Abstract
The Lense-Thirring effect from spinning neutron stars in double neutron star binaries contributes to the periastron advance of the orbit. This extra term involves the moment of inertia of the neutron stars. The moment of inertia, on the other hand, depends on the mass and spin of the neutron star, as well as the equation of state of the matter. If at least one member of the double neutron star binary (better the faster one) is a radio pulsar, then accurate timing analysis might lead to the estimation of the contribution of the Lense-Thirring effect to the periastron advance, which will lead to the measurement of the moment of inertia of the pulsar. The combination of the knowledge on the values of the moment of inertia, the mass and the spin of the pulsar will give a new constraint on the equation of state. Pulsars in double neutron star binaries are the best for this purpose as short orbits and moderately high eccentricities make the Lense-Thirring effect substantial, whereas tidal effects are negligible (unlike pulsars with main sequence or white-dwarf binaries). The most promising pulsars are PSR J0737 − 3039A and PSR J1757 − 1854. The spin-precession of pulsars due to the misalignment between the spin and the orbital angular momentum vectors affect the contribution of the Lense-Thirring effect to the periastron advance. This effect has been explored for both PSR J0737 − 3039A and PSR J1757 − 1854, and as the misalignment angles for both of these pulsars are small, the variation in the Lense-Thirring term is not much. However, to extract the Lense-Thirring effect from the observed rate of the periastron advance, more accurate timing solutions including precise proper motion and distance measurements are essential.
1. Introduction
Timing analysis of binary pulsars leads to the measurement of pulsar’s spin, Keplerian orbital parameters (the orbital period , the orbital eccentricity e, the longitude of periastron , the projected semi-major axis of the orbit , where is the semi-major axis of the pulsar orbit and i is the angle between the orbit and the sky-plane, and the epoch of the periastron passage1), as well as post-Keplerian (PK) parameters like the Einstein parameter (), Shapiro range (r) and shape (s) parameters, the rate of the periastron advance , the rate of change of the orbital period , the relativistic deformation of the orbit , etc. [4]. Sometimes, the Shapiro delay is parametrized differently, with parameters and [5], or with r and [6], and these parameters can easily be expressed in terms of conventional parameters s and r.
Measurement of PK parameters leads to estimation of masses of the pulsars and their companions, as well as tests of various theories of gravity [7,8]. Note that, in principle, measurements of only two PK parameters are enough to extract two unknowns, i.e., the masses of the pulsar and the companion, while measurements of more than two PK parameters lead to tests of gravity theory through consistency. However, the uncertainty in measurement is not equal for every PK parameter, and usually the two most accurate parameters are used to obtain the best mass estimates (e.g., Figure 1 of [9]). Additionally, relativistic binary pulsars have the potential to constrain the Equation of State (EoS) of matter at extreme densities. Measurements of masses of two pulsars being around have already ruled out many soft EsoS [10,11]. On the other hand, the recent analysis of the gravitational wave event GW170817 from the merger of two neutron stars ruled out some extremely stiff EsoS [12,13]. Still, a large number of EsoS is allowed, including several hybrid [14] and strange quark matter [15] EsoS in addition to standard hadronic ones. Therefore, further progress on this issue is essential, and that is expected in the near future as, on the one hand more, neutron star-neutron star mergers are expected to be detected in future runs of the advanced LIGO, and on the other hand, many binary pulsars are being timed regularly and accurately. Besides, upcoming radio telescopes like MeerKAT and the Square Kilometre Array (SKA) will lead to significant improvement in pulsar timing.
Among all of the PK parameters, in the present article, I concentrate mainly on the periastron advance, which has the potential to constrain the dense matter equation of state due to the Lense– Thirring effect. Neutron star-neutron star binaries or ‘Double Neutron Star’ (DNS) systems are the best for this purpose as these systems are compact enough to display effects of strong field gravity, yet wide enough to have negligible tidal effects. Moreover, due to the high compactness of neutron stars, spin-induced quadrupole moments are also negligible. On the other hand, as these neutron stars are rapidly spinning (spin periods of most of the pulsars in DNSs are less than 100 milliseconds), the Lense-Thirring effect is significant. That is why I concentrate on DNSs in this article, although the mathematical formulations are valid for any kind of general relativistic binaries with the possibility of additional effects depending on the nature of the objects in the binaries. There are about seventeen DNSs known at the present time, including the first discovered binary pulsar: the Hulse–Taylor binary, PSR B1913+16. For one DNS, PSR J0737 − 3039A/B, both members are radio pulsars, and the system is known as a double pulsar 2.
For a long period of time, the double pulsar was the most relativistic binary. However, the recently- discovered DNS, PSR J1757 − 1854 shows even stronger effects of general relativity in some aspects, i.e., and [17], due to its high eccentricity combined with a small orbital period. In fact, its eccentricity is 6.9-times and orbital period 1.8-times larger than those of PSR J0737 − 3039A/B. It is noteworthy that is larger for PSR J0737 − 3039A/B than PSR J1757 − 1854 where the contribution of eccentricity is less dominant; see Lorimer and Kramer [4] for expressions for PK parameters.
PSR J1906 + 0746 is another DNS having the second smallest value of , just after PSR J0737 − 3039A/B. However, its is slightly (1.1-times) and e is significantly (7.1-times) smaller than those of PSR J1757 − 1854. That is why although PSR J1906 + 0746 has the third largest value of , other PK parameters are small, even smaller than most of the other DNSs. Finally, the latest discovered DNS, PSR J1946 + 2052, has broken all the records by having the smallest value of and the largest value of [18].
2. Precession in Double Neutron Star Binaries
Precessions (of both the spin and the orbit) of neutron stars in DNSs are very important. Following Barker and O’Connell [19], the rate of the change of the unit spin vector () of a spinning neutron star (a) in a binary can be written as:
where the angular spin-precession frequency can be written as:
is the angular spin-precession frequency of the neutron star due to the space-time curvature around its companion and can be calculated within the ‘Post-Newtonian’ (PN) formalism. is the angular spin-precession frequency of that neutron star due to the Lense-Thirring effect of its spinning companion. We can further write:
where is the unit vector along the orbital angular momentum, is the orbital angular momentum, and:
Here, if a is the neutron star under consideration, is its companion. The amplitudes in Equations (3) and (4) are given by:
where G is the gravitational constant, c is the speed of light in a vacuum and is the angular orbital frequency. is the mass; is the moment of inertia; is the spin period of the a-th neutron star; and
For pulsars in DNSs, the Lense-Thirring term () can be ignored. Even for the case of the slow pulsar (B) of the double pulsar, where the Lense-Thirring effect due to the spin of the fast pulsar (A) contributes to , I find and (using the values of the parameters given in Table 1). This leads to using the fact that is almost parallel to [20,21], and hence, , which is close to the observed median value of [22]. It is unlikely that companions of other pulsars would be much faster than PSR A, and hence, can be neglected. Therefore, Equation (1) becomes:
where is the angle between and and is a unit vector perpendicular to the plane containing and in the direction given by the right-hand rule. Therefore, the measurement of the spin-precession of a pulsar helps estimate when other parameters involved in Equation (5) are already known.

Table 1.
Relevant observed parameters for known pulsars in DNSs. See the references for these parameters with more significant digits and uncertainties. The timing model (e.g., DDGR) is mentioned when more than one timing solution is available in the original reference.
Similarly, neglecting the tidal and the spin-quadrupole effects, as well as the spin-spin interaction, the orbital angular precession frequency can be written as:
where and are contributions from the space-time curvature and the Lense-Thirring effect, respectively. Note that both members of the binary contribute to each term. leads to the precession of both the Laplace–Runge–Lenz vector , as well as , but none is directly observable. Damour and Schafer [23] first studied the manifestation of in terms of observable parameters by decomposing as:
where is the unit vector along the line-of-sight, i.e., from the Earth to the a-th neutron star (the pulsar), is the unit vector along the line of the ascending node, is the longitude of the ascending node of the a-th neutron star and i is the angle between the orbit and the sky-plane. Damour and Schafer [23] has also given:
As already mentioned, is the parameter of interest as it has the potential to put constraints on the dense matter EoS. Therefore, I explore properties of in the next and subsequent sections.
Periastron Advance
The observed rate of the periastron advance () of the a-th member of a relativistic binary can be written as:
where is due to the space-time curvature caused by both members of the binary, is due to the Lense-Thirring effect of the star a and is due to the Lense-Thirring effect of the star . These three terms together come into the expressions of (Equation (12)) caused by the precession of the orbit. is a secular variation due to the gradual change of the apparent orientation of the orbit with respect to the line-of-sight due to the proper motion of the barycenter of the binary [24]. The expressions for different terms are:
where only the first and the second order terms are retained in the expression of . and are the proper motion of the barycenter of the binary (which is measured as the proper motion of the visible object) in the right ascension and the declination respectively, both expressed in units of milliarcseconds per year. All other parameters are in SI units. The parameters introduced in Equations (15)–(17) are as follow:
where , is the total mass of the system. is defined in Equation (7), and
where is the angle between and (see Figure 1). It is obvious from Equation (20) that the maximum value of occurs when is parallel to the vector , giving:
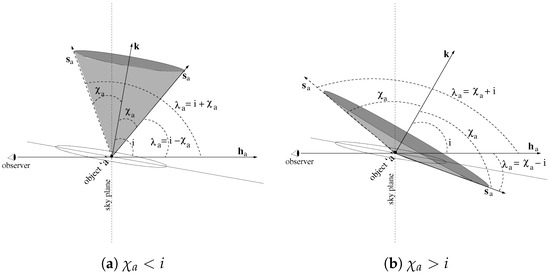
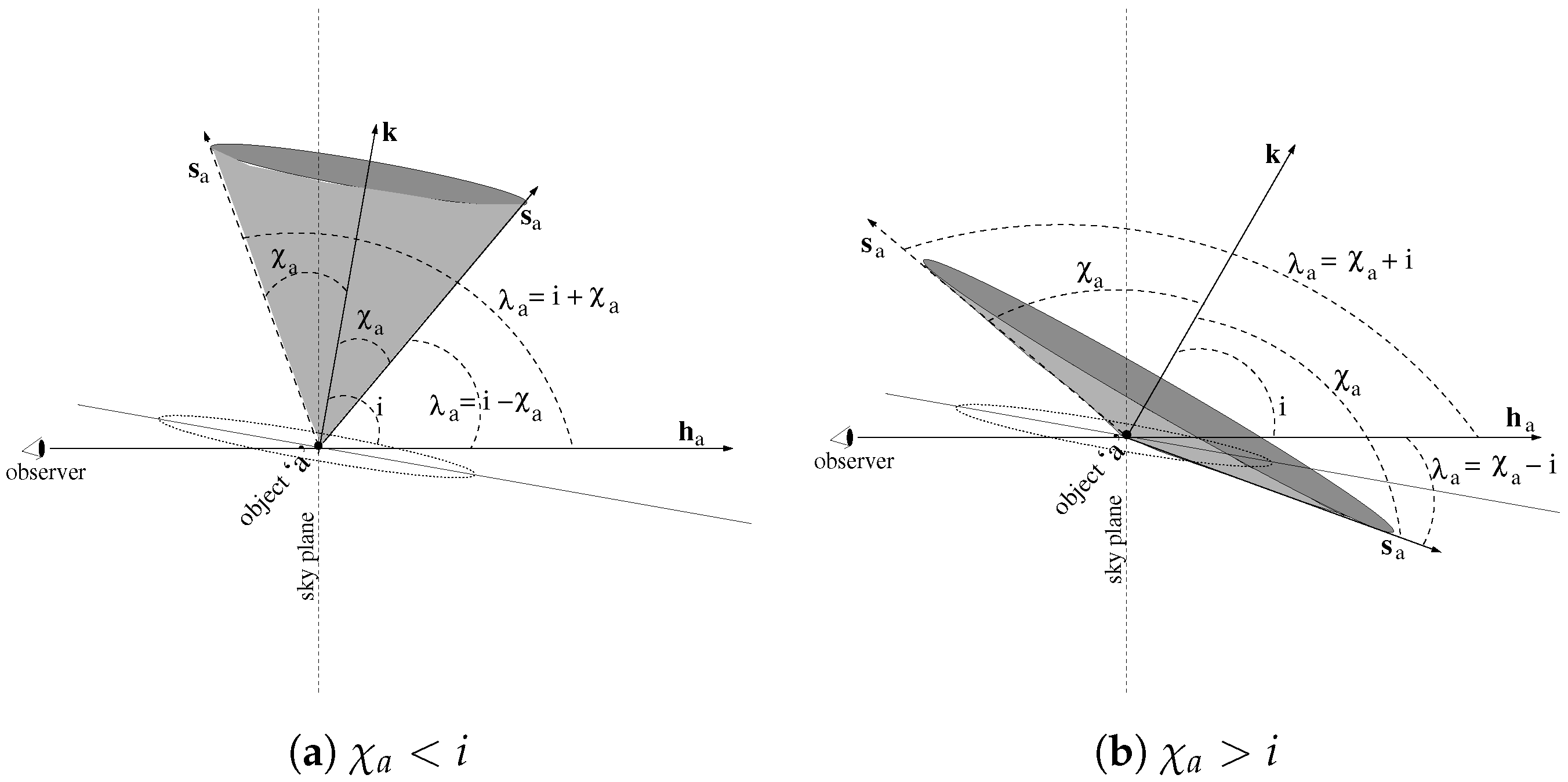
Figure 1.
Orientation of different vectors relevant for the estimation of where the subscript a refers to the object being observed, i.e., the pulsar (so the companion would be represented by the subscript ). The vectors are as follow: is the unit vector along the orbital angular momentum, is the unit vector along the line-of-sight and is the unit spin vector. The angles in the figures are: i is the inclination angle between the orbit of the pulsar and the sky-plane, as well as the angle between and , is the angle between and and is the angle between and . The left and right panels are for and , respectively. In both panels, two positions of are shown corresponding to maximum and minimum values of (see the text). The pulsar, i.e., the object a, is located at the vertex of the fiducial cone (gray in color) made by the precessing around .
If , i.e., and :
Using the expression of in Equation (16), I get , and using the expression of , I get . The negative sign in the Lense-Thirring term (Equation (16)) implies the fact that actually is the minimum value. However, depending on the values of i, , and , (Equation (20)) can be negative making (Equation (16)) positive. Note that the Lense-Thirring effects from both the pulsar and the companion come in the total periastron advance rate (Equations (14) and (16)). However, if the companion is much slower than the pulsar, as in the case of the double pulsar, then the contribution from the companion can be neglected. Due to the non-detection of any pulsation, we do not know the values of the spin periods of the companions for other DNSs and cannot rule out the possibility of significant Lense-Thirring effect from those companions. However, most of the pulsars in DNSs are recycled (at least mildly), suggesting the fact that pulsars were born as neutron stars earlier than their companions. The companions, i.e., the second born neutron stars in DNSs, are expected to be slow; because even if neutron stars are born with spin periods in the range of a few tens of milliseconds up to a few hundred milliseconds, they quickly spin down to periods of a few seconds unless they gain angular momentum via mass accretion from their Roche lobe filling giant companions and become fast rotators. Such spin-up is possible only for the first born neutron star in a DNS. That is why in the present article, I ignore the Lense-Thirring effect from the companions of pulsars in DNSs.
In such a case, i.e., when is negligible, can be extracted by subtracting from (Equation (14)). One can estimate the value of from if all other relevant parameters like , e, , , , , are known (Equations (7), (18)–(20)). Then, from the knowledge of , and , a new constraint on the EoS can be placed, as it is a well-known fact that the moment of inertia of a neutron star depends on its mass, spin-period and the EoS (see [25] and the references therein). For this purpose, DNSs with large values of (larger than the measurement uncertainty in ) are preferable. Large values of the orbital eccentricity e and small values of and make larger.
The procedure is actually a bit trickier than it seems at first. Usually, timing analysis of a binary pulsar reports the most accurate measurement of out of all PK parameters, and the masses of the pulsar and the companion are estimated by equating with and using the second most accurately-measured PK parameter. If is large, then this procedure would become erroneous. One should instead estimate masses using two PK parameters other than , and these mass values should also be accurate enough to give a precise estimate of . Accurate measurements of proper motion are also needed to evaluate . Only then, can be subtracted from the observed to get the value of . In short, one needs very precise measurements of at least three PK parameters, and two more, as well as the distance and the proper motion of the pulsar (the a-th neutron star).
Because of its small values of and , PSR J0737 − 3039A is expected to have a large value of in spite of its low eccentricity. Similarly, as PSR J1757−1854 has a slightly larger , slightly smaller and much larger e, it is also expected to have a large value of . For this reason, in the next section, I explore for these two DNSs in detail. Note that, although, PSR J1946 + 2052 might be a useful system for this purpose, it is not possible to extend my study for this system due to lack of knowledge of masses of the pulsar and the companion.
One should also remember the dependence of (via ) on the orientation of with respect to and (Equation (20)). If I assume that the a-th neutron star is the pulsar, then all ‘a’s in the subscripts of the above equations will be replaced by ‘p’s, e.g., , , etc. Most of the time, the value of is estimated in the literature. However, at least for some pulsars, . In such cases, the values of and can be measured by analyzing the change of the pulse profile shape and the polarization. Conventionally, is denoted by , and is denoted by . Note that, even if is a constant over time, would vary due to the spin precession and can be written as [26]:
where is the angular spin precession frequency (amplitude of in Equation (2)), t is the epoch of the observation and is the epoch of the precession phase being zero. Note that i itself might change with time as given in Equation (13).
In Table 1, with other relevant parameters, I compile values of wherever available. I do not compile values of , although available in some cases, as it is a time-dependent parameter. From Figure 1, it is clear that the spin would precess in such a way that it would lie on the surface of a fiducial cone with the vertex at the pulsar and having the half-opening angle as . The constraint on is: (i) if , then and (Figure 1a), (ii) if , then and (Figure 1b).
3. Results
For the purpose of demonstration, I compute the value of the moment of inertia () for the two most interesting pulsars, PSR J0737 − 3039A and PSR J1757 − 1854 using the Akmal-Pandharipande- Ravenhall (APR) equation of state [27] and the RNS code3 [28]. I find that, both of these pulsars have . I use this value in my calculations, remembering the fact that the true values of would be different depending on the true EoS, and we are actually seeking an answer whether it would be possible to know the value of by singling out from the total observed .
I tabulate values of , and for all pulsars in DNSs in Table 2. I exclude candidate DNSs, i.e., PSR B1820−11 and PSR J1753 − 2240 from this calculation due to poor mass constraints. For other cases, I use the limiting mass values where actual values are unavailable. Only can be calculated for the systems with undetermined/unpublished values of . As expected, PSR J0737 − 3039A shows the largest Lense-Thirring effect, followed by PSR J1757 − 1854. In fact, is slightly larger for PSR J1757 − 1854 () than that for PSR J0737 − 3039A (). This fact makes it a very interesting system, and I investigate this system in detail. The discovery paper [17] also mentioned the large Lense-Thirring effect causing significant amount of (Equation (13)).

Table 2.
Values of , and for known pulsars in DNSs using and neglecting the Lense-Thirring effect of the companion. To show the difference between and , I keep values up to five decimal places even for the cases where is known with less accuracy.
I find that, for PSR J1757 − 1854, is achieved for , . However, as the value of for this system is not yet known (although Cameron et al. [17] obtained a constraint based on their simulation of the kick velocity), I vary in the range of –. It is obvious that depends more on than on as the absolute value of the factor (see Equation (20)) with , i.e., , is larger than that of the factor with , i.e., . Furthermore, the measured value of gives two values of i (as ), and I use the larger one to get a bigger range of . The minimum value of is achieved for , . If I fix strictly as , then the maximum and minimum values of are and , for and , respectively. In Figure 2, I show the variation of for in the range of –, and for each value of , varies in the range of . On the other hand, as PSR J0737 − 3039A has [20], always remains close to . The maximum and minimum values of are at , ; and at , . To check the validity of my assumption that the Lense-Thirring effect from the companion could be ignored, I find that using , where the subscript ‘c’ stands for the companion, i.e., the slow PSR J0737 − 3039B. Varying in the range of [20], I find that the minimum value of is . These results support my argument that the Lense-Thirring effect from the companion of a pulsar in a DNS would have a negligible contribution to the rate of the periastron advance of the binary.
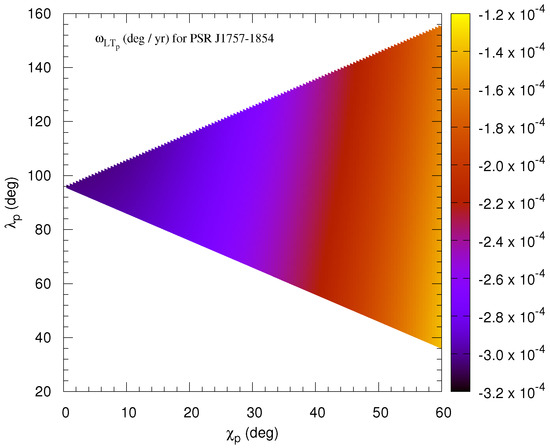
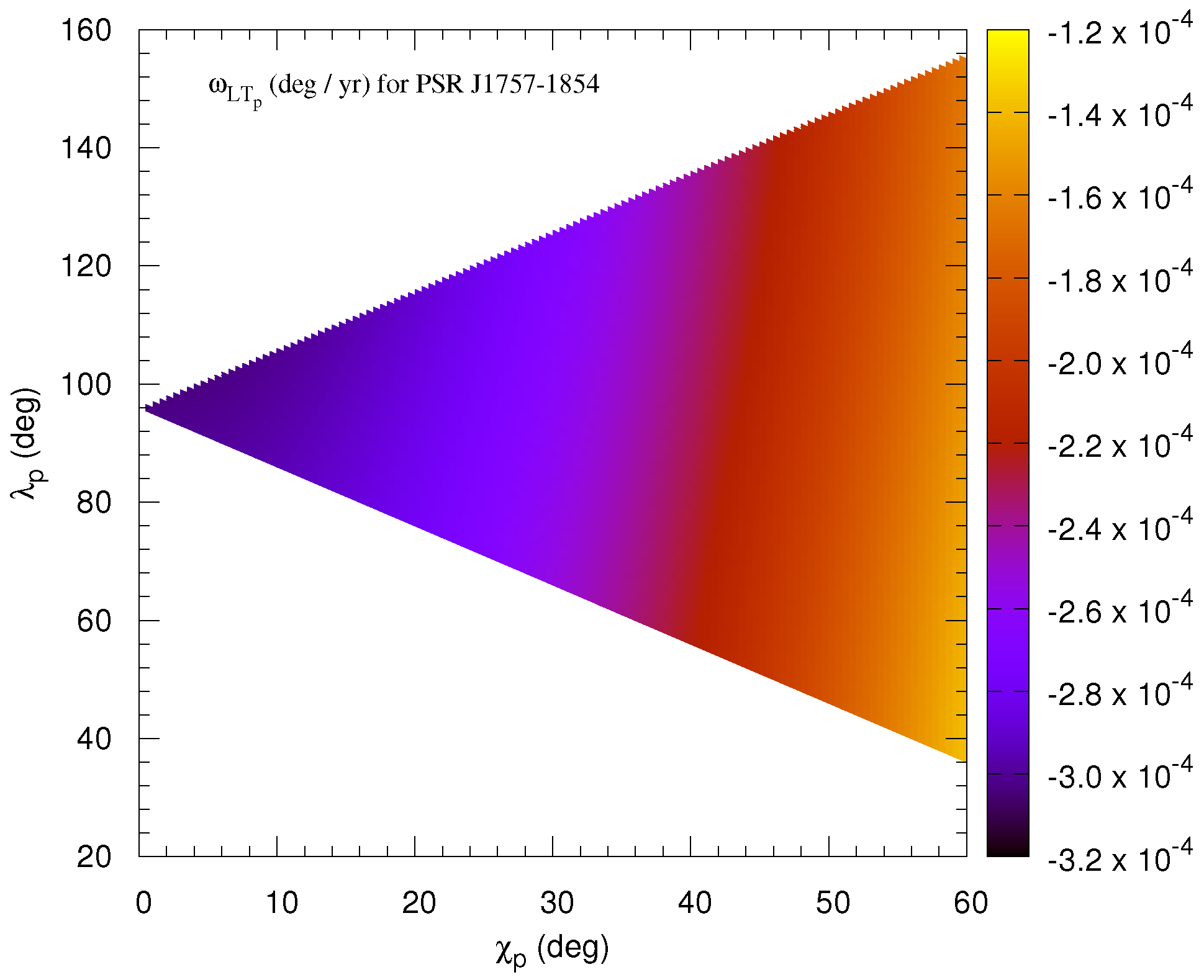
Figure 2.
Variation of with (in degrees) along the horizontal axis and (in degrees) along the vertical axis for PSR J1757 − 1854. The color code represents values of in .
As Table 2 shows, for PSR J0737 − 3039A is around 1.4-times smaller than the presently published accuracy, where the uncertainty is twice the formal value obtained in the timing solution [9]. The uncertainties in other PK parameters are even poorer (Table 1 of [9]), so if we exclude , the mass estimates would be less accurate and should not be used to calculate . Therefore, to achieve the goal of estimating , lowering only the uncertainty in would not be enough; one needs to improve the accuracy of at least two other parameters that can be used to get masses at least as precise as the ones already published. It is impossible to improve the accuracy of the Keplerian parameter R used by Kramer et al. [9] in combination with to report the values of the masses, because involves , the projected semi-major axis of the companion (PSR B), which is not visible presently and even when it was visible, it was not a good timer like PSR A. Solving the expressions for PK parameters, I find that the combination of s and is the best choice left when and R are excluded, i.e., gives the narrowest ranges of masses , using the published values of the uncertainties. I also find the fact that, to get masses as accurate as the ones reported by Kramer et al. [9], the uncertainty in should be reduced at least to assuming that s and relevant Keplerian parameters (, e, ) would also be improved by at least an order of magnitude. The published uncertainty in is . However, the question arises whether for such an improved measurement of , the dynamical contribution coming from the proper motion of the pulsar (Shklovskii effect) and the relative acceleration between the pulsar and the solar system barycenter could be ignored. Using the proper motion reported by Kramer et al. [9] and the distance (1.1 kpc) estimated by Deller et al. [29] using the Very-long-baseline interferometry (VLBI) parallax measurement, I find that , where I have used a realistic model of the galactic potential [30]. The improvement required in the timing solution of PSR J0737 − 3039A is expected by 2030 [31,32] accompanied by an improvement in . Fortunately, is smaller than ; using the proper motion reported in Kramer et al. [9], I find that it can be at most (I could not calculate the actual value, as is unknown). However, one will still need better estimates of and to be able to extract the value of the moment of inertia of the pulsar from the .
On the other hand, for PSR J1757 − 1854, both and are about 1.5-times larger than the presently-published accuracy, . However, even this system cannot be used at present to estimate , not only because of the unknown values of and , but also because of the less accurate values of other PK parameters. If one uses and , then the uncertainties in these parameters should be improved by one and two orders of magnitudes respectively to get the uncertainty in masses of about . This seems plausible, as the present accuracy in is only [17]. However, due to the lack of measurements of the proper motion and the parallax distance, I could not calculate for this pulsar and only can give rough estimates based on the distance guessed from the dispersion measure using two different models of the galactic electron density, e.g., the NE2001 model [33,34] and the YMW16 model [35]. The contribution due to the relative acceleration is for the NE2001 distance (7.4 kpc) and for the YMW16 distance (19.6 kpc). Both of the values seem to be too large to be canceled out by the Shklovskii term. Measurements of the proper motion and the distance (using parallax) are essential to estimate . The measurement of the proper motion will also help estimate .
4. Summary and Conclusions
Measurement of the moment of inertia of a pulsar will provide yet another constraint on the dense matter equation of state. This issue has been discussed in the literature in the past (see [32,51,52] and the references therein), but unfortunately, the effect of the misalignment between the spin and the orbital angular momentum vectors has not been explored in detail mainly because these two vectors are almost parallel for PSR J0737 − 3039, the only suitable system existing until recently.
However, even a small misalignment angle would have significant consequences, because for a particular neutron star; the theoretical values of the moment of inertia using different EsoS are sometimes very close (depending on the stiffness of the EoS). One can see Figure 1 of Bejger et al. [53] for predicted values of the moment of inertia for PSR J0737 − 3039A using a sample of EsoS. The present article extensively studied the effects of such misalignment.
I have demonstrated the fact that the recently-discovered DNS, PSR J1757 − 1854, is almost as good as PSR J0737 − 3039A regarding the prospect of determining the moment of inertia of the pulsar from . For PSR J0737 − 3039A, lies in the range of – , whereas for PSR J1757 − 1854 lies in the range of – . Future measurement of for PSR J1757 − 1854 will narrow down the range of .
For both of the systems, significant improvements in the timing solution are needed. Moreover, the proper motion and the parallax measurements for PSR J1757 − 1854 are crucial. Additionally, it is essential to measure and for PSR J1757 − 1854; hence, long-term studies of polarization properties and profile variation would be very useful.
Note that, although all of the calculations presented in this article are within the framework devised by Barker & O’Connell [19] and Damour & Schäfer [23], alternative formalisms to incorporate the Lense-Thirring effect in exist. One example is Iorio [54], but for systems with , , these two formalisms take similar forms. Precisely, Iorio [54] reports for PSR J0737 − 3039A using , which is close to what I get, i.e., if I use the same value of instead of used in this article. A fundamentally different idea, i.e., to incorporate the Lense-Thirring effect into the delays in the pulse arrival times, has been proposed recently [55]. If this can be implemented in future algorithms for pulsar timing, the effect of the Lense-Thirring effect could be measured directly.
Finally, if the measurement accuracy of improves by a few orders of magnitudes, one will need to subtract the Kopeikin term (the secular variation due to the proper motion). The measurement of the proper motion of PSR J1757 − 1854 will help us calculate this term. Moreover, in order to use to estimate masses accurately, one needs to subtract the contributions from the proper motion and the relative acceleration between the pulsar and the solar system barycenter. A package to perform these tasks based on the realistic potential of the Milky Way has been recently developed [30], and gradual improvement in the model of the galactic potential is expected with the help of Gaia data.
Acknowledgments
The author thanks the organizers of ‘Compact stars in the QCD phase diagram VI’ (especially David Blashcke) for their excellent hospitality, all three reviewers for extensive suggestions on the earlier version of the manuscript and ANI Technologies Pvt. Ltd. and Uber Technologies Inc. for helping to survive in Chennai.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Van Straten, W.; Bailes, M.; Britton, M.; Kulkarni, S.R.; Anderson, S.B.; Manchester, R.N.; Sarkissian, J. A test of general relativity from the three-dimensional orbital geometry of a binary pulsar. Nature 2001, 412, 158–160. [Google Scholar] [CrossRef] [PubMed]
- Deller, A.T.; Boyles, J.; Lorimer, D.R.; Kaspi, V.M.; McLaughlin, M.A.; Ransom, S.; Stairs, I.H.; Stovall, K. VLBI Astrometry of PSR J2222 − 0137: A Pulsar Distance Measured to 0.4% Accuracy. Astrophys. J. 2013, 770, 145. [Google Scholar] [CrossRef]
- Deller, A.T.; Vigeland, S.J.; Kaplan, D.L.; Goss, W.M.; Brisken, W.F.; Chatterjee, S.; Cordes, J.M.; Janssen, G.H.; Lazio, T.J.W.; Petrov, L.; et al. Microarcsecond VLBI Pulsar Astrometry with PSRπ. I. Two Binary Millisecond Pulsars with White Dwarf Companions. Astrophys. J. 2017, 828, 8. [Google Scholar] [CrossRef]
- Lorimer, D.; Kramer, M. Handbook of Pulsar Astronomy; Cambridge Observing Handbooks for Research Astronomers; Cambridge University Press: Cambridge, UK, 2005; pp. 32–58. [Google Scholar]
- Freire, P.C.C.; Wex, N. The orthometric parametrization of the Shapiro delay and an improved test of general relativity with binary pulsars. Mon. Not. R. Astron. Soc. 2010, 409, 199–212. [Google Scholar] [CrossRef]
- Kramer, M.; Stairs, I.H.; Manchester, R.N. Strong-field tests of gravity with the double pulsar. Annalen der Physik 2006, 15, 34–42. [Google Scholar] [CrossRef]
- Stairs, I. Testing General Relativity with Pulsar Timing. Living Rev. Relat. 2003, 6, 5. [Google Scholar] [CrossRef] [PubMed]
- Kramer, M. Pulsars as probes of gravity and fundamental physics. Int. J. Mod. Phys. 2016, 25, 1630029–1630061. [Google Scholar] [CrossRef]
- Kramer, M.; Stairs, I.H.; Manchester, R.N. Tests of General Relativity from Timing the Double Pulsar. Science 2006, 314, 97–102. [Google Scholar] [CrossRef] [PubMed]
- Demorest, P.B.; Pennucci, T.; Ransom, S.M.; Roberts, M.S.E.; Hessels, J.W.T. A two-solar-mass neutron star measured using Shapiro delay. Nature 2010, 467, 1081–1083. [Google Scholar] [CrossRef] [PubMed]
- Antoniadis, J.; Freire, P.C.C.; Wex, N.; Tauris, T.M.; Lynch, R.S. A Massive Pulsar in a Compact Relativistic Binary. Science 2013, 340, 1233232. [Google Scholar] [CrossRef] [PubMed]
- Abbott, B.P. GW170817: Observation of Gravitational Waves from a Binary Neutron Star Inspiral. Phys. Rev. Lett. 2017, 119, 161101. [Google Scholar] [CrossRef] [PubMed]
- Annala, E.; Gorda, T.; Kurkela, A.; Vuorinen, A. Gravitational-wave constraints on the neutron-star-matter Equation of State. arXiv 2017, arXiv:1711.02644. [Google Scholar]
- Ayriyan, A.; Bastian, N.U.; Blaschke, D.; Grigorian, H.; Maslov, K.; Voskresensky, D.N. How robust is a third family of compact stars against pasta phase effects? arXiv 2017, arXiv:1711.03926. [Google Scholar]
- Kurkela, A.; Romatschke, P.; Vuorinen, A. Cold quark matter. Phys. Rev. D 2010, 81, 105021. [Google Scholar] [CrossRef]
- Perera, B.B.P.; McLaughlin, M.A.; Kramer, M.; Stairs, I.H.; Ferdman, R.D.; Freire, P.C.C.; Possenti, A.; Breton, R.P.; Manchester, R.N.; Burgay, M.; et al. The Evolution of PSR J0737 − 3039B and a Model for Relativistic Spin Precession. Astrophys. J. 2010, 721, 1193–1205. [Google Scholar] [CrossRef]
- Cameron, A.D.; Champion, D.J.; Kramer, M.; Bailes, M.; Barr, E.D. The High Time Resolution Universe Pulsar Survey—XIII. PSR J1757 − 1854, the most accelerated binary pulsar. 2018, 475, L57–L61. [Google Scholar] [CrossRef]
- Stovall, K.; Freire, P.C.C.; Chatterjee, S.; Demorest, P.B.; Lorimer, D.R. PALFA Discovery of a Highly Relativistic Double Neutron Star Binary. Astrophys. J. 2018, 231, 453. [Google Scholar]
- Barker, B.M.; O’Connell, R.F. The gravitational interaction: Spin, rotation, and quantum effects—A review. Gen. Relat. Gravit. 1979, 11, 149–175. [Google Scholar] [CrossRef]
- Perera, B.B.P.; Kim, C.; McLaughlin, M.A.; Ferdman, R.D.; Kramer, M.; Stairs, I.H.; Freire, P.C.C.; Possenti, A. Realistic Modeling of the Pulse Profile of PSR J0737 − 3039A. Astrophys J. 2014, 787, 51. [Google Scholar] [CrossRef]
- Pol, N.; McLaughlin, M.; Kramer, M.; Stairs, I.; Perera, B.B.P.; Possenti, A. A direct measurement of sense of rotation of PSR J0737 − 3039A. Astrophys. J. 2018, 853, 73. [Google Scholar] [CrossRef]
- Breton, R.P.; Kaspi, V.M.; Kramer, M. Relativistic Spin Precession in the Double Pulsar. Science 2008, 321, 104–107. [Google Scholar] [CrossRef] [PubMed]
- Damour, T.; Schafer, G. Higher-order relativistic periastron advances and binary pulsars. Nuovo Cim. B 1988, 101, 127–176. [Google Scholar] [CrossRef]
- Kopeikin, S.M. Proper Motion of Binary Pulsars as a Source of Secular Variations of Orbital Parameters. Astrophys. J. 1996, 467, L93. [Google Scholar] [CrossRef]
- Bagchi, M. Rotational parameters of strange stars in comparison with neutron stars. New Astron. 2010, 15, 126–134. [Google Scholar] [CrossRef]
- Ferdman, R.D.; Stairs, I.H.; Kramer, M.; Breton, R.P.; McLaughlin, M.A.; Freire, P.C.C.; Possenti, A.; Stappers, B.W.; Kaspi, V.M.; Manchester, R.N.; et al. The Double Pulsar: Evidence for Neutron Star Formation without an Iron Core-collapse Supernova. Astrophys. J. 2013, 767, 85. [Google Scholar] [CrossRef]
- Akmal, A.; Pandharipande, V.R.; Ravenhall, D.G. Equation of state of nucleon matter and neutron star structure. Phys. Rev. C 1998, 58, 1804–1828. [Google Scholar] [CrossRef]
- Nozawa, T.; Stergioulas, N.; Gourgoulhon, E.; Eriguchi, Y. Construction of highly accurate models of rotating neutron stars—Comparison of three different numerical schemes. Astron. Astrophys. Suppl. Ser. 1998, 132, 431–454. [Google Scholar] [CrossRef]
- Deller, A.T.; Bailes, M.; Tingay, S.J. Implications of a VLBI Distance to the Double Pulsar J0737-3039A/B. Science 2009, 323, 1327–1329. [Google Scholar] [CrossRef] [PubMed]
- Pathak, D.; Bagchi, M. GalDynPsr: A package to estimate dynamical contributions in the rate of change of the period of radio pulsars. arXiv 2017, arXiv:1712.06590. [Google Scholar]
- Kramer, M.; Wex, N. TOPICAL REVIEW: The double pulsar system: A unique laboratory for gravity. Class. Quantum Gravity 2009, 26, 073001. [Google Scholar] [CrossRef]
- Kehl, M.S.; Wex, N.; Kramer, M.; Liu, K. Future measurements of the Lense-Thirring effect in the Double Pulsar. In Proceedings of the Fourteenth Marcel Grossmann Meeting, Rome, Italy, 12–18 July 2015. [Google Scholar]
- Cordes, J.M.; Lazio, T.J.W. NE2001.I. A New Model for the Galactic Distribution of Free Electrons and its Fluctuations. arXiv 2001, arXiv:astro-ph/0207156. [Google Scholar]
- Cordes, J.M.; Lazio, T.J.W. NE2001. II. Using Radio Propagation Data to Construct a Model for the Galactic Distribution of Free Electrons. arXiv 2003, arXiv:astro-ph/0301598. [Google Scholar]
- Yao, J.M.; Manchester, R.N.; Wang, N. A New Electron-density Model for Estimation of Pulsar and FRB Distances. Astrophys. J. 2017, 835, 29. [Google Scholar] [CrossRef]
- Weisberg, J.M.; Huang, Y. Relativistic measurements from timing the binary pulsar PSR B1913 + 16. Astrophys. J. 2016, 829, 55. [Google Scholar] [CrossRef]
- Martinez, J.G.; Stovall, K.; Freire, P.C.C.; Deneva, J.S.; Jenet, F.A.; McLaughlin, M.A.; Bagchi, M.; Bates, S.D.; Ridolfi, A. Pulsar J0453+1559: A Double Neutron Star System with a Large Mass Asymmetry. Astrophys. J. 2015, 812, 143. [Google Scholar] [CrossRef]
- Martinez, J.G.; Stovall, K.; Freire, P.C.C.; Deneva, J.S.; Tauris, T.M.; Ridolfi, A.; Wex, N.; Jenet, F.A.; McLaughlin, M.A.; Bagchi, M. Pulsar J1411+2551: A Low-mass Double Neutron Star System. Astrophys. J. 2017, 851, L29. [Google Scholar] [CrossRef]
- Janssen, G.H.; Stappers, B.W.; Kramer, M.; Nice, D.J.; Jessner, A.; Cognard, I.M.B.; Purver, M.B. Multi-telescope timing of PSR J1518 + 4904. Astron. Astrophys. 2008, 490, 753–761. [Google Scholar]
- Fonseca, E.; Stairs, I.H.; Thorsett, S.E. A Comprehensive Study of Relativistic Gravity Using PSR B1534 + 12. Astrophys. J. 2014, 787, 82. [Google Scholar] [CrossRef]
- Keith, M.J.; Kramer, M.; Lyne, A.G.; Eatough, R.P.; Stairs, I.H.; Possenti, A.; Camilo, F.; Manchester, R.N. PSR J1753 − 2240: A mildly recycled pulsar in an eccentric binary system. Mon. Not. R. Astron. Soc. 2009, 393, 623–627. [Google Scholar] [CrossRef]
- Ferdman, R.D.; Stairs, I.H.; Kramer, M.; Janssen, G.H.; Bassa, C.G.; Stappers, B.W.; Demorest, P.B.; Cognard, I.; Desvignes, G.; Theureau, G.; et al. PSR J1756 − 2251: A pulsar with a low-mass neutron star companion. Mon. Not. R. Astron. Soc. 2014, 443, 2183–2196. [Google Scholar] [CrossRef]
- Lynch, R.S.; Freire, P.C.C.; Ransom, S.M.; Jacoby, B.A. The Timing of Nine Globular Cluster Pulsars. Astrophys. J. 2012, 745, 109. [Google Scholar] [CrossRef]
- Corongiu, A.; Kramer, M.; Stappers, B.W.; Lyne, A.G.; Jessner, A.; Possenti, A.; D’Amico, N.; Löhmer, O. The binary pulsar PSR J1811 − 1736: Evidence of a low amplitude supernova kick. Astron. Astrophys. 2007, 462, 703–709. [Google Scholar] [CrossRef]
- Hobbs, G.; Lyne, A.G.; Kramer, M.; Martin, C.E.; Jordan, C. Long-term timing observations of 374 pulsars. Mon. Not. R. Astron. Soc. 2004, 353, 1311–1344. [Google Scholar] [CrossRef]
- Champion, D.J.; Lorimer, D.R.; McLaughlin, M.A.; Cordes, J.M.; Arzoumanian, Z.; Weisberg, J.M.; Taylor, J.H. PSR J1829 + 2456: A relativistic binary pulsar. Mon. Not. R. Astron. Soc. 2004, 350, L61–L65. [Google Scholar] [CrossRef]
- Van Leeuwen, J.; Kasian, L.; Stairs, I.H.; Lorimer, D.R.; Camilo, F. The Binary Companion of Young, Relativistic Pulsar J1906+0746. Astrophys. J. 2015, 798, 118. [Google Scholar] [CrossRef]
- Weisberg, J.M.; Nice, D.J.; Taylor, J.H. Timing Measurements of the Relativistic Binary Pulsar PSR B1913 + 16. Astrophys. J. 2010, 722, 1030–1034. [Google Scholar] [CrossRef]
- Swiggum, J.K.; Rosen, R.; McLaughlin, M.A.; Lorimer, D.R.; Heatherly, S. PSR J1930 − 1852: A Pulsar in the Widest Known Orbit around Another Neutron Star. Astrophys. J. 2015, 805, 156. [Google Scholar] [CrossRef]
- Jacoby, B.A.; Cameron, P.B.; Jenet, F.A.; Anderson, S.B.; Murty, R.N.; Kulkarni, S.R. Measurement of Orbital Decay in the Double Neutron Star Binary PSR B2127 + 11C. Astrophys. J. 2006, 644, L113–L116. [Google Scholar] [CrossRef]
- Iorio, L. Prospects for measuring the moment of inertia of pulsar J0737-3039A. New Astron. 2009, 1, 40–43. [Google Scholar] [CrossRef]
- O’Connell, R.F. Proposed New Test of Spin Effects in General Relativity. Phys. Rev. Lett. 2004, 93, 081103. [Google Scholar] [CrossRef] [PubMed]
- Bejger, M.; Bulik, T.; Haensel, P. Constraints on the dense matter equation of state from the measurements of PSR J0737 − 3039A moment of inertia and PSR J0751 + 1807 mass. Mon. Not. R. Astron. Soc. 2005, 364, 635–639. [Google Scholar] [CrossRef]
- Iorio, L. General relativistic spin-orbit and spin-spin effects on the motion of rotating particles in an external gravitational field. Gen. Relat. Gravit. 2012, 44, 719–736. [Google Scholar] [CrossRef]
- Iorio, L. Post-Keplerian perturbations of the orbital time shift in binary pulsars: an analytical formulation with applications to the galactic center. Eur. Phys. J. C 2017, 77, 439. [Google Scholar] [CrossRef]
| 1. | The remaining Keplerian parameter, the longitude of the ascending node , does not come in the standard pulsar timing algorithm. It can be measured via proper motion only in very special cases; see [1,2,3] for details. |
| 2. | Although for the last few years, the slow pulsar of the system is not visible and is believed to be beaming away from the Earth due to its spin-precession [16]. |
| 3. | RNS stands for ‘Rapidly Rotating Neutron Star’, a package to calculate different properties of rotating neutron stars, freely available at http://www.gravity.phys.uwm.edu/rns/. |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).