1. Remnants
The possibility that remnants of evaporated black holes form a component of dark matter was suggested by MacGibbon [
1] 30 years ago and has been explored by many authors [
2,
3,
4,
5,
6,
7,
8,
9]. There are no strong observational constraints on this possible contribution to dark matter [
10]; the weak point of this scenario has been, so far, the obscurity of the physical nature of the remnants.
The situation has changed recently because of the realisation that conventional physics provides a candidate for remnants: small-mass white holes with large interiors [
11,
12,
13]. In addition, quantum gravity indicates that these are indeed produced at the end of the evaporation [
14,
15,
16,
17,
18]. Here we show that the remnant lifetime predicted in [
16] is remarkably consistent with the production of primordial black holes at the end of inflation. More precisely, the rather strict constraints that the model sets on the time scales of the lifetime of black and white holes happen to match with a cosmological window where primordial black hole production is expected. A preliminary version of this result was posted in [
19].
Open questions are the stability and the eventual quantum properties of these remnants. It was suggested in [
16] that these remnants may be stable because quantum gravity dumps the Planck scale perturbations required to trigger their instability. Here we analyse the situation a bit more in detail by studying the stability of the remnants using a simple quantum model that captures the dynamical processes that black and white holes can undergo. The model indicates that a quantum superposition of Planck size white and black holes should be stable, because of the large interior volume and the area gap, i.e., the presence of a minimal non-vanishing eigenvalue in the area spectrum according to Loop Quantum Gravity.
These two results support the hypothesis that a component of dark matter could be formed by small black hole remnants.
2. White Holes
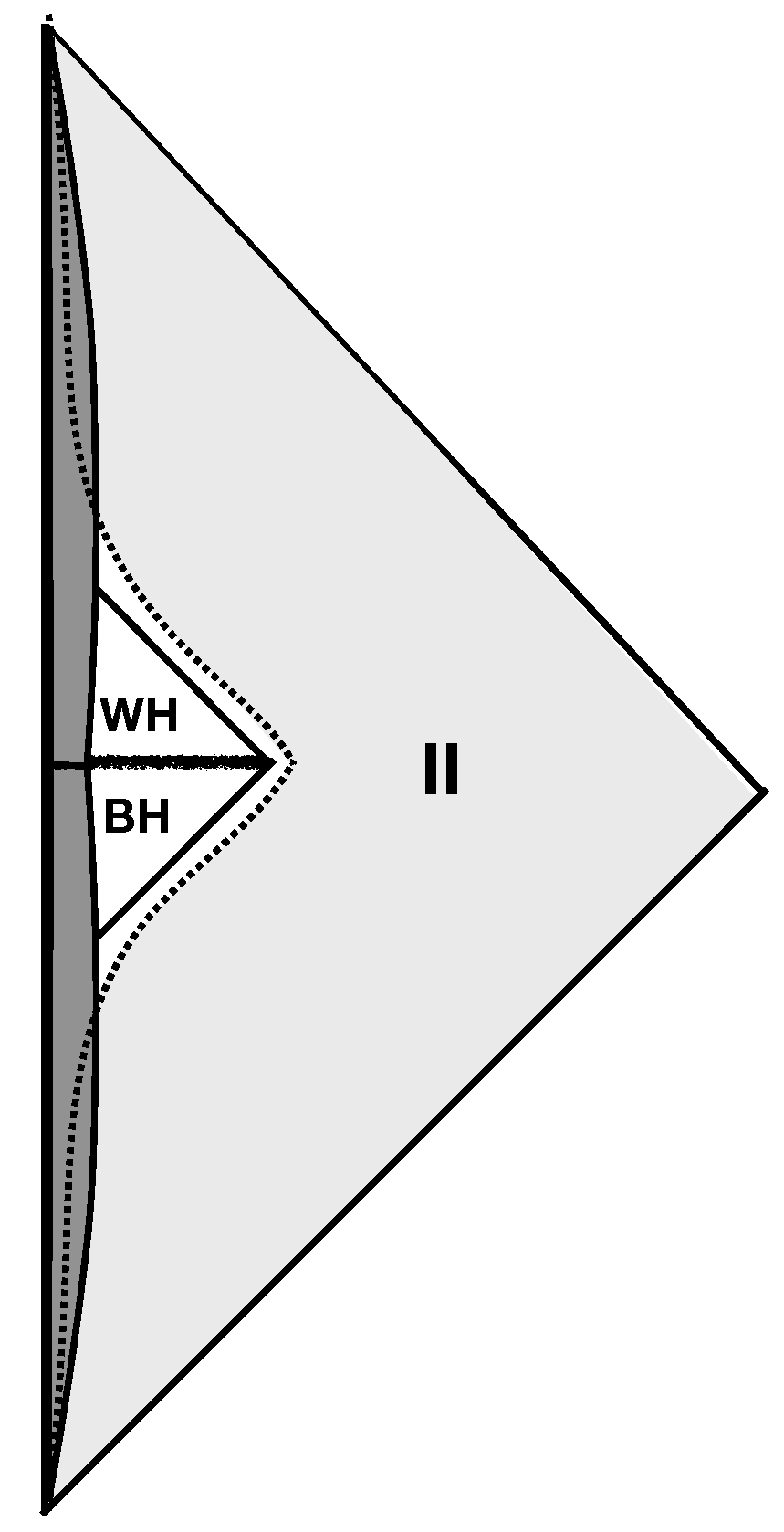
The difference between a black hole and a white hole is not very pronounced. Observed from the outside (say from the exterior of a sphere of radius , where m is the mass of the hole) and for a finite amount of time, a white hole cannot be distinguished from a black hole.
This is clear from the usual Schwarzschild line element, which is symmetric under time reversal, and therefore describes equally well the exterior of a black hole and the exterior of a white hole. Equivalently, zone II of the maximal extension of the Schwarzschild solution is equally the outside of a black hole and the outside of a white hole (see
Figure 1, Left). Analogous considerations hold for the Kerr solution. In other words, the continuation inside the radius
of an external
stationary black hole metric contains both a trapped region (a black hole) and an anti-trapped region (a white hole).
What then distinguishes a black hole from a white hole? The objects in the sky we call ‘black holes’ are described by a stationary metric only approximately, and for a limited time. In their past, at least their metric was definitely non-stationary, as they were produced by gravitational collapse. In this case, the continuation of the metric inside the radius
contains a trapped region, but not an anti-trapped region (see
Figure 1, Center). Vice versa, a white hole is an object that is indistinguishable from a black hole from the exterior and for a finite time, but in the future ceases to be stationary and there is no trapped region in its future (see
Figure 1, Right).
3. Quantum Processes and Time Scales
The classical prediction that the black is forever stable is not reliable. In the uppermost band of the central diagram of
Figure 1, quantum theory dominates. The death of a black hole is therefore a quantum phenomenon. The same is true for a white hole, reversing time direction. That is, the birth of a white hole is in a region where quantum gravitational phenomena are strong.
This consideration eliminates a traditional objection to the physical existence of white holes: How would they originate? They originate from a region where quantum phenomena dominate the behaviour of the gravitational field.
Such regions are generated in particular by the end of the life of a black hole, as mentioned above. Hence a white hole can in principle be originated by a dying black hole. This scenario has been shown to be concretely compatible with the exact external Einstein dynamics in [
12] and has been explored in [
13,
14,
15,
16,
17,
18]. The causal diagram of the spacetime giving the full life cycle of the black-white hole is given below in
Figure 2.
In particular, the result of [
16] indicates that the black-to-white process is asymmetric in time [
13] and the time scales of the durations of the different phases are determined by the initial mass of the black hole
. The lifetime
of the black hole is known from Hawking radiation theory to be at most of the order
in Planck units
. This time can be as shorter as
because of quantum gravitational effects [
11,
12,
13,
14,
15] (see also [
20,
21,
22,
23,
24]) but we disregard this possibility here. The lifetime
of the white hole phase is longer [
16]:
in Planck units. That is, in arbitrary units:
where
is the Planck mass. The tunnelling process itself from black to white takes a time of the order of the current mass at transition time [
15]. The area of the horizon of the black hole decreases with time because of Hawking evaporation, decreasing from
to the Planck mass
. At this point the transition happens and a white hole of mass of the order of the Planck mass is formed.
4. Timescales
Consider the hypothesis that white-hole remnants are a constituent of dark matter. To give an idea of the density of these objects, a local dark matter density of the order of
corresponds to approximately one Planck-scale remnant, with the weight of half an inch of human hair, per each 10.000 Km
. For these objects to be still present, we now need their lifetime to be larger or equal to the Hubble time
, that is
On the other hand, since the possibility of many larger black holes is constrained by observation, we expect remnants to be produced by already evaporated black holes, therefore the lifetime of the black hole must be shorter than the Hubble time. Therefore,
This gives an estimate on the possible value of
:
These are the masses of primordial black holes that could have given origin to dark matter present today in the form of remnants. Their Schwarzschild radius is in the range
According to a commonly considered theory of primordial black-hole formation, black holes of a given mass could have formed when their Schwarzschild radius was of the order of the cosmological horizon. Remarkably, the horizon was presumably in the above range at the end of inflation, during or just after reheating. Which happens to be precisely the epoch where we expect primordial black hole formation, namely shortly after reheating. This concordance supports the plausibility of the proposed scenario; that is, if the lifetimes in the model we are considering are correct, the black holes formed in that period are around us as remnants: they have already ended the Hawking evaporation but the resulting white holes have not had the time to dissipate yet.
5. Stability
Large classical white holes are unstable (see for instance Chapter 15 in [
25] and references therein). The reason can be understood as follows. The spacetime depicted in the center panel of
Figure 1 does not change much under a small arbitrary modification of its initial conditions on past null infinity, but it is drastically modified if we modify its final conditions on future null infinity. This is intuitively simple to grasp: if we sit on future null infinity and look back towards the hole, we see a black disk. This is the final condition. A slightly perturbed final condition includes the possibility of seeing radiation arriving from this disk. This is impossible in the spacetime of the center panel of
Figure 1, because of the huge red shift of the radiation moving next to the horizon, but it is possible in the left panel spacetime, because the radiation may have crossed over from the other asymptotic region.
The same is true for a white hole, reversing the time direction. In the spacetime depicted in the right panel, with some radiation, there is necessarily a dark spot in the incoming radiation from past null infinity. If we perturb this configuration, and add some incoming radiation in this dark spot, the evolution generically gives the spacetime of the left panel. Physically, what happens is that this radiation moves along the horizon, is blue shifted, can meet radiation coming out of the white hole and this is more mass than m at a radius : it is mass inside its Schwarzschild radius. At this point the region is trapped, and a black hole forms. Consequently, the evolution of the perturbed initial conditions yields the spacetime of the left, not the one of the right: the white hole is unstable and decays into a black hole.
This is the standard ‘instability of white holes’. How does this instability affect the remnants formed at the end of a black hole evaporation? The wavelength of the perturbation needed to trigger the instability must be smaller that the the size of the hole [
25]. It was observed in [
16] that to trigger the instability of a Planck size white hole we need trans-Planckian radiation, and this is likely not allowed by quantum gravity. Below we explore the issue in more detail, building a quantum model to describe the processes involving black and white holes.
6. Black and White Hole Processes
Consider a (spherically symmetric) Cauchy surface
in an extended Schwarzschild spacetime with mass
m.
can cut the horizon below or above the central sphere (the bifurcating horizon). See the left panel of
Figure 3. If above, we say that
contains a black hole; if below, we say it contains a white hole. In either case, the left asymptotic region and a portion of the interior of the hole can be replaced by a finite matter-filled interior. In this case, the interior portion of
has a finite volume
v. See
Figure 3. One possibility is to fix this interior portion of
to have a constant trace of the exterior curvature, or, equivalently, maximal volume [
26,
27,
28,
29]. Then the surface is determined by its intersection with the horizon (other interesting gauge fixings are possible).
Let
where
(for ‘Black’ and ‘White’) denote a coherent (semiclassical) quantum state of matter and geometry on the portion of
that lies inside the horizon, corresponding respectively to the center and right panels of
Figure 3, namely entering respectively the trapped (
) or anti-trapped (
) regions. Here
m and
v are the (expectation values of) mass and interior volume of the Schwarzschild geometry. We take here an approximation where these are the only relevant degrees of freedom. We assume black hole states
and white hole states
to be orthogonal states in the common Hilbert space
of the quantum states of geometry and matter inside a sphere, of Schwarzschild radius
. This is a reduced model since we disregard internal degrees of freedom other than
v. We are interested in the evolution of the state as the surface
moves up in time.
Let’s label the position of
with a temporal parameter t. For a black hole, it is natural to identify
t with the advanced time v and for a white hole, it is natural to identify it with the retarded time
. So let’s define
with an arbitrary origin for the t label. A number of processes can occur as the surface
moves up in time. We list them here using relativistic units
and keeping
ℏ explicit to distinguish classical from quantum phenomena.
Black hole volume increase and white hole volume decrease This is simply determined by the Einstein’s equations if nothing else happens. The variation is computed in [
26] to be governed by
where
is the initial mass of the black hole and the sign is plus for a black hole and minus for a white hole.
White to black instability This process is allowed by classical general relativity in the absence of any perturbation when there is a second asymptotic region, as it is apparent from the Left panel of
Figure 3; but it can also be triggered by an external perturbation [
25]. Notice that the volume does not change: this is due to the fact that this is a local process in the horizon region, which does not modify the interior. The lifetime of a white hole under decay to a black hole has been estimated to be proportional to its Schwarzschild radius [
25]:
This is equivalent to a transition probability per unit of time
This is a process that decreases the mass of a black hole, produced by negative energy entering the hole when a Hawking quantum is radiated. It is a phenomenon described by the classical backreaction on the geometry of the dynamics of a quantum field. Hawking radiation theory gives
Giving the lifetime for a massive black hole
Black to white tunnelling This is a genuine quantum gravitational process [
11,
16,
30]. Its probability per unit of time is still unclear. We take here the conservative estimate derived in [
15] using covariant Loop Quantum Gravity [
31], which agrees with the semiclassical expectation for tunnelling phenomena, namely that this probability is suppressed by the semiclassical standard tunnelling factor
where
S is a typical action for the transition. On dimensional grounds, this suggests a tunnelling probability per unit time
Here we have assumed for simplicity that the internal volume
v is conserved in this transition. A more precise account of this process will be studied elsewhere (for the tentative phenomenology derived from this process, see [
32,
33,
34,
35,
36,
37,
38]).
7. Dynamical Evolution
The ensemble of the processes listed above can be described as an evolution in t
for a two component state
governed by the Hamiltonian
where we have added also a diagonal energy term proportional to the mass in order to obtain the standard energy phase evolution, and
c and
b are constants of order unit.
We now ask what are the stable or semi-stable states of the hole as seen from the exterior.
A macroscopic black hole with mass m much larger than the Planck mass is stable when seen from the exterior for a (long) time span of the order , which is the Hawking evaporation time. The stability is due to the fact that process (1) does not affect the exterior, process (2) does not concern black holes and process (4) is strongly suppressed for macroscopic holes.
A macroscopic white hole, on the other hand, is not so stable, because of the fast instability of process (2). As basic physics is invariant under time reversal, one may wonder what breaks time reversal invariance here. What breaks time reversal invariance is the notion of stability that we are using. This is a stability under small fluctuations of the past boundary conditions. If instead we asked about stability under small fluctuations of the future boundary conditions, we would obviously obtain the opposite result: macroscopic white holes would be stable while macroscopic black holes would not.
The question we are interested in is what happens (generically) to a large macroscopic black hole if it is not fed by incoming mass. Then two processes are in place: its Hawking evaporation for a time (process 3) and the internal growth of v (process 1). This continues until process (4) becomes relevant, which happens when the mass is reduced to the order of Planck mass. At this point the black hole has a probability of order one to tunnel into a white hole under process (4). However, a white hole in unstable under process (2), giving it a finite probability of returning back to a black hole. Both processes (4) and (2) are fast at this point. Notice that this happens at large v, therefore in a configuration that classically is very distant from flat space, even if the overall mass involved is small.
As energy is constantly radiated away and no energy is fed into the system, the system evolves towards low m. However, m cannot vanish, because of the presence of the interior: in the classical theory, a geometry with larger v and small m is not contiguous to a Minkowski geometry, even if the mass is small. Therefore, in the large v region we have . Alternatively, this can be seen as a hypothesis ruling out macroscopic topology change.
However,
m cannot be arbitrarily small either, because of quantum gravity. The quantity
m is defined locally by the area of the horizon
and
A is quantized. According to Loop Quantum Gravity [
39], the eigenvalues of the area of
any surface are [
40]
where we have taken the Immirzi parameter to be the unit for simplicity. The minimal non-vanishing eigenvalue is
and is called the ‘area gap’ in loop quantum cosmology [
41]. This gives a minimal non-vanishing mass
defined by
, that is
(we have momentarily restored
for clarity.) Radiating energy away brings down the system to the
eigenspace. Consider now states that are
eigenstates of
m with the minimal value
and denote them
and
. The dynamics governed by the above Hamiltonian allows transition between black and white components. This is a typical quantum mechanical situation where two states, here
and
, can dynamically turn into one another. Let us disregard for a moment
v, which is invisible from the exterior, and project
down to a smaller state space
with basis states
. This is a two dimensional Hilbert space with basis vectors
and
. Seen from the exterior, the state of
will converge to
.
The Hamiltonian acting on this subspace is
where
. Quantum mechanics indicates that in a situation where the system can radiate energy away and there are possible transitions between these two states, the actual state will converge to a quantum state which is a quantum superposition of the two given by the lowest eigenstate of
H. This is
(
R for ‘Remnant’) and has eigenvalue
. If the amplitude
b of going from black to white is larger than the amplitude
a of going from white to black (as it seems plausible), the state is dominated by the white hole component. A related picture was been considered in [
42,
43,
44]: a classical oscillation between black and white hole states.
In a fully stationary situation, the mass
m is equal to the Bondi mass, which generates time translations at large distance from the hole in the frame determined by the hole. (Quantum gravity is locally Lorentz invariant [
45,
46] and has no preferred time [
47] but a black hole in a large nearly-flat region determines a preferred frame and a preferred time variable.) Keeping possible transitions into account, there is a subtle difference between the mass
m, determined locally by the horizon area, and the energy of the system, which is determined by the full Hamiltonian that includes the interaction terms. Being an eigenstate of the energy,
is a stationary state, as far as the external dynamics is concerned, and as long as the internal volume remains large. This is the stable remnant that forms after the end of Hawking evaporation.
On a time scale of order , on the other hand, the internal volume of the white hole component of this state can shrink to zero, and a transition to Minkowski space becomes probable, a process not explicitly contemplated by the simple model given.
8. Conclusions
We have computed the formation time of primordial black holes that could have given rise to remnants forming a component of dark matter today, and we have found that this formation time sits at a cosmological epoch after the end of inflation, compatible with the current observation of dark matter.
We have addressed the issue of remnant stability by building a simple quantum model that takes white hole instability explicitly into account, and shown that its only consequence is to induce a quantum superposition between Planckian-area quantum white and black hole states.
This is a preliminary crude quantum model. It disregards the detailed dynamics around the minimal radius [
17] and in the tunnelling region [
15,
18] and, importantly, the internal dynamics generated by the in-falling component by the Hawking’s radiation. The consistency of this picture depends on the hypothesis that there is no macroscopic topology change and a large black hole interior does not just magically disappear into nothing.
Still, its preliminary indications support the possibility of stable remnants, making it fairly clear that white hole instability is not an issue for their existence, and therefore remnants may well be components of the observed dark matter.
An alternative possibility, where dark matter is formed by remnants from a pre-big-bang phase in a bouncing cosmology, is explored in a companion paper [
48].