New Constraints on Spatial Variations of the Fine Structure Constant from Clusters of Galaxies
Abstract
:1. Introduction
2. Data
3. Methodology
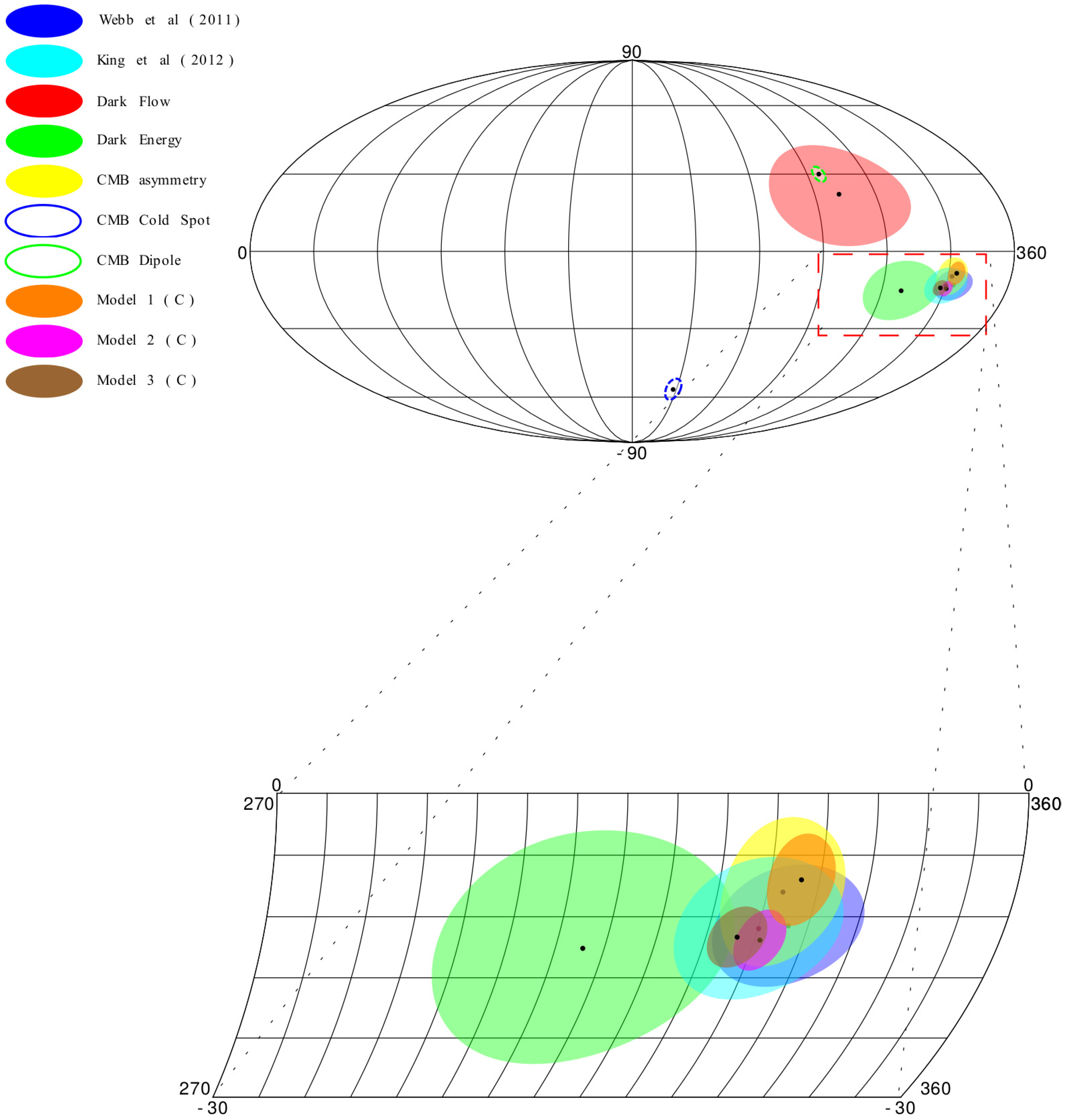
4. Results and Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Webb, J.K.; King, J.A.; Murphy, M.T.; Flambaum, V.V.; Carswell, R.F.; Bainbridge, M.B. Indications of a Spatial Variation of the Fine Structure Constant. Phys. Rev. Lett. 2011, 107, 191101. [Google Scholar] [CrossRef] [PubMed]
- King, J.A.; Webb, J.K.; Murphy, M.T.; Flambaum, V.V.; Carswell, R.F.; Bainbridge, M.B.; Wilczynska, M.R.; Koch, F.E. Spatial variation in the fine-structure constant—New results from VLT/UVES. Mon. Not. R. Astron. Soc. 2012, 422, 3370–3414. [Google Scholar] [CrossRef]
- Berengut, J.C.; Flambaum, V.V.; King, J.A.; Curran, S.J.; Webb, J.K. Is there further evidence for spatial variation of fundamental constants? Phys. Rev. D 2011, 83, 123506. [Google Scholar] [CrossRef]
- Berengut, J.C.; Kava, E.M.; Flambaum, V.V. Is there a spatial gradient in values of the fine-structure constant? A reanalysis of the results. Astron. Astrophys. 2012, 542, A118. [Google Scholar] [CrossRef]
- Pinho, A.M.M.; Martins, C.J.A.P. Updated constraints on spatial variations of the fine-structure constant. Phys. Lett. B 2016, 756, 121–125. [Google Scholar] [CrossRef]
- Mariano, A.; Perivolaropoulos, L. Is there correlation between fine structure and dark energy cosmic dipoles? Phys. Rev. D 2012, 86, 083517. [Google Scholar] [CrossRef]
- Mariano, A.; Perivolaropoulos, L. CMB maximum temperature asymmetry axis: Alignment with other cosmic asymmetries. Phys. Rev. D 2013, 87, 043511. [Google Scholar] [CrossRef]
- Planck Collaboration. Planck intermediate results. XXIV. Constraints on variation of fundamental constants. Astron. Astrophys. 2015, 580, A22. [Google Scholar]
- O’Bryan, J.; Smidt, J.; De Bernardis, F.; Cooray, A. Constraints on Spatial Variations in the Fine-structure Constant from Planck. Astrophys. J. 2015, 798, 18. [Google Scholar] [CrossRef]
- Iorio, L. Orbital effects of spatial variations of fundamental coupling constants. Mon. Not. R. Astron. Soc. 2011, 417, 2392–2400. [Google Scholar] [CrossRef]
- Sunyaev, R.A.; Zeldovich, Y.B. The Observations of Relic Radiation as a Test of the Nature of X-Ray Radiation from the Clusters of Galaxies. Comments Astrophys. Space Phys. 1972, 4, 173–178. [Google Scholar]
- Avgoustidis, A.; Martins, C.J.A.P.; Monteiro, A.M.R.V.L.; Vielzeufb, P.E.; Luzzi, G. Cosmological effects of scalar-photon couplings: Dark energy and varying-α Models. J. Cosmol. Astropart. Phys. 2014, 2014, 062. [Google Scholar] [CrossRef]
- De Martino, I.; Génova-Santos, R.T.; Atrio-Barandela, F.; Ebeling, H.; Kashlinsky, A.; Kocevski, D.; Martins, C.J.A.P. Constraining the Redshift Evolution of the Cosmic Microwave Background Blackbody Temperature with PLANCK Data. Astrophys. J. 2015, 808, 128. [Google Scholar] [CrossRef]
- Böhringer, H.; Schuecker, P.; Guzzo, L.; Collins, C.A.; Voges, W.; Cruddace, R.G.; Ortiz-Gil, A.; Chincarini, G.; De Grandi, S.; Edge, A.C.; et al. The ROSAT-ESO Flux Limited X-ray (REFLEX) Galaxy cluster survey. V. The cluster catalogue. Astron. Astrophys. 2004, 425, 367–383. [Google Scholar] [CrossRef]
- Ebeling, H.; Edge, A.C.; Böhringer, H.; Allen, S.W.; Crawford, C.S.; Fabian, A.C.; Voges, W.; Huchra, J.P. The ROSAT Brightest Cluster Sample—I. The compilation of the sample and the cluster log N-log S distribution. Mon. Not. R. Astron. Soc. 1998, 301, 881–914. [Google Scholar] [CrossRef]
- Ebeling, H.; Edge, A.C.; Allen, S.W.; Crawford, C.S.; Fabian, A.C.; Huchra, J.P. The ROSAT Brightest Cluster Sample—IV. The extended sample. Mon. Not. R. Astron. Soc. 2000, 318, 333–340. [Google Scholar] [CrossRef]
- Ebeling, H.; Mullis, C.R.; Tully, R.B. A Systematic X-Ray Search for Clusters of Galaxies behind the Milky Way. Astrophys. J. 2002, 580, 774–788. [Google Scholar] [CrossRef]
- Górski, K.M.; Hivon, E.; Banday, A.J.; Wandelt, B.D.; Hansen, F.K.; Reinecke, M.; Bartelmann, M. HEALPix: A Framework for High-Resolution Discretization and Fast Analysis of Data Distributed on the Sphere. Astrophys. J. 2005, 622, 759–771. [Google Scholar] [CrossRef]
- De Martino, I.; Atrio-Barandela, F. SZ/X-ray scaling relations using X-ray data and Planck Nominal maps. Mon. Not. R. Astron. Soc. 2016, 461, 3222–3232. [Google Scholar] [CrossRef]
- De Martino, I. A f(R)-gravity model of the Sunyaev-Zeldovich profile of the Coma cluster compatible with Planck data. Phys. Rev. D 2016, 93, 124043. [Google Scholar] [CrossRef]
- Hastings, W.K. Monte Carlo Sampling Methods Using Markov Chains and Their Applications. Biometrika 1970, 57, 97–109. [Google Scholar] [CrossRef]
- Metropolis, N.; Rosenbluth, A.W.; Rosenbluth, M.N.; Teller, A.H.; Teller, E. Equation of State Calculations by Fast Computing Machines. J. Chem. Phys. 1953, 21, 1087–1092. [Google Scholar] [CrossRef]
- Gelman, A.; Rubin, D.B. Inference from Iterative Simulation Using Multiple Sequences. Stat. Sci. 1992, 7, 457–472. [Google Scholar] [CrossRef]
- Verde, L.; Peiris, H.V.; Spergel, D.N.; Nolta, M.R.; Bennett, C.L.; Halpern, M.; Hinshaw, G.; Jarosik, N.; Kogut, A.; Limon, M.; et al. First Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Parameter Estimation Methodology. Astrophys. J. Suppl. Ser. 2003, 148, 195–211. [Google Scholar] [CrossRef]
- De Martino, I.; Martins, C.J.A.P.; Ebeling, H.; Kocevski, D. Constraining spatial variations of the fine structure constant using clusters of galaxies and Planck data. Phys. Review D 2016, 94, 083008. [Google Scholar] [CrossRef]
- Galli, S. Clusters of galaxies and variation of the fine structure constant. Phys. Rev. D 2013, 87, 123516. [Google Scholar] [CrossRef]
- Kashlinsky, A.; Atrio-Barandela, F.; Kocevski, D.; Ebeling, H. A Measurement of Large-Scale Peculiar Velocities of Clusters of Galaxies: Results and Cosmological Implications. Astrophys. J. Lett. 2008, 686, L49. [Google Scholar] [CrossRef]
- Kogut, A.; Lineweaver, C.; Smoot, G.F.; Bennett, C.L.; Banday, A.; Boggess, N.W.; Cheng, E.S.; de Amici, G.; Fixsen, D.J.; Hinshaw, G.; et al. Dipole Anisotropy in the COBE Differential Microwave Radiometers First-Year Sky Maps. Astrophys. J. 1993, 419, 1–6. [Google Scholar] [CrossRef]
- Vielva, P.; Martinez-Gonzalez, E.; Barreiro, R.B.; Sanz, J.L.; Cayon, L. Detection of non-gaussianity in the Wilkinson microwave anisotropy probe first-year data using spherical wavelets. Astrophys. J. 2004, 609, 22–34. [Google Scholar] [CrossRef]
- Kashlinsky, A.; Atrio-Barandela, F.; Ebeling, H.; Edge, A.; Kocevski, D. A New Measurement of the Bulk Flow of X-Ray Luminous Clusters of Galaxies. Astrophys. J. Lett. 2010, 712, L81. [Google Scholar] [CrossRef]
- Kashlinsky, A.; Atrio-Barandela, F.; Ebeling, H. Measuring the Dark Flow with Public X-ray Cluster Data. Astrophys. J. 2011, 732, 1. [Google Scholar] [CrossRef]
- Kashlinsky, A.; Atrio-Barandela, F.; Ebeling, H. Measuring bulk motion of X-ray clusters via the kinematic Sunyaev-Zeldovich effect: Summarizing the “dark flow” evidence and its implications. arXiv, 2012; arXiv:1202.0717v1. [Google Scholar]
- Atrio-Barandela, F.; Kashlinsky, A.; Ebeling, H.; Fixsen, D.J.; Kocevski, D. Probing the Dark Flow Signal in WMAP 9 -Year and Planck Cosmic Microwave Background Maps. Astrophys. J. 2015, 810, 143. [Google Scholar] [CrossRef]
- Ade, P.A.; Aghanim, N.; Armitage-Caplan, C.; Arnaud, M.; Ashdown, M.; Atrio-Barandela, F.; Aumont, J.; Baccigalupi, C.; Banday, A.J.; Barreiro, R.B.; et al. Planck 2013 results. XXIII. Isotropy and statistics of the CMB. Astron. Astrophys. 2014, 571, A23. [Google Scholar]
- Naselsky, P.; Zhao, W.; Kim, J.; Chen, S. Is the Cosmic Microwave Background Asymmetry due to the Kinematic Dipole? Astrophys. J. 2012, 749, 31. [Google Scholar] [CrossRef]
- Zhao, W.; Wu, P.X.; Zhang, Y. Anisotropy of Cosmic Acceleration. Int. J. Mod. Phys. D 2013, 22, 1350060. [Google Scholar] [CrossRef]
- Zhao, W. Directional dependence of CMB parity asymmetry. Phys. Rev. D 2014, 89, 023010. [Google Scholar] [CrossRef]
- Zhao, W.; Santos, L. Preferred axis in cosmology. Universe 2016, 3, 9–33. [Google Scholar]
- Cheng, C.; Zhao, W.; Huang, Q.-G.; Santos, L. Preferred axis of CMB parity asymmetry in the masked maps. Phys. Lett. B 2016, 757, 445–453. [Google Scholar] [CrossRef]
| m | d | RA (°) | DEC (°) | ||
|---|---|---|---|---|---|
| Model 1 | (A) | 0.0 | 261.0 | ||
| (B) | 261.0 | ||||
| (C) | 0.0 | ||||
| (D) | |||||
| Model 2 | (A) | 0.0 | 261.0 | ||
| (B) | 261.0 | ||||
| (C) | 0.0 | ||||
| (D) | |||||
| Model 3 | (A) | 1.0 | 261.0 | ||
| (B) | 261.0 | ||||
| (C) | 1.0 | ||||
| (D) |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
De Martino, I.; Martins, C.J.A.P.; Ebeling, H.; Kocevski, D. New Constraints on Spatial Variations of the Fine Structure Constant from Clusters of Galaxies. Universe 2016, 2, 34. https://doi.org/10.3390/universe2040034
De Martino I, Martins CJAP, Ebeling H, Kocevski D. New Constraints on Spatial Variations of the Fine Structure Constant from Clusters of Galaxies. Universe. 2016; 2(4):34. https://doi.org/10.3390/universe2040034
Chicago/Turabian StyleDe Martino, Ivan, Carlos J. A. P. Martins, Harald Ebeling, and Dale Kocevski. 2016. "New Constraints on Spatial Variations of the Fine Structure Constant from Clusters of Galaxies" Universe 2, no. 4: 34. https://doi.org/10.3390/universe2040034
APA StyleDe Martino, I., Martins, C. J. A. P., Ebeling, H., & Kocevski, D. (2016). New Constraints on Spatial Variations of the Fine Structure Constant from Clusters of Galaxies. Universe, 2(4), 34. https://doi.org/10.3390/universe2040034







