Warm Inflation

Abstract

I show here that there are some interesting differences between the predictions of warm and cold inflation models focusing in particular upon the scalar spectral index $n_s$ and the tensor-to-scalar ratio r. The first thing to be noted is that the warm inflation models in general predict a vanishingly small value of r. Cold inflationary models with the potential $V=M^4{\left(\varphi /M_P\right)}^p$ and a number of e-folds $N=60$ predict ${\delta }_{nsC}\equiv 1-n_s\approx \left(p+2\right)/120$, where $n_s$ is the scalar spectral index, while the corresponding warm inflation models with constant value of the dissipation parameter $\mathrm{\Gamma }$ predict ${\delta }_{nsW}=\left[\left(20+p\right)/\left(4+p\right)\right]/120$. For example, for $p=2$ this gives ${\delta }_{nsW}=1.1{\delta }_{nsC}$. The warm polynomial model with $\mathrm{\Gamma }=V$ seems to be in conflict with the Planck data. However, the warm natural inflation model can be adjusted to be in agreement with the Planck data. It has, however, more adjustable parameters in the expressions for the spectral parameters than the corresponding cold inflation model, and is hence a weaker model with less predictive force. However, it should be noted that the warm inflation models take into account physical processes such as dissipation of inflaton energy to radiation energy, which is neglected in the cold inflationary models.

1. Introduction

In the usual (cold) inflationary models, dissipative effects with decay of inflaton energy into radiation energy are neglected. However, during the evolution of warm inflation dissipative effects are important, and inflaton field energy is transformed to radiation energy. This produces heat and viscosity, which make the inflationary phase last longer. Warm inflation models were introduced and developed by Berera and coworkers [1,2,3,4,5,6,7,8,9,10,11,12,13,14]. However, even earlier inflation models with dissipation of inflaton energy to radiation and particles had been considered [15,16,17,18,19,20,21,22]. Introductions to warm inflation models and references to works prior to 2009 on warm inflation are found in [8] and [23]. For later works, see [9] and [24] and references in these articles. Further developments are found in the articles [25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43].

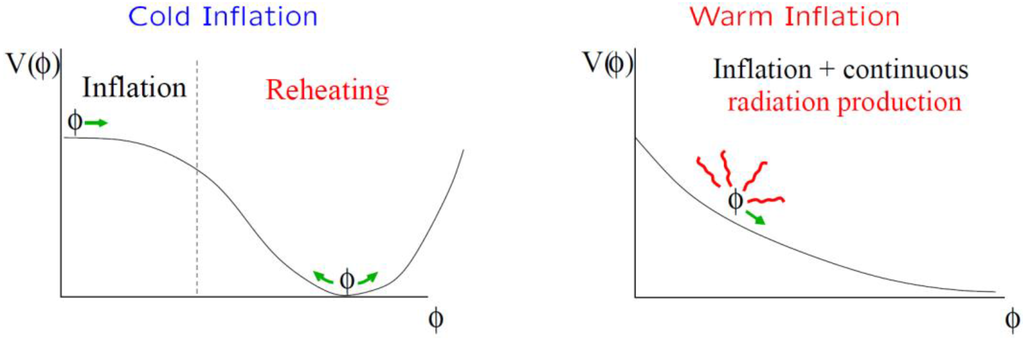
In this scenario, there is no need for a reheating at the end of the inflationary era. The universe heats up and becomes radiation dominated during the inflationary era, so there is a smooth transition to a radiation dominated phase (Figure 1).

In the present work, I will review the foundations of warm inflation and some of the most recent phenomenological models of this type, focusing in particular on the comparison with the experimental measurements of the scalar spectral index $n_s$ and the tensor to scalar ratio r by the Planck observatory.

The article is organized as follows. In Section 2, the definition and current measurements of these quantities are given. Then, the optical parameters in the warm inflation scenario are considered. We go on and study some phenomenological models in the subsequent sections: monomial-, natural- and viscous inflation. The models are compared in Section 7, and the results are summarized in the final section.

2. Definition and Measured Values of the Optical Parameters

We shall here briefly review a few of the mathematical quantities that are used to describe the temperature fluctuations in the CMB. The power spectra of scalar and tensor fluctuations are represented by [44]

$$\begin{array}{ll}{P}_S=A_S\left(k_{*}\right){\left(\frac{k}{k_{\ast }}\right)}^{n_S-1+\left(1/2\right){\alpha }_S\ln \left(k/k_{*}\right)+\cdot \cdot \cdot },& P_T=A_T\left(k_{*}\right){\left(\frac{k}{k_{\ast }}\right)}^{n_T+\left(1/2\right){\alpha }_T\ln \left(k/k_{*}\right)+\cdot \cdot \cdot },\\ A_S=\frac{V}{24{\pi }^2\epsilon M_P^4}={\left(\frac{H^2}{2\pi \dot{\varphi }}\right)}^2,& A_T=\frac{2V}{3{\pi }^2{M}_P^4}=\epsilon {\left(\frac{2H^2}{\pi \dot{\varphi }}\right)}^2\end{array}$$

(2.1)

Here, k is the wave number of the perturbation which is a measure of the average spatial extension for a perturbation with a given power, and $k_{\ast }$ is the value of k at a reference scale usually chosen as the scale at horizon crossing, called the pivot scale. One often writes $k=\dot{a}=aH$, where a is the scale factor representing the ratio of the physical distance between reference particles in the universe relative to their present distance. The quantities $A_S$ and $A_T$ are amplitudes at the pivot scale of the scalar- and tensor fluctuations, and $n_S$ and $n_T$ are the spectral indices of the corresponding fluctuations. We shall represent the scalar spectral index by the quantity ${\delta }_{ns}\equiv 1-n_S$. The quantities $n_S$ and $n_T$ are called the tilt of the power spectrum of curvature perturbations and tensor modes, respectively, because they represent the deviation of the values ${\delta }_{ns}=n_t=0$ that represent a scale invariant spectrum.

The quantities ${\alpha }_S$ and ${\alpha }_T$ are factors representing the k-dependence of the spectral indices. They are called the running of the spectral indices and are defined by

$${\alpha }_S=\frac{d{n}_S}{d\ln k},{\alpha }_T=\frac{d{n}_T}{d\ln k}$$

(2.2)

They will, however, not be further considered in this article.

As mentioned above, if $n_S=1$ the spectrum of the scalar fluctuations is said to be scale invariant. An invariant mass-density power spectrum is called a Harrison-Zel’dovich spectrum. One of the predictions of the inflationary universe models is that the cosmic mass distribution has a spectrum that is nearly scale invariant, but not exactly. The observations and analysis of the Planck team [45] have given the result $n_S=0.968\pm 0.006$. Hence, we shall use $n_S=0.968$ as the preferred value of $n_S.$ Different inflationary models will be evaluated against the Planck 2015 value of the tilt of the scalar curvature fluctuations, ${\delta }_{ns}=\mathrm{0.032.}$

The tensor-to-scalar ratio r is defined by

$$r\equiv \frac{P_T\left(k_{\ast }\right)}{P_S\left(k_{\ast }\right)}=\frac{A_T}{A_S}$$

(2.3)

As noted by [46], the tensor-to-scalar ratio is a measure of the energy scale of inflation, $V^{1/4}={\left(100r\right)}^{1/4}{10}^{16}GeV$. From Equations (2.1) and (2.3), we have

$$r=16\epsilon$$

(2.4)

The Planck observational data have given $r<0.11$.

3. Optical Parameters in Warm Inflation

During the warm inflation era, both the inflaton field energy with density ${\rho }_{\varphi }$ and the electromagnetic radiation with energy density ${\rho }_r$ are important for the evolution of the universe. The first Friedmann equation takes the form

$$H^2=\frac{\kappa }{3}\left({\rho }_{\varphi }+{\rho }_r\right)$$

(3.1)

We shall here use units so that $\kappa =1/M_P^2$ where $M_P$ is the reduced Planck mass. In these models, the continuity equations for the inflaton field and the radiation take the form

$${\dot{\rho }}_{\varphi }+3H\left({\rho }_{\varphi }+p_{\varphi }\right)=-\mathrm{\Gamma }{\dot{\varphi }}^2,{\dot{\rho }}_r+4H{\rho }_r=\mathrm{\Gamma }{\dot{\varphi }}^2$$

(3.2)

respectively, where the dot denotes differentiation with respect to cosmic time, and $\mathrm{\Gamma }$ is a dissipation coefficient of a process which transforms inflaton energy into radiation. In general, $\mathrm{\Gamma }$ is temperature dependent. The density and pressure of the inflaton field are given in terms of the kinetic and potential energy of the inflaton field as

$${\rho }_{\varphi }=\frac{{\dot{\varphi }}^2}{2}+V,p_{\varphi }=\frac{{\dot{\varphi }}^2}{2}-V$$

(3.3)

During warm inflation, the dark energy predominates over radiation, i.e., ${\rho }_{\varphi }>>{\rho }_r$, and $H,\varphi$ and $\mathrm{\Gamma }$ are slowly varying so that the production of radiation is quasi-static, $\ddot{\varphi }<<H\dot{\varphi },$ ${\dot{\rho }}_r<<4H{\rho }_r$ and ${\dot{\rho }}_r<<\mathrm{\Gamma }{\dot{\varphi }}^2$. Note that in the slow roll era the kinetic energy of the inflaton field energy can be neglected compared to its potential energy. Then, the inflaton field obeys the equation of state $p_{\varphi }\approx -{\rho }_{\varphi }$. Also, in this era, the second of Equation (3.2) gives ${\rho }_r=0$ in the case of vanishing dissipation, $\mathrm{\Gamma }=0$, i.e., in the warm inflation model all of the radiation is produced by dissipation of the inflaton energy. Then, the first Friedmann equation and the equation for the evolution of the inflaton field take the form

$$3H^2=\kappa {\rho }_{\varphi }=\kappa V,\left(3H+\mathrm{\Gamma }\right)\dot{\varphi }=-V^{\prime }$$

(3.4)

respectively. Here, a prime denotes differentiation with respect to the inflaton field $\varphi$.

Defining the so-called dissipative ratio by

$$Q\equiv \mathrm{\Gamma }/3H$$

(3.5)

the last of Equation (3.4) may be written as

$$3H\left(1+Q\right)\dot{\varphi }=-V^{\prime }$$

(3.6)

The quantity Q represents the effectiveness at which inflaton energy is transformed to radiation energy. If $Q>>1$ one says that there is a strong, dissipative regime, and if $Q<<1$ there is a weak dissipative regime.

During warm inflation, the second of the Equation (3.2) reduces to

$${\rho }_r=\left(3/4\right)Q{\dot{\varphi }}^2$$

(3.7)

In the warm inflation scenario, a thermalized radiation component is present with $T>H$, where both T and H are expressed in units of energy. Then, the tensor-to-scalar ratio defined in Equation (2.3), is modified with respect to standard cold inflation, so that [12]

$$r_W=\frac{H/T}{{\left(1+Q\right)}^{5/2}}r$$

(3.8)

Hence, the tensor-to-scalar ratio is suppressed by the factor $\left(T/H\right){\left(1+Q\right)}^{5/2}$ compared with the standard cold inflation.

Hall, Moss and Berera [9] have calculated the spectral index in warm inflation for the strong dissipative regime with $Q>>1$ or $\mathrm{\Gamma }>>3H$. We shall here follow Visinelli [47] and permit arbitrary values of $Q$. Differentiating the first of the Equation (3.4) and using Equation (3.6) gives

$$\dot{H}=-\left(\kappa /2\right)\left(1+Q\right){\dot{\varphi }}^2$$

(3.9)

Hence $\dot{H}<0$.

We define the potential slow roll parameters $\epsilon$ and $\eta$ by

$$\epsilon \equiv \frac{1}{2\kappa }{\left(\frac{V^{\prime }}{V}\right)}^2,\eta \equiv \frac{1}{\kappa }\frac{V^{″}}{V}$$

(3.10)

These expressions are to be evaluated at the beginning of the slow roll era. Using Equations (3.4), (3.6) and (3.9) and the first of Equation (3.10) we get

$$\epsilon =-\left(1+Q\right)\frac{\dot{H}}{H^2}$$

(3.11)

Differentiation of Equation (3.6) and using that ${\left(\dot{\varphi }\right)}^{\prime }=\ddot{\varphi }/\dot{\varphi }$ gives

$$V^{″}=\frac{{\mathrm{\Gamma }}^{\prime }{V}^{\prime }}{\mathrm{\Gamma }+3H}-3H\left(1+Q\right)\frac{\ddot{\varphi }}{\dot{\varphi }}-3\dot{H}$$

(3.12)

Dividing by $\kappa V$ and using the first of Equation (3.4) in the two last terms leads to

$$\eta =\frac{Q}{1+Q}\frac{1}{\kappa }\frac{{\mathrm{\Gamma }}^{\prime }{V}^{\prime }}{\mathrm{\Gamma }V}-\frac{1+Q}{H}\frac{\ddot{\varphi }}{\dot{\varphi }}-\frac{\dot{H}}{H^2}$$

(3.13)

Defining

$$\beta \equiv \frac{1}{\kappa }\frac{{\mathrm{\Gamma }}^{\prime }{V}^{\prime }}{\mathrm{\Gamma }V}$$

(3.14)

and using Equation (3.12) we get

$$\frac{\ddot{\varphi }}{H\dot{\varphi }}=-\frac{1}{1+Q}\left(\eta -\beta +\frac{\beta -\eta }{1+Q}\right)$$

(3.15)

in agreement with Equation (3.14) of Visinelli [47] .

It follows from Equation (3.6) that

$$\frac{d}{d\varphi }=-\frac{3H\left(1+Q\right)}{V^{\prime }}\frac{d}{dt}$$

(3.16)

From Equation (3.5) and the first of Equation (3.4) we have

$$H\mathrm{\Gamma }=\kappa VQ$$

(3.17)

Using Equations (3.14), (3.16) and (3.17) can be written as

$$\frac{\dot{\mathrm{\Gamma }}}{H\mathrm{\Gamma }}=-\frac{\beta }{1+Q}$$

(3.18)

During slow roll the second of the Equation (3.2) reduces to

$$4H{\rho }_r=\mathrm{\Gamma }{\dot{\varphi }}^2$$

(3.19)

Differentiation gives

$$\frac{{\dot{\rho }}_r}{H{\rho }_r}=\frac{\dot{\mathrm{\Gamma }}}{H\mathrm{\Gamma }}+2\frac{\ddot{\varphi }}{H\dot{\varphi }}-\frac{\dot{H}}{H^2}$$

(3.20)

Inserting Equations (3.11), (3.15) and (3.18) into Equation (3.20) gives

$$\frac{{\dot{\rho }}_r}{H{\rho }_r}=-\frac{1}{1+Q}\left(2\eta -\beta -\epsilon +2\frac{\beta -\epsilon }{1+Q}\right)$$

(3.21)

We now define ${\delta }_{ns}\equiv 1-n_s$, where $n_s$ is the scalar spectral index. Visinelli [48] has deduced

$${\delta }_{ns}=4\frac{\dot{H}}{H^2}-2\frac{\ddot{\varphi }}{H\dot{\varphi }}-\frac{\dot{\omega }}{H\left(1+\omega \right)}$$

(3.22)

where

$$\omega =\frac{T}{H}\frac{2\sqrt{3}\pi Q}{\sqrt{3+4\pi Q}}$$

(3.23)

Since ${\rho }_r\propto T^4$ we have that

$$\omega \propto \frac{{\rho }_r^{1/4}Q}{H\sqrt{3+4\pi Q}}$$

(3.24)

Differentiating this we get

$$\frac{\dot{\omega }}{H\omega }=\frac{1}{4}\frac{{\rho }_r}{H{\rho }_r}-\frac{\dot{H}}{H^2}+\frac{3+2\pi Q}{3+4\pi Q}\frac{\dot{Q}}{HQ}$$

(3.25)

Differentiating Equation (3.5) gives

$$\frac{\dot{Q}}{HQ}=\frac{\dot{\mathrm{\Gamma }}}{H\mathrm{\Gamma }}-\frac{\dot{H}}{H^2}$$

(3.26)

Using Equations (3.11) and (3.18) then leads to

$$\frac{\dot{Q}}{HQ}=\frac{\epsilon -\beta }{1+Q}$$

(3.27)

Inserting Equations (3.11), (3.21) and (3.27) into Equation (3.25) gives

$$\dot{\omega }=-\frac{H\omega }{1+Q}\left[\frac{2\eta -\beta -5\epsilon }{4}+\frac{1}{2}\frac{\beta -\epsilon }{1+Q}+\frac{3+2\pi Q}{3+4\pi Q}\left(\beta -\epsilon \right)\right]$$

(3.28)

Visinelli has rewritten this as follows

$$\dot{\omega }=-\frac{H\omega }{1+Q}\left[\frac{2\eta +\beta -7\epsilon }{4}+\frac{6+\left(3+4\pi \right)Q}{\left(1+Q\right)\left(3+4\pi Q\right)}\left(\beta -\epsilon \right)\right]$$

(3.29)

Inserting the expressions (3.11), (3.15) and (3.29) into Equation (3.22) gives

$${\delta }_{ns}=\frac{1}{1+Q}\left[4\epsilon -2\left(\eta -\beta +\frac{\beta -\epsilon }{1+Q}\right)+\frac{\omega }{1+\omega }\left(\frac{2\eta +\beta -7\epsilon }{4}+\frac{6+\left(3+4\pi \right)Q}{\left(1+Q\right)\left(3+4\pi Q\right)}\left(\beta -\epsilon \right)\right)\right]$$

(3.30)

The usual cold inflation is found in the limit $Q\to 0$ and $T<<H$, i.e., $\omega \to 0$. Then,

$${\delta }_{ns}\to 2\left(3\epsilon -\eta \right)$$

(3.31)

In the strong regime of warm inflation, $Q>>1$, $\omega >>1$ we get

$${\delta }_{ns}=\frac{3}{2Q}\left[\frac{3}{2}\left(\epsilon +\beta \right)-\eta \right]$$

(3.32)

In the weak regime, $Q<<1$, Equation (3.16) leads to

$${\delta }_{ns}=2\left(3\epsilon -\eta \right)-\frac{\omega /4}{1+\omega }\left(15\epsilon -2\eta -9\beta \right)$$

(3.33)

It may be noted that in warm inflation the condition for slow roll is that the absolute values of $\epsilon ,\eta$ and $\beta$ are much smaller than $1+Q$.

Visinelli has found that the tensor-to-scalar ratio in warm inflation is

$$r=\frac{16\epsilon }{{\left(1+Q\right)}^2\left(1+\omega \right)}$$

(3.34)

In the cold inflation limit, this reduces to

$$r\to 16\epsilon$$

(3.35)

In the strong dissipation regime warm inflation gives in general

$$r\to \frac{16}{Q^2\omega }\epsilon <<\epsilon$$

(3.36)

Hence, all the warm inflation models predict an extremely small tensor-to-scalar-ratio in the strong dissipation regime with $Q>>1$ and $\omega >>1$.

4. Warm Monomial Inflation

Visinelli [48] has investigated warm inflation with a polynomial potential which we write in the form

$$V=M^4{\left(\varphi /M_P\right)}^p$$

(4.1)

since the potential and the inflaton field have dimensions equal to the fourth and first power of energy, respectively. Here, M represents the energy scale of the potential when the inflaton field has Planck mass. Furthermore he assumes that the dissipative term is also monomial

$$\mathrm{\Gamma }={\mathrm{\Gamma }}_0{\left(\varphi /M_P\right)}^{q/2}$$

(4.2)

He considered models with $p>0$ and $q>p$. However, in the present article, we shall also consider polynomial models with $p<0$. From Equations (3.3) and (3.4) we have

$$Q=Q_0{\left(\frac{\varphi }{M_P}\right)}^{\frac{q-p}{2}},Q_0=\frac{{\mathrm{\Gamma }}_0{M}_P}{\sqrt{3}{M}^2}$$

(4.3)

The constant $Q_0$ represents the strength of the dissipation. For $q=p$ the dissipative ratio is constant, $Q=Q_0$. We shall here consider the strong dissipative regime where $Q>>1$. Then, the second of Equation (3.3) reduces to

$$\dot{\varphi }=-\frac{V^{\prime }}{\mathrm{\Gamma }}$$

(4.4)

Inserting Equations (4.1) and (4.2) gives

$$\dot{\varphi }=-\frac{p{M}^4}{{\mathrm{\Gamma }}_0{M}_P}{\left(\frac{\varphi }{M_P}\right)}^{p-\frac{q}{2}-1}$$

(4.5)

Integration leads to

$$\varphi \left(t\right)={\left[\frac{4+q-2p}{2}\left(K-\frac{p{M}^4}{{\mathrm{\Gamma }}_0{M}^{p-\frac{q}{2}}}t\right)\right]}^{\frac{2}{4+q-2p}},q>2\left(p-2\right)$$

(4.6)

where K is a constant of integration. The initial condition $\varphi \left(0\right)=0$ gives $K=0$.

The special cases (i) $\mathrm{\Gamma }=V/M_P^3$, i.e., ${\mathrm{\Gamma }}_0=M^4/M_P^3,q=2p$ and (ii) $\mathrm{\Gamma }={\mathrm{\Gamma }}_0$, i.e., $q=0$, both with the initial condition $\varphi \left(0\right)=0$, i.e., $K=0$, have been considered by Sharif and Saleem (2015). For these cases, the condition $\varphi \left(t\right)>0$ requires $p<0$. In the first case, Equation (3.6) reduces to

$$\varphi =M_P\sqrt{-2p{M}_{P}t}$$

(4.7)

Note that the time has dimension inverse mass with the present units, so that $M_{P}t$ is dimensionless.

Visinelli, however, has considered polynomial models with $p>0$. Then, we have to change the initial condition. The corresponding solution of Equation (4.5) with $q=2p$ and the inflaton field equal to the Planck mass at the Planck time gives

$$\varphi =M_P\sqrt{1-2p{M}_P\left(t-t_P\right)}$$

(4.8)

It may be noted that $q=2\left(p-2\right)$ gives a different time evolution of the inflaton field. Then, Equation (3.5) with the boundary condition $\varphi \left(t_P\right)=M_P$ has the solution

$$\varphi =M_P\exp \left[-\frac{p{M}^4}{{\mathrm{\Gamma }}_0{M}_P^2}\left(t-t_P\right)\right]$$

(4.9)

In this case, the inflaton field decreases or increases exponentially, depending upon the sign of $p$.

Inserting Equations (4.1) and (4.2) into Equations (3.9) and (3.13), the slow-roll parameters are

$$\epsilon =\frac{p^2}{2}{\left(\frac{M_P}{\varphi }\right)}^2,\eta =\frac{2\left(p-1\right)}{p}\epsilon ,\beta =\frac{q}{p}\epsilon$$

(4.10)

With these expressions Equation (3.32) valid in the regime of strong dissipation, $Q>>1$, gives

$${\delta }_{ns}=\frac{3\left(4+3q-p\right)}{4p}\frac{\epsilon }{Q}$$

(4.11)

The slow-roll regime ends when at least one of the parameters (4.10) is not much smaller than $1+Q$. In the strong dissipative regime $Q>>1$ and ${\epsilon }_f=Q_f$. Using Equations (4.3) and (4.10) we then get

$${\varphi }_f=M_P{\left(\frac{p^2}{2Q_0}\right)}^{\frac{2}{4+q-p}}$$

(4.12)

The number of e-folds, N, in the slow roll era for this model has been calculated by Visinelli [48] . It is defined by

$$N=\ln \frac{a_f}{a}={\displaystyle \underset{t}{\overset{t_f}{\int }}Hdt={\displaystyle \underset{\varphi }{\overset{{\varphi }_f}{\int }}\frac{H}{\dot{\varphi }}d\varphi }}$$

(4.13)

Using Equations (3.3) and (3.5) we get

$$N=\frac{1}{M_P^2}{\displaystyle \underset{{\varphi }_f}{\overset{\varphi }{\int }}\left(1+Q\right)\frac{V}{V^{\prime }}d\varphi }$$

(4.14)

Inserting the potential (4.1), performing the integration and considering the strong dissipative regime gives

$$N\approx \frac{2Q_0}{p\left(4+q-p\right)}\left[{\left(\frac{\varphi }{M_P}\right)}^{\frac{4+q-p}{2}}-{\left(\frac{{\varphi }_f}{M_P}\right)}^{\frac{4+q-p}{2}}\right]$$

(4.15)

The time dependence of the inflaton field is given by Equation (4.6) when $p<0$ showing that ${\varphi }_f>\varphi$ in this case, and by Equation (4.8) when $p>0$ implying ${\varphi }_f<\varphi$ in that case, showing that $N>0$ in both cases (not dot here)

$$\frac{\varphi }{M_P}\approx {\left(\frac{p\left(4+q-p\right)N}{2Q_0}\right)}^{\frac{2}{4+q-p}}$$

(4.16)

Inserting this into the first of Equations (4.10) and (4.3) gives

$$\epsilon \approx \frac{p^2}{2}{\left[\frac{2Q_0}{p\left(4+q-p\right)N}\right]}^{\frac{4}{4+q-p}},Q\approx Q_0{\left[\frac{p\left(4+q-p\right)N}{2Q_0}\right]}^{\frac{q-p}{4+q-p}}$$

(4.17)

Inserting these expressions into Equation (4.11) gives

$${\delta }_{ns}\approx \frac{3\left(4+3q-p\right)}{4\left(4+q-p\right)}\frac{1}{N}$$

(4.18)

Note that with $q=0$, i.e., a constant value of the dissipation parameter $\mathrm{\Gamma }$, Equation (4.18) reduces to

$${\delta }_{ns}=\frac{3}{4N}$$

(4.19)

for all values of p. Then $N=60$ gives ${\delta }_{ns}=0.012$ which is smaller than the preferred value from the Planck data, ${\delta }_{ns}=0.032$. Inserting $q=2p$ in Equation (4.18) and solving the equation with respect to p gives,

$$p=\frac{4\left(4N{\delta }_{ns}-3\right)}{15-4N{\delta }_{ns}}$$

(4.20)

The Planck values ${\delta }_{ns}=0.032,N=60$ give $p=2.56$ and $q=5.11$.

Panotopoulos and Videla [24] have investigated the tensor-to-scalar ratio in warm in inflation for inflationary models with an inflaton field given by the potential

$$V={\left(M/M_P\right)}^4{\varphi }^4$$

(4.21)

where M is the energy scale of the potential when the inflaton field has Planck mass, $M_P$. Let us choose $p=q=4$ in the monomial models above. Inserting this in Equation (3.18) gives ${\delta }_{ns}=9/4N$. With ${\delta }_{ns}=0.032$ we get $N=70$.

In this case ${\delta }_{ns}=2/N$ for cold inflation. For ${\delta }_{ns}=0.032$ this corresponds to $N\approx 62$ which is an acceptable number of e-folds. Then, the tensor-to-scalar ratio is $r=0.32$, which is much larger than allowed by the Planck observations [45]. Panotopoulos and Videla found the corresponding ${\delta }_{ns},r-$ relation in warm inflation with $\mathrm{\Gamma }=aT$, where a is a dimensionless parameter. They considered two cases.

(A) The weak dissipative regime. In this case $Q<<1$ and Equation (3.7) reduces to $r_W=\left(H/T\right)r$. They then found

$$r_W\approx \frac{0.01}{\sqrt{a}}{\delta }_{ns}$$

(4.22)

With the Planck values ${\delta }_{ns}=0.032$ and $r_W<0.12$ this requires $a>7·{10}^{-6}$. However, they also found that in this case ${\delta }_{ns}=1/N$ giving $N=31$ which is too small to be compatible with the standard inflationary scenario.

(B) The strong dissipative regime. Then, $R>>1$ and $r_W\approx \left(H/T{R}^{5/2}\right)r$. They then found

$${\delta }_{ns}=\frac{45}{28N},r_W=\frac{3.8·{10}^{-7}}{a^4}{\delta }_{ns}$$

(4.23)

Then $N=50$ and $a>1.8·{10}^{-2}$, so this is a promising model.

5. Warm Natural Inflation

Visinelli [47] has also investigated warm natural inflation with the potential

$$V\left(\varphi \right)=V_0\left(1+\cos \tilde{\varphi }\right)=2V_0{\cos }^2\left(\tilde{\varphi }/2\right)$$

(5.1)

where $\tilde{\varphi }=\varphi /M$, and M is the spontaneous symmetry breaking scale, and $M>M_P$ in order for inflation to occur. The constant $V_0$ is a characteristic energy scale for the model. The potential $V$ has a minimum at $\tilde{\varphi }=\pi$. Inserting the potential (5.1) into the expressions (3.9) we get

$$\epsilon =\frac{b}{2}\frac{1-\cos {\tilde{\varphi }}_i}{1+\cos {\tilde{\varphi }}_i},\eta =\epsilon -\frac{b}{2},b={\left(\frac{M_P}{M}\right)}^2$$

(5.2)

From Equation (3.3) with the potential (5.1) we have

$$H=\sqrt{\left(\kappa /3\right)V_0\left(1+\cos \tilde{\varphi }\right)}$$

(5.3)

Equations (3.4) and (5.3) then give

$$Q=\frac{\mathrm{\Gamma }{M}_P}{\sqrt{3V_0\left(1+\cos \tilde{\varphi }\right)}}$$

(5.4)

During the slow roll era we must have $\epsilon <<R$. Using the expressions (5.2) and (5.4) we find that this corresponds to

$$\frac{1-\cos \tilde{\varphi }}{\sqrt{1+\cos \tilde{\varphi }}}<<1/\beta ,\beta =\frac{\sqrt{6V_0}}{\mathrm{\Gamma }{M}_P}b$$

(5.5)

Inserting Equations (5.2) and (5.4) into Equation (3.31) with $\beta =0$ gives in the strong dissipative regime

$${\delta }_{ns}=\frac{3}{4\alpha }\frac{3+\cos {\tilde{\varphi }}_i}{\sqrt{1+\cos {\tilde{\varphi }}_i}}$$

(5.6)

We shall now express the ${\delta }_{ns}$ in terms of the number of e-folds of expansion during the slow roll era for this inflationary universe model, again following Visinelli. Assuming that the dissipation parameter $\mathrm{\Gamma }$ is independent of $\varphi$, i.e., that $\beta =0$, the number of e-folds is given by

$$N=-\mathrm{\Gamma }{\displaystyle \underset{{\varphi }_i}{\overset{{\varphi }_f}{\int }}\frac{H\left(\varphi \right)}{V^{\prime }\left(\varphi \right)}d}\varphi$$

(5.7)

Differentiating the potential (5.1) and inserting Equation (5.3) we get

$$N=\frac{\alpha }{2}{\displaystyle \underset{{\tilde{\varphi }}_i}{\overset{{\tilde{\varphi }}_f}{\int }}\frac{\sqrt{1+\cos x}}{\sin x}dx=\frac{\alpha }{\sqrt{2}}\ln \frac{\tan \left({\tilde{\varphi }}_f/4\right)}{\tan \left({\tilde{\varphi }}_i/4\right)}}$$

(5.8)

Hence,

$$\tan \frac{{\tilde{\varphi }}_i}{4}=\tan \frac{{\tilde{\varphi }}_f}{4}exp\left(-\frac{\beta N}{2}\right)$$

(5.9)

Visinelli has argued that

$${\tilde{\varphi }}_f=\pi -\beta$$

(5.10)

giving

$$\tan \frac{{\tilde{\varphi }}_f}{4}=\frac{1-\tan \left(\beta /4\right)}{1+\tan \left(\beta /4\right)}$$

(5.11)

Inserting this into Equation (5.9) gives

$$\tan \frac{{\tilde{\varphi }}_i}{4}=\gamma exp\left(-\frac{\beta N}{2}\right),\gamma =\frac{1-\tan \left(\beta /4\right)}{1+\tan \left(\beta /4\right)}$$

(5.12)

Applying the trigonometric identity

$$\sqrt{1+\cos \theta }=\sqrt{2}\frac{1-{\tan }^2\left(\theta /4\right)}{1+{\tan }^2\left(\theta /4\right)}$$

(5.13)

in the expression (5.12) and inserting the result into Equation (5.6) we finally arrive at

$${\delta }_{ns}=\frac{3}{8}\beta \frac{exp\left(2\beta N\right)+{\gamma }^4}{exp\left(2\beta N\right)-{\gamma }^4}$$

(5.14)

Here, we must have $\beta <<1$ in order to give the Planck value ${\delta }_{ns}=0.032$ for $N=60$. Hence, Equation (5.12) gives $\gamma \approx 1$. A good approximation for ${\delta }_{ns}$ is therefore

$${\delta }_{ns}\approx \left(3/8\right)\beta \coth \left(\beta N\right)$$

(5.15)

Inserting ${\delta }_{ns}=0.032$ and $N=60$ gives $\beta =0.08$.

Visinelli (2011) further found that the tensor-to-scalar ratio for this inflationary model is

$$r=128\kappa \sqrt{\frac{\pi }{\mathrm{\Gamma }}}\frac{{\dot{\varphi }}^2}{T\sqrt{H}}$$

(5.16)

Differentiating the expression (5.3) gives

$$\dot{H}=-\frac{\kappa V_0}{6M}\frac{s_{\varphi }\dot{\varphi }}{H},s_{\varphi }\equiv \sin \tilde{\varphi }$$

(5.17)

Combining this with Equation (3.8) in the strong dissipative regime and using Equation (3.4) gives

$$\dot{\varphi }=\frac{3V_0{s}_{\varphi }}{M\mathrm{\Gamma }}$$

(5.18)

The energy density of the radiation is

$${\rho }_{\gamma }=a{T}^4$$

(5.19)

where a = 7.5657 × 10⁻¹⁶ J·m⁻³·K⁻⁴ = 4.69 × 10⁻⁶ GeV·m⁻³·K⁻⁴ is the radiation constant. Combining with Equation (3.6) we get

$$T={\left(\frac{\mathrm{\Gamma }}{4aH}\right)}^{1/4}{\dot{\varphi }}^{1/2}$$

(5.20)

Equations (5.15), (5.18) and (5.19) give

$$r=B\frac{s_{\varphi }^{3/2}}{{\left(1+\cos \tilde{\varphi }\right)}^{1/8}},B=\frac{384·3^{5/8}{\kappa }^{7/8}\sqrt{6\pi }{V}^{11/8}{a}^{1/4}}{M^{3/2}{\mathrm{\Gamma }}^{9/4}}$$

(5.21)

Visinelli [47] has evaluated the constant B and concluded that for this type of inflationary universe model the expected value of r is extremely low. If observations give a value $r>{10}^{-14}$ this model has to be abandoned. On the other hand, the predictions of this model are in accordance with the observations so far.

6. Warm Viscous Inflation

As noted by del Campo, Herrera and Pavón [29], it has been usual, for the sake of simplicity, to study warm inflation models containing an inflaton field and radiation, only, (comma here) ignoring the existence of particles with mass that will appear due to the decay of the inflaton field. However, these particles modify the fluid pressure in two ways: (i) The relationship between pressure and energy density is no longer $p=\left(1/3\right)\rho$ as it is for radiation. A simple generalization is to use the equation of state $p=w\rho$, where w is a constant with value $0\le w\le 1$; (ii) Due to interactions between the particles and the radiation there will appear a bulk viscosity so that the effective pressure takes the form

$$p_{eff}=p-3\varsigma H$$

(6.1)

where $\varsigma$ is a coefficient of bulk viscosity.

We shall now consider isotropic universe models corresponding to the anisotropic models considered by Sharif and Saleem [37]. Equation (3.8) can be written

$$\dot{\varphi }=\pm M_P\sqrt{-2\dot{H}/\left(1+Q\right)}$$

(6.2)

For these models, the time dependence of the scale factor during the inflationary era may be written

$$a\left(t\right)=a_0\exp {\left(\frac{t}{t_1}\right)}^{\beta },0<\beta \le 1,$$

(6.3)

where $a_0$ is the value of the scale factor at $t=0$ before the slow roll era has started, and $t_1$ is the Hubble time of the corresponding De Sitter model having $\beta =1$. The Hubble parameter and its rate of change with time is

$$H=\frac{\beta }{t_1}{\left(\frac{t}{t_1}\right)}^{\beta -1},\dot{H}=\frac{\beta \left(\beta -1\right)}{t_1^2}{\left(\frac{t}{t_1}\right)}^{\beta -2}$$

(6.4)

Note that $\dot{H}<0$ for $\beta <1$. Inserting the second expression into Equation (6.2) gives

$$\dot{\varphi }=\pm \frac{M_P}{t_1}\sqrt{\frac{2\beta \left(1-\beta \right)}{1+Q}}{\left(\frac{t}{t_1}\right)}^{\frac{\beta }{2}-1}$$

(6.5)

Sharif and Saleem considered two cases. In the first one $\mathrm{\Gamma }=\mathrm{\Gamma }\left(\varphi \right)=\kappa V\left(\varphi \right)/M_P$. Equations (3.3) and (3.4) then gives $Q=H/M_P$. Furthermore, for several reasons, they restricted their analysis to the strong dissipative regime where $Q>>1$. Equation (6.5) then reduces to

$$\dot{\varphi }=\pm M_P\sqrt{2M_P\left(1-\beta \right)}{t}^{-1/2}$$

(6.6)

Integrating with the initial condition $\varphi \left(0\right)=0$ and assuming that $\varphi \left(t\right)>0$ we get

$$\varphi \left(t\right)=2M_P\sqrt{2M_P\left(1-\beta \right)t}$$

(6.7)

Hence, $\varphi$ is an increasing function of time. Inserting the first of the expressions (6.4) into the first of the Equation (3.3) gives

$$V\left(t\right)=3{\left(\frac{\beta M_P}{t_1}\right)}^2{\left(\frac{t}{t_1}\right)}^{2\left(\beta -1\right)}$$

(6.8)

Combining this with Equation (6.7) leads to

$$V\left(\varphi \right)=3{\left(\frac{\beta M_P}{t_1}\right)}^2{\left(\frac{\varphi }{2M_P\sqrt{2\left(1-\beta \right)M_P{t}_1}}\right)}^{4\left(\beta -1\right)}$$

(6.9)

Sharif and Saleem used the Hubble slow roll parameters,

$${\epsilon }_H\equiv -\frac{\dot{H}}{H^2}=\frac{1}{2\left(1+Q\right)}{\left(\frac{V^{\prime }}{V}\right)}^2,{\eta }_H\equiv -\frac{\ddot{H}}{2H\dot{H}}=\frac{1}{1+Q}\left[\frac{V^{″}}{V}-\frac{1}{2}{\left(\frac{V^{\prime }}{V}\right)}^2\right]$$

(6.10)

Note that ${\epsilon }_H=1+q$, where q is the deceleration parameter. In the present case and in the strong dissipative regime, we can replace $1+Q$ by $H=\sqrt{\kappa V/3}$. Then ${\epsilon }_H=\left(1/Q\right)\epsilon$ and ${\eta }_H=\left(1/Q\right)\left(\eta -\epsilon \right)$. Differentiating the expression (6.9) then gives

$${\epsilon }_H=\frac{1-\beta }{\beta }{\left(\frac{\varphi }{2M_P\sqrt{2\left(1-\beta \right)M_P{t}_1}}\right)}^{-2\beta },{\eta }_H=\frac{3-2\beta }{2\beta }{\left(\frac{\varphi }{2M_P\sqrt{2\left(1-\beta \right)M_P{t}_1}}\right)}^{-2\beta }=\frac{3-2\beta }{2\left(1-\beta \right)}{\epsilon }_H$$

(6.11)

The slow roll era ends when the inflaton field has a value ${\varphi }_f$ so that ${\epsilon }_H\left({\varphi }_f\right)=1$, corresponding to $\epsilon \left({\varphi }_f\right)=Q$, which gives

$${\left(\frac{{\varphi }_f}{2M_P\sqrt{2\left(1-\beta \right)M_P{t}_1}}\right)}^{2\beta }=\frac{1-\beta }{\beta }$$

(6.12)

The number of e-folds is given by Equation (4.15), which in the present case takes the form

$$N=\frac{1}{\sqrt{3}{M}_P}{\displaystyle \underset{{\varphi }_f}{\overset{\varphi }{\int }}\frac{V^{3/2}}{V^{\prime }}d\varphi }$$

(6.13)

Inserting the potential (6.9) and integrating gives

$$N={\left(\frac{{\varphi }_f}{2M_P\sqrt{2\left(1-\beta \right)M_P{t}_1}}\right)}^{2\beta }-{\left(\frac{\varphi }{2M_P\sqrt{2\left(1-\beta \right)M_P{t}_1}}\right)}^{2\beta }=\frac{1-\beta }{\beta }-{\left(\frac{\varphi }{2M_P\sqrt{2\left(1-\beta \right)M_P{t}_1}}\right)}^{2\beta }$$

(6.14)

Hence

$${\left(\frac{\varphi }{2M_P\sqrt{2\left(1-\beta \right)M_P{t}_1}}\right)}^{2\beta }=\frac{1-\beta }{\beta }-N$$

(6.15)

Since the left hand side is positive, this requires that $N<\left(1-\beta \right)/\beta$ or $\beta <1/\left(N+1\right)$. For $N>50$ this means that $0<\beta <0.02$.

Sharif and Saleem have calculated the scalar spectral index with the result

$${\delta }_{ns}=\frac{3\beta -2}{\beta }{\left(\frac{\varphi }{2M_P\sqrt{2\left(1-\beta \right)M_P{t}_1}}\right)}^{-2\beta }$$

(6.16)

Using Equation (6.15) we get

$${\delta }_{ns}=\frac{3\beta -2}{1-\beta -\beta N}\approx \frac{2-3\beta }{\beta }\frac{1}{N}$$

(6.17)

This equation can be written

$$\beta \approx \frac{2}{3+N{\delta }_{ns}}$$

(6.18)

Inserting the Planck value ${\delta }_{ns}=0.032$ and $N=60$, give $\beta =0.41$ corresponding to $p=-2.36$. This value of $\beta$ is not allowed by Equation (6.15).

In the second case, Sharif and Saleem assumed that $\mathrm{\Gamma }={\mathrm{\Gamma }}_0$. Equations (3.3) and (3.4) then give $Q={\mathrm{\Gamma }}_0/3H$. Using Equations (6.2) and (6.4) and integrating with the initial condition $\varphi \left(0\right)=0$, leads to

$$\varphi \left(t\right)=\lambda {\left(\frac{t}{t_1}\right)}^{\beta -1/2},V\left(\varphi \right)=3{\left(\frac{\beta M_P}{t_1}\right)}^2{\left(\frac{\varphi }{\lambda }\right)}^{\frac{4\left(1-\beta \right)}{2\beta -1}},\lambda =\frac{2\beta M_P}{2\beta -1}\sqrt{\frac{6\left(1-\beta \right)}{t_1{\mathrm{\Gamma }}_0}}$$

(6.19)

In this case ${\epsilon }_H$ and ${\eta }_H$ becomes

$${\epsilon }_H=\frac{1-\beta }{\beta }{\left(\frac{\varphi }{\lambda }\right)}^{-\frac{2\beta }{2\beta -1}},{\eta }_H=\frac{2-\beta }{\beta }{\left(\frac{\varphi }{\lambda }\right)}^{-\frac{2\beta }{2\beta -1}}=\frac{2-\beta }{1-\beta }{\epsilon }_H$$

(6.20)

The final value of ${\varphi }_f$ is given by

$${\left(\frac{{\varphi }_f}{\lambda }\right)}^{\frac{2\beta }{2\beta -1}}=\frac{1-\beta }{\beta }$$

(6.21)

The number of e-folds is

$$N={\left(\frac{\varphi }{\lambda }\right)}^{\frac{2\beta }{2\beta -1}}-{\left(\frac{{\varphi }_f}{\lambda }\right)}^{\frac{2\beta }{2\beta -1}}={\left(\frac{\varphi }{\lambda }\right)}^{2\beta }-\frac{1-\beta }{\beta }$$

(6.22)

Hence

$${\left(\frac{\varphi }{\lambda }\right)}^{\frac{2\beta }{2\beta -1}}=N+\frac{1-\beta }{\beta }$$

(6.23)

The scalar spectral index is

$${\delta }_{ns}=\frac{4+\beta }{2\beta }{\left(\frac{\varphi }{\lambda }\right)}^{-\frac{2\beta }{2\beta -1}}=\frac{4+\beta }{2\left(\beta N+1-\beta \right)}\approx \frac{4+\beta }{2\beta }\frac{1}{N}$$

(6.24)

which can be written

$$\beta =\frac{4}{2N{\delta }_{ns}-1}$$

(6.25)

Inserting the Planck value ${\delta }_{ns}=0.032$ and $N=60$ gives $\beta =1.4$ outside the range $\beta <1$ which requires $N>78$. However, in the anisotropic case considered by Sharif and Saleem, one may obtain agreement with the Planck data for $\beta <1$. As noted above, the tensor to scalar ratio has a very small value in these models. The time evolution of the inflaton field is given by Equation (6.7).

7. Comparison of Models

The models of Sharif and Saleem are a class of the monomial models. Comparing Equations (4.1) and (6.9) we have $p=4\left(\beta -1\right)$ or $\beta =1+p/4$. Hence, for $\beta <1$ we must have $p<0$ while Visinelli considered models with $p>0$. Furthermore, in the first case of Sharif and Saleem with $\mathrm{\Gamma }=V$ we have $q=2p$ and in the case with $\mathrm{\Gamma }={\mathrm{\Gamma }}_0$ we have $q=0$. Also, it should be noted that Visinelly has deduced the expression for the spectral parameters from the potential slow roll parameters, while Sharif and Saleem have used the Hubble slow roll parameters, and they have got slightly different expressions.

Let us consider an isotropic monomial model with scale as given in Equation (6.3). Then, we have two formulae for the potential—Equations (4.1) and (6.9). Hence

$$t_1={\left(\sqrt{3}\beta \right)}^{\frac{1}{\beta }}{\left[8\left(1-\beta \right)\right]}^{\frac{1-\beta }{\beta }}{\left(\frac{M_P}{M}\right)}^{2/\beta }{t}_P$$

(7.1)

where $t_P=1/M_P$ is the Planck time. As mentioned above in Sharif and Saleem’s first case $\mathrm{\Gamma }=\mathrm{\Gamma }\left(\varphi \right)=\kappa V\left(\varphi \right)/M_P$. Combining this with the first Equation (3.3) we get $\mathrm{\Gamma }=3H^2/M_P$. Furthermore they considered the strong dissipative regime with $\mathrm{\Gamma }>>3H$. Hence $H>>M_P$. The slow roll era begins at a point of time, $t_i$, when the inflaton field is given by Equation (6.23). This leads to

$$t_i={\left(N+\frac{1-\beta }{\beta }\right)}^{1/\beta }{t}_1$$

(7.2)

The Hubble parameter is given by the first equation in (6.4) with a maximal value at the beginning of the inflationary era. Hence, the condition $H>>M_P$ requires that

$$t_i={\left(\frac{\beta }{M_P{t}_1}\right)}^{\frac{1}{1-\beta }}{t}_1$$

(7.3)

Inserting the expression (7.2) for $t_1$ we arrive at

$$t_i<<\left(\beta N+1-\beta \right)t_P$$

(7.4)

Hence in this model with for example $\beta =1/2$ and $N=60$ the inflationary era begins much earlier than at around 30 Planck times. Inserting the inequality (7.4) into Equation (7.1) we get

$$M>>\sqrt{\sqrt{3}{\left[8\left(1-\beta \right)\right]}^{1-\beta }\left(\beta N+1-\beta \right)}{M}_P$$

(7.5)

Hence $M>>M_P$, so these models are large field inflation models.

V. Kamali and M. R. Setare [49] have considered warm viscous inflation models in the context of brane cosmology using the so-called chaotic potential (3.1) with $p=2$, i.e., $\beta =3/2$. We have considered the corresponding models in ordinary (not brane) spacetime which corresponds to taking the limit that the brane tension $\lambda \to \infty$ in their equations. They first considered the case $\mathrm{\Gamma }={\mathrm{\Gamma }}_0$, i.e., $q=0$. Then, the time evolution of the inflaton field is given by Equation (4.9) with $p=2$. As noted above, in this case ${\delta }_{ns}=0.012$ which is smaller than the preferred value from the Planck data. It may be noted that Kamali and M. R. Setare got a different result. Letting $\lambda \to \infty$ in their Equation (68) gives ${\delta }_{ns}=0$, i.e., a scale invariant spectrum.

Next, they considered the case $\mathrm{\Gamma }=\mathrm{\Gamma }\left(\varphi \right)=\alpha V\left(\varphi \right)$. With $\alpha =1$ this corresponds to the first case considered by Sharif and Saleem [37].

8. Conclusions

Warm inflation is a promising model of inflation, taking account of dissipative processes that are neglected in the usual, cold inflationary models. In warm inflation, radiation is produced by dissipation of the inflaton field, and reheating is not necessary. This type of inflationary model was introduced and developed initially by Berera and coworkers. Also, interactions between the inflaton field and the radiation provide a mechanism for producing viscosity.

In this article, I have given a review of some recent models with particular emphasis on their predictions of optical parameters, making it possible to evaluate the models against the observational data obtained by the Planck team. In particular, power law potential inflation, PI, and natural inflation, NI, in the warm inflation scenario have been considered.

I have emphasized that there are some interesting differences between the predictions of these models and the corresponding cold inflation models. The first thing to be noted is that the warm inflation models in general predict a vanishingly small value of the tensor-to-scalar ratio, r. I the present paper I have parametrized the scalar spectral index $n_s$ by ${\delta }_{ns}=1-n_s$. The Planck data favor the value ${\delta }_{ns}=0.032$, $r<0.11$ and a number of e-folds $N=60$.

Cold PI with the potential (4.1) predicts ${\delta }_{ns}=\frac{2\left(p+2\right)}{p+4N}$ and $r=\frac{16p}{p+4N}$. Inserting ${\delta }_{ns}=0.032$ and $N=60$ gives $p=1.8$ and $r=0.12$. The corresponding warm PI model with constant value of the dissipation parameter $\mathrm{\Gamma }$ predicts, according to Equation (6.24), ${\delta }_{ns}=\frac{20+p}{4+p}\frac{1}{2N}$ giving $p=2.8$. The corresponding model with $\mathrm{\Gamma }=\mathrm{\Gamma }\left(\varphi \right)=V\left(\varphi \right)$ predicts ${\delta }_{ns}=-\frac{4+3p}{4+p}\frac{1}{N}$ giving $p=-2.36$. However, according to Equation (6.15), this model is only consistent for $-4<p<-3.92$. Hence, this model is in conflict with the Planck data.

Cold natural inflation predicts

$${\delta }_{ns}=b\frac{\left(2+b\right)e^{bN}+b}{\left(2+b\right)e^{bN}-b},r=\frac{8b^2}{\left(2+b\right)e^{bN}-b},b={\left(\frac{M_P}{M}\right)}^2$$

(8.1)

Inserting ${\delta }_{ns}=0.032$ and $N=60$ gives $b=0.032$ or $M=5.5M_P$, giving $r=0.0006$. Since $M>M_P$ this is large field inflation according to the standard definition of this classification (Lyth [50], Dine and Pack [51]). The corresponding warm natural inflation model has two parameters, $\mathrm{\Gamma }$ and $V_0$, contained in $\beta$ in the expression for ${\delta }_{ns}$. Hence, some assumption concerning the relationship between $\mathrm{\Gamma }$ and $V_0$, is needed to make a prediction of the value of ${\delta }_{ns}$ in this model.