The Impact of Stellar Initial Mass Function on the Epoch of Reionization: Insights from Semi-Analytic Galaxy Modeling
Abstract
1. Introduction
2. Method
2.1. SAM Model
2.2. Dark Matter Simulations
2.3. Stellar Initial Mass Function
3. Result
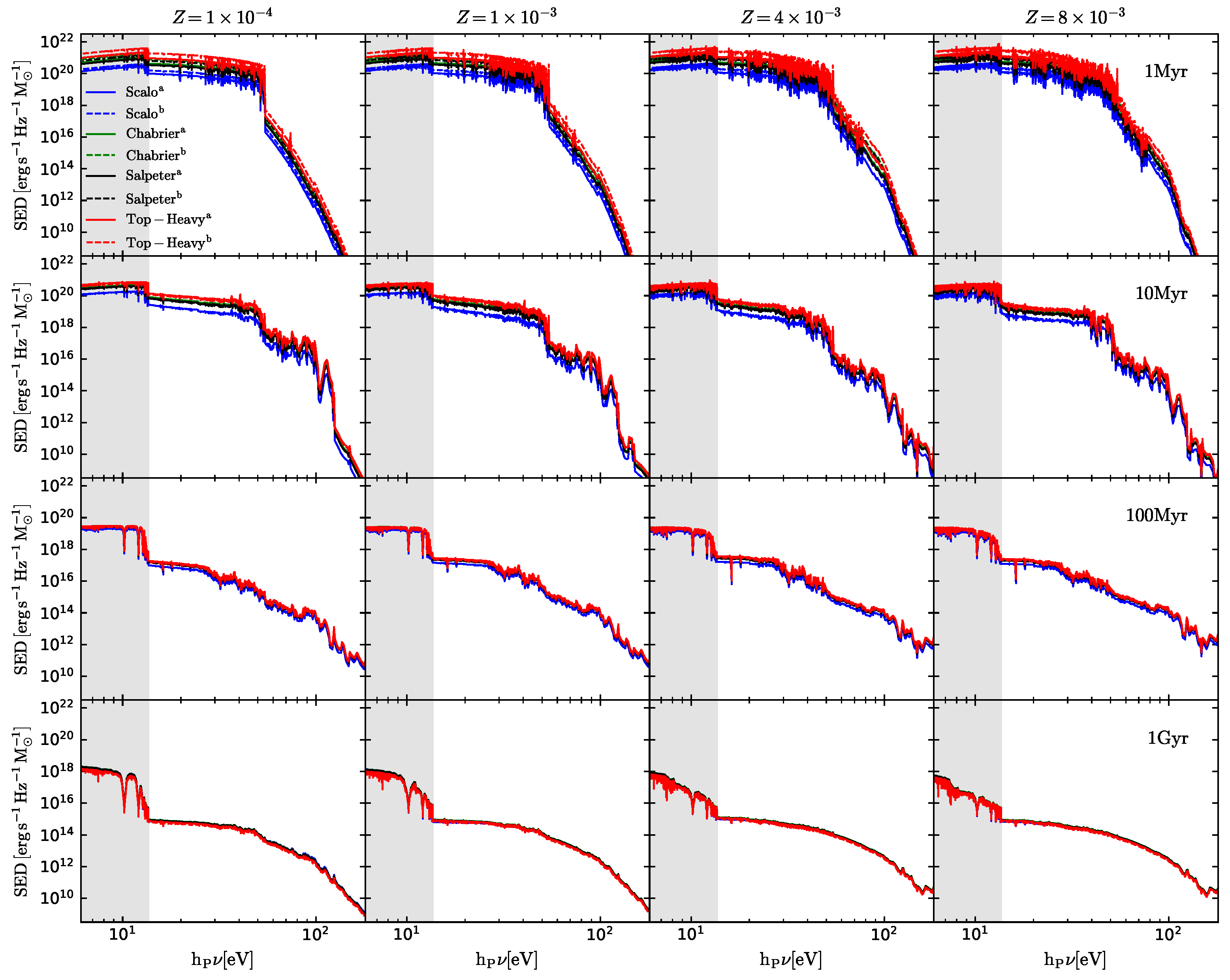
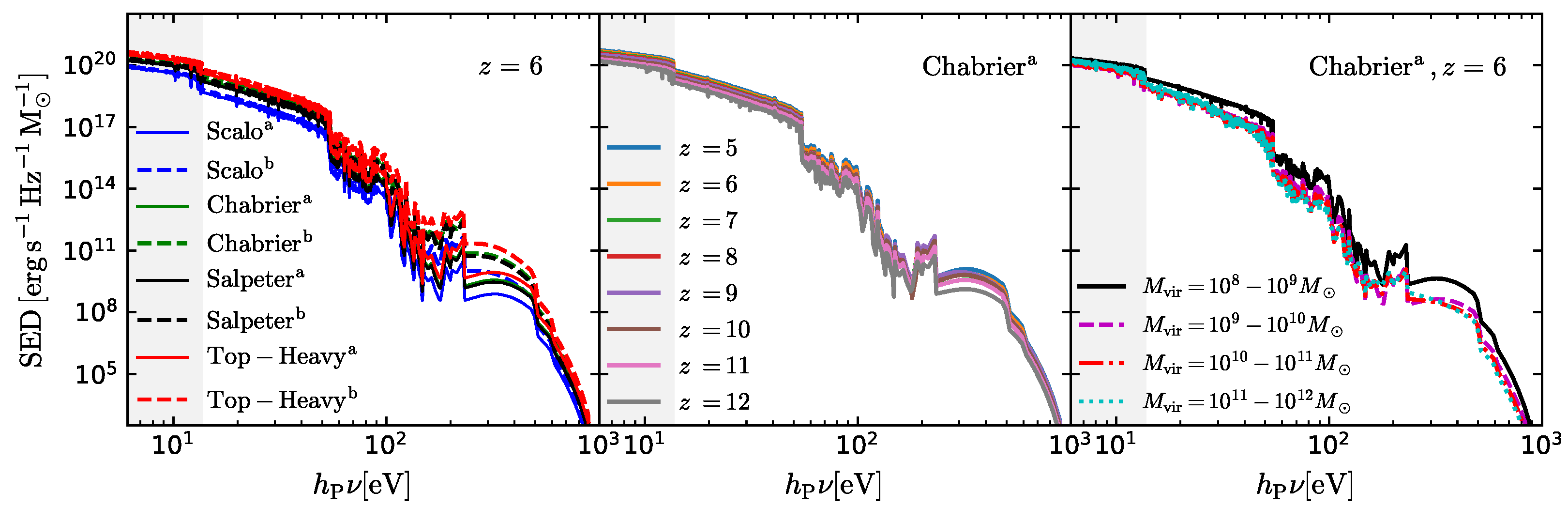
3.1. SED of High-z Galaxies
3.2. UVLF of the Galaxy
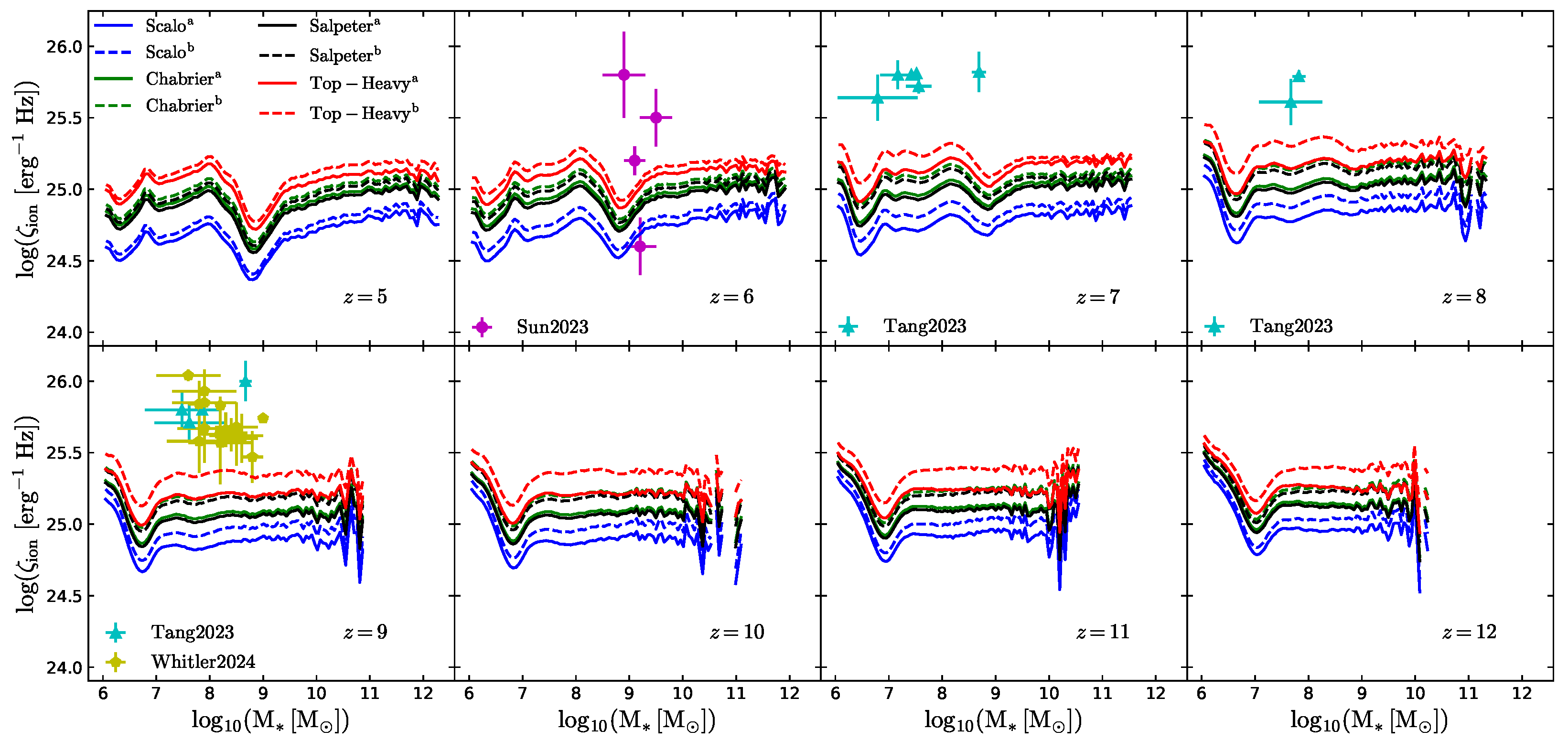
3.3. Budget of Ionizing Photons
4. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. SPS SED of 8 IMF Models from BPASS
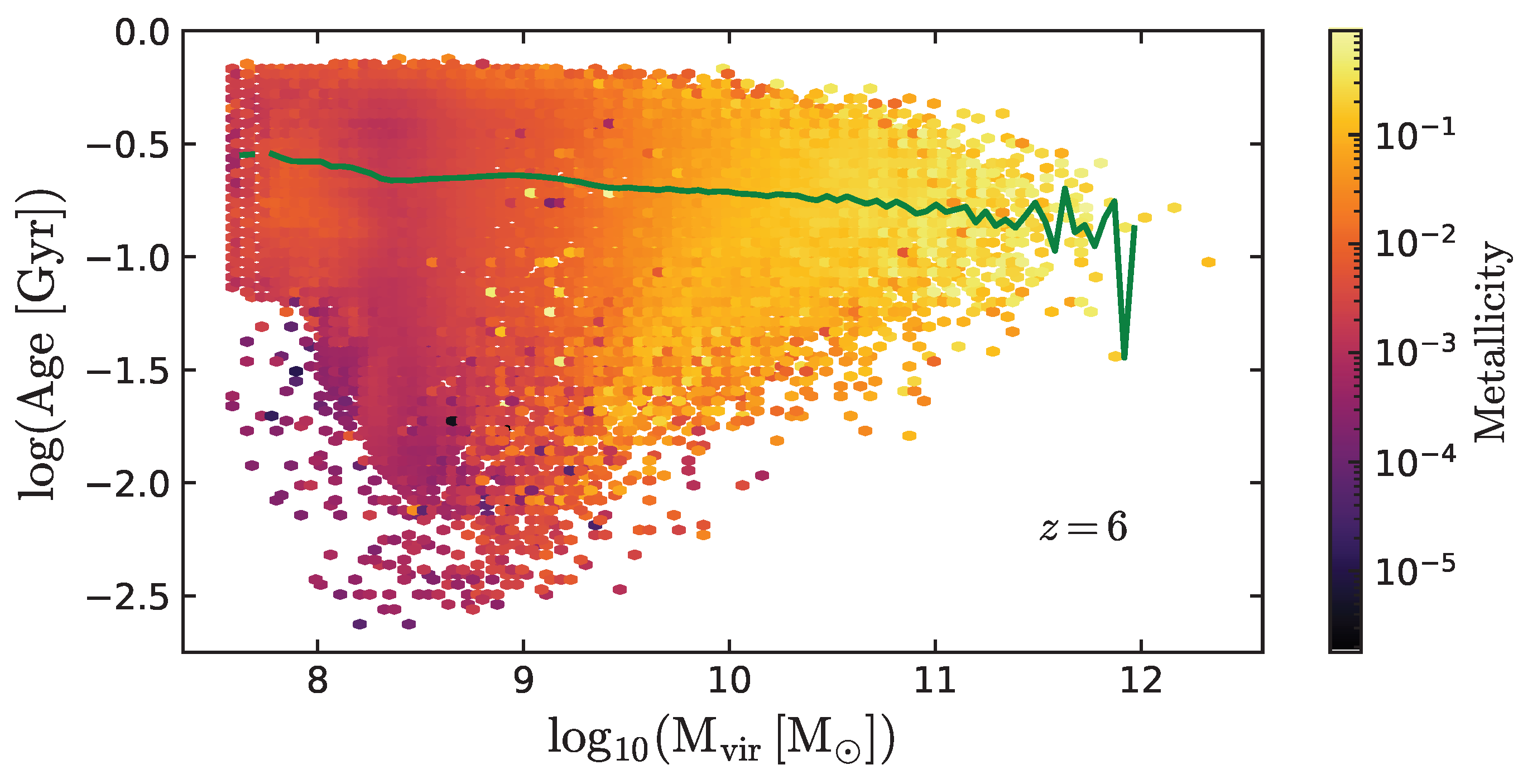
Appendix B. Mass Weighted Galaxy Age
References
- Hennawi, J.F.; Kist, T.; Davies, F.B.; Tamanas, J. Precisely Measuring the Cosmic Reionization History from IGM Damping Wings Towards Quasars. arXiv 2024, arXiv:2406.12070. [Google Scholar] [CrossRef]
- Bhagwat, A.; Costa, T.; Ciardi, B.; Pakmor, R.; Garaldi, E. SPICE: The connection between cosmic reionization and stellar feedback in the first galaxies. Mon. Not. R. Astron. Soc. 2024, 531, 3406–3430. [Google Scholar] [CrossRef]
- Fan, X.; Carilli, C.L.; Keating, B. Observational Constraints on Cosmic Reionization. Annu. Rev. Astron. Astrophys. 2006, 44, 415–462. [Google Scholar] [CrossRef]
- Yang, J.; Wang, F.; Fan, X.; Hennawi, J.F.; Davies, F.B.; Yue, M.; Eilers, A.C.; Farina, E.P.; Wu, X.B.; Bian, F.; et al. Measurements of the z ∼ 6 Intergalactic Medium Optical Depth and Transmission Spikes Using a New z > 6.3 Quasar Sample. Astrophys. J. 2020, 904, 26. [Google Scholar] [CrossRef]
- Bosman, S.E.I.; Davies, F.B.; Becker, G.D.; Keating, L.C.; Davies, R.L.; Zhu, Y.; Eilers, A.C.; D’Odorico, V.; Bian, F.; Bischetti, M.; et al. Hydrogen reionization ends by z = 5.3: Lyman-α optical depth measured by the XQR-30 sample. Mon. Not. R. Astron. Soc. 2022, 514, 55–76. [Google Scholar] [CrossRef]
- Lu, T.Y.; Goto, T.; Hashimoto, T.; Santos, D.J.D.; Wong, Y.H.V.; Kim, S.J.; Hsiao, T.Y.Y.; Kilerci, E.; Ho, S.C.C.; Nagao, T.; et al. Subaru High-z Exploration of Low-Luminosity Quasars (SHELLQs) - XV. Constraining the cosmic reionization at 5.5 < z < 7. Mon. Not. R. Astron. Soc. 2022, 517, 1264–1281. [Google Scholar] [CrossRef]
- Rinaldi, P.; Caputi, K.I.; Iani, E.; Costantin, L.; Gillman, S.; Perez Gonzalez, P.G.; Östlin, G.; Colina, L.; Greve, T.R.; Nørgard-Nielsen, H.U.; et al. MIDIS: Unveiling the Role of Strong Hα Emitters During the Epoch of Reionization with JWST. Astrophys. J. 2024, 969, 12. [Google Scholar] [CrossRef]
- Bromm, V.; Larson, R.B. The First Stars. Annu. Rev. Astron. Astrophys. 2004, 42, 79–118. [Google Scholar] [CrossRef]
- Alvarez, M.A.; Bromm, V.; Shapiro, P.R. The H II Region of the First Star. Astrophys. J. 2006, 639, 621–632. [Google Scholar] [CrossRef]
- Bouwens, R.J.; Illingworth, G.D.; Oesch, P.A.; Caruana, J.; Holwerda, B.; Smit, R.; Wilkins, S. Reionization After Planck: The Derived Growth of the Cosmic Ionizing Emissivity Now Matches the Growth of the Galaxy UV Luminosity Density. Astrophys. J. 2015, 811, 140. [Google Scholar] [CrossRef]
- Whitler, L.; Stark, D.P.; Endsley, R.; Chen, Z.; Mason, C.; Topping, M.W.; Charlot, S. Insight from JWST/Near Infrared Camera into galaxy overdensities around bright Lyman-alpha emitters during reionization: Implications for ionized bubbles at z 9. Mon. Not. R. Astron. Soc. 2024, 529, 855–872. [Google Scholar] [CrossRef]
- Chen, N.; Motohara, K.; Spitler, L.; Nakajima, K.; Terao, Y. Toward Unveiling Cosmic Reionization: The Ionizing Photon Production Efficiency (ξion) of Low-mass Hα Emitters at z ∼ 2.3. Astrophys. J. 2024, 968, 32. [Google Scholar] [CrossRef]
- Meiksin, A. Constraints on the ionization sources of the high-redshift intergalactic medium. Mon. Not. R. Astron. Soc. 2005, 356, 596–606. [Google Scholar] [CrossRef]
- Bolton, J.S.; Haehnelt, M.G. The observed ionization rate of the intergalactic medium and the ionizing emissivity at z >= 5: Evidence for a photon-starved and extended epoch of reionization. Mon. Not. R. Astron. Soc. 2007, 382, 325–341. [Google Scholar] [CrossRef]
- Srbinovsky, J.A.; Wyithe, J.S.B. Constraining the quasar contribution to the reionization of cosmic hydrogen. Mon. Not. R. Astron. Soc. 2007, 374, 627–633. [Google Scholar] [CrossRef]
- Jiang, L.; Ning, Y.; Fan, X.; Ho, L.C.; Luo, B.; Wang, F.; Wu, J.; Wu, X.B.; Yang, J.; Zheng, Z.Y. Definitive upper bound on the negligible contribution of quasars to cosmic reionization. Nat. Astron. 2022, 6, 850–856. [Google Scholar] [CrossRef]
- Dayal, P.; Volonteri, M.; Choudhury, T.R.; Schneider, R.; Trebitsch, M.; Gnedin, N.Y.; Atek, H.; Hirschmann, M.; Reines, A. Reionization with galaxies and active galactic nuclei. Mon. Not. R. Astron. Soc. 2020, 495, 3065–3078. [Google Scholar] [CrossRef]
- Yung, L.Y.A.; Somerville, R.S.; Finkelstein, S.L.; Hirschmann, M.; Davé, R.; Popping, G.; Gardner, J.P.; Venkatesan, A. Semi-analytic forecasts for JWST–V. AGN luminosity functions and helium reionization at z = 2–7. Mon. Not. R. Astron. Soc. 2021, 508, 2706–2729. [Google Scholar] [CrossRef]
- Yeh, J.Y.C.; Smith, A.; Kannan, R.; Garaldi, E.; Vogelsberger, M.; Borrow, J.; Pakmor, R.; Springel, V.; Hernquist, L. The THESAN project: Ionizing escape fractions of reionization-era galaxies. Mon. Not. R. Astron. Soc. 2023, 520, 2757–2780. [Google Scholar] [CrossRef]
- Wilkins, S.M.; Feng, Y.; Di-Matteo, T.; Croft, R.; Stanway, E.R.; Bouwens, R.J.; Thomas, P. The Lyman-continuum photon production efficiency in the high-redshift Universe. Mon. Not. R. Astron. Soc. 2016, 458, L6–L9. [Google Scholar] [CrossRef]
- Conroy, C.; Gunn, J.E.; White, M. The Propagation of Uncertainties in Stellar Population Synthesis Modeling. I. The Relevance of Uncertain Aspects of Stellar Evolution and the Initial Mass Function to the Derived Physical Properties of Galaxies. Astrophys. J. 2009, 699, 486–506. [Google Scholar] [CrossRef]
- Bruzual, G.; Charlot, S. Stellar population synthesis at the resolution of 2003. Mon. Not. R. Astron. Soc. 2003, 344, 1000–1028. [Google Scholar] [CrossRef]
- Zhang, F.; Han, Z.; Li, L.; Hurley, J.R. Evolutionary population synthesis for binary stellar populations. Astron. Astrophys. 2004, 415, 117–122. [Google Scholar] [CrossRef]
- Zhang, F.; Han, Z.; Li, L.; Hurley, J.R. Inclusion of binaries in evolutionary population synthesis. Mon. Not. R. Astron. Soc. 2005, 357, 1088–1103. [Google Scholar] [CrossRef]
- Maraston, C. Evolutionary population synthesis: Models, analysis of the ingredients and application to high-z galaxies. Mon. Not. R. Astron. Soc. 2005, 362, 799–825. [Google Scholar] [CrossRef]
- Leitherer, C.; Schaerer, D.; Goldader, J.D.; Delgado, R.M.G.; Robert, C.; Kune, D.F.; de Mello, D.F.; Devost, D.; Heckman, T.M. Starburst99: Synthesis Models for Galaxies with Active Star Formation. Astrophys. J. Suppl. Ser. 1999, 123, 3–40. [Google Scholar] [CrossRef]
- Leitherer, C.; Ekström, S.; Meynet, G.; Schaerer, D.; Agienko, K.B.; Levesque, E.M. The Effects of Stellar Rotation. II. A Comprehensive Set of Starburst99 Models. Astrophys. J. Suppl. Ser. 2014, 212, 14. [Google Scholar] [CrossRef]
- Stanway, E.R.; Eldridge, J.J. Re-evaluating old stellar populations. Mon. Not. R. Astron. Soc. 2018, 479, 75–93. [Google Scholar] [CrossRef]
- Stanway, E.R.; Eldridge, J.J.; Becker, G.D. Stellar population effects on the inferred photon density at reionization. Mon. Not. R. Astron. Soc. 2016, 456, 485–499. [Google Scholar] [CrossRef]
- Woodrum, C.; Rieke, M.; Ji, Z.; Baker, W.M.; Bhatawdekar, R.; Bunker, A.J.; Charlot, S.; Curtis-Lake, E.; Eisenstein, D.J.; Hainline, K.; et al. JADES: Using NIRCam Photometry to Investigate the Dependence of Stellar Mass Inferences on the IMF in the Early Universe. arXiv 2023, arXiv:2310.18464. [Google Scholar] [CrossRef]
- Harvey, T.; Conselice, C.; Adams, N.J.; Austin, D.; Juodzbalis, I.; Trussler, J.; Li, Q.; Ormerod, K.; Ferreira, L.; Duan, Q.; et al. EPOCHS IV: SED Modelling Assumptions and their impact on the Stellar Mass Function at 6.5 <z <13.5 using PEARLS and public JWST observations. arXiv 2024, arXiv:2403.03908. [Google Scholar] [CrossRef]
- Liu, B.; Hartwig, T.; Sartorio, N.S.; Dvorkin, I.; Costa, G.; Santoliquido, F.; Fialkov, A.; Klessen, R.S.; Bromm, V. Gravitational waves from mergers of Population III binary black holes: Roles played by two evolution channels. Mon. Not. R. Astron. Soc. 2024, 534, 1634–1667. [Google Scholar] [CrossRef]
- Harikane, Y.; Inoue, A.K.; Ellis, R.S.; Ouchi, M.; Nakazato, Y.; Yoshida, N.; Ono, Y.; Sun, F.; Sato, R.A.; Ferrami, G.; et al. JWST, ALMA, and Keck Spectroscopic Constraints on the UV Luminosity Functions at z~7-14: Clumpiness and Compactness of the Brightest Galaxies in the Early Universe. arXiv 2024, arXiv:2406.18352. [Google Scholar] [CrossRef]
- Seeyave, L.T.C.; Wilkins, S.M.; Kuusisto, J.K.; Lovell, C.C.; Irodotou, D.; Simmonds, C.; Vijayan, A.P.; Thomas, P.A.; Roper, W.J.; Byrne, C.M.; et al. First light and reionization epoch simulations (FLARES) X III: The lyman-continuum emission of high-redshift galaxies. Mon. Not. R. Astron. Soc. 2023, 525, 2422–2440. [Google Scholar] [CrossRef]
- Lapi, A.; Gandolfi, G.; Boco, L.; Gabrielli, F.; Massardi, M.; Haridasu, B.S.; Baccigalupi, C.; Bressan, A.; Danese, L. Constraining the Initial Mass Function in the Epoch of Reionization from Astrophysical and Cosmological Data. Universe 2024, 10, 141. [Google Scholar] [CrossRef]
- Kroupa, P.; Gjergo, E.; Jerabkova, T.; Yan, Z. The initial mass function of stars. arXiv 2024, arXiv:2410.07311. [Google Scholar] [CrossRef]
- Cullen, F.; Carnall, A.C.; Scholte, D.; McLeod, D.J.; McLure, R.J.; Arellano-Córdova, K.Z.; Stanton, T.M.; Donnan, C.T.; Dunlop, J.S.; Shapley, A.E.; et al. The JWST EXCELS survey: An extremely metal-poor galaxy at z=8.271 hosting an unusual population of massive stars. arXiv 2025, arXiv:2501.11099. [Google Scholar] [CrossRef]
- Cai, Z.Y.; De Zotti, G.; Bonato, M. High-z Dusty Star-forming Galaxies: A Top-heavy Initial Mass Function? Astrophys. J. 2020, 891, 74. [Google Scholar] [CrossRef]
- Ziegler, J.J.; Edwards, T.D.P.; Suliga, A.M.; Tamborra, I.; Horiuchi, S.; Ando, S.; Freese, K. Non-universal stellar initial mass functions: Large uncertainties in star formation rates at z ≈ 2–4 and other astrophysical probes. Mon. Not. R. Astron. Soc. 2022, 517, 2471–2484. [Google Scholar] [CrossRef]
- Clauwens, B.; Schaye, J.; Franx, M. Implications of a variable IMF for the interpretation of observations of galaxy populations. Mon. Not. R. Astron. Soc. 2016, 462, 2832–2846. [Google Scholar] [CrossRef][Green Version]
- Mowla, L.; Iyer, K.; Asada, Y.; Desprez, G.; Tan, V.Y.Y.; Martis, N.; Sarrouh, G.; Strait, V.; Abraham, R.; Bradač, M.; et al. Formation of a low-mass galaxy from star clusters in a 600-million-year-old Universe. Nature 2024, 636, 332–336. [Google Scholar] [CrossRef] [PubMed]
- Bouwens, R.J.; Oesch, P.A.; Stefanon, M.; Illingworth, G.; Labbé, I.; Reddy, N.; Atek, H.; Montes, M.; Naidu, R.; Nanayakkara, T.; et al. New Determinations of the UV Luminosity Functions from z 9 to 2 Show a Remarkable Consistency with Halo Growth and a Constant Star Formation Efficiency. Astron. J. 2021, 162, 47. [Google Scholar] [CrossRef]
- Donnan, C.T.; McLeod, D.J.; Dunlop, J.S.; McLure, R.J.; Carnall, A.C.; Begley, R.; Cullen, F.; Hamadouche, M.L.; Bowler, R.A.A.; Magee, D.; et al. The evolution of the galaxy UV luminosity function at redshifts z≃8-15 from deep JWST and ground-based near-infrared imaging. Mon. Not. R. Astron. Soc. 2023, 518, 6011–6040. [Google Scholar] [CrossRef]
- Harikane, Y.; Ouchi, M.; Oguri, M.; Ono, Y.; Nakajima, K.; Isobe, Y.; Umeda, H.; Mawatari, K.; Zhang, Y. A Comprehensive Study of Galaxies at z 9-16 Found in the Early JWST Data: Ultraviolet Luminosity Functions and Cosmic Star Formation History at the Pre-reionization Epoch. Astrophys. J. Suppl. Ser. 2023, 265, 5. [Google Scholar] [CrossRef]
- Leung, G.C.K.; Bagley, M.B.; Finkelstein, S.L.; Ferguson, H.C.; Koekemoer, A.M.; Pérez-González, P.G.; Morales, A.; Kocevski, D.D.; Yang, G.; Somerville, R.S.; et al. NGDEEP Epoch 1: The Faint End of the Luminosity Function at z 9-12 from Ultradeep JWST Imaging. Astrophys. J. Lett. 2023, 954, L46. [Google Scholar] [CrossRef]
- Finkelstein, S.L.; Leung, G.C.K.; Bagley, M.B.; Dickinson, M.; Ferguson, H.C.; Papovich, C.; Akins, H.B.; Arrabal Haro, P.; Dave, R.; Dekel, A.; et al. The Complete CEERS Early Universe Galaxy Sample: A Surprisingly Slow Evolution of the Space Density of Bright Galaxies at z ~8.5–14.5. arXiv 2023, arXiv:2311.04279. [Google Scholar] [CrossRef]
- McLeod, D.J.; Donnan, C.T.; McLure, R.J.; Dunlop, J.S.; Magee, D.; Begley, R.; Carnall, A.C.; Cullen, F.; Ellis, R.S.; Hamadouche, M.L.; et al. The galaxy UV luminosity function at z≃11 from a suite of public JWST ERS, ERO, and Cycle-1 programs. Mon. Not. R. Astron. Soc. 2024, 527, 5004–5022. [Google Scholar] [CrossRef]
- Harikane, Y.; Nakajima, K.; Ouchi, M.; Umeda, H.; Isobe, Y.; Ono, Y.; Xu, Y.; Zhang, Y. Pure Spectroscopic Constraints on UV Luminosity Functions and Cosmic Star Formation History from 25 Galaxies at z spec = 8.61–13.20 Confirmed with JWST/NIRSpec. Astrophys. J. 2024, 960, 56. [Google Scholar] [CrossRef]
- Donnan, C.T.; McLure, R.J.; Dunlop, J.S.; McLeod, D.J.; Magee, D.; Arellano-Córdova, K.Z.; Barrufet, L.; Begley, R.; Bowler, R.A.A.; Carnall, A.C.; et al. JWST PRIMER: A new multi-field determination of the evolving galaxy UV luminosity function at redshifts z≃ 9–15. arXiv 2024, arXiv:2403.03171. [Google Scholar] [CrossRef]
- Adams, N.J.; Conselice, C.J.; Austin, D.; Harvey, T.; Ferreira, L.; Trussler, J.; Juodžbalis, I.; Li, Q.; Windhorst, R.; Cohen, S.H.; et al. EPOCHS. II. The Ultraviolet Luminosity Function from 7.5 < z < 13.5 Using 180 arcmin2 of Deep, Blank Fields from the PEARLS Survey and Public JWST Data. Astrophys. J. 2024, 965, 169. [Google Scholar] [CrossRef]
- Liu, P.; Ma, Q.; Han, Y.; Luo, R. A Quantification of the Effects Using Different Stellar-population Synthesis Models for Epoch of Reionization. Astrophys. J. 2024, 968, 13. [Google Scholar] [CrossRef]
- Planck Collaboration; Aghanim, N.; Akrami, Y.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; et al. Planck 2018 results. VI. Cosmological parameters. Astron. Astrophys. 2020, 641, A6. [Google Scholar] [CrossRef]
- Henriques, B.M.B.; Yates, R.M.; Fu, J.; Guo, Q.; Kauffmann, G.; Srisawat, C.; Thomas, P.A.; White, S.D.M. L-GALAXIES 2020: Spatially resolved cold gas phases, star formation, and chemical enrichment in galactic discs. Mon. Not. R. Astron. Soc. 2020, 491, 5795–5814. [Google Scholar] [CrossRef]
- Boylan-Kolchin, M.; Springel, V.; White, S.D.M.; Jenkins, A.; Lemson, G. Resolving cosmic structure formation with the Millennium-II Simulation. Mon. Not. R. Astron. Soc. 2009, 398, 1150–1164. [Google Scholar] [CrossRef]
- White, S.D.M. Observable signatures of young galaxies. In The Epoch of Galaxy Formation; Frenk, C.S., sEllis, R.S., Shanks, T., Heavens, A.R., Peacock, J.A., Eds.; NATO Advanced Study Institute (ASI) Series C; Springer: Dordrecht, The Netherlands, 1989; Volume 264, p. 15. [Google Scholar]
- Kauffmann, G.; White, S.D.M.; Guiderdoni, B. The formation and evolution of galaxies within merging dark matter haloes. Mon. Not. R. Astron. Soc. 1993, 264, 201–218. [Google Scholar] [CrossRef]
- Springel, V.; White, S.D.M.; Jenkins, A.; Frenk, C.S.; Yoshida, N.; Gao, L.; Navarro, J.; Thacker, R.; Croton, D.; Helly, J.; et al. Simulations of the formation, evolution and clustering of galaxies and quasars. Nature 2005, 435, 629–636. [Google Scholar] [CrossRef]
- Henriques, B.M.B.; White, S.D.M.; Thomas, P.A.; Angulo, R.; Guo, Q.; Lemson, G.; Springel, V.; Overzier, R. Galaxy formation in the Planck cosmology—I. Matching the observed evolution of star formation rates, colours and stellar masses. Mon. Not. R. Astron. Soc. 2015, 451, 2663–2680. [Google Scholar] [CrossRef]
- Fu, J.; Kauffmann, G.; Huang, M.l.; Yates, R.M.; Moran, S.; Heckman, T.M.; Davé, R.; Guo, Q.; Henriques, B.M.B. Star formation and metallicity gradients in semi-analytic models of disc galaxy formation. Mon. Not. R. Astron. Soc. 2013, 434, 1531–1548. [Google Scholar] [CrossRef]
- Springel, V. The cosmological simulation code GADGET-2. Mon. Not. R. Astron. Soc. 2005, 364, 1105–1134. [Google Scholar] [CrossRef]
- More, S.; Kravtsov, A.V.; Dalal, N.; Gottlöber, S. The Overdensity and Masses of the Friends-of-friends Halos and Universality of Halo Mass Function. Astrophys. J. Suppl. Ser. 2011, 195, 4. [Google Scholar] [CrossRef]
- Springel, V.; White, S.D.M.; Tormen, G.; Kauffmann, G. Populating a cluster of galaxies—I. Results at z = 0. Mon. Not. R. Astron. Soc. 2001, 328, 726–750. [Google Scholar] [CrossRef]
- Chabrier, G. The Initial Mass Function: From Salpeter 1955 to 2005. In The Initial Mass Function 50 Years Later; Corbelli, E., Palla, F., Zinnecker, H., Eds.; Springer: Dordrecht, The Netherlands, 2005; Volume 327, p. 41. [Google Scholar] [CrossRef]
- Salpeter, E.E. The Luminosity Function and Stellar Evolution. Astrophys. J. 1955, 121, 161. [Google Scholar] [CrossRef]
- Han, Z.W.; Ge, H.W.; Chen, X.F.; Chen, H.L. Binary Population Synthesis. Res. Astron. Astrophys. 2020, 20, 161. [Google Scholar] [CrossRef]
- Yung, L.Y.A.; Somerville, R.S.; Popping, G.; Finkelstein, S.L. Semi-analytic forecasts for JWST - III. Intrinsic production efficiency of Lyman-continuum radiation. Mon. Not. R. Astron. Soc. 2020, 494, 1002–1017. [Google Scholar] [CrossRef]
- Ma, Q.B.; Fiaschi, S.; Ciardi, B.; Busch, P.; Eide, M.B. A CRASH simulation of the contribution of binary stars to the epoch of reionization. Mon. Not. R. Astron. Soc. 2022, 513, 1513–1525. [Google Scholar] [CrossRef]
- Scalo, J.M. The Stellar Initial Mass Function. Fundam. Cosm. Phys. 1986, 11, 1–278. [Google Scholar]
- Chabrier, G. Galactic Stellar and Substellar Initial Mass Function. Publ. Astron. Soc. Pac. 2003, 115, 763–795. [Google Scholar] [CrossRef]
- Vanzella, E.; Loiacono, F.; Bergamini, P.; Meštrić, U.; Castellano, M.; Rosati, P.; Meneghetti, M.; Grillo, C.; Calura, F.; Mignoli, M.; et al. An extremely metal-poor star complex in the reionization era: Approaching Population III stars with JWST. Astron. Astrophys. 2023, 678, A173. [Google Scholar] [CrossRef]
- Maiolino, R.; Übler, H.; Perna, M.; Scholtz, J.; D’Eugenio, F.; Witten, C.; Laporte, N.; Witstok, J.; Carniani, S.; Tacchella, S.; et al. JADES. Possible Population III signatures at z = 10.6 in the halo of GN-z11. Astron. Astrophys. 2024, 687, A67. [Google Scholar] [CrossRef]
- Cameron, A.J.; Katz, H.; Witten, C.; Saxena, A.; Laporte, N.; Bunker, A.J. Nebular dominated galaxies: Insights into the stellar initial mass function at high redshift. Mon. Not. R. Astron. Soc. 2024, 534, 523–543. [Google Scholar] [CrossRef]
- Mason, C.A.; Trenti, M.; Treu, T. The Galaxy UV Luminosity Function before the Epoch of Reionization. Astrophys. J. 2015, 813, 21. [Google Scholar] [CrossRef]
- Finkelstein, S.L.; Ryan, R.E., Jr.; Papovich, C.; Dickinson, M.; Song, M.; Somerville, R.S.; Ferguson, H.C.; Salmon, B.; Giavalisco, M.; Koekemoer, A.M.; et al. The Evolution of the Galaxy Rest-frame Ultraviolet Luminosity Function over the First Two Billion Years. Astrophys. J. 2015, 810, 71. [Google Scholar] [CrossRef]
- Inayoshi, K.; Harikane, Y.; Inoue, A.K.; Li, W.; Ho, L.C. A Lower Bound of Star Formation Activity in Ultra-high-redshift Galaxies Detected with JWST: Implications for Stellar Populations and Radiation Sources. Astrophys. J. Lett. 2022, 938, L10. [Google Scholar] [CrossRef]
- Trinca, A.; Schneider, R.; Valiante, R.; Graziani, L.; Ferrotti, A.; Omukai, K.; Chon, S. Exploring the nature of UV-bright z ≳ 10 galaxies detected by JWST: Star formation, black hole accretion, or a non-universal IMF? Mon. Not. R. Astron. Soc. 2024, 529, 3563–3581. [Google Scholar] [CrossRef]
- Yung, L.Y.A.; Somerville, R.S.; Finkelstein, S.L.; Wilkins, S.M.; Gardner, J.P. Are the ultra-high-redshift galaxies at z > 10 surprising in the context of standard galaxy formation models? Mon. Not. R. Astron. Soc. 2024, 527, 5929–5948. [Google Scholar] [CrossRef]
- Ventura, E.M.; Qin, Y.; Balu, S.; Wyithe, J.S.B. Semi-analytic modelling of Pop. III star formation and metallicity evolution—I. Impact on the UV luminosity functions at z = 9–16. Mon. Not. R. Astron. Soc. 2024, 529, 628–646. [Google Scholar] [CrossRef]
- Ma, Q.B.; Ghara, R.; Ciardi, B.; Iliev, I.T.; Koopmans, L.V.E.; Mellema, G.; Mondal, R.; Zaroubi, S. POLAR-I: Linking the 21-cm signal from the epoch of reionization to galaxy formation. Mon. Not. R. Astron. Soc. 2023, 522, 3284–3297. [Google Scholar] [CrossRef]
- Sun, F.; Egami, E.; Pirzkal, N.; Rieke, M.; Baum, S.; Boyer, M.; Boyett, K.; Bunker, A.J.; Cameron, A.J.; Curti, M.; et al. First Sample of Hα+[O III]λ5007 Line Emitters at z > 6 Through JWST/NIRCam Slitless Spectroscopy: Physical Properties and Line-luminosity Functions. Astrophys. J. 2023, 953, 53. [Google Scholar] [CrossRef]
- Tang, M.; Stark, D.P.; Chen, Z.; Mason, C.; Topping, M.; Endsley, R.; Senchyna, P.; Plat, A.; Lu, T.Y.; Whitler, L.; et al. JWST/NIRSpec spectroscopy of z = 7–9 star-forming galaxies with CEERS: New insight into bright Lyα emitters in ionized bubbles. Mon. Not. R. Astron. Soc. 2023, 526, 1657–1686. [Google Scholar] [CrossRef]
- Simmonds, C.; Tacchella, S.; Hainline, K.; Johnson, B.D.; McClymont, W.; Robertson, B.; Saxena, A.; Sun, F.; Witten, C.; Baker, W.M.; et al. Low-mass bursty galaxies in JADES efficiently produce ionizing photons and could represent the main drivers of reionization. Mon. Not. R. Astron. Soc. 2024, 527, 6139–6157. [Google Scholar] [CrossRef]
- Shivaei, I.; Reddy, N.A.; Siana, B.; Shapley, A.E.; Kriek, M.; Mobasher, B.; Freeman, W.R.; Sanders, R.L.; Coil, A.L.; Price, S.H.; et al. The MOSDEF Survey: Direct Observational Constraints on the Ionizing Photon Production Efficiency, ξion, at z ∼ 2. Astrophys. J. 2018, 855, 42. [Google Scholar] [CrossRef]
- Schaerer, D.; Guibert, J.; Marques-Chaves, R.; Martins, F. Observable and ionizing properties of star-forming galaxies with very massive stars and different initial mass functions. Astron. Astrophys. 2025, 693, A271. [Google Scholar] [CrossRef]
- Mauerhofer, V.; Dayal, P.; Haehnelt, M.G.; Kimm, T.; Rosdahl, J.; Teyssier, R. Synergising semi-analytical models and hydrodynamical simulations to interpret JWST data from the first billion years. arXiv 2025, arXiv:2502.02647. [Google Scholar] [CrossRef]
- Li, Y.; Leja, J.; Johnson, B.D.; Tacchella, S.; Naidu, R.P. No Top-heavy Stellar Initial Mass Function Needed: The Ionizing Radiation of GS9422 Can Be Powered by a Mixture of an Active Galactic Nucleus and Stars. Astrophys. J. Lett. 2024, 969, L5. [Google Scholar] [CrossRef]
- Hutter, A.; Cueto, E.R.; Dayal, P.; Gottlöber, S.; Trebitsch, M.; Yepes, G. ASTRAEUS: X. Indications of a top-heavy initial mass function in highly star-forming galaxies from JWST observations at z > 10. Astron. Astrophys. 2025, 694, A254. [Google Scholar] [CrossRef]


| Model | IMF | |||
|---|---|---|---|---|
| (0.1–M1) | (M1–) | () | ||
| 170-100 | Scaloa | −1.30 | −2.70 | 100 |
| 170-300 | Scalob | −1.30 | −2.70 | 300 |
| chab100 | Chabriera | - | −2.30 | 100 |
| chab300 | Chabrierb | - | −2.30 | 300 |
| 135-100 | Salpetera | −2.35 | −2.35 | 100 |
| 135-300 | Salpeterb | −2.35 | −2.35 | 300 |
| 100-100 | Top-Heavya | −1.30 | −2.00 | 100 |
| 100-300 | Top-Heavyb | −1.30 | −2.00 | 300 |
| z | Scaloa | Scalob | Chabriera | Chabrierb | Salpetera | Salpeterb | Top-Heavya | Top-Heavyb |
|---|---|---|---|---|---|---|---|---|
| 9 | 134.49 | 131.57 | 75.29 | 81.95 | 84.14 | 76.03 | 173.71 | 226.94 |
| 10 | 120.74 | 117.78 | 42.09 | 38.25 | 59.09 | 46.29 | 72.08 | 142.16 |
| 11 | 90.38 | 90.16 | 73.99 | 60.10 | 80.27 | 77.61 | 46.99 | 36.97 |
| 12 | 36.25 | 34.93 | 31.26 | 30.00 | 31.11 | 31.13 | 20.81 | 16.58 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, Q.; Liu, L.; Liu, P. The Impact of Stellar Initial Mass Function on the Epoch of Reionization: Insights from Semi-Analytic Galaxy Modeling. Universe 2025, 11, 129. https://doi.org/10.3390/universe11040129
Ma Q, Liu L, Liu P. The Impact of Stellar Initial Mass Function on the Epoch of Reionization: Insights from Semi-Analytic Galaxy Modeling. Universe. 2025; 11(4):129. https://doi.org/10.3390/universe11040129
Chicago/Turabian StyleMa, Qingbo, Lei Liu, and Peiai Liu. 2025. "The Impact of Stellar Initial Mass Function on the Epoch of Reionization: Insights from Semi-Analytic Galaxy Modeling" Universe 11, no. 4: 129. https://doi.org/10.3390/universe11040129
APA StyleMa, Q., Liu, L., & Liu, P. (2025). The Impact of Stellar Initial Mass Function on the Epoch of Reionization: Insights from Semi-Analytic Galaxy Modeling. Universe, 11(4), 129. https://doi.org/10.3390/universe11040129







