Scaling Invariance of Perturbations in k-Inflation Models
Abstract
1. Introduction
2. Hamilton Formalism
A Few Useful Relations
3. k-Essence Inflation Models
3.1. Model A
The Klein-Gordon Equation
3.2. Model B
The Tachyon Model
4. Curvature Perturbations
4.1. Mukhanov–Sasaki Equation
4.1.1. Rough Estimates
4.1.2. Initial Conditions
4.2. Redefinition of the Input Parameters and Fields
4.3. Approximate Spectrum
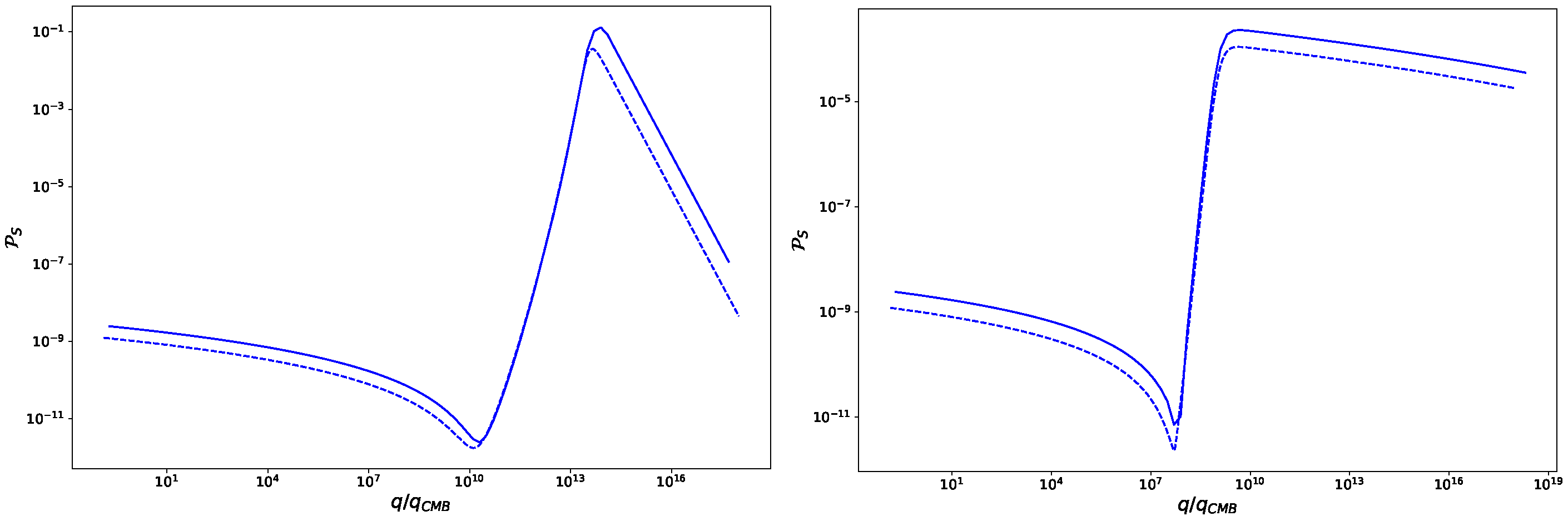
4.4. Integration of the Mukhanov–Sasaki Equation
4.4.1. Input Parameters
4.4.2. Note on the Numerical Routines
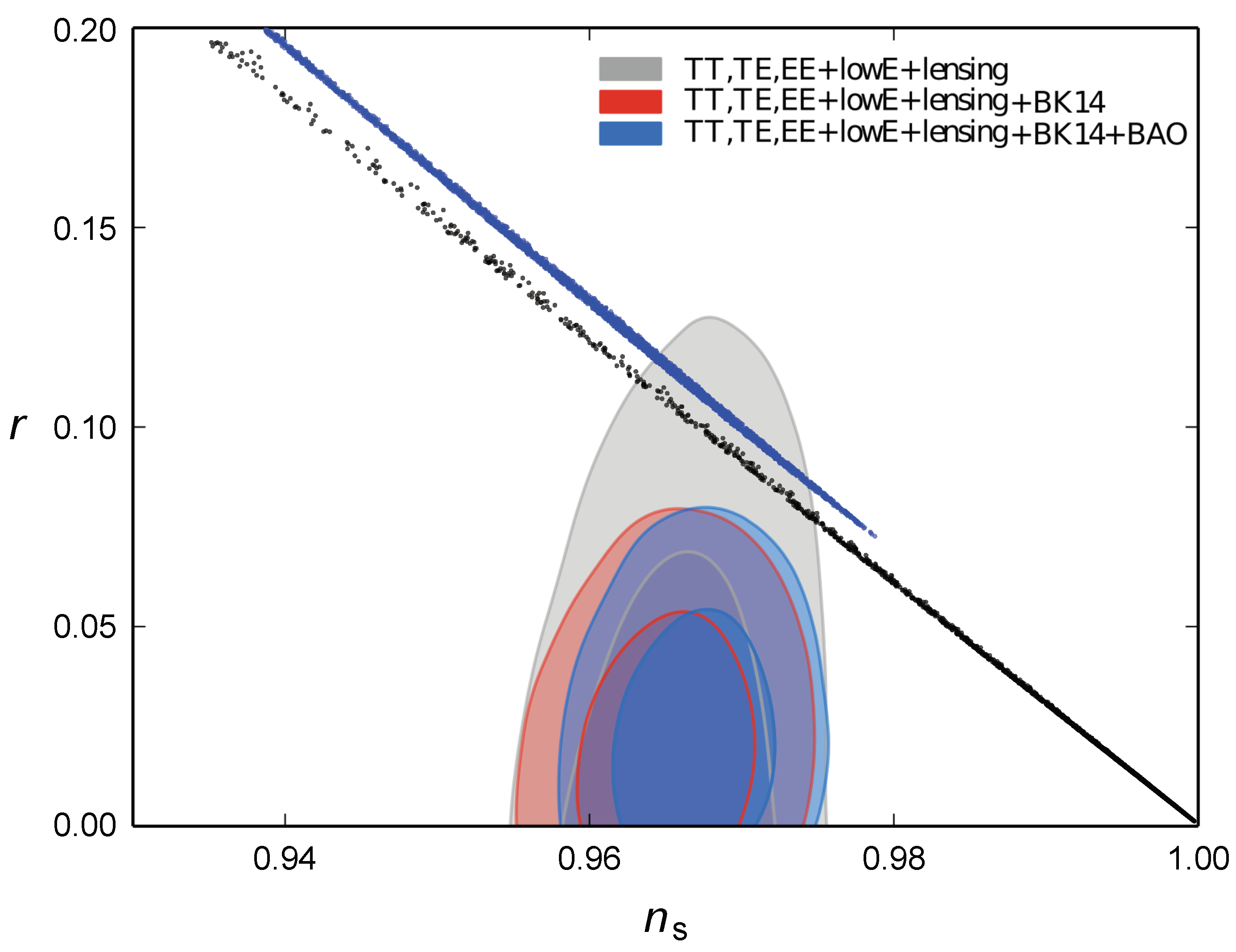
5. Summary and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Armendariz-Picon, C.; Mukhanov, V.F.; Steinhardt, P.J. A dynamical solution to the problem of a small cosmological constant and late-time cosmic acceleration. Phys. Rev. Lett. 2000, 85, 4438. [Google Scholar] [CrossRef] [PubMed]
- Armendariz-Picon, C.; Damour, T.; Mukhanov, V.F. k-inflation. Phys. Lett. B 1999, 458, 209. [Google Scholar] [CrossRef]
- Kamenshchik, A.Y.; Moschella, U.; Pasquier, V. An Alternative to quintessence. Phys. Lett. B 2001, 511, 265–268. [Google Scholar] [CrossRef]
- Bilic, N.; Tupper, G.B.; Viollier, R.D. Unification of dark matter and dark energy: The Inhomogeneous Chaplygin gas. Phys. Lett. B 2002, 535, 17–21. [Google Scholar] [CrossRef]
- Fairbairn, M.; Tytgat, M.H.G. Inflation from a tachyon fluid? Phys. Lett. B 2002, 546, 1–17. [Google Scholar] [CrossRef]
- Frolov, A.V.; Kofman, L.; Starobinsky, A.A. Prospects and problems of tachyon matter cosmology. Phys. Lett. B 2002, 545, 8. [Google Scholar] [CrossRef]
- Shiu, G.; Wasserman, I. Cosmological constraints on tachyon matter. Phys. Lett. B 2002, 541, 6. [Google Scholar] [CrossRef]
- Sami, M.; Chingangbam, P.; Qureshi, T. Aspects of tachyonic inflation with exponential potential. Phys. Rev. D 2002, 66, 043530. [Google Scholar] [CrossRef]
- Shiu, G.; Tye, S.H.H.; Wasserman, I. Rolling tachyon in brane world cosmology from superstring field theory. Phys. Rev. D 2003, 67, 083517. [Google Scholar] [CrossRef]
- Kofman, L.; Linde, A.D. Problems with tachyon inflation. J. High Energy Phys. 2002, 0207, 004. [Google Scholar] [CrossRef]
- Cline, J.M.; Firouzjahi, H.; Martineau, P. Reheating from tachyon condensation. J. High Energy Phys. 2002, 0211, 041. [Google Scholar] [CrossRef]
- Salamate, F.; Khay, I.; Safsafi, A.; Chakir, H.; Bennai, M. Observational Constraints on the Chaplygin Gas with Inverse Power Law Potential in Braneworld Inflation. Mosc. Univ. Phys. Bull. 2018, 73, 405. [Google Scholar] [CrossRef]
- Barbosa-Cendejas, N.; Cartas-Fuentevilla, R.; Herrera-Aguilar, A.; Mora-Luna, R.R.; da Rocha, R. A de Sitter tachyonic braneworld revisited. J. Cosmol. Astropart. Phys. 2018, 2018, 005. [Google Scholar] [CrossRef]
- Dantas, D.M.; da Rocha, R.; Almeida, C.A.S. Monopoles on string-like models and the Coulomb’s law. Phys. Lett. B 2018, 782, 149. [Google Scholar] [CrossRef]
- Steer, D.A.; Vernizzi, F. Tachyon inflation: Tests and comparison with single scalar field inflation. Phys. Rev. D 2004, 70, 043527. [Google Scholar] [CrossRef]
- Bilic, N.; Dimitrijevic, D.D.; Djordjevic, G.S.; Milosevic, M.; Stojanovic, M. Tachyon inflation in the holographic braneworld. J. Cosmol. Astropart. Phys. 2019, 08, 034. [Google Scholar] [CrossRef]
- Papanikolaou, T.; Lymperis, A.; Lola, S.; Saridakis, E.N. Primordial black holes and gravitational waves from non-canonical inflation. J. Cosmol. Astropart. Phys. 2023, 03, 003. [Google Scholar] [CrossRef]
- Garcia-Bellido, J.; Morales, E.R. Primordial black holes from single field models of inflation. Phys. Dark Univ. 2017, 18, 47–54. [Google Scholar] [CrossRef]
- Kannike, K.; Marzola, L.; Raidal, M.; Veermäe, H. Single Field Double Inflation and Primordial Black Holes. J. Cosmol. Astropart. Phys. 2017, 09, 020. [Google Scholar] [CrossRef]
- Germani, C.; Musco, I. Abundance of Primordial Black Holes Depends on the Shape of the Inflationary Power Spectrum. Phys. Rev. Lett. 2019, 122, 141302. [Google Scholar] [CrossRef]
- Gibbons, G.W. Thoughts on tachyon cosmology. Class. Quant. Grav. 2003, 20, S321. [Google Scholar] [CrossRef]
- Sen, A. Supersymmetric world volume action for nonBPS D-branes. J. High Energy Phys. 1999, 9910, 008. [Google Scholar] [CrossRef]
- Sen, A. Tachyon matter. J. High Energy Phys. 2002, 07, 065. [Google Scholar] [CrossRef]
- Shandera, S.E.; Tye, S.-H.H. Observing brane inflation. J. Cosmol. Astropart. Phys. 2006, 2006, 007. [Google Scholar] [CrossRef]
- Bilić, N.; Domazet, S.; Djordjevic, G. Tachyon with an inverse power-law potential in a braneworld cosmology. Class. Quant. Grav. 2017, 34, 165006. [Google Scholar] [CrossRef]
- Garriga, J.; Mukhanov, V.F. Perturbations in k-inflation. Phys. Lett. B 1999, 458, 219–225. [Google Scholar] [CrossRef]
- Bertini, N.R.; Bilic, N.; Rodrigues, D.C. Primordial perturbations and inflation in holographic cosmology. Phys. Rev. D 2020, 102, 123505, Erratum in Phys. Rev. D 2022, 105, 129901. [Google Scholar] [CrossRef]
- De, A.; Mahbub, R. Numerically modeling stochastic inflation in slow-roll and beyond. Phys. Rev. D 2020, 102, 123509. [Google Scholar] [CrossRef]
- Bunch, T.S.; Davies, P.C.W. Quantum Field Theory in de Sitter Space: Renormalization by Point Splitting. Proc. R. Soc. Lond. A 1978, 360, 117–134. [Google Scholar] [CrossRef]
- Lola, S.; Lymperis, A.; Saridakis, E.N. Inflation with non-canonical scalar fields revisited. Eur. Phys. J. C 2021, 81, 719. [Google Scholar] [CrossRef]
- Akrami, Y. et al. [Planck] Planck 2018 results. X. Constraints on inflation. Astron. Astrophys. 2020, 641, A10. [Google Scholar] [CrossRef]
- Cole, P.S.; Gow, A.D.; Byrnes, C.T.; Patil, S.P. Primordial black holes from single-field inflation: A fine-tuning audit. J. Cosmol. Astropart. Phys. 2023, 08, 031. [Google Scholar] [CrossRef]
- Inomata, K.; Braglia, M.; Chen, X.; Renaux-Petel, S. Questions on calculation of primordial power spectrum with large spikes: The resonance model case. J. Cosmol. Astropart. Phys. 2023, 04, 011, Erratum in J. Cosmol. Astropart. Phys. 2023, 09, E01. [Google Scholar] [CrossRef]
- Kristiano, J.; Yokoyama, J. Constraining Primordial Black Hole Formation from Single-Field Inflation. Phys. Rev. Lett. 2024, 132, 221003. [Google Scholar] [CrossRef]
- Choudhury, S.; Panda, S.; Sami, M. Quantum loop effects on the power spectrum and constraints on primordial black holes. J. Cosmol. Astropart. Phys. 2023, 11, 066. [Google Scholar] [CrossRef]
- Ballesteros, G.; Egea, J.G. One-loop power spectrum in ultra slow-roll inflation and implications for primordial black hole dark matter. J. Cosmol. Astropart. Phys. 2024, 07, 052. [Google Scholar] [CrossRef]
- Franciolini, G.; Iovino, A., Jr.; Taoso, M.; Urbano, A. Perturbativity in the presence of ultraslow-roll dynamics. Phys. Rev. D 2024, 109, 123550. [Google Scholar] [CrossRef]
- Firouzjahi, H.; Riotto, A. Primordial Black Holes and loops in single-field inflation. J. Cosmol. Astropart. Phys. 2024, 02, 021. [Google Scholar] [CrossRef]
| PLLS Model, | Tachyon Model | |||
|---|---|---|---|---|
| Original | Redefined | Original | Redefined | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bilić, N.; Dimitrijević, D.D.; Djordjević, G.S.; Milošević, M.; Stojanović, M. Scaling Invariance of Perturbations in k-Inflation Models. Universe 2025, 11, 128. https://doi.org/10.3390/universe11040128
Bilić N, Dimitrijević DD, Djordjević GS, Milošević M, Stojanović M. Scaling Invariance of Perturbations in k-Inflation Models. Universe. 2025; 11(4):128. https://doi.org/10.3390/universe11040128
Chicago/Turabian StyleBilić, Neven, Dragoljub D. Dimitrijević, Goran S. Djordjević, Milan Milošević, and Marko Stojanović. 2025. "Scaling Invariance of Perturbations in k-Inflation Models" Universe 11, no. 4: 128. https://doi.org/10.3390/universe11040128
APA StyleBilić, N., Dimitrijević, D. D., Djordjević, G. S., Milošević, M., & Stojanović, M. (2025). Scaling Invariance of Perturbations in k-Inflation Models. Universe, 11(4), 128. https://doi.org/10.3390/universe11040128






