Abstract
In this paper, we apply several latest results from statistical physics on the probability and energy of knotting to study the knotted field lines in solar corona. Since the solar magnetic field in small scale can be seen as nearly random, by assuming that the magnetic field lines behave similarly to random loops, we find the probability P of certain knot type K for the field line knotting as a function to the distance L between the foot-points of sunspots, which is . From the equation, we find that the variety of knot type increases with the distance. Since knotting is the topological resemblance to magnetic helicity, which is an invariant for ideal MHD, our result enriches the understanding of the probability of magnetic helicity as well as field line structure in active regions. Based on the relation between knotting and magnetic energy, we provide support to the high variety of field line knot types.
1. Introduction
Outstanding solar activities such as coronal mass ejection (CME) have a strong impact on the Earth, such as sometimes causing geomagnetic storms. In order to better understand CMEs, it is necessary to study the magnetic flux rope and filament eruption, because over of filament eruptions lead to CME [1]. A common understanding of flux rope is for it to be seen as set of magnetic field lines winding around the same core [1,2], and thus have the same connectivity to the foot-point. Since the eruption is caused by the evolving external magnetic field, there have been different proposed mechanisms for it, such as emerging flux [3], reconnection [4], and kink-instability [5]. Among these different mechanisms, it is universally acknowledged that the knottiness plays an important role, because a reconnection process is a topological change to the knot type, while the kink-instability implies that there is a threshold for twisting such that the eruption takes place when the degree of twisting exceeds that threshold. Thus, both flux rope and filament eruption processes are fundamentally related to the twisted magnetic field [1,2,6,7]. Furthermore, the CME and its counterpart in space, which is the magnetic cloud, are also twisted [2]. The evolution from CME to magnetic cloud can be very complex as the magnetic flux can be replaced by reconnection, and it is frequently observed that the flux rope is not coherent during the CME process, sometimes even completely substituted [8]. Therefore, for the dynamics of various solar and space magnetic activities, the twisted magnetic field lines are crucial factors.
To characterize these twisted magnetic field lines and their influence to the dynamics, the magnetic helicity has been found as an invariance for ideal magnetohydrodynamics (MHD) [9,10,11]. The magnetic helicity is defined as
with B being the magnetic field and A its potential. The magnetic helicity has been measured using various method, such as the optical flow method [12,13,14,15] and nonlinear force-free reconstruction based on the magnetogram [16,17,18,19]. These abundant measurements provide a solid ground for studying magnetic helicity in solar magnetic field. On the other hand, from the topological perspective, the magnetic helicity can be studied through investigations on knots. A knot is a topological invariant in three-dimensional space. Knotted field lines contribute to the helicity. In terms of the knotting topology, helicity can also be written as [20]
where and are the twist and writhe of the field lines, n is the linking number, and is the magnetic flux in the tube. Therefore, helicity measures the degree of knottiness in a given system. If the field lines are highly complex knotted, then the system has a large helicity.
The magnetic field topology may change during the evolution, and such change may be studied by the change of the knot type and the linking number. From Equation (2), we find the time-derivative of linking number as
If the magnetic flux is nearly constant, it becomes
In measurement, it is usually preferred to measure the relative helicity of certain region against its neighborhood region [10], which is an invariant under specific boundary, and its time-derivative is given as [12]
where is the vector potential and U is the horizontal velocity field. There have been measurements [13,15] on the the time-derivative of the linking number, yet there is still a lack of a general analysis on the knot types and the degree of knotting of the magnetic field lines. Thus, in this paper we provide a new perspective by studying the probability and energy of field line knotting. In Section 2, by assuming that the field lines are behaving similarly to random curves, we find the probability equation of field line knotting. In Section 3, we apply the relation between knotting and energy to discuss the variety of knot types in solar magnetic fields.
2. Knot Probability of Random Magnetic Field Lines
While it is difficult to observe the solar activity process in great detail due to the limited image resolution, we can exploit statistical physics methods and apply the recent results on knot probability to the analysis of solar physics, as knots and helicity are foundations to turbulent solar dynamics. According to the dynamo theory [21], which studies the solar magnetic field based on the mean-field theory, the turbulent magnetic field can be decomposed into a combination of the mean field and fluctuation:
Meanwhile, if the fluctuation term is mainly Gaussian random waves, it can be written as a superposition of random waves:
In this framework, the solar magnetic field has a certain degree of randomness in local scale, while the global flow is determined by dominant MHD equations. Consequently, when the complex solar magnetic field is interpreted as a superposition of random waves in Equations (6) and (7), the field lines behave like random loops. There have already been a broad range of systems justified and applied to this perspective of random loops, such as quantum chaos [22] and quantum turbulence [23]. While the physical materials may be different among different systems, there are similar mathematical formulations, and thus the zero-set (such as vortices and field lines) are studied as random loops. Globally, random loops are structured as topologically one-dimensional sphere (), while locally the field lines have a geometry of random curves such that, between two points on a given curve, the Euclidean distance between them is proportional to the square-root of the arc-length between them. Therefore, random loops are not simple random curves, but rather an ensemble of topologically and geometrically specified curves.
There have been analyses of solar magnetic field lines between sunspots as random loops [24], where the predictions based on random loop assumption are verified by observations. In this work [24], researchers derived a power-law index of for magnetic helicity distribution based on the assumption of treating field lines between sunspots as random loops, and the theory is supported by observations of newly emerged active regions during the 23rd and 24th solar cycle. Therefore, there have been published observations that support the analysis of solar magnetic field lines as random loops. The scale for the random loop model is manifested within the same loop between the foot-points of sunspots. At the global scale, the loops are structured, but within the same loop the field lines and tubes are curved randomly. Depending on the magnitude and cycle of solar activity, the span of the field lines connecting between sunspot foot-points may vary, and thus the scales for them to be randomly curved also vary accordingly. There is no conflict between a dominant MHD dynamic and the random loop approximation, and there is no conflict between the loop structure and its randomly curved geometry. Before the emergence of active regions in the corona, the magnetic field lines are already formed and intertwined in the convective zone. Since the flows in the convective zone are highly turbulent and fully convective, it is reasonable to model the knotted field lines as nearly random [25]. Then, when the pressure exceeds the threshold, the magnetic field lines emerge as active regions. During such emergence, while the magnetic tube may be relaxed, the helicity remains nearly invariant, thus the random loop approximation to the field line’s knottiness remains valid. Furthermore, after the formation of loops in the active region, the geometry of the field lines is also randomly curved due to the fluctuation in the MHD, which is a direct outcome of the nature of turbulence flow. The framework of this model is consistent with previous studies on coronal loops in MHD turbulence, such as [26,27], where the magnetic energy of coronal loops under fluctuation is studied.
In this paper, we study the probability of knotting in solar active regions based on a recent work on the knot probability in three-dimensional random walks [28]. This recent paper studies the knot probability of closed random walks in (Euclidean space) verified by a very large amount of data, which contained simulation data sampling number in magnitude. The closed random walks are generated for different edge (step) numbers, and for each edge number the random walks are distinguished by the Alexander polynomial for the knot type, and thus the probability of different knot types are obtained. The knot types are basically classified by the number of composition and crossings. For a single knot, which is also called prime knot, the knot type is classified by the number of crossings, which is a fundamental topological invariant. The simplest single knot is knot , meaning that it has three crossings, and is the first of its type, even though there is only one type of its kind. After the and knots, there are two type of five crossing knots, each labeled and . After that are the , , and knots, and six seven-crossing knots, to . The combination of multiple knots is called a composite knot. The simplest composite knot would be two trefoil knots () combined together, labeled as . There could be a knot and a knot together, forming composite knot , while there could also be three trefoil knots together forming . The composition of composite knots can have a large variety. Through a combination of theoretical analysis and large data fitting, it has been shown [28] that there is a universal probability equation for different knot types. For a certain knot type K, the probability for its existence as a function of the number of random walk step number N is
where is the amplitude coefficient for each knot type K, for being a constant based on the probability of the unknot, and the number of composite knot component, such as for a single knot, for a composite knot with two components, for a composite knot with three components, and so on. depends on the mechanism of the generation of random knots, such as whether the knots are formed by random walks with equal step length, or if the step length follows certain statistical distribution. Since it is an asymptotic expansion, there are correction terms in the equation, but if the correction term is much smaller than the main term, we may neglect it and consider only the main term for practical calculation.
Based on the knowledge of random knot probability, and the assumption that solar magnetic field lines may locally behave like random curves, we now consider the knot probability of magnetic field lines between two foot-points of distance L of a given sunspot. Since the magnetic field lines between two sunspots have a shape that roughly equals a semi-circle, we know that the distance between the two sunspots is linearly proportional to the semi-circle circumference of the field line. In statistical physics, it is known that, for two points on a random curve, the arc length between them is proportional to the square of the Euclidean distance between them. Therefore, if we consider the field line as a discretized random walk, its step number N is , where L is proportional to the distance between the two foot-points of the sunspot. By omitting the correction term, we may write the probability of certain knot type K between sunspots as
where , within which is the power-law constant for the probability of the unknot, and is the number of components in the composite knot. is a constant if the mechanism for the generation of random field line is universal in the solar active regions. The spatial scale for this equation’s application is the same as the distance between foot-pints of the same sunspot, which may vary from to kilometers, and is proportional to L. In this way, when the span of the foot-point is large, it is more likely to observe complexly knotted field lines. Among the probability of different knot types, perhaps the probability of the unknot is a primal concern in many scenarios. Explicitly, the probability of the unknot is
In the previous analysis of three-dimensional random walk [28], is found to be around for both equal-lateral and non-equal lateral case, so it is speculated to be universal. This equation describes the probability of a given field line between sunspots of distance L to be unknotted, so naturally the probability of field lines being knotted between sunspots is . With the increase of the length L, the probability for it being knotted increases exponentially, and thus it become almost certainly knotted as L tends to infinity,
As shown in Figure 1, we plot schematically the knot probability of different knot types as a function to the distance L. indicates the probability of the field line being knotted, and it is natural that, with the increase of the distance, the probability of the field lines being knotted increases. Furthermore, represent the probability of a single knot, while and represent the probability of composite knots with two and three components. With the increase of the number of component, the position of the peak of the probability curve shifts right, and the amplitude decreases. This suggests that when L is small, the dominant knot type is prime knots, which are knots with only one component; while when L increases, it is more common to find composite knots, which is the combination of multiple knots. Therefore, with the increase of distance, the variety of knot type increases as they are dominantly composite knots.
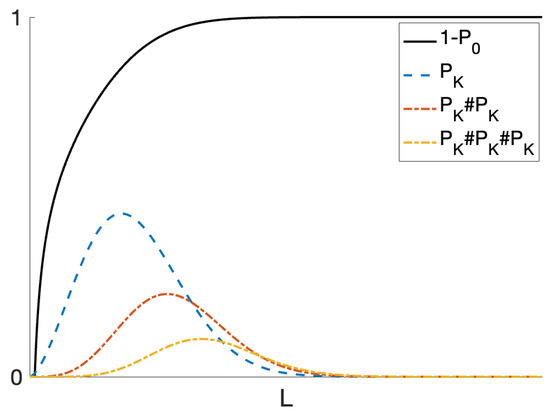
Figure 1.
A schematic plot for the knot probability of field lines as function to distance L between foot-points of sunspot. The probability of different knot types are plotted in different colors and patterns.
Based on Equation (9), we find the ratio of the probability of two knot types, and , to be
if is a constant. Furthermore, since , where is the number of component, we may further simplify the equation and get
Thus, if we consider the ratio of the probability of a two-component composite knot whose is 2, over a single knot whose is 1, then it would be
and the ratio of the probability of two single knots, since , is a constant
independent to length L. The probability amplitude decreases with the knot’s crossing in an exponential trend in three-dimensional random walks [28]. In measurement, the constant ratio of two certain knots with the same number of component could serve as a calibration to the randomness of local solar magnetic fields.
In a recent study [29], it is shown that solar dynamo activities begin near the surface, and have a high resemblance of near-surface instability. This result suggests that the magnetic rope may start being knotted near the surface. Based on this result, Equation (9) suggests that there is a minimum distance threshold for sunspots to have knotted field lines. According to Equation (9), if the distance between the two ends of a magnetic field line is very short, the field lines cannot be knotted, and thus have zero helicity. Therefore, Equation (9) suggests that active regions with non-zero magnetic helicity must not be too small, which agrees with previous observations.
3. Relation Between Knotting and Magnetic Energy
As we have discussed the knot probability of random magnetic field lines in Section 2, in this section we emphasize its physical meaning by discussing its relation to magnetic energy. Magnetic energy M is defined as
and it is found that the magnetic energy M has a logarithmic increase with the crossing number of the knot [30]. Tight knots are knots under relaxation and the radius of the tube reaches the possible maximum, so that the tubes are thick enough so that they are squeezing one another. When the knots are sorted based on their crossing number, the knot type indices are denoted as . Through the analysis of simulation on tight knots, the best fit relation is found [30] to be
where for knots, and for links. This result reveals the relation between the magnetic energy of knotted field lines and the complexity of knots. While there are different values of b in the equation, it is universal for knotted field lines that the energy increases logarithmically with the knot type crossing number . Meanwhile, from [28], we find the probability in terms of as
suggesting that, with the increase of , the probability for its existence decreases exponentially. These two equations together suggests a description of the energy probability distribution of knotted field lines based on tight prime knots. In terms of tight prime knots, with the increases of crossing number, the energy increases slowly in Log function, while its probability decreases exponentially quickly. In this case, if one considers a random set of prime knots, it would have a very low probability for high energy knots, because the energy increases logarithmically slowly with the crossing number, while such probability decreases exponentially quickly, and would thus lead to a almost evenly distributed energy spectrum for knots.
Therefore, this analysis suggests that, in order to explain the strong and abrupt activities in solar corona, the knotted field lines are not always tight prime knots in static equilibrium, but rather a diverse state of knotting, and further including a frequent change of knot type through reconnections. This is because, if the solar magnetic field lines are mainly simple prime knots, then they would have a very similar amount of energy, which is contradictory to observation [31] that the energy distribution falls into a power-law crossing several magnitudes. Therefore, the field lines must have a great variety of knotting, yet so far with current observation resolution we are unable to tell the specific twisting and self-linking of the field lines directly. Rather than simple prime knots, the field lines need to form various composite knots, including through reconnections, so that the energy of different magnetic ropes could be different in magnitude from one another. In the future, we may further investigate the knotted field lines through the reconstruction of magnetic fields from magnetograms, and with a higher resolution observation we may better find the knotting situation of field lines, so we would have a more precise knowledge regarding the relation between energy and knotting probability of flied lines.
4. Conclusions and Discussion
In this paper, we study the knotting probability of magnetic field lines based on the knowledge of the knotting probability of random walks. We find a universal probability equation for different knot types as a function to the length between the foot-points of sunspot in Equation (9), and their relative probability ratio in Equation (12). We discuss the relation between knot probability and the statistical behavior of solar magnetic fields, such as the scale range of the randomness in the magnetic field. Furthermore, through the relation between the crossing number of knots and the corresponding magnetic energy of tight knots, we study the relation between knot probability and energy, and provide statistical analysis to support the assumption that the field lines form a variety of composite knots rather than simple tight prime knots, and there are reconnections to change the knot type. Even though the specific field line knotting cannot be directly observed in great detail with current tools, in the future, with higher resolution images and reconstruction of the magnetic field based on magnetogram, such as by the nonlinear-force-free-field method [19], we may further investigate the knotting and energy of magnetic field lines in active regions. We hope this result helps future statistical analysis on solar magnetic topology and dynamics.
Author Contributions
A.X., S.Y. and X.L. proposed the research and wrote the paper. All authors have read and agreed to the published version of the manuscript.
Funding
This research is supported by the National Key R&D Program of China (grant Nos. 2022YFF0503800, 2021YFA1600500, 2022YFF0503001); the National Natural Science Foundation of China (grant Nos. 12250005, 12073040, 12273059, 11973056, 12003051, 11573037, 12073041, 11427901, 11572005 and 11611530679); the Strategic Priority Research Program of the Chinese Academy of Sciences (grant Nos. XDB0560000, XDA15052200, XDB09040200, XDA15010700, XDB0560301, and XDA15320102); by the Chinese Meridian Project (CMP); and by Beijing Natural Science Foundation (grant Nos. IS23030, Z180007).
Data Availability Statement
The data is available from the author.
Acknowledgments
We thank Renzo Ricca and Mark Dennis for valuable discussions.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Schmieder, B.; Démoulin, P.; Aulanier, G. Solar filament eruptions and their physical role in triggering Coronal Mass Ejections. Adv. Space Res. 2012, 51, 1967–1980. [Google Scholar]
- Liu, R. Magnetic Flux Ropes in the Solar Corona: Structure and Evolution toward Eruption. Res. Astron. Astrophys. 2020, 20, 165. [Google Scholar]
- Chen, J. Theory of prominence eruption and propagation: Interplanetary consequences. J. Geophys. Res. 1996, 101, 27499–27520. [Google Scholar]
- Moore, R.L.; Sterling, A.C.; Hudson, H.S.; Lemen, J.R. Onset of the magnetic explosion in solar flares and coronal mass ejections. Astrophys. J. 2001, 552, 833–848. [Google Scholar]
- Török, T.; Kliem, B. Confined and Ejective Eruptions of Kink-unstable Flux Ropes. Astrophys. J. 2005, 630, 97–100. [Google Scholar] [CrossRef]
- Wang, W.; Qiu, J.; Liu, R.; Zhu, C.; Yang, K.E.; Hu, Q.; Wang, Y. Investigating pre-eruptive magnetic properties at the footprints of erupting magnetic flux ropes. Astrophys. J. 2023, 943, 80. [Google Scholar]
- Zhao, A.; Wang, Y.; Feng, H.; Xu, M.; Zhao, Y.; Zhao, G.; Hu, Q. The twist profile in the cross-section of interplanetary magnetic clouds. Astrophys. J. Lett. 2018, 869, L13. [Google Scholar] [CrossRef]
- Gou, T.; Liu, R.; Veronig, A.M.; Zhuang, B.; Li, T.; Wang, W.; Xu, M.; Wang, Y. Complete replacement of magnetic flux in a flux rope during a coronal mass ejection. Nat. Astron. 2023, 7, 815–824. [Google Scholar]
- Woltjer, L. A Theorem on Force-Free Magnetic Fields. Proc. Natl. Acad. Sci. USA 1958, 44, 489–491. [Google Scholar] [CrossRef]
- Berger, M. Introduction to magnetic helicity. Plasma Phys. Control. Fusion 1999, 12, B167. [Google Scholar]
- Zhang, H. Solar Magnetism; Springer: Singapore.
- Chae, J.; Wang, H.; Qiu, J.; Goode, P.R.; Strous, L.; Yun, H.S. The formation of a prominence in active region NOAA 8668. I. SOHO/MDI observations of magnetic field evolution. Astrophys. J. 2001, 12, 476. [Google Scholar]
- Yang, S.; Zhang, H.; Büchner, J. Magnetic helicity accumulation and tilt angle evolution of newly emerging active regions. Astron. Astrophys. 2009, 9, 333–340. [Google Scholar] [CrossRef]
- Yang, S.; Liu, S.; Su, J.; Deng, Y. Comparison of Relative Magnetic Helicity Flux Calculation Results Based on the Line-of-Sight Magnetograms of ASO-S/FMG and SDO/HMI. Sol. Phys. 2025, 300, 1–12. [Google Scholar] [CrossRef]
- LaBonte, B.J.; Georgoulis, M.K.; Rust, D.M. Survey of Magnetic Helicity Injection in Regions Producing X-Class Flares. Astrophys. J. 2007, 671, 955. [Google Scholar] [CrossRef]
- Wang, Q.; Yang, S.; Zhang, M.; Yang, X. Comparison of Two Methods for Calculating Magnetic Helicity in the Solar Corona. Astrophys. J. 2022, 929, 122. [Google Scholar]
- Yang, S.; Buechner, J.; Santos, J.C.; Skala, J.; Zhang, H. Relative Alpha in the Magneto-Hydro-Dynamics (MHD) with open magnetic field boundary and its application to the solar eruption. Astrophys. J. 2025, 980, 206. [Google Scholar]
- Nakariakov, V.M.; Ofman, L.; Deluca, E.E.; Roberts, B.; Davila, J.M. TRACE Observation of Damped Coronal Loop Oscillations: Implicating for Coronal Heating. Science 1999, 285, 862–864. [Google Scholar] [CrossRef]
- Wiegelmann, T.; Sakurai, T. Solar force-free magnetic fields. Living Rev. Sol. Phys. 2021, 18, 1. [Google Scholar] [CrossRef]
- Moffatt, H.K.; Ricca, R.L. Helicity and the Călugăreanu invariant. Proc. R. Soc. A 1992, 11, 411–429. [Google Scholar]
- Roberts, P.H. Lectures on Solar and Planetary Dynamos; Proctor, M.R.E., Gilbert, A.D., Eds.; Cambridge University Press: Cambridge, UK, 1994; pp. 1–58. [Google Scholar]
- Taylor, A.; Dennis, M. Vortex knots in tangled quantum eigenfunctions. Nat. Commun. 2016, 7, 12346. [Google Scholar]
- Barenghi, C.F.; Skrbek, L.; Sreenivasan, K.R. Quantum Turbulence; Cambridge University Press: Cambridge, UK, 2023. [Google Scholar]
- Xiong, A.; Yang, S.; Wang, Q.; Liu, X. Fractality of Magnetic Helicity Distribution in the Solar Corona. Astrophys. J. 2025, 980, 266. [Google Scholar] [CrossRef]
- Fan, Y. Magnetic fields in the solar convection zone. Living Rev. Sol. Phys. 2021, 18, 5. [Google Scholar] [CrossRef]
- Nigro, G.; Malara, F.; Veltri, P. Resonant Behavior and Fluctuating Energy Storage in Coronal Loops. Astrophys. J. 2008, 685, 606–621. [Google Scholar] [CrossRef]
- Cadavid1, A.C.; Lawrence1, J.K.; Christian1, D.J.; Jess, D.B.; Nigro, G. Heating Mechanisms for Intermittent Loops in Active Region Cores from AIA/SDO EUV Observations. Astrophys. J. 2014, 795, 48. [Google Scholar] [CrossRef]
- Xiong, A.; Taylor, A.J.; Dennis, M.R.; Whittington, S.G. Knot probabilities in equilateral random polygons. J. Phys. Math. Theor. 2021, 9, 405001. [Google Scholar] [CrossRef]
- Vasil, G.M.; Lecoanet, D.; Augustson, K.; Burns, K.J.; Oishi, J.S.; Brown, B.P.; Brummell, N.; Julien, K. The solar dynamo begins near the surface. Nature 2021, 629, 769–772. [Google Scholar] [CrossRef]
- Ricca, R.; Maggioni, F. On the groundstate energy spectrum of magnetic knots and links. J. Phys. Math. Theor. 2014, 47, 205501. [Google Scholar] [CrossRef]
- Parnell, C.E.; Jupp, P.E. Statistical Analysis of the Energy Distribution of Nanoflares in the Quiet Sun. Astrophys. J. 2000, 529, 554–569. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).