Black Holes and de Sitter Space as Time Mirrors

Abstract

It is usually assumed that matter disappears together with the spacetime at the center of a Schwarzschild black hole (BH). Here, we find that if we impose a boundary condition that the field does not disappear at the BH center (that is, field flux into the singularity vanishes), the BH acts as a time mirror that totally reflects the infalling light and matter outside the BH. Namely, the reflected field propagates backward in time, passes the event horizon and moves away from the BH. In this case, a BH can be used as a time machine that allows us to send a signal into the past. We also show that de Sitter spacetime acts as a time mirror provided particles do not disappear from the spacetime at $r=\infty$.

1. Introduction

It was pointed out long ago that the existence of particles moving faster than light in a vacuum is not in contradiction with special relativity [1,2,3]. Feinberg called these hypothetical particles tachyons [3]. A generalization of the Lorentz transformation for the region $V>c$ has been proposed [4].

Despite many qualms in the physics community and the lack of direct experimental evidence, the possibilities and implications of tachyons have been a subject of interest among physicists [5,6,7,8]. For example, it has been claimed that some neutrinos may be tachyons [9,10,11].

If we disregard gravity, the geometry of our spacetime is described by the Minkowski metric. In the case of a 1 + 1 dimension, the interval reads

$$d{s}^2=d{t}^2-d{x}^2,$$

(1)

which is invariant under the Lorentz transformation of coordinates. In Equation (1), we set $c=1$ to make the time and space coordinates have the same units. Physically, the difference between t and x appears when we calculate the derivative $dx/dt$ along a worldline of a massive particle. If $|dx/dt|<1$, we associate t with the time coordinate and x with the spatial coordinate. Otherwise, t and x should be interchanged.

It is tacitly assumed that physical processes can “flow” only unidirectionally with time, from the past into the future, which is chosen as the positive direction on the time axis. This implies that the past affects the future, but the future can not affect the past. Mathematically, this assumption is formulated as the Cauchy problem, which consists of finding the solution of the evolution differential equations subject to the initial conditions at some value $t=t_0$. In the Cauchy problem, the initial conditions at $t=t_0$ can be imposed in a way that leaves no possibility for propagation backward in time, breaking the time-reversal invariance of the classical evolution equations.

In this paper, we do not restrict our analysis to the Cauchy problem and consider examples with time boundaries for which the solution of the evolution equations can be uniquely obtained without specifying initial conditions. We show that there are situations when propagation occurs backward in time and the future affects the past. Along the spatial coordinates, the physical processes can proceed in any direction. Then, why along the time coordinate can they not proceed in both directions as well?

We first consider the reflection of a massless scalar field $\varphi$ from a hypothetical “tachyonic” boundary (mirror) that propagates faster than light in a vacuum, and we impose a boundary condition that the field vanishes at the mirror surface. By making a conventional Lorentz transformation with subluminal velocity, one can choose an inertial frame in which the superluminal boundary has the worldline $t=t_0$. In this frame, the boundary condition reduces to $\varphi \left(t_0\right)=0$ everywhere in space.

Such a Lorentz transformation exists if the boundary moves at a speed greater than the speed of light in vacuum c. For example, a worldline

$$x+ut=0,u>c,$$

under Lorentz transformation

$$t={\displaystyle \frac{t^{\prime }-\beta x^{\prime }/c}{\sqrt{1-{\beta }^2}}},x={\displaystyle \frac{x^{\prime }-\beta c{t}^{\prime }}{\sqrt{1-{\beta }^2}}},$$

where $\beta =c/u<1$, transforms into the worldline $t^{\prime }=0$.

We show that we can satisfy the boundary condition only if we allow the reflected field to propagate backward in time. This is analogous to reflection from a static mirror for which the boundary condition is satisfied only if the field can move in both directions along the spatial coordinate.

The boundary condition $\varphi =0$ applies to the problem of light reflection from a moving perfect conductor. Indeed, in the Lorenz gauge, Maxwell’s equations read

$$\left({\displaystyle \frac{{\partial }^2}{\partial t^2}}-{\nabla }^2\right)\mathbf{A}={\mu }_0\mathbf{j},$$

where $\mathbf{A}$ is the vector potential, and $\mathbf{j}$ is the electric current density. For the problem of the reflection of electromagnetic waves from the surface of a perfect conductor at normal incidence, the vector potential $\mathbf{A}$ vanishes at the metal surface. This boundary condition for $\mathbf{A}$ (but not for the electric field $\mathbf{E}$) remains valid if the conductor is moving perpendicular to its flat surface at any speed.

Thus, in our analysis, the boundary condition $\varphi =0$ models the interaction of the field with a perfectly reflecting moving mirror. However, it is not clear how to realize such a boundary condition at superluminal mirror motion in laboratory experiments since the existence of tachyons remains questionable.

One should note that inhomogeneities in the refractive index partially reflect light and behave like mirrors. The reflection and transmission of a light pulse when passing through the superluminal inhomogeneities of the refractive index yield interesting phenomena, which have been investigated theoretically [12,13,14,15,16]. Such superluminal boundaries have also been demonstrated experimentally. For example, superluminal ionization fronts have been used to generate electromagnetic radiation [17]. In a nonlinear medium, one can make refractive index inhomogeneities propagate faster than light by creating interference between two laser beams with differing frequencies (flying mirrors). Recently, a temporal reflection at photonic time interfaces has been observed experimentally [18,19].

However, in these studies, the inhomogeneities did not yield the perfectly reflecting boundary condition at the superluminal surface, which allows transmission of the pulse through the interface. In this case, one can satisfy the boundary conditions assuming no backward-in-time reflected pulse and two transmitted pulses propagating in opposite directions.

However, in Section 3, we show that centers of static black holes act like perfectly reflecting superluminal mirrors if we impose a boundary condition that the field remains finite at the center. This boundary condition implies that the field does not disappear at the black hole center. Hence, the present problem could have applications in astrophysics.

Moreover, in Section 4, we show that de Sitter spacetime acts as a time mirror provided particles do not disappear from spacetime at $r=\infty$. This problem might be relevant to the early universe because the exponential expansion of space during cosmic inflation can be described by the de Sitter metric.

To gain insights into the physics of black holes and de Sitter space geometries, in the next section, we consider a fictitious superluminal perfect mirror in Minkowski spacetime. Since there is no evidence that the latter object can exist in nature, one can treat the problem as a simplified mathematical model of light reflection from the black hole center or the de Sitter space boundary.

2. Reflection of Light Backward in Time from a Superluminal Mirror

In this section, we consider hypothetical perfectly reflecting superluminal mirrors by imposing boundary condition $\varphi =0$ at the surface. In this case, there is no transmitted wave. We do not argue that such mirrors can (or cannot) be realized experimentally but rather study how light is reflected from them. As we show below, the backward-in-time reflection produced by such superluminal mirror yields a possibility of constructing a time machine that allows us to send a signal into the past. This leads to logical contradictions associated with time travel paradoxes, which might be an argument against the existence of time mirrors. Yet, the possibility of new physics cannot be ruled out.

To avoid ambiguities with field quantization, we consider a classical massless complex scalar field $\varphi (t,x)$ with 1 + 1 dimensions obeying a wave equation with a source located at the origin of the $t-x$ coordinate system

$$\left({\displaystyle \frac{{\partial }^2}{\partial t^2}}-{\displaystyle \frac{{\partial }^2}{\partial x^2}}\right)\varphi (t,x)={\delta }^{\prime }\left(t\right)\delta \left(x\right),$$

(2)

where $\delta \left(x\right)$ is the Dirac delta function, and prime denotes the derivative of the delta function with respect to its argument. In this and the following section, we set $c=1$. The time derivative on the right-hand side in Equation (2) appears because the corresponding action must be invariant under Lorentz transformations. Indeed, Equation (2) can be obtained by taking the variation in the Lorentz invariant action

$$S=\int dtdx\left({\displaystyle \frac{\partial \varphi }{\partial t}}{\displaystyle \frac{\partial {\varphi }^{\ast }}{\partial t}}-{\displaystyle \frac{\partial \varphi }{\partial x}}{\displaystyle \frac{\partial {\varphi }^{*}}{\partial x}}-g\left(t\right)\delta \left(x\right){\displaystyle \frac{\partial }{\partial t}}\left(\varphi +{\varphi }^{*}\right)\right)$$

with respect to ${\varphi }^{*}$, where $g\left(t\right)=\delta \left(t\right)$ is a scalar coupling constant. Thus, Equation (2) can describe certain physical models. For example, the source in Equation (2) can be a two-level atom located at $x=0$ for which coupling with field $g\left(t\right)$ is suddenly turned on and turned off at $t=0$ as a delta function $\delta \left(t\right)$ [20]. From the perspective of the atom, the proper time of the atom determines the positive direction of the time axis t, and we adopt this convention here.

The general solution of Equation (2) reads

$$\varphi (t,x)={\displaystyle \frac{1}{2}}\delta (t-|x\left|\right)+F_1(t-x)+F_2(t+x),$$

(3)

where $F_1$ and $F_2$ are arbitrary functions.

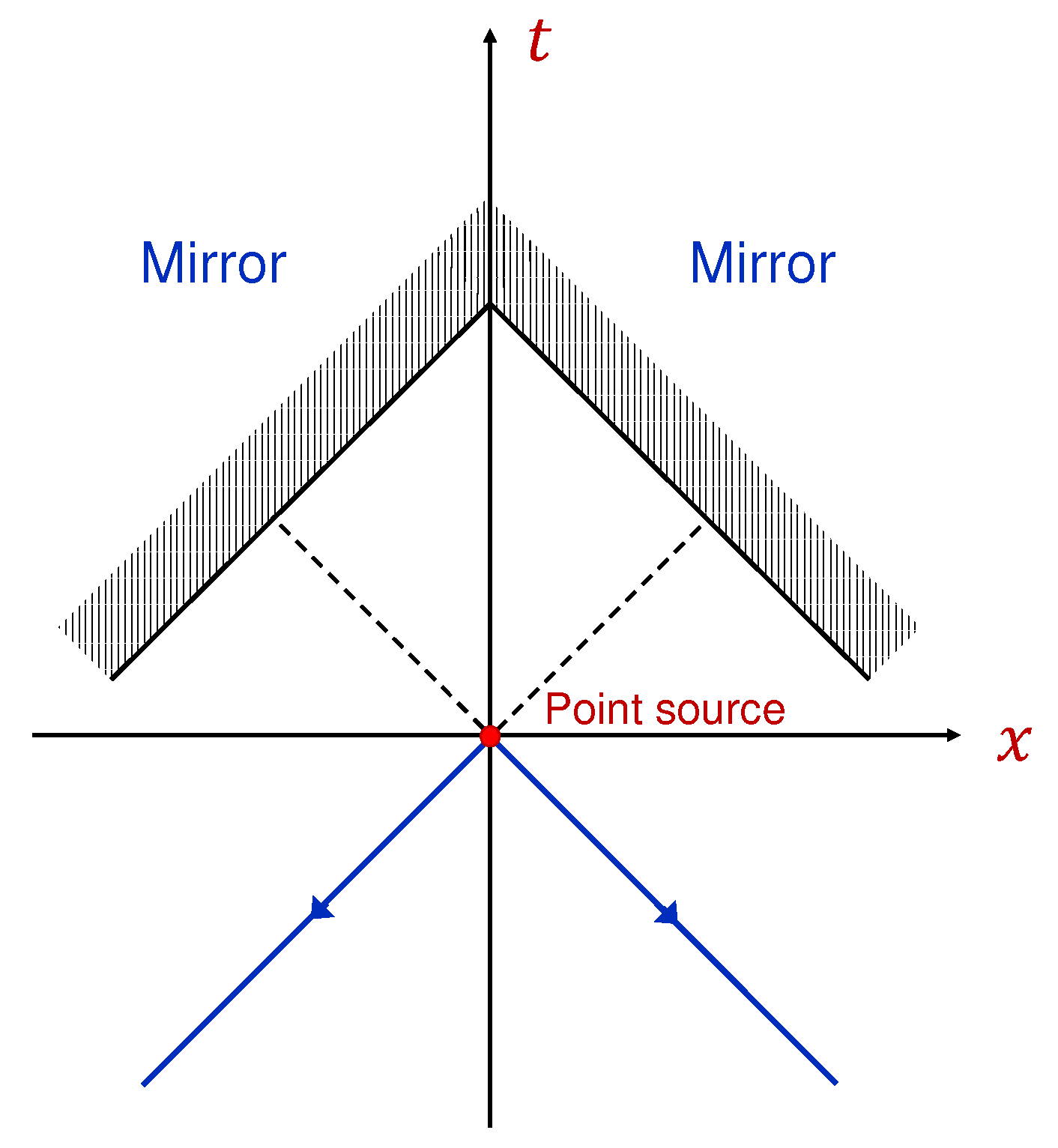
As the first example, we consider a situation for which $F_1$ and $F_2$ can be obtained uniquely without specifying the initial condition for the field. Namely, we assume that there are two hypothetical mirrors propagating with the speed of light along trajectories (see Figure 1)

$$t=d\pm x,$$

(4)

where $d>0$ (d is the time at which the mirrors pass the point $x=0$). At the position of the mirrors, the field $\varphi (t,x)$ must vanish; that is, $\varphi (d\pm x,x)=0$. This boundary condition yields the following constraints on $F_1$ and $F_2$:

$$F_1(t-x)=-{\displaystyle \frac{1}{2}}\delta (t-x)+F_1\left(d\right),$$

(5)

$$F_2(t+x)=-{\displaystyle \frac{1}{2}}\delta (t+x)-F_1\left(d\right).$$

(6)

Plugging Equations (5) and (6) into Equation (3) gives that the solution satisfying the boundary condition at the mirror’s surfaces is unique and is given by

$$\varphi (t,x)=-{\displaystyle \frac{1}{2}}\left[\delta (t-x)\theta (-x)+\delta (t+x)\theta \left(x\right)\right],$$

(7)

where $\theta \left(x\right)$ is the Heaviside step function. Solution (7) can be written as

$$\varphi (t,x)={\varphi }_1(t,x)+{\varphi }_2(t,x),$$

(8)

where

$${\varphi }_1(t,x)={\displaystyle \frac{1}{2}}\delta (t-|x\left|\right)={\displaystyle \frac{1}{2}}\delta (t-x)\theta \left(x\right)+{\displaystyle \frac{1}{2}}\delta (t+x)\theta (-x)$$

(9)

is a solution of Equation (2) with no mirrors that satisfies the “natural” initial condition $\partial {\varphi }_1(0,x)/\partial t={\varphi }_1(0,x)=0$, and

$${\varphi }_2(t,x)=-{\displaystyle \frac{1}{2}}\left[\delta (t-x)+\delta (t+x)\right].$$

(10)

Equation (8) can be interpreted as follows: The point source on the right-hand side in Equation (2) generates two $\delta$ - pulses propagating to the left and to the right toward the mirrors. This is described by the function ${\varphi }_1(t,x)$. The pulses are then reflected from the mirrors and propagate backward in time, which is described by ${\varphi }_2(t,x)$. Thus, the mirrors act as time mirrors. In the region $t>0$, the incident and reflected pulses cancel each other ($\varphi =0$). The net field propagates backward in time from the source into the region where $t<0$ (see Figure 1). If pulses could propagate only forward in time, then, in the region where $t<0$, the field must be equal to zero, which is not the case according to the unique solution (7).

This example demonstrates that the presence of the mirrors in the future affects how the source radiates in the past (at $t=0$), namely, no field appears in the region where $t>0$. If there are many point sources, then none of them would generate a field into the future region.

One can also interpret solution (7) as if two pulses are propagating from $t=-\infty$ forward in time toward the source and are absorbed by the source. However, in such interpretation, the two pulses are not generated by the source on the right-hand side in Equation (2), which is not the problem we are considering. Moreover, in such interpretation, the mirrors play no role because the pulses do not reach the mirrors.

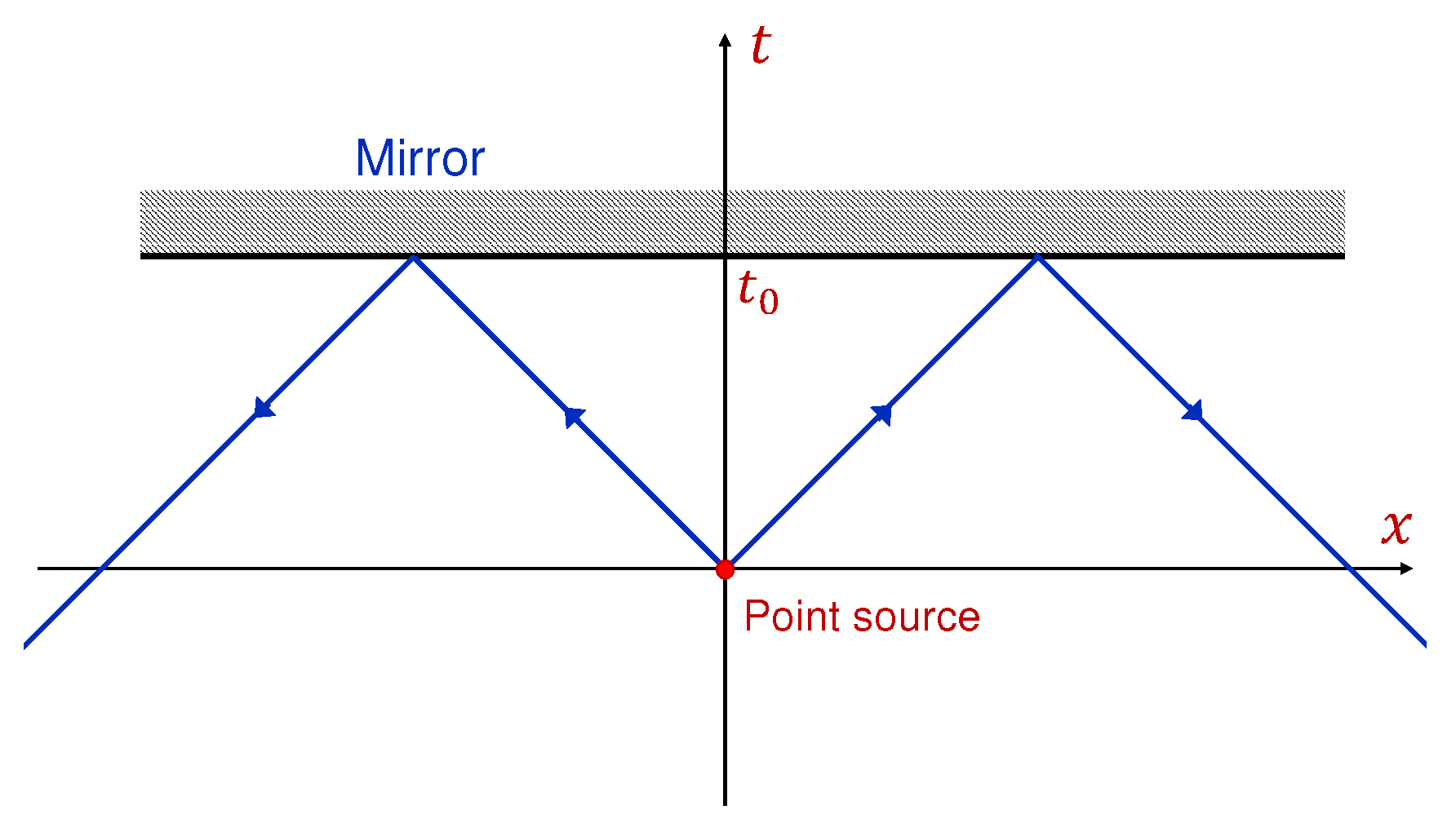
In the next example, we consider a hypothetical mirror moving along a trajectory $t=t_0>0$ (see Figure 2). That is, the field must satisfy the boundary condition

$$\varphi (t_0,x)=0$$

(11)

for any x. Plugging this boundary condition into the general solution (3) yields the following constraint:

$${\displaystyle \frac{1}{2}}\delta (t_0-\left|x\right|)+F_1(t_0-x)+F_2(t_0+x)=0.$$

(12)

The symmetry of the problem implies that $F_1=F_2$. As the pulse generated by the source on the right-hand side in Equation (2) is a combination of $\delta$-functions and the pulse trajectory must pass through the source, Equation (12) gives

$$F_1\left(y\right)=F_2\left(y\right)=-{\displaystyle \frac{C}{2}}\delta \left(y\right)-{\displaystyle \frac{1-C}{2}}\delta (y-2t_0),$$

where C is an arbitrary constant. Thus, the general solution of Equation (2) satisfying boundary condition (11) is

$$\varphi (t,x)={\displaystyle \frac{1}{2}}\delta (t-|x\left|\right)-{\displaystyle \frac{C}{2}}\left[\delta (t-x)+\delta (t+x)\right]-{\displaystyle \frac{1-C}{2}}\left[\delta (t-x-2t_0)+\delta (t+x-2t_0)\right].$$

(13)

The first term on the right-hand side in Equation (13) is a solution of Equation (2) with no mirror, which describes the left and right propagating $\delta$-pulses generated by the source. Since it is a solution with no mirror, we interpret these $\delta$-pulses as propagating forward in time. At $t=t_0$, the pulses are reflected from the mirror. The reflection produces $\delta$-pulses propagating backward in time along the same spacetime trajectory (the second term proportional to C) and along the reflected trajectory (the last term in Equation (13)).

In this example, the boundary condition at the mirror surface is not sufficient to specify the value of the integration constant C. However, for the present geometry, the problem of the field interaction with the mirror is transitionally invariant along the x-axis, which yields the conservation of the field momentum during reflection. Therefore, we must take $C=0$. Then, solution (13) reduces to

$$\varphi (t,x)={\displaystyle \frac{1}{2}}\delta (t-|x\left|\right)-{\displaystyle \frac{1}{2}}\left[\delta (t-x-2t_0)+\delta (t+x-2t_0)\right],$$

(14)

which is sketched in Figure 2. Solution (14) has the following interpretation: the point source generates left and right propagating $\delta$-pulses moving forward in time (the first term), which are reflected from the mirror at $t=t_0$ and propagate backward in time (the second term).

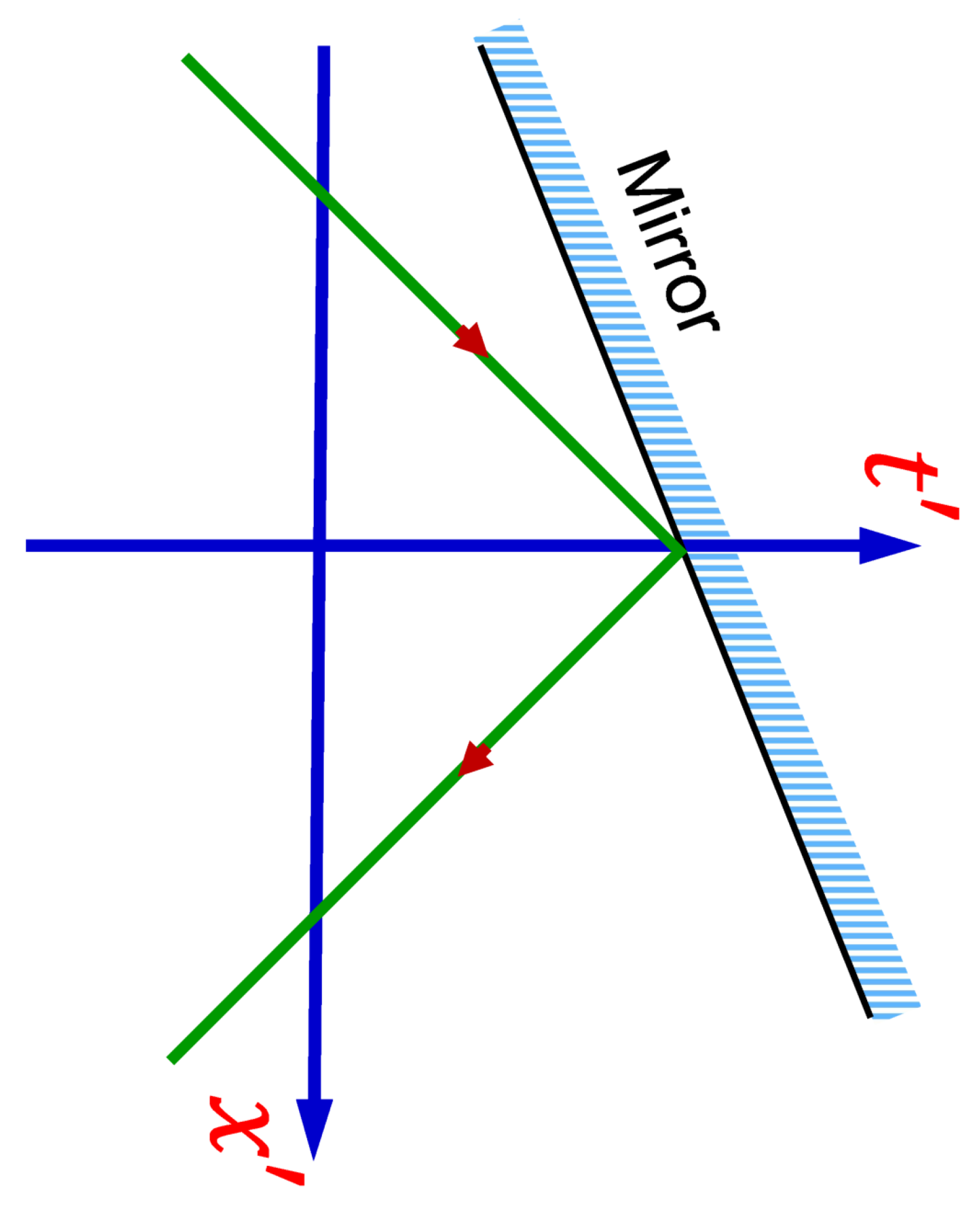
Thus, the $t=t_0$ mirror acts as a time mirror: after reflection from such a mirror, the field propagates backward in time. It turns out that any superluminal mirror, with the boundary condition $\varphi =0$ at the mirror surface, acts as a time mirror. Indeed, let us consider part of the solution (14) for $x>0$, that is,

$${\varphi }_{+}={\displaystyle \frac{1}{2}}\delta (t-x)-{\displaystyle \frac{1}{2}}\delta (t+x-2t_0),$$

(15)

in a moving frame by making the Lorentz transformation of the coordinates

$$x={\displaystyle \frac{x^{\prime }-V{t}^{\prime }}{\sqrt{1-V^2}}},t={\displaystyle \frac{t^{\prime }-V{x}^{\prime }}{\sqrt{1-V^2}}},$$

(16)

where $V<1$. In the new coordinates, Equation (15) becomes

$${\varphi }_{+}\propto {\displaystyle \frac{1}{2}}\delta (t^{\prime }-x^{\prime })-{\displaystyle \frac{1}{2}}\delta \left(t^{\prime }+x^{\prime }-{\displaystyle \frac{2\sqrt{1+V}}{\sqrt{1-V}}}{t}_0\right),$$

(17)

while the mirror is moving along trajectory

$$x^{\prime }={\displaystyle \frac{1}{V}}\left(t^{\prime }-\sqrt{1-V^2}{t}_0\right)$$

with superluminal speed $u=d{x}^{\prime }/d{t}^{\prime }=1/V>1$. Solution (17) is sketched in Figure 3.

Equation (17) shows that the $\delta$-pulse produced by the source and propagating forward in time (the first term) is reflected from the superluminal mirror at the spacetime point

$$x^{\prime }=t^{\prime }={\displaystyle \frac{\sqrt{1+V}}{\sqrt{1-V}}}{t}_0$$

and then propagates backward in time (the second term). Thus, the superluminal mirrors act as the time mirrors.

Pulses propagating backward in time interact differently with atoms. Namely, such pulses behave as if they have negative energy, and, as a result, ground-state atoms cannot become excited by absorbing them. Instead, the process looks like a ground-state atom becoming excited by emitting a photon. Indeed, the interaction Hamiltonian between a two-level atom located at $x=x_0$ and a classical field $\varphi (t,x)$ reads

$$\hat{V}\left(t\right)=g\left(\hat{\sigma }{e}^{-i\omega t}+{\hat{\sigma }}^{†}{e}^{i\omega t}\right)\varphi (t,x_0),$$

(18)

where $\omega >0$ is the atomic transition frequency, $\hat{\sigma }$ and ${\hat{\sigma }}^{†}$ are the atomic lowering and raising operators, g is the atom–field coupling constant, and field $\varphi (t,x)$ is taken at the atom’s location $x_0$. If there is a time mirror at $t=0$, then the plane-wave modes of the field satisfying boundary condition $\varphi (0,x)=0$ at the mirror surface are

$${\varphi }_{\nu }(t,x)=e^{-i\nu t+i\nu x}-e^{i\nu t+i\nu x},$$

(19)

where $\nu$ is a parameter that we assume to be positive ($\nu >0$). The first term in the right hand side of Equation (19) describes a plane wave with positive energy propagating toward the mirror. This wave can yield the excitation of the ground-state atom through the term ${\hat{\sigma }}^{†}{e}^{i\omega t}{e}^{-i\nu t+i\nu x_0}$ in the Hamiltonian, which becomes time-independent under the resonance condition $\nu =\omega$. In contrast, the wave reflected from the mirror (the second term in Equation (19)) cannot excite the atom because the part of the Hamiltonian describing the atom’s excitation ${\hat{\sigma }}^{†}{e}^{i\omega t}{e}^{i\nu t+i\nu x_0}$ is a fast oscillating function of time for any $\nu >0$. If $\nu =\omega$, the reflected wave can yield resonant de-excitation of the excited atom through the term $\hat{\sigma }{e}^{-i\omega t}{e}^{i\nu t+i\nu x_0}$ in the Hamiltonian, which implies that the wave has negative energy.

From the perspective of a subluminal (e.g., fixed in space) observer, the field is evolving in the forward direction of the observer’s proper time, and the latter process looks as if the ground-state atom becomes excited by emitting a negative-energy pulse (photon). One should note that negative-energy photons appear in various physical problems [21,22,23,24,25]. For example, in the reference frame moving faster than the speed of light in a medium, photons propagating inside the Cherenkov cone have negative energy [20,26]. This leads to Cherenkov radiation. Similar effects occur in the case of surface waves, for example, surface plasmons. In the moving frame, the surface plasmon frequency is Doppler-shifted, and, for large wave numbers, the shifted frequency becomes negative. As a result, a ground-state atom moving above a metal surface can become excited by emitting a negative-energy surface plasmon [27]. The negative energy of the surface plasmon ensures energy conservation in the process of atom excitation.

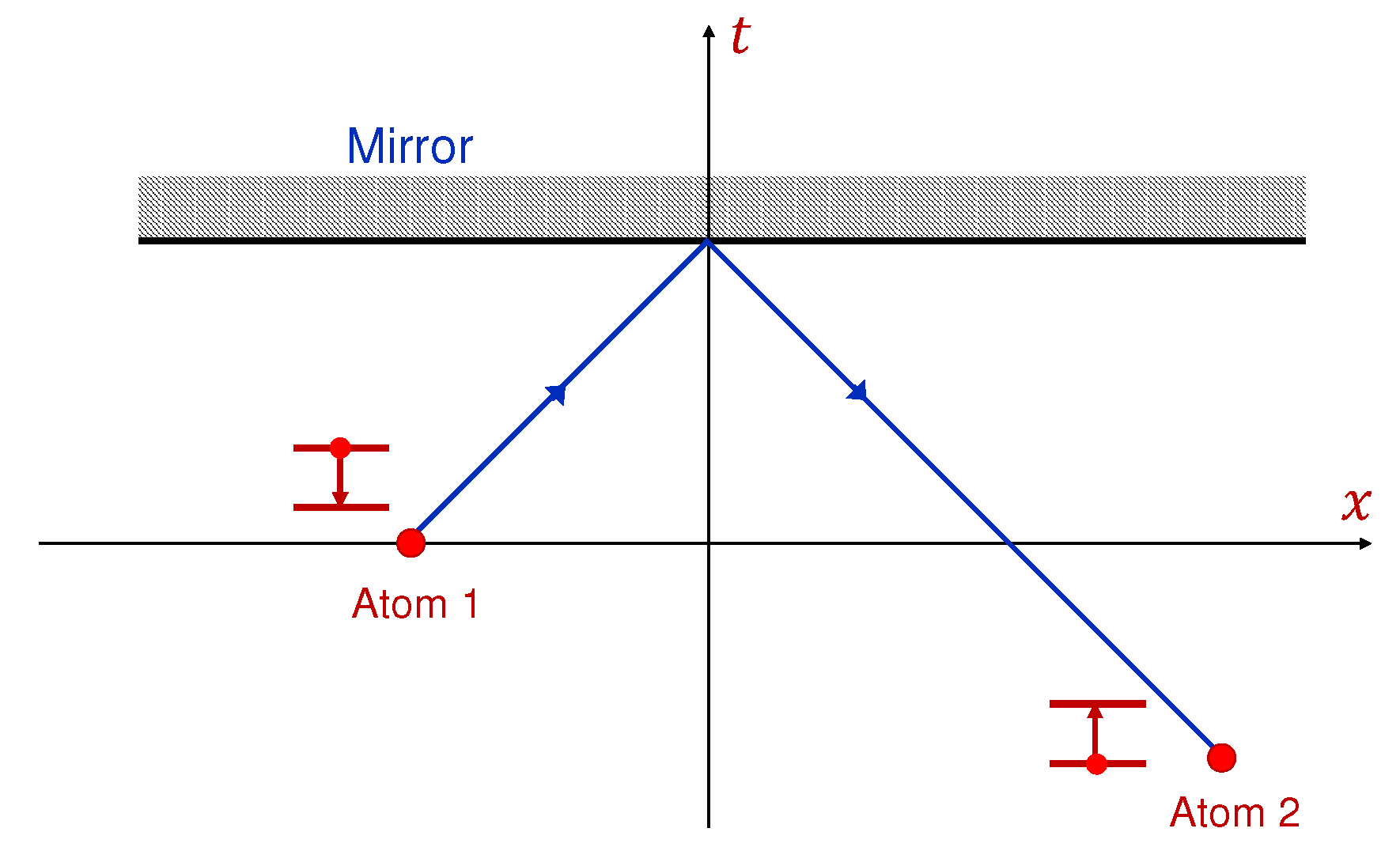
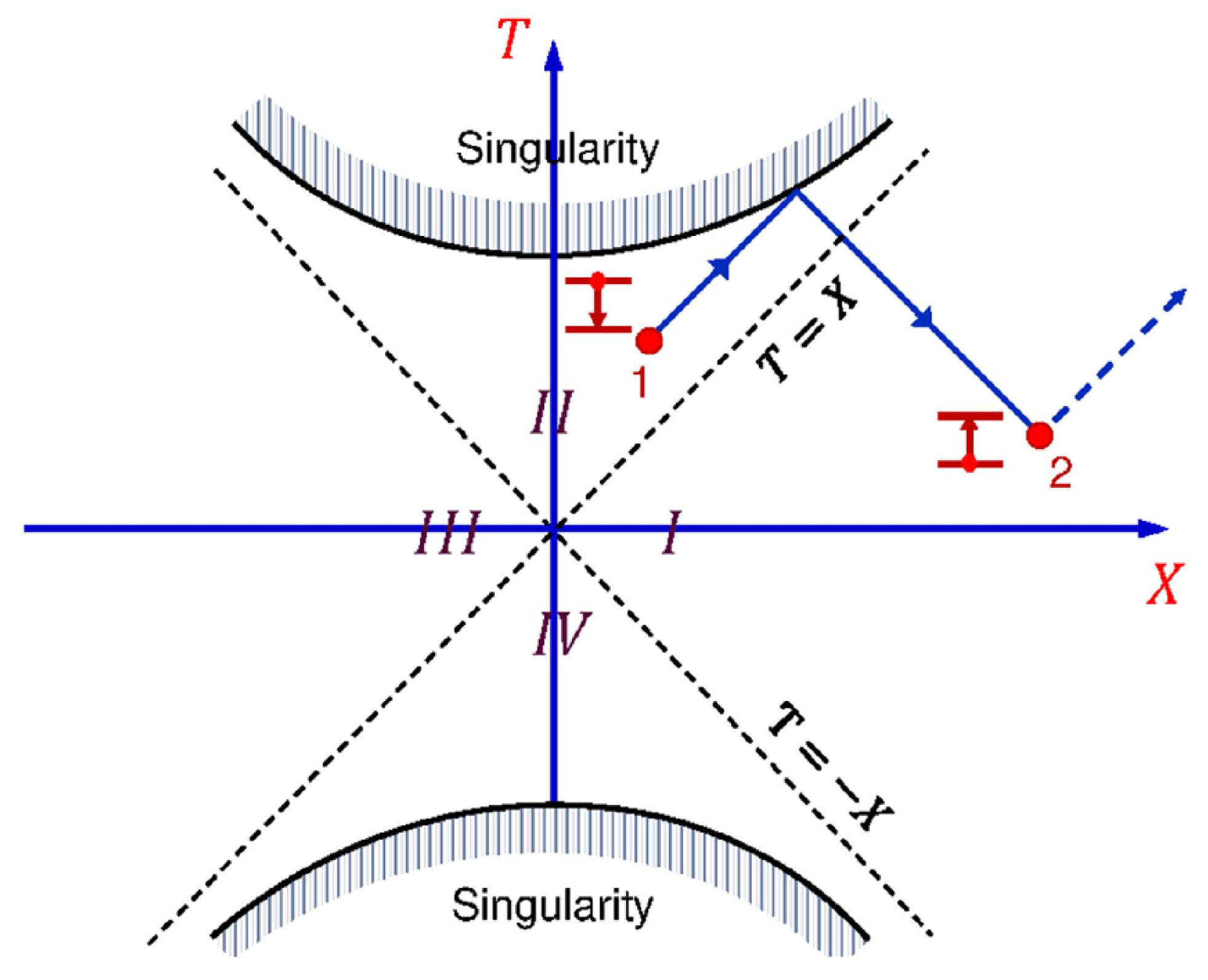
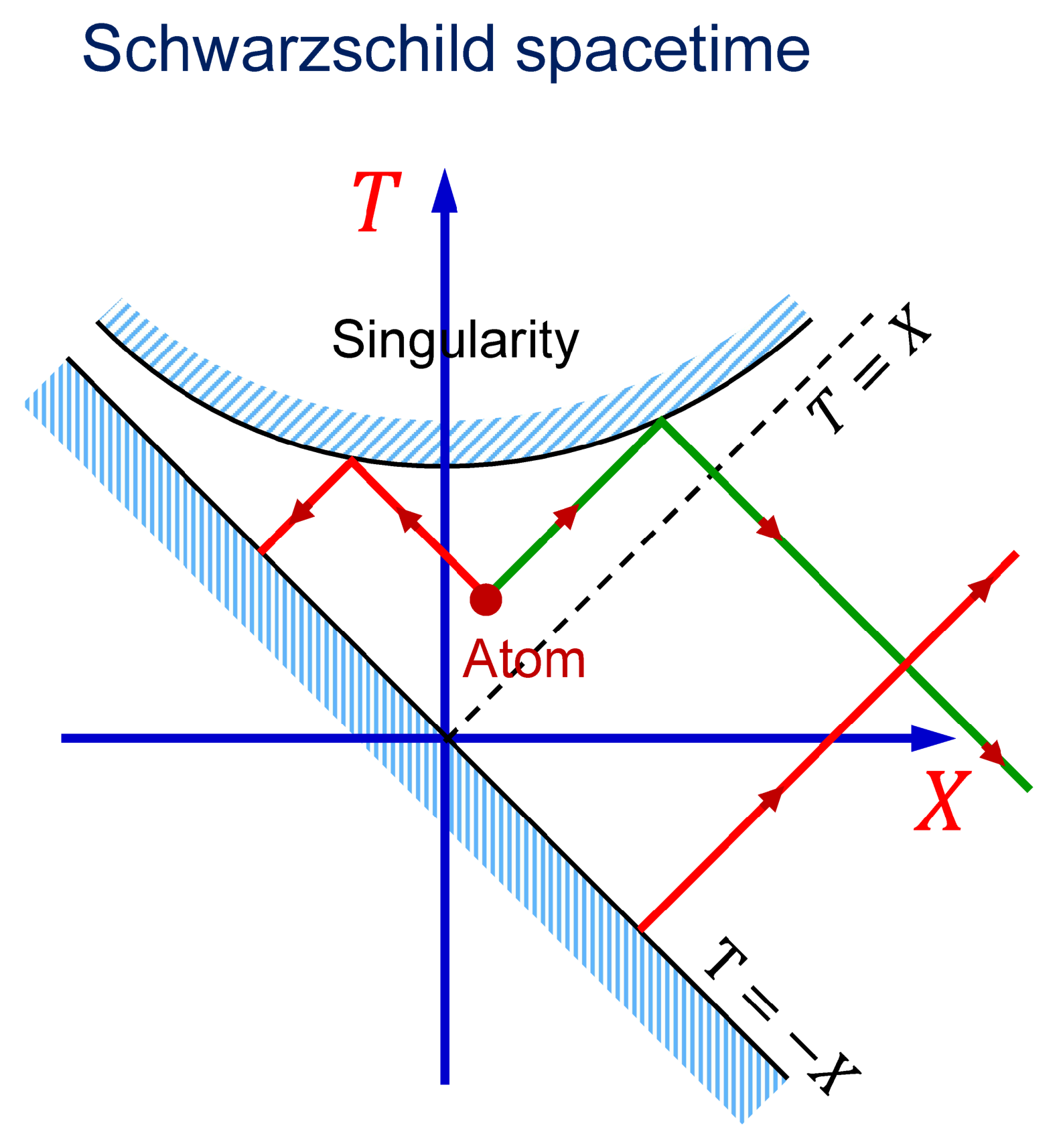
Despite similarities, the mentioned negative-energy excitations are different from the pulses propagating backward in time. The latter have negative energy in the lab frame and can violate causality; that is, the future can affect the past. Figure 4 shows an excited atom 1, which at time $t_1$ spontaneously emits a photon propagating forward in time. After reflection from the superluminal mirror ($t=t_0$), the photon propagates backward in time and can excite an atom 2 at $t_2<t_1$. The process looks like atom 2 becomes excited by emitting a photon. However, the cause of the excitation of atom 2 is photon emission by atom 1 at a later moment in time.

One should note that in the quantum description of the field, the appearance of negative frequencies in field mode functions (19) implies particle production. That is, a superluminal mirror generates photons [16]. In the present classical treatment, this effect does not appear.

Changing the sign of the frequency of a wave reflected from a superluminal mirror can be also understood considering the reflection of plane waves. The net field is the sum of the incident (right propagating) and reflected (left propagating) waves, with frequencies ${\nu }_i>0$ and ${\nu }_r$, respectively,

$$\varphi (t,x)=A_i{e}^{-i{\nu }_{i}t+i{k}_{i}x}+A_r{e}^{-i{\nu }_{r}t-i{k}_{r}x},$$

where $k_i={\nu }_i/c$, and $k_r={\nu }_r/c$. At the surface of a mirror moving with velocity u to the left ($z=-ut$), the field vanishes, which yields

$${\nu }_r={\displaystyle \frac{c+u}{c-u}}{\nu }_i.$$

(20)

Equation (20) shows that if the mirror is superluminal ($u>c$), the frequency of the reflected wave is negative.

3. Black Hole Center as a Superluminal Mirror

In this section, we show that the centers of static black holes (BHs) act like perfectly reflecting superluminal mirrors if we impose a boundary condition that the field remains finite at the center. This boundary condition implies that the field does not disappear at the BH center. That is, the field flux through a sphere with small radius r vanishes at the limit $r\to 0$. After reflection from the BH center, infalling light and matter propagate backward in time and escape from the BH. If true, accreting BHs could be bright rather than dark objects in the sky.

To gain insight into the effect, we first consider a scalar field $\varphi$ in flat Minkowski spacetime in 3 + 1 dimensions. Field $\varphi$ obeys the wave equation

$$\left({\displaystyle \frac{{\partial }^2}{\partial t^2}}-{\nabla }^2\right)\varphi =0.$$

(21)

For spherically symmetric solutions, the origin of the spherical coordinate system $r=0$ acts as a mirror, where r is the spherical radial coordinate. Indeed, in spherical coordinates, Equation (21) reduces to

$${\displaystyle \frac{{\partial }^2\varphi }{\partial t^2}}-{\displaystyle \frac{{\partial }^2\varphi }{\partial r^2}}-{\displaystyle \frac{2}{r}}{\displaystyle \frac{\partial \varphi }{\partial r}}=0.$$

(22)

Introducing a new function

$$\tilde{\varphi }=r\varphi ,$$

(23)

we find that $\tilde{\varphi }$ obeys the one-dimensional wave equation

$${\displaystyle \frac{{\partial }^2\tilde{\varphi }}{\partial t^2}}-{\displaystyle \frac{{\partial }^2\tilde{\varphi }}{\partial r^2}}=0,$$

(24)

and, according to Equation (23), it satisfies the mirror-like boundary condition

$${\left.\tilde{\varphi }\right|}_{r=0}=0.$$

(25)

That is, $\tilde{\varphi }(t,r)$ describes waves propagating in free space with a mirror boundary at $r=0$.

Often, for simplicity, spherically symmetric problems in 3 + 1 dimensions are modeled by truncating spacetime into 1 + 1 dimensions. In this procedure, Equation (21) is written in 1 + 1 dimensions, which yields

$${\displaystyle \frac{{\partial }^2\varphi }{\partial t^2}}-{\displaystyle \frac{{\partial }^2\varphi }{\partial r^2}}=0.$$

(26)

The truncated spacetime is confined into the region $r\ge 0$. Equation (26), however, does not specify the boundary condition for field $\varphi$ at the spacetime boundary. One can obtain the boundary condition from Equation (22) in 3 + 1 dimensions by writing it as

$${\displaystyle \frac{\partial \varphi }{\partial r}}={\displaystyle \frac{r}{2}}\left({\displaystyle \frac{{\partial }^2\varphi }{\partial t^2}}-{\displaystyle \frac{{\partial }^2\varphi }{\partial r^2}}\right).$$

(27)

Requiring the field derivatives to be finite everywhere, and taking the limit $r\to 0$ in Equation (27), we obtain the boundary condition for $\varphi$:

$${\left.{\displaystyle \frac{\partial \varphi }{\partial r}}\right|}_{r=0}=0,$$

(28)

which can be used in the truncated 1 + 1-dimensional model to mimic spherical symmetry of the original 3 + 1-dimensional problem. Equations (26) and (28) in truncated spacetime can be mapped into the exact 3 + 1-dimensional Equations (24) and (25) by introducing anew function $\tilde{\varphi }=\partial \varphi /\partial r$, which obeys Equations (24) and (25). Thus, the truncated spacetime model can capture the essential physics provided we impose the proper boundary condition.

General relativity predicts the existence of BHs. An eternal static BH of mass M in 3 + 1 dimensions in Schwarzschild coordinates is described by the metric

$$d{s}^2=\left(1-{\displaystyle \frac{r_g}{r}}\right)d{t}^2-{\displaystyle \frac{1}{1-\frac{r_g}{r}}}d{r}^2-r^2\left(d{\theta }^2+{sin}^2\theta d{\phi }^2\right),$$

(29)

where $r_g=2GM/c^2$ is the gravitational radius.

BH spacetime has an event horizon at $r=r_g$. If it would be possible to hold a mirror at a fixed r inside the event horizon, such a mirror would act as a time mirror. Next, we show that the problem of reflection from the BH center ($r=0$) is mathematically similar to the reflection from the fictitious superluminal mirror in Minkowski spacetime discussed in the previous section.

BHs have a curvature singularity at $r=0$, which, however, is not responsible for the present effect. Namely, the mirror-like boundary condition at $r=0$ appears due to the spherical symmetry of the 3 + 1 dimensional problem, while the mirror trajectory is superluminal because it is located inside the event horizon.

Here, we consider a massless scalar field $\varphi$ in Schwarzschild spacetime that obeys the covariant wave equation

$${\displaystyle \frac{1}{\sqrt{-g}}}{\displaystyle \frac{\partial }{\partial x^{\mu }}}\left(\sqrt{-g}{g}^{\mu \nu }{\displaystyle \frac{\partial \varphi }{\partial x^{\nu }}}\right)=0,$$

(30)

where $g^{\mu \nu }$ is the spacetime metric given by the interval (29), namely,

$$g^{tt}={\displaystyle \frac{1}{1-\frac{r_g}{r}}},g^{rr}={\displaystyle \frac{r_g}{r}}-1,\sqrt{-g}=r^{2}sin\theta .$$

In the following, we use the gravitational radius as a unit of length and $r_g/c$ as a unit of time. To make a straightforward analogy with the superluminal mirror, we use the Kruskal–Szekeres coordinates, which are defined in terms of the Schwarzschild coordinates t, r as

$$T=\sqrt{r-1}{e}^{\frac{r}{2}}sinh\left({\displaystyle \frac{t}{2}}\right),X=\sqrt{r-1}{e}^{\frac{r}{2}}cosh\left({\displaystyle \frac{t}{2}}\right),$$

for $r>1$, and

$$T=\sqrt{1-r}{e}^{\frac{r}{2}}cosh\left({\displaystyle \frac{t}{2}}\right),X=\sqrt{1-r}{e}^{\frac{r}{2}}sinh\left({\displaystyle \frac{t}{2}}\right),$$

(31)

for $0<r<1$. With these coordinates, the BH center ($r=0$) is a space-like line $T^2-X^2=1$ along which $|dX/dT|=T/\sqrt{T^2-1}>1$. The line $T^2-X^2=1$ sets a boundary on Schwarzschild spacetime in Kruskal–Szekeres coordinates (see Figure 5). With these coordinates, the Schwarzschild metric reads

$$d{s}^2={\displaystyle \frac{4}{r}}{e}^{-r}\left(d{T}^2-d{X}^2\right)-r^2\left(d{\theta }^2+{sin}^2\theta d{\phi }^2\right),$$

(32)

and, for a spherically symmetric problem (no dependence on angles $\theta$ and $\phi$), Equation (30) reduces to

$${\displaystyle \frac{{\partial }^2\varphi }{\partial T^2}}-{\displaystyle \frac{{\partial }^2\varphi }{\partial X^2}}-{\displaystyle \frac{4}{r^2}}{e}^{-r}\left(X{\displaystyle \frac{\partial \varphi }{\partial X}}+T{\displaystyle \frac{\partial \varphi }{\partial T}}\right)=0,$$

(33)

where the dependence of r on T and X is given by

$$\left(r-1\right)e^r=X^2-T^2.$$

(34)

In contrast to the Schwarzschild coordinates, in the Kruskal–Szekeres coordinates, Equation (33) and metric (32) are regular at the BH horizon ($r=1$), and, hence, the singular behavior of the metric (29) at $r=1$ is a coordinate effect.

3.1. Black Hole Model in Truncated Spacetime

If spacetime is truncated to 1 + 1 dimensions, T and X, the Schwarzschild metric in Kruskal–Szekeres coordinates is conformally invariant to the Minkowski metric

$$d{s}^2={\displaystyle \frac{4}{r}}{e}^{-r}\left(d{T}^2-d{X}^2\right),$$

(35)

and the scalar field $\varphi$ obeys the same wave equation as in Minkowski spacetime

$$\left({\displaystyle \frac{{\partial }^2}{\partial T^2}}-{\displaystyle \frac{{\partial }^2}{\partial X^2}}\right)\varphi =0.$$

(36)

Equation (36) does not specify the boundary condition for field $\varphi$ at the spacetime boundary $T^2-X^2=1$. As a consequence, many authors have not imposed any boundary condition. This implies that the field can freely propagate through the spacetime boundary as if it is totally absorbed by the BH center (singularity). Usually, the presumption that the BH singularity must absorb everything falling into it is based on the argument that, otherwise, the Cauchy problem is not well defined. However, if we allow propagation backward in time, the problem with the boundary conditions at the superluminal spacetime boundary $T^2-X^2=1$ becomes well formulated. That is, the boundary conditions determine whether propagation backward in time occurs in a particular physical situation.

With the correct treatment, the boundary condition must be properly derived from the equations. The spacetime boundary in the simplified 1 + 1 dimensional model corresponds to the origin of the spherical coordinates in the exact 3 + 1 dimensional description. Thus, the boundary condition must be obtained from 3 + 1 dimensional equations. Taking the limit $r\to 0$ in field Equation (33) in 3 + 1 dimensions, we find the following boundary condition:

$${\left.\left(T{\displaystyle \frac{\partial \varphi }{\partial T}}+X{\displaystyle \frac{\partial \varphi }{\partial X}}\right)\right|}_{T^2-X^2=1}=0.$$

(37)

To obtain Equation (37) from Equation (33), we need to assume that ${\partial }^2\varphi /\partial T^2$ and ${\partial }^2\varphi /\partial X^2$ are finite at the boundary. Later, we give an exact solution of the problem in 3 + 1 dimensions, imposing the boundary condition that scalar field $\varphi$ must be finite at the boundary, which yields the same solution. The latter condition (finite field) is independent of the coordinate choice since the field is scalar.

In the following, we adopt boundary condition (37) for the Schwarzschild BH in the simplified 1 + 1 dimensional model. Boundary condition (37) can be also obtained directly in 1 + 1 dimensions from the requirement that the field flux through spacetime boundary $T^2-X^2=1$ is equal to zero.

Introducing a new scalar field $\tilde{\varphi }$

$$\tilde{\varphi }=T{\displaystyle \frac{\partial \varphi }{\partial T}}+X{\displaystyle \frac{\partial \varphi }{\partial X}},$$

and taking into account that

$${\displaystyle \frac{{\partial }^2\tilde{\varphi }}{\partial T^2}}-{\displaystyle \frac{{\partial }^2\tilde{\varphi }}{\partial X^2}}=\left(T{\displaystyle \frac{\partial }{\partial T}}+X{\displaystyle \frac{\partial }{\partial X}}+2\right)\left({\displaystyle \frac{{\partial }^2\varphi }{\partial T^2}}-{\displaystyle \frac{{\partial }^2\varphi }{\partial X^2}}\right),$$

we find that $\tilde{\varphi }$ obeys the wave equation

$$\left({\displaystyle \frac{{\partial }^2}{\partial T^2}}-{\displaystyle \frac{{\partial }^2}{\partial X^2}}\right)\tilde{\varphi }=0$$

subject to the mirror-like boundary condition at the superluminal (space-like) line

$${\left.\tilde{\varphi }\right|}_{T^2-X^2=1}=0.$$

(38)

That is, for field $\tilde{\varphi }$, the BH center $T^2-X^2=1$ acts as a superluminal mirror. As $\tilde{\varphi }$ obeys the same wave equation as in Minkowski spacetime and for the same boundary condition, the results obtained in the previous section can be applied here as well. One should mention that boundary condition (38) was introduced in Ref. [28] without derivation in connection with the Hawking radiation problem.

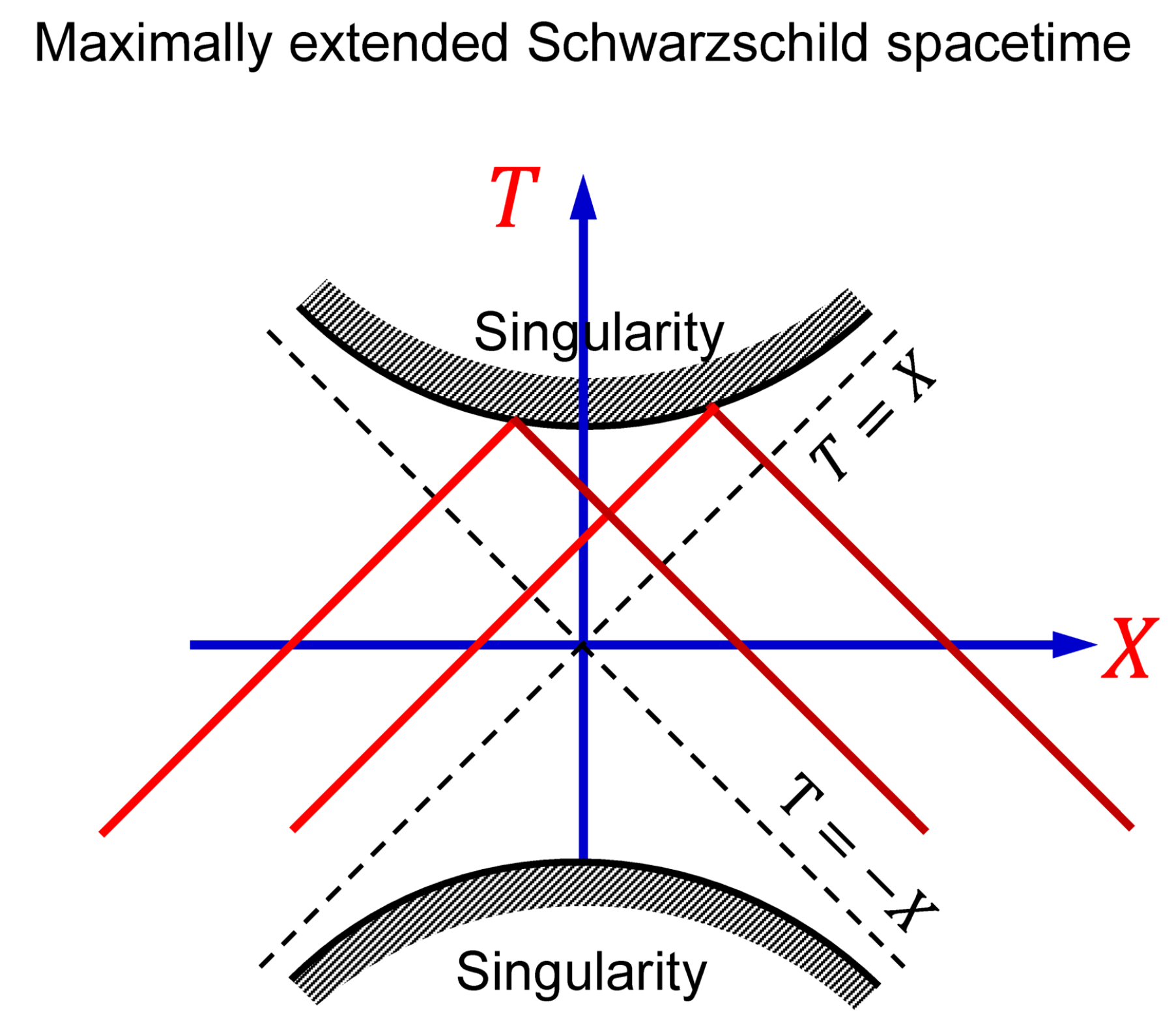
Figure 5 illustrates a maximally extended Schwarzschild spacetime of a static BH in Kruskal–Szekeres coordinates T, X. The hyperbolas that bound the top and the bottom of the diagram are the BH and white hole centers, respectively, which act as superluminal time mirrors. After reflection from the center, the field propagates backward in time and escapes the BH. In particular, the photons emitted by the atoms inside the BH event horizon escape from the BH and can excite atoms in the exterior region (see Figure 5).

The backward-in-time propagating photons excite atoms in an unusual manner. Namely, since the proper time of the atom determines the positive direction of the time axis, the process looks like a ground-state atom becomes excited by emitting a photon (Cherenkov-like radiation [20]). However, the emitted photon cannot be detected because its future path until the BH center is determined, and, hence, it cannot be absorbed before it hits the center. Such a photon can only be emitted sufficiently close to the center so that there is nothing on its path to interact with. Light reflected from the BH center and propagating away from the BH backward in time is interpreted by a distant observer as usual radiation coming from a point source. Such radiation can excite ground-state atoms, which can then spontaneously decay back to the ground state by emitting photons propagating forward in time (see Figure 5).

The general solution of Equation (36) satisfying the boundary condition (37) reads

$$\varphi (T,X)=f(T-X)+f\left({\displaystyle \frac{1}{T+X}}\right),$$

(39)

where f is an arbitrary function. It is insightful to consider solutions in the form

$${\varphi }_{\nu }(T,X)=e^{-2i\nu ln(T-X)}\theta (T-X)+e^{2i\nu ln(T+X)}\theta (T+X),$$

(40)

where $\nu$ is the frequency of the wave far away from the BH in Schwarzschild coordinates. Mode functions analogous to Equation (40) have been discussed in connection with a uniformly accelerated mirror in Minkowski spacetime [29]. The first (second) term on the right-hand side in Equation (40) is nonzero only above the horizon $T=X$ ($T=-X$). Solutions (40) describe waves falling into the top spacetime boundary $T^2-X^2=1$, which are then totally reflected from the boundary and propagate backward in time (see Figure 6). Which term in Equation (40) is interpreted as an incident (reflected) wave is determined by the location of the source generating such a wave.

To make the set of modes (40) complete, one should add mode functions describing the reflection of waves propagating backward in time from the white hole center (bottom spacetime boundary in Figure 5),

$${\varphi }_{\nu }(T,X)=e^{-2i\nu ln(X-T)}\theta (X-T)+e^{2i\nu ln(-T-X)}\theta (-T-X),$$

(41)

which are a superposition of the terms that are nonzero in the opposite half-plane from the corresponding horizons $T=\pm X$. After reflection from the whitehole center, the wave propagates forward in time.

The Schwarzschild coordinate system can only cover regions I and II in the Kruskal–Szekeres diagram in Figure 5. Regions III and IV describe extension of Schwarzschild spacetime into a “parallel” universe. Solutions (40) and (41) describe the propagation of waves into (from) the parallel universe. When such a wave crosses the boundary of the parallel universe, it disappears from Schwarzschild spacetime (regions I and II). If the parallel universe does not exist, then we must choose mode functions that would not terminate in Schwarzschild spacetime. Such mode functions can be constructed by taking the sum of Equations (40) and (41), which yields

$${\varphi }_{\nu }(T,X)=e^{-2i\nu ln|T-X|}+e^{2i\nu ln|T+X|},$$

(42)

or, in the Schwarzschild coordinates,

$${\varphi }_{\nu }(t,r)=e^{i\nu (t-r)-i\nu ln|1-r|}+e^{i\nu (t+r)+i\nu ln|1-r|},$$

(43)

where we use

$${|T+X|}^2=e^{t+r}{|1-r|,|T-X|}^2=e^{r-t}|1-r|.$$

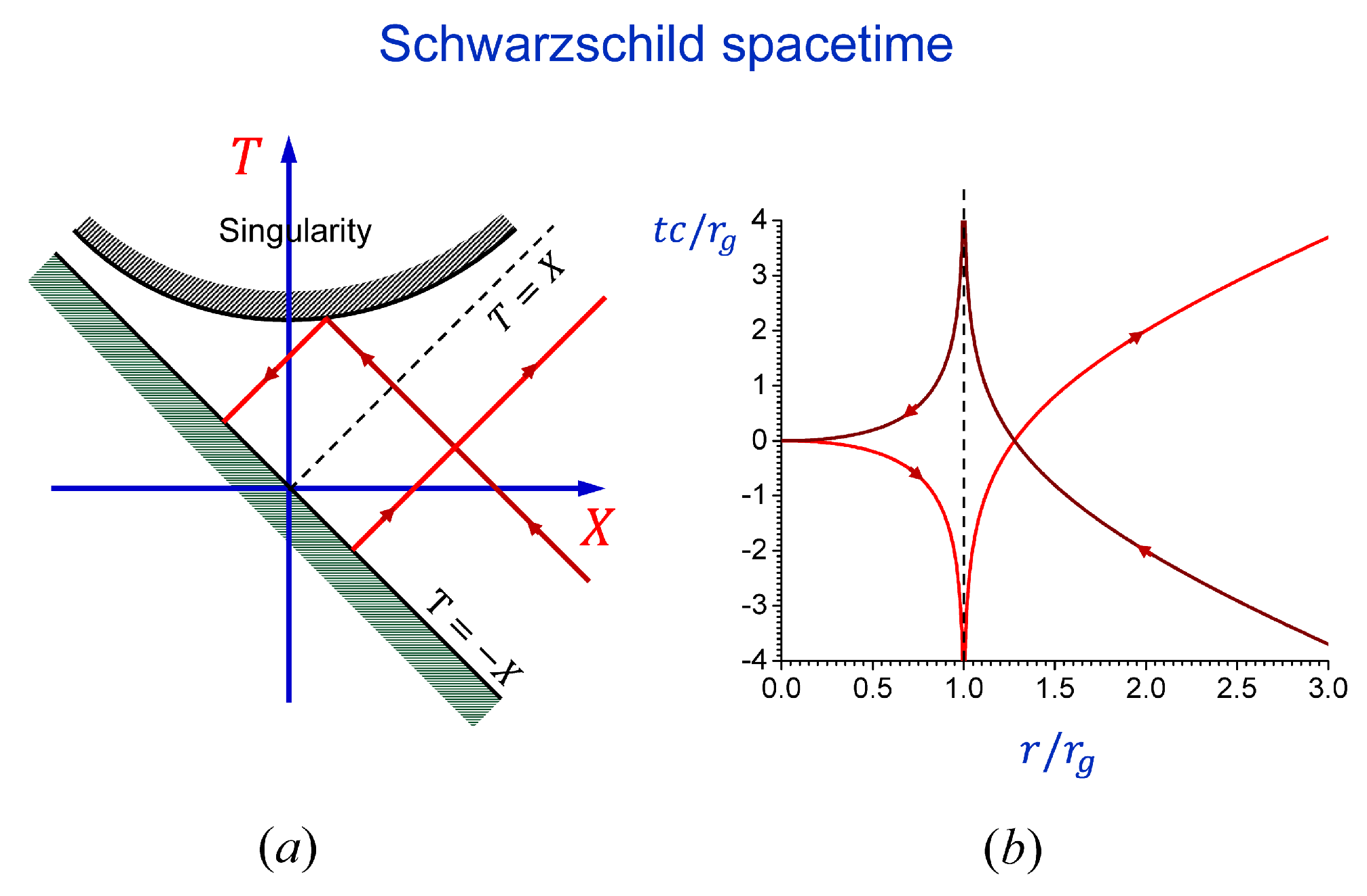
Equation (43) describes a wave falling into the BH (first term) that is totally reflected from the center and propagates away from the BH (second term). The lines of the constant phase of such waves (light rays) in Kruskal–Szekeres and Schwarzschild coordinates are shown in Figure 7. Figure 7 shows that when the reflected wave emerges from the BH horizon, it begins to propagate forward in time. That is, from the perspective of a distant observer, the BH acts as a usual perfectly reflecting static point-like mirror. Namely, far from the center $r\gg r_g$, both the ingoing and the outgoing waves propagate forward in time.

If a short pulse is sent to the BH, which can be approximated as a $\delta$-function, the corresponding solution for the field reads

$$\varphi (T,X)={\displaystyle \frac{a}{2}}\delta \left(|T-X|-a\right)+{\displaystyle \frac{1}{2a}}\delta \left(|T+X|-{\displaystyle \frac{1}{a}}\right),$$

where $a>0$ is a constant determined by the position of the pulse at $T=0$. In Schwarzschild coordinates, we obtain

$$\varphi (t,r)=\delta \left[r-t+ln|1-r|-2lna\right]+\delta \left[t+r+ln|1-r|+2lna\right].$$

The worldline of the $\delta$-function pulse coincides with the light rays shown in Figure 7. Using the general solution (39), one can construct other types of pulses, e.g., Gaussian pulses.

3.2. Exact Solution in 3 + 1 Dimensions

To demonstrate that the effect is not a fluke of the simplified truncated spacetime model, we here present an exact solution of the problem in 3 + 1 dimensions. Namely, we present solutions analogous to the modes (43). To obtain such solutions, it is convenient to start from field Equation (30) in Schwarzschild coordinates. In 3 + 1 dimensions, for spherical symmetry, Equation (30) reduces to

$${\displaystyle \frac{r^3}{1-r}}{\displaystyle \frac{{\partial }^2\varphi }{\partial t^2}}-r\left(1-r\right){\displaystyle \frac{{\partial }^2\varphi }{\partial r^2}}-\left(1-2r\right){\displaystyle \frac{\partial \varphi }{\partial r}}=0.$$

(44)

One can separate variables by looking for solutions in the form

$$\varphi (t,r)=e^{i\nu t}\varphi \left(r\right),$$

which yields the following equation for $\varphi \left(r\right)$:

$$r\left(1-r\right){\displaystyle \frac{{\partial }^2\varphi }{\partial r^2}}+\left(1-2r\right){\displaystyle \frac{\partial \varphi }{\partial r}}+{\displaystyle \frac{{\nu }^2{r}^3}{1-r}}\varphi =0.$$

(45)

This equation can be solved exactly, with its solutions being expressed in terms of confluent Heun functions HeunC [30]. Two independent solutions of Equation (45) are given by

$${\left(1-r\right)}^{i\nu }{e}^{i\nu r}\mathit{Heun}\mathrm{C}\left(-2i\nu ,2i\nu ,0,-2{\nu }^2,2{\nu }^2,1-r\right),$$

(46)

and its complex conjugate. The confluent Heun function in Equation (46) logarithmically diverges at $r=0$ but is regular elsewhere. The pre-factor ${\left(1-r\right)}^{i\nu }=e^{i\nu ln(1-r)}$ has a logarithmic phase singularity at horizon $r=1$.

Next, we note that if ${\varphi }_0(t,r)$ is a solution of Equation (44), then functions ${\varphi }_0(t,r)\theta (1-r)$ and ${\varphi }_0(t,r)\theta (r-1)$ are also solutions of Equation (44). This property allows us to construct mode functions that are regular along the wave propagation in Kruskal–Szekeres coordinates by replacing the pre-factor ${\left(1-r\right)}^{i\nu }$ in Equation (46) with ${|1-r|}^{i\nu }$, which yields another solution. Taking a linear combination of this solution with its complex conjugate, we obtain the following solutions of Equation (44)

$${\varphi }_{\nu }(t,r)=e^{i\nu (t+r)+i\nu ln|1-r|}f\left(r\right)+C_{\nu }{e}^{i\nu (t-r)-i\nu ln|1-r|}{f}^{*}\left(r\right),$$

(47)

which are analogous to mode functions (43). In Equation (47),

$$f\left(r\right)=\mathit{Heun}\mathrm{C}\left(-2i\nu ,2i\nu ,0,-2{\nu }^2,2{\nu }^2,1-r\right).$$

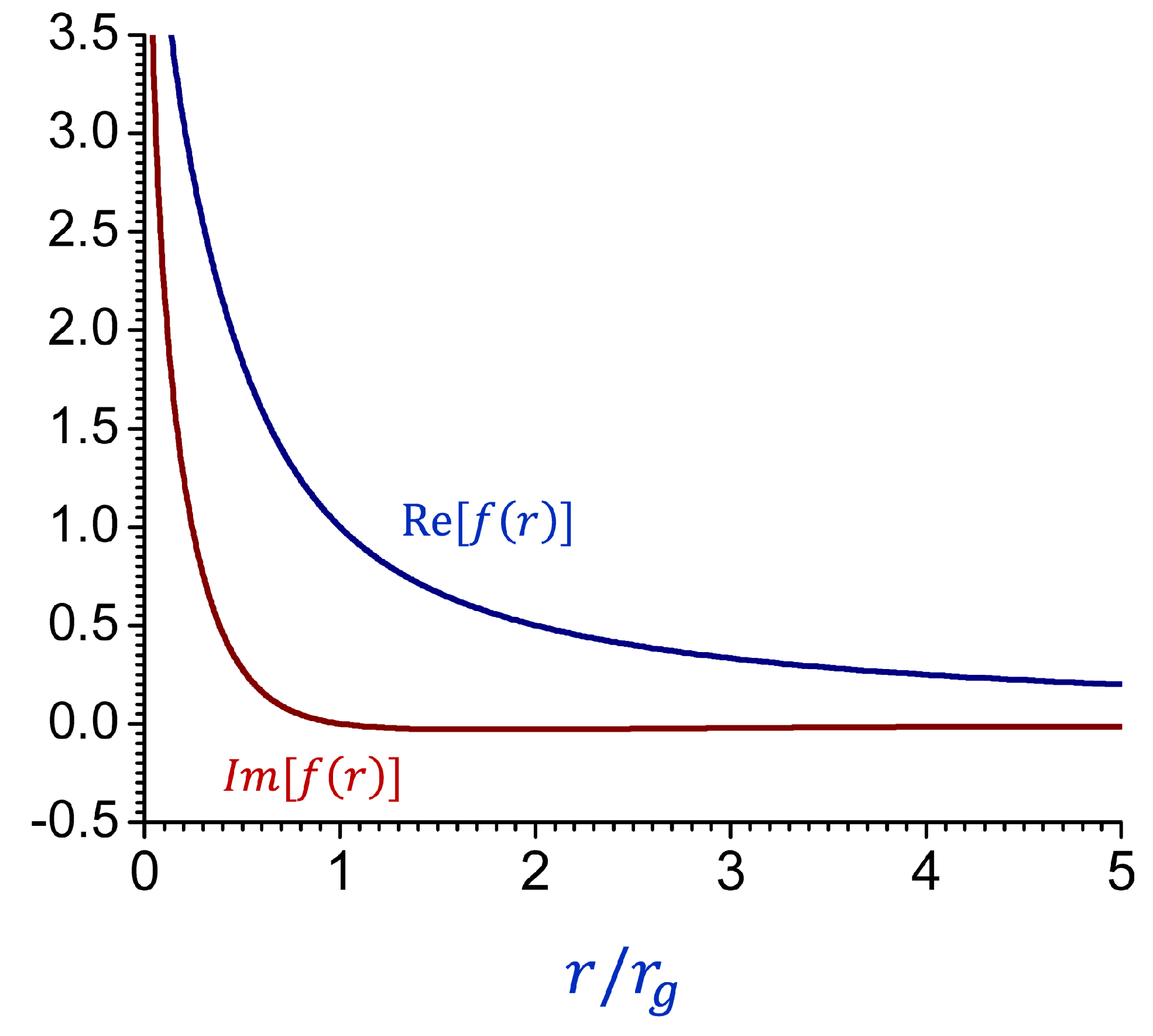
In Figure 8, we plot the real and imaginary parts of $f\left(r\right)$ as a function of r, which shows their regular behavior everywhere, apart from the logarithmic divergence at $r=0$.

The complex constant $C_{\nu }$ is obtained from the requirement that functions ${\varphi }_{\nu }(t,r)$ must be finite at $r=0$. Taking into account the asymptotic of the confluent Heun function for $r\to 0$

$$\mathit{Heun}\mathrm{C}\left(-2i\nu ,2i\nu ,0,-2{\nu }^2,2{\nu }^2,1-r\right)ln\left(r\right),$$

(48)

we find

$$|C_{\nu }|=1.$$

The phase of $C_{\nu }$ can be calculated numerically, but it is irrelevant for the present discussion.

The asymptotic (48) can be found from Equation (45) by taking the limit $r\to 0,$ which yields

$$r{\displaystyle \frac{{\partial }^2\varphi }{\partial r^2}}+{\displaystyle \frac{\partial \varphi }{\partial r}}+{\nu }^2{r}^3\varphi =0,$$

whose solutions are combinations of Bessel functions

$$\varphi \left(r\right)=A_1{J}_0\left({\displaystyle \frac{\nu r^2}{2}}\right)+A_2{Y}_0\left({\displaystyle \frac{\nu r^2}{2}}\right).$$

The Bessel function of the second kind $Y_0$ leads to logarithmic divergence at $r\to 0$.

One should note that the requirement of rhe boundedness of the field at $r=0$ can be obtained by calculating the flux of the field current

$$j^r=i{g}^{rr}\left({\varphi }^{*}{\displaystyle \frac{\partial \varphi }{\partial r}}-\varphi {\displaystyle \frac{\partial {\varphi }^{*}}{\partial r}}\right)=i\left({\displaystyle \frac{r_g}{r}}-1\right)\left({\varphi }^{*}{\displaystyle \frac{\partial \varphi }{\partial r}}-\varphi {\displaystyle \frac{\partial {\varphi }^{*}}{\partial r}}\right)$$

through a sphere with a small radius r and taking the limit $r\to 0$.The flux vanishes only if the field is finite at the BH center. nonzero flux implies that the field simply disappears at the BH center.

The asymptotic of the confluent Heun function for $r\to \infty$ is [31]

$$\mathit{Heun}\mathrm{C}\left(-2i\nu ,2i\nu ,0,-2{\nu }^2,2{\nu }^2,1-r\right){\displaystyle \frac{1}{r}}\left[1+C_{1\nu }{r}^{-2i\nu }\right],$$

where $C_{1\nu }$ is a constant that depends on $\nu$. Thus, far from the BH, the mode functions (47) decay as

$${\varphi }_{\nu }\propto {\displaystyle \frac{e^{i\nu (t+r)}}{r}}\left[r^{i\nu }+C_{1\nu }{r}^{-i\nu }\right]+C_{\nu }{\displaystyle \frac{e^{i\nu (t-r)}}{r}}\left[r^{-i\nu }+C_{1\nu }^{*}{r}^{i\nu }\right].$$

(49)

Equation (49) shows that an ingoing spherical wave is totally reflected from the BH center (since $|C_{\nu }|=1$) and propagates away to infinity. In Kruskal-Szekeres coordinates, the mode functions (47) read

$${\varphi }_{\nu }(T,X)=e^{2i\nu ln|T+X|}f\left(r\right)+C_{\nu }{e}^{-2i\nu ln|T-X|}{f}^{*}\left(r\right),$$

where the dependence of r on T and X is given by Equation (34).

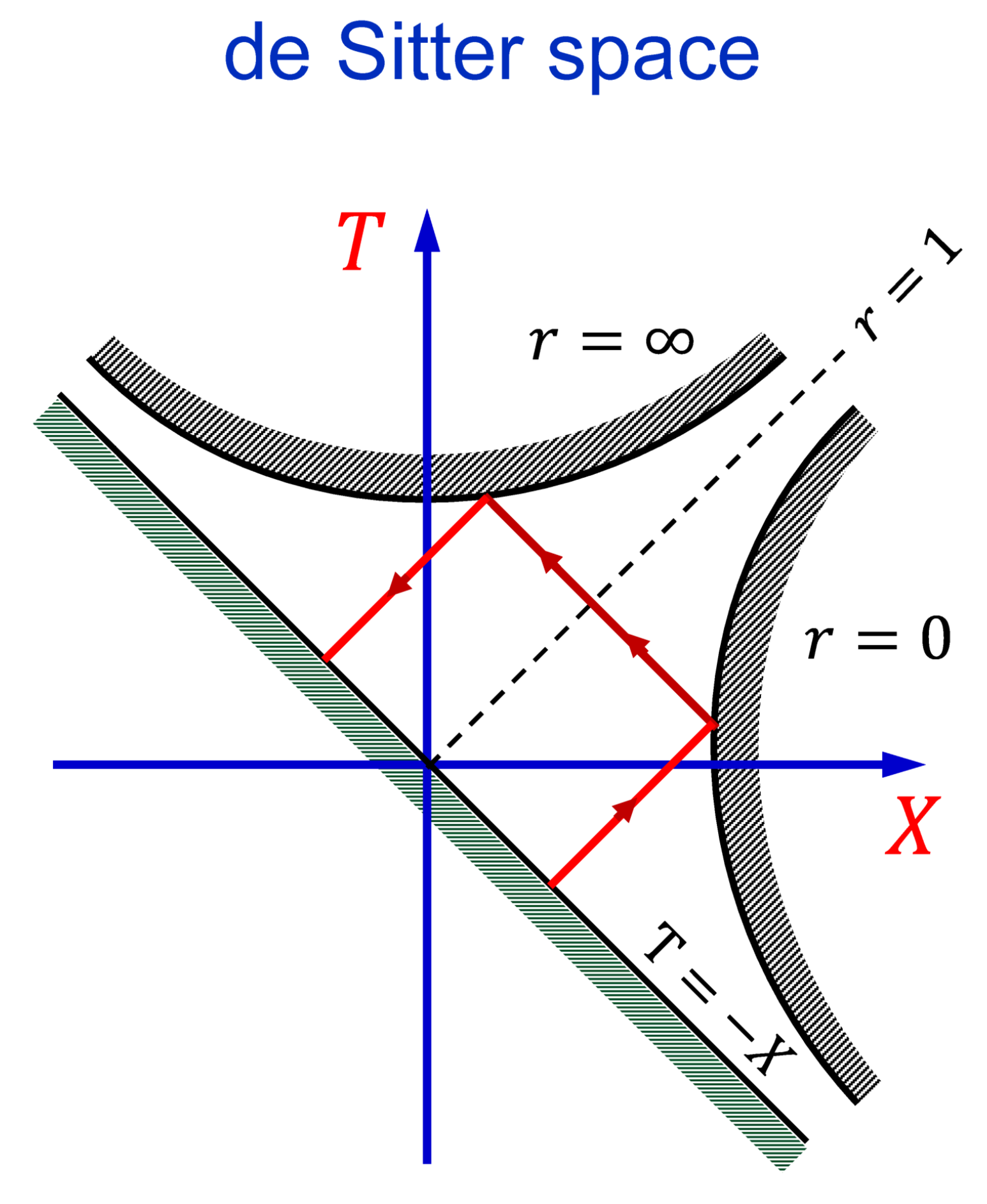
4. Backward-in-Time Reflection from de Sitter Space Boundary

The de Sitter metric in static coordinates describes the spacetime produced by uniform matter density permeating an infinite, homogeneous medium: [32]

$$d{s}^2=\left(1-r^2/r_0^2\right)d{t}^2-{\displaystyle \frac{1}{1-r^2/r_0^2}}d{r}^2-r^2\left(d{\theta }^2+{sin}^2\theta d{\phi }^2\right),$$

(50)

where $r_0$ is the de Sitter radius, which describes the limiting distance beyond which the spacetime curvature prevents any signal moving forward in time from ever reaching us (the event horizon). At this distance, the enclosed mass is sufficient to turn it into a Schwarzschild radius for an observer at the origin of the spherical coordinates. De Sitter space can be defined by a hyperbola embedded in 4+1 dimensional Minkowski space [33].

During the cosmic inflation of the early universe, the exponential expansion of space can also be described by the de Sitter metric [33,34]. Namely, the region $0<r<r_0$ can be mapped into the metric of the inflationary cosmological model

$$d{s}^2=d{\tau }^2-e^{2H\tau }\left[d{\rho }^2+{\rho }^2\left(d{\theta }^2+{sin}^2\theta d{\phi }^2\right)\right],$$

(51)

where $H=1/r_0$. The coordinate transformation connecting (50) and (51) is

$$\tau =t+{\displaystyle \frac{1}{2H}}ln\left(1-H^2{r}^2\right),\rho ={\displaystyle \frac{r{e}^{-Ht}}{\sqrt{1-H^2{r}^2}}}.$$

The outside region $r>r_0$ can be mapped into the metric (51) by the coordinate transformation

$$\tau =t+{\displaystyle \frac{1}{2H}}ln\left(H^2{r}^2-1\right),\rho ={\displaystyle \frac{r{e}^{-Ht}}{\sqrt{H^2{r}^2-1}}}.$$

In space that expands exponentially with time, any pair of free-floating objects that are initially at rest move apart from each other at an accelerating rate (if the objects are not bound together). From the point of view of one such object, spacetime is something like an inside-out Schwarzschild black hole – each object is surrounded by a spherical event horizon. According to conventional wisdom, once the other object has fallen through this horizon, it can never return, and even the light signals it sends never reach the first object.

In this section, we show that signals moving outside the horizon ($r>r_0$) can be reflected back in time from the de Sitter space boundary (at $r=\infty$) similarly to the time reflection from the BH center. Such backward-in-time propagating signals can pass the event horizon and reach the interior region $r<r_0$.

One should note that spacetimes described by metrics (50) and (51) are physically different. The point is that spacetime (51) covers only part of spacetime (50) (inside or outside the sphere $r=r_0$, depending on which coordinate transformation we choose). The effect we discuss in this paper is the property of the extended spacetime (50). This is important because the inflationary stage of universe expansion described by metric (51) is a real physical spacetime, and backward-in-time propagation is not what we are used to in physics.

In the following, we use $r_0$ as a unit of length and $r_0/c$ as a unit of time. To make a straightforward analogy with the superluminal mirror, we make the following coordinate transformation of metric (50):

$$T=\sqrt{{\displaystyle \frac{1+r}{1-r}}}sinh\left(t\right),X=\sqrt{{\displaystyle \frac{1+r}{1-r}}}cosh\left(t\right),$$

for $0<r<1$, and

$$T=\sqrt{{\displaystyle \frac{r+1}{r-1}}}cosh\left(t\right),X=\sqrt{{\displaystyle \frac{r+1}{r-1}}}sinh\left(t\right),$$

for $r>1$. In these coordinates, the de Sitter space boundary ($r=\infty$) is a space-like line $T^2-X^2=1$ along which $|dX/dT|=T/\sqrt{T^2-1}>1$,while the origin ($r=0$) is a time-like line $X^2-T^2=1$. In coordinates T and X, metric (50) reads

$$d{s}^2={\left(1-r\right)}^2\left(d{T}^2-d{X}^2\right)-r^2\left(d{\theta }^2+{sin}^2\theta d{\phi }^2\right).$$

(52)

If spacetime is truncated to 1 + 1 dimensions, T and X, metric (52) is conformally invariant to the Minkowski metric

$$d{s}^2={\left(1-r\right)}^2\left(d{T}^2-d{X}^2\right),$$

and the scalar field $\varphi$ obeys the same wave equation as in Minkowski spacetime

$$\left({\displaystyle \frac{{\partial }^2}{\partial T^2}}-{\displaystyle \frac{{\partial }^2}{\partial X^2}}\right)\varphi =0.$$

Figure 9 shows a diagram of truncated de Sitter space in T and X coordinates. The space is bound by the lines $X=\sqrt{1+T^2}$ ($r=0$), $T=\sqrt{1+X^2}$ ($r=\infty$), and $T=-X$. The latter two boundaries are the same as in the case of Schwarzschild spacetime in Kruskal-Szekeres coordinates (see Figure 7a). The horizon is drawn as a dashed line in Figure 9.

The solid line indicates a wave ray traveling in the de Sitter space. If particles do not disappear from the spacetime at the boundaries, they undergo backward-in-time reflection from the superluminal boundary $r=\infty$. The reflected wave crosses the horizon and propagates into the interior region $r<1$. In contrast to BHs, in the present case, the spacetime is not singular at the superluminal boundary.

In 3 + 1 dimensions, for spherical symmetry, the wave equation for the scalar field (30) in metric (50) reduces to

$${\displaystyle \frac{r^2}{1-r^2}}{\displaystyle \frac{{\partial }^2\varphi }{\partial t^2}}-{\displaystyle \frac{\partial }{\partial r}}\left(r^2\left(1-r^2\right){\displaystyle \frac{\partial \varphi }{\partial r}}\right)=0,$$

which has the following solution analogous to the mode function (47):

$${\varphi }_{\nu }(t,r)={\displaystyle \frac{e^{i\nu t}}{r}}\left(e^{\frac{i\nu }{2}ln\left|\frac{r-1}{r+1}\right|}\left(1-{\displaystyle \frac{ir}{\nu }}\right)\right.+\left.C{e}^{-\frac{i\nu }{2}ln\left|\frac{r-1}{r+1}\right|}\left(1+{\displaystyle \frac{ir}{\nu }}\right)\right),$$

(53)

where C is an integration constant. For solution (53,) the flux of the field current through a sphere of radius r is independent of r and proceeds as $C^2-1$. Thus, flux vanishes if $C=\pm 1$. For $r\ll 1$, Equation (53) has the asymptote

$${\varphi }_{\nu }(t,r)\approx {\displaystyle \frac{e^{i\nu (t-r)}}{r}}+C{\displaystyle \frac{e^{i\nu (t+r)}}{r}},$$

which is finite at the origin if $C=-1$. Hence, we obtain that, for $C=-1$, Equation (53) describes a standing spherical wave formed by reflection at the center ($r=0$) and backward-in-time reflection from the superluminal boundary at $r=\infty$. Thus, de Sitter space acts as a cavity that traps electromagnetic radiation.

5. Summary and Discussion

In this paper, we consider the reflection of light, approximating it as a massless scalar field $\varphi$, from a perfect fictitious mirror that propagates faster than light in a vacuum, and we impose the boundary condition that the field vanishes at the mirror surface. In this case, there are no transmitted pulses, and a reflected pulse must be present to satisfy the boundary condition. We find that light propagates backward in time after reflection from such a mirror, which can affect the past. Namely, using a superluminal mirror, one can send information into the past. This leads to logical contradictions associated with time travel paradoxes – the grandfather paradox, causal loops, etc.

Here, we prefer not to speculate whether time travel is possible but want to mention that it is not clear how to realize a superluminal mirror with the perfectly reflecting boundary condition in laboratory experiments. The superluminal motion of inhomogeneities (e.g., medium refractive index or ionization fronts in plasma) in a fixed medium has been realized experimentally [17]. However, the parameter inhomogeneity (for example, discontinuity in the permittivity) traveling at a velocity exceeding the speed of light does not yield the perfectly reflecting boundary conditions at the superluminal surface, and, as a result, the boundary conditions can be satisfied without backward-in-time reflection that can affect the past [12,13,14,16].

We also found that centers of hypothetical BHs might act as time mirrors. Namely, in Kruskal–Szekeres coordinates, the center of a Schwarzschild BH moves along the superluminal (space-like) trajectory $T^2-X^2=1$. According to general relativity, spacetime disappears at the BH center. It is usually assumed that matter disappears together with the spacetime. Here, we impose a boundary condition that the field does not disappear at the BH center (or, equivalently, it remains finite at the center). In this case, as we show, light is totally reflected from the center. The reflected field propagates backward in time, passes through the event horizon, and moves away from the BH.

We find that due to the peculiar structure of Schwarzschild spacetime, the photons reflected from the BH center can propagate both forward and backward in time in the exterior region. In particular, from the perspective of a distant observer, the BH acts as a usual static and perfectly reflecting point-like mirror. Namely, in the exterior region, both the ingoing and the outgoing waves propagate forward in time (see Figure 7). If the wave source is located inside the event horizon, then, depending on which direction the wave is emitted, after reflection from the center, the wave can propagate into the exterior region as forward or backward in time or as a combination of those two (see Figure 10). Photons propagating backward in time excite atoms in an unusual way. Namely, the process looks like the ground-state atom becomes excited by emitting a negative-energy photon, which is analogous to Cherenkov radiation [20].

We also show that a similar situation occurs in de Sitter space. Namely, the space boundary $r=\infty$ acts as a time mirror. Particles reflected from the boundary propagate backward in time and pass the event horizon into the interior region. In contrast to BHs, de Sitter space is not singular at the superluminal boundary.

If BH centers are time mirrors, BHs are at odds with the generally accepted wisdom that BHs are spacetime regions from which nothing can escape to infinity. Namely, light emitted inside the event horizon can never reach the external observer, and anything that passes through the event horizon from the observer’s side is never seen again by the observer. This conclusion results from not imposing the boundary condition for the field at the BH center, assuming that it simply disappears. Imposing no boundary condition leads to the acceptance of divergent solutions for the field as meaningful. Please note that the scalar field itself diverges at the center, which is independent of the choice of coordinates since the field is scalar. For such divergent solutions, the flux of the field into the BH singularity is nonzero.

If we want to avoid the divergence of the field in Schwarzschild spacetime (and nonzero field flux into the BH center), we must allow solutions propagating backward in time. One should mention that authors of Refs. [35,36,37,38] also noticed that if the boundedness of the field is required at the BH center, then there are two different arrows of time, in agreement with our results. Moreover, it has been demonstrated that a vanishing boundary condition at the BH center can be natural [39]. It has been also shown that the boundary conditions at the BH singularity prevent a loss of quantum mechanical information from spacetime, which might be a possible way to resolve the BH information paradox [40,41,42,43,44,45]. However, the BH information paradox can be also resolved without backward-in-time propagation [46].

If BHs are time mirrors, the existence of BHs is somewhat at odds with astronomical observations. For example, when matter, e.g., atoms, fall into the BH center (singularity), the coupling between atoms and light changes nonadiabatically on a time scale of the light oscillation period. Such nonadiabatic change in coupling yields the emission of bursts of radiation by the atoms inside the event horizon. After reflection from the BH center, such radiation bursts propagate backward in time and escape from the BH. Due to this radiation mechanism, accreting BHs could look intrinsically bright, which contradicts the observations of BH candidates in binary systems or supermassive BHs in galactic centers. To resolve the issue one can, e.g., argue that there is an optically thick gas cloud around the BH center that absorbs photons propagating backward in time before they reach the event horizon, and, hence, photons cannot escape. Proper modeling of such systems can shed more light on this problem.

Another issue is the following: if the BH center reflects infalling light and matter, then BHs cannot grow by consuming the accreting mass. This contradicts to observations of supermassive objects at galactic centers, which are believed to become supermassive by consuming accreted matter. Moreover, the problem of gravitational collapse itself must be reconsidered if we allow backward-in-time propagation. If only forward-in-time propagation is permitted, once the surface of the star has entered the Schwarzschild sphere during gravitational collapse, one has a BH. The matter of the star and its radiation are then permanently trapped in the BH [47]. However, backward-in-time propagation permits matter escape at any stage of the collapse. The inner part of an unstable star first contracts and then expands. What kind of object is formed under these conditions is a question for future study.

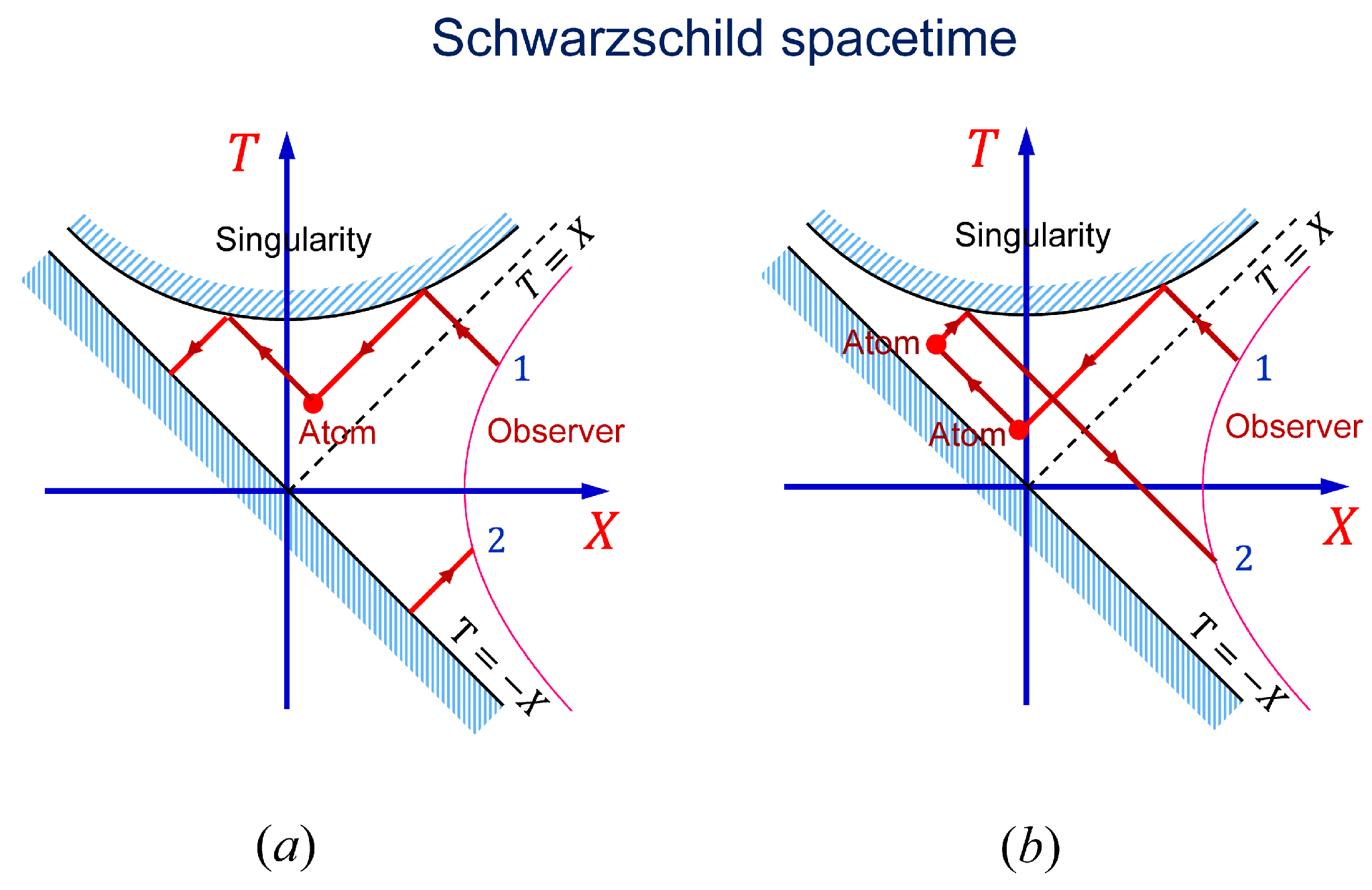
If a BH acts as a perfect mirror, then there is no information loss, and, hence, no BH information paradox. However, in this case, BHs can be used to construct a time machine that allows us to send a signal into the past, yielding logical contradictions, and the associated time travel paradoxes arise. An example of a BH-based time machine is shown in Figure 11. A distant observer, which we assume is located at fixed $r\gg r_g$, sends a signal (light pulse) into the BH at point 1 of its trajectory. After reflection from the BH center, the pulse propagates backward in time away from the center and is absorbed by an atom located inside the event horizon. The atom re-emits the pulse toward the center, and the pulse is reflected from the center one more time (Figure 11a). After that, the pulse propagates away from the BH and crosses the observer’s trajectory at point 2, which is earlier in time than the original point 1. That is, the observer can send information to itself in the past. In another version of the machine, the pulse re-emitted by the atom hits another atom that redirects the pulse into a different trajectory, which leads to a similar result (Figure 11b).

One should mention that in the framework of general relativity, time machines have been proposed based on the traversable wormholes of Morris and Thorne [48,49,50] as well as on Gott’s cosmic string construction [51]. For more details on time-machines, see, e.g., Refs. [52,53,54,55], while a discussion of time travel paradoxes can be found, e.g., in [56,57,58,59].

The point of our paper is that, in the case of BHs, the field equations have nonsingular solutions if we allow backward-in-time propagation. We prefer not to speculate which solution, singular or nonsingular, should be chosen in BH models. This question should be addressed through experiments. In either case, classical BHs do not obey the physics we are used to, or they are singular objects for which matter disappears together with spacetime at the singularity, or they are nonsingular but the associated backward-in-time propagation yields time travel paradoxes.

In addition to exploring unconventional BH physics, one should look for alternatives of general relativity that predict no event horizons, no singularities, and, thus, no unusual physics. BHs have never been observed directly and the usually cited evidence of their existence is based on the assumption that general relativity provides the correct description of strong field gravitation. Until signatures of event horizons are found, the existence of BHs will not be proven.

The vector theory of gravity is the viable alternative [60,61]. The theory assumes that gravity is a vector field in fixed four-dimensional Euclidean background space, which effectively alters the spacetime geometry of the universe. Despite fundamental differences, vector gravity also passes all available gravitational tests, including the detection of gravitational waves by LIGO and Virgo [60]. In addition, vector gravity provides an explanation of dark energy as the energy of the longitudinal gravitational field induced by the expansion of the universe and yields, with no free parameters, the value of ${\mathrm{\Omega }}_{\mathrm{\Lambda }}=2/3$ [61], which agrees with the results of Planck collaboration [62] and the results of the Dark Energy Survey. Thus, vector gravity solves the dark energy problem.

In strong fields, vector gravity deviates substantially from general relativity and yields no BHs. In particular, since the theory predicts no event horizons, the end point of a gravitational collapse is a stable star with a reduced mass. It has been shown that the properties of supermassive objects at galactic centers can be explained well in the framework of vector gravity, including their images by the Event Horizon Telescope [63,64].

Moreover, it has been recently found that the data on gravitational wave (GW) detection of binary neutron star event GW170817, the only event so far whose source location was determined precisely by concurrent electromagnetic observations, are inconsistent with the tensor GW polarization predictions of general relativity, and Einstein’s theory is ruled out at a 99% confidence level [64]. At the same time, vector GW polarization, predicted by vector theory of gravity, is supported by GW detection data [64]. If true, future GW detections for which the GW source is identified should confirm this conclusion with greater accuracy.

Finally, our preliminary results indicate that vector gravity, with no free parameters, yields value of the electron and muon masses in agreement with experiment. If so, this leaves no doubt that general relativity is ruled out and BHs do not exist in nature.