Restrictions on Regularized Fisher and Dilatonic Spacetimes Implied by High-Frequency Quasiperiodic Oscillations Observed in Microquasars and Active Galactic Nuclei
Abstract
1. Introduction
2. Regularized Spacetimes
2.1. Regularized Fisher Spacetime
2.2. Regularized Dilatonic Spacetime
3. Circular Geodesics in the Regularized Spacetimes
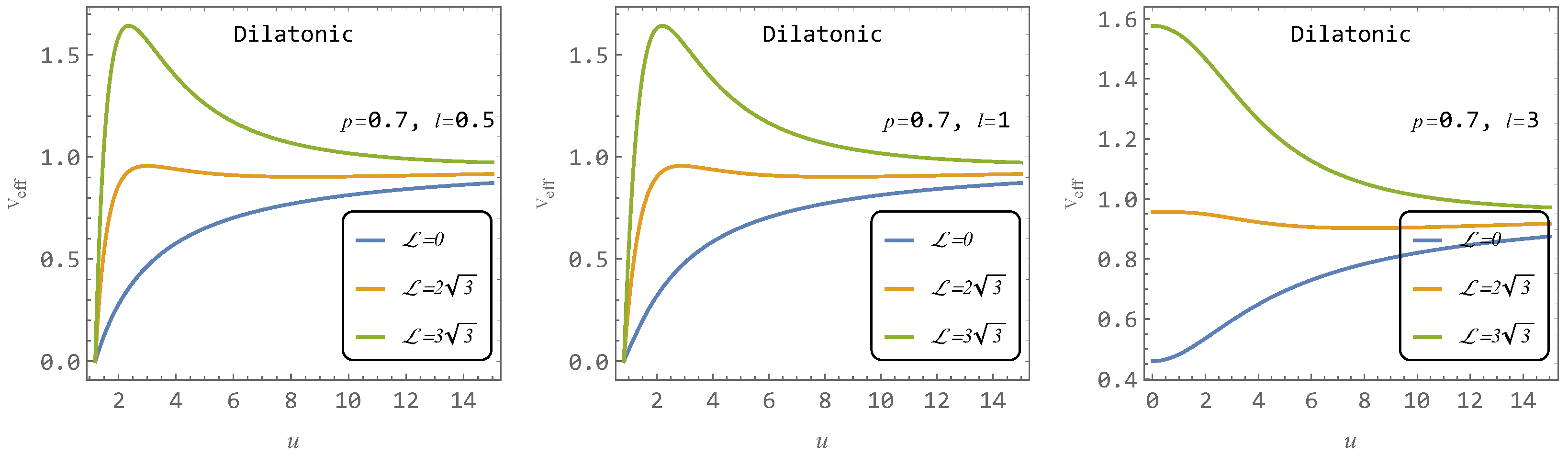
3.1. Effective Potential
3.2. Circular Geodesics
3.2.1. Regions of Existence
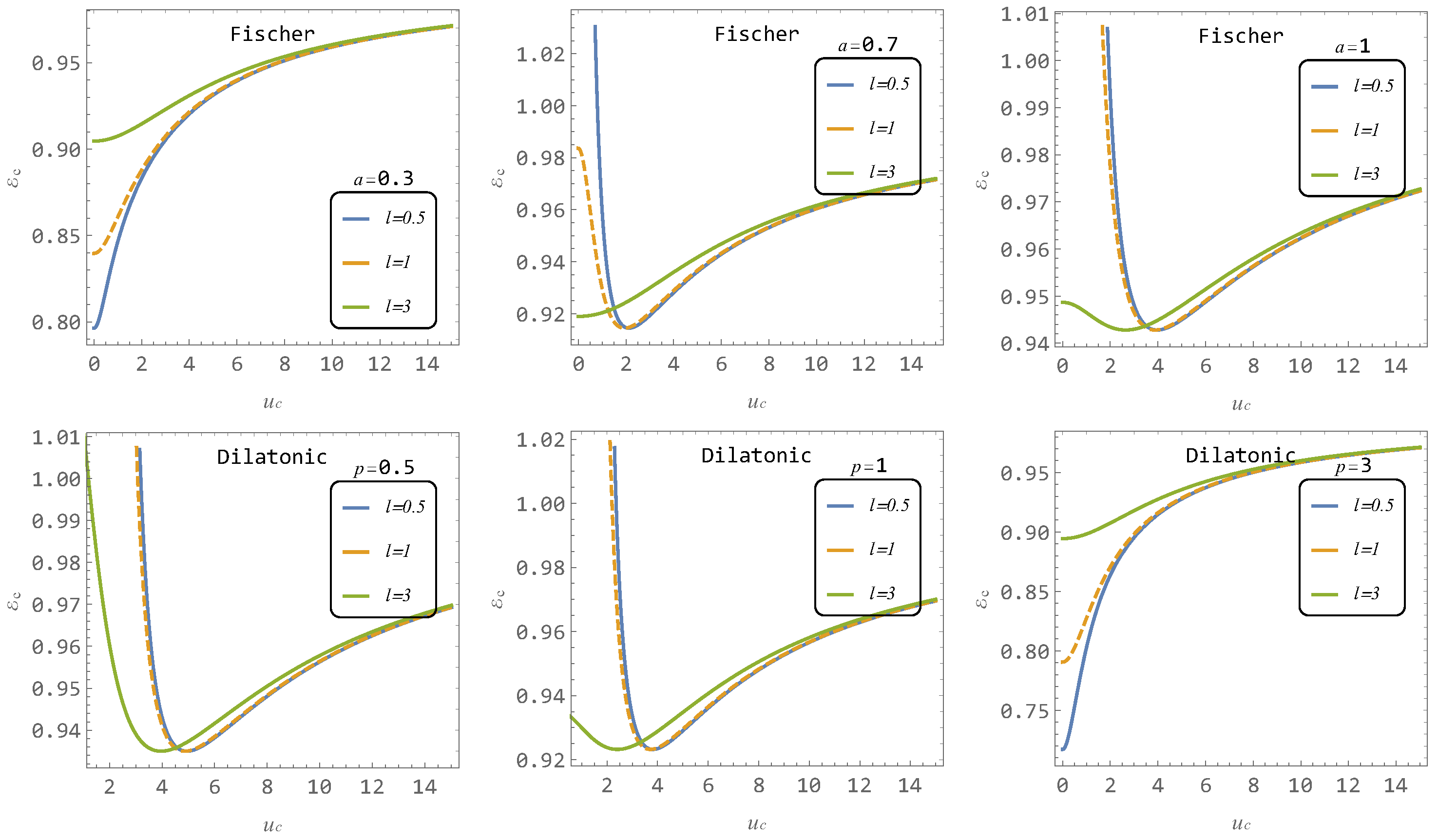
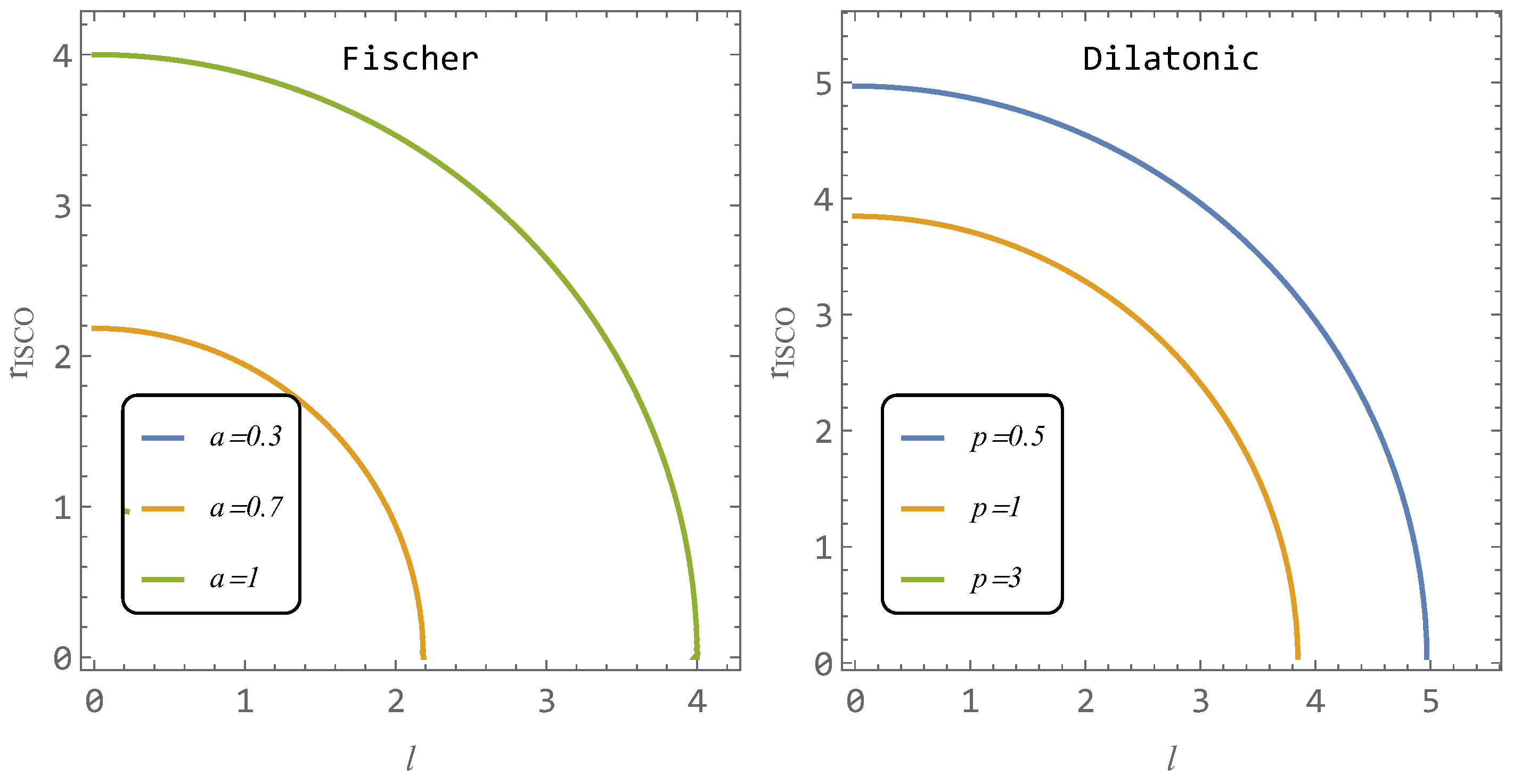
3.2.2. ISCO
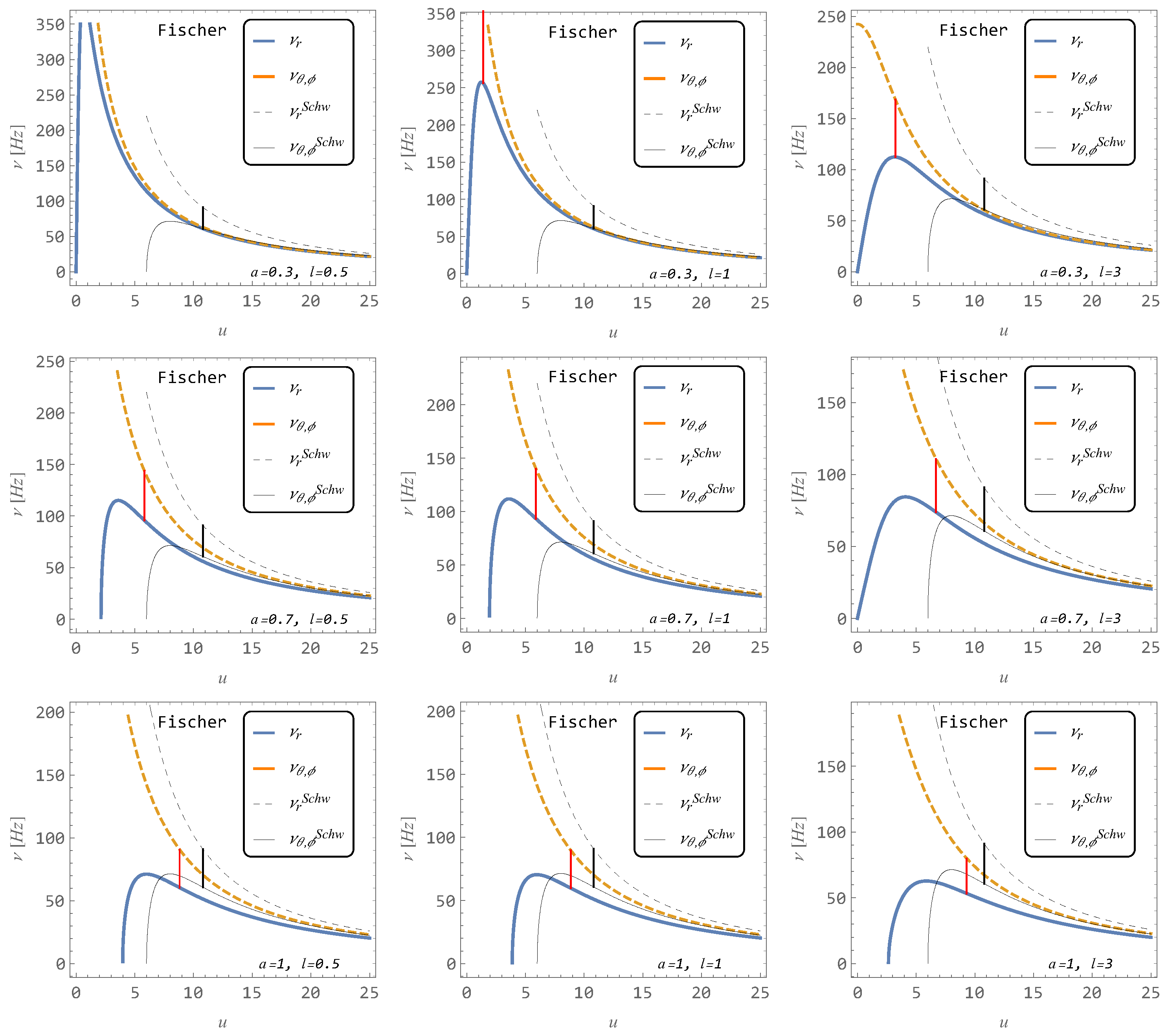
4. Epicyclic Oscillations Around Stable Circular Geodesics of the Regularized Spacetimes
5. Restrictions on the Regularized Spacetime Parameters Due to Fits to the HF QPOs Observed in Microquasars and Active Galactic Nuclei
5.1. Geodesic Model of HF QPOs
5.2. Comparison of Observational Data from Microquasars with the Geodesic Model of Twin HF QPOs Applied for the Regularized Spacetimes
5.3. Comparison of Observational Data from Active Galactic Nuclei with the Geodesic Model of HF QPOs Model Applied to the Regularized Spacetimes
6. Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
| 1 | The black bounces are contained in a variety of black holes that contain beyond their horizon an expanding asymptotically isotropic universe [10,11,12]. In general relativity, or its extensions, such bounced solutions can be obtained, if phantom scalar fields are considered the source [13,14,15,16]. |
| 2 | It is important that the frequencies of the oscillations are independent of the electromagnetic field governed by non-linear electrodynamic models being fully governed by the spacetime geometry, but the optical phenomena depend on the non-linear electrodynamics—the photons are not following the null geodesics of the spacetime [47,48,49]. |
| 3 | Some alternatives to the geodesic model of HF QPOs are the diskoseismic model relating the QPOs to the global oscillations of thin accretion disks [65,66,67,68,69,70,71], and the string loop oscillation model [72]. Of special interest is the magnetically modified geodesic model where epicyclic motion is considered for slightly charged matter orbiting a magnetized black hole or neutron star along stable circular orbits [43,73,74]. |
References
- Bronnikov, K.A. Black bounces, wormholes, and partly phantom scalar fields. Phys. Rev. D 2022, 106, 064029. [Google Scholar] [CrossRef]
- Born, M. On the Quantum Theory of the Electromagnetic Field. Proc. R. Soc. Lond. Ser. A 1934, 143, 410–437. [Google Scholar] [CrossRef]
- Born, M.; Infeld, L. Foundations of the New Field Theory. Proc. R. Soc. Lond. Ser. A 1934, 144, 425–451. [Google Scholar] [CrossRef]
- Bronnikov, K.A. Regular magnetic black holes and monopoles from nonlinear electrodynamics. Phys. Rev. D 2001, 63, 044005. [Google Scholar] [CrossRef]
- Bronnikov, K.A. Nonlinear electrodynamics, regular black holes and wormholes. Int. J. Mod. Phys. D 2018, 27, 1841005. [Google Scholar] [CrossRef]
- Fan, Z.Y.; Wang, X. Construction of regular black holes in general relativity. Phys. Rev. D 2016, 94, 124027. [Google Scholar] [CrossRef]
- Toshmatov, B.; Stuchlík, Z.; Ahmedov, B. Comment on “Construction of regular black holes in general relativity”. Phys. Rev. D 2018, 98, 028501. [Google Scholar] [CrossRef]
- Kruglov, S.I. Universe acceleration and nonlinear electrodynamics. Phys. Rev. D 2015, 92, 123523. [Google Scholar] [CrossRef]
- Simpson, A.; Visser, M. Black-bounce to traversable wormhole. J. Cosmol. Astropart. Phys. 2019, 2019, 042. [Google Scholar] [CrossRef]
- Bronnikov, K.A.; Fabris, J.C. Regular Phantom Black Holes. Phys. Rev. Lett. 2006, 96, 251101. [Google Scholar] [CrossRef]
- Bronnikov, K.A.; Dehnen, H.; Melnikov, V.N. Regular black holes and black universes. Gen. Relativ. Gravit. 2007, 39, 973–987. [Google Scholar] [CrossRef]
- Bolokhov, S.V.; Bronnikov, K.A.; Skvortsova, M.V. Magnetic black universes and wormholes with a phantom scalar. Class. Quantum Gravity 2012, 29, 245006. [Google Scholar] [CrossRef]
- Clément, G.; Fabris, J.C.; Rodrigues, M.E. Phantom black holes in Einstein-Maxwell-dilaton theory. Phys. Rev. D 2009, 79, 064021. [Google Scholar] [CrossRef]
- Azreg-Aïnou, M.; Clément, G.; Fabris, J.C.; Rodrigues, M.E. Phantom black holes and sigma models. Phys. Rev. D 2011, 83, 124001. [Google Scholar] [CrossRef]
- Bronnikov, K. Scalar Fields as Sources for Wormholes and Regular Black Holes. Particles 2018, 1, 5. [Google Scholar] [CrossRef]
- Nishonov, I.; Zahid, M.; Khan, S.U.; Rayimbaev, J.; Abdujabbarov, A. Dynamics and collision of particles in modified black-bounce geometry. Eur. Phys. J. C 2024, 84, 829. [Google Scholar] [CrossRef]
- Haggard, H.M.; Rovelli, C. Quantum-gravity effects outside the horizon spark black to white hole tunneling. Phys. Rev. D 2015, 92, 104020. [Google Scholar] [CrossRef]
- Modesto, L. Semiclassical Loop Quantum Black Hole. Int. J. Theor. Phys. 2010, 49, 1649–1683. [Google Scholar] [CrossRef]
- Franzin, E.; Liberati, S.; Mazza, J.; Simpson, A.; Visser, M. Charged black-bounce spacetimes. J. Cosmol. Astropart. Phys. 2021, 2021, 036. [Google Scholar] [CrossRef]
- Mazza, J.; Franzin, E.; Liberati, S. A novel family of rotating black hole mimickers. J. Cosmol. Astropart. Phys. 2021, 2021, 082. [Google Scholar] [CrossRef]
- Xu, Z.; Tang, M. Rotating spacetime: Black-bounces and quantum deformed black hole. Eur. Phys. J. C 2021, 81, 863. [Google Scholar] [CrossRef]
- Churilova, M.S.; Stuchlík, Z. Ringing of the regular black-hole/wormhole transition. Class. Quantum Gravity 2020, 37, 075014. [Google Scholar] [CrossRef]
- Guerrero, M.; Mora-Pérez, G.; Olmo, G.J.; Orazi, E.; Rubiera-Garcia, D. Charged BTZ-type solutions in Eddington-inspired Born-Infeld gravity. J. Cosmol. Astropart. Phys. 2021, 2021, 025. [Google Scholar] [CrossRef]
- Tsukamoto, N. Gravitational lensing in the Simpson-Visser black-bounce spacetime in a strong deflection limit. Phys. Rev. D 2021, 103, 024033. [Google Scholar] [CrossRef]
- Bronnikov, K.A.; Konoplya, R.A. Echoes in brane worlds: Ringing at a black hole-wormhole transition. Phys. Rev. D 2020, 101, 064004. [Google Scholar] [CrossRef]
- Furtado, C.; Nascimento, J.R.; Petrov, A.Y.; Porfírio, P.J.; Soares, A.R. Strong gravitational lensing in a spacetime with topological charge within the Eddington-inspired Born-Infeld gravity. Phys. Rev. D 2021, 103, 044047. [Google Scholar] [CrossRef]
- Stuchlík, Z.; Vrba, J. Epicyclic Oscillations around Simpson-Visser Regular Black Holes and Wormholes. Universe 2021, 7, 279. [Google Scholar] [CrossRef]
- Abdulkhamidov, F.; Nedkova, P.; Rayimbaev, J.; Kunz, J.; Ahmedov, B. Parameter constraints on traversable wormholes within beyond Horndeski theories through quasiperiodic oscillations. Phys. Rev. D 2024, 109, 104074. [Google Scholar] [CrossRef]
- Bronnikov, K.A.; Walia, R.K. Field sources for Simpson-Visser spacetimes. Phys. Rev. D 2022, 105, 044039. [Google Scholar] [CrossRef]
- Fisher, I.Z. Scalar mesostatic field with regard for gravitational effects. arXiv 1999, arXiv:gr-qc/9911008. [Google Scholar] [CrossRef]
- Janis, A.I.; Newman, E.T.; Winicour, J. Reality of the Schwarzschild Singularity. Phys. Rev. Lett. 1968, 20, 878–880. [Google Scholar] [CrossRef]
- Bronnikov, K.A.; Shikin, G.N. Interacting fields in general relativity theory. Russ. Phys. J. 1977, 20, 1138–1143. [Google Scholar] [CrossRef]
- Garfinkle, D.; Horowitz, G.T.; Strominger, A. Charged black holes in string theory. Phys. Rev. D 1991, 43, 3140–3143, Erratum in 1992, 45, 3888. https://doi.org/10.1103/PhysRevD.45.3888. [Google Scholar] [CrossRef]
- Gibbons, G.W.; Maeda, K.I. Black holes and membranes in higher-dimensional theories with dilaton fields. Nucl. Phys. B 1988, 298, 741–775. [Google Scholar] [CrossRef]
- Belloni, T.M.; Sanna, A.; Méndez, M. High-frequency quasi-periodic oscillations in black hole binaries. Mon. Not. RAS 2012, 426, 1701–1709. [Google Scholar] [CrossRef]
- Belloni, T.M.; Stella, L. Fast Variability from Black-Hole Binaries. Space Sci. Rev. 2014, 183, 43–60. [Google Scholar] [CrossRef]
- Remillard, R.A.; McClintock, J.E. X-Ray Properties of Black-Hole Binaries. Annu. Rev. Astron. Astrophys. 2006, 44, 49–92. [Google Scholar] [CrossRef]
- Smith, K.L.; Tandon, C.R.; Wagoner, R.V. Confrontation of Observation and Theory: High-frequency QPOs in X-Ray Binaries, Tidal Disruption Events, and Active Galactic Nuclei. Astrophys. J. 2021, 906, 92. [Google Scholar] [CrossRef]
- Dai, D.C.; Starkman, G.D.; Stojkovic, B.; Stojkovic, D.; Weltman, A. Using Quasars as Standard Clocks for Measuring Cosmological Redshift. Phys. Rev. Lett. 2012, 108, 231302. [Google Scholar] [CrossRef]
- Solomon, R.; Stojkovic, D. Variability in quasar light curves: Using quasars as standard candles. J. Cosmol. Astropart. Phys. 2022, 2022, 060. [Google Scholar] [CrossRef]
- Dainotti, M.G.; Bargiacchi, G.; Lenart, A.L.; Capozziello, S.; Ó Colgáin, E.; Solomon, R.; Stojkovic, D.; Sheikh-Jabbari, M.M. Quasar Standardization: Overcoming Selection Biases and Redshift Evolution. Astrophys. J. 2022, 931, 106. [Google Scholar] [CrossRef]
- Stuchlík, Z.; Kotrlová, A.; Török, G. Multi-resonance orbital model of high-frequency quasi-periodic oscillations: Possible high-precision determination of black hole and neutron star spin. Astron. Astrophys. 2013, 552, A10. [Google Scholar] [CrossRef]
- Stuchlík, Z.; Kološ, M.; Kovář, J.; Slaný, P.; Tursunov, A. Influence of Cosmic Repulsion and Magnetic Fields on Accretion Disks Rotating around Kerr Black Holes. Universe 2020, 6, 26. [Google Scholar] [CrossRef]
- van der Klis, M. A comparison of the power spectra of Z and atoll sources, pulsars and black hole candidates. Astron. Astrophys. 1994, 283, 469–474. [Google Scholar]
- Motta, S.E.; Rouco Escorial, A.; Kuulkers, E.; Muñoz-Darias, T.; Sanna, A. Links between quasi-periodic oscillations and accretion states in neutron star low-mass X-ray binaries. Mon. Not. RAS 2017, 468, 2311–2324. [Google Scholar] [CrossRef]
- Belloni, T.; Homan, J.; Motta, S.; Ratti, E.; Méndez, M. Rossi XTE monitoring of 4U1636-53—I. Long-term evolution and kHz quasi-periodic oscillations. Mon. Not. RAS 2007, 379, 247–252. [Google Scholar] [CrossRef]
- Novello, M.; de Lorenci, V.A.; Salim, J.M.; Klippert, R. Geometrical aspects of light propagation in nonlinear electrodynamics. Phys. Rev. D 2000, 61, 045001. [Google Scholar] [CrossRef]
- De Lorenci, V.A.; Klippert, R.; Novello, M.; Salim, J.M. Light propagation in non-linear electrodynamics. Phys. Lett. B 2000, 482, 134–140. [Google Scholar] [CrossRef]
- Stuchlík, Z.; Schee, J. Shadow of the regular Bardeen black holes and comparison of the motion of photons and neutrinos. Eur. Phys. J. C 2019, 79, 44. [Google Scholar] [CrossRef]
- Bronnikov, K.; Rubin, S. Black Holes, Cosmology and Extra Dimensions; Information and Interdisciplinary Subjects Series; World Scientific: Singapore, 2013. [Google Scholar]
- Bronnikov, K.A. On Spherically Symmetric Solutions in D-Dimensional Dilaton Gravity. Gravit. Cosmol. 1995, 1, 67–78. [Google Scholar]
- Misner, C.W.; Thorne, K.S.; Wheeler, J.A. Gravitation; W. H. Freeman Princeton University Press: Princeton, NJ, USA, 1973. [Google Scholar]
- Chowdhury, A.N.; Patil, M.; Malafarina, D.; Joshi, P.S. Circular geodesics and accretion disks in the Janis-Newman-Winicour and gamma metric spacetimes. Phys. Rev. D 2012, 85, 104031. [Google Scholar] [CrossRef]
- Gyulchev, G.; Nedkova, P.; Vetsov, T.; Yazadjiev, S. Image of the Janis-Newman-Winicour naked singularity with a thin accretion disk. Phys. Rev. D 2019, 100, 024055. [Google Scholar] [CrossRef]
- Vieira, R.S.S.; Schee, J.; Kluźniak, W.; Stuchlík, Z.; Abramowicz, M. Circular geodesics of naked singularities in the Kehagias-Sfetsos metric of Hořava’s gravity. Phys. Rev. D 2014, 90, 024035. [Google Scholar] [CrossRef]
- Stuchlík, Z.; Kološ, M. Acceleration of the charged particles due to chaotic scattering in the combined black hole gravitational field and asymptotically uniform magnetic field. Eur. Phys. J. C 2016, 76, 32. [Google Scholar] [CrossRef]
- Abramowicz, M.A.; Kluźniak, W.; McClintock, J.E.; Remillard, R.A. The Importance of Discovering a 3:2 Twin-Peak Quasi-periodic Oscillation in an Ultraluminous X-Ray Source, or How to Solve the Puzzle of Intermediate-Mass Black Holes. Astrophys. J. Lett. 2004, 609, L63–L65. [Google Scholar] [CrossRef]
- Ingram, A.R.; Motta, S.E. A review of quasi-periodic oscillations from black hole X-ray binaries: Observation and theory. New Astron. Rev. 2019, 85, 101524. [Google Scholar] [CrossRef]
- Belloni, T.; Méndez, M.; Homan, J. The distribution of kHz QPO frequencies in bright low mass X-ray binaries. Astron. Astrophys. 2005, 437, 209–216. [Google Scholar] [CrossRef]
- Török, G.; Abramowicz, M.A.; Kluźniak, W.; Stuchlík, Z. The orbital resonance model for twin peak kHz quasi periodic oscillations in microquasars. Astron. Astrophys. 2005, 436, 1–8. [Google Scholar] [CrossRef]
- Stuchlík, Z.; Kološ, M. Models of quasi-periodic oscillations related to mass and spin of the GRO J1655-40 black hole. Astron. Astrophys. 2016, 586, A130. [Google Scholar] [CrossRef]
- Stella, L.; Vietri, M. kHz Quasiperiodic Oscillations in Low-Mass X-Ray Binaries as Probes of General Relativity in the Strong-Field Regime. Phys. Rev. Lett. 1999, 82, 17–20. [Google Scholar] [CrossRef]
- Rezzolla, L.; Yoshida, S.; Zanotti, O. Oscillations of vertically integrated relativistic tori—I. Axisymmetric modes in a Schwarzschild space-time. Mon. Not. RAS 2003, 344, 978–992. [Google Scholar] [CrossRef]
- Rezzolla, L.; Yoshida, S.; Maccarone, T.J.; Zanotti, O. A new simple model for high-frequency quasi-periodic oscillations in black hole candidates. Mon. Not. RAS 2003, 344, L37–L41. [Google Scholar] [CrossRef]
- Okazaki, A.T.; Kato, S.; Fukue, J. Global trapped oscillations of relativistic accretion disks. Publ. Astron. Soc. Jpn. 1987, 39, 457–473. [Google Scholar]
- Nowak, M.A.; Wagoner, R.V. Diskoseismology: Probing Accretion Disks. II. G-Modes, Gravitational Radiation Reaction, and Viscosity. Astrophys. J. 1992, 393, 697. [Google Scholar] [CrossRef]
- Kato, S. Basic Properties of Thin-Disk Oscillations. Publ. Astron. Soc. Jpn. 2001, 53, 1–24. [Google Scholar] [CrossRef]
- Kato, S. Resonant Excitation of Disk Oscillations by Warps: A Model of kHz QPOs. Publ. Astron. Soc. Jpn. 2004, 56, 905–922. [Google Scholar] [CrossRef]
- Lai, D.; Tsang, D. Corotational instability of inertial-acoustic modes in black hole accretion discs and quasi-periodic oscillations. Mon. Not. RAS 2009, 393, 979–991. [Google Scholar] [CrossRef]
- Horák, J.; Lai, D. Corotation resonance and overstable oscillations in black hole accretion discs: General relativistic calculations. Mon. Not. RAS 2013, 434, 2761–2771. [Google Scholar] [CrossRef]
- Kato, S.; Fukue, J. Trapped Radial Oscillations of Gaseous Disks around a Black Hole. Publ. Astron. Soc. Jpn. 1980, 32, 377. [Google Scholar] [CrossRef]
- Stuchlík, Z.; Kološ, M. String loops oscillating in the field of Kerr black holes as a possible explanation of twin high-frequency quasiperiodic oscillations observed in microquasars. Phys. Rev. D 2014, 89, 065007. [Google Scholar] [CrossRef]
- Shaymatov, S.; Vrba, J.; Malafarina, D.; Ahmedov, B.; Stuchlík, Z. Charged particle and epicyclic motions around 4 D Einstein-Gauss-Bonnet black hole immersed in an external magnetic field. Phys. Dark Universe 2020, 30, 100648. [Google Scholar] [CrossRef]
- Stuchlík, Z.; Kološ, M.; Tursunov, A. Large-scale magnetic fields enabling fitting of the high-frequency QPOs observed around supermassive black holes. Publ. Astron. Soc. Jpn. 2022, 74, 1220–1233. [Google Scholar] [CrossRef]
- Abramowicz, M.A.; Kluźniak, W. A precise determination of black hole spin in GRO J1655-40. Astron. Astrophys. 2001, 374, L19–L20. [Google Scholar] [CrossRef]
- Abramowicz, M.A.; Karas, V.; Kluzniak, W.; Lee, W.H.; Rebusco, P. Non-Linear Resonance in Nearly Geodesic Motion in Low-Mass X-Ray Binaries. Publ. Astron. Soc. Jpn. 2003, 55, 467–471. [Google Scholar] [CrossRef]
- Horák, J. Weak nonlinear coupling between epicyclic modes in slender tori. Astron. Astrophys. 2008, 486, 1–8. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifschits, E.M. The Classical Theory of Fields; Course of Theoretical Physics; Pergamon Press: Oxford, UK, 1975; Volume 2. [Google Scholar]
- Shahzadi, M.; Kološ, M.; Saleem, R.; Stuchlík, Z. Testing alternative spacetimes by high-frequency quasi-periodic oscillations observed in microquasars and active galactic nuclei. Class. Quantum Gravity 2024, 41, 075014. [Google Scholar] [CrossRef]
- Stuchlík, Z.; Vrba, J. Epicyclic orbits in the field of Einstein-Dirac-Maxwell traversable wormholes applied to the quasiperiodic oscillations observed in microquasars and active galactic nuclei. Eur. Phys. J. Plus 2021, 136, 1127. [Google Scholar] [CrossRef]
- Shafee, R.; McClintock, J.E.; Narayan, R.; Davis, S.W.; Li, L.X.; Remillard, R.A. Estimating the Spin of Stellar-Mass Black Holes by Spectral Fitting of the X-Ray ContinuumF. Astrophys. J. Lett. 2006, 636, L113–L116. [Google Scholar] [CrossRef]
- Reid, M.J.; McClintock, J.E.; Steiner, J.F.; Steeghs, D.; Remillard, R.A.; Dhawan, V.; Narayan, R. A Parallax Distance to the Microquasar GRS 1915+105 and a Revised Estimate of its Black Hole Mass. Astrophys. J. 2014, 796, 2. [Google Scholar] [CrossRef]




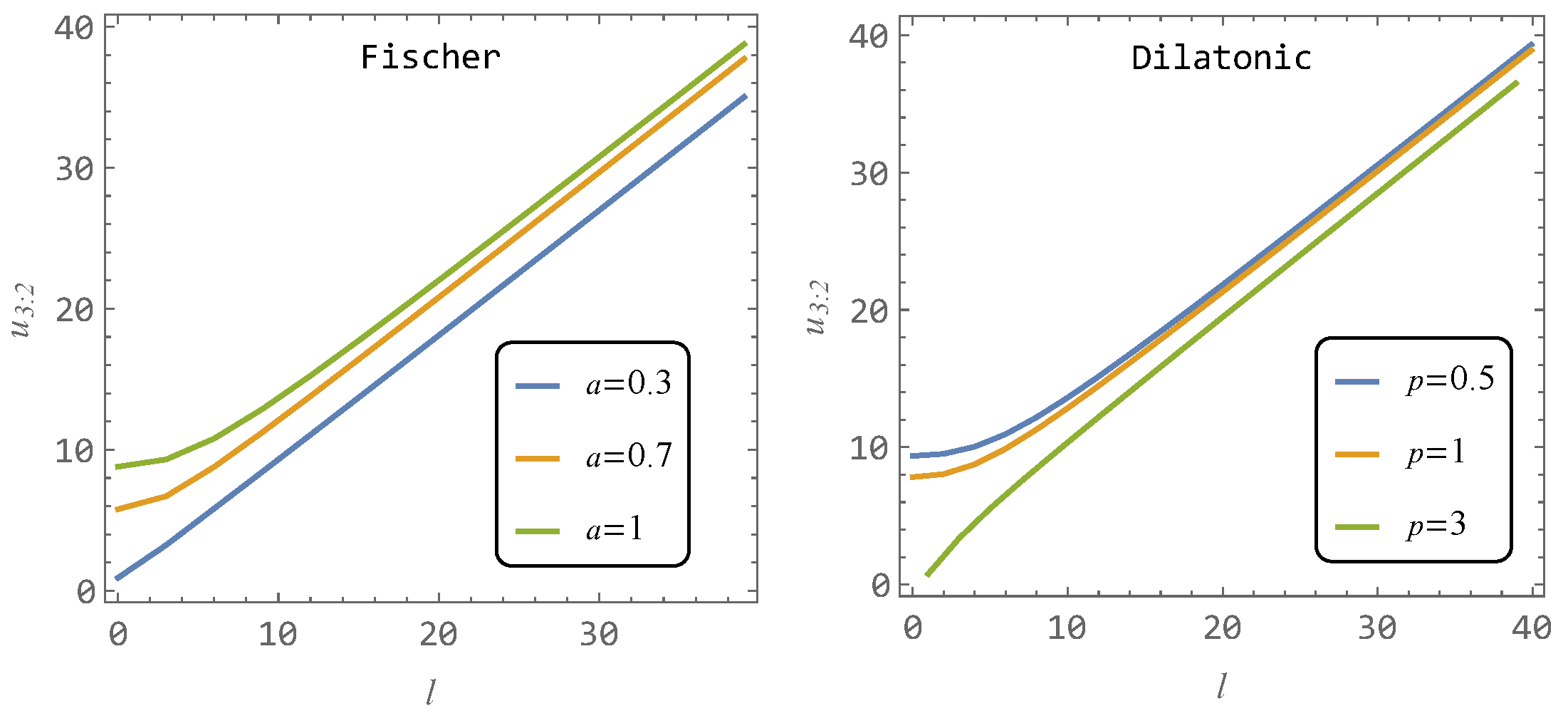
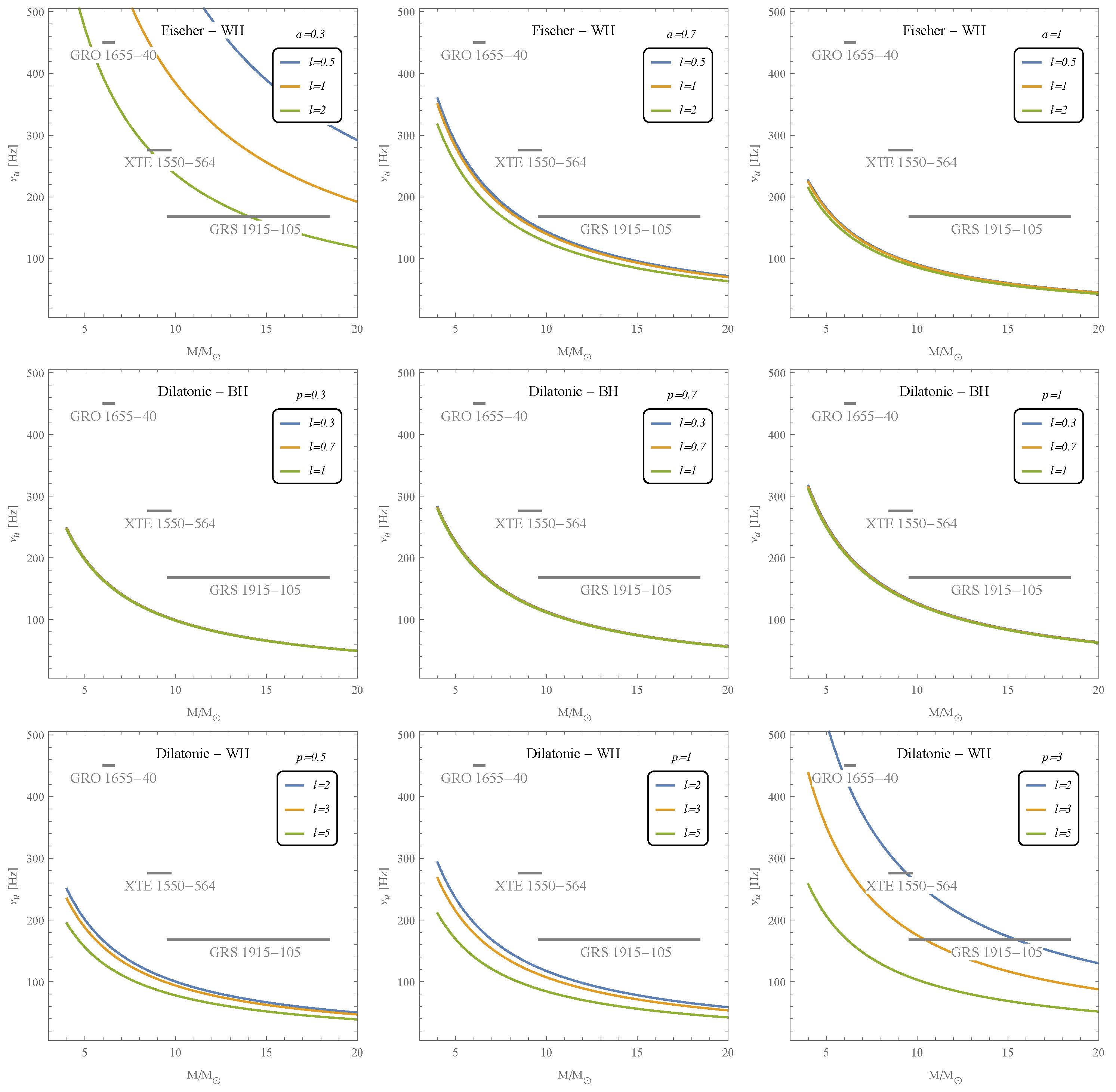
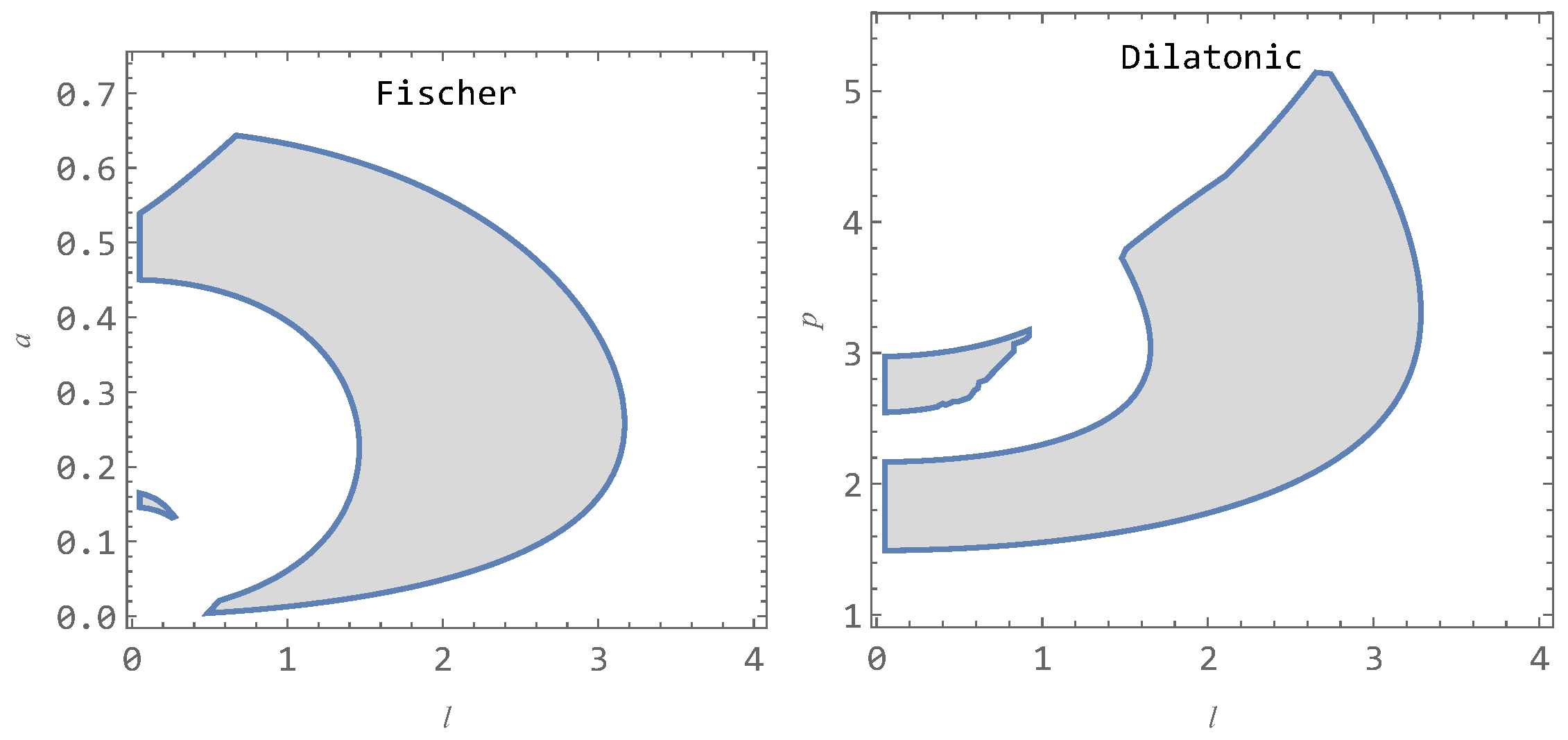
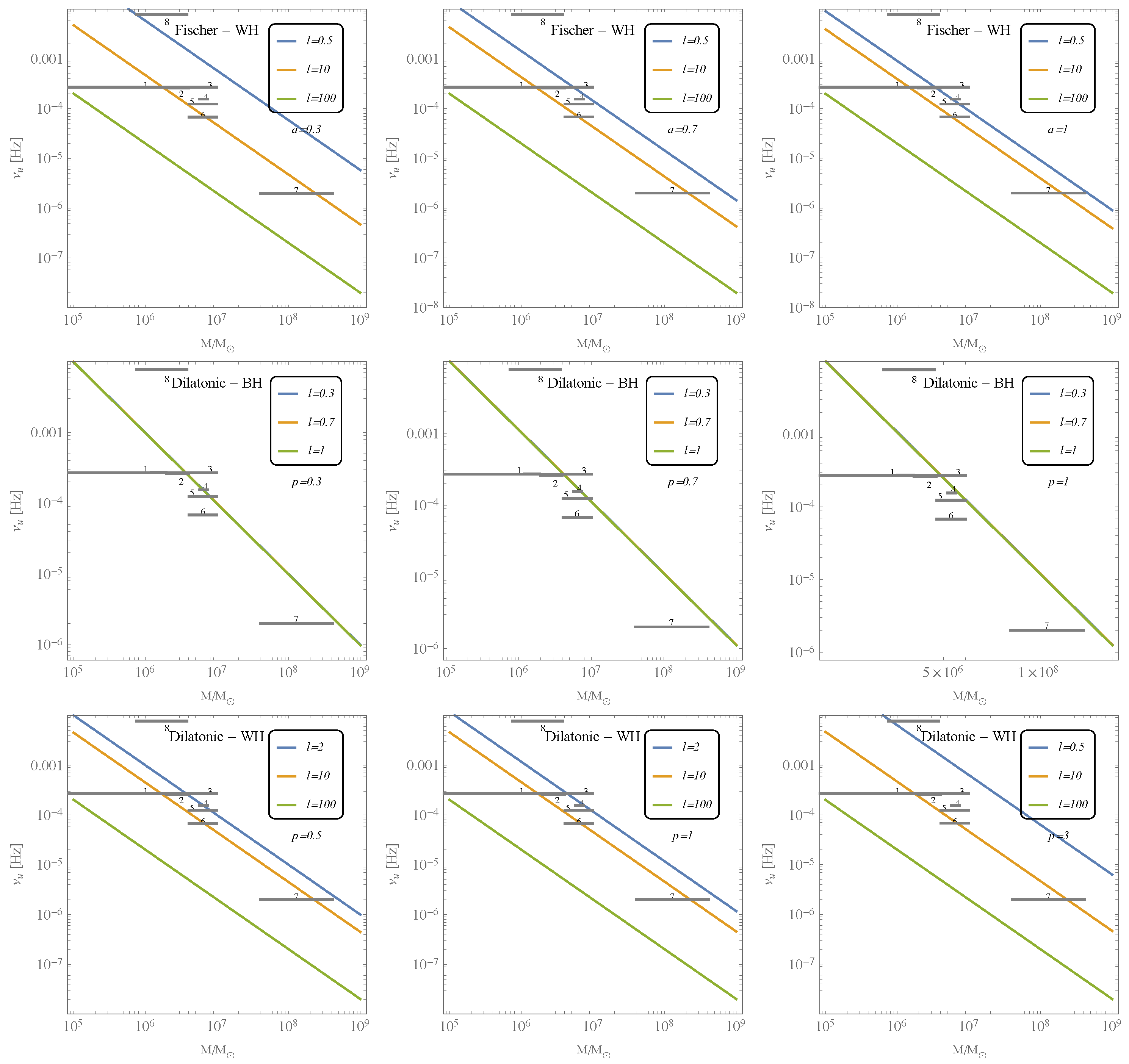

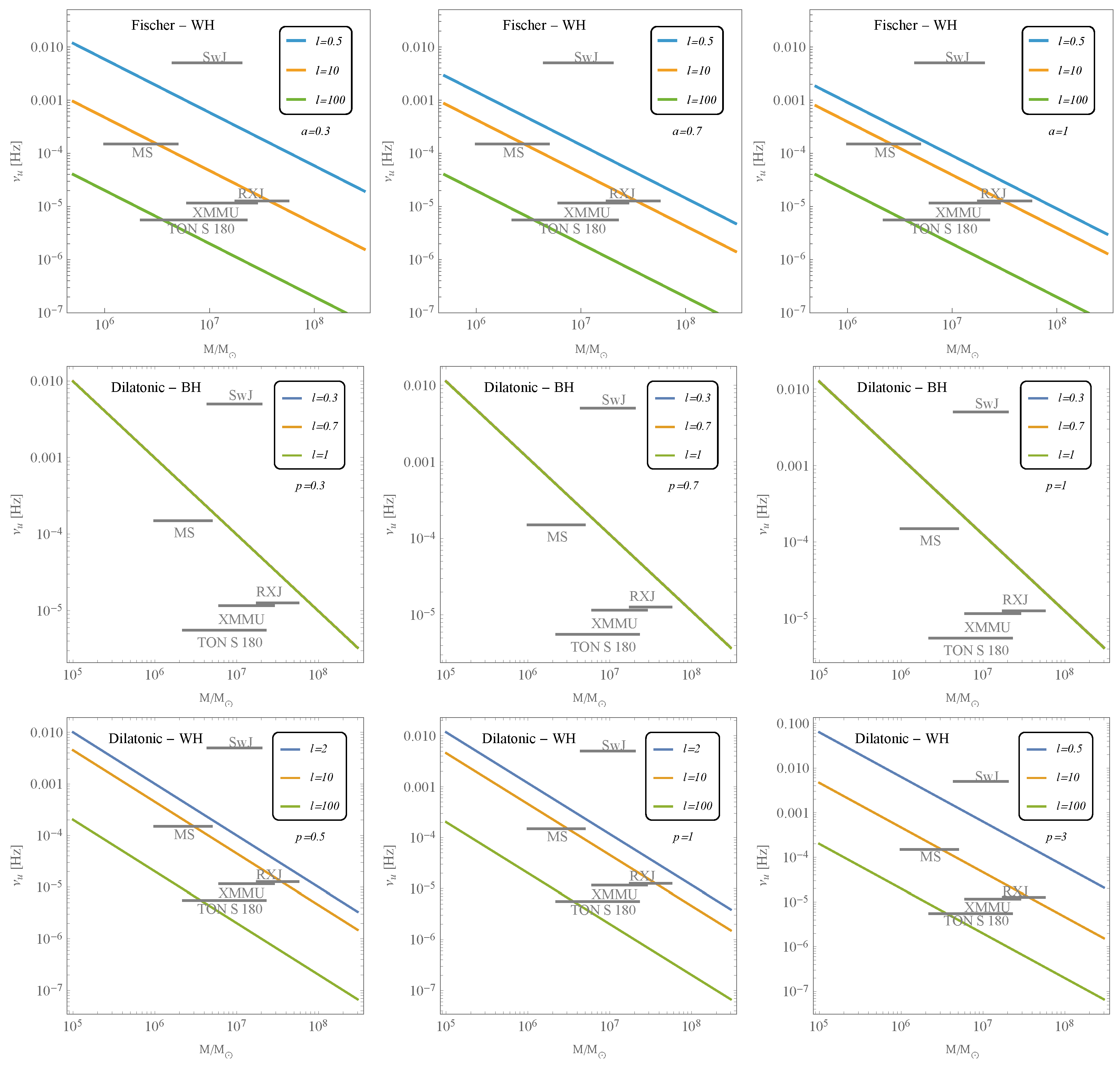
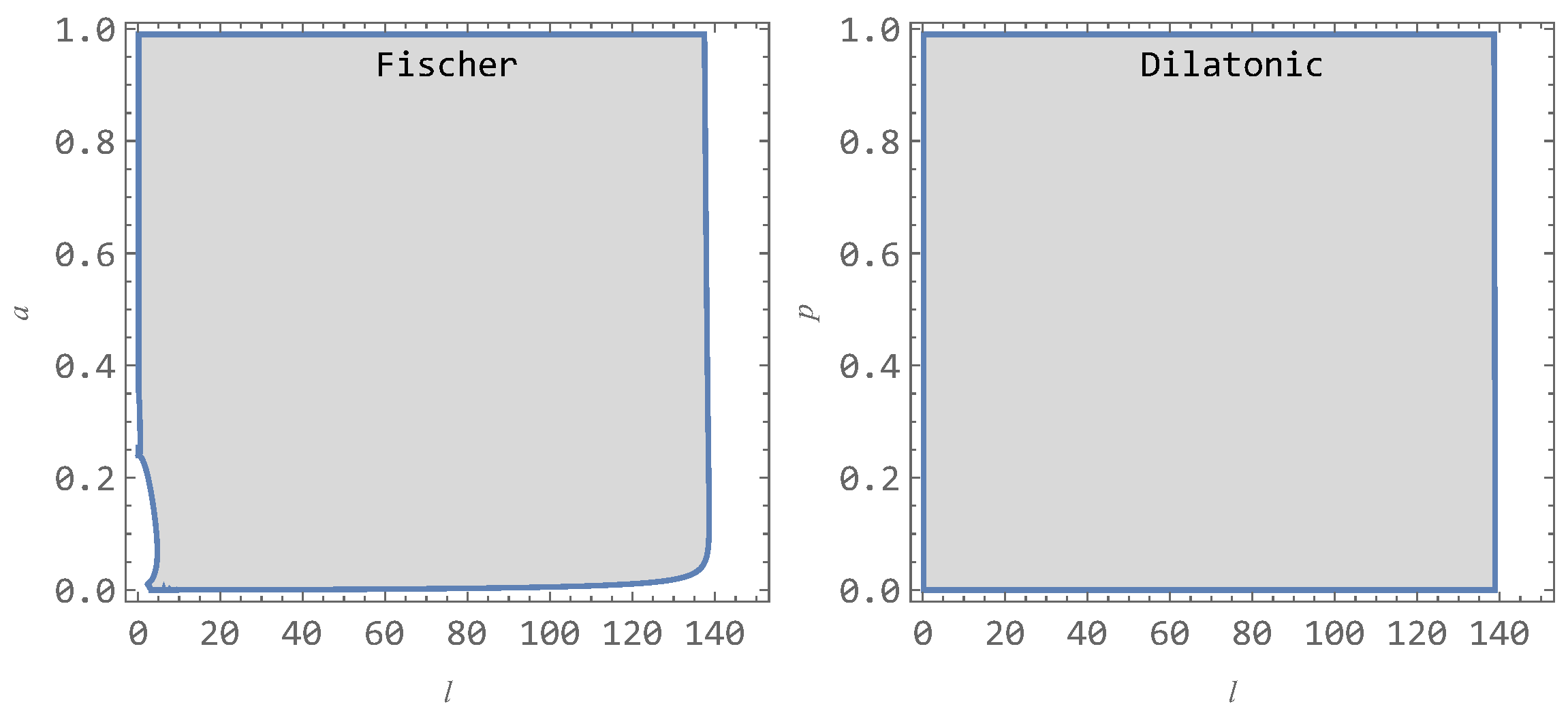
| Source | [Hz] | [Hz] | |
|---|---|---|---|
| GRO 1655-40 | 447–453 | 295–305 | 6.03–6.57 |
| XTE 1550-564 | 273–279 | 179–189 | 8.5–9.7 |
| GRS 1915+105 | 165–171 | 108–118 | 9.6–18.4 |
| Number | Name | BH Spin | log () | (Hz) |
|---|---|---|---|---|
| 1 | RE J1034+396 | 0.998 | ||
| 2 | 1H0707-495 | >0.976 | ||
| 3 | MCG-06-30-15 | >0.917 | ||
| 4 | Mrk 766 | >0.92 | ||
| 5 | ESO 113-G010 | 0.998 | ||
| 6 | ESO 113-G010b | 0.998 | ||
| 7 | 1H0419-577 | >0.98 | ||
| 8 | ASASSN-14li | >0.7 | ||
| - | TON S 180 | <0.4 | ||
| - | RXJ 0437.4-4711 | - | ||
| - | XMMU J134736.6+173403 | - | ||
| - | MS 2254.9-3712 | - | ||
| - | Sw J164449.3+573451 | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vrba, J.; Stuchlík, Z. Restrictions on Regularized Fisher and Dilatonic Spacetimes Implied by High-Frequency Quasiperiodic Oscillations Observed in Microquasars and Active Galactic Nuclei. Universe 2025, 11, 99. https://doi.org/10.3390/universe11030099
Vrba J, Stuchlík Z. Restrictions on Regularized Fisher and Dilatonic Spacetimes Implied by High-Frequency Quasiperiodic Oscillations Observed in Microquasars and Active Galactic Nuclei. Universe. 2025; 11(3):99. https://doi.org/10.3390/universe11030099
Chicago/Turabian StyleVrba, Jaroslav, and Zdeněk Stuchlík. 2025. "Restrictions on Regularized Fisher and Dilatonic Spacetimes Implied by High-Frequency Quasiperiodic Oscillations Observed in Microquasars and Active Galactic Nuclei" Universe 11, no. 3: 99. https://doi.org/10.3390/universe11030099
APA StyleVrba, J., & Stuchlík, Z. (2025). Restrictions on Regularized Fisher and Dilatonic Spacetimes Implied by High-Frequency Quasiperiodic Oscillations Observed in Microquasars and Active Galactic Nuclei. Universe, 11(3), 99. https://doi.org/10.3390/universe11030099








