Abstract
We model compact objects of known stellar mass and radius made of isotropic matter within Einstein’s gravity. The interior solution describing hydrostatic equilibrium we are using throughout the manuscript corresponds to the Tolman IV exact analytic solution obtained a long time ago. The three free parameters of the solutions are determined by imposing the matching conditions for objects of known stellar mass and radius. Finally, using well established criteria, it is shown that, contrary to the Kohler Chao solution, the Tolman IV solution is compatible with all requirements for well-behaved and realistic solutions, except for the relativistic adiabatic index that diverges at the surface of stars. The divergence of the index Γ may be resolved, including a thin crust assuming a polytropic equation of state, which is precisely the case seen in studies of neutron stars. To the best of our knowledge, we model here for the first time the recently discovered massive pulsar PSR J0740+6620 and the strangely light HESS compact object via the Tolman IV solution. The present work may be of interest to model builders as well as a useful reference for future research.
1. Introduction
General relativity (GR), formulated by A. Einstein more than 100 years ago [1], is globally accepted as a beautiful and, at the same time, very successful gravitational theory, thanks to which we nowadays can understand and describe different aspects of astrophysics and cosmology. Many of its remarkable predictions have been confirmed observationally, starting from the classical tests in the old days [2,3], and more recently with the historical LIGO’s direct detection of gravitational waves emitted from black hole mergers in binaries [4,5,6]. For a recent review on the tests of GR, see, e.g., [7].
Despite the mathematical elegance of GR, the analysis of problems corresponding to realistic physical situations is highly non-trivial in most of the cases of interest, as the field equations are non-linear coupled partial differential equations. The principle of superposition, valid in linear differential equations, does not apply here, and therefore, finding exact analytic solutions has been always an interesting and challenging topic, keeping researchers busy for decades. For known exact solutions to Einstein’s field equations, see [8].
In studies of compact relativistic astrophysical objects, the authors usually focus their attention on stars made of an isotropic fluid, where there is a unique pressure along all spatial dimensions, . However, celestial bodies are not always made of isotropic fluids only. In fact, under certain conditions, the matter content of the star may become anisotropic. The review article of Ruderman [9] a long time ago mentioned for the first time such a possibility: there the author makes the observation that relativistic particle interactions in very dense media could lead to the generation of anisotropies. In the years to follow, the study of anisotropies in relativistic stars received a boost by the subsequent work of [10]. Indeed, anisotropies may arise in different physical situations of dense matter media, for example, phase transitions [11], pion condensation [12], or in the presence of type 3A super-fluid [13], to mention just a few.
A new and elegant method [14], which permits us to obtain new solutions starting from a known one, has been applied extensively over the years. The so-called minimal geometric deformation (MGD) approach, which was originally introduced in [15] in the context of the brane-world scenario [16,17], has been proven to be a powerful tool in the investigation of the properties of self-gravitating objects, such as relativistic stars or black holes [18,19,20,21] (see also [22,23,24,25,26,27]). The MGD approach was later extended in [28], and applied in [29], demonstrating the power and potential of that technique. More recently, a method to obtain the isotropic generator of any anisotropic solution was developed in [30], and applied in [31].
Moreover, recently, the concept of complexity for self-gravitating systems within GR was introduced in [32]. The so called complexity factor, which is a measure of complexity, appears in the orthogonal splitting of the Riemann tensor. Obviously, it vanishes for homogeneous energy densities and isotropic fluid spheres, but it may also vanish when the two terms containing density inhomogeneity and anisotropic pressure cancel each other (see, for instance, [33,34,35,36,37,38,39,40,41,42,43] for works on anisotropic stars within the complexity factor formalism).
Yet another approach to obtain exact analytic solutions to the field equations describing hydrostatic equilibrium of relativistic stars is via the Karmarkar condition in gravity [44], which works well both for isotropic and anisotropic objects. If one of the metric potentials is assumed, then the Karmarkar condition allows us to obtain the other metric potential, and after that, the energy density and pressures of the fluid may be computed using the field equations. Within this approach, no equation of state for the matter content is assumed. For an incomplete list of works obtaining interior solutions via the Karmarkar condition in gravity, see, e.g., [45,46,47,48,49,50,51,52,53,54,55].
Regarding the composition and inner structure of compact objects, the most massive pulsars [56,57,58] observed over the last 15 years or so are putting constraints on different equations of state, since any mass-to-radius relationship that predicts a highest mass lower than the observed ones must be ruled out. In order to model a certain star, it would be advantageous to know both its mass and its radius, which is not always the case, as measuring the radius is much more difficult. There are some good strange quark star candidates (see, e.g., Table 5 of [59] or Table 1 of [60]), and also the recently discovered massive pulsar PSR J0740+6620 [61,62,63] and the strangely light object HESS [64], where both the stellar mass and radius are known observationally.
The exact analytic solution obtained within one of the aforementioned approaches must be physically relevant, that is, it must be well behaved and realistic, fulfilling all the well established criteria, and it should be capable of modeling one or more of the observed stars of known mass and radius. In this work, we propose to model the massive pulsar PSR J0740+6620 [61,62,63] and the strangely light HESS [64] compact object via the Tolman IV exact analytic solution of GR, assuming stars made of isotropic matter.
In the present article, our work is organized as follows. After this introduction, in the next section we briefly review the structure equations, while in Section 3, we summarize the Tolman IV and the Kohler Chao exact analytic solutions. In Section 4, we model two objects of known mass and radius and check weather or not the corresponding solution is realistic and well behaved. Finally, we conclude our work in Section 5. Throughout the manuscript we adopt the mostly positive metric signature, , as well as geometrical units, in which both the speed of light in a vacuum and Newton’s constant are set to unity, .
2. Anisotropic Relativistic Stars in GR
The most general form of a static, spherically symmetric geometry in Schwarzschild-like coordinates, , is given by
where, for interior solutions (, R being the radius of the star), are two independent functions of the radial coordinate. In the discussion to follow, it is more convenient to work with the mass function, , defined by
To obtain interior solutions describing hydrostatic equilibrium of relativistic stars, one needs to integrate the Tolman–Oppenheimer–Volkoff equations [65,66],
where a prime denotes differentiation with respect to r, and the matter content is described by a stress–energy tensor of the form
where is the radial pressure of the fluid, is its tangential pressure, and is the energy density of matter content, while the anisotropic factor is defined by
The function may be computed by
with M being the mass of the star. Equations (3)–(5) are to be integrated, imposing at the center of the star appropriate conditions
where is the central pressure. In addition, the following matching conditions must be satisfied at the surface of the object
taking into account that the exterior vacuum solution () is given by the Schwarzschild geometry [67]
3. Kohler Chao and Tolman IV Solutions
If the metric tensor satisfies the Karmarkar condition [44], it can represent an embedding class one spacetime
with different than zero. This condition leads to a differential equation given by [45]
Upon integration, we obtain the relationship between the metric potentials as follows [45]
where A and B are arbitrary constants of integration.
Finally, the anisotropic factor is computed to be [45]
Notice that the anisotropic factor vanishes when at least one of the expressions in the parentheses vanishes. Moreover, it is easy to verify that the factor being zero corresponds to the Schwarzschild solution.
In the discussion to follow, we shall seek interior solutions describing hydrostatic equilibrium of stars made of isotropic matter. Demanding that the second parenthesis vanishes,
then the metric potential, , is found to be
where the constants are two free parameters, the first being dimensionless and the other having dimensions of length. Therefore, we recover an existing solution obtained a long time ago [68]. Thanks to the Karmarkar condition, the second metric potential is computed to be
while the mass function is given by
Next, using the structure equations, the pressure and the energy density of the fluid may be computed, and they are given by
where the central values are found to be finite. Finally, the speed of sound, , and the relativistic adiabatic index, , are computed to be
Clearly, neither the energy density nor the pressure become zero at any finite radius, and therefore the Kohler Chao solution is not suitable for describing stellar interiors in hydrostatic equilibrium. This is why in the discussion to follow we shall switch to the Tolman IV analytic solution. We comment in passing that since we shall not be working with the Kohler Chao solution in the following, we could have omitted the discussion altogether. Nevertheless, we have decided to include it in order to demonstrate that modeling stars is not a trivial job, and that not every analytic solution is good enough.
As far as the Tolman IV solution is concerned, we may start assuming a metric potential of the form
Next, using the definition of the mass function as well the first structure equation, the energy density and the mass function are computed to be
Finally, making use of the other two structure equations, the pressure of the fluid and the other metric potential, , are found to be [26]
As a check, it is straightforward to verify that all structure equations are satisfied. We see that both the pressure and the energy density remain finite at the center of the star, while at the same time the pressure becomes zero at a finite radius R, which is found to be
Finally, the speed of sound, , and the relativistic adiabatic index, , for the Tolman IV solution are found to be
We notice that, contrary to the sound speed that always remains finite throughout the star, the index becomes infinite at the surface of the star.
4. Modeling Objects of Known Mass and Radius
4.1. Criteria for Realistic Solutions
Before an attempt to model the massive pulsar J0740+6620 and the light object HESS J1731-347 is made, let us first report here the requirements for well-behaved solutions capable of describing realistic astrophysical configurations. Those are the following:
- Causality, that is, the sound speed cannot exceed the speed of light in vacuum
- Stability based on the adiabatic relativistic index, that is, its mean value must be larger than a critical valuewhere the critical value is given by [69]while the mean value is computed by [69]
- The energy conditions are the constraints on the energy–momentum tensor of the matter content within a given theory of gravity. The standard acceptable conditions assumed for the energy–momentum tensor are: weak energy condition (WEC), dominant energy condition (DEC), null energy condition (NEC), and strong energy condition (SEC) (see, for instance, [70,71,72]). If and are arbitrary time-like and null vectors, respectively, then the conditions for the energy–momentum tensor are expressed with the following inequalitiesIn particular, in the case of a perfect fluid, the energy conditions require that [73,74]
4.2. Case I: Massive Pulsar J0740+6620
The analytic solution presented in the previous subsection is characterized by three free parameters, A, with dimensions of length, and B, which is dimensionless. Their numerical values may be determined by imposing the matching conditions
and hence the values of are found to be
considering stellar mass and radius and , respectively. Next, we compute the mean value of the adiabatic relativistic index as well as its critical value, which are found to be
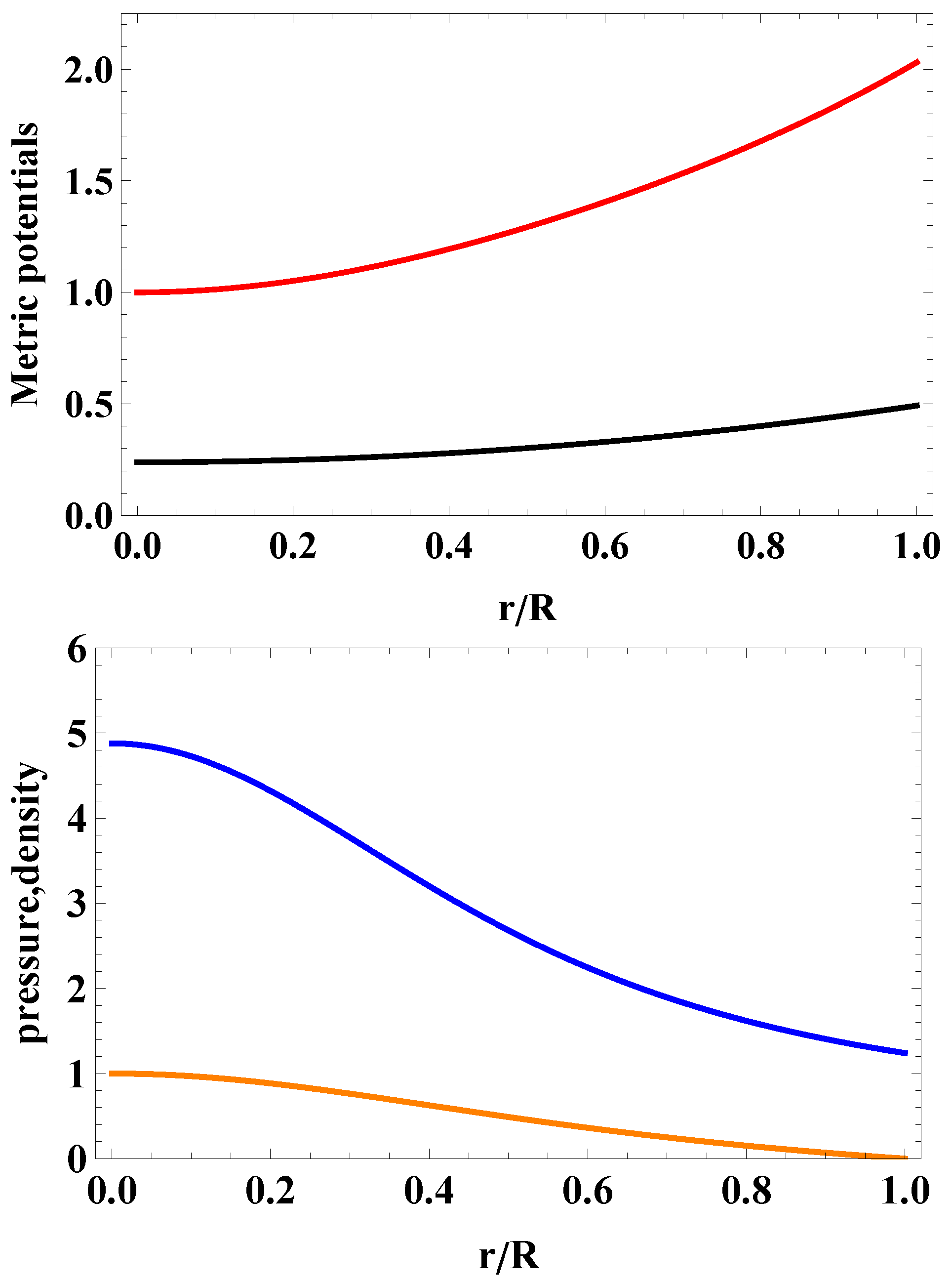
Finally, the metric potentials, the energy density, the pressure, the speed of sound, and the adiabatic relativistic index as a function of the radial coordinate are displayed in Figure 1 and Figure 2 below. We notice that both the pressure and the energy density are finite at the center, and they monotonically decrease throughout the star from the center to the surface. Furthermore, causality is not violated, and all energy conditions are fulfilled as well. Moreover, since , we conclude that the stability criterion, too, is met by the solution adopted here.
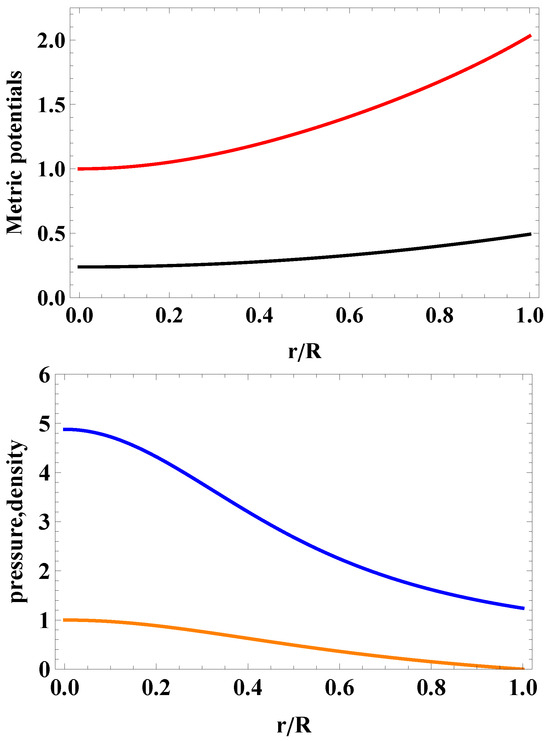
Figure 1.
Metric potentials (upper panel) and normalized pressure and energy density (lower panel) versus dimensionless radial coordinate, , for the massive pulsar J0740+6620. The pressure vanishes at .
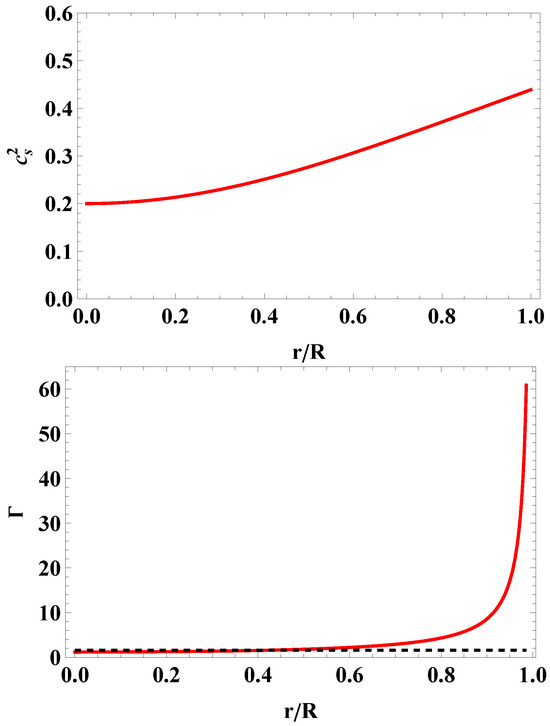
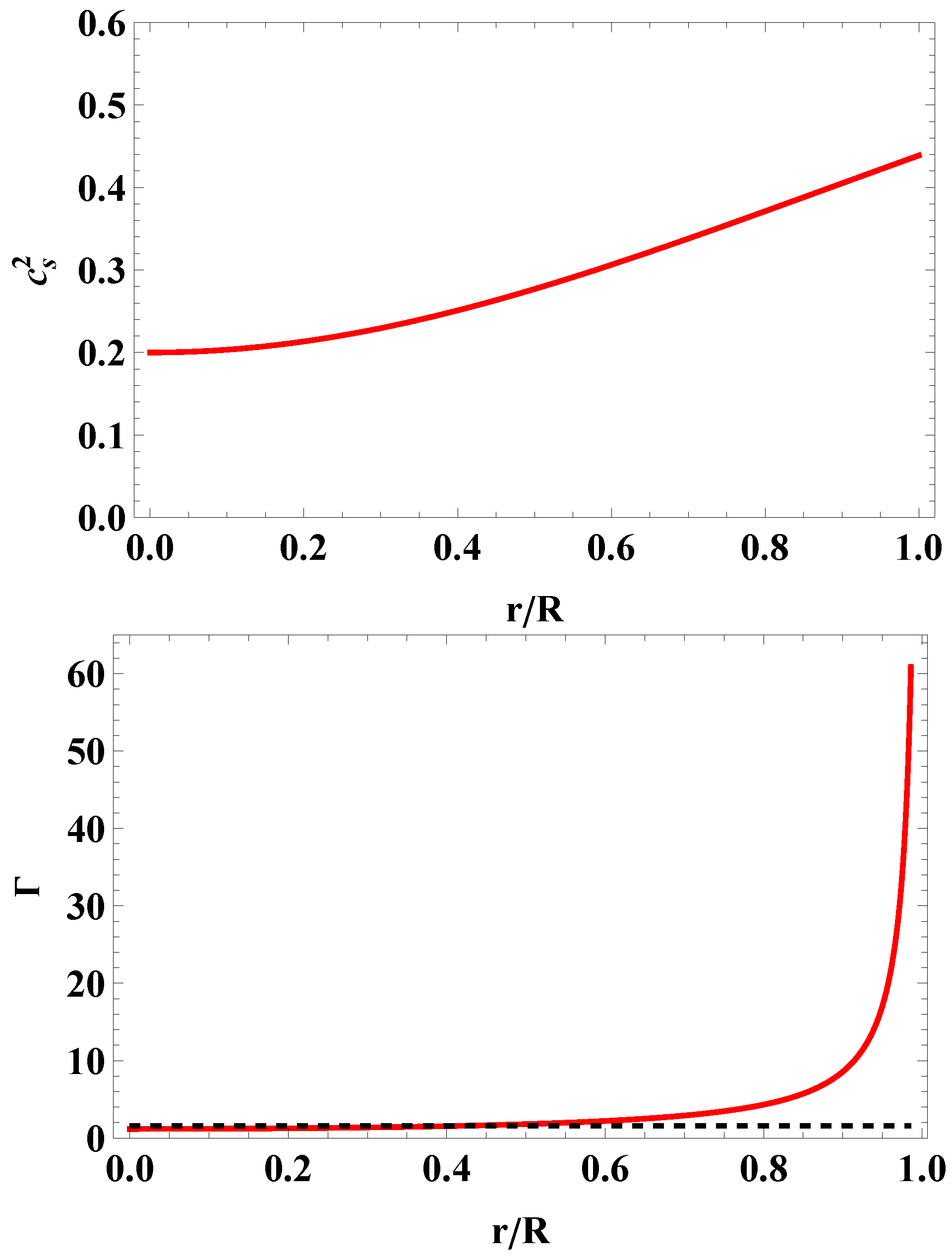
Figure 2.
Speed of sound (upper panel) and relativistic adiabatic index (lower panel) versus dimensionless radial coordinate, , for the massive pulsar J0740+6620. The horizontal dashed line corresponds to the critical value.
4.3. Case II: Light Object HESS J1731-347
As in the previous case, imposing the matching conditions, we find the following values of the free parameters
considering stellar mass and radius and , respectively. After that, we compute both the mean value of the adiabatic relativistic index and its critical value, and they are found to be
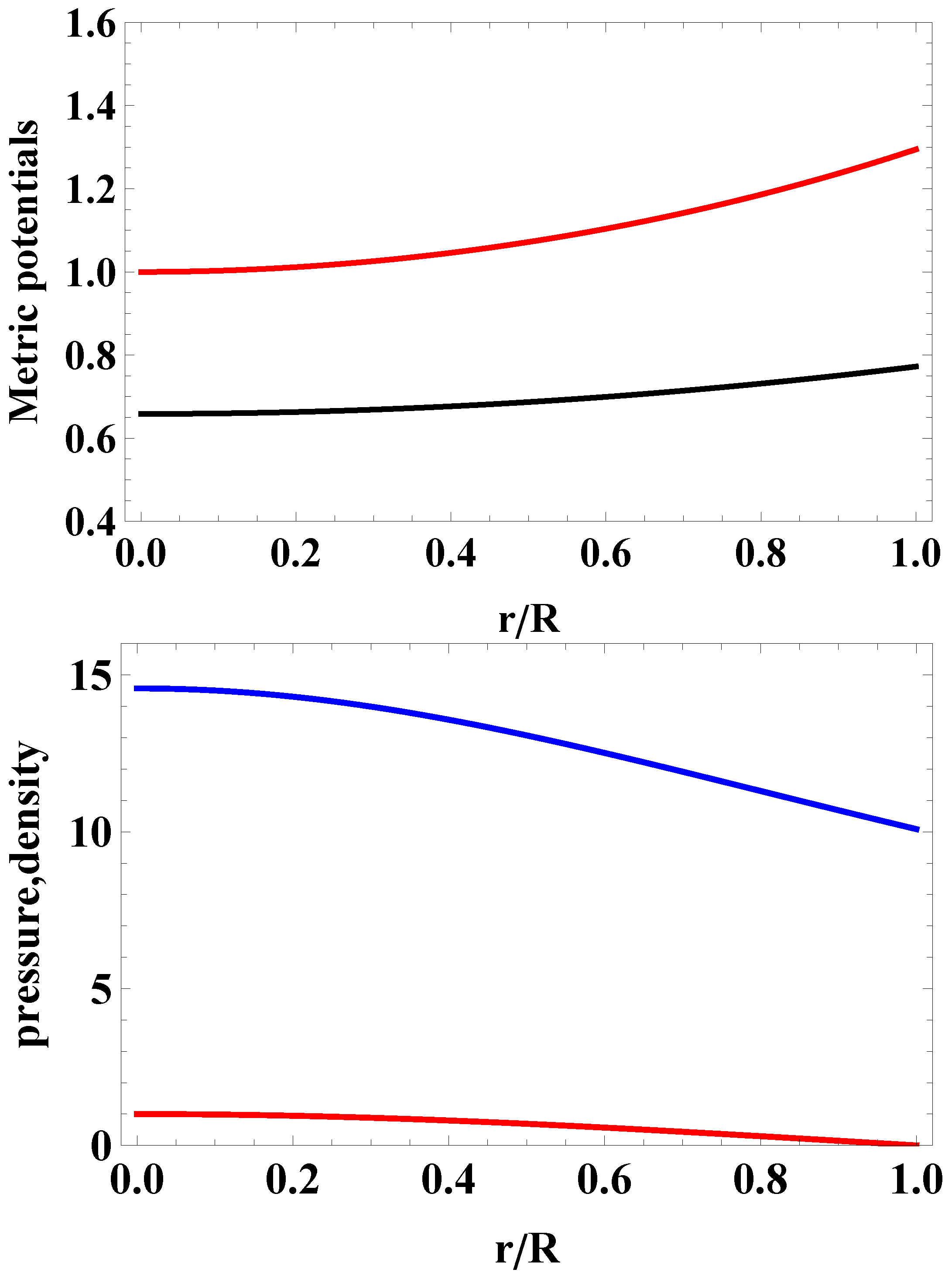
Next, the quantities of interest, namely the metric potentials, the energy density, the pressure, the speed of sound and the adiabatic relativistic index, as a function of the radial coordinate, are displayed in Figure 3 and Figure 4 below. A behavior very similar to the previous case is observed, although the central (normalized) energy density is now three times larger, while at the same time the adiabatic relativistic index takes higher values as we approach the surface of the star. We observe that causality is not violated, and that all the energy conditions are fulfilled as well. In addition to that, both the pressure and the energy density of the fluid are finite at the origin, and they monotonically decrease with r. Finally, since , we conclude that the stability criterion is met as well.
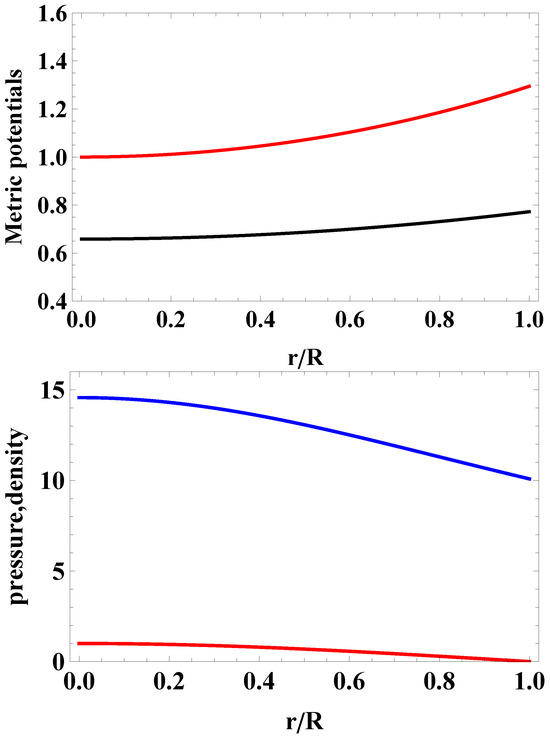
Figure 3.
Metric potentials (upper panel) and normalized pressure and energy density (lower panel) versus dimensionless radial coordinate, , for the HESS J1731-347 compact object. The pressure vanishes at .
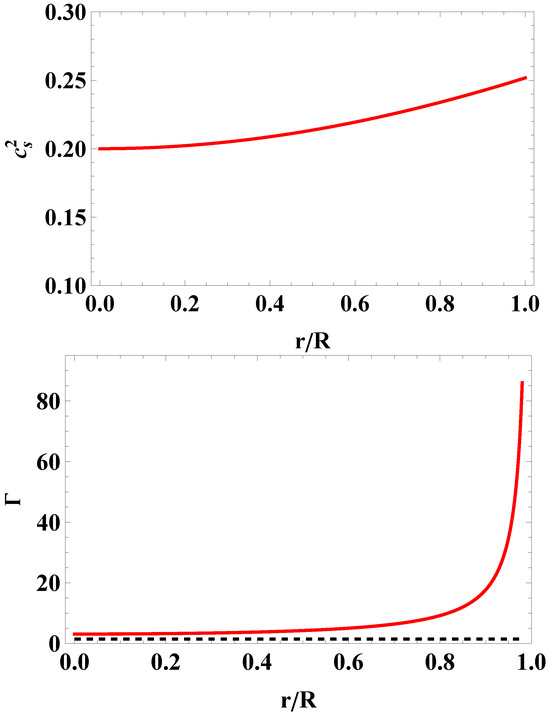
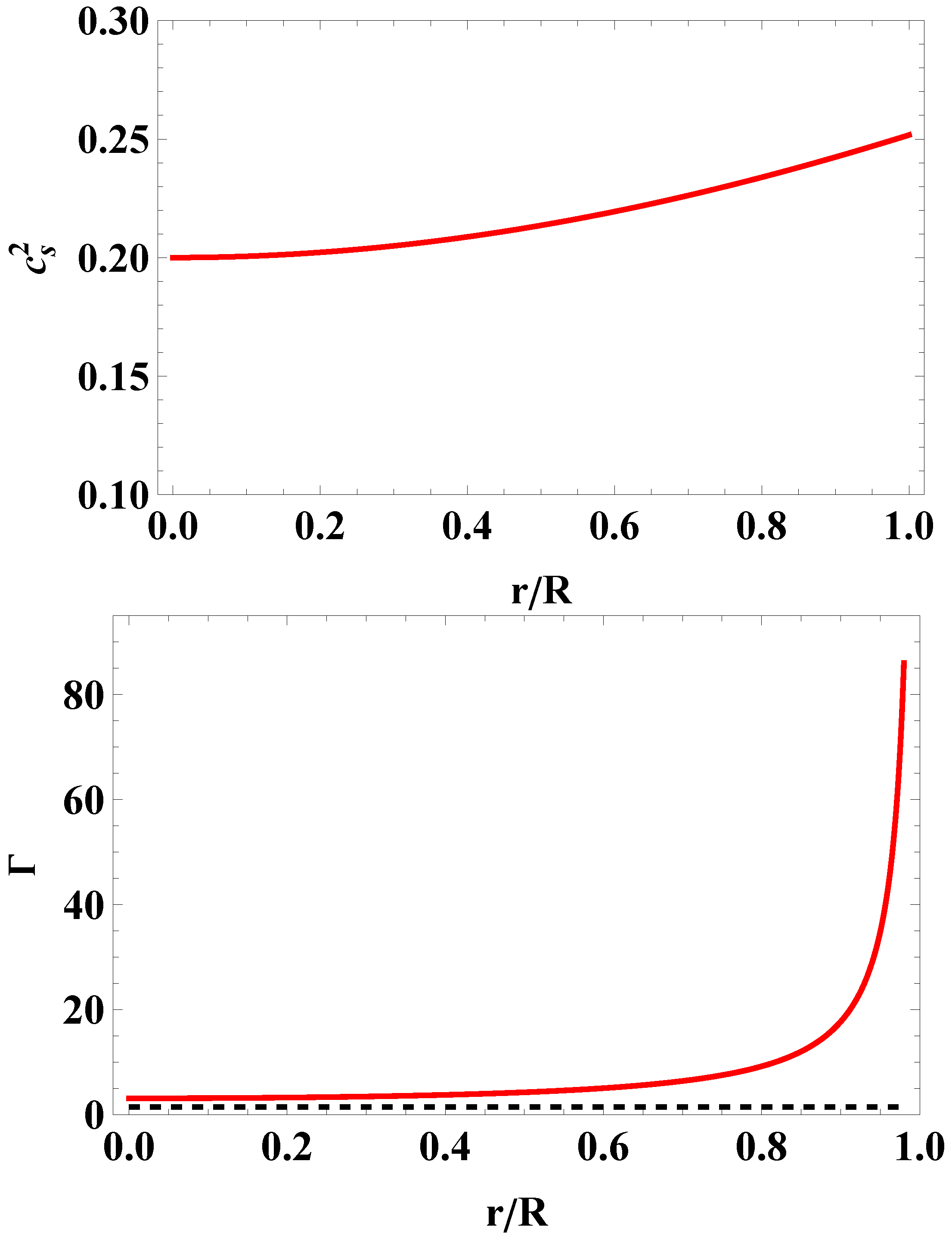
Figure 4.
Speed of sound (upper panel) and relativistic adiabatic index (lower panel) versus dimensionless radial coordinate, , for the HESS J1731-347 compact object. The horizontal dashed line corresponds to the critical value.
Before we conclude our work, a couple of comments are in order. The first one has to do with the matter content of the stars and the underlying equation of state. The exact analytic solution adopted here does not assume any equation of state, although it may be obtained in parametric form, , and, in principle, it could be studied in a future work. Despite that, given the behavior of the energy density, the sound speed, and the relativistic adiabatic index shown in the figures, one may assume that the objects modeled in this work are made either of dark energy, based on the extended Chaplygin gas (ECG) equation of state [75], or of quark matter in the color-flavor locked (CFL) phase [76]. The ECG EoS is the following
while the CFL EoS in parametric form , with being the quark chemical potential, is of the following form [77]
where the constant is given by
while the numerical values of the parameters are as follows: . This is one of the 19 viable models (CFL3) shown in Table I of [77].
Notice that, given the form of the equations of state above, only the pressure vanishes at the surface of the star, whereas the energy density acquires a non-vanishing surface value.
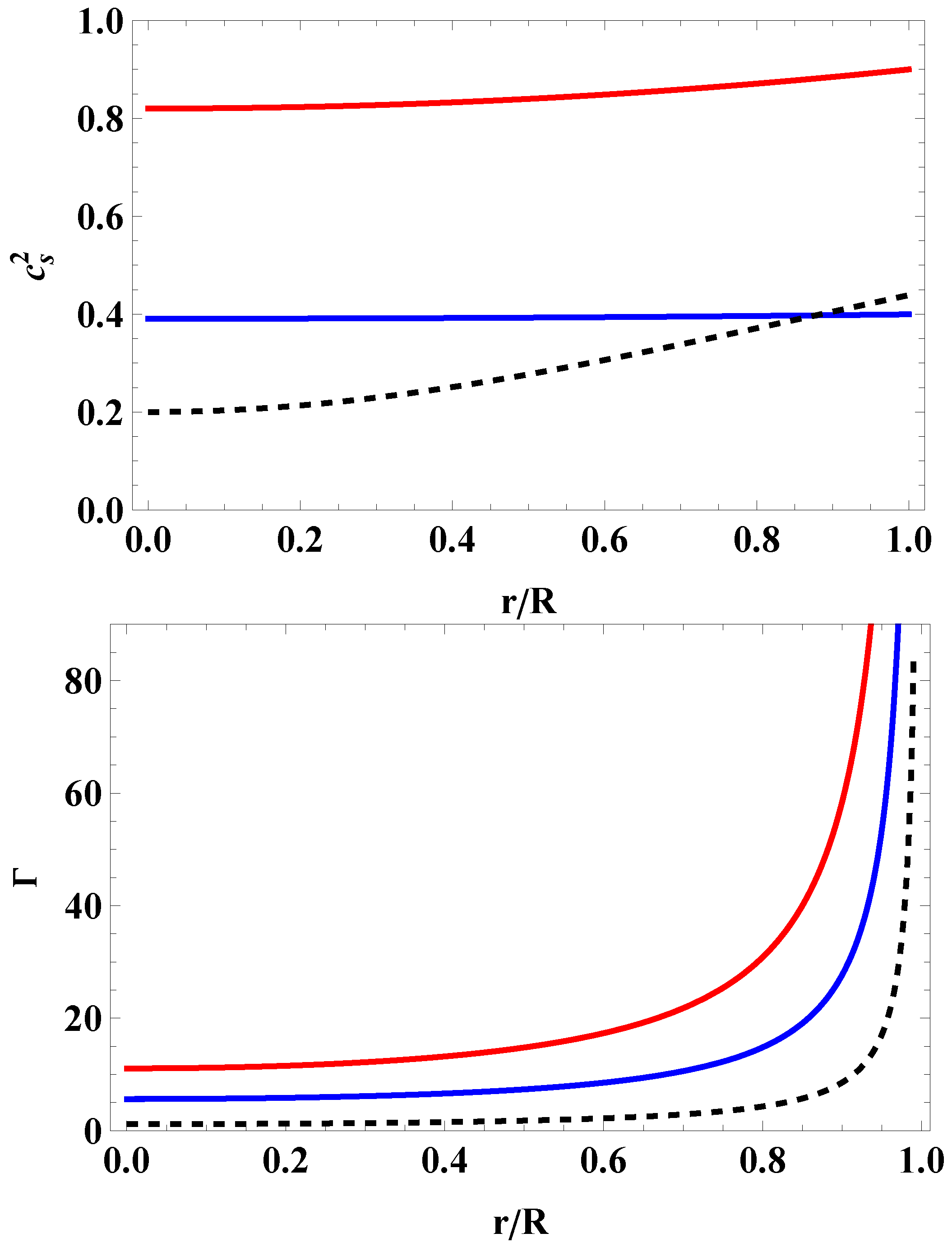
In Figure 5, we show the speed of sound as well as the relativistic adiabatic index for both matter contents and for the Tolman solution, as well as in the case of the massive pulsar J0740+6620. Clearly, the speed of sound of the dark energy content is too large, and so quark matter in the CFL phase is more likely. The behavior of the index observed here is the typical behavior whenever the pressure and the energy density cannot be zero at the same time at . This may be resolved by including a second layer, such as a thin crust, assuming a polytropic equation of state, and so both the energy density and the pressure vanish at the surface of the star. Therefore, the relativistic adiabatic index turns out to be finite. This happens, for instance, in studies of neutron stars.
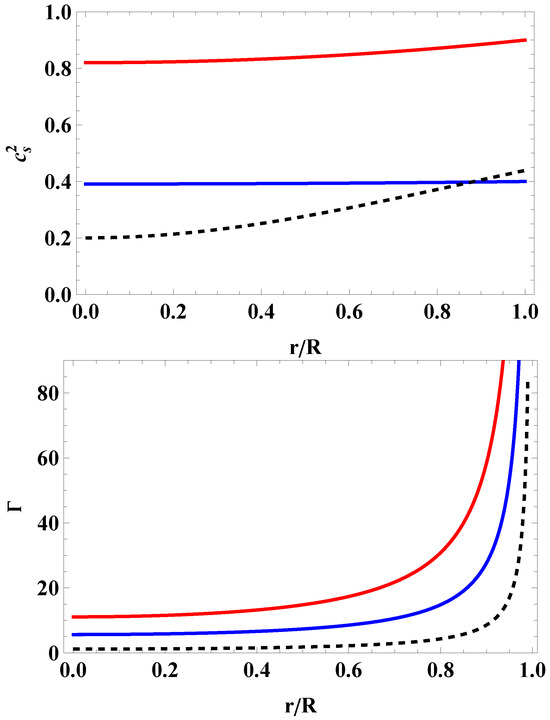
Figure 5.
Speed of sound (upper panel) and relativistic adiabatic index (lower panel) versus dimensionless radial coordinate, , for the CFL quark matter (curve in blue), the extended Chaplygin gas equation of state (curve in red) and the Tolman IV solution (black dashed curve). Both panels correspond to the case of the massive pulsar J0740+6620, considering a stellar mass .
Finally, in the present work, we have assumed stars made of isotropic matter with Einstein’s general relativity. In principle, one may consider an alternative theory of gravity. In the latter case, the new field equations will give rise to generalized TOV equations. Therefore, the quantities of interest will be given by different expressions. Moreover, the exterior (vacuum solution), generically speaking, will be different than the Schwarzschild geometry. Hence, as a future work, it would be interesting to extend this study to other objects of known masses and radii, and also to consider modeling relativistic stars made of anisotropic matter and/or within modified theories of gravity. We hope we can address those issues in forthcoming works in the near future.
5. Conclusions
To summarize our work, we have modeled astronomical objects of known masses and radii within GR via the Tolman IV solution. First, the general description of relativistic stars made of anisotropic matter within Einstein’s gravity was reviewed. Next, the so called Kohlar–Chao solution, which was obtained a long time ago and which is not suitable for describing stellar interior solutions, was recovered, assuming stars made of isotropic matter. After that, we presented the Tolman IV solution, and we summarized well established criteria for realistic solutions capable of describing astrophysical configurations. Next, considering the massive pulsar J0740+6620, the three free parameters of the solution were determined by imposing the appropriate matching conditions at the surface of the star. Then, the behavior of the solution was displayed graphically. According to our results, the quantities of interest were found to be finite (except for the relativistic adiabatic index that diverges at the surface of the star) and at the same time smooth, continuous functions of the radial coordinate throughout the pulsar. Moreover, well-established criteria, such as energy conditions, causality, and stability based on the adiabatic relativistic index, were shown to be fulfilled. Finally, going through the same steps, we demonstrated that the light HESS J1731-347 compact object, too, may be successfully modeled, as all the quantities of interest were found to be smooth and continuous functions of the radial coordinate throughout the object, while at the same time, all the well established criteria are met. The divergence of the index Γ may be resolved by including a thin crust and assuming a polytropic equation of state, which is precisely the case seen in studies of neutron stars.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in the study are included in the article. Further inquiries can be directed to the corresponding author.
Acknowledgments
The author wishes to thank the anonymous reviewers for useful comments and suggestions.
Conflicts of Interest
The author declare no conflict of interest.
References
- Einstein, A. The Field Equations of Gravitation; Sitzungsberichte der Preussischen Akademie der Wissenschaften: Berlin, Germany, 1915; pp. 844–847. [Google Scholar]
- Weinberg, S. Gravitation and Cosmology: Principles and Applications of the General Theory of Gravitation; John Wiley and Sons: Hoboken, NJ, USA, 1972. [Google Scholar]
- Meisner, C.W.; Thorne, K.S.; Wheeler, J.A. Gravitation; Princeton University Press: Princeton, NJ, USA, 1973. [Google Scholar]
- Abbott, B.P.; LIGO Scientific and Virgo. Observation of Gravitational Waves from a Binary Black Hole Merger. Phys. Rev. Lett. 2016, 116, 061102. [Google Scholar] [CrossRef]
- Abbott, B.P.; LIGO Scientific and Virgo. GW151226: Observation of Gravitational Waves from a 22-Solar-Mass Binary Black Hole Coalescence. Phys. Rev. Lett. 2016, 116, 241103. [Google Scholar] [CrossRef] [PubMed]
- Abbott, B.P.; LIGO Scientific and VIRGO. GW170104: Observation of a 50-Solar-Mass Binary Black Hole Coalescence at Redshift 0.2. Phys. Rev. Lett. 2017, 118, 221101, Erratum in: Phys. Rev. Lett. 2018, 121, 129901. [Google Scholar] [CrossRef] [PubMed]
- Asmodelle, E. Tests of General Relativity: A Review. arXiv 2004, arXiv:1705.04397. [Google Scholar]
- Stephani, H.; Kramer, D.; Maccallum, M.; Hoenselaers, C.; Herlt, E. Exact Solutions of Einstein’s Field Equations; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Ruderman, R. Pulsars: Structure and dynamics. Ann. Rev. Astron. Astrophys. 1972, 10, 427. [Google Scholar] [CrossRef]
- Bowers, R.L.; Liang, E.P.T.; Astrophys, J. Anisotropic spheres in general relativity. Astrophys. J. 1974, 188, 657. [Google Scholar] [CrossRef]
- Sokolov, A.I. Fazovye perekhody v sverkhtekuchej nejtronno zhidkosti. J. Exp. Theor. Phys. 1980, 79, 1137. [Google Scholar]
- Sawyer, R.F. Condensed Π-Phase in Neutron-Star Matter. Phys. Rev. Lett. 1972, 29, 382. [Google Scholar] [CrossRef]
- Kippenhahn, R.; Weigert, A. Stellar Structure and Evolution; Springer: Berlin, Germany, 1990. [Google Scholar]
- Ovalle, J. Decoupling gravitational sources in general relativity: From perfect to anisotropic fluids. Phys. Rev. D 2017, 95, 104019. [Google Scholar] [CrossRef]
- Ovalle, J. Searching exact solutions for compact stars in braneworld: A Conjecture. Mod. Phys. Lett. A 2008, 23, 3247–3263. [Google Scholar] [CrossRef]
- Randall, L.; Sundrum, R. A Large mass hierarchy from a small extra dimension. Phys. Rev. Lett. 1999, 83, 3370–3373. [Google Scholar] [CrossRef]
- Randall, L.; Sundrum, R. An Alternative to compactification. Phys. Rev. Lett. 1999, 83, 4690–4693. [Google Scholar] [CrossRef]
- Estrada, M.; Tello-Ortiz, F. A new family of analytical anisotropic solutions by gravitational decoupling. Eur. Phys. J. Plus 2018, 133, 453. [Google Scholar] [CrossRef]
- Morales, E.; Tello-Ortiz, F. Compact Anisotropic Models in General Relativity by Gravitational Decoupling. Eur. Phys. J. C 2018, 78, 841. [Google Scholar] [CrossRef]
- Estrada, M.; Prado, R. The Gravitational decoupling method: The higher dimensional case to find new analytic solutions. Eur. Phys. J. Plus 2019, 134, 168. [Google Scholar] [CrossRef]
- Ovalle, J.; Casadio, R.; da Rocha, R.; Sotomayor, A.; Stuchlik, Z. Black holes by gravitational decoupling. Eur. Phys. J. C 2018, 78, 960. [Google Scholar] [CrossRef]
- Ovalle, J. Non-uniform Braneworld Stars: An Exact Solution. Int. J. Mod. Phys. D 2009, 18, 837–852. [Google Scholar] [CrossRef]
- Ovalle, J. The Schwarzschild’s Braneworld Solution. Mod. Phys. Lett. A 2010, 25, 3323–3334. [Google Scholar] [CrossRef]
- Casadio, R.; Ovalle, J. Brane-world stars and (microscopic) black holes. Phys. Lett. B 2012, 715, 251–255. [Google Scholar] [CrossRef]
- Casadio, R.; Ovalle, J. Brane-world stars from minimal geometric deformation, and black holes. Gen. Rel. Grav. 2014, 46, 1669. [Google Scholar] [CrossRef]
- Ovalle, J.; Linares, F. Tolman IV solution in the Randall-Sundrum Braneworld. Phys. Rev. D 2013, 88, 104026. [Google Scholar] [CrossRef]
- Ovalle, J.; Gergely, L.; Casadio, R. Brane-world stars with a solid crust and vacuum exterior. Class. Quant. Grav. 2015, 32, 045015. [Google Scholar] [CrossRef]
- Ovalle, J. Decoupling gravitational sources in general relativity: The extended case. Phys. Lett. B 2019, 788, 213–218. [Google Scholar] [CrossRef]
- Fernandes-Silva, A.; Ferreira-Martins, A.J.; da Rocha, R. Extended quantum portrait of MGD black holes and information entropy. Phys. Lett. B 2019, 791, 323–330. [Google Scholar] [CrossRef]
- Contreras, E. Minimal Geometric Deformation: The inverse problem. Eur. Phys. J. C 2018, 78, 678. [Google Scholar] [CrossRef]
- Contreras, E.; Bargueño, P. Minimal Geometric Deformation in asymptotically (A-)dS space-times and the isotropic sector for a polytropic black hole. Eur. Phys. J. C 2018, 78, 985. [Google Scholar] [CrossRef]
- Herrera, L. New definition of complexity for self-gravitating fluid distributions: The spherically symmetric, static case. Phys. Rev. D 2018, 97, 044010. [Google Scholar] [CrossRef]
- Abbas, G.; Nazar, H. Complexity Factor for Static Anisotropic Self-Gravitating Source in f(R) Gravity. Eur. Phys. J. C 2018, 78, 510. [Google Scholar] [CrossRef]
- Sharif, M.; Butt, I.I. Complexity Factor for Charged Spherical System. Eur. Phys. J. C 2018, 78, 688. [Google Scholar] [CrossRef]
- Abbas, G.; Nazar, H. Complexity Factor for Anisotropic Source in Non-minimal Coupling Metric f(R) Gravity. Eur. Phys. J. C 2018, 78, 957. [Google Scholar] [CrossRef]
- Nazar, H.; Abbas, G. Complexity factor for dynamical spherically symmetric fluid distributions in f(R) gravity. Int. J. Geom. Meth. Mod. Phys. 2019, 16, 1950170. [Google Scholar] [CrossRef]
- Sharif, M.; Majid, A. Complexity factor for static sphere in self-interacting Brans–Dicke gravity. Chin. J. Phys. 2019, 61, 38–46. [Google Scholar] [CrossRef]
- Sharif, M.; Majid, A.; Nasir, M.M.M. Complexity factor for self-gravitating system in modified Gauss–Bonnet gravity. Int. J. Mod. Phys. A 2019, 34, 1950210. [Google Scholar] [CrossRef]
- Khan, S.; Mardan, S.A.; Rehman, M.A. Framework for generalized polytropes with complexity factor. Eur. Phys. J. C 2019, 79, 1037. [Google Scholar] [CrossRef]
- Nazar, H.; Alkhaldi, A.H.; Abbas, G.; Shahzad, M.R. Complexity factor for anisotropic self-gravitating sphere in Rastall gravity. Int. J. Mod. Phys. A 2021, 36, 2150233. [Google Scholar] [CrossRef]
- Arias, C.; Contreras, E.; Fuenmayor, E.; Ramos, A. Anisotropic star models in the context of vanishing complexity. Ann. Phys. 2022, 436, 168671. [Google Scholar] [CrossRef]
- Rincon, A.; Panotopoulos, G.; Lopes, I. Anisotropic Quark Stars with an Interacting Quark Equation of State within the Complexity Factor Formalism. Universe 2023, 9, 72. [Google Scholar] [CrossRef]
- Rincon, A.; Panotopoulos, G.; Lopes, I. Anisotropic stars made of exotic matter within the complexity factor formalism. Eur. Phys. J. C 2023, 83, 116. [Google Scholar] [CrossRef]
- Karmarkar, K.R. Gravitational metrics of spherical symmetry and class one. Proc. Ind. Acad. Sci. A 1948, 27, 56. [Google Scholar] [CrossRef]
- Maurya, S.K.; Gupta, Y.K.; Smitha, T.T.; Rahaman, F. A new exact anisotropic solution of embedding class one. Eur. Phys. J. A 2016, 52, 191. [Google Scholar] [CrossRef]
- Singh, K.N.; Bhar, P.; Pant, N. A new solution of embedding class I representing anisotropic fluid sphere in general relativity. Int. J. Mod. Phys. D 2016, 25, 1650099. [Google Scholar] [CrossRef]
- Bhar, P.; Maurya, S.K.; Gupta, Y.K.; Manna, T. Modelling of anisotropic compact stars of embedding class one. Eur. Phys. J. A 2016, 52, 312. [Google Scholar] [CrossRef]
- Maurya, S.K.; Gupta, Y.K.; Ray, S.; Deb, D. A new model for spherically symmetric charged compact stars of embedding class 1. Eur. Phys. J. C 2017, 77, 45. [Google Scholar] [CrossRef]
- Bhar, P.; Govender, M. Anisotropic charged compact star of embedding class I. Int. J. Mod. Phys. D 2016, 26, 1750053. [Google Scholar] [CrossRef]
- Maurya, S.K.; Maharaj, S.D. Anisotropic fluid spheres of embedding class one using Karmarkar condition. Eur. Phys. J. C 2017, 77, 328. [Google Scholar] [CrossRef]
- Bhar, P.; Singh, K.N.; Manna, T. A new class of relativistic model of compact stars of embedding class I. Int. J. Mod. Phys. D 2017, 26, 1750090. [Google Scholar] [CrossRef]
- Tello-Ortiz, F.; Maurya, S.K.; Errehymy, A.; Singh, K.N.; Daoud, M. Anisotropic relativistic fluid spheres: An embedding class I approach. Eur. Phys. J. C 2019, 79, 885. [Google Scholar] [CrossRef]
- Jasim, M.K.; Maurya, S.K.; Al-Sawaii, A.S.M. A generalised embedding class one static solution describing anisotropic fluid sphere. Astrophys. Space Sci. 2020, 365, 9. [Google Scholar] [CrossRef]
- Baskey, L.; Das, S.; Rahaman, F. An analytical anisotropic compact stellar model of embedding class I. Mod. Phys. Lett. A 2021, 36, 2150028. [Google Scholar] [CrossRef]
- Zubair, M.; Waheed, S.; Javaid, H. A Generic Embedding Class-I Model via Karmarkar Condition in Gravity. Adv. Astron. 2021, 2021, 6685578. [Google Scholar] [CrossRef]
- Demorest, P.; Pennucci, T.; Ransom, S.; Roberts, M.; Hessels, J. Shapiro Delay Measurement of A Two Solar Mass Neutron Star. Nature 2010, 467, 1081–1083. [Google Scholar] [CrossRef]
- Antoniadis, J.; Freire, P.C.C.; Wex, N.; Tauris, T.M.; Lynch, R.S.; van Kerkwijk, M.H.; Kramer, M.; Bassa, C.; Dhillon, V.S.; Driebe, T.; et al. A Massive Pulsar in a Compact Relativistic Binary. Science 2013, 340, 6131. [Google Scholar] [CrossRef] [PubMed]
- Sullivan, A.G.; Romani, R.W. A Joint X-ray and Optical Study of the Massive Redback Pulsar J2215+5135. arXiv 2024, arXiv:2405.13889v. [Google Scholar] [CrossRef]
- Weber, F. Strange quark matter and compact stars. Prog. Part. Nucl. Phys. 2005, 54, 193–288. [Google Scholar] [CrossRef]
- Aziz, A.; Ray, S.; Rahaman, F.; Khlopov, M.; Guha, B.K. Constraining values of bag constant for strange star candidates. Int. J. Mod. Phys. D 2019, 28, 1941006. [Google Scholar] [CrossRef]
- Miller, M.C.; Lamb, F.K.; Dittmann, A.J.; Bogdanov, S.; Arzoumanian, Z.; Gendreau, K.C.; Guillot, S.; Ho, W.C.G.; Lattimer, J.M.; Loewenstein, M.; et al. The Radius of PSR J0740+6620 from NICER and XMM-Newton Data. Astrophys. J. Lett. 2021, 918, L28. [Google Scholar] [CrossRef]
- Riley, T.E.; Watts, A.L.; Ray, P.S.; Bogdanov, S.; Guillot, S.; Morsink, S.M.; Bilous, A.V.; Arzoumanian, Z.; Choudhury, D.; Deneva, J.S.; et al. A NICER View of the Massive Pulsar PSR J0740+6620 Informed by Radio Timing and XMM-Newton Spectroscopy. Astrophys. J. Lett. 2021, 918, L27. [Google Scholar] [CrossRef]
- Salmi, T.; Vinciguerra, S.; Choudhury, D.; Riley, T.E.; Watts, A.L.; Remillard, R.A.; Ray, P.S.; Bogdanov, S.; Guillot, S.; Arzoumanian, Z.; et al. The Radius of PSR J0740+6620 from NICER with NICER Background Estimates. Astrophys. J. 2022, 941, 150. [Google Scholar] [CrossRef]
- Doroshenko, V.; Suleimanov, V.; Pühlhofer, G.; Santangelo, A. A strangely light neutron star within a supernova remnant. Nat. Astron. 2022, 6, 1444–1451. [Google Scholar] [CrossRef]
- Tolman, R.C. Static solutions of Einstein’s field equations for spheres of fluid. Phys. Rev. 1939, 55, 364–373. [Google Scholar] [CrossRef]
- Oppenheimer, J.R.; Volkoff, G.M. On massive neutron cores. Phys. Rev. 1939, 55, 374–381. [Google Scholar] [CrossRef]
- Schwarzschild, K. On the Gravitational Field of a Mass Point According to Einstein’s Theory; Sitzungsberichte der Preussischen Akademie der Wissenschaften: Berlin, Germany, 1916; pp. 189–196. [Google Scholar]
- Kohler, M.; Chao, K.L. Zentralsymmetrische statische Schwerefelder mit Räumen der Klasse 1. Z. Naturforsch. Ser. A 1965, 20, 1537. [Google Scholar] [CrossRef]
- Moustakidis, C.C. The stability of relativistic stars and the role of the adiabatic index. Gen. Rel. Grav. 2017, 49, 68. [Google Scholar] [CrossRef]
- Hawking, S.W.; Ellis, G.F.R. The Large Scale Structure of Space-Time; Cambridge University Press: Cambridge, UK, 2023. [Google Scholar]
- Wald, R.M. General Relativity; Chicago University Press: Chicago, IL, USA, 1984. [Google Scholar]
- Frolov, V.P.; Novikov, I.D. Black Hole Physics: Basic Concepts and New Developments; Springer: Dordrecht, The Netherlands, 1998. [Google Scholar]
- Panotopoulos, G.; Vernieri, D.; Lopes, I. Quark stars with isotropic matter in Hořava gravity and Einstein–æther theory. Eur. Phys. J. C 2020, 80, 537. [Google Scholar] [CrossRef]
- Balart, L.; Panotopoulos, G.; Rincon, A. Regular Charged Black Holes, Energy Conditions, and Quasinormal Modes. Fortsch. Phys. 2023, 71, 2300075. [Google Scholar] [CrossRef]
- Pourhassan, B.; Kahya, E.O. Extended Chaplygin gas model. Results Phys. 2014, 4, 101–102. [Google Scholar] [CrossRef]
- Alford, M.G.; Schmitt, A.; Rajagopal, K.; Schäfer, T. Color superconductivity in dense quark matter. Rev. Mod. Phys. 2008, 80, 1455–1515. [Google Scholar] [CrossRef]
- Flores, C.V.; Lugones, G. Constraining color flavor locked strange stars in the gravitational wave era. Phys. Rev. C 2017, 95, 025808. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).