Screening Mechanisms on White Dwarfs: Symmetron and Dilaton
Abstract
1. Introduction
2. Framework
2.1. Scalar–Tensor Theory
2.2. Equation of State
2.3. Equilibrium Equations
3. Models
3.1. Symmetron Screening
3.2. Dilaton Screening
3.3. Boundary Conditions
3.4. Shooting Method
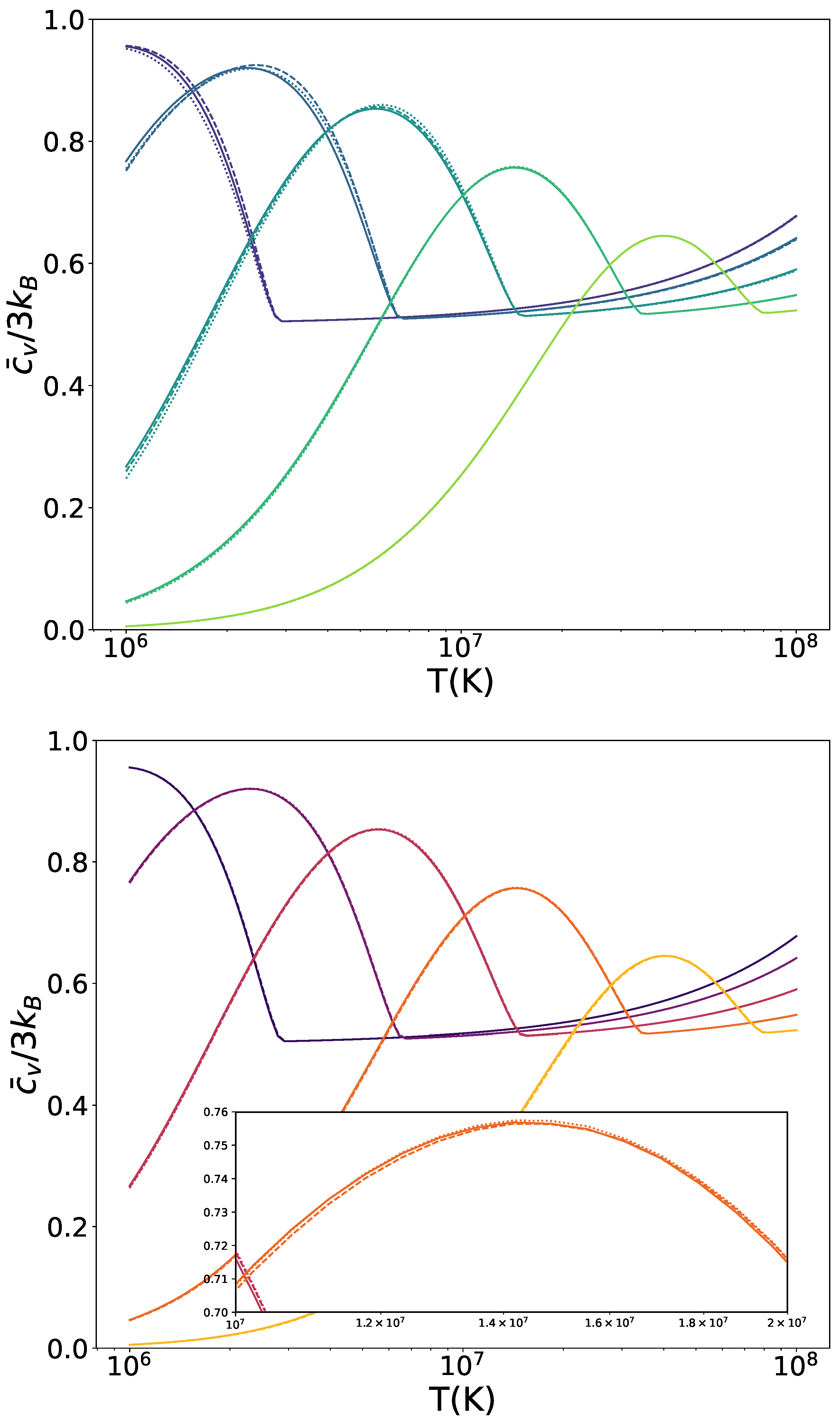
4. Results
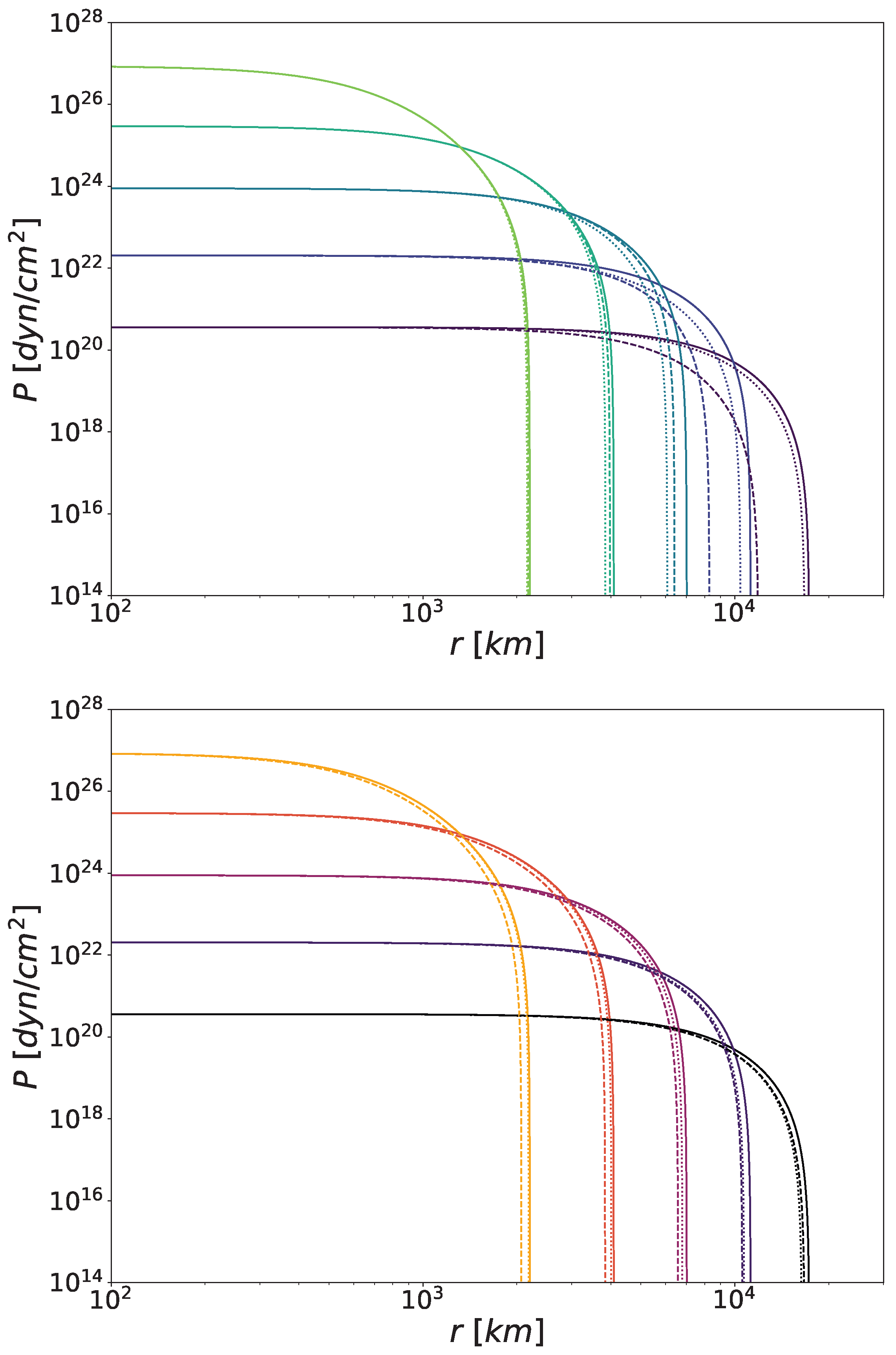
4.1. Pressure Profiles
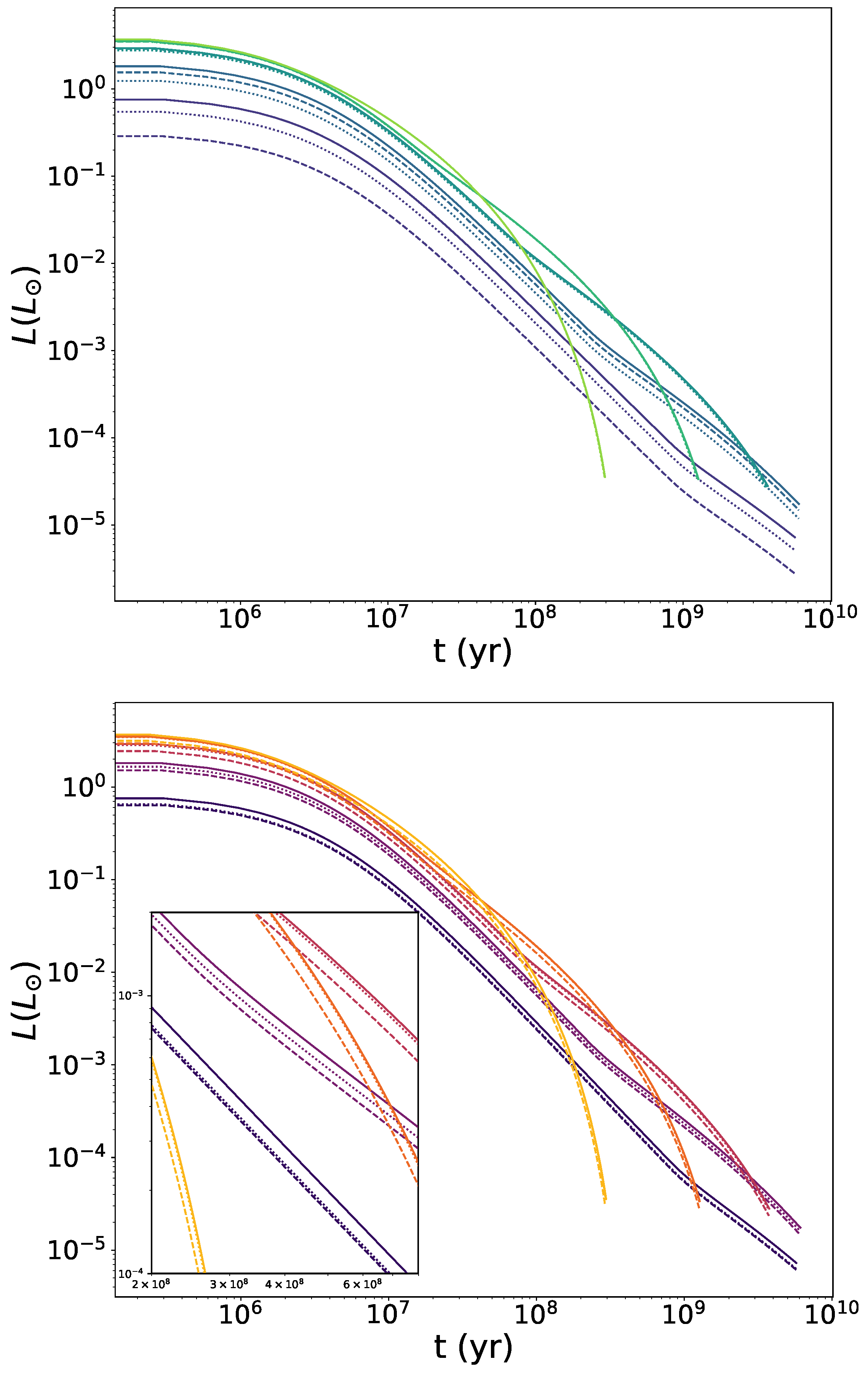
4.2. Cooling Time
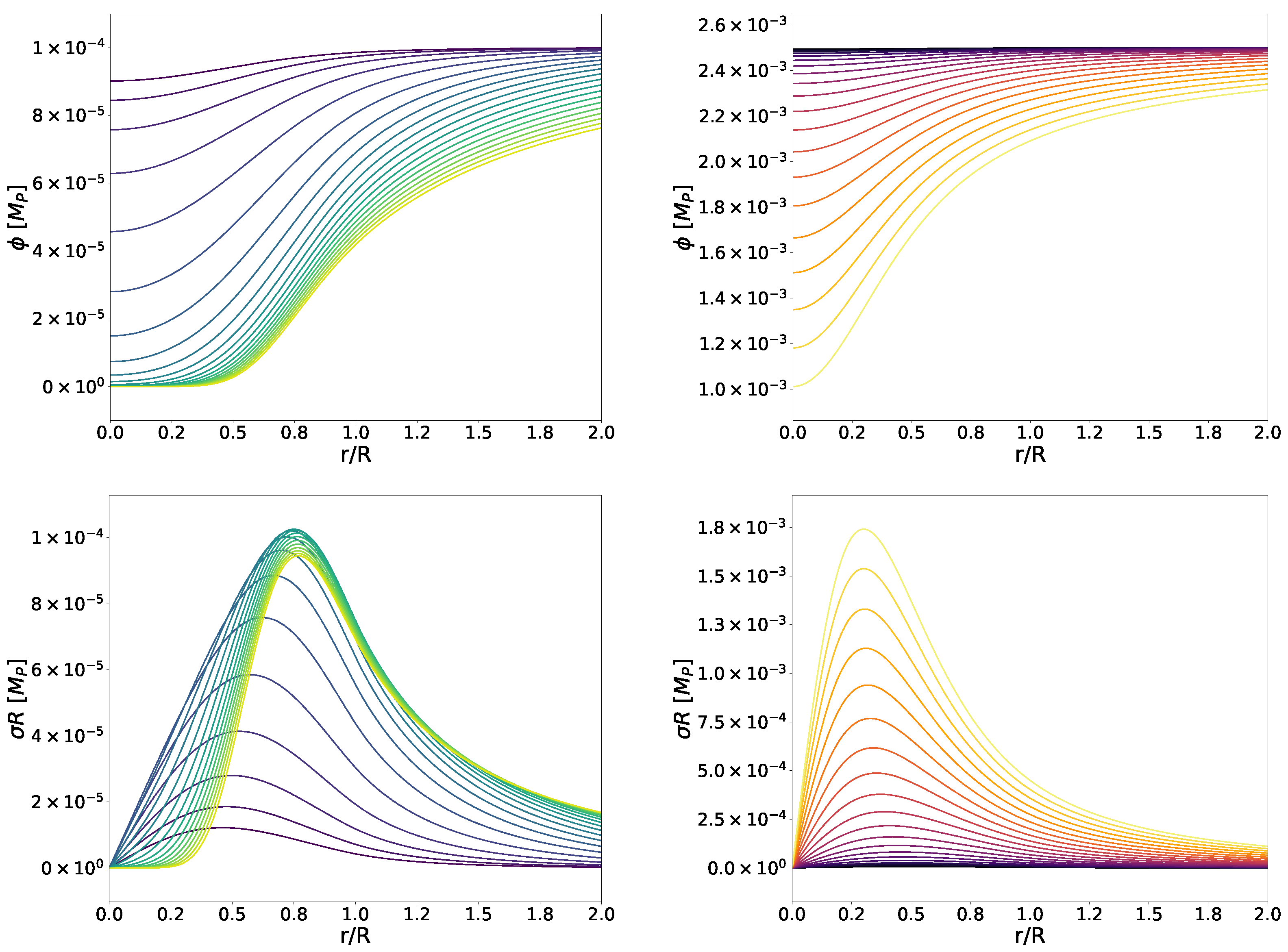
4.3. Scalar Profiles
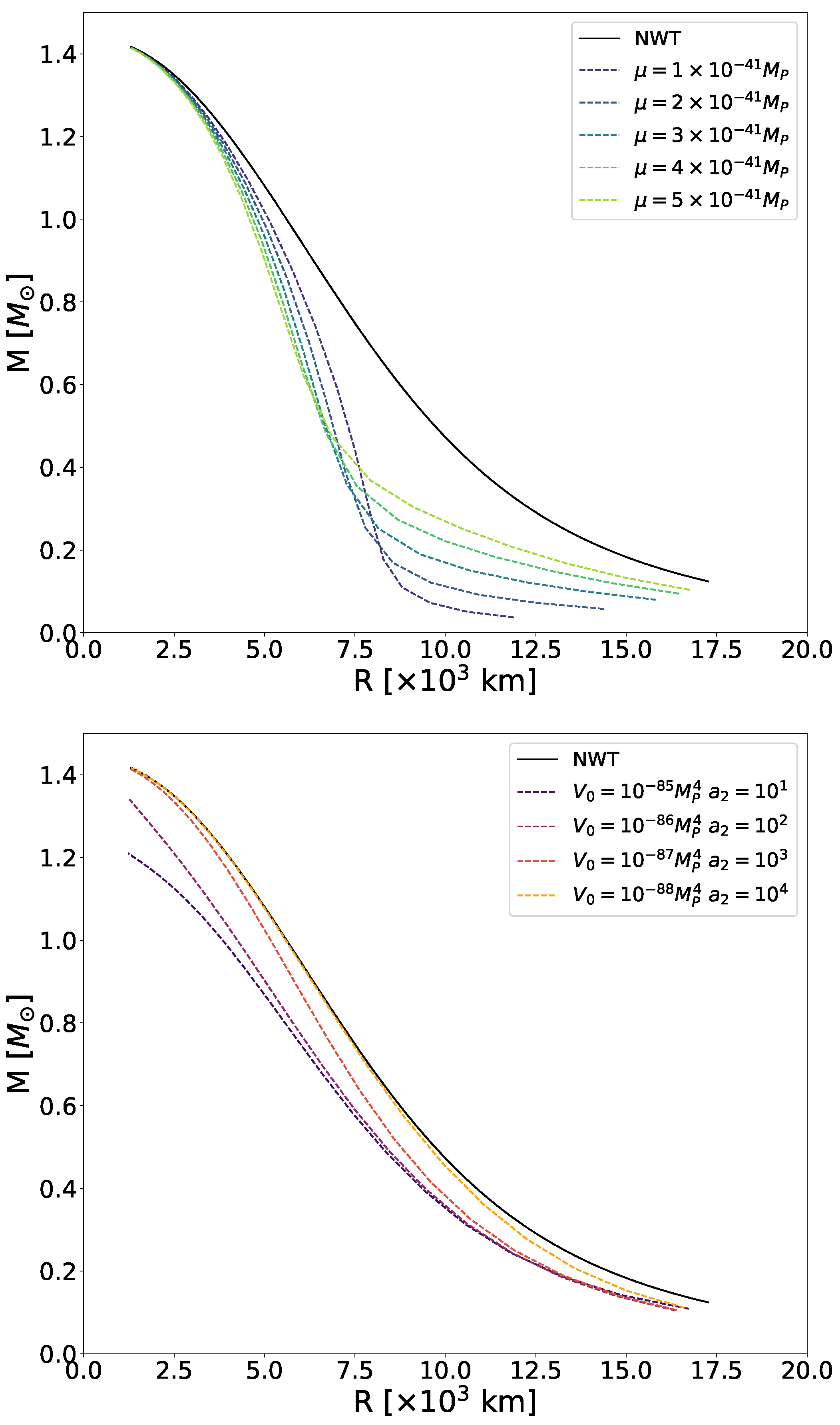
4.4. Mass–Radius Relation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Shooting Method Pseudocode
| Algorithm A1 Shooting method for Equations (14)–(18) and the ODE system. |
|
| 1 |
References
- Burrage, C.; Sakstein, J. Tests of chameleon gravity. Living Rev. Relativ. 2018, 21, 1–58. [Google Scholar] [CrossRef]
- Brax, P.; Casas, S.; Desmond, H.; Elder, B. Testing Screened Modified Gravity. Universe 2021, 8, 11. [Google Scholar] [CrossRef]
- Fischer, H.; Käding, C.; Pitschmann, M. Screened Scalar Fields in the Laboratory and the Solar System. Universe 2024, 10, 297. [Google Scholar] [CrossRef]
- Will, C.M. Theory and Experiment in Gravitational Physics; Cambridge University Press: Cambridge, UK, 2018. [Google Scholar]
- Amendola, L.; Rubio, J.; Wetterich, C. Primordial black holes from fifth forces. Phys. Rev. D 2018, 97, 081302. [Google Scholar] [CrossRef]
- Savastano, S.; Amendola, L.; Rubio, J.; Wetterich, C. Primordial dark matter halos from fifth forces. Phys. Rev. D 2019, 100, 083518. [Google Scholar] [CrossRef]
- Goh, L.W.K.; Bachs-Esteban, J.; Gómez-Valent, A.; Pettorino, V.; Rubio, J. Observational constraints on early coupled quintessence. Phys. Rev. D 2024, 109, 023530. [Google Scholar] [CrossRef]
- Wetterich, C. The Cosmon model for an asymptotically vanishing time dependent cosmological ‘constant’. Astron. Astrophys. 1995, 301, 321–328. [Google Scholar] [CrossRef]
- Wetterich, C. Growing neutrinos and cosmological selection. Phys. Lett. B 2007, 655, 201–208. [Google Scholar] [CrossRef]
- Amendola, L.; Baldi, M.; Wetterich, C. Quintessence cosmologies with a growing matter component. Phys. Rev. D 2008, 78, 023015. [Google Scholar] [CrossRef]
- Casas, S.; Pettorino, V.; Wetterich, C. Dynamics of neutrino lumps in growing neutrino quintessence. Phys. Rev. D 2016, 94, 103518. [Google Scholar] [CrossRef]
- Garcia-Bellido, J.; Rubio, J.; Shaposhnikov, M.; Zenhausern, D. Higgs-Dilaton Cosmology: From the Early to the Late Universe. Phys. Rev. D 2011, 84, 123504. [Google Scholar] [CrossRef]
- Ferreira, P.G.; Hill, C.T.; Ross, G.G. No fifth force in a scale invariant universe. Phys. Rev. D 2017, 95, 064038. [Google Scholar] [CrossRef]
- Casas, S.; Karananas, G.K.; Pauly, M.; Rubio, J. Scale-invariant alternatives to general relativity. III. The inflation-dark energy connection. Phys. Rev. D 2019, 99, 063512. [Google Scholar] [CrossRef]
- Copeland, E.J.; Millington, P.; Muñoz, S.S. Fifth forces and broken scale symmetries in the Jordan frame. J. Cosmol. Astropart. Phys. 2022, 2, 16. [Google Scholar] [CrossRef]
- Hinterbichler, K.; Khoury, J. Screening Long-Range Forces through Local Symmetry Restoration. Phys. Rev. Lett. 2010, 104, 231301. [Google Scholar] [CrossRef] [PubMed]
- Brax, P.; van de Bruck, C.; Davis, A.C.; Shaw, D. The Dilaton and Modified Gravity. Phys. Rev. D 2010, 82, 063519. [Google Scholar] [CrossRef]
- Khoury, J.; Weltman, A. Chameleon cosmology. Phys. Rev. D 2004, 69, 044026. [Google Scholar] [CrossRef]
- Vainshtein, A.I. To the problem of nonvanishing gravitation mass. Phys. Lett. B 1972, 39, 393–394. [Google Scholar] [CrossRef]
- Burrage, C.; Coltman, B.; Padilla, A.; Saadeh, D.; Wilson, T. Massive Galileons and Vainshtein screening. J. Cosmol. Astropart. Phys. 2021, 2021, 50. [Google Scholar] [CrossRef]
- Babichev, E.; Deffayet, C.; Ziour, R. k-Mouflage gravity. Int. J. Mod. Phys. D 2009, 18, 2147–2154. [Google Scholar] [CrossRef]
- Brax, P.; Valageas, P. The effective field theory of K-mouflage. J. Cosmol. Astropart. Phys. 2016, 2016, 20. [Google Scholar] [CrossRef]
- Brax, P.; Burrage, C.; Davis, A.-C. Screening fifth forces in k-essence and DBI models. J. Cosmol. Astropart. Phys. 2013, 2013, 20. [Google Scholar] [CrossRef]
- ter Haar, L.; Bezares, M.; Crisostomi, M.; Barausse, E.; Palenzuela, C. Dynamics of Screening in Modified Gravity. Phys. Rev. Lett. 2021, 126, 091102. [Google Scholar] [CrossRef]
- Luongo, O.; Mengoni, T. Generalized K-essence inflation in Jordan and Einstein frames. Class. Quantum Gravity 2024, 41, 105006. [Google Scholar] [CrossRef]
- D’Agostino, R.; Luongo, O.; Muccino, M. Healing the cosmological constant problem during inflation through a unified quasi-quintessence matter field. Class. Quantum Gravity 2022, 39, 195014. [Google Scholar] [CrossRef]
- Chang, P.; Hui, L. Stellar Structure and Tests of Modified Gravity. Astrophys. J. 2011, 732, 25. [Google Scholar] [CrossRef]
- Sakstein, J. Stellar oscillations in modified gravity. Phys. Rev. D 2013, 88, 124013. [Google Scholar] [CrossRef]
- Brito, R.; Terrana, A.; Johnson, M.; Cardoso, V. Nonlinear dynamical stability of infrared modifications of gravity. Phys. Rev. D Part. Fields Gravit. Cosmol. 2014, 90, 124035. [Google Scholar] [CrossRef]
- Babichev, E.; Koyama, K.; Langlois, D.; Saito, R.; Sakstein, J. Relativistic Stars in Beyond Horndeski Theories. Class. Quant. Grav. 2016, 33, 235014. [Google Scholar] [CrossRef]
- de Aguiar, B.F.; Mendes, R.F. Highly compact neutron stars and screening mechanisms: Equilibrium and stability. Phys. Rev. D 2020, 102, 024064. [Google Scholar] [CrossRef]
- de Aguiar, B.F.; Mendes, R.F.P.; Falciano, F.T. Neutron Stars in the Symmetron Model. Universe 2021, 8, 6. [Google Scholar] [CrossRef]
- Panotopoulos, G.; Rubio, J.; Lopes, I. On the impact of nonlocal gravity on compact stars. Int. J. Mod. Phys. D 2023, 32, 2250139. [Google Scholar] [CrossRef]
- Dima, A.; Bezares, M.; Barausse, E. Dynamical chameleon neutron stars: Stability, radial oscillations, and scalar radiation in spherical symmetry. Phys. Rev. D 2021, 104, 084017. [Google Scholar] [CrossRef]
- Saltas, I.D.; Sawicki, I.; Lopes, I. White dwarfs and revelations. J. Cosmol. Astropart. Phys. 2018, 2018, 28. [Google Scholar] [CrossRef]
- Alam, K.; Islam, T. White dwarf mass-radius relation in theories beyond general relativity. J. Cosmol. Astropart. Phys. 2023, 8, 81. [Google Scholar] [CrossRef]
- Kalita, S.; Sarmah, L.; Wojnar, A. Metric-affine effects in crystallization processes of white dwarfs. Phys. Rev. D 2023, 107, 044072. [Google Scholar] [CrossRef]
- Camenzind, M. Compact Objects in Astrophysics: White Dwarfs, Neutron Stars and Black Holes; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Jiménez-Esteban, F.M.; Torres, S.; Rebassa-Mansergas, A.; Skorobogatov, G.; Solano, E.; Cantero, C.; Rodrigo, C. A white dwarf catalogue from Gaia-DR2 and the Virtual Observatory. Mon. Not. R. Astron. Soc. 2018, 480, 4505–4518. [Google Scholar] [CrossRef]
- Tremblay, P.E.; Cukanovaite, E.; Gentile Fusillo, N.P.; Cunningham, T.; Hollands, M.A. Fundamental parameter accuracy of DA and DB white dwarfs in Gaia Data Release 2. Mon. Not. R. Astron. Soc. 2018, 482, 5222–5232. [Google Scholar] [CrossRef]
- Kilic, M.; Bergeron, P.; Kosakowski, A.; Brown, W.R.; Agüeros, M.A.; Blouin, S. The 100 pc White Dwarf Sample in the SDSS Footprint. Astrophys. J. 2020, 898, 84. [Google Scholar] [CrossRef]
- Bachs-Esteban, J.; Lopes, I.; Rubio, J. Structural Implications of the Chameleon Mechanism on White Dwarfs. arXiv 2024, arXiv:2407.04791. [Google Scholar]
- Bettoni, D.; Rubio, J. Quintessential Inflation: A Tale of Emergent and Broken Symmetries. Galaxies 2022, 10, 22. [Google Scholar] [CrossRef]
- Chandrasekhar, S. The highly collapsed configurations of a stellar mass (Second paper). Mon. Not. Roy. Astron. Soc. 1935, 95, 207–225. [Google Scholar] [CrossRef]
- Hamada, T.; Salpeter, E.E. Models for Zero-Temperature Stars. Astrophys. J. 1961, 134, 683. [Google Scholar] [CrossRef]
- Vidal, S.; Wojnar, A.; Järv, L.; Doneva, D. Crystallized white dwarf stars in scalar-tensor gravity. arXiv 2024, arXiv:2408.15937. [Google Scholar] [CrossRef]
- Das, U.; Mukhopadhyay, B. Maximum mass of stable magnetized highly super-Chandrasekhar white dwarfs: Stable solutions with varying magnetic fields. J. Cosmol. Astropart. Phys. 2014, 6, 50. [Google Scholar] [CrossRef]
- Roy, S.K.; Mukhopadhyay, S.; Lahiri, J.; Basu, D.N. Relativistic Thomas-Fermi equation of state for magnetized white dwarfs. Phys. Rev. D 2019, 100, 063008. [Google Scholar] [CrossRef]
- Fontaine, G.; Brassard, P.; Bergeron, P. The Potential of White Dwarf Cosmochronology. Publ. Astron. Soc. Pac. 2001, 113, 409. [Google Scholar] [CrossRef]
- Misner, C.W.; Thorne, K.S.; Wheeler, J.A. Gravitation; W. H. Freeman: San Francisco, CA, USA, 1973. [Google Scholar]
- Hinterbichler, K.; Khoury, J.; Levy, A.; Matas, A. Symmetron Cosmology. Phys. Rev. D 2011, 84, 103521. [Google Scholar] [CrossRef]
- Frohlich, J.; Morchio, G.; Strocchi, F. Higgs Phenomenon without Symmetry Breaking Order Parameter. Nucl. Phys. B 1981, 190, 553–582. [Google Scholar] [CrossRef]
- Babichev, E.; Langlois, D. Relativistic stars in f(R) and scalar-tensor theories. Phys. Rev. D 2010, 81, 124051. [Google Scholar] [CrossRef]
- Brax, P.; Davis, A.C.; Jha, R. Neutron Stars in Screened Modified Gravity: Chameleon vs. Dilaton. Phys. Rev. D 2017, 95, 083514. [Google Scholar] [CrossRef]
- Brush, S.G.; Sahlin, H.L.; Teller, E. Monte Carlo Study of a One-Component Plasma. I. J. Chem. Phys. 1966, 45, 1727895. [Google Scholar] [CrossRef]
- Koester, D. Outer Envelopes and Cooling of White Dwarfs. Astron. Astrophys. 1972, 16, 459–470. [Google Scholar]
- Koester, D.; Chanmugam, G. Physics of white dwarf stars. Rep. Prog. Phys. 1990, 53, 837. [Google Scholar] [CrossRef]
- Sotani, H.; Kokkotas, K.D. Stellar oscillations in scalar-tensor theory of gravity. Phys. Rev. D 2005, 71, 124038. [Google Scholar] [CrossRef]
| Scalar Field | |||
|---|---|---|---|
| Chameleon | |||
| Symmetron | |||
| Dilaton |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bachs-Esteban, J.; Lopes, I.; Rubio, J. Screening Mechanisms on White Dwarfs: Symmetron and Dilaton. Universe 2025, 11, 158. https://doi.org/10.3390/universe11050158
Bachs-Esteban J, Lopes I, Rubio J. Screening Mechanisms on White Dwarfs: Symmetron and Dilaton. Universe. 2025; 11(5):158. https://doi.org/10.3390/universe11050158
Chicago/Turabian StyleBachs-Esteban, Joan, Ilídio Lopes, and Javier Rubio. 2025. "Screening Mechanisms on White Dwarfs: Symmetron and Dilaton" Universe 11, no. 5: 158. https://doi.org/10.3390/universe11050158
APA StyleBachs-Esteban, J., Lopes, I., & Rubio, J. (2025). Screening Mechanisms on White Dwarfs: Symmetron and Dilaton. Universe, 11(5), 158. https://doi.org/10.3390/universe11050158











