Revisiting Holographic Dark Energy from the Perspective of Multi-Messenger Gravitational Wave Astronomy: Future Joint Observations with Short Gamma-Ray Bursts
Abstract
1. Introduction
2. Cosmological Model
2.1. The HDE Model
2.2. The RDE Model
3. Methodology
3.1. Simulations of GW Events
3.2. Detection of GW Events
3.3. Detection of Short GRBs
3.4. Fisher Information Matrix and Error Analysis
4. Results and Discussion
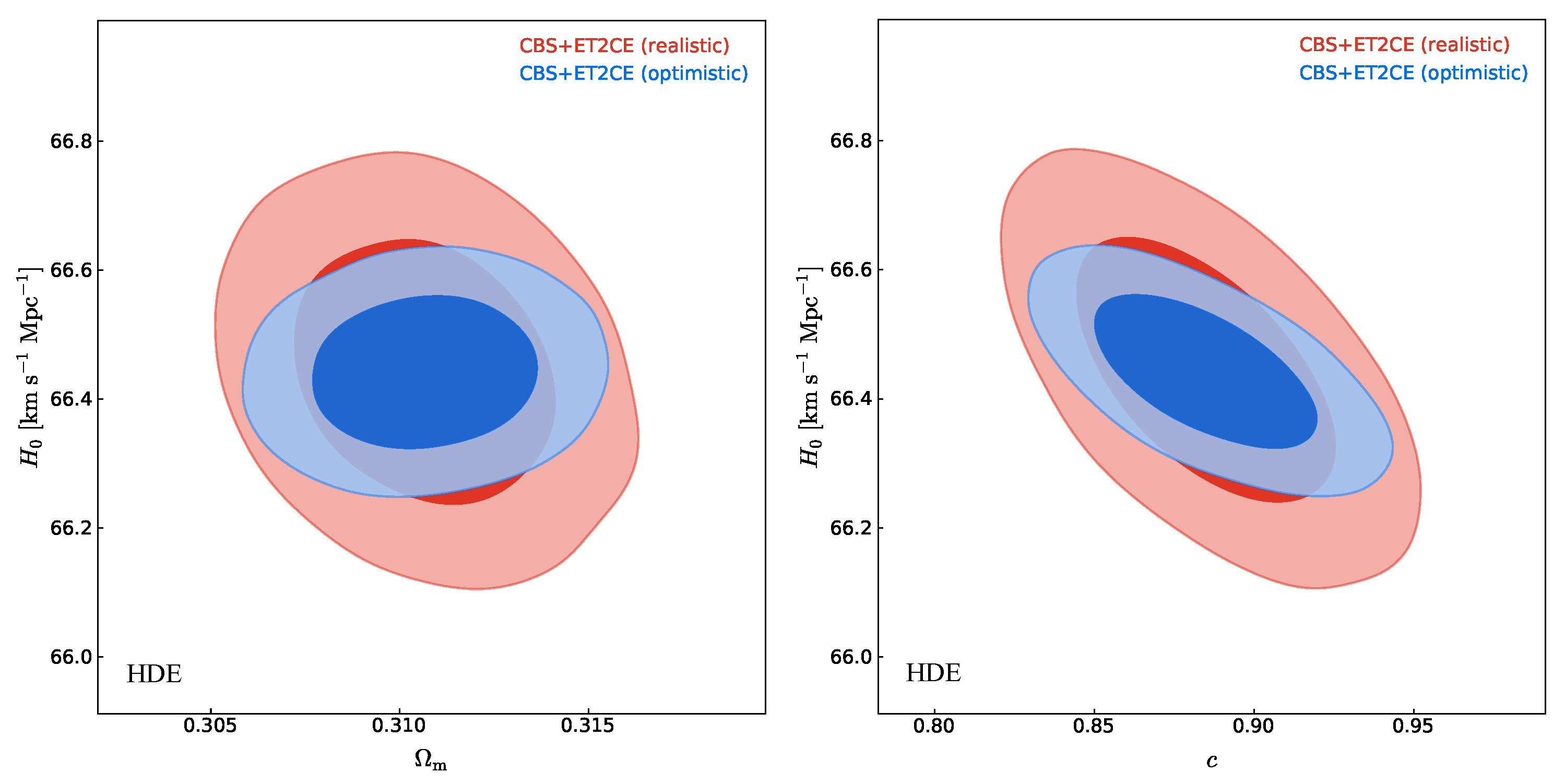
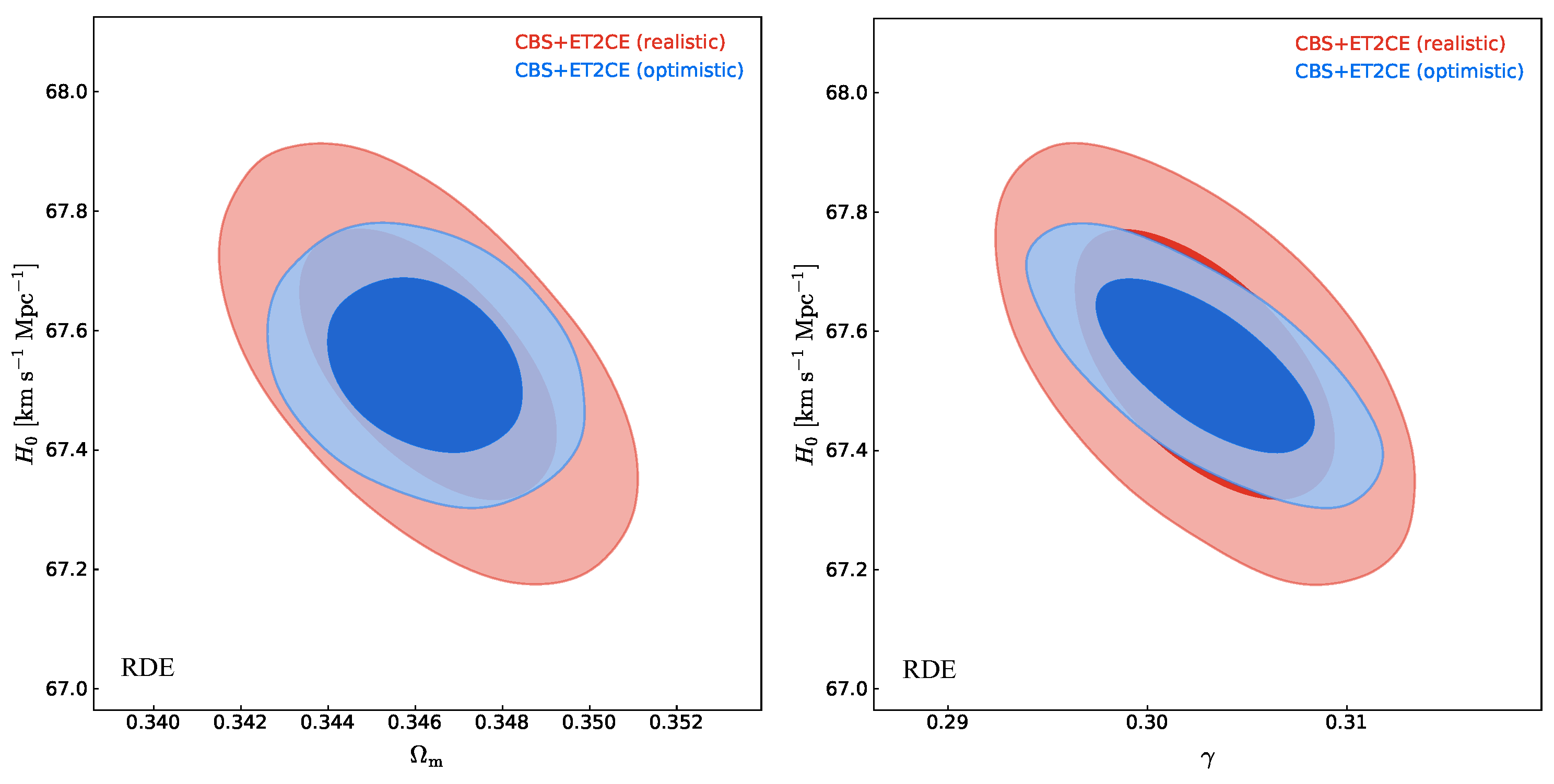
4.1. Constraint Results in Optimistic Scenario
4.2. Constraint Results in Realistic Scenario
4.3. Methodological Improvements Compared to Previous Work
4.4. Constraint Results Compared to Previous Works
4.5. Challenges of the HDE Model
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Riess, A.G.; Filippenko, A.V.; Challis, P.; Clocchiatti, A.; Diercks, A.; Garnavich, P.M.; Gilliland, R.L.; Hogan, C.J.; Jha, S.; Kirshner, R.P.; et al. Observational evidence from supernovae for an accelerating universe and a cosmological constant. Astron. J. 1998, 116, 1009–1038. [Google Scholar] [CrossRef]
- Perlmutter, S.; Aldering, G.; Goldhaber, G.; Knop, R.A.; Nugent, P.; Castro, P.G.; Deustua, S.; Fabbro, S.; Goobar, A.; Groom, D.E.; et al. Measurements of Ω and Λ from 42 high redshift supernovae. Astrophys. J. 1999, 517, 565–586. [Google Scholar] [CrossRef]
- Sahni, V.; Starobinsky, A.A. The Case for a positive cosmological Lambda term. Int. J. Mod. Phys. D 2000, 9, 373–444. [Google Scholar] [CrossRef]
- Caldwell, R.R. A Phantom menace? Phys. Lett. B 2002, 545, 23–29. [Google Scholar] [CrossRef]
- Padmanabhan, T. Cosmological constant: The Weight of the vacuum. Phys. Rept. 2003, 380, 235–320. [Google Scholar] [CrossRef]
- Peebles, P.J.E.; Ratra, B. The Cosmological Constant and Dark Energy. Rev. Mod. Phys. 2003, 75, 559–606. [Google Scholar] [CrossRef]
- Copeland, E.J.; Sami, M.; Tsujikawa, S. Dynamics of dark energy. Int. J. Mod. Phys. D 2006, 15, 1753–1936. [Google Scholar] [CrossRef]
- Li, M.; Li, X.D.; Wang, S.; Wang, Y. Dark Energy. Commun. Theor. Phys. 2011, 56, 525–604. [Google Scholar] [CrossRef]
- Bamba, K.; Capozziello, S.; Nojiri, S.; Odintsov, S.D. Dark energy cosmology: The equivalent description via different theoretical models and cosmography tests. Astrophys. Space Sci. 2012, 342, 155–228. [Google Scholar] [CrossRef]
- Weinberg, S. The Cosmological Constant Problem. Rev. Mod. Phys. 1989, 61, 1–23. [Google Scholar] [CrossRef]
- Carroll, S.M. The Cosmological constant. Living Rev. Rel. 2001, 4, 1. [Google Scholar] [CrossRef]
- Li, M. A Model of holographic dark energy. Phys. Lett. B 2004, 603, 1. [Google Scholar] [CrossRef]
- Cohen, A.G.; Kaplan, D.B.; Nelson, A.E. Effective field theory, black holes, and the cosmological constant. Phys. Rev. Lett. 1999, 82, 4971–4974. [Google Scholar] [CrossRef]
- Zhang, X.; Wu, F.Q. Constraints on holographic dark energy from Type Ia supernova observations. Phys. Rev. D 2005, 72, 043524. [Google Scholar] [CrossRef]
- Zhang, X.; Wu, F.Q. Constraints on Holographic Dark Energy from Latest Supernovae, Galaxy Clustering, and Cosmic Microwave Background Anisotropy Observations. Phys. Rev. D 2007, 76, 023502. [Google Scholar] [CrossRef]
- Huang, Q.G.; Gong, Y.G. Supernova constraints on a holographic dark energy model. JCAP 2004, 08, 006. [Google Scholar] [CrossRef]
- Wang, B.; Abdalla, E.; Su, R.K. Constraints on the dark energy from holography. Phys. Lett. B 2005, 611, 21–26. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Unifying phantom inflation with late-time acceleration: Scalar phantom-non-phantom transition model and generalized holographic dark energy. Gen. Rel. Grav. 2006, 38, 1285–1304. [Google Scholar] [CrossRef]
- Chang, Z.; Wu, F.Q.; Zhang, X. Constraints on holographic dark energy from x-ray gas mass fraction of galaxy clusters. Phys. Lett. B 2006, 633, 14–18. [Google Scholar] [CrossRef]
- Zhang, J.f.; Zhang, X.; Liu, H.y. Holographic dark energy in a cyclic universe. Eur. Phys. J. C 2007, 52, 693–699. [Google Scholar] [CrossRef]
- Li, Y.H.; Wang, S.; Li, X.D.; Zhang, X. Holographic dark energy in a Universe with spatial curvature and massive neutrinos: A full Markov Chain Monte Carlo exploration. JCAP 2013, 02, 033. [Google Scholar] [CrossRef]
- Zhang, J.F.; Zhao, M.M.; Cui, J.L.; Zhang, X. Revisiting the holographic dark energy in a non-flat universe: Alternative model and cosmological parameter constraints. Eur. Phys. J. C 2014, 74, 3178. [Google Scholar] [CrossRef]
- Landim, R.C.G. Holographic dark energy from minimal supergravity. Int. J. Mod. Phys. D 2016, 25, 1650050. [Google Scholar] [CrossRef]
- Wang, S.; Wang, Y.; Li, M. Holographic Dark Energy. Phys. Rept. 2017, 696, 1–57. [Google Scholar] [CrossRef]
- Li, M.; Li, X.; Zhang, X. Comparison of dark energy models: A perspective from the latest observational data. Sci. China Phys. Mech. Astron. 2010, 53, 1631–1645. [Google Scholar] [CrossRef]
- Xu, Y.Y.; Zhang, X. Comparison of dark energy models after Planck 2015. Eur. Phys. J. C 2016, 76, 588. [Google Scholar] [CrossRef]
- Li, H.L.; Zhang, J.F.; Feng, L.; Zhang, X. Reexploration of interacting holographic dark energy model: Cases of interaction term excluding the Hubble parameter. Eur. Phys. J. C 2017, 77, 907. [Google Scholar] [CrossRef]
- Feng, L.; Li, Y.H.; Yu, F.; Zhang, J.F.; Zhang, X. Exploring interacting holographic dark energy in a perturbed universe with parameterized post-Friedmann approach. Eur. Phys. J. C 2018, 78, 865. [Google Scholar] [CrossRef]
- Li, M.; Li, X.D.; Ma, Y.Z.; Zhang, X.; Zhang, Z. Planck Constraints on Holographic Dark Energy. JCAP 2013, 09, 021. [Google Scholar] [CrossRef]
- Wang, S.; Li, M. Theoretical aspects of holographic dark energy. Commun. Theor. Phys. 2023, 75, 117401. [Google Scholar] [CrossRef]
- Li, T.N.; Li, Y.H.; Du, G.H.; Wu, P.J.; Feng, L.; Zhang, J.F.; Zhang, X. Revisiting holographic dark energy after DESI 2024. arXiv 2024, arXiv:2411.08639v1. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Covariant Generalized Holographic Dark Energy and Accelerating Universe. Eur. Phys. J. C 2017, 77, 528. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D.; Oikonomou, V.K.; Paul, T. Unifying Holographic Inflation with Holographic Dark Energy: A Covariant Approach. Phys. Rev. D 2020, 102, 023540. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D.; Paul, T. Different Faces of Generalized Holographic Dark Energy. Symmetry 2021, 13, 928. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D.; Paul, T. Barrow entropic dark energy: A member of generalized holographic dark energy family. Phys. Lett. B 2022, 825, 136844. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D.; Saridakis, E.N. Holographic inflation. Phys. Lett. B 2019, 797, 134829. [Google Scholar] [CrossRef]
- Gao, C.; Wu, F.; Chen, X.; Shen, Y.G. A Holographic Dark Energy Model from Ricci Scalar Curvature. Phys. Rev. D 2009, 79, 043511. [Google Scholar] [CrossRef]
- Zhang, X. Holographic Ricci dark energy: Current observational constraints, quintom feature, and the reconstruction of scalar-field dark energy. Phys. Rev. D 2009, 79, 103509. [Google Scholar] [CrossRef]
- Cai, R.G.; Hu, B.; Zhang, Y. Holography, UV/IR Relation, Causal Entropy Bound and Dark Energy. Commun. Theor. Phys. 2009, 51, 954–960. [Google Scholar] [CrossRef]
- Fu, T.F.; Zhang, J.F.; Chen, J.Q.; Zhang, X. Holographic Ricci dark energy: Interacting model and cosmological constraints. Eur. Phys. J. C 2012, 72, 1932. [Google Scholar] [CrossRef]
- Cui, J.L.; Zhang, J.F. Comparing holographic dark energy models with statefinder. Eur. Phys. J. C 2014, 74, 2849. [Google Scholar] [CrossRef]
- Zhang, J.F.; Cui, J.L.; Zhang, X. Diagnosing holographic dark energy models with statefinder hierarchy. Eur. Phys. J. C 2014, 74, 3100. [Google Scholar] [CrossRef]
- Yu, F.; Cui, J.L.; Zhang, J.F.; Zhang, X. Statefinder hierarchy exploration of the extended Ricci dark energy. Eur. Phys. J. C 2015, 75, 274. [Google Scholar] [CrossRef]
- Riess, A.G.; Yuan, W.; Macri, L.M.; Scolnic, D.; Brout, D.; Casertano, S.; Jones, D.O.; Murakami, Y.; Anand, G.S.; Breuval, L.; et al. A Comprehensive Measurement of the Local Value of the Hubble Constant with 1 km s-1 Mpc-1 Uncertainty from the Hubble Space Telescope and the SH0ES Team. Astrophys. J. Lett. 2022, 934, L7. [Google Scholar] [CrossRef]
- Cai, R.G. Editorial. Sci. China Phys. Mech. Astron. 2020, 63, 290401. [Google Scholar] [CrossRef]
- Guo, R.Y.; Zhang, J.F.; Zhang, X. Inflation model selection revisited after a 1.91% measurement of the Hubble constant. Sci. China Phys. Mech. Astron. 2020, 63, 290406. [Google Scholar] [CrossRef]
- Yang, W.; Pan, S.; Di Valentino, E.; Nunes, R.C.; Vagnozzi, S.; Mota, D.F. Tale of stable interacting dark energy, observational signatures, and the H0 tension. JCAP 2018, 09, 019. [Google Scholar] [CrossRef]
- Vagnozzi, S. New physics in light of the H0 tension: An alternative view. Phys. Rev. D 2020, 102, 023518. [Google Scholar] [CrossRef]
- Di Valentino, E.; Melchiorri, A.; Mena, O.; Vagnozzi, S. Nonminimal dark sector physics and cosmological tensions. Phys. Rev. D 2020, 101, 063502. [Google Scholar] [CrossRef]
- Di Valentino, E.; Melchiorri, A.; Mena, O.; Vagnozzi, S. Interacting dark energy in the early 2020s: A promising solution to the H0 and cosmic shear tensions. Phys. Dark Univ. 2020, 30, 100666. [Google Scholar] [CrossRef]
- Liu, M.; Huang, Z.; Luo, X.; Miao, H.; Singh, N.K.; Huang, L. Can Non-standard Recombination Resolve the Hubble Tension? Sci. China Phys. Mech. Astron. 2020, 63, 290405. [Google Scholar] [CrossRef]
- Zhang, X.; Huang, Q.G. Measuring H0 from low-z datasets. Sci. China Phys. Mech. Astron. 2020, 63, 290402. [Google Scholar] [CrossRef]
- Ding, Q.; Nakama, T.; Wang, Y. A gigaparsec-scale local void and the Hubble tension. Sci. China Phys. Mech. Astron. 2020, 63, 290403. [Google Scholar] [CrossRef]
- Lin, M.X.; Hu, W.; Raveri, M. Testing H0 in Acoustic Dark Energy with Planck and ACT Polarization. Phys. Rev. D 2020, 102, 123523. [Google Scholar] [CrossRef]
- Hryczuk, A.; Jodłowski, K. Self-interacting dark matter from late decays and the H0 tension. Phys. Rev. D 2020, 102, 043024. [Google Scholar] [CrossRef]
- Cai, R.G.; Guo, Z.K.; Li, L.; Wang, S.J.; Yu, W.W. Chameleon dark energy can resolve the Hubble tension. Phys. Rev. D 2021, 103, 121302. [Google Scholar] [CrossRef]
- Vagnozzi, S.; Pacucci, F.; Loeb, A. Implications for the Hubble tension from the ages of the oldest astrophysical objects. JHEAp 2022, 36, 27–35. [Google Scholar] [CrossRef]
- Vagnozzi, S. Consistency tests of ΛCDM from the early integrated Sachs-Wolfe effect: Implications for early-time new physics and the Hubble tension. Phys. Rev. D 2021, 104, 063524. [Google Scholar] [CrossRef]
- Riess, A.G. The Expansion of the Universe is Faster than Expected. Nat. Rev. Phys. 2019, 2, 10–12. [Google Scholar] [CrossRef]
- Verde, L.; Treu, T.; Riess, A.G. Tensions between the Early and the Late Universe. Nat. Astron. 2019, 3, 891. [Google Scholar] [CrossRef]
- Li, T.N.; Wu, P.J.; Du, G.H.; Jin, S.J.; Li, H.L.; Zhang, J.F.; Zhang, X. Constraints on Interacting Dark Energy Models from the DESI Baryon Acoustic Oscillation and DES Supernovae Data. Astrophys. J. 2024, 976, 1. [Google Scholar] [CrossRef]
- Schutz, B.F. Determining the Hubble Constant from Gravitational Wave Observations. Nature 1986, 323, 310–311. [Google Scholar] [CrossRef]
- Holz, D.E.; Hughes, S.A. Using gravitational-wave standard sirens. Astrophys. J. 2005, 629, 15–22. [Google Scholar] [CrossRef]
- Zhao, W.; Van Den Broeck, C.; Baskaran, D.; Li, T.G.F. Determination of Dark Energy by the Einstein Telescope: Comparing with CMB, BAO and SNIa Observations. Phys. Rev. D 2011, 83, 023005. [Google Scholar] [CrossRef]
- Zhang, X.N.; Wang, L.F.; Zhang, J.F.; Zhang, X. Improving cosmological parameter estimation with the future gravitational-wave standard siren observation from the Einstein Telescope. Phys. Rev. D 2019, 99, 063510. [Google Scholar] [CrossRef]
- Jin, S.J.; He, D.Z.; Xu, Y.; Zhang, J.F.; Zhang, X. Forecast for cosmological parameter estimation with gravitational-wave standard siren observation from the Cosmic Explorer. JCAP 2020, 03, 051. [Google Scholar] [CrossRef]
- Li, H.L.; He, D.Z.; Zhang, J.F.; Zhang, X. Quantifying the impacts of future gravitational-wave data on constraining interacting dark energy. JCAP 2020, 06, 038. [Google Scholar] [CrossRef]
- Cai, R.G.; Liu, T.B.; Liu, X.W.; Wang, S.J.; Yang, T. Probing cosmic anisotropy with gravitational waves as standard sirens. Phys. Rev. D 2018, 97, 103005. [Google Scholar] [CrossRef]
- Cai, R.G.; Yang, T. Estimating cosmological parameters by the simulated data of gravitational waves from the Einstein Telescope. Phys. Rev. D 2017, 95, 044024. [Google Scholar] [CrossRef]
- Zhang, J.F.; Dong, H.Y.; Qi, J.Z.; Zhang, X. Prospect for constraining holographic dark energy with gravitational wave standard sirens from the Einstein Telescope. Eur. Phys. J. C 2020, 80, 217. [Google Scholar] [CrossRef]
- Jin, S.J.; Zhang, Y.Z.; Song, J.Y.; Zhang, J.F.; Zhang, X. Taiji-TianQin-LISA network: Precisely measuring the Hubble constant using both bright and dark sirens. Sci. China Phys. Mech. Astron. 2024, 67, 220412. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, C.; Adya, V.B.; Affeldt, C.; Agathos, M.; et al. Prospects for observing and localizing gravitational-wave transients with Advanced LIGO, Advanced Virgo and KAGRA. Living Rev. Rel. 2018, 21, 3. [Google Scholar] [CrossRef]
- Song, J.Y.; Wang, L.F.; Li, Y.; Zhao, Z.W.; Zhang, J.F.; Zhao, W.; Zhang, X. Synergy between CSST galaxy survey and gravitational-wave observation: Inferring the Hubble constant from dark standard sirens. Sci. China Phys. Mech. Astron. 2024, 67, 230411. [Google Scholar] [CrossRef]
- Han, T.; Jin, S.J.; Zhang, J.F.; Zhang, X. A comprehensive forecast for cosmological parameter estimation using joint observations of gravitational waves and short γ-ray bursts. Eur. Phys. J. C 2024, 84, 663. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Adhikari, R.X.; Ananyeva, A.; Anderson, S.B.; Appert, S.; Arai, K.; Araya, M.C.; Barayoga, J.C.; Barish, B.C.; et al. A gravitational-wave standard siren measurement of the Hubble constant. Nature 2017, 551, 85–88. [Google Scholar] [CrossRef]
- ET. Available online: https://www.et-gw.eu (accessed on 5 March 2025).
- Punturo, M.; Abernathy, M.; Acernese, F.; Allen, B.; Andersson, N.; Arun, K.; Barone, F.; Barr, B.; Barsuglia, M.; Beker, M.; et al. The Einstein Telescope: A third-generation gravitational wave observatory. Class. Quant. Grav. 2010, 27, 194002. [Google Scholar] [CrossRef]
- CE. Available online: https://cosmicexplorer.org/ (accessed on 5 March 2025).
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Ackley, K.; Adams, C.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; Affeldt, C.; et al. Exploring the Sensitivity of Next Generation Gravitational Wave Detectors. Class. Quant. Grav. 2017, 34, 044001. [Google Scholar] [CrossRef]
- Evans, M.; Adhikari, R.X.; Afle, C.; Ballmer, S.W.; Biscoveanu, S.; Borhanian, S.; Brown, D.A.; Chen, Y.; Eisenstein, R.; Gruson, A.; et al. A Horizon Study for Cosmic Explorer: Science, Observatories, and Community. arXiv 2021, arXiv:2109.09882. [Google Scholar] [CrossRef]
- Amati, L.; O’Brien, P.T.; Götz, D.; Bozzo, E.; Santangelo, A.; Tanvir, N.; Frontera, F.; Mereghetti, S.; Osborne, J.P.; Blain, A.; et al. The THESEUS space mission: Science goals, requirements and mission concept. Exper. Astron. 2021, 52, 183–218. [Google Scholar] [CrossRef]
- Amati, L.; O’Brien, P.; Götz, D.; Bozzo, E.; Tenzer, C.; Frontera, F.; Ghirlanda, G.; Labanti, C.; Osborne, J.P.; Stratta, G.; et al. The THESEUS space mission concept: Science case, design and expected performances. Adv. Space Res. 2018, 62, 191–244. [Google Scholar] [CrossRef]
- Stratta, G.; Ciolfi, R.; Amati, L.; Bozzo, E.; Ghirlanda, G.; Maiorano, E.; Nicastro, L.; Rossi, A.; Vinciguerra, S.; Frontera, F.; et al. THESEUS: A key space mission concept for Multi-Messenger Astrophysics. Adv. Space Res. 2018, 62, 662–682. [Google Scholar] [CrossRef]
- Stratta, G.; Amati, L.; Ciolfi, R.; Vinciguerra, S. THESEUS in the era of Multi-Messenger Astronomy. Mem. Soc. Ast. It. 2018, 89, 205–212. [Google Scholar] [CrossRef]
- ’t Hooft, G. Dimensional reduction in quantum gravity. Conf. Proc. C 1993, 930308, 284–296. [Google Scholar] [CrossRef]
- Susskind, L. The World as a hologram. J. Math. Phys. 1995, 36, 6377–6396. [Google Scholar] [CrossRef]
- Vitale, S.; Farr, W.M.; Ng, K.; Rodriguez, C.L. Measuring the star formation rate with gravitational waves from binary black holes. Astrophys. J. Lett. 2019, 886, L1. [Google Scholar] [CrossRef]
- Belgacem, E.; Dirian, Y.; Foffa, S.; Howell, E.J.; Maggiore, M.; Regimbau, T. Cosmology and dark energy from joint gravitational wave-GRB observations. JCAP 2019, 08, 015. [Google Scholar] [CrossRef]
- Yang, T. Gravitational-Wave Detector Networks: Standard Sirens on Cosmology and Modified Gravity Theory. JCAP 2021, 05, 044. [Google Scholar] [CrossRef]
- Madau, P.; Dickinson, M. Cosmic Star Formation History. Ann. Rev. Astron. Astrophys. 2014, 52, 415–486. [Google Scholar] [CrossRef]
- Virgili, F.J.; Zhang, B.; O’Brien, P.; Troja, E. Are all short-hard gamma-ray bursts produced from mergers of compact stellar objects? Astrophys. J. 2011, 727, 109. [Google Scholar] [CrossRef]
- D’Avanzo, P.; Salvaterra, R.; Bernardini, M.G.; Nava, L.; Campana, S.; Covino, S.; D’Elia, V.; Ghirlanda, G.; Ghisellini, G.; Melandri, A.; et al. A complete sample of bright Swift short Gamma-Ray Bursts. Mon. Not. Roy. Astron. Soc. 2014, 442, 2342–2356. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, C.; Adhikari, R.; Adya, V.; LIGO Scientific Collaboration and Virgo Collaboration; et al. GWTC-1: A Gravitational-Wave Transient Catalog of Compact Binary Mergers Observed by LIGO and Virgo during the First and Second Observing Runs. Phys. Rev. X 2019, 9, 031040. [Google Scholar] [CrossRef]
- Abbott, R.; Abbott, T.; Acernese, F.; Ackley, K.; Adams, C.; Adhikari, N.; Adhikari, R.; Adya, V.; Affeldt, C.; LIGO Scientific Collaboration, Virgo Collaboration, and KAGRA Collaboration; et al. Population of Merging Compact Binaries Inferred Using Gravitational Waves through GWTC-3. Phys. Rev. X 2023, 13, 011048. [Google Scholar] [CrossRef]
- Wen, L.; Chen, Y. Geometrical Expression for the Angular Resolution of a Network of Gravitational-Wave Detectors. Phys. Rev. D 2010, 81, 082001. [Google Scholar] [CrossRef]
- Cutler, C.; Apostolatos, T.A.; Bildsten, L.; Finn, L.S.; Flanagan, E.E.; Kennefick, D.; Markovic, D.M.; Ori, A.; Poisson, E. The Last three minutes: Issues in gravitational wave measurements of coalescing compact binaries. Phys. Rev. Lett. 1993, 70, 2984–2987. [Google Scholar] [CrossRef]
- Sathyaprakash, B.S.; Schutz, B.F. Physics, Astrophysics and Cosmology with Gravitational Waves. Living Rev. Rel. 2009, 12, 2. [Google Scholar] [CrossRef]
- Zhao, W.; Wen, L. Localization accuracy of compact binary coalescences detected by the third-generation gravitational-wave detectors and implication for cosmology. Phys. Rev. D 2018, 97, 064031. [Google Scholar] [CrossRef]
- Blanchet, L.; Iyer, B.R. Hadamard regularization of the third post-Newtonian gravitational wave generation of two point masses. Phys. Rev. D 2005, 71, 024004. [Google Scholar] [CrossRef]
- Maggiore, M. Gravitational Waves. Vol. 1: Theory and Experiments; Oxford Master Series in Physics; Oxford University Press: Oxford, UK, 2007. [Google Scholar]
- Howell, E.J.; Ackley, K.; Rowlinson, A.; Coward, D. Joint gravitational wave—Gamma-ray burst detection rates in the aftermath of GW170817. Mon. Not. R. Astron. Soc. 2018. [Google Scholar] [CrossRef]
- Wanderman, D.; Piran, T. The rate, luminosity function and time delay of non-Collapsar short GRBs. Mon. Not. Roy. Astron. Soc. 2015, 448, 3026–3037. [Google Scholar] [CrossRef]
- Meszaros, P.; Meszaros, A. The Brightness distribution of bursting sources in relativistic cosmologies. Astrophys. J. 1995, 449, 9–16. [Google Scholar] [CrossRef]
- Meszaros, A.; Ripa, J.; Ryde, F. Cosmological effects on the observed flux and fluence distributions of gamma-ray bursts: Are the most distant bursts in general the faintest ones? Astron. Astrophys. 2011, 529, A55. [Google Scholar] [CrossRef]
- Band, D.L. Comparison of the gamma-ray burst sensitivity of different detectors. Astrophys. J. 2003, 588, 945–951. [Google Scholar] [CrossRef]
- Hirata, C.M.; Holz, D.E.; Cutler, C. Reducing the weak lensing noise for the gravitational wave Hubble diagram using the non-Gaussianity of the magnification distribution. Phys. Rev. D 2010, 81, 124046. [Google Scholar] [CrossRef]
- Tamanini, N.; Caprini, C.; Barausse, E.; Sesana, A.; Klein, A.; Petiteau, A. Science with the space-based interferometer eLISA. III: Probing the expansion of the Universe using gravitational wave standard sirens. JCAP 2016, 04, 002. [Google Scholar] [CrossRef]
- Speri, L.; Tamanini, N.; Caldwell, R.R.; Gair, J.R.; Wang, B. Testing the Quasar Hubble Diagram with LISA Standard Sirens. Phys. Rev. D 2021, 103, 083526. [Google Scholar] [CrossRef]
- Kocsis, B.; Frei, Z.; Haiman, Z.; Menou, K. Finding the electromagnetic counterparts of cosmological standard sirens. Astrophys. J. 2006, 637, 27–37. [Google Scholar] [CrossRef]
- He, J.H. Accurate method to determine the systematics due to the peculiar velocities of galaxies in measuring the Hubble constant from gravitational-wave standard sirens. Phys. Rev. D 2019, 100, 023527. [Google Scholar] [CrossRef]
- Chen, L.; Huang, Q.G.; Wang, K. Distance Priors from Planck Final Release. JCAP 2019, 02, 028. [Google Scholar] [CrossRef]
- Beutler, F.; Blake, C.; Colless, M.; Jones, D.H.; Staveley-Smith, L.; Campbell, L.; Parker, Q.; Saunders, W.; Watson, F. The 6dF Galaxy Survey: Baryon Acoustic Oscillations and the Local Hubble Constant. Mon. Not. Roy. Astron. Soc. 2011, 416, 3017–3032. [Google Scholar] [CrossRef]
- Ross, A.J.; Samushia, L.; Howlett, C.; Percival, W.J.; Burden, A.; Manera, M. The clustering of the SDSS DR7 main Galaxy sample – I. A 4 per cent distance measure at z=0.15. Mon. Not. Roy. Astron. Soc. 2015, 449, 835–847. [Google Scholar] [CrossRef]
- Alam, S.; Ata, M.; Bailey, S.; Beutler, F.; Bizyaev, D.; Blazek, J.A.; Bolton, A.S.; Brownstein, J.R.; Burden, A.; Chuang, C.; et al. The clustering of galaxies in the completed SDSS-III Baryon Oscillation Spectroscopic Survey: Cosmological analysis of the DR12 galaxy sample. Mon. Not. Roy. Astron. Soc. 2017, 470, 2617–2652. [Google Scholar] [CrossRef]
- Brout, D.; Scolnic, D.; Popovic, B.; Riess, A.G.; Carr, A.; Zuntz, J.; Kessler, R.; Davis, T.M.; Hinton, S.; Jones, D.; et al. The Pantheon+ Analysis: Cosmological Constraints. Astrophys. J. 2022, 938, 110. [Google Scholar] [CrossRef]
- Available online: https://www.et-gw.eu/index.php/etsensitivities/ (accessed on 5 March 2025).
- Available online: https://cosmicexplorer.org/sensitivity.html (accessed on 5 March 2025).
- Zhu, J.P.; Wu, S.; Yang, Y.; Liu, C.; Zhang, B.; Song, H.; Gao, H.; Cao, Z.; Yu, Y.; Kang, Y.; et al. Kilonovae and Optical Afterglows from Binary Neutron Star Mergers. II. Optimal Search Strategy for Serendipitous Observations and Target-of-opportunity Observations of Gravitational Wave Triggers. Astrophys. J. 2023, 942, 88. [Google Scholar] [CrossRef]
- Adame, A.G.; Aguilar, J.; Ahlen, S.; Alam, S.; Alexander, D.M.; Alvarez, M.; Alves, O.; Anand, A.; Andrade, U.; Armengaud, E.; et al. DESI 2024 III: Baryon Acoustic Oscillations from Galaxies and Quasars. arXiv 2024, arXiv:2404.03000. [Google Scholar] [CrossRef]
- Adame, A.G.; Aguilar, J.; Ahlen, S.; Alam, S.; Alexander, D.M.; Alvarez, M.; Alves, O.; Anand, A.; Andrade, U.; Armengaud, E.; et al. DESI 2024 IV: Baryon Acoustic Oscillations from the Lyman Alpha Forest. arXiv 2024, arXiv:2404.03001. [Google Scholar] [CrossRef]
- Ahumada, R.; Prieto, C.A.; Almeida, A.; Anders, F.; Anderson, S.F.; Andrews, B.H.; Anguiano, B.; Arcodia, R.; Armengaud, E.; Aubert, M.; et al. The 16th Data Release of the Sloan Digital Sky Surveys: First Release from the APOGEE-2 Southern Survey and Full Release of eBOSS Spectra. Astrophys. J. Suppl. 2020, 249, 3. [Google Scholar] [CrossRef]
- Scolnic, D.M.; Jones, D.O.; Rest, A.; Pan, Y.C.; Chornock, R.; Foley, R.J.; Huber, M.E.; Kessler, R.; Narayan, G.; Riess, A.G.; et al. The Complete Light-curve Sample of Spectroscopically Confirmed SNe Ia from Pan-STARRS1 and Cosmological Constraints from the Combined Pantheon Sample. Astrophys. J. 2018, 859, 101. [Google Scholar] [CrossRef]
- Hogan, C.J. Measurement of Quantum Fluctuations in Geometry. Phys. Rev. D 2008, 77, 104031. [Google Scholar] [CrossRef]
- Hogan, C.J. Indeterminacy of Holographic Quantum Geometry. Phys. Rev. D 2008, 78, 087501. [Google Scholar] [CrossRef]
- Available online: https://www.esa.int/Science_Exploration/Space_Science/Integral_challenges_physics_beyond_Einstein (accessed on 5 March 2025).
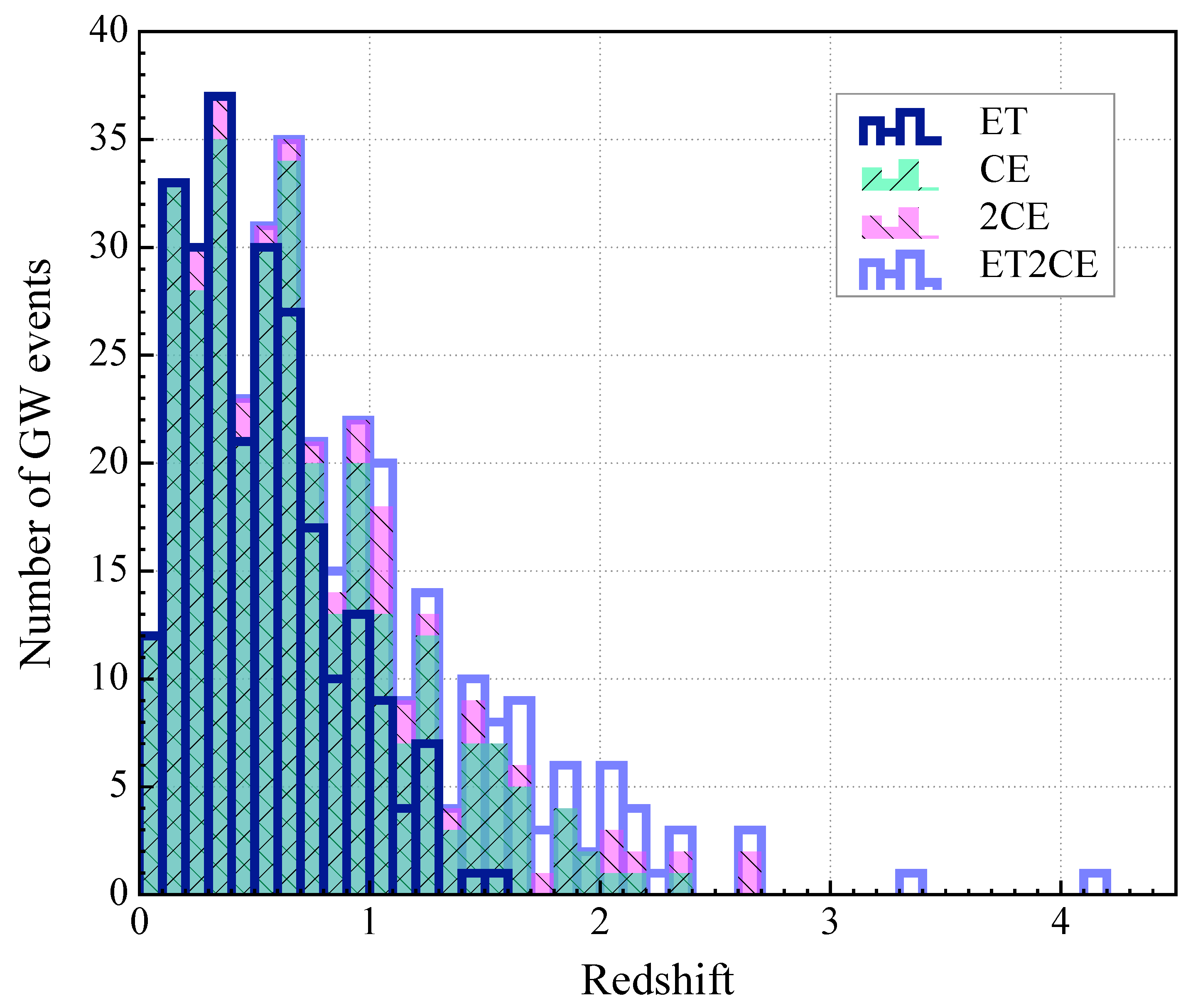
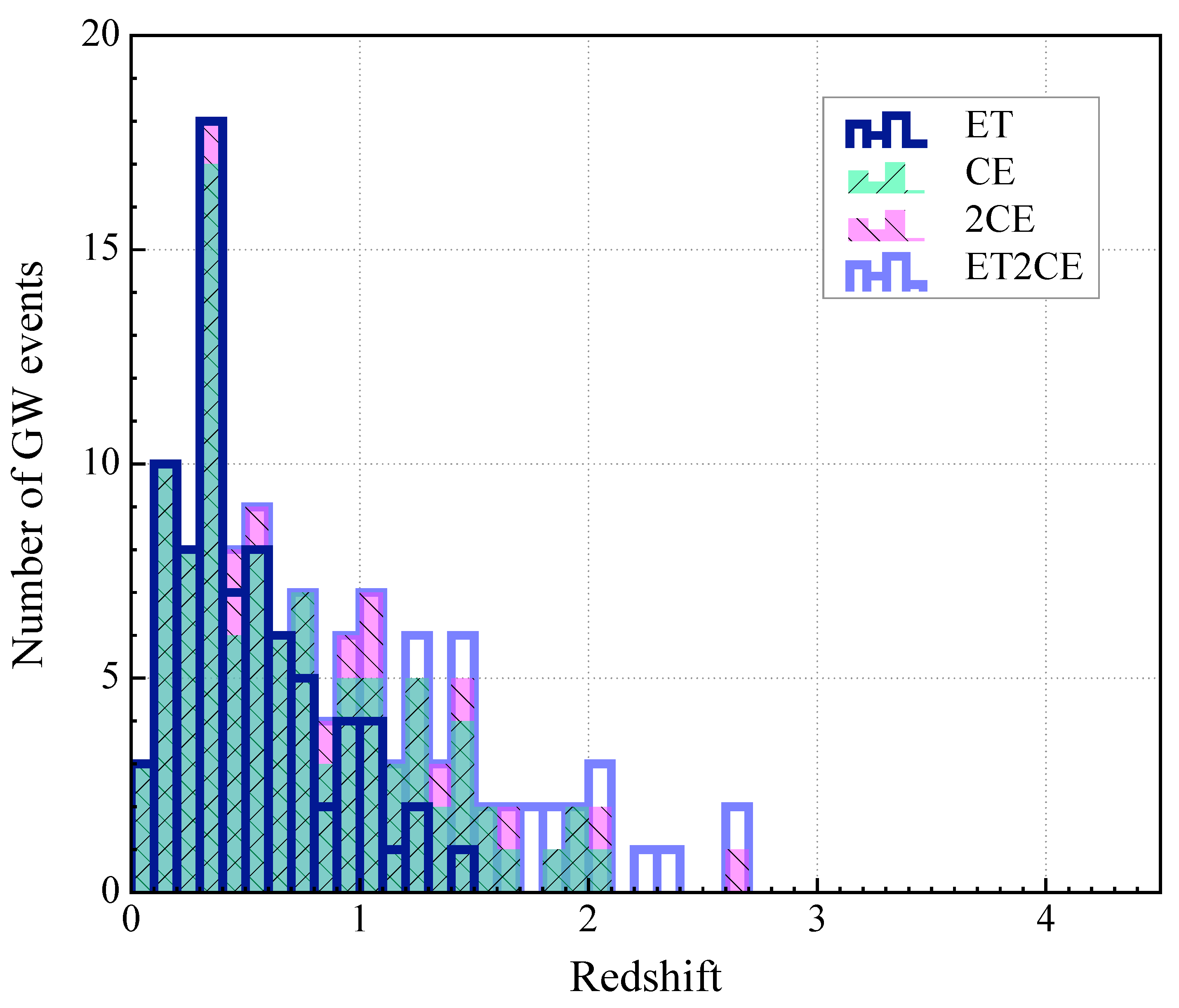
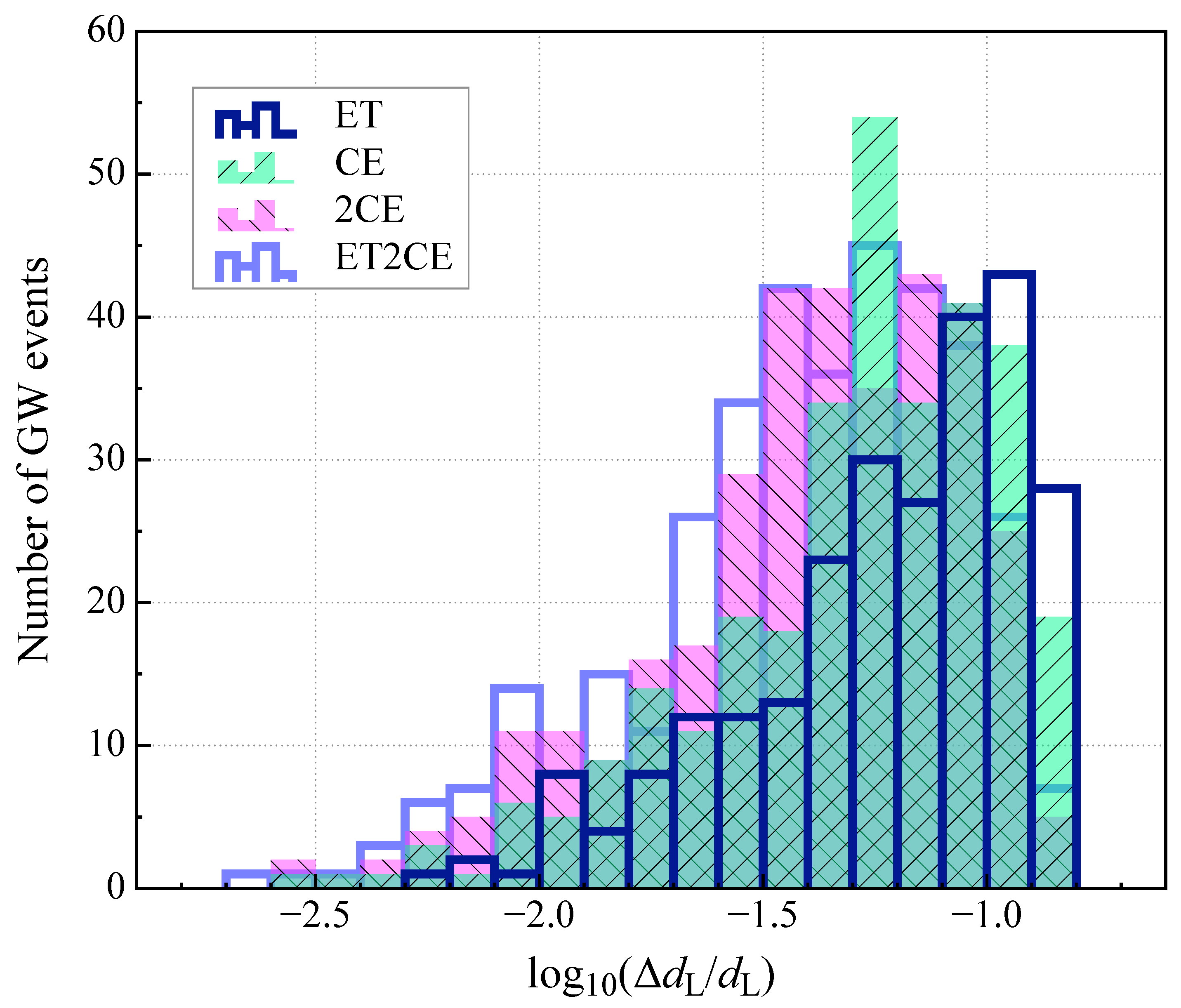
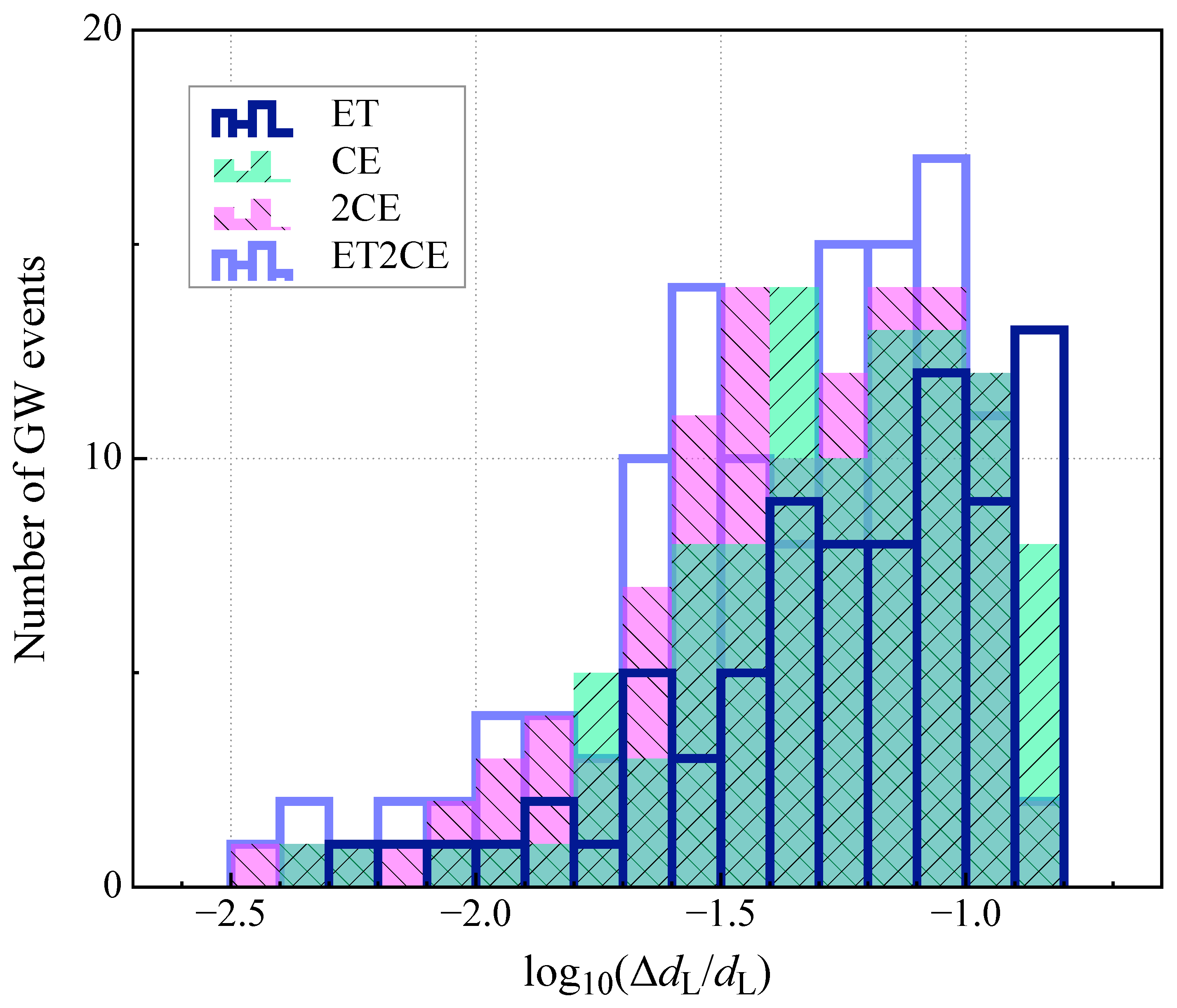
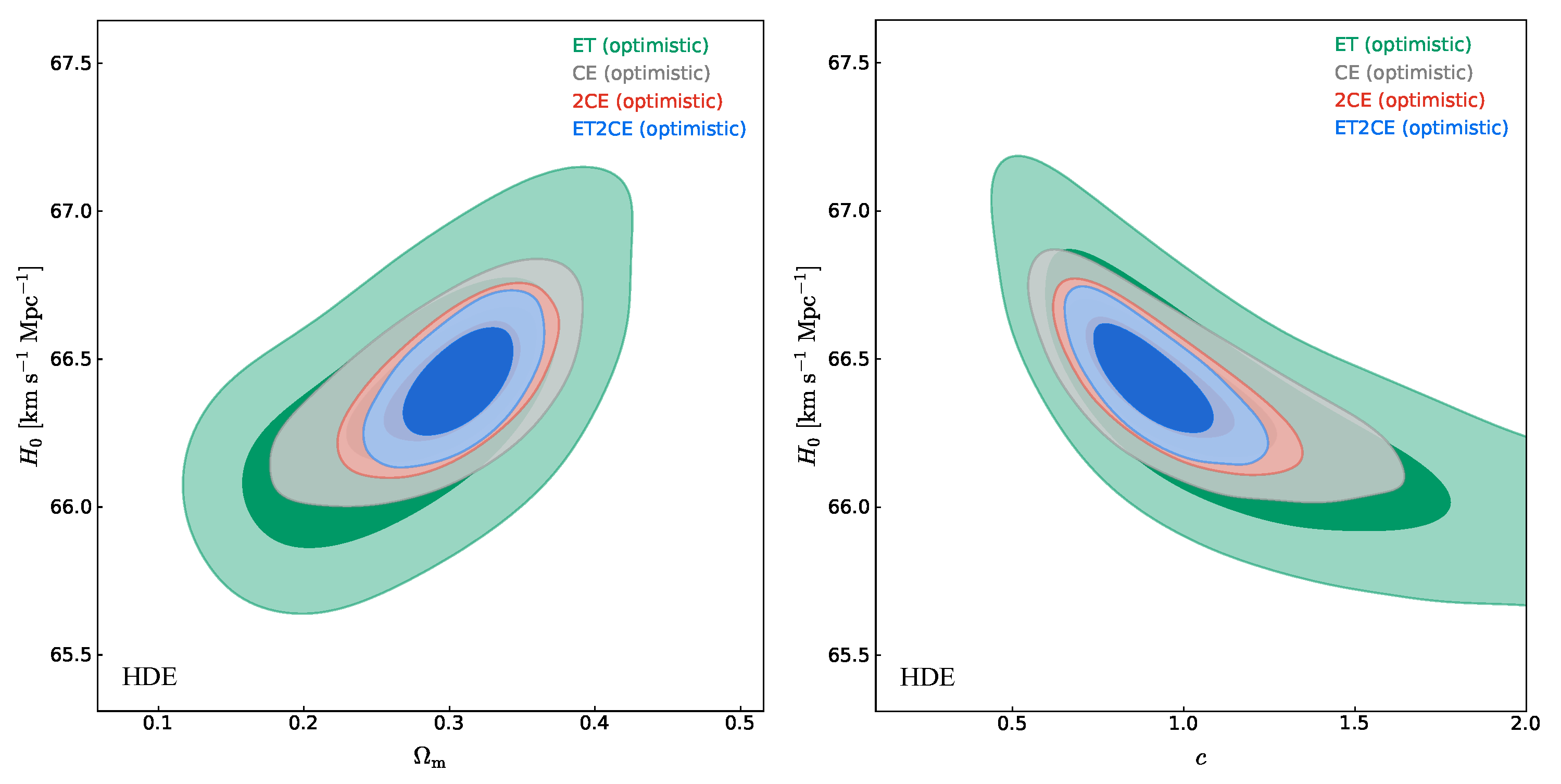
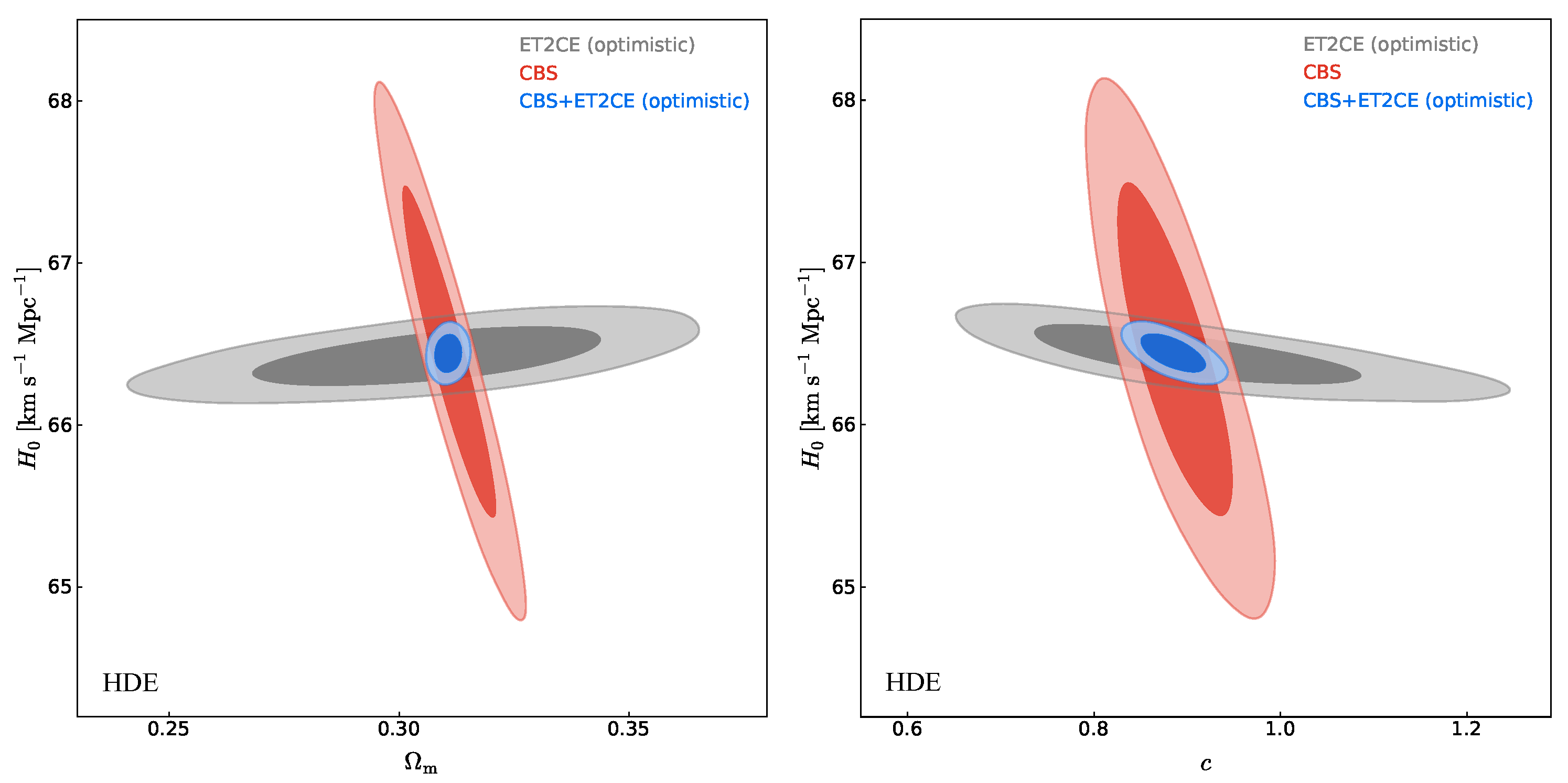
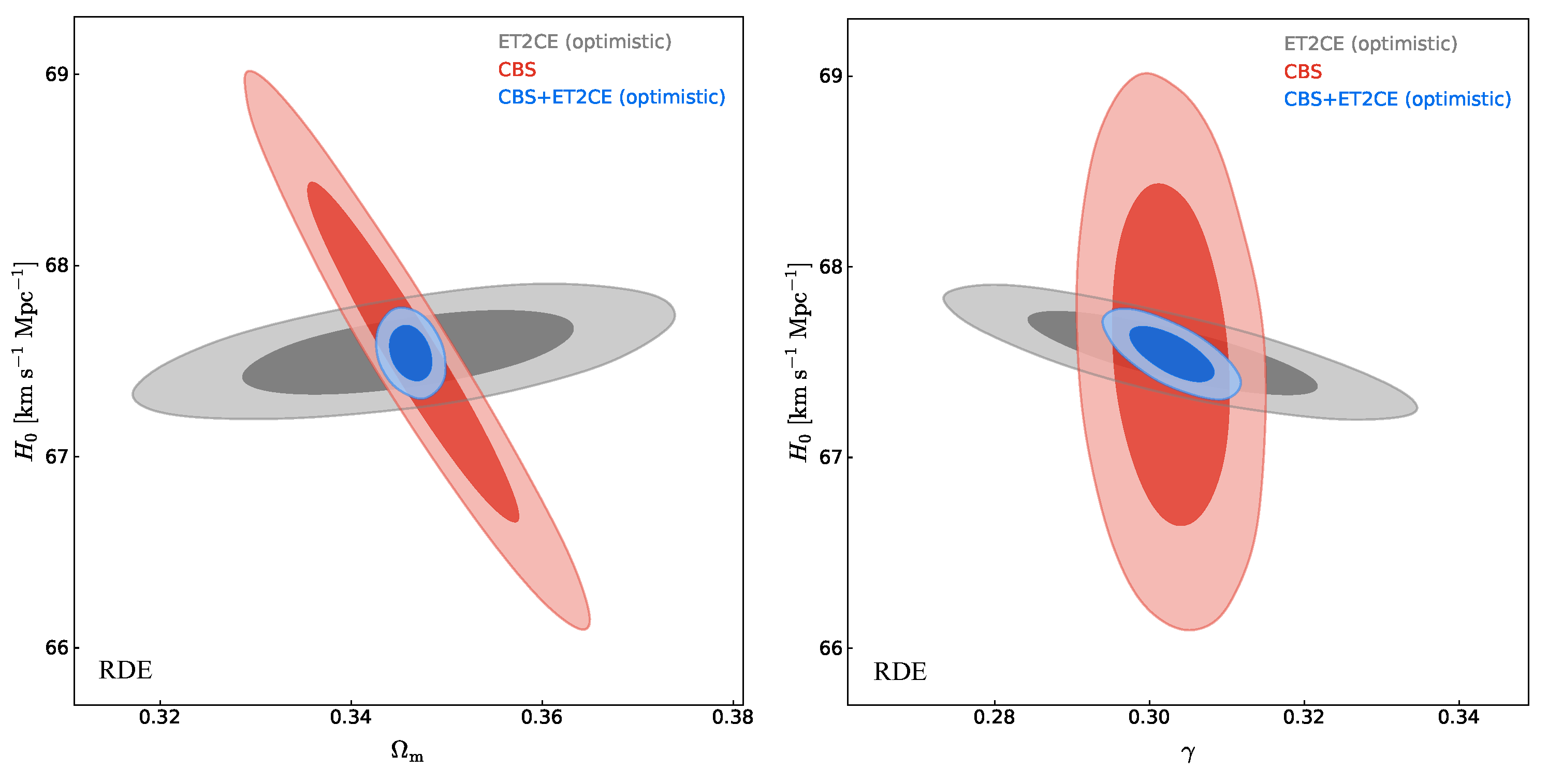
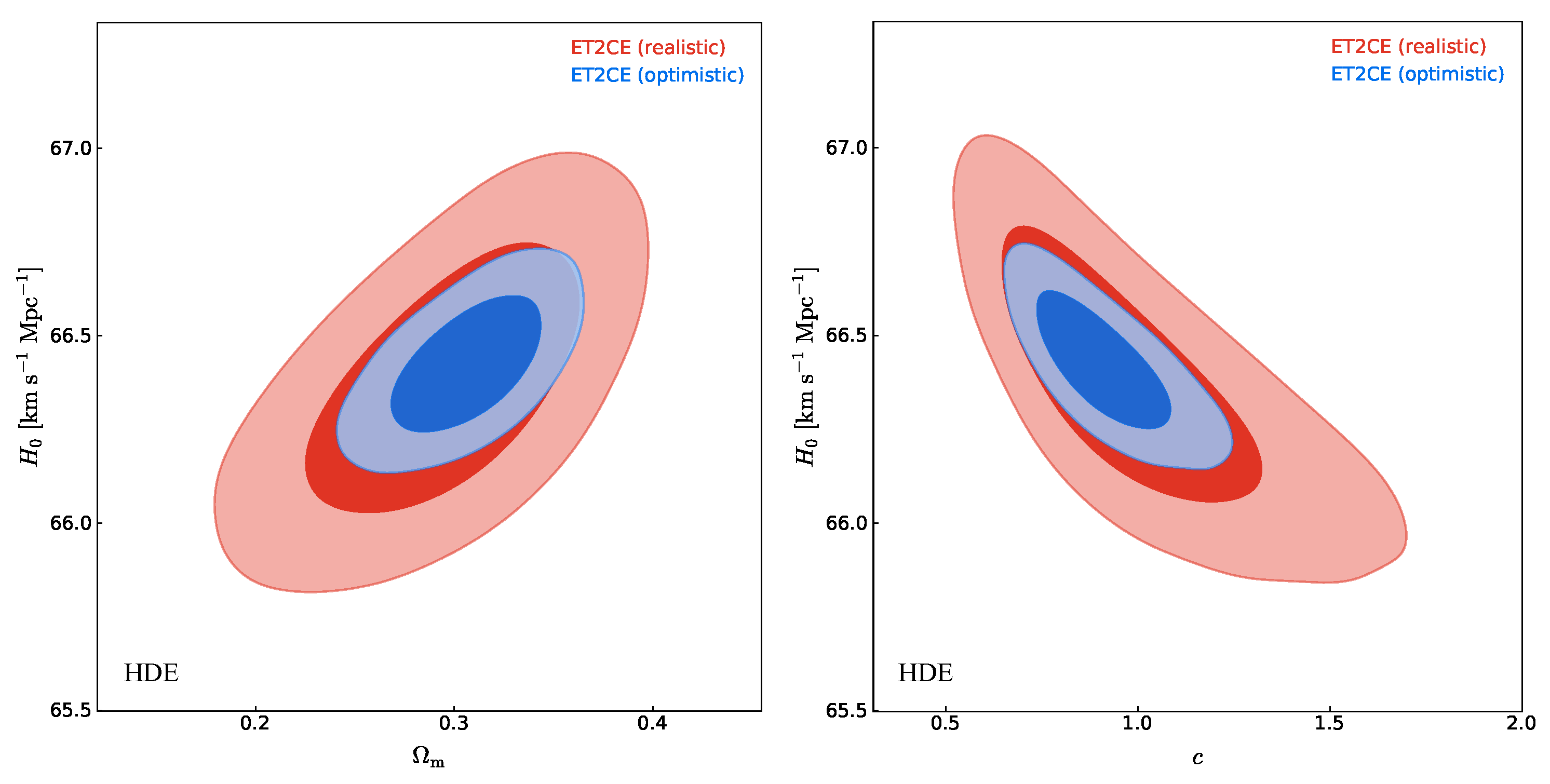
| Detection Strategy | ET | CE | 2CE | ET2CE |
|---|---|---|---|---|
| Optimistic scenario | 252 | 309 | 340 | 363 |
| Realistic scenario | 79 | 99 | 112 | 121 |
| Model | Error | ET | CE | 2CE | ET2CE | CBS | CBS + ET | CBS + CE | CBS + 2CE | CBS + ET2CE |
|---|---|---|---|---|---|---|---|---|---|---|
| HDE | ||||||||||
| RDE | ||||||||||
| Model | Error | ET | CE | 2CE | ET2CE | CBS | CBS + ET | CBS + CE | CBS + 2CE | CBS + ET2CE |
|---|---|---|---|---|---|---|---|---|---|---|
| HDE | ||||||||||
| RDE | ||||||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, T.; Li, Z.; Zhang, J.-F.; Zhang, X. Revisiting Holographic Dark Energy from the Perspective of Multi-Messenger Gravitational Wave Astronomy: Future Joint Observations with Short Gamma-Ray Bursts. Universe 2025, 11, 85. https://doi.org/10.3390/universe11030085
Han T, Li Z, Zhang J-F, Zhang X. Revisiting Holographic Dark Energy from the Perspective of Multi-Messenger Gravitational Wave Astronomy: Future Joint Observations with Short Gamma-Ray Bursts. Universe. 2025; 11(3):85. https://doi.org/10.3390/universe11030085
Chicago/Turabian StyleHan, Tao, Ze Li, Jing-Fei Zhang, and Xin Zhang. 2025. "Revisiting Holographic Dark Energy from the Perspective of Multi-Messenger Gravitational Wave Astronomy: Future Joint Observations with Short Gamma-Ray Bursts" Universe 11, no. 3: 85. https://doi.org/10.3390/universe11030085
APA StyleHan, T., Li, Z., Zhang, J.-F., & Zhang, X. (2025). Revisiting Holographic Dark Energy from the Perspective of Multi-Messenger Gravitational Wave Astronomy: Future Joint Observations with Short Gamma-Ray Bursts. Universe, 11(3), 85. https://doi.org/10.3390/universe11030085












