Abstract
In this work, we present a study on the long time-scale period variations of four single-mode high-amplitude delta Scuti stars (HADS) via the classical analysis. The target HADS are (i) XX Cygni, (ii) YZ Bootis, (iii) GP Andromedae, and (iv) ZZ Microscopii. The newly determined times of maximum light came from the Transiting Exoplanet Survey Satellite (TESS), American Association of Variable Star Observers (AAVSO), and Bundesdeutsche Arbeitsgemeinschaft für Veränderliche Sterne (BAV) projects. Together with the times of maximum light obtained in the historical literature, the analysis was performed on these HADS, in which we obtained the linear period variation rates as , , , and , respectively. Based on these results and some earlier research, we also discuss the evolutionary stages and the mechanisms of the period variation of these four HADS.
1. Introduction
Delta Scuti stars are pulsators located in the classical Cepheid instability strip crossing the main sequence and sometimes in the region between the main sequence and the giant branch. The mass of delta Scuti stars ranges from 1.4 to 2.5 , and their pulsation period ranges from to days [1]. As a subclass of delta Scuti stars, the High Amplitude Delta Scuti stars (HADS) generally have larger amplitude (≥0.1 mag) and slow rotation speed () [2], which can be Population I or II stars. Most of the HADS exhibit one or two radial pulsation modes, while some of them display three radial pulsation modes and even some non-radial modes [3,4,5,6,7,8]. For those HADS which exhibit only one dominant radial pulsation mode (see, e.g., [9]), we can use the deviation of their times of maximum light (TML) between the observed and calculated ones to study their period variations ( analysis).
The analysis provides us an opportunity to study the period variation details of these stars. Theoretically, for HADS, the period variation rates caused by stellar evolution should be in the range of to [10]. If the observed value is of the same order of magnitude as the theoretical one, it indicates that the period variation of this star could be attributed to stellar evolution; if not, the period variation may be influenced by other mechanisms such as nonlinear mode interaction, mass transfer or the light-travel time effect in binary systems [5,6,7,10,11,12,13,14]. Consequently, the investigation into the period variation of HADS will help us have a better understanding of their evolutionary stage and reveal the unknown mechanisms behind it.
In this work, we chose four single-mode HADS as the targets to study their period variation rates, which have been observed by different projects many times in history and recent years. The basic information about these four HADS is listed as follows.
XX Cygni (XX Cyg, , ) [15], a Population II HADS [16,17,18]. The linear period variation rate obtained by refs. [15,19] are both at the order .
YZ Bootis (YZ Boo, , ) [20], a Population I HADS [21]. In the most recent analysis on YZ Boo [20], the authors obtained a period variation rate of = . However, they also declared that the second-order polynomial curve fitting does not show sufficient advantage compared to linear fitting, which indicates that it is hard to say whether the period of YZ Boo is varying or not.
GP Andromedae (GP And, , ) [22], a Population I HADS [10]. In the latest research of its period variation rate, ref. [22] not only gave a result of = , but also confirmed an amplitude variability in GP And. Two other recent studies for GP And [23,24] showed increasing pulsation period variations with a rate of ∼. All these results are much larger than the theoretical values [25].
ZZ Microscopii (ZZ Mic, , ), was first discovered by [26]. In ref. [27], they conducted an analysis on ZZ Mic and obtained that its period was increasing at a constant rate. However, in the latest research of this star [28], the authors claimed that the period of ZZ Mic was increasing at a constant rate during the years 1960 to 2003, and it has been decreasing since 2003.
All of these stars have unsolved problems about their period variations. Thus, we expected to acquire a better understanding on the period variations of them with more data. This paper is organized as follows. In Section 2, we introduce the data sources and the reduction procedures. In Section 3, we show the results of four target stars and their linear period variation rates. In Section 4, we discuss the behaviors and the origins of the period variation rates. In Section 5, we list the conclusions.
2. Data Sources and Data Reduction
The Transiting Exoplanet Survey Satellite (TESS), a NASA mission launched in 2018, is designed to discover exoplanets by detecting transits while simultaneously advancing asteroseismology through its high-precision photometric observations of host stars, enabling scientists to study stellar interiors and oscillations for deeper insights into stellar evolution and structure [29].
In this work, we collected the TML based on the light curves from TESS (from MAST Portal1, which were processed by the TESS Science Processing Operations Center (SPOC) [30,31]), AAVSO2, BAV3 projects, and the historical literature. The overview of the data from TESS, AAVSO, and BAV is listed in Table 1.

Table 1.
Overview of the data from TESS, AAVSO, and BAV.
For the light curves from TESS, we downloaded the Sectors with an exposure time of 120 s and normalized them using thepython package Lightkurve v2.4.2 [32]. Then, we used the module optimize.curve_fit in thepackage SciPy v1.14.0 [33] to fit the data points around each of the peaks in the light curve with a polynomial to determine the time of maximum light. Due to the profiles of the light curves, we used a third- or fourth-order polynomial, generally, and sometimes a fifth-order polynomial, depending on the quality of the data and the goodness of fit.
Because Julian Days (JD) are used in the AAVSO data, we converted them into Heliocentric Julian Days (HJD) with the help of an online applet4. Moreover, a Monte Carlo simulation was constructed to estimate the uncertainties of each time of maximum light.
For the TML, from the historical literature without uncertainties, we used the following rules to estimate the uncertainties: when the the data value has n decimals, we set the uncertainty as (i.e., for , for ). All the TML in this work were converted to BJD with the help of the online applet hjd2bjd5.
3. Analysis
All the TML used in this work were collected in a data file, which was uploaded to the Zenodo website (https://zenodo.org/records/14950457, accessed on 1 March 2025). The indicators of the historical literature in the data file are listed in Appendix A.
3.1. Analysis of XX Cyg
For XX Cyg, a total of 905 TML were obtained, of which 360 were determined from TESS, 90 were determined from AAVSO, 36 were determined from BAV, and 419 of them were collected from the historical literature of this star. In order to calculate the values and their corresponding cycle numbers, we adopted the linear ephemeris [15]
to obtain a new linear ephemeris
Then, we fit the values (the residuals of the linear fitting) with a second-order polynomial and obtained the result , which has a linear period variation rate of . The fitting results of the values and corresponding residuals are shown in Figure 1.
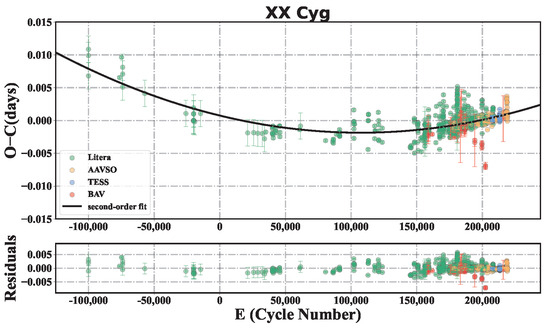
Figure 1.
values of XX Cyg and the corresponding residuals. The black line represents the second-order polynomial fit of the values. The different colors of the points represent data from different sources.
3.2. Analysis of YZ Boo
For YZ Boo, a total of 736 TML were obtained, of which 434 were determined from TESS, 28 were determined from AAVSO, 63 were determined from BAV, and 211 were collected from the historical literature. In order to calculate the values and their corresponding cycle numbers, we adopted the linear ephemeris [20]
to obtain a new linear ephemeris
Then, we fit the values (the residuals of the linear fitting) with a second-order polynomial and obtained the result . The obtained linear period variation rate is , which is similar to the result in Ref. [20]. The fitting results of the values and corresponding residuals are shown in Figure 2.
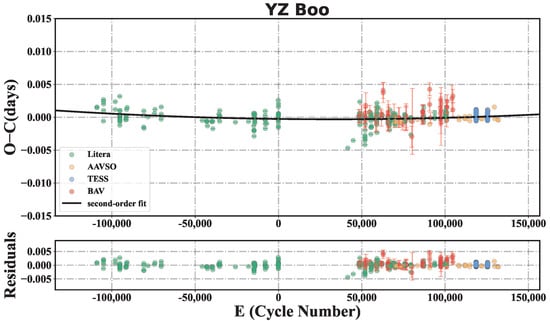
Figure 2.
values of YZ Boo and the corresponding residuals. The black line represents the second-order polynomial fit of the values. The different colors of the points represent data from different sources.
3.3. Analysis of GP And
For GP And, a total of 591 TML were obtained (from 1970 to 2023), of which 268 of were determined from TESS, 33 were determined from AAVSO, 92 were determined from BAV, and 198 of them were collected from the historical literature. In order to calculate the values and their corresponding cycle numbers, we adopted the linear ephemeris [22]
to obtain a new linear ephemeris
Then, we fit the values (the residuals of the linear fitting) with a second-order polynomial and obtained the result .
The obtained linear period variation rate is , and the fitting results of the values and corresponding residuals are shown in Figure 3.
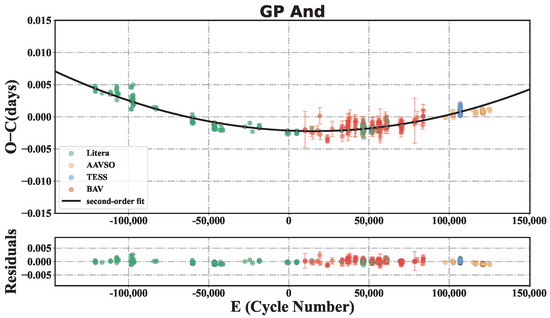
Figure 3.
values of GP And and the corresponding residuals. The black line represents the second-order polynomial fit of the values. The different colors of the points represent data from different sources.
3.4. Analysis of ZZ Mic
For ZZ Mic, we determined 667 TML from TESS and 2 from AAVSO. Moreover, we also collected 48 TML from the historical literature. Based on the above 717 TML, we determined the new linear ephemeris as
Then, we fit the values (the residuals of the linear fitting) with a second-order polynomial and obtained the result .
The obtained linear period variation rate is , and the fitting results of the values and corresponding residuals are shown in Figure 4.
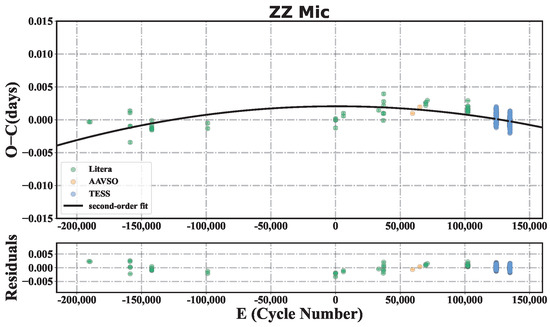
Figure 4.
values of ZZ Mic and the corresponding residuals. The black line represents the second-order polynomial fit of the values. The different colors of the points represent data from different sources.
4. Discussion
4.1. Discussion of XX Cyg
The linear period variation rate we obtained in this work was , which is similar to the theoretical evolutionary results in ref. [15]. In this post-mean sequence (post-MS) evolutionary stage, the envelope absorbs energy produced by the hydrogen burning shell and then expands, which leads to an expansion of the star. As it well known, the period of the fundamental mode in HADS mainly depends on the mean density of the star itself. So the increase in the stellar radius means an increase in the period.
In some earlier research (see, e.g., ref. [34]), researchers claimed that XX Cyg experienced a sudden period variation in 1942. However, even though the jumping of period variation is allowed by stellar evolution theory [35], our result indicates that it should be due to the limited data points.
In addition, some other HADS that were suspected to exhibit period jumps have now been proved to have a continuous period variation, or the previously considered ‘jump’ was actually caused by the light-travel time effect (LTTE) (such as CY Aqr [36,37]).
4.2. Discussion of YZ Boo
Different from the other three stars in this work, we found that the second-order polynomial trend in the diagram of YZ Boo was not very significant. Therefore, an F-test was performed to test the advantage of the second-order fitting comparing to the linear one. Based on the routine from Statology6, we used the residuals of the linear and second-order fittings to calculate the p value. It produced , and then we obtained , which indicates that the goodness-of-fit of the second-order fitting was not significant. As a result, we cannot conclude that YZ Boo exhibited significant period variation in 1955–2024. This result is similar to the conclusion in ref. [20].
However, if we take the linear period variation rate of YZ Boo obtained in this work seriously, it is consistent with the theoretical calculations of the period variation rate in ref. [20], which indicates that YZ Boo is in the post-MS evolutionary stage. In the case of YZ Boo, we need more data to obtain results with higher confidence.
4.3. Discussion of GP And
Although the linear period variation rate of GP And () falls into the range of the theoretical prediction ( to ) and indicates the star is in the post-MS evolutionary stage, a detailed stellar evolutionary model for this star is also needed to explain the exact value of and its evolutionary stage.
Ref. [38] calculated the linear period variation rates of GP And (including both MS and post-MS models) in three cases, and all the results were at the order of . Ref. [24] estimated a theoretical value of about from the results in ref. [10]. On the other hand, the observed linear period variation rate of GP And was [22] and [39] in some recent literature.
Why are the theoretical values of the period variation rate of GP And we mentioned above much larger than the observed ones? Here we give two possibilities: (i) First, more accurate and detailed theoretical evolutionary models need to be constructed for GP And, which could give us a more reasonable theoretical prediction of ; (ii) Second, an accumulation of the TML in a longer time-scale is also needed to test whether the observed is caused by LTTE. Because a quasi-sinusoidal curve is locally similar to a polynomial curve, the observed second-order polynomial trend could be a superposition of a quasi-sinusoidal trend (from LTTE) and a weak second-order polynomial trend (from stellar evolution) (see, e.g., refs. [7,40]).
4.4. Discussion of ZZ Mic
The situation in ZZ Mic is more complex than that of the other three stars. Historically, some researchers obtained an increasing period [27] and even employed a third-order polynomial to fit the values. The negative linear period variation rate obtained in this work indicates that ZZ Mic has a decreasing period. The different results might come from the lack of TML in cycles from to 0, which prevents us from obtaining high-confidence results on the period variation of ZZ Mic.
If we ascribe the decreasing period to stellar evolution, it demands that ZZ Mic is in an overall contraction evolutionary stage. In this stage, the star has exhausted all the hydrogen in its core and starts to contract due to gravity. Although some works reported pre-MS stars (which show delta Scuti-type pulsations) can also have negative period variation [41,42,43], the linear period variation rate of ZZ Mic is so small that it can only be a post-MS star [10].
The fitting residuals of the O-C values of ZZ Mic are presented in Figure 5, in which we can find a potential periodic trend. However, the data points were not sufficient to cover a complete cycle. As the TML continues to be accumulated from different observations, we expect to solve out the potential orbital parameters via the values affected by LTTE in this multi-star system (see, e.g., refs. [7,44]) and study some other interesting mechanisms like the magnetic braking effect (which is an important physical mechanism that influences material accretion, spin-down, and evolutionary paths of binary stars [45,46]) in other types of multi-star systems.
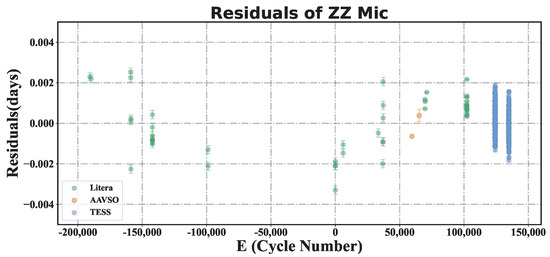
Figure 5.
Residuals of the second-order fitting of the values from ZZ Mic.
5. Conclusions
In this work, we collected TML of four HADS over several decades and obtained the linear period variation rates of these stars via the analysis as follows: (i) XX Cyg, ; (ii) YZ Boo, ; (iii) GP And, ; (iv) ZZ Mic, .
For XX Cyg and YZ Boo, the period variation rates we obtained are similar to the results in the latest research, which could be ascribed to stellar evolution. For GP And, although the observed period variation rate is in the range of the general theoretical prediction from stellar evolution, some discrepancy appears between the the observed value and some previous specialized studies on this star. More in-depth studies are necessary in the future, based on more observations.
For ZZ Mic, we obtained a negative linear period variation rate, which is different from previous studies and indicates that the star is in an overall contraction evolutionary stage. Moreover, we found a potential periodic (quasi-sinusoidal) trend in the residuals of diagram, which might be caused by LTTE in a multi-star system.
More observations in the future will provide us further opportunity to study these HADS in-depth, including their evolutionary stages and their nature in multi-star systems.
Author Contributions
Conceptualization, J.-S.N. and H.-F.X.; methodology, J.-S.N. and H.-F.X.; software, T.-F.M.; validation, T.-F.M., J.-S.N. and H.-F.X.; formal analysis, T.-F.M.; investigation, T.-F.M.; resources, J.-S.N.; data curation, T.-F.M.; writing—original draft preparation, T.-F.M.; writing—review and editing, J.-S.N. and H.-F.X.; visualization, T.-F.M.; supervision, J.-S.N. and H.-F.X.; project administration, J.-S.N. and H.-F.X.; funding acquisition, H.-F.X. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the National Natural Science Foundation of China (NSFC: No. 12303036).
Data Availability Statement
All the data obtained in this work can be found on the Zenodo website (https://zenodo.org/records/14950457, accessed on 1 March 2025).
Acknowledgments
H.F.X. acknowledges support from the National Natural Science Foundation of China (NSFC) (No. 12303036). All the authors acknowledge the TESS Science team and everyone who has contributed to making the TESS mission possible. We also acknowledge with thanks the variable star observations from the AAVSO International Database contributed by observers worldwide and used in this research.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A. Times of Maximum Light Used in This Work
All the TML used in this work were collected in a file and uploaded on the Zenodo website (doi: 10.5281/zenodo.14950457, https://zenodo.org/records/14950457).
The indicators of the historical literature in the data file are listed as follows.
For XX Cyg: (1) [47]; (2) [48]; (3) [49]; (4) [50]; (5) [51]; (6) [52]; (7) [52], from unpublished data of L. Detre; (8) [53]; (9) [54]; (10) [55]; (11) [17]; (12) [56]; (13) [57]; (14) [25]; (15) [58]; (16) [59]; (17) [60]; (18) [61]; (19) [34]; (20) [62]; [63]; (21) [64]; (22) [65]; (23) [66]; (24) [65]; (25) [67]; (26) [68]; (27) [69]; (28) [15]; (29) [19].
For YZ Boo: (1) [70]; (2) [71]; (3) [72]; (4) [73]; (5) [74]; (6) [53]; (7) [75]; (8) [76]; (9) collected from [77], the original source cannot be found; (10) [52]; (11) [21]; (12) [78]; (13) [79]; (14) [80]; (15) [57]; (16) [81]; (17) [60]; (18) [82]; (19) [83]; (20) [84]; (21) [62]; (22) [85]; (23) [64]; (24) [65]; (25) [77]; (26) [20].
For GP And: (1) [86]; (2) [87], the TML were derived from [25]; (3) [88], the TML were derived by [25]; (4) [25]; (5) [89]; (6) [90]; (7) collected from [23]; (8) [23]; (9) [22].
For ZZ Mic: (1) [26]; (2) [91]; (3) [92]; (4) [93]; (5) [27]; (6) [28].
Notes
| 1 | https://mast.stsci.edu/portal/Mashup/Clients/Mast/Portal.html, accessed on 1 May 2024 |
| 2 | https://www.aavso.org/, accessed on 1 June 2024 |
| 3 | https://www.bav-astro.eu/index.php, accessed on 1 July 2024 |
| 4 | https://doncarona.tamu.edu/apps/jd/, accessed on 15 June 2024 |
| 5 | https://astroutils.astronomy.osu.edu/time/hjd2bjd.html, accessed on 15 July 2024 |
| 6 | https://www.statology.org/f-test-python/, accessed on 15 September 2024 |
References
- Netzel, H.; Smolec, R. Modelling of multimode radially pulsating high-amplitude δ Scuti stars from the OGLE Galactic bulge sample. Mon. Not. R. Astron. Soc. 2022, 515, 4574–4586. [Google Scholar] [CrossRef]
- Breger, M. δ Scuti stars (Review). In Astronomical Society of the Pacific Conference Series, Proceedings of the Delta Scuti and Related Stars, Vienna, Austria, 4–7 August 1999; Breger, M., Montgomery, M., Eds.; BiblioGov: Ottawa, ON, Canada, 2000; Volume 210, p. 3. [Google Scholar]
- Wils, P.; Rozakis, I.; Kleidis, S.; Hambsch, F.J.; Bernhard, K. Photometry of GSC 762-110, a new triple-mode radially pulsating star. Astron. Astrophys. 2008, 478, 865–868. [Google Scholar] [CrossRef]
- Niu, J.S.; Fu, J.N.; Zong, W.K. Pulsation analysis of the high amplitude δ Scuti star CW Serpentis. Res. Astron. Astrophys. 2013, 13, 1181–1188. [Google Scholar] [CrossRef][Green Version]
- Niu, J.S.; Fu, J.N.; Li, Y.; Yang, X.H.; Zong, W.; Xue, H.F.; Zhang, Y.P.; Liu, N.; Du, B.; Zuo, F. AE Ursae Majoris—A δ Scuti star in the Hertzsprung Gap. Mon. Not. R. Astron. Soc. 2017, 467, 3122–3139. [Google Scholar] [CrossRef]
- Xue, H.F.; Fu, J.N.; Fox-Machado, L.; Shi, J.R.; Zhou, Y.T.; Zhang, J.B.; Michel, R.; Yan, H.L.; Niu, J.S.; Zong, W.K.; et al. Asteroseismology of the Double-mode High-amplitude δ Scuti Star VX Hydrae. Astrophys. J. 2018, 861, 96. [Google Scholar] [CrossRef]
- Xue, H.F.; Niu, J.S. DY Pegasi: An SX Phoenicis Star in a Binary System with an Evolved Companion. Astrophys. J. 2020, 904, 5. [Google Scholar] [CrossRef]
- Daszyńska-Daszkiewicz, J.; Walczak, P.; Pamyatnykh, A.A.; Szewczuk, W. Asteroseismology of the double-radial mode δ Scuti star BP Pegasi. Mon. Not. R. Astron. Soc. 2022, 512, 3551–3565. [Google Scholar] [CrossRef]
- Xue, W.; Niu, J.S.; Xue, H.F.; Yin, S. Pulsation Analysis of High-Amplitude δ Scuti Stars with TESS. Res. Astron. Astrophys. 2023, 23, 075002. [Google Scholar] [CrossRef]
- Breger, M.; Pamyatnykh, A.A. Period changes of delta Scuti stars and stellar evolution. Astron. Astrophys. 1998, 332, 958–968. [Google Scholar] [CrossRef]
- Bowman, D.M.; Kurtz, D.W.; Breger, M.; Murphy, S.J.; Holdsworth, D.L. Amplitude modulation in δ Sct stars: Statistics from an ensemble study of Kepler targets. Mon. Not. R. Astron. Soc. 2016, 460, 1970–1989. [Google Scholar] [CrossRef]
- Bowman, D.M.; Hermans, J.; Daszyńska-Daszkiewicz, J.; Holdsworth, D.L.; Tkachenko, A.; Murphy, S.J.; Smalley, B.; Kurtz, D.W. KIC 5950759: A high-amplitude δ Sct star with amplitude and frequency modulation near the terminal age main sequence. Mon. Not. R. Astron. Soc. 2021, 504, 4039–4053. [Google Scholar] [CrossRef]
- Niu, J.S.; Xue, H.F. A Rapidly Evolving High-amplitude δ Scuti Star Crossing the Hertzsprung Gap. Astrophys. J. Lett. 2022, 938, L20. [Google Scholar] [CrossRef]
- Xue, H.F.; Niu, J.S.; Fu, J.N. Precise Evolutionary Asteroseismology of High-Amplitude δ Scuti Star AE Ursae Majoris. Res. Astron. Astrophys. 2022, 22, 105006. [Google Scholar] [CrossRef]
- Yang, X.H.; Fu, J.N.; Zha, Q. Stellar Pulsations and Period Changes in the SX Phoenicis Star XX Cygni. Astron. J. 2012, 144, 92. [Google Scholar] [CrossRef]
- Ceraski, W. Une nouvelle variable 14.1904 Cygni. Astron. Nachrichten 1904, 165, 61. [Google Scholar] [CrossRef]
- Joner, M.D. The nature of the DWARF cepheid XX CYG. Publ. Astron. Soc. Pac. 1982, 94, 289. [Google Scholar] [CrossRef]
- Hintz, E.G.; Joner, M.D. Fourier decomposition of the light curves of three DWARF CEPHEIDS: CY AQUARII, XX CYGNI, AND V798 CYGNI. Publ. Astron. Soc. Pac. 1997, 109, 639. [Google Scholar] [CrossRef][Green Version]
- Withers, S.; Kantorowitz-Sapers, A.; Parsons, J.; Wu, J.Y.; Delaney, P.A. Photometric Monitoring and Period Changes in SX Phoenicis Star XX Cygni. IV. J. R. Astron. Soc. Can. 2021, 115, 238. [Google Scholar]
- Yang, T.Z.; Esamdin, A.; Fu, J.N.; Niu, H.B.; Feng, G.J.; Song, F.F.; Liu, J.Z.; Ma, L. Pulsations of the High-Amplitude δ Scuti star YZ Bootis. Res. Astron. Astrophys. 2018, 18, 002. [Google Scholar] [CrossRef]
- Joner, M.D.; McNamara, D.H. A photometric and spectrographic study of YZ Bootis. Publ. Astron. Soc. Pac. 1983, 95, 433–439. [Google Scholar] [CrossRef]
- Zhou, A.Y.; Jiang, S.Y. Period and Amplitude Variability of the High-amplitude δ Scuti Star GP Andromedae. Astron. J. 2011, 142, 100. [Google Scholar] [CrossRef]
- Szeidl, B.; Schnell, A.; Pocs, M.D. The high-amplitude delta Scuti star GP Andromedae. Inf. Bull. Var. Stars 2006, 5718, 1. [Google Scholar]
- Pop, A.; Liteanu, V.; Moldovan, D. On the period variability of GP Andromedae. Astrophys. Space Sci. 2003, 284, 1207–1222. [Google Scholar] [CrossRef]
- Rodriguez, E.; Rolland, A.; Lopez de Coca, P. Simultaneous uvby-beta photometry of GP Andromedae. Astron. Astrophys. Suppl. 1993, 101, 421. [Google Scholar]
- Churms, J.; Evans, D.S. HD 199757: A variable stars of extremely short period. Observatory 1961, 81, 25–29. [Google Scholar]
- Kim, C.; Moon, B.K. A Photometric Study of ZZ Microscopium. Publ. Astron. Soc. Pac. 2009, 121, 478. [Google Scholar] [CrossRef]
- Axelsen, R.A.; Napier-Munn, T. Recently Determined Light Elements for the delta Scuti Star ZZ Microscopii. J. Am. Assoc. Var. Star Obs. 2015, 43, 50. [Google Scholar]
- Ricker, G.R.; Winn, J.N.; Vanderspek, R.; Latham, D.W.; Bakos, G.Á.; Bean, J.L.; Berta-Thompson, Z.K.; Brown, T.M.; Buchhave, L.; Butler, N.R.; et al. Transiting Exoplanet Survey Satellite (TESS). J. Astron. Telesc. Instrum. Syst. 2015, 1, 014003. [Google Scholar] [CrossRef]
- Jenkins, J.M.; Twicken, J.D.; McCauliff, S.; Campbell, J.; Sanderfer, D.; Lung, D.; Mansouri-Samani, M.; Girouard, F.; Tenenbaum, P.; Klaus, T.; et al. The TESS science processing operations center. In Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series, Proceedings of the Software and Cyberinfrastructure for Astronomy IV, Edinburgh, UK, 26–30 June 2016; Chiozzi, G., Guzman, J.C., Eds.; SPI: Bellingham, WA, USA, 2016; Volume 9913, p. 99133E. [Google Scholar] [CrossRef]
- Caldwell, D.A.; Tenenbaum, P.; Twicken, J.D.; Jenkins, J.M.; Ting, E.; Smith, J.C.; Hedges, C.; Fausnaugh, M.M.; Rose, M.; Burke, C. TESS Science Processing Operations Center FFI Target List Products. Res. Notes Am. Astron. Soc. 2020, 4, 201. [Google Scholar] [CrossRef]
- Cardoso, J.V.d.M. et al. [Lightkurve Collaboration] Lightkurve: Kepler and TESS time series analysis in Python. Astrophysics Source Code Library, record ascl:1812.013, 2018. Available online: http://ascl.net/1812.013 (accessed on 1 February 2024).
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental algorithms for scientific computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef]
- Kiss, L.L.; Derekas, A. Period Variation of XX Cygni Revisited. Inf. Bull. Var. Stars 2000, 4950, 1. [Google Scholar]
- Breger, M. Mode and period changes in pulsating stars near the main sequence: δ Scuti stars. New Astron. Rev. 1999, 43, 441–447. [Google Scholar] [CrossRef]
- Powell, J.M.; Joner, M.D.; McNamara, D.H. The Long-Term Period Variations of the SX Phoenicis Star CY Aquarii. Publ. Astron. Soc. Pac. 1995, 107, 225. [Google Scholar] [CrossRef]
- Fang, W.J.; Luo, Z.Q.; Zhang, X.B.; Deng, L.C.; Wang, K.; Luo, Y.P.; Pan, Y.; Peng, Y.J. The high-amplitude δ Scuti variable CY Aqr is probably a triple system. Res. Astron. Astrophys. 2016, 16, 96. [Google Scholar] [CrossRef]
- Rodriguez, E.; Rolland, A.; Lopez de Coca, P. Period change in GP And. Delta Scuti Star Newsl. 1993, 6, 10. [Google Scholar]
- Boonyarak, C.; Fu, J.N.; Khokhuntod, P.; Jiang, S.Y. On the period variations of several low declination high amplitude delta Scuti variables. Astrophys. Space Sci. 2011, 333, 125–131. [Google Scholar] [CrossRef]
- Li, G.; Fu, J.; Su, J.; Fox-Machado, L.; Michel, R.; Guo, Z.; Liu, J.; Feng, G. Pulsations and period variations of the δ Scuti star AN Lyncis in a possible three-body system. Mon. Not. R. Astron. Soc. 2018, 473, 398–411. [Google Scholar] [CrossRef]
- Breger, M. Pre-Main Stars. I. Light Variability, Shells, and Pulsation in NGC 2264. Astrophys. J. 1972, 171, 539. [Google Scholar] [CrossRef]
- Díaz-Fraile, D.; Rodríguez, E.; Amado, P.J. Searching for δ Scuti-type pulsation and characterising northern pre-main-sequence field stars. Astron. Astrophys. 2014, 568, A32. [Google Scholar] [CrossRef]
- Zwintz, K.; Fossati, L.; Ryabchikova, T.; Guenther, D.; Aerts, C.; Barnes, T.G.; Themeßl, N.; Lorenz, D.; Cameron, C.; Kuschnig, R.; et al. Echography of young stars reveals their evolution. Science 2014, 345, 550–553. [Google Scholar] [CrossRef]
- Zong, P.; Esamdin, A.; Fu, J.N.; Biao Niu, H.; Jie Feng, G.; Zhi Yang, T.; Hai Bai, C.; Zhang, Y.; Liu, J.Z. Pulsations of the SX Phe Star BL Camelopardalis. Publ. Astron. Soc. Pac. 2019, 131, 064202. [Google Scholar] [CrossRef]
- Deng, Z.L.; Gao, Z.F.; Li, X.D.; Shao, Y. On the Formation of PSR J1640+2224: A Neutron Star Born Massive? Astrophys. J. 2020, 892, 4. [Google Scholar] [CrossRef]
- Deng, Z.L.; Li, X.D.; Gao, Z.F.; Shao, Y. Evolution of LMXBs under Different Magnetic Braking Prescriptions. Astrophys. J. 2021, 909, 174. [Google Scholar] [CrossRef]
- Parkhurst, J.A.; Jordan, F.C. Photographic photometry of short-period variable stars. Astrophys. J. 1906, 23, 79–91. [Google Scholar] [CrossRef]
- Shapley, H.; Shapley, M.B. A study of the lightcurve of XX Cygni. Astrophys. J. 1915, 42, 148–162. [Google Scholar] [CrossRef]
- Jordan, F.C. Photographic photometry with the thirty-inch Thaw refractor: The light curves of twenty nine Cepheid variables. Publ. Allegh. Obs. Univ. Pittsburgh 1929, 7, 1–124. [Google Scholar]
- Kleissen, E. Untersuchungen über Gesetzmäßigkeiten des Lichtwechsels der RR Lyrae-Sterne. Astron. Nachrichten 1938, 267, 137. [Google Scholar] [CrossRef]
- Detre, L. XX Cygni. Astron. Nachrichten 1936, 258, 329. [Google Scholar] [CrossRef]
- Szeidl, B.; Mahdy, H.A. Period Changes in Dwarf Cepheids, II. YZ Bootis, XX Cygni and DY Herculis. Commun. Konkoly Obs. Hung. 1981, 75, 1–35. [Google Scholar]
- Fitch, W.S.; Wisniewski, W.Z.; Johnson, H.L. Photoelectric UBV observations of RR Lyr variable stars. Commun. Lunar Planet. Lab. 1966, 5, 71. [Google Scholar]
- Romano, G.; Perissinotto, M. Observations of Some Variable Stars. Inf. Bull. Var. Stars 1982, 2161, 1. [Google Scholar]
- McNamara, D.H.; Feltz, K.A. A photometric and spectrographic study of XX Cyg. Publ. Astron. Soc. Pac. 1980, 92, 195–201. [Google Scholar] [CrossRef]
- Sadun, A.C.; Ressler, M. Photometric observations of the dwarf cepheid XX Cygni. Publ. Astron. Soc. Pac. 1986, 98, 504–506. [Google Scholar] [CrossRef]
- Kim, C.; Joner, M.D. VRc Photometry of Dwarf Cepheids (I). Observation. Astrophys. Space Sci. 1994, 218, 113–135. [Google Scholar] [CrossRef]
- Acerbi, F.; Barani, C. CCD observations of the variable star of SX Phe type, XX Cyg. In Proceedings of the 27th Conference on Variable Star Research, Brno, Czech Republic, 10–12 November 1995; Zejda, M., Ed.; Astronomical Institute, Slovak Academy of Science: Tatranská Lomnica, The Slovak Republic, 1996; pp. 18–22. [Google Scholar]
- Blake, R.M.; Delaney, P.; Khosravani, H.; Tome, J.; Lightman, M. Period Changes in SX Phoenicis Stars. II. XX Cygni. Publ. Astron. Soc. Pac. 2003, 115, 212–217. [Google Scholar] [CrossRef]
- Agerer, F.; Hubscher, J. Photoelectric Minima of Selected Eclipsing Binaries and Maxima of Pulsating Stars. Inf. Bull. Var. Stars 2000, 4912, 1. [Google Scholar]
- Zhou, A.Y.; Jiang, S.Y.; Chayan, B.; Du, B.T. Amplitude and period changes in the SX Phoenicis star XX Cygni. Astrophys. Space Sci. 2002, 281, 699–714. [Google Scholar] [CrossRef]
- Hubscher, J. Photoelectric Minima of Selected Eclipsing Binaries and Maxima of Pulsating Stars. Inf. Bull. Var. Stars 2005, 5643, 1. [Google Scholar]
- Hubscher, J.; Paschke, A.; Walter, F. Photoelectric Minima of Selected Eclipsing Binaries and Maxima of Pulsating Stars. Inf. Bull. Var. Stars 2005, 5657, 1. [Google Scholar]
- Klingenberg, G.; Dvorak, S.W.; Robertson, C.W. Times of Maxima for Selected Delta Scuti Stars. Inf. Bull. Var. Stars 2006, 5701, 1. [Google Scholar]
- Hubscher, J.; Paschke, A.; Walter, F. Photoelectric Minima of Selected Eclipsing Binaries and Maxima of Pulsating Stars. Inf. Bull. Var. Stars 2006, 5731, 1. [Google Scholar]
- Biro, I.B.; Borkovits, T.; Csizmadia, S.; Hegedus, T.; Klagyivik, P.; Kiss, Z.T.; Kovacs, T.; Lampens, P.; Patkos, L.; Pal, A.; et al. New Times of Minima of Eclipsing Binary Systems and of Maximum of SXPHE Type Stars. Inf. Bull. Var. Stars 2006, 5684, 1. [Google Scholar]
- Derekas, A.; Kiss, L.L.; Bedding, T.R.; Ashley, M.C.B.; Csák, B.; Danos, A.; Fernandez, J.M.; Fűrész, G.; Mészáros, S.; Szabó, G.M.; et al. Binarity and multiperiodicity in high-amplitude δ Scuti stars. Mon. Not. R. Astron. Soc. 2009, 394, 995–1008. [Google Scholar] [CrossRef]
- Fiacconi, D.; Tinelli, L. Light curve analysis of XX Cygni from data taken using DSLR. Open Eur. J. Var. Stars 2009, 114, 1. [Google Scholar]
- Conidis, G.J.; Sadavoy, S.I.; Maxwell, A.J.; Delaney, P.A.; Manzer, L.H. Period Changes in SX Phoenicis Stars. III. XX Cygni. Publ. Astron. Soc. Pac. 2011, 123, 26. [Google Scholar] [CrossRef]
- Eggen, O.J. A New Short-Period Variable Star. Publ. Astron. Soc. Pac. 1955, 67, 354. [Google Scholar] [CrossRef]
- Broglia, P.; Masani, A. Osservazioni fotoelettriche in due colori della variabile BD + 37°2635. Mem. Soc. Astron. Ital. 1957, 28, 13. [Google Scholar]
- Spinrad, H. Photoelectric Observations of RR Lyrae Stars. Astrophys. J. 1959, 130, 539. [Google Scholar] [CrossRef]
- Broglia, P. Sui periodi di alcune variabiliti di tipo RR Lyr. Mem. Soc. Astron. Ital. 1961, 32, 7. [Google Scholar]
- Heiser, A.M.; Hardie, R.H. Three-Color Photometry of YZ Boötis. Astrophys. J. 1964, 140, 694. [Google Scholar] [CrossRef]
- Gieren, W.; Gieseking, F.; Hoffmann, M. Three-colour Photometry of the RR Lyrae-Star YZ Bootis. Astron. Astrophys. 1974, 37, 443. [Google Scholar]
- Langford, W.R. Intermediate-Band Photometry of Short Period Dwarf Cepheid Variables; Provided by the SAO/NASA Astrophysics Data System. Ph.D. Thesis, Brigham Young University, Provo, UT, USA, 1976. [Google Scholar]
- Ward, R.; Delaney, P.; Sadavoy, S.; Maxwell, A.; Senthilnathan, S.; Hsu, S. Period Changes for the β Scuti Star YZ Boo. J. R. Astron. Soc. Can. 2008, 102, 134. [Google Scholar]
- Jiang, S.Y. The period variation of YZ Boo. Acta Astron. Sin. 1985, 26, 297–300. [Google Scholar]
- Peniche, R.; Gonzalez, S.F.; Pena, J.H. Photometry and period determination of the delta Scuti star YZ Bootis. Publ. Astron. Soc. Pac. 1985, 97, 1172–1177. [Google Scholar] [CrossRef]
- Hamdy, M.A.; Mahdy, H.A.; Soliman, M.A. On the Period Variation of YZ Boo. Inf. Bull. Var. Stars 1986, 2963, 1. [Google Scholar]
- Agerer, F.; Dahm, M.; Hubscher, J. Photoelectric Minima of Selected Eclipsing Binaries and Maxima of Pulsating Stars. Inf. Bull. Var. Stars 1999, 4712, 1. [Google Scholar]
- Derekas, A.; Kiss, L.L.; Székely, P.; Alfaro, E.; Csák, B.; Mészáros, S.; Rodriguez, E.; Rolland, A.; Sárneczky, K.; Szabó, G.M.; et al. A photometric monitoring of bright high-amplitude δ Scuti stars-II. Period updates for seven stars. Astron. Astrophys. 2003, 402, 733–743. [Google Scholar] [CrossRef][Green Version]
- Agerer, F.; Hubscher, J. Photoelectric Maxima of Selected Pulsating Stars. Inf. Bull. Var. Stars 2003, 5485, 1. [Google Scholar]
- Jin, H.; Kim, S.L.; Kwon, S.G.; Youn, J.H.; Lee, C.U.; Lee, D.J.; Kim, K.S. Multiband photometric re-classification of ROTSE-I δ Scuti type stars. Astron. Astrophys. 2003, 404, 621–629. [Google Scholar] [CrossRef]
- Zhou, A.Y. Stability in period and amplitude: The High-amplitude δ Scuti Star YZ Boötis. Astrophys. Space Sci. 2006, 301, 11–20. [Google Scholar] [CrossRef]
- Splittgerber, E. 18 Maxima von GP Andromedae. Zentralinstitut Astrophys. Sternwarte Sonneb. Mitteilungen Veraenderliche Sterne 1976, 7, 137–138. [Google Scholar]
- Gieseking, F.; Hoffmann, M.; Nelles, B. Photoelectric photometry of the RRs-variable GP And. Astron. Astrophys. Suppl. 1979, 36, 457–463. [Google Scholar]
- Eggen, O.J. Intermediate Band and Hbeta Photometry of Ultrashort Period Cepheids. Inf. Bull. Var. Stars 1978, 1517, 1. [Google Scholar]
- Burchi, R.; de Santis, R.; di Paolantonio, A.; Piersimoni, A.M. Photoelectric photometry of field variables. I. Astron. Astrophys. Suppl. 1993, 97, 827–834. [Google Scholar]
- Schmidt, E.G.; Chab, J.R.; Reiswig, D.E. The Behlen Observatory Variable Star Survey. Paper III. Astron. J. 1995, 109, 1239. [Google Scholar] [CrossRef]
- Leung, K.C. Dwarf cepheid HD 199757. Astron. J. 1968, 73, 500–503. [Google Scholar] [CrossRef]
- Chambliss, C.R. Photoelectric Photometry of the Dwarf Cepheid HD 199757. Astrophys. J. 1971, 165, 365. [Google Scholar] [CrossRef]
- Balona, L.A.; Martin, W.L. The radius of the dwarf cepheid ZZ Mic. Mon. Not. R. Astron. Soc. 1978, 184, 11–15. [Google Scholar] [CrossRef][Green Version]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).