On the Yang-Mills Propagator at Strong Coupling

Abstract

About twelve years ago, the use of standard functional manipulations was demonstrated to imply an unexpected property satisfied by the fermionic Green’s functions of $QCD$. This non-perturbative phenomenon has been dubbed an effective locality. In a much simpler way than in $QCD$, the most remarkable and intriguing aspects of effective locality have been presented in a recent publication on the Yang-Mills theory on Minkowski spacetime. While quickly recalled in the current paper, these results are used to calculate the problematic gluonic propagator in the Yang-Mills non-perturbative regime. This paper is dedicated to the memory of Professor Herbert M. Fried (1929–2023), whose inspiring manner, impressive command of functional methods in quantum field theories, enthusiasm for a broad range of topics in Theoretical Physics, and warm friendship are missed greatly by the authors.

1. Introduction

A new property of QCD was discovered fourteen years ago and was named “effective locality”, or $EL$ for short [1]. In the case of QCD specifically, this property has often been phrased as follows:

For any fermionic $2n$-point Green’s functions and related amplitudes, when the full sum of all interactions is completed, the resulting structure is that of a local contact-type interaction term. This local interaction is mediated by a tensorial field which is antisymmetric both in Lorentz and colour indices. Moreover, the evoked sum happens to be gauge-invariant [2].

The $EL$ property is non-perturbative and its derivation makes it clear that it is specifically due to non-abelian structure interactions: no possible track of it could ever be found in an abelian situation.

The qualification of “effective” refers to the fact that a complete integration of elementary gluonic degrees of freedom is carried out, while “locality” refers to the unexpected contact-type resulting interaction. Does this mean that one should think of effective locality as a dual form of the originally formulated $QCD$ theory? The answer is certainly negative [3] in spite of the preliminary results obtained thirty years ago in the Euclidean Yang–Mills case and at the first non-trivial order of a semi-classical expansion [4].

Since its discovery, the property of effective locality has been explored both at theoretical and phenomenological levels. The $EL$’s first outputs appear quite interesting and mostly in line with the expected features of the $QCD$ non-perturbative regime, but also involve some new predictions, more specific to the $EL$ property itself. For example, fermionic Green’s functions have displayed an extra dependence on the trilinear Casimir operator of the $S{U}_c\left(3\right)$ algebra [2], which, however sub-leading, has elsewhere been recognised as a hallmark of the non-abelian non-perturbative regime [5]. These results have been summarised in a recent review article [2].

However, only the full $QCD$ case has been considered so far, as, in certain approximation schemes at least, the fermionic sector enjoys valuable simplifications; and also, because elementary gluon fields have been integrated out, the effective locality form presents itself under the form of an effective quark model.

Now, the full $QCD$ case somewhat obscures the most essential aspects of the $EL$ derivation, which are related to the gluonic sector of $QCD$. For example, the crucial issue of the non-abelian gauge invariance, which would posit $EL$ as a sound and most promising property, can be read off the simpler Yang-Mills case.

In a recent paper devoted to the Yang-Mills theory on Minkowski spacetime, the gluon Green’s function generating functional was derived in full detail in order to display the striking $EL$ property [6]. Concerning concrete calculations, however, the efficiency of the Yang-Mills gluon Green’s function generating functional obtained in this way can be questioned.

The goal of the current paper is therefore to rely on the generating functional derived in [6] in order to obtain insights on the first and simpler Green’s function: the non-perturbative gluon propagator in the strong coupling regime.

It may be worth recalling that the formal context of the whole matter is that of standard functional methods within Lagrangian quantum field theories [7].

The current paper is organised as follows. The next section summarises as quickly as possible the derivation of [6], while Section 3 takes advantage of it to estimate the gluonic propagator at strong coupling, with a result which clearly supports previous expectations [8]. Particular emphasis is put on the feasibility and rigour the $EL$ context offers to concrete calculations. Such an example is clearly offered by the Section 3.1, in which the quite technical calculation of the one-point Green’s function is given in detail. The final section, Section 4, concludes our paper.

Of course, Yang-Mills theory has been the focus of an impressive amount of work and publications that the present paper does not list.

2. Gluon Green’s Function Generating Functional

In this section, a brief summary of the essential steps at the origin of the effective locality form of the gluon Green’s function generating functional is given, whose full details can be found in [6].

In Minkowski spacetime, the $YM$ Lagrangian density reads

$${\mathcal{L}}_{YM}\left(x\right)=-{\displaystyle \frac{1}{4}}{F}_{\mu \nu }^a\left(x\right)F^{a\mu \nu }\left(x\right)$$

(1)

where the $F_{\mu \nu }^a\left(x\right)$ are the customary non-abelian field strength tensors:

$$F_{\mu \nu }^a\left(x\right)={\partial }_{\mu }{A}_{\nu }^a\left(x\right)-{\partial }_{\nu }{A}_{\mu }^a\left(x\right)+g{f}^{abc}{A}_{\mu }^b\left(x\right)A_{\nu }^c\left(x\right)$$

(2)

where $A_{\mu }^a\left(x\right)$ is the gluon fields—$a=(1,\cdots ,8)$—and $f^{abc}$ is the totally antisymmetric structure constants of the $S{U}_c\left(3\right)$–Lie algebra. An integration by parts yields

$$\int {\mathcal{L}}_{YM}=-{\displaystyle \frac{1}{4}}\int F^2={\displaystyle \frac{1}{2}}\int {\displaystyle A_{\mu }^a\left(x\right){\delta }^{ab}\left(g^{\mu \nu }{\partial }^2-{\partial }^{\mu }{\partial }^{\nu }\right)A_{\nu }^b\left(x\right)}+\int {\mathcal{L}}_{int}\left[A\right]$$

(3)

In a standard manner [7], this separation allows one to obtain the full gluon generating functional out of the free field one:

$$\begin{array}{ccc}\hfill Z_{YM}\left[j\right]& \equiv & {}_{\mathrm{in}}<0\left|{Te}^{{\displaystyle -i\int d^{4}x{j}_{\mu }^a\left(x\right)A_{\mu }^a\left(x\right)}}\right|0{>}_{\mathrm{in}}\hfill \\ & =& {Ne}^{{\displaystyle i\int {\mathrm{d}}^{4}x{\mathcal{L}}_{\mathrm{int}}\left[i\frac{\delta }{\delta j_{\rho }^c\left(x\right)}\right]}}{e}^{{\displaystyle -\frac{i}{2}\int {\mathrm{d}}^{4}x{\mathrm{d}}^{4}y{j}_{\mu }^a\left(x\right)D_{ab}^{\mu \nu }(x-y)j_{\nu }^b\left(y\right)}}\hfill \end{array}$$

(4)

where the constant N is such that $Z_{YM}\left[0\right]=1$, and provided that the distribution $D_{ab}^{\mu \nu }(x-y)$ exists. Now, this is the point, because $D_{ab}^{\mu \nu }$ is supposed to satisfy the equation

$${\displaystyle \left[g^{\mu \rho }{\partial }_x^2-{\partial }_x^{\mu }{\partial }_x^{\rho }\right]D_{\rho }^{ab\nu }(x-y)=g^{\mu \nu }{\delta }^{ab}{\delta }^{\left(4\right)}(x-y)}$$

(5)

As is well known, the operator ${\partial }^2-\partial \otimes \partial$ cannot be inverted and $D_{ab}^{\mu \nu }$ is accordingly not defined. In $QED$ as well as in perturbative $QCD$, solutions to this problem are well known, preserving Lorentz invariance and breaking momentarily the local gauge invariance of ${\mathcal{L}}_{YM}$ by means of a gauge-fixing term. In a second step, local gauge invariance is restored and checked through the Ward–Takahashi and Slavnov–Taylor identities satisfied by Green’s functions, in the respective cases of $QED$ and $QCD$. These are textbook materials and define the well-controlled perturbative framework of these theories.

Now, the non-abelian structure of ${\mathcal{L}}_{YM}$ offers a possibility which has no abelian equivalent. For example, adding and subtracting a term to (1),1

$${\mathcal{L}}_{YM}⟶{\mathcal{L}}_{YM}+{\displaystyle \frac{1}{2\zeta }}{(\partial ·A)}^2-{\displaystyle \frac{1}{2\zeta }}{(\partial ·A)}^2$$

(6)

the original full gauge invariance of (1) is obviously preserved, while one of the two extra terms of (6) can be used to turn the undefined expression of (5) into the well-defined covariant propagator: $D_{\mathrm{F}}^{\left(\zeta \right)}$

$${\left({D_{\mathrm{F}}^{\left(\zeta \right)}}^{-1}\right)}_{\mu \nu }^{ab}={\delta }^{ab}\left[g_{\mu \nu }{\partial }^2-\left(1-{\displaystyle \frac{1}{\zeta }}\right){\partial }_{\mu }{\partial }_{\nu }\right]$$

(7)

Then, using (3) to re-express the density of interaction ${\mathcal{L}}_{int.}$, one arrives at

$$\begin{array}{c}\hfill Z_{YM}\left[j\right]=N{\left.e^{{\displaystyle -\frac{i}{4}\int F^2-\frac{i}{2}\int {\displaystyle A_{\mu }^a\left(x\right)\left(g^{\mu \nu }{\partial }^2-(1-\frac{1}{\zeta }){\partial }^{\mu }{\partial }^{\nu }\right)A_{\nu }^a\left(x\right)}}}\right|}_{{\displaystyle A=\frac{1}{i}\frac{\delta }{\delta j}}}{e}^{{\displaystyle -\frac{i}{2}\int j·D_{\mathrm{F}}^{\left(\zeta \right)}·j}}\end{array}$$

(8)

A convenient rearrangement of (8) can be obtained in a standard functional way [7]:

$$\begin{array}{ccc}\hfill Z_{YM}\left[j\right]& =& N{e}^{{\displaystyle -\frac{i}{2}\int j·D_{\mathrm{F}}^{\left(\zeta \right)}·j}}\hfill \\ & ·& {\left.e^{{\displaystyle {\mathfrak{D}}_A^{\left(\zeta \right)}}}{e}^{{\displaystyle -\frac{i}{4}\int F^2-\frac{i}{2}\int A·{\left(D_{\mathrm{F}}^{\left(\zeta \right)}\right)}^{-1}·A}}\right|}_{{\displaystyle A=\int D_{\mathrm{F}}^{\left(\zeta \right)}·j}}\hfill \end{array}$$

(9)

where the functional operator $exp{\mathfrak{D}}_A$ reads

$$exp{\mathfrak{D}}_A^{\left(\zeta \right)}=exp{\displaystyle \frac{i}{2}}\int {\mathrm{d}}^{4}x\int {\mathrm{d}}^{4}y{\displaystyle \frac{\delta }{\delta A\left(x\right)}}·D_{\mathrm{F}}^{\left(\zeta \right)}(x-y)·{\displaystyle \frac{\delta }{\delta A\left(y\right)}}$$

(10)

In order to proceed with doable exact calculations, one must introduce a “linearisation” of the $\int F^2$ term, which appears in the right-hand side of (9). This is achieved by using the famous Halpern’s representation [9] (also known as the Hubbard–Stratonovich transformation in solid state physics [10,11]), which rests on the introduction of eight antisymmetric-in-spacetime indices $\mu$ and $\nu$, and tensor fields ${\chi }_{\mu \nu }^a\left(x\right)$, $a=(1,\cdots ,8)$:

$$e^{{\displaystyle -\frac{i}{4}\int F^2}}=N^{\prime }\int \mathrm{d}\left[\chi \right]e^{{\displaystyle \frac{i}{4}\int {\chi }_{\mu \nu }^a{\chi }^{a\mu \nu }+\frac{i}{2}\int {\chi }^{a\mu \nu }{F}_{\mu \nu }^a}}$$

(11)

allowing one to bring (9) into the form

$$\begin{array}{ccc}\hfill Z_{YM}\left[j\right]& =& \mathcal{N}{e}^{{\displaystyle -\frac{i}{2}\int j·D_{\mathrm{F}}^{\left(\zeta \right)}·j}}\int \mathrm{d}\left[\chi \right]e^{{\displaystyle \frac{i}{4}\int {\chi }_{\mu \nu }^a{\chi }^{a\mu \nu }}}\hfill \\ & ·& {\left.e^{{\displaystyle {\mathfrak{D}}_A^{\left(\zeta \right)}}}{e}^{{\displaystyle \frac{i}{2}\int \chi ·F-\frac{i}{2}\int A·{\left(D_{\mathrm{F}}^{\left(\zeta \right)}\right)}^{-1}·A}}\right|}_{{\displaystyle A=\int D_{\mathrm{F}}^{\left(\zeta \right)}·j}}\hfill \end{array}$$

(12)

where $\mathcal{N}=N{N}^{\prime }$, and (12) yields, as a final result, the gluon Green’s function generating functional of [6]

$$\begin{array}{cc}\hfill & {\displaystyle Z_{YM}\left[j\right]=\mathcal{N}\int \mathrm{d}\left[\chi \right]e^{{\displaystyle \frac{i}{4}\int {\chi }_{\mu \nu }^a{\chi }^{a\mu \nu }}}{\left[det\left(gf\chi \right)\right]}^{-\frac{1}{2}}}\\ & ·e^{{\displaystyle -\frac{i}{2}\int {\mathrm{d}}^{4}x\left(j_{\mu }^a\left(x\right)+{\partial }^{\lambda }{\chi }_{\lambda \mu }^a\right)\left(x\right){\left[{\left(gf\chi \right)}^{-1}\right]}_{ab}^{\mu \nu }\left(x\right)\left(j_{\nu }^b\left(x\right)+{\partial }^{\sigma }{\chi }_{\sigma \nu }^b\right)\left(x\right)}}\end{array}$$

(13)

The normalisation condition $Z_{YM}\left[0\right]=1$ leads to

$${\mathcal{N}}^{-1}=\int \mathrm{d}\left[\chi \right]e^{{\displaystyle \frac{i}{4}\int {\chi }_{\mu \nu }^a{\chi }^{a\mu \nu }}}{\left[det\left(gf\chi \right)\right]}^{-{\displaystyle \frac{1}{2}}}{e}^{{\displaystyle -\frac{i}{2}\int {\mathrm{d}}^{4}x{\partial }^{\lambda }{\chi }_{\lambda \mu }^a\left(x\right){\left[{\left(gf\chi \right)}^{-1}\right]}_{ab}^{\mu \nu }\left(x\right){\partial }^{\sigma }{\chi }_{\sigma \nu }^b\left(x\right)}}$$

(14)

One may note that the form (13) is not completely unknown. This was observed more than thirty years ago in an attempt at deriving a form dual to (1) within an instanton-based calculation [4]; but most importantly, a final integration on the same $\chi$-field remained constrained by a gauge-fixing condition with all of the ensuing well-known complications [12].

3. Insights Obtained Out of the Effective Locality ${\mathit{Z}}_{\mathit{YM}}\left[\mathit{j}\right]$

One may expect the effective locality $Z_{YM}\left[j\right]$ to provide interesting informations on the strong coupling non-perturbative regime of the $YM$ theory, and to lend itself to tractable calculations. This is what is investigated in the present section.

3.1. Calculation of $\langle A_a^{\mu }\left(x\right)\rangle$

This example will pave the route to the next section’s considerations and set up the framework of effective locality calculations, while exhibiting the rigour of the calculation’s developments offered by the $EL$ context.

3.1.1. Presentation

From (13), one obtains the “one-point” Green’s function by means of one functional differentiation over $Z_{YM}$:

$$\begin{array}{c}{\displaystyle {\displaystyle \langle A_a^{\mu }\left(x\right)\rangle }=i\frac{\delta }{\delta j_{\mu }^a\left(x\right)}{Z}_{YM}\left[j\right]{|}_{j=0}=\mathcal{N}\int d\left[\chi \right]e^{{\displaystyle \frac{i}{4}\int d^{4}u{\left({\chi }_{\mu \nu }^a\left(u\right)\right)}^2}}{\left[det\left(gf\chi \right)\right]}^{-\frac{1}{2}}}\\ {\displaystyle ·\frac{1}{g}{\partial }_{\alpha }{\chi }_{\alpha \nu }^b\left(x\right){\left[{\left(f\chi \right)}^{-1}\right]}_{\nu \mu }^{ba}\left(x\right)e^{{\displaystyle -\frac{i}{2}\int d^{4}u{\partial }_{\alpha }{\chi }_{\alpha \mu }^a\left(u\right){\left[{\left(gf\chi \right)}^{-1}\right]}_{\mu \nu }^{ab}\left(u\right){\partial }_{\beta }{\chi }_{\beta \nu }^b\left(u\right)}}}\hfill \end{array}$$

(15)

Calculating (15) is a formidable task which could be undertaken in a future publication. For the current purpose, it is put to a more accessible form in the limit of strong coupling, $g>>1$. This is particularly consistent with the non-perturbative regime inherent to the $EL$ property and its (partial) duality aspect [6]. As will be proven elsewhere in the case of $QCD$, at a first non-trivial order at least, this property allows one to rely on an ultraviolet and infrared well-behaved expansion in power of $g^{-1}$.

At strong coupling, only the term of order $g^{-1}$ will be kept. The exponential, expanded in power of $g^{-1}$, is therefore taken to unity. At leading order, $\langle A\rangle$ reads

$${\displaystyle {\displaystyle \langle A_a^{\mu }\left(x\right)\rangle }={\mathcal{N}}_1\int d\left[\chi \right]e^{{\displaystyle \frac{i}{4}\int d^{4}u{\left({\chi }_{\mu \nu }^a\left(u\right)\right)}^2}}{\left[det\left(gf\chi \right)\right]}^{-\frac{1}{2}}\left(\frac{1}{g}\right){\partial }^{\alpha }{\chi }_{\alpha \lambda }^c\left(x\right){\left[{\left(f\chi \right)}^{-1}\right]}_{ca}^{\lambda \mu }\left(x\right)}$$

(16)

At the same order of approximation, the normalisation is

$${\mathcal{N}}_1^{-1}=\int \mathrm{d}\left[\chi \right]e^{{\displaystyle \frac{i}{4}\int {\chi }_{\mu \nu }^a{\chi }^{a\mu \nu }}}{\left[det\left(gf\chi \right)\right]}^{-{\displaystyle \frac{1}{2}}}$$

(17)

3.1.2. A Few Formal Steps: The Matrix $\mathbb{M}$

To proceed with concrete calculations, a series of previous analyses summarised in [2] have proven that it is convenient to take advantage of (an analytically continued) Random Matrix integration [13] of (16) and (17). This is achieved by defining the hermitian matrix:

$${\displaystyle \mathbb{M}\left(x\right)=i\sum _{a=1}^8{\chi }^a\left(x\right)\otimes T^a}$$

(18)

where ${\chi }^a$ represents the $4\times 4$ antisymmetric matrices of matrix elements, ${\chi }_{\mu \nu }^a$. The $T^a$s are the eight Lie algebra generators of $S{U}_c\left(3\right)$ taken in the $8\times 8$ dimensional adjoint representation, where the matrix representation of these hermitian generators is given by the $S{U}_c\left(3\right)$–Lie algebra structure constants:

$${\left(T^a\right)}^{bc}=-i{f}^{abc}$$

(19)

Equations (18) and (19) lead to

$${\left(\mathbb{M}\right)}_{ab}^{\mu \nu }={\left(f\chi \right)}_{ab}^{\mu \nu }$$

(20)

One has now replaced the unmanageable ${\left(f\chi \right)}_{ab}^{\mu \nu }$ term, and its $\chi$ integration, by an algebraic quantity that will turn out to be effective for computational purposes.

So, $\mathbb{M}$ is the sum of eight matrices, each of them being composed of $4\times 4$ blocks of dimension $8\times 8$. Its elements have the form ${\left(\mathbb{M}\right)}_{ab}^{\mu \nu }$ with both pairs of indices being antisymmetric. Nonetheless, $\mathbb{M}$ turns out to be a real, traceless, symmetric matrix, of dimension $N\times N$, that is $32\times 32$, at $D=4$ spacetime dimensions and $N_c=3$ colours, with $N=D(N_c^2-1)$.

Being a real symmetric matrix, $\mathbb{M}\left(x\right)$ can be diagonalised, $\mathbb{M}\left(x\right)={}^t\mathcal{O}\left(x\right)D\left(x\right)\mathcal{O}\left(x\right)$, where ${}^t\mathcal{O}\left(x\right)$ is the transpose of $\mathcal{O}\in O_N\left(\mathbb{R}\right)$, the orthogonal group, and where the matrix $D\left(x\right)$ is the real diagonal matrix $D\left(x\right)=\mathrm{diag}\left({\xi }_1,{\xi }_2,\dots ,{\xi }_{N-1},{\xi }_N\right)$. Formally, one also has ${\mathbb{M}}^{-1}={}^t\mathcal{O}\left(x\right)D^{-1}\left(x\right)\mathcal{O}\left(x\right)$ with $D^{-1}\left(x\right)=\mathrm{diag}\left({{\xi }_1}^{-1},{{\xi }_2}^{-1},\dots ,{{\xi }_{N-1}}^{-1},{{\xi }_N}^{-1}\right)$. With $\mathbb{M}\left(x\right)$ such as defined above, it is easy to check that for all point x in $\mathcal{M}$, the eigenvalue $\xi =0$ belongs to the spectrum of $\mathbb{M}\left(x\right)$; this, however, will not induce difficulties in the subsequent integration processes [2].

As displayed in (23), the property of effective locality allows one to transform the initial functional measure of integration $\mathrm{d}\left[\chi \right]$ into the product of an integration on the spectrum of $\mathbb{M}$, $\mathrm{Sp}\left(\mathbb{M}\right)$, times an integration on the orthogonal group $O_N\left(\mathbb{R}\right)$; symbolically,

$$\mathrm{d}\left[\chi \right]⟶\mathrm{d}\mathrm{Sp}\left(\mathbb{M}\right)\times \mathrm{d}{O}_N\left(\mathbb{R}\right)$$

(21)

In this way, in effect, the symbolic functional measure of integration $\mathrm{d}\left[\chi \right]$ with

$$\int \mathrm{d}\left[\chi \right]=\prod _{z\in \mathcal{M}}\prod _{a=1}^{N_c^2-1}\prod _{0=\mu <\nu }^3\int \mathrm{d}\left[{\chi }_{\mu \nu }^a\left(z\right)\right],$$

(22)

where $\mathcal{M}$ is the spacetime manifold, is turned into a well-defined measure of integration on the finite dimensional space of $\mathbb{M}$ matrices:

$$\begin{array}{ccc}\hfill \mathrm{d}\left(i\sum _{a=1}^8{\chi }^a\left(x\right)\otimes T^a\right)& \equiv & \mathrm{d}\mathbb{M}\left(x\right)=\mathrm{d}{M}_{11}\mathrm{d}{M}_{12}\cdots \mathrm{d}{M}_{NN}\hfill \\ & =& \left|{\displaystyle \frac{\partial (M_{11},\cdots ,M_{NN})}{\partial ({\xi }_1,\cdots ,{\xi }_N,p_1,\cdots ,p_{N(N-1)/2})}}\right|\mathrm{d}{\xi }_1\cdots \mathrm{d}{\xi }_N\mathrm{d}{p}_1\cdots \mathrm{d}{p}_{N(N-1)/2}\hfill \\ & =& \prod _{i=1}^N\mathrm{d}{\xi }_i\prod _{1\le i<j}^N{|{\xi }_i-{\xi }_j|}^{\beta }\mathrm{d}{p}_1..\mathrm{d}{p}_{N(N-1)/2}f\left(\mathbf{p}\right)\hfill \end{array}$$

(23)

In this equation, $\beta =1$, and the very last factors of (23) stand for a Haar measure of integration on the orthogonal group $O_N\left(\mathbb{R}\right)$.

Note that in (23), the value $\beta =1$ could be quite concerning as it seems to compromise the analyticity. This is not so, however, because it turns out that the matrix $\mathbb{M}$ also possesses eigenvalue spectra formed of $N/2$ pairs of equal and opposite eigenvalues. For instance, they can be ordered in the following way:

$$\mathrm{Sp}\mathbb{M}=\left\{({\xi }_i,{\xi }_{N-i+1}=-{\xi }_i)\right\},\forall i=1,2,\dots ,N/2.$$

(24)

Taking this property into account, the apparently non-analytic Vandermonde determinant can be rewritten as

$$\begin{array}{c}\hfill \prod _{1\le i<j}^N{|{\xi }_i-{\xi }_j|}^{\beta }={\left[\prod _{i=1}^{N/2}2\left|{\xi }_i\right|\right]}^{\beta }{\left[\prod _{1\le i<j}^{N/2}{({\xi }_i^2-{\xi }_j^2)}^2\right]}^{\beta }\end{array}$$

(25)

which, even at $\beta =1$, will give rise to an analytic function of its eigenvalues because the first term in the right-hand side of (25), involving absolute values, is exactly compensated by the term ${\left[det\left(gf\chi \right)\right]}^{-{\displaystyle \frac{1}{2}}}$. This applies to both (16) and (17).

3.1.3. Calculating $\langle A_a^{\mu }\left(x\right)\rangle$

Referring to $\langle A_a^{\mu }\left(x\right)\rangle$, once one has replaced ${\left(f\chi \right)}_{ab}^{\mu \nu }\left(x\right)$ by ${\left(\mathbb{M}\right)}_{ab}^{\mu \nu }$ in (16), one needs to then deal with the ${\partial }^{\alpha }{\chi }_{\alpha \beta }^a\left(x\right)$ term that has to be expressed in the function of $\mathbb{M}$ as well.

From definition (18) and (19), one can prove (and easily check in the simpler case of $SU\left(2\right)$) the following relation:

$${\chi }_{\alpha \lambda }^c\left(x\right)={\displaystyle \frac{1}{N_c}}\mathrm{Tr}\left[\mathbb{M}\left(x\right)\left({\mathbb{I}}_{\alpha \lambda }\otimes i{T}^c\right)\right]$$

(26)

where the $4\times 4$ matrix ${\mathbb{I}}_{\alpha \lambda }$ has null matrix elements except for the element at row $\alpha$ and column $\lambda$, which has a value of 1. In view of the antisymmetry of ${\chi }_{\alpha \lambda }^c$, one necessarily has $\alpha \ne \lambda$. The matrix ${\mathbb{I}}_{\alpha \lambda }$ is therefore non-symmetric, guaranteeing the non-triviality of (26), and has zeros on its diagonal:

$${\left({\mathbb{I}}_{\alpha \lambda }\right)}^{\rho \rho }=0,\forall \rho =0,1,2,3.$$

(27)

In order to provide calculations with a convenient covariant-like form, it is appropriate to pass from the $\mu ,\nu =0,1,2,3$ spacetime indices and the $a,b=1,2,\dots ,8$ colour indices to indices of an enlarged linear space2 of dimension $4\times 8=32$3, on which matrices $\mathbb{M}\left(x\right)$ would operate as endomorphisms. One can define the covariant indices i and r4:

$$i\equiv a+\mu n,r\equiv c+\lambda n,n\equiv N_c^2-1=8,i,r=1,2,\dots ,32$$

(28)

and these new indices relate to the previous ones through the one-to-one mapping:

$$(\mu ,a)\to i=a+\mu n,i\to (\mu ={\displaystyle \frac{i-i_{m^{\left(o\right)}n}}{n}},a=i_{m^{\left(o\right)}n}),$$

(29)

where the notation $i_{m^{\left(o\right)}n}$ stands for i modulo n. The last terms of (16) can now be rewritten as

$${\displaystyle \frac{1}{g{N}_c}}{\left[\mathbb{M}{\left(x\right)}^{-1}\right]}_{ca}^{\lambda \mu }{\partial }^{\alpha }\mathrm{Tr}\left(\mathbb{M}\left(x\right){\mathbb{P}}_{\alpha \lambda }^c\right)={\displaystyle \frac{1}{g{N}_c}}{\left[\mathbb{M}{\left(x\right)}^{-1}\right]}^{ir}{\partial }^{\alpha }\mathrm{Tr}\left(\mathbb{M}\left(x\right){\mathbb{P}}_{\alpha }^r\right)$$

(30)

where shorthands ${\mathbb{P}}_{\alpha \lambda }^c$ and ${\mathbb{P}}_{\alpha }^r$ are introduced for the $N\times N$ matrix ${\mathbb{I}}_{\alpha \lambda }\otimes i{T}^c$, which achieves the projection of $\mathbb{M}\left(x\right)$ on ${\chi }_{\alpha \lambda }^c\left(x\right)$ according to (26). In view of (27), one also has

$${\left({\mathbb{P}}_{\alpha }^r\right)}^{ii}=0,\forall i=1,2,\dots ,32.$$

(31)

The right-hand side of Equation (30) can be written as

$${\displaystyle \frac{1}{g{N}_c}}\left[{\left({}^t\mathcal{O}\right)}^{iu}\left({\displaystyle \frac{{\delta }^{us}}{{\xi }_s}}\right){\mathcal{O}}^{sr}\right]{\partial }^{\alpha }\left[{\left({}^t\mathcal{O}\right)}^{hk}\left({\delta }^{kl}{\xi }_k\right){\mathcal{O}}^{lm}{\left({\mathbb{P}}_{\alpha }^r\right)}^{mh}\right]$$

(32)

where the orthogonal matrix $\mathcal{O}$ and eigenvalues ${\xi }_{i}s$ are taken at $x\in \mathcal{M}$ and all the indices except i are summed over.

Carrying out the discrete summations on u and l in (32), one obtains

$${\displaystyle \frac{1}{g{N}_c}}{\left[\mathbb{M}{\left(x\right)}^{-1}\right]}^{ir}{\partial }^{\alpha }\mathrm{Tr}\left(\mathbb{M}\left(x\right){\mathbb{P}}_{\alpha }^r\right)={\displaystyle \frac{1}{g{N}_c}}\left[{\mathcal{O}}^{si}{\displaystyle \frac{1}{{\xi }_s}}{\mathcal{O}}^{sr}\right]{\partial }^{\alpha }\left[{\xi }_k{\mathcal{O}}^{kh}{\mathcal{O}}^{km}{\left({\mathbb{P}}_{\alpha }^r\right)}^{mh}\right].$$

(33)

The ${\partial }^{\alpha }$ derivatives must be taken before integration on $O_N\left(\mathbb{R}\right)$ and $\mathrm{Sp}\left(\mathbb{M}\right)$, and bear on ${\mathcal{O}}^{kh}{\mathcal{O}}^{km}\left(x\right)$ and on ${\xi }_k\left(x\right)$.

In both cases, in order to proceed, it will be essential to work on a basis where the orthogonal matrix is block diagonal, the blocks being $2\times 2$ matrices of rotation in 2-dimensional subspaces mutually orthogonal to each other. The orthonormal basis of the $\mathbb{M}\left(x\right)$ matrix eigenvectors can be used, where $\mathbb{M}\left(x\right)$ can be expanded as ${\sum }_{k=1}^N{\xi }_k{u}_k{}^{t}u_k$, and the basis vectors re-ordered in such a way that in the newly ordered proper basis, one has $\mathbb{M}\left(x\right)=diag\left(({\xi }_1,{\xi }_2=-{\xi }_1),({\xi }_3,{\xi }_4=-{\xi }_3),\dots ,({\xi }_{N-1},{\xi }_N=-{\xi }_{N-1})\right)$. A linear algebra theorem [14] then asserts that $N/2$ angles exist, ${\Theta }_i=1,3,5,\dots N-1$ such that each of them parametrises a rotation or an inversion in a given 2-dimensional subspace.

For example, in the subspace spanned by the two eigenvectors $u_{2k+1},u_{2k+2}$ corresponding to the eigenvalues ${\xi }_{2k+1}$ and ${\xi }_{2k+2}=-{\xi }_{2k+1}$, one will have the $2\times 2$ rotation $R\left({\Theta }_{2k+1}\right)$, or the inversion $I\left({\Theta }_{2k+1}\right)$, as the $(k+1)$-th block diagonal matrix representing, in this basis, the orthogonal matrix $\mathcal{O}$, with $0\le k\le N/2-1$.

$$\begin{array}{ccccccc}0& \dots & 0& cos{\Theta }_{2k+1}-sin{\Theta }_{2k+1}& 0& \dots & 0\\ 0& \dots & 0& sin{\Theta }_{2k+1}cos{\Theta }_{2k+1}& 0& \dots & 0\\ 0& \dots & 0& 0& 0& \ddots \\ 0& \dots & 0\end{array}$$

(34)

Each row and each column of the orthogonal matrix $\mathcal{O}$, contains only two non-zero coefficients that are either $cos{\Theta }_{2k+1}$ and $-sin{\Theta }_{2k+1}$ or $cos{\Theta }_{2k+1}$ and $sin{\Theta }_{2k+1}$, in both cases of a rotation and an inversion, whose matrix reads as

$$I\left({\Theta }_{2k+1}\right)=\left(\begin{array}{c}cos{\Theta }_{2k+1}sin{\Theta }_{2k+1}\\ sin{\Theta }_{2k+1}-cos{\Theta }_{2k+1}\end{array}\right)$$

Referring to (33), a first contribution of ${\partial }^{\alpha }$ acting on ${\xi }_k$ only is thus given by the expression

$${\displaystyle \frac{1}{g{N}_c}}\left[{\displaystyle \frac{{\partial }^{\alpha }{\xi }_k}{{\xi }_i}}\right]\left[O^{ii}{O}^{ir}{O}^{kh}{O}^{km}\right]{\left({\mathbb{P}}_{\alpha }^r\right)}^{mh},$$

(35)

Integration on $O_N\left(\mathbb{R}\right)$ can be performed—see [2] for instance—yielding

$$\left[{\partial }^{\alpha }ln{\xi }_i\right]\left[{\delta }^{ir}{\delta }^{hm}+{\delta }^{ih}{\delta }^{rm}+{\delta }^{im}{\delta }^{rh}\right]{\left({\mathbb{P}}_{\alpha }^r\right)}^{mh}=\left[{\partial }^{\alpha }ln{\xi }_i\right]\sum _r\left[{\left({\mathbb{P}}_{\alpha }^r\right)}^{ri}+{\left({\mathbb{P}}_{\alpha }^r\right)}^{ir}\right],$$

(36)

where (31) is used for the first couple of $\delta$-constraints. For the two remaining terms in the right-hand side of (36), one has

$${\left({\mathbb{P}}_{\alpha }^r\right)}^{ri}={\left({\mathbb{P}}_{\alpha }^r\right)}^{ir}=0$$

(37)

This can be proven by inspection. The index i is fixed and choices of indices $\alpha$ and $\lambda$ can be made among $(16-4=12)/2=6$ possibilities. A given choice of $\alpha$ and $\lambda$ allows for deciding the location of the $8\times 8$ matrix $T^c$, among the sixteen $8\times 8$ blocks composing the full projector ${\mathbb{P}}_{\alpha \lambda }^c$, with the diagonal being excluded5.

The matrix elements of $\left({\mathbb{P}}_{\alpha }^r\right)={\mathbb{P}}_{\alpha \lambda }^c$ with entries $ir$ or $ri$ are either zero systematically (see the endnote above), or non-zero a priori. In this latter case, however, at entries $ir$ or $ri$, the matrix elements of ${\mathbb{P}}_{\alpha \lambda }^c$ coincide with elements of the matrix of $T^c$, taken at two identical entries and this is zero by antisymmetry of the generators $T^c$. This is seen as follows. One has, for all index i, for all $c=1,2,\dots ,8,$ and all $r=1,2,\dots ,N$,

$$r=c+\lambda n⟺r=cm{}^{\left(o\right)}n⟹{\left({\mathbb{P}}_{\alpha \lambda }^c\right)}^{ir}={\left(T^c\right)}^{ic}=0,$$

(38)

In the specific case of $\alpha =2$ and $\lambda =1$, for instance, ${\left({\mathbb{P}}_{\alpha \lambda }^c\right)}^{ir}$ is identically 0 by construction, in the most trivial situation where $i>8$. This is why in the last term of (38), the “covariant” index i is preserved, in a somewhat hybrid way, instead of $im{}^{\left(o\right)}n$ of (28). This applies identically to the reverse entries $ri$.

The other contribution to (33) reads

$${\displaystyle \frac{1}{g{N}_c}}{O}^{si}{O}^{sr}{\partial }^{\alpha }{O}^{sh}{O}^{sm}{\left({\mathbb{P}}_{\alpha }^r\right)}^{mh}$$

(39)

This reduction of (33)–(39) is due to the fact that if $k\ne s$, then the odd character of the ${\xi }_k$-integration yields a vanishing result6.

Now, with the index i fixed, the sum on $s,h,m$ in (39) is very restricted; for an even value of i, one obtains in effect,

$$O^{i-1,i}{O}^{i-1,i-1}{\partial }^{\alpha }{O}^{i-1,i}{O}^{i-1,i-1}{\left({\mathbb{P}}_{\alpha }^{i-1}\right)}^{i-1,i}+O^{ii}{O}^{i,i-1}{\partial }^{\alpha }{O}^{ii}{O}^{i,i-1}{\left({\mathbb{P}}_{\alpha }^{i-1}\right)}^{i,i-1}=0$$

(40)

and a similar expression for an odd value of index i,

$$O^{ii}{O}^{i,i+1}{\partial }^{\alpha }{O}^{ii}{O}^{i,i+1}{\left({\mathbb{P}}_{\alpha }^{i+1}\right)}^{i,i+1}+O^{i+1,i}{O}^{i+1,i+1}{\partial }^{\alpha }{O}^{i+1,i}{O}^{i+1,i+1}{\left({\mathbb{P}}_{\alpha }^{i+1}\right)}^{i,i+1}=0.$$

(41)

Both expressions cancel each other because of (38), but would also yield a vanishing result upon integration over the angles ${\Theta }_{2k+1}$. At the end, because of (36), (37), (40), and (41), one finds

$$\langle A_a^{\mu }\left(x\right)\rangle =0,$$

(42)

as is expected [15].

3.2. The Yang-Mills Propagator at Strong Coupling

3.2.1. Presentation

The gluon 2-point Green’s function is obtained from (13) by means of two functional differentiations:

$${\displaystyle \langle T\left(A_{\mu }^a\left(x\right)A_{\nu }^b\left(y\right)\right)\rangle =i\frac{\delta }{\delta j_{\mu }^a\left(x\right)}i\frac{\delta }{\delta j_{\nu }^b\left(y\right)}{\mathcal{Z}}_{YM}\left[j\right]{|}_{j=0}}$$

(43)

and, accordingly, reads

$$\begin{array}{cc}\hfill & {\displaystyle \langle T\left(A_{\mu }^a\left(x\right)A_{\nu }^b\left(y\right)\right)\rangle =\mathcal{N}\int \mathrm{d}\left[\chi \right]e^{{\displaystyle \frac{i}{4}\int {\chi }_{\mu \nu }^a{\chi }^{a\mu \nu }}}{\left[det\left(gf\chi \right)\right]}^{-\frac{1}{2}}}\\ & ·\left[i{\left[{\left(gf\chi \right)}^{-1}\right]}_{\mu \nu }^{ab}\left(x\right){\delta }^{\left(4\right)}(x-y)+{\partial }^{\alpha }{\chi }_{\alpha \lambda }^c\left(x\right){\left[{\left(gf\chi \right)}^{-1}\right]}_{\lambda \mu }^{ca}\left(x\right){\partial }^{\beta }{\chi }_{\beta \rho }^d\left(y\right){\left[{\left(gf\chi \right)}^{-1}\right]}_{\rho \nu }^{db}\left(y\right)\right]\\ & ·e^{{\displaystyle -\frac{i}{2}\int {\mathrm{d}}^{4}x{\partial }^{\lambda }{\chi }_{\lambda \mu }^a\left(x\right){\left[{\left(gf\chi \right)}^{-1}\right]}_{ab}^{\mu \nu }\left(x\right){\partial }^{\sigma }{\chi }_{\sigma \nu }^b\left(x\right)}}\end{array}$$

(44)

At strong coupling, the first term in the squared brackets is of order $g^{-1}$, while the second term is of order $g^{-2}$ and is thus a sub-leading correction. The leading-order gluon propagator is therefore given by the simpler expression

$$\langle T\left(A_{\mu }^a\left(x\right)A_{\nu }^b\left(y\right)\right)\rangle ={\mathcal{N}}_1{\displaystyle \frac{i}{g}}{\delta }^{\left(4\right)}(x-y)\int \mathrm{d}\left[\chi \right]e^{{\displaystyle \frac{i}{4}\int {\chi }_{\mu \nu }^a{\chi }^{a\mu \nu }}}{\left[det\left(gf\chi \right)\right]}^{-{\displaystyle \frac{1}{2}}}{\left[{\left(f\chi \right)}^{-1}\right]}_{\mu \nu }^{ab}\left(x\right)$$

(45)

where the exponential, expanded in power of $g^{-1}$, is therefore taken to unity and the normalisation factor ${\mathcal{N}}_1$ given by (17).

That is, if the right-hand sides of both (45) and (17) are well defined, then the leading-order contribution (45) to the $YM$ gluon propagator at strong coupling would indicate an absence of propagation and a possible gluon condensate; as recalled in our concluding remarks, the importance of this conclusion has been analysed and stressed in [8] in regard to the crucial non-perturbative properties of mass gap [16] and quark confinement.

3.2.2. Using the Matrix $\mathbb{M}$

Obviously, the $\chi$ integral of (45) differs from that of (16), with the divergence term ${\partial }^{\alpha }{\chi }_{\alpha \lambda }^c\left(x\right)$ being absent in (45). This will lead to very different kinds of computations between $\langle A_a^{\mu }\left(x\right)\rangle$ and $\langle T\left(A_{\mu }^a\left(x\right)A_{\nu }^b\left(y\right)\right)\rangle$.

For (17) and (45), the integration on the functional space of ${\chi }_{\mu \nu }^a$ field configurations is now translated into an integration on $\mathbb{M}$, as in the previous section, and using Formulas (20)–(25), one obtains

$$\begin{array}{c}\hfill \langle T\left(A_{\mu }^a\left(x\right)A_{\nu }^b\left(y\right)\right)\rangle ={\mathcal{N}}_1{\displaystyle \frac{i}{g}}{\delta }^{\left(4\right)}(x-y){\displaystyle \frac{1}{g^{N/2}}}\prod _{i=1}^N{\int }_{-\infty }^{+\infty }{\displaystyle \frac{\mathrm{d}{\xi }_i}{\sqrt{{\xi }_i}}}\prod _{i=1}^{N/2}\delta ({\xi }_i+{\xi }_{N-i+1})\\ \hfill ·\prod _{j=1}^{N/2}2\left|{\xi }_j\right|\prod _{1\le k<l}^{N/2}{({\xi }_k^2-{\xi }_l^2)}^2{e}^{{\displaystyle \frac{i}{8N_c}\sum _1^N\Delta {\xi }_i^2}}{\int }_{O_N\left(\mathbb{R}\right)}\mathrm{d}O{\left({\mathbb{M}}^{-1}\left(x\right)\right)}_{\mu \nu }^{ab},\end{array}$$

(46)

and in the same way, for (17),

$$\begin{array}{c}\hfill {\mathcal{N}}_1^{-1}={\displaystyle \frac{1}{g^{N/2}}}\prod _{i=1}^N{\int }_{-\infty }^{+\infty }{\displaystyle \frac{\mathrm{d}{\xi }_i}{\sqrt{{\xi }_i}}}\prod _{i=1}^{N/2}\delta ({\xi }_i+{\xi }_{N-i+1})\\ \hfill ·\prod _{j=1}^{N/2}2\left|{\xi }_j\right|\prod _{1\le k<l}^{N/2}{({\xi }_k^2-{\xi }_l^2)}^2{e}^{{\displaystyle \frac{i}{8N_c}\sum _1^N\Delta {\xi }_i^2}}{\int }_{O_N\left(\mathbb{R}\right)}\mathrm{d}O.\end{array}$$

(47)

Because the eigenvalues ${\xi }_{i}s$ are dimensional quantities, extra dimensions are brought in by the constraints $\delta ({\xi }_i+{\xi }_{N-i+1})$, which cancel out in the ratio of (46) and (47) and are accordingly omitted. In the argument of the exponential term, a parameter $\Delta$ with a dimension of (length)⁴ must be introduced to keep the argument dimensionless (see comments (ii) and (iii) below).

As was performed in the previous section, the original matrix element ${\left({\mathbb{M}}^{-1}\right)}_{\mu \nu }^{ab}$ will be replaced by the new matrix element ${\left({\mathbb{M}}^{-1}\right)}^{ij}$ with new indices $i=a+n\mu$ and $j=b+n\nu$ (see (28)). The right-hand side of (46), can therefore be written as

$${\mathcal{N}}_1{\displaystyle \frac{i}{g}}{\delta }^{\left(4\right)}(x-y){\displaystyle \frac{2^{N/2}}{g^{N/2}}}\prod _{i=1}^{N/2}{\int }_{-\infty }^{+\infty }\mathrm{d}{\xi }_i\prod _{1\le i<j}^{N/2}{({\xi }_i^2-{\xi }_j^2)}^2{e}^{{\displaystyle \frac{i}{4N_c}\sum _1^{N/2}\Delta {\xi }_i^2}}{\int }_{O_N\left(\mathbb{R}\right)}\mathrm{d}O{\left({}^{t}O\right)}^{ik}{D}_{kl}^{-1}{O}^{lj}.$$

(48)

The last integration on $O_N\left(\mathbb{R}\right)$ is straightforward and yields [2]

$${\int }_{O_N\left(\mathbb{R}\right)}\mathrm{d}O\sum _{k=1}^N{\left({}^{t}O\right)}^{ik}{D}_{kl}^{-1}{O}^{lj}={\int }_{O_N\left(\mathbb{R}\right)}\mathrm{d}O\sum _{k=1}^N{\left({}^{t}O\right)}^{ik}{\displaystyle \frac{{\delta }_{kl}}{{\xi }_k+i\epsilon }}{O}^{lj}=-i\pi {\delta }^{ij}\mathrm{vol}\left(O_N\left(\mathbb{R}\right)\right)\sum _{k=1}^{N/2}\delta \left({\xi }_k\right)$$

(49)

where in the right-hand side, the full volume of the orthogonal group $O_N\left(\mathbb{R}\right)$ appears [17]:

$$\mathrm{vol}\left(O_N\left(\mathbb{R}\right)\right)={\displaystyle \frac{2^N{\pi }^{N(N+1)/4}}{{\prod }_1^N\Gamma \left(k/2\right)}}$$

and where the poles at ${\xi }_k=0$ are displaced by an infinitesimal amount of $+i\epsilon$ and the usual identity has been used, i.e., $1/(x+i\epsilon )=v.p.(1/x)-i\pi \delta \left(x\right)$, the first term of which being the Cauchy’s principal value distribution7.

The eigenvalues ${\xi }_i$ have a (mass)² dimension, i.e., ${\xi }_i={\Lambda }^2{\xi }_i^{\prime }$, with $\Lambda$ as some mass scale. Keeping the same symbol ${\xi }_i$, the right-hand side of (48) can eventually be written in terms of dimensionless integration variables:

$$\begin{array}{cc}\hfill & {\displaystyle \langle T\left(A_{\mu }^a\left(x\right)A_{\nu }^b\left(y\right)\right)\rangle ={\mathcal{N}}_1\frac{\pi }{g}{\delta }^{\left(4\right)}(x-y){\delta }^{ij}\frac{N}{2}{\Lambda }^{-2}\mathrm{vol}\left(O_N\left(\mathbb{R}\right)\right)\frac{2^{N/2}}{g^{N/2}}{\Lambda }^N{\Lambda }^{N(N-1)(N-2)/2}}\\ & {\displaystyle ·{\int }_{-\infty }^{+\infty }\mathrm{d}{\xi }_1\delta \left({\xi }_1\right){\int }_{-\infty }^{+\infty }\mathrm{d}{\xi }_2\cdots {\int }_{-\infty }^{+\infty }\mathrm{d}{\xi }_{\frac{N}{2}}\prod _{1\le k<l}^{N/2}{({\xi }_k^2-{\xi }_l^2)}^2{e}^{{\displaystyle \frac{i}{4N_c}\Delta {\Lambda }^4\sum _1^{N/2}{\xi }_i^2}}}\end{array}$$

(50)

and the normalisation can be calculated in the same way:

$$\begin{array}{cc}\hfill & {\displaystyle {\mathcal{N}}_1^{-1}=\mathrm{vol}\left(O_N\left(\mathbb{R}\right)\right).\frac{2^{N/2}}{g^{N/2}}.{\Lambda }^N{\Lambda }^{N(N-1)(N-2)/2}}\\ & {\displaystyle ·{\int }_{-\infty }^{+\infty }\mathrm{d}{\xi }_1{\int }_{-\infty }^{+\infty }\mathrm{d}{\xi }_2\cdots {\int }_{-\infty }^{+\infty }\mathrm{d}{\xi }_{\frac{N}{2}}\prod _{1\le k<l}^{N/2}{({\xi }_k^2-{\xi }_l^2)}^2{e}^{{\displaystyle \frac{i}{4N_c}\Delta {\Lambda }^4\sum _1^{N/2}{\xi }_i^2}}}\end{array}$$

(51)

At the $g^{-1}$ leading order, the result for the Yang-Mills propagator at strong coupling can therefore be put into the following form:

$$\langle T\left(A_{\mu }^a\left(x\right)A_{\nu }^b\left(y\right)\right)\rangle ={\displaystyle \frac{\pi N}{2g}}{\displaystyle \frac{I_1(\Delta {\Lambda }^4)}{I_2(\Delta {\Lambda }^4)}}{\displaystyle \frac{1}{{\Lambda }^2}}{\delta }^{ab}{g}_{\mu \nu }{\delta }^{\left(4\right)}(x-y)+\mathcal{O}\left({\displaystyle \frac{1}{g^2}}\right),$$

(52)

where the functions $I_1$ and $I_2$ of $\Delta {\Lambda }^4$ are the integrals which appear in the right-hand sides of the expressions (50) and (51), respectively, and where the mapping (29) has been used to recover the original spacetime and internal colour indices8.

Some preliminary remarks are in order:

(i)

Result (52) is clearly non-perturbative, as it should. Not only because it is on the order of $g^{-1}$, but as advertised before, because it also indicates an absence of propagation, in sharp contradistinction to the perturbative regime where gluon degrees of freedom propagate.

(ii)

In (52), two parameters show up: a mass, $\Lambda$, and a correlated dimensionless parameter $\Delta {\Lambda }^4$. In these derivations, nothing determines what $\Lambda$ should precisely be. However, that such a mass term should be present is a clear output of the current analysis and this is a non-trivial point for a theory which is massless from the start [16]. The only mass scale one can think of in a quantum Yang-Mills theory is that of the asymptotic freedom ${\Lambda }_{YM}$ parameter, e.g., which is a renormalisation group invariant. There should not be any inconsistency in assuming the relation $\Lambda \simeq {\Lambda }_{YM}$, as ${\Lambda }_{YM}$ is the scale below which non-perturbative effects are expected to come into play.

(iii)

The second parameter, $\Delta {\Lambda }^4$, is a pure numerical factor, which involves some volume element $\Delta$ inherent to the definition of the initial measure (22) on the spacetime manifold $\mathcal{M}$. In a canonical way [18], in effect, the measure (22) definition assumes a decomposition of $\mathcal{M}$ into a collection of elementary cells of infinitesimal volume $\delta$, centred around each point of $\mathcal{M}$. The extension $\delta$, a a meshing parameter, could therefore appear to be the infinitesimal element met in mathematics, which is a formal indefinite quantity, that is, deprived of any definite measure. In physical theories though, things must often be re-interpreted. In the current case, the formal indefinite elementary volume extension $\delta$ must be turned into a physical elementary volume extension $\Delta$, relative to the effective locality distance scale [2]—given 2 points x and y in $\mathcal{M}$, in effect, fields’ correlations are sensitive to non-perturbative effects beyond a distance $L\ge {\Lambda }_{YM}^{-1}$ only. At this point, one may observe that such a situation would normally preclude an interpretation of the effective locality form as a form dual to the original $YM$ case, at least in the most canonical definition of duality.

3.2.3. Computations: Definiteness and Calculability

To begin with, a simple rescaling of the integration variables is enough to determine the dependence of the ratio $I_1/I_2$ on the parameter $\Delta {\Lambda }^4$. One obtains

$$\langle T\left(A_{\mu }^a\left(x\right)A_{\nu }^b\left(y\right)\right)\rangle ={\displaystyle \frac{\pi N}{2g}}{\displaystyle \frac{C_1}{C_2}}\sqrt{{\displaystyle \frac{\Delta }{4N_c}}}{\delta }^{ab}{g}_{\mu \nu }{\delta }^{\left(4\right)}(x-y)+\mathcal{O}\left({\displaystyle \frac{1}{g^2}}\right)$$

(53)

where

$$C_1={\int }_{-\infty }^{+\infty }\mathrm{d}{\xi }_1\delta \left({\xi }_1\right){\int }_{-\infty }^{+\infty }\mathrm{d}{\xi }_2\cdots {\int }_{-\infty }^{+\infty }\mathrm{d}{\xi }_{N/2}\prod _{1\le k<l}^{N/2}{({\xi }_k^2-{\xi }_l^2)}^2{e}^{{\displaystyle i\sum _1^{N/2}{\xi }_i^2}}$$

(54)

and

$$C_2={\int }_{-\infty }^{+\infty }\mathrm{d}{\xi }_1{\int }_{-\infty }^{+\infty }\mathrm{d}{\xi }_2\cdots {\int }_{-\infty }^{+\infty }\mathrm{d}{\xi }_{N/2}\prod _{1\le k<l}^{N/2}{({\xi }_k^2-{\xi }_l^2)}^2{e}^{{\displaystyle i\sum _1^{N/2}{\xi }_i^2}}$$

(55)

Note that in (53), the mass parameter $\Lambda$ has disappeared to the exclusive benefit of the meshing parameter $\Delta$.

This striking result indicates that if the meshing parameter is sent to zero, then, the non-perturbative effective locality contributions to the gluon 2-point function at strong coupling simply vanish. This is of course consistent with the $YM$ asymptotic freedom property relevant to the short-distance limit, which is that of $\Delta \to 0$.

Hence, as compared to the previous expression (52), (53) displays in a more cogent manner that the meshing parameter cannot be the indefinite $\delta$ parameter if (53) is to make sense. And rightly so, as discussed above in remark (iii), the meshing parameter relates to the $YM$ scale ${\Lambda }_{YM}$ through the simple relation $\Delta {\Lambda }_{YM}^4\ge 1$.

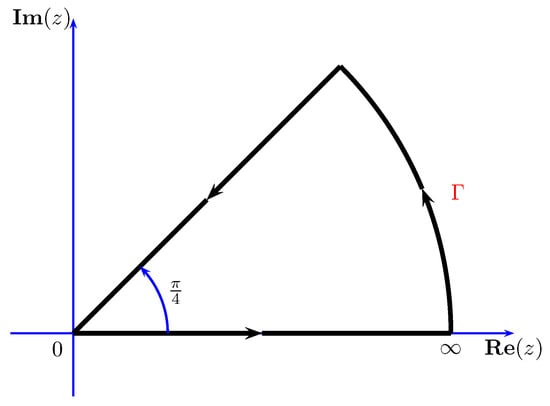
If (53) is to make physical sense now, the ratio $C_1/C_2$ must be defined and computable. For immediate purpose, Cauchy’s theorem is used on the contour of Figure 1 in order to establish the analytical continuation of the ${\xi }_k$ to the integration variables ${\Theta }_k$: ${\xi }_k\to \sqrt{i}{\Theta }_k$, with ${\Theta }_k\in \mathbb{R}$ [2]. One obtains

$$C_1={\sqrt{i}}^{N/2-1}{\int }_{-\infty }^{+\infty }\mathrm{d}{\Theta }_1\delta \left({\Theta }_1\right){\int }_{-\infty }^{+\infty }\mathrm{d}{\Theta }_2\cdots {\int }_{-\infty }^{+\infty }\mathrm{d}{\Theta }_{N/2}\prod _{1\le k<l}^{N/2}{({\Theta }_k^2-{\Theta }_l^2)}^2{e}^{{\displaystyle -\sum _1^{N/2}{\Theta }_i^2}}.$$

(56)

and likewise, for $C_2$,

$$C_2={\sqrt{i}}^{N/2}{\int }_{-\infty }^{+\infty }\mathrm{d}{\Theta }_1{\int }_{-\infty }^{+\infty }\mathrm{d}{\Theta }_2\cdots {\int }_{-\infty }^{+\infty }\mathrm{d}{\Theta }_{N/2}\prod _{1\le k<l}^{N/2}{({\Theta }_k^2-{\Theta }_l^2)}^2{e}^{{\displaystyle -\sum _1^{N/2}{\Theta }_i^2}}$$

(57)

The first output of this analytical continuation is to make clear that $C_1$ and $C_2$ are non-vanishing numbers. The ratio $C_1/C_2$ is therefore a well-defined number:

$${\displaystyle \frac{C_1}{C_2}}={\displaystyle \frac{1}{\sqrt{i}}}\left|{\displaystyle \frac{C_1}{C_2}}\right|.$$

(58)

However, the difficulty in calculating $C_1$ and $C_2$ lies in the Vandermonde determinant ${\prod }_{1\le k<l}^{N/2}{({\Theta }_k^2-{\Theta }_l^2)}^2$, which entails as much as $2^{N(N-2)/8}$ monomials, alternate in signs, that is, $2^{120}$ terms.

Each monomial of the Vandermonde expansion might be integrated out exactly over the whole $\mathrm{Sp}\left(\mathbb{M}\right)$, relying on the integration formula:

$${\int }_{-\infty }^{+\infty }\mathrm{d}\Theta {\Theta }^{2p}{e}^{-a{\Theta }^2}={\displaystyle \frac{(2p-1)!!}{{\left(2a\right)}^p}}\sqrt{{\displaystyle \frac{\pi }{a}}}$$

though not encountering any difficulty of principle. It remains that the control of such a huge number of terms, alternate in signs, is a formidable task, most likely out of reach practically.

3.2.4. Connecting to the Random Matrix Formalism

On the other hand, the analytical continuation ${\xi }_k\to \sqrt{i}{\Theta }_k$ just introduced makes it possible to rely on the powerful Random Matrix Theory and the Wigner’s semi-circle law in order to bind the constants $C_1$ and $C_2$ within definite intervals.

In order to see this, some Random Matrix Theory definitions must be introduced [13]:

$$P_{N\beta }({\Theta }_1,\dots ,{\Theta }_N)\equiv C_{N\beta }\prod _{i<j}^N{|{\Theta }_l-{\Theta }_j|}^{\beta }{e}^{-\beta /2{\sum }_1^N{\Theta }_i^2},$$

(59)

$$C_{N\beta }^{-1}={\left({\displaystyle \frac{2\pi }{\beta }}\right)}^{N/2}{\beta }^{-\beta N(N-1)/4}[\Gamma (1+{\displaystyle \frac{\beta }{2}}){]}^{-N}\prod _{j=1}^N\Gamma (1+{\displaystyle \frac{\beta }{2}}j),\mathrm{at}\beta =1,2,4$$

(60)

where the constants $C_{N_{\beta }}$ are normalisation constants while, in the Random Matrix formalism, the values of $\beta =1,2,4$ refer to the so-called orthogonal, unitary, and symplectic ensembles, respectively. The cases of $YM$ and $QCD$ theories, as we have seen, are relevant to the “orthogonal value” $\beta =1$9. One defines

$$\left[\prod _{j=2}^N{\int }_{-\infty }^{+\infty }\mathrm{d}{\Theta }_j\right]P_{N_{\beta }}({\Theta }_1,\dots ,{\Theta }_N)\equiv N^{-1}{\sigma }_N\left({\Theta }_1\right).$$

(61)

and Wigner’s semi-circle law, valid at large N values, is the following statement [13]:

$${\sigma }_N(\Theta )⟶\sqrt{2N-{\Theta }^2},\mathrm{for}-\sqrt{2N}\le \Theta \le +\sqrt{2N},{\sigma }_N(\Theta )=0,\mathrm{otherwise}.$$

(62)

Using these relations and observing that integrations on the ${\Theta }_i$s are saturated on the intervals $|{\Theta }_i|\le 1$ because of the strong suppression operated by the Gaussian terms $exp-{\displaystyle \frac{\beta }{2}}{\Theta }_i^2$, beyond ${\Theta }_i=\sqrt{2/\beta }$, upper and lower bounds on $|C_1|$ and $|C_2|$ can be deduced:

$${\displaystyle \frac{2}{\sqrt{N}}}{C}_{N,4}^{-1}\le |C_1|\le 4·2^{N(N-2)/4}{C}_{N,2}^{-1},2\pi C_{N,4}^{-1}\le \left|C_2\right|\le \pi 2^{N(N-2)/4}{C}_{N,2}^{-1}$$

(63)

A few remarks are in order:

-

Proceeding in this way, the intractable sum of monomials generated by expanding the Vandermonde determinant of (59) is circumvented within a few lines of calculations.

-

Moreover, using Wigner’s semi-circle law appears to be the more appropriate method as its universality is recognised to extend far beyond the realm of its original derivation [19].

-

Now, whereas (62) is obtained at $N\to \infty$, while one has $N=32$ in the current case, corrections to the asymptotic limit of $N\to \infty$ can be calculated in a systematic, algorithmic manner [13].

-

As in the case of $QCD$ [2], this shows how the powerful Random Matrix formalism connects to the effective locality non-abelian property to allow for well-defined and calculable estimates.

3.2.5. On the Way to a Numerical Outlook

Relying on the normalisation constant definitions (61), the absolute value of the ratio $C_1/C_2$ can eventually be bound as follows:

$${\displaystyle \frac{2^{1+N-\frac{5}{8}{N}^2}}{\pi \sqrt{N}}}{\left({\displaystyle \frac{2}{\sqrt{\pi }}}\right)}^{N/2}\prod _{j=1}^{{\displaystyle \frac{N}{2}}}\Gamma (j+{\displaystyle \frac{1}{2}})\le \left|{\displaystyle \frac{C_1}{C_2}}\right|\le {\displaystyle \frac{2^{1-\frac{N}{2}+\frac{3}{8}{N}^2}}{\pi }}{\left({\displaystyle \frac{\sqrt{\pi }}{2}}\right)}^{N/2}\prod _{j=1}^{{\displaystyle \frac{N}{2}}}{\displaystyle \frac{1}{\Gamma (j+\frac{1}{2})}}$$

(64)

Numerically, the numbers involved in both sides of (64) are still enormous numbers. That is, besides an issue of existence which is definitely established, (64) would not be very helpful for a comparison to numerical estimates.

Rather, taking again advantage of the strong suppression operated by the Gaussian terms $exp-{\displaystyle \frac{\beta }{2}}{\Theta }_i^2$ beyond ${\Theta }_i$ values greater than ${\Theta }_i=\sqrt{2/\beta }$, a much easier approximation consists of ignoring the squared powers of the variables ${({\Theta }_k^2-{\Theta }_l^2)}^2$ in the expressions (57) and (56) corresponding to $C_2$ and $C_1$, replacing them by ${({\Theta }_k-{\Theta }_l)}^2$. In this way, using Wigner’s semi-circle law (62), one obtains simply

$$|{\displaystyle \frac{C_1}{C_2}}|\simeq {\displaystyle \frac{1}{\pi }}\sqrt{{\displaystyle \frac{2}{N}}}$$

(65)

and one may expect to bring (53) in a form more amenable to possible comparisons with lattice numerical simulations, as will be seen shortly (Section 3.2.7):

$$\langle T\left(A_{\mu }^a\left(x\right)A_{\nu }^b\left(y\right)\right)\rangle \simeq {\displaystyle \frac{{\displaystyle e^{-\frac{i\pi }{4}}}}{2}}\sqrt{{\displaystyle \frac{N}{2g^2{N}_c}}}\sqrt{\Delta }{\delta }^{\left(4\right)}(x-y){\delta }^{ab}{g}_{\mu \nu }+\mathcal{O}\left({\displaystyle \frac{1}{g^2}}\right)$$

(66)

where the sign of approximate equality refers to (65) and to the use of the Wigner semi-circle law (62).

3.2.6. Another (Drastic) Way of Estimating the Gluon Propagator

Since the first article on the $EL$ matter [1], much more approximated and simplified techniques have been used for computing amplitudes with surprisingly good results [2]. The trick consists of substituting a single positive variable, R, say, for the involved structure of ${\left(f\chi \right)}_{\mu \nu }^{ab}\left(x\right)$, averaging over all colour and spacetime indices. A crude approximation which may find justifications in some cases, is the one of elastic quark–quark scattering amplitudes, for instance. Concerning the 2-point gluon Green’s function, it works as follows: the measure $\mathrm{d}\left[\chi \right]$ proceeds into $R^7\mathrm{d}R$, and $det\left(f\chi \right)$ into $R^8$.

Within this approximation, the first-order gluon 2-point Green’s function is found to be

$$\langle T\left(A_{\mu }^a\left(x\right)A_{\nu }^b\left(y\right)\right)\rangle ={\mathcal{N}}_0{\displaystyle \frac{i}{g}}{\delta }^{\left(4\right)}(x-y){\delta }^{ab}{g}_{\mu \nu }{\int }_0^{\infty }{\displaystyle \frac{R^7\mathrm{d}R}{R^4}}{e}^{{\displaystyle \frac{i}{4}}\Delta R^2}\left({\displaystyle \frac{1}{R}}\right)$$

(67)

with the same meshing parameter $\Delta$ as introduced in (46) and (47), and a normalisation factor, which reads simply

$${\mathcal{N}}_0^{-1}={\int }_0^{\infty }{R}^3\mathrm{d}R{e}^{{\displaystyle \frac{i}{4}}\Delta R^2}$$

(68)

Both integrals are straightforward and yield

$$\langle T\left(A_{\mu }^a\left(x\right)A_{\nu }^b\left(y\right)\right)\rangle ={\displaystyle \frac{1}{g}}{\displaystyle \frac{{\displaystyle e^{+\frac{i\pi }{4}}\sqrt{\pi }}}{4}}\sqrt{\Delta }{\delta }^{\left(4\right)}(x-y){\delta }^{ab}{g}_{\mu \nu }$$

(69)

where the ${\delta }^{ab}{g}_{\mu \nu }$ structure comes from the full treatment leading to our main result (53), while the dimensional factors of $\sqrt{\Delta }{\delta }^{\left(4\right)}(x-y)$ are correctly reproduced.

A difference of phase remains with a factor of $\sqrt{i}$ instead of its inverse in (53). Its origin is easily traced back to this approximation’s artefact: In effect, replacing ${\left({\mathbb{M}}^{-1}\left(x\right)\right)}_{\mu \nu }^{ab}$ by $1/R$ misses the factor of $-i$ which comes from the integration on $O_N\left(\mathbb{R}\right)$ of the right-most piece of (46) to yield (49). Of course, such an approximation cannot always be a reliable one: in the case of the current paper, for example, a conclusion like that of Equation (42) was far from being reached in this way.

3.2.7. Proposing a Physical Picture and a Numerical Estimate of the Meshing Parameter

The main result (53) is correct at the dimensional level, but its interpretation is not obvious. This is due to the product of the non-zero meshing parameter $\sqrt{\Delta }$ with the constraint of ${\delta }^{\left(4\right)}(x-y)$. These two elements seem to be contradictory.

In effect, if y must be as close as possible to x, then $EL$ has nothing to bring about, but Perturbation Theory only. At face value, the association in a product of the $EL$-length scale, with a constraint of ${\delta }^{\left(4\right)}(x-y)$, appears as a quirk.

We will venture here that it is not so.

Things may be understood as follows. The $YM$ quantum system is originally postulated on the spacetime manifold $\mathcal{M}$, where the two points x and y are labelled. As the elementary gluonic excitations are integrated out, one leaves the perturbative for the non-perturbative regime of the $YM$ theory, whose interactions are now mediated by the ${\chi }_{\mu \nu }^a$-fields, whereas references to the same spacetime manifold $\mathcal{M}$ keep applying unmodified.

This is where the contradiction comes from. In the non-perturbative $YM$ regime, such as described by any effective form,10 y can no longer be taken as close as possible to x, but a certain minimal distance away from it, here related to $\Delta$.

One has learned to know that functional integrations “do the job, but do not warn that they do it”.11

In the current situation, the functional integration process delivers no explicit information that in the effective formulation (13), the same original points x and y should be understood as rescaled points X and Y, fuzzed from the original x and y points to an extent $\Delta$.

That is, ${\delta }^{\left(4\right)}(x-y)$ should be understood as ${\delta }^{\left(4\right)}(X-Y)$ and the $EL$ form (13) postulated on a new spacetime manifold, made out of such points $X,Y,Z,\dots$.

This interpretation is reminiscent of the resolution power of the microscopes being used to describe the $YM$ dynamics, or, in a more formal way, reminiscent of the Wilson renormalisation group and related block–spin integration procedures used for Ising models [20].

A consequence of this interpretation of the result (53) amounts to its rewriting as

$$\langle T\left(A_{\mu }^a\left(x\right)A_{\nu }^b\left(y\right)\right)\rangle ={\displaystyle \frac{\pi N}{4\sqrt{g^2{N}_c}}}{\displaystyle \frac{C_1}{C_2}}{\delta }^{ab}{g}_{\mu \nu }{\displaystyle \frac{1}{\sqrt{\Delta }}}{\delta }^{\left(4\right)}(\widehat{X}-\widehat{Y})+\mathcal{O}\left({\displaystyle \frac{1}{g^2}}\right)$$

(70)

with $X\equiv \Delta \widehat{X}$, so that ${\delta }^{\left(4\right)}(\widehat{X}-\widehat{Y})$ is dimensionless.

In this way, the gluonic condensation which can be read off (53) is seen to proceed like the inverse squared root of the $EL$-resolution or meshing parameter $\Delta$, that is, like ${\Lambda }_{YM}^2$ at most, if one keeps sticking to an estimation of $\Delta {\Lambda }_{YM}^4\ge 1$.

In the literature, not so many numerical estimates can be found based on the gluon propagator and relating to a possible value of ${\langle {\mathcal{A}}_{\mu }^2\rangle }_R$12. In [8], though, a numerical simulation suggests a value of ${\left(2.76\mathrm{GeV}\right)}^2$ for the expression $g_R^2{\langle {\mathcal{A}}_{\mu }^2\rangle }_R$ in the case of $S{U}_c\left(3\right)$ [21], where the subscript R refers to “renormalised” (which are all of the expressions dealt with in any $EL$ calculation [22]).

Now, up to a numerical factor of $N_c/N$ and based on an Operator Product Expansion calculation, it turns out that in the Landau gauge, the term $g_R^2{\langle {\mathcal{A}}_{\mu }^2\rangle }_R$ is the mass acquired by all gluons and ghost fields due to gluon condensation; while, remarkably enough, these masses preserve both BRST symmetry and Slavnov–Taylor identities [8]. This opens the route to a sensible comparison of our main result (53) and/or (70) to the numerical simulation just mentioned.

To begin with, if in (69) the strong coupling constant $g_R$ is taken at a value of 10, then it is quite amusing to discover that the inverse squared root of the meshing parameter $\Delta$ comes out to be

$${\displaystyle \frac{1}{\sqrt{\Delta }}}={\left(230\mathrm{MeV}\right)}^2$$

(71)

that is, close enough to the $YM$ scale of ${\Lambda }_{YM}=259\mathrm{MeV}$ found by a full lattice $QCD$ calculation at zero flavour number $n_f=0$ [23].

Using our main result (53) now, approximated by (66), the same value of the inverse squared root of the meshing parameter (71) is obtained at a smaller value of the strong renormalised coupling constant, that is, at $g_R\simeq 4$, which is still, admittedly, a strong coupling value.

As advocated in [8], a result like (53), which can be phrased as “gluon condensation”, is proposed to be the origin of mass gap in the $YM$ theory and of quark confinement in $QCD$.

4. Conclusions

In this paper, the property of effective locality is explored in the case of pure Minkowskian Yang-Mills theory. As compared to $QCD$, where the property was first discovered, the Yang-Mills case is simpler and preserves some of the most salient features of the non-abelian dynamics, perturbative and non-perturbative.

In a recent article [6], the Green’s function generating functional of the Yang-Mills theory has been constructed in full detail, relying on standard proven functional methods, e.g., Equation (13) of the current paper, whose derivation has been quickly summarised.

The very purpose of this article was to see whether the formal derivation of $Z_{YM}\left[j\right]$ in Equation (13) lends itself to doable concrete calculations. This calls for quite technical developments which, if not the simplest, can nevertheless be carried out with a satisfying degree of mathematical rigour. In particular, as in the case of $QCD$, it turns out to be possible to rely on the powerful Random Matrix Theory in order to complete an integration process and to circumvent the intractable difficulties induced by a complicated Vandermonde determinant.

The first and elementary gluon Green’s function calculation is that of $\langle A_{\mu }^a\left(x\right)\rangle$, the vacuum expectation value of the gluon field. The proof that it is vanishing, i.e., $\langle A_{\mu }^a\left(x\right)\rangle =0$, is not trivial, but allows one to set up the general framework of subsequent Green’s function calculations.

This framework is then used to investigate the gluon propagator in the non-perturbative strong coupling regime of the Yang-Mills theory. At the leading order of a strong coupling expansion (in powers of the inverse coupling $1/g$), it is found that $\langle T{A}_{\mu }^a\left(x\right)A_{\nu }^b\left(y\right)\rangle$ comes out proportional to a factor of ${\delta }^{\left(4\right)}(x-y)$, and hence, displays no propagation, contrarily to the perturbative regime. Since the result also exhibits an isotropy in the internal and spacetime indices, the non-perturbative gluon propagator could point out the formation of a gluonic condensate of dimension “mass-squared”.

It is interesting to observe that a similar conclusion is met within a thermodynamical analysis of quantum $YM$ theory [24]; namely, an exclusion of gluon propagation and the emergence of a massive structure (there identified to emergent fermionic–self-intersecting centre–vortex loops), strolling above a confining ground state. Since, in all possible situations, the $T\to 0$ temperature limit has always been found to be a continuous one, this similarity is worth quoting.

As seen from Perturbation Theory (renormalisation group-improved), results (53) or (70) compare reasonably well with the non-vanishing mass acquired by ghosts and gluons in the Landau gauge of the Lorentz-type gauge fixing condition [8,21].

It is stressed that the $YM$ effective locality calculations cannot make sense in the absence of a mass or distance scale, which turns out to be given by the meshing parameter $\Delta$ introduced in a canonical way in order to define the functional measure of integration on the $\chi$-space of functions defined on the spacetime manifold $\mathcal{M}$. One finds in effect a result of the form $\langle T{A}_{\mu }^a\left(x\right)A_{\nu }^b\left(y\right)\rangle \sim \sqrt{\Delta }{\delta }^{\left(4\right)}(x-y)$. Would the parameter $\Delta$ be taken to zero, the supposed gluon condensate would vanish altogether, in agreement with the short-distance perturbative regime of the $YM$ theory.

That is, like in $QCD$ [2], the property of effective locality is clearly associated to a given mass scale beyond which the $EL$ property just fades away, leaving the place to the perturbative regimes of both theories, $YM$ and $QCD$.

Because of the length scale dependence of the $EL$ property, one may think that contrarily to appearances (such as advocated decades ago in the Euclidean case [4]), the effective locality form displayed in Equation (13) should hardly be thought of as a form really dual to the original $YM$ formulation.

Unfortunately, comparisons to other existing approaches like Gribov’s horizon and Dyson–Schwinger-type calculations are rendered uneasy because of their Euclidean rather than Minkowskian formulations, to begin with, not forgetting a lack of control on gauge invariance. Furthermore, as noticed already in the case of $QCD$, the $EL$ analyses would indicate a sort of disconnection from Perturbation Theory. In effect, while perturbation theories require well-defined free gauge-field propagators out of which Feynman rules are devised, nothing like this can be met within the current treatment of the $YM$ theory and/or the pure glue sector of $QCD$.

This fate could be suggestive of a real disconnection between Perturbation Theory and the $EL$ non-perturbative approaches to both $YM$ and $QCD$. In this respect, it is worth recalling that a Dyson–Schwinger non-truncated analysis [25] is able to point out such an irreducible disconnection regarding the $\beta$-function of $QCD$; and in the same line, that a similar “uneasy connection” is perceived also in the light-front approach to $QCD$ [26].

Another approach based on Quantum Mechanics first principles is a variational attempt at describing the non-perturbative regimes of $QCD$ and $YM$ theories and enforces gauge invariance by construction [27]. A quite important number of approximations, guesses, known perturbative, and assumed non-perturbative inputs are implemented in the wave function construction. Then, the “best wave function” is determined in a variational way with respect to a mass parameter M which separates the perturbative from the non-perturbative sectors, and turns out to also be the dynamically generated scale of the theory. In this approach, devised to capture non-perturbative features of the non-abelian dynamics, inputs and approximations are found to satisfy global consistency checks in regard to the results.

However, whereas the current paper assumes a non-perturbative threshold of $L\ge {\Lambda }_{YM}^{-1}$, the dynamically generated scale found in [27] proceeds the opposite way, $L\sim M^{-1}<<{\Lambda }_{QCD}^{-1}$, rendering an uneasy comparison to the current approach outputs. One may also observe that this result comes out in contradistinction to those of [25], where the reliability of Perturbation Theory is shown to extend beyond the usual short distances of ${\Lambda }_{QCD}^{-1}$.

Despite the Euclidean approach, one can nevertheless note some similarities, which probably do not happen just by chance. In [27], in effect, the square of “the best wave function” defines a partition function of a non-linear $\sigma$-model. In the paper introducing our present $YM$ analysis [6], such a partition function of a non-linear $\sigma$-model was acknowledged, read off (13) at zero sources $j_{\mu }^a\left(x\right)=0$:

…the $j_{\mu }^a\left(x\right)$-source free $Z_{YM}\left[j\right]$ above, can be written in a form which is strongly reminiscent of a non-linear sigma model (while not complying exactly with the most general definition of these models at $D\ge 2$)… As these models and (13) both aim at describing the non-perturbative regimes of $YM/QCD$ theories, it is possible that this coincidence happens to be not by chance solely [6].

This paper offers another example of effective locality calculations whose connections to the Random Matrix calculus, by means of analytical continuation, allow one to proceed in a systematic way and a satisfying level of mathematical rigour. It could be worth examining if sub-leading-order contributions, $\mathcal{O}(1/g^2)$, would display residual propagation effects, possibly associated to some glueball picture.

Be it as it may, this treatment of the pure glue sector of $QCD$ should allow one to improve on previous $QCD$ estimates [2], where, to begin with simpler calculations, these gluonic terms had been omitted to the exclusive benefit of fermionic ones.