Abstract
We study the dynamics of a coherent state of closed type II string gravitons within the framework of the Steepest Entropy Ascent Quantum Thermodynamics, an effective model where the quantum evolution is driven by a maximal increase of entropy. We find that by perturbing the pure coherent state of gravitons by the presence of other states in the string spectrum, there exist conditions upon which the system undergoes decoherence by reaching thermodynamical equilibrium. This suggests the instability of the coherent state of gravitons. We identify the time scale it takes the system to reach equilibrium consisting of a mixed state of fields in the string spectrum and compare it with the quantum-break time. Also we find that in such final state the quantum-break time seems to be larger than the classical break-time.
1. Introduction
The current accelerated expansion of our Universe is nicely described in a classical approximation by a 4-dimensional de-Sitter (dS) space-time. However, its construction from fundamental structures in a quantum gravity theory, such as string theory, has been challenging. One of the first proposals to construct a stable dS vacuum was given almost 20 years ago by Kachru, Kallosh, Linde, and Trivedi, known as the KKLT solution [1], whose viability is still in debate at present day. There have been as well more unorthodox constructions such as the incorporation of non-geometric fluxes [2,3,4,5], which nevertheless present important limitations [6,7].
The difficulty to find a stable fully controlled dS vacuum in string theory has opened up the possibility of other scenarios. One of the most intriguing is the suggestion about the non-existence of dS in string theory [8] or in any framework of quantum gravity [9,10,11] through the (Refined) dS conjectures within the Swampland Program [12,13,14,15] in which the existence of a stable dS solution is compromised at Planckian energies and, in consequence, at the string landscape. These proposals suggest, in turn, that dS space could be unstable or metastable.
In order to describe the possible instability of dS space, it was proposed in [16] (see also [17,18,19]) that the classical dS space-time can be visualized, at the weak gravity limit, as a coherent state of gravitons over the Minkowski space-time. The authors in [16] argue that coherent states of gravitons can represent a de Sitter (dS) space in the semi-classical limit by reproducing key properties of such space-time, including the redshift of probe particles and the thermal Gibbons-Hawking radiation. By utilizing scattering amplitudes, the interactions of gravitons in a coherent superposition effectively reconstruct the dS geometry and encode the curvature radius associated with the cosmological constant. This framework provides a bridge between quantum field theory and general relativity, shedding light on the quantum-to-classical transition and the stability of dS space-time. Such semiclassical construction of dS space has been further elaborated in the context of string theory by [20,21].
As the theory incorporates non-linearities, the coherent dynamics departs from the classical dynamics, defining a breakdown of this relation at some time, called the classical break time , which for the case of dS space goes as
with H the Hubble constant. However, there is also a quantum dynamics leading to instability. In the presence of other particles interacting with the gravitons, the system undergoes decoherence indicating that dS space is no longer described by a classical mean field evolution. The time at which this happens is called the quantum break time and goes as
Therefore, dS space, identified as a coherent state of gravitons scattering to other particles, is unstable. The relation between both times goes as , where . The decoherence of dS space within the framework of string theory as well as the connection with the swampland Refined dS conjecture was addressed in [22].
Motivated by these results, we construct a coherent state of gravitons in type II superstring theory and study its quantum evolution by an effective model which modifies the Schrödinger equation by adding a dissipation term. The evolution is then driven by the increase of entropy among the quantum states conforming the system. Specifically, the coherent states, constituting pure quantum states, can be dissipated by the presence of other orthogonal states, as typically happens in the closed string by the presence of the extra fields coming from the Neveu-Schwarz-Neveu-Schwarz (NS-NS) sector itself and the other sectors: Neveu-Schwarz-Ramond (NS-R), Ramond-Neveu-Schwarz (R-NS) and Ramond-Ramond (RR) fields, all of them forming a set of orthogonal states to the coherent state of gravitons.
The referred framework considers a non-linear dynamics called the Steepest Entropy Ascent Quantum Thermodynamics (SEAQT) and it was proposed in [23]. In this formulation, the system evolves not according to unitary, reversible dynamics, but instead in a direction that maximizes the rate of entropy production, constrained by the principles of quantum mechanics. In this scenario, the state of the system follows a trajectory of steepest entropy ascent, driving it toward thermodynamic equilibrium. This proposal is an effective model which allows describing how the initial coherent state of gravitons in string theory undergoes decoherence. In this context, it is possible to apply the SEAQT framework, study the stability of a coherent state of gravitons in string theory, thinking of such system as the whole universe.
The application of SEAQT to the universe as a whole rests on the assumption that the universe can be treated as a self-contained, closed system, with its dynamics governed by the same statistical and thermodynamic principles that apply to subsystems. SEAQT, as a framework, can incorporate interactions between a quantum system and its environment, but it is not limited to such scenarios. Instead, it provides a generalized description of non-equilibrium dynamics and entropy generation, which are intrinsic to the evolution of any system, including the universe. Furthermore, SEAQT is constructed upon the foundational principles of quantum mechanics, with the additional assumption of entropy generation as a fundamental feature of the trajectory of the system through state space. This perspective aligns with the thermodynamic arrow of time and offers a natural framework to describe the evolution of the universe from low-entropy initial conditions to the higher-entropy states observed today.
Basically what this framework tells us is the following: consider a system conformed by orthogonal quantum states . A pure state, let us say would be stable, with zero entropy as far as it does not interact with the other states. When the interaction occurs, the entropy would increase, driving the system to one formed by mixed states. Our claim is that this is precisely the situation that occurs in string theory when one considers a coherent state of gravitons, since one must take into account all states in the other string sectors. Under this perspective it is expected that a coherent state of gravitons must evolve into a mixed state of all possible closed string states, implying the decoherence of the initial state and, in consequence, its instability.
Let us then summarize our main results:
- We effectively describe the evolution of a quantum system conformed by a coherent state of gravitons, using the SEAQT framework.
- In this context, the evolution is driven by the increase of entropy. For that it is essential to have orthogonal coherent states interacting with the initial state of coherent gravitons. This scenario is given in the closed superstring theories, where the RR fields are orthogonal to the graviton by construction.
- By studying the effective evolution of the system, we find that there exists a time scale at which the system can reach equilibrium by undergoing decoherence and ending in a mixed state conformed by fields in the NS-NS and RR sectors.
- The time in which the coherent state of gravitons is not longer described by a dynamics of a quantum coherent state is called quantum-break time and denoted . We suggest that could be essentially related to the difference on mean energy values among different orthogonal states. Also, in the equation of motion describing the effective evolution of the system, it appears a parameter in time units which seems to be independent of the quantum process but that nevertheless determines how long it takes the system to evolve into decoherence. We therefore propose identify this parameter with the classical break-time recently studied in literature [16].
- Closed to equilibrium when the system is a mixed state, one can see that , a condition that could suggests, upon an identification of the coherent state of gravitons to some classical space, that such space cannot undergo a quantum process, since the classical-break time is the time scale at which the system is destroyed by classical non-linearities which apart the theory from the weak coupling limit.
The outline of our work is as follows. In Section 2 we implement the so-called Steepest-Entropy-Ascent Quantum Thermodynamics (SEAQT) framework to a system of coherent states of gravitons within the context of type II string theory and review the most important characteristics of this proposal. Section 3 is devoted to applying this framework to a pure state constructed from closed string gravitons in the presence of other states. We show how the decoherence is natural due to the presence of orthogonal states such as the B-field and the dilaton in the NS-NS sector and all the massless states in the RR one. We show that such a state is unstable and compute the time scale in which equilibrium is restored. Finally, we shall discuss some implications on the stability of a coherent state of gravitons over the Minkowski space and the possible association of a classical and a quantum break time. The motivation behind this study is precisely the possible identification of a coherent state of gravitons with the dS space. This last point is not addressed in the present work, though. However, we shall comment on it in the final section. Similar topics are covered recently in [24].
2. The SEAQT Framework
In this section, we describe the generalities about the framework we shall use to study the stability of a coherent quantum state. It is important to notice that this framework is an effective proposal to describe the dynamical evolution of a quantum system by assuming that it is driven by an increment of entropy. The model was proposed in [25] and it has been successful in providing an effective description of quantum systems by incorporating thermodynamic irreversibilities directly into the system dynamics. For instance, the SEAQT framework has been successfully applied to predict a flip-change process, essential during heat interactions with an environment, and pure dephasing [26,27], which is related in this framework solely to internal entropy generation. It also models atom-photon field interactions in cavity quantum electrodynamics (CQED), accurately predicting the decay of coherence in photon fields and agreeing with experimental observations [28] as well as the relaxation of non-resonant excitation transfer processes [29]. Notice that for pure dephasing, as well as during the decay of coherence, the system under consideration is isolated. Therefore, the assumption of entropy increase provides an accurate description of these phenomena.
Let us review the basics of this framework. Consider a nonlinear extension of the Schrödinger (von Neumann) equation, which incorporates a dissipative term inducing an increase in entropy. This method proposes that the system follows the path in Hilbert space along which the entropy increases most rapidly, providing a quantum channel compatible with the second law of thermodynamics [30]. Specifically, it involves projecting the gradient of the entropy onto the orthogonal direction to a constrained space or manifold, spanned by the usual quantum dynamics without dissipative terms. This manifold is defined by the conserved observables, which act as generators of motion. Typical examples of these generators include the identity operator, the Hamiltonian operator , and particle number operators [23,25,31,32]. For a single, indivisible system, this means that the usual symplectic dynamics is modified by including a nonlinear dissipative term, resulting in an evolution equation of the form
where the Hermitian operator describes the presence of dissipation associated with the quantum state, and it is given by
where is the density matrix operator, and is a free parameter. Consequently is the square-root state operator obtained from the spectral expansion of the density matrix by substituting its eigenvalues with their positive square roots. Finally, encodes the dissipative process that we proceed to describe. The quantum dynamics of non-dissipative (i.e., a system where the entropy does not increase) can be thought of as dynamics on a manifold generated by the basis of operators and . The idea is then to consider an orthogonal direction, along which the quantum system takes a path (which inherently implies the increase of entropy). Therefore, one can say that must be of the form
where represents the linear manifold spanned by all real combinations of the set of operators . In this way, the dissipative process is encoded in the operator , i.e., if is the identity operator, we have a maximal dissipation where is totally aligned along the orthogonal direction given by which is chosen in order to correctly reproduce the von Neumann entropy. The idea is that along this direction, the entropy increases. Hence, if the quantum states are not projected into such a direction, the entropy is null. This indicates that the Von Neumann entropy can be written in terms of a projector acting on all quantum states as
When is the identity and we have maximal dissipation, the entropy operator acts on all states.
For a system evolving to a state of larger entropy, the most general form of the operator is , where projects onto those states that have zero eigenvalues with respect to . This orthogonality condition ensures that both trace and energy are preserved along all dynamics. In this way, the operator D (which contrary to , is non-hermitian) can be constructed by the Gram-Schmidt process through the non-recursive formula
where , is the Gram determinant and as usual, .
The expansion of the determinant gives us
where is the identity operator. For convenience, we define at this point the parameter as
since, as we shall see, can be related to the (non-equilibrium) inverse temperature of the system. Therefore, the Hermitian operator takes the form
where is the anti-commutator and where we use the shorthand notation for a general quantum state . Notice that can be written as the difference between the average free energy and the operator free energy as
with ,
Also observe that under this non-linear extension, quantum states are said to be in equilibrium if and . If , the kernel of the density matrix is non-empty, and the operator . This case represents limit cycles of the dynamics, known as partial equilibrium states, which are unstable (see Figure 1). However, when the states reach stable limit cycles that coincide with the thermal equilibrium state, the kernel of the density matrix is empty and [23].
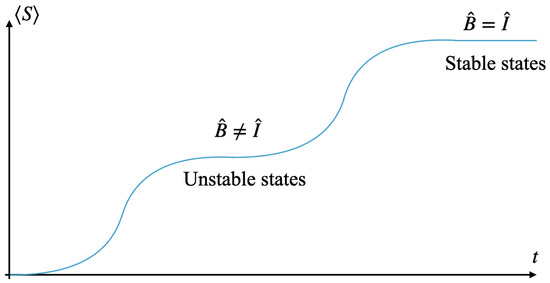
Figure 1.
Diagrammatic description of the unstable states in the SEAQT framework. For an initial pure state, the entropy is zero. However, within the SEAQT framework, such states are unstable and tend to evolve toward a thermodynamic equilibrium state. As the density matrix evolves, intermediate unstable states, known as partial equilibrium states, may also emerge.
Notice that the opposite is not always true, i.e., when the system is perturbed such that it contains all possible states, the operator is actually the identity, but the perturbation could take some time to reach stable equilibrium.
2.1. Non-Dissipative States and Equilibrium
Under this dynamics, all solutions for are called non-dissipative, and it follows from Equation (10) and the expression of in terms of in Equation (6) that
By considering , we effectively restrict to the support of , making the expression finite and well-defined. This is equivalent to replacing . In this way, the operator eliminates contributions from the null space where is undefined. Let us define a modified operator:
which makes invertible and ensures that is finite. Thus, Equation (13), can be written as
where is the partition function. By exponentiation and multiplying on the left and right by the projector to ensure that is restricted to its rank. Notice, that the Born rule, recovered in the Lindblad formulation at late times [33], can emerge under this dynamics through entropy maximization within the partially canonical states which has the form
This implies that the dissipative dynamics leads to the canonical (or partial-canonical) distributions, i.e., is given in terms of equilibrium states denoted . Therefore, we can identify the related parameter as the inverse of the thermodynamic temperature. Furthermore, for such cases the expectation values and are no longer independent, and thus
It is important to remark that equilibrium states for which dissipation is null could have some associated entropy, contrary to a pure state, for which the entropy is zero, as it follows from Equation (17) for . Moreover, we can immediately identify a (particularly important) configuration leading to this situation, i.e., having a non-pure state in equilibrium. This happens for a mixed state formed by orthogonal states.
2.2. Pure State of Gravitons
Let us now consider a single coherent state of gravitons (over the Minkowski space) as our whole quantum system. At this point, it is important to emphasize two relevant conditions in our work:
- According to the framework we are considering, it is very important to have a scenario in which the graviton coexists with other states which actually are orthogonal to it or to a coherent state formed by them. This is precisely what does happen in string theory. The graviton belongs to the massless symmetric excited state in the NS-NS sector along with the B-field and the dilaton. In type II theories the RR sector also contains massless fields which by construction are orthogonal to those in the NS-NS sector. Therefore, string theory provides a natural scenario in which there are orthogonal quantum states to the graviton, which could lead (we shall see that it does) an instability of a system formed purely by a coherent state of gravitons.
- Motivated by the possible representation of a coherent state of gravitons with a classical space we compute the time-scale after which the quantum evolution departs from the classical mean field evolution described by the dynamics of the coherent state of gravitons. This scale is called the quantum time-break and it is inversely proportional to the number of particle species. The reason behind the fact that the quantum evolution can not be longer described by a classical theory after some time is due to the scattering process among different quantum states and in consequence undergoes decoherence. Within the SQEAT framework, the quantum evolution is effectively described by the dissipation term in Equation (3). Therefore, we expect that the quantum process of scattering would increase the entropy driving the system into a mixed state.
Based on the above expectations, it seems viable to effectively describe the quantum evolution of a coherent state of gravitons under the SEAQT framework with the goal to interpret the results, in a future work, in terms of the stability of a classical space.
Then, let us consider a coherent state of massless gravitons, denoted and given by
where is a nilpotent traceless symmetric constant tensor and
with and being the fermionic mode operators for the left and right modes respectively in the NS-NS sector of the closed string. Specifics about the construction of the coherent state are given in Appendix A.
We want to study the stability of this state in the presence of other states orthogonal to it. For that, we start by analyzing its stability and considering it as a single state in our system (i.e., for the moment we do not consider the presence of the other states).
Since our system is solely formed by a coherent state of gravitons, we depart from the pure state . Then the partition function is
For the operator given by , the associated density matrix at partial equilibrium is
which matches with the pure state density matrix. Therefore the matrix operator is actually a pure state of the form . Thus, under the non-linear dynamics, the pure state generated by the coherent states of gravitons corresponds to partially canonical states. Such states have zero entropy since they represent states of complete knowledge and are non-dissipative. Furthermore, since they are projectors of eigenvectors of the Hamiltonian, it leads to a zero contribution of the symplectic term in the SEAQT equation of motion, and in consequence its dynamics is trivial, i.e., . However, as we shall see, this solution is unstable (in the Lyapunov sense [23]), since any perturbation leads to an evolution of the density matrix.
3. Instability of a Coherent State of Gravitons in String Theory
In string theory, the graviton states are part of the NS-NS sector together with the B-field and the dilaton. Besides, we also have bosonic fields constructed in the RR sector. As known, those states are orthogonal to any state belonging to the NS-NS sector, in particular to the coherent state of gravitons. This structure is actually the one that under the SEAQT framework allows us to study the dynamical evolution of a system formed by a mixture state of coherent states. Therefore, we shall depart from a coherent state of gravitons slightly perturbed by orthogonal states, into a mixed state. We analyze under which conditions this system reaches a thermodynamic equilibrium.
3.1. Perturbations
Consider an initial system formed by a coherent state of gravitons such that as well as coherent states denoted constructed from the rest of the fields in the NS-NS and RR sectors. Notice that these states are orthogonal to the coherent state of gravitons. After some time, we expect the system to be perturbed by the presence of these modes. Therefore, after some perturbation of the pure state, the matrix density operator is given by
where n refers to the number of coherent states orthogonal to the graviton with (in the context of string theory we can construct coherent states related to the B-field, the dilaton and the RR fields). To preserve the trace of the density matrix, we demand that . In this sense, the dissipative term in the equation of motion Equation (3) is non-zero. It is important to observe that under this perturbation, the Kernel of the matrix operator is null, for which from this point forward we shall take .
We now proceed to compute all terms in Equation (10) by employing the replica trick. First, notice that the n-power of the perturbed density matrix is
Next, we aim to approximate the term , by expanding the logarithmic terms for small giving us
Thus, the average expectation value for the entropy operator is
Next, we construct the free energy operator , which combines the contribution of the Hamiltonian , and the entropy operator , as well as the thermodynamical parameter , given in Equation (12). We find
whereas its expectation value is given by
where we use the shorthand , where · is an operator , denotes the expectation value for the coherent states . The quantity is now a function on all and it is approximately (up to linear terms in ) given by
For latter purposes, consider the contribution of the free energy operator in the graviton sector
as well as the contribution from the B-field and dilaton sectors,
Using the free energy contributions and the SEAQT framework, we derive the evolution equations for and . This is done by direct substitution of the free energy operator, given by Equation (26) and the average free energy, given by the Equation (27). This is, in general, a complicated differential equation which contains the contribution of the perturbations and . To separate each contribution, we can take the separate contribution of the average value of the free energy in the graviton sector as well as in the orthogonal states; this allows us to write the evolution of the perturbations as
as well as
To further simplify, we expand the evolution equations to first order in the perturbations. After simplifying, this reduces to
Under the assumption of homogeneity on the perturbations, this equation can be reduced to a dynamical evolution of perturbations in the form
with . Although this is a difficult equation to solve analytically, we can infer some interesting features.
For instance, if the energy difference , meaning that the scattering between different coherent states occurs among those with the same mean energy value, Equation (34) implies that the equilibrium solution is achieved when . It follows that for small perturbations below , the rate of change of is positive, driving upward towards equilibrium. Conversely, deviations above result in a negative rate of change, which drives back to equilibrium. Specifically, for the case where , the system is unstable, and the perturbation grows over time as
However, we can see that, in this case, the growth of the perturbation velocity depends solely on the parameter . For large values of the perturbation grows very slowly. Actually, one can see that even if the scattering process is almost stopped, with a very small dissipation, the parameter determines how rapid the system becomes unstable. Since it seems that is a characteristic of the system not belonging to the quantum process, must be related to some classical behavior of the theory. This is indeed a strong assumption that requires a more profound analysis but provides an effective way to compare it with the time the system takes to undergo decoherence due to quantum processes.
3.2. Reaching the Equilibrium
We have now all the necessary expressions to determine whether there are conditions upon which a coherent state of gravitons evolves and reaches thermodynamical equilibrium as a mixed state. From Equation (31) we see that if the perturbation grows over time, the final state would be a mixed state among the coherent states in the NS-NS and RR sectors (decoherence of the initial state). On the contrary, if decreases in size, we can say that the system reaches the equilibrium by restoring coherence in the graviton states.
From Equation (34) we see that the equilibrium would be reached when , this is when . Observe that such a condition is possible to reach, since for a finite (and small) number of orthogonal coherent states to the graviton. Therefore it is possible to get the necessary equilibrium condition such that, after some time .
Let us then study the required conditions around this special region where equilibrium is near to be reached. Our strategy is as follows: according to our previous discussion, we shall assume that the growth velocity of the perturbations can take very small values. When this occurs we want to see if the size of the perturbation shrinks, freezes, or continues growing. For the first option, we can have a stable equilibrium, while for the latter ones, the system would be unstable with respect to the original perturbed state of coherent gravitons.
Let us then define and express it as
where is a very small constant indicating that the velocity of change in the perturbation is very close to zero. We want to see if there are stable conditions for a perturbation which barely changes in size. Therefore, near equilibrium, the function G can be ignored. However, far from equilibrium, must contain the dynamics and particularities of how fast the perturbation evolves.
Hence, near the equilibrium when is very small, we can approximate
for a small value of the quotient . Substituting in Equation (34), we get
where is the initial value of the perturbation and
where the integration is taken from a perturbation close to equilibrium to the perturbation with .
At the time when the system is almost in equilibrium (but not quite there since although very small is not zero), and we can say that
For the perturbation , although presenting a small growth velocity (since by assumption) grows exponentially over time, indicating the system is unstable with respect to perturbations in the i-th state, and the density matrix evolves towards a mixed state, consisting of all other states in the NS-NS sector, as well as the RR one in the case of type II string theory. The equilibrium is reached, but it is an unstable equilibrium with respect to a pure state of coherent states of gravitons. This can also be seen from entropy Equation (25), which can get a constant value as the perturbations continue growing even with a small velocity.
On the other hand, if the perturbations shrink over time. However, in this case, the entropy Equation (25) decreases to zero. Therefore, this case is not to be considered.
Notice that the time required to reach the equilibrium, rather the system evolves to a mixed state or goes back to a pure state of gravitons, is of the order
Since the origin of such evolution is given by quantum scattering among the states of the string, we propose to identify this time as the quantum break time . Together with the identification of the classical break time with , we infer that
meaning that the factor connecting both time scales is given basically by which according to [16] can be interpreted as a quantum coupling which powers suppress classical non-linearities corrections. For a small , i.e., when the system is closed to equilibrium conformed by a mixture of coherent states, .
4. Final Comments and Conclusions
The dynamics of a coherent state of string gravitons within the effective framework of the Steepest-Entropy-Ascent Quantum Thermodynamics (SEAQT) is described. Coherent states of gravitons, being pure states with zero entropy, are inherently unstable under the non-linear dynamics prescribed by the SEAQT equation of motion in the presence of other orthogonal states, as naturally happens in the context of string theory. This instability arises since any small perturbation of the system, consisting in the presence of other states, induces an increase in entropy. This is described by a dissipative term in the SEAQT equation driving the system toward states of higher entropy and moving it away from the initial coherent state.
As the system evolves, it naturally progresses toward a stable equilibrium state that is a statistical mixture of states available in the theory. For the case of (type II) superstring theories, the massless available states are contained in the so-called NS-NS and RR sectors. Under the non-linear SEAQT dynamics, these fields would also contribute to the system’s evolution toward a thermodynamic equilibrium state. This equilibrium would involve a mixture of all relevant massless modes, including both bosonic and fermionic degrees of freedom inherent in supersymmetric theories. The mixing of these states would lead to stable configurations that are consistent with supersymmetric backgrounds.
Therefore, we have presented a framework in which we can effectively study the stability of a coherent state of gravitons and infer the time scale it takes the system to undergo decoherence. Under the SEAQT framework, the coherent states evolve by increasing the associated entropy resembling the quantum scattering among gravitons and all other fields (mainly those in the RR sector). In this sense, by considering a small dissipation, or equivalently, a small rate of scattering, a perturbation of the original coherent pure state grows over time, rendering the system unstable. The velocity of such evolution is encoded in the effective time . Since its value seems to be independent of the quantum processes, we propose to identify it with the classical break-time associated with a classical space which can be described by a dynamics of some specific construction of coherent states of gravitons. Although we have not given specifics on such coherent state, we are motivated by the construction presented in [16], where the dS space is identified with some coherent state of gravitons.
We also studied the conditions upon which a thermodynamical equilibrium is reached. This happens when , where is the perturbation along one of the orthogonal directions of the graviton (i.e., a perturbation driven by the dilaton and the B-field), and is the difference of the energy mean values related to the state of gravitons and the orthogonal ones and is the effective inverse temperature associated during the dynamical process into equilibrium. Hence, if the product of this effective temperature with the energy difference grows as , the system would approach the equilibrium. As we mentioned, there are conditions to expect this would happen. Hence, near the equilibrium we can see that the system is unstable and the time scale in which the system undergoes decoherence into a mixed state is given by . We propose to identify this scale with the quantum break-time , since it essentially depends on the quantum scattering between gravitons and orthogonal states producing a non-zero value for .
Finally we observe that for divergent (with an almost zero thermodynamical temperature indicating the closeness to equilibrium) the coherent state of graviton is unstable, reaching the equilibrium in mixed states conformed of massless fields in the NS-NS and RR sectors of type II string theories. In that case
The instability of a coherent state in string theory seems to be natural within this framework. Any coherent state in the presence of other orthogonal states would evolve into a mixed state, increasing the entropy and going into decoherence. That is the principal conclusion we want to remark. The reason we consider such observation to be interesting is that we expect to relate a classical space-time in the weak gravity to some dynamics of coherent state of gravitons as proposed and studied in [16]. Under such identification, one could explore the stability of interesting space-time solutions, as the dS space. The Swampland conjectures posit that certain low-energy effective field theories cannot be consistently embedded into a quantum theory of gravity, effectively “swamping” them out of the landscape of viable theories. Specifically, it suggests through the dS-conjectures that stable dS (dS) vacua are difficult to achieve in string theory, while Minkowski and AdS vacua are more natural. The tendency of the SEAQT dynamics to favor equilibrium states corresponding to Minkowski or AdS backgrounds aligns with this aspect of the swampland conjecture, reinforcing the idea that only certain spacetime configurations are consistent with quantum gravity.
In conclusion, the SEAQT dynamics provide valuable insights into the interplay between quantum thermodynamics and string theory. The instability of coherent states under the SEAQT framework and the resulting evolution toward an equilibrium mixture of massless modes are consistent with the principles of thermodynamics, particularly the tendency of systems to evolve toward states of maximum entropy. This behavior aligns with string theory phenomenology, where Minkowski and AdS spacetimes emerge naturally as stable backgrounds. Moreover, it could offer support for the swampland conjecture by demonstrating how non-linear dynamics favor certain spacetime configurations over others.
Author Contributions
Conceptualization, C.D. and O.L.-B.; Methodology, C.D. and O.L.-B.; Writing—original draft preparation, C.D. and O.L.-B.; Writing—review and editing, C.D. and O.L.-B. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by CONAHCYT under the project CF-2023-I-682.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Acknowledgments
We thank Nana Cabo-Bizet for useful discussions around these topics.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A. Construction of a Coherent State of Gravitons in String Theory
For completeness, we show that a coherent state of fields formed by massless states created by symmetric, antisymmetric, and scalar operators in the NS-NS sector, are indeed orthogonal to each other. We elaborate on the case of a coherent state of gravitons and one constructed by states corresponding to the B-field. Extension to the dilaton and states in the RR sector for type II superstrings are commented on at the end.
Consider the algebra of the fermionic annihilation and creation mode operators for the NS-NS sector, namely
for . The annihilation modes act as
for annihilating the left and right ground states of the NS sector of the closed string. Let us define the closed string ground state as
The massless graviton is given as (with )
Massive symmetric states are expressed by the action of rising modes for all . Therefore, the most general coherent state one can think of is constructed by the action of all rising fermionic modes on the ground state (for simplicity, we do not consider the bosonic part of the spectrum). In contrast, with quantum field theory where there is a unique rising operator acting on the quantum states in string theory there are infinity number of rising and lowering operators, actually, one for each string mode. In this manner the coherent state is given by
where the rising operator and the corresponding lowering operator are defined as
with being a traceless symmetric tensor depending on the mode n. is known as the coherence parameter, and in the case of fermionic modes satisfies
is an operator that creates symmetric states (with respect to and ) while acts as an annihilator operator for each mode n. The anticommuting algebra, which is compatible with the simple fermionic oscillator, requires the eingenvalue of a coherent state to be a Grassmann number. Notice that the presence of both left-moving and right-moving operators is required due to the level-matching.
Then, we want to see if is actually a coherent state with respect to the annihilator operators . For that, we must show that is indeed an eigenstate of the operator
this is
for some numbers . Using the Baker-Campbell-Hausdorff formula we have
where the nested commutator is given by
A similar calculation shows that the third term applied to the ground state is
However, due to the nilpotency of all terms involving a squared or higher order on vanish. Therefore, since annihilates the ground state,
from which we conclude that is indeed a coherent state with respect to the annihilator operator . Notice that for this state to be coherent it is required the nilpotency on the polarization tensor .
In the paper, we focus on the state formed by massless gravitons for clarity. This is
which is an eigenstate of the operator ,
In the NS-NS sector are then many states orthogonal to a coherent state of gravitons, rather we include all modes or just the massless graviton. Moreover, by construction in string theory, the existence of other three sectors in the Hilbert space, as the Neveu-Schwarz-Ramond (NS-R), Ramond-Neveu-Schwarz (R-NS) and Ramond-Ramond (RR) provide with a plethora of many other orthogonal states. We refer to those states as . It is important to notice that this environment of having the existence of many orthogonal states to the graviton coherent state appears naturally in string theory, providing with the required conditions to apply the SEAQT framework.
References
- Kachru, S.; Kallosh, R.; Linde, A.D.; Trivedi, S.P. De Sitter vacua in string theory. Phys. Rev. D 2003, 68, 046005. [Google Scholar] [CrossRef]
- Damian, C.; Diaz-Barron, L.R.; Loaiza-Brito, O.; Sabido, M. Slow-Roll Inflation in Non-geometric Flux Compactification. J. High Energy Phys. 2013, 2013, 109. [Google Scholar] [CrossRef]
- Damian, C.; Loaiza-Brito, O. More stable de Sitter vacua from S-dual nongeometric fluxes. Phys. Rev. D 2013, 88, 046008. [Google Scholar] [CrossRef]
- Leontaris, G.K.; Shukla, P. Seeking de Sitter vacua in the string landscape. PoS 2023, CORFU2022, 058. [Google Scholar] [CrossRef]
- AbdusSalam, S.; Gao, X.; Leontaris, G.K.; Shukla, P. Systematic exploration of the non-geometric flux landscape. arXiv 2024, arXiv:2410.22444. [Google Scholar]
- Damian, C.; Loaiza-Brito, O. Galois groups of uplifted de Sitter vacua. Ann. Phys. 2024, 467, 169697. [Google Scholar] [CrossRef]
- Prieto, D.; Quirant, J.; Shukla, P. On the limitations of non-geometric fluxes to realize dS vacua. J. High Energy Phys. 2024, 5, 8. [Google Scholar] [CrossRef]
- Danielsson, U.H.; Van Riet, T. What if string theory has no de Sitter vacua? Int. J. Mod. Phys. D 2018, 27, 1830007. [Google Scholar] [CrossRef]
- Garg, S.K.; Krishnan, C. Bounds on Slow Roll and the de Sitter Swampland. J. High Energy Phys. 2019, 11, 75. [Google Scholar] [CrossRef]
- Obied, G.; Ooguri, H.; Spodyneiko, L.; Vafa, C. De Sitter Space and the Swampland. arXiv 2018, arXiv:1806.08362. [Google Scholar]
- Ooguri, H.; Palti, E.; Shiu, G.; Vafa, C. Distance and de Sitter Conjectures on the Swampland. Phys. Lett. B 2019, 788, 180–184. [Google Scholar] [CrossRef]
- Palti, E. The Swampland: Introduction and Review. Fortsch. Phys. 2019, 67, 1900037. [Google Scholar] [CrossRef]
- van Beest, M.; Calderón-Infante, J.; Mirfendereski, D.; Valenzuela, I. Lectures on the Swampland Program in String Compactifications. Phys. Rep. 2022, 989, 1–50. [Google Scholar] [CrossRef]
- Graña, M.; Herráez, A. The Swampland Conjectures: A Bridge from Quantum Gravity to Particle Physics. Universe 2021, 7, 273. [Google Scholar] [CrossRef]
- Agmon, N.B.; Bedroya, A.; Kang, M.J.; Vafa, C. Lectures on the string landscape and the Swampland. arXiv 2022, arXiv:2212.06187. [Google Scholar]
- Dvali, G.; Gomez, C.; Zell, S. Quantum Break-Time of de Sitter. J. Cosmol. Astropart. Phys. 2017, 6, 028. [Google Scholar] [CrossRef]
- Dvali, G.; Gomez, C.; Zell, S. Quantum Breaking Bound on de Sitter and Swampland. Fortschr. Phys. 2019, 67, 1800094. [Google Scholar] [CrossRef]
- Berezhiani, L.; Dvali, G.; Sakhelashvili, O. de Sitter space as a BRST invariant coherent state of gravitons. Phys. Rev. D 2022, 105, 25022. [Google Scholar] [CrossRef]
- Berezhiani, L.; Dvali, G.; Sakhelashvili, O. Consistent Canonical Quantization of Gravity: Recovery of Classical GR from BRST-invariant Coherent States. arXiv 2024, arXiv:2409.18777. [Google Scholar]
- Brahma, S.; Dasgupta, K.; Tatar, R. de Sitter space as a Glauber-Sudarshan state. J. High Energy Phys. 2021, 2021, 104. [Google Scholar] [CrossRef]
- Brahma, S.; Dasgupta, K.; Tatar, R. Four-dimensional de Sitter space is a Glauber-Sudarshan state in string theory. J. High Energy Phys. 2021, 2021, 114. [Google Scholar] [CrossRef]
- Blumenhagen, R.; Kneissl, C.; Makridou, A. De Sitter quantum breaking, swampland conjectures and thermal strings. J. High Energy Phys. 2021, 10, 157. [Google Scholar] [CrossRef]
- Beretta, G.P. Nonlinear quantum evolution equations to model irreversible adiabatic relaxation with maximal entropy production and other nonunitary processes. Rep. Math. Phys. 2009, 64, 139–168. [Google Scholar] [CrossRef]
- Brahma, S.; Calderón-Figueroa, J.; Luo, X.; Seery, D. The special case of slow-roll attractors in de Sitter: Non-Markovian noise and evolution of entanglement entropy. arXiv 2024, arXiv:2411.08632. [Google Scholar]
- Beretta, G.P. Nonlinear model dynamics for closed-system, constrained, maximal-entropy-generation relaxation by energy redistribution. Phys. Rev. E—Stat. Nonlinear Soft Matter Phys. 2006, 73, 026113. [Google Scholar] [CrossRef]
- Montañez-Barrera, J.; von Spakovsky, M.R.; Damian Ascencio, C.E.; Cano-Andrade, S. Decoherence predictions in a superconducting quantum processor using the steepest-entropy-ascent quantum thermodynamics framework. Phys. Rev. 2022, 106, 032426. [Google Scholar] [CrossRef]
- Montanez-Barrera, J.; Damian-Ascencio, C.E.; von Spakovsky, M.R.; Cano-Andrade, S. Loss-of-entanglement prediction of a controlled-PHASE gate in the framework of steepest-entropy-ascent quantum thermodynamics. Phys. Rev. 2020, 101, 052336. [Google Scholar] [CrossRef]
- Cano-Andrade, S.; Beretta, G.P.; von Spakovsky, M.R. Steepest-entropy-ascent quantum thermodynamic modeling of decoherence in two different microscopic composite systems. Phys. Rev. 2015, 91, 013848. [Google Scholar] [CrossRef]
- Morishita, T.; Kobayashi, K.; Ishikawa, A. Relaxation dynamics of nonresonant excitation transfer processes assisted by coherent phonon environment. Jpn. J. Appl. Phys. 2023, 62, 102005. [Google Scholar] [CrossRef]
- Witten, E. A mini-introduction to information theory. Riv. Nuovo C. 2020, 43, 187–227. [Google Scholar] [CrossRef]
- Beretta, G.P. Steepest entropy ascent model for far-nonequilibrium thermodynamics: Unified implementation of the maximum entropy production principle. Phys. Rev. 2014, 90, 042113. [Google Scholar] [CrossRef] [PubMed]
- Beretta, G.P. The fourth law of thermodynamics: Steepest entropy ascent. Philos. Trans. R. Soc. 2020, 378, 20190168. [Google Scholar] [CrossRef] [PubMed]
- Weinberg, S. What happens in a measurement? Phys. Rev. A 2016, 93, 032124. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).