Conclusions Not Yet Drawn from the Unsolved 4/3-Problem—How to Get a Stable Classical Electron

Abstract

It has been known for over 100 years that there is a discrepancy between Maxwell’s electrodynamics and the idea of a classical electron as the “atom” of electricity. This incompatibility is known under the terms 4/3 problem of the classical electron and radiation reaction force and was circumvented in the currently most successful theories, the quantum field theories, by limit value considerations, by the mutual subtraction of infinities, i.e., by purely mathematical methods that eliminate obvious contradictions but are not really based on an intuitive understanding of its physical causes. The actual origin of the problems mentioned lies in the instability of the classical electron. Stabilization cannot be achieved within the framework of Maxwell’s electrodynamics. This raises the question of what a minimal change to the fundamentals of electrodynamics should look like, which contains Maxwell’s theory as a limiting case. A detailed analysis of the 4/3 problem points to models that fulfill these requirements.

1. Introduction

The discussion about the origin of the problems of the classical electron is essentially about the concept of particles. The question is whether the idea of assuming atoms of electricity to describe electrodynamic phenomena, as Helmholtz had already suggested, is expedient. Stoney suggested the name “electron” for these “atoms”. In formulating this description, classical electrodynamics encountered two unsolvable problems, the 4/3 problem and the problem of radiation reaction force [1,2]. In this article, we focus in particular on the cause of the 4/3 problem and examine what conclusions can be drawn from the form of the discrepancy and what kind of models can solve both problems of classical electrodynamics.

Early on in the formulation of the dynamics of electrons, an idea emerged that is still generally accepted today: a distinction is made between the dynamics of electromagnetic fields, the dynamics of electrons and the interaction between particles and fields. According to the special theory of relativity, the mass of particles is expected to increase with velocity according to the well-known Equation (4) with the $\gamma$ factor. It is a characteristic of moving particles that are described in a “stationary” three-dimensional Euclidean reference system $\mathrm{\Sigma }$, see Section 2 and Figure 1, that the velocity vector $u^{\mu }\stackrel{\left(\right)}{=}\gamma (c,\overrightarrow{v})$ does not have to be orthogonal to the position vectors $x^{\mu }:=(0,\overrightarrow{x})$, i.e., the scalar product 1

$$u_{\mu }{x}^{\mu }:=-\gamma \overrightarrow{v}\overrightarrow{x}\le 0.$$

(1)

does not have to vanish. The equal sign only applies to particles at rest.

For electrons, which are described by electromagnetic fields, such a particle behavior was already expected by Lorentz and Abraham [2,3]. Rohrlich clearly demonstrated in [4,5] that the formalism of special relativity only guarantees that the four-momentum of a field distribution behaves Lorentz-covariantly. However, the 4/3 problem already established by Abraham [1] shows that it was not possible to consistently represent electrons moving in $\mathrm{\Sigma }$ by fields. The reason lies in the instability of the classical electron. To discuss the 4/3 problem, it is sufficient to consider electrons moving at constant speed. The result of such a field description of the classical electron is given in Section 2 in order to be able to discuss in Section 3 which minimal changes lead to a stable model of classical electrons, so that the energy–momentum relationships also apply in reference systems that are not orthogonal to $u^{\mu }$, as the inequality (1) allows. In such a model, which allows a stable classical electron to be formulated, no divergences occur. Maxwell’s electrodynamics would thus no longer contradict Millikan’s famous experiment, which proved the quantization of the electric charge before quantum mechanics moved quantization to the center of scientific interest, as explained in Section 3.

2. Particle and Field Description of the Classical Electron

Particles are lumps of matter that remain undestroyed when scattered with sufficiently low energies. Such particles can be assigned an invariant mass $m_0$ and the concepts of kinematics can be applied without contradiction. To understand what this means, it is helpful to look at the definitions and relationships of relativistic kinematics and their relationship to the non-relativistic terms, see Appendix A.

From the assignment of the space–time coordinates $x^{\mu }$ to time t and the position vector $\overrightarrow{x}$

$$x:=(c_{0}t,\overrightarrow{x})$$

(2)

and the four-momentum $p^{\mu }$ to the energy E and the spatial momentum $\overrightarrow{p}$

$$p:=({\displaystyle \frac{E}{c_0}},\overrightarrow{p})$$

(3)

it follows that the mass m of the particles depends on the ratio of their velocity v to the speed of light $c_0$

$$m\left(\beta \right)\stackrel{\left(A12\right)}{=}\gamma m_0\mathrm{with}\gamma :={\displaystyle \frac{1}{\sqrt{1-{\beta }^2}}}\mathrm{and}\beta :={\displaystyle \frac{v}{c_0}}$$

(4)

so the four-momentum results in

$$\begin{array}{c}\hfill p\stackrel{\left(A12\right)}{=}\gamma m_0(c_0,\overrightarrow{v}).\end{array}$$

(5)

A closer look shows that definition (3) follows from definition (2) if a suitable action function for a free particle is defined and the momentum is derived from it as the temporal component of the energy–momentum tensor

$$p^{\mu }\stackrel{\left(A32\right)}{=}{\int }_{\mathrm{\Sigma }}{\mathrm{\Theta }}^{\mu 0}\left(x\right){\mathrm{d}}^3\sigma .$$

(6)

The integration here takes place over that three-dimensional space-like volume $\mathrm{\Sigma }$ in which the velocities $\overrightarrow{v}$ are determined, i.e., in principle over any three-dimensional space-like volume. Precisely this arbitrariness of $\mathrm{\Sigma }$ is obviously one of the characteristics of a particle, see Figure 1.

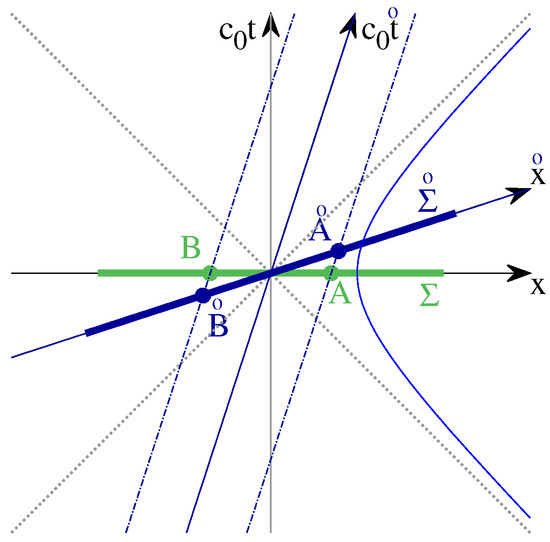
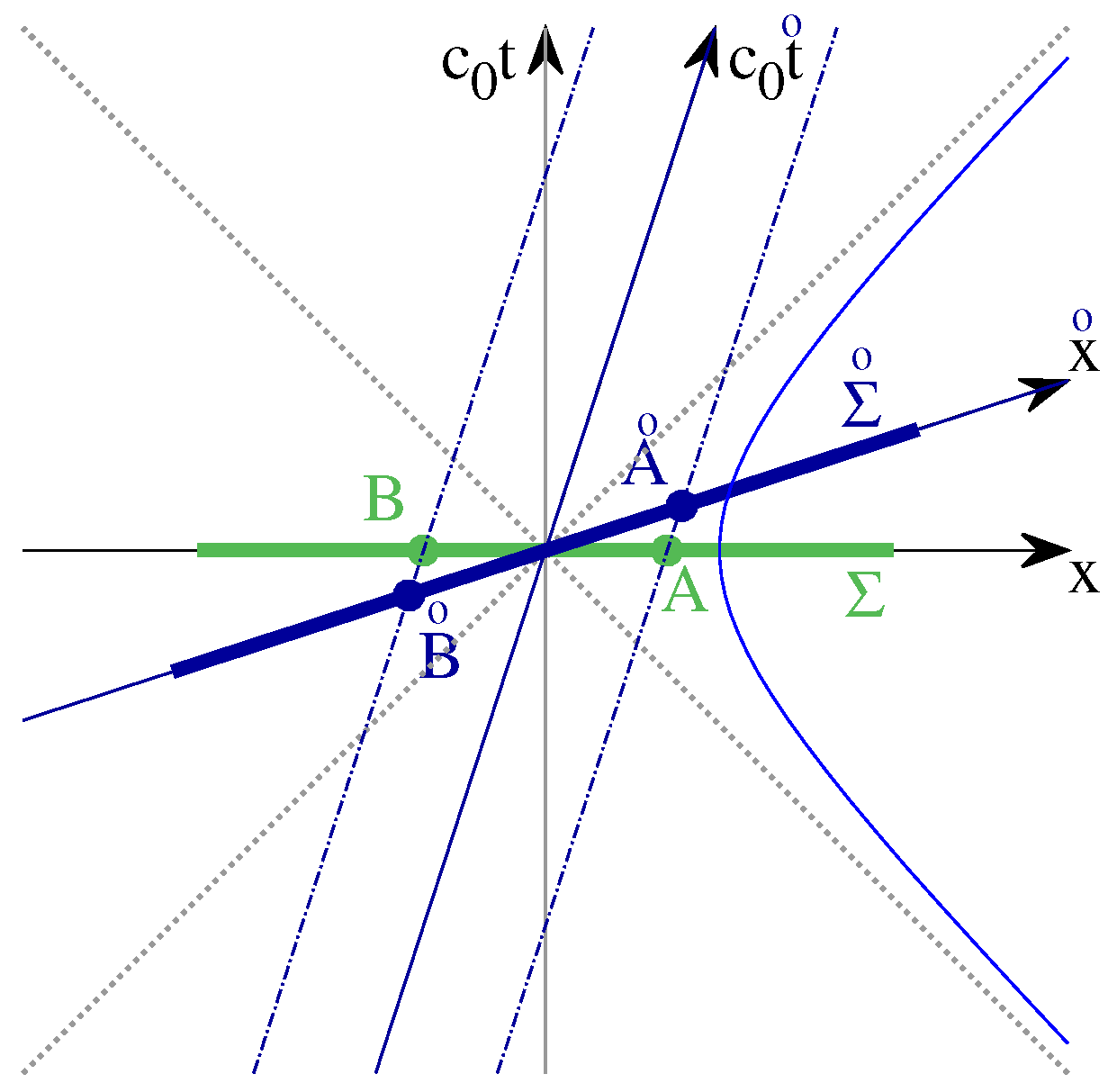
Figure 1. We describe an electron in the laboratory system $\mathrm{\Sigma }$ and in the comoving system $\stackrel{\circ }{\mathrm{\Sigma }}$ according to the rules of special relativity, as shown in this Minkowski diagram. Note that the points A and $\stackrel{\circ }{A}$ connected by dashed lines have the same spatial coordinates $\stackrel{\circ }{x}$ and only differ in time $\stackrel{\circ }{t}$. Since the electron is at rest in the comoving system, the field strengths measured in the comoving system are the same at A as in $\stackrel{\circ }{A}$. To determine the field strength measured in $\mathrm{\Sigma }$ at A, the coordinates x and t at A must be taken into account and the field strength tensor must be transformed according to the transformation rules of a tensor. The relationships valid for A apply accordingly for B.

Figure 1. We describe an electron in the laboratory system $\mathrm{\Sigma }$ and in the comoving system $\stackrel{\circ }{\mathrm{\Sigma }}$ according to the rules of special relativity, as shown in this Minkowski diagram. Note that the points A and $\stackrel{\circ }{A}$ connected by dashed lines have the same spatial coordinates $\stackrel{\circ }{x}$ and only differ in time $\stackrel{\circ }{t}$. Since the electron is at rest in the comoving system, the field strengths measured in the comoving system are the same at A as in $\stackrel{\circ }{A}$. To determine the field strength measured in $\mathrm{\Sigma }$ at A, the coordinates x and t at A must be taken into account and the field strength tensor must be transformed according to the transformation rules of a tensor. The relationships valid for A apply accordingly for B.

In the field description, we assume, like Abraham [1], that the mass of the electron is purely electromagnetic in nature, see Appendix B, and calculate energy and momentum according to Equation (6) for the field of a charge $e=-e_0$ from the symmetric energy–momentum tensor

$${\mathrm{\Theta }}^{\mu \nu }\stackrel{\left(A35\right)}{=}-{\displaystyle \frac{1}{{\mu }_0}}{\eta }^{\mu \kappa }{F}_{\kappa \lambda }{F}^{\nu \lambda }+{\displaystyle \frac{1}{4{\mu }_0}}{\eta }^{\mu \nu }{F}_{\kappa \lambda }{F}^{\kappa \lambda }.$$

(7)

In a reference frame $\mathrm{\Sigma }$, in which the electron moves at a speed $\overrightarrow{v}=c\overrightarrow{\beta }$, see Figure 1, the field strengths transform according to the Lorentz transformation of the field strength tensor $F^{\mu \nu }$ to

$$\begin{array}{c}\hfill \begin{array}{c}\overrightarrow{E}\left(\overrightarrow{\beta }\right)\stackrel{\left(A46\right)}{=}{\overrightarrow{E}}_{\Vert }\left(0\right)+\gamma {\overrightarrow{E}}_{\perp }\left(0\right)\mathrm{with}{\overrightarrow{E}}_{\Vert }:={\displaystyle \frac{\overrightarrow{\beta }\left(\overrightarrow{\beta }\overrightarrow{E}\right)}{{\beta }^2}},{\overrightarrow{E}}_{\perp }:=\overrightarrow{E}-{\overrightarrow{E}}_{\Vert },\hfill \\ c\overrightarrow{B}\left(\overrightarrow{\beta }\right)\stackrel{\left(A46\right)}{=}\gamma \overrightarrow{\beta }\times \overrightarrow{E}\left(0\right).\hfill \end{array}\end{array}$$

(8)

For a charge at rest, each of the three electric field components contributes to the energy density (A36) with one third of the rest energy density ${\mathcal{E}}_0\left(\overrightarrow{r}\right)$. This leads to an energy of the moving charge e

$$E_e\left(\beta \right)\stackrel{\left(A49\right)}{=}{E}_e\left(0\right){\displaystyle \frac{4{\gamma }^2-1}{3\gamma }},$$

(9)

that does not have the form expected for particles (5), $E_e\left(\beta \right)=\gamma E_e\left(0\right)$. The momentum

$${\overrightarrow{P}}_e\left(\overrightarrow{\beta }\right)\stackrel{\left(A51\right)}{=}{\displaystyle \frac{{\epsilon }_0}{c_0}}{\int }_{\stackrel{\circ }{\mathrm{\Sigma }}}{\mathrm{d}}^3\stackrel{\circ }{\sigma }\left[-{\overrightarrow{E}}_{\perp }\left(0\right)\left({\overrightarrow{E}}_{\Vert }\left(0\right)\overrightarrow{\beta }\right)+\gamma \overrightarrow{\beta }{\overrightarrow{E}}_{\perp }^2\left(0\right)\right]\stackrel{\left(A52\right)}{=}\overrightarrow{\beta }\gamma {\displaystyle \frac{4}{3}}{\displaystyle \frac{E_e\left(0\right)}{c_0}}$$

(10)

shows momentum densities normal to the velocity

$$-{\displaystyle \frac{{\epsilon }_0}{c_0}}{\overrightarrow{E}}_{\perp }\left(0\right)\left({\overrightarrow{E}}_{\Vert }\left(0\right)\overrightarrow{\beta }\right)$$

(11)

and thus internal stresses in the classical electron, which cancel each other out and therefore do not contribute to the total momentum. The factor 4/3 in ${\overrightarrow{P}}_e\left(\overrightarrow{\beta }\right)$ means a discrepancy between the gravitational mass $E_e\left(0\right)/c_0^2$ and the inertial mass ${\displaystyle \frac{4}{3}}{E}_e\left(0\right)/c_0^2$ of the classical electron, which can be read from expression (10). This is in obvious contrast to the particle description of a classical electron according to Equation (5). The cause of this contradiction lies in the instability of the classical electron described by the electromagnetic fields of Maxwell’s electrodynamics, as has been known for over 100 years [6] and is explained in detail in Section 3. Furthermore, conclusions are drawn in this section as to how a model of a stable classical electron can be formulated.

The fact that the discrepancy discussed in this paper, which is over 100 years old, is not a violation of the rules of special relativity is confirmed by the calculation of the four-momentum of the moving electron, if the coordinates $(c_{0}t,\overrightarrow{x})$ are used for the calculation, but integrated over the space-like volume $\stackrel{\circ }{\mathrm{\Sigma }}$, which are simultaneous for the electron at rest. This integration leads to

$$P^{\mu }\left(\overrightarrow{\beta }\right)\stackrel{\left(A53\right)}{=}{\displaystyle \frac{E_e\left(0\right)}{c_0}}(\gamma ,\overrightarrow{\beta }\gamma ),$$

(12)

and relates to the four-momentum of the electron at rest as expected. That the rules of special relativity also apply to the unstable classical electron was emphasized by Rohrlich with his calculations in Ref. [5].

3. Conclusions from the Problems

An interpretation of the frustrating result (9) for the energy of the moving electron is facilitated by a comparison with the Sine–Gordon model, a Lorentz-invariant, topologically interesting, field model in one space and one time dimension, which is illustrated very clearly in Ref. [7]. According to Equation (6.23) of Ref. [7] the rest energy $E_{\mathrm{SG}}\left(0\right)$ of a Sine–Gordon soliton increases for a moving soliton to

$$E_{\mathrm{SG}}\left(\beta \right)=E_{\mathrm{SG}}\left(0\right){\displaystyle \frac{{\gamma }^2+\stackrel{{\gamma }^2}{\overbrace{1+{\gamma }^2{\beta }^2}}}{2\gamma }}=\gamma E_{\mathrm{SG}}\left(0\right).$$

(13)

The stress energy $\propto \gamma$, the potential energy $\propto 1/\gamma$ and the kinetic energy $\propto \gamma {\beta }^2$ are listed here in sequence. This result, $E_{\mathrm{SG}}\left(\beta \right)=\gamma E_{\mathrm{SG}}\left(0\right)$, for the energy of the Sine–Gordon soliton fulfills the expectations of a particle that is subject to the laws of relativistic kinematics. It is also stable because the stress term broadening a particle ≡ Sine–Gordon soliton and the compressing potential energy keep each other in equilibrium. In the soliton at rest, these two energy contributions must be equal in order for stability to occur according to the Hobart–Derrick theorem [8,9]. This results from the one-dimensional integration over the real axis and the number of derivatives, as the stress term contains two derivatives and the potential term contains no derivative. The stress energy is therefore proportional and the potential energy indirectly proportional to the diameter of the soliton.

When comparing the energy expressions (9) and (13), it is noticeable that adding an energy contribution of one third of the rest energy and with a $1/\gamma$ behavior, i.e., of ${\displaystyle \frac{E_e\left(0\right)}{3\gamma }}$, to the energy $E_e\left(\beta \right)$ in Equation (9) leads to the behavior expected for a stabilized classical electron

$$E_e\left(\beta \right)\to E_{\mathrm{stab}}\left(\beta \right):=E_e\left(\beta \right)+{\displaystyle \frac{E_e\left(0\right)}{3\gamma }}\stackrel{\left(9\right)}{=}{\displaystyle \frac{4}{3}}\gamma E_e\left(0\right).$$

(14)

The addition of this contribution thus leads to the energy value required by the momentum calculation (10) of the moving classical electron. The added energy ${\displaystyle \frac{E_e\left(0\right)}{3\gamma }}$ is obviously the energy contribution required for stabilization. After taking it into account, the energy $E_e\left(0\right)$ of the electric field is only 3/4th of the rest energy of a stable classical electron. The size of the added contribution, one third of the electromagnetic field energy for a particle at rest, shows that this contribution must not have any Lorentz indices, i.e., it must be a potential energy. This is because only such a contribution

$$E_{\mathrm{pot}}\left(0\right):=\int {\mathrm{d}}^{3}r{\mathcal{E}}_{\mathrm{pot}}\left(\overrightarrow{r}\right)$$

(15)

to the energy of a particle at rest scales under the substitution $r\to \lambda r$ as one third of the electric field energy of a particle at rest, $E_{\mathrm{pot}}\left(0\right)\stackrel{\left(16\right)}{=}{E}_e\left(0\right)/3$,

$${\displaystyle \frac{\mathrm{d}}{\mathrm{d}\lambda }}{\left[\int {\mathrm{d}}^3\left(\lambda r\right){\mathcal{E}}_0\left(\lambda r\right)\right]}_{\lambda =1}+{\displaystyle \frac{\mathrm{d}}{\mathrm{d}\lambda }}{\left[\int {\mathrm{d}}^3\left(\lambda r\right){\mathcal{E}}_{\mathrm{pot}}\left(\lambda r\right)\right]}_{\lambda =1}=-E_e\left(0\right)+3E_{\mathrm{pot}}\left(0\right)=0,$$

(16)

if the total energy $E_{\mathrm{stab}}\left(\beta \right)=E_e\left(\beta \right)+E_{\mathrm{pot}}\left(\beta \right)$ has a minimum at $\lambda =1$. Such an energy contribution $E_{\mathrm{pot}}\left(\beta \right)$ also contributes nothing to the momentum ${\overrightarrow{P}}_e\left(\overrightarrow{\beta }\right)$ of a moving electron.

We conclude from this comparison with the Sine–Gordon model that the solution of the 4/3 problem requires a formulation of the degrees of freedom of an electron that allows the field values that occur in the center of the electron to have a high potential energy density and thus prevent an unlimited increase in the size of the central region. This is only possible with a formulation of electrodynamics in which the vector fields $A_{\mu }$ are not the fundamental fields, but with vector fields based on a scalar field (Higgs field) $Q\left(x\right)$, with which a suitable potential energy density ${\mathcal{E}}_{\mathrm{pot}}\left(0\right)$ can be formulated, which disappears sufficiently quickly at infinity. The trick is to find a formulation in which the dynamics of the scalar field is formulated by the vector field $A_{\mu }$ in the usual form with four Lorentz indices.

We can draw another important conclusion from the internal stresses that we have determined in connection with the calculation of the momentum of a moving classical electron in Equation (10). These stresses are formulated in the first term in the square brackets in Equation (10). Although they cancel each other out in the calculation of the total momentum, they reflect the instability of the classical electron. These stresses only disappear if the field strength components ${\overrightarrow{E}}_{\Vert }\left(0\right)$ and ${\overrightarrow{E}}_{\perp }\left(0\right)$ are everywhere orthogonal to each other in some additional, internal space. This can be achieved in non-abelian formulations, when the field strength tensors take values in the Lie algebra of some nonabelian group, as they occur in quantum chromodynamics or in the su(2) algebra, in which such field components can belong to orthogonal directions in the algebra.

The 4/3 problem shows that within the Maxwell-Lorentz theory it is impossible to describe electrons as particles localized in a small volume with a quantized charge whose field extends to infinity or to oppositely charged particles. It therefore follows that a modification of the theory is absolutely necessary. This modification should lead to a simple model, but what does simple mean? A simple description is characterized by its intuitiveness, i.e., its direct comprehensibility resulting from an idea or a comparison. The fewer defining fields a description contains, the fewer relations between these fields need to be chosen. As far as electrodynamics and the description of electrons are concerned, there are four scales invented by humans: time, length, mass and charge. Since 2019 they have been formulated in the SI by the numerical values of $c_0,e_0,\hslash \mathrm{and}\mathrm{\Delta }\nu$ of Cs. The conversion between the four associated natural scales of a model and the SI scales can only be obtained by comparison with the experiment. These four scale parameters are not free parameters. A simple model should require as few adjustable parameters as possible. As Einstein’s description of gravitation shows, a simple model does not necessarily lead to simple calculations. Due to possible non-linearity, even a simple model may require complicated calculations.

As a result of the above analyses, I would like to set the following requirements for a simple modified classic model of the electron and electrodynamics:

1.

There is no division of the field degrees of freedom between degrees of freedom for electrons and degrees of freedom for electromagnetic fields, no division of the Lagrangian function into a dynamics of free fields, a dynamics of free particles and an interaction term between these free fields, as exemplified by the Sine–Gordon model. In experiments, electrons are inseparable from their fields. There are no electrons without fields. This is also how electrons should be described.

2.

Electrons should be purely electromagnetic in nature, so their dynamics should be describable by a maximum of three field degrees of freedom as in Maxwell’s electrodynamics. Of the four $A_{\mu }$ fields, one of the degrees of freedom is only a gauge degree of freedom and is therefore described as unphysical. The Maxwell-Diracian description uses four fields for the photon field $A_{\mu }$ and 8-1 degrees of freedom for the complex, normalized four-component Dirac spinors.

3.

As was concluded in connection with Equation (14), the Lagrangian density sought should contain, in addition to the dynamic term with four derivatives that seeks to smear electrons, a potential term without derivatives that holds the electron together. The field itself, which describes the electrons, is uncharged. The problem of the instability of the classical electron, which has remained unsolved for 100 years, cannot be attributed to the repulsion of charged regions inside the electron, as is often assumed [10]. The topological structure of the field of charges should lead to attraction or repulsion and quantization of the charges due to the terms in the Lagrangian.

4.

The dynamic term with four derivatives should asymptotically transform the field into the structure of the field of a point charge e, i.e., into a field that can be described in Abelian terms. The potential term should only have a short-range effect and modify the Coulomb law at small distances, i.e., cause the charge to run due to the geometry.

5.

The description of electrons following from the Lagrangian should bosonize Maxwell-Dirac’s formulation of electrodynamics.

In addition to the stabilization of electrons, a potential term in the Lagrangian would allow further interesting conclusions to be drawn. It already classically leads to a non-vanishing trace of the energy–momentum tensor [11]. The “trace anomaly” of QED would thus find an explanation. Anomalies are symmetries of the Lagrangian, i.e., of the classical description, which are lost in quantum theory. Scale transformations lead to the vanishing of this trace in the classical description of electrodynamics for massless electrons. In QED, however, this trace remains non-zero even for vanishing fermion mass, as explained in more detail in Section 19.5 of Peskin-Schröder [12] with reference to the original work [13]. The trace anomaly can therefore be seen as an indication of the absence of the potential term in classical electrodynamics.

QED suffers from the serious problem that it cannot explain the vacuum energy density of the universe. From the measurements of the Planck Collaboration [14], its value is 0.69 ${\rho }_{\mathrm{crit}}$, whereby the critical energy density is $4.9{\displaystyle \frac{\mathrm{GeV}}{{\mathrm{m}}^3}}$. The many fluctuations of the quantum fields could in principle contribute to the vacuum energy density. However, if they are taken into account, they result in a value that is dozens of powers of ten too high. There is no consensus on the value, but factors of up to 120 powers of ten are mentioned. The usual alternative in quantum field theory of subtracting vacuum expectation values leads to an error at least as large, namely the disappearance of the value. This is known as the “cosmological constant problem”. With a potential term in the Lagrangian of nonlinear electrodynamics, each particle would contribute directly to the vacuum energy density and Einstein’s cosmological constant should result as the spatial average of these contributions.

There are many papers on the 4/3 problem [4,5,6,10,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38], as well as other studies cited in these works. Some of them also deal with the second problem of classical electrodynamics, the radiation reaction problem. For a formulation of electrodynamics with only one non-Abelian field, following the above conditions, this second problem is irrelevant. A single fundamental non-Abelian field with a suitable Lagrangian function as proposed above cannot have a reaction on itself, but can only follow its dynamics as formulated in the Lorentz invariant Lagrangian. As far as the Lagrangian is a Lorentz scalar, no contradiction with special relativity can occur due to the consistency of the theory. Each scientist will form their own image and decide for themselves which image is most likely to be developed further. The above considerations show what minimal changes sould be made to Maxwell’s electrodynamics in order to eliminate the inconsistencies, which are more than a hundred years old. Maxwell’s electrodynamics should then turn out to be a clever linear approximation to this nonlinear theory. It should be interesting to investigate models with such properties [39,40].

We can then ask ourselves how fundamental theoretical physics would have developed if a stable field configuration for an electron had been found soon after the investigations of Abraham and Lorentz, for a model of a classical electron whose far field corresponds to the Coulomb field of classical electrodynamics for a point-shaped electron, as suggested by Equation (A42). There would then have been no singularity that would have had to be regularized. I think it is quite unlikely that the path proposed by Kramers at the Shelter Island Conference in 1947 would have been taken. As Veltman put it in a lecture [41], Kramers said: “Well, let’s do it like follows: Let’s not try to understand everything. Let’s just say the experimental mass, that’s something we can measure and God knows what goes on in the electron at small distances and the like. Why don’t we just skip that part of the problem?” I also don’t assume that the great physicists of the past and present would not have come up with anything to explain the experiments in such a model.