1. Introduction
Since long ago, investigations on de Sitter and quasi-de Sitter cosmic solutions have attracted much attention along different research lines. Such studies were somewhat inspired by the possible avoidance of the primeval singular state ordinarily predicted by “big-bang” models, and the decaying vacuum emerging from a plethora of inflationary models driven by scalar fields including or excluding quadratic corrections to Einstein gravity [
1,
2,
3,
4,
5,
6,
7]. A different approach analysed the possible creation of the universe from “nothing” (in the sense of Vilenkin [
8]), with the classical universe emerging as a de Sitter solution from an expected, but still observationally unavailable, quantum gravity regime. This primeval state without ordinary matter may be characterised by a physical energy scale,
, or equivalently, by a vacuum energy density,
, where
GeV is the reduced Planck mass (in our units,
).
It is also widely known that a non-singular de Sitter spacetime is structurally unstable both from quantum and classical viewpoints, at least due to three different effects: quantum corrections on the geometric sector of general relativity [
4], the existence of thermal fluctuations [
9], and the process of gravitational particle creation in the expanding universe [
7,
10,
11,
12,
13,
14], Henceforth, due to its simplicity and interesting physical consequences for the evolution of the emergent classical initial vacuum state, the presence of thermal instabilities conjoined with an irreversible flow of energy, matter, and entropy forming the thermal bath will be taken for granted. Additional reasons will be outlined ahead.
More recently, independent astronomical observations have shown that the cosmic concordance model (
CDM + Inflation) provides a quite reasonable and predictive description of the current universe driven by a rigid vacuum energy density,
. However, the incredible discrepancy with what is expected from quantum field theory (QFT) as compared to current astronomical observations,
, gave rise to the cosmological constant problem (CCP) [
15]. Furthermore, according to the cosmic concordance model, the dominance of rigid vacuum (
, where
is the matter density) took place at a redshift
(see, e.g., [
16]) thereby leading to the so-called coincidence problem (CP). Another well-known consequence of the rigid vacuum
CDM cosmology is the inexorable evolution of the current universe to a final de Sitter spacetime. Here, it is characterised by an extremely low vacuum energy density, say,
, where the Hubble parameter
provides the final de Sitter constant energy scale, which will be attained only for
.
Currently, the standard rigid vacuum cosmology is also being observationally challenged by the
and
tensions. In the case of
, local determinations of the Hubble constant (
) using Cepheid-calibrated supernovae of the SHOES collaboration [
17], measurements at intermediate redshifts from a combination of tests [
18,
19] and strong lensing time-delays [
20], which, in comparison with the independent prediction of Planck collaboration plus
CDM, shows a clear-cut tension around 5
[
21]. In addition, estimates based on cosmic shear evaluations from weak lensing are favouring values of the parameter
, where
measures the current mass fluctuation in 8 h
−1Mpc, which are lower than the ones provided by early time probes [
22,
23,
24].
In this context, it seems natural to advocate that the whole classical evolution of the universe would be analytically described between two de Sitter stages defined by a pair of extreme and constant energy scales,
and
. In this case, for all theoretical purposes, we may also consider that the second de Sitter vacuum state of very low energy density is the true vacuum state. In certain sense, the structural instability of the primeval de Sitter (
) is somewhat driving the evolution of the observed universe to its ‘ground state’, corresponding to the final de Sitter vacuum,
, where the sub-index 0 refers to present day quantities. Thus, it is not surprising that a lot of attention has been paid to running vacuum cosmologies in the last decade by several reasons, among them: (i) a simple solution to the singularity problem, as well as the old CCP and CP puzzles; (ii) a complete cosmology (from de Sitter to de Sitter) with two accelerating stages driven by the same actor, described by the running vacuum energy density,
, departing slightly at all phases from the rigid vacuum model plus slow-roll inflation; and (iii) a possible solution to the current
and
observational tensions plaguing the current standard cosmology provided by the
CDM model, which at late times model is driven by a rigid vacuum [
25,
26,
27,
28,
29,
30,
31,
32].
As we shall see, a suitable
-term uniting both de Sitter phases can be deduced using non-equilibrium thermodynamics and the Einstein field equations (EFE). The classical evolution of the universe can also be analytically described, and some of the questions outlined above are answered. Perhaps more interestingly, we demonstrate that a minimally coupled ordinary scalar field cannot describe the irreversible two-fluid approach of the running vacuum scenario. However, the whole evolution can perfectly be mimicked by a single minimally coupled non-canonical field when interpreted as a mixture of two minimally coupled interacting perfect fluids [
33,
34,
35,
36,
37,
38,
39,
40,
41,
42].
The paper is organised as follows. In
Section 2, we set up the Einstein equations for an interacting mixture of running vacuum medium plus a perfect fluid. In
Section 3, the irreversible thermodynamic approach for such a mixture is discussed in detail. In particular, by taking into account only the thermal effects of the interacting mixture, a viable expression for
(
H) is phenomenological deduced based on Einstein’s equations and non-equilibrium thermodynamics. The equation governing the entire classical evolution of the universe from
to
is also determined.
Section 4 is dedicated to the basic results of the cosmic eras, and the solutions to some cosmological problems are also discussed. In
Section 5, a representation of the whole process in terms of a non-canonical scalar field and the associated dynamics is investigated. The article is closed in
Section 6 with the final comments and conclusions. In
Appendix C, the two basic parameters of the non-canonical scalar field potential are calculated in terms of
,
,
, and the mass scale (
M) of the scalar field.
2. Basic Equations
In what follows we consider a class of Friedmann–Lemaître–Roberson–Walker (FLRW) cosmologies described by a flat geometry:
where
is the scale factor. In such a background, the EFE for a perfect fluid plus a running vacuum can be written as
where
and
p are the energy density and pressure of the ordinary fluid component, while a dot means a comoving time derivative. Now, by adopting the “
-law” equation of state (EoS),
it is readily seen that Equations (
2)–(
4) imply that the cosmic dynamics is driven by the “H-equation of motion”
where
is the vacuum density parameter.
In principle, for
, it is possible to have two extreme de Sitter solutions (
) describing the initial and final vacuum states (say,
and
) and, as such, two accelerating cosmic states (early and late time inflation) may result from the same actor [
26,
27,
32]. The initial de Sitter spacetime (
) works like a “repeller” (unstable solution) at early times. However, due to the cosmic evolution, energy, particles and entropy are continuously being transferred to the fluid component, thereby giving rise to an attractor de Sitter spacetime in the distant future, characterised by a very low energy scale (
). Accordingly,
implies that the fluid energy densities for both extreme scales are nullified, i.e.,
.
Of course, the complete evolution driven by Equation (
5), linked to the subsequent radiation-vacuum and matter-vacuum dominated phases, only comes out if the expression for
is known. Next, it will be derived by combining the EFE, non-equilibrium thermodynamics, and the limiting ‘boundary’ constraints provided by the extreme de Sitter solutions.
3. Running Vacuum: A Thermal Approach
Let us now consider the energy flow from the decaying vacuum creating particles and entropy to the fluid component. Following standard lines, the thermodynamic states for the interacting mixture is defined by the energy conservation law (
) and the balance equations for the number of particles and entropy fluxes,
and
:
where
n and
s are the particle concentration and entropy density, and
is the particle creation rate, being the same for particle number and entropy. Thus, the entropy of the fluid is also a pure consequence of the decaying vacuum and, as such, the bulk viscosity process and gravitational matter creation have been neglected [
43]. In principle, one may argue that the second law of thermodynamics should be applied for both components. However, the vacuum fluid behaves like a condensate carrying no entropy, as happens in the two-fluid description ordinarily employed in superfluid dynamics [
44]. The vacuum state is assumed to have energy, but no entropy and real particles.
In the course of the decaying vacuum process, one may see from (7) and (8) that the specific entropy,
, remains constant (
). Such an interesting result becomes more clear when rewritten as (see
Appendix A):
This inequality implies that the decaying vacuum (due to its own energy density) can only produce matter in the space-time (), while the reverse process is thermodynamically forbidden.
The condition
has another remarkable consequence. Actually, by combining Gibbs’ law,
, with (4) and (5), we find a key result in this framework:
The second equality above is a typical first-order thermodynamic relation uniting the stress (“flux”) to its thermodynamic force . The above coefficient of is the fluid enthalpy density which, due to the weak energy condition, satisfies the inequality .
Notice that by adding
EFE (
2) and (
3), we find
, which means that
. Thus, since
from Equation (
9), it follows that the constraint
must be obeyed. In this thermal approach, a decaying vacuum from the primeval de Sitter state is also required by the second law of thermodynamics.
Now, by inserting
h into Equation (
10), a new and interesting result is derived:
where
B is a constant to be fixed by the de Sitter ‘boundary conditions’. To the best of our knowledge, the above integral expression defining
(
H) in terms of the creation rate
has not been found before. Thus, in order to obtain a complete description (from
to
), an expression for
needs to be specified.
At this point, it should be remarked that, until now, only classical macroscopic tools were explored, namely EFE and non-equilibrium thermodynamics. It is also well known that particle creation from a perturbed vacuum state is essentially a microscopic phenomenon. Hence, from a more rigorous viewpoint, an expression for in this context cannot be macroscopically deduced. Nevertheless, under the proviso that the dimension of , a simple possibility would be , where the factor 3 is introduced for mathematical convenience, and is a dimensionless positive free parameter, in principle, restricted on the interval .
Furthermore, such a linear expression generates a term
. However, it is not enough for describing the unified cosmic history from de Sitter to de Sitter, since it generates a singular initial state [
38]. At late times, due to the very low expansion rate,
is taken as a constant parameter. However, it may be a function of
H at early times, thereby implying a more intense transference of energy, particles, and entropy to the material component. This is needed for the formation of the primeval thermal bath, both in the macroscopic approach [
26] and for a possible scalar field description [
45].
In this connection, a renormalized vacuum energy density proportional to
has been derived long ago [
7]. This is also the next term obtained by Shapiro and Solà based on the covariance of the renormalized action [
46]. From Equation (
11), we also see that a term proportional to
can also be generated by a creation rate
. Therefore, inspired by such studies, and also some ad hoc treatments for
[
25,
26,
32], a quadratic correction, namely
, where the arbitrary
, is added to the natural term, based on dimensional grounds. In particular, for
it follows that
whereas
, as given by Equation (
11), reads:
As a simple check of such expressions, one may compute directly
(see
Appendix B for a more detailed calculation, including both de Sitter boundary conditions).
Now, it is easy to see that the expressions for the density parameters take the form
where
is the matter density parameter. Now, by inserting
or
into Equation (
5), it is readily seen that the classical evolution of the model between the two extreme de Sitter phases is governed by
The above equation depends on two pairs of positive parameters (
) and two energy scales (
). Like in the rigid vacuum model,
is differently fixed by the description of the cosmic eras
(radiation) and
(dust). So, it cannot rigorously be considered a new free parameter. For the remaining three parameters, we remark that the energy scale
has a natural upper bound given by the reduced Planck mass
(see
Section 1), while the final
scale can be determined in order to solve the CCP problem, by assuming, for instance, that
. It can also be calculated by the model in terms of
.
Figure 1 schematically displays the complete evolution of the whole classical scenario. Observe that Equation (
16) remains valid, even for
, since this minimal model is also defined by the same extreme constant physical scales (
,
). The only difference is that the late time evolution for
happens in such a way that CMB photons are not produced any more. Moreover, it is easy to see that the scenario becomes the standard, rigid
CDM cosmology, described here in terms of the constant final scale
. Thus, only the early inflationary stage is modified, because it started from a pure de Sitter vacuum solution. The details of each transition describing the evolution (from de Sitter to de Sitter) through different cosmic eras will be discussed next.
5. Running Vacuum Cosmology: A Non-Canonical Scalar Field Description
Let us now consider a pure scalar field
minimally coupled with gravity. In the framework of general relativity, the total action for a non-canonical field can be written as
where
is a functional of the standard kinetic term
.
In what follows, it will be assumed that the dominant energy contribution in the primeval universe comes from the non-canonical scalar field, which is described by the Lagrangian [
49]
where the scale
M has dimension of mass,
is the potential, and
a real positive number. The energy–momentum tensor (EMT),
−
, is diagonal, with components
where
is a non-canonical kinetic term, and a dot means a time derivative. It is also easy to show that the following equation of motion drives the evolution of the non-canonical scalar field:
which can also be obtained from the total energy conservation law (
).
Let us now prove that a canonical scalar field cannot describe both the smooth dynamic and thermodynamics of a running (H)-term (from de Sitter to de Sitter), as discussed in the previous sections.
5.1. The Failure of the Canonical Case
The generic non-canonical Lagrangian Equation (
40) can also be seen as non-linear extension of the ordinary scalar field Lagrangian, which is readily recovered by taking
in Equation (
40). One finds
As should be expected, the energy density (
41) and pressure (
42) of the field now reduces to
where
and
are, respectively, the kinetic energy density and pressure of the ordinary canonical scalar field.
On the other hand, it is also widely known that such a scalar field can be interpreted as a mixture of
two interacting perfect fluids with different equations of state, namely a material Zeldovich’s stiff fluid [
50], where (
), plus a pure vacuum (
-term) obeying an EoS
(see, e.g., ref. [
51] for a more detailed discussion with examples). Therefore, as happens in the running vacuum model, by assuming that both components are gravitationally coupled, in principle, there will be no local energy–momentum conservation for each perfect fluid component separately. Only the total energy–momentum tensor of the system as a whole is conserved.
Nevertheless, under such an interpretation, whether the potential of the unstable vacuum dominates (maximum scale
) and decays spontaneously through a non-adiabatic decaying process conserving the specific entropy (as discussed in
Section 3), the energy stored in the field will be transferred to a stiff component. In this way, the standard thermal bath formed by ultra-relativistic particles (
) is not generated. An inevitable consequence is that a new phase transition needs to be hypothesised (perhaps through a new coupling term), thereby forcing the formation of a thermal bath, with the universe finally entering in the standard radiation phase. Naturally, in this case, the two-fluid description without additional assumption is unable to faithfully describe the complete scenario driven by the running vacuum cosmology.
Such a scenario will happen naturally when the coherent field oscillation phase is absent, with the vacuum field ( term) continuously approaching its final, very low (but finite!) value, which is defined by the scale . As we shall see next, such a picture allow us to represent an evolution driven by the same scalar field (from de Sitter to de Sitter) based on a non-canonical scalar field, and mimicking the running vacuum term, as discussed in previous sections.
5.2. The Non-Canonical Case
Let us now consider the generic non-standard case. To begin with, we remark from Equations (
41) and (
42) that the general EoS parameter for the kinetic term (the material fluid) can be defined as
Therefore, based on the two-fluid interpretation, the kinetic term for
exactly obeys the radiation EoS.
2 Thus, by assuming, as before, that the classical universe emerged from the quantum gravity regime as a de Sitter-like solution with scale
(see
Figure 1), this means that
, and the unstable potential
must decay directly in ultra-relativistic particles. Interestingly, the inflationary process is not adiabatic, since the primeval thermal bath is a consequence of the energy transfer from the potential
or, equivalently, the
(
H)-term to the radiation-created component (see
Section 3). In a certain sense, this inflationary scenario resembles some variants of the warm inflationary process, because the primeval accelerating expansion is not adiabatic. However, it is somewhat different, because the whole thermal bath here is a consequence of the running vacuum process (de Sitter instability), and not related to an initial singular state, as assumed in some warm inflationary scenarios [
54,
55,
56,
57].
Now, let us demonstrate that the general equation of motion for the running
cosmology Equation (
16) is reproduced by the non-canonical scalar field based on the two-fluid interpretation, as proposed above. In this case, the
EFE Equations (
2) and (
3) now take the form
where
and
are the kinetic energy density and pressure of the fluid satisfying the EoS (
47), while
must be determined in such a way that
. Interestingly, the above equations imply that the cosmic dynamics is also driven by
where the equation of state
was used, and
is the vacuum density parameter. The above equation should be compared with (5) in
Section 2.
Once the two-fluid interpretation is assumed, the ‘H-equation of motion’ is independent of the particular expression of the potential. Nevertheless, an expression for needs to be given, and the scalar field solution properly derived.
Inspired by the derived expression (
13) for
, let us discuss the potential contributions emulating the different cosmic phases, starting from the primeval de Sitter state.
5.3. From de Sitter to the Radiation-Vacuum Dominated Era
To begin with, let us consider
. The energy density and pressure of the non-canonical scalar field becomes
with the kinetic component emulating the radiation EoS. Now, in order to describe the initial de Sitter configuration and its transition to a radiation dominated phase, let us also assume the following scalar field potential:
where
and the constant
is a dimensional parameter, [
. Its value is calculated in
Appendix CIn order to obtain the expression for the radiation energy density, let us assume the
ansatz . Inserting this into Equation (
51), we obtain
and
Now, by inserting the expression for
above into Equations (
53) and (
55), one can show that
thereby recovering the expressions (
19) and (
21) shown in
Section 4. Hence, the proposed potential Equation (
53) emulates completely the cosmological dynamics of the vacuum-radiation dominated era Equation (
17). In particular, we see that there is no a thermal bath for
since, in this case,
.
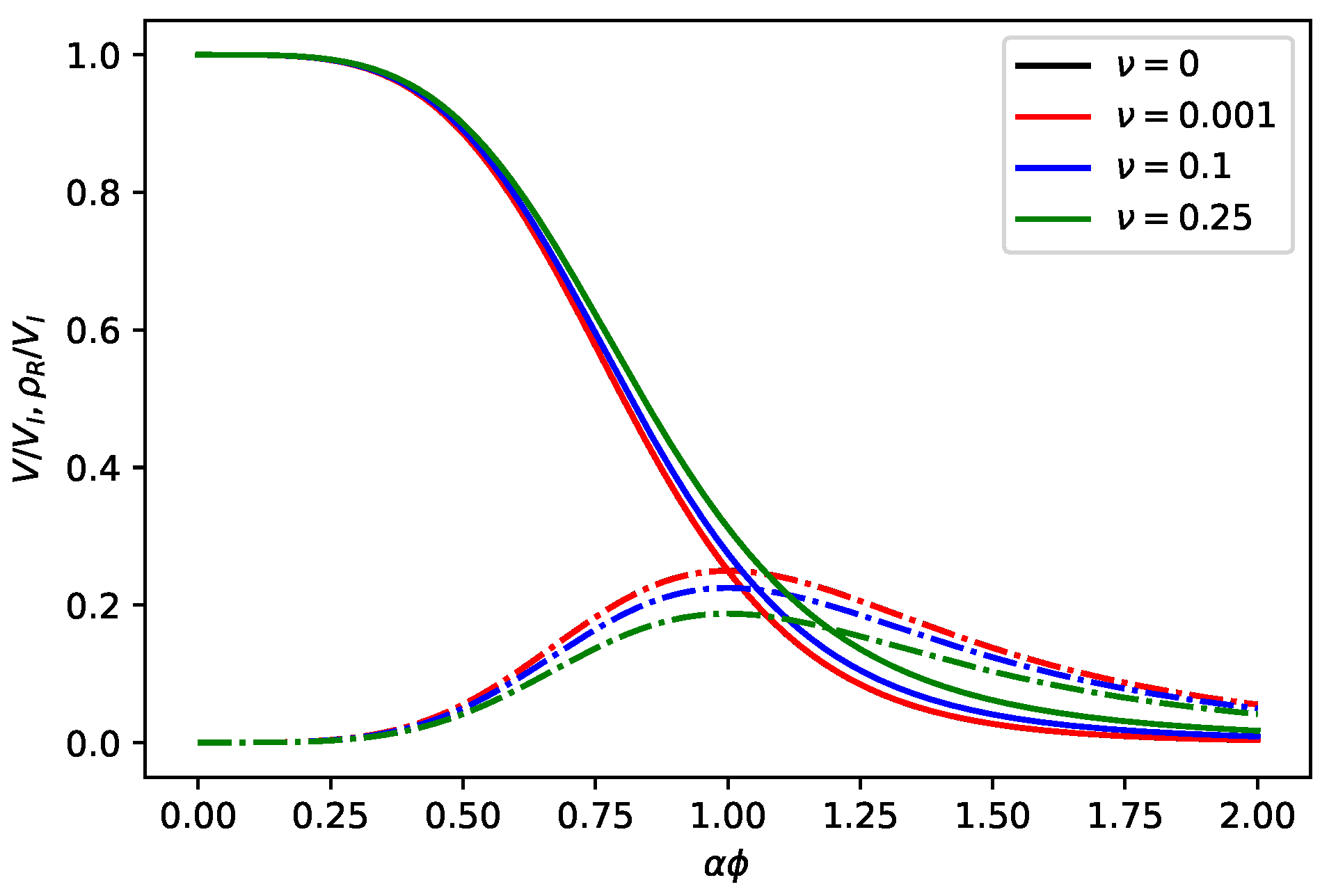
In
Figure 2, we display the evolution of the basic dimensionless quantities, namely the potential scalar field and the kinetic term
. The latter one describes the created component forming the thermal bath of effectively massless particles (
). As one may check, the transition from vacuum to the radiation-vacuum phase is also determined by the condition
[see discussion below Equation (
24)].
5.4. From Matter-Vacuum to the Final de Sitter Era
In this case,
, which means that
in Equation (
47). Now, based on the expression (
13) for
, we propose the following potential
to the matter dominated era:
where
, and
is also a dimensional parameter as before,
. As a function of the scales
and
M, and the parameter
, it is given by (see
Appendix C)
In order to obtain the expression for the matter energy density, we will again consider a similar
ansatz of the transition from de Sitter (
) to the radiation-vacuum dominated phase, namely
. Now, keeping this in mind, it is easy to show that
and
By substituting the expression for
above in both Equations (
59) and (
61), one can show that
recovering the expressions (
27) and (
28) shown in
Section 4. As it happens for the early universe, the potential (
59) recovers the cosmological dynamics of the matter-vacuum era (
25).
Figure 3 shows the time behaviour of the basic dimensionless quantities as defined in
Figure 2.
6. Final Remarks and Conclusions
Entropy is the quantity which allows us to describe the progress of non-equilibrium dissipative processes. A special ingredient of our scenario discussed here is that it takes into account the second law of thermodynamics from the very beginning. For instance, the non-equilibrium thermodynamics was explicitly used to establish an integral relation uniting
and the particle creation rate
. The running vacuum emerges from an unknown quantum gravity regime as a primeval de Sitter vacuum. Due to a structural thermal instability, it transfers irreversibly energy, particles, and entropy to the spacetime, forming the primeval thermal bath at the expenses of its own energy density at scale, which is initially defined by
, which is smaller than the reduced Planck mass. In this connection, see also [
45], where the dynamic evolution of this phase forming the thermal bath was investigated for
.
Subsequently, the evolution departs slightly from the standard radiation- and matter-dominated phases sustained by a softer generation of entropy. Since the scale is incredibly low, for all practical purposes, the final vacuum state will be eternal.
There are also two interesting aspects of the scenario proposed here. Firstly, the irreversible evolution of the running vacuum generating a complete cosmology can also be described by a single minimally coupled non-canonical scalar field when it is interpreted as a mixture of two interacting perfect fluids, as suggested long ago (see
Section 5). Secondly, all of the energy scales appearing in the potential, and also in the non-canonical kinetic term, are sub-Planckian with no fine-tuning.
Finally, we stress that the mild deviation from the rigid (i.e., non-dynamical) vacuum model (CDM) may also provide an explanation to the current and tensions, perhaps simpler than other phenomenological dark energy interacting models. Studies along these lines are in progress and, naturally, still deserves a closer scrutiny.