Constraint on the Cosmic Curvature in a Model with the Schwarzschild–de Sitter Metric from Supernovae and Gamma-Ray Burst Observational Data

Abstract

In developing his cosmological model of 1917, de Sitter theoretically predicted the phenomenon of cosmological redshift (the de Sitter effect), which he did long before the discovery of this phenomenon in observations. The de Sitter effect is gravitational by its nature, as it is due to differences between the coordinate systems of the observer and the distant source. However, the relationship between the redshift and distance derived from the de Sitter metric is at odds with observations, since this relationship is nonlinear (quadratic) for small redshifts, while the observed relationship between the same quantities is strictly linear. This paper discusses the possibility that cosmological redshift is gravitational by its nature, as in de Sitter’s 1917 model. At the same time, here, as in de Sitter’s model, an elliptical space is used, the main characteristic of which is the identification of its antipodal points. But, unlike de Sitter’s model, here, in order to ensure strict linear dependence of the redshift on distance, the origin of the reference system is transferred to the observer’s antipodal point. The Schwarzschild–de Sitter metric used in this model allows you to estimate the curvature of space from observational data. To achieve this, a theoretical Hubble diagram is built within the framework of the model with the Schwarzschild–de Sitter metric, which is compared with observations from the Pantheon+ catalogue of type Ia supernovae and the Amati catalogue of gamma-ray bursts in the redshift range of $0<z<8$. As a result of this comparison, we found that the lower estimate of the radius of curvature of space was quite large: $2.4\times {10}^{15}$ Mpc. This means that the observational data indicate a negligible curvature of space.

1. Introduction

The first exact solutions of Einstein’s field equations were spherically symmetric. The Schwarzschild metric [1] corresponds to the following interval in spherical coordinates $r,\theta ,\varphi$:

$$d{s}^2=g_{tt}^{\mathrm{Sch}}{c}^{2}d{t}^2-{\displaystyle \frac{d{r}^2}{g_{tt}^{\mathrm{Sch}}}}-r^2(d{\theta }^2+{sin}^2\theta d{\phi }^2),$$

(1)

with its metric coefficient associated with time

$$g_{tt}^{\mathrm{Sch}}=1-{\displaystyle \frac{r_g}{r}},$$

(2)

where $r_g=2 GM/c^2$ is the gravitational radius, M is the central mass, c is the speed of light, and G is the gravitational constant. This solution is symmetric with respect to the local centre of spherical mass distribution. Two other exact solutions to Einstein’s field equations were found, one by Einstein [2]:

$$d{s}^2=c^{2}d{t}^2-d{r}^2-R^2{sin}^2{\displaystyle \frac{r}{R}}(d{\theta }^2+{sin}^2\theta d{\phi }^2)$$

(3)

and the other by de Sitter [3]:

$$d{s}^2={cos}^2{\displaystyle \frac{r}{R}}{c}^{2}d{t}^2-d{r}^2-R^2{sin}^2{\displaystyle \frac{r}{R}}(d{\theta }^2+{sin}^2\theta d{\phi }^2).$$

(4)

These two solutions are also spherically symmetrical, but their symmetry is not local because the solutions are not related to the preferred centre of curvature or the central mass distribution. The curvature $R^{-2}$ is global by definition, so the symmetry of these models is spherical with respect to any arbitrary point in space.

In the Schwarzschild solution (1), the metric coefficient $g_{tt}$ implies a transformation (dilation) of time along the radial coordinate r. It follows from the coefficient (2) that this transformation leads to a complete halt in the flow of time at the Schwarzschild radius $r=r_g$. A similar cessation of time is inherent in the de Sitter metric (4), since the time coordinate in this metric is also subject to dilatation along the radial coordinate r due to the metric coefficient

$$g_{tt}^{\mathrm{dS}}={cos}^2{\displaystyle \frac{r}{R}}={cos}^2\chi .$$

(5)

Here, the projective angle $\chi$ is such that

$$r=R\chi .$$

(6)

Thus, according to the expression (5), time stops at a large distance from the observer, corresponding to $\chi ={\displaystyle \frac{\pi }{2}}$, when $cos\chi =0$. At closer distances to the observer, time dilation leads to a decrease in the frequencies of the spectral lines of light sources. On the basis of this property, de Sitter theoretically predicted the possibility of cosmological redshift, which was called the de Sitter effect. This prediction was experimentally confirmed ten years later by Lemaître [4], and then by Hubble, who wrote that the observed “velocity-distance relation may represent the de Sitter effect” [5].

As can be seen from the comparison of metrics (1) and (4), the de Sitter effect is gravitational by its nature, since it is caused by the difference between the coordinate systems of the source and the observer in curved spacetime, similar to what happens in the Schwarzschild metric. But, unlike the gravitational redshift in the Schwarzschild metric, the de Sitter gravitational redshift is global and isotropic: its character remains the same, regardless of the choice of the observer’s point in space and the direction of observation.

In Einstein’s metric (3), the metric coefficient associated with time is identical to unity; therefore, in Einstein’s cosmological model, there is no effect of time dilation, and time is universal for all space. Einstein’s metric (3) corresponds to the Riemannian space ${\mathbb{S}}^3$ with a constant positive curvature $\lambda =R^{-2}$, due to the presence of a non-zero density of matter distribution over space, $\rho >0$. In the case of the de Sitter metric (4), $\lambda =3R^{-2}$, and ${\rho }_0=0$ (i.e., the space is empty). The distance $d_{os}$ from the observer (o) to the source (s) is measured by the radial coordinate r:

$${\displaystyle \underset{\phantom{--}|r=0}{o}}{\displaystyle \stackrel{r=R\chi \equiv d_{os}}{\to }}s{\displaystyle \stackrel{}{\to }}a.$$

(7)

The notation ‘a’ is used here for the observer’s antipodal point in space ${\mathbb{S}}^3$. This point corresponds to the projective angle $\chi =\pi$, which marks a very large distance from the observer. In principle, light from the source can reach the observer from this point as well, although in practice, this is unlikely due to the presence of horizons, which will be discussed below. In addition, there is coordinate ambiguity for $\chi >\pi /2$, as discussed by de Sitter in [3].

To avoid this ambiguity, de Sitter replaced the Riemannian sphere ${\mathbb{S}}^3$ with an elliptical (projective) space, the main property of which is the identification of its antipodal points ($o\equiv a$). The same elliptical space was used in subsequent cosmological models by Lemaître [4], Tolman [6] and Robertson [7,8,9], from where elliptical space transitioned into the standard cosmological model of cold dark matter $\mathsf{\Lambda }$CDM with the cosmological term $\mathsf{\Lambda }$.

In 1939, R.C. Tolman proposed a general method for finding exact solutions to Einstein’s field equations [10]. One of the new solutions found by Tolman combines the Schwarzschild metric with the de Sitter metric (SdS):

$$d{s}^2=g_{tt}{c}^{2}d{t}^2-{\displaystyle \frac{d{r}^2}{g_{tt}}}-R^2{sin}^2{\displaystyle \frac{r}{R}}(d{\theta }^2+{sin}^2\theta d{\phi }^2).$$

(8)

In this metric, the metric coefficient associated with time

$$g_{tt}=1-{\displaystyle \frac{r_g}{r}}-{\displaystyle \frac{r^2}{R^2}}$$

(9)

includes the curvature parameter $R^{-2}$. Therefore, the SdS solution can be used to estimate the curvature of space. However, this cannot be carried out directly, because, as with the Schwarzschild metric, the SdS metric is local and anisotropic. This problem is solved by using the main property of elliptical space, i.e., the connectivity between its antipodal points. In this case, it is also necessary to transfer the origin of the coordinate system from the point where the observer is located to their antipodal point. We will discuss this in Section 2, and then, in Section 3, we will estimate the R parameter by calculating the theoretical distance moduli for the SdS metric and comparing them to the distance moduli derived from observations of distant sources such as supernovae and gamma-ray bursts.

2. Materials and Methods

2.1. Elliptical Space

The luminosity distances calculated with the use of the metric coefficient

$$g_{tt}^{\mathrm{d}S}={cos}^2{\displaystyle \frac{r}{R}}$$

(10)

in the de Sitter metric are not consistent with the observations because here, the theoretical relationship between luminosity distances and redshifts is nonlinear (quadratic) near the origin. At the same time, the observational data show a strictly linear relationship between luminosity distances and redshifts at low redshifts.

Notwithstanding, one can avoid nonlinearity by moving the origin of the coordinate system from the observer point (o) to the antipodal point (a):

$$o{\displaystyle \stackrel{d_{so}}{\leftarrow }}s{\displaystyle \stackrel{r=r_s}{\leftarrow }}{\displaystyle \underset{r=0|\phantom{--}}{a}}\equiv o$$

(11)

Compared with the Hubble diagram (7), in this coordinate system, distances are calculated as in the normal coordinate system associated with an observer. Here, $r_s$ is the radial distance between the antipodal point (a) and the source location (s). In order to use the Schwarzschild–de Sitter metric in the calculations, let us bring to bear the main property of elliptical space, the connectivity between its antipodal points (see below). Our goal is to calculate the source-to-observer distance ($d_{so}$) in the SdS metric and compare it with the redshift z of the source. Using the above notations, we obtain the distance between the observer and their antipodal point in the form

$$r_o=r_s+d_{so}.$$

(12)

In this configuration, the centre of symmetry of the SdS metric is located at the observer’s antipodal point (a). From the observer’s perspective, this point looks like a distant sphere with a large (or infinite) radius. It encompasses the entire celestial sphere ($4\pi$ steradian) around the observer. In this way, the SdS metric becomes spherically symmetric and isotropic for any arbitrary point in space, provided that the antipodal points are endowed with this metric.

Endowing an elliptical space with the SdS metric is possible if the mathematical identification of distant points is materialised through their physical connectivity by means of a structure with a metric that is an exact solution of Einstein’s field equations. Such an exact solution to the field equations was found in 1935 by Einstein and Rosen [11]. This solution interconnects two different spaces or two different regions of the same space. Therefore, it was called the Einstein–Rosen bridge, but more often, it is called the “wormhole” [12]. In the simplest case, the exterior space around a wormhole is described by the Schwarzschild metric or by the Schwarzschild–de Sitter metric (if space has a curvature of $R^{-2}$). In both metrics, the redshift is gravitational by its nature, so it can be calculated using the metric coefficient (9). Such a calculation within the scheme (11) makes it possible to obtain theoretical cosmological redshifts of distant sources.

As shown by Morris, Thorne and Yurtsever [13], it is most likely that wormholes are microscopic objects with dimensions in the order of the Planck–Wheeler length, ${\mathrm{𝓁}}_{\mathrm{P}}=\sqrt{G\hslash /c^3}=1.62\times {10}^{-33}$ cm. This determines the scale of the difference between the idealised (mathematical) elliptical space and its physical counterpart, the space whose antipodal regions are connected through microscopic Einstein–Rosen wormholes.

There is a widespread belief that wormholes are unstable and that even the slightest disturbance associated with the passage of particles of matter or radiation through their throats destroys them. However, most publications on the stability or instability of wormholes are based on the concept of their traversability [14,15,16]. Other publications discuss this topic either in terms of exotic theories of gravity [17], or within the framework of the theory of quantum gravity [18], which does not yet exist. Therefore, such publications can be disregarded.

In classical general relativity, wormholes are the smallest possible objects. As such, they are not traversable and, therefore, they are stable by definition. Moreover, according to the ideas of Einstein, Rosen and Wheeler, the answer to the question of the relationship between the discrete (particles of matter) and the continuous (space) lies precisely in the possibility of the existence of microscopic structures within the framework of general relativity. Thus, the question of where matter particles and radiation can come from at all is clarified by the possibility of the existence of microscopic wormholes, proven by Einstein and Rosen.

A static wormhole is described by the Schwarzschild metric (1). But our goal here is to estimate the curvature of space $R^{-2}$, which is encoded in the Schwarzschild–de Sitter metric (8). Therefore, we use this metric, with its free parameter R to be evaluated using observations.

The observer is located near one of the throats of the wormhole (hereinafter referred to as the near throat), and the observed source is somewhere between the observer and the far throat of the observer’s antipodal point. According to our choice of coordinate system, any distance is now measured from the origin of that coordinate system (a) to the source ($r_s$) and to the observer ($r_o$), with the origin being a large antipodal sphere surrounding the observer. Our goal is to find the relationship between the redshift of the source (z) and the distance from the source to the observer:

$$d_{so}\left(z\right)=r_o-r_s.$$

(13)

Since the origin of the coordinates for these calculations is located on the surface of a distant sphere with radius $r_o$, regardless of the direction to the source, this distance remains the same when observing any source (for example, a supernova). But the distance to the source $r_s$ from the origin can vary, depending on the source redshift All distances are counted along the line of sight to the source (a supernova). The global (cosmological) redshift of the source is given by the Schwarzschild metric with a gravitational radius $r_g$, calculated from the origin a (any point on the antipodal sphere).

In this case, the effect of cosmological gravitational redshift is caused by the local distribution of masses in the vicinity of the observer due to the connectivity between the region of elliptical space adjacent to the observer and the region around the observer’s antipodal point. In elliptical space, with its identified antipodal points, the centre of the local mass distribution (as well as all other points of this mass distribution, including the points of the Schwarzschild horizons of each mass) are geometrically transformed into a huge sphere around the observer. The radius of this sphere is so large that any local differences in the positions of the mass distributions correspond to negligible relative displacements of the distant sphere surfaces, including the surfaces of the Schwarzschild horizons.

In this way, a collective spherically symmetrical horizon of radius $r_g$ is formed around each point in space, and all points in space are equivalent in this respect. So, the universe looks the same to any arbitrarily chosen observer. In such a scheme, all masses within some vicinity of the observer contribute to the global collective gravitational redshift through their antipodal points. From the point of view of an observer, the size of this neighbourhood can be very large. It includes matter in the form of local and distant galaxies, as well as possibly distant clusters of galaxies. However, compared to the gravitational radius $r_g$, the size of this region around the observer is negligible.

2.2. Redshift–Distance Relationship

In our scheme (11), there are two unknown distances, $r_o$ and $r_s$. The latter quantity can be replaced by the source-to-observer distance $d_{so}=r_o-r_s$, which is the sought theoretical quantity to be compared with observational data. The gravitational radius $r_g$ and the global radius of curvature R are the unknowns. Thus, in total, our model has three free parameters: $r_o$, $r_g$ and R, which should be determined from observations.

Both the source and the observer are in the SdS metric (8) with its redshift-defining coefficient (9). In this case, the redshift z of the source with respect to the observer is calculated using the following expression:

$$z=\sqrt{{\displaystyle \frac{g_{tt}^o}{g_{tt}^s}}}-1$$

(14)

or, taking into account (9),

$${(z+1)}^2=\left[1-{\displaystyle \frac{r_g}{r_o}}-{\displaystyle \frac{r_o^2}{R^2}}\right]{\left[1-{\displaystyle \frac{r_g}{r_s}}-{\displaystyle \frac{r_s^2}{R^2}}\right]}^{-1}.$$

(15)

2.2.1. Approximate Solution

Expression (15) can be converted to the desired functional dependence of the distance $d_{so}=r_o-r_s$ on the source redshift z by regrouping the terms included in this expression and temporarily taking $r_g$ as the distance unit: $r_g=1$. Later, this parameter can be translated into some generally accepted units of distance measurement, for example, in light years or megaparsecs. By rearranging Equation (15), we obtain

$${\left(1+z\right)}^2=\left(1-r_o^{-1}-r_o^2{R}^{-2}\right){\left(1-r_s^{-1}-r_s^2{R}^{-2}\right)}^{-1}.$$

(16)

Replacing $r_s$ in (16) with $r_s=r_o-d_{so}$, we obtain an expression containing only the sought parameters $r_o$, $d_{so}$ and R, as well as the redshift z, which is the input argument:

$${(r_o-d_{so})}^{-1}=1-(1-r_o^{-1}-r_o^2{R}^{-2}){(1+z)}^{-2}-{(r_o-d_{so})}^2{R}^{-2}.$$

(17)

Then, the distance $d_{so}$ as a function of redshift z reads

$$d_{so}=r_o-{\left[1-(1-r_o^{-1}-r_o^2{R}^{-2}){(1+z)}^{-2}-{(r_o-d_{so})}^2{R}^{-2}\right]}^{-1}.$$

(18)

This simple solution is recursive; hence, it is approximate. Given that the value of $R^2$ in the denominator of the last term in (18) is known to be extremely large (from observations), the distances $d_{so}$ can be calculated by successive approximations. In the zero-order approximation, the last term in expression (18) can be neglected:

$$d_{so}^{\left(0\right)}=r_o-{\left[1-(1-r_o^{-1}-r_o^2{R}^{-2}){(1+z)}^{-2}\right]}^{-1}.$$

(19)

This depends only on z and can be substituted on the right-hand side of the expression (18) to calculate the required distances $d_{so}$.

2.2.2. Exact Solution

An exact solution to Equation (15) also exists (the author must acknowledge that it was proposed by the reviewer of this paper). The solution is achieved by converting Equation (15) into a reduced cubic equation,

$$r_s^3+3p{r}_s+2q=0$$

(20)

using the coefficients $p=-{\displaystyle \frac{1}{3}}\left[1-{\displaystyle \frac{r_g}{r_o}}-{\displaystyle \frac{r_o^2}{R^2}}\right]{(1+z)}^{-2}{R}^2$ and $q={\displaystyle \frac{r_g{R}^2}{2}}$. Since $|p^3|>|q^2|$, while $p<0$, the discriminant of (20) is negative, $p^3+q^2<0$, which means that (20) has three real solutions [19]:

$$r_s=2\sqrt{-p}cos{\displaystyle \frac{\phi }{3}},\phantom{--}\mathrm{and}\phantom{--}{r}_s^{\pm }=-2\sqrt{-p}cos{\displaystyle \frac{\phi \pm \pi }{3}},$$

(21)

with $\phi =arccos(-q/\sqrt{-p^3})$. Like in (18), the required source-to-observer distance is calculated as $d_{so}=r_o-r_s$ using one of the exact solutions (21):

$$d_{so}=r_o-2\sqrt{-p}cos{\displaystyle \frac{\phi }{3}},\phantom{--}\mathrm{or}\phantom{--}{d}_{so}^{\pm }=r_o+2\sqrt{-p}cos{\displaystyle \frac{\phi \pm \pi }{3}}$$

(22)

The choice between these three solutions can be made by comparing them with the approximate solution (18), since it is the only one. It turns out that the first of these solutions results in distances decreasing with the growth of z, while the third ($d_{so}^{-}$) leaves the distances approximately constant within the redshift range $0<z<0.1$. Both contradict observational facts. The only solution that corresponds to the observations is the second solution $d_{so}^{+}$. It also coincides with the approximate solution from Section 2.2.1.

2.2.3. Luminosity Distance

The luminosity distance comparable with that of the source, is obtained from the expressions (18) or (22) by multiplying these expressions by the scaling factor ${(1+z)}^2$:

$$d_L\left(z\right)=d_{so}{\left(1+z\right)}^2,$$

(23)

with one of the $(1+z)$-factors accounting for the loss of luminosity due to the cosmological redshift z, as well as for the lower rate at which the photons reach the observer because of the cosmological time dilatation due to the non-unit metric coefficient $g_{tt}$. The other $(1+z)$-factor takes into account the distortion of the photon’s trajectory (coefficient $g_{tt}^{-1}$ in the Schwarzschild–de Sitter metric). The expression (23) can be used to determine the free parameters of our model by comparing the theoretical distance moduli

$${\mu }^{\mathrm{theor}}=5log{d}_L+25$$

(24)

(in stellar magnitudes) with the distance moduli obtained from observations. The numerical coefficients in (24) correspond to the luminosity distances $d_L$, expressed in Mpc.

2.3. Observational Data

The Formulas (18)–(24) describe the theoretical relationship between distances to remote sources and redshifts. Distances are expressed as the photometric properties of sources. Thus, the assessment of theoretical parameters should be based on observational photometric data for a wide range of cosmological redshifts. One of the most accurate sets of observational data of this kind is the photometric catalogue Pantheon+ [20,21], which contains data on 1701 type Ia supernovae in the redshift range of $0<z_{\mathrm{SN}}<2.26$.

Yet, this range of redshifts is not wide enough to indicate differences between cosmological models, since these differences are manifested significantly only for redshifts $z>3$. The range of redshifts can be expanded by using additional observational data from the gamma-ray burst (GRB) catalogue compiled by Amati et al. [22]. This catalogue contains 193 moduli of gamma-ray burst distances ${\mu }_{\mathrm{GRB}}$, calculated and calibrated using the Amati relation [23]. The range of redshifts covered by this catalogue, $0.03<z_{\mathrm{GRB}}<8.1$, is significantly wider than in the case of type Ia supernovae.

The ${\mu }_{\mathrm{GRB}}$ data are much noisier than ${\mu }_{\mathrm{SNe}}$, and they are also slightly systematically biased within the redshift range $0<z<0.7$, where all cosmological models and data must coincide. This bias is calculated to be $-0.258$ [mag] by minimising the Pearson’s ${\chi }^2$ for 27 GRBs within the mentioned redshift range (the GRB data are corrected for this bias).

3. Results

Calculations using the Formulas (18)–(24) give estimates of the parameters R, $r_o$ and $r_g$ within the framework of the SdS model. The parameters are estimated by minimising the ${\chi }^2$ Pearson criterion [21]

$${\chi }^2=\Delta {\mathbf{D}}^T{C}^{-1}\Delta \mathbf{D},$$

(25)

in which C is the covariance matrix and $\Delta \mathbf{D}$ is the vector of residuals between theoretical and observational distance moduli:

$$\Delta {\mathbf{D}}_i={\mu }_i^{\mathrm{theor}}\left(z_i\right)-{\mu }_i.$$

(26)

The length of this vector is $N=1701$, which corresponds to the length of the Pantheon+ catalogue, which provides the observational ${\mu }_i$ of type Ia supernovae. The theoretical distance moduli are calculated for the SdS model by using the Formulas (18), (22) and (24), as described in the previous section. For comparison purposes, ${\mu }_i^{\mathrm{theor}}\left(z_i\right)$ is also calculated by using the standard formalism of the $\mathsf{\Lambda }$CDM model, applying the cosmological parameters estimated by the authors of the Pantheon+ catalogue [21].

Since here, we extend the range of available source redshifts by using an additional catalogue of calibrated GRBs, which provides only the uncertainties of the GRB distance moduli instead of the full covariance matrix, we can use a simplified $\chi$-squared calculation

$${\chi }^2={(\mathrm{diag}{C}^T\Delta \mathbf{D})}^2={\displaystyle \sum _{i=1}^N}{\displaystyle \frac{\Delta {\mathbf{D}}_i^2}{{\sigma }_{{\mu }_i}^2}},$$

(27)

where ${\sigma }_{{\mu }_i}^2$ are the uncertainties of ${\mu }_i$ corresponding to the diagonal of the covariance matrix (see, e.g., [24], § IIIc for theoretical work or [25,26] for practical examples of using (27) for comparison of various cosmological models between each other).

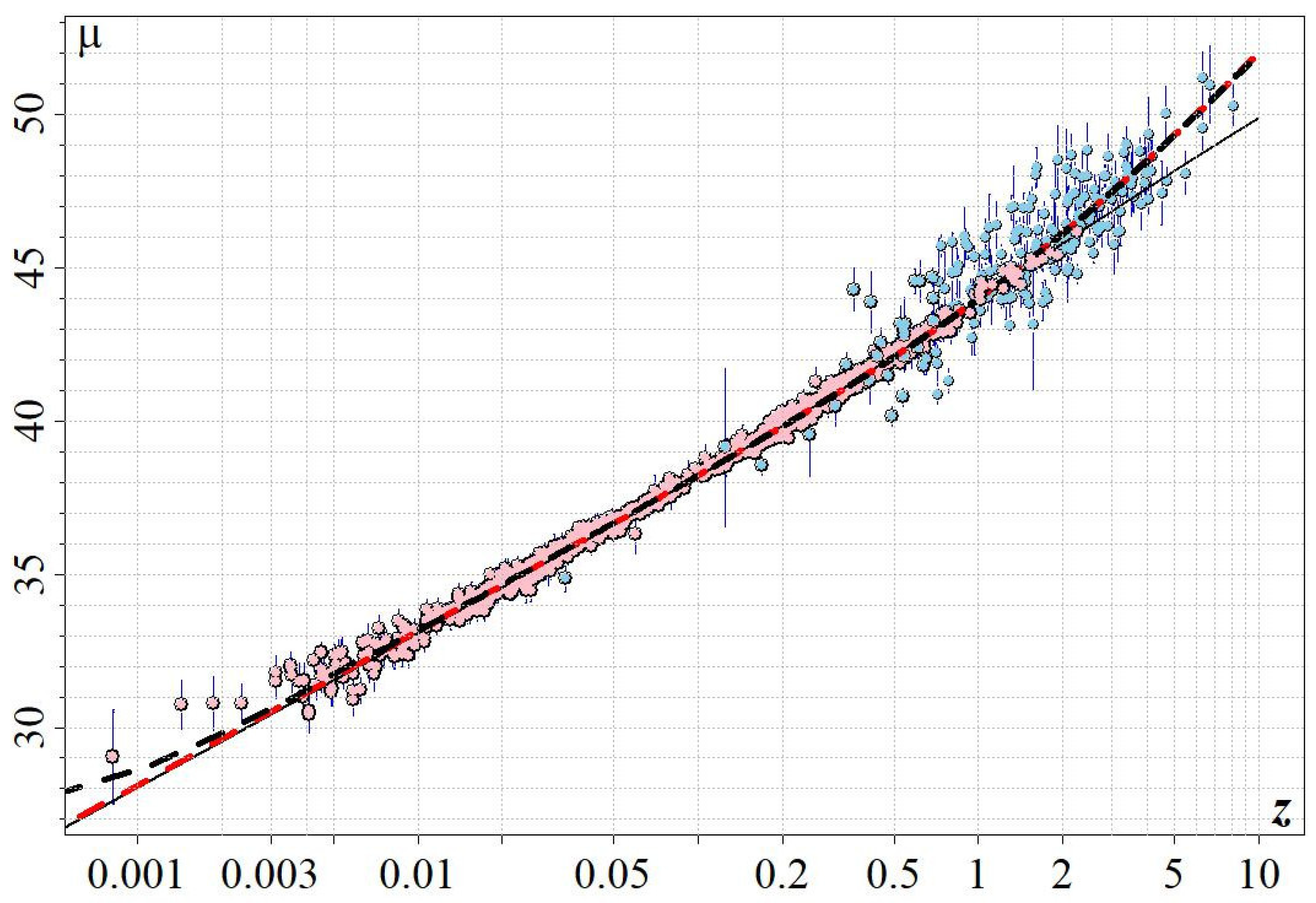
The parameters of the standard $\mathsf{\Lambda }$CDM model, as estimated in [21] by using the Pantheon+ sample, are $H_0=73.6\pm 1.1$ [km/s/Mpc], ${\mathsf{\Omega }}_M=0.334\pm 0.018$ and ${\mathsf{\Omega }}_k=0$. The theoretical distance moduli curve corresponding to these parameters is indicated in Figure 1 by the thin solid curve. It matches fairly well with the observational type Ia distance moduli (pink circles in this plot), with Pearson’s ${\chi }_{\mathsf{\Lambda }\mathrm{CDM}}^2=906.1$.

The theoretical parameters $r_g$, $r_o$ and R for the SdS model are obtained by minimising Pearson’s ${\chi }^2$, which is achieved by the global descent method with consecutive iterations. These parameters based on 1701 type Ia supernova data are given in the second column of

Table 1. Fitting of the SdS theoretical model to the observational data.

Parameter	SNe	SNe+GRB	Units
Approximate solution
R	$(1.{08}_{-0.83}^{+\infty })\times {10}^5$	$(1.{17}_{-0.94}^{+\infty })\times {10}^5$	[$r_g$] 1
$r_o-1$	$(9.91\pm 0.15)\times {10}^{-8}$	$(9.{91}_{-0.06}^{+0.18})\times {10}^{-8}$	[$r_g$]
$r_g$	$\left(2.13\pm 0.03\right)\times {10}^{10}$	$\left({2.13}_{-0.04}^{+0.03}\right)\times {10}^{10}$	[Mpc]
${\chi }_{\min }^2$	887.6	2033.7	–
Exact solution
R	$(1.{127}_{-0.85}^{+5.2})\times {10}^5$	$(1.{127}_{-0.89}^{+5.9})\times {10}^5$	[$r_g$]
$r_o-1$	$(9.914\pm 0.009)\times {10}^{-8}$	$(9.914\pm 0.011)\times {10}^{-8}$	[$r_g$]
$r_g$	$\left(2.12\pm 0.03\right)\times {10}^{10}$	$(2.12\pm 0.04)\times {10}^{10}$	[Mpc]
${\chi }_{\min }^2$	871.3	2018.0	–

¹ Only the lower limit is determinable.

. The one-sigma confidence intervals for these parameters are calculated by varying the parameters and taking those of their values that correspond to a Pearson’s probability of 68.3%. These values are divided by the square root of the number of degrees of freedom, $\sqrt{N-n_{\mathrm{p}}}$, where $n=3$ is the number of free parameters, and $N=1701$ is the number of sources in the sample.

The calculated theoretical distance moduli for the SdS model are shown as two dashed bold curves in Figure 1, with the red curve corresponding to the approximate solution of (15), while the black dashed curve represents the exact solution. The quality of the SdS-model fit into the observational data is characterised by the minimum value of the Pearson criterion, which turns out to be ${\chi }^2=887.6$ for the approximate solution and ${\chi }^2=871.3$ for the exact solution. These values indicate slightly better binding of the theory discussed here to the observational data, in comparison with the $\mathsf{\Lambda }$CDM model.

The additional distance moduli extending the observational redshift range to $z\approx 8$ are 193 data points from the Amati catalogue. They are shown in Figure 1 as blue circles. With this joint data sample of SNe+GRB containing 1894 data points, the number of degrees of freedom is $N-n=1891$. In the case of the approximate solution, the tolerance intervals of the parameters for the type Ia SNe and for the joint data sample of SNe+GRB remain approximately the same as for the SNe alone, because the photometric accuracy of SNe is much higher than that of GRBs. With the exact solution, the tolerances are smaller when the more accurate SN data are used for determining the model parameters.

Nevertheless, the GRB data confirm the parameter values for $r_o$ and $r_g$ obtained from SNe (compare the second and third columns of Table 1). The first four rows of this Table provide the outcome of the approximate solution, and the last four rows correspond to the more accurate results of the exact solution.

The estimated value of the SdS model parameter $R=(1.{127}_{-0.85}^{+5.2})\times {10}^5$, shown in the second column of Table 1, is the lower estimate of the radius of curvature of the universe, since the upper tolerance interval of R is very wide (even being indefinite in the case of the approximate solution). The value of R (in units of $r_g$) combined with the scale factor $r_g$ suggests that the spatial curvature of the universe is constrained from above by the value $1/R^2\approx 1.75\times {10}^{-31}$ Mpc⁻².

4. Discussion

Observations of 1701 type Ia supernovae collected in the Pantheon+ catalogue, combined with observations of 193 gamma-ray bursts from the Amati catalogue, make it possible to determine the lowest possible value of the radius of curvature of the universe in a cosmological model with the Schwarzschild–de Sitter metric. It turns out to be very large: $2.4\times {10}^{15}$ Mpc. Accordingly, the curvature of space in this model is constrained from above by the value $1.75\times {10}^{-31}$ Mpc⁻². That is, the observational data used in this work for these estimates are compatible with the possibility that space is flat.

In this paper, we discuss the origin of cosmological redshift in an alternative way: the redshift of remote galaxies is interpreted as a manifestation of the static Schwarzschild–de Sitter metric. Many studies will disagree with this interpretation because it is commonly believed that the universe cannot be static. The point is that the standard cosmological model, with its interpretation of redshift as the result of space expansion described by the dynamic Friedmann–Lemaître–Robertson–Walker (FLRW) metric, can explain a large variety of observational facts. Therefore, since the late 1990s, the standard model has been dubbed the concordance cosmological model, which puts all the observations together.

The current general view is that static cosmological models have long been a thing of the past and that it is not worth interpreting astrophysical observations in terms of static models, since they allegedly cannot explain such theoretically and observationally substantiated facts, such as Big Bang nucleosynthesis, the initial annihilation of matter and antimatter, the recombination of plasma in the process of the universe’s expansion, the process of structure formation and the subsequent reionisation of the medium during the formation of the first stars and galaxies.

However, a static model is discussed here for good reasons: the observational facts obtained over the past two years by the James Webb Space Telescope (JWST) have disarranged the entire coherent picture of concordance cosmology and made us think about the nature of cosmological redshift.

The light-gathering power and high angular resolution of the JWST provide exquisitely detailed information about the physical processes that took place in the universe 13 billion years ago and earlier—a glimpse into the so-called “dark ages”, when, according to the concept of the expanding universe, the process of recombination ended and the process of reionisation should have begun.

The generally accepted view was that the process of the formation of the first stars and the beginning of reionisation corresponded to redshifts $z\sim 20$. But the JWST observations have shown that at distances corresponding to these redshifts, there are a large number of massive galaxies (with masses $>{10}^{10}$ M_⊙) that formed less than 700 million years after the beginning of the universe. The observed large number density of massive galaxies with $z>10$ [27] is at odds with the predictions of the theory of galaxy formation. The recently published UNCOVER catalogue of JWST galaxies [28,29] contains a very large number of galaxies with $z\approx 20$, while, according to the $\mathsf{\Lambda }$CDM model, this is the redshift where the first stars and galaxies are expected to be formed. Therefore, at this redshift, corresponding to the universe’s age of ∼160–200 million years, there should be much fewer galaxies, which are expected to be shapeless and small in size.

These observational facts are currently explained by galaxy evolution. But there is a problem here, because the JWST observations show that galaxies with $z>10$ are fully formed, with disks and bulges, containing large amounts of dust and heavy chemical elements. They are look-alikes of the late-universe galaxies, but with one exception: the physical sizes of remote galaxies are much smaller than those of the galaxies next to us. This is an illusion due to the geometry of the expanding scaling factor. By contrast, in the geometry of a static coordinate system, the galaxies have quite normal sizes, in accordance with their masses and luminosities.

Additional confirmation that the small angular sizes of high-redshift galaxies are not due to their evolution comes from a recently discovered contradiction between the reionisation rate of the early universe known from pre-JWST observations and the new reionisation rate based on the JWST observations. The observed large number density of high-redshift massive galaxies necessarily implies—within the framework of $\mathsf{\Lambda }$CDM—an extremely high rate of star formation, since the $\mathsf{\Lambda }$CDM-based time that has elapsed since the Big Bang is very short (a few hundred million years).

It follows that the density of ionising photons must then be very high. According to the calculations in [30], reionisation should not only have begun much earlier than the standard model suggests, but should have already been completed by the time the galaxies observed by the JWST telescope formed. This is at odds with other observational facts, like the large abundance of neutral hydrogen at redshifts $z\approx$ 13–17. For example, the discovery of an anomalously strong neutral hydrogen absorption line in the redshift range $z\approx$ 13–17 [31] indicates the presence of a large amount of neutral hydrogen, which is incompatible with the $\mathsf{\Lambda }$CDM-based theory of reionisation. By contrast, in static or slowly-evolving coordinates, such a problem does not occur, since in these cases, the volume of space for $z\approx$ 13–17 in which the observed galaxies are located turns out to be much larger than in the case of the $\mathsf{\Lambda }$CDM model. Accordingly, the number density of galaxies per unit volume is lower in a static model, and there can be much more neutral hydrogen within this volume, which is consistent with observations and which removes all the contradictions.

Consequently, the reionisation process based on the JWST observations is now in very strong tension with the cosmic microwave background (CMB) and the Lyman-$\alpha$ forest [32]. This is a new kind of tension (CMB-based reionisation optical depth tension), which adds to the previous CMB-based issues discussed intensively in the literature, including Hubble constant tension, ${\sigma }_8$-tension, the CMB Cold Spot problem, and many other issues, which we are not going to discuss here. But, taken altogether, plus the lack of evolution time from the beginning of the universe for the high-redshift galaxies discovered by the JWST, this all indicates a profound crisis of the $\mathsf{\Lambda }$CDM, which must somehow be resolved.

As for the other observational facts, in the past, static cosmological models were not only supported by the same observational phenomena as $\mathsf{\Lambda }$CDM, but they predicted that such phenomena existed. In the literature, there are plenty of papers discussing how static-universe models solve challenging observational facts in alternative ways to $\mathsf{\Lambda }$CDM. So, there is no need to review these topics in detail here.

And for those researchers who are convinced that without the expansion of the universe, it is impossible to explain all the observed facts, there is a palliative solution. The fact is that the static Schwarzschild–de Sitter metric is mathematically equivalent to the dynamic McVittie metric [33,34]. The latter is the Schwarzschild metric (like in the model discussed here) embedded in the FLRW metric of the expanding universe. Thus, all arguments regarding the Big Bang’s nucleosynthesis, structure formation, etc., remain valid for the McVittie (≡SdS) metric, as for the metric of $\mathsf{\Lambda }$CDM.

The only difference between McVittie’s solutions and $\mathsf{\Lambda }$CDM is that most of the cosmological redshift in the McVittie metric is due to the gravitational effect (as in the SdS metric discussed here), and only a small fraction is due to the effect associated with space expansion. Therefore, the Hubble constant $H_0$ in this case becomes very small, which is equivalent to a very large value of the parameter R obtained here in the SdS metric. Accordingly, the age of the universe is estimated to be several orders of magnitude larger than the 13.8 billion years suggested in the $\mathsf{\Lambda }$CDM model. We will discuss this option elsewhere.

Nevertheless, we will mention explanations of some observational facts as they are seen within the framework of static cosmological models. For example, the cosmological redshift phenomenon was itself predicted theoretically by de Sitter for a static cosmological model well before the appearance of any dynamical cosmological models. Moreover, de Sitter warned in his 1917 paper that the lines of spectra systematically displaced towards the red might give rise to a spurious positive radial velocity interpretation [3]. In 1923, Eddington repeated this warning by writing the following: in de Sitter’s theory, there is the general displacement of spectral lines to the red in distant objects due to the slowing down of atomic vibrations which would be erroneously interpreted as a motion of recession [35].

Then, in 1926, Eddington predicted thermalised background radiation to exist with $T=3$ K for a static-universe model [36]. Later, in 1937, a similar prediction with respect to the CMB temperature $T=2.8$ K within a static-universe framework was proposed by W. Nernst [37]. Only much later, in 1953, did G. Gamow make his prediction with respect to the CMB and its temperature $T=7$ K for the expanding-universe model [38]. The abundances of light elements in a static universe were explained by G.R. Burbidge and F. Hoyle [39,40], R. Salvaterra and A. Ferrara [41] and others, although there are some unresolved issues for both the static and dynamic universe models. For example, the expanding universe model predicts that the synthesis of deuterium from hydrogen occurred only during the short period of nucleosynthesis after the Big Bang. In the future, the synthesis of deuterium cannot occur—it can only be destroyed in the interior of stars [42]. For this reason, the observed abundance of deuterium must be gradually diminishing with time. The Big Bang nucleosynthesis theory predicts the same evolution for lithium. But, contrary to this theory, observations show that the abundance of lithium is growing with time. This fact is attributed to the phenomenon of cosmic-ray spallation [43].

As for the process of structure formation in the universe, it is believed that the initial inhomogeneities that subsequently give rise to structures such as galaxy clusters and filaments arose at the inflationary stage due to quantum fluctuations, and then due to baryonic acoustic oscillations at the initial stage of the expansion of the universe, when the density of matter was sufficiently high. It is believed that in a static universe, there can be no process of structure formation. However, according to the classical scenarios, structure formation in static universe models occurs due to the mechanism of gravitational instability. Initial fluctuations in the homogeneous gas of primordial hydrogen grow exponentially into large-scale structures [44,45]. In the early years of cosmology, when static cosmological models were considered to be on a par with expanding-universe models, these scenarios agreed with observations. But when Eddington published a paper in 1930 showing that Einstein’s static model of the universe was unstable [46], static models fell out of fashion. Nevertheless, in 1970, N. Rosen, the collaborator of Einstein, proved that Eddington’s judgment was not well founded and that static universe models are stable [47]. This reopened the possibility of exploring the structure-formation process in models with static metrics.

These studies continued throughout the 1980s to the beginning of the 2000s. It was found that in static models, matter aggregation is likely to be fractal [48,49], which was later confirmed by statistical studies of CMB maps [50] and of the matter distribution in the universe [51,52]. Opposite to this, in the standard model of an expanding universe, structures cannot be fractal. Therefore, the reasons for the existence of the largest structures in the universe (the filaments and wall-like super-clusters, with huge voids between them) still cannot be explained within the framework of $\mathsf{\Lambda }$CDM.

Based on the newly recognised strong $\mathsf{\Lambda }$CDM tension called “the reionisation optical depth tension’’, one can confidently conclude that the model-dependent cosmological parameters derived from the “Planck”-mission CMB measurements cannot be fully trusted. Thence, the $H_0$-tension is resolved and is supportive of the type Ia supernova value of $H_0=73.5$ km s⁻¹ Mpc⁻¹. The corresponding age of the universe is then reduced to 12.4 Gyr (instead of the commonly accepted value of 13.8 Gyr deduced from the CMB Plank cosmology). This means that the galaxies with $z\approx 20$ observed by the JWST are as young as 160 million years old, which highlights to the extreme degree the impossibility of constructing a physically meaningful galaxy-formation model predicting a well-developed galaxy to be built in such a short time. This suggests that the universe’s age, according to the $\mathsf{\Lambda }$CDM model, is likely to be incorrect. The only alternative to solving this problem is to revise the standard cosmological model, which would make it possible to determine the real (larger) age of the universe.

Some people would be tempted to relegate the gravitational redshift hypothesis discussed here as an “amusing curiosity”, not worthy of being seriously discussed. Then, they would also have to agree that the hypothesis of the late 1970s of the inflationary universe by Starobinsky, Linde, Guth and others, which, according to the authors themselves in those years, was considered an “amusing curiosity”, also had no right to be discussed. However, that hypothesis (still a hypothesis that has not been confirmed by any observations) has now become the basis of the standard cosmological model.

The main problem with the two hundred or so existing inflation models is that they are quite successful in explaining current experimental data, but they do not allow for the prediction of the results of future measurements. In contrast to these hypotheses, the model discussed in this manuscript makes a clear testable prediction of the results of future measurements. The graph in Figure 1 shows that supernovae with redshifts $z=3$ or more, when they are detected, will be dimmer, compared to what $\mathsf{\Lambda }$CDM predicts for these redshifts. But in order to explain the additional dimming of supernovae from $z>1$, in relation to the simple model of an expanding universe, the concept of an unobservable physical entity called “dark energy” was introduced into the standard model. Its energy density, as determined by the supernova distance moduli, turned out to be ${10}^{120}$ times less than the vacuum energy density determined experimentally in elementary particle physics.

The cosmological model presented here does not need to introduce unobservable physical entities. It predicts the photometric parameters of distant sources, depending on their redshifts, and the observed quantities follow the predictions exactly based on gravitational redshift formalism.