The Intrinsic Correlations between Prompt Emission and X-ray Flares of Gamma-Ray Bursts
Abstract
1. Introduction
2. Data and Method
3. Statistical Analysis
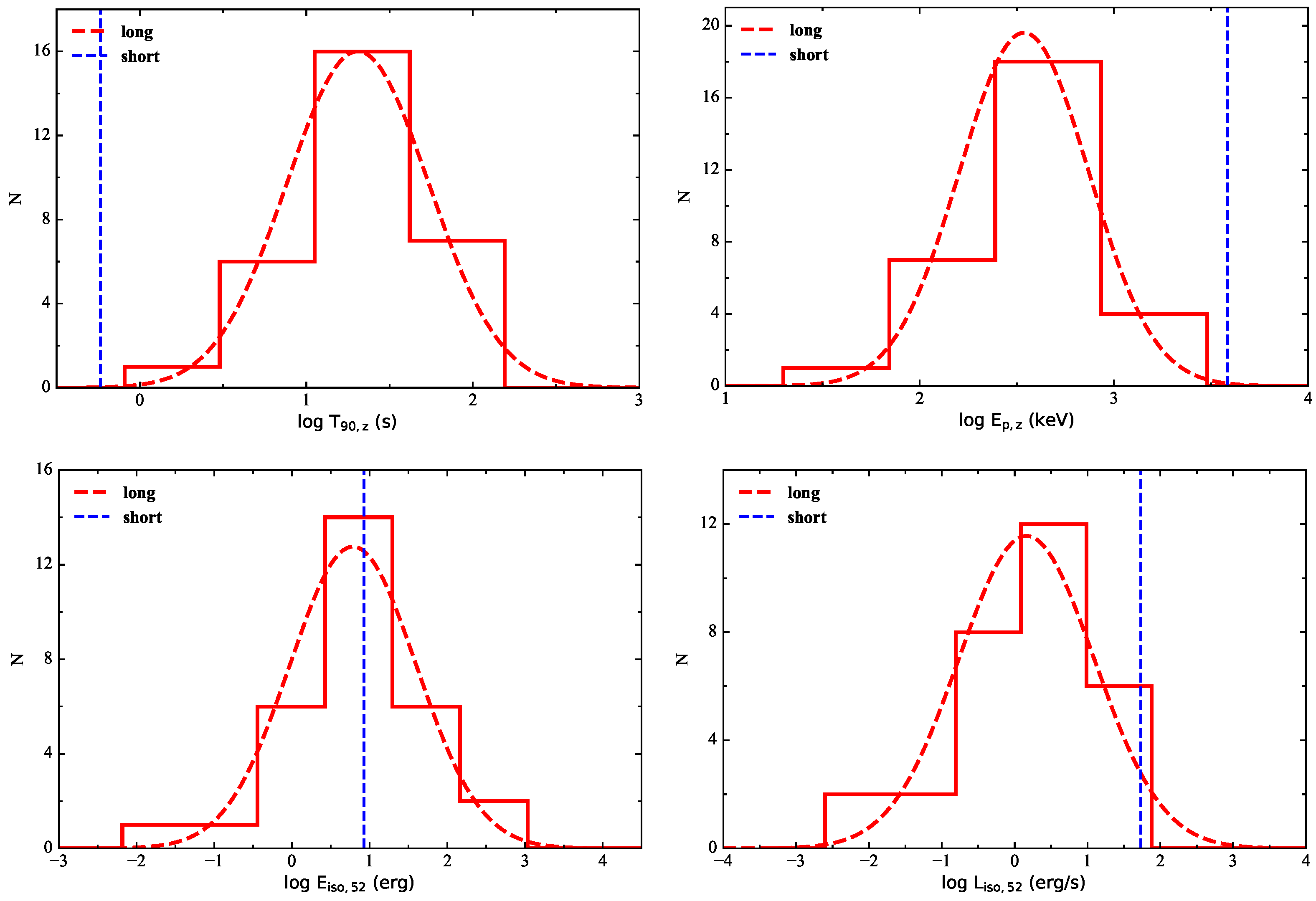
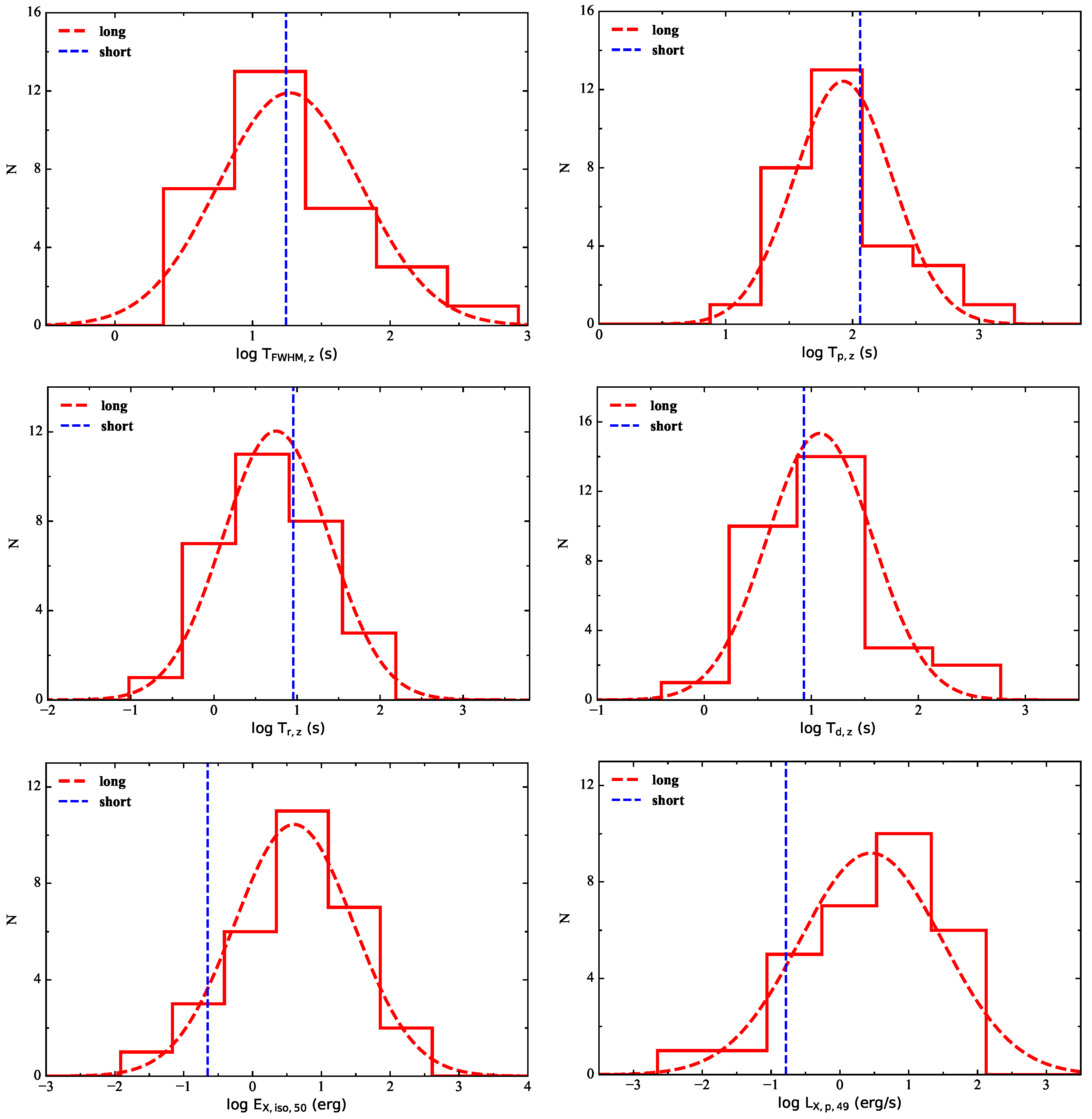
3.1. Parameter Distributions
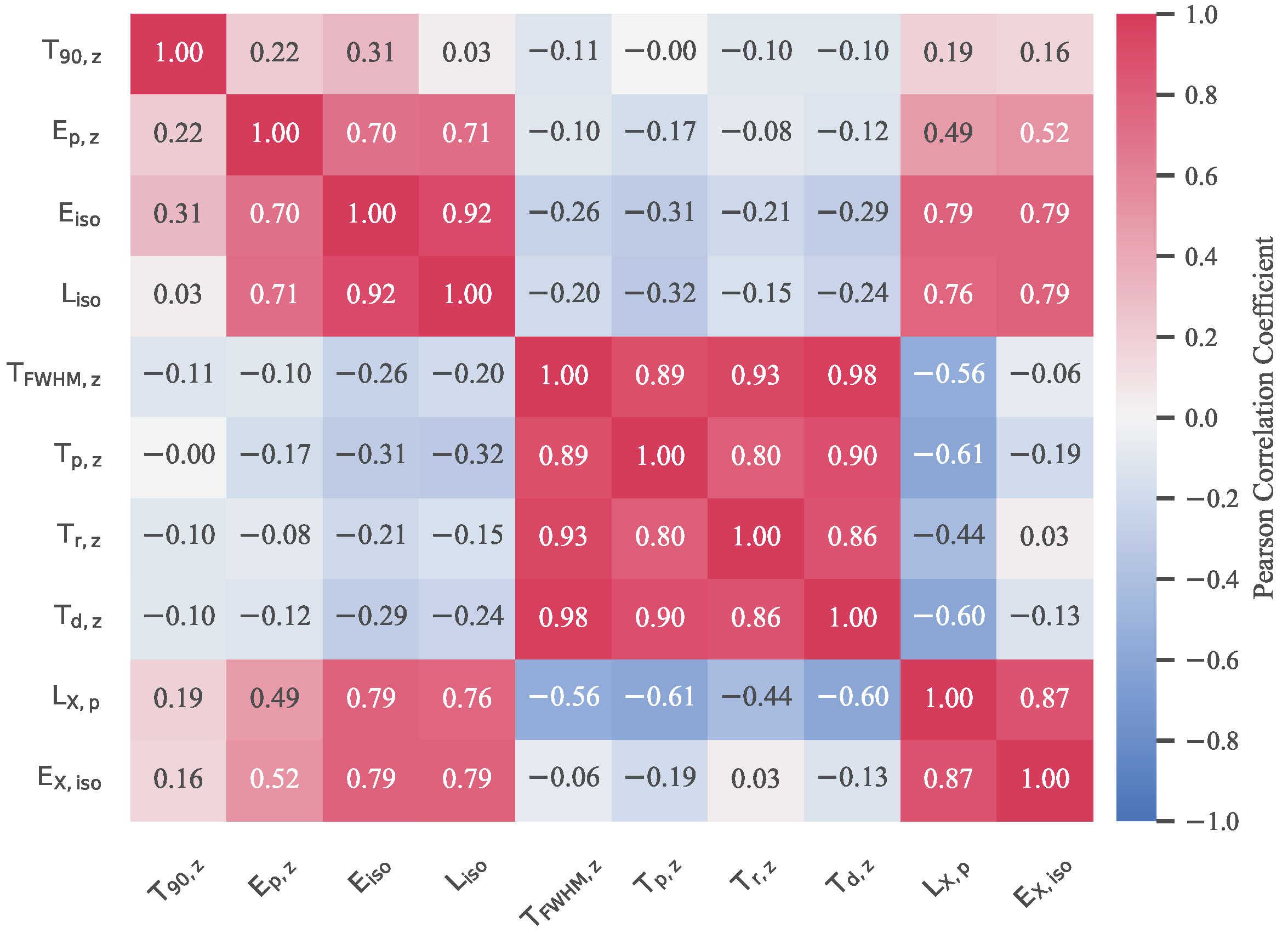
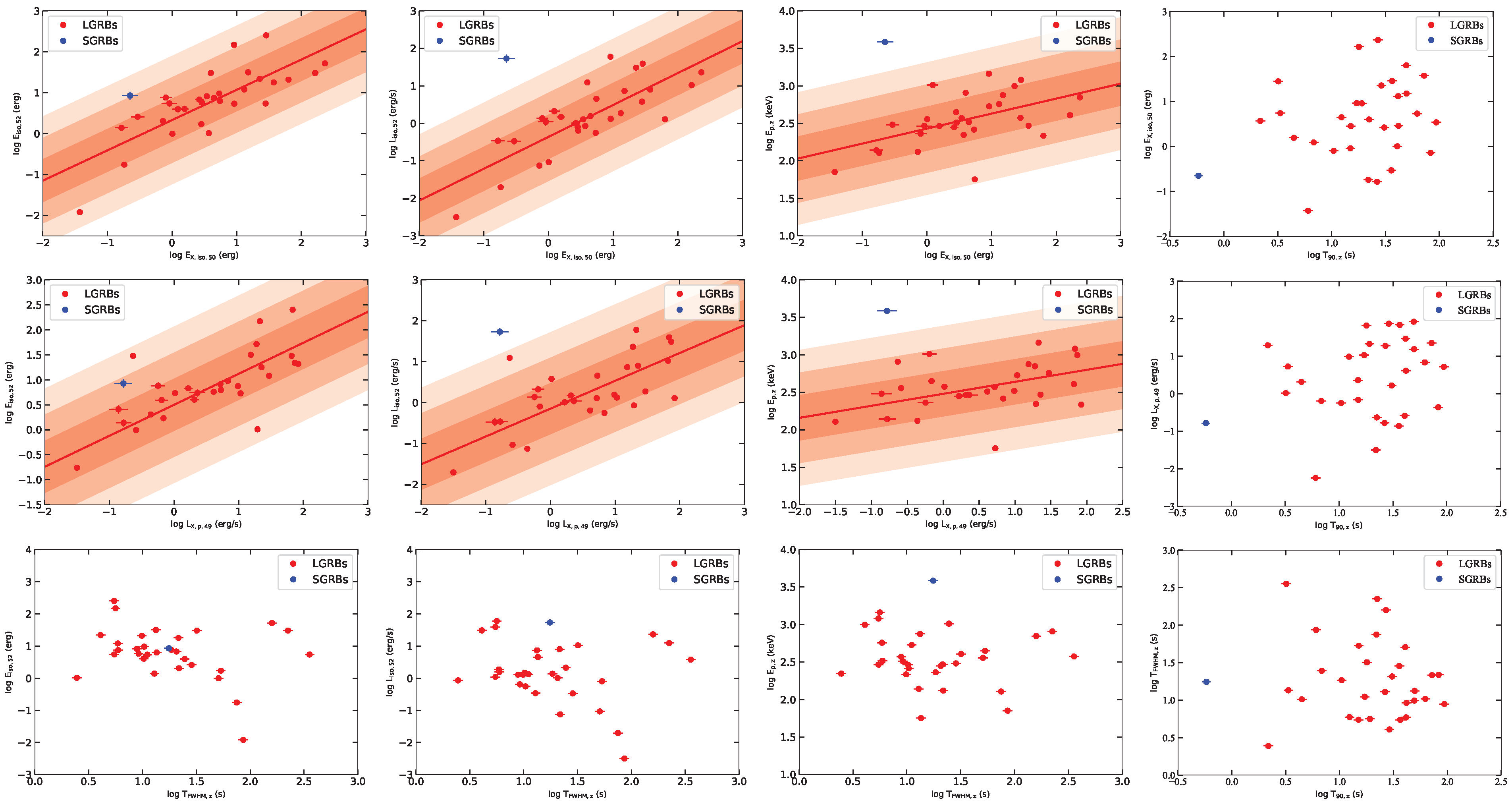
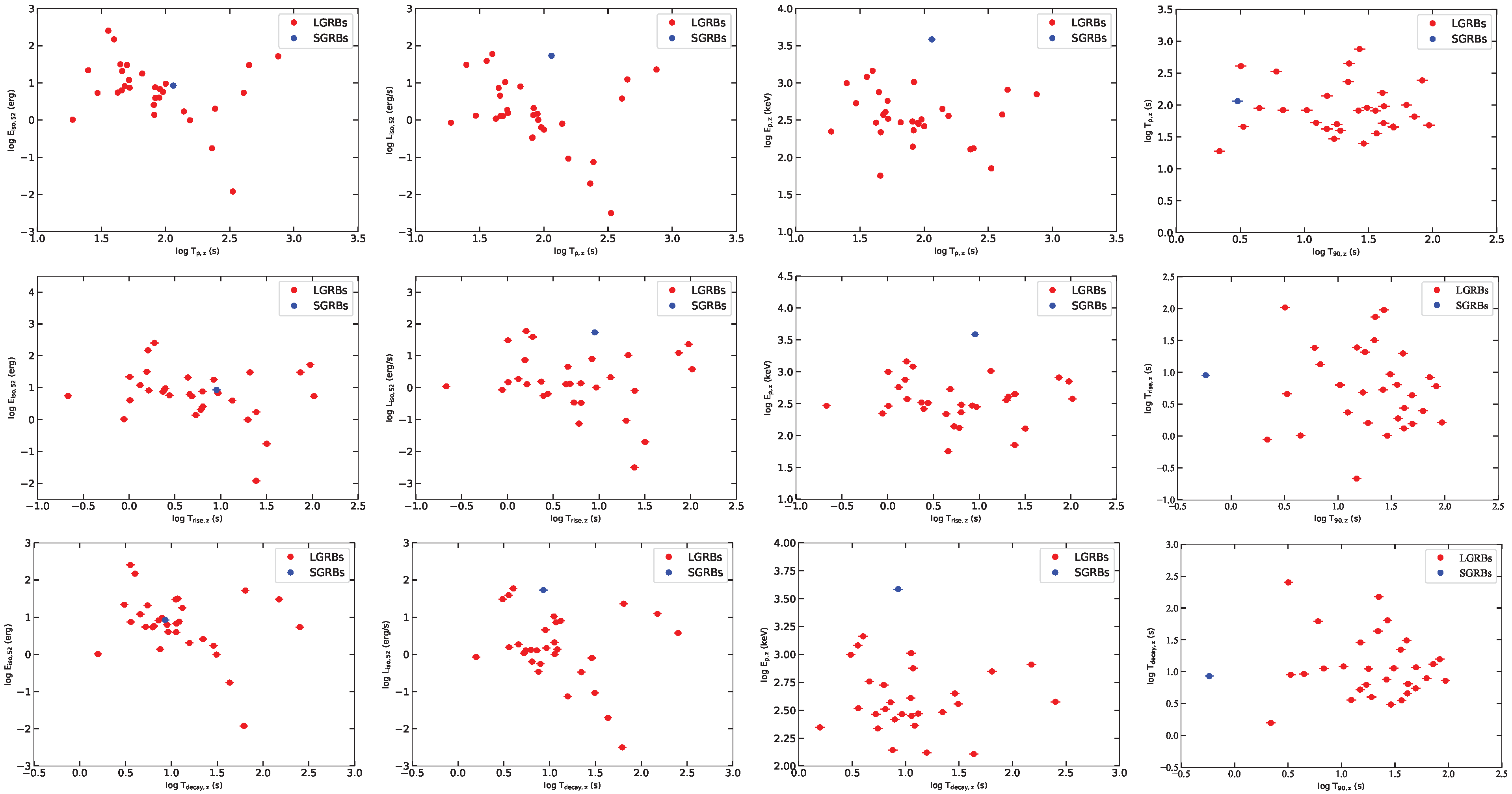
3.2. Two-Parameter Correlations
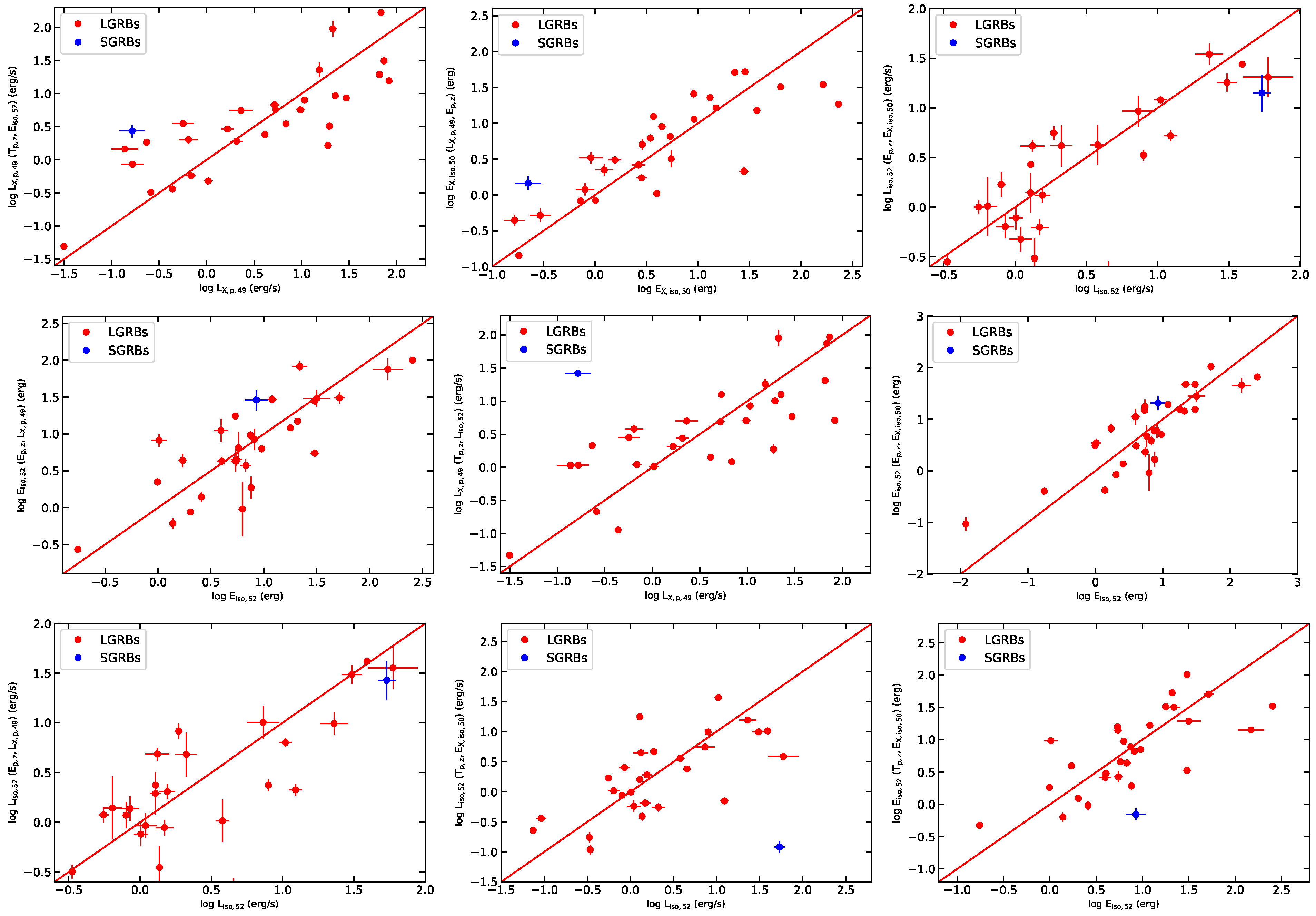
3.3. Three-Parameter Correlations
4. Summary
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
| 1 | https://heasarc.gsfc.nasa.gov/W3Browse/fermi/fermigbrst.html, accessed on 1 May 2024. |
| 2 | https://gcn.nasa.gov/, accessed on 1 May 2024. |
| 3 | https://pypi.python.org/pypi/emcee, accessed on 1 May 2024. |
References
- Kouveliotou, C.; Meegan, C.A.; Fishman, G.J.; Bhat, N.P.; Briggs, M.S.; Koshut, T.M.; Paciesas, W.S.; Pendleton, G.N. Identification of Two Classes of Gamma-Ray Bursts. Astrophys. J. Lett. 1993, 413, L101. [Google Scholar] [CrossRef]
- Paczynski, B. Gamma-ray bursters at cosmological distances. Astrophys. J. Lett. 1986, 308, L43. [Google Scholar] [CrossRef]
- Kochanek, C.S.; Piran, T. Gravitational Waves and gamma-Ray Bursts. Astrophys. J. Lett. 1993, 417, L17. [Google Scholar] [CrossRef]
- Woosley, S.E. Gamma-Ray Bursts from Stellar Mass Accretion Disks around Black Holes. Astrophys. J. 1993, 405, 273. [Google Scholar] [CrossRef]
- Kumar, P.; Zhang, B. The physics of gamma-ray bursts & relativistic jets. Phys. Rep. 2015, 561, 1. [Google Scholar] [CrossRef]
- Gehrels, N.; Chincarini, G.; Giommi, P.; Mason, K.O.; Nousek, J.A.; Wells, A.A.; White, N.E.; Barthelmy, S.D.; Burrows, D.N.; Cominsky, L.R.; et al. The Swift Gamma-Ray Burst Mission. Astrophys. J. 2004, 611, 1005. [Google Scholar] [CrossRef]
- Zhang, B.; Fan, Y.Z.; Dyks, J.; Kobayashi, S.; Mészáros, P.; Burrows, D.N.; Nousek, J.A.; Gehrels, N. Physical Processes Shaping Gamma-Ray Burst X-ray Afterglow Light Curves: Theoretical Implications from the Swift X-ray Telescope Observations. Astrophys. J. 2006, 642, 354. [Google Scholar] [CrossRef]
- Campana, S.; Tagliaferri, G.; Lazzati, D.; Chincarini, G.; Covino, S.; Page, K.; Romano, P.; Moretti, A.; Cusumano, G.; Mangano, V.; et al. The X-ray Afterglow of the Short Gamma Ray Burst 050724. Astron. Astrophys. 2006, 454, 113. [Google Scholar] [CrossRef][Green Version]
- Falcone, A.D.; Burrows, D.N.; Lazzati, D.; Campana, S.; Kobayashi, S.; Zhang, B.; Mészáros, P.; Page, K.L.; Kennea, J.A.; Romano, P.; et al. The Giant X-ray Flare of GRB 050502B: Evidence for Late-Time Internal Engine Activity. Astrophys. J. 2006, 641, 1010. [Google Scholar] [CrossRef]
- Nousek, J.A.; Kouveliotou, C.; Grupe, D.; Page, K.L.; Granot, J.; Ramirez-Ruiz, E.; Patel, S.K.; Burrows, D.N.; Mangano, V.; Barthelmy, S.; et al. Evidence for a Canonical Gamma-Ray Burst Afterglow Light Curve in the Swift XRT Data. Astrophys. J. 2006, 642, 389. [Google Scholar] [CrossRef]
- Margutti, R.; Chincarini, G.; Granot, J.; Guidorzi, C.; Berger, E.; Bernardini, M.G.; Gehrels, N.; Soderberg, A.M.; Stamatikos, M.; Zaninoni, E. X-ray Flare Candidates in Short Gamma-Ray Bursts. Mon. Not. R. Astron. Soc. 2011, 417, 2144. [Google Scholar] [CrossRef][Green Version]
- Yi, S.-X.; Xi, S.-Q.; Yu, H.; Wang, F.Y.; Mu, H.-J.; Lü, L.Z.; Liang, E.-W. Comprehensive Study of the X-ray Flares from Gamma-Ray Bursts Observed by Swift. Astrophys. J. Suppl. Ser. 2016, 224, 20. [Google Scholar] [CrossRef]
- Shi, Y.-R.; Ding, X.-K.; Zhu, S.-Y.; Sun, W.-P.; Zhang, F.-W. Statistical Properties of X-ray Flares in Gamma-Ray Bursts. Universe 2022, 8, 358. [Google Scholar] [CrossRef]
- Curran, P.A.; Starling, R.L.C.; O’Brien, P.T.; Godet, O.; van der Horst, A.J.; Wijers, R.A.M.J. On the nature of late X-ray flares in Swift gamma-ray bursts. Astron. Astrophys. 2008, 487, 533. [Google Scholar] [CrossRef]
- Bernardini, M.G.; Margutti, R.; Chincarini, G.; Guidorzi, C.; Mao, J. Gamma-Ray Burst Long Lasting X-ray Flaring Activity. Astron. Astrophys. 2011, 526, A27. [Google Scholar] [CrossRef]
- Mészáros, P.; Rees, M.J. Optical and Long-Wavelength Afterglow from Gamma-Ray Bursts. Astrophys. J. 1997, 476, 232. [Google Scholar] [CrossRef]
- Kobayashi, S.; Zhang, B.; Mészáros, P.; Burrows, D. Inverse Compton X-ray Flare from Gamma-Ray Burst Reverse Shock. Astrophys. J. 2007, 655, 391. [Google Scholar] [CrossRef][Green Version]
- Chincarini, G.; Moretti, A.; Romano, P.; Falcone, A.D.; Morris, D.; Racusin, J.; Campana, S.; Covino, S.; Guidorzi, C.; Tagliaferri, G.; et al. The First Survey of X-ray Flares from Gamma-Ray Bursts Observed by Swift: Temporal Properties and Morphology. Astrophys. J. 2007, 671, 1903. [Google Scholar] [CrossRef]
- Rees, M.J.; Mészáros, P. Refreshed Shocks and Afterglow Longevity in Gamma-Ray Bursts. Astrophys. J. Lett. 1998, 496, L1. [Google Scholar] [CrossRef]
- Ioka, K.; Kobayashi, S.; Zhang, B. Variabilities of Gamma-Ray Burst Afterglows: Long-acting Engine, Anisotropic Jet, or Many Fluctuating Regions? Astrophys. J. 2005, 631, 429. [Google Scholar] [CrossRef]
- Zhang, B.; Mészáros, P. Gamma-Ray Bursts with Continuous Energy Injection and Their Afterglow Signature. Astrophys. J. 2002, 566, 712. [Google Scholar] [CrossRef]
- Burrows, D.N.; Romano, P.; Falcone, A.; Kobayashi, S.; Zhang, B.; Moretti, A.; O’Brien, P.T.; Goad, M.R.; Campana, S.; Page, K.L.; et al. Bright X-ray Flares in Gamma-Ray Burst Afterglows. Science 2005, 309, 1833. [Google Scholar] [CrossRef] [PubMed]
- Chincarini, G.; Mao, J.; Margutti, R.; Bernardini, M.G.; Guidorzi, C.; Pasotti, F.; Giannios, D.; Della Valle, M.; Moretti, A.; Romano, P.; et al. Unveiling the Origin of X-ray Flares in Gamma-Ray Bursts. Mon. Not. R. Astron. Soc. 2010, 406, 2113. [Google Scholar] [CrossRef]
- Falcone, A.D.; Morris, D.; Racusin, J.; Chincarini, G.; Moretti, A.; Romano, P.; Burrows, D.N.; Pagani, C.; Stroh, M.; Grupe, D.; et al. The First Survey of X-ray Flares from Gamma-Ray Bursts Observed by Swift: Spectral Properties and Energetics. Astrophys. J. 2007, 671, 1921. [Google Scholar] [CrossRef]
- Lü, L.-Z.; Liang, E.-W.; Cordier, B. The Spectral Evolution Patterns and Implications of Gamma-Ray Burst X-ray Flares. Astrophys. J. 2022, 941, 99. [Google Scholar] [CrossRef]
- Margutti, R.; Guidorzi, C.; Chincarini, G.; Bernardini, M.G.; Genet, F.; Mao, J.; Pasotti, F. Lag-luminosity relation in gamma-ray burst X-ray flares: A direct link to the prompt emission. Mon. Not. R. Astron. Soc. 2010, 406, 2149. [Google Scholar] [CrossRef]
- Sonbas, E.; MacLachlan, G.A.; Shenoy, A.; Dhuga, K.S.; Parke, W.C. A New Correlation between GRB X-ray Flares and the Prompt Emission. Astrophys. J. Lett. 2013, 767, L28. [Google Scholar] [CrossRef][Green Version]
- Chang, X.Z.; Peng, Z.Y.; Chen, J.M.; Yin, Y.; Wang, D.Z.; Wu, H. A Comprehensive Study of Multiflare GRB Spectral Lag. Astrophys. J. 2021, 922, 34. [Google Scholar] [CrossRef]
- Peng, F.-K.; Liang, E.-W.; Wang, X.-Y.; Hou, S.-J.; Xi, S.-Q.; Lu, R.-J.; Zhang, J.; Zhang, B. Photosphere Emission in the X-ray Flares of Swift Gamma-Ray Bursts and Implications for the Fireball Properties. Astrophys. J. 2014, 795, 155. [Google Scholar] [CrossRef]
- Wang, Y.; Aimuratov, Y.; Moradi, R.; Peresano, M.; Ruffini, R.; Shakeri, S. Revisiting the Statistics of X-ray Flares in Gamma-Ray Bursts. Mem. Soc. Astron. Ital. 2018, 89, 293. [Google Scholar] [CrossRef]
- Yi, S.-X.; Xie, W.; Ma, S.-B.; Lei, W.-H.; Du, M. Constraining Properties of GRB Central Engines with X-ray Flares. Mon. Not. R. Astron. Soc. 2021, 507, 1047. [Google Scholar] [CrossRef]
- Yi, S.-X.; Du, M.; Liu, T. Statistical Analyses of the Energies of X-ray Plateaus and Flares in Gamma-Ray Bursts. Astrophys. J. 2022, 924, 69. [Google Scholar] [CrossRef]
- Saji, J.; Iyyani, S.; Mazde, K. Statistical Analysis of Long GRBs’ Prompt Emission and X-ray Flares: Multivariate Clustering and Correlations. Astrophys. J. Suppl. Ser. 2023, 269, 2. [Google Scholar] [CrossRef]
- Wang, F.Y.; Dai, Z.G. Self-organized Criticality in X-ray Flares of Gamma-Ray-Burst Afterglows. Nat. Phys. 2013, 9, 465. [Google Scholar] [CrossRef]
- Schaefer, B.E. The Hubble Diagram to Redshift >6 from 69 Gamma-Ray Bursts. Astrophys. J. 2007, 660, 16. [Google Scholar] [CrossRef]
- Band, D.; Matteson, J.; Ford, L.; Schaefer, B.; Palmer, D.; Teegarden, B.; Cline, T.; Briggs, M.; Paciesas, W.; Pendleton, G.; et al. BATSE Observations of Gamma-Ray Burst Spectra. I. Spectral Diversity. Astrophys. J. 1993, 413, 281. [Google Scholar] [CrossRef]
- D’Agostini, G. Fits, and especially linear fits, with errors on both axes, extra variance of the data points and other complications. arXiv 2005, arXiv:physics/0511182. [Google Scholar]
- Xu, M.; Huang, Y.F. New three-parameter correlation for gamma-ray bursts with a plateau phase in the afterglow. Astron. Astrophys. 2012, 538, A134. [Google Scholar] [CrossRef]
- Tang, C.-H.; Huang, Y.-F.; Geng, J.-J.; Zhang, Z.-B. Statistical Study of Gamma-Ray Bursts with a Plateau Phase in the X-ray Afterglow. Astrophys. J. Suppl. Ser. 2019, 245, 1. [Google Scholar] [CrossRef]
- Foreman-Mackey, D.; Hogg, D.W.; Lang, D.; Goodman, J. emcee: The MCMC Hammer. Publ. Astron. Soc. Pac. 2013, 125, 306. [Google Scholar] [CrossRef]
- Norris, J.P.; Nemiroff, R.J.; Bonnell, J.T.; Scargle, J.D.; Kouveliotou, C.; Paciesas, W.S.; Meegan, C.A.; Fishman, G.J. Attributes of Pulses in Long Bright Gamma-Ray Bursts. Astrophys. J. 1996, 459, 393. [Google Scholar] [CrossRef]
- Dainotti, M.G.; Ostrowski, M.; Willingale, R. Towards a standard gamma-ray burst: Tight correlations between the prompt and the afterglow plateau phase emission. Mon. Not. R. Astron. Soc. 2011, 418, 2202. [Google Scholar] [CrossRef]
- Ding, X.-K.; Shi, Y.-R.; Zhu, S.-Y.; Sun, W.-P.; Zhang, F.-W. Statistical properties of the X-ray afterglow shallow decay phase and their relationships with the prompt gamma-ray emission of gamma-ray bursts. Astrophys. Space Sci. 2022, 367, 58. [Google Scholar] [CrossRef]
- Deng, C.; Huang, Y.-F.; Xu, F. Pseudo-redshifts of Gamma-Ray Bursts Derived from the L-T-E Correlation. Astrophys. J. 2023, 943, 126. [Google Scholar] [CrossRef]
- Dainotti, M.G.; Postnikov, S.; Hernandez, X.; Ostrowski, M. A Fundamental Plane for Long Gamma-Ray Bursts with X-ray Plateaus. Astrophys. J. Lett. 2016, 825, L20. [Google Scholar] [CrossRef]
- Si, S.-K.; Qi, Y.-Q.; Xue, F.-X.; Liu, Y.-J.; Wu, X.; Yi, S.-X.; Tang, Q.-W.; Zou, Y.-C.; Wang, F.-F.; Wang, X.-G. The Three-parameter Correlations About the Optical Plateaus of Gamma-Ray Bursts. Astrophys. J. 2018, 863, 50. [Google Scholar] [CrossRef]
| GRB | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| (s) | (keV) | (erg) | (erg/s) | (s) | (s) | (s) | (s) | (erg/s) | (erg) | |
| 050908 | 4.47 ± 0.45 | 291.18 ± 29.12 | 4.02 ± 0.39 | 1.48 ± 0.21 | 10.26 ± 1.03 | 89.22 ± 0.20 | 1.02 ± 0.10 | 9.24 ± 0.92 | 2.07 ± 0.30 | 1.56 ± 0.22 |
| 060115 | 30.82 ± 3.08 | 280.86 ± 45.30 | 6.74 ± 0.75 | 1.01 ± 0.11 | 20.67 ± 2.07 | 90.38 ± 3.53 | 9.33 ± 0.93 | 11.34 ± 1.13 | 1.66 ± 0.26 | 2.64 ± 0.39 |
| 060204B | 41.75 ± 4.15 | 323.24 ± 136.91 | 5.76 ± 0.38 | 0.64 ± 0.10 | 9.21 ± 0.92 | 95.34 ± 0.42 | 2.76 ± 0.28 | 6.45 ± 0.65 | 4.11 ± 0.27 | 2.88 ± 0.14 |
| 060418 | 41.42 ± 4.14 | 572.47 ± 57.25 | 11.99 ± 1.20 | 1.86 ± 0.11 | 5.90 ± 0.59 | 51.85 ± 0.12 | 1.32 ± 0.13 | 4.58 ± 0.46 | 29.50 ± 1.07 | 13.10 ± 0.40 |
| 060707 | 14.96 ± 1.50 | 292.05 ± 44.25 | 5.49 ± 0.65 | 1.09 ± 0.20 | 5.47 ± 0.547 | 42.20 ± 0.14 | 0.22 ± 0.02 | 5.25 ± 0.53 | 2.30 ± 0.63 | 0.91 ± 0.24 |
| 060719 | 26.42 ± 2.64 | 138.96 ± 13.90 | 1.38 ± 0.09 | 0.34 ± 0.03 | 12.89 ± 1.29 | 81.54 ± 4.18 | 5.33 ± 0.53 | 7.56 ± 0.76 | 0.17 ± 0.04 | 0.17 ± 0.04 |
| 060814 | 49.71 ± 4.97 | 751.19 ± 169.53 | 31.58 ± 9.27 | 7.31 ± 1.89 | 13.30 ± 1.33 | 44.40 ± 0.40 | 1.55 ± 0.16 | 11.74 ± 1.17 | 15.40 ± 0.79 | 15.00 ± 0.52 |
| 070318 | 40.63 ± 4.06 | 360.20 ± 35.99 | 0.99 ± 0.04 | 0.09 ± 0.01 | 50.87 ± 5.09 | 154.93 ± 2.51 | 19.78 ± 1.98 | 31.09 ± 3.11 | 0.26 ± 0.01 | 1.01 ± 0.04 |
| 080210 | 12.36 ± 1.24 | 329.44 ± 32.94 | 7.46 ± 0.41 | 1.56 ± 0.20 | 5.95 ± 0.60 | 52.47 ± 0.55 | 2.35 ± 0.24 | 3.61 ± 0.36 | 9.74 ± 0.10 | 4.46 ± 0.40 |
| 081008 | 62.49 ± 6.25 | 261.23 ± 26.12 | 9.53 ± 0.44 | 0.56 ± 0.04 | 10.40 ± 1.04 | 100.22 ± 0.25 | 2.48 ± 0.25 | 7.92 ± 0.79 | 6.84 ± 0.28 | 5.37 ± 0.17 |
| 091029 | 10.45 ± 1.05 | 230.37 ± 65.66 | 7.59 ± 0.32 | 1.37 ± 0.08 | 18.49 ± 1.85 | 82.82 ± 3.40 | 6.33 ± 0.63 | 12.16 ± 1.22 | 0.57 ± 0.14 | 0.80 ± 0.16 |
| 101219B | 21.94 ± 2.19 | 128.03 ± 7.15 | 0.17 ± 0.01 | 0.02 ± 0.00 | 75.08 ± 7.51 | 229.84 ± 7.44 | 31.78 ± 3.18 | 43.30 ± 4.33 | 0.03 ± 0.01 | 0.18 ± 0.01 |
| 111107A | 6.83 ± 0.68 | 1026.76 ± 299.15 | 3.94 ± 0.58 | 2.11 ± 0.37 | 24.64 ± 2.46 | 83.25 ± 4.75 | 13.37 ± 1.34 | 11.27 ± 1.13 | 0.64 ± 0.14 | 1.23 ± 0.24 |
| 131030A | 17.91 ± 1.79 | 406.22 ± 22.95 | 30.14 ± 1.83 | 10.48 ± 1.05 | 31.96 ± 3.20 | 49.97 ± 0.61 | 20.82 ± 2.08 | 11.14 ± 1.11 | 65.90 ± 2.43 | 164.00 ± 4.93 |
| 131117A | 2.18 ± 0.22 | 221.85 ± 37.31 | 1.02 ± 0.16 | 0.85 ± 0.12 | 2.460 ± 0.25 | 18.86 ± 0.18 | 0.88 ± 0.09 | 1.58 ± 0.16 | 19.0 ± 1.67 | 3.70 ± 0.26 |
| 140419A | 19.11 ± 1.91 | 1452.11 ± 416.30 | 148.26 ± 48.57 | 59.54 ± 24.07 | 5.62 ± 0.56 | 39.64 ± 0.33 | 1.61 ± 0.16 | 4.01 ± 0.40 | 21.30 ± 1.91 | 9.10 ± 0.61 |
| 140515A | 3.20 ± 0.32 | 375.52 ± 107.60 | 5.42 ± 0.55 | 3.79 ± 0.42 | 356.23 ± 35.62 | 406.37 ± 2.80 | 104.06 ± 10.41 | 252.17 ± 25.22 | 1.04 ± 0.11 | 28.00 ± 2.87 |
| 140907A | 35.84 ± 3.58 | 303.21 ± 17.25 | 2.57 ± 0.09 | 0.33 ± 0.02 | 28.57 ± 2.86 | 81.12 ± 4.58 | 6.38 ± 0.64 | 22.19 ± 2.22 | 0.14 ± 0.04 | 0.29 ± 0.07 |
| 141221A | 15.05 ± 1.51 | 446.44 ± 78.39 | 1.71 ± 0.16 | 0.80 ± 0.05 | 53.36 ± 5.34 | 138.96 ± 6.71 | 24.50 ± 2.45 | 28.86 ± 2.89 | 0.69 ± 0.08 | 2.83 ± 0.31 |
| 150206A | 26.95 ± 2.70 | 703.84 ± 108.05 | 51.87 ± 6.01 | 22.98 ± 5.16 | 159.11 ± 15.91 | 754.59 ± 3.43 | 94.87 ± 9.49 | 64.24 ± 6.42 | 18.90 ± 0.45 | 232.00 ± 4.38 |
| 151111A | 17.10 ± 1.71 | 533.24 ± 43.43 | 5.37 ± 0.35 | 1.32 ± 0.26 | 11.08 ± 1.11 | 29.47 ± 0.93 | 4.83 ± 0.48 | 6.25 ± 0.63 | 10.70 ± 0.75 | 9.18 ± 0.67 |
| 160804A | 83.06 ± 8.31 | 131.68 ± 4.88 | 2.03 ± 0.05 | 0.07 ± 0.01 | 21.80 ± 2.18 | 243.15 ± 0.97 | 6.06 ± 0.61 | 15.74 ± 1.57 | 0.48 ± 0.03 | 0.72 ± 0.40 |
| 161117A | 49.31 ± 4.93 | 216.76 ± 4.39 | 20.83 ± 0.27 | 1.29 ± 0.05 | 9.86 ± 0.99 | 45.89 ± 0.22 | 4.36 ± 0.44 | 5.49 ± 0.55 | 83.30 ± 2.06 | 63.40 ± 1.51 |
| 161219B | 6.05 ± 0.61 | 71.03 ± 19.28 | 0.01 ± 0.00 | 0.003 ± 0.00 | 86.26 ± 8.63 | 333.94 ± 2.57 | 24.33 ± 2.43 | 61.93 ± 6.19 | 0.01 ± 0.00 | 0.04 ± 0.00 |
| 170405A | 36.52 ± 3.65 | 1204.23 ± 41.89 | 253.07 ± 2.55 | 39.11 ± 0.84 | 5.46 ± 0.55 | 35.77 ± 0.23 | 1.89 ± 0.19 | 3.57 ± 0.36 | 68.50 ± 3.65 | 28.60 ± 1.23 |
| 170705A | 72.19 ± 7.22 | 294.61 ± 23.01 | 17.84 ± 0.54 | 7.96 ± 0.18 | 21.56 ± 2.16 | 65.65 ± 0.29 | 8.37 ± 0.84 | 13.18 ± 1.32 | 22.60 ± 0.38 | 37.40 ± 0.59 |
| 180325A | 28.97 ± 2.90 | 993.89 ± 126.67 | 21.83 ± 3.45 | 30.60 ± 4.85 | 4.08 ± 0.41 | 24.89 ± 0.23 | 1.01 ± 0.10 | 3.07 ± 0.31 | 73.70 ± 4.69 | 22.70 ± 1.19 |
| 180620B | 93.88 ± 9.39 | 371.90 ± 105.43 | 8.17 ± 0.22 | 1.28 ± 0.11 | 8.88 ± 0.89 | 48.02 ± 0.55 | 1.64 ± 0.16 | 7.24 ± 0.72 | 5.20 ± 0.56 | 3.44 ± 0.26 |
| 191221B | 22.35 ± 2.24 | 809.80 ± 62.29 | 30.20 ± 3.02 | 12.33 ± 1.30 | 224.02 ± 22.40 | 447.20 ± 11.49 | 73.92 ± 7.39 | 150.10 ± 15.01 | 0.23 ± 0.01 | 3.98 ± 0.16 |
| 210411C | 3.346 ± 0.34 | 56.62 ± 41.32 | 6.27 ± 0.52 | 4.53 ± 0.28 | 13.55 ± 1.36 | 45.52 ± 0.94 | 4.58 ± 0.46 | 8.97 ± 0.90 | 5.32 ± 0.42 | 5.50 ± 0.35 |
| 160410A | 0.58 ± 0.05 | 3847.27 ± 967.25 | 8.49 ± 2.12 | 53.82 ± 7.69 | 17.54 ± 1.75 | 114.84 ± 7.13 | 8.90 ± 0.90 | 8.54 ± 0.854 | 0.17 ± 0.05 | 0.22 ± 0.07 |
| Parameter | Median Value | Dispersion |
|---|---|---|
| 20.35 s | 0.43 | |
| 344.61 keV | 0.33 | |
| 6.11 × erg | 0.82 | |
| 1.45 × erg | 0.93 | |
| 18.58 s | 0.52 | |
| 84.49 s | 0.39 | |
| 5.57 s | 0.64 | |
| 12.04 s | 0.49 | |
| 4.02 × erg | 0.86 | |
| 2.84 × erg | 1.04 |
| Relation | Expression | r | |
|---|---|---|---|
| 0.53 | 0.79 | ||
| 0.53 | 0.79 | ||
| 0.60 | 0.79 | ||
| 0.64 | 0.76 | ||
| 0.25 | 0.52 | ||
| 0.26 | 0.49 |
| Relation | Expression | r | |
|---|---|---|---|
| 0.54 | 0.87 | ||
| 0.51 | 0.81 | ||
| 0.31 | 0.66 | ||
| 0.45 | 0.87 | ||
| 0.56 | 0.87 | ||
| 0.26 | 0.53 | ||
| 0.41 | 0.86 | ||
| 0.56 | 0.79 | ||
| 0.17 | 0.72 | ||
| 0.41 | 0.86 | ||
| 0.68 | 0.79 | ||
| 0.20 | 0.71 | ||
| 0.58 | 0.85 | ||
| 0.62 | 0.78 | ||
| 0.32 | 0.64 | ||
| 0.43 | 0.85 | ||
| 0.57 | 0.79 | ||
| 0.20 | 0.70 | ||
| 0.43 | 0.85 | ||
| 0.72 | 0.77 | ||
| 0.16 | 0.72 | ||
| 0.58 | 0.81 | ||
| 0.56 | 0.79 | ||
| 0.39 | 0.34 | ||
| 0.52 | 0.80 | ||
| 0.57 | 0.79 | ||
| 0.40 | 0.32 | ||
| 0.33 | 0.62 | ||
| 0.27 | 0.51 | ||
| 0.77 | 0.51 | ||
| 0.26 | 0.53 | ||
| 0.78 | 0.53 | ||
| 0.41 | 0.21 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhong, X.-T.; Zhu, S.-Y.; Zhuo, L.-M.; Zhang, Z.; Zhang, F.-W. The Intrinsic Correlations between Prompt Emission and X-ray Flares of Gamma-Ray Bursts. Universe 2024, 10, 343. https://doi.org/10.3390/universe10090343
Zhong X-T, Zhu S-Y, Zhuo L-M, Zhang Z, Zhang F-W. The Intrinsic Correlations between Prompt Emission and X-ray Flares of Gamma-Ray Bursts. Universe. 2024; 10(9):343. https://doi.org/10.3390/universe10090343
Chicago/Turabian StyleZhong, Xing-Ting, Si-Yuan Zhu, Li-Ming Zhuo, Zeng Zhang, and Fu-Wen Zhang. 2024. "The Intrinsic Correlations between Prompt Emission and X-ray Flares of Gamma-Ray Bursts" Universe 10, no. 9: 343. https://doi.org/10.3390/universe10090343
APA StyleZhong, X.-T., Zhu, S.-Y., Zhuo, L.-M., Zhang, Z., & Zhang, F.-W. (2024). The Intrinsic Correlations between Prompt Emission and X-ray Flares of Gamma-Ray Bursts. Universe, 10(9), 343. https://doi.org/10.3390/universe10090343






