Lifetime of Long-Lived Sunspot Groups
Abstract
1. Introduction
2. Materials and Methods
3. Results
3.1. Recurrent Sunspot Groups
3.1.1. Lifetimes of Recurrent Sunspot Groups
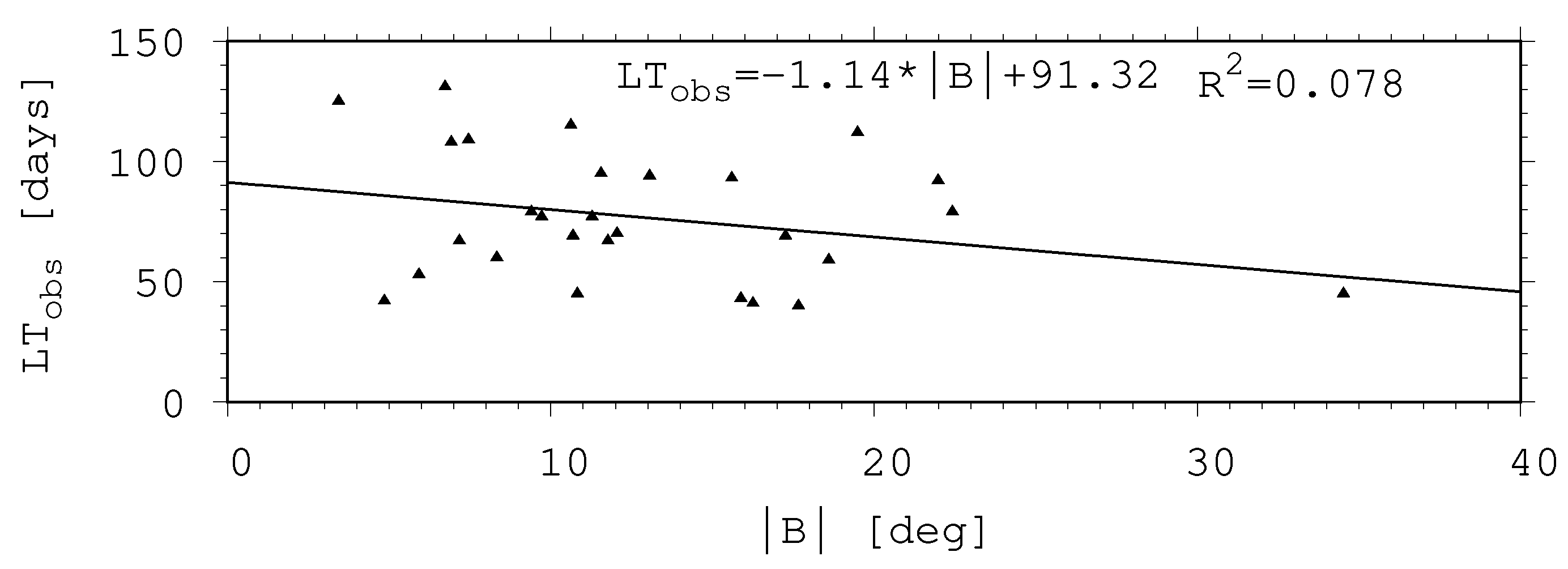
3.1.2. Cycle Phase Dependence
3.2. Active Nests
4. Conclusions
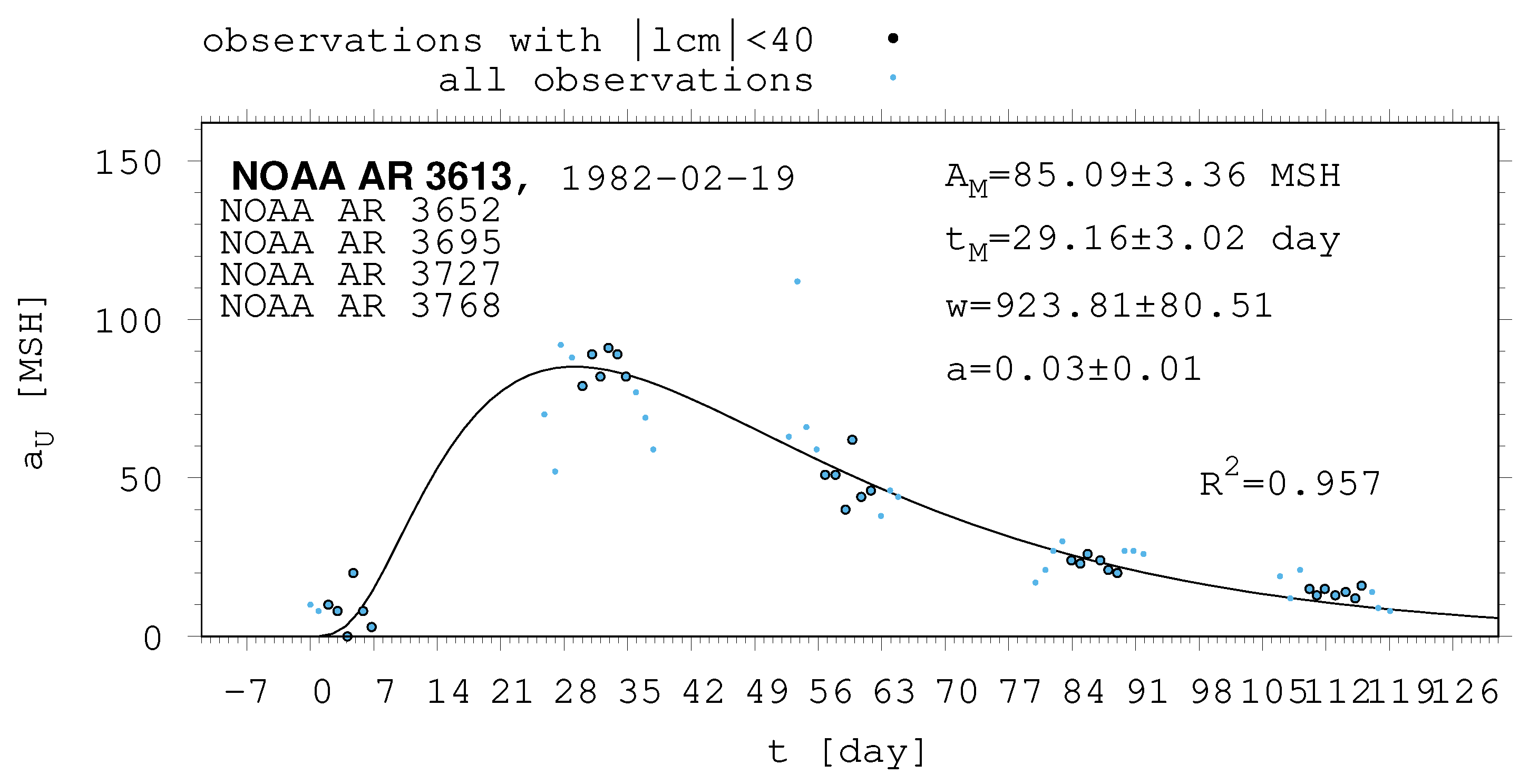
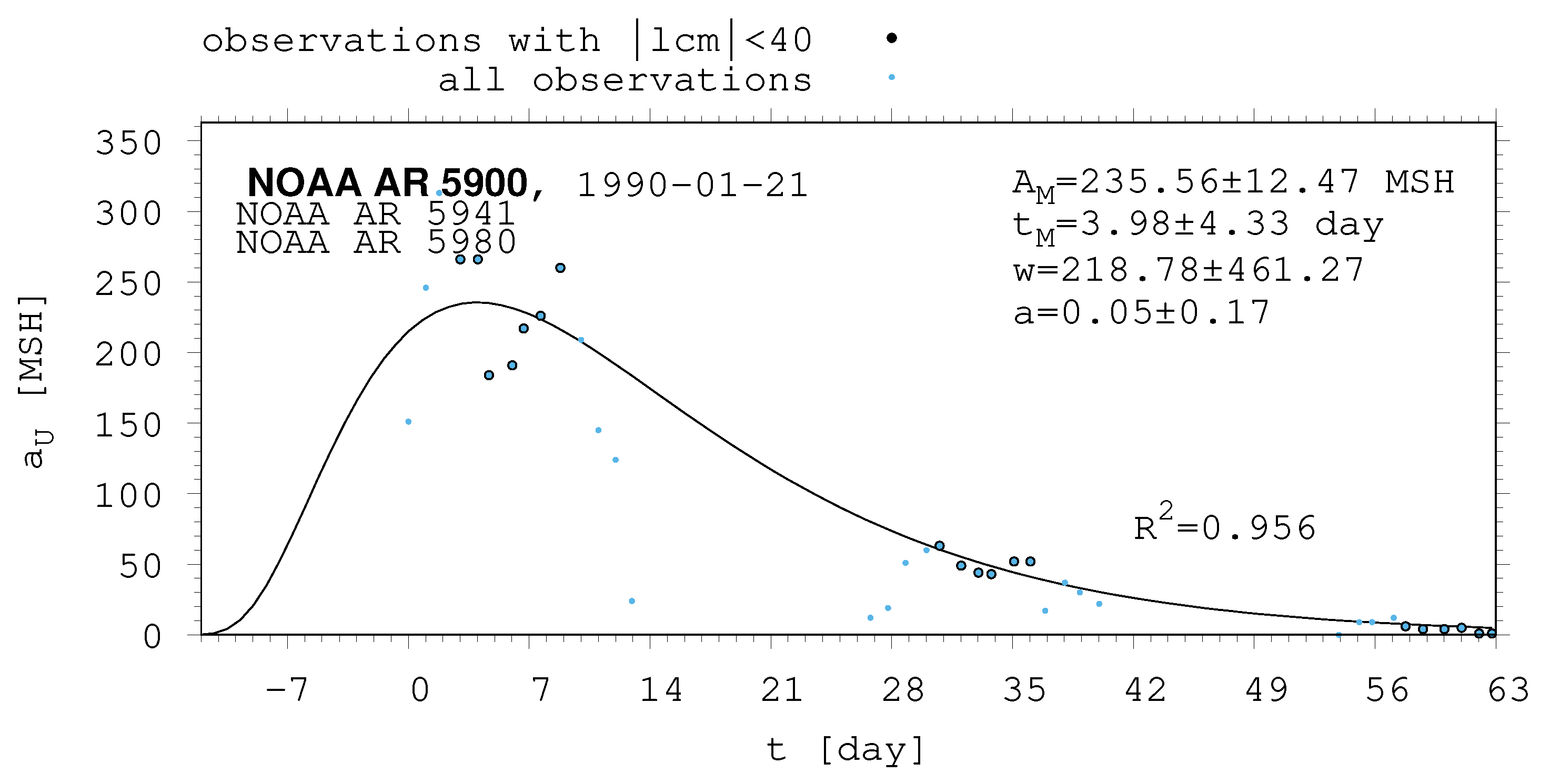
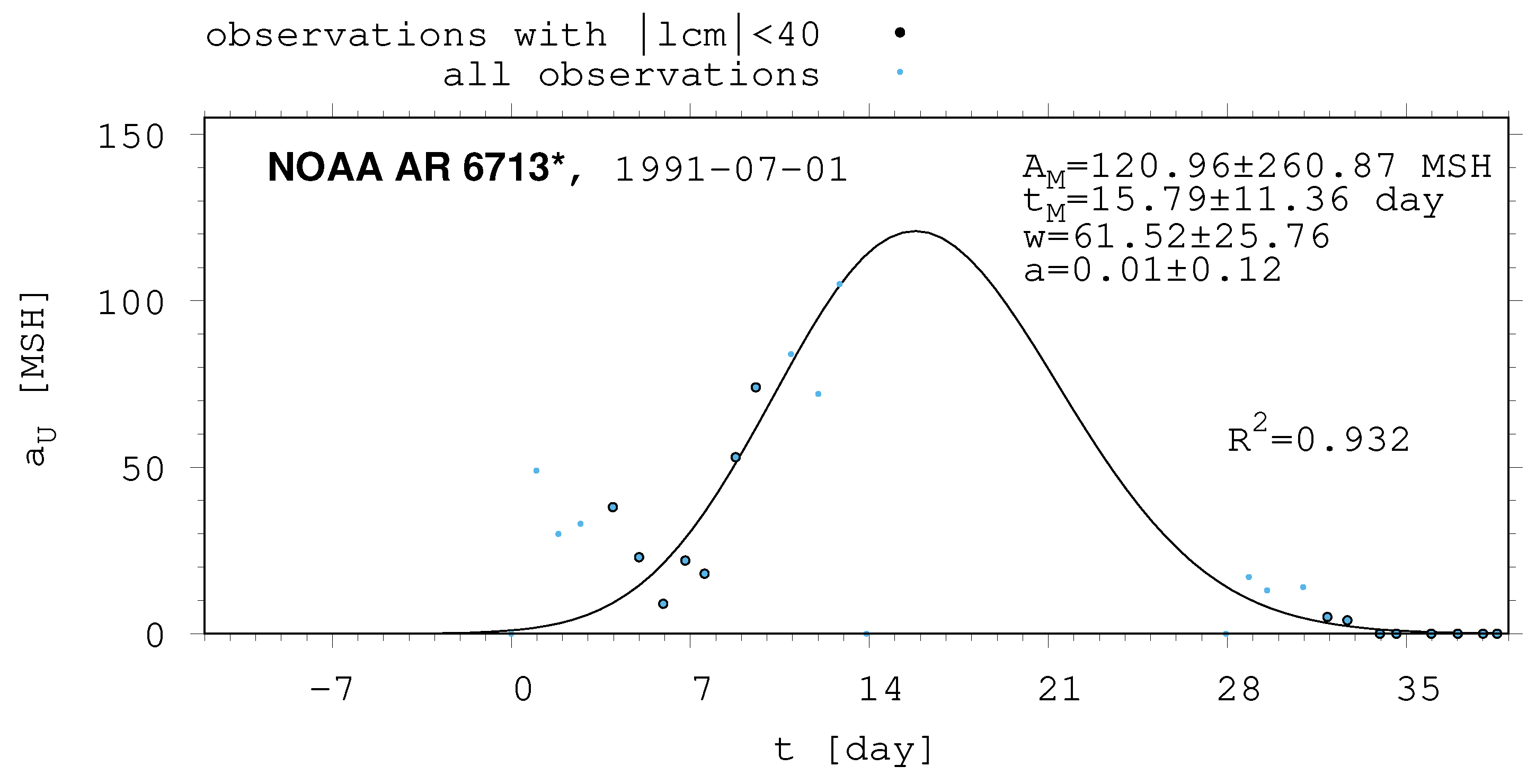
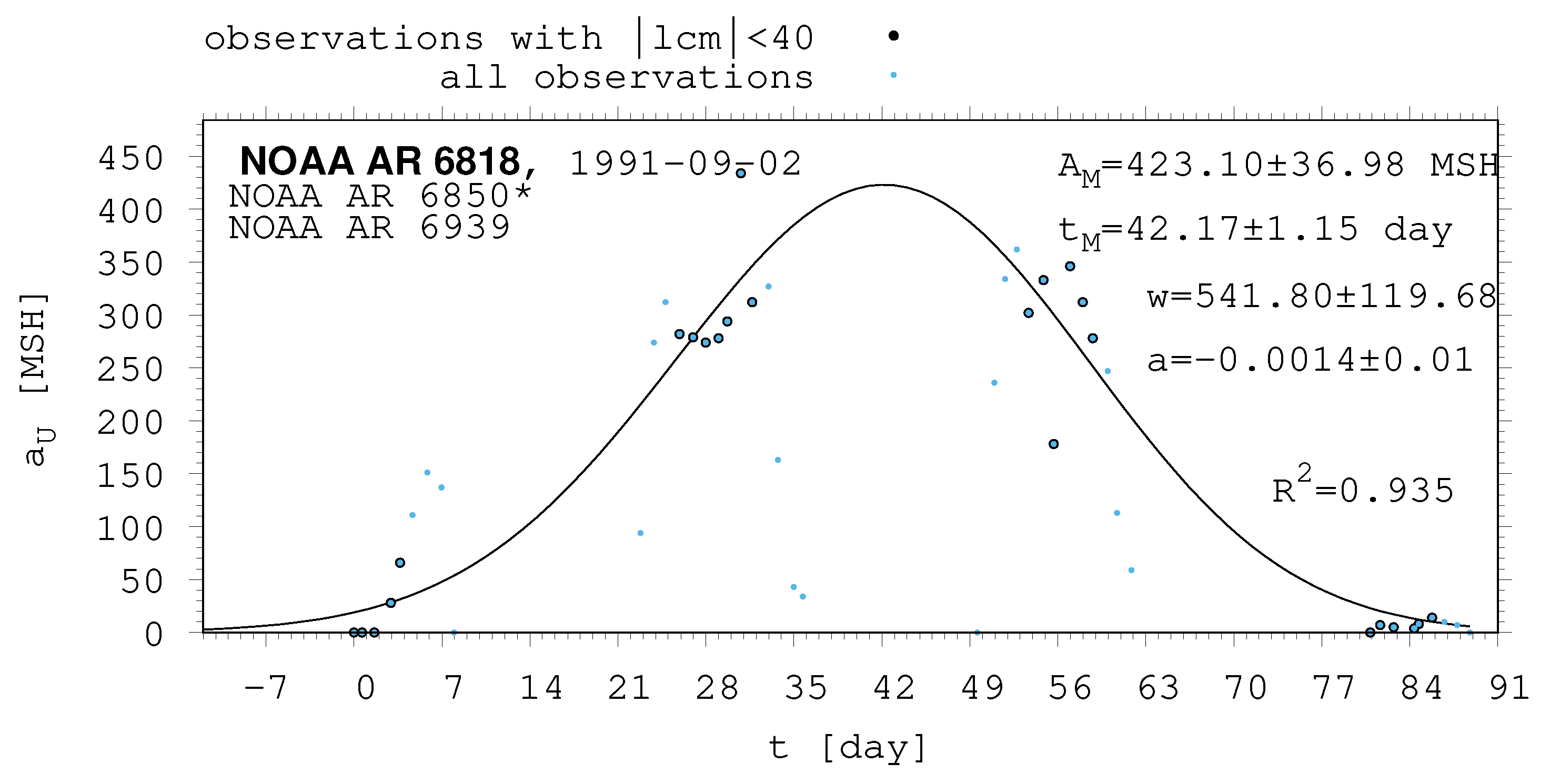
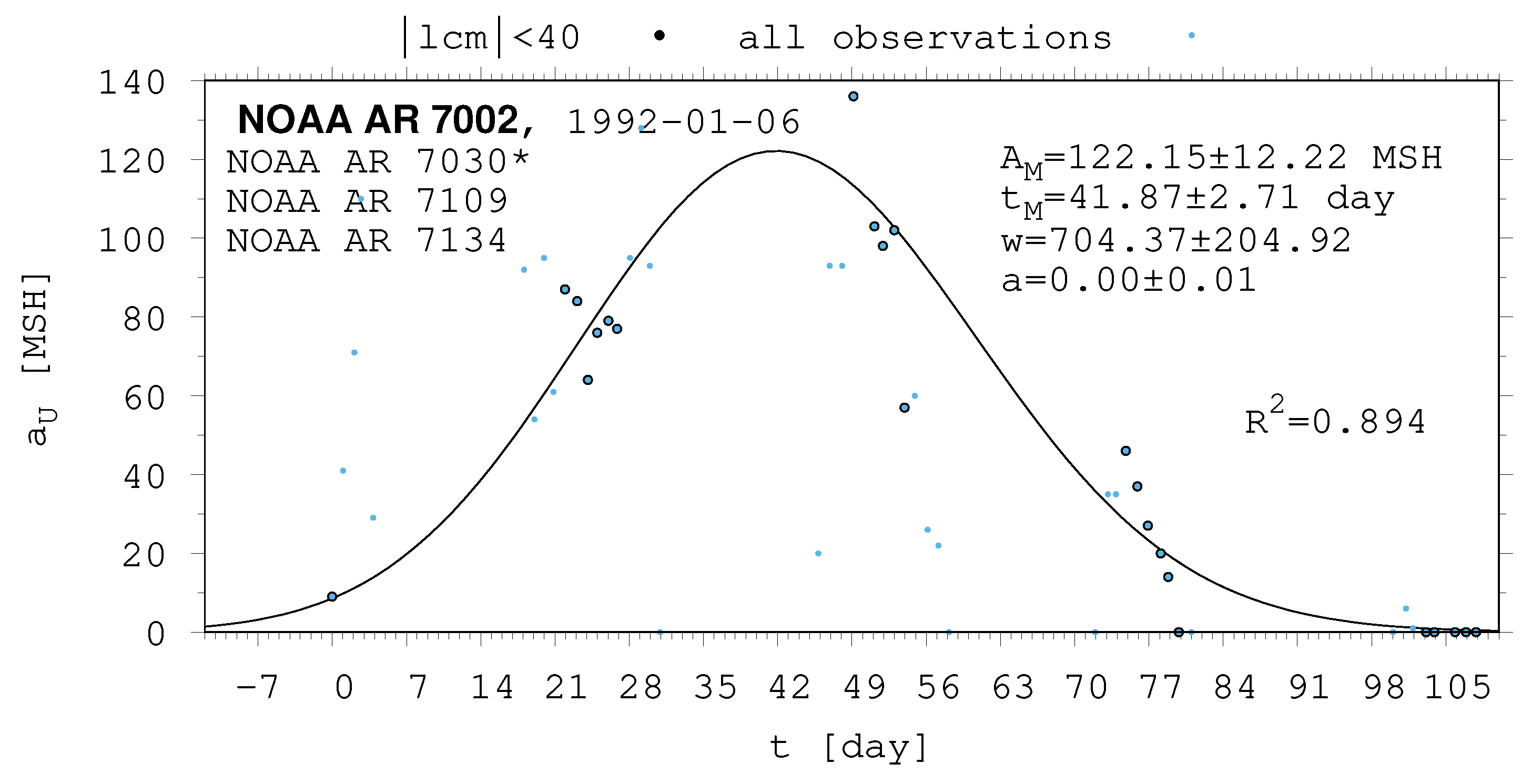
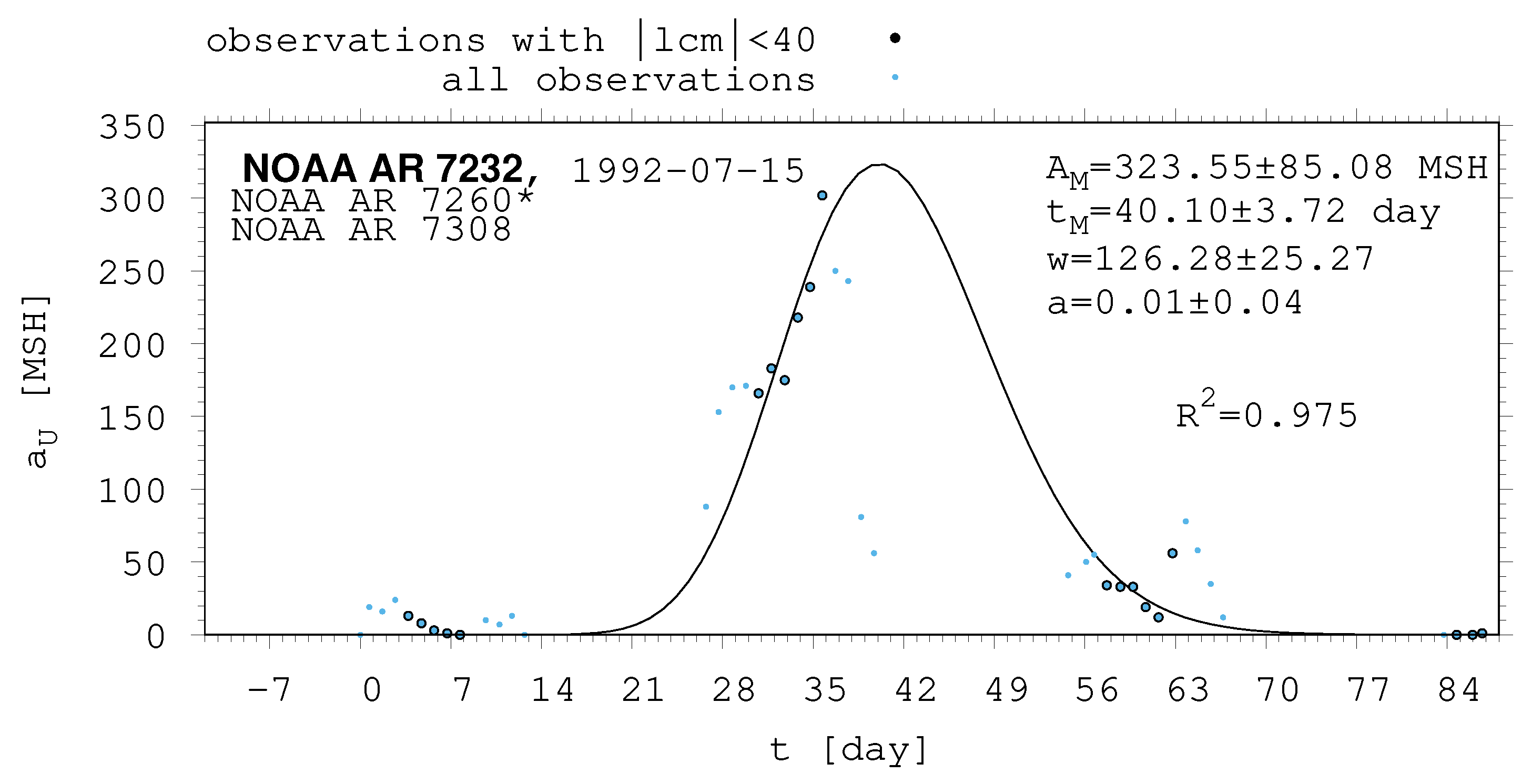
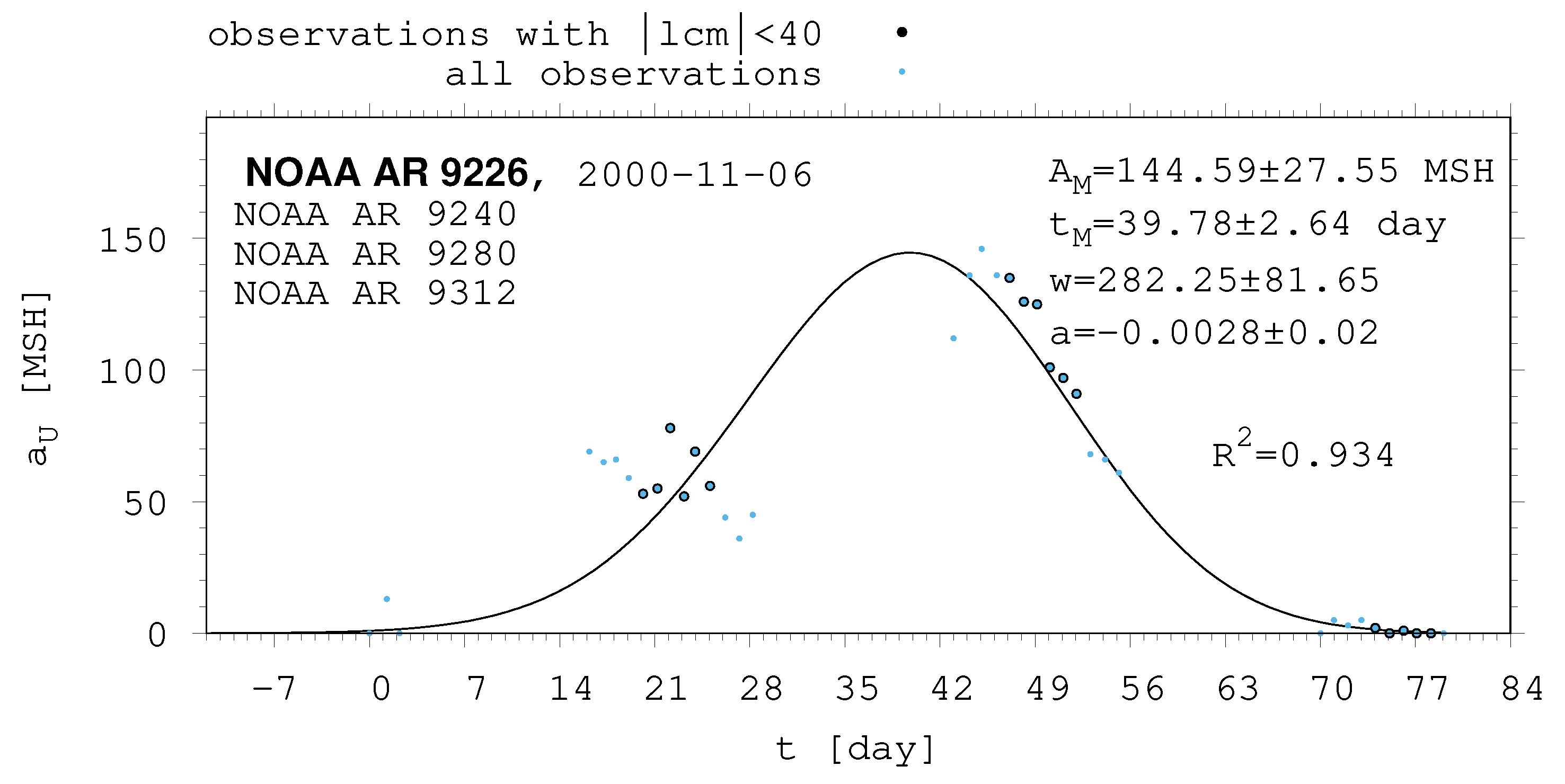
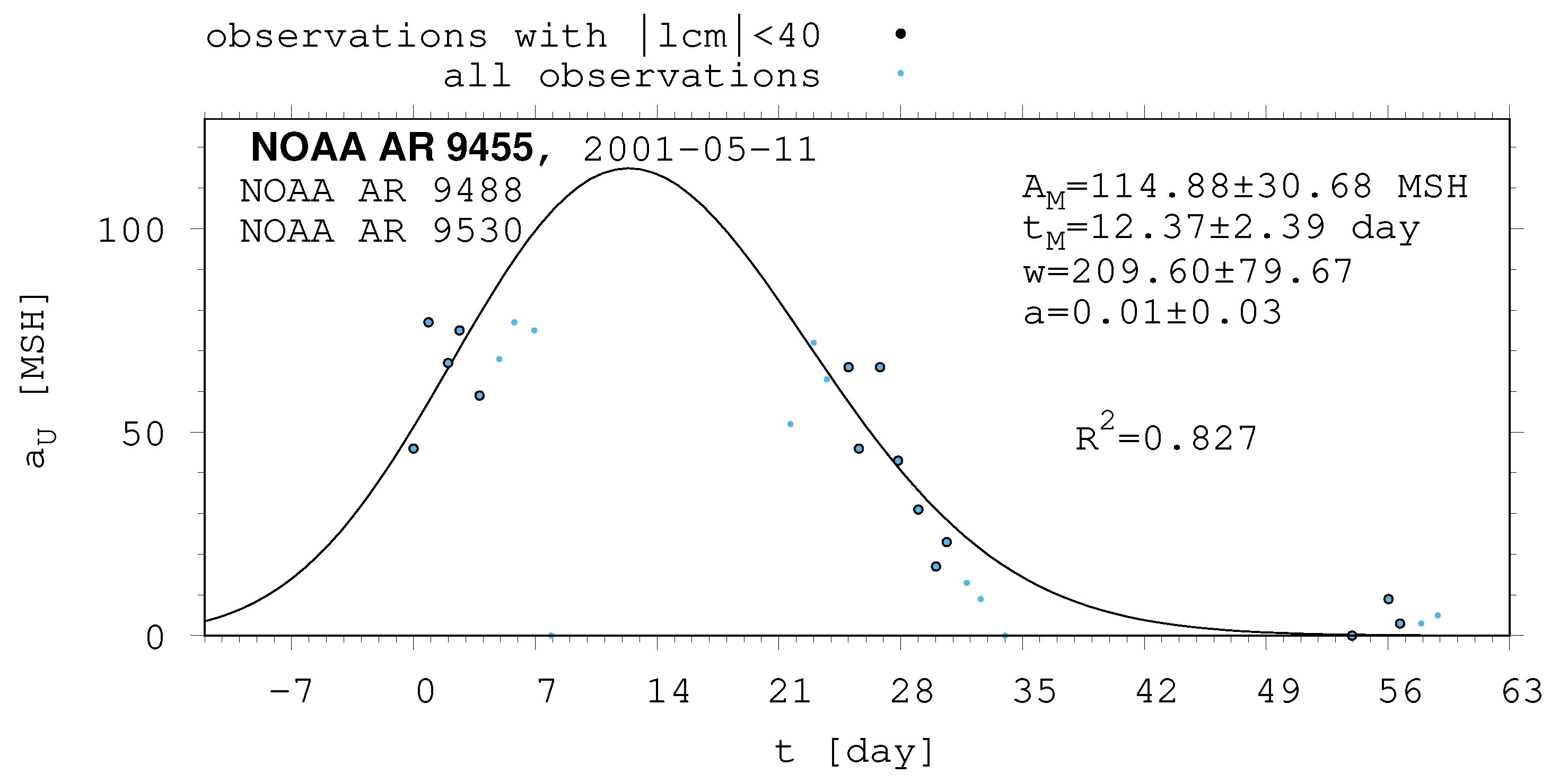
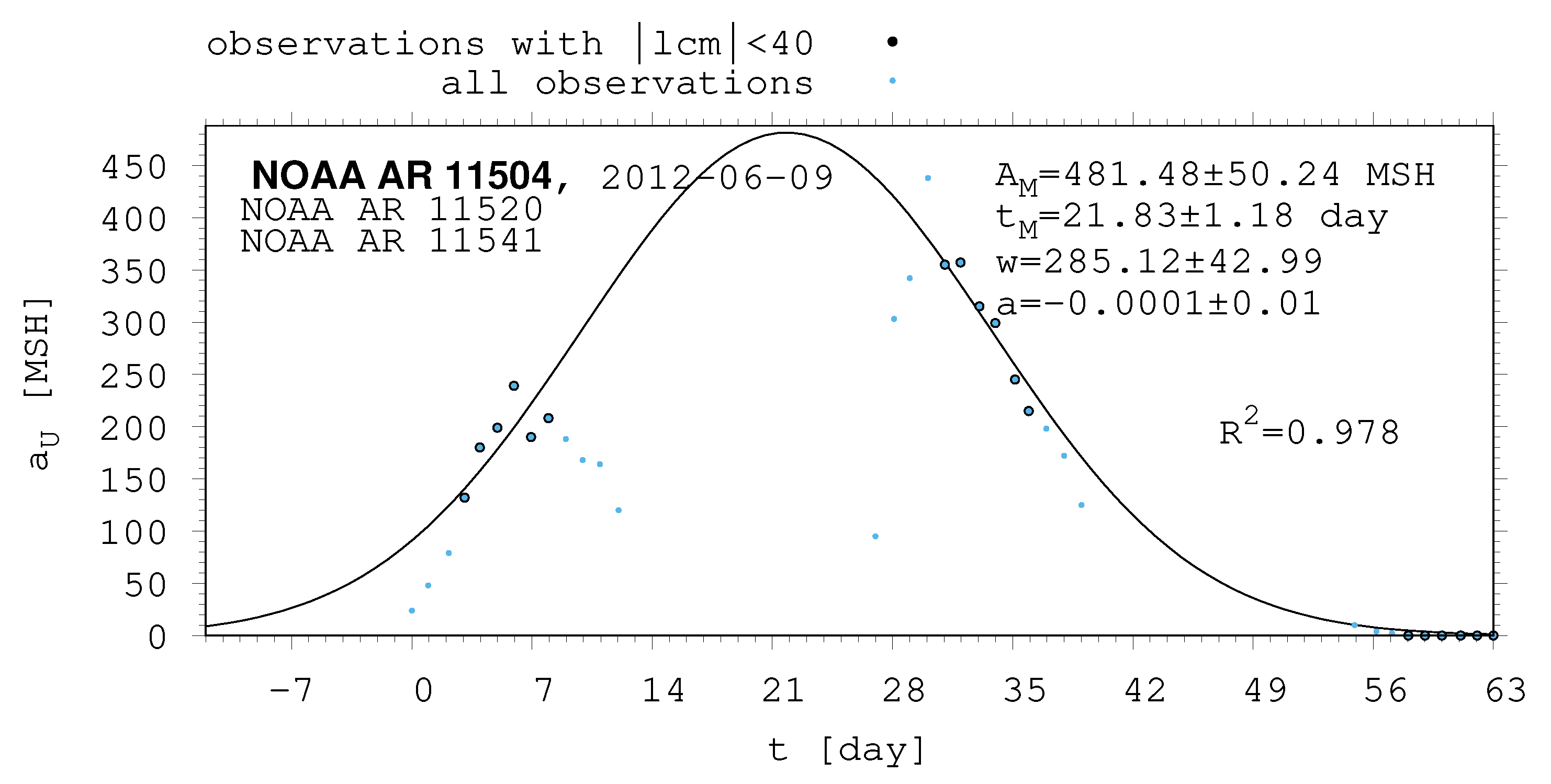
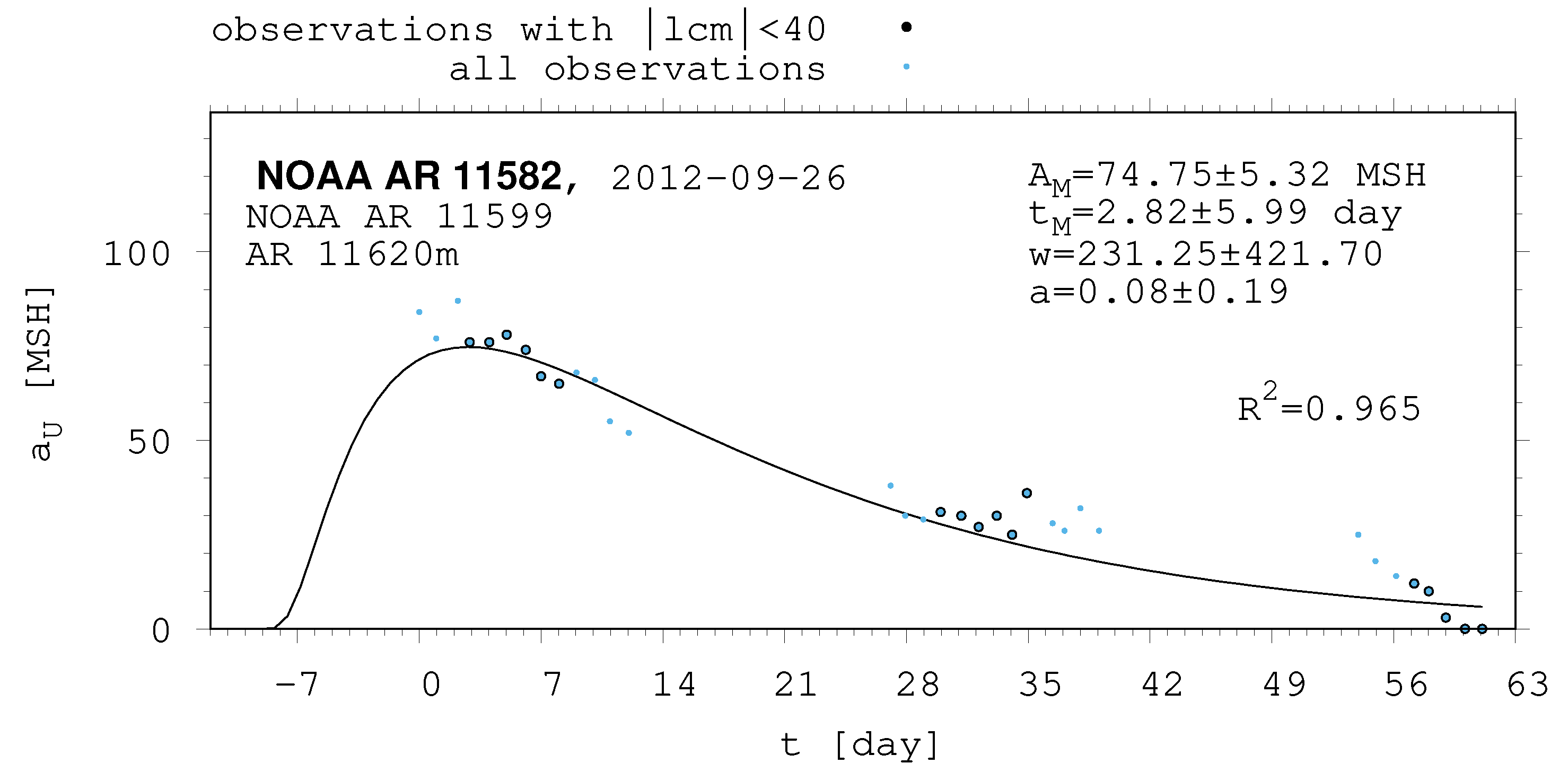
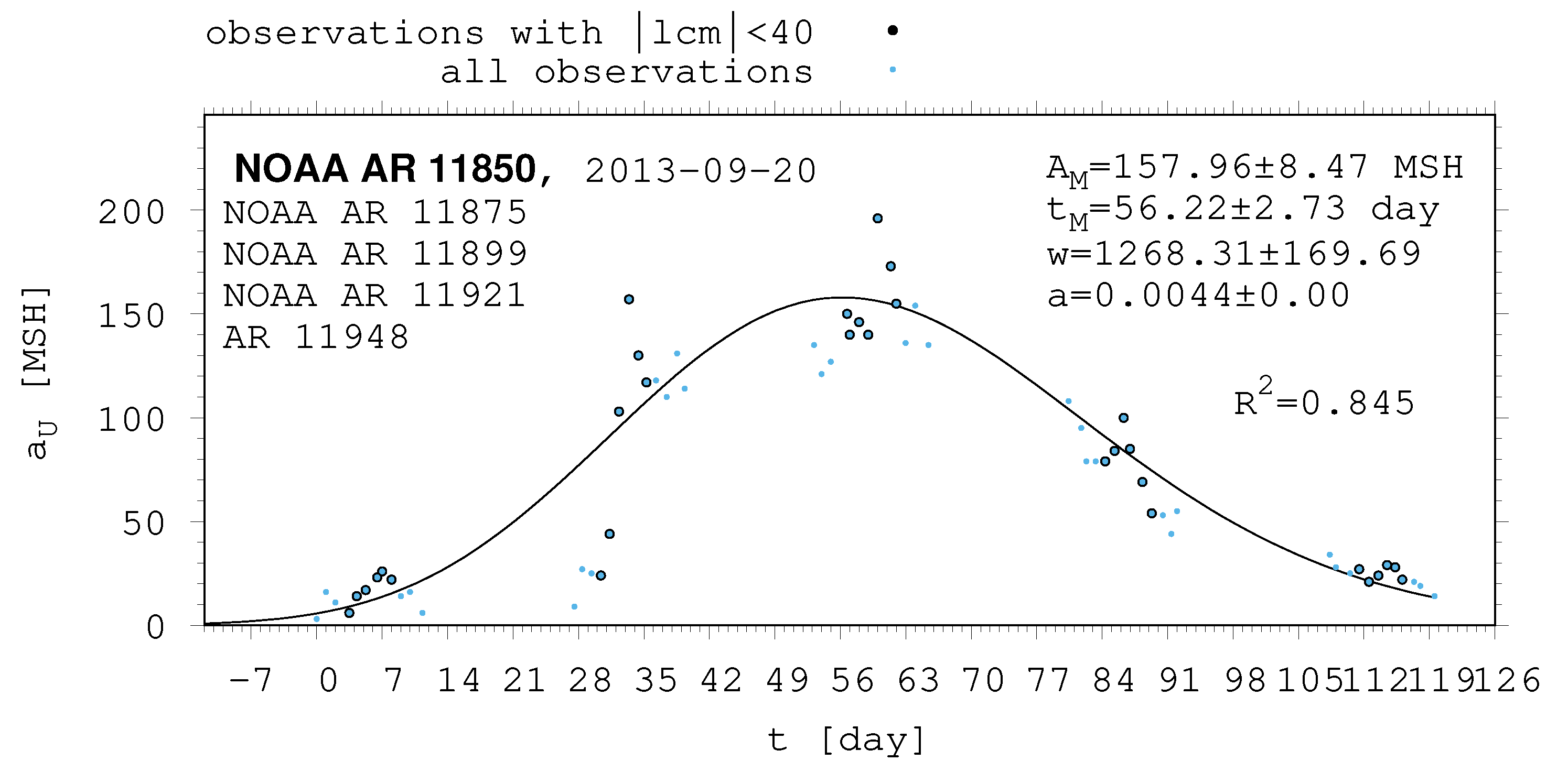
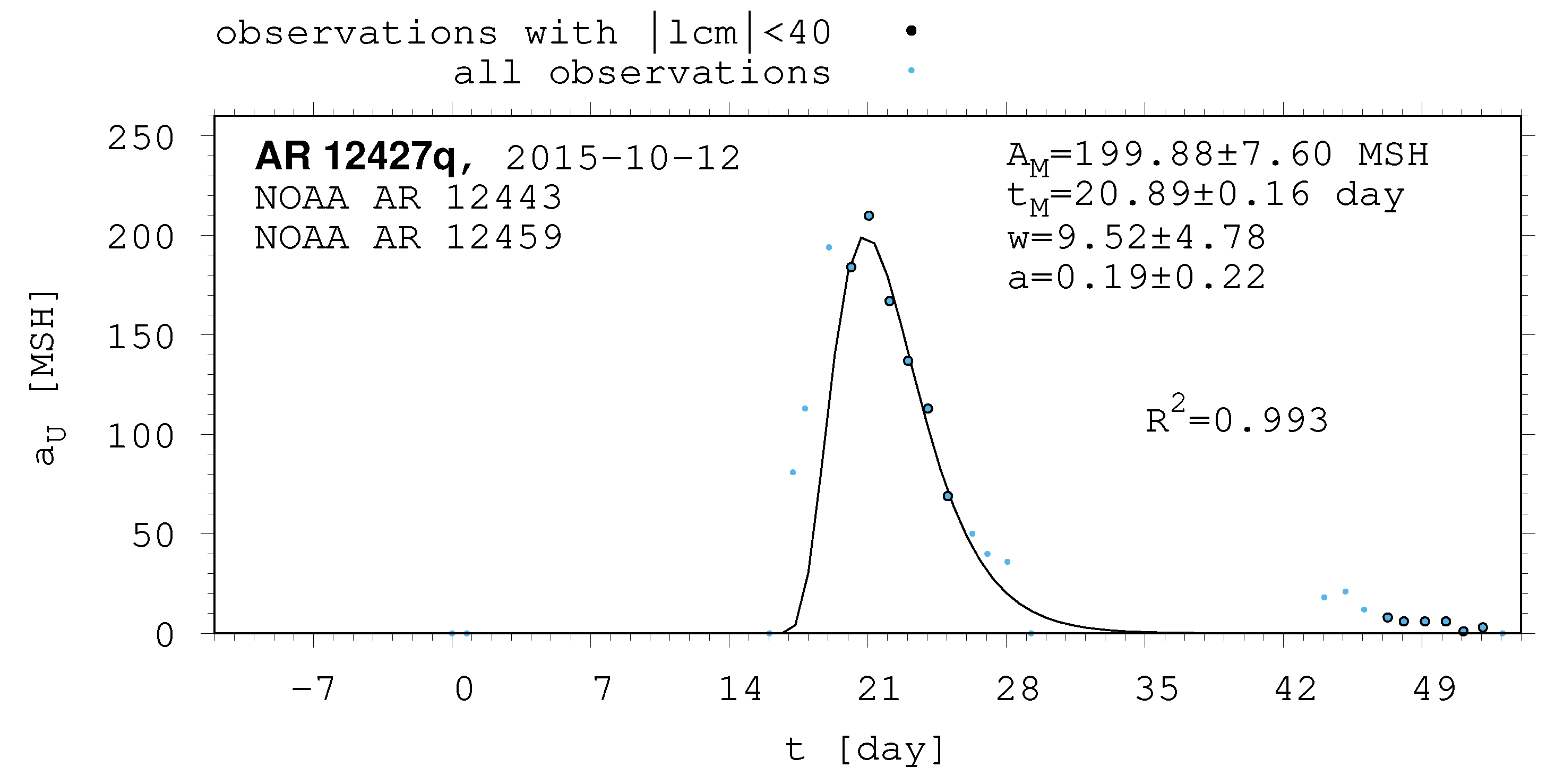
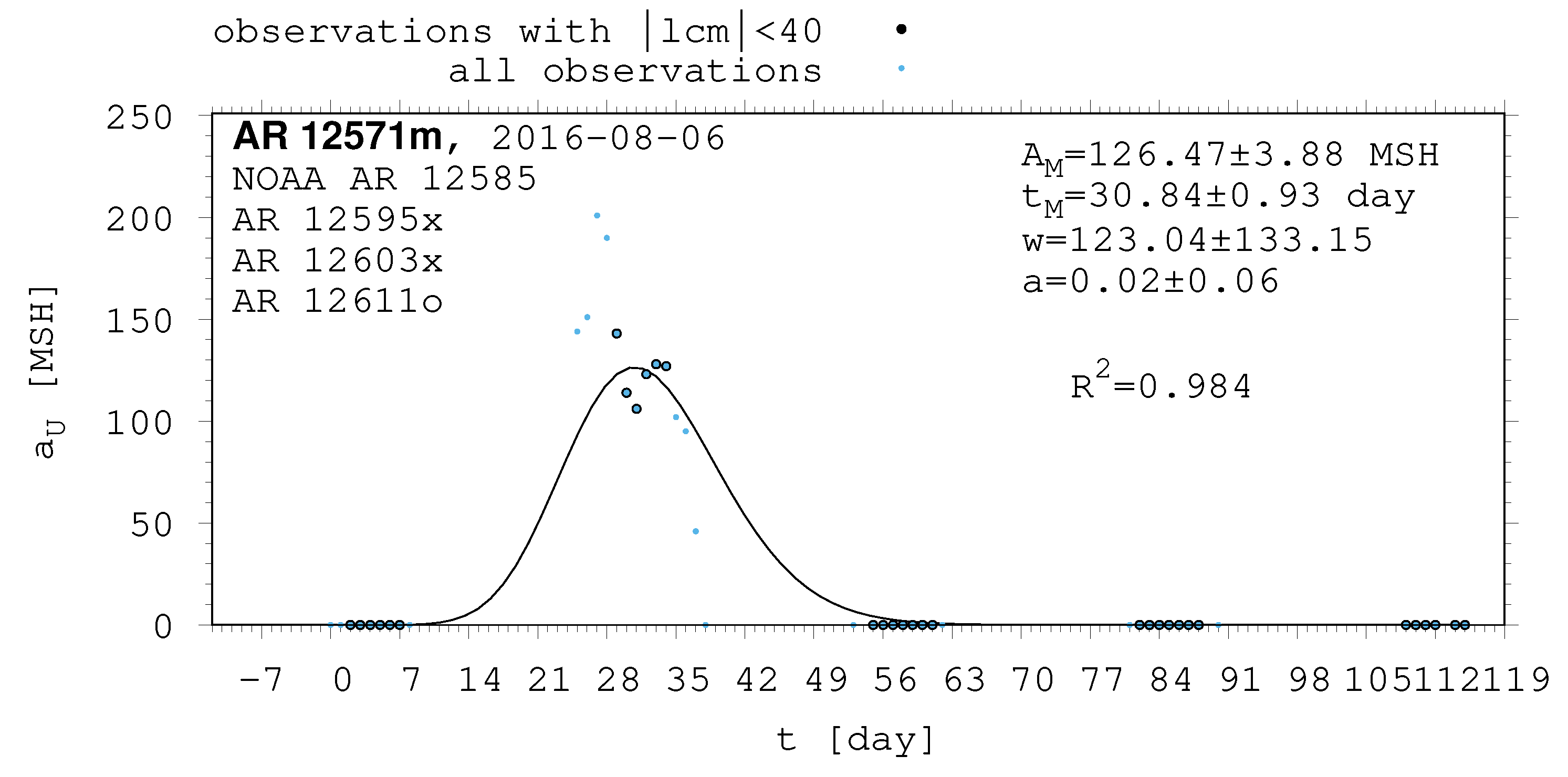
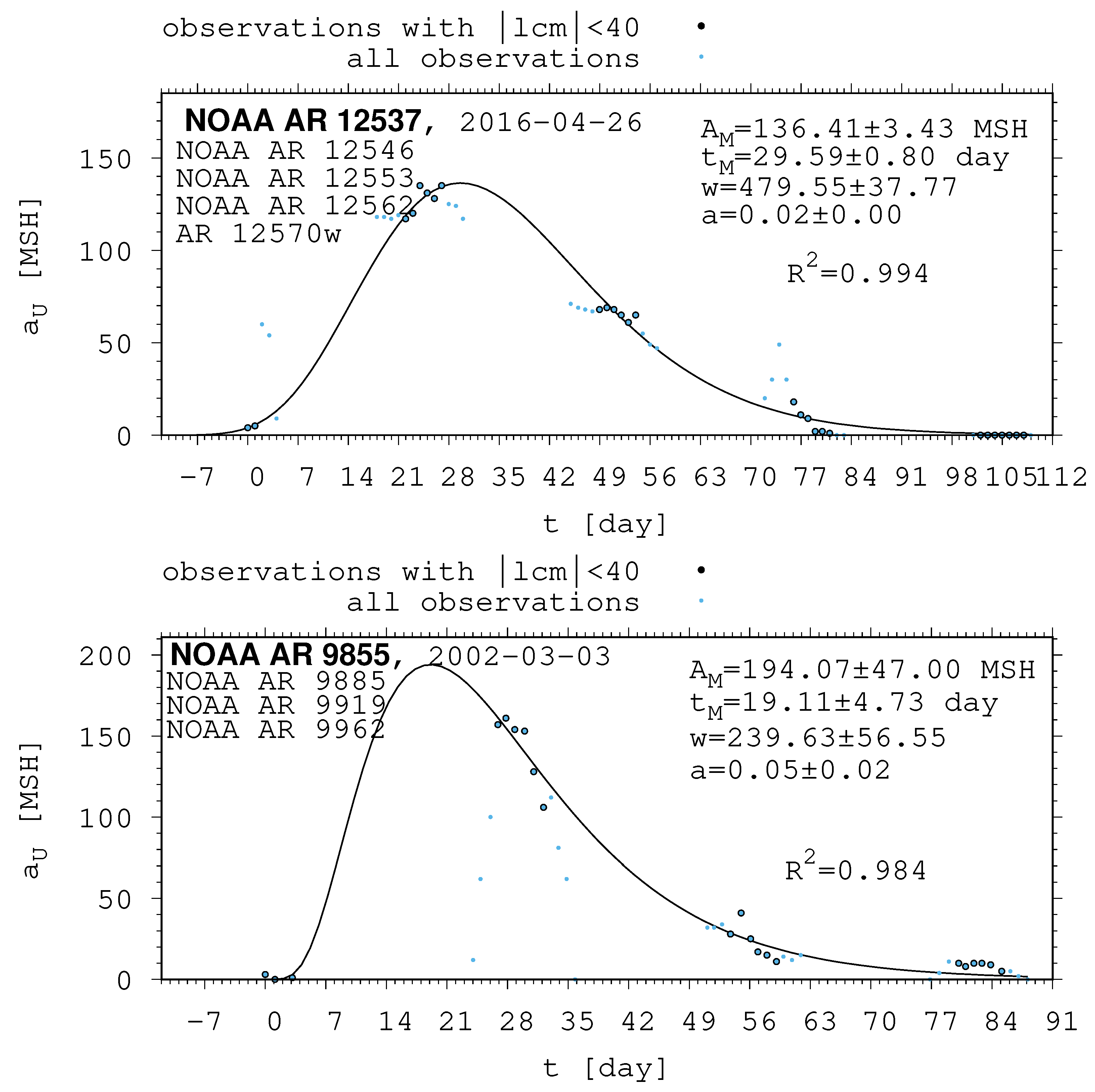
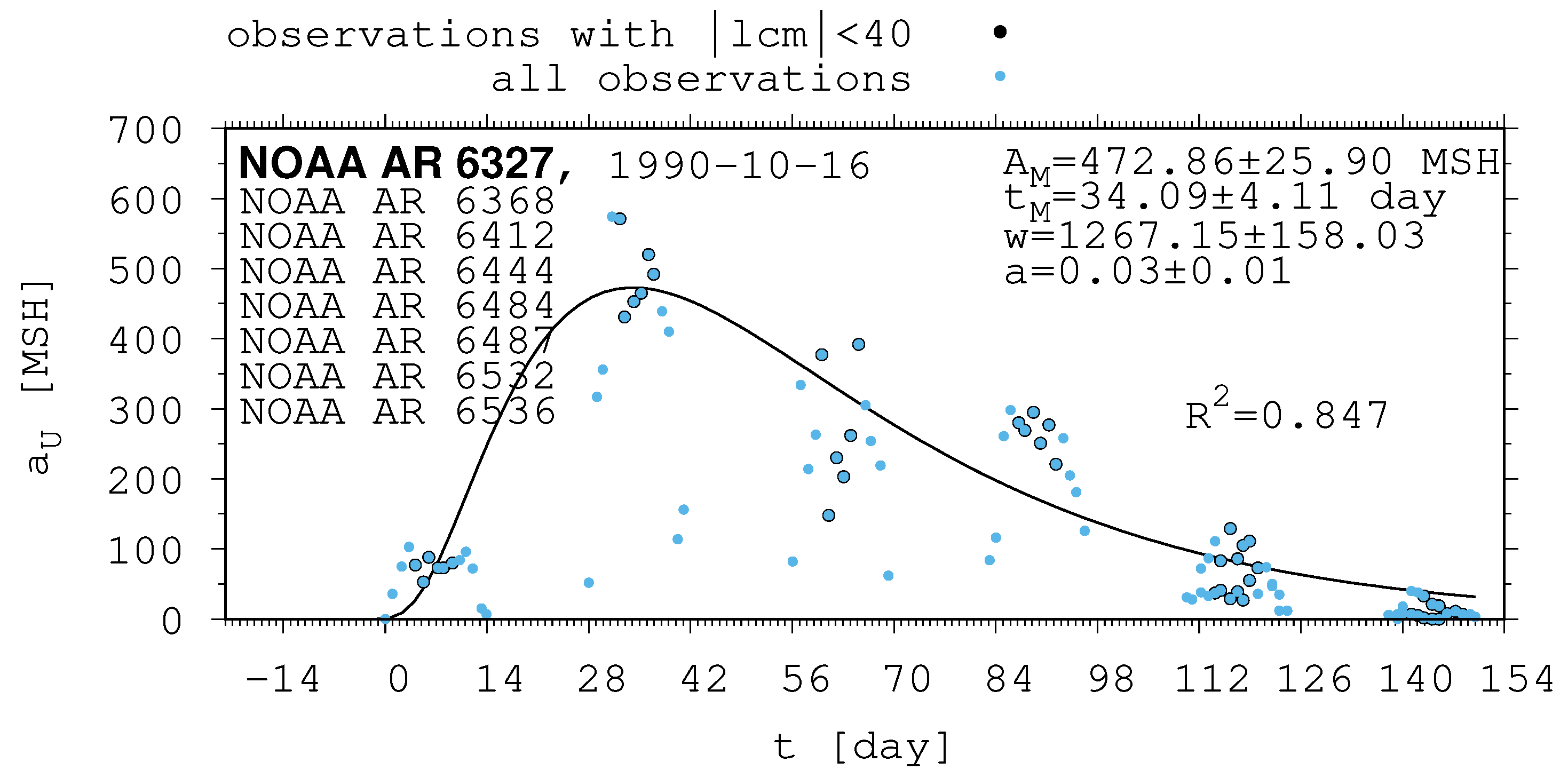
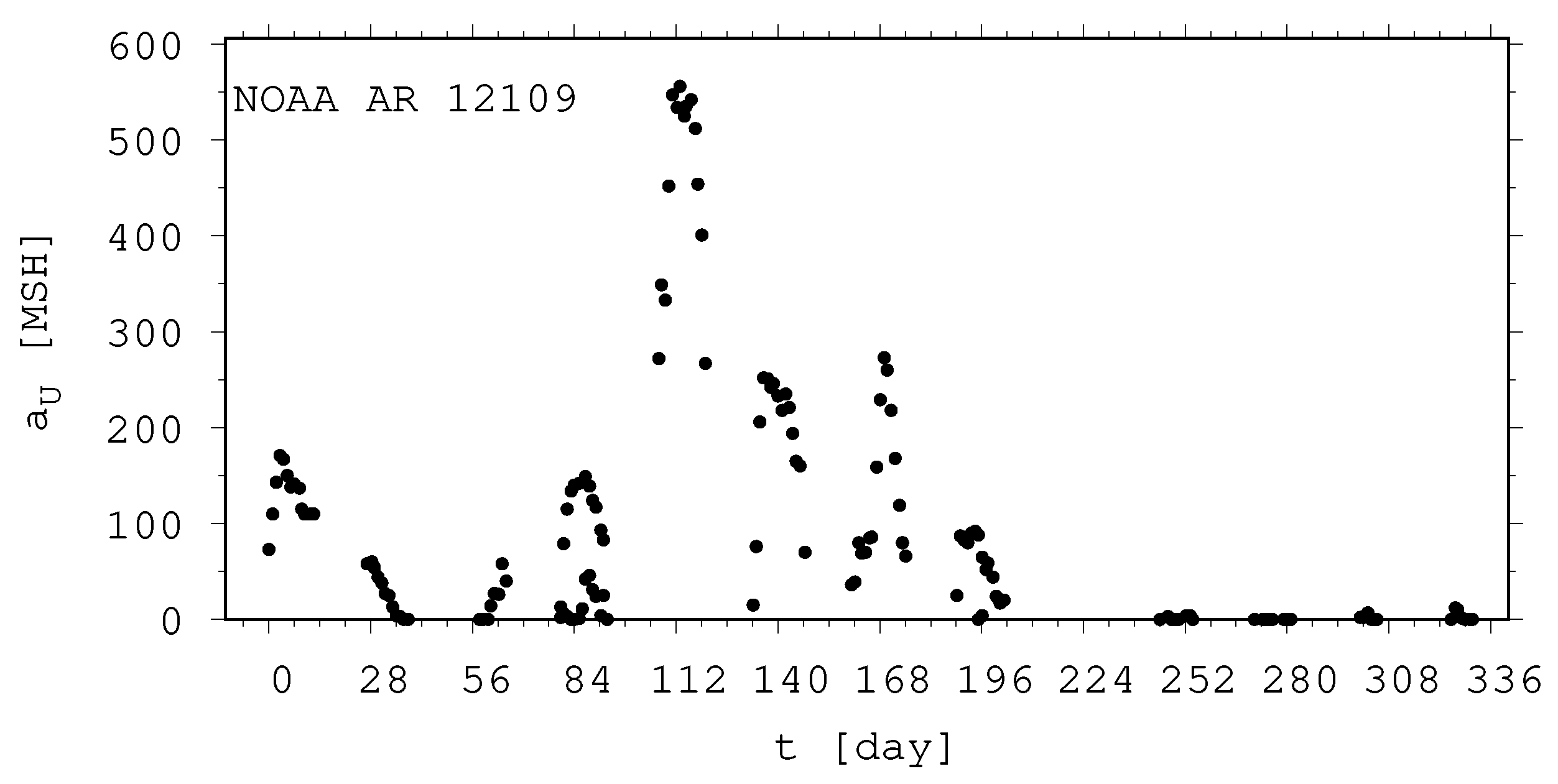
- The shape of the evolution of a long-lived recurrent sunspot group can be described by the same asymmetric Gaussian function that is suitable for the cases of short-lived active regions whose entire lifetimes are observed on the visible disc (Muraközy et al. [16], Muraközy [17]). If the returning active region is identical with that observed in the previous rotation. then its data have a surprisingly good fit to this curve (Figure 2).
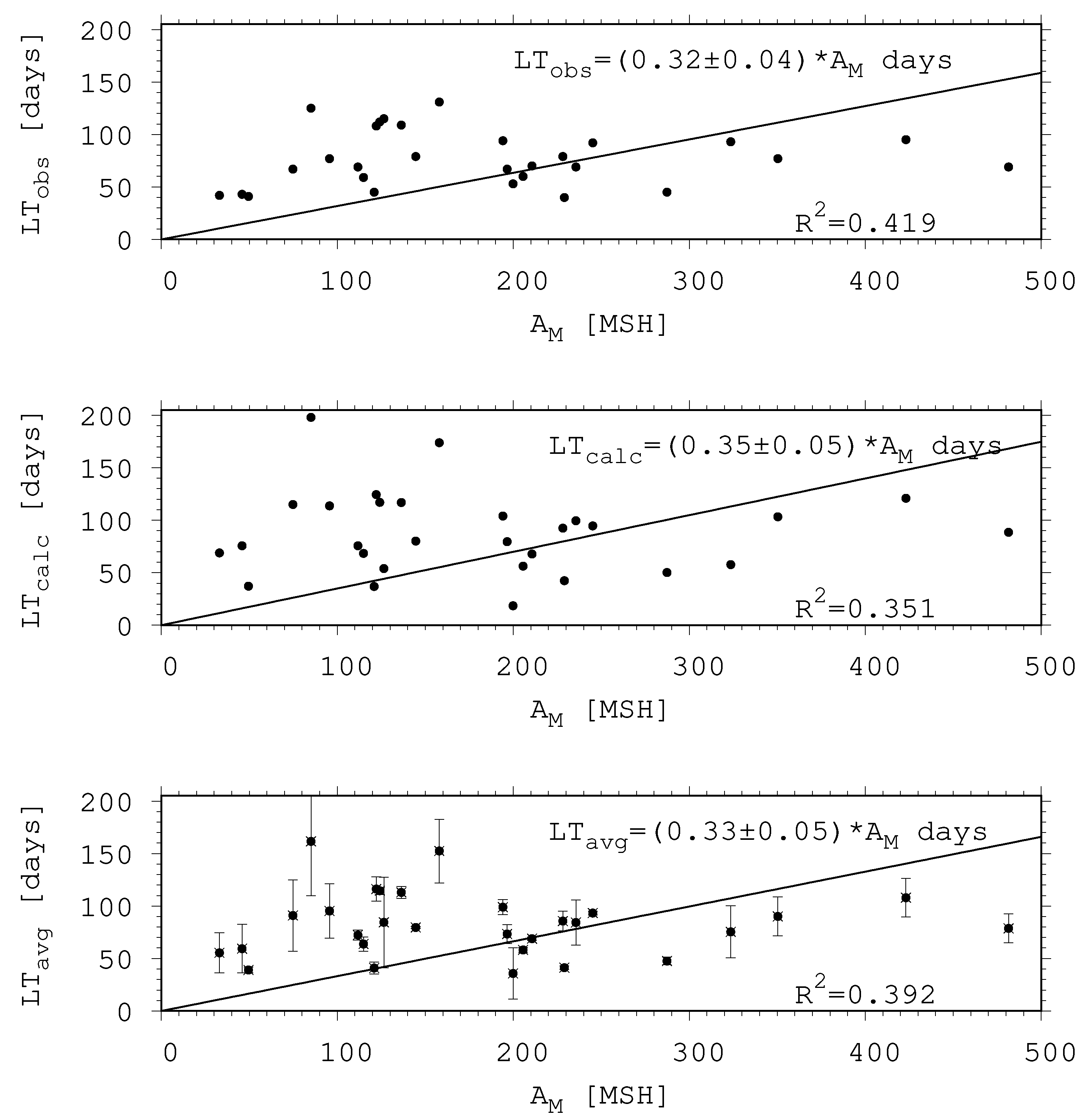
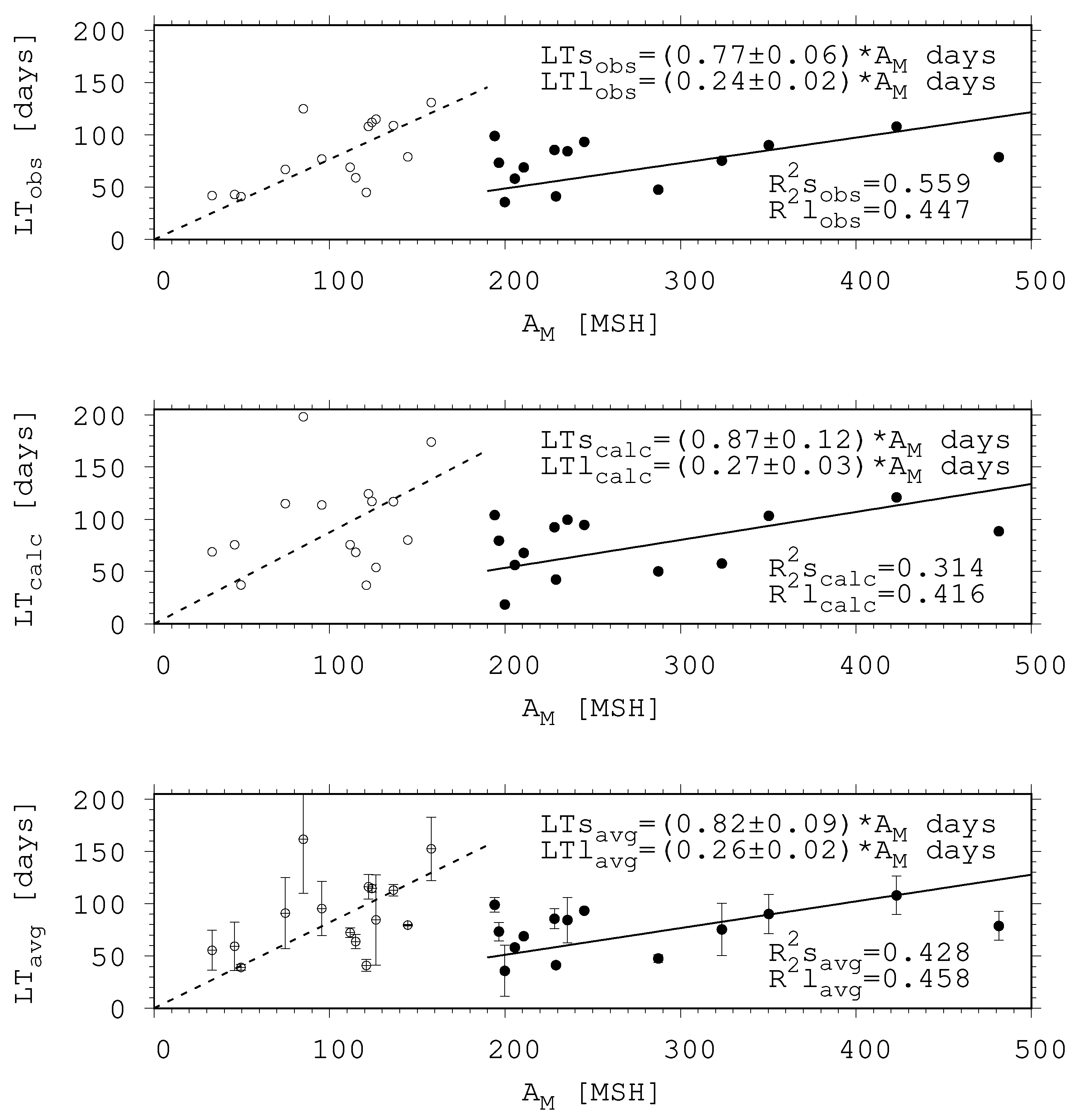
- The lifetimes of sunspot groups depend on their peak area; the larger the sunspot group, the longer its lifetime. Two groups of active region sizes can be distinguished, separated by size (AM ≈ 190 MSH) (Figure 4).
- While recurrent sunspot groups live for about 4–5 solar rotations, active nests can be tracked for a longer time, even through 12–13 rotations. They can be distinguished from a single recurrent sunspot group by the asymmetric Gaussian, as the data of the active domain in consecutive rotations do not have a good fit to the curve.
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| DPD | Debrecen Photoheliographic Data |
| SC | Solar Cycle |
| AR | Active Region |
| lcm | Longitudinal distance from the Sun’s central meridian |
| MSH | Millionths of Solar Hemisphere |
Appendix A









References
- Gnevyshev, M.N. On the nature of solar activity. Izv. Gl. Astron. Obs. Pulkove 1938, 16, 36–45. [Google Scholar]
- Waldmeier, M. Ergebnisse und Probleme der Sonnenforschung. 1955. Available online: https://ui.adsabs.harvard.edu/abs/1955epds.book.....W/abstract (accessed on 4 July 2024).
- Petrovay, K.; van Driel-Gesztelyi, L. Making Sense of Sunspot Decay. I. Parabolic Decay Law and Gnevyshev-Waldmeier Relation. Sol. Phys. 1997, 176, 249–266. [Google Scholar] [CrossRef]
- Henwood, R.; Chapman, S.C.; Willis, D.M. Increasing Lifetime of Recurrent Sunspot Groups within the Greenwich Photoheliographic Results. Sol. Phys. 2010, 262, 299–313. [Google Scholar] [CrossRef]
- Javaraiah, J. Relationship between Magnetic Structures of Small and Large Sunspot Groups. In Proceedings of the Current Theoretical Models and Future High Resolution Solar Observations: Preparing for ATST; Pevtsov, A.A., Uitenbroek, H., Eds.; Astronomical Society of the Pacific Conference Series; 2003; Volume 286, p. 325. Available online: http://prints.iiap.res.in/handle/2248/4603 (accessed on 4 July 2024).
- Namekata, K.; Maehara, H.; Notsu, Y.; Toriumi, S.; Hayakawa, H.; Ikuta, K.; Notsu, S.; Honda, S.; Nogami, D.; Shibata, K. Lifetimes and Emergence/Decay Rates of Star Spots on Solar-type Stars Estimated by Kepler Data in Comparison with Those of Sunspots. Astrophys. J. 2019, 871, 187. [Google Scholar] [CrossRef]
- Yazev, S.A.; Isaeva, E.S.; Ishmukhametova, Y.V. Active Regions on the Sun with Increased Flare Activity in Cycle 24. Astron. Rep. 2021, 65, 507–517. [Google Scholar] [CrossRef]
- Pojoga, S.; Cudnik, B. The Clustering Properties of Active Regions during the First Part of Solar Cycle 23. Sol. Phys. 2002, 208, 17–32. [Google Scholar] [CrossRef]
- Nagovitsyn, Y.A.; Ivanov, V.G.; Skorbezh, N.N. Refinement of the Gnevyshev-Waldmeier Rule Based on a 140-Year Series of Observations. Astron. Lett. 2019, 45, 396–401. [Google Scholar] [CrossRef]
- Forgács-Dajka, E.; Dobos, L.; Ballai, I. Time-dependent properties of sunspot groups. I. Lifetime and asymmetric evolution. Astron. Astrophys. 2021, 653, A50. [Google Scholar] [CrossRef]
- Nagovitsyn, Y.A.; Pevtsov, A.A. On the Presence of Two Populations of Sunspots. Astrophys. J. 2016, 833, 94. [Google Scholar] [CrossRef]
- Baranyi, T.; Gyori, L.; Ludmány, A. On-line Tools for Solar Data Compiled at the Debrecen Observatory and Their Extensions with the Greenwich Sunspot Data. Sol. Phys. 2016, 291, 3081–3102. [Google Scholar] [CrossRef]
- Tlatov, A.G. Lifetime of Sunspots and Pores. Sol. Phys. 2023, 298, 93. [Google Scholar] [CrossRef]
- Tlatov, A.G. The Lifetime of Sunspot. Geomagn. Aeron. 2024, 63, 1116–1119. [Google Scholar] [CrossRef]
- Du, Z. The Shape of Solar Cycle Described by a Modified Gaussian Function. Sol. Phys. 2011, 273, 231–253. [Google Scholar] [CrossRef]
- Muraközy, J.; Baranyi, T.; Ludmány, A. Sunspot Group Development in High Temporal Resolution. Sol. Phys. 2014, 289, 563–577. [Google Scholar] [CrossRef][Green Version]
- Muraközy, J. Study of the Decay Rates of the Umbral Area of Sunspot Groups Using a High-resolution Database. Astrophys. J. 2020, 892, 107. [Google Scholar] [CrossRef]
- Muraközy, J. On the Decay of Sunspot Groups and Their Internal Parts in Detail. Astrophys. J. 2021, 908, 133. [Google Scholar] [CrossRef]
- Iglesias, F.A.; Cremades, H.; Merenda, L.A.; Mandrini, C.H.; López, F.M.; López Fuentes, M.C.; Ugarte-Urra, I. Analysis of a long-duration AR throughout five solar rotations: Magnetic properties and ejective events. Adv. Space Res. 2020, 65, 1641–1653. [Google Scholar] [CrossRef]
- Wan, M.; Gao, P.X.; Zeng, S.G.; Deng, L.H. Differential Rotation for Different-sized Sunspot Groups Early Observed by the OGAUC. Astrophys. J. 2023, 956, 53. [Google Scholar] [CrossRef]

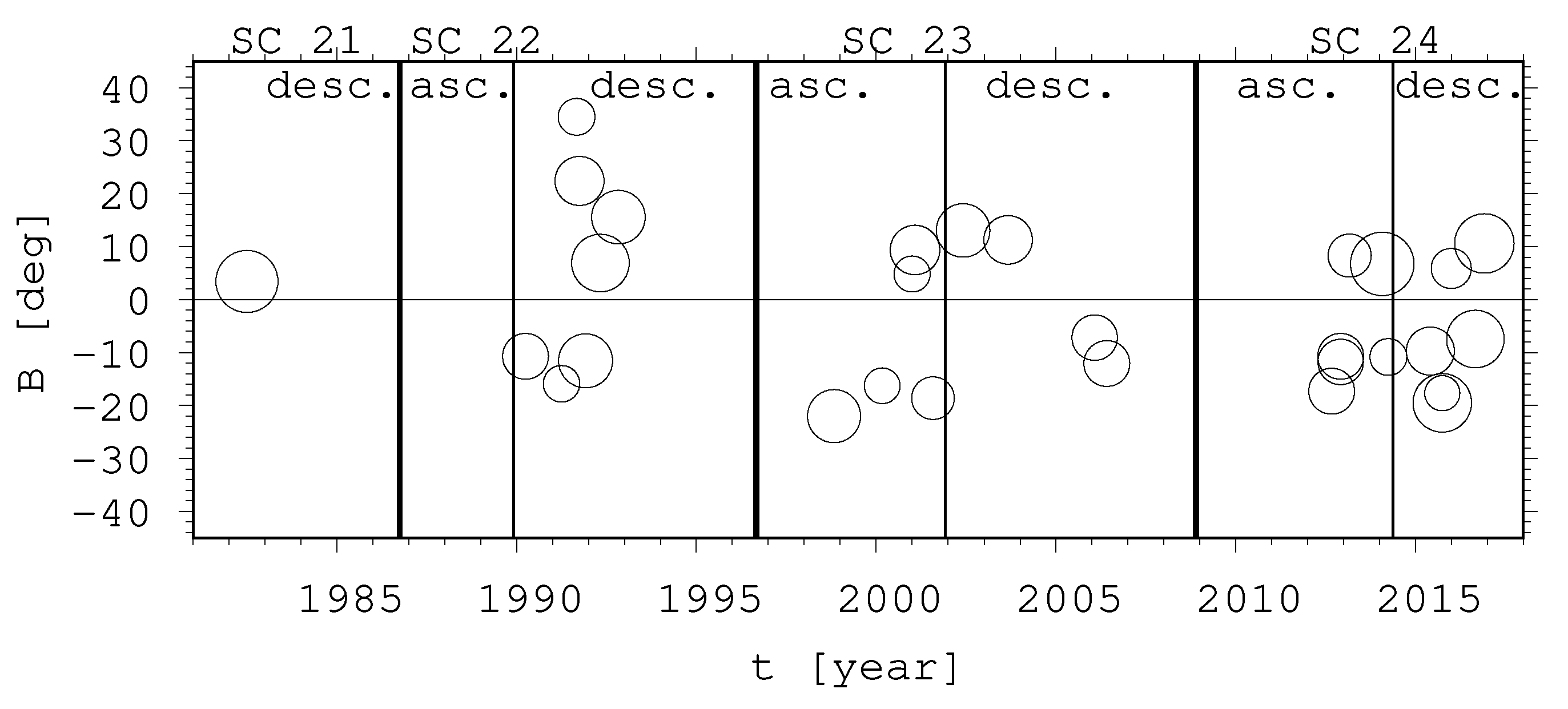
| NOAA AR1/FD1 | NOAA AR2/FD2 | NOAA AR3/FD3 | NOAA AR4/FD4 | NOAA AR5/FD5 |
|---|---|---|---|---|
| 3613 | 3652 | 3695 | 3727 | 3768 |
| 1982-02-19 | 1982-03-17 | 1982-04-13 | 1982-05-10 | 1982-06-06 |
| 5900 | 5941 | 5980 | ||
| 1990-01-21 | 1990-02-17 | 1990-03-16 | ||
| 6504 * | ||||
| 1991-02-15 | ||||
| 6711 | 6757 * | |||
| 1991-07-01 | 1991-07-28 | |||
| 6713 * | ||||
| 1991-07-01 | ||||
| 6818 | 6850 * | 6939 | ||
| 1991-09-02 | 1991-09-25 | 1991-11-22 | 1991-11-19 | |
| 7002 | 7030 * | 7109 | 7134 | |
| 1992-01-06 | 1992-01-24 | 1992-03-18 | 1992-04-15 | |
| 7232 | 7260 * | 7308 | ||
| 1992-07-15 | 1992-08-11 | 1992-10-07 | ||
| 8293 | 8323 | 8346a | 8367a | |
| 1998-08-02 | 1998-08-28 | 1998-09-26 | 1998-10-27 | |
| 8813 | 8849 | |||
| 1999-12-28 | 2000-01-28 | |||
| 9219 | 9245 | |||
| 2000-10-31 | 2000-11-28 | |||
| 9226 | 9240 | 9280 | 9312 | |
| 2000-11-06 | 2000-11-22 | 2000-12-19 | 2001-01-15 | |
| 9455 | 9488 | 9530 | ||
| 2001-05-11 | 2001-06-02 | 2001-07-04 | ||
| 9855 | 9885 | 9919 | 9962 | |
| 2002-03-03 | 2002-03-27 | 2002-04-23 | 2002-05-19 | |
| 10375 | 10397 | 10420 | ||
| 2003-06-01 | 2003-06-27 | 2003-07-24 | ||
| 10822 | 10834 | 10845n | ||
| 2005-11-12 | 2005-12-09 | 2006-01-10 | ||
| 10865 | 10875 | 10890 | ||
| 2006-03-28 | 2006-04-23 | 2006-05-24 | ||
| 11504 | 11520 | 11541 | ||
| 2012-06-09 | 2012-07-06 | 2012-08-03 | ||
| 11579 | 11598 | 11618n | ||
| 2012-09-24 | 2012-10-21 | 2012-11-21 | ||
| 11582 | 11599 | 11620m | ||
| 2012-09-26 | 2012-10-23 | 2012-11-19 | ||
| 11631m | 11654 | 11669 | ||
| 2012-12-15 | 2013-01-08 | 2013-02-05 | ||
| 11850 | 11875 | 11899 | 11921 | 11948 |
| 2013-09-20 | 2013-10-17 | 2013-11-12 | 2013-12-09 | 2014-01-06 |
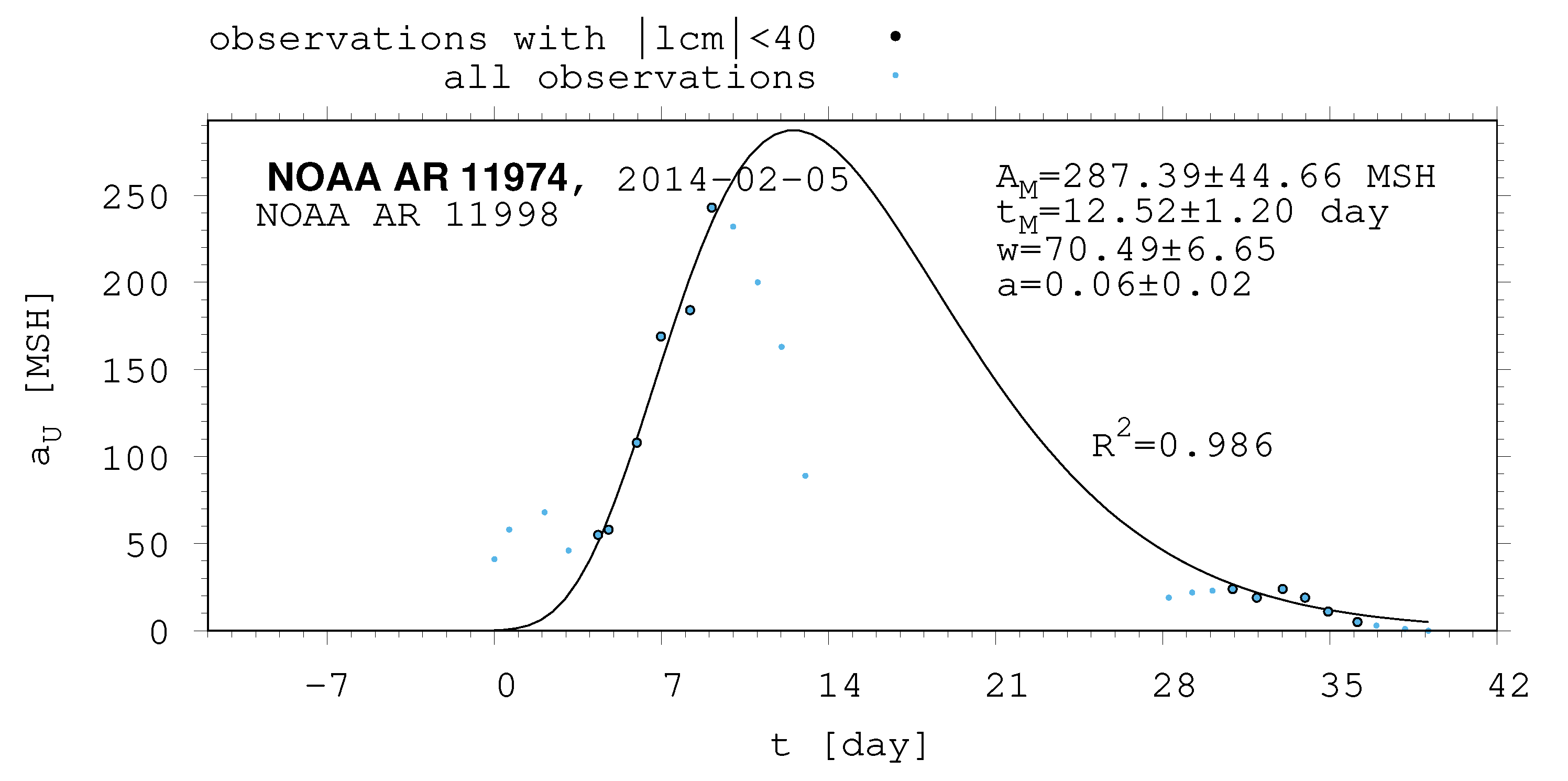
| 11974 | 11998 | |||
| 2014-02-05 | 2014-03-05 | |||
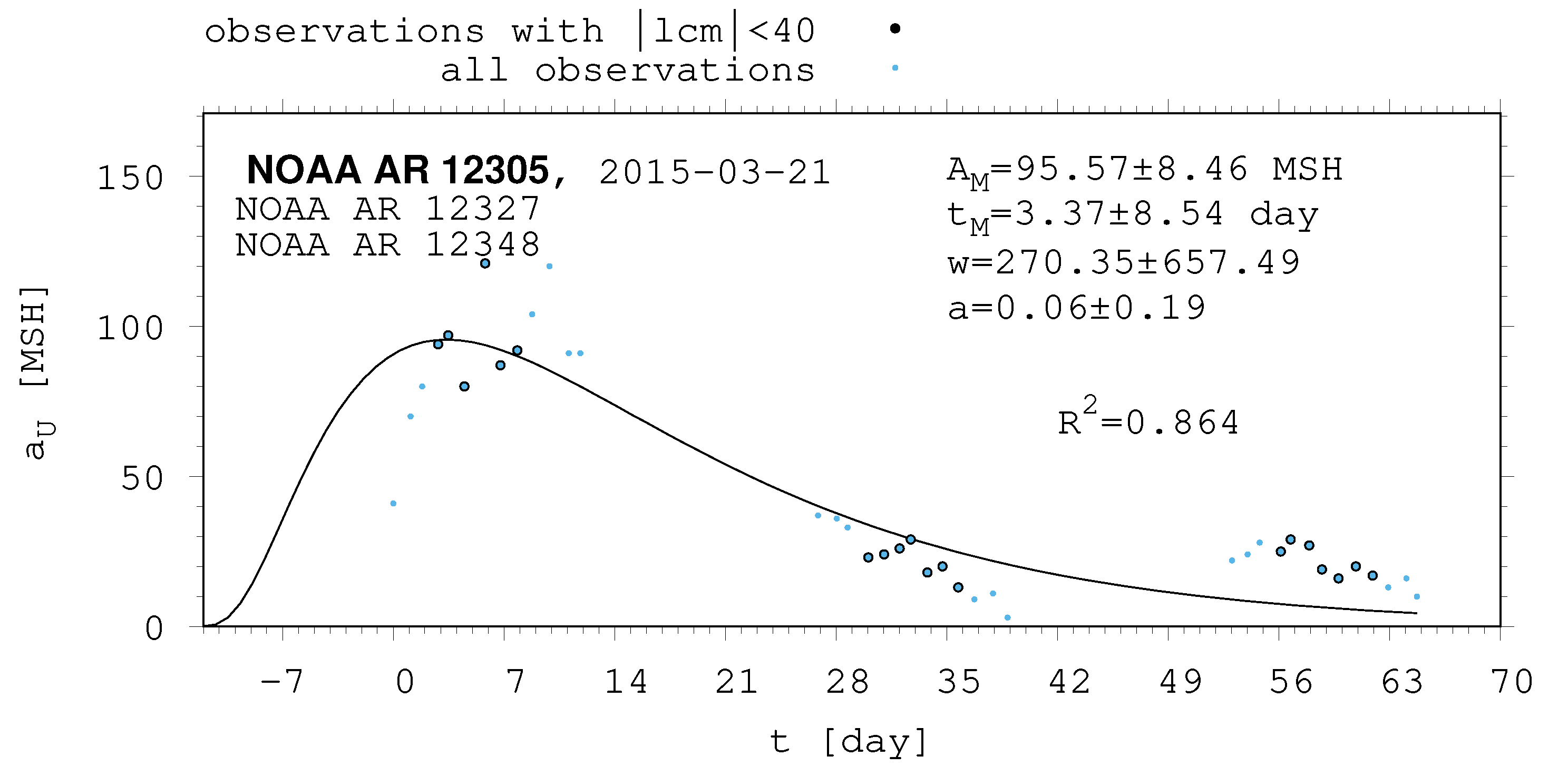
| 12305 | 12327 | 12348 | ||
| 2015-03-21 | 2015-04-29 | 2015-05-13 | ||
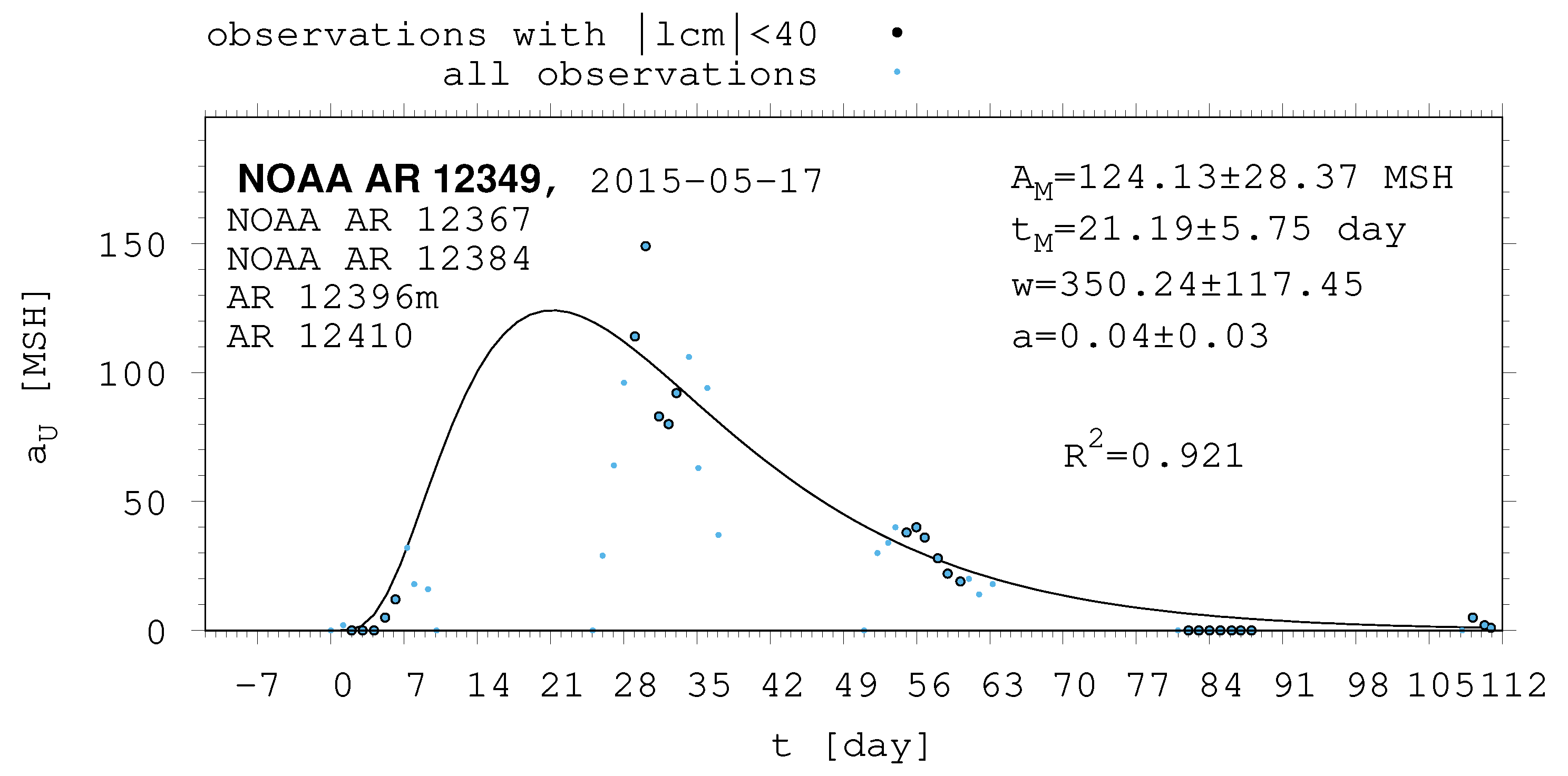
| 12349 | 12367 | 12384 | 12396m | 12410 |
| 2015-05-17 | 2015-06-11 | 2015-07-07 | 2015-08-06 | |
| 12396 | 12406q | |||
| 2015-08-03 | 2015-09-02 | |||
| 12427q | 12443 | 12459 | ||
| 2015-10-12 | 2015-10-28 | 2015-11-25 | ||
| 12537 | 12546 | 12553 | 12562 | 12570w |
| 2016-04-26 | 2016-05-14 | 2016-06-10 | 2016-07-07 | 2016-08-05 |
| 12571m | 12585 | 12595x | 12603x | 12611o |
| 2016-08-06 | 2016-08-31 | 2016-09-28 | 2016-10-26 | 2016-11-23 |
| NOAA AR1 | AM | eAM | tM | etM | w | ew | a | ea |
|---|---|---|---|---|---|---|---|---|
| 3613 | 85.09 | 3.36 | 29.16 | 3.02 | 923.81 | 80.51 | 0.03 | 0.01 |
| 5900 | 235.56 | 12.47 | 3.98 | 4.33 | 218.78 | 461.27 | 0.05 | 0.17 |
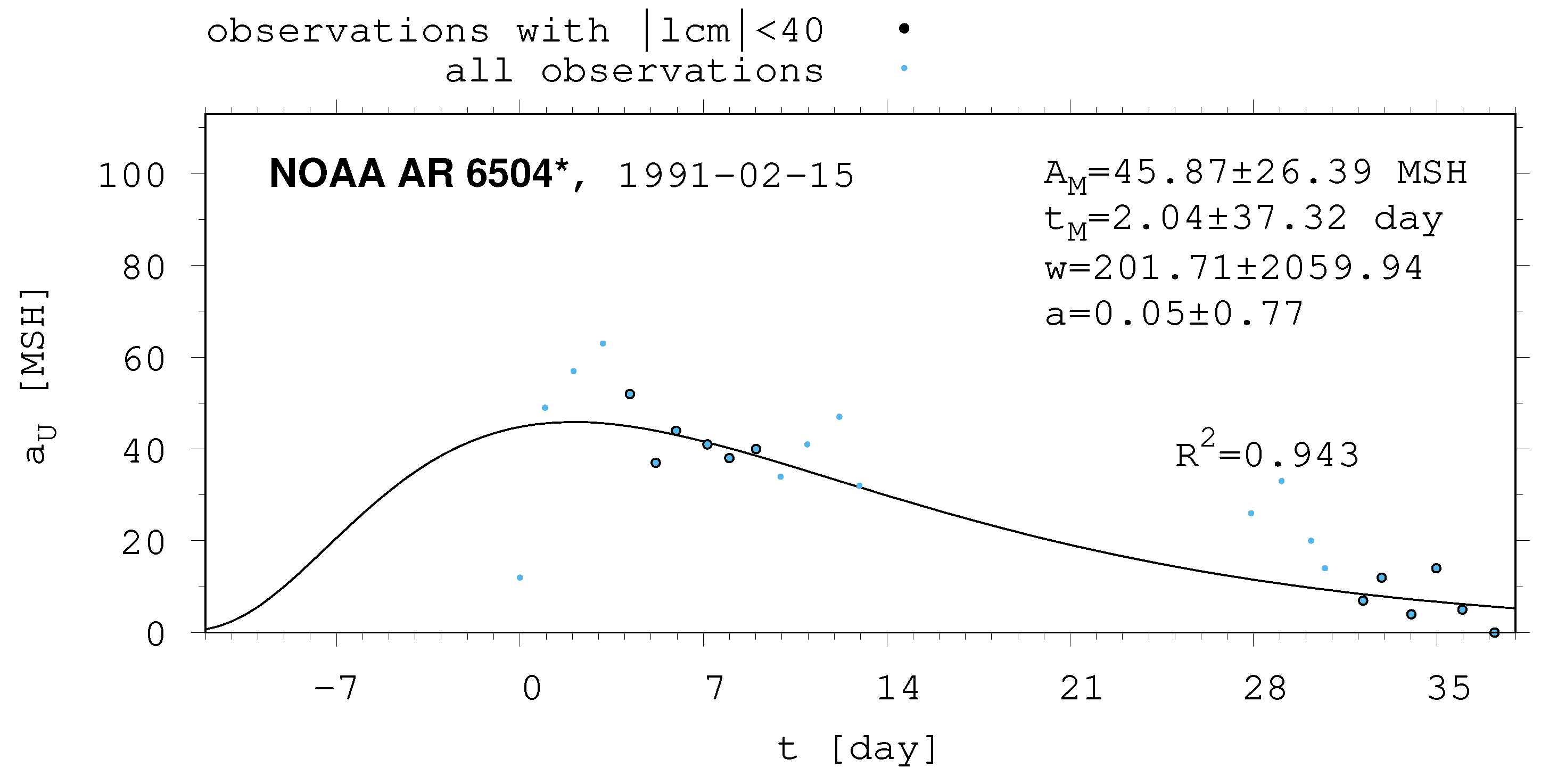
| 6504 | 45.87 | 26.39 | 2.04 | 37.32 | 201.71 | 2059.94 | 0.05 | 0.77 |
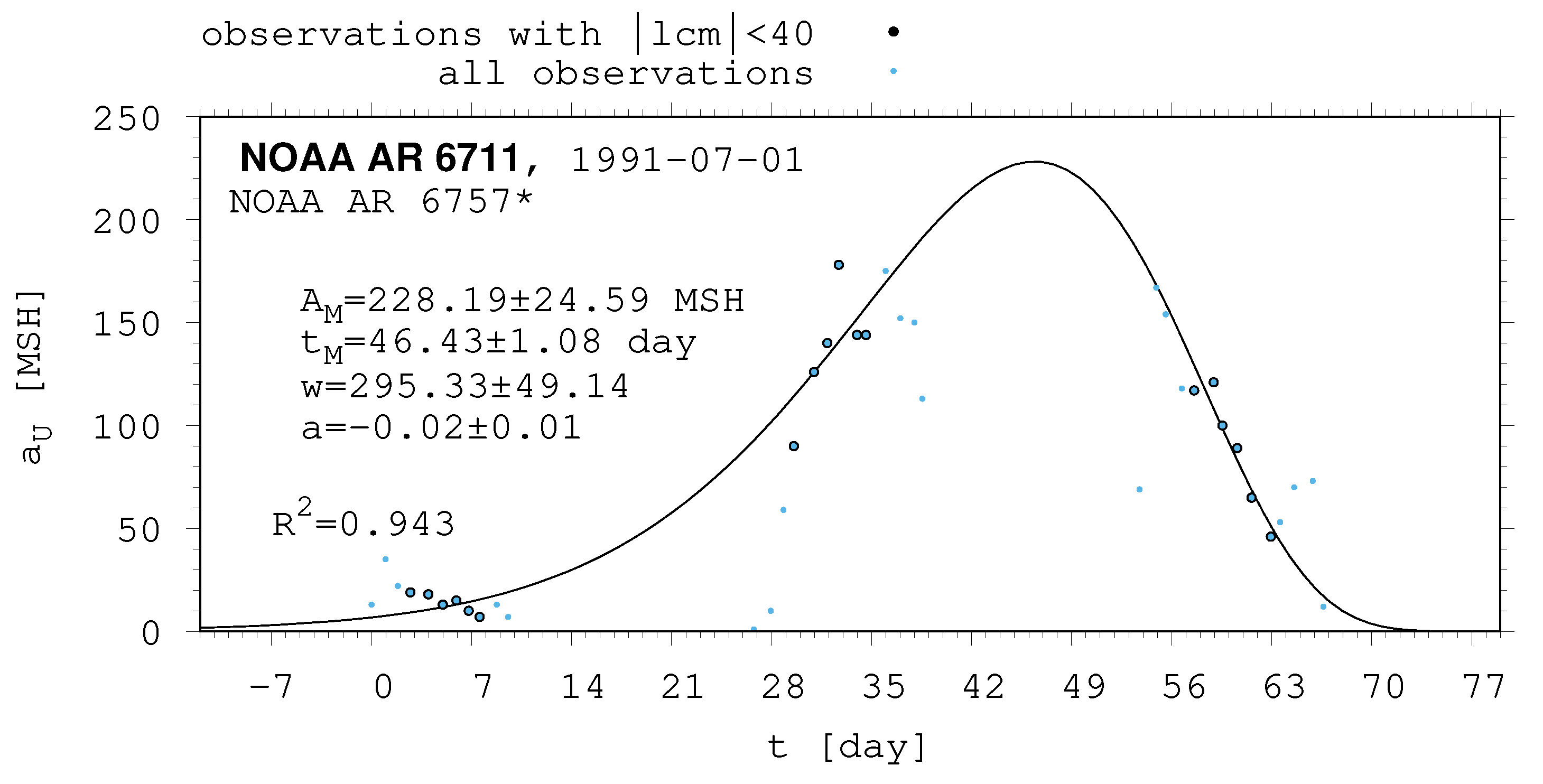
| 6711 | 228.19 | 24.59 | 46.43 | 1.08 | 295.33 | 49.14 | −0.02 | 0.01 |
| 6713 | 120.96 | 260.87 | 15.79 | 11.36 | 61.52 | 25.76 | 0.01 | 0.12 |
| 6818 | 423.10 | 36.98 | 42.17 | 1.15 | 541.80 | 119.68 | 0.00 | 0.01 |
| 7002 | 122.15 | 12.22 | 41.87 | 2.71 | 704.37 | 204.92 | 0.00 | 0.01 |
| 7232 | 323.55 | 85.08 | 40.10 | 3.72 | 126.28 | 25.27 | 0.01 | 0.04 |
| 8293 | 245.14 | 34.01 | 24.09 | 2.77 | 343.38 | 93.93 | −0.01 | 0.02 |
| 8813 | 49.53 | 29.30 | 10.66 | 5.65 | 63.80 | 44.56 | 0.05 | 0.11 |
| 9219 | 33.08 | 2.60 | 5.70 | 1.79 | 107.90 | 303.57 | 0.11 | 0.42 |
| 9226 | 144.59 | 27.55 | 39.78 | 2.64 | 282.25 | 81.65 | 0.00 | 0.02 |
| 9455 | 114.88 | 30.68 | 12.37 | 2.39 | 209.60 | 79.67 | 0.01 | 0.03 |
| 9855 | 194.07 | 47.00 | 19.11 | 4.73 | 239.63 | 56.55 | 0.05 | 0.02 |
| 10375 | 350.33 | 59.35 | 15.18 | 1.20 | 191.46 | 38.97 | 0.06 | 0.02 |
| 10822 | 196.50 | 227.69 | −0.31 | 38.92 | 133.87 | 992.95 | 0.07 | 0.67 |
| 10865 | 210.63 | 35.53 | 14.54 | 1.22 | 156.69 | 20.17 | 0.03 | 0.01 |
| 11504 | 481.48 | 50.24 | 21.83 | 1.18 | 285.12 | 42.99 | 0.00 | 0.01 |
| 11579 | 111.71 | 23.96 | 22.70 | 2.47 | 264.16 | 90.89 | 0.00 | 0.02 |
| 11582 | 74.75 | 5.32 | 2.82 | 5.99 | 231.25 | 421.70 | 0.08 | 0.19 |
| 11631m | 205.55 | 14.87 | 26.85 | 2.85 | 129.33 | 125.13 | 0.01 | 0.04 |
| 11850 | 157.96 | 8.47 | 56.22 | 2.73 | 1268.31 | 169.69 | 0.00 | 0.00 |
| 11974 | 287.39 | 44.66 | 12.52 | 1.20 | 70.49 | 6.65 | 0.06 | 0.02 |
| 12305 | 95.57 | 8.46 | 3.37 | 8.54 | 270.35 | 657.49 | 0.06 | 0.19 |
| 12349 | 124.13 | 28.37 | 21.19 | 5.75 | 350.24 | 117.45 | 0.04 | 0.03 |
| 12396 | 229.02 | 5.91 | 5.84 | 0.36 | 35.57 | 8.02 | 0.14 | 0.03 |
| 12427q | 199.88 | 7.60 | 20.89 | 0.16 | 9.52 | 4.78 | 0.19 | 0.22 |
| 12537 | 136.41 | 3.43 | 29.59 | 0.80 | 479.55 | 37.77 | 0.02 | 0.00 |
| 12571m | 126.47 | 3.88 | 30.84 | 0.93 | 123.04 | 133.15 | 0.02 | 0.06 |
| AR1 | t1c | t2c | LTcalc | lE | lD | t1o | t2o | LTobs | LTavg | STD.LT |
|---|---|---|---|---|---|---|---|---|---|---|
| 3613 | 1.28 | 199.40 | 198.11 | d | f | 0.00 | 125.00 | 125.00 | 161.56 | 51.70 |
| 5900 | −12.15 | 87.44 | 99.60 | f | d | −6.00 | 63.00 | 69.00 | 84.30 | 21.64 |
| 6504 | −13.00 | 62.65 | 75.65 | f | d | −6.00 | 37.00 | 43.00 | 59.33 | 23.09 |
| 6711 | −17.86 | 74.56 | 92.42 | f | f | −6.00 | 73.00 | 79.00 | 85.71 | 9.49 |
| 6713 | −0.97 | 35.93 | 36.91 | f | d | −6.00 | 39.00 | 45.00 | 40.95 | 5.72 |
| 6818 | −20.87 | 100.10 | 120.97 | d | f | 0.00 | 95.00 | 95.00 | 107.99 | 18.37 |
| 7002 | −20.36 | 104.10 | 124.47 | d | d | 0.00 | 108.00 | 108.00 | 116.23 | 11.64 |
| 7232 | 15.31 | 73.07 | 57.76 | f | d | −6.00 | 87.00 | 93.00 | 75.38 | 24.92 |
| 8293 | −33.88 | 60.79 | 94.66 | f | d | −6.00 | 86.00 | 92.00 | 93.33 | 1.88 |
| 8813 | −0.64 | 36.62 | 37.25 | f | d | −6.00 | 35.00 | 41.00 | 39.13 | 2.65 |
| 9219 | −10.62 | 58.29 | 68.91 | f | d | −6.00 | 36.00 | 42.00 | 55.45 | 19.03 |
| 9226 | −2.52 | 77.6 | 80.11 | d | d | 0 | 79 | 79 | 79.56 | 0.79 |
| 9455 | −16.17 | 52.30 | 68.47 | d | d | 0.00 | 59.00 | 59.00 | 63.74 | 6.70 |
| 9855 | 2.82 | 106.82 | 104.00 | d | f | 0.00 | 94.00 | 94.00 | 99.00 | 7.07 |
| 10375 | 1.13 | 104.49 | 103.36 | f | f | −6.00 | 71.00 | 77.00 | 90.18 | 18.64 |
| 10822 | −12.11 | 67.47 | 79.58 | f | d | −6.00 | 61.00 | 67.00 | 73.29 | 8.89 |
| 10865 | −5.15 | 62.64 | 67.78 | f | d | −6.00 | 64.00 | 70.00 | 68.89 | 1.57 |
| 11504 | −22.53 | 65.99 | 88.52 | f | d | −6.00 | 63.00 | 69.00 | 78.76 | 13.80 |
| 11579 | −14.89 | 60.72 | 75.60 | f | d | −6.00 | 63.00 | 69.00 | 72.30 | 4.67 |
| 11582 | −8.34 | 106.61 | 114.95 | f | d | −6.00 | 61.00 | 67.00 | 90.97 | 33.90 |
| 11631m | 2.57 | 58.91 | 56.34 | d | d | 0.00 | 60.00 | 60.00 | 58.17 | 2.59 |
| 11850 | −14.66 | 159.21 | 173.87 | f | f | −6.00 | 125.00 | 131.00 | 152.43 | 30.31 |
| 11974 | 0.89 | 51.03 | 50.14 | f | f | −6.00 | 39.00 | 45.00 | 47.57 | 3.63 |
| 12305 | −10.91 | 102.85 | 113.76 | f | f | −6.00 | 71.00 | 77.00 | 95.38 | 25.99 |
| 12349 | 1.31 | 118.33 | 117.02 | d | d | 0.00 | 112.00 | 112.00 | 114.51 | 3.55 |
| 12396 | −0.13 | 42.32 | 42.46 | f | d | −6.00 | 34.00 | 40.00 | 41.23 | 1.74 |
| 12427q | 17.01 | 35.60 | 18.59 | d | d | 0.00 | 53.00 | 53.00 | 35.79 | 24.33 |
| 12537 | −1.94 | 114.91 | 116.84 | d | d | 0.00 | 109.00 | 109.00 | 112.92 | 5.55 |
| 12571m | 10.68 | 64.61 | 53.93 | d | d | 0 | 115 | 115 | 84.47 | 43.18 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Muraközy, J. Lifetime of Long-Lived Sunspot Groups. Universe 2024, 10, 318. https://doi.org/10.3390/universe10080318
Muraközy J. Lifetime of Long-Lived Sunspot Groups. Universe. 2024; 10(8):318. https://doi.org/10.3390/universe10080318
Chicago/Turabian StyleMuraközy, Judit. 2024. "Lifetime of Long-Lived Sunspot Groups" Universe 10, no. 8: 318. https://doi.org/10.3390/universe10080318
APA StyleMuraközy, J. (2024). Lifetime of Long-Lived Sunspot Groups. Universe, 10(8), 318. https://doi.org/10.3390/universe10080318






