Measuring a Mass: The Puzzling History of an Elusive Particle
Abstract
1. Introduction
[…] in order to understand that -emission is possible, we want to try to construct a theory of the emission of lightweight particles from the nucleus in analogy with the theory of emission of light quanta from an excited atom by the usual radiation process. In radiation theory, the total number of light quanta is not constant. Light quanta are created when they are emitted from an atom, and are annihilated when they are absorbed.([10], p. 1151)
- Direct method for neutrino mass determination.At the heart of direct neutrino mass determination, there is kinematics of weak decays of a number of isotopes, so the neutrino mass is obtained by means of the relativistic energy–momentum formula . In principle, the method is sensitive to the neutrino mass squared and dates back to Fermi’s suggestion [7,8,9,10], independently pointed out by Perrin [14], of the investigation of the endpoint region of a -decay spectrum or an electron capture. Usually the measurement of the charged decay products leads to the determination of the average electron neutrino mass as the incoherent sum over all the neutrino mass eigenstates , , where there is no contribution from the phases of the neutrino mixing matrix . The direct method is still the most sensitive one aimed to determine the absolute neutrino mass scale and it has the advantage of being model-independent.9 Unfortunately, it cannot say anything about the nature of neutrinos.
- Neutrinoless double -decay.The discovery of nonzero neutrino masses brought to the attention of scientists the fundamental and longstanding issue of the nature of neutrinos, and the related issue of the conservation of the lepton number L. In fact, if a neutrino is a Majorana fermion, the conservation of L is not an exact law of nature and its violation holds on [56]. Vice versa, the conservation of L is an exact law of nature for a Dirac fermion and , processes are strictly forbidden. The best experimental probe of lepton number conservation is, without any doubt, the neutrinoless double -decay [57,58,59,60]. Here, the neutrino behaves as a virtual exchange particle and only two electrons are expected to be observed in the final state characterized by an energy sum close to the Q-value of the decay. Neutrinoless double -decay is really a very rare and challenging process to observe and may occur only if the massive neutrino is a Majorana particle. In fact, the lifetime of the process is related to the effective Majorana neutrino mass . Here, the presence of the -violating Majorana phases could make the sum zero even in the presence of nonzero single neutrino masses. The process is also sensitive to the absolute scale of neutrino masses and to the mass hierarchy.
- Cosmology and astrophysics.The actual structure of the universe is the result of fluctuations in the primordial universe. Relic neutrinos affect the distribution of matter in the universe, leaving a fingerprint on the cosmic microwave background, on the large-scale clustering of cosmological structure and finally on the primordial abundance of light elements. In fact, they smeared out fluctuations at small scales, whose order of magnitude could be found starting from the free streaming length of neutrinos, a function of their mass. Thus, information on the total neutrino mass , can be gathered from satellite data as WMAP [61] and PLANCK [62], as well as from large galaxy surveys such as SDSS [63]. In this way, upper limits on the total neutrino mass have been obtained, the last one being eV at confidence level, albeit model- and analysis-dependent.Information about neutrino mass can be gathered also using neutrinos from very strong sources, such as astrophysical events like a core-collapse supernova. Very long baselines are also required in order to carry out time-of-flight measurements. The supernova explosion SN1987A in the Large Magellanic Cloud, which has been the only one detected via neutrinos, provided the following limits on the electron antineutrino mass, eV [64] and eV [65], at confidence level, depending on the underlying supernova model as well as on the chosen data analysis techniques. Currently, nearby supernova explosions are extremely rare and the underlying mechanism still lacks a complete understanding. These considerations make direct laboratory neutrino-mass experiments the best experimental choice to obtain a determination of the neutrino mass.
2. Direct Neutrino Mass Determination
2.1. The -Decay Spectrum and Early Experiments
He also added a footnote, pointing out that analogous conclusions had been drawn by F. Perrin in a recent publication [14]. Then, in the simplest case of a neutrino with zero rest mass, from Equation (1) (where was taken), he obtained the simplified expression:The greatest similarity to the empirical curves is given by the theoretical curve for . Hence, we conclude that the rest mass of the neutrino is either zero or, in any case, very small in comparison to the mass of the electrons.([10], p. 1156)
The experimental points […] are consistent with a neutrino rest mass of zero. Within the limits of error one can certainly say that the mass of the neutrino is less than one percent the mass of the electron.([99], p. 552)
It seems to be futile to try to apply the corrections which would be necessary for the interpretation of the Leipunski experiment. Nevertheless the experiment had great value in that a successful method of detecting recoil nuclei was found for the first time, and the way was thereby opened for a succession of experiments on the momentum relations in the beta-decay.([16], p. 285)
The thesis that the maximum -energy can only be determined with the same accuracy as can the mass of the neutrino, has here been illustrated in the special case of the Fermi theory, which fits experimental data rather closely, but it is not restricted to this theory alone.([88], p. 452)
2.2. The -Spectrum of 3H: Early Experiments
Can the present limit on , from -decay be improved? It has been argued in this paper that an inherent limitation on the accuracy imposed by atomic effects is at a much lower level than in the magnetic-spectrometer measurements, and that the main uncertainty therefore is statistical. The statistical accuracy is strongly influenced by the resolution, the radiation dose that the detector can tolerate, and the length of time which is used for recording the spectrum. In fact, if the present experiment were carried out for one tritium half-life, all other things remaining the same, the limit on , could be reduced to about 20 eV ( confidence). (One might implant a dozen detectors and count for about a year, achieving again about 20 eV as a limit.) The resolution can be improved only marginally, so that at the moment work is in progress toward an experiment with higher count rate.([126], p. 639)
2.3. Orbital Electron Capture Experiments
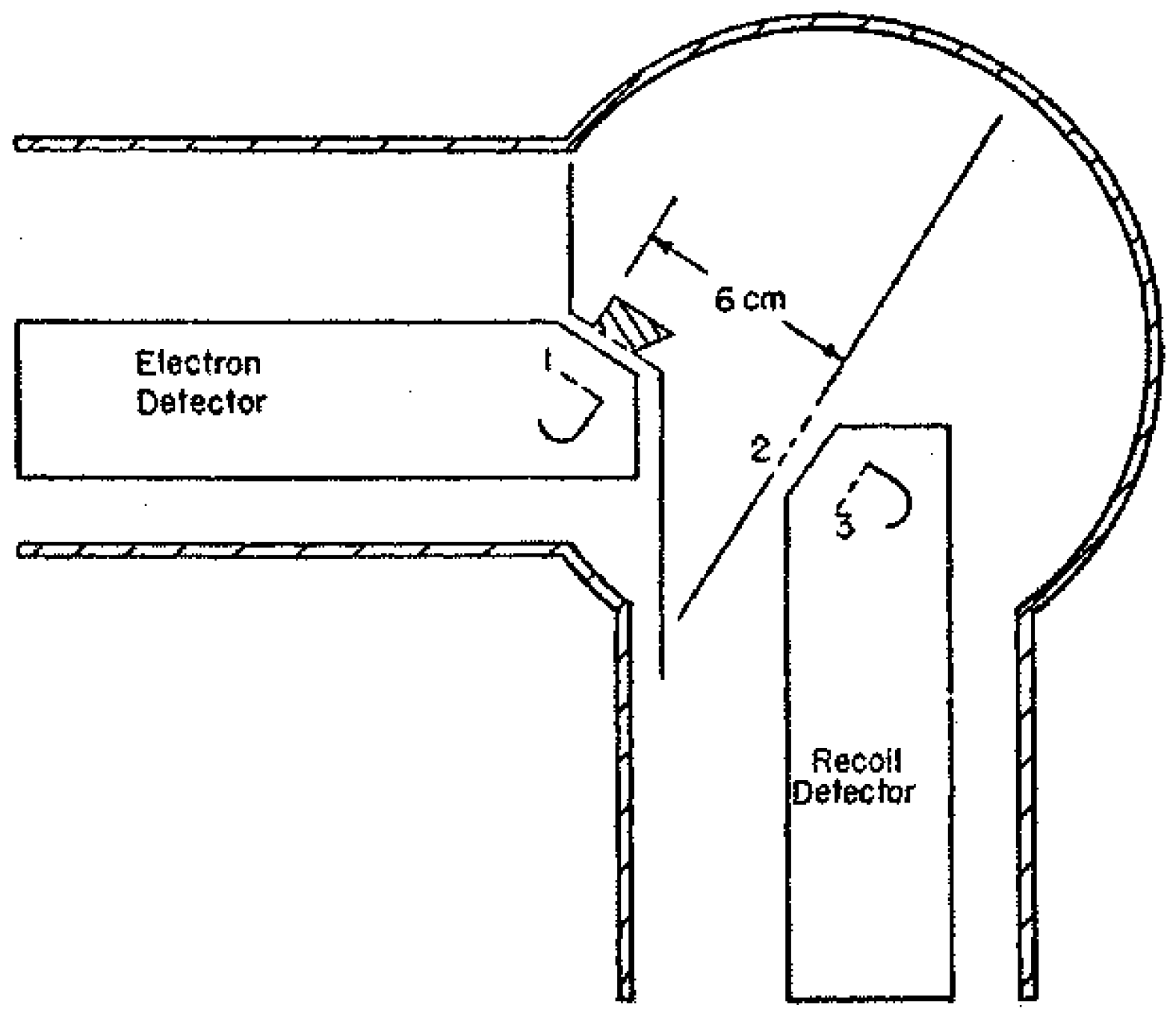
The measurement of the recoil in a K-capture process is the one experiment which can distinguish sharply between the emission of single and multiple neutrinos. If the single neutrino picture is correct, the momentum spectrum of recoils will be a line spectrum since the energy of the transformation is not shared between an electron and a neutrino but is taken by the neutrino alone. If no gamma-rays are emitted, the recoil spectrum will consist of a single line. In contrast, the multiple neutrino picture would, clearly, give a continuous distribution of recoil momenta. Second, recoil experiments can tell something about the angular correlation between the directions of emission of the electron and the neutrino.([16], p. 281)
The energy which a neutral silver recoil must have to escape from the metal surface can be estimated reliably from the heats of vaporization of the metals involved, and is several electron volts. The maximum recoil energies obtainable from the x-rays and Auger electrons which follow the K-capture are only eV and eV, respectively. Therefore the fact that the recoils do escape from the surface, and that quantitatively the number collected is of the right order of magnitude, is strong evidence that momentum is acquired by the atom in accord with the neutrino hypothesis.([16], p. 283)
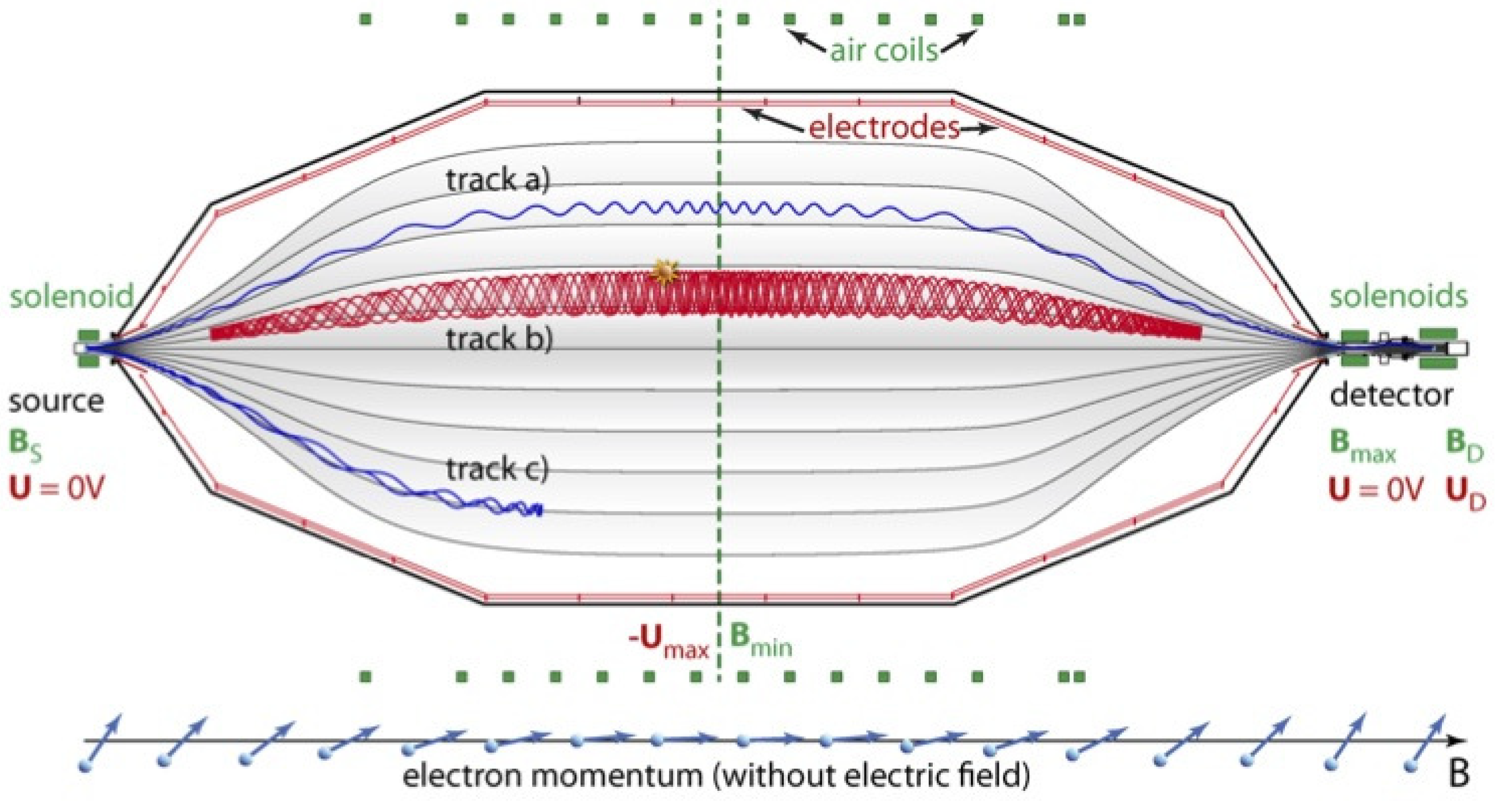
2.4. Pushing Limits below 50 eV: Recent Experiments on Tritium, Rhenium and Holmium
3. Neutrinoless Double -Decay
3.1. Early Theoretical Issues
A disintegration with the simultaneous emission of two electrons and two neutrinos will then be in strong analogy to the Raman effect, or, even more closely, to the simultaneous emission of two light quanta, and can be calculated in essentially the same manner, namely, from the second-order terms in the perturbation theory. The process will appear as the simultaneous occurrence of two transitions, each of which does not fulfill the law of conservation of energy separately.([204], p. 512)
Majorana has recently shown by using a special set of Dirac matrices that the symmetry properties of the Dirac equations make possible the elimination of the negative energy states in the case of a free particle. […] Majorana also showed how his ideas can be applied in the theory of the neutral particle to obtain a formalism essentially different from that of the ordinary Dirac theory. Qualitatively the difference appears in the number of states having the same momentum. In the Dirac theory as used at present there are four such states, corresponding to two alternatives for the spin orientation and to the possible existence of both the particles in question and their “antiparticles”? e.g., neutrinos and antineutrinos. In the Majorana theory there are just two states for a given momentum, corresponding to the two possibilities for the spin: there are no “antiparticles” and, in the final formulation, no mention of negative energy states. […] For the neutrino, however, the Majorana theory is a priori just as acceptable as the ordinary Dirac theory. It is interesting to find that it is possible to accomplish all the purposes for which the neutrino theory was devised, including the discussion of both electron emission and positron emission, without the introduction of antineutrinos.([205], p. 56)
In the ordinary theory one type of -decay involves the emission of neutrinos and the other the emission of antineutrinos, but in the Majorana theory use is made of neutrinos only. It should be possible to settle which theory is preferable by considering processes in which neutrinos are absorbed as well as emitted, but actually this does not seem feasible at present. Differences would presumably appear in the results of using the light particle fields to account for the forces between heavy particles, but this part of the subject is in such an unsatisfactory state owing to divergence difficulties that it seems to offer no hope of a decision, and indeed it seems quite doubtful that nuclear forces are to be explained in this way. Another possibility of deciding between the two theories is offered in principle by the phenomenon of -decay with absorption of a light neutral particle instead of its emission, the -ray accordingly having more energy than the limit of the spectrum instead of less. Here, as Racah has remarked, there is an obvious qualitative difference between the two theories. On the ordinary Dirac theory, a positron emitter can be “stimulated” only by an electron emitter, and vice versa, but on the Majorana theory any emission may “stimulate” any other emission, whether of the same or of opposite type. But since the cross section of a radioactive nucleus for capture of a neutrino is of order of magnitude between and cm2, it seems unlikely that this effect, which would not only serve to decide the question of the existence of antineutrinos but would provide experimental evidence of the best sort for the neutrino hypothesis itself, can ever be observed.([205], p. 67)
We prove here that the condition of self charge-conjugation is incompatible with the usual invariance requirements; identity of a field with its charge-conjugate is impossible, because they transform differently under space reversal. Clearly, this suffices to rule out the Majorana theory.([208], p. 564)
Coming back to physics, we wish to point out, finally, that the rejection of the Majorana theory for the neutrino would not forbid the interpretation of double beta-decay phenomena, should they be definitely proved to occur.([208], p. 565)
3.2. Experiments
- (A)
- In this theory it is clear that the neutrino state and the antineutrino state cannot be the same. A Majorana theory for such a neutrino is therefore impossible.
- (B)
- The mass of the neutrino and the antineutrino in this theory is necessarily zero. This is true for the physical mass even with the inclusion of all interactions. To see this, one need only observe that all the one-particle physical states consisting of one neutrino (or one antineutrino) must belong to a representation of the inhomogeneous proper Lorentz group identical with the representation to which the free neutrino states discussed above belong. For such a representation to exist at all, the mass must be zero ([23], p. 1672).
We would like to suggest that further attempts to measure the double beta-decay process may be “indeed … worth-while.” The discovery that the law of conservation of parity is violated in the weak interactions has led us to believe in the completely longitudinally-polarized “two-component” neutrino and the consequent law of lepton conservation in the weak interactions. It is certainly worth-while to measure the double beta-decay process for in doing so it is possible that someone will find the answer to the question we raise, “Are leptons conserved?” If only the two-neutrino mode of decay is found to occur in nature, then lepton conservation becomes much more firmly established than is now evident. If the neutrino less mode of decay is found to occur in nature, the principle of lepton conservation is not valid, more will be learned about the interaction […], and possibly a lower limit on the neutrino’s mass could be established.([225], p. 530)
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| F-K | Fermi-Kurie |
| G-M | Geiger-Mueller |
| ITEP | Institute of Theoretical and Experimental Physics |
| LANL | Los Alamos National Laboratory |
| LNL | Livermore National Laboratories |
| INS | Institute of Nuclear Studies |
| MAC-E Filter | Magnetic Adiabatic Collimation with an Electrostatic Filter |
| KATRIN | Karlsruhe Tritium Neutrino |
| CRES | Cyclotron Radiation Emission Spectroscopy |
| MARE | Microcalorimeter Arrays for a Rhenium Experiment |
| IBEC | internal bremsstrahlung in electron capture |
| GUTs | grand unified theories |
| PMNS | Pontecorvo Maki Nakagawa Sakata |
| HPGe | High Purity Germanium |
| 1 | Pauli’s proposal was put forward in an open letter addressed to Hans W. Geiger and Lise Meitner at a meeting in Tübingen in December 1930 [1], and later publicly expressed at the American Physical Society meeting held in Pasadena in June 1931. In fact, in 1933 at the Solvay Conference in Brussels, Pauli recalled “In June 1931, during a conference in Pasadena, I proposed the following interpretation: the conservation laws hold, the emission of beta particles occurring together with the emission of a very penetrating radiation of neutral particles, which has not been observed yet. The sum of the energies of the beta particle and the neutral particle (or the neutral particles, since one does not know whether there is one or many) emitted by the nucleus in one process, will be equal to the energy which corresponds to the upper limit of the beta spectrum” ([2], p. 324). |
| 2 | This feature followed as a result of the existing model of nuclei, consisting of protons and electrons. Indeed, according to this picture and the Ehrenfest–Oppenheimer rule [3], the 14N nucleus was built of fourteen protons and seven electrons, leading to a half-integer spin and then to Fermi–Dirac statistics, at odds with experimental observations, consistent with spin-1 and Bose–Einstein statistics. |
| 3 | This critical position was shared by Niels Bohr, who had also questioned the validity of the energy conservation, in an attempt to look for a solution to the -decay puzzle [4]. |
| 4 | A corresponding penetrating power of km in solid matter was predicted, which led Bethe and Peierls to the pessimistic conclusion: “It is therefore absolutely impossible to observe processes of this kind with the neutrinos created in nuclear transformations” ([13], p. 532). |
| 5 | The starting point of Pontecorvo’s method was the consideration that radioactive atoms produced by inverse -ray processes and irradiated atoms have different chemical properties. Several elements can be used for neutrino irradiation, among which 37Cl, and the experiment proposed by Pontecorvo is based on the following reactions: + 37Cl + 37Ar and 37Ar → 37Cl, the last one being an electron capture decay. It required the irradiation of a large volume of Chlorine or Carbon Tetra-Chloride for about one month, followed by the extraction of radioactive 37Ar by boiling. Then, the radioactive isotope 37Ar had to be introduced inside a small counter with a counting efficiency close to [17]. |
| 6 | Reines and Cowan’s experiment was based on the reaction . According to Fermi’s theory the cross section for an inverse -decay process had to depend on the energy. As such, for antineutrinos with average energy of 3 MeV, a cross section equal to cm2 with an uncertainty of about 25 percent (due to the uncertainty of the energy spectrum of antineutrinos) was predicted. The cross section measured by Reines and Cowan was in agreement with the predicted value within 5 percent [21]. |
| 7 | The muon neutrino was detected for the first time in 1962 at Brookhaven [33]. |
| 8 | |
| 9 | |
| 10 | Throughout this subsection and the following one the historical notation for the neutrino rest mass is adopted. |
| 11 | In general, the matrix element is different from zero if the difference between the angular momentum and spin of the primary and secondary nuclei is equal to zero or one. |
| 12 | Alvarez investigated the K-electron capture process for several isotopes by focusing, in particular, on the transition from 67Ga nucleus to the stable 67Zn nucleus [80]. |
| 13 | See Ref. [107] for a complete survey of the main results of the theoretical and experimental studies on the fundamental reactions involving light nuclei carried out until 1950. In particular, the endpoint energy estimates for the -spectrum here quoted vary from keV to keV. |
| 14 | The finite resolution of spectrometers required the correction of the experimental points in order to obtain the true -spectrum. Such a correction was shown to depend on the energy derivatives of the observed energy distribution and on the observed resolution characteristics. Ad hoc procedures were developed in order to face this problem [115,116]. |
| 15 | Otherwise the absorption of low-energy electrons could introduce distortions in the measured spectra. |
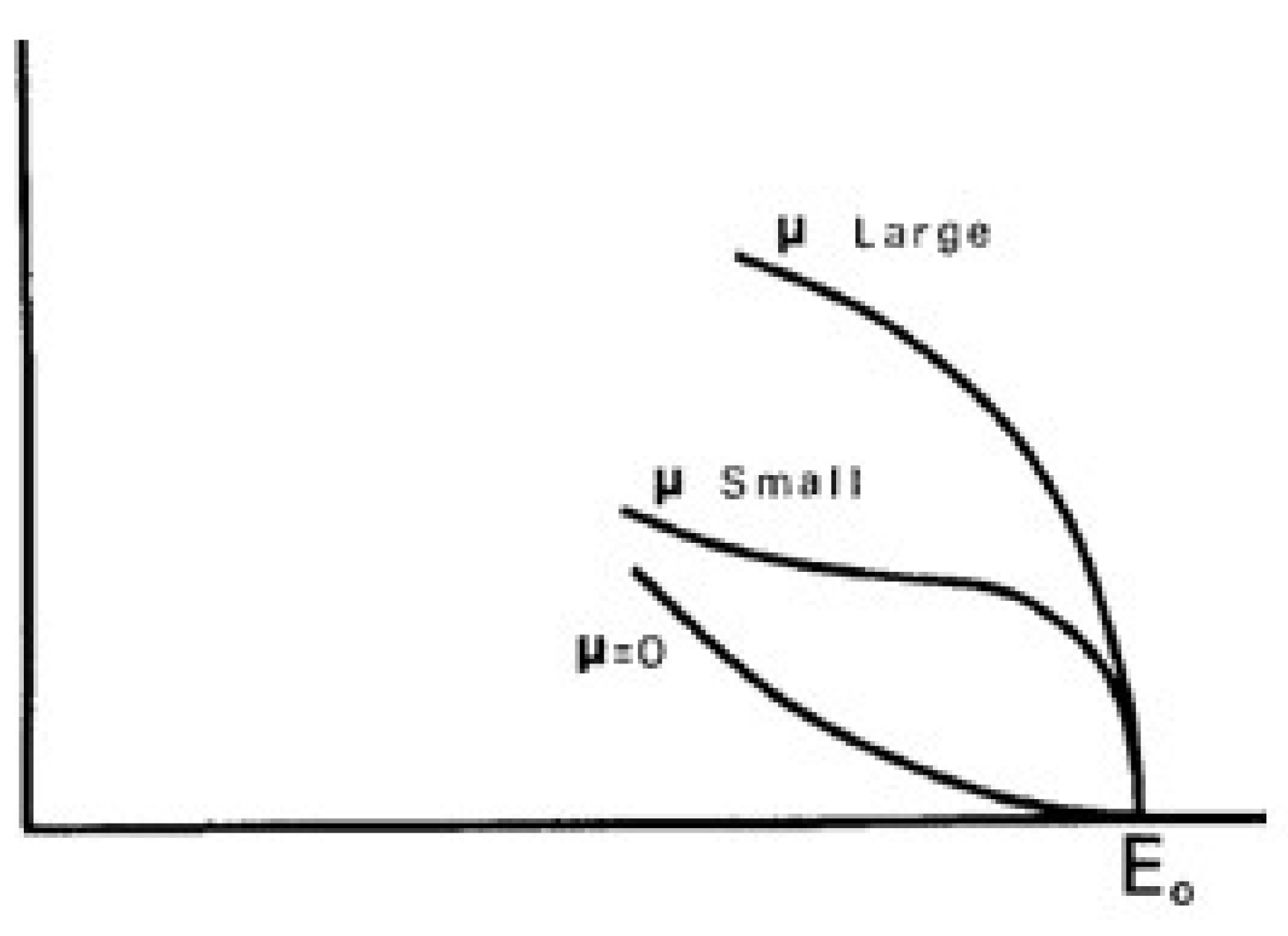
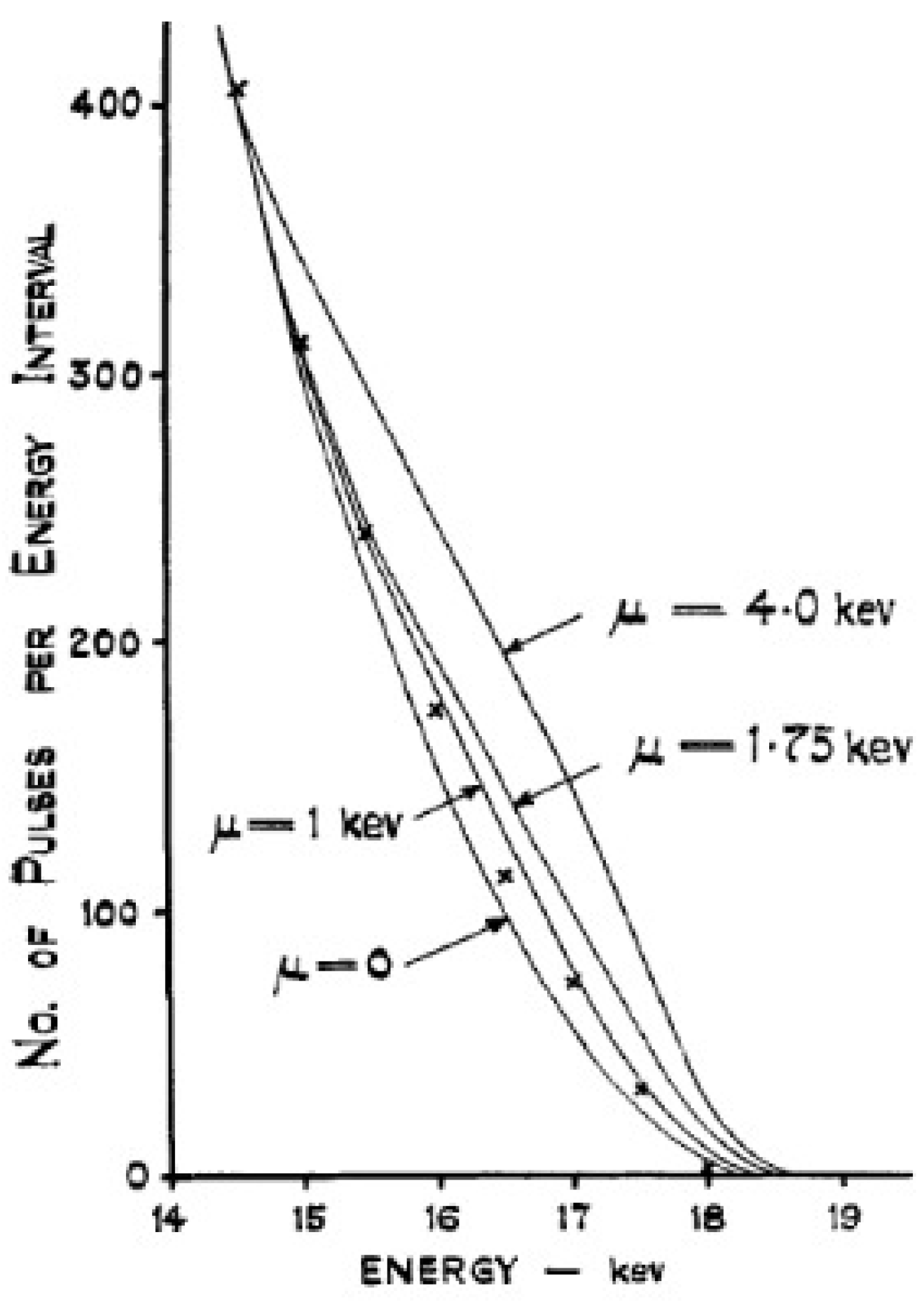
| 16 | A finite neutrino mass was shown to influence essentially the region close to the endpoint of the -spectrum [114], which led to an F-K plot turning sharply towards the energy axis. The distance between the theoretical endpoint and the endpoint obtained by the straight line extrapolation of the spectrum at low energies was equal to and for Dirac antineutrino and neutrino, respectively, while being equal to in the case of a Majorana neutrino. In Ref. [114] the upper limit obtained was compatible with a Dirac neutrino picture. |
| 17 | The interesting history of the experimental efforts conducted by the ITEP group and of the general skepticism which accompanied them throughout the years is retraced in Ref. [50], pp. 196–199, to which we refer the interested reader. |
| 18 | |
| 19 | |
| 20 | |
| 21 | This circumstance was pointed out by B. Pontecorvo in Ref. [207]. |
| 22 | From its very beginning, the story of experimental searches for double -decay has been characterized by false discoveries, which would have been superseded by subsequent attempts. A collection of these unfortunate efforts can be found in Ref. [215], to which we refer the interested reader. |
| 23 |
References
- Pauli, W. Letter to a physicists’ gathering at Tübingen, December 4, 1930. In W. Pauli, Collected Scientific Papers; Kronig, R., Weisskopf, V., Eds.; Interscience: New York, NY, USA, 1964; Volume 2, p. 1313. [Google Scholar]
- Pauli, W. In Discussion du rapport de M. Heisenberg. In Structure et Propriétés des Noyaux Atomiques: Rapports et Discussions du Septiéme Conseil de Physique Tenu à Bruxelles du 22 au 29 Octobre 1933; Institut International de Physique Solvay Edition; Gauthier-Villars: Paris, France, 1934; p. 324. [Google Scholar]
- Ehrenfest, P.; Oppenheimer, J.R. Note on the Statistic of Nuclei. Phys. Rev. 1931, 37, 333–338. [Google Scholar] [CrossRef]
- Bohr, N. Faraday Lecture. Chemistry and the Quantum Theory of Atomic Constitution. J. Chem. Soc. 1932, 349–384. [Google Scholar] [CrossRef]
- Chadwick, J. The existence of a neutron. Proc. R. Soc. Lond. A 1932, 136, 692–708. [Google Scholar]
- Chadwick, J. Possible Existence of a Neutron. Nature 1932, 129, 312. [Google Scholar] [CrossRef]
- Fermi, E. Tentativo di una teoria dell’emissione dei raggi beta. Ric. Sci. 1933, 4, 491–495. [Google Scholar]
- Fermi, E. Tentativo di una teoria dei raggi β. Il Nuovo C. 1934, 11, 1–19. [Google Scholar] [CrossRef]
- Fermi, E. Versuch einer Theorie der β-Strahlen. 1. Z. Phys. 1934, 88, 161–171. [Google Scholar] [CrossRef]
- Wilson, F.L. Fermi’s Theory of Beta Decay. Am. J. Phys. 1968, 36, 1150–1160. [Google Scholar] [CrossRef]
- Heisenberg, W. Über den Bau der Atomkerne 1. Z. Phys. 1932, 77, 1–11. [Google Scholar] [CrossRef]
- Majorana, E. Teoria simmetrica dell’elettrone e del positrone. Il Nuovo C. 1937, 14, 171–184. [Google Scholar] [CrossRef]
- Bethe, H.; Peierls, R. The “Neutrino”. Nature 1934, 133, 532. [Google Scholar] [CrossRef]
- Perrin, F. Possibilité d’ émission de particules neutres de masse intrinsèque nulle dans les radioactivités β. Comptes Rendus 1933, 197, 1625–1627. [Google Scholar]
- Crane, H.R. An Attempt to Observe the Absorption of Neutrinos. Phys. Rev. 1939, 55, 501–502. [Google Scholar] [CrossRef]
- Crane, H.R. The Energy and Momentum Relations in the Beta-Decay, and the Search for the Neutrino. Rev. Mod. Phys. 1948, 20, 278–295. [Google Scholar] [CrossRef]
- Pontecorvo, B.M. Inverse β Process; Report PD-205; National Research Council of Canada, Division of Atomic Energy: Chalk River, ON, Canada, 1946. [Google Scholar]
- Ageno, M.; Chiozzotto, M.; Querzoli, R. Scintillations in Liquids and Solutions. Phys. Rev. 1950, 79, 720. [Google Scholar] [CrossRef]
- Kallmann, H. Scintillation Counting with Solutions. Phys. Rev. 1950, 78, 621. [Google Scholar] [CrossRef]
- Reynolds, G.I.; Harrison, F.B.; Salvini, G. Liquid Scintillation Counters. Phys. Rev. 1950, 78, 488. [Google Scholar] [CrossRef]
- Cowan, C.L.; Reines, F.; Harrison, F.B.; Kruse, H.W.; McGuire, A.D. Detection of the Free Neutrino: A Confirmation. Science 1956, 124, 103–104. [Google Scholar] [CrossRef]
- Wu, C.S.; Ambler, E.; Hayward, R.W.; Hoppes, D.D.; Hudson, R.P. Experimental Test of Parity Conservation in Beta Decay. Phys. Rev. 1957, 105, 1413–1414. [Google Scholar] [CrossRef]
- Lee, T.D.; Yang, C.N. Parity Nonconservation and a Two-Component Theory of the Neutrino. Phys. Rev. 1957, 105, 1671–1675. [Google Scholar] [CrossRef]
- Landau, L.D. On the Conservation Laws for Weak Interactions. Nucl. Phys. 1957, 30, 127–131. [Google Scholar] [CrossRef]
- Salam, A. On parity conservation and neutrino mass. Il Nuovo C. 1957, 5, 299–301. [Google Scholar] [CrossRef]
- Goldhaber, M.; Grodzins, L.; Sunyar, A.W. Helicity of Neutrinos. Phys. Rev. 1958, 109, 1015–1016. [Google Scholar] [CrossRef]
- Feynman, R.P.; Gell-Mann, M. Theory of the Fermi Interaction. Phys. Rev. 1958, 109, 193–197. [Google Scholar] [CrossRef]
- Sudarshan, E.C.G.; Marshak, R.E. Chirality Invariance and the Universal Fermi Interaction. Phys. Rev. 1958, 109, 1860. [Google Scholar] [CrossRef]
- Davis, R.; Harmer, D.S. Attempt to observe the Cl37(ν¯e−)Ar37 reaction induced by reactor antineutrinos. Bull. Am. Phys. Soc. 1959, 4, 217. [Google Scholar]
- Pontecorvo, B.M. Mesonium and Antimesonium. Sov. Phys. JETP 1958, 6, 429–431. [Google Scholar]
- Pontecorvo, B.M. Inverse Beta Processes and Nonconservation of Lepton Charge. Sov. Phys. JETP 1958, 7, 172–173. [Google Scholar]
- Pontecorvo, B.M. Neutrino Experiments and the Problem of Conservation of Leptonic Charge. Sov. Phys. JETP 1968, 26, 984–988. [Google Scholar]
- Danby, G.; Gaillard, J.M.; Goulianos, K.; Lederman, L.M.; Mistry, M.; Schwartz, M.; Steinberger, J. Observation of High-Energy Neutrino Reactions and the Existence of Two Kinds of Neutrinos. Phys. Rev. Lett. 1962, 9, 36–44. [Google Scholar] [CrossRef]
- Bilenky, S.M.; Pontecorvo, B.M. Lepton Mixing and Neutrino Oscillations. Phys. Rep. 1978, 41, 225–261. [Google Scholar] [CrossRef]
- Katayama, Y.; Matumoto, K.; Tanaka, S.; Yamada, E. Possible Unified Models of Elementary Particles with Two Neutrinos. Prog. Theor. Phys. 1962, 28, 675–689. [Google Scholar] [CrossRef][Green Version]
- Maki, Z.; Nakagawa, M.; Sakata, S. Remarks on the Unified Model of Elementary Particles. Progress Theor. Phys. 1962, 28, 870–880. [Google Scholar] [CrossRef]
- Nakagawa, M.; Okonogi, H.; Sakata, S.; Toyoda, A. Possible Existence of a Neutrino with Mass and Partial Conservation of Muon Charge. Progress Theor. Phys. 1963, 30, 727–729. [Google Scholar] [CrossRef][Green Version]
- Fukuda, Y. et al. [Super-Kamiokande Collaboration] Evidence for oscillation of atmospheric neutrinos. Phys. Rev. Lett. 1998, 81, 1562–1567. [Google Scholar] [CrossRef]
- Allison, W.W.M. et al. [Soudan-2 Collaboration] The atmospheric neutrino flavor ratio from a 3.9 fiducial kiloton-year exposure of Soudan 2. Phys. Lett. B 1999, 449, 137–144. [Google Scholar] [CrossRef]
- Ambrosio, M. et al. [MACRO Collaboration] Matter effects in upward-going muons and sterile neutrino oscillations. Phys. Lett. B 2001, 517, 59–66. [Google Scholar] [CrossRef]
- Cleveland, B.T.; Daily, T.; Davis, R.; Distel, J.R.; Lande, K.; Lee, C.K.; Wilderhain, P.S.; Ullman, J. Measurement of the Solar Electron Neutrino Flux with the Homes- take Chlorine Detector. Astrophys. J. 1998, 496, 505–526. [Google Scholar] [CrossRef]
- Hampel, W. et al. [GALLEX Collaboration] GALLEX solar neutrino observations: Results for GALLEX IV. Phys. Lett. B 1999, 447, 127–133. [Google Scholar] [CrossRef]
- Altmann, M. et al. [GNO Collaboration] GNO solar neutrino observations: Results for GNO I. Phys. Lett. B 2000, 490, 16–26. [Google Scholar] [CrossRef]
- Abdurashitov, J.N. et al. [SAGE Collaboration] Measurement of the solar neutrino capture rate with gallium metal. Phys. Rev. C 1999, 60, 055801. [Google Scholar] [CrossRef]
- Smy, M.B. et al. [Super-Kamiokande Collaboration] Solar neutrino precision measurements using all 1496 days of Super-Kamiokande-I data. Nucl. Phys. B Proc. Suppl. 2003, 118, 25–32. [Google Scholar] [CrossRef]
- Ahmad, Q.R. et al. [SNO Collaboration] Direct evidence for neutrino flavor transformation from neutral-current interactions in the Sudbury Neutrino Observatory. Phys. Rev. Lett. 2002, 89, 011301. [Google Scholar] [CrossRef] [PubMed]
- Ahmad, Q.R. et al. [SNO Collaboration] Measurement of day and night neutrino energy spectra at SNO and constraints on neutrino mixing parameters. Phys. Rev. Lett. 2002, 89, 011302. [Google Scholar] [CrossRef] [PubMed]
- Eguchi, K. et al. [KamLAND Collaboration] First results from KamLAND: Evidence for reactor anti-neutrino disappearance. Phys. Rev. Lett. 2003, 90, 021802. [Google Scholar] [CrossRef] [PubMed]
- Kodama, K. et al. [DONUT Collaboration] Observation of tau neutrino interactions. Phys. Lett. B 2001, 504, 218–224. [Google Scholar] [CrossRef]
- Robertson, R.G.H.; Knapp, D.A. Direct measurements of neutrino mass. Annu. Rev. Nucl. Part. Sci. 1988, 38, 185–215. [Google Scholar] [CrossRef]
- Holzschuh, E. Measurement of the neutrino mass from tritium beta decay. Rep. Prog. Phys. 1992, 55, 1035–1091. [Google Scholar] [CrossRef]
- Otten, R.; Weinheimer, C. Neutrino mass limit from tritium β decay. Rep. Prog. Phys. 2008, 71, 086201. [Google Scholar] [CrossRef]
- Drexlin, G.; Hannen, V.; Mertens, S.; Weinheimer, C. Current direct neutrino mass experiments. Adv. High Energy Phys. 2013, 2013, 293986. [Google Scholar] [CrossRef]
- Allen, J.S. The Neutrino; Princeton University Press: Princeton, NJ, USA, 1958. [Google Scholar]
- Formaggio, J.A.; de Gouvea, A.L.C.; Robertson, R.G.H. Direct Measurements of Neutrino Mass. Phys. Rep. 2021, 914, 1–54. [Google Scholar] [CrossRef]
- Kayser, B. Majorana neutrinos. Comments Nucl. Part. Phys. 1985, 14, 69–86. [Google Scholar]
- Furry, W.H. On Transition Probabilities in Double Beta-Disintegration. Phys. Rev. 1939, 56, 1184–1193. [Google Scholar] [CrossRef]
- Giuliani, A.; Poves, A. Neutrinoless Double-Beta Decay. Adv. High Energy Phys. 2012, 2012, 857016. [Google Scholar] [CrossRef]
- Petcov, S.T. The Nature of the Neutrino (Dirac/Majorana) and Double Beta Decay with or without Neutrinos. In Proceedings of the International Conference on History of the Neutrino, Paris, France, 5–7 September 2018; p. 417. [Google Scholar]
- Barabash, A.S. Double Beta Decay: Historical Review of 75 Years of Research. Phys. At. Nucl. 2011, 74, 603–613. [Google Scholar] [CrossRef]
- Komatsu, E. et al. [WMAP Collaboration] Seven-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Cosmological Interpretation. Astrophys. J. Suppl. Ser. 2011, 192, 18. [Google Scholar] [CrossRef]
- Aghanim, N. et al. [PLANCK Collaboration] Planck 2018 results. VI. Cosmological parameters. Astron. Astrophys. 2020, 641, A6. [Google Scholar] [CrossRef]
- Aihara, H. et al. [SDSS Collaboration] The Eighth Data Release of the Sloan Digital Sky Survey: First Data from SDSS-III. Astrophys. J. Suppl. Ser. 2011, 193, 26, Erratum in Astrophys. J. Suppl. Ser. 2011, 195, 26. [Google Scholar]
- Loredo, T.J.; Lamb, D.Q. Bayesian analysis of neutrinos observed from supernova SN1987A. Phys. Rev. D 2002, 65, 063002. [Google Scholar] [CrossRef]
- Pagliaroli, G.; Rossi-Torres, F.; Vissani, F. Neutrino mass bound in the standard scenario for supernova electronic antineutrino emission. Astropart. Phys. 2010, 33, 287–291. [Google Scholar] [CrossRef]
- Bilenky, S.M. Neutrino. History of a unique particle. Eur. Phys. J. H 2013, 38, 345–404. [Google Scholar] [CrossRef]
- Rajasekaran, G. The Story of the Neutrino. arXiv 2016, arXiv:1606.08715. [Google Scholar]
- Bettini, A. Chapter 1: A Brief History of Neutrino. In The State of the Art of Neutrino Physics; Ereditato, A., Ed.; World Scientific Publishing: Singapore, 2018; pp. 1–36. [Google Scholar]
- Bilenky, S.M. The History of Neutrino Oscillations. Phys. Scr. 2005, T121, 17–22. [Google Scholar] [CrossRef]
- Bilenky, S.M. Bruno Pontecorvo–Pioneer of neutrino oscillations. Il Nuovo Cimento C 2014, 37, 21–28. [Google Scholar]
- Bilenky, S.M. Neutrino oscillations: From a historical perspective to the present status. Nucl. Phys. B 2016, 908, 2–13. [Google Scholar] [CrossRef]
- Bernabeu, J. On the history of the PMNS Matrix … with today’s perspective. Il Nuovo Cimento C 2014, 37, 145–154. [Google Scholar]
- Konopinski, E.J. H3 and the Mass of the Neutrino. Phys. Rev. 1947, 72, 518–519. [Google Scholar] [CrossRef]
- Arenz, M. et al. [KATRIN Collaboration] Commissioning of the vacuum system of the KATRIN Main Spectrometer. J. Instrum. 2016, 11, P04011. [Google Scholar] [CrossRef]
- Ellis, C.D.; Wooster, W.A. The Average Energy of Disintegration of Radium E. Proc. R. Soc. Lond. A 1927, 117, 109–123. [Google Scholar]
- Konopinski, E.J. Beta-Decay. Rev. Mod. Phys. 1943, 15, 209–245. [Google Scholar] [CrossRef]
- Cook, C.S.; Owen, G.E. The allowed Beta-Spectrum. Am. J. Phys. 1950, 18, 453–462. [Google Scholar] [CrossRef]
- Wick, G.C. Sugli elementi radioattivi di F. Joliot e I. Curie. Atti Accad. Dei Lincei Rend. 1934, 19, 319–324. [Google Scholar]
- Alvarez, L.W. Nuclear K Electron Capture. Phys. Rev. 1937, 52, 134–135. [Google Scholar] [CrossRef]
- Alvarez, L.W. The Capture of Orbital Electrons by Nuclei. Phys. Rev. 1938, 54, 486–497. [Google Scholar] [CrossRef]
- Ellis, C.D.; Henderson, W.J. Artificial Radioactivity. Proc. R. Soc. Lond. A 1934, 146, 206–216. [Google Scholar]
- Konopinski, E.J.; Uhlenbeck, G.E. On the Fermi Theory of β-Radioactivity. Phys. Rev. 1935, 48, 7–12. [Google Scholar] [CrossRef]
- Kurie, F.N.D.; Richardson, J.R.; Paxton, H.C. The Radiations Emitted from Artificially Produced Radioactive Substances. I. The Upper Limits and Shapes of the β-Ray Spectra from Several Elements. Phys. Rev. 1936, 49, 368–381. [Google Scholar] [CrossRef]
- Henderson, W.J. The Upper Limits of the Continuous β-Ray Spectra of Thorium C and C". Proc. R. Soc. Lond. A 1934, 147, 572–582. [Google Scholar]
- Ellis, C.D.; Mott, N.F. Energy Relations in the β-Ray Type of Radioactive Disintegration. Proc. R. Soc. Lond. A 1933, 141, 502–511. [Google Scholar]
- Crane, H.R.; Delsasso, L.A.; Fowler, W.A.; Lauritsen, C.C. The Emission of Negative Electrons from Boron Bombarded by Deuterons. Phys. Rev. 1935, 47, 887–888. [Google Scholar] [CrossRef]
- Bethe, H.A.; Bacher, R.F. Nuclear Physics. A. Stationary States of Nuclei. Rev. Mod. Phys. 1936, 8, 82–229. [Google Scholar] [CrossRef]
- Kofoed-Hansen, O. Maximum β-Energies and the Mass of the Neutrino. Phys. Rev. 1947, 71, 451–452. [Google Scholar] [CrossRef]
- Bethe, H.A.; Morrison, P. Elementary Nuclear Theory; John Wiley & Sons: New York, NY, USA, 1947. [Google Scholar]
- Allen, J.S. The Search for the Neutrino through Nuclear Recoil Experiments. Am. J. Phys. 1948, 16, 451–461. [Google Scholar] [CrossRef]
- Haxby, R.O.; Shoupp, W.E.; Stephens, W.E.; Wells, W.H. Thresholds for the Proton-Neutron Reactions of Lithium, Beryllium, Boron, and Carbon. Phys. Rev. 1940, 58, 1035–1042. [Google Scholar] [CrossRef]
- Lyman, E.M. The β-Ray Spectrum of N13 and the Mass of the Neutrino. Phys. Rev. 1939, 55, 234. [Google Scholar]
- Hughes, D.J.; Eggler, C. The reaction He3(n, p)H3 and the Neutrino Mass. Phys. Rev. 1948, 73, 809–810. [Google Scholar] [CrossRef]
- Watts, R.J.; Williams, D. Beta-Rays from H3. Phys. Rev. 1946, 70, 640–642. [Google Scholar] [CrossRef]
- Tyler, A.W. The Beta- and Gamma-Radiations from Copper64 and Europium152. Phys. Rev. 1939, 56, 125–130. [Google Scholar] [CrossRef]
- Albert, R.D.; Wu, C.S. The Beta-Spectrum of S35. Phys. Rev. 1948, 74, 847–848. [Google Scholar] [CrossRef]
- Wu, C.S.; Albert, R.D. The Beta-Ray Spectra of Cu64. Phys. Rev. 1949, 75, 315–316. [Google Scholar]
- Wu, C.S.; Albert, R.D. The Beta-Ray Spectra of Cu64 and the Ratio of N+/N-. Phys. Rev. 1949, 75, 1107–1108. [Google Scholar] [CrossRef]
- Cook, C.S.; Langer, L.M.; Price, H.C. Study of the Beta–Spectra of C14 and S35. Phys. Rev. 1948, 74, 548–552. [Google Scholar] [CrossRef]
- Leipunski, A.I. Determination of the Energy Distribution of Recoil Atoms During β Decay and the Existence of the Neutrino. Math. Proc. Camb. Philos. Soc. 1936, 32, 301–303. [Google Scholar] [CrossRef]
- Crane, H.R.; Halpern, J. New Experimental Evidence for the Existence of a Neutrino. Phys. Rev. 1938, 53, 789–794. [Google Scholar] [CrossRef]
- Crane, H.R.; Halpern, J. Further Experiments on the Recoil of the Nucleus in Beta-Decay. Phys. Rev. 1939, 56, 232–237. [Google Scholar] [CrossRef]
- Bloch, F.; Moller, C. Recoil by β-decay. Nature 1935, 136, 911–912. [Google Scholar] [CrossRef]
- Hamilton, D.R. Electron-Neutrino Angular Correlation in Beta-Decay. Phys. Rev. 1947, 71, 456–457. [Google Scholar] [CrossRef]
- Sherwin, C.W. Momentum Conservation in the Beta-Decay of P32 and the Angular Correlation of Neutrinos with Electrons. Phys. Rev. 1948, 73, 216–225. [Google Scholar] [CrossRef]
- Sherwin, C.W. The Conservation of Momentum in the Beta-Decay of Y90. Phys. Rev. 1948, 73, 1173–1177. [Google Scholar] [CrossRef]
- Hornyak, W.F.; Lauritsen, T.; Morrison, P.; Fowler, W.A. Energy Levels of Light Nuclei. III. Rev. Mod. Phys. 1950, 22, 291–372. [Google Scholar] [CrossRef]
- Pruett, J.R. H3 and the Mass of the Neutrino. Phys. Rev. 1948, 73, 1219. [Google Scholar]
- Curran, S.C.; Angus, J.; Cockroft, A.L. Beta Spectrum of Tritium. Nature 1948, 162, 302–303. [Google Scholar] [CrossRef] [PubMed]
- Curran, S.C.; Angus, J.; Cockroft, A.L., III. Investigation of soft radiations–II. The beta spectrum of tritium. Philos. Mag. J. Sci. 1949, 40, 53–60. [Google Scholar] [CrossRef]
- Curran, S.C.; Angus, J.; Cockroft, A.L. The Beta-Spectrum of Tritium. Phys. Rev. 1949, 76, 853–854. [Google Scholar] [CrossRef]
- Hanna, G.C.; Pontecorvo, B. The β-Spectrum of H3. Phys. Rev. 1949, 75, 983–984. [Google Scholar] [CrossRef]
- Hanna, G.C.; Kirkwood, D.H.W.; Pontecorvo, B. High Multiplication Proportional Counters for Energy Measurements. Phys. Rev. 1949, 75, 985–986. [Google Scholar] [CrossRef]
- Langer, L.M.; Moffat, R.J.D. The Beta-Spectrum of Tritium and the Mass of the Neutrino. Phys. Rev. 1952, 88, 689–694. [Google Scholar] [CrossRef]
- Owen, G.E.; Primakoff, H. Relation between Apparent Shapes of Monoenergetic Conversion Lines and of Continuous β-Spectra in a Magnetic Spectrometer. Phys. Rev. 1948, 74, 1406–1412. [Google Scholar] [CrossRef]
- Owen, G.E.; Primakoff, H. Relation between Apparent Shapes of Monoenergetic Conversion Lines and Continuous Beta-Spectra in a Magnetic Spectrometer. II. Rev. Sci. Instruments 1950, 21, 447–450. [Google Scholar] [CrossRef]
- Hamilton, D.R.; Alford, W.P.; Gross, L. Upper Limits on the Neutrino Mass from the Tritium Beta Spectrum. Phys. Rev. 1953, 92, 1521–1525. [Google Scholar] [CrossRef]
- Hamilton, D.R.; Gross, L. An Electrostatic Beta-Spectrograph. Rev. Sci. Instruments 1950, 21, 912–917. [Google Scholar] [CrossRef] [PubMed]
- Lillie, A.B.; Conner, J.P. Preparation of Thin Tritium Targets. Rev. Sci. Instrum. 1951, 22, 210–211. [Google Scholar] [CrossRef]
- Salgo, R.C.; Staub, H.H. Re-determination of the β-energy of tritium and its relation to the neutrino rest mass and the Gamow-Teller matrix element. Nucl. Phys. A 1969, 138, 417–428. [Google Scholar] [CrossRef]
- Daris, R.; St-Pierre, C. Beta decay of tritium. Nucl. Phys. A 1969, 138, 545–555. [Google Scholar] [CrossRef]
- Bergkvist, K.E. A high-luminosity, high-resolution study of the end-point behaviour of the tritium beta-spectrum (i). basic experimental procedure and analysis with regard to neutrino mass and neutrino degeneracy. Nucl. Phys. B 1972, 39, 317–370. [Google Scholar] [CrossRef]
- Bergkvist, K.E. A high-luminosity, high-resolution study of the end-point behaviour of the tritium beta-spectrum (ii). the end-point energy of the spectrum. comparison of the experimental axial-vector matrix element with predictions based on pcac. Nucl. Phys. B 1972, 39, 371–406. [Google Scholar] [CrossRef]
- Bergkvist, K.E. On Some Atomic Effects in the Tritium β-Spectrum. Phys. Scr. 1971, 4, 23–31. [Google Scholar] [CrossRef]
- Röde, B.; Daniel, H. Measurement of the 3H β-ray spectrum and determination of an upper limit for the electron-antineutrino rest mass. Lett. Nuovo C. 1972, 5, 139–143. [Google Scholar] [CrossRef]
- Simpson, J.J. Measurement of the β-energy spectrum of 3H to determine the antineutrino mass. Phys. Rev. D 1981, 23, 649–662. [Google Scholar] [CrossRef]
- Wang, K.C. A Suggestion on the Detection of the Neutrino. Phys. Rev. 1942, 61, 97. [Google Scholar] [CrossRef]
- Rumbaugh, L.H.; Roberts, R.B.; Hafstad, L.R. Nuclear Transmutations of the Lithium Isotope. Phys. Rev. 1938, 54, 657–680. [Google Scholar] [CrossRef]
- Zaffarano, D.J.; Kern, B.D.; Mitchell, A.C.G. Energy of the Be7 Gamma-Ray. Phys. Rev. 1948, 74, 105–106. [Google Scholar] [CrossRef]
- Allen, J.S. Experimental Evidence for the Existence of a Neutrino. Phys. Rev. 1942, 61, 692–697. [Google Scholar] [CrossRef]
- Smith, P.B.; Allen, J.S. Nuclear Recoils Resulting from the Decay of Be7*. Phys. Rev. 1951, 81, 381–385. [Google Scholar] [CrossRef]
- Davis, R. Nuclear Recoil Following Neutrino Emission from Beryllium 7*. Phys. Rev. 1952, 86, 976–985. [Google Scholar] [CrossRef]
- Richards, H.T.; Smith, R.V.; Browne, C.P. Proton-Neutron Reactions and Thresholds. Phys. Rev. 1950, 80, 524–530. [Google Scholar] [CrossRef]
- Taschek, R.F.; Jarvis, G.A.; Argo, H.V.; Hemmendinger, A. Neutron-Hydrogen Mass Difference from the T3(p, n)He3 Reaction Threshold. Phys. Rev. 1949, 75, 1268–1269. [Google Scholar] [CrossRef]
- Rodeback, G.W.; Allen, J.S. Neutrino Recoils Following the Capture of Orbital Electrons in A37. Phys. Rev. 1952, 86, 446–450. [Google Scholar] [CrossRef]
- Kofoed-Hansen, O. Neutrino Recoil Spectrometer. Investigation of A37. Phys. Rev. 1954, 96, 1045–1050. [Google Scholar] [CrossRef]
- Snell, A.H.; Pleasonton, F. Spectrometry of Recoils from Neutrino Emission in Argon-37. Phys. Rev. 1955, 97, 246–248. [Google Scholar] [CrossRef]
- Snell, A.H.; Pleasonton, F. Spectrometry of the Neutrino Recoils of Argon-37. Phys. Rev. 1955, 100, 1396–1403. [Google Scholar] [CrossRef]
- Alvarez, L.W.; Helmholz, A.C.; Wright, B.T. Recoil from K Capture. Phys. Rev. 1941, 60, 160. [Google Scholar]
- Wright, B.T. Recoil of Silver Nuclei Due to K-Capture in Cadmium. Phys. Rev. 1947, 71, 839–841. [Google Scholar] [CrossRef]
- Bradt, H.; Gugelot, P.C.; Huber, O.; Medicus, H.; Preiswerk, P.; Scherrer, P.; Steffen, R. Die Silberkerne Ag107 und Ag109. Helv. Phys. Acta 1946, 19, 218–219. [Google Scholar]
- Lubimov, V.A.; Novikov, E.G.; Nozik, V.Z.; Tretjakov, E.F.; Kosik, V.F. An estimate of the νe mass from the β-spectrum of tritium in the valine molecule. Phys. Lett. B 1980, 94, 266–268. [Google Scholar] [CrossRef]
- Lubimov, V.A.; Novikov, E.G.; Nozik, V.Z.; Tretjakov, E.F.; Kosik, V.F.; Myasoedov, N.F. Estimation of the neutrino rest mass from measurements of the tritium β spectrum. Sov. Phys. JETP 1981, 54, 616–628. [Google Scholar]
- Boris, S.; Golutvin, A.; Laptin, L.; Lubimov, V.A.; Nagovizin, V.; Novikov, E.G.; Nozik, V.Z.; Soloshenko, V.; Tihomirov, I.; Tretjakov, E.F. The neutrino mass from the tritium beta spectrum in valine. Phys. Lett. B 1985, 159, 217–222. [Google Scholar] [CrossRef]
- Boris, S.; Golutvin, A.; Laptin, L.; Lubimov, V.A.; Nagovizin, V.; Nozik, V.Z.; Novikov, E.G.; Soloshenko, V.; Tihomirov, I.; Tretjakov, E.F.; et al. Neutrino Mass from the Beta Spectrum in the Decay of Tritium. Phys. Rev. Lett. 1987, 58, 2019–2022, Erratum in Phys. Rev. Lett. 1988, 61, 245. [Google Scholar] [CrossRef] [PubMed]
- Fritschi, M.; Holzschuh, E.; Kuendig, W.; Petersen, J.W.; Pixley, R.E.; Stussi, H. An upper limit for the mass of from tritium β-decay. Phys. Lett. B 1986, 173, 485–489. [Google Scholar] [CrossRef]
- Holzschuh, E.; Fritschi, M.; Kuendig, W. Measurement of the electron-neutrino mass from tritium beta decay. Phys. Lett. B 1992, 287, 381–388. [Google Scholar] [CrossRef]
- Wilkerson, J.F.; Bowles, T.J.; Browne, J.C.; Maley, M.P.; Robertson, R.G.H.; Cohen, J.S.; Martin, R.L.; Knapp, D.A.; Helffrich, J.A. Limit on Mass from Free-Molecular-Tritium Beta Decay. Phys. Rev. Lett. 1987, 58, 2023–2026. [Google Scholar] [CrossRef] [PubMed]
- Robertson, R.G.H.; Bowles, T.J.; Stephenson, G.J.; Wark, D.L.; Wilkerson, J.F.; Knapp, D.A. Limit on mass from observation of the β-decay of molecular tritium. Phys. Rev. Lett. 1991, 67, 957–960. [Google Scholar] [CrossRef] [PubMed]
- Van Dyck, R.S.; Farnham, D.L.; Schwinberg, P.B. Tritium-helium-3 mass difference using the Penning trap mass spectroscopy. Phys. Rev. Lett. 1993, 70, 2888–2891. [Google Scholar] [CrossRef] [PubMed]
- Nagy, S.; Fritioff, T.; Björkhage, M.; Bergström, I.; Schuch, R. On the Q-value of the tritium β-decay. Europhys. Lett. 2006, 74, 404–410. [Google Scholar] [CrossRef]
- Lippmaa, E.; Pikver, R.; Suurmaa, E.; Past, J.; Puskar, J.; Koppel, I.; Tammik, A. Precise 3H-3He Mass Difference for Neutrino Mass Determination. Phys. Rev. Lett. 1985, 54, 285–288. [Google Scholar] [CrossRef] [PubMed]
- Stoeffl, W.; Decman, D.J. Anomalous Structure in the Beta Decay of Gaseous Molecular Tritium. Phys. Rev. Lett. 1995, 75, 3237–3240. [Google Scholar] [CrossRef] [PubMed]
- Kawakami, H.; Nisimura, K.; Ohshima, T.; Shibata, S.; Shoji, Y.; Sugai, I.; Ukai, K.; Yasuda, T.; Monikawa, N.; Nogawa, N. An upper limit for the mass of the electron anti-neutrino from the INS experiment. Phys. Lett. B 1987, 187, 198–204. [Google Scholar] [CrossRef]
- Kawakami, H.; Kato, S.; Naito, F.; Nisimura, K.; Ohshima, T.; Shibata, S.; Suzuki, T.; Ukai, K.; Morikawa, N.; Nogawa, N.; et al. Neutrino Mass and End Point Energy of 3H Beta Decay. J. Phys. Soc. Jpn. 1988, 57, 2873–2876. [Google Scholar] [CrossRef]
- Kawakami, H.; Kato, S.; Ohshima, T.; Shibata, S.; Ukai, K.; Morikawa, N.; Nogawa, N.; Haga, K.; Nagafuchi, T.; Shigeta, M.; et al. New upper bound on the electron anti-neutrino mass. Phys. Lett. B 1991, 256, 105–111. [Google Scholar] [CrossRef]
- Bodine, L.I.; Parno, D.S.; Robertson, R.G.H. Assessment of molecular effects on neutrino mass measurements from tritium beta decay. Phys. Rev. C 2015, 91, 035505. [Google Scholar] [CrossRef]
- Saenz, A.; Jonsell, S.; Froelich, P. Improved Molecular Final-State Distribution of HeT+ for the β-Decay Process of T2. Phys. Rev. Lett. 2000, 84, 242–245. [Google Scholar] [CrossRef]
- Doss, N.; Tennyson, J.; Saenz, A.; Jonsell, S. Molecular effects in investigations of tritium molecule β decay endpoint experiments. Phys. Rev. C 2006, 73, 025502. [Google Scholar] [CrossRef]
- Froelich, P.; Jeziorski, B.; Kokos, W.; Monkhorst, H.; Saenz, A.; Szalewicz, K. Probability distribution of excitations to the electronic continuum of HeT+ following the β decay of the T2 molecule. Phys. Rev. Lett. 1993, 71, 2871–2874. [Google Scholar] [CrossRef] [PubMed]
- Weinheimer, C.; Przynembel, M.; Backe, H.; Barth, H.; Bonn, J.; Degan, B.; Eding, T.; Fischer, H.; Fleischmann, L.; Gross, J.U.; et al. Improved limit on the electron anti-neutrino rest mass from tritium beta decay. Phys. Lett. B 1993, 300, 210–216. [Google Scholar] [CrossRef]
- Weinheimer, C.; Degenddag, B.; Bielle, A.; Bonn, J.; Bornschein, L.; Kazachenko, O.; Kovalik, A.; Otten, E.W. High precision measurement of the tritium β spectrum near its endpoint and upper limit on the neutrino mass. Phys. Lett. B 1999, 460, 219–226. [Google Scholar] [CrossRef]
- Belesev, A.I.; Bleule, A.I.; Geraskin, E.V.; Golubev, A.A.; Golubev, N.A.; Kazachenko, O.V.; Kiev, E.P.; Kuznetsov, Y.E.; Lobashev, B.M.; Ovchinnikov, B.M.; et al. Results of the Troitsk experiment on the search for the electron antineutrino rest mass in tritium beta-decay. Phys. Lett. B 1995, 350, 263–272. [Google Scholar] [CrossRef]
- Lobashev, V.M.; Assev, V.N.; Belesev, A.I.; Berlev, A.I.; Geraskin, E.V.; Golubev, A.A.; Kazachencko, O.V.; Kuznetsov, Y.E.; Ostroumov, R.P.; Rivkis, L.A.; et al. Direct search for mass of neutrino and anomaly in the tritium beta-spectrum. Phys. Lett. B 1999, 460, 227–235. [Google Scholar] [CrossRef]
- Kraus, C.; Bornschein, B.; Bornschein, L.; Bonn, J.; Flatt, B.; Kovalik, A.; Ostrick, B.; Otten, E.W.; Schall, J.P.; Thummier, T.; et al. Final results from phase II of the Mainz neutrino mass search in tritium β decay. Eur. Phys. J. C 2005, 40, 447–468. [Google Scholar] [CrossRef]
- Aseev, V.N.; Belesev, A.I.; Berlev, A.I.; Geraskin, E.V.; Golubev, A.A.; Likhovid, N.A.; Lobashev, V.M.; Nozik, A.A.; Pantuev, V.S.; Parfenov, V.I.; et al. Upper limit on the electron antineutrino mass from the Troitsk experiment. Phys. Rev. D 2011, 84, 112003. [Google Scholar] [CrossRef]
- Hsu, T.; Hirshfield, J.L. Electrostatic energy analyser using a nonuniform axial magnetic field. Rev. Sci. Instruments 1976, 47, 236–238. [Google Scholar] [CrossRef]
- Beamson, G.; Porter, H.Q.; Turner, D.W. The collimating and magnifying properties of a superconducting field photolectron spectrometer. J. Phys. E Sci. Instruments 1980, 13, 64–66. [Google Scholar] [CrossRef]
- Kruit, P.; Read, F.H. Magnetic field paralleliser for 2π electron-spectrometer and electron-image amplifier. J. Phys. E Sci. Instruments 1983, 16, 313–324. [Google Scholar] [CrossRef]
- Picard, A.; Backe, H.; Barth, H.; Bonn, J.; Degen, B.; Edling, T.; Haid, R.; Hermanni, A.; Leiderer, P.; Loeken, T.; et al. A solenoid retarding spectrometer with high resolution and transmission for keV electrons. Nucl. Instrum. Methods B 1992, 63, 345–358. [Google Scholar] [CrossRef]
- Lobashev, V.M. The search for the neutrino mass by direct method in the tritium beta-decay and perspectives of study it in the project KATRIN. Nucl. Instruments Methods A 2003, 719, 153–160. [Google Scholar] [CrossRef]
- Kleesiek, M.; Behrens, J.; Drexlin, G.; Eitel, K.; Erhard, M.; Formaggio, J.A.; Glück, F.; Groh, S.; Hötzel, M.; Mertens, S.; et al. β-Decay Spectrum, Response Function and Statistical Model for Neutrino Mass Measurements with the KATRIN Experiment. Eur. Phys. J. C 2019, 79, 204. [Google Scholar] [CrossRef]
- Angrik, J. KATRIN Design Report 2004; Wissenschaftliche Berichte, FZ Karlsruhe 7090; Forschungszentrum Jülich: Jülich, Germany, 2005. [Google Scholar]
- Aker, M. et al. [KATRIN Collaboration] Improved Upper Limit on the Neutrino Mass from a Direct Kinematic Method by KATRIN. Phys. Rev. Lett. 2019, 123, 221802. [Google Scholar] [CrossRef] [PubMed]
- Monreal, B.; Formaggio, J.A. Relativistic cyclotron radiation detection of tritium decay electrons as a new technique for measuring the neutrino mass. Phys. Rev. D 2009, 80, 051301. [Google Scholar] [CrossRef]
- Ashtari Esfahani, A. et al. [Project 8 Collaboration] Determining the neutrino mass with cyclotron radiation emission spectroscopy–Project 8. J. Phys. G 2017, 44, 054004. [Google Scholar] [CrossRef]
- Ashtari Esfahani, A. et al. [Project 8 Collaboration] Electron radiated power in cyclotron radiation emission spectroscopy experiments. Phys. Rev. C 2019, 99, 055501. [Google Scholar] [CrossRef]
- Asner, D.M. et al. [Project 8 Collaboration] Single-Electron Detection and Spectroscopy via Relativistic Cyclotron Radiation. Phys. Rev. Lett. 2015, 114, 162501. [Google Scholar] [CrossRef]
- Formaggio, J.A. Project 8: Using Radio-Frequency Techniques to Measure Neutrino Mass. Nucl. Phys. B Proc. Suppl. 2012, 229-232, 371–375. [Google Scholar] [CrossRef]
- Ferri, E. et al. [MARE Collaboration] The Status of the MARE Experiment with 187Re and 187Ho Isotopes. Phys. Procedia 2015, 61, 227–231. [Google Scholar] [CrossRef]
- De Rujula, A.; Lusignoli, M. Calorimetric measurements of 163 holmium decay as tools to determine the electron neutrino mass. Phys. Lett. B 1982, 118, 429–434. [Google Scholar] [CrossRef][Green Version]
- Brodzinski, R.L.; Conway, D.C. Decay of rhenium-187. Phys. Rev. 1965, 138, B1368–B1371. [Google Scholar] [CrossRef]
- Huster, E.; Verbeek, H. Das β-spektrum des natürlichen rhenium 187. Z. Phys. 1967, 203, 435–442. [Google Scholar] [CrossRef]
- Cosulich, E.; Gallinaro, G.; Gatti, F.; Vitale, S. Detection of 187Re beta decay with a cryogenic microcalorimeter. Preliminary results. Phys. Lett. B 1992, 295, 143–147. [Google Scholar] [CrossRef]
- Gatti, F.; Fontanelli, F.; Galeazzi, M.; Swift, A.M.; Vitale, S. Detection of environmental fine structure in the low-energy beta-decay spectrum of 187Re. Nature 1999, 307, 137–139. [Google Scholar] [CrossRef]
- Arnaboldi, C. et al. [MiBETA Collaboration] Measurement of the p to s wave branching ratio of 187Re β decay from beta environmental fine structure. Phys. Rev. Lett. 2006, 96, 042503. [Google Scholar] [CrossRef] [PubMed]
- Sisti, M. et al. [MiBETA Collaboration] New limits from the Milano neutrino mass experiment with thermal microcalorimeters. Nucl. Instruments Methods A 2004, 520, 125–131. [Google Scholar] [CrossRef]
- Nucciotti, A. The MARE Project. J. Low Temp. Phys. 2008, 151, 597–602. [Google Scholar] [CrossRef]
- Hopke, P.K.; Evans, J.S.; Naumann, R.A. Decay of Ho163. Phys. Rev. 1968, 171, 1290–1292. [Google Scholar] [CrossRef]
- Bennett, C.L.; Hallin, A.L.; Naumann, R.A.; Springer, P.T.; Witherell, M.S.; Chrien, R.E.; Baisden, P.A.; Sisson, D.H. The X-ray spectrum following 163Ho M electron capture. Phys. Lett. B 1981, 107, 19–22. [Google Scholar] [CrossRef]
- De Rujula, A. A new way to measure neutrino mass. Nucl. Phys. B 1981, 188, 414–458. [Google Scholar] [CrossRef][Green Version]
- Springer, P.T.; Bennett, C.L.; Baisden, P.A. Measurement of the neutrino mass using the inner bremsstrahlung emitted in the electron-capture decay of 163Ho. Phys. Rev. A 1987, 35, 679–689. [Google Scholar] [CrossRef] [PubMed]
- Yasumi, S.; Maezawa, H.; Shima, K.; Inagaki, Y.; Mukoyama, T.; Mizogawa, T.; Sera, K.; Kishimoto, S.; Fujioka, M.; Ishi, K.; et al. The mass of the electron neutrino from electron capture in Ho-163. Phys. Lett. B 1994, 334, 229–233. [Google Scholar] [CrossRef]
- Velte, C.; Ahrens, F.; Barth, A.; Blaum, K.; Bras, M.; Door, M.; Dorner, H.; Dullmann, C.E.; Eliseev, S.; Enss, C.; et al. High-resolution and low-background 163Ho spectrum: Interpretation of the resonance tails. Eur. Phys. J. C 2019, 79, 1026. [Google Scholar] [CrossRef]
- Gallucci, G. et al. [HOLMES Collaboration] Status of the HOLMES experiment to directly measure the electron neutrino mass with a calorimetric approach. Proc. Sci. (NuFact2019) 2020, 369, 106. [Google Scholar]
- Croce, M. et al. [NUMECS Collaboration] Development of holmium-163 electron-capture spectroscopy with transition-edge sensors. J. Low Temp. Phys. 2016, 184, 958–968. [Google Scholar] [CrossRef]
- Primakoff, H.; Rosen, S.P. Double Beta Decay. Rep. Prog. Phys. 1959, 22, 121–166. [Google Scholar] [CrossRef]
- Zdesenko, Y.G. The future of double beta decay research. Rev. Mod. Phys. 2002, 74, 663–684. [Google Scholar] [CrossRef]
- Vergados, J.D.; Ejiri, H.; Simkovic, F. Neutrinoless double beta decay and neutrino mass. Int. J. Mod. Phys. E 2016, 25, 1630007. [Google Scholar] [CrossRef]
- Engel, J.; Menéndez, J. Status and future of nuclear matrix elements for neutrinoless double-Beta decay: A review. Rep. Prog. Phys. 2017, 80, 046301. [Google Scholar] [CrossRef] [PubMed]
- Jones, B. The Physics of Neutrinoless Double Beta Decay: A Beginners Guide. Proc. Sci. (TASI2020) 2021, 388, 007. [Google Scholar]
- Simkovic, F.; Krivoruchenko, M.I.; Faessler, A. Neutrinoless double-beta decay and double-electron capture. Prog. Part. Nucl. Phys. 2011, 66, 446–451. [Google Scholar] [CrossRef]
- Blaum, K.; Eliseev, S.; Danevich, F.A.; Tretyak, V.I.; Kovalenko, S.; Krivoruchenko, M.I.; Novikov, Y.N.; Suhonen, J. Neutrinoless Double-Electron Capture. Rev. Mod. Phys. 2020, 92, 045007. [Google Scholar] [CrossRef]
- Goeppert-Mayer, M. Double Beta-Disintegration. Phys. Rev. 1935, 48, 512–516. [Google Scholar] [CrossRef]
- Furry, W.H. Note on the Theory of the Neutral Particle. Phys. Rev. 1938, 54, 56–67. [Google Scholar] [CrossRef]
- Racah, G. Sulla simmetria tra particelle e antiparticelle. Il Nuovo C. 1937, 14, 322–328. [Google Scholar] [CrossRef]
- Pontecorvo, B. Fifty years of neutrino physics: A Few Episodes. Priroda 1983, 1, 43. [Google Scholar]
- Caianiello, E.R. An Argument Against the Majorana Theory of Neutral Particles. Phys. Rev. 1952, 86, 564–565. [Google Scholar] [CrossRef]
- Fireman, E.L. Double Beta Decay. Phys. Rev. 1948, 74, 1238. [Google Scholar]
- Fireman, E.L. A measurement of the Half-Life of Double Beta-Decay from 50Sn124. Phys. Rev. 1949, 75, 323–324. [Google Scholar] [CrossRef]
- Kalkstein, M.I.; Libby, W.F.S. An investigation of the Double Beta-Decay of 50Sn124. Phys. Rev. 1952, 85, 368–369. [Google Scholar] [CrossRef]
- Pearce, R.W.; Darby, E.R. Double beta-decay of Sn124. Phys. Rev. 1952, 86, 1049–1050. [Google Scholar] [CrossRef]
- Fireman, E.L.; Schwarzer, D. A Re-Investigation of the Double Beta-Decay from Sn124. Phys. Rev. 1952, 86, 451–453. [Google Scholar] [CrossRef]
- McCarthy, J.A. Search for Double Beta-Decay in Sn124 and Zr96. Phys. Rev. 1953, 90, 853–856. [Google Scholar] [CrossRef]
- Tretyak, V.I. False Starts in History of Searches for 2β Decay, or Discoverless Double Beta Decay. AIP Conf. Proc. 2011, 1417, 129–133. [Google Scholar]
- Fremlin, J.H.; Walters, M.C. An Experimental Investigation of the Stability of Nuclei against Double Beta-Disintegration. Proc. Phys. Soc. London, Sect. A 1952, 65, 911–915. [Google Scholar] [CrossRef]
- Berthelot, M.M.A.; Chaminade, R.; Levi, C.; Papineau, L.; Joliot, F. Recherche d’une double capture K dons le zinc (64). Comptes Rendus 1953, 236, 1769–1772. [Google Scholar]
- Winter, R.G. Search for Double Beta Decay in Cadmium and Molybdenum. Phys. Rev. 1955, 99, 88–91. [Google Scholar] [CrossRef]
- Georgi, H.; Glasjow, S.L.; Nussinov, S. Unconventional model of neutrino masses. Nucl. Phys. B 1981, 193, 297–316. [Google Scholar] [CrossRef]
- Voloshin, M.B.; Mitsel’maker, G.V.; Eramzhyan, R.A. Conversion of an atomic electron into a positron and double β+ decay. JETP Lett. 1982, 35, 656–659. [Google Scholar]
- Bernabeu, J.; De Rujula, A.; Jarlskog, C. Neutrinoless double electron capture as a tool to measure the electron neutrino mass. Nucl. Phys. B 1983, 223, 15–28. [Google Scholar] [CrossRef]
- Inghram, M.G.; Reynolds, J.H. On the Double Beta-Process. Phys. Rev. 1949, 76, 1265–1266. [Google Scholar] [CrossRef]
- Inghram, M.G.; Reynolds, J.H. Double Beta-Decay of Te120. Phys. Rev. 1950, 78, 822–823. [Google Scholar] [CrossRef]
- Levine, C.B.; Griorso, A.; Seaborg, G.T. The title of the cited article. Phys. Rev. 1950, 77, 296. [Google Scholar] [CrossRef]
- Greuling, E.; Whitten, R.C. Lepton Conservation and Double Beta-Decay. Ann. Phys. 1960, 11, 510–533. [Google Scholar] [CrossRef]
- der Mateosian, E.; Goldhaber, M. Limits for Lepton-Conserving and Lepton-Nonconserving Double Beta Decay in Ca48. Phys. Rev. 1966, 146, 810–815. [Google Scholar] [CrossRef]
- Fiorini, E.; Pullia, A.; Bertolini, G.; Cappellani, F.; Restelli, G. A search for lepton non-conservation in double beta decay with a germanium detector. Phys. Lett. B 1967, 25, 602–603. [Google Scholar] [CrossRef]
- Fiorini, E.; Pullia, A.; Bertolini, G.; Cappellani, F.; Restelli, G. Neutrinoless double-beta decay of 76Ge. Il Nuovo Cimento A 1973, 13, 747–763. [Google Scholar] [CrossRef]
- Bardin, R.K.; Gollon, P.J.; Ullman, J.D.; Wu, C.S. Double beta decay in 48Ca and the conservation of leptons. Phys. Lett. B 1967, 26, 112–116. [Google Scholar] [CrossRef]
- Cleveland, B.T.; Leo, W.R.; Wu, C.S.; Kasday, L.R.; Rushton, A.M.; Gollon, P.J.; Ullman, J.D. Lepton Conservation in the Double β Decay of 82Se. Phys. Rev. Lett. 1975, 35, 757–760. [Google Scholar] [CrossRef]
- Takaoka, N.; Ogata, K. The half-life of Te-130 double beta-decay. Z. Naturforsch. A 1966, 21, 84–90. [Google Scholar] [CrossRef]
- Kirsten, T.; Gentner, W.; Muller, O. Isotopenanalyse der Edelgase in einem Tellurerz von Boliden (Schweden). Z. Naturforsch. A 1967, 22, 1783–1792. [Google Scholar] [CrossRef]
- Kirsten, T.; Gentner, W.; Schaeffer, O.A. Massenspektrometrischer Nachweis von ββ-Zerfallsprodukten. Z. Phys. 1967, 202, 273–292. [Google Scholar] [CrossRef]
- Hennecke, E.W.; Manuel, O.K.; Sabu, D.D. Double beta decay of 128Te. Phys. Rev. C 1975, 11, 1378–1384. [Google Scholar] [CrossRef]
- Bilenky, S.M.; Pontecorvo, B. Again on Neutrino Oscillations. Lett. Nuovo C. 1976, 17, 569–574. [Google Scholar] [CrossRef]
- Konetschny, W.; Kummer, W. Nonconservation of Total Lepton Number with Scalar Bosons. Phys. Lett. B 1977, 70, 433–435. [Google Scholar] [CrossRef]
- Fukugita, M.; Yanagida, T. Baryogenesis without ground unification. Phys. Lett. B 1986, 174, 45–47. [Google Scholar] [CrossRef]
- Gomez-Cadenas, J.J.; Martin-Albo, J.; Sorel, M.; Ferrario, P.; Monrabal, F.; Munoz-Vidal, J.; Novella, P.; Poves, A. Sense and sensitivity of double beta decay experiments. J. Cosmol. Astropart. Phys. 2011, 2011, 007. [Google Scholar] [CrossRef]
- Dolinski, M.J.; Poon, A.W.; Rodejohann, W. Neutrinoless double-beta decay: Status and prospects. Annu. Rev. Nucl. Part. Sci. 2019, 69, 219–251. [Google Scholar] [CrossRef]
- Caldwell, D.O. Double Beta Decay-Present and Future. J. Phys. G Nucl. Part. Phys. 1991, 17, S137–S144. [Google Scholar] [CrossRef]
- Vasenko, A.A.; Kirpichnikov, I.V.; Kuznetsov, A.A.; Starostin, A.S.; Dzhanian, A.G.; Markosian, G.E.; Oganesian, V.M.; Pogosov, V.S.; Tamanian, A.G.; Shakhazizian, S.R. New Results in the ITEP/YePI Double Beta-Decay Experiment with Enriched Germanium Detectors. Mod. Phys. Lett. A 1990, 5, 1299–1306. [Google Scholar] [CrossRef]
- Klapdor-Kleingrothaus, H.V. et al. [HEIDELBERG-MOSCOW Collaboration] Latest results from the HEIDELBERG-MOSCOW double beta decay experiment. Eur. Phys. J. A 2001, 12, 147–154. [Google Scholar] [CrossRef]
- Aalseth, C.E. et al. [IGEX Collaboration] IGEX 76Ge neutrinoless double-beta decay experiment: Prospects for next generation experiments. Phys. Rev. D 2002, 65, 092007. [Google Scholar] [CrossRef]
- Barabash, A.S.; Brudanin, V.B. Investigation of Double-Beta Decay with the NEMO-3 Detector. Phys. At. Nucl. 2011, 74, 312–317. [Google Scholar] [CrossRef]
- Andreotti, E. et al. [CUORICINO Collaboration] 130Te neutrinoless double-beta decay with CUORICINO. Astroparticle Physics 2011, 34, 822–831. [Google Scholar] [CrossRef]
- Bollen, G. First absolute mass measurement of short-lived isotopes. Hyperfine Interact. 1987, 38, 793–802. [Google Scholar] [CrossRef][Green Version]
- Blaum, K. High-accuracy mass spectrometry with stored ions. Phys. Rep. 2006, 425, 1–78. [Google Scholar] [CrossRef]
- Blaum, K.; Dilling, J.; Nörtershäuser, W. Precision atomic physics techniques for nuclear physics with radioactive beams. Phys. Scr. T 2013, 152, 014017. [Google Scholar] [CrossRef]
- Kretzschmar, M. Theoretical investigations of different excitation modes for Penning trap mass spectrometry. Int. J. Mass Spectrom. 2013, 349-350, 227–239. [Google Scholar] [CrossRef]
- Eliseev, S.; Blaum, K.; Block, M.; Droese, C.; Goncharov, M.; Minaya Ramirez, E.; Nesterenko, D.A.; Novikov, Y.N.; Schweikhard, L. Phase-Imaging Ion-Cyclotron-Resonance Measurements for Short-Lived Nuclides. Phys. Rev. Lett. 2013, 110, 082501. [Google Scholar] [CrossRef] [PubMed]
- Abgrall, N. et al. [LEGEND Collaboration] The large enriched germanium experiment for neutrinoless double beta decay (LEGEND). AIP Conf. Proc. 2017, 1894, 020027. [Google Scholar]

| Group and Date | Spectrometer | Mass (eV) |
|---|---|---|
| Curran et al., 1949 [111] | Proportional Counter | <1000 |
| Hanna, Pontecorvo 1949 [112] | Proportional Counter | <500 |
| Langer, Moffat 1952 [114] | Magnetic | <250 |
| Hamilton et al., 1953 [117] | Electrostatic | <200 |
| Daris, St. Pierre 1969 [121] | Magnetic | <75 |
| Bergkvist 1972 [122,123] | Magnetic | <55 |
| ITEP 1980 [142,143] | Magnetic | = |
| Simpson 1981 [126] | Si(Li) | <65 |
| Zurich 1986 [146] | Magnetic | <18 |
| ITEP 1987 [145] | Magnetic | = |
| LANL 1987 [148] | Magnetic | <27 |
| INS 1991 [156] | Magnetic | <13 |
| LANL 1991 [149] | Magnetic | <9.3 |
| Mainz 1993 [161] | MAC-E | <7.2 |
| Troitsk 1994 [163] | MAC-E | <4.35 |
| Mainz 2005 [165] | MAC-E | <2.3 |
| Troitsk 2011 [166] | MAC-E | <2.05 |
| KATRIN 2020 [174] | MAC-E | <1.1 |
| Group and Date | Isotope | Half-Life Bound (yr) |
|---|---|---|
| Mateosian, Goldhaber 1966 [226] | 48Ca | > |
| Fiorini et al., 1967 [227] | 76Ge | > |
| Bardin et al., 1967 [229] | 48Ca | > |
| Fiorini et al., 1973 [228] | 76Ge | > |
| Cleveland et al., 1975 [230] | 82Se | > |
| Caldwell 1989 [240] | 76Ge | > |
| ITEP-ErPI 1990 [241] | 76Ge | > |
| Heidelberg-Moscow 2001 [242] | 76Ge | > |
| IGEX 2002 [243] | 76Ge | > |
| NEMO-3 2010 [244] | 100Mo | > |
| CUORICINO 2011 [245] | 130Te | > |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Di Grezia, E.; Esposito, S.; Naddeo, A. Measuring a Mass: The Puzzling History of an Elusive Particle. Universe 2024, 10, 317. https://doi.org/10.3390/universe10080317
Di Grezia E, Esposito S, Naddeo A. Measuring a Mass: The Puzzling History of an Elusive Particle. Universe. 2024; 10(8):317. https://doi.org/10.3390/universe10080317
Chicago/Turabian StyleDi Grezia, Elisabetta, Salvatore Esposito, and Adele Naddeo. 2024. "Measuring a Mass: The Puzzling History of an Elusive Particle" Universe 10, no. 8: 317. https://doi.org/10.3390/universe10080317
APA StyleDi Grezia, E., Esposito, S., & Naddeo, A. (2024). Measuring a Mass: The Puzzling History of an Elusive Particle. Universe, 10(8), 317. https://doi.org/10.3390/universe10080317






