Direct and Indirect Measurements of the 19F(p,α)16O Reaction at Astrophysical Energies Using the LHASA Detector and the Trojan Horse Method
Abstract
1. Introduction
2. Direct Approach: The LHASA Detector
3. Indirect Approach: Trojan Horse Method
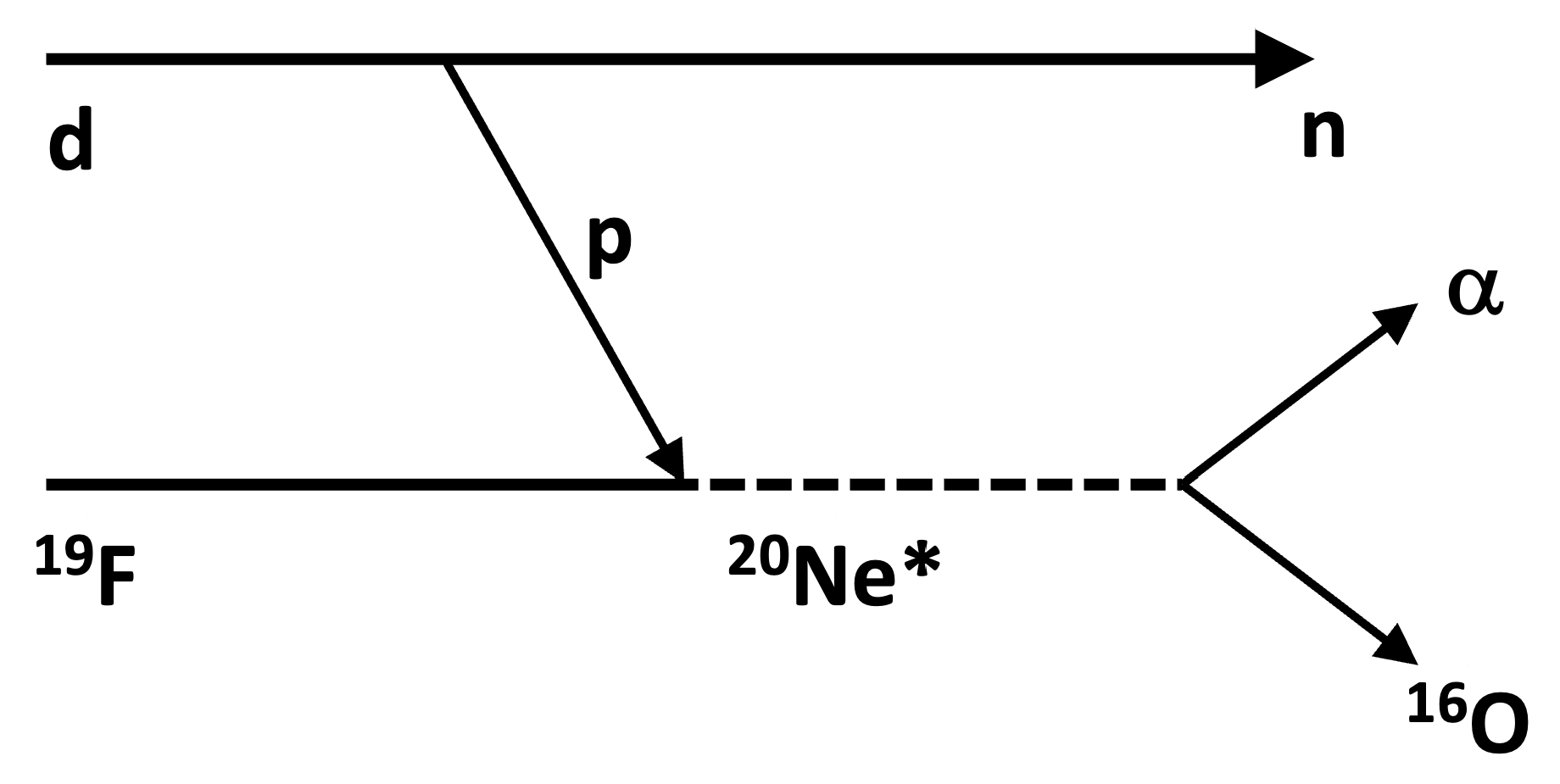
3.1. (p,)16O via THM
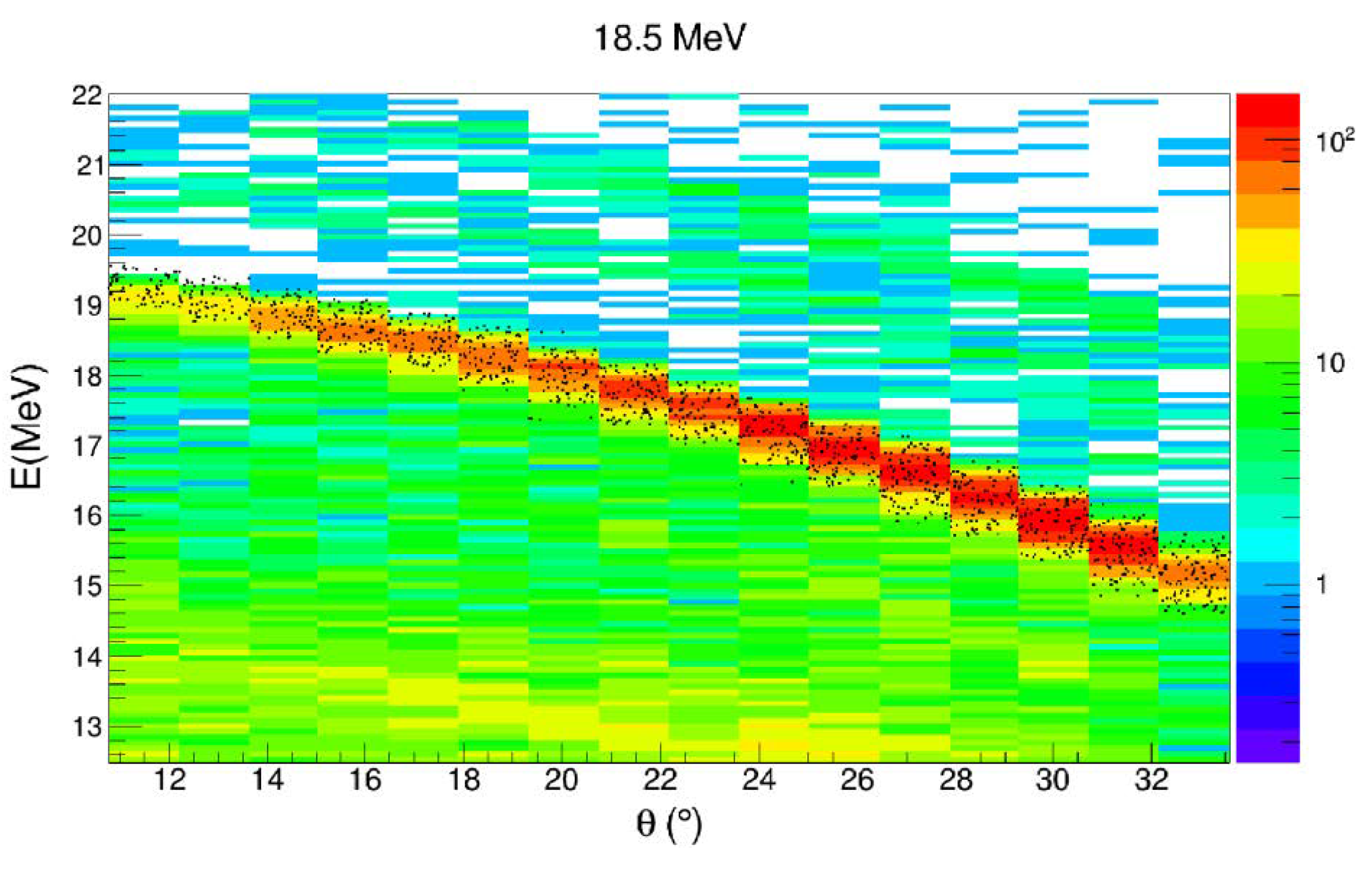
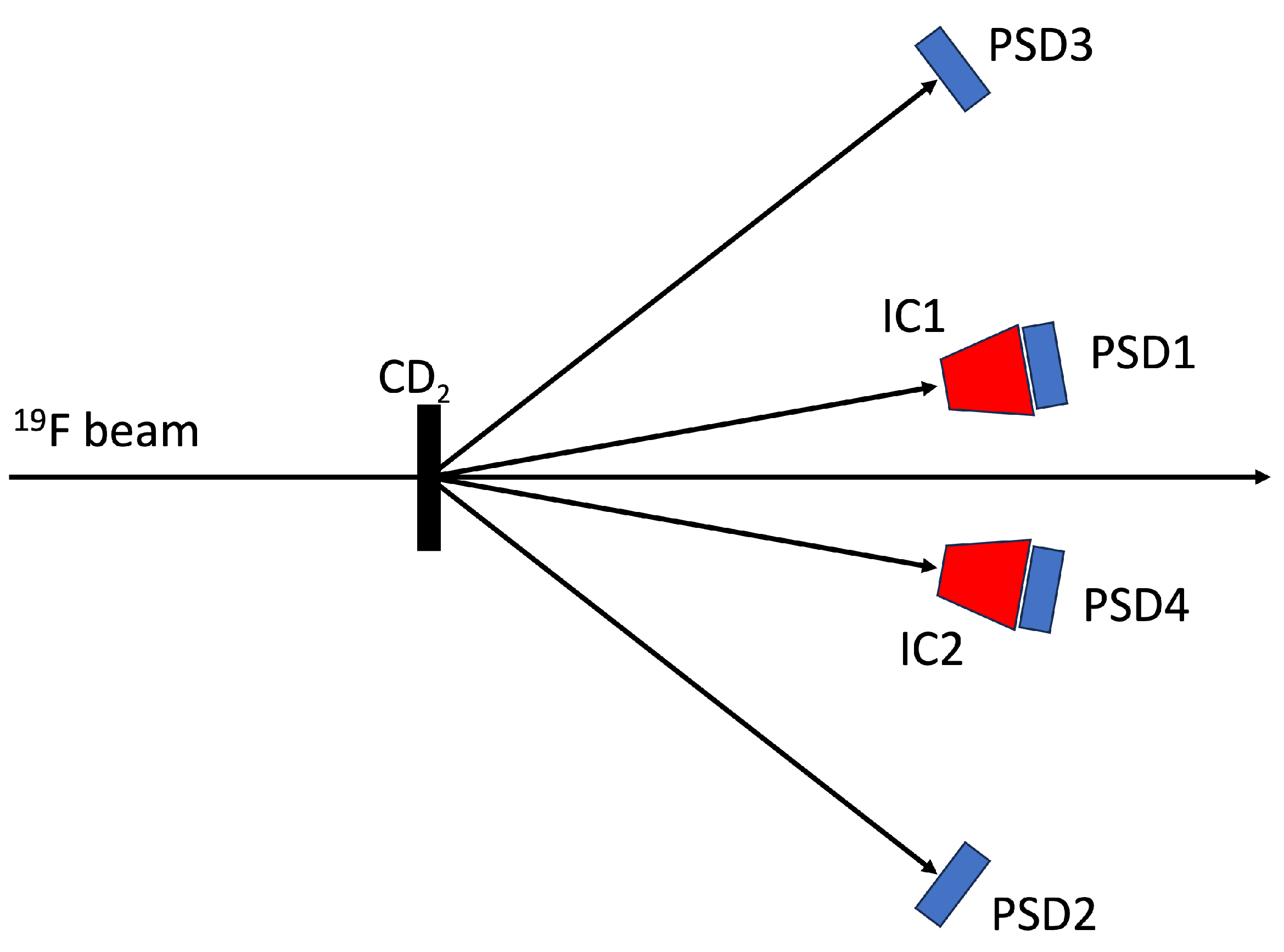
3.1.1. Experimental Setup
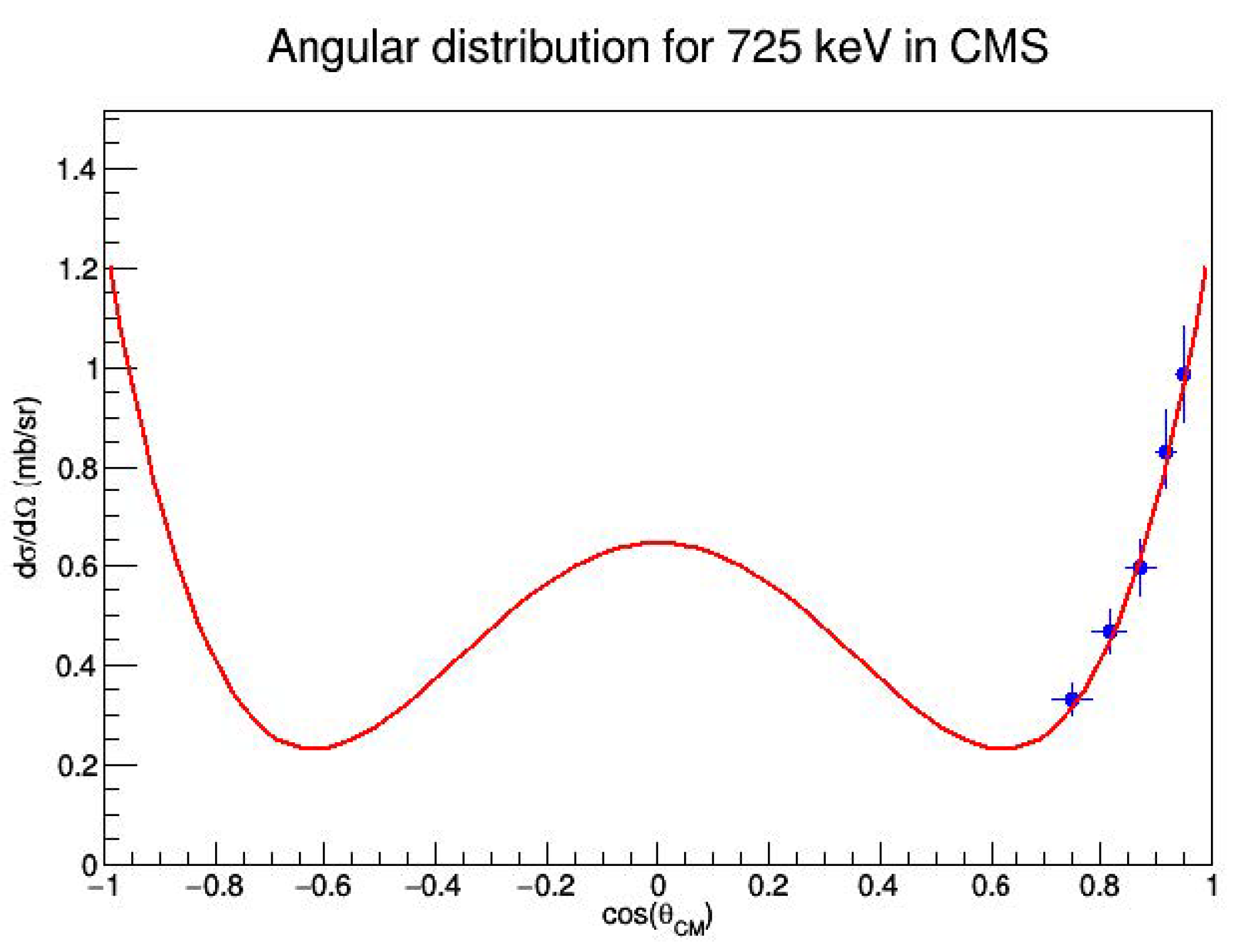
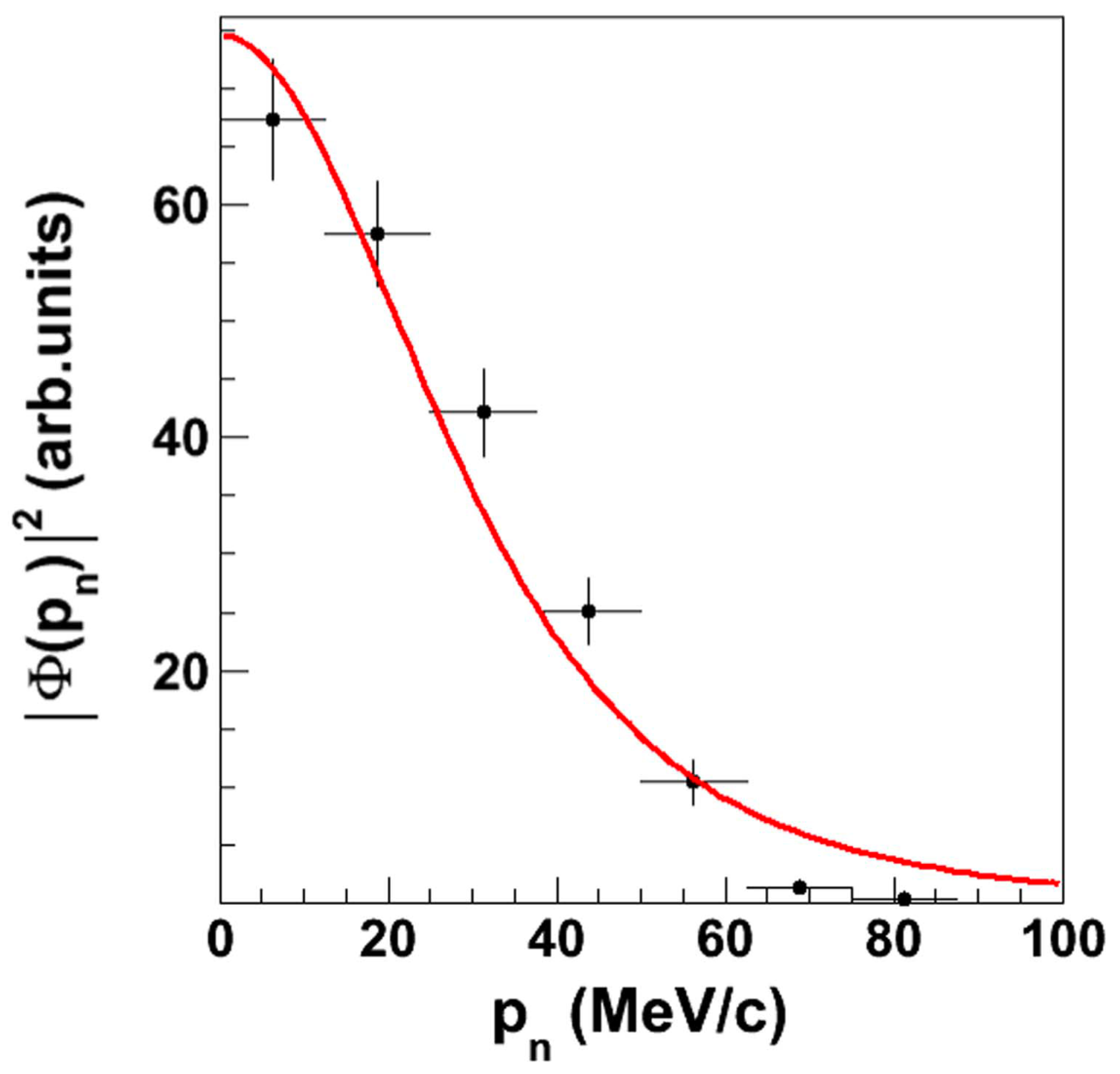
3.1.2. Selection of the Reaction Channel and Mechanism
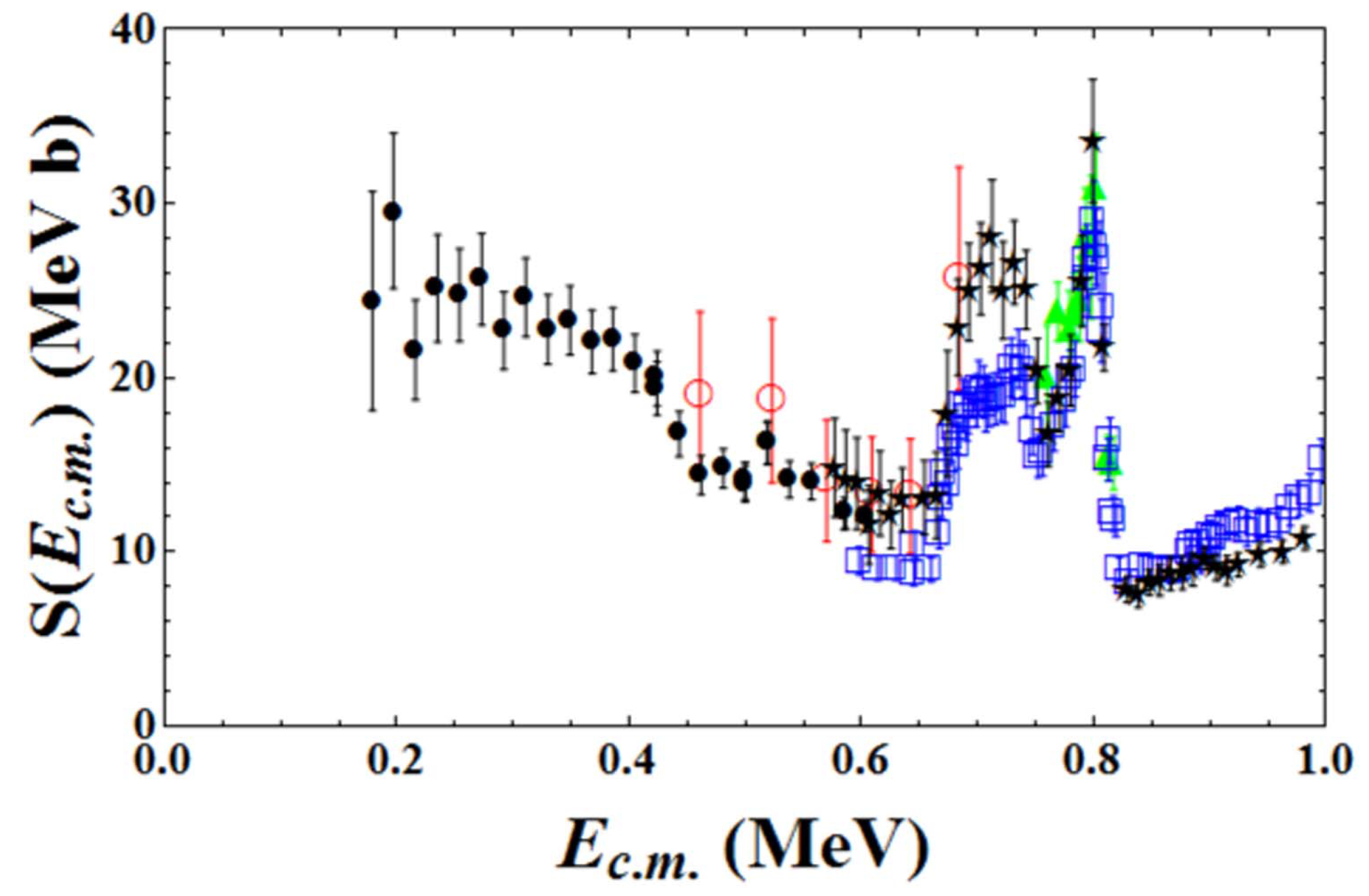
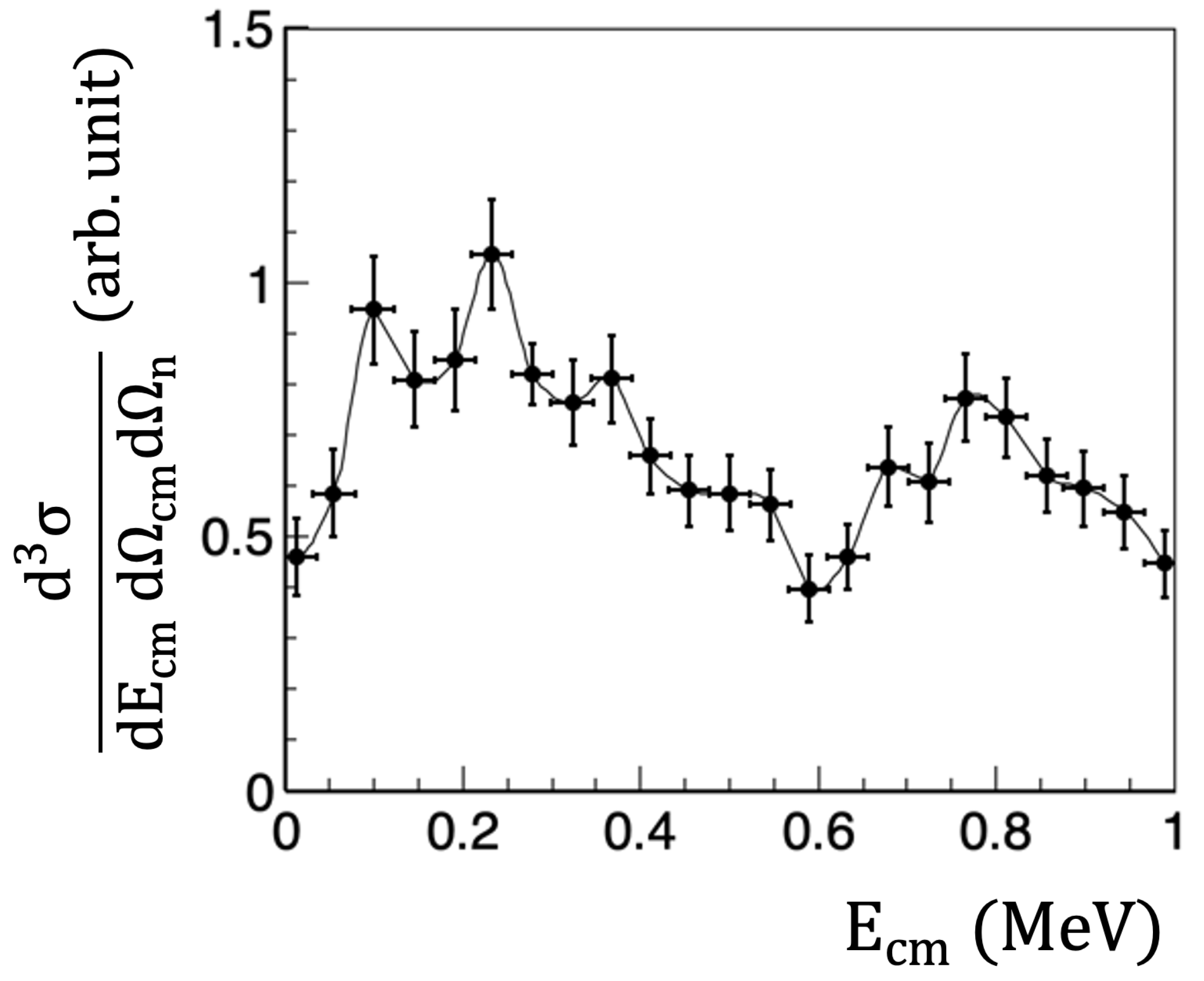
3.1.3. Extraction of the Astrophysical S(E)-Factor
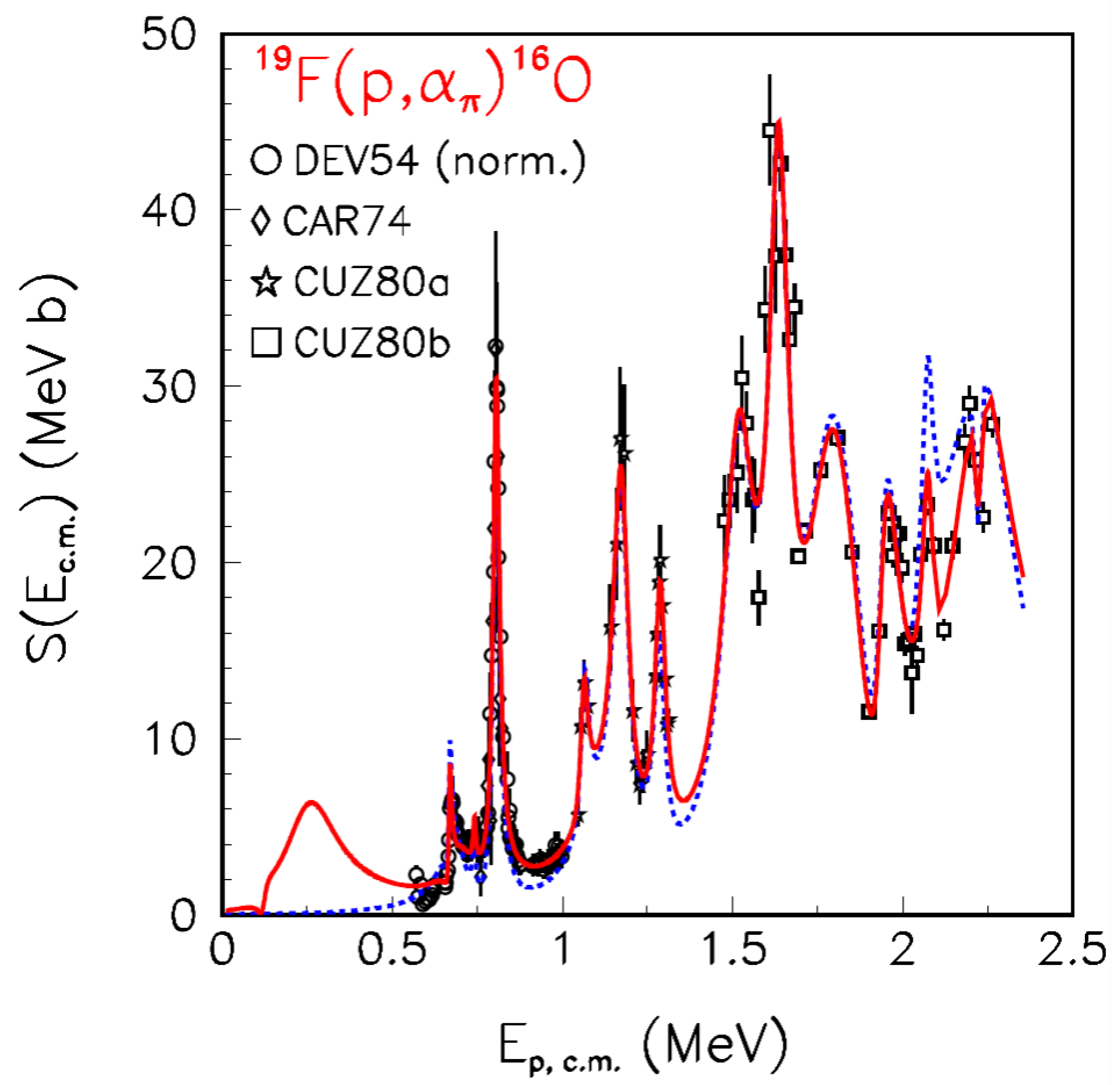
4. Direct Data and THM Data: Comparison
4.1. Direct Approach: LHASA + ELISSA Detectors
4.2. Indirect Approach via THM
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cristallo, S.; Straniero, O.; Gallino, R.; Piersanti, L.; Domínguez, I.; Lederer, M.T. Evolution, nucleosynthesis and yields of low-mass Asymptotic Giant Branch stars at different metallicities. Astrophys. J. 2009, 696, 797. [Google Scholar] [CrossRef]
- Jonsson, H.; Ryde, N.; Spitoni, E.; Matteucci, F.; Cunha, K.; Smith, V.; Hinkle, K.; Schultheis, M. Fluorine in the solar neighborhood: No evidence for the neutrino process. Astrophys. J. 2017, 835, 50. [Google Scholar] [CrossRef]
- Abia, C.; Cunha, K.; Cristallo, S.; Laverny, P. The origin of fluorine: Abundances in AGB carbon stars revisited. A&A 2015, 581, A88. [Google Scholar]
- Lugaro, M.; Ugalde, C.; Karakas, A.I.; Gorres, J.; Wiescher, M.; Lattanzio, J.C.; Cannon, R.C. Reaction Rate Uncertainties and the Production of 19F in Asymptotic Giant Branch Stars. Astrophys. J. 2004, 615, 934. [Google Scholar] [CrossRef]
- Palmerini, S.; D’Agata, G.; La Cognata, M.; Indelicato, I.; Pizzone, R.G.; Trippella, O.; Vescovi, D. 19F(p, α)16O and 19F(α,p)22Ne Reaction Rate Measured via THM and Fluorine Nucleosynthesis in AGB stars. J. Phys. Conf. Ser. 2019, 1308, 012016. [Google Scholar] [CrossRef]
- La Cognata, M.; Mukhamedzhanov, A.M.; Spitaleri, C.; Indelicato, I.; Aliotta, M.; Burjan, V.; Cherubini, S.; Coc, A.; Gulino, M.; Hons, Z.; et al. The fluorine destruction in stars: First experimental study of the 19F(p,α0)16O reaction at astrophysical energies. Astrophys. J. Lett. 2011, 739, L54. [Google Scholar] [CrossRef]
- Indelicato, I.; La Cognata, M.; Spitaleri, C.; Burjan, V.; Cherubini, S.; Gulino, M.; Hayakawa, S.; Hons, Z.; Kroha, V.; Lamia, L.; et al. New Improved Indirect Measurement of the 19F(p,α)16O Reaction at Energies of Astrophysical Relevance. Astrophys. J. 2017, 19, 845. [Google Scholar] [CrossRef]
- Angulo, C.; Arnould, M.; Rayet, M.; Descouvemont, P.; Baye, D.; Leclercq-Willain, C.; Coc, A.; Barhoumi, S.; Aguer, P.; Rolfs, C.; et al. A compilation of charged-particle induced thermonuclear reaction rates. Nucl. Phys. A 1999, 656, 3. [Google Scholar] [CrossRef]
- Clarkson, O.; Herwig, F. Convective H-He interactions in massive population III stellar evolution models. Mon. Not. R. Astron. Soc. 2021, 500, 2685–2703. [Google Scholar] [CrossRef]
- Zhang, L.Y.; Su, J.; He, J.J.; Wiescher, M.; deBoer, R.J.; Kahl, D.; Chen, Y.J.; Li, X.Y.; Wang, J.G.; Zhang, L.; et al. Direct Measurement of the Astrophysical 19F(p,αγ)16O Reaction in the Deepest Operational Underground Laboratory. Phys. Rev. Lett. 2021, 127, 152702. [Google Scholar] [CrossRef]
- Zhang, L.Y.; He, J.; deBoer, R.J.; Wiescher, M.; Heger, A.; Kahl, D.; Su, J.; Odell, D.; Chen, Y.; Li, X.; et al. Measurement of 19F(p,γ)20Ne reaction suggests CNO breakout in first stars. Nature 2022, 610, 656. [Google Scholar] [CrossRef] [PubMed]
- Wiescher, M.; Görres, J.; Schatz, H. Break-out reactions from the CNO cycles. J. Phys. G Nucl. Part. Phys. 1999, 25, R133. [Google Scholar] [CrossRef]
- Abia, C.; Recio-Blanco, A.; de Laverny, P.; Cristallo, S.; Domínguez, I.; Straniero, O. Fluorine in AGB Carbon Stars Revisited. Astrophys. J. 2009, 694, 971. [Google Scholar] [CrossRef]
- Abia, C.; Cunha, K.; Cristallo, S.; de Laverny, P.; Domínguez, I.; Eriksson, K.; Gialanella, L.; Hinkle, K.; Imbriani, G.; Recio-Blanco, A.; et al. Fluorine abundances in galactic Asymptotic Giant Branch stars. Astrophys. J. 2010, 715, L94. [Google Scholar] [CrossRef]
- Breuer, G. Messung und Analyse von Winkelverteilung und Wirkungsquerschnitt der Reaktion F19(p,α0)O16 im Energiebereich 0,4 bis 0,72 MeV. Z. Phys. 1959, 154, 339. [Google Scholar] [CrossRef]
- Isoya, A. Analysis of the yield curves and the angular distributions of the reactions F19 (p, α0) O16 and F19 (p, απ) O16. Nucl. Phys. A 1959, 7, 126. [Google Scholar] [CrossRef]
- Caracciolo, R.; Cuzzocrea, P.; DeRosa, A.; Inglima, G.; Perillo, E.; Sandoli, M.; Spadaccini, G. The 13.645 MeV state in20Ne. Lett. Nuovo Cimento 1974, 11, 33. [Google Scholar] [CrossRef]
- Cuzzocrea, P.; De Rosa, A.; Inglima, G.; Perillo, E.; Rosato, E.; Sandoli, M.; Spadaccini, G. Quartet states in20Ne. Lett. Nuovo Cimento 1980, 28, 515. [Google Scholar] [CrossRef]
- Lombardo, I.; Dell’Aquila, D.; Di Leva, A.; Indelicato, I.; La Cognata, M.; La Commara, M.; Ordine, A.; Rigato, V.; Romoli, M.; Rosato, M.; et al. Toward a reassessment of the 19F(p,α0)16O reaction rate at astrophysical temperatures. Phys. Lett. B 2015, 748, 178. [Google Scholar] [CrossRef]
- Lombardo, I.; Dell’Aquila, D.; Campajola, L.; Rosato, E.; Spadaccini, G.; Vigilante, M. Analysis of the 19F(p, α0)16O reaction at low energies and the spectroscopy of 20Ne. J. Phys. G Nucl. Part. Phys. 2013, 40, 125102. [Google Scholar] [CrossRef]
- Micron Semiconductor, General Catalogue. Available online: https://www.micronsemiconductor.co.uk/silicon-detector-catalogue/ (accessed on 14 July 2024).
- Guardo, G.L.; Lattuada, D.; Petruse, T. Developing system arrays for new experimental approach in nuclear astrophysics. J. Phys. Conf. Ser. 2023, 2619, 012009. [Google Scholar] [CrossRef]
- Lattuada, D.; Balabanski, D.L.; Chesnevskaya, S.; Costa, M.; Crucillà, V.; Guardo, G.L.; La Cognata, M.; Matei, C.; Pizzone, R.G.; Romano, S.; et al. A fast and complete GEANT4 and ROOT Object-Oriented Toolkit: GROOT. EPJ Web Conf. 2017, 165, 01034. [Google Scholar] [CrossRef][Green Version]
- Brun, R.; Rademakers, F. ROOT: An object oriented data analysis framework. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrom. Detect. Assoc. Equip. 1997, 389, 81. [Google Scholar] [CrossRef]
- Guardo, G.L.; Petruse, T.; Lattuada, D.; La Cognata, M.; Balabanski, D.L.; Açıksöz, E.; Acosta, L.; Capponi, L.; Carbone, D.; Cherubini, S.; et al. Direct measurement of the 19F(p,α0)16O reaction at E = 0.4–0.9 MeV using the LHASA detector array. Eur. Phys. J. A 2023, 59, 65. [Google Scholar] [CrossRef]
- Petruse, T.; Guardo, G.L.; Lattuada, D.; La Cognata, M.; Balabanski, D.L.; Açıksöz, E.; Acosta, L.; Capponi, L.; Carbone, D.; Cherubini, S.; et al. Submitted to EPJ, tag number EPJA-107832, Under Review.
- Spitaleri, C.; La Cognata, M.; Lamia, L.; Pizzone, R.G.; Tumino, A. Astrophysics studies with the Trojan Horse Method. Eur. Phys. J. A 2019, 55, 161. [Google Scholar] [CrossRef]
- Pizzone, R.G.; Bertulani, C.A.; Lamia, L.; La Cognata, M.; Sergi, M.L.; Spartá, R.; Tumino, A. Clusters and their fundamental role for Trojan Horse Method. Eur. Phys. J. A 2020, 56, 283. [Google Scholar] [CrossRef]
- Tumino, A.; Bertulani, C.A.; La Cognata, M.; Lamia, L.; Pizzone, R.G.; Romano, S.; Typel, S. The Trojan Horse Method: A Nuclear Physics Tool for Astrophysics. Annu. Rev. Nucl. Part. Sci. 2021, 71, 345–376. [Google Scholar] [CrossRef]
- Tribble, R.E.; Bertulani, C.A.; Mukhamedzhanov, A.M.; Spitaleri, C. Indirect techniques in nuclear astrophysics: A review. Rep. Prog. Phys. 2014, 77, 106901. [Google Scholar] [CrossRef] [PubMed]
- Mukhamedzhanov, A.M.; Blokhintsev, L.D.; Irgaziev, B.F.; Kadyrov, A.S.; La Cognata, M.; Spitaleri, C.; Tribble, R.E. Trojan Horse as an indirect technique in nuclear astrophysics. J. Phys. G Nucl. Part. Phys. 2008, 35, 014016. [Google Scholar] [CrossRef][Green Version]
- Rapisarda, G.G.; Spitaleri, C.; Cvetinović, A.; Spartà, R.; Cherubini, S.; Guardo, G.L.; Gulino, M.; La Cognata, M.; Lamia, L.; Pizzone, R.G.; et al. Study of the 10B(p,α1)7Be reaction by means of the Trojan Horse Method. Eur. Phys. J. A 2018, 54, 189. [Google Scholar] [CrossRef]
- Cvetinovic, A.; Spitaleri, C.; Spartá, R.; Rapisarda, G.G.; Puglia, S.M.R.; La Cognata, M.; Cherubini, S.; Guardo, G.L.; Gulino, M.; Lamia, L.; et al. Trojan horse measurement of the 10B(p,α0)7Be cross section in the energy range from 3 keV to 2.2 MeV. Phys. Rev. C 2018, 97, 065801. [Google Scholar] [CrossRef]
- Palmerini, S.; La Cognata, M.; Hammache, F.; Acosta, L.; Alba, R.; Burjan, V.; Chávez, E.; Cherubini, S.; Cvetinović, A.; D’Agata, G.; et al. The 27Al(p,α)24Mg reaction at astrophysical energies studied by means of the Trojan Horse Method applied to the 2H(27Al,α24Mg)n reaction. Eur. Phys. J. Plus 2021, 136, 898. [Google Scholar] [CrossRef]
- La Cognata, M.; Palmerini, S.; Adsley, P.; Hammache, F.; Di Pietro, A.; Figuera, P.; Dell’Agli, F.; Alba, R.; Cherubini, S.; Guardo, G.L.; et al. A New Reaction Rate of the 27Al(p,α)24Mg Reaction Based on Indirect Measurements at Astrophysical Energies and Implications for 27Al Yields of Intermediate-mass Stars. Astrophys. J. 2022, 941, 96. [Google Scholar] [CrossRef]
- Guardo, G.L.; Spitaleri, C.; Lamia, L.; Spartá, R.; Carlin, N.; Cherubini, S.; Del Santo, G.; Indelicato, I.; La Cognata, M.; Lattuada, D.; et al. The 10B(n,α)7Li cross sections at ultra-low energy through the Trojan Horse Method applied to the 2H(10B,α7Li)1H. Eur. Phys. J. A 2019, 55, 211. [Google Scholar] [CrossRef]
- Pizzone, R.G.; Spampinato, C.; Spartá, R.; Couder, M.; Tan, W.; Burjan, V.; D’Agata, G.; Guardo, G.L.; La Cognata, M.; Lamia, L.; et al. Indirect measurement of the 3He (n,p)3H reaction cross section at Big Bang energies. Eur. Phys. J. A 2020, 56, 199. [Google Scholar] [CrossRef]
- Spartá, R.; Lamia, L.; La Cognata, M.; Spitaleri, C.; Rapisarda, G.G.; Guardo, G.L.; Cherubini, S.; D’Agata, G.; Di Pietro, A.; Figuera, P.; et al. 10B(n,α0)7Li and 10B(n,α1)7Li reactions measured via Trojan Horse Method. Eur. Phys. J. A 2021, 57, 170. [Google Scholar]
- Spartá, R.; Pizzone, R.G.; Bertulani, C.A.; Hou, S.; Lamia, L.; Tumino, A. Direct and Indirect Measurements for a Better Understanding of the Primordial Nucleosynthesis. Front. Astron. Space Sci. 2020, 7, 560149. [Google Scholar] [CrossRef]
- Rapisarda, G.G.; Lamia, L.; Caciolli, A.; Chengbo, L.; Degl’Innocenti, S.; Depalo, R.; Palmerini, S.; Pizzone, R.G.; Romano, S.; Spitaleri, C.; et al. Experimental Nuclear Astrophysics With the Light Elements Li, Be and B: A Review. Front. Astron. Space Sci. 2021, 7, 589240. [Google Scholar] [CrossRef]
- Sergi, M.L.; D’Agata, G.; Guardo, G.L.; Rapisarda, G.G.; Burjan, V.; Cherubini, S.; Gulino, M.; Indelicato, I.; La Cognata, M.; Lamia, L.; et al. Trojan Horse Investigation for AGB Stellar Nucleosynthesis. Universe 2022, 8, 128. [Google Scholar] [CrossRef]
- Spartá, R.; La Cognata, M.; Guardo, G.L.; Palmerini, S.; Sergi, M.L.; D’Agata, G.; Lamia, L.; Lattuada, D.; Oliva, A.A.; Pizzone, R.G.; et al. Neutron-Driven Nucleosynthesis in Stellar Plasma. Front. Phys. 2022, 10, 896011. [Google Scholar] [CrossRef]
- Lamia, L.; La Cognata, M.; Spitaleri, C.; Irgaziev, B.; Pizzone, R.G. Influence of the d-state component of the deuteron wave function on the application of the Trojan horse method. Phys. Rev. C 2012, 85, 025805. [Google Scholar] [CrossRef]
- Shapiro, I.S. Interaction of High-Energy Particles with Nuclei; Academitices: New York, NY, USA, 1967; p. 210. [Google Scholar]
- Devons, S.; Goldring, G. Emission of Electron-Positron Pairs from Light Nuclei II: γ-Transitions in 8Be, 10B and 16O. Proc. Phys. Soc. A 1954, 67, 413. [Google Scholar] [CrossRef]
- Cuzzocrea, P.; De Rosa, A.; Inglima, G.; Perillo, E.; Rosato, E.; Sandoli, M.; Spadaccini, G. The 19F(p,α)16O Reaction and the Quartet Model. INFN Report INFN/BE-80/5. 1980. Available online: https://www.lnf.infn.it/sis/preprint/getfilepdf.php?filename=INFN-BE-80-5.pdf (accessed on 14 July 2024).
- Lombardo, I.; Dell’Aquila, D.; He, J.J.; Spadaccini, G.; Vigilante, M. New analysis of p+19F reactions at low energies and the spectroscopy of natural-parity states in 20Ne. Phys. Rev. C 2019, 100, 044307. [Google Scholar] [CrossRef]
- Chesnevskaya, S.; Balabanski, D.L.; Choudhury, D.; Constantin, P.; Filipescu, D.M.; Ghita, D.G.; Guardo, G.L.; Lattuada, D.; Matei, M.; Rotaru, A.; et al. Performance studies of X3 silicon detectors for the future ELISSA array at ELI-NP. J. Instrum. 2018, 13, T05006. [Google Scholar] [CrossRef]
- Guardo, G.L.; Anzalone, A.; Balabanski, D.L.; Chesnevskaya, S.; Crucillá, V.; Filipescu, D.; Gulino, M.; La Cognata, M.; Lattuada, D.; Matei, C.; et al. Development of the ELISSA array: Prototype testing at Laboratori Nazionali del Sud. EPJ Web Conf. 2018, 184, 02006. [Google Scholar] [CrossRef]





| E*(MeV) | J | keV |
|---|---|---|
| 12.957 | 2+ | 113 |
| 13.095 | 2+ | 251 |
| 13.222 a | 0+ | |
| 13.224 a | 1− | 380 |
| 13.226 a | 3+ | |
| 13.529 a | 2+ | 696 |
| 13.586 a | 2+ | 739 |
| 13.642 | 2+ | 798 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guardo, G.L.; Rapisarda, G.G.; Balabanski, D.L.; D’Agata, G.; Di Pietro, A.; Figuera, P.; La Cognata, M.; La Commara, M.; Lamia, L.; Lattuada, D.; et al. Direct and Indirect Measurements of the 19F(p,α)16O Reaction at Astrophysical Energies Using the LHASA Detector and the Trojan Horse Method. Universe 2024, 10, 304. https://doi.org/10.3390/universe10070304
Guardo GL, Rapisarda GG, Balabanski DL, D’Agata G, Di Pietro A, Figuera P, La Cognata M, La Commara M, Lamia L, Lattuada D, et al. Direct and Indirect Measurements of the 19F(p,α)16O Reaction at Astrophysical Energies Using the LHASA Detector and the Trojan Horse Method. Universe. 2024; 10(7):304. https://doi.org/10.3390/universe10070304
Chicago/Turabian StyleGuardo, Giovanni L., Giuseppe G. Rapisarda, Dimiter L. Balabanski, Giuseppe D’Agata, Alessia Di Pietro, Pierpaolo Figuera, Marco La Cognata, Marco La Commara, Livio Lamia, Dario Lattuada, and et al. 2024. "Direct and Indirect Measurements of the 19F(p,α)16O Reaction at Astrophysical Energies Using the LHASA Detector and the Trojan Horse Method" Universe 10, no. 7: 304. https://doi.org/10.3390/universe10070304
APA StyleGuardo, G. L., Rapisarda, G. G., Balabanski, D. L., D’Agata, G., Di Pietro, A., Figuera, P., La Cognata, M., La Commara, M., Lamia, L., Lattuada, D., Matei, C., Mazzocco, M., Oliva, A. A., Palmerini, S., Petruse, T., Pizzone, R. G., Romano, S., Sergi, M. L., Spartá, R., ... Vukman, N. (2024). Direct and Indirect Measurements of the 19F(p,α)16O Reaction at Astrophysical Energies Using the LHASA Detector and the Trojan Horse Method. Universe, 10(7), 304. https://doi.org/10.3390/universe10070304









