Laboratory Magnetoplasmas as Stellar-like Environment for 7Be β-Decay Investigations Within the PANDORA Project
Abstract
1. Introduction
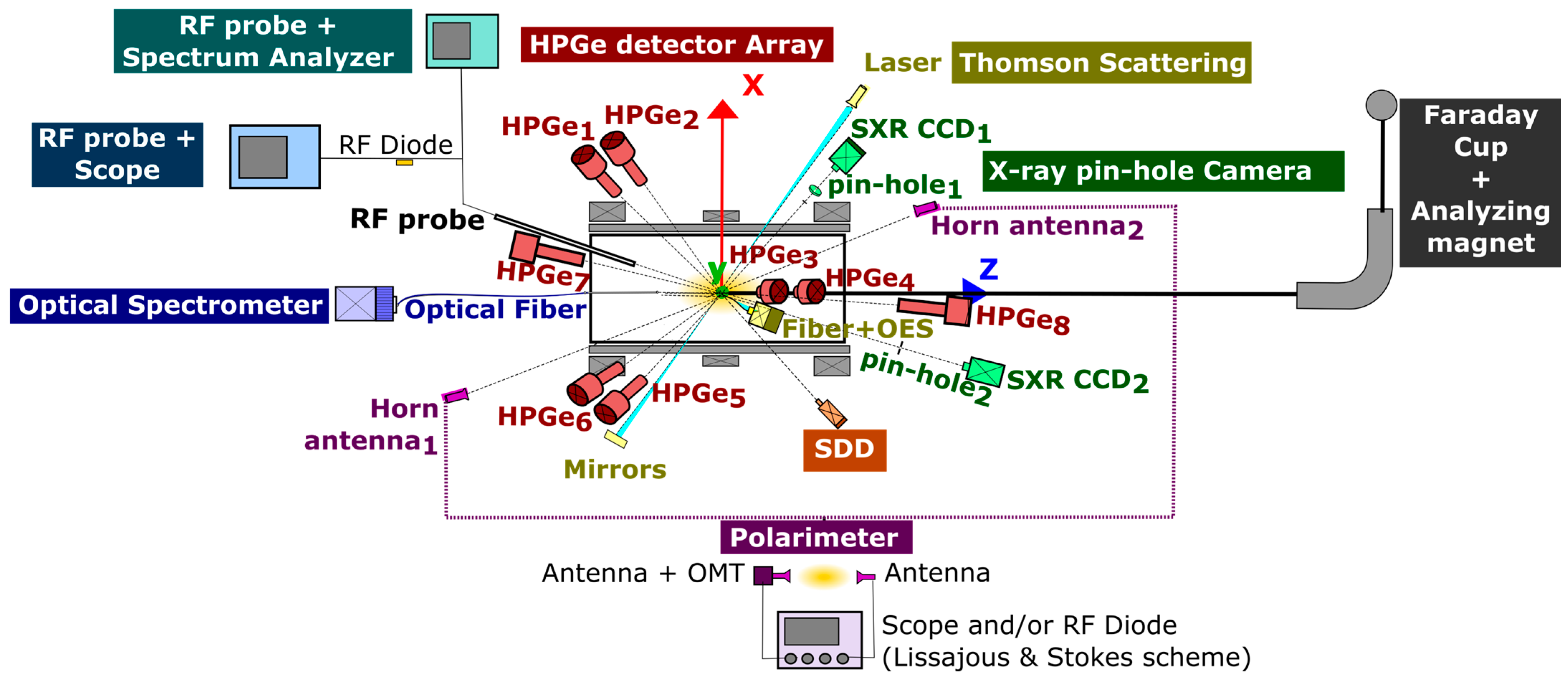
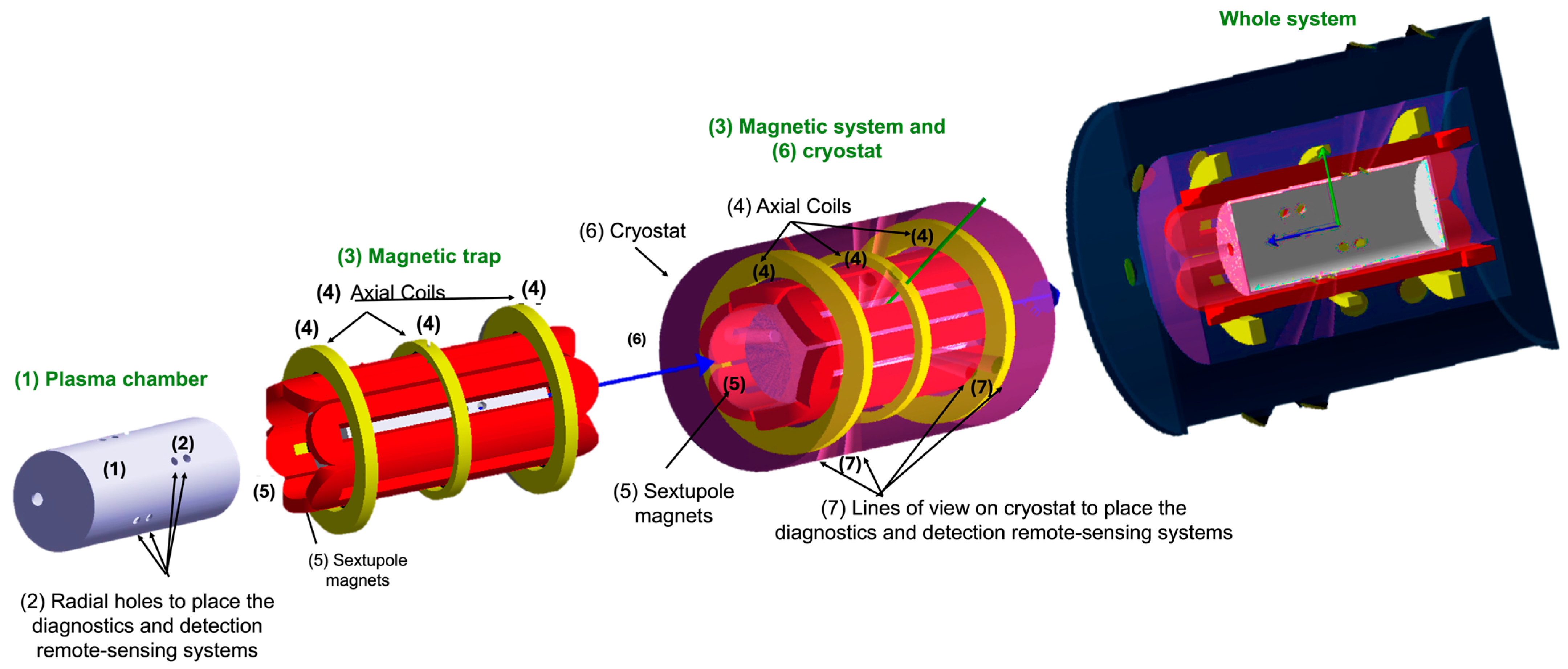
2. The PANDORA Facility: Conceptual Design and the Novel Experimental Approach
- A buffer plasma of He, O, or Ar is created using ECR heating, reaching densities up to 1013 cm−3.
- The plasma trap is designed to accommodate metal injection systems that vaporize metal isotopes (176Lu, 134Cs, 94Nb) to densities ranging from 106 to 1011 cm−3. Simulations have also evaluated the diffusion [43] of these atoms within the plasma chamber, along with plasma interaction and transport phenomena.
- Other isotope injection solutions have been considered for the case of 7Be, due to its larger activity compared to the other physics cases mentioned. A feasibility study based on the principles of the Charge-Breeder technique and of the ISOL technique has been already performed. The isotope injection in plasma will be based on the construction of an in-flight injection line of radioactive ion beams (RIBs) into the plasma trap. The 7Be nuclei can be produced by an accelerated proton beam hitting a boron nitride compound; fragmentation reaction will produce the isotope from boron. Then, effusing nuclei will be extracted at 1+ charge state and subsequently injected into a radio-frequency quadrupole cooler to optimize the beam envelope properties, longitudinal matching and energy, before entering the plasma potential and penetrate in the plasma core.
- The plasma can be maintained in magnetohydrodynamic (MHD) equilibrium for extended periods (days). The number of γ-rays emitted from the decay of daughter nuclei produced in the β-decay process can be expressed as Nγ(tm) = λniVptm, where λ is the isotope’s nuclear decay constant, ni is the isotope ion density, Vp is the plasma volume, and tm is the measurement time. Nγ(tm) scales linearly with tm, and once ni and Vp are known, λ can be determined.
- The emitted γ-rays are detected by the array of HPGe detectors.
- The in-plasma radioactivity is correlated with plasma parameters using the non-invasive multi-diagnostic setup able to monitor the plasma parameters online.
3. Methods
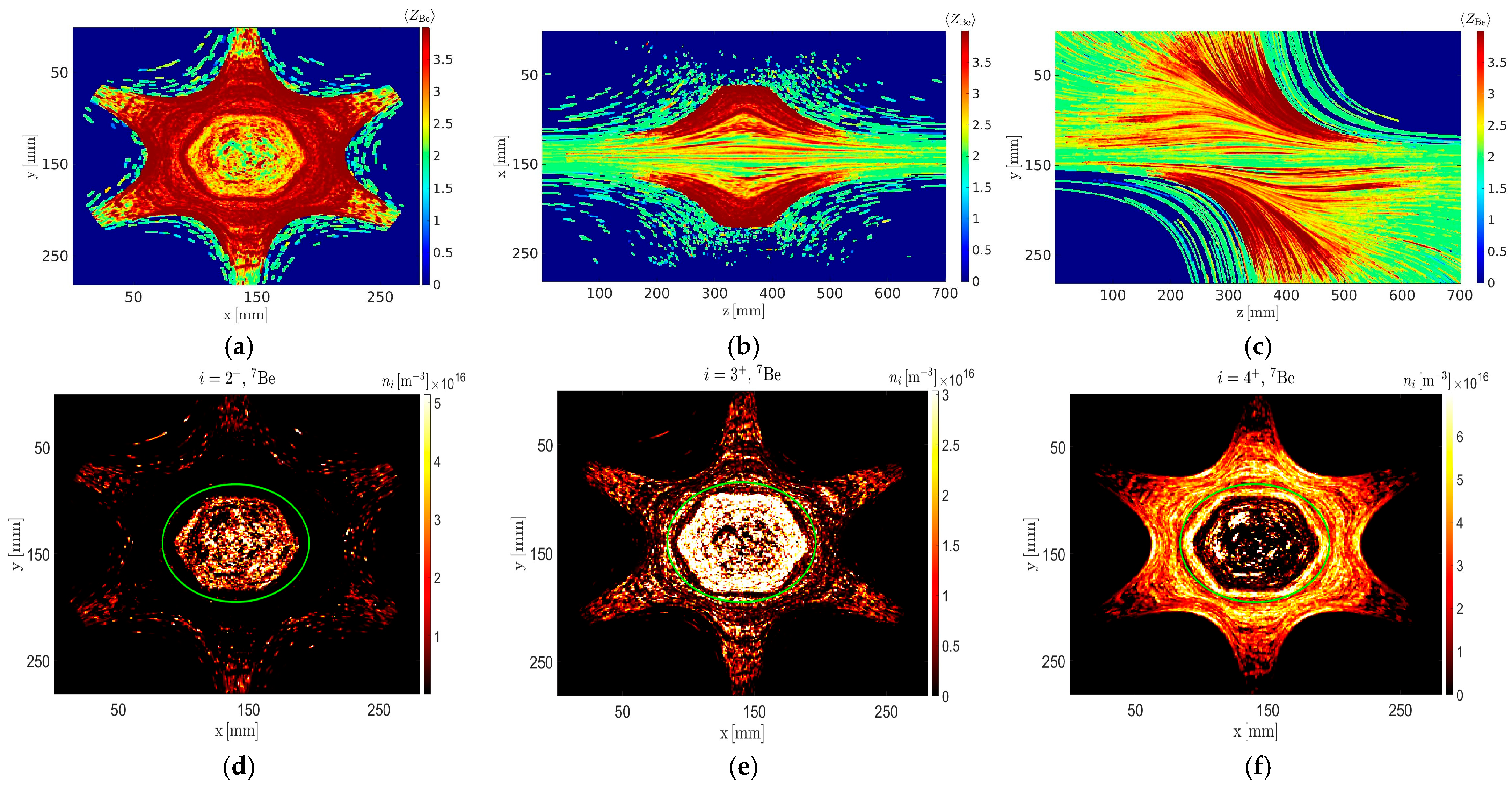
3.1. Spatial Distribution of 7Be CSD
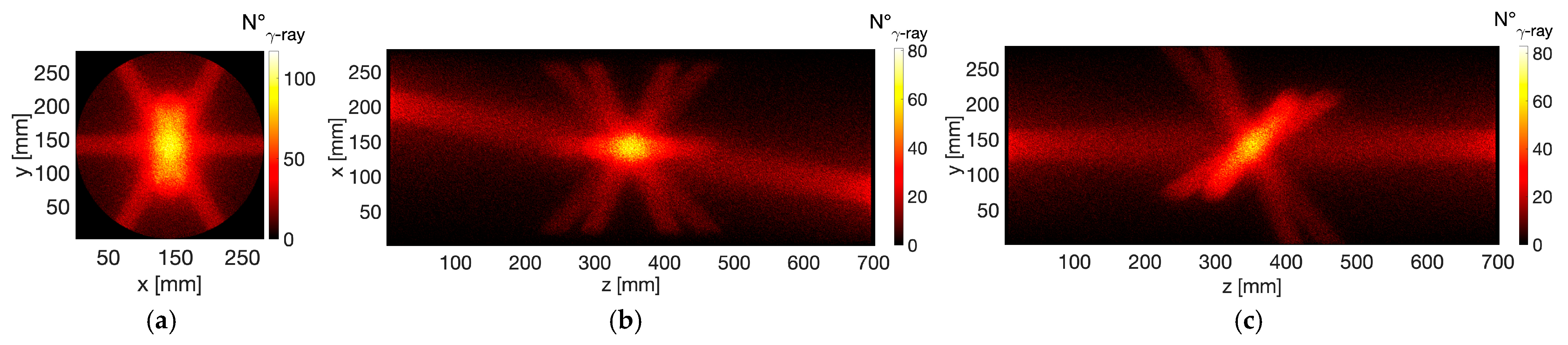
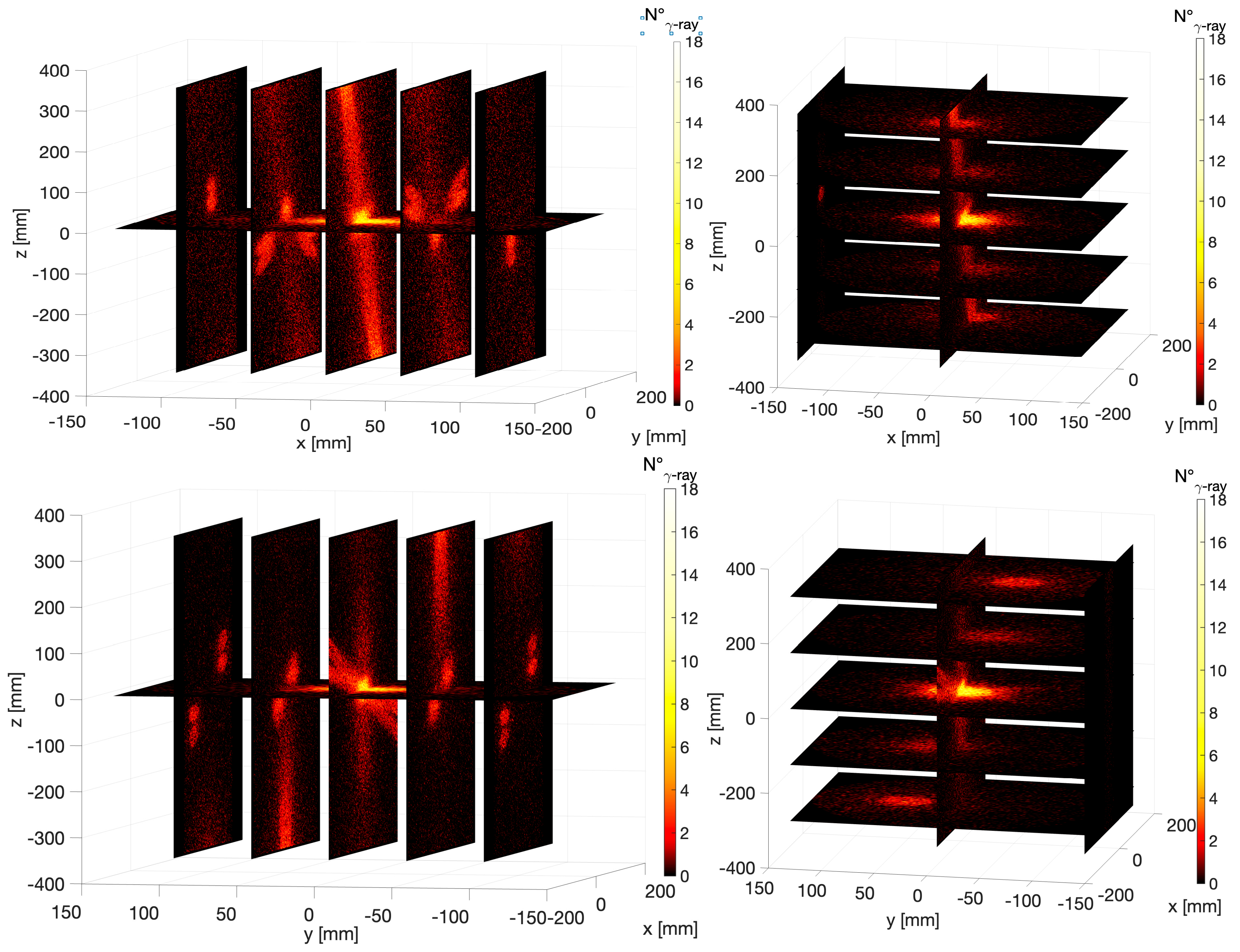
3.2. GEANT4 Simulations for the Evaluation of the 3D Array Efficiency Map
4. Results
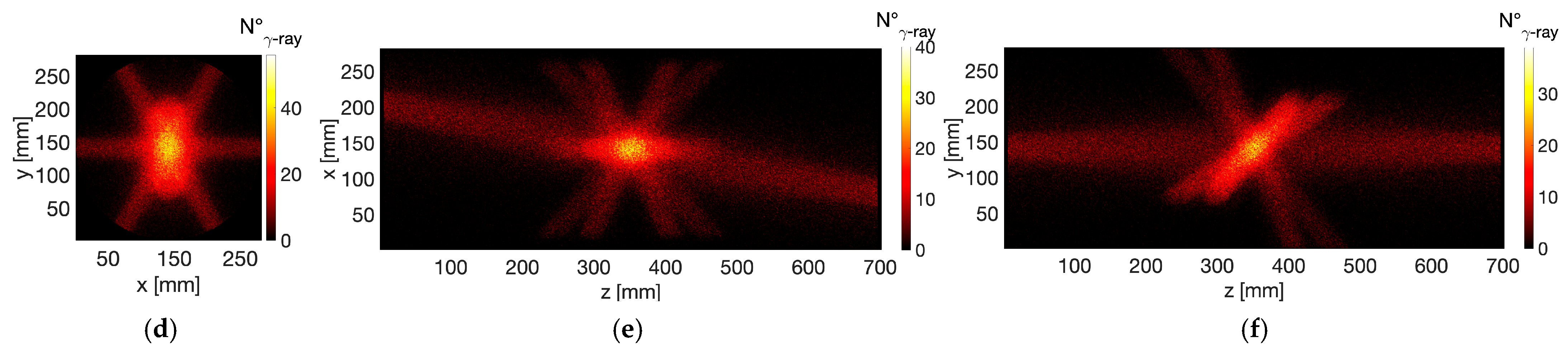
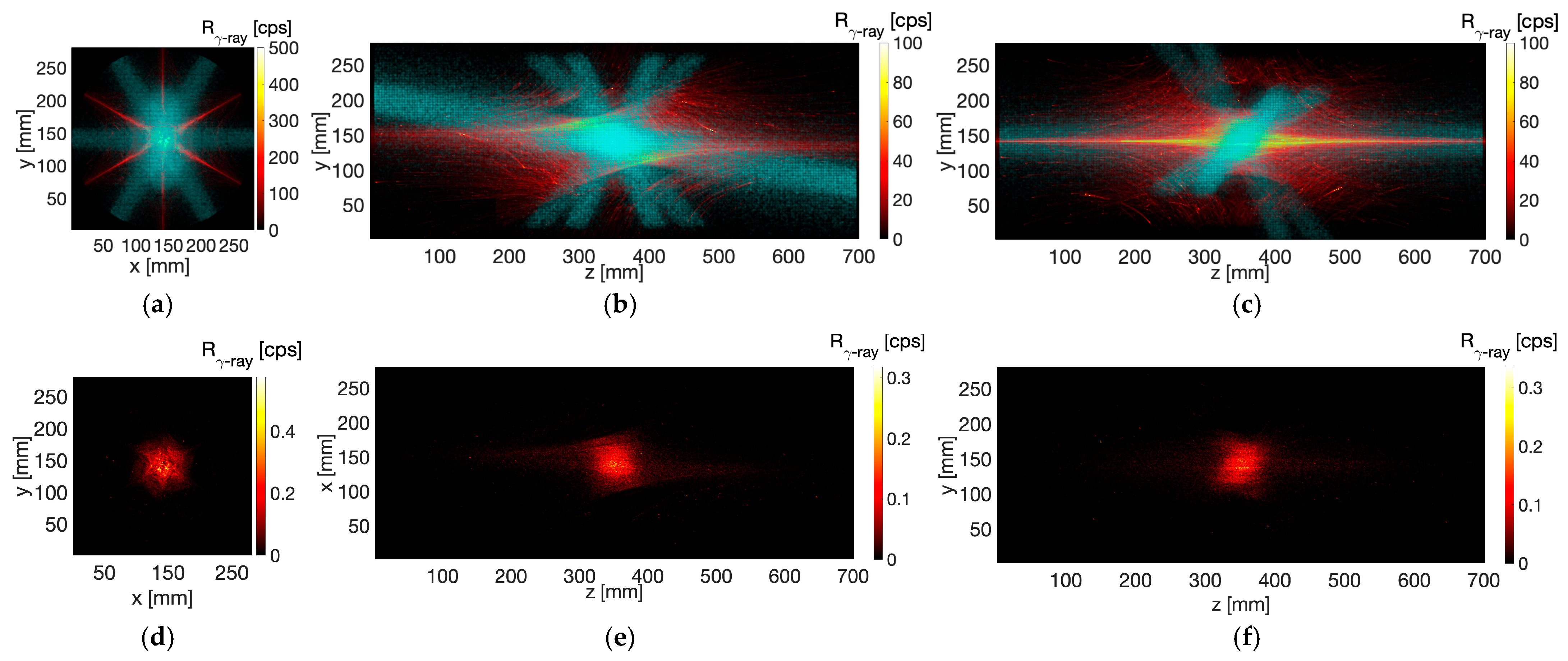
4.1. Spatial Distribution of Secondary γ-Emission
4.2. Local g-Ray Detector Array Efficiency
- Bremsstrahlung X-rays (): these originate from plasma self-emission and are particularly intense in loss-cone regions caused by axial and radial losses impinging on the plasma chamber walls.
- γ-rays from excited 7Li nuclei following the β-decay of neutral 7Be (): these result from the γ-decay of daughter 7Li nuclei following the β-decay of neutral 7Be continuously injected into the plasma trap. This contribution cannot be experimentally distinguished from the γ-decay of ionized nuclei within the plasma (, where i is a given ionization state), which constitutes the signal of interest. This overlap undermines and limits the accuracy of in-plasma β-decay rate measurements attributed solely to ionized nuclei.
5. Discussion
- Reasonable measurement durations;
- Manageable material quantities and doses (considering cost, availability, and handling limitations for radioprotection issues);
- The dependency of the uncertainty in the decay constant of ionized atoms on measurement time.
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Käppeler, F.; Mengoni, A. Nuclear input for the s process: Progress with experiments and theory. Nucl. Phys. A 2006, 777, 291–310. [Google Scholar] [CrossRef]
- Kolbe, E.; Langanke, K.; Martinez-Pinedo, G.; Vogel, P. Neutrino-nucleus reactions and nuclear structure. J. Phys. G Nucl. Part. Phys. 2003, 29, 2569. [Google Scholar] [CrossRef]
- Langanke, K.; Thielemann, F.-K.; Wiescher, M. Nuclear Astrophysics and Nuclei Far from Stability. Lect. Notes Phys. 2004, 651, 383. [Google Scholar]
- Käppeler, F.; Thielemann, F.-K.; Wiescher, M. Current quests in nuclear astrophysics and experimental approaches. Annu. Rev. Nucl. Part. Sci. 1998, 48, 175–251. [Google Scholar] [CrossRef]
- Thielemann, F.-K.; Frohlich, C.; Hirschi, R.; Liebendorfer, M.; Dillmann, I.; Mocelj, D.; Rauscher, T.; Martinez-Pinedo, G.; Langanke, K.; Farouqi, K.; et al. Production of intermediate-mass and heavy nuclei. Prog. Part. Nucl. Phys. 2007, 59, 74–93. [Google Scholar] [CrossRef]
- Daudel, R. Alteration of radioactive periods of the elements with the aid of chemical methods. Rev. Sci. 1947, 85, 510. [Google Scholar]
- Segré, E.; Wiegard, C.E. Experiments on the Effect of Atomic Electrons on the Decay Constant of Be7. Phys. Rev. 1949, 75, 39. [Google Scholar] [CrossRef]
- Emery, G.T. Perturbation of Nuclear Decay Rates. Annu. Rev. Nucl. Part. Sci. 1972, 22, 165–202. [Google Scholar] [CrossRef]
- Mazaki, H.; Nagatomo, T.; Shimizu, S. Effect of Pressure on the Decay Constant of 99mTc. Phys. Rev. C 1972, 5, 1718. [Google Scholar] [CrossRef]
- Bosch, F.; Faestermann, T.; Friese, J.; Heine, F.; Kienle, P.; Wefers, E.; Zeitelhack, K.; Beckert, K.; Franzke, B.; Klepper, O.; et al. Observation of Bound-State β− Decay of Fully Ionized 187Re: 187Re−187Os Cosmochronometry. Phys. Rev. Lett. 1996, 77, 5190. [Google Scholar] [CrossRef]
- Jung, M.; Bosch, F.; Beckert, K.; Eickhoff, H.; Folger, H.; Franzke, B.; Gruber, A.; Kienle, P.; Klepper, O.; Koenig, W.; et al. First observation of bound-state β− decay. Phys. Rev. Lett. 1992, 69, 2164. [Google Scholar] [CrossRef] [PubMed]
- Takahashi, K.; Yokoi, K. Nuclear β-Decays of Highly Ionised Heavy toms in Stellar Interiors. Nucl. Phys. A 1983, 404, 578–598. [Google Scholar] [CrossRef]
- Palmerini, S.; Busso, M.; Vescovi, D.; Naselli, E.; Pidatella, A.; Mucciola, R.; Cristallo, S.; Mascali, D.; Mengoni, A.; Simonucci, S.; et al. Presolar grain isotopic ratios as constraints to nuclear and stellar parameters of asymptotic giant branch star nucleosynthesis. Astrophys. J. 2021, 921, 7. [Google Scholar] [CrossRef]
- Busso, M.M.; Kratz, K.-L.; Palmerini, S.; Akram, W.; Antonuccio-Delogu, V. Production of solar abundances for nuclei beyond Sr: The s- and r-process perspectives. Front. Astron. Space Sci. 2022, 9, 956633. [Google Scholar] [CrossRef]
- Mishra, B.; Galatà, A.; Pidatella, A.; Biri, S.; Mauro, G.S.; Naselli, E.; Rácz, R.; Torrisi, G.; Mascali, D. Modeling space-resolved ion dynamics in ECR plasmas for predicting in-plasma β-decay rates. Front. Phys. 2022, 10, 932448. [Google Scholar] [CrossRef]
- Mishra, B. Electron Captures and Bound-State β-Decays in Ions and Plasma. Phys. Rev. C, 2025; under review. [Google Scholar]
- Mascali, D.; Santonocito, D.; Amaducci, S.; Andò, L.; Antonuccio, A.; Biri, S.; Bonanno, A.; Bonanno, V.P.; Briefi, S.; Busso, M.; et al. A Novel Approach to β-Decay: PANDORA, a New Experimental Setup for Future In-Plasma Measurements. Universe 2022, 8, 80. [Google Scholar] [CrossRef]
- Naselli, E. Experimental study of ECR plasmas in stationary versus turbulent regimes for in-plasma β-decay investigations. Eur. Phys. J. Plus 2023, 138, 599. [Google Scholar] [CrossRef]
- Naselli, E.; Santonocito, D.; Amaducci, S.; Celona, L.; Galatà, A.; Mauro, G.S.; Mazzaglia, M.; Mishra, B.; Pidatella, A.; Torrisi, G.; et al. GEANT4 simulations for γ-ray detector array design for in plasma β-decays studies of nuclear astrophysics interest. EPJ Web Conf. 2023, 279, 13006. [Google Scholar] [CrossRef]
- Naselli, E. Laboratory magnetoplasmas as an ideal experimental environment for nuclear astrophysics β-decay studies. EPJ Web Conf. 2023, 275, 02008. [Google Scholar] [CrossRef]
- Mascali, D.; Santonocito, D.; Busso, M.; Celona, L.; Galatà, A.; La Cognata, M.; Mauro, G.S.; Mengoni, A.; Naselli, E.; Odorici, F.; et al. A new approach to β-decays studies impacting nuclear physics and astrophysics: The PANDORA setup. EPJ Web Conf. 2023, 279, 06007. [Google Scholar] [CrossRef]
- Mascali, D.; Naselli, E.; Torrisi, G. Techniques for electron cyclotron resonance plasma diagnostics. Rev. Sci. Instrum. 2022, 93, 033302. [Google Scholar] [CrossRef] [PubMed]
- Naselli, E.; Santonocito, D.; Amaducci, S.; Celona, L.; Galatà, A.; Goasduff, A.; Mauro, G.S.; Mazzaglia, M.; Mishra, B.; Napoli, D.R.; et al. Design study of a HPGe detector array for β-decay investigation in laboratory ECR plasma. Front. Phys. 2022, 10, 935728. [Google Scholar] [CrossRef]
- Mascali, D.; Musumarra, A.; Leone, F.; Romano, F.P.; Galatà, A.; Gammino, S.; Massimi, C. PANDORA, a new facility for interdisciplinary in-plasma physics. Eur. Phys. J. A 2017, 53, 145. [Google Scholar] [CrossRef]
- Adelberger, E.G.; Balantekin, A.B.; Bemmerer, D.; Bertulani, C.A.; Chen, J.-W.; Costantini, H.; Couder, M.; Cyburt, R.; Davids, B.; Freedman, S.J.; et al. Solar fusion cross sections. II. The pp chains and CNO cycles. Rev. Mod. Phys. 2011, 83, 195. [Google Scholar] [CrossRef]
- Broggini, C.; Canton, L.; Fiorentini, G.; Villante, F.L. The cosmological 7Li problem from a nuclear physics perspective. J. Cosmol. Astropart. Phys. 2012, 2012, 030. [Google Scholar] [CrossRef]
- Vescovi, D.; Piersanti, L.; Cristallo, S.; Busso, M.; Vissani, F.; Palmerini, S.; Simonucci, S.; Taioli, S. Effects of a revised 7Be e−-capture rate on solar neutrino fluxes. Astron. Astrophys. 2019, 623, 7. [Google Scholar] [CrossRef]
- Quarati, P.; Scarafone, A.M. Nuclear electron capture rate in stellar interiors and the case of 7Be. J. Phys. G Nucl. Part. Phys. 2008, 36, 025203. [Google Scholar] [CrossRef]
- Simonucci, S.; Taioli, S.; Palmerini, S.; Busso, M. Theoretical estimates of stellar e− captures. I. The half-life of 7Be in evolved stars. Astrophys. J. 2013, 764, 118. [Google Scholar] [CrossRef]
- Palmerini, S.; Busso, M.; Simonucci, S.; Taioli, S. Lithium abundances in AGB stars and a new estimate for the 7Be life-time. J. Phys. Conf. Ser. 2016, 665, 012014. [Google Scholar] [CrossRef]
- Mishra, B.; Pidatella, A.; Taioli, S.; Simonucci, S.; Mascali, D. Plasma Induced Variation of Electron Capture and Bound-State β Decays. arXiv 2024, arXiv:2407.01787. [Google Scholar]
- Morresi, T.; Taioli, S.; Simonucci, S. Relativistic Theory and Ab Initio Simulations of Electroweak Decay Spectra in Medium-Heavy Nuclei and of Atomic and Molecular Electronic Structure. Adv. Theory Simul. 2018, 1, 11. [Google Scholar] [CrossRef]
- Gupta, D. The 7Be destruction reactions and the cosmological lithium problem. Eur. Phys. J. Spec. Topics. 2024, 233, 2823–2829. [Google Scholar] [CrossRef]
- Mauro, G.S.; Celona, L.; Torrisi, G.; Pidatella, A.; Naselli, E.; Russo, F.; Mazzaglia, M.; Galatà, A.; Maimone, F.; Lang, R.; et al. An Innovative Superconducting Magnetic Trap for Probing β-decay in Plasmas. Front. Phys. 2022, 10, 931953. [Google Scholar] [CrossRef]
- Torrisi, G.; Naselli, E.; Mascali, D.; Di Donato, L.; Sorbello, G. Mm-wave polarimeter and profilometry design study for retrieving plasma density in the PANDORA experiment. Front. Astron. Space Sci. 2022, 9, 949920. [Google Scholar] [CrossRef]
- Tsikata, S.; Maunoury, L.; Ducret, J.-E. Incoherent Thomson scattering: Future implementation and measurement capabilities on the PANDORA experiment. Front. Astron. Space Sci. 2022, 9, 936532. [Google Scholar] [CrossRef]
- Vincent, B. Incoherent Thomson Scattering Investigations in Hall Thruster, Planar Magnetron and ECR Ion Source Plasmas. Ph.D. Thesis, Plasma Physics Université d’Orléans, Orléans, France, 2019. [Google Scholar]
- Torrisi, G.; Mascali, D.; Sorbello, G.; Castro, G.; Gammino, S. Numerical and Experimental Characterization of RF Waves Propagation in Ion Sources Magnetoplasmas. IEEE Trans. Antennas Propag. 2019, 67, 2884807. [Google Scholar] [CrossRef]
- Pidatella, A.; Mascali, D.; Bezmalinovich, M.; Emma, G.; Mazzaglia, M.; Mishra, B.; Finocchiaro, G.; Galatà, A.; Marletta, S.; Mauro, G.S.; et al. Experimental and numerical investigation of magneto-plasma optical properties toward measurements of opacity relevant for compact binary objects. Front. Astron. Space Sci. 2022, 9, 931744. [Google Scholar] [CrossRef]
- Biri, S.; Rácz, R.; Perduk, Z.; Pálinkjás, J.; Naselli, E.; Mazzaglia, M.; Torrisi, G.; Castro, G.; Celona, L.; Gammino, S.; et al. Innovative experimental setup for X-ray imaging to study energetic magnetized plasmas. J. Instrum. 2021, 16, P03003. [Google Scholar] [CrossRef]
- Mascali, D.; Castro, G.; Altana, C.; Caliri, C.; Mazzaglia, M.; Romano, F.P.; Leone, F.; Musumarra, A.; Naselli, E.; Reitano, R.; et al. Electromagnetic diagnostics of ECR-Ion Sources plasmas: Optical/X-ray imaging and spectroscopy. J. Instrum. 2017, 12, C12047. [Google Scholar] [CrossRef]
- Goasduff, A.; Santonocito, D.; Menegazzo, R.; Capra, S.; Pullia, A.; Raniero, W.; Rosso, D.; Toniolo, N.; Zago, L.; Naselli, E.; et al. A high resolution γ-ray array for the Pandora plasma trap. Front. Phys. 2022, 10, 936081. [Google Scholar] [CrossRef]
- Pidatella, A.; Mascali, D.; Galatà, A.; Mishra, B.; Naselli, E.; Celona, L.; Lang, R.; Maimone, F.; Mauro, G.S.; Santonocito, D.; et al. Metal evaporation dynamics in electron cyclotron resonance ion sources: Plasma role in the atom diffusion, ionisation, and transport. Plasma Phys. Control. Fusion 2024, 66, 035016. [Google Scholar] [CrossRef]
- Taioli, S.; Vescovi, D.; Busso, M.; Palmerini, S.; Cristallo, S.; Mengoni, A.; Simonucci, S. Theoretical Estimate of the Half-Life for the Radioactive 134Cs and 135Cs in Astrophysical Scenarios. Astrophys. J. 2022, 933, 158. [Google Scholar] [CrossRef]
- Galatà, A.; Mascali, D.; Mishra, B.; Naselli, E.; Pidatella, A.; Torrisi, G. On the Numerical Determination of the Density and Energy Spatial Distributions relevant for in-Plasma β-Decay Emission Estimation. Front. Phys. 2022, 10, 947194. [Google Scholar] [CrossRef]
- Mascali, D.; Torrisi, G.; Neri, L.; Sorbello, G.; Castro, G.; Celona, L.; Gammino, S. 3D-Full Wave and Kinetics Numerical Modelling of Electron Cyclotron Resonance Ion Sources Plasma: Steps Towards Self-Consistency. Eur. Phys. J. D 2015, 69, 27. [Google Scholar] [CrossRef]
- Chung, H.-K.; Chen, M.H.; Morgan, W.L.; Raichenko, Y.; Lee, R.W. FLYCHK: Generalized population kinetics and spectral model for rapid spectroscopic analysis for all elements. High Energy Density Phys. 2005, 1, 3–12. [Google Scholar] [CrossRef]
- Tilley, D.R.; Cheves, C.M.; Godwin, J.L.; Hale, G.M.; Hofmann, H.M.; Kelley, J.H.; Sheu, C.G.; Weller, H.R. Energy levels of light nuclei A=5, 6, 7. Nucl. Phys. A 2002, 708, 3–163. [Google Scholar]
- Gumberidze, A.; Trassinelli, M.; Adrouche, N.; Szabo, C.I.; Indelicato, P.; Haranger, F.; Isac, J.-M.; Lamour, E.; Le Bigot, E.-O.; Mérot, J.; et al. Electronic temperatures, densities, and plasma X-ray emission of a 14.5 GHz electron-cyclotron resonance ion source. Rev. Sci. Instrum. 2010, 81, 033303. [Google Scholar] [CrossRef]
- Di Leva, A. Reducing experimental uncertainties on production and destruction of 7 Be in hydrogen burning. In Proceedings of the XII International Symposium on Nuclei in the Cosmos, Vol. NIC XII, Cairns, Australia, 5–12 August 2012; p. 112. [Google Scholar]
- Limata, B.N.; Gialanella, L.; Di Leva, A.; De Cesare, N.; D’Onofrio, A.; Gyurky, G.; Rolfs, C.; Romano, M.; Rogalla, D.; Rossi, C.; et al. 7Be radioactive beam production at CIRCE and its utilization in basic and applied physics. Nucl. Instrum. Methods Phys. Res. B 2008, 266, 2117–2121. [Google Scholar] [CrossRef]
- Tóth, Á.; Gyürky, G.; Papp, E.; Szücs, T. Experimental 7Be production cross section from the Li7(p,n)7Be reaction at Ep=3.5−13 MeV. Nucl. Phys. A 2024, 1041, 122778. [Google Scholar] [CrossRef]
- Cosentino, L.; Musumarra, A.; Barbagallo, M.; Pappalardo, A.; Colonna, N.; Damone, L.; Piscopo, M.; Finocchiaro, P.; Maugeri, E.; Heinitz, S.; et al. Experimental setup and procedure for the measurement of the 7Be(n,α)α reaction at n_TOF. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2016, 830, 197–205. [Google Scholar] [CrossRef]
- Mascali, D.; Naselli, E.; Biri, S.; Finocchiaro, G.; Galatà, A.; Mauro, G.S.; Mazzaglia, M.; Mishra, B.; Passarello, S.; Pidatella, A.; et al. The Multi-Detectors System of the PANDORA Facility: Focus on the Full-Field Pin-Hole CCD System for X-ray Imaging and Spectroscopy. Condens. Matter 2024, 9, 28. [Google Scholar] [CrossRef]
- Tarvainen, O.; Izotov, I.; Mansfeld, D.; Skalyga, V.; Golubev, S.; Kalvas, T.; Koivisto, H.; Komppula, J.; Kronholm, R.; Laulainen, J.; et al. Beam current oscillations driven by cyclotron instabilities in a minimum-B electron cyclotron resonance ion source plasma. Plasma Sources Sci. Technol. 2014, 23, 025020. [Google Scholar] [CrossRef]
- Naselli, E.; Mascali, D.; Mazzaglia, M.; Biri, S.; Rácz, R.; Pálinkás, J.; Perduk, Z.; Galatá, A.; Castro, G.; Celona, L.; et al. Impact of two-close-frequency heating on ECR ion source plasma radio emission and stability. Plasma Sources Sci. Technol. 2019, 28, 085021. [Google Scholar] [CrossRef]
- Li, L.X.; Li, J.B.; Ma, J.D.; Guo, H.; Guo, B.; Hitz, D.; Feng, Y.C.; Lu, W.; Guo, J.W.; Fang, X.; et al. Production of intense pulsed beams of highly charged ions from a superconducting electron cyclotron resonance ion source. Phys. Rev. Accel. Beams 2022, 25, 063402. [Google Scholar] [CrossRef]
- Leitner, D.; Lyneis, C.M.; Abbott, S.R.; Collins, D.B.; Dwinell, R.D.; Galloway, M.L.; Leitner, M.; Todd, D.S. Next generation ECR ion sources: First results of the superconducting 28 GHz ECRIS - VENUS. Nucl. Instrum. Methods B 2005, 235, 486–493. [Google Scholar] [CrossRef]
- Zhao, H.W.; Sun, L.T.; Guo, J.W.; Lu, W.; Xie, D.Z.; Hitz, D.; Zhang, X.Z.; Yang, Y. Intense Highly Charged Ion Beam Production and Operation with a Superconducting Electron Cyclotron Resonance Ion Source. Phys. Rev. Accel. Beams 2017, 20, 094801. [Google Scholar] [CrossRef]





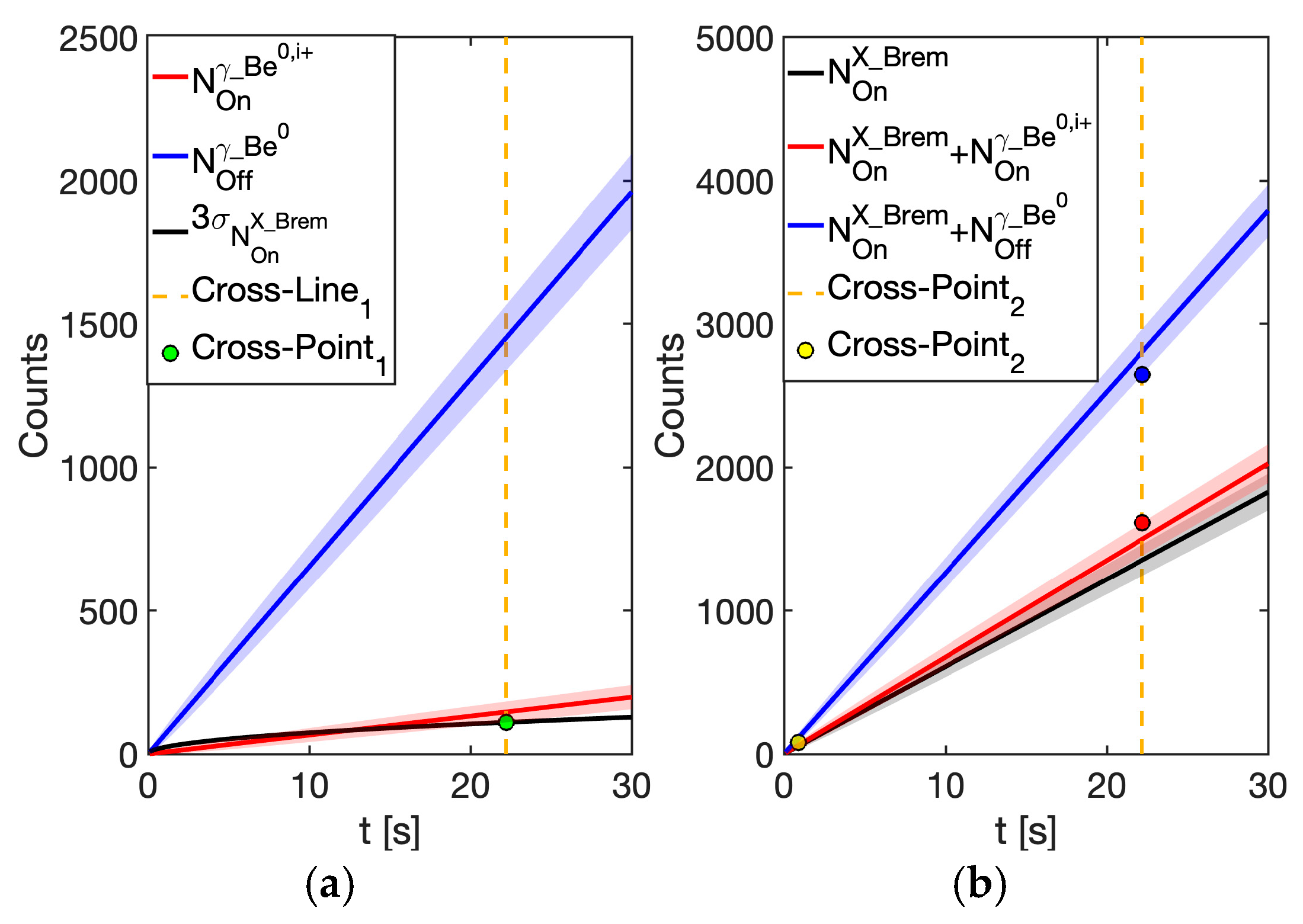
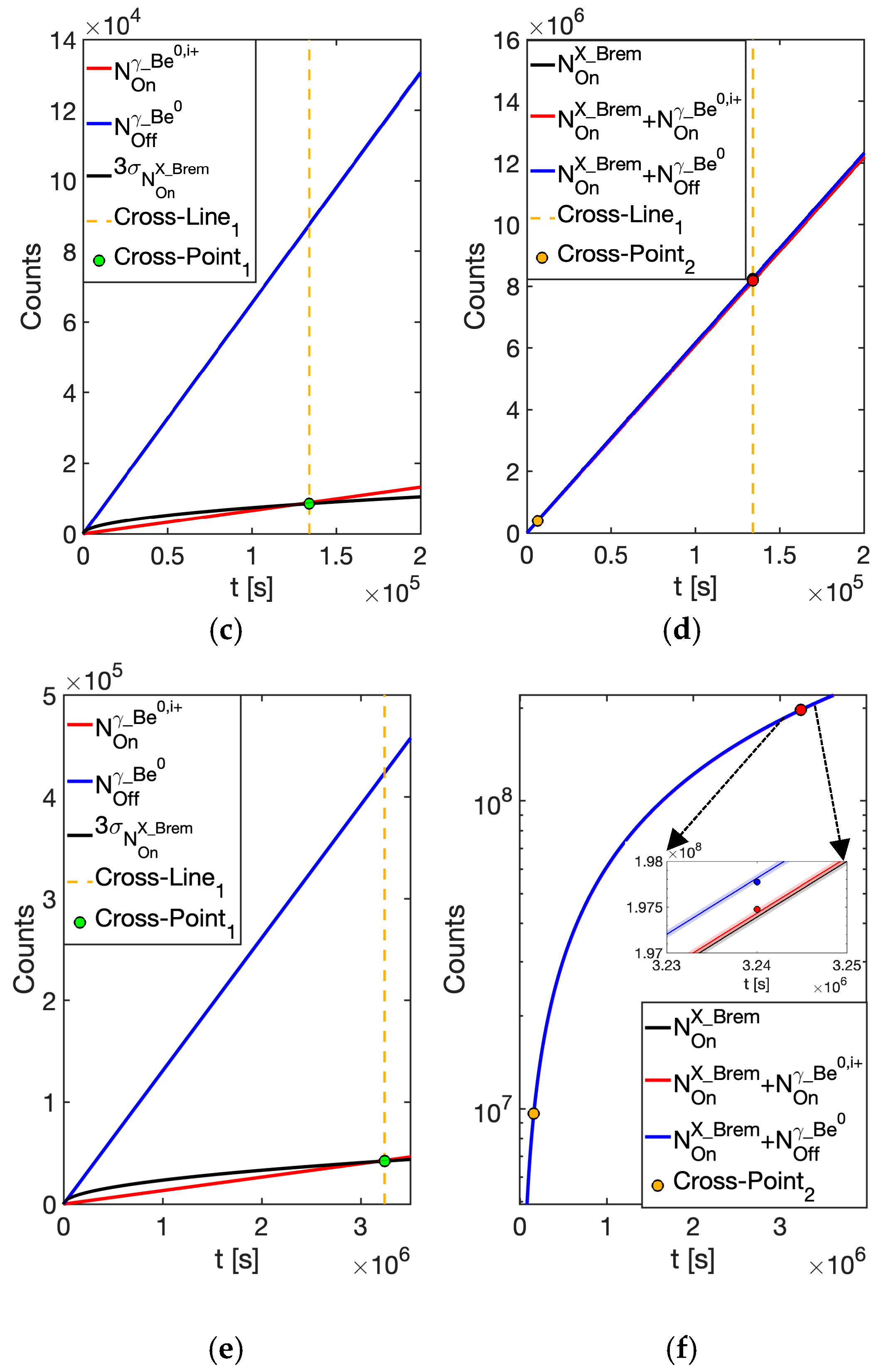

| Physical Cases | Isotope | t1/2 | Type of Decay | Daughter Nuclei | Eγ [keV] |
|---|---|---|---|---|---|
| PANDORA Phase-1 | 176Lu | 3.78 · 1010 [yr] | β- | 176Hf | 202.88 & 306.78 |
| 134Cs | 2.06 [yr] | β- | 134Ba | 795.86 | |
| 94Nb | 2.03 · 104 [yr] | β- | 94Mo | 871.09 | |
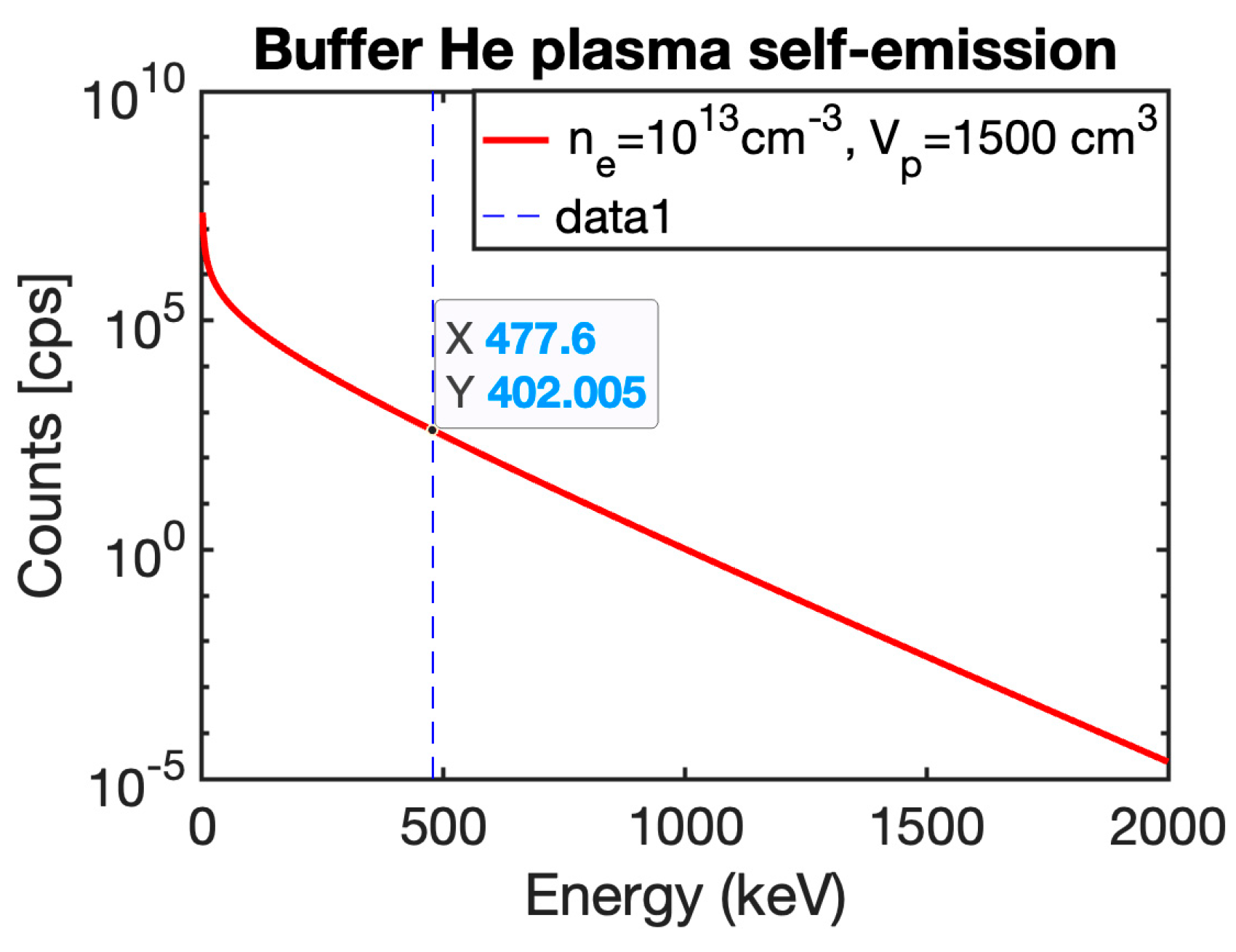
| PANDORA Phase-2 | 7Be | 53.2 [days] | EC | 7Li | 477.60 |
| SDD | CCD Pin-Hole System | HPGe Detector Array | Optical Spectrometer | RF Probe + Spectrum Analyzer | RF Probe + Scope | Polarimeter | Microwave Imaging Profilometry | Thomson Scattering | Analyzing Magnet + Faraday Cup | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
|
1–30 keV
(Soft X-Ray) |
0.4–20 keV
(soft X-Ray) |
30–2000 keV
(Hard X, g-Ray) |
1–12 eV
(Visible) |
10–26.5 GHz
(RF) |
10–26.5 GHz
(RF) |
90–100 GHz
(mm-Wave) |
60–100 GHz
(mm-Wave) |
1–1000 eV
(vis., UV, EUV) | // | ||
| Warm Electrons | Warm Electrons | Hot Electrons | Cold Electrons | // | // | Whole Electrons | Whole Electrons | Cold Electrons | |||
| Electron density ne | Volumetric | ene∼7% ∆E∼120 eV @ 8 keV | ene∼15–20% ∆E∼260 eV @ 8 keV | ene∼7% ∆E∼2.4 keV @ 1.3 MeV | ene∼10% Δλ = 0.035 nm, R = 13,900 | ene∼28% | ene∼10% ∆E∼0.009/1.24 eV @ 4.67/608 eV | ||||
| Space-resolved & Imaging | ene∼15–20% ∆s∼460 mm | ene∼1–13% | |||||||||
| Electron temperature Te | Volumetric | eTe∼5% ∆E∼120 eV @ 8 keV | eTe∼15–20% ∆E∼260 eV | eTe∼5% ∆E∼2.4 keV @ 1.3 MeV | eTe∼25–30% Δλ = 0.035 nm, R = 13,900 | eTe∼10% ∆E∼0.009/1.24 eV @ 4.67/608 eV | |||||
| Space- resolved & Imaging | eTe∼15–20% ∆s∼460 mm | ||||||||||
| Instable vs. stable regimes | Monitoring | Instability strengh, RBW 3 MHz, ∆t ≲ ms | Instability strengh, 80 Gs, ∆t ≲ ns | ||||||||
| Other info | soft X-ray bursts | plasma losses vs. core emissions | hard X-ray bursts | visible light bursts | RF bursts | RF bursts | |||||
| b-decay tagging | Technique | By g-ray tagging (sensitivity 3 s) | By mass spectrometry dq/dm = 1/200 | ||||||||
| CSD | Details | Online Δλ = 0.003 nm R = 164,000 | By beam extraction dq/dm = 1/200 | ||||||||
| Other info | Details | plasma structure, dynamics of losses and confinement | Local EM field intensity, e∼0.07–0.14 dB | EEDF, electron drift velocity | |||||||
| Charge State (i) | Electronic Configuration | Electron Capture Decay Rate [s−1] |
|---|---|---|
| 0+ | 1s22s2 | 1.51 × 10−7 |
| 1+ | 1s22s1 | 1.51 × 10−7 |
| 2+ | 1s2 | 1.46 × 10−7 |
| 3+ | 1s1 | 6.53 × 10−8 |
| 4+ | - | 0 |
| 7Be | ||||
| t0 [days] | 53.3 | |||
| Concentration | 10−6 | 5 × 10−6 | 5 × 10−5 | 5 × 10−4 |
| [cps] | 100 | 500 | 5010 | 50,039 |
| A [MBq] | 22,311 | 4683 | 555 | 80 |
| M [mg] | 1720 | 0.361 | 0.043 | 0.006 |
| [cps] | 40 | 199 | 1990 | 19,900 |
| Detected [cps] | 0.007 | 0.066 | 0.656 | 6552 |
| Concentration | 1 × 10−6 | 5 × 10−6 | 5 × 10−5 | 5 × 10−4 | |||||
|---|---|---|---|---|---|---|---|---|---|
| tm | 37.04 days | 100 days | 1.6 h | 15 days | 1600 s | 1 day | 23 s | 5 min | 1 h |
| 47% | 28% | 46% | 15% | 42% | 6% | 36% | 10% | 3% | |
| Relative | 0.01% | 0.004% | 0.03% | 0.01% | 0.32% | 0.04% | 2.7% | 0.7% | 0.2% |
| Δl* | 62.6% | 39.6% | 61.3% | 23.5% | 56.7% | 15.46% | 49.2% | 18.76% | 14.03% |
| A [GBq] | 22.31 | 60.24 | 4.68 | 45.09 | 0.55 | 29.97 | 0.08 | 1.04 | 12.49 |
| M [mg] | 1.72 | 4.64 | 0.36 | 3.48 | 0.043 | 2.31 | 0.006 | 0.08 | 0.96 |
| F | 10% | ||||||||
| N0 | 10% | ||||||||
| Δtm | 1 s | ||||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Naselli, E.; Mishra, B.; Pidatella, A.; Galatà, A.; Mauro, G.S.; Santonocito, D.; Torrisi, G.; Mascali, D. Laboratory Magnetoplasmas as Stellar-like Environment for 7Be β-Decay Investigations Within the PANDORA Project. Universe 2025, 11, 195. https://doi.org/10.3390/universe11060195
Naselli E, Mishra B, Pidatella A, Galatà A, Mauro GS, Santonocito D, Torrisi G, Mascali D. Laboratory Magnetoplasmas as Stellar-like Environment for 7Be β-Decay Investigations Within the PANDORA Project. Universe. 2025; 11(6):195. https://doi.org/10.3390/universe11060195
Chicago/Turabian StyleNaselli, Eugenia, Bharat Mishra, Angelo Pidatella, Alessio Galatà, Giorgio S. Mauro, Domenico Santonocito, Giuseppe Torrisi, and David Mascali. 2025. "Laboratory Magnetoplasmas as Stellar-like Environment for 7Be β-Decay Investigations Within the PANDORA Project" Universe 11, no. 6: 195. https://doi.org/10.3390/universe11060195
APA StyleNaselli, E., Mishra, B., Pidatella, A., Galatà, A., Mauro, G. S., Santonocito, D., Torrisi, G., & Mascali, D. (2025). Laboratory Magnetoplasmas as Stellar-like Environment for 7Be β-Decay Investigations Within the PANDORA Project. Universe, 11(6), 195. https://doi.org/10.3390/universe11060195







