Dissipative Kinematics in Binary Neutron Star Mergers

Abstract

We highlight the recent progress in the calculation of transport coefficients pertinent to binary neutron star mergers. Specifically, we analyze the bulk viscosity coefficient driven by both the DURCA and MURCA processes and electron transport coefficients in dense and hot plasma relevant to the merger scenario. The study considers high temperatures ($T>6\times {10}^{10}$ K) and dense environments ($n_B\sim n_0-3n_0$). Bulk viscosity exhibits resonant behavior, with peak values and peak positions dependent on particle interaction rates and thermodynamic susceptibilities. Susceptibilities are calculated by modeling the nuclear matter in the density functional approach. The bulk viscosity coefficient peaks at $T\sim {10}^{11}$ K, with a compression–rarefaction oscillation dissipation time scale of 20–50 ms. Electrical transports incorporate frequency-dependent dynamical screening in quantized electron–ion scattering rates. Consequently, dynamical screening reduces the maxima of electrical and thermal conductivities, shortening corresponding dissipation time scales. These results highlight the crucial role of dissipation coefficients in understanding binary neutron star mergers.

1. Introduction

The recent identification of gravitational waves by the LIGO–Virgo collaboration, from the multi-messenger binary neutron star merger (BNSM) event GW170817, prompts research in the field of the transport properties of dense nuclear matter under extreme scenarios of temperatures and densities relevant to this merger scenario [1,2,3]. BNSMs and collider experiments stand as the most extreme manifestations of matter in the universe, characterized by temperatures several tens of MeVs and a density of 5–7 times the nuclear saturation density $n_0\approx 0.16$ ${\mathrm{fm}}^{-3}$. Furthermore, the detection of short gamma-ray bursts (SGRBs) by the Fermi satellite GRB170817A hints at the presence of extreme magnetic fields during these merger events [4,5], making them important sources of gravitational radiation, electromagnetic emissions and neutrinos [6], thus offering a remarkable window into the study of nonlinear gravitational effects and intricate microphysical processes, akin to Einstein’s natural laboratory [7].

In BNSMs, immediately after the merger, the resulting dense object undergoes oscillations and dissipates energy through the emission of gravitational radiation until it eventually collapses into a black hole. Understanding neutron star mergers mandates expertise in General Relativistic Magneto Hydrodynamics (GRMHD) [6,8,9,10,11]. These advanced numerical simulations provide valuable insights into the post-merger object at the extremities of matter density and temperature limits. In this high-density environment, the significance of the dissipative effect through a specific transport coefficient is examined by analyzing the dissipation timescales during which these transport coefficients would influence the dynamics of the medium evolution. If this timescale aligns with the merger timescale, which spans tens to hundreds of milliseconds, the process may be considered relevant to mergers [12]. Recently, attempts have been made to study the significance of dissipative mechanisms in merger simulations in various studies [12,13,14,15,16,17,18,19,20,21,22,23,24]. A recent study by Alford et al. [12] explored the bulk viscosity coefficient ($\zeta$) arising from the MURCA process in the neutrino-transparent regime of BNSM. The authors have found that this mechanism leads to a dissipation timescale comparable to the merger’s survival time (milliseconds). Complementing this work, another study by Alford et al. [13] evaluated the bulk viscosity coefficient due to the URCA process within the neutrino-trapped regime.

In [21,22,25], the authors have extended the initial analyses by Alford et al. [12] by incorporating a more realistic appraisal of the bulk viscosity’s contribution to the pressure within a state-of-the-art neutron star merger simulation. This enables the identification of the specific stages and spatial regions where bulk viscosity has significant influence. Recently, in [18], the authors presented the magnetohydrodynamic (MHD) equations in both generic and curved spacetimes, addressing both the ideal-MHD limit and the presence of resistivity equations. Additionally, authors in ref. [19] have studied the impact of finite-temperature effects in numerical-relativity simulations of binary neutron star mergers, utilizing a full Bayesian analysis with microphysical equations of state and neutrino transport. In light of all of the studies mentioned, this review will focus on the relevance of bulk viscous dissipation, thermal conduction, and electrical conduction in the context of BNSM.

The bulk viscosity of these stars markedly influences the dissipation time-scale of stellar vibrations in neutron stars and the maximum rotation rate of millisecond pulsars. Vibrational and rotational instabilities induce density changes in vibrating stars, altering species concentrations primarily through direct URCA (DURCA) and modified URCA (MURCA) processes. Dissipation peaks when the rates of microscopic reactions align with the oscillation rates of the chemical potential. Recent investigations into the bulk viscosity in BNSM play an important role in estimation of dissipative time scales [12,25]. One of the aims of our study is to review the estimation of bulk viscous dissipation time scales due to the DURCA and MURCA process in high-temperature and high-density plasma, relevant to BNS mergers [13,26,27].

In most of the GRMHD simulations of merged objects [6,8,9,10,11], the framework of ideal MHD is employed. However, recent research [28] highlights the significant role of the Hall effect in the magnetic field decay of merged objects, suggesting the need to integrate this effect into ideal MHD simulations. In Ref. [15], the authors have reported the effects of dynamical screening on electrical conductivity, and in Ref. [29], the effects of dynamical screening on thermal conductivity in the context of BNSMs. Considering these insights, we review the calculations of electrical and thermal conductivities in fully ionized plasma by solving the Boltzmann equation. The current review employs modified Hard-Dense-Loop (HDL) propagators in the calculation of a relativistic medium. Key to our analysis is the quantification of transport coefficients, including Landau damping in quantized particle interaction rates in relativistic, magnetized hot and dense plasma. The significance of transport coefficients will be evaluated by comparing damping timescales to the characteristic duration of the post-merger phase (approximately 10–100 ms), alongside the timescales for thermal transport and dissipation.

The current review is organized as follows, in Section 2 we present the formalism of Bulk viscosity in hot and dense baryonic matter. Section 3 presents the results of Bulk viscosity. In Section 4 we present the microphysics of electrical conduction. Electrical conduction results have been presented in Section 5.

2. Bulk Viscosity in Hot and Dense Baryonic Matter

In this section, we review the significance of bulk viscosity in the context of BNSM. It might be recalled that bulk viscosity arises as a response to repetitive cycles of compression and rarefaction within a system. These oscillations lead to fluctuations in the density of conserved quantities, such as baryon number density, consequently affecting beta equilibration rates [24]. Thus the system’s response to changes in baryon number density is primarily determined by weak interaction rates. Weak interaction processes equilibrate at rates comparable to the frequency of density oscillations in compact objects, while strong interactions have a minimal impact [24].

This study considers the basic components of baryonic matter, specifically focusing on neutrons (n), protons (p), electrons (e), and neutrinos (${\nu }_e$), across density ranges from $0.5n_0$ to $3n_0$ (where $n_0$ is about $0.16$ ${\mathrm{fm}}^{-3}$) and temperature ranges from 5 to 50 MeV. However, as temperatures rise above 5 MeV, ${\nu }_e$ mean free path reduces to less than a kilometer and, hence, neutrinos become trapped. Notably, positrons are virtually absent in these conditions because the electron chemical potential is around 100 MeV. This significantly reduces the weak processes involving positrons by an approximate factor of $exp(-{\mu }_{{\nu }_e}/T)$.

Beta equilibration, in this context, occurs through DURCA and MURCA processes. In these two processes, if there is a proton deficit, protons are generated through neutron decay processes, as mentioned below [13,24],

$$\begin{array}{cc}\hfill n\to p+e^{-}+{\overline{\nu }}_e& \mathrm{Direct}\mathrm{Urca}\end{array}$$

(1)

$$\begin{array}{cc}\hfill n+N\to N+p+e+{\overline{\nu }}_e,& \mathrm{Modified}\mathrm{Urca}\end{array}$$

(2)

in the above equation, N represents a spectator neutron.

In DURCA and MURCA processes, if a deficit of neutrons exists, neutrons are produced through electron capture processes as written below [13,24],

$$\begin{array}{cc}\hfill e^{-}+p\to n+{\nu }_e& \mathrm{Direct}\mathrm{Urca}\end{array}$$

(3)

$$\begin{array}{cc}\hfill N+p+e\to N+n+{\nu }_e& \mathrm{Modified}\mathrm{Urca}\end{array}$$

(4)

In the dynamic environment of a neutron star merger, due to compression and decompression cycles, the baryonic matter deviates from $\beta$-equilibrium, which can be quantified by a non-zero chemical potential as defined below:

$$\begin{array}{c}\hfill {\mu }_{\Delta }\equiv {\mu }_n+{\mu }_{{\nu }_e}-{\mu }_p-{\mu }_e.\end{array}$$

(5)

In the above expression, ${\mu }_{\Delta }$ is non-zero due to density fluctuation, and re-equilibration of this quantity leads to bulk viscosity. The fluctuations of the chemical potential is given by

$$\begin{array}{c}\hfill \delta {\mu }_{\Delta }={\left.{\displaystyle \frac{\partial {\mu }_{\Delta }}{\partial n_B}}\right|}_x\delta n_B+{\left.{\displaystyle \frac{\partial {\mu }_{\Delta }}{\partial x}}\right|}_{n_B}\delta x.\end{array}$$

(6)

Now, taking the time derivative of ${\mu }_{\Delta }$, we arrive at

$$\begin{array}{c}\hfill {\displaystyle \frac{d{\mu }_{\Delta }}{dt}}=\mathcal{C}\omega {\displaystyle \frac{\Delta n_B}{{\overline{n}}_B}}cos\left(\omega t\right)+\mathcal{B}{\overline{n}}_B{\displaystyle \frac{dx}{dt}},\end{array}$$

(7)

where $\omega$ is the frequency of density oscillation, $n_B$ is the equilibrium baryon density, $\Delta n_B$ is the deviation of baryon density, and $\delta x$ is the deviation of the baryon density fraction from the equilibrium value. $\mathcal{B}$ represents the “beta-off-equilibrium–proton-fraction” susceptibility, which quantifies the relationship between the chemical potential deviating from beta equilibrium and the corresponding variation in the proton fraction. On the other hand, $\mathcal{C}$ denotes the “beta-off-equilibrium–baryon-density” susceptibility, which assesses the variation in off-equilibrium chemical potential concerning changes in baryon density while maintaining a fixed proton fraction,

$$\begin{array}{c}\hfill \mathcal{C}\equiv {\overline{n}}_B{\left.{\displaystyle \frac{\partial {\mu }_{\Delta }}{\partial n_B}}\right|}_x,\mathcal{B}\equiv {\displaystyle \frac{1}{{\overline{n}}_B}}{\left.{\displaystyle \frac{\partial {\mu }_{\Delta }}{\partial x}}\right|}_{n_B}.\end{array}$$

(8)

These two susceptibilities depend on the equation of state (EoS) of the system. To quantify the amount of dissipation due to bulk viscosity in the medium, we first estimate the susceptibilities of the medium. In the neutrino trapped baryonic medium, the susceptibilities are given by [13,24]

$$\begin{array}{ccc}\hfill \mathcal{B}& =& {\displaystyle \frac{1}{{\overline{n}}_B}}\left({\displaystyle \frac{\partial {\mu }_{{\nu }_e}}{\partial x_n}}{|}_{n_B}+{\displaystyle \frac{\partial {\mu }_n}{\partial x_n}}{|}_{n_B}-{\displaystyle \frac{\partial {\mu }_p}{\partial x_n}}{|}_{n_B}-{\displaystyle \frac{\partial {\mu }_e}{\partial x_n}}{|}_{n_B}\right),\hfill \end{array}$$

(9)

$$\begin{array}{ccc}\hfill \mathcal{C}& =& {\overline{n}}_B\left({\displaystyle \frac{\partial {\mu }_{{\nu }_e}}{\partial n_B}}{|}_{x_n}+{\displaystyle \frac{\partial {\mu }_n}{\partial n_B}}{|}_{x_n}-{\displaystyle \frac{\partial {\mu }_p}{\partial n_B}}{|}_{x_n}-{\displaystyle \frac{\partial {\mu }_e}{\partial n_B}}{|}_{x_n}\right).\hfill \end{array}$$

(10)

In the above equation, ${\mu }_n,{\mu }_p,{\mu }_e,{\mu }_{{\nu }_e}$ are the chemical potentials for neutron, proton, electron and neutrino, respectively, and $x_n$ is the neutron fraction. The net equilibration rate for a typical process can be written as follows:

$${\mathsf{\Gamma }}^{(\leftrightarrow )}\equiv {\mathsf{\Gamma }}^{(\to )}-{\mathsf{\Gamma }}^{(\leftarrow )}={\overline{n}}_B{\displaystyle \frac{\partial x}{\partial t}},$$

(11)

where ${\mathsf{\Gamma }}^{(\to )}$ is the forward weak interaction rate and ${\mathsf{\Gamma }}^{(\leftarrow )}$ is the backward weak interaction rate. The differential equation involving chemical fluctuation in Equation (7) can be expressed as follows:

$$\begin{array}{c}\hfill {\displaystyle \frac{dA\left(\varphi \right)}{d\varphi }}=dcos\left(\varphi \right)+{\displaystyle \frac{\mathcal{B}{\mathsf{\Gamma }}^{\leftrightarrow }}{\omega T}}.\end{array}$$

(12)

In the above equation, $\varphi \equiv \omega t$, $A\left(\varphi \right)={\mu }_{\Delta }/T$ with the pre-factors given by

$$\begin{array}{c}\hfill d\equiv {\displaystyle \frac{\mathcal{C}}{T}}{\displaystyle \frac{\delta n_B}{{\overline{n}}_B}},f\equiv {\displaystyle \frac{\mathcal{B}\tilde{\mathsf{\Gamma }}{T}^6}{\omega }}.\end{array}$$

(13)

$A\left(\varphi \right)$ can be evaluated by solving the differential Equation (12). The fluid within the post-merged object experiences repetitive cycles of compression and rarefaction, leading to energy dissipation. The rate of energy dissipation per unit volume due to these oscillations is expressed as [24]

$${\displaystyle \frac{dϵ}{dt}}=\zeta {\left(\overrightarrow{\nabla }·\overrightarrow{v}\right)}^2$$

(14)

where $\overrightarrow{v}$ is the local velocity of the fluid, $\zeta$ is the bulk viscosity. In the hydrodynamic limit after averaging the energy dissipation rate per volume over one time period the bulk viscosity can be written as

$$\zeta =-{\displaystyle \frac{1}{\pi }}{\displaystyle \frac{{\overline{n}}_B^3}{\Delta n_B}}{\int }_0^{\tau }{\displaystyle \frac{\partial {\mu }_{\Delta }}{\partial n_B}}{\int }_0^t{\displaystyle \frac{dx}{d{t}^{\prime }}}d{t}^{\prime }cos\left(\omega t\right)dt.$$

(15)

A detailed derivation of the bulk viscosity can be found in Ref. [24]. In the sub-thermal limit (${\mu }_{\Delta }/T\ll 1$), by expanding the interaction rate in Equation (11) in this limit of ${\mu }_{\Delta }/T$ while keeping terms only up to linear in powers of the expansion parameter, one can solve Equation (12) in order to obtain the bulk viscosity as [13,24]

$$\begin{array}{c}\hfill \zeta ={\displaystyle \frac{{\mathcal{C}}^2}{\mathcal{B}}}{\displaystyle \frac{{\mathsf{\Gamma }}^{\leftrightarrow }\mathcal{B}}{{\omega }^2+{\mathsf{\Gamma }}^{\leftrightarrow 2}{\mathcal{B}}^2}}.\end{array}$$

(16)

The above expression demonstrates the classic resonant form, governed by two components: the pre-factor, a ratio of susceptibilities ${\mathcal{C}}^2/\mathcal{B}$ solely dependent on the equation of state, and the relaxation rate ${\mathsf{\Gamma }}^{\leftrightarrow }$, which is determined by the rate of weak interactions. In the following sections, we present the detailed expressions of interaction rates of DURCA and MURCA processes.

2.1. DURCA Rate

In nuclear matter, the occurrence of DURCA and MURCA processes is dependent on specific density, as well as temperature conditions. Depending upon the equation of states, DURCA and MURCA start to occur at different baryonic densities [12]. In the trapped baryonic matter, the microscopic beta-equilibration rates for the neutron decay DURCA interaction rate ($n\to p+e^{-}+{\overline{\nu }}_e$ ) is defined as ${\mathsf{\Gamma }}_{1U}^{\leftrightarrow }$, whereas electron capture DURCA interaction rate ($e^{-}+p\to n+{\nu }_e$) is defined as ${\mathsf{\Gamma }}_{2U}^{\leftrightarrow }$. The twelve dimension interaction rates are given by [13]

$$\begin{array}{ccc}\hfill {\mathsf{\Gamma }}_{1U}^{\leftrightarrow }& =& {\mathsf{\Gamma }}_{1U}^{\to }-{\mathsf{\Gamma }}_{1U}^{\leftarrow }={\int }_{p_n,p_p,p_e,p_{{\nu }_e}}\sum {\left|{\mathcal{M}}_{DURCA}\right|}^2{\mathcal{P}}_{1U}{\left(2\pi \right)}^4{\delta }^{\left(4\right)}(p_p+p_e+p_{{\nu }_e}-p_n)\hfill \end{array}$$

(17)

$$\begin{array}{ccc}\hfill {\mathsf{\Gamma }}_{2U}^{\leftrightarrow }& =& {\mathsf{\Gamma }}_{2U}^{\to }-{\mathsf{\Gamma }}_{2U}^{\leftarrow }={\displaystyle \frac{1}{2}}{\int }_{p_n,p_p,p_e,p_{{\nu }_e}}\sum {\left|{\mathcal{M}}_{DURCA}\right|}^2{\mathcal{P}}_{2U}{\left(2\pi \right)}^4\delta (p_p-p_{{\nu }_e}+k_e-p_n),\hfill \end{array}$$

(18)

where the phase-space factors ${\mathcal{P}}_{1U}$ and ${\mathcal{P}}_{2U}$ are written as ${\mathcal{P}}_{1U}=f\left(p_n\right)[1-f\left(p_{{\nu }_e}\right)][1-f\left(p_{{\nu }_e}\right)][1-f\left(p_p\right)]-f\left(p_e\right)f\left(p_{{\nu }_e}\right)f\left(p_p\right)[1-f\left(p_n\right)]$, ${\mathcal{P}}_{2U}=f\left(p_n\right)f\left(p_{{\nu }_e}\right)[1-f\left(p_e\right)][1-f\left(p_p\right)]-f\left(p_{{\nu }_e}\right)f\left(p_p\right)[1-f\left(p_n\right)][1-f\left(p_{{\nu }_e}\right)]$, respectively. Explicitly, $f_i=1/(1+exp[({ϵ}_i-{\mu }_i)/T])$ are the Fermi–Dirac distributions for the species ($i=n,p,e$) with the chemical potential ${\mu }_i$. $p^{\prime }$, p are the four-momenta of the neutron and proton, respectively, and k and $k^{\prime }$ refer to the four-momenta of neutrino (antineutrino) and electron, respectively. In the above expression, the matrix element is given by [13]

$$\begin{array}{c}\hfill \sum |{\mathcal{M}}_{DURCA}{|}^2=32{\tilde{G}}^2(k·p^{\prime })(p·k^{\prime }),\end{array}$$

(19)

where ${\tilde{G}}^2=G_F^{2}cos{\theta }_c^2=1.29\times {10}^{-22}$ MeV⁻⁴ and $g_A=1.26$. For subsequent calculations, one can conveniently write the energy conserving delta functions as ${\delta }^{\left(4\right)}(p_p-p_n+q)=\delta ({\overrightarrow{p}}_p-{\overrightarrow{p}}_n+\overrightarrow{q})\delta ({ϵ}_p-{ϵ}_{p_n}+\omega )$, ${\delta }^{\left(4\right)}(p_e\pm p_{{\nu }_e}-q)=\delta (\overrightarrow{p_e}\pm \overrightarrow{p_{{\nu }_e}}-\overrightarrow{q})\delta ({ϵ}_{p_e}\pm {ϵ}_{p_{{\nu }_e}}-\omega )$. The energy delta function can be expressed as $\delta ({ϵ}_p\pm {ϵ}_{\overline{{\nu }_e}/{\nu }_e}+{ϵ}_e-{ϵ}_n-{\mu }_{\Delta })$, where, the argument of the $\delta$-function involves addition and subtraction of ${\mu }_{\Delta }$ and $p_0={ϵ}_p-\mu$.

Incorporating above changes, one can write the phase space factor as follows [13]:

$$\begin{array}{ccc}\hfill {\mathcal{P}}_{1U}& =& f\left(p^{\prime }\right)[1-f\left(p_e\right)][1-f\left(p_{{\nu }_e}\right)][1-f\left(p_p\right)]-f\left(p_e\right)f\left(p_{{\nu }_e}\right)f\left(p_p\right)[1-f\left(p_n\right)]\hfill \\ & =& g\left(q\right)[f\left({ϵ}_p\right)-f({ϵ}_p+\tilde{\omega })][1-f(\omega -{ϵ}_{p_{{\nu }_e}})][1-f\left({ϵ}_{p_{{\nu }_e}}\right)]\hfill \\ & -& f(\omega -{ϵ}_{{\nu }_e})f\left({ϵ}_{{\nu }_e}\right)[1+g\left(q\right)][f({ϵ}_p+\tilde{\omega })-f\left({ϵ}_p\right)],\hfill \end{array}$$

(20)

where $\tilde{\omega }=\omega -{\mu }_{\Delta }$, $g\left(q\right)$ is the Bose–Einstein distribution function. In the above expression, $p^{\prime }$ and $k^{\prime }$ integrations are performed using the three delta functions $\delta (\overrightarrow{p}-{\overrightarrow{p}}_n+\overrightarrow{q})$ and $\delta ({\overrightarrow{p}}_e-{\overrightarrow{p}}_{{\nu }_e}-\overrightarrow{q})$. After performing the integrations, the interaction rate becomes [13]

$$\begin{array}{ccc}\hfill {\mathsf{\Gamma }}_{1U}^{\leftrightarrow }& =& \int {\displaystyle \frac{d\omega }{2\pi }}\int {\displaystyle \frac{d^{3}q}{{\left(2\pi \right)}^3}}g(\omega -{\mu }_{\Delta }){\displaystyle \frac{m^{★2}T}{2\pi q}}ln\left|{\displaystyle \frac{1+exp\left(-\frac{{ϵ}_{\min }}{T}\right)}{1+exp\left(-\frac{{ϵ}_{\min }+\omega -{\mu }_{\Delta }}{T}\right)}}\right|\int {\displaystyle \frac{p_{{\nu }_e}^{2}d{p}_{{\nu }_e}}{{\left(2\pi \right)}^5}}[1-f(\omega -{ϵ}_{p_{{\nu }_e}})][1-f\left({ϵ}_{p_{{\nu }_e}}\right)]\hfill \\ & & {\int }_{-1}^{1}d{y}^{\prime }\delta \left(p_{{\nu }_e}+\sqrt{p_{{\nu }_e}^2+q^2-2p_{{\nu }_e}q{y}^{\prime }}-{\omega }^{\prime }\right),\hfill \end{array}$$

(21)

where $y^{\prime }$ is the angel between ${\mathbf{p}}_{{\nu }_e}$ and $\mathbf{q}$, ${\omega }^{\prime }=\omega +{\mu }_e-{\mu }_{{\nu }_e}$. After changing the variables $x=({ϵ}_{{\overline{\nu }}_e}+{\mu }_{{\nu }_e})/T$, $y=\omega /T$, $z=q/T$, ${\alpha }_{n,p,e,{\nu }_e}={\mu }_{n,p,e,{\nu }_e}/T$ and ${ϵ}_{\min }=p_{\min }^2/2m^{★}-{\mu }_p=(m^{★}/2q^2)\times {\left({\mu }_n^{★}-{\mu }_p^{★}+\omega -{\mu }_{\Delta }-{\displaystyle \frac{q^2}{2m^{★}}}\right)}^2-{\mu }_p^{★}$ [13,30]. For a detailed derivation, see also [13]. Now, the interaction rates can be further simplified as

$$\begin{array}{ccc}\hfill {\mathsf{\Gamma }}_{1U}^{\leftrightarrow }& =& {\displaystyle \frac{m^{★2}{\tilde{G}}^2}{8{\pi }^5}}{T}^6{\int }_{-{\alpha }_e+{\alpha }_{{\nu }_e}}^{\infty }dyg\left(y\right){\int }_0^{y+{\alpha }_e-{\alpha }_{\nu }}dzln\left|{\displaystyle \frac{1+exp\left(-y_0\right)}{1+exp\left(-y_0-y\right)}}\right|\hfill \\ & & \times {\int }_{(y+{\alpha }_e+{\alpha }_{{\nu }_e}-z)/2}^{(y+{\alpha }_e+{\alpha }_{\nu }+z)/2}dx(x-{\alpha }_{{\nu }_e})(y+{\alpha }_e-x)f(x-y)[1-f\left(x\right)],\hfill \end{array}$$

(22)

$$\begin{array}{ccc}\hfill {\mathsf{\Gamma }}_{2U}^{\leftrightarrow }& =& {\displaystyle \frac{m^{★2}{\tilde{G}}^2}{8{\pi }^5}}{T}^6{\int }_{-\infty }^{\infty }dyg\left(y\right){\int }_{|y+{\alpha }_e-{\alpha }_{\nu }|}^{\infty }dzln\left|{\displaystyle \frac{1+exp\left(-y_0\right)}{1+exp\left(-y_0-y)\right)}}\right|\hfill \\ & & {\int }_{-(y+{\alpha }_e+{\alpha }_{{\nu }_e}-z)/2}^{\infty }dx(x+{\alpha }_{\nu })(y+{\alpha }_e+x)f\left(x\right)[1-f(x+y)].\hfill \end{array}$$

(23)

In the above two equations, $y_0=(q^2-{\omega }^{\prime 2}+2{\omega }^{\prime }{p}_{{\nu }_e})/2kq$. The above two integrals are now evaluated numerically to obtain the numerical results presented in the Results of Bulk viscosity section later in this review paper.

2.2. MURCA Rate

The MURCA reactions entail both strong and weak interactions. In the neutrino trapped baryonic matter, the interaction rates for the neutron decay $n+N\to N+p+e+{\overline{\nu }}_e$ and the electron capture process $n+N\to N+p+e+{\overline{\nu }}_e$ are given by ${\mathsf{\Gamma }}_{1MU}^{\leftrightarrow }$ and ${\mathsf{\Gamma }}_{2MU}^{\leftrightarrow }$, respectively, and the form of these two reactions are mentioned below:

$$\begin{array}{cc}\hfill {\mathsf{\Gamma }}_{1MU}^{\leftrightarrow }& ={\mathsf{\Gamma }}_{1MU}^{\to }-{\mathsf{\Gamma }}_{1MU}^{\leftarrow }=\int {\displaystyle \frac{d^3{p}_n}{{\left(2\pi \right)}^3}}{\displaystyle \frac{d^3{p}_N}{{\left(2\pi \right)}^3}}{\displaystyle \frac{d^3{p}_N^{\prime }}{{\left(2\pi \right)}^3}}{\displaystyle \frac{d^3{p}_p}{{\left(2\pi \right)}^3}}{\displaystyle \frac{d^3{p}_e}{{\left(2\pi \right)}^3}}{\displaystyle \frac{d^3{p}_{{\nu }_e}}{{\left(2\pi \right)}^3}}\sum {\left|{\mathcal{M}}_{MURCA}\right|}^2{\mathcal{P}}_{1MU}\\ & {\left(2\pi \right)}^4{\delta }^4\left(p_n+p_N-p_N^{\prime }-p_p-p_e-p_{{\overline{\nu }}_e}\right),\end{array}$$

(24)

$$\begin{array}{cc}\hfill {\mathsf{\Gamma }}_{2MU}^{\leftrightarrow }& ={\mathsf{\Gamma }}_{2MU}^{\to }-{\mathsf{\Gamma }}_{2MU}^{\leftarrow }=\int {\displaystyle \frac{d^3{p}_n}{{\left(2\pi \right)}^3}}{\displaystyle \frac{d^3{p}_N}{{\left(2\pi \right)}^3}}{\displaystyle \frac{d^3{p}_N^{\prime }}{{\left(2\pi \right)}^3}}{\displaystyle \frac{d^3{p}_p}{{\left(2\pi \right)}^3}}{\displaystyle \frac{d^3{p}_e}{{\left(2\pi \right)}^3}}{\displaystyle \frac{d^3{p}_{{\nu }_e}}{{\left(2\pi \right)}^3}}\sum {\left|{\mathcal{M}}_{MURCA}\right|}^2{\mathcal{P}}_{2MU}\\ & {\left(2\pi \right)}^4{\delta }^4(p_n+p_p+p_e-p_N^{\prime }-p_n-p_{{\nu }_e}).\end{array}$$

(25)

In the above two equations, the phase space factors ${\mathcal{P}}_{1MU}$ and ${\mathcal{P}}_{2MU}$ are given by

$$\begin{array}{ccc}\hfill {\mathcal{P}}_{1MU}& =& [f\left(p_n\right)f\left(p_N\right)(1-f\left(p_N\right))(1-f\left(p_p\right))(1-f\left(p_{{\overline{\nu }}_e}\right))(1-f\left(p_e\right))\hfill \\ & -& f\left(p_N\right)f\left(p_p\right)f\left(p_e\right)f\left(p_{{\overline{\nu }}_e}\right)(1-f\left(p_N\right))(1-f\left(p_n\right))],\hfill \end{array}$$

(26)

$$\begin{array}{ccc}\hfill {\mathcal{P}}_{2MU}& =& [f\left(p_n\right)f\left(p_p\right)f\left(p_e\right)(1-f\left(p_N\right))(1-f\left(p_p\right))(1-f_{{\nu }_e})\hfill \\ & -& f\left(p_N\right)f\left(p_n\right)f\left(p_{{\overline{\nu }}_e}\right)(1-f\left(p_n\right))(1-f\left(p_p\right))(1-f\left(p_e\right))].\hfill \end{array}$$

(27)

The squared scattering matrix element $\sum |{\mathcal{M}}_{MURCA}{|}^2$ in Equations (24) and (25) is given by [31]

$$\begin{array}{c}\hfill \sum |{\mathcal{M}}_{MURCA}{|}^2=16G^2{\displaystyle \frac{21}{4}}{\left({\displaystyle \frac{f}{m_{\pi }}}\right)}^4{\displaystyle \frac{g_A^2}{{ϵ}_e^2}}{\displaystyle \frac{p_{fn}^4}{{(p_{fn}^2+m_{\pi }^2)}^2}},\end{array}$$

(28)

where $f\sim 1$ is the p-wave $\pi N$ coupling constant in the one pion exchange theory of N – N interaction, $m_{\pi }$ is the mass of pion and ${ϵ}_e$ is the energy of the electron.

To perform the energy integral, we use the following replacements in two delta functions. For the neutron decay process, the delta function takes the following form [27]:

$$\begin{array}{ccc}& & \delta (p_n+p_N-p_N^{\prime }-p_p-p_e-p_{{\overline{\nu }}_e})=\delta (x_1+x_2+x_3+x_4+x_5+(-x_6+{\mu }_{\Delta }/T))/T.\hfill \end{array}$$

(29)

In the above equation, $x_1=\beta ({ϵ}_n-{\mu }_n)$, $x_2=\beta ({ϵ}_N-{\mu }_N)$, $x_3=-\beta ({ϵ}_N^{\prime }-{\mu }_N)$, $x_4=-\beta ({ϵ}_e-{\mu }_e)$, $x_5=-\beta ({ϵ}_p-{\mu }_p)$, $x_6=\beta ({ϵ}_{{\overline{\nu }}_e}+{\mu }_e)$ [27]. For the electron capture process, the delta function can be written as shown below:

$$\begin{array}{c}\hfill \delta (p_N+p_p+p_e+p_{{\overline{\nu }}_e}-p_N^{\prime }-p_n)=\delta \left(x_1+x_2+x_3+x_4+x_5+\left(-x_6-{\mu }_{\Delta }/T\right)\right)/T,\end{array}$$

(30)

where $x_1=\beta ({ϵ}_n-{\mu }_n)$, $x_2=\beta ({ϵ}_p-{\mu }_p)$, $x_3=\beta ({ϵ}_e-{\mu }_e)$, $x_4=-\beta ({ϵ}_e-{\mu }_n)$, $x_5=-\beta ({ϵ}_N^{\prime }-{\mu }_N)$, $x_6=\beta ({ϵ}_{{\nu }_e}-{\mu }_{{\nu }_e})$.

In a concise notation, we express the interaction rate as ${\mathsf{\Gamma }}^{\to }-{\mathsf{\Gamma }}^{\leftarrow }=AI$, where A contains information about the angular integral, while I pertains to the energy integral. For the neutron decay process the energy integral is written as follows:

$$\begin{array}{ccc}& & I_1=\mathcal{C}onst{T}^7\int d{x}_{{\nu }_e}{x}_{{\nu }_e}^2\int {\mathsf{\Pi }}_{i=1}^{5}d{x}_i\hfill \\ & & [{(1+e^{x_i})}^{-1}(1-f_{{\overline{\nu }}_e})-{(1+e^{x_i})}^{-1}{f}_{{\overline{\nu }}_e}]\delta (x_1+x_2+x_3+x_4+x_5+(-x_6+{\mu }_{\Delta }/T))/T\hfill \\ & & =I_{10}-I_2\left(\nu \right)-I_3\left(\nu \right),\hfill \end{array}$$

(31)

where $\mathcal{C}onst=p_{fn}{m}_n{p}_{fN}{m}_N{p}_{fn}{m}_n{p}_{fp}{m}_p{p}_{fe}^2$. In the above equation, the contribution arising from terms containing antineutrino distribution functions ($I_2\left(\nu \right)$ and $I_3\left(\nu \right)$) are suppressed. Here, we have used $x_{{\nu }_e}=E_{{\nu }_e}/T$. The five dimensional integral for the neutron, proton, electron and spectator neutrons are evaluated following [27,32]:

$$\begin{array}{ccc}& & \int {\mathsf{\Pi }}_{i=1}^{5}d{x}_i{\left(1+e^{x_i}\right)}^{-1}\hfill \\ & & \delta \left(x_1+x_2+x_3+x_4+x_5+\left(-x_6+{\mu }_{\Delta }/T\right)\right)+\delta \left(x_1+x_2+x_3+x_4+x_5+\left(-x_6-{\mu }_{\Delta }/T\right)\right)\hfill \\ & =& [{\displaystyle \frac{1}{1+e^{(-x_6+{\mu }_{\Delta }/T)}}}{\displaystyle \frac{1}{4!}}({(-x_6+{\mu }_{\Delta }/T)}^4+10{\pi }^2{(-x_6+{\mu }_{\Delta }/T)}^2+9{\pi }^4)\hfill \\ & +& {\displaystyle \frac{1}{1+e^{(x_6+{\mu }_{\Delta }/T)}}}{\displaystyle \frac{1}{4!}}({(x_6+{\mu }_{\Delta }/T)}^4+10{\pi }^2{(x_6+{\mu }_{\Delta }/T)}^2+9{\pi }^4)].\hfill \end{array}$$

(32)

The above integrations have been performed by employing the following method [32]:

$$\begin{array}{c}\hfill \int {\mathsf{\Pi }}_{i=1}^{5}d{x}_i{\left(1+e^{x_i}\right)}^{-1}\delta \left(x_i+y\right)={\displaystyle \frac{1}{e^{-y}4!}}\left(y^4+10{\pi }^2{y}^2+9{\pi }^4\right).\end{array}$$

(33)

For the other MURCA process $N+p+e\leftrightarrow N+n+{\nu }_e$, the energy integral in the interaction rate (${\mathsf{\Gamma }}_2^{\leftrightarrow }$) is written as [27]

$$\begin{array}{ccc}& & I_2=\mathcal{C}onst{T}^7\int d{x}_{{\nu }_e}{x}_{{\nu }_e}^2\int {\mathsf{\Pi }}_{i=1}^{5}d{x}_i\hfill \\ & & \left[{\left(1+e^{x_j}\right)}^{-1}\left(1-f_{{\nu }_e}\right)-{\left(1+e^{x_j}\right)}^{-1}{f}_{{\nu }_e}\right]\delta \left(x_1+x_2+x_3+x_4+x_5+\left(-x_6-{\mu }_{\Delta }/T\right)\right)/T\hfill \\ & =& I_{20}-I_4\left(\nu \right)-I_5\left(\nu \right).\hfill \end{array}$$

(34)

The final expression for MURCA equilibration rate thus becomes [27]

$$\begin{array}{ccc}\hfill {\mathsf{\Gamma }}^{\leftrightarrow }& =& {\mathsf{\Gamma }}_1^{\leftrightarrow }+{\mathsf{\Gamma }}_2^{\leftrightarrow }=\tilde{\mathsf{\Gamma }}{T}^7\int d{x}_{{\nu }_e}{x}_{{\nu }_e}^2{\displaystyle \frac{1}{1+e^{(-x_6+{\mu }_{\Delta }/T)}}}{\displaystyle \frac{1}{4!}}\left[\left({\displaystyle \frac{{\mu }_{\Delta }}{T}}-x_6{)}^4+10{\pi }^2{\left({\displaystyle \frac{{\mu }_{\Delta }}{T}}-x_6\right)}^2+9{\pi }^4\right)\right]\hfill \\ & +& {\displaystyle \frac{1}{1+e^{(-x_{{\nu }_e}+{\mu }_{{\nu }_e}/T)}}}{\displaystyle \frac{1}{1+e^{(-x_6-{\mu }_{\Delta }/T)}}}{\displaystyle \frac{1}{4!}}\left[\left({\displaystyle \frac{{\mu }_{\Delta }}{T}}+x_6{)}^4+10{\pi }^2{({\displaystyle \frac{{\mu }_{\Delta }}{T}}+x_6)}^2+9{\pi }^4\right)\right]\hfill \\ & -& {\displaystyle \frac{1}{1+e^{(x_{{\nu }_e}-{\mu }_{{\nu }_e}/T)}}}{\displaystyle \frac{1}{1+e^{(-x_6-\frac{{\mu }_{\Delta }}{T})}}}{\displaystyle \frac{1}{4!}}\left[\left({\displaystyle \frac{{\mu }_{\Delta }}{T}}+x_6{)}^4+10{\pi }^2{({\displaystyle \frac{{\mu }_{\Delta }}{T}}+x_6)}^2+9{\pi }^4\right)\right],\hfill \end{array}$$

(35)

where $\tilde{\mathsf{\Gamma }}=4.68\times {10}^{-19.0}{(x_p{n}_B/n_0)}^{1/3}{\mathrm{M}\mathrm{e}\mathrm{V}}^{-4}$ ($x_p$ is the proton fraction).

3. Results

Bulk Viscosity

In this section, we quantify the dissipation arising from bulk viscous effects. Our medium comprises nuclear matter constituents such as neutrons, protons, electrons, and electron neutrinos. Following a neutron star merger, the temperature surpasses the trapped neutrino temperature, thus necessitating consideration of non-zero neutrino chemical potentials. These chemical potentials for constituent particles are obtained from the equation of state like NL3 [33]. NL3 features density-independent meson-nucleon couplings and nonlinear parametrization. Analytical expressions for chemical potentials in the medium are given by [13,24,27]

$$\begin{array}{ccc}\hfill {\mu }_n^{★}& =& \sqrt{m_n^2+{\left(3{\pi }^2{x}_n{n}_B\right)}^{2/3}}+g_{\omega }{\omega }_0-{\displaystyle \frac{1}{2}}{g}_{\rho }{\rho }_0^3,\hfill \\ \hfill {\mu }_p^{★}& =& \sqrt{m_p^2+{\left(3{\pi }^2{x}_n{n}_B\right)}^{2/3}}+g_{\omega }{\omega }_0+{\displaystyle \frac{1}{2}}{g}_{\rho }{\rho }_0^3\hfill \\ \hfill {\mu }_e^{★}& =& {\left(3{\pi }^2{x}_p{n}_B\right)}^{1/3},\hfill \\ \hfill {\mu }_{{\nu }_e}^{★}& =& {\left(3{\pi }^2{\overline{x}}_{{\nu }_e}{n}_B\right)}^{1/3},\hfill \end{array}$$

(36)

where $x_p$, $x_n$ and $x_{{\nu }_e}$ are the protons, neutrons and neutrinos fractions, respectively. $m_n$ and $m_p$ are the mass of neutrons and protons, respectively. $g_{\omega }$ and $g_{\rho }$ are the couplings of the $\omega$ and $\rho$ mesonic fields. The bulk viscosity can be derived from susceptibilities $\mathcal{B}$ and $\mathcal{C}$, obtained through the chemical potentials defined above Equation (10) [13,27].

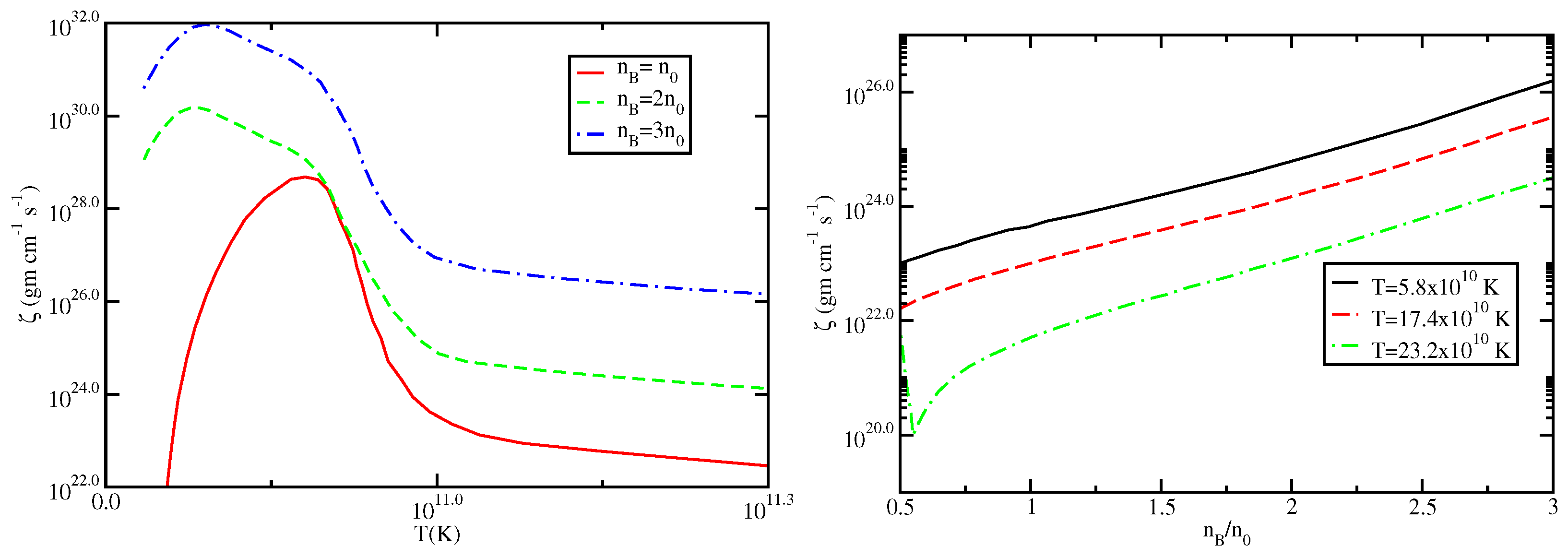
In Figure 1, the temperature and density variations in $\zeta$ driven by the DURCA process have been presented in the left and right panel, respectively [13]. In the left panel of the figure, the solid red line corresponds to $n_B=n_0$, the green dashed line corresponds to $n_B=2n_0$, and the blue dashed dotted line corresponds to $n_B=3n_0$. The bulk viscosity, which is a function of the temperature at a fixed oscillation frequency $\omega$, follows the standard resonant form, thus exhibiting a maximum when the beta relaxation rate matches with $\omega$ as $8.48$ kHz, corresponding to the oscillation frequency of the quadrupole r-mode of a neutron star [24]. The temperature dependence of $\zeta$ mainly arises from the ${\mathsf{\Gamma }}^{\leftrightarrow }$, via the relation ${\mathsf{\Gamma }}^{\leftrightarrow }\propto T^2$. Hence, increasing temperature leads to a higher relaxation rate from phase space expansion. This results in a bulk viscosity that decreases quadratically with temperature following $\zeta \propto T^{-2}$.

The right panel of Figure 1 illustrates the density dependence of the bulk viscosity across various temperature values. In Figure 1, we present the curves for three different temperatures, where the solid black curve corresponds to $T=5.8\times {10}^{10}$ K, and the red dashed curve corresponds to $T=17.4\times {10}^{10}$ K and $T=23.2\times {10}^{10}$ K. Since the beta relaxation rate is nearly independent upon the baryon density, the density dependence of the bulk viscosity mirrors that of the susceptibilities and, thus, increases with density [13]. The prefactor ${\mathcal{C}}^2/\mathcal{B}$ in Equation (16) gradually increases with density (please see Figure 6 of Ref. [13]). Consequently, $\zeta$ also increases with density, following the same pattern.

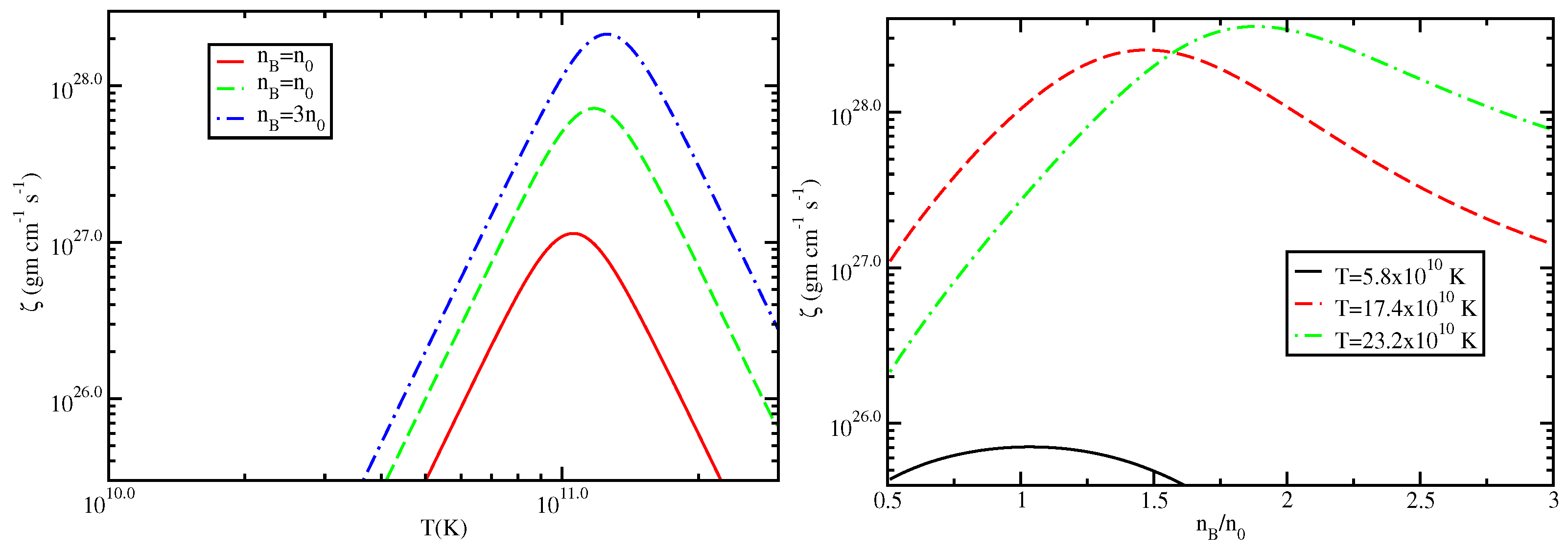
In Figure 2, we present plots showing the variation in $\zeta$ with temperature, considering the MURCA interaction rate both in neutrino transparent and neutrino trapped matter. The black, red, and green curves represent the bulk viscosity of baryonic matter without trapped neutrinos. The resonant curve for the zeta particle interaction rate emerges when the interaction rate aligns with $\omega$. Specifically, the black solid curve corresponds to $n_B=n_0$, the red dashed curve to $n_B=2n_0$, and the green dashed-dotted curve to $n_B=3n_0$. The blue, orange, and dark green curves represent the bulk viscosity of baryonic matter with trapped neutrinos. The blue dotted curve corresponds to $n_B=n_0$, the orange double dot-dashed curve to $n_B=2n_0$, and the dark green double dashed-dotted curve to $n_B=3n_0$. From these curves, it can be seen that the maximum bulk viscosity occurs at a temperature of $4.84\times {10}^{10}$ K, with a value of $1.14\times {10}^{27}$ g cm⁻¹ s⁻¹ for $n_B=n_0$ when the neutrino chemical potential is zero. With a non-zero ${\nu }_e$, the maximum bulk viscosity shifts to $10.21\times {10}^{10}$ K, with a value of $\sim {10}^{28}$ g cm⁻¹ ${\mathrm{s}}^{-1}$. The calculation employs two equations of state (EoS): a free-hadron EoS for the neutrino-transparent matter, and NL3 EoS for the neutrino-trapped matter. The position of the peak changes with the inclusion of neutrinos, shifting the peak position by a factor of $2.10$ compared to the neutrino transparent scenario. This is because the inclusion of neutrinos alters the interaction rate, and the peak position of the curve primarily depends on the particle interaction rate.

In Figure 3, the variation in $\zeta$ with temperature is plotted for different densities using NL3 EoS. Specifically, the solid red curve, green dashed curve, and blue dashed-dotted curve correspond to $n_B=n_0$, $n_B=2n_0$, and $n_B=3n_0$, respectively. It is observed that the height of the maxima changes with the density. This is due to the fact that the height of the peak depends upon the density dependent factors like the susceptibilities ($\mathcal{B},\mathcal{C}$) of the medium. The temperature and density of the hadronic medium are chosen to ensure that the degeneracy condition ${\mu }_i\ll T$ (i = n, p, e, ${\nu }_e$) is maintained. Insights into the density dependence of $\zeta$ are presented in the right panel of Figure 3. Examination of $\zeta$ suggests that the interaction rate demonstrates minimal density dependence, whereas the plots mirrors the combined characteristics of both $\mathcal{B}$ and $\mathcal{C}$. For both temperature-dependent and density-dependent plots, we have considered the frequency of density oscillation as $8.48$ kHz. The dissipation time scale is calculated using ${\tau }_{\zeta }=K{n}_B{t}_{dns}^2/\left(36{\pi }^2{\zeta }_{max}\right)$ [12]. ${\tau }_{\zeta }\sim 50$ ms considering K as the nuclear compressibility ($\sim 250$ MeV), $t_{dns}\sim 1$ ms, and ${\zeta }_{max}$ as the maxima of the bulk viscosity.

4. Electrical Conduction

This section presents transport theory formulation for the electrical ($\sigma$) and thermal conductivity ($\kappa$) coefficients in magnetized electron–ion plasmas. In compact objects, intense magnetic fields cause the electron motion to become quantized within the QED plasma. Under these conditions, both thermal and electrical conductivities exhibit anisotropy, and the conductivity tensor is represented as follows [34]:

$$\sigma /\kappa =\left(\begin{array}{ccc}{\sigma }_{\perp }/{\kappa }_{\perp }& -{\sigma }_H/{\kappa }_H& 0\\ {\sigma }_H/{\kappa }_H& {\sigma }_{\perp }/{\kappa }_{\perp }& 0\\ 0& 0& {\sigma }_{\Vert }/{\kappa }_{\Vert }\end{array}\right).$$

(37)

In the above expression, ${\sigma }_{\Vert }/{\kappa }_{\Vert }$ is the parallel component and ${\sigma }_{\perp }/{\kappa }_{\perp }$ is the perpendicular component of electrical/thermal conductivity in presence of external magnetic field along the z direction. ${\sigma }_H/{\kappa }_H$ is defined as the Hall coefficient. Next, we calculate the expressions of the quantized ${\sigma }_{\Vert }/{\kappa }_{\Vert }$ in the electron–ion plasma.

$\sigma$ and $\kappa$ are related to the electric current (j) and thermal current (q) via hydrodynamic constitutive relations $j=\sigma E$ (where E is the electric field), $q=-\kappa \nabla T$. From kinetic theory, the current density (j) and thermal currents (q) are given by

$$\begin{array}{ccc}\hfill j& =& {\displaystyle \frac{em{\omega }_B}{4{\pi }^2}}\sum _{n=0}^{\infty }\sum _{s=\pm }{\int }_{m{c}^2}^{\infty }{\mathsf{\Phi }}_{n,p_z,s}d{ϵ}_p,\hfill \\ \hfill q& =& {\displaystyle \frac{m{\omega }_B}{4{\pi }^2}}\sum _{n=0}^{\infty }\sum _{s=\pm }{\int }_{m{c}^2}^{\infty }({ϵ}_p-\mu ){\mathsf{\Phi }}_{n,p_z,s}d{ϵ}_p,\hfill \end{array}$$

(38)

where m, e are the mass and charge of an electron, respectively. ${\omega }_B=eB/m$, n being the number of the quantized electronic level in presence of magnetic field, $p_z$ is the z component of electron’s momentum, ${ϵ}_p$ is the energy of electron, and s is the spin. ${\mathsf{\Phi }}_{n,p_z,s}$ contains the information of the off-equilibrium distribution function arising because of the presence of an electromagnetic field in the plasma. By solving the Boltzmann equation in the presence of a magnetic field, one can calculate ${\mathsf{\Phi }}_{n,p_z,s}$. Because of presence of a magnetic field along the z direction in plasma, the symmetry of the system is broken. The transport equation for electrons present in the plasma follows from the Boltzmann equation in magnetic field and is given by [34]

$${\displaystyle \frac{\partial f_{n{p}_{z}s}}{\partial t}}+v_z{\displaystyle \frac{\partial f_{n{p}_{z}s}}{\partial z}}-\dot{\mathbf{p}}.{\displaystyle \frac{\partial f_{n{p}_{z}s}}{\partial p_z}}=\mathcal{C}\left[f\right].$$

(39)

In the above equation, $f_{n,p_z,s}$ describes the population of electrons which are defined by the quantum state $n,s,p_z$. The right hand side of the equation represents the collisional integral involving the particle interaction rates,

$$\begin{array}{c}\hfill \mathcal{C}\left[f\right]={\displaystyle \frac{\partial f_{n,p_z,s}}{\partial t}}{|}_{coll}=\sum _f{I}_{fi}\left(f_{n,p_z,s\to n^{\prime },p_z^{\prime },s^{\prime }}\right).\end{array}$$

(40)

The collision integral consists of the interaction of electrons and ions and the form of the integral is given below:

$$\begin{array}{ccc}\hfill I_{fi}& =& {\displaystyle \frac{1}{2{ϵ}_p}}\int {\displaystyle \frac{d^3{p}^{\prime }}{{\left(2\pi \right)}^{3}2{ϵ}_{p^{\prime }}}}\int {\displaystyle \frac{d^{3}k}{{\left(2\pi \right)}^{3}2{ϵ}_k}}\int {\displaystyle \frac{d^3{k}^{\prime }}{{\left(2\pi \right)}^{3}2{ϵ}_{k^{\prime }}}}\left[f_{n,p_z,s}{g}_k(1-f_{n^{\prime },p_z^{\prime },s^{\prime }})-f_{n^{\prime },p_z^{\prime },s^{\prime }}{g}_{k^{\prime }}(1-f_{n,p_z,s})\right]\hfill \\ & & {\left(2\pi \right)}^4{\delta }^4\left(p+k-p^{\prime }-k^{\prime }\right){\left|{\mathcal{M}}_{fi}\right|}^2\hfill \end{array}$$

(41)

where ${\mathcal{M}}_{fi}$ is the electron–ion scattering matrix and $g_k$ is distribution function of ions. Now, ${\mathcal{M}}_{fi}$ can be written as [35]

$$\begin{array}{c}\hfill {\mathcal{M}}_{fi}=-{\Delta }_L{J}_0{J}_0^{\prime }+{\Delta }_T{J}_t{J}_t^{\prime }=-{\mathcal{M}}_L+{\mathcal{M}}_T,\end{array}$$

(42)

where $J^{\mu }$ and $J^{\prime \mu }$ are the components of currents given by $J^{\mu }=-e^{*}\overline{u}\left(p^{\prime }\right){\gamma }^{\mu }u\left(p\right)$ and $J^{\prime \mu }=Z{e}^{*}{v}_k^{\mu }=Z{e}^{*}(1,\overrightarrow{k}/M)$. Also, $e^{★}=\sqrt{4\pi }e$, and $v_k$ is the velocity of the ion having momentum k. In the above equation, ${\Delta }_T$ and ${\Delta }_L$ are transverse and longitudinal HDL effective photon propagators, respectively, given explicitly by

$$\begin{array}{c}\hfill {\Delta }_L={\displaystyle \frac{1}{q^2-3m_D^2\left[1-y^2-\frac{y(1-y^2)}{2}ln\left(\frac{y+1}{y-1}\right)\right]}},{\Delta }_T={\displaystyle \frac{1}{q^2-3m_D^2\left[\frac{y^2}{2}+\frac{y(1-y^2)}{2}ln\left(\frac{y+1}{y-1}\right)\right]}}.\end{array}$$

(43)

In the above expression, q represents the exchanged four-momentum, with $y=q_0/q$, and $m_D$ denotes the Debye mass. The final form of magnetically modified interaction rate is mentioned below [15,29]:

$$\begin{array}{ccc}\hfill I_{fi}& =& {\displaystyle \frac{n_i}{2}}\sum _{n^{\prime },p_z^{\prime },s^{\prime }}\int du\left({\mathsf{\Phi }}_{n,p_z,s}-{\mathsf{\Phi }}_{n^{\prime },p_z^{\prime },s^{\prime }}\right)\left[{\displaystyle \frac{1}{3(\xi +\frac{m_D^2}{3})(\xi +m_D^2)}}-{\displaystyle \frac{v_k^2}{6\xi (\xi +\frac{m_D^2}{3})}}\right]\mathcal{F}.\hfill \end{array}$$

(44)

where $\xi =m_D^2/2m{\omega }_B$ and

$$\begin{array}{ccc}\hfill & & \mathcal{F}={\displaystyle \frac{4\pi {\sigma }_0}{m^2}}\sum _{n^{\prime },p_z^{\prime },s^{\prime }}[1+s{s}^{\prime }+{\displaystyle \frac{m^2}{{ϵ}_p^2}}(1-s{s}^{\prime })[1+s{s}^{\prime }-{\displaystyle \frac{1}{2}}{\displaystyle \frac{s{s}^{\prime }}{{ϵ}_p^2-m^2}}{({\eta }^{\prime }{p}_{n^{\prime }}-p_z)}^2]\hfill \\ & & [F_{n^{\prime },n}^2\left(u\right)+F_{n^{\prime }-1,n-1}^2\left(u\right)]]-{\displaystyle \frac{s{s}^{\prime }u{\omega }_{B}m}{{ϵ}_p^2-m^2}}[F_{n^{\prime }-1,n}^2\left(u\right)+F_{n^{\prime },n-1}^2\left(u\right)]\hfill \\ & & -{\displaystyle \frac{s{p}_z+s^{\prime }{\eta }^{\prime }{p}_n^{\prime }}{\sqrt{{ϵ}_p^2-m^2}}}[F_{n^{\prime },n}^2\left(u\right)-F_{n^{\prime }-1,n-1}^2\left(u\right)].\hfill \end{array}$$

(45)

The energy states are denoted by quantum numbers $ϵ,p_z,n,s$. $s=\pm 1$ is the helicity, and n enumerates the Landau levels. ${\eta }^{\prime }=\pm$, $F_{n^{\prime },n}\left(u\right)=ex{p}^{-u/2}{u}^{{\displaystyle \frac{n-n^{\prime }}{2}}}\sqrt{{\displaystyle \frac{n^{\prime }!}{n!}}}{L}_{n^{\prime }}^{n-n^{\prime }}$ and $u={\displaystyle \frac{1}{2m{\omega }_B}}(q_x^2+q_y^2)$. The functions $L_{n^{\prime }}^{n-n^{\prime }}\left(u\right)$ are Laguerre polynomials, and $F_{n^{\prime },n}\left(u\right)$ are normalized to ${\int }_0^{\infty }{F}_{n^{\prime },n}^{2}du=1$.

To determine the transport coefficients, it is beneficial to introduce a dimensionless scattering rate and a dimensionless alteration to the distribution function,

$$\begin{array}{ccc}\hfill & & {\displaystyle \frac{I_{fi}}{n_i{v}_z{\sigma }_0}}=a,\hfill \\ & & {\displaystyle \frac{eE}{{\sigma }_0{n}_i}}{\displaystyle \frac{\partial f_0}{\partial {ϵ}_p}}\mathsf{\Psi }=\mathsf{\Phi },\hfill \end{array}$$

(46)

where ${\sigma }_0=\pi Z^2{e}^4/{\omega }_B^2$, $n_i$ is the number density of ions, and $v_z$ is the z component of the particle velocity. The final result can be expressed in the form [15,29]

$$\left(\begin{array}{c}\sigma \\ \kappa \end{array}\right)=\left(\begin{array}{c}{\displaystyle \frac{{\delta }_0}{\theta }}{\int }_1^{\infty }\mathsf{\Psi }{f}_0(1-f_0)d\mathcal{E}\\ {\displaystyle \frac{{\pi }^{2}T}{3e^2}}\left[{\displaystyle \frac{{\delta }_0}{\theta }}{\int }_1^{\infty }{{\displaystyle \frac{({ϵ}_p-\mu )}{T^2}}}^2\mathsf{\Psi }{f}_0(1-f_0)d\mathcal{E}-{\displaystyle \frac{{\delta }_0}{T\theta }}{\displaystyle \frac{{\int }_1^{\infty }({ϵ}_p-\mu )\mathsf{\Psi }{f}_0(1-f_0)d\mathcal{E}}{{\int }_1^{\infty }\mathsf{\Psi }{f}_0(1-f_0)d\mathcal{E}}}\right]\end{array}\right).$$

(47)

where $\mathcal{E}={ϵ}_p/m$, $\mathsf{\Psi }=({\mathcal{E}}^2-1)/2Q_2$, ${\delta }_0$ is a constant and is given by ${\delta }_0=m^4{b}^2/8{\pi }^3{Z}^2{e}^2{n}_i$, $\theta =T/m$ and $b=B/B_c$, $B_c$ is the critical field given by $4.413\times {10}^{13}$ G.

5. Results

Electrical and Thermal Conductivity

In this section, we present the plots for the quantized longitudinal electronic transport coefficients in dense and hot magnetized QED plasma, pertinent to BNS merger simulations. The analysis accounts for electron–ion scattering through screened electromagnetic interaction in plasma. Plots illustrating the variation in transport coefficients with density, temperature, and magnetic field are presented for Fe. The plotted scales adhere to conditions of relativistic electrons at densities $\rho >{10}^6$ g cm⁻³, and temperatures $T>5.93\times {10}^9$ K. The specified density and temperature, combined with a magnetic field of approximately ${10}^{17}$ G, meet the criteria for the zeroth Landau level population, as dictated by the equation $\sqrt{({\mathcal{E}}^2-1)}/2b\ll 1$. These constraints validate the high magnetic field and low-density regime of BNS mergers as the physical domain for our calculations.

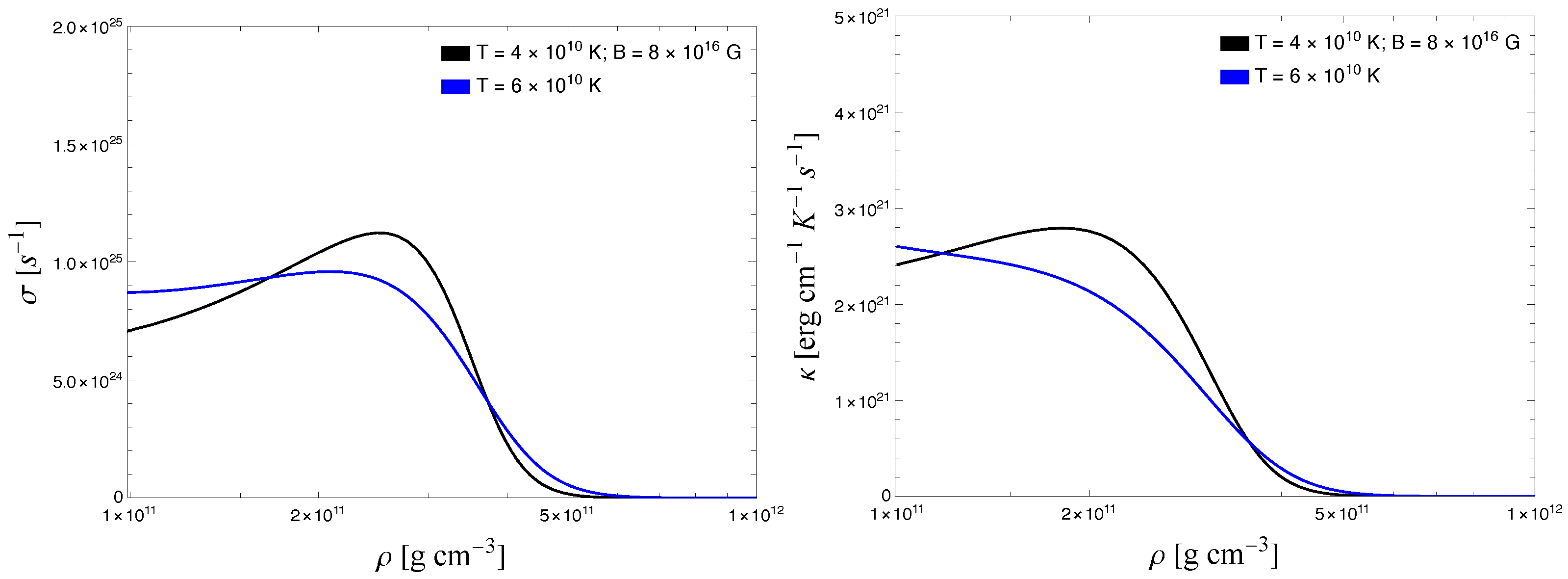
In Figure 4, we present the plots for the variation in $\sigma$ and $\kappa$ obtained by numerically evaluating Equation (47) with $\rho$ for two temperatures and a fixed magnetic field. Since the electrons need to be relativistic, the density and temperatures are chosen as $\rho \gg {10}^{11}$ g cm⁻³ and $T\sim {10}^{10}$ K, respectively. The parameters influencing the population of the zeroth Landau level include: $T_{\mathrm{c}e}\approx 1.343\times {10}^8{B}_{12}\mathrm{K}$, ${\rho }_B=7.045\times {10}^3{\displaystyle \frac{A}{Z}}{\left(B_{12}\right)}^{3/2}\mathrm{g}{\mathrm{cm}}^{-3}$, and $B_{12}=B/{10}^{12}$, and ${\omega }_{ce}$ is the cyclotron frequency for electrons. B is strongly quantizing if $\rho <{\rho }_B$ and $T\ll T_{ce}$, to ensure the population of the zeroth Landau level. The weak degeneracy condition ($|{ϵ}_p-\mu |\sim T$) of the electron distribution function causes the feature of the differentiated Fermi function at $T\ll \mu$. The hump in the curve at temperatures $T=4\times {10}^{10}$ K and $T=6\times {10}^{10}$ K arise due to satisfying the weak degeneracy condition of the electron distribution function. Both the curves resemble the shape of a differentiated Fermi function. It is observed from the plots that, with increasing temperature, electrons become non-degenerate leading to broadening of the hump.

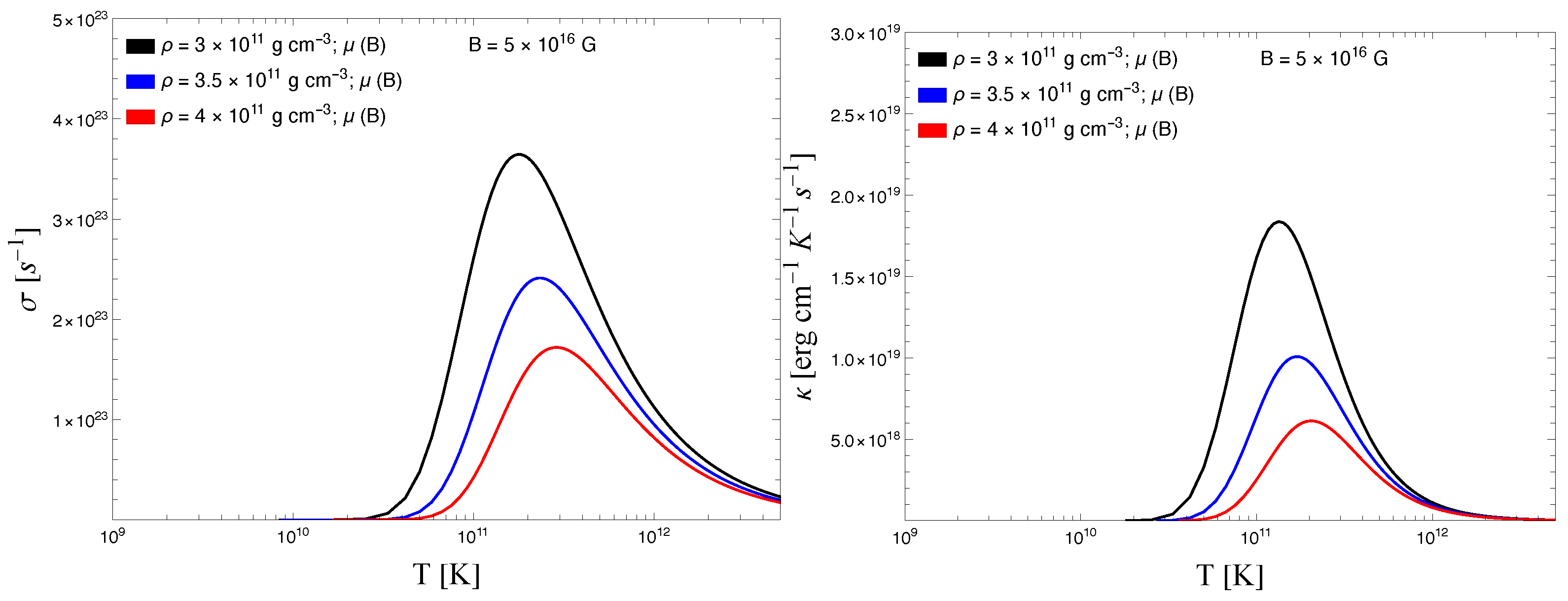
Next, Figure 5 shows the results of $\sigma$ and $\kappa$ with T for three different densities at a fixed magnetic field. The variation in $\sigma$ follows the temperature dependence through the relation $\sigma ={(a+b\times T^c)}^{-1}$, whereas at low temperatures, the effect of $T^c$ is found to be small, leading to constant $\sigma$. However, at high temperatures, $\sigma \propto T^{-c}$ and decreases with the temperature.

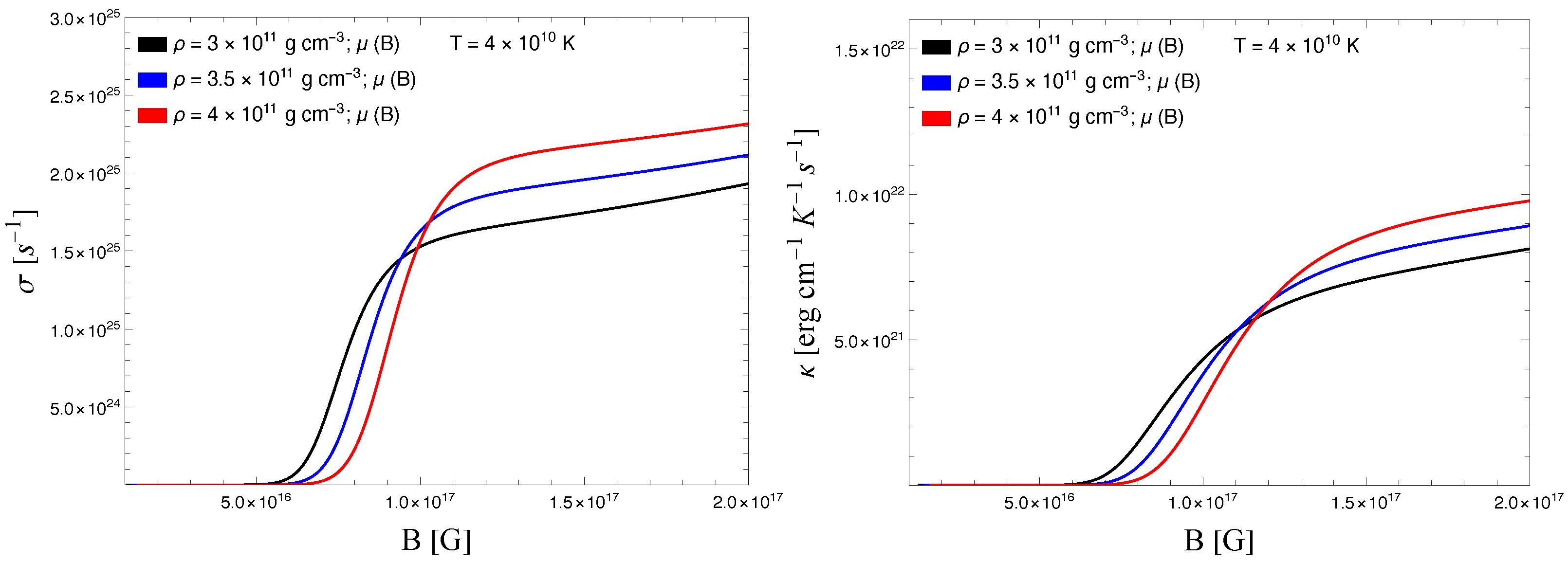
In Figure 6, we plot the variation in $\sigma$ and $\kappa$ with the magnetic field. The choice of densities are same as in Figure 5. We note that, on increasing the magnetic field, $\sigma$ and $\kappa$ increase with the B, followed by a gradual saturation. The onset of saturation coincides with the point where the weak degeneracy condition is met, $({ϵ}_p-\mu )\sim T$. This temperature remains constant for all three curves shown in the figure. The location of the saturation regime shifts because $\mu$ depends on both the density and the magnetic field strength. An increase in density leads to a higher chemical potential, while an increase in the magnetic field has the opposite effect, lowering the chemical potential. As a consequence, saturation starts at a lower B for lower densities and at a higher B for higher densities.

The magnetic field decay timescale due to Ohmic dissipation is defined by the expression ${\tau }_{\sigma }=4\pi \sigma {\lambda }_B^2/c^2$, where ${\lambda }_B$ the magnetic field scale height [28,36]. ${\lambda }_B$ is determined by comparing with electron mean free path ${\lambda }_{mfp}$. The kinetic theory definition of ${\lambda }_{mfp}$ is given by ${\lambda }_{mfp}=A{m}_n\sigma 3T/\left(Z{e}^{2}c\rho \right)\sim {10}^8$ cm ($m_n$ atomic mass unit, c velocity of light). The hydrodynamic condition is maintained if ${\lambda }_{mfp}\ge {\lambda }_B$ [28]. We consider a typical value of ${\lambda }_B\approx {10}^{-4}$ cm following the above constraint to obtain ${\tau }_{\sigma }\approx 2$ ms. This duration falls within the typical survival time of a neutron star merger. In a non-relativistic plasma, considering only the static Debye screened propagator, the electrical conductivity becomes $\sigma \sim {10}^{27}$ s⁻¹ [29]. With this conductivity and ${\lambda }_B\approx {10}^{-4}$ cm, this results in ${\tau }_{\sigma }\approx 600$ ms. Our analysis highlights the significant reduction in timescale when dynamical screening is included, compared to the scenario of electron–ion interactions mediated by longitudinal plasmons.

The thermal conduction timescale is given by ${\tau }_{\kappa }=c_v\Delta z^2/6\kappa$, where $c_v$ represents the specific heat and $\Delta z$ denotes the region hotter than its surroundings by a temperature difference $\Delta T$. The contribution of degenerate relativistic electrons to the specific heat is expressed as $c_v=5.4\times {10}^{19}{\left({\displaystyle \frac{n_e}{n_0}}\right)}^{2/3}{T}_9$ erg cm⁻³ K⁻¹, where $n_e$ is the electron number density, $n_0$ is the nuclear saturation density, and $T_9=T/{10}^9$. For $n_e=5.15\times {10}^{34}{\mathrm{cm}}^{-3}$, $T=6\times {10}^{10}$ K, and $\Delta z\sim {10}^{-1}$ cm, the thermal equilibration timescale is approximately ∼2 ms, which aligns with the timescale of the merged object [29]. However, for $\Delta z\sim$1 km, the timescale is noted to be much greater than the survival time period of the merged compact star [12].

6. Discussion

In this article, we have reviewed the relevance of different transport coefficients like $\zeta$, $\sigma$ and $\kappa$ in BNSM. During simulations of BNSM, densities can escalate to several times the nuclear saturation density, while temperatures can escalate dramatically, reaching up to ${10}^{12}$ K. Under such extreme conditions, neutrinos become trapped within the baryonic matter. Notably, at around $T\sim 5.8\times {10}^{10}$ K, the neutrino mean free path falls below the radius of the star, resulting in a non-zero chemical potential for neutrinos. For our analysis, we focus on a neutrino-trapped baryonic medium of up to approximately $T\sim 6\times {10}^{11}$ K and a density of around ∼$3n_0$.

The bulk viscosity study is structured around two primary objectives: initially, establishing the underlying medium using a neutrino-trapped nuclear equation of state; subsequently, we calculate the bulk viscosity by assessing the interaction rate of neutrino-trapped DURCA and MURCA processes. In this study, we concentrate on determining the bulk viscosity of baryonic media with neutrinos trapped through the DURCA and MURCA processes. While the DURCA process has a faster interaction rate, making it a more significant contributor to the overall bulk viscosity, its activity is limited. DURCA is restricted by specific conditions on the Fermi momentum of involved particles, and only functions above a certain density threshold. Conversely, the MURCA process is not hindered by such limitations. Both URCA and MURCA reaction rates are dependent on the density, temperature and ${\mu }_{\Delta }$.

In neutrino-trapped baryonic matter, the temperature dependence of the bulk viscosity driven by DURCA process mainly arises from the temperature dependence of the beta relaxation rate; consequently, in the neutrino-trapped regime, the bulk viscosity decreases as $\zeta \propto T^{-2}$. Thus, in neutrino-trapped matter, the DURCA driven bulk viscosity is thousand times smaller than that of neutrino-transparent matter, making the corresponding dissipation times likely too long to affect a merger.

The MURCA-driven bulk viscosity displays a resonant behavior as a function of temperature at a fixed oscillation frequency. In the neutrino-transparent matter, the maximum of $\zeta$ occurs at a lower temperature. Both the height and position of the peak change in the presence of trapped neutrinos. Changes in the EoS and the interaction rates influence both the height and the position of the resonant curve, shifting the peak to higher temperatures around $T_{{\zeta }_{max}}\sim {10}^{11}$ K. The density dependence of $\zeta$ is primarily dictated by the susceptibilities, which are dependent on the underlying EoS. Specifically, $\mathcal{B}$ exhibits a weak density dependence, while $\mathcal{C}$ shows a strong density dependence. Consequently, the behavior of bulk viscosity with density variation closely reflects that of $\mathcal{C}$. The time scale during which dissipation remains effective is found out to vary between ${\tau }_{\zeta }\sim$ 18–50 ms with the variation in density from $n_B\sim n_0-3n_0$. The values of $T_{{\zeta }_{max}}$ and ${\tau }_{\zeta }$ suggest that the neutrino-trapped MURCA process could be a potential mechanism for bulk viscous dissipation in BNSM. This is because the maximum temperature reached in a BNSM is of the order of $T\sim {10}^{11}$ K, and the survival time of the merged object is within hundreds of milliseconds.

In this study, alongside $\zeta$, we have also reviewed the quantized longitudinal electronic transport coefficients within a dynamically screened, hot, and dense magnetized quantum electrodynamics plasma, relevant to BNSM simulations. Our calculations account for the scattering of electrons with ions through screened electromagnetic forces in electron–ion plasma.

To compute both electrical and thermal conductivities, we have assumed that particles are slightly out of equilibrium, enabling us to numerically solve the Boltzmann equation. The electron–ion scattering amplitude was calculated by taking into consideration the screened electromagnetic interaction of magnetically modified spinors. The off-equilibrium distribution function was derived by solving the Boltzmann kinetic equation using the relaxation time approximation.

In relativistic BNSM plasmas, we found that considering the frequency dependence HDL propagator has a significant impact. It increases the rate of collisions between particles within the plasma. This, in turn, reduces $\sigma$ and $\kappa$. As a result, the timescales associated with these transport coefficients, ${\tau }_{\sigma }$ and ${\tau }_{\kappa }$, become shorter compared to non-relativistic plasma with static screening model.

In summary, our calculations signify a crucial advancement in integrating the detailed microphysical phenomena in plasma with GRMHD simulations. Furthermore, the transport theory framework outlined here can be expanded to encompass relativistic, magnetized QCD matter with necessary adjustments, including the incorporation of the QCD coupling constant, strong interaction diagrams, and accurate vertex corrections.