Theoretical Perspectives on Viscous Nature of Strongly Interacting Systems
Abstract
1. Introduction
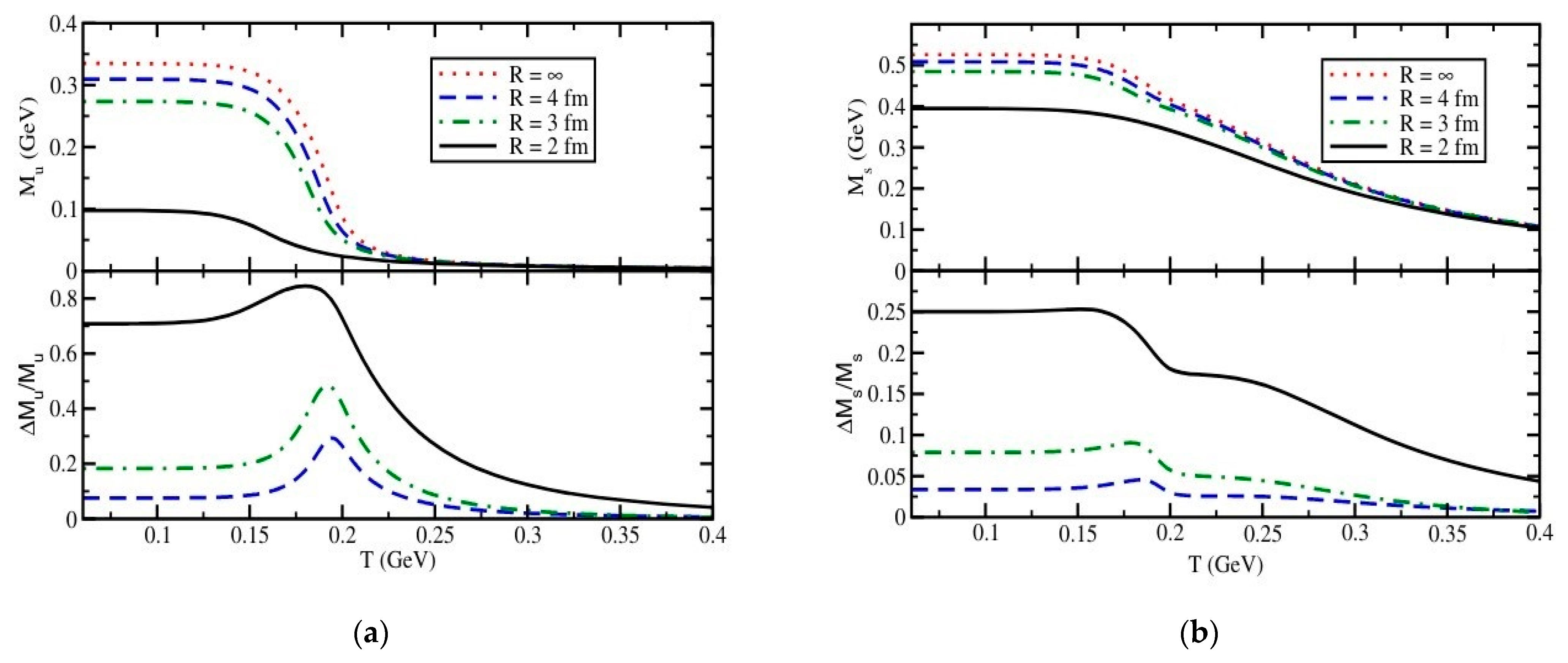
2. The Model Framework
3. Transport Coefficients
4. Results
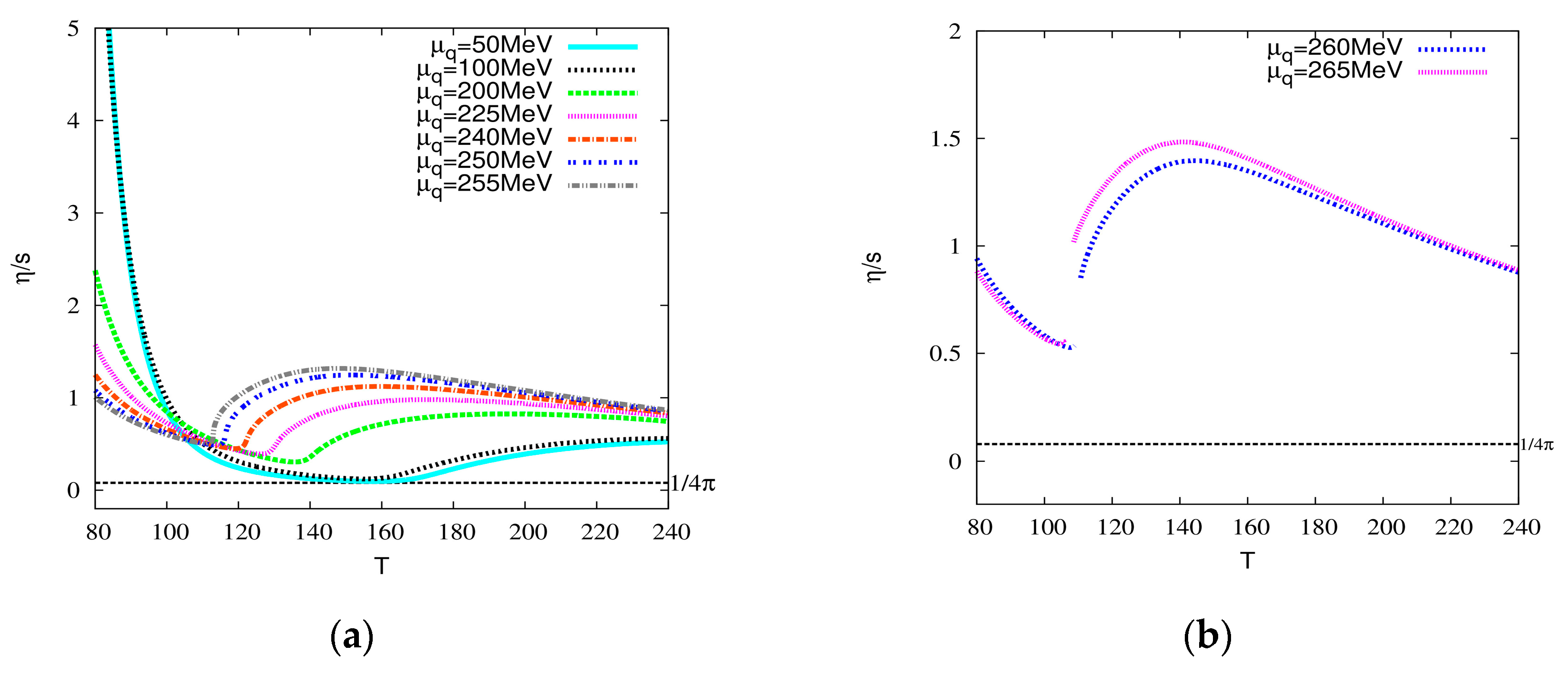
4.1. Shear Viscosity
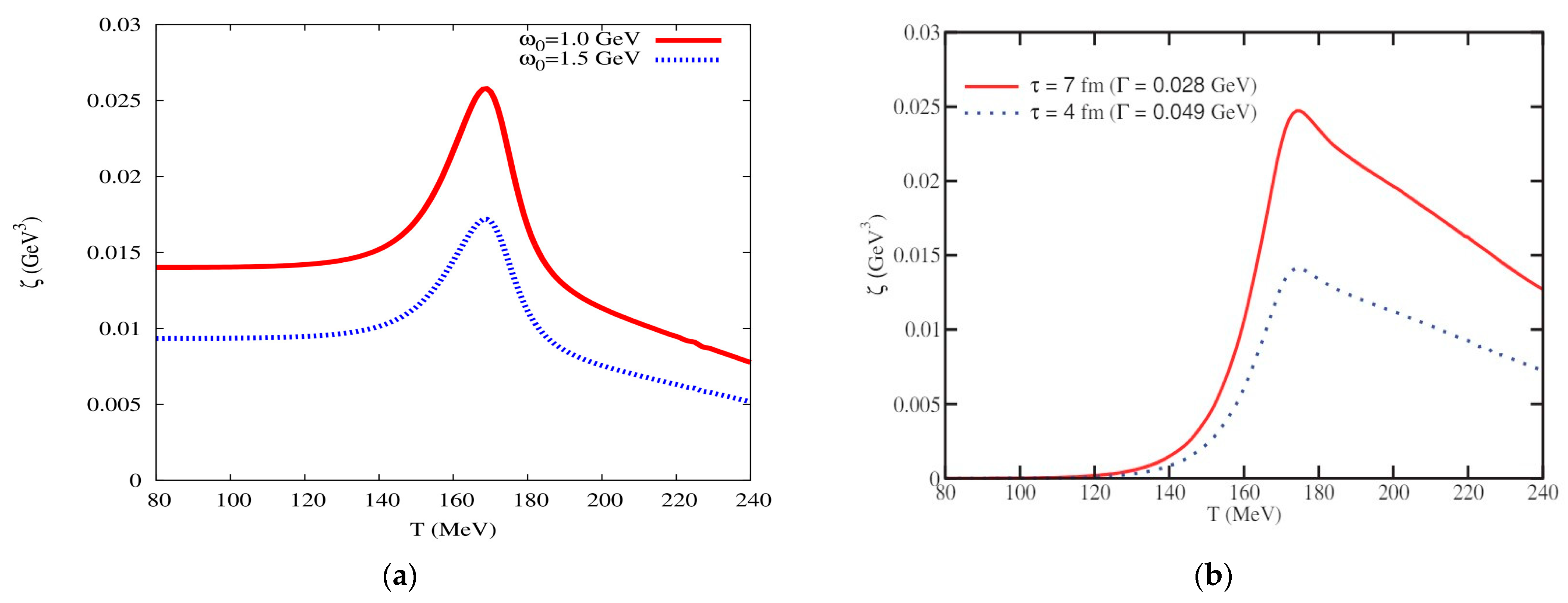
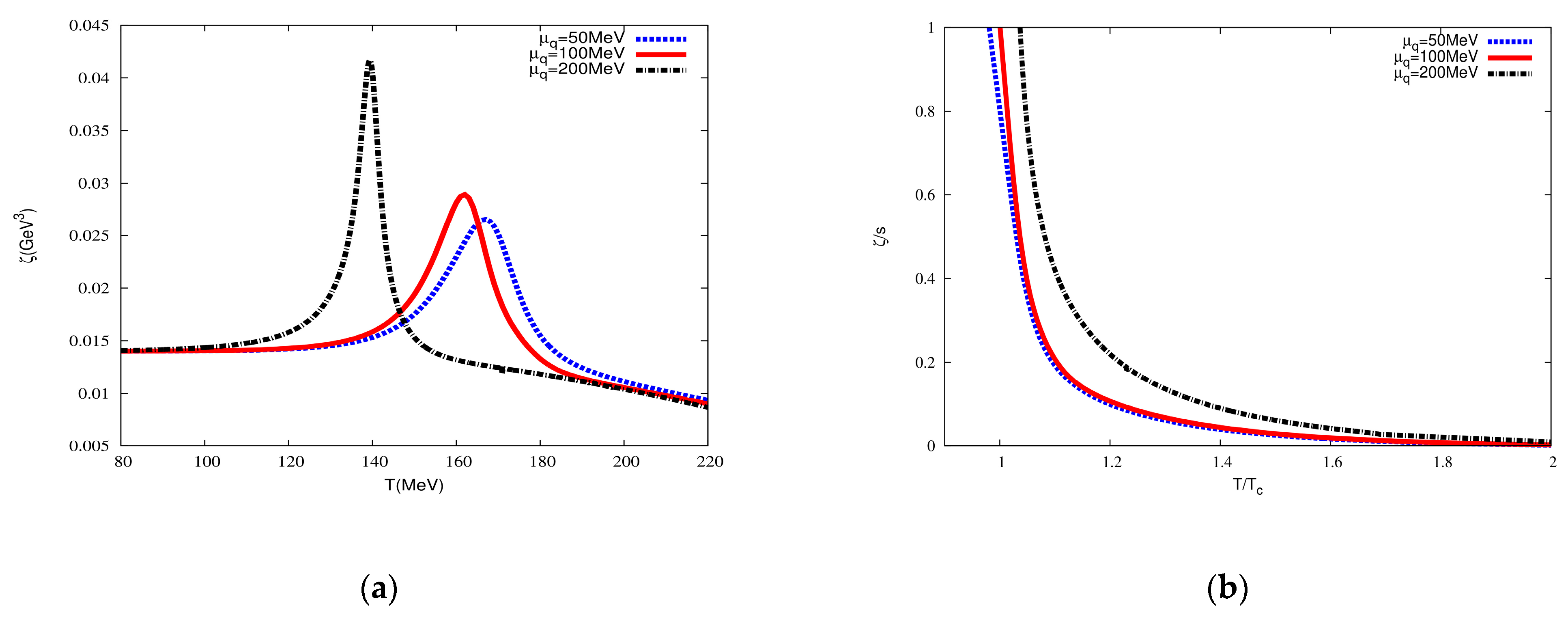
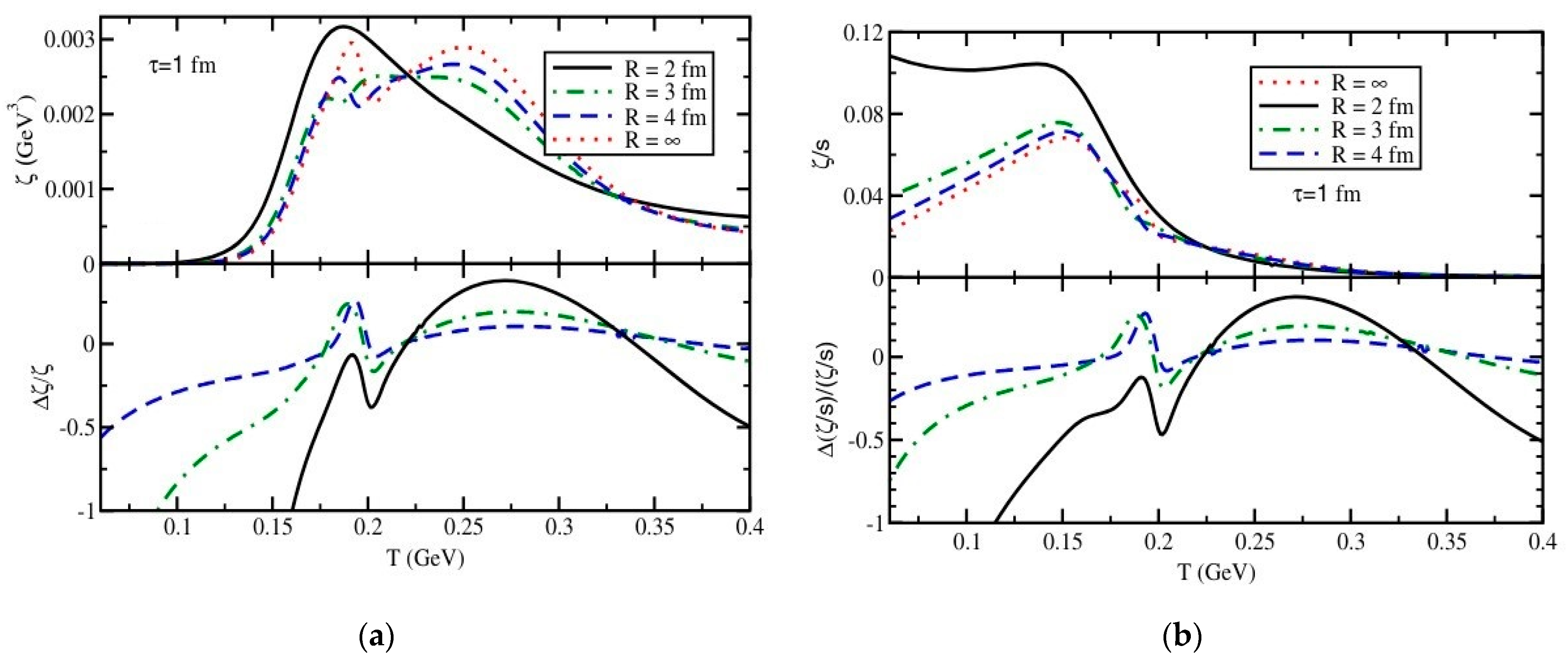
4.2. Bulk Viscosity
5. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bożek, P.; Wyskiel, I. Directed flow in ultrarelativistic heavy-ion collisions. Phys. Rev. C 2010, 81, 054902. [Google Scholar] [CrossRef]
- Steinheimer, J.; Auvinen, J.; Petersen, H.; Bleicher, M.; Stöcker, H. Examination of directed flow as a signal for a phase transition in relativistic nuclear collisions. Phys. Rev. C 2014, 89, 054913. [Google Scholar] [CrossRef]
- Ollitrault, J.-Y. Anisotropy as a signature of transverse collective flow. Phys. Rev. D 1992, 46, 229–245. [Google Scholar] [CrossRef] [PubMed]
- Policastro, G.; Son, D.T.; Starinets, A.O. Shear Viscosity of Strongly Coupled N = 4 Supersymmetric Yang-Mills Plasma. Phys. Rev. Lett. 2001, 87, 081601. [Google Scholar] [CrossRef] [PubMed]
- Kovtun, P.K.; Son, D.T.; Starinets, A.O. Viscosity in Strongly Interacting Quantum Field Theories from Black Hole Physics. Phys. Rev. Lett. 2005, 94, 111601. [Google Scholar] [CrossRef] [PubMed]
- Ferdinand, E.; Fisher, M.E. Bounded and Inhomogeneous Ising Models. I. Specific-Heat Anomaly of a Finite Lattice. Phys. Rev. 1969, 185, 832. [Google Scholar] [CrossRef]
- Fisher, M.E.; Barber, M.N. Scaling Theory for Finite-Size Effects in the Critical Region. Phys. Rev. Lett. 1972, 28, 1516. [Google Scholar] [CrossRef]
- Luscher, M. Volume dependence of the energy spectrum in massive quantum field theories. I. Stable particle states. Commun. Math. Phys. 1986, 104, 177. [Google Scholar] [CrossRef]
- Elze, H.T.; Greiner, W. Finite size effects for quark-gluon plasma droplets. Phys. Lett. B 1986, 179, 385. [Google Scholar] [CrossRef]
- Gasser, J.; Leutwyler, H. Thermodynamics of chiral symmetry. Phys. Lett. B 1987, 188, 477. [Google Scholar] [CrossRef]
- Spieles, C.; Stoecker, H.; Greiner, C. Phase transition of a finite quark-gluon plasma. Phys. Rev. C 1998, 57, 908. [Google Scholar] [CrossRef]
- Gopie, A.; Ogilvie, M.C. First principles estimate of finite size effects in quark-gluon plasma formation. Phys. Rev. D 1999, 59, 034009. [Google Scholar] [CrossRef]
- Kiriyama, O.; Hosaka, A. Chiral phase properties of finite size quark droplets in the Nambu–Jona-Lasinio model. Phys. Rev. D 2003, 67, 085010. [Google Scholar] [CrossRef]
- Fischer, C.S.; Pennington, M.R. Finite volume effects in a quenched lattice-QCD quark propagator. Phys. Rev. D 2006, 73, 034029. [Google Scholar] [CrossRef]
- Luecker, J.; Fischer, C.S.; Williams, R. Volume behavior of quark condensate, pion mass, and decay constant from Dyson Schwinger equations. Phys. Rev. D 2010, 81, 094005. [Google Scholar] [CrossRef]
- Palhares, L.F.; Fraga, E.S.; Kodama, T. Chiral transition in a finite system and possible use of finite-size scaling in relativistic heavy ion collisions. J. Phys. G 2011, 38, 085101. [Google Scholar] [CrossRef]
- Braun, J.; Klein, B.; Piasecki, P. On the scaling behavior of the chiral phase transition in QCD in finite and infinite volume. Eur. Phys. J. C 2011, 71, 1576. [Google Scholar] [CrossRef]
- Fraga, E.S.; Palhares, L.F.; Sorensen, P. Finite-size scaling as a tool in the search for the QCD critical point in heavy ion data. Phys. Rev. C 2011, 84, 011903. [Google Scholar] [CrossRef]
- Marty, R.; Bratkovskaya, E.; Cassing, W.; Aichelin, J.; Berrehrah, H. Transport coefficients from the Nambu–Jona-Lasinio model for SU(3)f. Phys. Rev. C 2013, 88, 045204. [Google Scholar] [CrossRef]
- Ratti, C.; Thaler, M.A.; Weise, W. Phases of QCD: Lattice thermodynamics and a field theoretical model. Phys. Rev. D 2006, 73, 014019. [Google Scholar] [CrossRef]
- Ghosh, S.K.; Mukherjee, T.K.; Mustafa, M.G.; Ray, R. Susceptibilities and speed of sound from the Polyakov-Nambu-Jona-Lasinio model. Phys. Rev. D 2006, 73, 114007. [Google Scholar] [CrossRef]
- Mukherjee, S.; Mustafa, M.G.; Ray, R. Thermodynamics of the Polyakov-Nambu-Jona-Lasinio model with nonzero baryon and isospin chemical potentials. Phys. Rev. D 2007, 75, 094015. [Google Scholar] [CrossRef]
- Ghosh, S.K.; Mukherjee, T.K.; Mustafa, M.G.; Ray, R. Polyakov-Nambu-Jona-Lasinio model with a Vandermonde term. Phys. Rev. D 2008, 77, 094024. [Google Scholar] [CrossRef]
- Meinsinger, P.N.; Ogilvie, M.C. Chiral symmetry restoration and ZN symmetry. Phys. Lett. B 1996, 379, 163–168. [Google Scholar] [CrossRef]
- Meisinger, P.N.; Ogilvie, M.C. Coupling the deconfining and chiral transitions. Nucl. Phys. B 1996, 47, 519–522. [Google Scholar] [CrossRef]
- Fukushima, K. Chiral effective model with the Polyakov loop. Phys. Lett. B 2004, 591, 277–284. [Google Scholar] [CrossRef]
- Megias, E.; Arriola, E.R.; Salcedo, L.L. Dimension two condensates and the Polyakov loop above the deconfinement phase transition. J. High Energy Phys. 2006, 1, 73. [Google Scholar] [CrossRef]
- Megías, E.; Arriola, E.R.; Salcedo, L.L. Chiral Lagrangian at finite temperature from the Polyakov-chiral quark model. Phys. Rev. D 2006, 74, 114014. [Google Scholar] [CrossRef]
- Megías, E.; Arriola, E.R.; Salcedo, L.L. Polyakov loop in chiral quark models at finite temperature. Phys. Rev. D 2006, 74, 065005. [Google Scholar] [CrossRef]
- Tsai, H.-M.; Müller, B. Phenomenology of the three-flavor PNJL model and thermal strange quark production. J. Phys. G 2009, 36, 075101. [Google Scholar] [CrossRef]
- Megias, E.; Arriola, E.R.; Salcedo, L.L. Polyakov Loop and the Hadron Resonance Gas Model. Phys. Rev. Lett. 2012, 109, 151601. [Google Scholar] [CrossRef] [PubMed]
- Megías, E.; Arriola, E.R.; Salcedo, L. Polyakov loop in various representations in the confined phase of QCD. Phys. Rev. D 2014, 89, 076006. [Google Scholar] [CrossRef]
- Deb, P.; Bhattacharyya, A.; Datta, S.; Ghosh, S.K. Mesonic excitations of QGP: Study with an effective model. Phys. Rev. C 2009, 79, 055208. [Google Scholar] [CrossRef]
- Bhattacharyya, A.; Ghosh, S.K.; Ray, R.; Saha, K.; Upadhaya, S. Polyakov–Nambu–Jona-Lasinio model in finite volumes. Europhys. Lett. 2016, 116, 52001. [Google Scholar] [CrossRef]
- Osipov, A.; Hiller, B.; da Providência, J. Multi-quark interactions with a globally stable vacuum. Phys. Lett. B 2006, 634, 48–54. [Google Scholar] [CrossRef]
- Osipov, A.; Hiller, B.; Blin, A.; da Providência, J. Effects of eight-quark interactions on the hadronic vacuum and mass spectra of light mesons. Ann. Phys. 2007, 322, 2021–2054. [Google Scholar] [CrossRef]
- Lang, R.; Weise, W. Shear viscosity from Kubo formalism: NJL model study. Eur. Phys. J. A 2014, 50, 63. [Google Scholar] [CrossRef]
- Fukutome, T.; Iwasaki, M. Effect of Soft Mode on Shear Viscosity of Quark Matter. Prog. Theor. Phys. 2008, 119, 991–1004. [Google Scholar] [CrossRef]
- Iwasaki, M.; Ohnishi, H.; Fukutome, T. Shear viscosity and spectral function of the quark matter. arXiv 2006, arXiv:hep-ph/0606192vl. [Google Scholar]
- Iwasaki, M.; Ohnishi, H.; Fukutome, T. Shear viscosity of the quark matter. J. Phys. G 2008, 35, 035003. [Google Scholar] [CrossRef]
- Ghosh, S.K.; Raha, S.; Ray, R.; Saha, K.; Upadhaya, S. Shear viscosity and phase diagram from Polyakov–Nambu–Jona-Lasinio model. Phys. Rev. D 2015, 91, 054005. [Google Scholar] [CrossRef]
- Kubo, R. Statistical-Mechanical Theory of Irreversible Processes. I. General Theory and Simple Applications to Magnetic and Conduction Problems. J. Phys. Soc. Jpn. 1957, 12, 570–586. [Google Scholar] [CrossRef]
- Kubo, R.; Yokota, M.; Nakajima, S. Statistical-Mechanical Theory of Irreversible Processes. II. Response to Thermal Disturbance. J. Phys. Soc. Jpn. 1957, 12, 1203–1211. [Google Scholar] [CrossRef]
- Shushpanov, I.A.; Kapusta, J.I.; Ellis, P.J. Low-energy theorems for QCD at finite temperature and chemical potential. Phys. Rev. C 1999, 59, 2931–2933. [Google Scholar] [CrossRef]
- Kharzeev, D.; Tuchin, K. Bulk viscosity of QCD matter near the critical temperature. J. High Energy Phys. 2008, 2008, 93. [Google Scholar] [CrossRef]
- Karsch, F.; Kharzeev, D.; Tuchin, K. Universal properties of bulk viscosity near the QCD phase transition. Phys. Lett. B 2008, 663, 217–221. [Google Scholar] [CrossRef]
- Fujii, H.; Kharzeev, D. Long-range forces of QCD. Phys. Rev. D 1999, 60, 114039. [Google Scholar] [CrossRef]
- Saha, K.; Upadhaya, S.; Ghosh, S. A comparative study on two different approaches of bulk viscosity in the Polyakov–Nambu–Jona-Lasinio model. Mod. Phys. Lett. A 2017, 32, 1750018. [Google Scholar] [CrossRef]
- Gavin, S. Transport coefficients in ultra-relativistic heavy-ion collisions. Nucl. Phys. A 1985, 435, 826–843. [Google Scholar] [CrossRef]
- Chakraborty, P.; Kapusta, J.I. Quasiparticle theory of shear and bulk viscosities of hadronic matter. Phys. Rev. C 2011, 83, 014906. [Google Scholar] [CrossRef]
- Ghosh, S.; Peixoto, T.C.; Roy, V.; Serna, F.E.; Krein, G. Shear and bulk viscosities of quark matter from quark-meson fluctuations in the Nambu–Jona-Lasinio model. Phys. Rev. C 2016, 93, 045205. [Google Scholar] [CrossRef]
- Fernández-Fraile, D.; Nicola, A.G. Bulk Viscosity and the Conformal Anomaly in the Pion Gas. Phys. Rev. Lett. 2009, 102, 121601. [Google Scholar] [CrossRef] [PubMed]
- Fernández-Fraile, D.; Nicola, A.G. Transport coefficients and resonances for a meson gas in Chiral Perturbation Theory. Eur. Phys. J. C 2009, 62, 37. [Google Scholar] [CrossRef]
- Bhattacharyya, A.; Deb, P.; Ghosh, S.K.; Maity, S.; Raha, S.; Ray, R.; Saha, K.; Upadhaya, S. Finite temperature properties of a modified Polyakov–Nambu–Jona-Lasinio model. Phys. Rev. D 2020, 102, 074006. [Google Scholar] [CrossRef]
- Zhao, Y.-P. Thermodynamic properties and transport coefficients of QCD matter within the nonextensive Polyakov–Nambu–Jona-Lasinio model. Phys. Rev. D 2020, 101, 096006. [Google Scholar] [CrossRef]
- Satapathy, S.; Paul, S.; Anand, A.; Kumar, R.; Ghosh, S. From non-interacting to interacting picture of thermodynamics and transport coefficients for quark gluon plasma. J. Phys. G 2020, 47, 045201. [Google Scholar] [CrossRef]
- Gao, F.; Liu, Y.-X. Temperature effect on shear and bulk viscosities of QCD matter. Phys. Rev. D 2018, 97, 056011. [Google Scholar] [CrossRef]
- Islam, C.A.; Mustafa, M.G.; Ray, R.; Singha, P. Consistent approach to study gluon quasiparticles. Phys. Rev. D 2022, 106, 054002. [Google Scholar] [CrossRef]
- Hua, L.-M.; Xu, J. Shear viscosity of nuclear matter in the spinodal region. Phys. Rev. C 2023, 107, 034601. [Google Scholar] [CrossRef]
- Ghosh, S.; Ghosh, S. One-loop Kubo estimations of the shear and bulk viscous coefficients for hot and magnetized bosonic and fermionic systems. Phys. Rev. D 2021, 103, 096015. [Google Scholar] [CrossRef]
- Ghosh, S.; Ghosh, S.; Bhattacharyya, S. Phenomenological bound on the viscosity of the hadron resonance gas. Phys. Rev. C 2018, 98, 045202. [Google Scholar] [CrossRef]
- Singha, P.; Abhishek, A.; Kadam, G.; Ghosh, S.; Mishra, H. Calculations of shear, bulk viscosities and electrical conductivity in the Polyakov-quark–meson model. J. Phys. G 2019, 46, 015201. [Google Scholar] [CrossRef]
- Saha, K.; Ghosh, S.; Upadhaya, S.; Maity, S. Transport coefficients in a finite volume Polyakov–Nambu–Jona-Lasinio model. Phys. Rev. D 2018, 97, 116020. [Google Scholar] [CrossRef]
- Ghosh, S. Electrical conductivity of hadronic matter from different possible mesonic and baryonic loops. Phys. Rev. D 2017, 95, 036018. [Google Scholar] [CrossRef]
- Muller, D.; Buballa, M.; Wambach, J. Quark propagator in the Nambu–Jona-Lasinio model in a self-consistent 1/Nc expansion. Phys. Rev. D 2010, 81, 094022. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saha, K. Theoretical Perspectives on Viscous Nature of Strongly Interacting Systems. Universe 2024, 10, 259. https://doi.org/10.3390/universe10060259
Saha K. Theoretical Perspectives on Viscous Nature of Strongly Interacting Systems. Universe. 2024; 10(6):259. https://doi.org/10.3390/universe10060259
Chicago/Turabian StyleSaha, Kinkar. 2024. "Theoretical Perspectives on Viscous Nature of Strongly Interacting Systems" Universe 10, no. 6: 259. https://doi.org/10.3390/universe10060259
APA StyleSaha, K. (2024). Theoretical Perspectives on Viscous Nature of Strongly Interacting Systems. Universe, 10(6), 259. https://doi.org/10.3390/universe10060259




