Nonlinear Dynamics in Variable-Vacuum Finsler–Randers Cosmology with Triple Interacting Fluids

Abstract

Considering the interaction among matter, vacuum, and radiation, this paper investigates the evolution of cosmic dynamics of the varying-vacuum model in a case of Finslerian geometry through dynamic analysis methods. Surprisingly, this model can alleviate the coincidence problem and allows for a stable later cosmological solution corresponding to the accelerating universe.

1. Introduction

Inspired by the significant discovery that the universe is expanding with acceleration [1,2,3,4,5], numerous cosmological theories and models have been proposed to account for this accelerated expansion. The simplest dark energy (DE) model, obtained by introducing a cosmological constant $\Lambda$ into the Einstein field equations, can cause this acceleration [6,7]. The corresponding cosmological scenario is known as $\Lambda$-cosmology, and it fits a series of observation data well. However, it suffers from the well-known cosmological constant and coincidence problems [8,9]. That is, it cannot explain why the current energy density of DE is on the same order of magnitude as that of matter, and the cosmological constant is many orders of magnitude smaller than the vacuum energy defined in particle physics.

Naturally, the appearance of new ideas in this framework is expected to extend $\Lambda$-cosmologies and address these two problems. The simplest of such ideas is to allow the $\Lambda$ term to vary with respect to cosmic time [10,11,12,13,14,15,16]. The resulting changing (running) vacuum scenarios favour the radiation- and matter-dominated eras and late-time accelerated expansion [14,15]. Running vacuum models incorporating an additional component X interacting with the vacuum has shown promise in resolving the cosmic coincidence problem. This model type was comprehensively examined in [17], where the extended cosmic coincidence ratio between vacuum and matter energy density remained sufficiently small. With the dynamics of running vacuum models, matter can be thought to interact with DE [18,19,20,21,22,23,24,25,26,27]. From a dynamic point of view, interacting varying-vacuum scenarios are investigated in [28], where the models obtained with interaction between dark matter and vacuum can describe various phases of cosmological evolution. The interacting running vacuum models in the Dvali–Gabadadze–Porrati (DGP) braneworld framework were studied in [29], which systematically presented seven distinct choices of interacting terms.

Finslerian geometry is of considerable interest when applying gravitation since it can be considered a generalization of Riemannian geometry [30,31,32,33,34]. Therefore, it is anticipated that gravitational theory based on Finslerian geometry can yield further information on the universe’s evolution. Over the last decade, cosmologies in Finslerian geometry have been of growing concern and have been widely investigated [35,36,37,38]. In the particular case of Finslerian geometry, the Finsler–Randers (FR) metric represents a locally anisotropic perturbation of Riemannian geometry. The field equations of FR cosmological models contain an extra geometric term, which can be possible candidates for DE [39]. Further work on FR cosmological models can be found in [40,41,42,43,44,45,46,47].

Recently, varying-vacuum models in an FR geometrical background with two interacting fluids (matter and vacuum) were investigated for the first time in [48], where a detailed dynamic analysis was presented, and the models could depict the basic eras of the observed universe. Motivated by [48], we consider a varying-vacuum cosmology in FR theory with three interacting fluids (matter, vacuum, and radiation). Although radiation is hardly coupled to matter, these two fluids can be hypothesized to interact with the vacuum. Thus, energy can be converted between radiation and matter by interacting with the vacuum. For this reason, radiation is included in the interacting fluids. Moreover, we focus on the influence of the strength of the interaction on the extra geometric term $Z_t/H$ and investigate the statefinder parameters as well as the classical stability of the model.

This work is organized as follows: in Section 2, we briefly review the main elements of FR theory and introduce an interacting varying-vacuum FR model. Section 3 covers the dynamics and cosmological evolution of the interacting model, as well as the analysis of the statefinder and the square of the sound speed parameters. Our concluding remarks are presented in Section 4.

2. Interacting Varying Vacuum in FR Geometry

The geometrical foundation of the FR cosmological model is Finslerian geometry [49,50,51], which generalizes the standard Riemannian geometry. Generally, a Finsler space can be obtained from a generating differentiable function $F(x,y)$ on a tangent bundle F:$TM\to R$, $TM=\tilde{T}\left(M\right)/\left\{0\right\}$ on a differentiable manifold M. The function F is a degree-one homogeneous function with respect to $y=dx/dt$, where t is the time variable. In other words, the Finsler space-time is a structure induced by F on the space-time manifold M. As a particular case, the metric function in FR space-time has the form

$$F(x,y)=\sigma (x,y)+u_{\mu }\left(x\right)y^{\mu },\sigma (x,y)\equiv \sqrt{a_{\mu \nu }{y}^{\mu }{y}^{\nu }},$$

(1)

where $u_{\mu }=\left(u_0,0,0,0\right)$ is a weak primordial vector field with $\left|\left|u_{\mu }\right|\right|\ll 1$, and $a_{\mu \nu }$ is the metric of the Riemannian space. Intrinsically, the geometrical contribution to Finsler space-time is provided by the vector field $u_{\mu }$, which offers a preferable direction in the referenced space-time [52].

In Finslerian geometry, the main object $F(x,dx)$ extends the Riemannian concept of distance, a quadratic function with respect to the infinitesimal increments $d{x}^a$ between two neighbouring points. Adding a nonquadratic distance measure to the postulate of Riemannian geometry, the Finslerian metric tensor can be written as

$$f_{\mu \nu }={\displaystyle \frac{1}{2}}{\displaystyle \frac{{\partial }^2{F}^2}{\partial y^{\mu }\partial y^{\nu }}},$$

(2)

with tangent $y^a={\displaystyle \frac{d{x}^a}{d\tau }}$. Using the metric tensor, we can derive a significant feature of Finslerian geometry, the Cartan tensor $C_{\mu \nu k}={\displaystyle \frac{1}{2}}{\displaystyle \frac{\partial f_{\mu \nu }}{\partial y^k}}$.

In the present paper, the energy–momentum of a cosmological fluid is given as

$$T_{\mu \nu }\left(x,y\left(x\right)\right)=(\rho +p)y_{\mu }\left(x\right)y_{\nu }\left(x\right)-p{f}_{\mu \nu }\left(x,y\left(x\right)\right),$$

(3)

where p and $\rho$ denote the cosmic fluid pressure and energy density, respectively.

For a local anisotropic structure, the extended gravitational field has more degrees of freedom. The related Friedmann equations contain both geometric notions, such as the Ricci tensor in [39], and the additional term ${\dot{u}}_0$, which describes the variation in the small anisotropic quantity. This form of the equation may shed light on the possible small anisotropies of the universe’s evolution.

In FR cosmology, the field equations are

$$L_{\mu \nu }=8\pi G\left(T_{\mu \nu }-{\displaystyle \frac{1}{2}}T{f}_{\mu \nu }\right),$$

(4)

where $L_{\mu \nu }$ is the Finslerian Ricci tensor, and T denotes the trace of the energy–momentum tensor.

Here, we consider a Finslerian perfect fluid with velocity 4-vector field $u_{\mu }$; then, the energy–momentum tensor becomes $T_{\mu \nu }=diag\left(\rho ,-p{f}_{ij}\right)$, where $\{\mu ,\nu \}\in \{0,1,2,3\}$ and $\{i,j\}\in \{1,2,3\}$. Substituting this form of the energy–momentum tensor into field Equation (4), for a spatially flat Friedmann–Lemaître–Robertson–Walker (FLRW) metric.

$$d{s}^2=-d{t}^2+a^2\left(t\right)\left(d{x}^2+d{y}^2+d{z}^2\right),$$

implies the modified Friedmann equations [39]:

$$\begin{array}{c}\dot{H}+H^2+{\displaystyle \frac{3}{4}}H{Z}_t=-{\displaystyle \frac{4\pi G}{3}}\left(\rho +3p\right),\end{array}$$

(5)

$$\begin{array}{c}\dot{H}+3H^2+{\displaystyle \frac{11}{4}}H{Z}_t=4\pi G\left(\rho -p\right),\end{array}$$

(6)

where $H\equiv \dot{a}\left(t\right)/a\left(t\right)$ represents the Hubble parameter, the overhead dot denotes the derivative with respect to the cosmic time t, and $Z_t$ is defined as $Z_t={\dot{u}}_0\left(t\right)$. Merging Equations (5) and (6), one obtains

$$H^2+H{Z}_t={\displaystyle \frac{8\pi G}{3}}\rho .$$

(7)

The additional term $Z{H}_t$, which represents the anisotropy of the universe, contributes to the dynamics of the universe. For the case of $u_0\equiv 0$, which leads to $Z_t=0$, the modified Friedmann equations reduce to the usual form.

Moreover, the Bianchi identities imply the conservation equation of

$$\dot{\rho }+3H(\rho +p)-Z_t\left(\rho +{\displaystyle \frac{3}{2}}p\right)=0.$$

(8)

The conservation equation does not take the usual form in the FR geometry. The additional term $Z_t\left(\rho +{\displaystyle \frac{3}{2}}p\right)$ reflects the effective matter creation, which is naturally incorporated in the FR geometry. Furthermore, the related effective matter creation rate $\Gamma$ can be given by $\Gamma =-Z_t$ [48].

Considering a universe comprising pressureless matter (including dark matter and baryons), a varying vacuum, and radiation, the fluid’s total pressure and energy density are expressed as

$$p=p_m+p_{\Lambda }+p_r,\rho ={\rho }_m+{\rho }_{\Lambda }+{\rho }_r,$$

(9)

where ${\rho }_m={\rho }_{dm}+{\rho }_b$. The field equations become

$$\begin{array}{c}1+{\displaystyle \frac{Z_t}{H}}={\displaystyle \frac{{\rho }_m}{3H^2}}+{\displaystyle \frac{{\rho }_{\Lambda }}{3H^2}}+{\displaystyle \frac{{\rho }_r}{3H^2}},\end{array}$$

(10)

$$\begin{array}{c}{\displaystyle \frac{\dot{H}}{H^2}}+1+{\displaystyle \frac{3Z_t}{4H}}=-{\displaystyle \frac{1}{6H^2}}\left({\rho }_m-2{\rho }_{\Lambda }+2{\rho }_r\right),\end{array}$$

(11)

where the assumptions $8\pi G\equiv 1$, $p_m=0$, $p_{\Lambda }=-{\rho }_{\Lambda }$, and $p_r={\rho }_r/3$ have been used.

Here, in addition to the interaction between dark matter and varying vacuum, we consider the interaction between the varying vacuum and radiation. Although the weak coupling between matter and radiation is negligible, the energy conversion between them can be obtained by interacting with the varying vacuum. To remove the nonlinear term $Z_t$, we take this term as part of the interaction term and move it to the right side of the equation. Thus, the continuity equations can be written as

$$\begin{array}{c}\hfill {\dot{\rho }}_{dm}+3H{\rho }_{dm}=Q_1,\\ \hfill {\dot{\rho }}_{\Lambda }=Q_2,\\ \hfill {\dot{\rho }}_r+4H{\rho }_r=Q_3,\end{array}$$

(12)

where $Q_1$ symbolizes the energy exchange between dark matter and vacuum, while $Q_3$ signifies the energy exchange between radiation and vacuum. These interactions collectively impact the universe’s evolution, as expressed by the relationship $Q_1+Q_2+Q_3=0$. For the subsequent analysis, we need to determine their explicit forms. There is no theoretical criterion for selecting a specific form of the interacting terms $Q_i(i=1,2,3)$. Hence, the explicit form of $Q_i$ adopted is phenomenological and empirical. For a more physical justification, the interacting model is anticipated to lead to accelerated scaling attractor solutions that alleviate the coincidence problem, so, to some extent, it is relevant to define the explicit form of $Q_i$. Given that this study does not account for the interaction between matter and radiation, the interaction terms $Q_1$ and $Q_3$ can be determined phenomenologically and mathematically as $Q_1=Q_1(H,{\rho }_{\Lambda },{\rho }_{dm})$, $Q_3=Q_3(H,{\rho }_{\Lambda },{\rho }_r)$, or in more specific forms like $Q_1=3\lambda H{\rho }_{\Lambda }$ (or $Q_1=3\lambda H{\rho }_{dm}$) (refer to [53,54,55]). Consequently, the interaction terms $Q_1$, $Q_3$ in this research can be represented as $Q_1=3\alpha H{\rho }_{\Lambda }$, $Q_3=3\beta H{\rho }_{\Lambda }$, with $Q_2=-3\alpha H{\rho }_{\Lambda }-3\beta H{\rho }_{\Lambda }$, where the dimensionless parameters $\alpha$ and $\beta$ denote the interaction strength. While the constraints imposed by the cosmic microwave background (CMB) on the interaction between radiation and vacuum may be stringent [56,57,58], we can select a sufficiently small value for the strength parameter $\beta$ to ensure that this model adheres to these constraints and remains physically feasible. Here, $\alpha$ and $\beta$ are regarded as free parameters in conjunction with other cosmological parameters. Typically, $\alpha$ is observed to be on the order of $\sim {10}^{-3}$ or lower, exemplified by values such as $\alpha =0.00013\pm 0.00018$ [59] or $\alpha =0.00014\pm 0.00103$ [60]. Meanwhile, $\beta$ is constrained to an upper limit of approximately $5.25\times {10}^{-5}$ [58].

3. Dynamic Analysis

In this section, a dynamic system analysis is used to investigate the behaviour of the cosmological model. This approach examines the critical points of the field equations that describe different cosmological eras. The stability of these eras is determined according to the eigenvalues for the particular critical points of the linearized system. This approach has been widely used in works on the dynamic behaviour of cosmological models and the universe’s evolution [61,62,63,64,65,66,67,68,69,70].

3.1. Dynamic System

To recast the field equations, we introduce four dimensionless variables

$${\Omega }_z={\displaystyle \frac{Z_t}{H}},{\Omega }_m={\displaystyle \frac{{\rho }_m}{3H^2}},{\Omega }_{\Lambda }={\displaystyle \frac{{\rho }_{\Lambda }}{3H^2}},{\Omega }_r={\displaystyle \frac{{\rho }_r}{3H^2}}.$$

(13)

Then, Equation (10) becomes

$$1+{\Omega }_z={\Omega }_m+{\Omega }_{\Lambda }+{\Omega }_r.$$

(14)

Additionally, using continuous Equation (12) and field Equations (10) and (11), we can obtain the dynamical system

$$\begin{array}{cc}\hfill & {\displaystyle \frac{d{\Omega }_m}{dN}}={\Omega }_m\left({\displaystyle \frac{5}{2}}{\Omega }_m-{\displaystyle \frac{1}{2}}{\Omega }_{\Lambda }+{\displaystyle \frac{7}{2}}{\Omega }_r-{\displaystyle \frac{5}{2}}\right)+3\alpha {\Omega }_{\Lambda },\hfill \\ \hfill & {\displaystyle \frac{d{\Omega }_{\Lambda }}{dN}}={\Omega }_{\Lambda }\left({\displaystyle \frac{5}{2}}{\Omega }_m-{\displaystyle \frac{1}{2}}{\Omega }_{\Lambda }+{\displaystyle \frac{7}{2}}{\Omega }_r+{\displaystyle \frac{1}{2}}\right)-3\alpha {\Omega }_{\Lambda }-3\beta {\Omega }_{\Lambda },\hfill \\ \hfill & {\displaystyle \frac{d{\Omega }_r}{dN}}={\Omega }_r\left({\displaystyle \frac{5}{2}}{\Omega }_m-{\displaystyle \frac{1}{2}}{\Omega }_{\Lambda }+{\displaystyle \frac{7}{2}}{\Omega }_r-{\displaystyle \frac{7}{2}}\right)+3\beta {\Omega }_{\Lambda },\hfill \end{array}$$

(15)

where $N=lna$. The deceleration parameter q used to highlight the universe expansion rate can be given by

$$q\equiv -1-{\displaystyle \frac{\dot{H}}{H^2}}={\displaystyle \frac{3}{4}}{\Omega }_z+{\displaystyle \frac{1}{2}}{\Omega }_m-{\Omega }_{\Lambda }+{\Omega }_r.$$

(16)

The universe acceleration or deceleration can be determined by the sign (negative or positive) of q. Naturally, the equation of the state parameter for the effective fluid can be written as

$${\omega }_{eff}=-{\displaystyle \frac{1}{3}}+{\displaystyle \frac{1}{2}}{\Omega }_z+{\displaystyle \frac{1}{3}}{\Omega }_m-{\displaystyle \frac{2}{3}}{\Omega }_{\Lambda }+{\displaystyle \frac{2}{3}}{\Omega }_r.$$

(17)

Assuming the right-hand side of the above equations to be zero, we obtain four critical points with coordinates $\left({\Omega }_z,{\Omega }_m,{\Omega }_{\Lambda },{\Omega }_r\right)$ of the dynamic system (15), and they are

$$\begin{array}{cccc}\hfill P_{A1}& =\left(-1,0,0,0\right),\hfill & \hfill P_{A2}& =\left(0,1,0,0\right),\hfill \\ \hfill P_{A3}& =\left(0,0,0,1\right),\hfill & \hfill P_{A4}& =\left(0,{\Omega }_m^{A4},{\Omega }_{\Lambda }^{A4},{\Omega }_r^{A4}\right),\hfill \end{array}$$

where

$${\Omega }_m^{A4}={\displaystyle \frac{\alpha (3\alpha +3\beta -4)}{3\alpha +4\beta -4}},{\Omega }_{\Lambda }^{A4}={\displaystyle \frac{-3{(\alpha +\beta )}^2+7(\alpha +\beta )-4}{3\alpha +4\beta -4}},{\Omega }_r^{A4}={\displaystyle \frac{3\beta (\alpha +\beta -1)}{3\alpha +4\beta -4}}.$$

Point $P_{A1}$ depicts an empty universe accelerating due to the additional term introduced through the FR geometry. This point always exists in the model with the equation of state ${\omega }_{eff}=-5/6$. The eigenvalues of the linearized system around $P_{A1}$ are derived as $\left\{-5/2,-7/2,1/2-3(\alpha +\beta )\right\}$. Hence, the point is stable when $\alpha +\beta >1/6$.

Point $P_{A2}$ describes a matter-dominated universe with ${\omega }_{eff}=0$. The corresponding eigenvalues are $\left\{5/2,-1,-3(\alpha +\beta -1)\right\}$. Since two of the eigenvalues of point $P_{A2}$ have different signs, it is an unstable point, or to be precise, a saddle point.

Point $P_{A3}$ is always physically accepted and corresponds to a radiation-dominated universe. The eigenvalues for this point are $\left\{7/2,1,4-3(\alpha +\beta )\right\}$. It is unstable, as point $P_{A3}$ admits two positive eigenvalues at least.

Point $P_{A4}$ describes a universe where matter, the cosmological constant, and radiation coexist. The cosmic triple coincidence problem can be alleviated for this solution. The equation of the state of the point is ${\omega }_{eff}=\alpha +\beta -1$, and the corresponding universe accelerates when $\alpha +\beta <2/3$. The point exists for $0\le {\Omega }_j^{A4}\le 1$, where $j=m,\Lambda ,r$. When $\alpha =0$ and $\beta =0$, point $P_{A4}$ becomes a de Sitter point, with ${\omega }_{eff}=-1$, representing the universe where only the cosmological constant term contributes to the evolution. The obtained eigenvalues are $\left\{3(\alpha +\beta )-1/2,3(\alpha +\beta )-3,3(\alpha +\beta )-4\right\}$; hence, $P_{A4}$ is stable for $\alpha +\beta <1/6$.

The above analysis of four critical points for the interaction model is summarized in

Table 1. Critical points of the model.

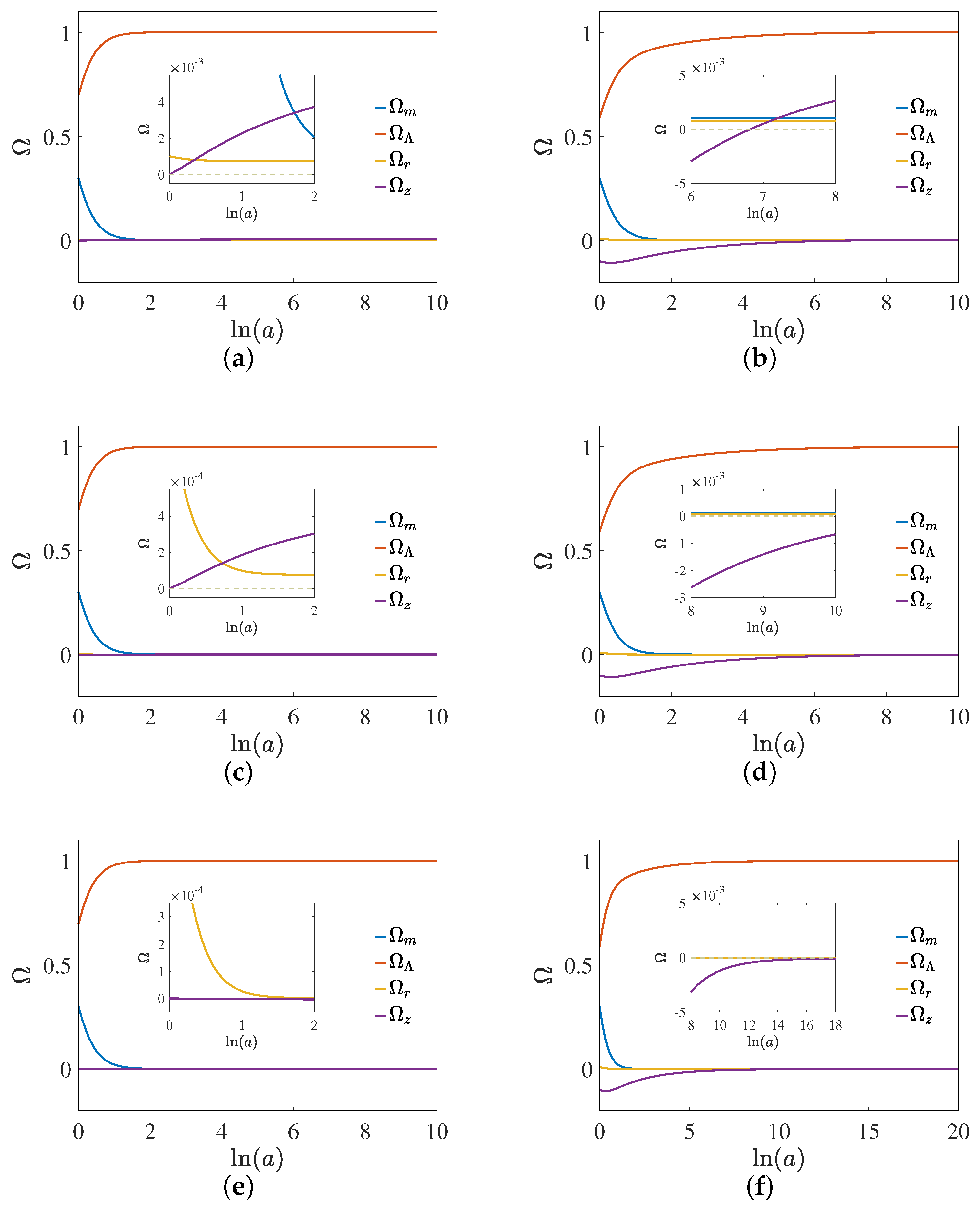
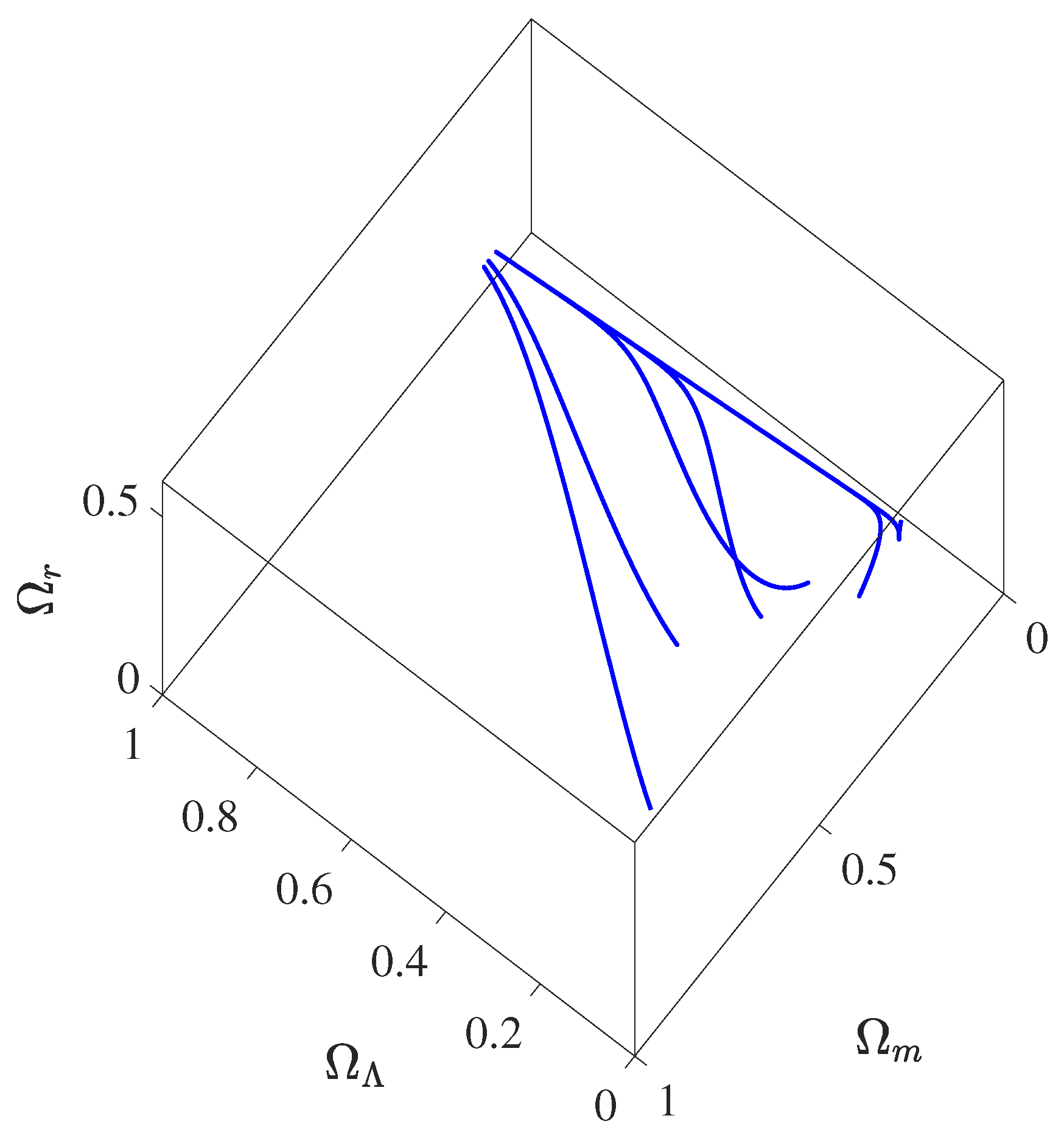
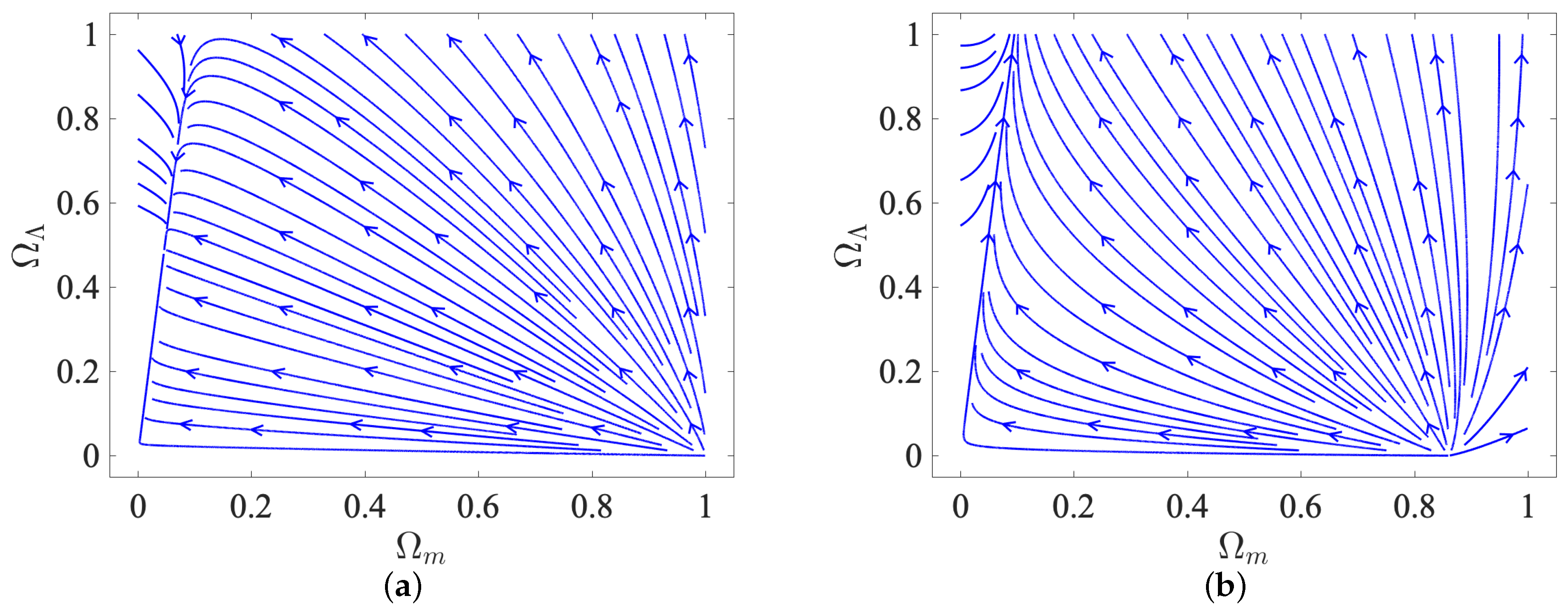
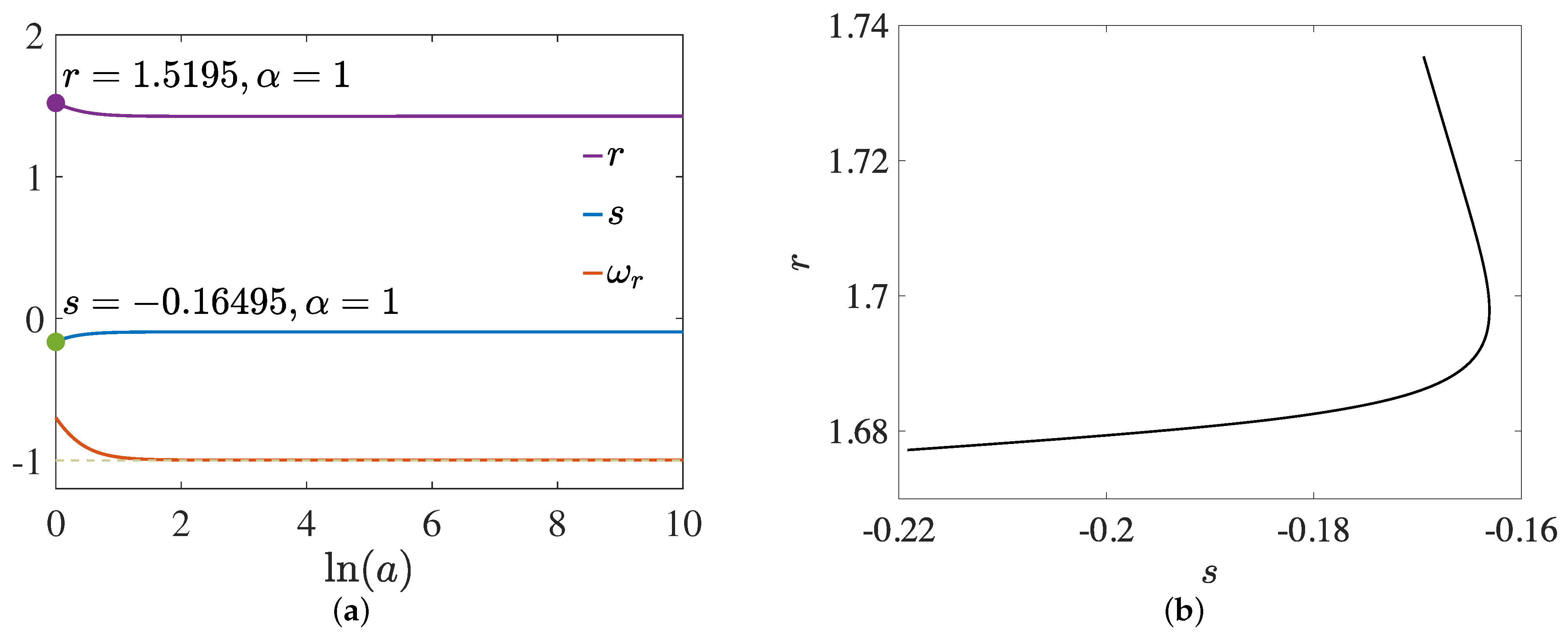
Point	$\left({\mathbf{\Omega }}_{\mathit{z}},{\mathbf{\Omega }}_{\mathit{m}},{\mathbf{\Omega }}_{\mathit{\Lambda }},{\mathbf{\Omega }}_{\mathit{r}}\right)$	Existence	${\mathit{\omega }}_{\mathit{eff}}$	Acceleration	Eigenvalues	Stability
$P_{A1}$	$\left(-1,0,0,0\right)$	Always	$-5/6$	True	$\left\{-5/2,-7/2,1/2-3(\alpha +\beta )\right\}$	Stable for $\alpha +\beta >1/6$
$P_{A2}$	$\left(0,1,0,0\right)$	Always	0	False	$\left\{5/2,-1,-3(\alpha +\beta -1)\right\}$	Unstable
$P_{A3}$	$\left(0,0,0,1\right)$	Always	$1/3$	False	$\left\{7/2,1,4-3(\alpha +\beta )\right\}$	Unstable
$P_{A4}$	$\left(0,{\Omega }_m^{A4},{\Omega }_{\Lambda }^{A4},{\Omega }_r^{A4}\right)$	$0\le {\Omega }_i^{A4}\le 1$	$\alpha +\beta -1$	True for $\alpha +\beta <2/3$	$\left\{3(\alpha +\beta )-1/2,3(\alpha +\beta )-3,3(\alpha +\beta )-4\right\}$	Stable for $\alpha +\beta <1/6$

. The cosmological evolution of the model is presented in Figure 1, Figure 2 and Figure 3. It is shown that vacuum, matter, and radiation coexist in the late stage of cosmological evolution which can alleviate the coincidence problem. Moreover, the extra term ${\Omega }_z$ plays an important role as well and has intriguing properties. It is obvious from the figures that ${\Omega }_z$ finally increases to a stable value, and this stable value increases as $\alpha$ increases or $\beta$ decreases while it does not depend on its initial value. When the values of $\alpha$ and $\beta$ are of the same order, ${\Omega }_z$ fades away at late times, which may signify that the interaction between fluids can counteract the small anisotropies of the evolution of the universe.

3.2. Statefinder Diagnostic

The statefinder parameter is a geometrical diagnostic tool which was developed from the scale factor and its derivatives directly. The statefinder diagnostic pair $(r,s)$ was proposed by Sahni et al. for the first time and defined as [71]

$$r={\displaystyle \frac{\stackrel{⃛}{a}}{a{H}^3}},s={\displaystyle \frac{r-1}{3(q-1/2)}}.$$

(18)

The trajectories of different cosmological models present different qualitative behaviours in the r–s plane, thus the diagnostic pair $(r,s)$ is conducive to segregate different DE models. The parameter pair ($r=1$, $s=1$) corresponds to the standard cold dark matter (SCDM) model while ($r=1$, $s=0$) is related to the $\Lambda$ cold dark matter ($\Lambda$CDM) model. The trajectories of quintessence and Chaplygin gas model lie in the regions $r<1$ and $s>0$ and $r>1$ and $s<0$, respectively [71,72]. In the terms of variables (13), the diagnostic parameters r and s can be written as

$$\begin{array}{c}r=8(5{\Omega }_m+5{\Omega }_{\Lambda }-36\alpha {\Omega }_{\Lambda }-48\beta {\Omega }_{\Lambda }+42{\Omega }_r+9),\end{array}$$

(19)

$$\begin{array}{c}s={\displaystyle \frac{5{\Omega }_m+5{\Omega }_{\Lambda }-36\alpha {\Omega }_{\Lambda }-48\beta {\Omega }_{\Lambda }+42{\Omega }_r+1}{6(5{\Omega }_m-{\Omega }_{\Lambda }+7{\Omega }_r-5)}}.\end{array}$$

(20)

The behaviour of statefinder parameters r and s is shown in Figure 4. The universe evolves with $r>1$ and $s<0$ at late times, implying that the evolution of the universe presents a behaviour similar to a Chaplygin gas model. The values of the statefinder parameters for the model are $r_0=1.519$ and $s_0=-0.165$ at the present epoch, which are in agreement with constraints from OHD+SNe+BAO ($r_0={1.11}_{-0.50}^{+0.51}$, $s_0=-{0.03}_{-0.14}^{+0.17}$) [73].

3.3. Classical Stability Analysis

To assess the classical stability of the current model against energy density perturbations, it is imperative to employ the square of the sound speed, denoted as

$$v_s^2={\displaystyle \frac{dp}{d\rho }}.$$

(21)

The model is classically stable when the square of its sound speed lies in the range $0\le v_s^2\le 1$. It is interesting to investigate the stability of the late-time mixed fluid since the extra geometrical term ${\Omega }_z$ undeniably contributes at that time. In the present model, the square of the sound speed $v_s^2$ has the form

$$v_s^2=-{\displaystyle \frac{9\alpha {\Omega }_{\Lambda }+10\beta {\Omega }_{\Lambda }-4{\Omega }_r}{9{\Omega }_m+12{\Omega }_r}}.$$

(22)

The behaviour of $v_s^2$ is depicted in Figure 5 for different values of $\beta$. The model in the non-interacting case is not classically stable, possibly due to the contribution of the extra term ${\Omega }_z$. While introducing interacting terms can help in smoothing the curves of $v_s^2$, it does not alter the instability of the model when subjected to energy density perturbations.

4. Discussion and Conclusions

This study delved into a varying-vacuum model within the framework of the Finsler–Randers geometry, employing a dynamic system analysis. Apart from examining the interaction between vacuum and matter, it also explored the interaction between a varying vacuum and radiation. The primary focus of this study was understanding the impact of the considered interaction terms on the critical points and classical stability of the model, as well as the evolution of the extra term ${\Omega }_z$.

The stability analysis of the four critical points $P_{Ai}(i=1,2,3,4)$ within the dynamic system of the model was detailed in Table 1, and the cosmological evolution of the model was visually depicted in Figure 1, Figure 2 and Figure 3. The point $P_{A1}$ described a universe dominated by the Finslerian dynamic term, and points $P_{A2}$ and $P_{A3}$ gave the limits of General Relativity (GR), representing the matter-dominated and radiation-dominated eras, respectively. The point $P_{A4}$ was the solution of GR, where matter, the cosmological constant term, and radiation contributed to the universe’s evolution. The interaction term under consideration led to modifications in the coordinates of point $P_{A4}$, consequently influencing the stability of both $P_{A1}$ and $P_{A4}$. In the absence of interaction (i.e., when the interaction strength parameters were zero), point $P_{A4}$ represented a stable De Sitter universe.

The extra term ${\Omega }_z$ assumed significance and exhibited intriguing characteristics at late times. Its value remained independent of the initial energy density values but was influenced by the interaction strength parameters $\alpha$ and $\beta$, representing the energy exchange rate between the corresponding fluids. It increased as the value of $\alpha$ increased, or that of $\beta$ decreased. The value of ${\Omega }_z$ vanished when $\alpha$ and $\beta$ were of the same order, signifying that the small anisotropies of the universe’s evolution may be counteracted by the interaction between fluids in the universe.

Using the statefinder parameters r and s, and the square of the sound speed $v_s^2$, we further analysed the properties of dark energy (DE) and the classical stability of the model. The model’s evolution was similar to that of the Chaplygin gas model. It exhibited instability in the non-interacting scenario when subjected to energy density perturbations, possibly attributed to the impact of the additional term ${\Omega }_z$. Even with the incorporation of interaction terms, the model’s instability persisted without alteration.