Fluctuations and Correlations of Conserved Charges Serving as Signals for QGP Production: An Overview from Polyakov Loop Enhanced Nambu–Jona-Lasinio Model
Abstract
1. Introduction
2. The Model Frameworks
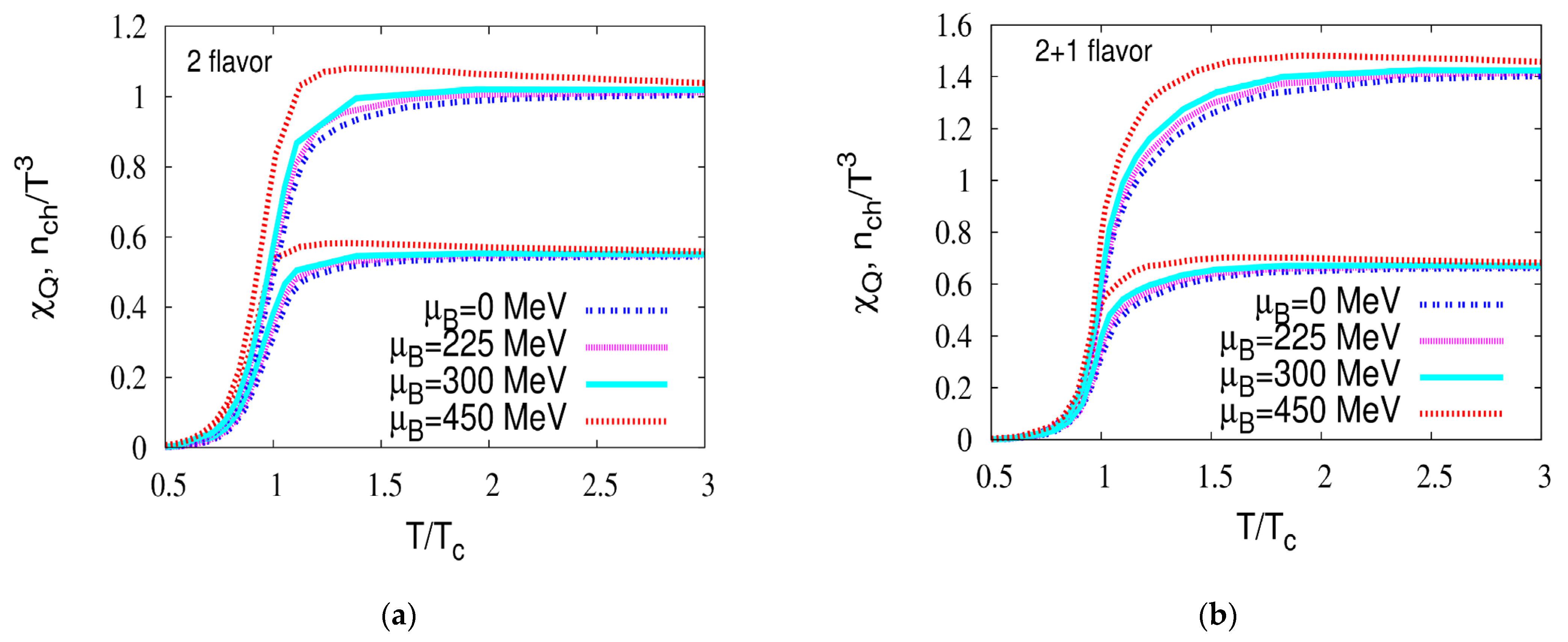
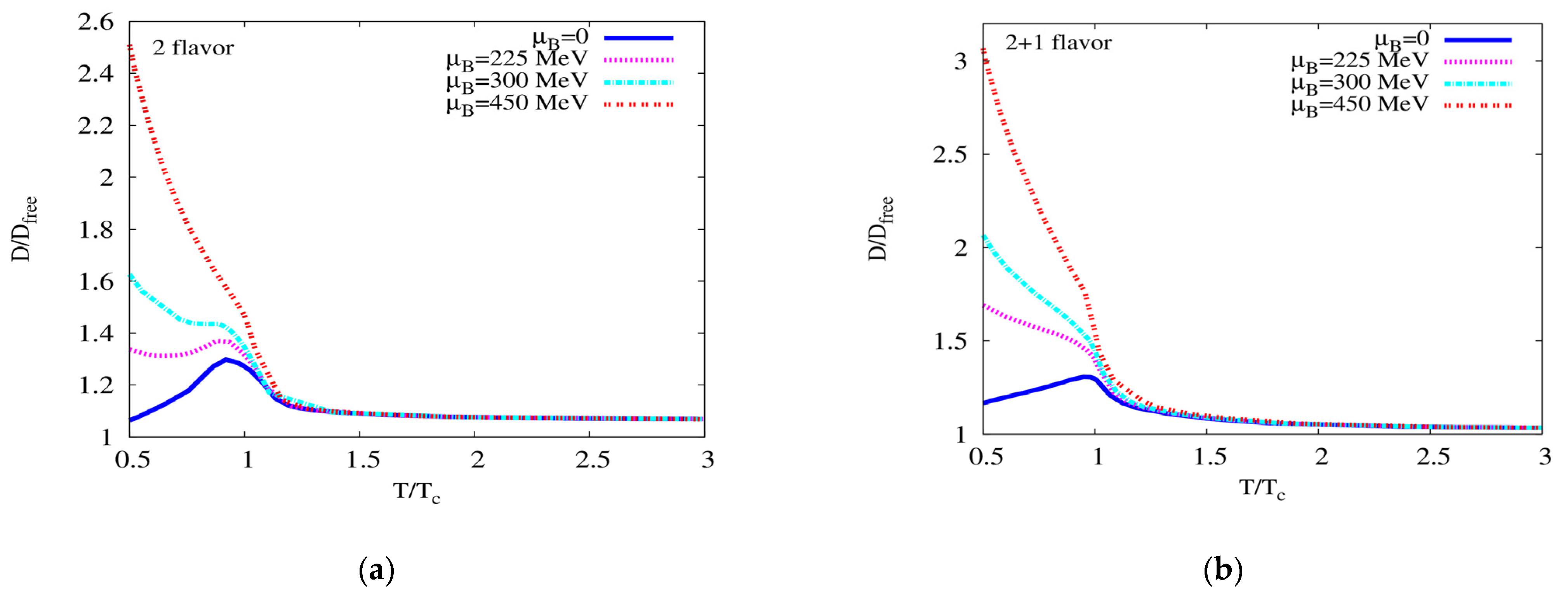
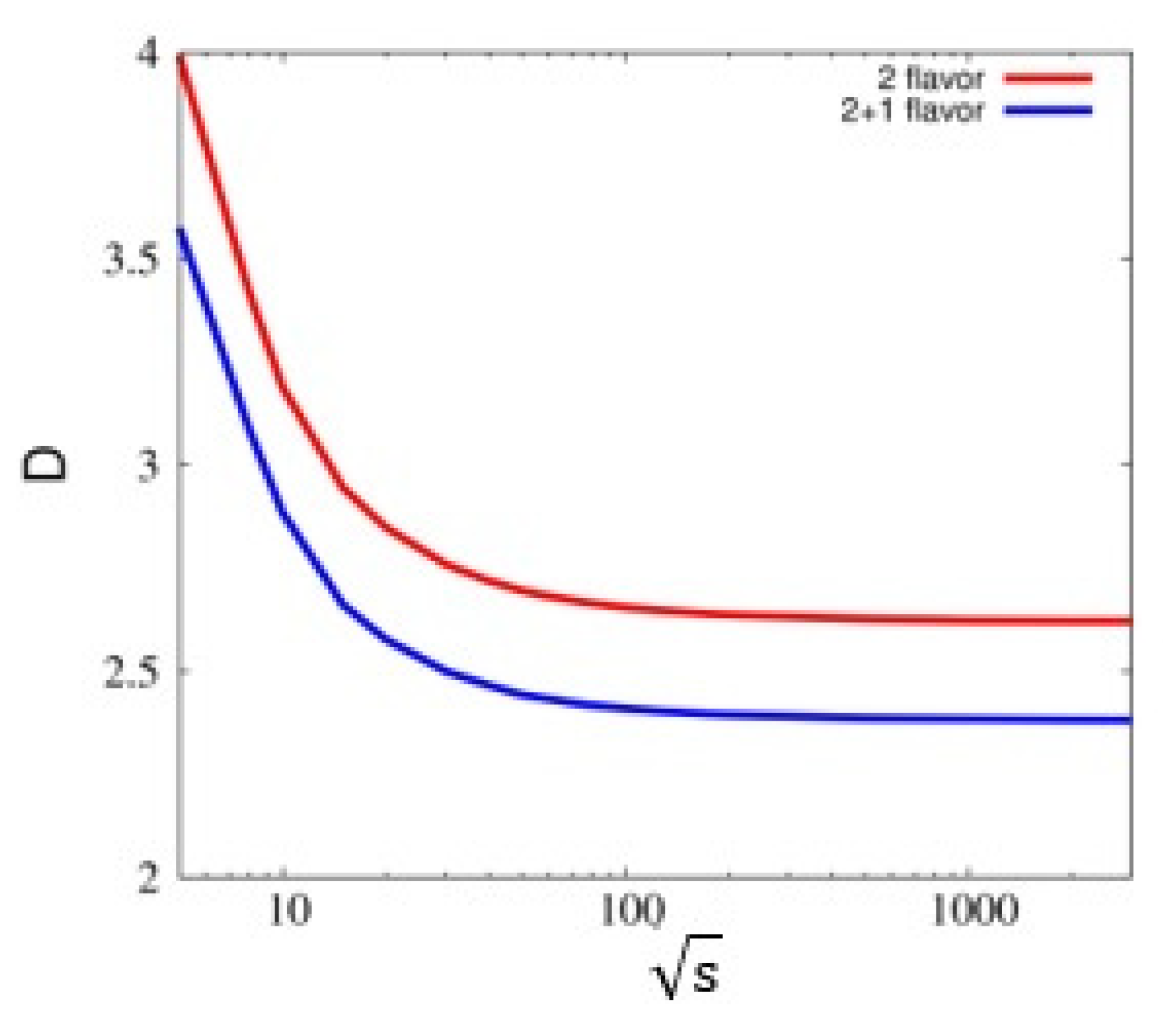
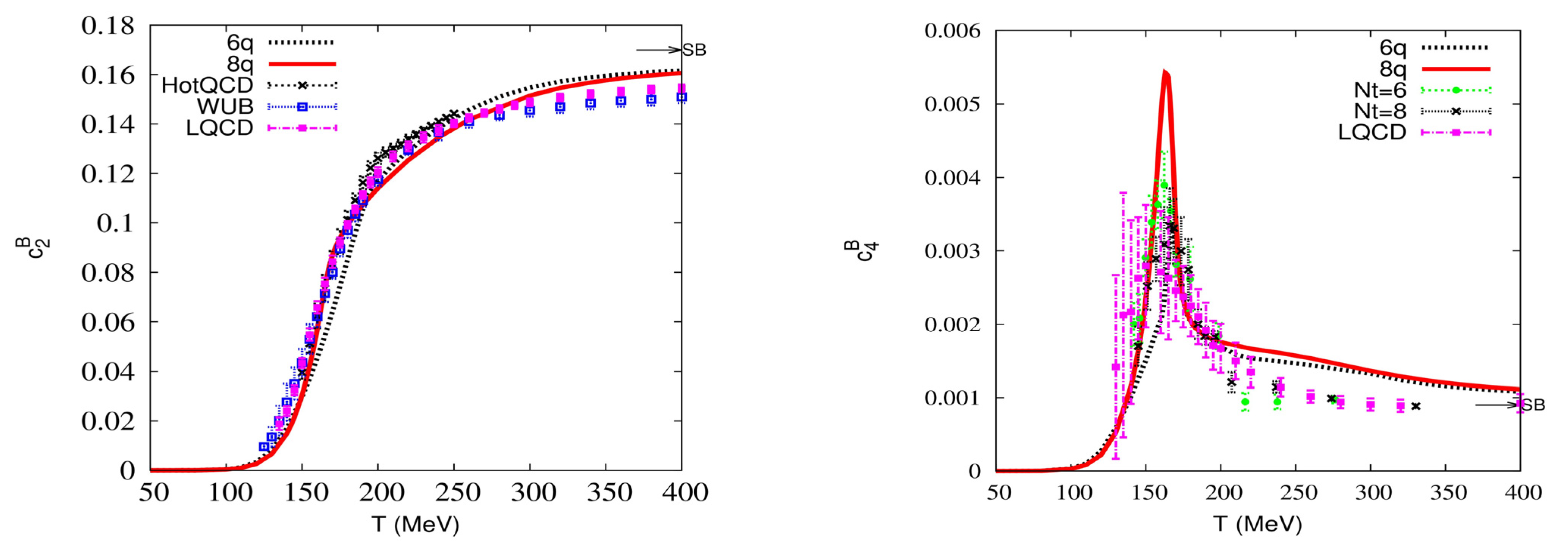
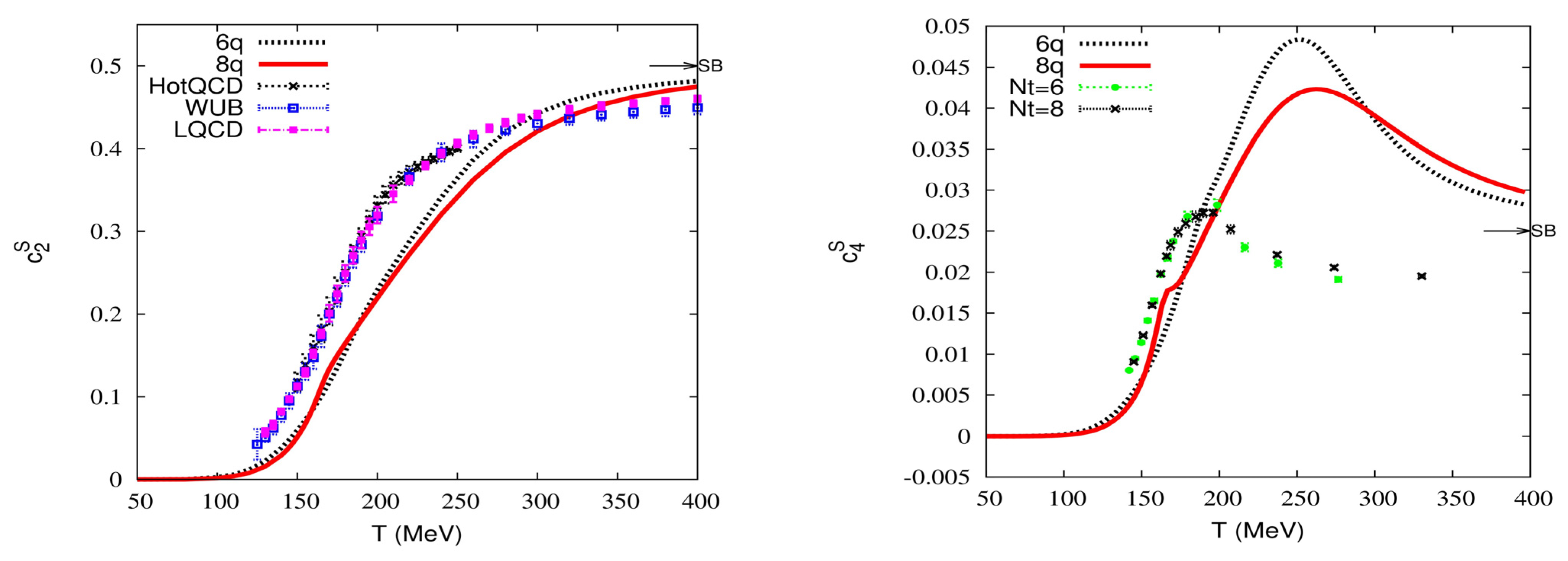
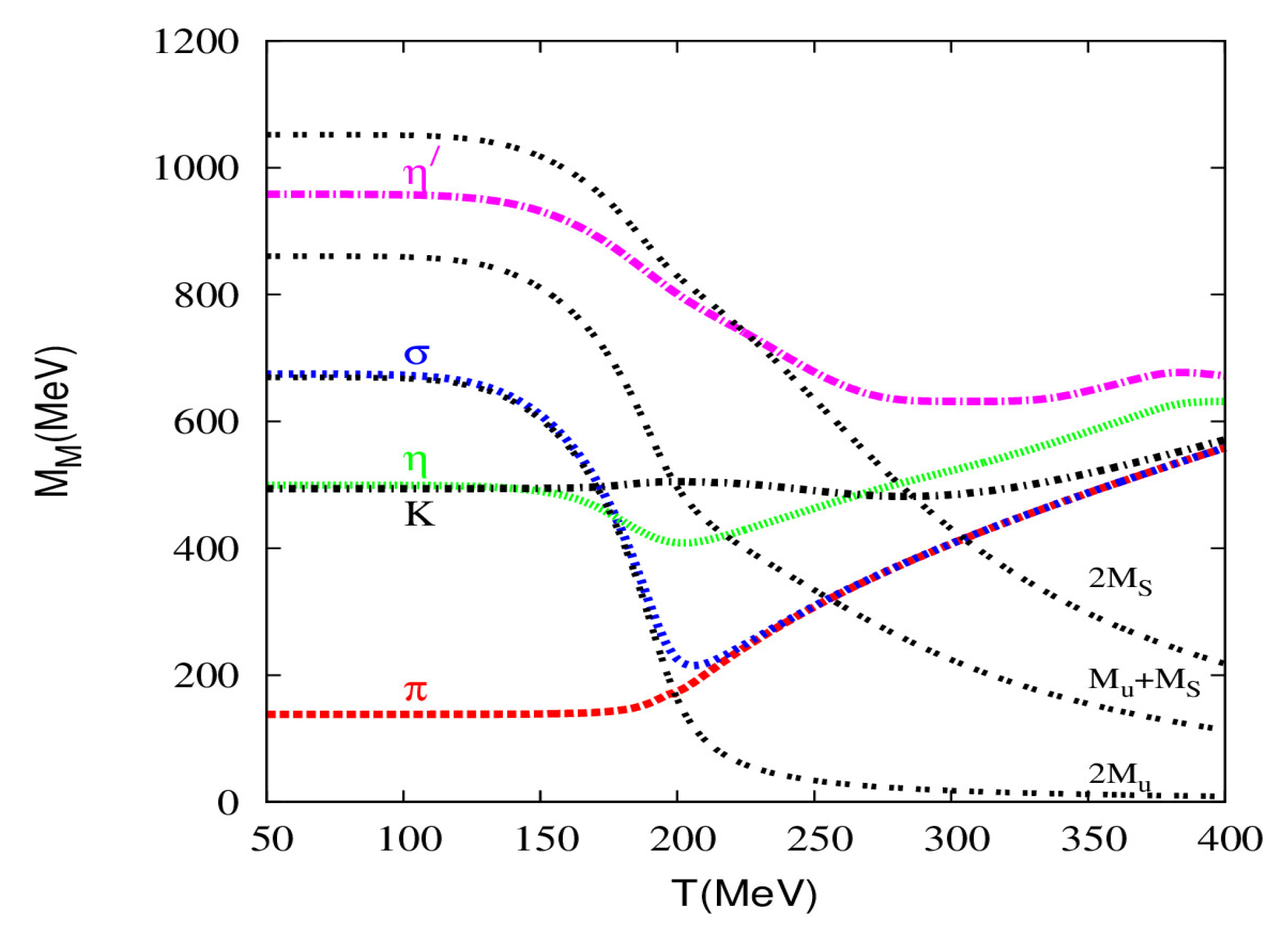
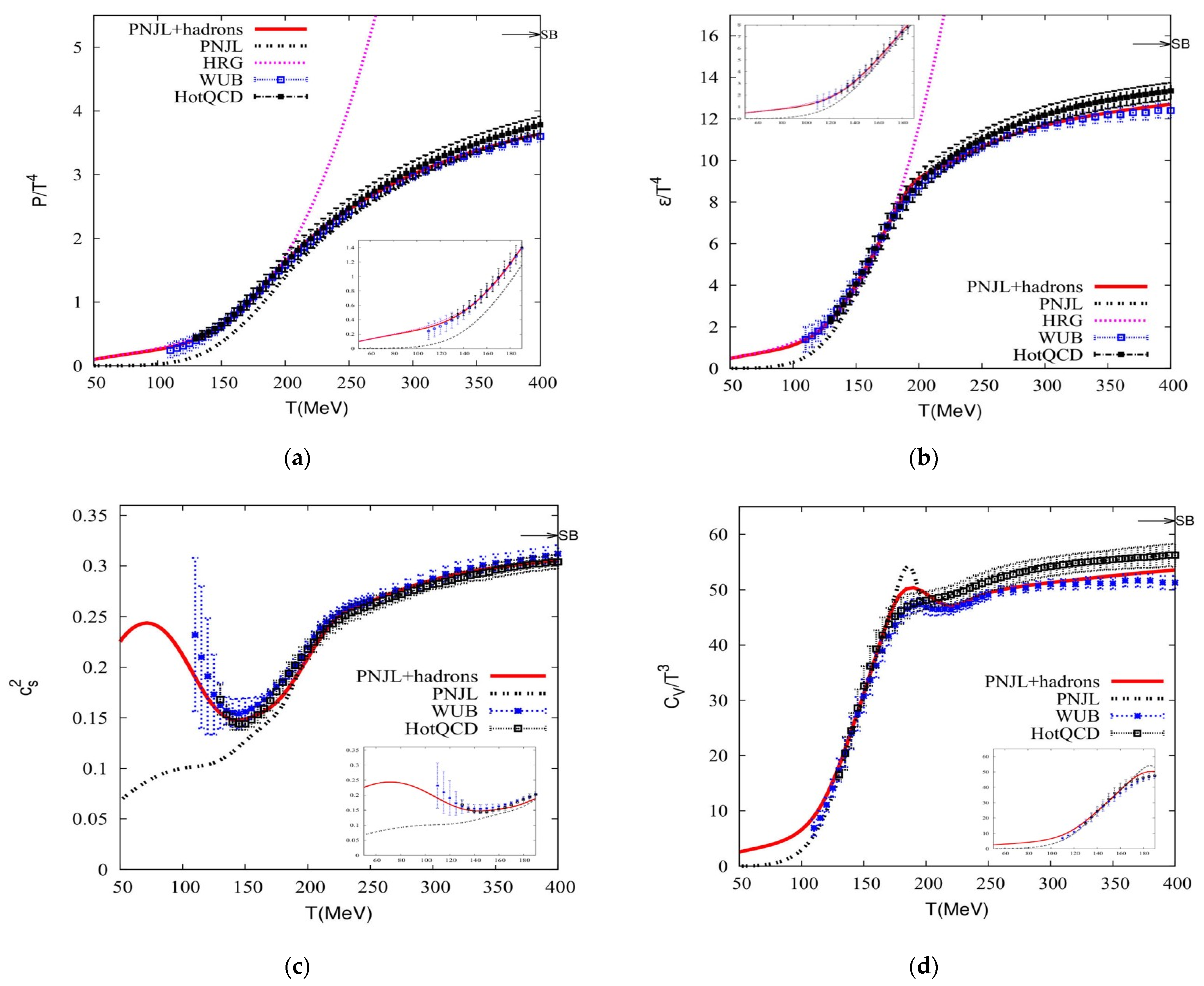
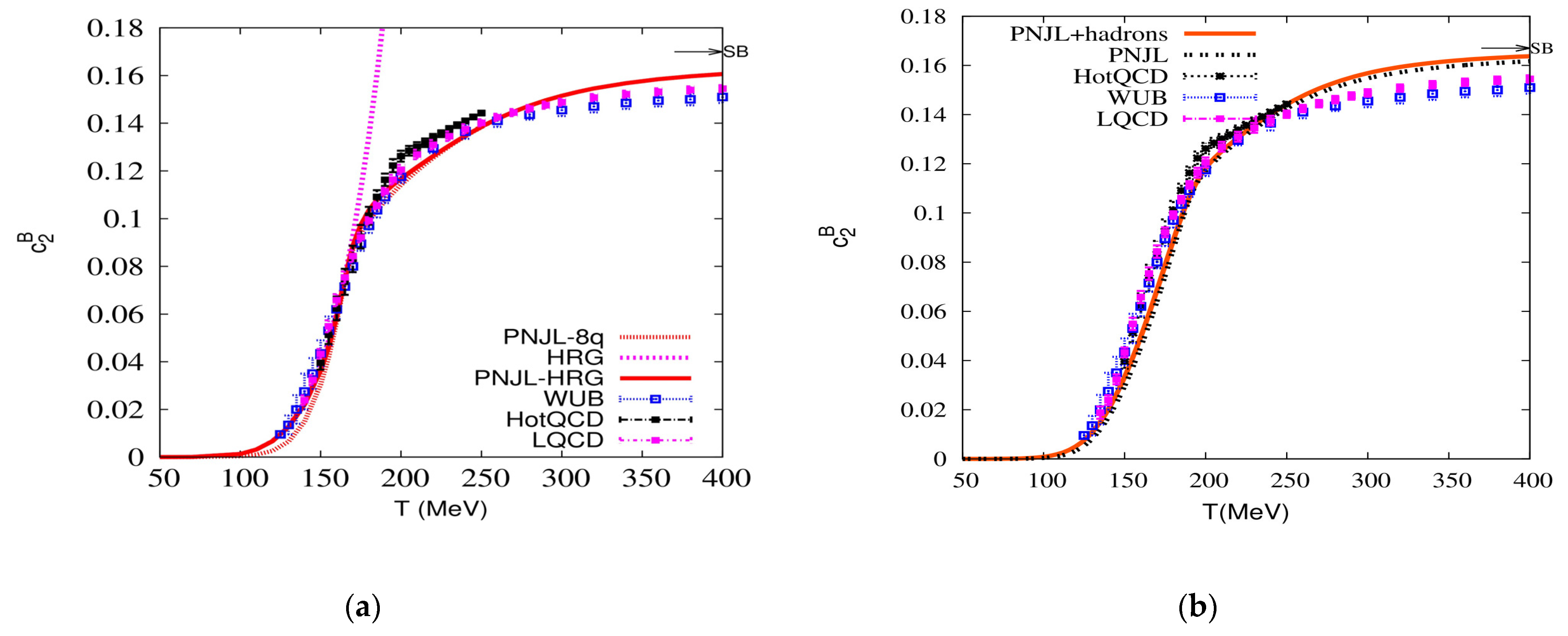
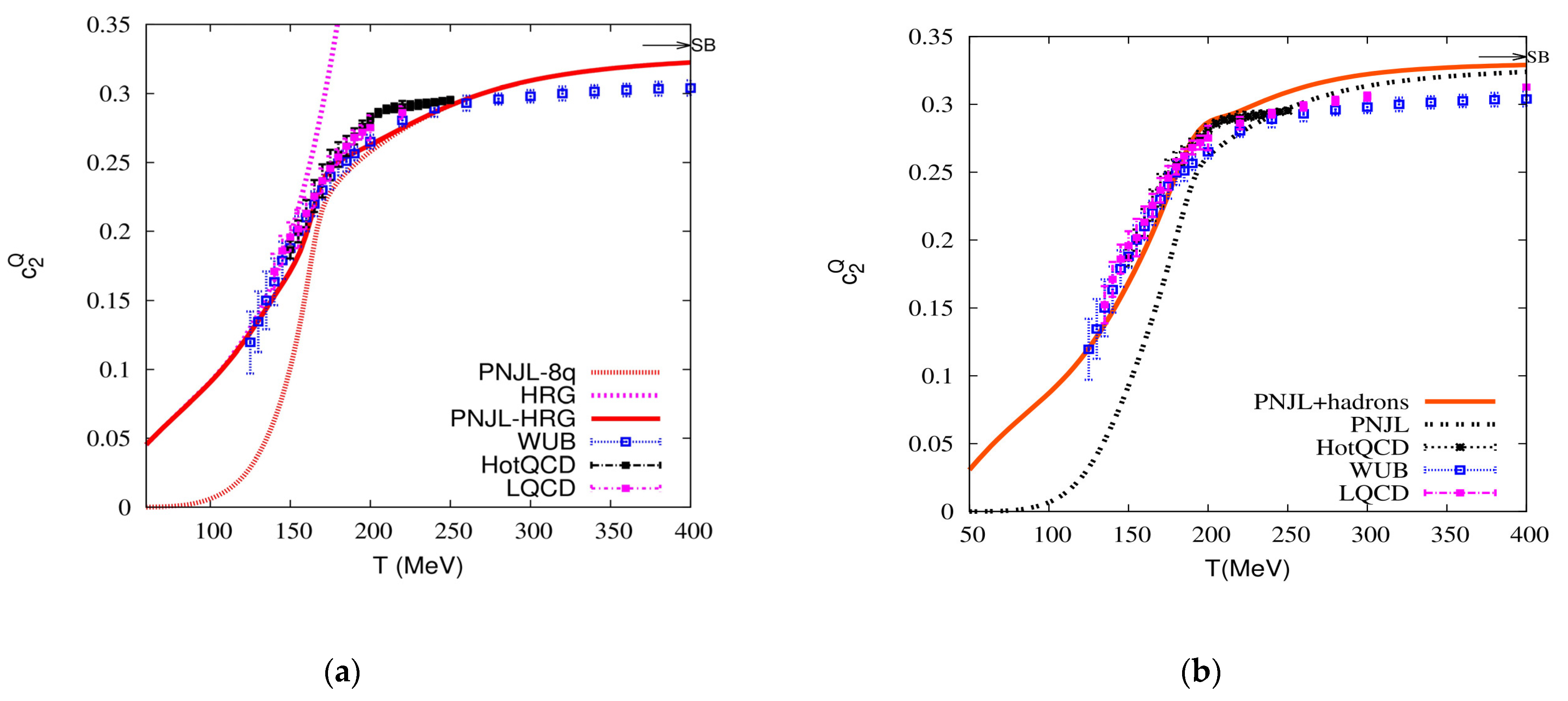
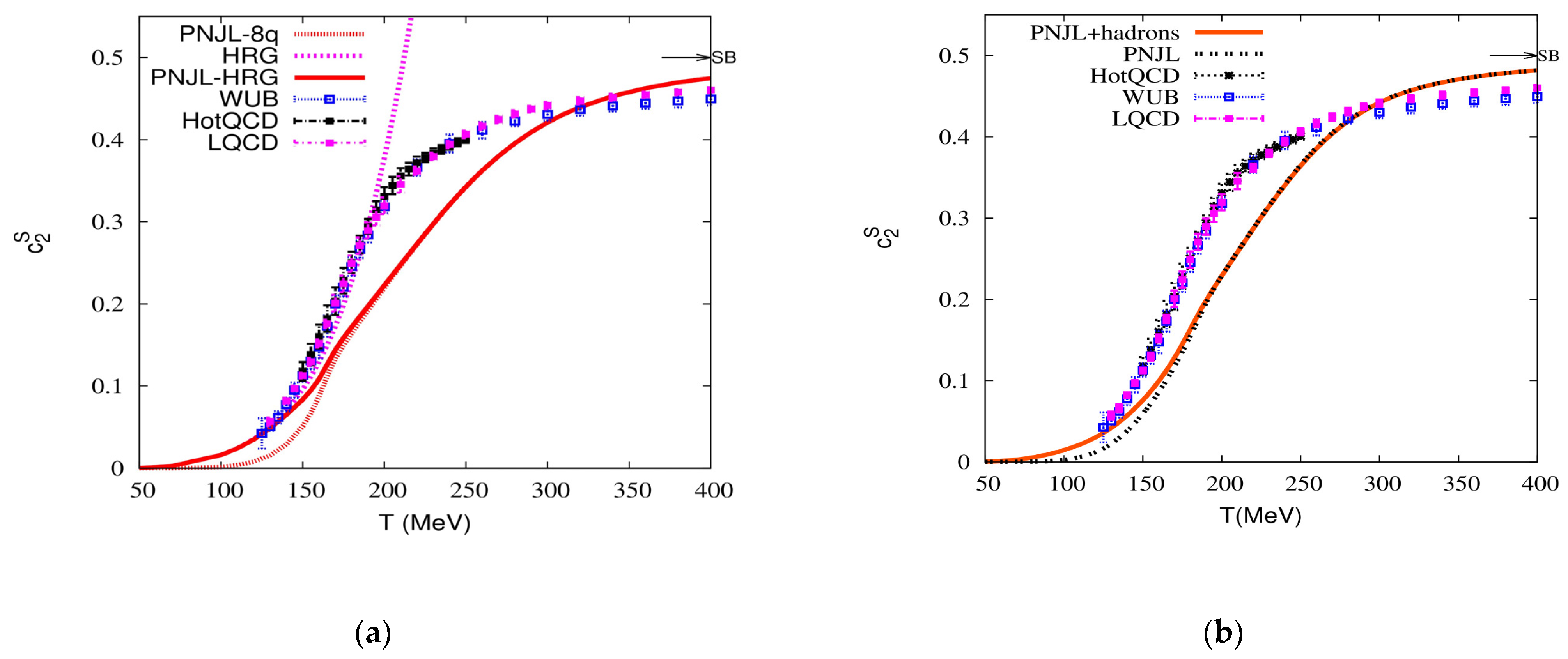
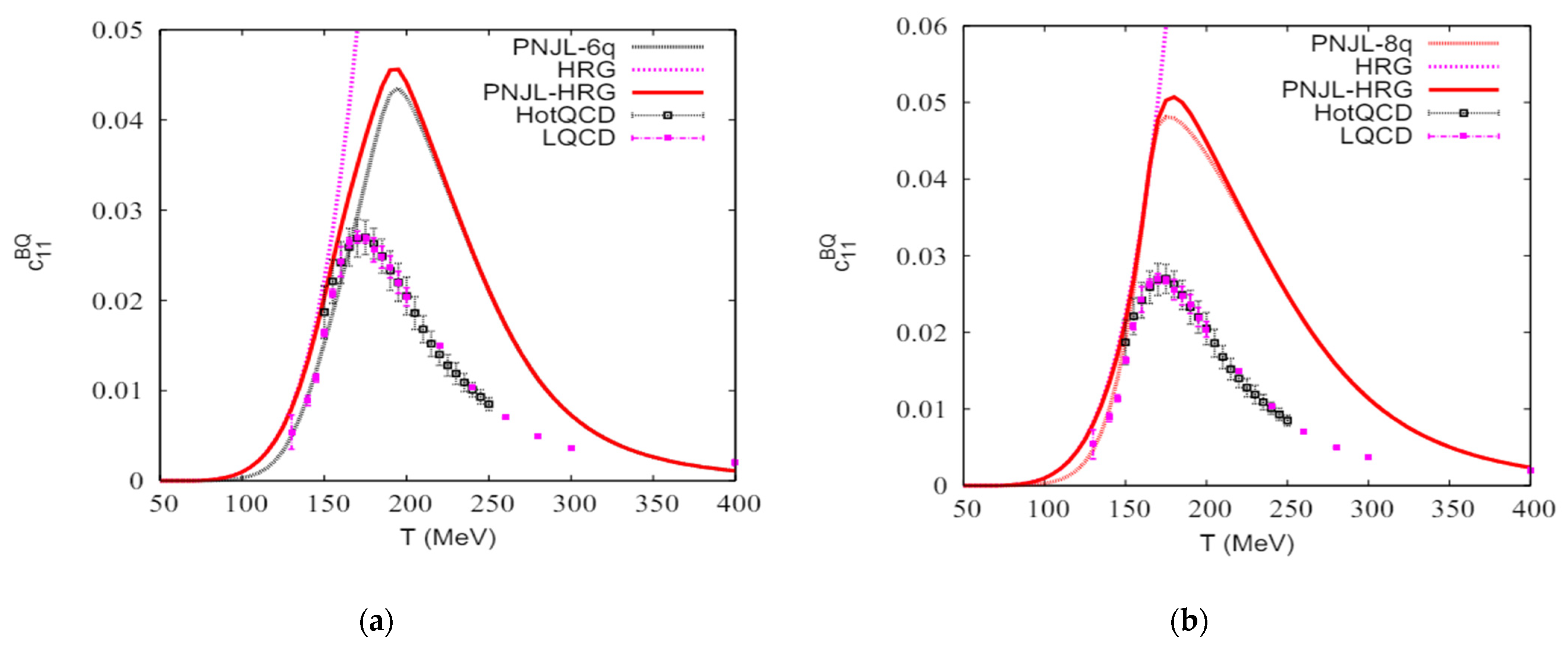
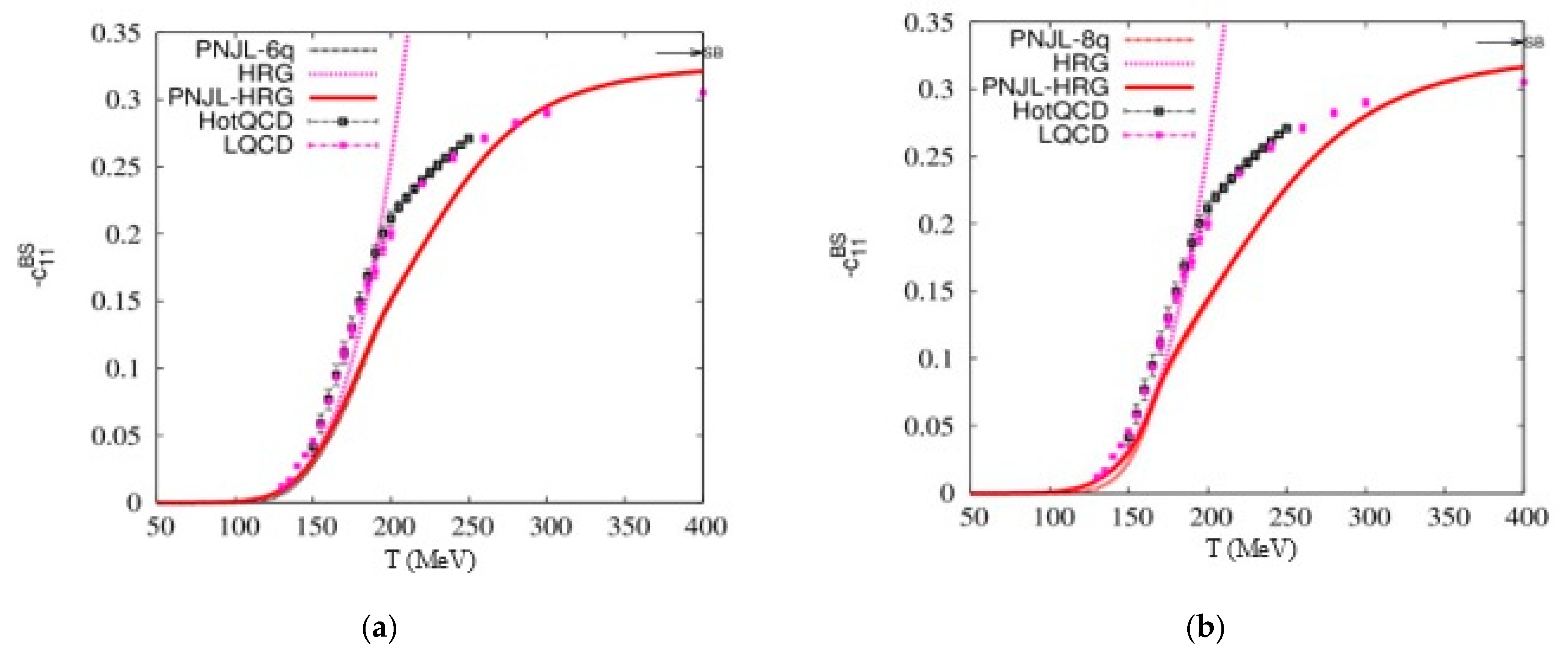
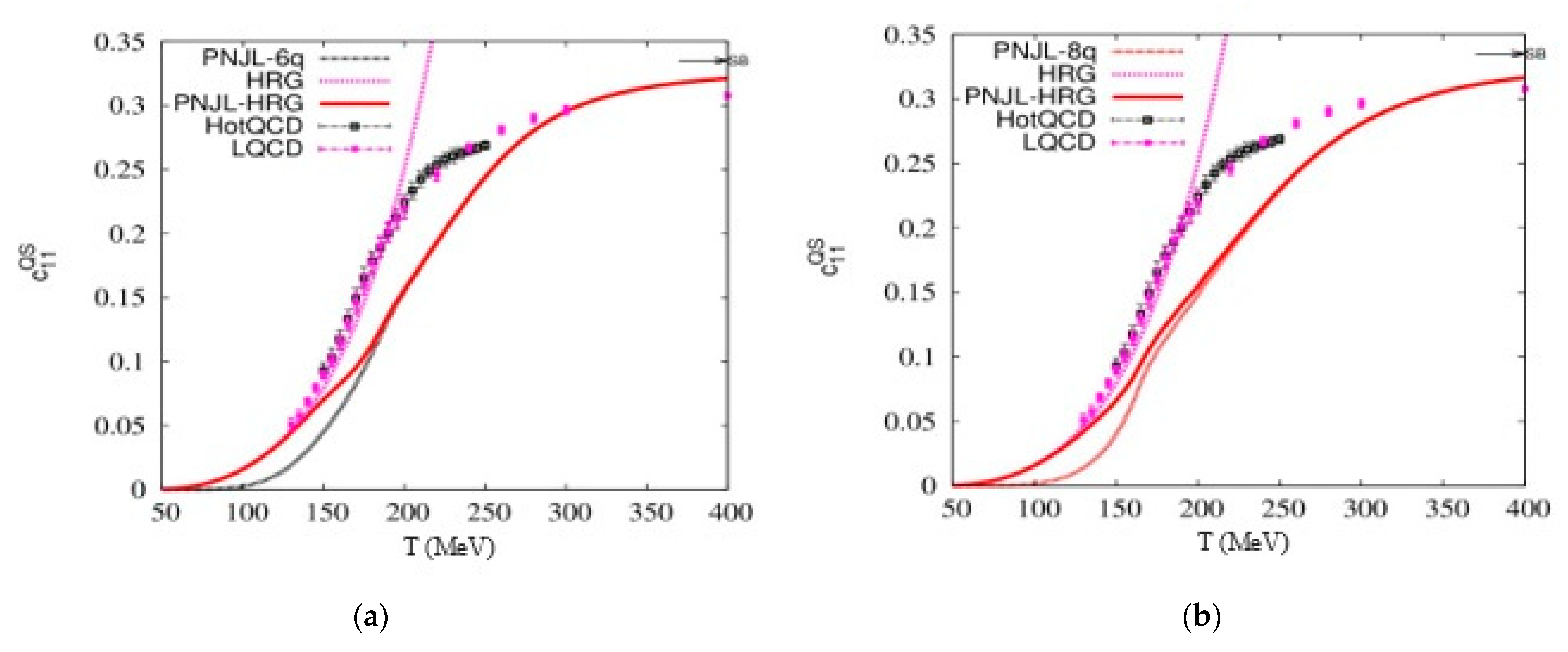
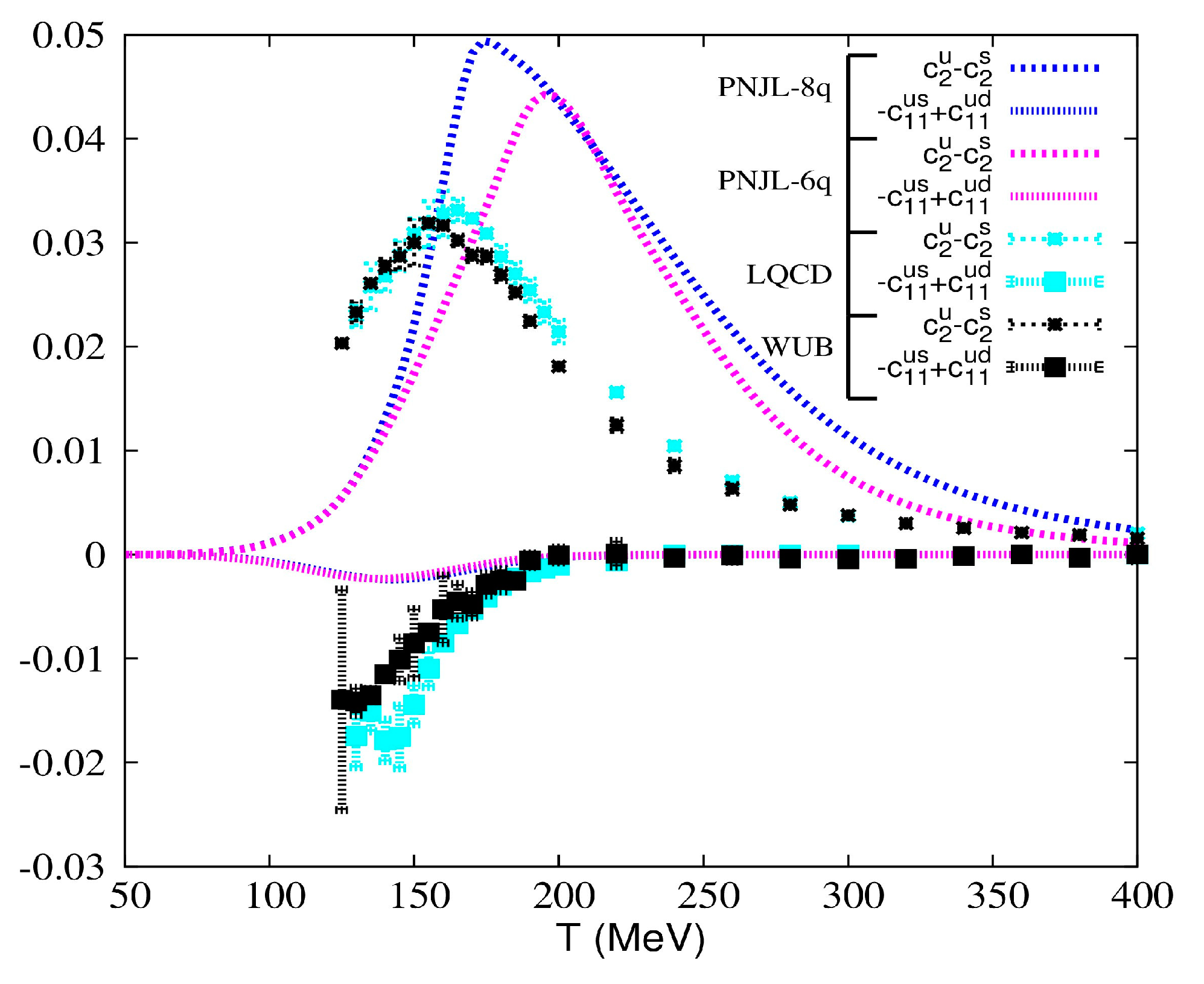
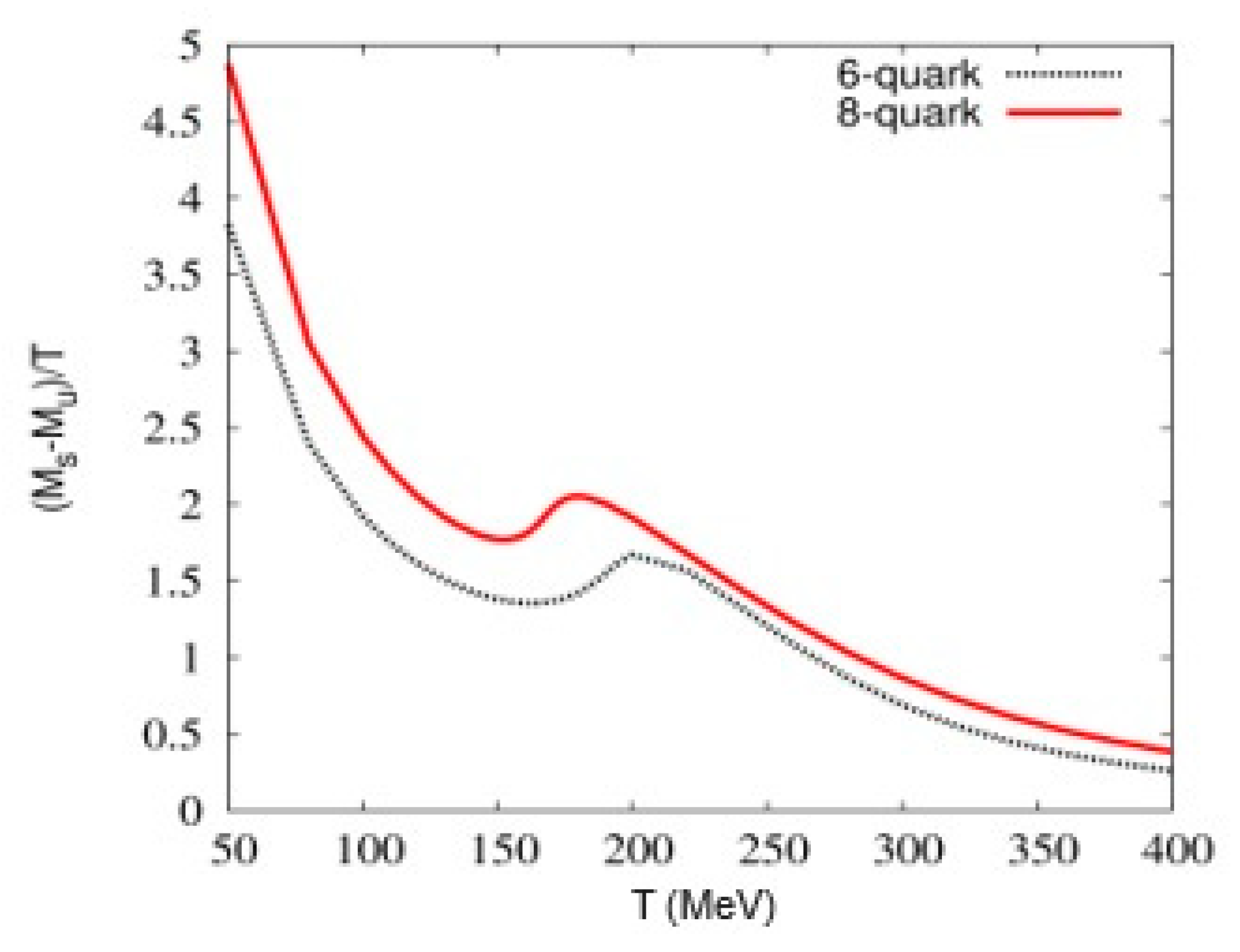
3. Results
4. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Boyd, G.; Engels, J.; Karsch, F.; Laermann, E.; Legeland, C.; Lugermeier, M.; Peterson, B. Thermodynamics of SU(3) lattice gauge theory. Nucl. Phys. B 1996, 469, 419–444. [Google Scholar] [CrossRef]
- Engels, J.; Kaczmarek, O.; Karsch, F.; Laermann, E. The quenched limit of lattice QCD at non-zero baryon number. Nucl. Phys. B 1999, 558, 307–326. [Google Scholar] [CrossRef][Green Version]
- Fodor, Z.; Katz, S.D. A new method to study lattice QCD at finite temperature and chemical potential. Phys. Lett. B 2002, 534, 87–92. [Google Scholar] [CrossRef]
- Fodor, Z.; Katz, S.D.; Szabo, K.K. The QCD equation of state at nonzero densities: Lattice result. Phys. Lett. B 2003, 568, 73–77. [Google Scholar] [CrossRef]
- Allton, C.R.; Ejiri, S.; Hands, S.J.; Kaczmarek, O.; Karsch, F.; Laermann, E.; Schmidt, C.; Scorzato, L. QCD thermal phase transition in the presence of a small chemical potential. Phys. Rev. D 2002, 66, 074507. [Google Scholar] [CrossRef]
- Bhattacharyya, A.; Das, S.; Ghosh, S.K.; Raha, S.; Ray, R.; Saha, K.; Upadhaya, S. Net Charge Fluctuations as a signal of QGP from Polyakov-Nambu-Jona-Lasinio model. arXiv 2012, arXiv:1212.6010. [Google Scholar]
- Jeon, S.; Koch, V. Fluctuations of Particle Ratios and the Abundance of Hadronic Resonances. Phys. Rev. Lett. 1999, 83, 5435. [Google Scholar] [CrossRef]
- Jeon, S.; Koch, V. Charged Particle Ratio Fluctuation as a Signal for Quark-Gluon Plasma. Phys. Rev. Lett. 2000, 85, 2076–2079. [Google Scholar] [CrossRef]
- Stock, R. Event by event analysis of ultrarelativistic nuclear collisions: A new method to search for critical fluctuations. In Proceedings of the NATO Advanced Study Workshop on Hot Hadronic Matter: Theory and Experiment, Divonne-les-Bains, France, 27 June–1 July 1994; Letessier, J., Gutbrod, H.H., Rafelski, J., Eds.; Plenum Press: New York, NY, USA, 1995. [Google Scholar]
- Stephanov, M.; Rajagopal, K.; Shuryak, E. Event-by-event fluctuations in heavy ion collisions and the QCD critical point. Phys. Rev. D 1999, 60, 114028. [Google Scholar] [CrossRef]
- Ding, H.-T.; Karsch, F.; Mukherjee, S. Thermodynamics of Strong-Interaction Matter from Lattice QCD. In Quark Gluon Plasma 5; Wang, X.N., Ed.; World Scientific: Singapore, 2016. [Google Scholar]
- Pereira, R.C.; Costa, P. Building models of quarks and gluons with an arbitrary number of colors using Cartan-Polyakov loop. Nucl. Phys. B 2024, 998, 116415. [Google Scholar] [CrossRef]
- Deb, P.; Varma, R. Fluctuations of conserved charges with finite size PNJL model. arXiv 2022, arXiv:2209.06297. [Google Scholar]
- Bühlmann, P.; Wenger, U. Heavy-dense QCD at fixed baryon number without a sign problem. In Proceedings of the ScienceVolume 396, 38th International Symposium on Lattice Field Theory, LATTICE 2021, Online, 26–30 July 2021; p. 584. [Google Scholar]
- Bhattacharya, T.; Buchoff, M.I.; Christ, N.H.; Ding, H.T.; Gupta, R.; Jung, C.; Karsch, F.; Lin, Z.; Mawhinney, R.D.; McGlynn, G.; et al. QCD Phase Transition with Chiral Quarks and Physical Quark Masses. Phys. Rev. Lett. 2014, 113, 082001. [Google Scholar] [CrossRef]
- Gottlieb, S.A.; Heller, U.M.; Kennedy, A.D.; Kim, S.; Kogut, J.B.; Liu, C.; Renken, R.L.; Sinclair, D.K.; Sugar, R.L.; Toussaint, D.; et al. Thermodynamics of lattice QCD with two light quark flavors on a 16**3 x 8 lattice. 2. Phys. Rev. D 1997, 55, 6852–6860. [Google Scholar] [CrossRef]
- Allton, C.R.; Ejiri, S.; Hands, S.J.; Kaczmarek, O.; Karsch, F.; Laermann, E.; Schmidt, C. Equation of state for two flavor QCD at nonzero chemical potential. Phys. Rev. D 2003, 68, 014507. [Google Scholar] [CrossRef]
- de Forcrand, P.; Philipsen, O. The QCD phase diagram for three degenerate flavors and small baryon density. Nucl. Phys. B 2003, 673, 170–186. [Google Scholar] [CrossRef]
- Aoki, Y.; Fodor, Z.; Katz, S.D.; Szabo, K.K. The QCD transition temperature: Results with physical masses in the continuum limit. Phys. Lett. B 2006, 643, 46–54. [Google Scholar] [CrossRef]
- Aoki, Y.; Endrodi, G.; Fodor, Z.; Katz, S.D.; Szabo, K.K. The Order of the quantum chromodynamics transition predicted by the standard model of particle physics. Nature 2006, 443, 675–678. [Google Scholar] [CrossRef] [PubMed]
- Aoki, Y.; Borsanyi, S.; Durr, S.; Fodor, Z.; Katz, S.D.; Krieg, S.; Szabo, K.K. The QCD transition temperature: Results with physical masses in the continuum limit II. J. High Energy Phys. 2009, 06, 088. [Google Scholar] [CrossRef]
- Borsanyi, S.; Fodor, Z.; Katz, S.D.; Krieg, S.; Ratti, C.; Szabo, K.K. Freeze-Out Parameters: Lattice Meets Experiment. Phys. Rev. Lett. 2013, 111, 062005. [Google Scholar] [CrossRef] [PubMed]
- Bazavov, A.; Bhattacharya, T.; Cheng, M.; DeTar, C.; Ding, H.T.; Gottlieb, S.; Gupta, R.; Hegde, P.; Heller, U.M.; Karsch, F.; et al. Chiral and deconfinement aspects of the QCD transition. Phys. Rev. D 2012, 85, 054503. [Google Scholar] [CrossRef]
- Bazavov, A.; Bhattacharya, T.; DeTar, C.; Ding, H.T.; Gottlieb, S.; Gupta, R.; Hegde, P.; Heller, U.M.; Karsch, F.; Laermann, E.; et al. Equation of state in (2 + 1)-flavor QCD. Phys. Rev. D 2014, 90, 094503. [Google Scholar] [CrossRef]
- Borsanyi, S.; Fodor, Z.; Hoelbling, C.; Katz, S.D.; Krieg, S.; Szabo, K.K. Full result for the QCD equation of state with 2 + 1 flavors. Phys. Lett. B 2014, 730, 99–104. [Google Scholar] [CrossRef]
- Hatta, Y.; Stephanov, M.A. Proton-Number Fluctuation as a Signal of the QCD Critical End Point. Phys. Rev. Lett. 2003, 91, 102003, Erratum in Phys. Rev. Lett. 2003, 91, 129901. [Google Scholar] [CrossRef]
- Gazdzicki, M.; Mrowczynski, S. A Method to study ‘equilibration’ in nucleus-nucleus collisions. Z. Phys. C 1992, 54, 127–132. [Google Scholar]
- Ejiri, S.; Karsch, F.; Redlich, K. Hadronic fluctuations at the QCD phase transition. Phys. Lett. B 2006, 633, 275–282. [Google Scholar] [CrossRef]
- Stephanov, M.A. Non-Gaussian fluctuations near the QCD critical point. Phys. Rev. Lett. 2009, 102, 032301. [Google Scholar] [CrossRef]
- Meisinger, P.N.; Ogilvie, M.C. Chiral symmetry restoration and ZN symmetry. Phys. Lett. B 1996, 379, 163–168. [Google Scholar] [CrossRef]
- Fukushima, K. Chiral effective model with the Polyakov loop. Phys. Lett. B 2004, 591, 277–284. [Google Scholar] [CrossRef]
- Ratti, C.; Thaler, M.A.; Weise, W. Phases of QCD: Lattice thermodynamics and a field theoretical model. Phys. Rev. D 2006, 73, 014019. [Google Scholar] [CrossRef]
- Ghosh, S.K.; Mukherjee, T.K.; Mustafa, M.G.; Ray, R. Susceptibilities and speed of sound from PNJL model. Phys. Rev. D 2006, 73, 114007. [Google Scholar] [CrossRef]
- Mukherjee, S.; Mustafa, M.G.; Ray, R. Thermodynamics of the Polyakov-Nambu-Jona-Lasinio model with nonzero baryon and isospin chemical potentials. Phys. Rev. D 2007, 75, 094015. [Google Scholar] [CrossRef]
- Ciminale, M.; Gatto, R.; Ippolito, N.D.; Nardulli, G.; Ruggieri, M. Three flavor Nambu–Jona-Lasinio model with Polyakov loop and competition with nuclear matter. Phys. Rev. D 2008, 77, 054023. [Google Scholar] [CrossRef]
- Shao, G.Y.; Tang, Z.D.; Di Toro, M.; Colonna, M.; Gao, X.Y.; Gao, N. Phase transition of strongly interacting matter with a chemical potential dependent Polyakov loop potential. Phys. Rev. D 2016, 94, 014008. [Google Scholar] [CrossRef]
- Shao, G.Y.; Tang, Z.D.; Di Toro, M.; Colonna, M.; Gao, X.Y.; Gao, N.; Zhao, Y.L. Entanglement interaction and the phase diagram of strongly interacting matter. Phys. Rev. D 2015, 92, 114027. [Google Scholar] [CrossRef]
- Ghosh, S.; Peixoto, T.C.; Roy, V.; Serna, F.E.; Krein, G. Shear and bulk viscosities of quark matter from quark-meson fluctuations in the Nambu–Jona-Lasinio model. Phys. Rev. D 2016, 93, 045205. [Google Scholar] [CrossRef]
- Islam, C.A.; Majumder, S.; Haque, N.; Mustafa, M.G. Vector meson spectral function and dilepton production rate in a hot and dense medium within an effective QCD approach. J. High Energy Phys. 2015, 1502, 11. [Google Scholar] [CrossRef][Green Version]
- Bellwied, R.; Borsanyi, S.; Fodor, Z.; Katz, S.D.; Pasztor, A.; Ratti, C.; Szabo, K.K. Fluctuations and correlations in high temperature QCD. Phys. Rev. D 2015, 92, 114505. [Google Scholar] [CrossRef]
- Bazavov, A.; Bhattacharya, T.; DeTar, C.E.; Ding, H.T.; Gottlieb, S.; Gupta, R.; Hegde, P.; Heller, U.M.; Karsch, F.; Laermann, E.; et al. Fluctuations and correlations of net baryon number, electric charge, and strangeness: A comparison of lattice QCD results with the hadron resonance gas model. Phys. Rev. D 2012, 86, 034509. [Google Scholar] [CrossRef]
- Borsányi, S.; Fodor, Z.; Katz, S.D.; Krieg, S.; Ratti, C.; Szabó, K. Fluctuations of conserved charges at finite temperature from lattice QCD. J. High Energy Phys. 2012, 1201, 138. [Google Scholar] [CrossRef]
- Bazavov, A.; Ding, H.T.; Hegde, P.; Kaczmarek, O.; Karsch, F.; Laermann, E.; Mukherjee, S.; Petreczky, P.; Schmidt, C.; Smith, D.; et al. Freeze-Out Conditions in Heavy Ion Collisions from QCD Thermodynamics. Phys. Rev. Lett. 2012, 109, 192302. [Google Scholar] [CrossRef]
- Schmidt, C. QCD bulk thermodynamics and conserved charge fluctuations with HISQ fermions. (for the BNL-Bielefeld Collaboration). J. Phys. Conf. Ser. 2012, 432, 012013. [Google Scholar] [CrossRef]
- Bazavov, A.; Ding, H.T.; Hegde, P.; Kaczmarek, O.; Karsch, F.; Laermann, E.; Maezawa, Y.; Mukherjee, S.; Ohno, H.; Petreczky, P.; et al. Strangeness at High Temperatures: From Hadrons to Quarks. Phys. Rev. Lett. 2013, 111, 082301. [Google Scholar] [CrossRef]
- Braun-Munzinger, P.; Redlich, K.; Stachel, J. Particle Production in Heavy Ion Collisions. arXiv 2003, arXiv:nucl-th/0304013. [Google Scholar]
- Karsch, F.; Redlich, K.; Tawfik, A. Thermodynamics at Non-Zero Baryon Number Density: A Comparison of Lattice and Hadron Resonance Gas Model Calculations. Phys. Lett. B 2003, 571, 67–74. [Google Scholar] [CrossRef]
- Tawfik, A. QCD phase diagram: A comparison of lattice and hadron resonance gas model calculations. Phys. Rev. D 2005, 71, 054502. [Google Scholar] [CrossRef]
- Andronic, A.; Braun-Munzinger, P.; Stachel, J.; Winn, M. Interacting hadron resonance gas meets lattice QCD. Phys. Lett. B 2012, 718, 80–85. [Google Scholar] [CrossRef]
- Huovinen, P.; Petreczky, P. Hadron resonance gas with repulsive interactions and fluctuations of conserved charges. Phys. Lett. B 2018, 777, 125–130. [Google Scholar] [CrossRef]
- Dashen, R.; Ma, S.-K.; Bernstein, H.J. S-Matrix Formulation of Statistical Mechanics. Phys. Rev. 1969, 187, 345–370. [Google Scholar] [CrossRef]
- Dashen, R.; Ma, S.-K. Scattering Theory and Current Correlations in Classical Gases. Phys. Rev. A 1971, 4, 700. [Google Scholar] [CrossRef]
- Braun-Munzinger, P.; Stachel, J.; Wessels, J.; Xu, N. Thermal equilibration and expansion in nucleus-nucleus collisions at the AGS. Phys. Lett. B 1995, 344, 43–48. [Google Scholar] [CrossRef]
- Cleymans, J.; Elliott, D.; Satz, H.; Thews, R.L. Thermal hadron production in Si-Au collisions. Z. Für Phys. C Part. Fields 1997, 74, 319–323. [Google Scholar] [CrossRef]
- Bhattacharyya, A.; Ghosh, S.K.; Maity, S.; Raha, S.; Ray, R.; Saha, K.; Samanta, S.; Upadhaya, S. Thermodynamics of strongly interacting matter in a hybrid model. Phys. Rev. C 2019, 99, 045207. [Google Scholar] [CrossRef]
- Schaefer, B.-J.; Wambach, J. Susceptibilities near the QCD (tri)critical point. Phys. Rev. D 2007, 75, 085015. [Google Scholar] [CrossRef]
- Scavenius, O.; Mócsy, Á.; Mishustin, I.N.; Rischke, D.H. Chiral phase transition within effective models with constituent quarks. Phys. Rev. C 2001, 64, 045202. [Google Scholar] [CrossRef]
- Schaffner-Bielich, J. Effective Restoration of the UA(1) Symmetry in the SU(3) Linear σ Model. Phys. Rev. Lett. 2000, 84, 3261. [Google Scholar] [CrossRef] [PubMed]
- Gupta, U.S.; Tiwari, V.K. Meson masses and mixing angles in the 2 + 1 flavor Polyakov quark meson sigma model and symmetry restoration effects. Phys. Rev. D 2010, 81, 054019. [Google Scholar] [CrossRef]
- Tawfik, A.; Magdy, N.; Diab, A. Polyakov linear SU(3) σ model: Features of higher-order moments in a dense and thermal hadronic medium. Phys. Rev. C 2014, 89, 055210. [Google Scholar] [CrossRef]
- Tawfik, A.N.; Diab, A.M.; Hussein, M.T. Quark-hadron phase structure, thermodynamics and magnetization of QCD matter. arXiv 2018, arXiv:1604.08174. [Google Scholar] [CrossRef]
- Tawfik, A.N.; Diab, A.M.; Ghoneim, M.T.; Anwer, H. SU(3) Polyakov linear-sigma model with finite isospin asymmetry: QCD phase diagram. Eur. J. Mod. Phys. A 2019, 34, 1950199. [Google Scholar] [CrossRef]
- Tawfik, A.N.; Greiner, C.; Diab, A.M.; Ghoneim, M.T.; Anwer, H. Polyakov linear-σ model in mean-field approximation and optimized perturbation theory. Phys. Rev. C 2020, 101, 035210. [Google Scholar] [CrossRef]
- Tawfik, A.N.; Diab, A.M. Chiral magnetic properties of QCD phase-diagram. Eur. Phys. J. A 2021, 57, 200. [Google Scholar] [CrossRef]
- Tawfik, A.N. QCD Phase Structure and In-Medium Modifications of Meson Masses in Polyakov Linear-Sigma Model with Finite Isospin Asymmetry. Universe 2023, 9, 276. [Google Scholar] [CrossRef]
- Tawfik, A.N.; Dabash, T.F.; Elshehri, A. Singularity attenuation with quantum-mechanically revised metric tensor. Astron. Nachr. 2024, 345, e240004. [Google Scholar] [CrossRef]
- Ayala, A.; Bashir, A.; Dominguez, C.A.; Gutierrez, E.; Loewe, M. QCD phase diagram from finite energy sum rules. Phys. Rev. D 2011, 84, 056004. [Google Scholar] [CrossRef]
- Gutierrez, E.; Ahmad, A.; Ayala, A.; Bashir, A.; Raya, A. The QCD phase diagram from Schwinger–Dyson equations. J. Phys. G 2014, 41, 075002. [Google Scholar] [CrossRef][Green Version]
- Contant, R.; Huber, M.Q. Phase structure and propagators at nonvanishing temperature for QCD and QCD-like theories. Phys. Rev. D 2017, 96, 074002. [Google Scholar] [CrossRef]
- Ahmad, A. Chiral symmetry restoration and deconfinement in the contact interaction model of quarks with parallel electric and magnetic fields. Chin. Phys. C 2021, 45, 073109. [Google Scholar] [CrossRef]
- Ahmad, A.; Bashir, A.; Dedolla, M.A.; Cobos-Martinez, J.J. Flavor, temperature and magnetic field dependence of the QCD phase diagram: Magnetic catalysis and its inverse. J. Phys. G 2021, 487, 075002. [Google Scholar] [CrossRef]
- Ahmad, A.; Farooq, A. Schwinger Pair Production in QCD from Flavor-Dependent Contact Interaction Model of Quarks. arXiv 2023, arXiv:2302.13265. [Google Scholar]
- Ahmad, A.; Azher, M.; Raya, A. Robust features of a QCD phase diagram through a contact interaction model for quarks: A view from the effective potential. Eur. Phys. J. A 2023, 59, 252. [Google Scholar] [CrossRef]
- Bhattacharyya, A.; Ghosh, S.K.; Ray, R.; Saha, K.; Upadhaya, S. Polyakov–Nambu–Jona-Lasinio model in finite volumes. Eur. Phys. Lett. 2016, 116, 52001. [Google Scholar] [CrossRef]
- Ghosh, S. Electrical conductivity of hadronic matter from different possible mesonic and baryonic loops. Phys. Rev. D 2017, 95, 036018. [Google Scholar] [CrossRef]
- Ghosh, S.; Ghosh, S.; Bhattacharyya, S. Phenomenological bound on the viscosity of the hadron resonance gas. Phys. Rev. C 2018, 98, 045202. [Google Scholar] [CrossRef]
- Saha, K.; Ghosh, S.; Upadhaya, S.; Maity, S. Transport coefficients in a finite volume Polyakov–Nambu–Jona-Lasinio model. Phys. Rev. D 2018, 97, 116020. [Google Scholar] [CrossRef]
- Singha, P.; Abhishek, A.; Kadam, G.; Ghosh, S.; Mishra, H. Calculations of shear, bulk viscosities and electrical conductivity in the Polyakov-quark–meson model. J. Phys. G 2019, 46, 015201. [Google Scholar] [CrossRef]
- Ghosh, S.; Ghosh, S. One-loop Kubo estimations of the shear and bulk viscous coefficients for hot and magnetized bosonic and fermionic systems. Phys. Rev. D 2021, 103, 096015. [Google Scholar] [CrossRef]
- Islam, C.A.; Mustafa, M.G.; Ray, R.; Singha, P. Consistent approach to study gluon quasiparticles. Phys. Rev. D 2022, 106, 054002. [Google Scholar] [CrossRef]
- Elze, H.T.; Greiner, W. Finite Size Effects for Quark—Gluon Plasma Droplets. Phys. Lett. B 1986, 179, 385–392. [Google Scholar] [CrossRef]
- Hua, L.M.; Xu, J. Shear viscosity of nuclear matter in the spinodal region. Phys. Rev. C 2023, 107, 034601. [Google Scholar] [CrossRef]
- Saha, K. Theoretical Perspectives on Viscous Nature of Strongly Interacting Systems. Universe 2024, 10, 259. [Google Scholar] [CrossRef]
- Bhattacharyya, A.; Deb, P.; Lahiri, A.; Ray, R. Susceptibilities with multi-quark interactions in PNJL model. Phys. Rev. D 2010, 82, 114028. [Google Scholar] [CrossRef]
- Bhattacharyya, A.; Deb, P.; Lahiri, A.; Ray, R. Correlation between conserved charges in PNJL Model with multi-quark interactions. Phys. Rev. D 2011, 83, 014011. [Google Scholar] [CrossRef]
- Ghosh, S.K.; Mukherjee, T.K.; Mustafa, M.G.; Ray, R. Polyakov-Nambu-Jona-Lasinio model with a Vandermonde term. Phys. Rev. D 2008, 77, 094024. [Google Scholar] [CrossRef]
- Bhattacharyya, A.; Deb, P.; Ghosh, S.K.; Ray, R. Investigation of the phase diagram and bulk thermodynamic properties using the Polyakov–Nambu–Jona-Lasinio model with eight-quark interactions. Phys. Rev. D 2010, 82, 014021. [Google Scholar] [CrossRef]
- Bhattacharyya, A.; Ghosh, S.K.; Maity, S.; Raha, S.; Ray, R.; Saha, K.; Upadhaya, S. Reparametrizing the Polyakov–Nambu–Jona-Lasinio model. Phys. Rev. D 2017, 95, 054005. [Google Scholar] [CrossRef]
- Jeon, S.; Koch, V.; Hwa, R.C. Event-by-Event Fluctuations; Quark gluon plasma. arXiv 2003, arXiv:hep-ph/0304012. [Google Scholar]
- Kumar, D.; Sarkar, N.; Bhaduri, P.P.; Jaiswal, A. Examination of thermalization of quarkonia at energies available at the CERN Large Hadron Collider. Phys. Rev. C 2023, 107, 064906. [Google Scholar]
- Braun-Munzinger, P.; Stachel, J. Production of strange clusters and strange matter in nucleus-nucleus collisions at the AGS. J. Phys. G 1995, 21, L17–L20. [Google Scholar] [CrossRef]
- Braun-Munzinger, P.; Heppe, I.; Stachel, J. Chemical equilibration in Pb+Pb collisions at the SPS. Phys. Lett. B 1999, 465, 15–20. [Google Scholar] [CrossRef]
- Cleymans, J.; Redlich, K. Chemical and thermal freeze-out parameters from 1A to 200A GeV. Phys. Rev. C 1999, 60, 054908. [Google Scholar] [CrossRef]
- Braun-Munzinger, P.; Magestro, D.; Redlich, K.; Stachel, J. Hadron production in Au–Au collisions at RHIC. Phys. Lett. B 2001, 518, 41–46. [Google Scholar] [CrossRef]
- Xu, N.; Kaneta, M. Hadron freeze-out conditions in high energy nuclear collisions. Nucl. Phys. A 2002, 698, 306–313. [Google Scholar] [CrossRef][Green Version]
- Becattini, F.; Manninen, J.; Gazdzicki, M. Energy and system size dependence of chemical freeze-out in relativistic nuclear collisions. Phys. Rev. C 2006, 73, 044905. [Google Scholar] [CrossRef]
- Andronic, A.; Braun-Munzinger, P.; Stachel, J. Hadron production in central nucleus-nucleus collisions at chemical freeze-out. Nucl. Phys. A 2006, 772, 167–199. [Google Scholar] [CrossRef]
- Cleymans, J.; Oeschler, H.; Redlich, K.; Wheaton, S. Comparison of chemical freeze-out criteria in heavy-ion collisions. Phys. Rev. C 2006, 73, 034905. [Google Scholar] [CrossRef]
- Andronic, A.; Braun-Munzinger, P.; Stachel, J. Thermal hadron production in relativistic nuclear collisions: The hadron mass spectrum, the horn, and the QCD phase transition. Phys. Lett. B 2009, 673, 142–145. [Google Scholar] [CrossRef]
- Andronic, A.; Braun-Munzinger, P.; Stachel, J. The horn, the hadron mass spectrum and the QCD phase diagram—The statistical model of hadron production in central nucleus-nucleus collisions. Nucl. Phys. A 2010, 834, 237c–240c. [Google Scholar] [CrossRef]
- Koch, V.; Bleicher, M.; Jeon, S. Event-by-event fluctuations and the QGP. Nucl. Phys. A 2002, 698, 261–268. [Google Scholar] [CrossRef][Green Version]
- Chatterjee, S.; Das, S.; Kumar, L.; Mishra, D.; Mohanty, B.; Sahoo, R.; Sharma, N. Freeze-Out Parameters in Heavy-Ion Collisions at AGS, SPS, RHIC, and LHC Energies. Adv. High Energy Phys. 2015, 2015, 349013. [Google Scholar] [CrossRef]
- Bhattacharyya, A.; Ghosh, S.K.; Ray, R.; Samanta, S. Exploring effects of magnetic field on the Hadron Resonance Gas. Euro. Phys. Lett. 2016, 115, 62003. [Google Scholar] [CrossRef]
- Bollweg, D.; Goswami, J.; Kaczmarek, O.; Karsch, F.; Mukherjee, S.; Petreczky, P.; Schmidt, C.; Scior, P.; HotQCD Collaboration. Second order cumulants of conserved charge fluctuations revisited: Vanishing chemical potentials. Phys. Rev. D 2021, 104, 074512. [Google Scholar]
- Bhattacharyya, A.; Das, S.; Ghosh, S.K.; Ray, R.; Samanta, S. Fluctuations and correlations of conserved charges in an excluded-volume hadron resonance gas model. Phys. Rev. C 2014, 90, 034909. [Google Scholar] [CrossRef]
- Sahoo, B.; Pradhan, K.K.; Sahu, D.; Sahoo, R. Effect of a magnetic field on the thermodynamic properties of a high-temperature hadron resonance gas with van der Waals interactions. Phys. Rev. D 2023, 108, 074028. [Google Scholar] [CrossRef]
- Hagedorn, R.; Rafelski, J. Hot hadronic matter and nuclear collisions. Phys. Lett. B 1980, 97, 136–142. [Google Scholar] [CrossRef]
- Rischke, D.H.; Gorenstein, M.I.; Stöcker, H.; Greiner, W. Excluded volume effect for the nuclear matter equation of state. Z. Für Phys. C Part. Fields 1991, 51, 485–489. [Google Scholar] [CrossRef]
- Cleymans, J.; I Gorenstein, M.; Stålnacke, J.; Suhonen, E. Excluded volume effect and the quark-hadron phase transition. Phys. Scr. 1993, 48, 277–280. [Google Scholar] [CrossRef]
- Singh, C.; Patra, B.; Singh, K. Thermodynamically consistent EOS for hot dense hadron gas. Phys. Lett. B 1996, 387, 680–684. [Google Scholar] [CrossRef]
- Yen, G.D.; Gorenstein, M.I.; Greiner, W.; Yang, S.N. Excluded volume hadron gas model for particle number ratios in A+A collisions. Phys. Rev. C 1997, 56, 2210. [Google Scholar] [CrossRef]
- Gorenstein, M.I.; Hauer, M.; Moroz, O.N. Viscosity in the excluded volume hadron gas model. Phys. Rev. C 2008, 77, 024911. [Google Scholar] [CrossRef]
- Fu, J. Statistical model analysis of particle ratio fluctuations in heavy-ion collisions. Phys. Rev. C 2012, 85, 064905. [Google Scholar] [CrossRef]
- Begun, V.V.; Gazdzicki, M.; Gorenstein, M.I. Hadron-resonance gas at freeze-out: Reminder on the importance of repulsive interactions. Phys. Rev. C 2013, 88, 024902. [Google Scholar] [CrossRef]
- Fu, J. Higher moments of net-proton multiplicity distributions in heavy ion collisions at chemical freeze-out. Phys. Lett. B 2013, 722, 144–150. [Google Scholar] [CrossRef]
- Tawfik, A. Constant-trace anomaly as a universal condition for the chemical freeze-out. Phys. Rev. C 2013, 88, 035203. [Google Scholar] [CrossRef]
- Hama, Y.; Kodama, T.; Socolowski, O. Topics on Hydrodynamic Model of Nucleus-Nucleus Collisions. Braz. J. Phys. 2005, 35, 24–51. [Google Scholar] [CrossRef]
- Werner, K.; Karpenko, I.; Pierog, T.; Bleicher, M.; Mikhailov, K. Event-by-event simulation of the three-dimensional hydrodynamic evolution from flux tube initial conditions in ultrarelativistic heavy ion collisions. Phys. Rev. C 2010, 82, 044904. [Google Scholar] [CrossRef]
- Merdeev, A.V.; Satarov, L.M.; Mishustin, I.N. Hydrodynamic modeling of the deconfinement phase transition in heavy-ion collisions in the NICA–FAIR energy domain. Phys. Rev. C 2011, 84, 014907. [Google Scholar] [CrossRef]
- Olive, K.A. Review of Particle Physics. (Particle Data Group). Chin. Phys. C 2014, 38, 090001. [Google Scholar] [CrossRef]
- Abelev, B.; Adam, J.; Adamova, D.; Adare, A.M.; Aggarwal, M.M.; Aglieri Rinella, G.; Agocs, A.G.; Agostinelli, A.; Aguilar Salazar, S.; Ahammed, Z.; et al. Net-Charge Fluctuations in Pb-Pb Collisions at √SNN=2.76 TeV. Phys. Rev. Lett. 2013, 110, 152301. [Google Scholar] [CrossRef]
- Bhattacharyya, A.; Deb, P.; Ghosh, S.K.; Maity, S.; Raha, S.; Ray, R.; Saha, K.; Upadhaya, S. Finite temperature properties of a modified Polyakov–Nambu–Jona-Lasinio model. Phys. Rev. D 2020, 102, 074006. [Google Scholar] [CrossRef]
- Karsch, F.; Redlich, K. Probing freeze-out conditions in heavy ion collisions with moments of charge fluctuations. Phys. Lett. B 2011, 695, 136–142. [Google Scholar] [CrossRef]
- Albright, M.; Kapusta, J.; Young, C. Matching excluded-volume hadron-resonance gas models and perturbative QCD to lattice calculations. Phys. Rev. C 2014, 90, 024915. [Google Scholar] [CrossRef]
- Miyahara, A.; Torigoe, Y.; Kouno, H.; Yahiro, M. Equation of state and transition temperatures in the quark-hadron hybrid model. Phys. Rev. D 2016, 94, 016003. [Google Scholar] [CrossRef]
- Miyahara, A.; Ishii, M.; Kouno, H.; Yahiro, M. Crossover-model approach to QCD phase diagram, equation of state and susceptibilities in the 2 + 1 and 2 + 1 + 1 flavor systems. Int. J. Mod. Phys. A 2017, 32, 1750205. [Google Scholar] [CrossRef]
- Yukalov, V.I.; Yukalova, E.P. Multichannel approach to clustering matter. Physica A 1997, 243, 382–414. [Google Scholar] [CrossRef][Green Version]
- Yukalov, V.I.; Yukalova, E.P. Thermodynamics of strong interactions. Phys. Part. Nucl. 1997, 28, 37. [Google Scholar] [CrossRef][Green Version]
- Yukalov, V.I.; Yukalova, E.P. Models of Mixed Matter. Phys. Part. Nucl. 2023, 54, 1–68. [Google Scholar] [CrossRef]
- Yukalov, V.I.; Yukalova, E. Phase transition in multicomponent field theory at finite temperature. arXiv 2015, arXiv:1502.07109. [Google Scholar]
- Yukalov, V.I.; Yukalova, E.P. Calculation of critical exponents by self-similar factor approximants. Eur. Phys. J. B 2007, 55, 93–99. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Upadhaya, S. Fluctuations and Correlations of Conserved Charges Serving as Signals for QGP Production: An Overview from Polyakov Loop Enhanced Nambu–Jona-Lasinio Model. Universe 2024, 10, 332. https://doi.org/10.3390/universe10080332
Upadhaya S. Fluctuations and Correlations of Conserved Charges Serving as Signals for QGP Production: An Overview from Polyakov Loop Enhanced Nambu–Jona-Lasinio Model. Universe. 2024; 10(8):332. https://doi.org/10.3390/universe10080332
Chicago/Turabian StyleUpadhaya, Sudipa. 2024. "Fluctuations and Correlations of Conserved Charges Serving as Signals for QGP Production: An Overview from Polyakov Loop Enhanced Nambu–Jona-Lasinio Model" Universe 10, no. 8: 332. https://doi.org/10.3390/universe10080332
APA StyleUpadhaya, S. (2024). Fluctuations and Correlations of Conserved Charges Serving as Signals for QGP Production: An Overview from Polyakov Loop Enhanced Nambu–Jona-Lasinio Model. Universe, 10(8), 332. https://doi.org/10.3390/universe10080332




