On Dark Matter and Dark Energy in CCC+TL Cosmology
Abstract
1. Introduction
2. Theoretical Background
3. Dark Matter and Dark Energy Estimates
4. Concerning Structure Formation
5. Discussion
6. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Riess, A.G.; Filippenko, A.V.; Challis, P.; Clocchiatti, A.; Diercks, A.; Garnavich, P.M.; Gilliland, R.L.; Hogan, C.J.; Jha, S.; Kirshner, R.P.; et al. Observational Evidence from Supernovae for an Accelerating Universe and a Cosmological Constant. Astron. J. 1998, 116, 1009–1038. [Google Scholar] [CrossRef]
- Perlmutter, S.; Aldering, G.; Goldhaber, G.; Knop, R.A.; Nugent, P.; Castro, P.G.; Deustua, S.; Fabbro, S.; Goobar, A.; Groom, D.E.; et al. Measurements of Ω and Λ from 42 High-Redshift Supernovae. Astrophys. J. 1999, 517, 565. [Google Scholar] [CrossRef]
- Jimenez, R.; Loeb, A. Constraining Cosmological Parameters Based on Relative Galaxy Ages. Astrophys. J. 2002, 573, 37–42. [Google Scholar] [CrossRef]
- Eisenstein, D.J.; Zehavi, I.; Hogg, D.W.; Scoccimarro, R.; Blanton, M.R.; Nichol, R.C.; Scranton, R.; Seo, H.; Tegmark, M.; Zheng, Z.; et al. Detection of the Baryon Acoustic Peak in the Large-Scale Correlation Function of SDSS Luminous Red Galaxies. Astrophys. J. 2005, 633, 560–574. [Google Scholar] [CrossRef]
- Betoule, M.; Kessler, R.; Guy, J.; Mosher, J.; Hardin, D.; Biswas, R.; Astier, P.; El-Hage, P.; Konig, M.; Kuhlmann, S.; et al. Improved cosmological constraints from a joint analysis of the SDSS-II and SNLS supernova samples. Astron. Astrophys. 2014, 568, A22. [Google Scholar] [CrossRef]
- Haridasu, B.S.; Luković, V.V.; D’agostino, R.; Vittorio, N. Strong evidence for an accelerating Universe. Astron. Astrophys. 2017, 600, L1. [Google Scholar] [CrossRef]
- Bahcall, N.A. Dark matter universe. Proc. Natl. Acad. Sci. USA 2015, 112, 12243. [Google Scholar] [CrossRef] [PubMed]
- Weinberg, D.H.; Bullock, J.S.; Governato, F.; de Naray, R.K.; Peter, A.H.G. Cold dark matter: Controversies on small scales. Proc. Natl. Acad. Sci. USA 2015, 112, 12249–12255. [Google Scholar] [CrossRef] [PubMed]
- Yang, M.; Zhu, L.; Lei, Y.; Boardman, N.; Weijmans, A.M.; Morganti, R.; Oosterloo, T.; Duc, P.A. Dark matter measurements combining stellar and HI kinematics: 30% 1−σ outliers with low dark matter content at 5Re. Mon. Not. R. Astron. Soc. 2024, 528, 5295–5308. [Google Scholar] [CrossRef]
- Boylan-Kolchin, M.; Bullock, J.S.; Kaplinghat, M. Too big to fail? The puzzling darkness of massive Milky Way subhaloes. Mon. Not. R. Astron. Soc. Lett. 2011, 415, L40–L44. [Google Scholar] [CrossRef]
- Navarro, J.F.; Frenk, C.S.; White, S.D.M. A Universal Density Profile from Hierarchical Clustering. Astrophys. J. 1997, 490, 493–508. [Google Scholar] [CrossRef]
- Bunker, A.J.; Saxena, A.; Cameron, A.J.; Willott, C.J.; Curtis-Lake, E.; Jakobsen, P.; Carniani, S.; Smit, R.; Maiolino, R.; Witstok, J.; et al. JADES NIRSpec Spectroscopy of GN-z11: Lyman-α emission and possible enhanced nitrogen abundance in a z = 10.60 luminous galaxy. Astron. Astrophys. 2023, 677, A88. [Google Scholar] [CrossRef]
- Goerdt, T.; Moore, B.; Read, J.I.; Stadel, J.; Zemp, M. Does the Fornax dwarf spheroidal have a central cusp or core? Mon. Not. R. Astron. Soc. 2006, 368, 1073–1077. [Google Scholar] [CrossRef]
- Klypin, A.; Kravtsov, A.V.; Valenzuela, O.; Prada, F. Where are the missing galactic satellites? Astrophys. J. 1999, 522, 82–92. [Google Scholar] [CrossRef]
- Lord, K. Baltimore Lectures on Molecular Dynamics and the Wave Theory of Light; C.J. Clay and Sons: London, UK, 1904; p. 274. [Google Scholar]
- Zwicky, F. Republication of: The redshift of extragalactic nebulae. Gen. Relativ. Gravit. 2009, 41, 207–224. [Google Scholar] [CrossRef]
- Rubin, V.C.; Ford, W.K., Jr. Rotation of the Andromeda Nebula from a Spectroscopic Survey of Emission Regions. Astrophys. J. 1970, 150, 379. [Google Scholar] [CrossRef]
- Rubin, V.C.; Ford, W.K., Jr.; Thonnard, N. Extended rotation curves of high-luminosity spiral galaxies. IV. Systematic dynamical properties, Sa through Sc. Astrophys. J. 1978, 225, L107–L111. [Google Scholar] [CrossRef]
- Bosma, A. 21-cm line studies of spiral galaxies. II. The distribution and kinematics of neutral hydrogen in spiral galaxies of various morphological types. Astron. J. 1981, 86, 1825–1846. [Google Scholar] [CrossRef]
- Sofue, Y.; Rubin, V. Rotation Curves of Spiral Galaxies. Annu. Rev. Astron. Astrophys. 2001, 39, 137–174. [Google Scholar] [CrossRef]
- De Blok, W.J.; Walter, F.; Brinks, E.; Trachternach, C.; Oh, S.H.; Kennicutt, R.C. High-Resolution Rotation Curves and Galaxy Mass Models from THINGS. Astron. J. 2008, 136, 2648. [Google Scholar] [CrossRef]
- Genzel, R.; Schreiber, N.M.F.; Übler, H.; Lang, P.; Naab, T.; Bender, R.; Tacconi, L.J.; Wisnioski, E.; Wuyts, S.; Alexander, T.; et al. Strongly baryon-dominated disk galaxies at the peak of galaxy formation ten billion years ago. Nature 2017, 543, 397–401. [Google Scholar] [CrossRef]
- Lang, P.; Schreiber, N.M.F.; Genzel, R.; Wuyts, S.; Wisnioski, E.; Beifiori, A.; Belli, S.; Bender, R.; Brammer, G.; Burkert, A.; et al. Falling outer rotation curves of star-forming galaxies at 0.6 ≲ Z ≲ 2.6 probed with KMOS3D and SINS/ZC-SINF. Astrophys. J. 2017, 840, 92. [Google Scholar] [CrossRef]
- Nelson, A.; Williams, P. Recent Observations of the Rotation of Distant Galaxies and the Implication for Dark Matter. arXiv 2024, arXiv:2401.13783. [Google Scholar] [CrossRef]
- Faber, S.M.; Jackson, R.E. Velocity dispersions and mass-to-light ratios for elliptical galaxies. Astrophys. J. 1976, 204, 668–683. [Google Scholar] [CrossRef]
- Binny, J.; Merrifield, M. Galactic Astronomy; Princeton University Press: Princeton, NJ, USA, 1998; p. 712. [Google Scholar]
- Allen, S.W.; Evrard, A.E.; Mantz, A.B. Cosmological Parameters from Observations of Galaxy Clusters. Annu. Rev. Astron. Astrophys. 2011, 49, 409–470. [Google Scholar] [CrossRef]
- Taylor, A.N.; Dye, S.; Broadhurst, T.J.; Benitez, N.; van Kampen, E. Gravitational Lens Magnification and the Mass of Abell 1689. Astrophys. J. 1998, 501, 539–553. [Google Scholar] [CrossRef][Green Version]
- Natarajan, P.; Chadayammuri, U.; Jauzac, M.; Richard, J.; Kneib, J.-P.; Ebeling, H.; Jiang, F.; Bosch, F.v.D.; Limousin, M.; Jullo, E.; et al. Mapping substructure in the HST Frontier Fields cluster lenses and in cosmological simulations. Mon. Not. R. Astron. Soc. 2017, 468, 1962–1980. [Google Scholar] [CrossRef]
- Hinshaw, G.; Weiland, J.L.; Hill, R.S.; Odegard, N.; Larson, D.; Bennett, C.L.; Dunkley, J.; Gold, B.; Greason, M.R.; Jarosik, N.; et al. Five-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Data Processing, Sky Maps, and Basic Results. Astrophys. J. Suppl. Ser. 2009, 180, 225. [Google Scholar] [CrossRef]
- Ade, P.A.; Aghanim, N.; Arnaud, M.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Banday, A.J.; Barreiro, R.B.; Bartlett, J.G.; Bartolo, N.; et al. Planck 2015 results. XIII. Cosmological parameters. Astron. Astrophys. 2016, 594, A13. [Google Scholar]
- Schramm, D.N. The age of the universe, dark matter, and structure formation. Proc. Natl. Acad. Sci. USA 1998, 95, 1. [Google Scholar] [CrossRef]
- Popolo, A.D. Dark matter and structure formation a review. Astron. Rep. 2007, 51, 169–196. [Google Scholar] [CrossRef]
- Mina, M.; Mota, D.F.; Winther, H.A. Solitons in the dark: First approach to non-linear structure formation with fuzzy dark matter. Astron. Astrophys. 2022, 662, A29. [Google Scholar] [CrossRef]
- Clowe, D.; Bradač, M.; Gonzalez, A.H.; Markevitch, M.; Randall, S.W.; Jones, C.; Zaritsky, D. A direct empirical proof of the existence of dark matter. Astrophys. J. 2006, 648, L109–L113. [Google Scholar] [CrossRef]
- Ding, Z.; Seo, H.-J.; Huff, E.; Saito, S.; Clowe, D. Detecting baryon acoustic oscillations in dark matter from kinematic weak lensing surveys. Mon. Not. R. Astron. Soc. 2019, 487, 253–267. [Google Scholar] [CrossRef]
- Gupta, R.P. Testing CCC+TL Cosmology with Observed BAO Features. arXiv 2024, arXiv:2401.09483. [Google Scholar]
- Aghanim, N.; Akrami, Y.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; Basak, S.; et al. [Planck Collaboration] Planck 2018 results. VI. Cosmological parameters. Astron. Astrophys. 2020, 641, A6. [Google Scholar]
- Gupta, R.P. JWST early Universe observations and ΛCDM cosmology. Mon. Not. R. Astron. Soc. 2023, 524, 3385–3395. [Google Scholar] [CrossRef]
- Chae, K.-H.; Lelli, F.; Desmond, H.; McGaugh, S.S.; Li, P.; Schombert, J.M. Testing the Strong Equivalence Principle: Detection of the External Field Effect in Rotationally Supported Galaxies. Astrophys. J. 2020, 904, 51. [Google Scholar] [CrossRef]
- Nadler, E.O.; Yang, D.; Yu, H.-B. A Self-interacting Dark Matter Solution to the Extreme Diversity of Low-mass Halo Properties. Astrophys. J. 2023, 958, L39. [Google Scholar] [CrossRef]
- Bose, B.; Carrilho, P.; Marinucci, M.; Moretti, C.; Pietroni, M.; Carella, E.; Piga, L.; Wright, B.S.; Vernizzi, F.; Carbone, C.; et al. [Euclid Collaboration] Euclid preparation. Modelling spectroscopic clustering on mildly nonlinear scales in beyond-ΛCDM models. arXiv 2023, arXiv:2311.13529. [Google Scholar]
- Adhikari, P.; Ajaj, R.; Alpízar-Venegas, M.; Auty, D.J.; Benmansour, H.; Bina, C.E.; Bonivento, W.; Boulay, M.G.; Cadeddu, M.; Cai, B.; et al. First Direct Detection Constraints on Planck-Scale Mass Dark Matter with Multiple-Scatter Signatures Using the DEAP-3600 Detector. Phys. Rev. Lett. 2022, 128, 011801. [Google Scholar] [CrossRef]
- Kane, G.; Watson, S. Dark matter and LHC: What is the connection? Mod. Phys. Lett. A 2008, 23, 2103–2123. [Google Scholar] [CrossRef]
- Fox, P.J.; Harnik, R.; Kopp, J.; Tsai, Y. LEP shines light on dark matter. Phys. Rev. D 2011, 84, 014028. [Google Scholar] [CrossRef]
- Mannheim, P.D. Alternatives to Dark Matter and Dark Energy Prog. Part. Nucl. Phys. 2006, 56, 340–445. [Google Scholar] [CrossRef]
- Milgrom, M. A modification of the Newtonian dynamics as a possible alternative to the hidden mass hypothesis. Astrophys. J. 1983, 270, 365–370. [Google Scholar] [CrossRef]
- Milgrom, M. Universal Modified Newtonian Dynamics Relation between the Baryonic and “Dynamical” Central Surface Densities of Disc Galaxies. Phys. Rev. Lett. 2016, 117, 141101. [Google Scholar] [CrossRef]
- Milgrom, M. MOND in galaxy groups: A superior sample. Phys. Rev. D 2019, 99, 044041. [Google Scholar] [CrossRef]
- Milgrom, M. MOND vs. dark matter in light of historical parallels. Stud. Hist. Philos. Sci. Part B Stud. Hist. Philos. Mod. Phys. 2020, 71, 170–195. [Google Scholar] [CrossRef]
- Kroupa, P. A modern view of galaxies and their stellar populations. arXiv 2023, arXiv:2310.01473. [Google Scholar]
- Milgrom, M. MOND as manifestation of modified inertia. arXiv 2023, arXiv:2310.14334. [Google Scholar]
- Kroupa, P.; Pawlowski, M.; Milgrom, M. The failures of the standard model of cosmology require a new paradigm. Int. J. Mod. Phys. D 2012, 21, 1230003. [Google Scholar] [CrossRef]
- Capozziello, S.; De Laurentis, M. The dark matter problem from f(R) gravity viewpoint. Ann. der Phys. 2012, 524, 545–578. [Google Scholar] [CrossRef]
- Farnes, J.S. A unifying Theory of Dark Energy and Dark Matter: Negative Masses and Matter Creation within a Modified ΛCDM Framework. Astron. Astrophys. 2018, 620, A92. [Google Scholar] [CrossRef]
- Verlinde, E. On the Origin of Gravity and the Laws of Newton. J. High Energy Phys. 2011, 2011, 29. [Google Scholar] [CrossRef]
- Gonzalo, E.; Montero, M.; Obied, G.; Vafa, C. Dark Dimension Gravitons as Dark Matter. J. High Energy Phys. 2023, 2023, 109. [Google Scholar] [CrossRef]
- Yahalom, A. The Geometrical Meaning of Time. Found. Phys. 2008, 38, 489–497. [Google Scholar] [CrossRef]
- Yahalom, A. The Effect of Retardation on Galactic Rotation Curves. J. Phys. Conf. Ser. 2019, 1239, 012006. [Google Scholar] [CrossRef]
- Wagman, M.; Horwitz, L.P.; Yahalom, A. Applying Retardation Theory to Galaxies. J. Phys. Conf. Ser. 2023, 2482, 012005. [Google Scholar] [CrossRef]
- Joyce, A.; Jain, B.; Khoury, J.; Trodden, M. Beyond the Cosmological Standard Model. Phys. Rep. 2015, 568, 1–98. [Google Scholar] [CrossRef]
- Skordis, C.; Złośnik, T. New Relativistic Theory for Modified Newtonian Dynamics. Phys. Rev. Lett. 2021, 127, 161302. [Google Scholar] [CrossRef] [PubMed]
- Naidu, R.P.; Oesch, P.A.; van Dokkum, P.; Nelson, E.J.; Suess, K.A.; Brammer, G.; Whitaker, K.E.; Illingworth, G.; Bouwens, R.; Tacchella, S.; et al. Two remarkably luminous galaxy candidates at z ≈ 10–12 revealed by JWST. Astrophys. J. Lett. 2022, 940, L14. [Google Scholar] [CrossRef]
- Naidu, R.P.; Oesch, P.A.; Setton, D.J.; Matthee, J.; Conroy, C.; Johnson, B.D.; Weaver, J.R.; Bouwens, R.J.; Brammer, G.B.; Dayal, P.; et al. Schrodinger’s Galaxy Candidate: Puzzlingly Luminous at z ≈ 17, or Dusty/Quenched at z ≈ 5? arXiv 2022, arXiv:2208.02794. [Google Scholar]
- Labbé, I.; van Dokkum, P.; Nelson, E.; Bezanson, R.; Suess, K.A.; Leja, J.; Brammer, G.; Whitaker, K.; Mathews, E.; Stefanon, M.; et al. A population of red candidate massive galaxies ~600 Myr after the Big Bang. Nature 2023, 616, 266–269. [Google Scholar] [CrossRef] [PubMed]
- Curtis-Lake, E.; Carniani, S.; Cameron, A.; Charlot, S.; Jakobsen, P.; Maiolino, R.; Bunker, A.; Witstok, J.; Smit, R.; Chevallard, J.; et al. Spectroscopic confirmation of four metal-poor galaxies at z = 10.3–13.2. Nat. Astron. 2023, 7, 622–632. [Google Scholar] [CrossRef]
- Hainline, K.N.; Johnson, B.D.; Robertson, B.; Tacchella, S.; Helton, J.M.; Sun, F.; Eisenstein, D.J.; Simmonds, C.; Topping, M.W.; Whitler, L.; et al. The Cosmos in Its Infancy: JADES Galaxy Candidates at z > 8 in GOODS-S and GOODS-N. Astrophys. J. 2024, 964, 71. [Google Scholar] [CrossRef]
- Robertson, B.E.; Tacchella, S.; Johnson, B.D.; Hainline, K.; Whitler, L.; Eisenstein, D.J.; Endsley, R.; Rieke, M.; Stark, D.P.; Alberts, S.; et al. Identification and properties of intense star-forming galaxies at redshifts z > 10. Nat. Astron. 2023, 7, 611–621. [Google Scholar] [CrossRef]
- Adams, N.J.; Conselice, C.J.; Ferreira, L.; Austin, D.; Trussler, J.A.; Juodžbalis, I.; Wilkins, S.M.; Caruana, J.; Dayal, P.; Verma, A.; et al. Discovery and properties of ultra-high redshift galaxies (9 < z < 12) in the JWST ERO SMACS 0723 Field. Mon. Not. R. Astron. Soc. 2023, 518, 4755–4766. [Google Scholar]
- Atek, H.; Chemerynska, I.; Wang, B.; Furtak, L.J.; Weibel, A.; Oesch, P.; Weaver, J.R.; Labbé, I.; Bezanson, R.; van Dokkum, P.; et al. JWST UNCOVER: Discovery of z > 9 Galaxy Candidates behind the Lensing Cluster Abell 2744. Mon. Not. R. Astron. Soc. 2023, 524, 5486–5496. [Google Scholar] [CrossRef]
- Chen, Z.; Stark, D.P.; Endsley, R.; Topping, M.; Whitler, L.; Charlot, S. JWST/NIRCam Observations of Stars and HII Regions in z ≃ 6−8 Galaxies: Properties of Star Forming Complexes on 150 pc Scales. Mon. Not. R. Astron. Soc. 2022, 518, 5607–5619. [Google Scholar] [CrossRef]
- Donnan, C.T.; McLeod, D.J.; Dunlop, J.S.; McLure, R.J.; Carnall, A.C.; Begley, R.; Cullen, F.; Hamadouche, M.L.; Bowler, R.A.; Magee, D.; et al. The evolution of the galaxy UV luminosity function at redshifts z ≃ 8–15 from deep JWST and ground-based near-infrared imaging. Mon. Not. R. Astron. Soc. 2022, 518, 6011–6040. [Google Scholar] [CrossRef]
- Finkelstein, S.L.; Bagley, M.B.; Haro, P.A.; Dickinson, M.; Ferguson, H.C.; Kartaltepe, J.S.; Papovich, C.; Burgarella, D.; Kocevski, D.D.; Iyer, K.G.; et al. A Long Time Ago in a Galaxy Far, Far Away: A Candidate z∼12 Galaxy in Early JWST CEERS Imaging. Astrophys. J. Lett. 2022, 940, L55. [Google Scholar] [CrossRef]
- Ono, Y.; Harikane, Y.; Ouchi, M.; Yajima, H.; Abe, M.; Isobe, Y.; Shibuya, T.; Wise, J.H.; Zhang, Y.; Nakajima, K.; et al. Morphologies of Galaxies at z ≳ 9 Uncovered by JWST/NIRCam Imaging: Cosmic Size Evolution and an Identification of an Extremely Compact Bright Galaxy at z∼12. Astrophys. J. 2023, 951, 72. [Google Scholar] [CrossRef]
- Tacchella, S.; Eisenstein, D.J.; Hainline, K.; Johnson, B.D.; Baker, W.M.; Helton, J.M.; Robertson, B.; Suess, K.A.; Chen, Z.; Nelson, E.; et al. JADES Imaging of GN-z11: Revealing the Morphology and Environment of a Luminous Galaxy 430 Myr after the Big Bang. Astrophys. J. 2023, 952, 74. [Google Scholar] [CrossRef]
- Tacchella, S.; Johnson, B.D.; Robertson, B.E.; Carniani, S.; D’eugenio, F.; Kumari, N.; Maiolino, R.; Nelson, E.J.; Suess, K.A.; Übler, H.; et al. JWST NIRCam + NIRSpec: Interstellar medium and stellar populations of young galaxies with rising star formation and evolving gas reservoirs. Mon. Not. R. Astron. Soc. 2023, 522, 6236–6249. [Google Scholar] [CrossRef]
- Wu, Y.; Cai, Z.; Sun, F.; Bian, F.; Lin, X.; Li, Z.; Li, M.; Bauer, F.E.; Egami, E.; Fan, X.; et al. The Identification of a Dusty Multiarm Spiral Galaxy at z = 3.06 with JWST and ALMA. Astrophys. J. Lett. 2022, 942, L1. [Google Scholar] [CrossRef]
- Yang, L.; Morishita, T.; Leethochawalit, N.; Castellano, M.; Calabro, A.; Treu, T.; Bonchi, A.; Fontana, A.; Mason, C.; Merlin, E.; et al. Early Results from GLASS-JWST. V: The First Rest-frame Optical Size–Luminosity Relation of Galaxies at z > 7. Astrophys. J. Lett. 2022, 938, L17. [Google Scholar] [CrossRef]
- Austin, D.; Adams, N.; Conselice, C.J.; Harvey, T.; Ormerod, K.; Trussler, J.; Li, Q.; Ferreira, L.; Dayal, P.; Juodžbalis, I. A Large Population of Faint 8 < z < 16 Galaxies Found in the First JWST NIRCam Observations of the NGDEEP Survey. Astrophys. J. 2023, 952, L7. [Google Scholar] [CrossRef]
- Baggen, J.F.; van Dokkum, P.; Labbé, I.; Brammer, G.; Miller, T.B.; Bezanson, R.; Leja, J.; Wang, B.; Whitaker, K.E.; Suess, K.A.; et al. Sizes and mass profiles of candidate massive galaxies discovered by JWST at 7 < z < 9: Evidence for very early formation of the central ~100 pc of present-day ellipticals. Astrophys. J. Lett. 2023, 955, L12. [Google Scholar]
- Haslbauer, M.; Kroupa, P.; Zonoozi, A.H.; Haghi, H. Has JWST Already Falsified Dark-matter-driven Galaxy Formation? Astrophys. J. 2022, 939, L31. [Google Scholar] [CrossRef]
- Inayoshi, K.; Harikane, Y.; Inoue, A.K.; Li, W.; Ho, L.C. A Lower Bound of Star Formation Activity in Ultra-high-redshift Galaxies Detected with JWST: Implications for Stellar Populations and Radiation Sources. Astrophys. J. 2022, 938, L10. [Google Scholar] [CrossRef]
- Kannan, R.; Springel, V.; Hernquist, L.; Pakmor, R.; Delgado, A.M.; Hadzhiyska, B.; Hernández-Aguayo, C.; Barrera, M.; Ferlito, F.; Bose, S.; et al. The MillenniumTNG Project: The galaxy population at z ≥ 8. Mon. Not. R. Astron. Soc. 2023, 524, 2594–2605. [Google Scholar] [CrossRef]
- Keller, B.W.; Munshi, F.; Trebitsch, M.; Tremmel, M. Can Cosmological Simulations Reproduce the Spectroscopically Confirmed Galaxies Seen at z ≥ 10? Astrophys. J. 2023, 943, L28. [Google Scholar] [CrossRef]
- Regan, J. Massive Star Formation in Overdense Regions of the Early Universe. arXiv 2022, arXiv:2210.04899. [Google Scholar] [CrossRef]
- Yajima, H.; Abe, M.; Fukushima, H.; Ono, Y.; Harikane, Y.; Ouchi, M.; Hashimoto, T.; Khochfar, S. FOREVER22: The first bright galaxies with population III stars at redshifts z ≃ 10–20 and comparisons with JWST data. Mon. Not. R. Astron. Soc. 2023, 525, 4832–4839. [Google Scholar] [CrossRef]
- Mason, C.A.; Trenti, M.; Treu, T. The brightest galaxies at cosmic dawn. Mon. Not. R. Astron. Soc. 2023, 521, 497–503. [Google Scholar] [CrossRef]
- Mirocha, J.; Furlanetto, S.R. Balancing the efficiency and stochasticity of star formation with dust extinction in z ≳ 10 galaxies observed by JWST. Mon. Not. R. Astron. Soc. 2022, 519, 843–853. [Google Scholar] [CrossRef]
- Whitler, L.; Stark, D.P.; Endsley, R.; Chen, Z.; Mason, C.; Topping, M.W.; Charlot, S. Insight from JWST/NIRCam into galaxy overdensities around bright Lyα emitters during reionization: Implications for ionized bubbles at z∼9. Mon. Not. R. Astron. Soc. 2023, 529, 855–872. [Google Scholar] [CrossRef]
- Whitler, L.; Endsley, R.; Stark, D.P.; Topping, M.; Chen, Z.; Charlot, S. On the ages of bright galaxies ∼500 Myr after the big bang. Mon. Not. R. Astron. Soc. 2023, 519, 157–171. [Google Scholar] [CrossRef]
- McCaffrey, J.; Hardin, S.; Wise, J.H.; Regan, J.A. No Tension: JWST Galaxies at z > 10 Consistent with Cosmological Simulations. arXiv 2023, arXiv:2304.13755. [Google Scholar] [CrossRef]
- Ellis, R.S. When Galaxies Were Born: The Quest for Cosmic Dawn; Princeton University Press: Princeton, NJ, USA, 2022. [Google Scholar]
- Reinoso, B.; Klessen, R.S.; Schleicher, D.; Glover, S.C.O.; Solar, P. Formation of supermassive stars in the first star clusters. Mon. Not. R. Astron. Soc. 2023, 521, 3553–3569. [Google Scholar] [CrossRef]
- Brummel-Smith, C.; Skinner, D.; Sethuram, S.S.; Wise, J.H.; Xia, B.; Taori, K. Inferred galaxy properties during Cosmic Dawn from early JWST photometry results. Mon. Not. R. Astron. Soc. 2023, 525, 4405–4425. [Google Scholar] [CrossRef]
- Dolgov, A.D. James Webb Space Telescope: Data, problems, and resolution. arXiv 2023, arXiv:2301.01365. [Google Scholar]
- Larson, R.L.; Finkelstein, S.L.; Kocevski, D.D.; Hutchison, T.A.; Trump, J.R.; Haro, P.A.; Bromm, V.; Cleri, N.J.; Dickinson, M.; Fujimoto, S.; et al. A CEERS Discovery of an Accreting Supermassive Black Hole 570 Myr after the Big Bang: Identifying a Progenitor of Massive z > 6 Quasars. Astrophys. J. Lett. 2023, 953, L29. [Google Scholar] [CrossRef]
- Maiolino, R.; Scholtz, J.; Witstok, J.; Carniani, S.; D’Eugenio, F.; de Graaff, A.; Übler, H.; Tacchella, S.; Curtis-Lake, E.; Arribas, S.; et al. A small and vigorous black hole in the early Universe. Nature 2024, 627, 59–63. [Google Scholar] [CrossRef] [PubMed]
- Dekel, A.; Sarkar, K.C.; Birnboim, Y.; Mandelker, N.; Li, Z. Efficient Formation of Massive Galaxies at Cosmic Dawn by Feedback-Free Starbursts. Mon. Not. R. Astron. Soc. 2023, 523, 3201–3218. [Google Scholar] [CrossRef]
- Boyett, K.; Trenti, M.; Leethochawalit, N.; Calabró, A.; Metha, B.; Roberts-Borsani, G.; Dalmasso, N.; Yang, L.; Santini, P.; Treu, T.; et al. A massive interacting galaxy 510 million years after the Big Bang. Nat. Astron. 2024, 8, 657–672. [Google Scholar] [CrossRef]
- Looser, T.J.; D’eugenio, F.; Maiolino, R.; Witstok, J.; Sandles, L.; Curtis-Lake, E.; Chevallard, J.; Tacchella, S.; Johnson, B.D.; Baker, W.M.; et al. A recently quenched galaxy 700 million years after the Big Bang. Nature 2024, 629, 53–57. [Google Scholar] [CrossRef] [PubMed]
- Long, A.S.; Antwi-Danso, J.; Lambrides, E.L.; Lovell, C.C.; de la Vega, A.; Valentino, F.; Zavala, J.A.; Casey, C.M.; Wilkins, S.M.; Yung, L.Y.; et al. Efficient NIRCam Selection of Quiescent Galaxies at 3 < z < 6 in CEERS. arXiv 2023, arXiv:2305.04662. [Google Scholar]
- Haro, P.A.; Dickinson, M.; Finkelstein, S.L.; Fujimoto, S.; Fernández, V.; Kartaltepe, J.S.; Jung, I.; Cole, J.W.; Burgarella, D.; Chworowsky, K.; et al. Spectroscopic Confirmation of CEERS NIRCam-selected Galaxies at z ≃ 8–10. Astrophys. J. Lett. 2023, 951, L22. [Google Scholar] [CrossRef]
- Eilers, A.-C.; Simcoe, R.A.; Yue, M.; Mackenzie, R.; Matthee, J.; Ďurovčíková, D.; Kashino, D.; Bordoloi, R.; Lilly, S.J. EIGER. III. JWST/NIRCam Observations of the Ultraluminous High-redshift Quasar J0100+2802. Astrophys. J. 2023, 950, 68. [Google Scholar] [CrossRef]
- Schneider, R.; Valiante, R.; Trinca, A.; Graziani, L.; Volonteri, M.; Maiolino, R. Are we surprised to find SMBHs with JWST at z > 9? Mon. Not. R. Astron. Soc. 2023, 526, 3250–3261. [Google Scholar] [CrossRef]
- Chen, Y.; Mo, H.J.; Wang, K. Massive dark matter haloes at high redshift: Implications for observations in the JWST era. Mon. Not. R. Astron. Soc. 2023, 526, 2542–2559. [Google Scholar] [CrossRef]
- Mauerhofer, V.; Dayal, P. The dust enrichment of early galaxies in the JWST and ALMA era. Mon. Not. R. Astron. Soc. 2023, 526, 2196–2209. [Google Scholar] [CrossRef]
- Dirac, P.A.M. The Cosmological Constants. Nature 1937, 139, 323. [Google Scholar] [CrossRef]
- Zwicky, F. On the redshift of spectral lines through interstellar space. Proc. Natl. Acad. Sci. USA 1929, 15, 773–779. [Google Scholar] [CrossRef]
- Scolnic, D.; Brout, D.; Carr, A.; Riess, A.G.; Davis, T.M.; Dwomoh, A.; Jones, D.O.; Ali, N.; Charvu, P.; Chen, R.; et al. The Pantheon+ Analysis: The Full Data Set and Light-curve Release. Astrophys. J. 2022, 938, 113. [Google Scholar] [CrossRef]
- Brout, D.; Scolnic, D.; Popovic, B.; Riess, A.G.; Carr, A.; Zuntz, J.; Kessler, R.; Davis, T.M.; Hinton, S.; Jones, D.; et al. The Pantheon+ Analysis: Cosmological Constraints. Astrophys. J. 2022, 938, 110. [Google Scholar] [CrossRef]
- Gupta, R.P. Varying Coupling Constants and Their Interdependence. Mod. Phys. Lett. A 2022, 37, 2250155, arXiv: 2201.11667 (corrected version). [Google Scholar] [CrossRef]
- Ryden, B.S. Introduction to Cosmology; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar]
- Baumann, D. Cosmology; Cambridge University Press: Cambridge, UK, 2022. [Google Scholar]
- Longair, M.S. Galaxy Formation, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 2023. [Google Scholar]
- Laursen, P. Galaxy formation from a timescale perspective. In Multiplicity of Time Scales in Complex Systems; Springer: Berlin/Heidelberg, Germany, 2023. [Google Scholar]
- Cao, S.; Ryan, J.; Ratra, B. Using Pantheon and DES supernova, baryon acoustic oscillation, and Hubble parameter data to constrain the Hubble constant, dark energy dynamics, and spatial curvature. Mon. Not. R. Astron. Soc. 2021, 504, 300–310. [Google Scholar] [CrossRef]
- Cao, S.; Ratra, B. H0 = 69.8 ± 1.3 km s−1 Mpc−1, Ωm0 = 0.288 ± 0.017, and other constraints from lower-redshift, non-CMB, expansion-rate data. Phys. Rev. D 2023, 107, 103521. [Google Scholar] [CrossRef]
- Peng, P. The Pantheon Sample analysis of cosmological constraints under new models. arXiv 2023, arXiv:2303.10095. [Google Scholar]
- Eappen, R.; Kroupa, P. The formation of compact massive relic galaxies in MOND. Mon. Not. R. Astron. Soc. 2024, 528, 4264–4271. [Google Scholar] [CrossRef]
- Garcia-Bellido, J.; Hawkins, M. Reanalysis of the MACHO constraints on PBH in the light of Gaia DR3 data. arXiv 2024, arXiv:2402.00212. [Google Scholar]
- Lee, S. Constraint on the minimally extended varying speed of light using time dilations in Type Ia supernovae. Mon. Not. R. Astron. Soc. 2023, 524, 4019–4023. [Google Scholar] [CrossRef]
- Lewis, G.F.; Brewer, B.J. Detection of the Cosmological Time Dilation of High-Redshift Quasars. Nat. Astron. 2023, 7, 1265–1269. [Google Scholar] [CrossRef]
- Hawkins, M.R.S. On time dilation in quasar light curves. Mon. Not. R. Astron. Soc. 2010, 405, 1940–1946. [Google Scholar] [CrossRef]
- Blondin, S.; Davis, T.M.; Krisciunas, K.; Schmidt, B.P.; Sollerman, J.; Wood-Vasey, W.M.; Becker, A.C.; Challis, P.; Clocchiatti, A.; Damke, G.; et al. Time Dilation in Type Ia Supernova Spectra at High Redshift. Astrophys. J. 2008, 682, 724–736. [Google Scholar] [CrossRef]
- Lesgourgues, J. The Cosmic Linear Anisotropy Solving System (CLASS) I: Overview. arXiv 2011, arXiv:1104.2932. [Google Scholar]
- Lewis, A.; Challinor, A.; Lasenby, A. Efficient Computation of Cosmic Microwave Background Anisotropies in Closed Friedmann-Robertson-Walker Models. Astrophys. J. 2000, 538, 473–476. [Google Scholar] [CrossRef]
- Wang, C.; Bolejko, K.; Lewis, G.F. The Instantaneous Redshift Difference of Gravitationally Lensed Images: Theory and Observational Prospects. Astrophys. J. 2022, 940, 16. [Google Scholar] [CrossRef]
- Wang, C.; Bolejko, K.; Lewis, G.F. The Redshift Difference in Gravitational Lensed Systems. Mon. Not. R. Astron. Soc. 2023, 525, 3006–3015. [Google Scholar] [CrossRef]
- Cao, S.; Qi, J.; Biesiada, M.; Zheng, X.; Xu, T.; Zhu, Z.-H. Testing the Speed of Light over Cosmological Distances: The Combination of Strongly Lensed and Unlensed Type Ia Supernovae. Astrophys. J. 2018, 867, 50. [Google Scholar] [CrossRef]
- Cao, S.; Qi, J.; Biesiada, M.; Liu, T.; Zhu, Z.-H. Precise Measurements of the Speed of Light with High-redshift Quasars: Ultra-compact Radio Structure and Strong Gravitational Lensing. Astrophys. J. 2020, 888, L25. [Google Scholar] [CrossRef]
- Gupta, R.P. Testing the Speed of Light Variation with Strong Gravitational Lensing of SNe 1a. Res. Notes AAS 2021, 5, 176. [Google Scholar] [CrossRef]
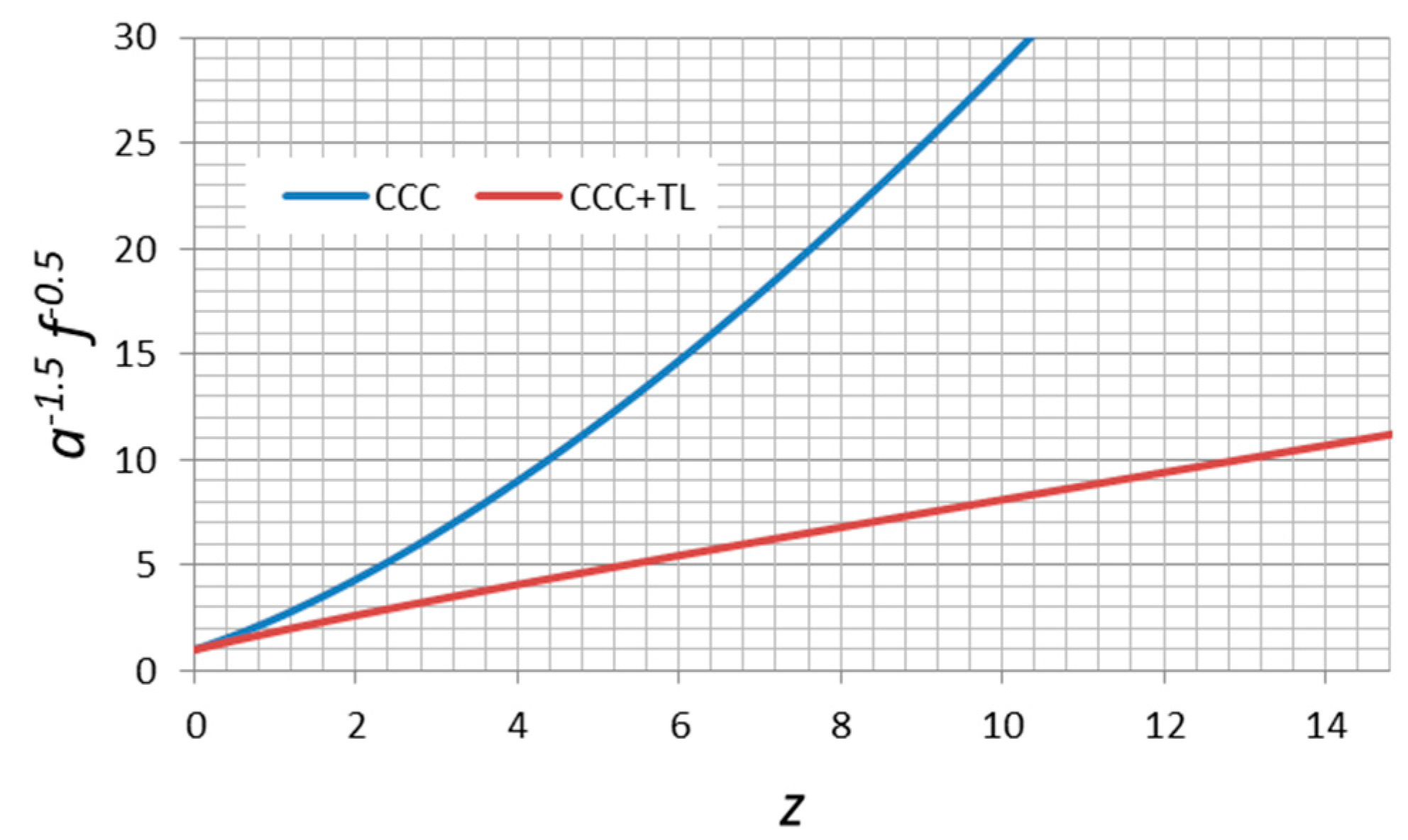
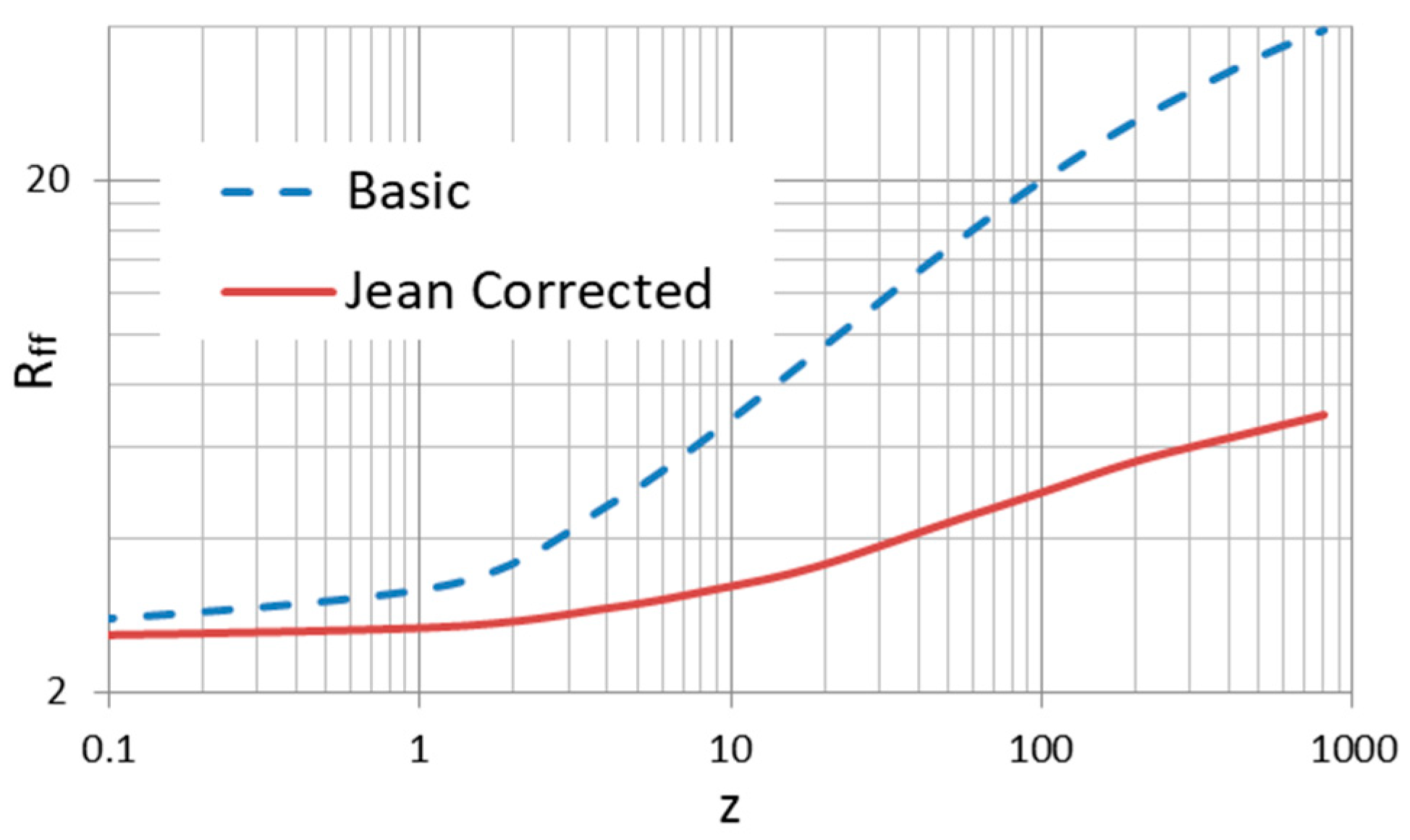

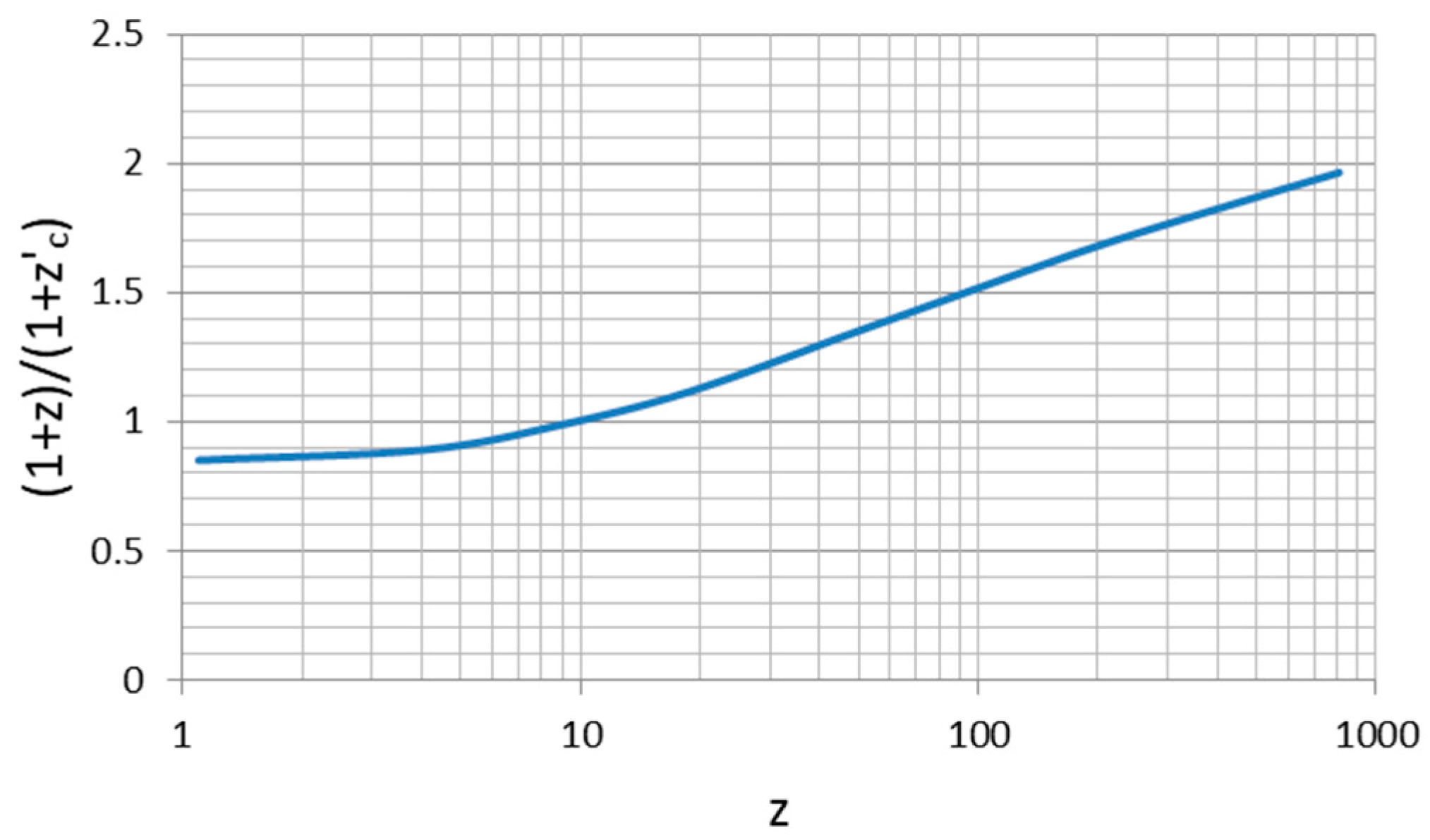

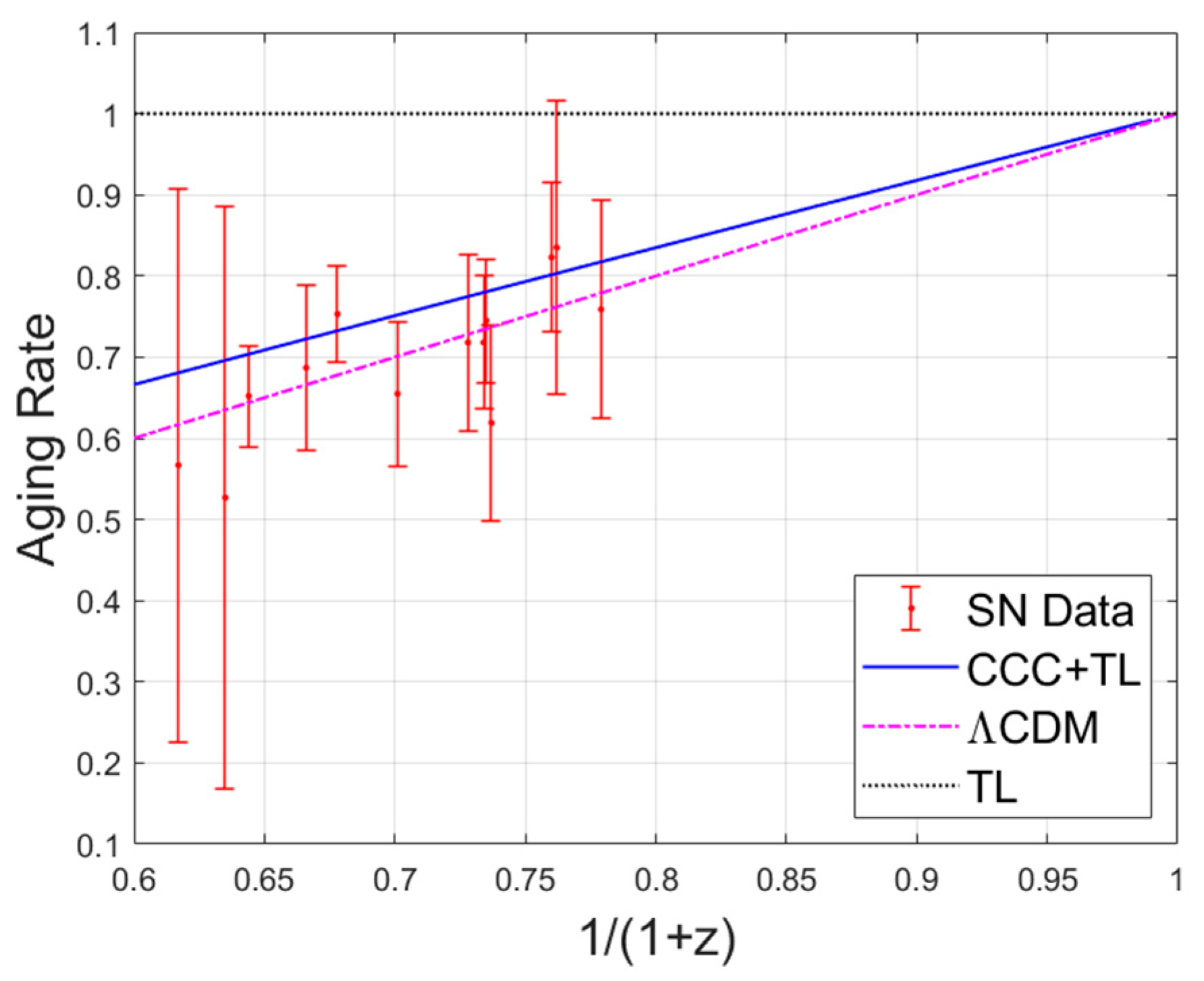
| Item\Model | CCC (Base) | CCC+TL (Base) | CCC (Expanded) | CCC+TL (Expanded) | LCDM |
|---|---|---|---|---|---|
| Critical density | |||||
| 0.25 | 0.03 | 1 | 0.67 | 1 | |
| 1 | 1 | 0.25 | 0.04 | [0.35] | |
| 0 | 0 | 0.25 | 0.64 | 0.65 | |
| 0 | 0 | 0.50 | 0.32 | NA | |
| Km s−1Mpc−1 | [72.7] | 72.6 | [72.7] | 72.6 | [73.0] |
| Km s−1Mpc−1 | 72.7 | [59.5] | 72.7 | [59.5] | 73.0 |
| [−0.50] | [−0.80] | [−0.50] | [−0.80] | NA | |
| 4600 | 10,000 | 4600 | 10,000 | 4000 | |
| NA | NA | 0.72 | 10 | NA | |
| NA | NA | <0 (future) | 1.2 | NA | |
| NA | NA | NA | NA | 0.23 | |
| at acceleration | 1.2 | 14.5 | 1.2 | 14.5 | 0.55 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gupta, R.P. On Dark Matter and Dark Energy in CCC+TL Cosmology. Universe 2024, 10, 266. https://doi.org/10.3390/universe10060266
Gupta RP. On Dark Matter and Dark Energy in CCC+TL Cosmology. Universe. 2024; 10(6):266. https://doi.org/10.3390/universe10060266
Chicago/Turabian StyleGupta, Rajendra P. 2024. "On Dark Matter and Dark Energy in CCC+TL Cosmology" Universe 10, no. 6: 266. https://doi.org/10.3390/universe10060266
APA StyleGupta, R. P. (2024). On Dark Matter and Dark Energy in CCC+TL Cosmology. Universe, 10(6), 266. https://doi.org/10.3390/universe10060266






