Abstract
In this paper, we examine the role played by topology, and some specific boundary conditions as well, on the physics of a higher-dimensional black hole. We analyze the line element of a five-dimensional non-extremal Reissner–Nordström black hole to obtain a new family of subspaces that are types of strong retractions and deformations, and then we extend these results to higher dimensions in order to deduce the relationship between various types of transformations. We also study the scalar field perturbations in the background under consideration and obtain an analytical expression for the quasibound state frequencies by using the Vieira–Bezerra–Kokkotas approach, which uses the polynomial conditions of the general Heun functions, and then we discuss the stability of the system and present the radial eigenfunctions. Our main goal is to discuss the physical meaning of these mathematical applications in such higher-dimensional effective metric.
Keywords:
strong retraction; folding; strong homotopy retract; Klein–Gordon equation; general Heun functions; wave eigenfunctions PACS:
02.30.Gp; 03.65.Ge; 04.20.Jb; 04.62.+v; 04.70.-s; 04.80.Cc; 47.35.Rs; 47.90.+a
1. Introduction
One of the most exciting areas of physics over the past ten years has been the study of black holes [1], in which it was proposed that rather than being viewed as mathematical constructs, black holes might be thought of as physical systems, and that information theory could be used to comprehend their physics. In order to study quantum gravity, one needs to combine classical mechanics and gravity, and quantum mechanics within the theory of black hole thermodynamics [2].
In addition, when combined with a negative cosmological constant, the Reissner–Nordström black hole (RNBH) has shown to be a valuable tool for research into the thermodynamical features of gravity [3,4], as well as to determine the effect of the changed radiation equation of state at the Planck scale on the Reissner–Nordström–anti-de Sitter black hole (RNAdSBH) [5]. Even though the RNBH in AdS spacetime is a universally efficient solution to many effective field theories of gravity, it still has a lot of baffling problems. It does not saturate the bootstrap bound, even at extremes or at absolute zero, unlike in asymptotically Minkowski spacetime. Without additional charged matter, its classical instability has not been explicitly demonstrated, but it may indicate that the extremal RN solution in AdS spacetime is unstable [6,7,8].
It is known that under charged large scalar perturbations, superradiant stability applies to all non-extremal RNBHs in five dimensions. According to this, all RNBHs in higher dimensions, under charged massive scalar perturbations, may be superradiantly stable [9]. On the other hand, the relaxation rate of the four-dimensional RNBH associated with the massless scalar field was analyzed in ref. [10].
Asymptotically flat charged black holes can support complex arrangements of both massive and massless scalar fields. These fields exhibit connections to the electromagnetic field tensor of the corresponding central charged black holes (for a review, see the highly fascinating ref. [11] and references therein). In the literature [12,13,14,15,16], mathematical studies have also been conducted on higher-dimensional RNBHs. A numerical approach was used to demonstrate that asymptotically flat RNBHs, in the range of dimensions , under massless scalar perturbations, remained relatively stable [17,18].
The present paper has two broad aims. First, to present some important results on both geometrical and topological aspects of the five-dimensional RNBH spacetime, by constructing different types of strong retractions and strong homotopy retracts on the background under consideration, which is mathematically denoted, for simplicity, by black hole. In addition, we use it to prove the existence of apparent horizons, which are crucial to the studies of wave phenomena on black hole spacetimes. Furthermore, we also show that the end limit of an black hole is a zero-dimensional non-extremal black hole. Second, to discuss the interaction between quantum charged massive scalar particles and the background under consideration, by obtaining the spectrum of quasibound states, which are related to the boundary conditions imposed on the radial wave solution. In addition, we also calculate the corresponding angular and radial wave eigenfunctions. Indeed, these are two very important interesting features from a mathematical physics point of view.
The main interesting field of topology is the theory of strong retracts, and this theory is used to describe the horizon as a subspace in the non-extremal 5DRNBH. In fact, from the theory of geodesics, we infer some types of strong retractions as a cross-sectional apparent horizon of the non-extremal 5DRNBH. Also, quasibound states are wave phenomena that occur near the exterior event horizon of a black hole. However, the relation between the algebraic topology on a non-extremal 5DRNBH and a spectrum of quasibound states comes from the way we can describe the horizons of the non-extremal 5DRNBH in these two different fields.
The quasibound states (or quasistationary levels) are localized in the black hole’s potential well, which means that there may exist a flux of particles crossing into the black hole’s exterior surface [19,20]. Therefore, the spectrum of quasibound states is constituted by complex frequencies, which are denoted by , where the imaginary part determines the stability of the system, and the real part is the oscillation frequency. In fact, the wave solution is said to be stable when the imaginary part of the frequency is negative (, decay rate), while the wave solution is said to be unstable when the imaginary part of the frequency is positive (, growth rate). In this work, the quasibound states are obtained by using the so-called Vieira–Bezerra–Kokkotas (VBK) approach [21,22] (for more details and applications, see also refs. [23,24,25,26,27,28]).
The paper is organized as follows. In Section 2, we introduce the general metric corresponding to D-dimensional RNBH spacetimes, and then we particularize it for the five-dimensional case. In Section 3, we investigate some geometrical and topological aspects of the black hole and the theory of retracts. In Section 4, we find exact solutions for the charged massive Klein–Gordon equation, and then we obtain an analytical expression for the quasibound states. Finally, in Section 5, we summarize the obtained results. At this point, we utilize the natural units where .
2. Higher-Dimensional Reissner–Nordström Black Holes
The standard four-dimensional black hole solutions to Einstein’s equations were generalized to higher dimensions by Myers and Perry in [29]. The higher-dimensional action, which is a generalization of the Einstein–Hilbert action, is given by
where is the D-dimensional gravitational constant, R is the Ricci scalar, is the Lagrangian density for any other fields one may wish to consider, and . Then, by varying this action with respect to the spacetime metric , we obtain the Einstein equations in higher dimensions
where is the Ricci tensor. Now, for simplicity and without loss of generality (WLOG), we may adopt the natural units where . Next, by imposing a harmonic gauge condition, a static, asymptotically flat and spherically symmetric vacuum solution of Equation (2), which generalizes the RNBH solution in D dimensions, has the following form
where the metric function, , and the solid angle element, , are given, respectively, by
and
The parameters and are related to the black hole’s mass M and charge Q, respectively, through the relations
and
with
where is the volume of a -dimensional unit sphere, and is the gamma function.
Observe that the solution (3) can be reduced to the standard Reissner–Nordström metric when , as well as to the Schwarzschild one for . This metric is Ricci flat and is simply called the D-dimensional Reissner–Nordström black hole (DDRNBH) spacetime. This study concentrates on the five-dimensional Reissner–Nordström black hole (5DRNBH). Thus, the explicit line element given by Equation (3) for reads
with
where and run over the range 0 to , and from 0 to . The causal structure of the 5DRNBH spacetime can be identified from the surface equation
whose solutions are the exterior (outer) and interior (inner) “event” horizons [30], given by and , respectively, and two negative non-physical solutions, given by and .
Then, since the wave phenomena occurring outside the event horizons of a black hole could give us some insight on the physics of these interesting objects, it is meaningful to investigate the existence of such singularities in the background under consideration. Afterward, we discuss a very special type of wave phenomena that occurs near a black hole, namely, the quasibound states of charged massive scalar particles.
In this work, we concentrate on the non-extreme case, that is, when . In fact, the 5DRNBH spacetime has apparent horizons (not event horizons, essentially); these horizons represent the outermost surface where outgoing photons become marginally trapped (for a comprehensive investigation about the radiating black hole horizons, see refs. [31,32] and references therein). Nevertheless, for simplicity, convenience, and WLOG, we refer to these solutions as the exterior, , and interior, , “event” horizons. The behavior of the function , as well as that of the horizons, is shown in Figure 1; Evidently, the surface equation has four (real) solutions.
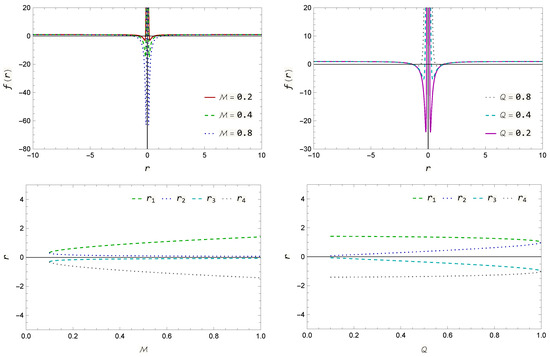
Figure 1.
Top panel: The metric function with and varying parameter (left), and with and varying parameter (right). Bottom panel: The horizons with as functions of the BH’s mass (left), and with as functions of the BH’s charge (right).
3. Geometric Topology and Theory of Retracts
Geometric topology is a field that focuses on exploring the properties of manifolds and maps. Specifically, we are dealing with embeddings of one manifold into another. Retraction is the continuous mapping from a topological space into a subspace by preserving the position of all points in that subspace, and hence the subspace is called a retract of the original space [33].
In summary, geometric topology concentrates on matters arising in special spaces such as manifolds and the theory of deformations and retractions. If W and V are topological spaces with , then a continuous function is a retraction if for all . It means that the function r collapses the space V onto its subset W. Whenever , the inclusion function can be defined by within the bigger space V. In fact, r is a retraction of onto , since any element is sent to itself by r [33,34,35]. As a result, the theory of retracts may be viewed as the concept of determining a class of functions related to topological properties.
In addition to being significant, these maps are more special than arbitrary continuous maps, and these maps are also significantly more generalized than homeomorphisms. Many additional topological aspects are also included in this theory, many of which have a definite geometrical aspect.
Next, we establish two intriguing topological requirements: strong retraction and strong homotopy retraction. After that, we utilize this theory to analyze the metric of a black hole (for details, please see ref. [32]).
3.1. Basic Definitions
At this point, we present some essential concepts concerning to the theory of deformations.
Definition 1.
Let W be an n-dimensional manifold with a subspace topology . A strong retraction is a continuous map for which
- (a)
- W is open;
- (b)
- ;
- (c)
- ;
- (d)
- is a manifold with constant curvature [32].
Definition 2.
A subset of a manifold W is called a strong homotopy retract if there exists a strong retraction and a homotopy for which
- (a)
- ;
- (b)
- ;
- (c)
- and [32].
Definition 3.
Suppose that and are two Riemannian manifolds of dimensions and , respectively. A map is called an isometric folding of into , if the induced path is a piecewise geodesic and of the same length as γ, whenever a path is a piecewise geodesic [36]. We shall just use the term folding to indicate an isometric folding. In what follows, we introduce the chain of limit folding as , for which is a chain of foldings. If is a Riemannian manifold of dimension n, and , then this type of folding is called folded conditionally.
3.2. Components of an Black Hole
In order to investigate some kinds of retractions on the black hole, we first determine some background parameters and then use the Lagrangian formalism to obtain a set of geodesic equations. Thus, the standard metric for a five-dimensional black hole solution can be written as
where the components () can be constructed by comparing Equations (9) and (14). Then, by solving (integrating) a system of differential equations, we can find that these components are given by
with
where () are constants (of integration) to be determined. Here, and are the elliptic integral of the first and second kind, respectively. For simplicity, we can define a five-vector as . Now, we want to obtain the components of the geodesic equation from the Lagrangian and Euler–Lagrange equation, which are given, respectively, by
and
where , and the dot “˙” indicates the derivative with respect to the proper length. Next, by using the relation
we can write
where we have used the identity . In fact, for null geodesics, we have , and for massive particles we get . Thus, the components of the geodesic equation are reduced to
where and are constants (of integration) to be determined, and the quotation marks “′” represents the derivative with respect to the radial coordinate r.
Then, from Equation (22), by considering , we obtain a time solution , where is also a constant (of integration) to be determined. Moreover, if we assume that , we have four surfaces, namely, (), which are the two event (apparent) horizons and the two non-physical solutions to the surface equation of a 5DRNBH spacetime. Therefore, the surfaces and describe the exterior and interior event (apparent) horizons of . Thus, the photons can escape from the exterior horizon and reach an arbitrary large distance from the black hole; this confirms that these surfaces are, in fact, apparent horizons, not the event horizons.
Now, by putting in Equation (26), we obtain at least one of , , or equal to zero. Hence, in the case of and , we have . Thus, we obtain a subspace , and the components have the following form
Therefore, we can write the first strong retraction as .
Now, by considering and , we obtain , and hence we have a subspace , whose components are given by
Therefore, the strong retraction can be represented as .
Next, under the condition that and , we can conclude that , which implies that (a special case), and then, there exists a subspace that contains the following components
Therefore, with this approach, we can find the other strong retraction, namely, .
3.3. Strong Homotopy Retracts
Here, we use all types of strong retractions stated above to introduce strong homotopy retracts of the black hole.
Thus, by using the strong retractions , , and , we can construct the homotopy retracts on as follows.
First, the strong homotopy retracts of onto a geodesic can be characterized by
where
which is valid and , with
Next, we can write the strong homotopy retracts of onto a geodesic as
where
which is valid and , with
Finally, we can achieve the strong homotopy retracts of onto a geodesic as
where
which is valid and , with
Therefore, based on these findings, we can infer that all the strong retractions, as a subspace of , induce strong homotopy retractions on . Furthermore, we deduce that every geodesic provides a strong retraction on a cross-sectional apparent horizon of the 5DRNBH. In addition, the subspaces are strongly homotopically retracted, and they are also contained within a subspace of . Thus, we have proved and substantiated (from a rigorous mathematical standpoint) the existence of apparent horizons in the 5DRNBH spacetime. Then, these findings allow us to investigate an interesting physical phenomenon which occurs in the gravity surface of an exterior (apparent) horizon, namely, the quasibound states at the black hole’s potential well. Since we have proved the existence of such an exterior horizon, we are able to investigate the boundary condition related to this surface, and at the spatial infinity as well, in order to discuss one of the physical meanings of this mathematical tool. In what follows, first, we conclude the topological studies by investigating the limit case of these transformations, and then we address the motion of scalar particles in the exterior region of the 5DRNBH spacetime by imposing some specific conditions on the radial solution.
3.4. Limit Transformation on a Non-Extremal D-Dimensional RNBH
Now, we look at the limit of strong retraction and the limit of folding on a D-dimensional non-extremal RNBH from the standpoint of commutative diagrams.
Theorem 1.
Suppose that is a D-dimensional non-extremal RNBH. Let be a subspace of . This yields chains of folded conditionally () and strong retractions (), with , such that , , …, , in which the end limit is a zero-dimensional non-extremal RNBH () with a zero-dimensional subspace ().
Proof.
In this approach, we introduce the following chains of strong retractions and conditionally folded foldings as commutative diagrams:
From the existence of the lower limit, we can consequently obtain the zero-dimensional non-extremal RNBH. □
4. Charged Massive Scalar Equation of Motion
In this section, our focus is on the fundamental attributes of the 5DRNBH spacetime, especially the ones related to their interaction with quantum scalar fields, in particular the classical scalar wave phenomena such as the quasibound states (QBSs). To this end, we consider the covariant, conformally coupled, charged massive Klein–Gordon equation, which is given by
where , is the five-dimensional scalar wave function, and and e are the mass and the charge of the scalar particle, respectively. Here, the electromagnetic five-vector of the 5DRNBH is given by [37]
Then, in order to obtain exact analytical solutions of Equation (39), due to the stationarity and axisymmetry of the 5DRNBH spacetime, we can use the following ansatz
where is the radial function, is an angular function, and is the frequency (energy, in the natural units). Thus, by using the 5DRNBH spacetime metric, the electromagnetic potential, and the separation of variables, given by Equations (9), (40), and (41), respectively, the equation of motion (39) can be separated into an angular and a radial equation as
and
where , and and are the separation constants. Thus, the general exact analytical solutions of the angular Equation (42) are provided by the generic formulas , where are the corresponding Legendre functions in four dimensions [38,39,40] with arbitrary degree and order l, in which , and are the spherical harmonics, with l and m being the angular and magnetic quantum numbers, respectively, for which . Next, we analytically solve the radial Equation (43) by applying the VBK approach, which means to rewrite it as a (general) Heun type differential equation [41].
4.1. Radial Equation
To solve the radial Equation (43), first, we need to find a more convenient form (parametrization) for the metric function given by Equation (10). In fact, the left-hand side of surface Equation (13) is a biquadratic equation, and we can “reduce” the number of singularities by defining a new radial coordinate, x, as
such that
and hence, we get the metric function through parametrization
whose (positive) solutions are now the exterior and interior “apparent horizons”, given by and . Thus, with this parametrized metric function, given by Equation (46), we demonstrate that Equation (43) is totally appropriate to study QBSs with purely ingoing boundary conditions at the exterior event horizon and decaying boundary conditions far from the BH at spatial infinity. The behavior of the metric function , including the horizons, is shown in Figure 2; we can see that the surface equation has two (real, positive) solutions.
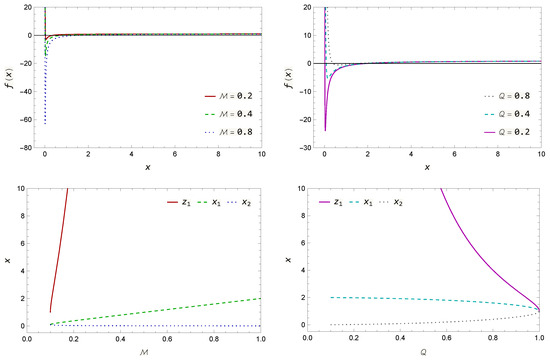
Figure 2.
Top panel: The metric function with and varying parameter (left), and with and varying parameter (right). Bottom panel: The horizons with as functions of the BH’s mass (left), and with as functions of the BH’s charge (right).
Now, by following the steps defined in the VBK approach, we can deduce the exact analytical solutions of Equation (43). First, we need to establish a new radial coordinate, z, as
such that
These new definitions move the three singularities to the points , as well as keeping a regular singularity at (spatial) infinity. Note that the regular singular point at is located outside . Then, the next step is to perform an F-homotopic transformation, such that by
where
with . Now, by substituting Equations (44)–(51) into Equation (43), we obtain
where
Equation (52) has the exact (canonical) form of a general Heun equation, where represents the general Heun function, which is the solution corresponding to the exponent 0 at when considering the value 1 there. Thus, if is not a negative integer, the existence of can be deduced from the Fuchs–Frobenius theory, which is analytic in the disk and represented by a Maclaurin series expansion:
where
with
Here, Karl Heun [42] adopted the normalization . Also, when is not a positive integer, the solution of Equation (52) corresponding to the exponent at is .
Hence, the exact solution for the radial part of the conformally coupled charged massive Klein–Gordon equation in the 5DRNBH spacetime can be represented as
where and are constants (to be determined), and labels the solution at all singular points. Consequently, we obtain a pair of linearly independent solutions at () through
Similarly, the pair of linearly independent solutions for exponents 0 and at () is provided by
The pair of linearly independent solutions for exponents 0 and at () is provided by
Finally, the pair of linearly independent solutions for exponents and at () is provided by
Next, by assuming a specific asymptotic behavior (boundary condition) on these exact solutions, namely, near the exterior black hole event horizon () and at the spatial infinity (), we can discuss the physical solutions related to the quasibound states.
4.2. Quasibound States
Now, we apply the VBK approach [21,22] to deduce the characteristic resonance equation and then determine the spectrum of QBS frequencies. To do this, we need to impose the following two boundary conditions on the radial solution: it should describe a purely ingoing wave at the exterior black hole event horizon and tend (decaying) to zero far from the black hole at spatial infinity. Since QBSs are mode solutions to the eigenvalue problem, we refer to QBSs as . In addition, it can be shown that the fact that at spatial infinity QBSs decay exponentially enables an analytic evaluation. Here, we only present the most important and final results, and hence we cordially invite the readers to check all the necessary calculations/steps on the VBK approach papers [21,22].
Thus, the general Heun function becomes a (class I) polynomial of degree n iff it satisfies two conditions [41], namely,
From the first condition, which is called -condition, we find the frequency eigenvalues. Moreover, based on the second condition, we determine the constant for all value of n, and then we use it to find the eigenvalues , as well as the radial and angular wave eigenfunctions. Therefore, by implementing Equation (69), we have that the exact analytical spectrum of QBSs is provided by
where n is now the overtone number, which can be called the principal quantum number. In fact, . On the other hand, by imposing Equation (70) for the fundamental mode when leads to
whose solution is
from which we can determine the angular eigenvalue for the ground state, as, for example, for , , , and .
In Figure 3 we show the behavior of the imaginary part of charged massive scalar QBSs in the 5DRNBH spacetime; The real part for the QBS is always constant and equal to .
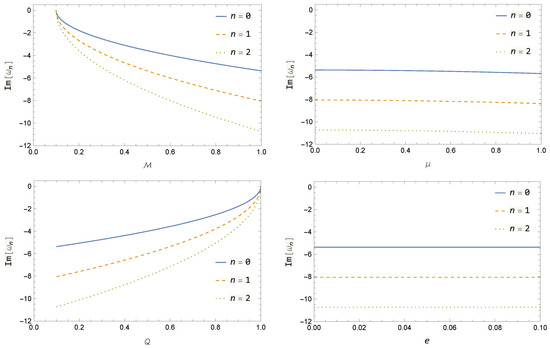
Figure 3.
Top panel: The imaginary part of the charged massive scalar QBSs of a five-dimensional non-extremal Reissner–Nordström black hole with respect to and varying the BH’s mass (left) and the field’s mass (right). Bottom panel: The imaginary part of the charged massive scalar QBSs of a five-dimensional non-extremal Reissner–Nordström black hole with respect to and varying the BH’s charge (left) and the field’s charge e (right).
4.3. Radial Wave Eigenfunctions
Finally, we introduce the radial wave eigenfunctions, which correspond to the charged massive scalar QBS frequencies in the 5DRNBH spacetime. To do this, we also follow the VBK approach.
Thus, the QBS radial wave eigenfunctions for charged massive scalar fields propagating in a 5DRNBH spacetime are given by
where is a constant to be determined, and are the general Heun polynomials.
In Figure 4, we present the squared radial wave eigenfunctions for the fundamental mode. We can see that these radial solutions tend to zero at spatial infinity and diverge (reaching a maximum value) at the exterior event horizon.
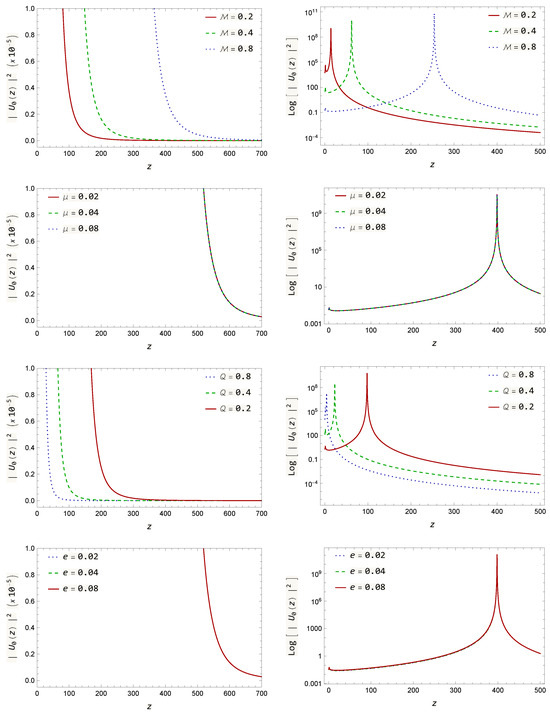
Figure 4.
The squared radial wave eigenfunctions (left) and their log-scale plots (right) for the fundamental of charged massive scalar QBS frequencies in a 5DRNBH spacetime as functions of , , , and e. The units are in multiples of .
5. Final Remarks
In this work, we investigated novel mathematical implications of concepts in geometric topology, retract theory, and physics, focusing on strong homotopy retracts in the five-dimensional non-extremal Reissner–Nordström black hole spacetime. From the metric describing the aforementioned background, we showed that the geodesics were strong retractions. In addition, we also proved that the end limit of folding on a D-dimensional non-extremal Reissner–Nordström black hole was a zero-dimensional non-extremal RNBH.
We used the theory of retracts to investigate the importance of geometric topology in the study of spacetime singularities, especially the apparent horizons of the five-dimensional non-extremal Reissner–Nordström black hole. We also looked at how quantum charged massive scalar fields behaved as they moved near the exterior event horizon of the five-dimensional non-extremal Reissner–Nordström black hole spacetime. We deduced the exact analytical solution for the radial part of the conformally coupled Klein–Gordon equation, provided in terms of the general Heun functions, and subsequently studied a significant physical phenomenon associated with the boundary conditions imposed on it, namely, the quasibound states. The spectrum of quasibound state frequencies for charged massive scalar fields was obtained by using the VBK approach.
Finally, we discussed the stability of the system. The system was stable, since the imaginary part of its resonant frequencies were negative. Here, it is worth emphasizing that these quasibound state frequencies were obtained directly from the general Heun functions by using their polynomial conditions, and, to our knowledge, there have not been any similar results in the literature for the background under consideration. In fact, there exist some results on bound states (not quasibound) of both 4D and 5D RNBHs obtained by Huang, Zhao, and Zou [37], where they imposed a bound state condition given by , which is a low-frequency limit, meaning that the particle was not absorbed by the black hole, and eventually, it could be emitted with a superradiant frequency; therefore, the spectrum of eigenfrequencies was just real, that is, , such that it did not depend on an overtone number n. Furthermore, in our case, the radial solution diverged near the exterior event horizon, and achieving a maximum value indicated that the scalar particles could cross into the black hole.
We hope that, in the near future, our results can be used to fit some astrophysical and/or experimental data and hence may shed some light on the physics of black holes and higher-dimensional theories of gravity as well.
Author Contributions
M.A.-S.: conceptualization, methodology, investigation, writing—original draft. H.S.V.: software, data curation, visualization, supervision, validation, writing—review and editing. L.H.C.B.: supervision, validation, writing—review editing. All authors have read and agreed to the published version of the manuscript.
Funding
H.S.V. is partially supported by the Alexander von Humboldt-Stiftung/Foundation (grant no. 1209836). This study was financed in part by the Conselho Nacional de Desenvolvimento Científico e Tecnológico—Brasil (CNPq)—research project no. 150410/2022-0 and funded by the Federal Ministry of Education and Research (BMBF) and the Baden-Württemberg Ministry of Science as part of the Excellence Strategy of the German Federal and State Governments—reference no. 1.-31.3.2/0086017037.
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Acknowledgments
It is a great pleasure to thank the Theoretical Astrophysics at Tübingen (TAT Group) for its wonderful hospitality and technological support (software licenses).
Conflicts of Interest
The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Bekenstein, J.D. Black Holes and Entropy. Phys. Rev. D 1973, 7, 2333. [Google Scholar] [CrossRef]
- Bardeen, J.M.; Carter, B.; Hawking, S.W. The four laws of black hole mechanics. Commun. Math. Phys. 1973, 31, 161. [Google Scholar] [CrossRef]
- Kastor, D.; Ray, S. Traschen, J. Enthalpy and the mechanics of AdS black holes. Class. Quantum Gravity 2009, 26, 195011. [Google Scholar] [CrossRef]
- Kubizňák, D.; Mann, R.B. P–V criticality of charged AdS black holes. J. High Energy Phys. 2012, 2012, 33. [Google Scholar] [CrossRef]
- Lobo, I.P.; Santos, L.C.N.; Bezerra, V.B.; Graça, J.P.M.; Moradpour, H. The extended phase space thermodynamics of Planck-scale-corrected Reissner-Nordström-anti-de Sitter black hole. Nucl. Phys. B 2021, 972, 115568. [Google Scholar] [CrossRef]
- Gubser, S.S.; Mitra, I. The evolution of unstable black holes in anti-de Sitter space. J. High Energy Phys. 2001, 2001, 18. [Google Scholar] [CrossRef]
- Konoplya, R.A.; Zhidenko, A. Stability of higher dimensional Reissner-Nordström-anti-de Sitter black holes. Phys. Rev. D 2008, 78, 104017. [Google Scholar] [CrossRef]
- Gwak, B.; Lee, B.H.; Ro, D. Instability of charged anti-de Sitter black holes. Phys. Lett. B 2016, 761, 437. [Google Scholar] [CrossRef]
- Huang, J.H.; Chen, W.X.; Huang, Z.Y.; Mai, Z.F. Superradiant stability of the Kerr black holes. Phys. Lett. B 2019, 798, 135026. [Google Scholar] [CrossRef]
- Hod, S. The Reissner–Nordström black hole with the fastest relaxation rate. Eur. Phys. J. C 2018, 78, 935. [Google Scholar] [CrossRef]
- Herdeiro, C.A.R.; Radu, E.; Gual, N.S.; Font, J.A. Spontaneous Scalarization of Charged Black Holes. Phys. Rev. Lett. 2018, 121, 101102. [Google Scholar] [CrossRef]
- Ishihara, H.; Kimura, M.; Konoplya, R.A.; Murata, K.; Soda, J.; Zhidenko, A. Evolution of perturbations of squashed Kaluza-Klein black holes: Escape from instability. Phys. Rev. D 2008, 77, 084019. [Google Scholar] [CrossRef]
- Ishibashi, A.; Kodama, H. Stability of Higher-Dimensional Schwarzschild Black Holes. Prog. Theor. Phys. 2003, 110, 901. [Google Scholar] [CrossRef]
- Kodama, H. Superradiance and Instability of Black Holes. Prog. Theor. Phys. Suppl. 2008, 172, 11. [Google Scholar] [CrossRef]
- Konoplya, R.A.; Zhidenko, A. Quasinormal modes of black holes: From astrophysics to string theory. Rev. Mod. Phys. 2011, 83, 793. [Google Scholar] [CrossRef]
- Konoplya, R.A.; Zhidenko, A. Instability of D-dimensional extremally charged Reissner-Nordstrøm (-de Sitter) black holes: Extrapolation to arbitrary D. Phys. Rev. D 2014, 89, 024011. [Google Scholar] [CrossRef]
- Konoplya, R.A.; Zhidenko, A. Instability of Higher-Dimensional Charged Black Holes in the de Sitter World. Phys. Rev. Lett. 2009, 103, 161101. [Google Scholar] [CrossRef]
- Huang, J.H.; Cao, T.T.; Zhang, M.Z. Superradiant stability of five and six-dimensional extremal Reissner-Nordstrom black holes. Eur. Phys. J. C 2021, 81, 904. [Google Scholar] [CrossRef]
- Damour, T.; Deruelle, N.; Ruffini, R. On quantum resonances in stationary geometries. Lett. Nuovo Cim. 1976, 15, 257. [Google Scholar] [CrossRef]
- Gaina, A.B.; Ionescu-Pallas, N.I. The fine and hyperfine structure of fermionic levels in gravitational fields. Rom. J. Phys. 1993, 38, 729. [Google Scholar]
- Vieira, H.S.; Bezerra, V.B. Confluent Heun functions and the physics of black holes: Resonant frequencies, Hawking radiation and scattering of scalar waves. Ann. Phys. 2016, 373, 28. [Google Scholar] [CrossRef]
- Vieira, H.S.; Kokkotas, K.D. Quasibound states of Schwarzschild acoustic black holes. Phys. Rev. D 2021, 104, 024035. [Google Scholar] [CrossRef]
- Vieira, H.S.; Destounis, K.; Kokkotas, K.D. Slowly-rotating curved acoustic black holes: Quasinormal modes, Hawking-Unruh radiation, and quasibound states. Phys. Rev. D 2022, 105, 045015. [Google Scholar] [CrossRef]
- Senjaya, D. Analytical quasibound states of black holes emerging from modified theories of gravity. Mod. Phys. Lett. A 2023, 38, 2350160. [Google Scholar] [CrossRef]
- Senjaya, D. Exact analytical quasibound states of a scalar particle around a slowly rotating black hole. J. High Energy Astrophys. 2023, 40, 49. [Google Scholar] [CrossRef]
- Vieira, H.S.; Destounis, K.; Kokkotas, K.D. Analog Schwarzschild black holes of Bose-Einstein condensates in a cavity: Quasinormal modes and quasibound states. Phys. Rev. D 2023, 107, 104038. [Google Scholar] [CrossRef]
- Senjaya, D. Exact massless spinor quasibound states of Schwarzschild black hole. Phys. Lett. B 2024, 854, 138714. [Google Scholar] [CrossRef]
- Senjaya, D. The Kerr–Bumblebee exact massive and massless scalar quasibound states and Hawking radiation. Eur. Phys. J. C 2024, 84, 424. [Google Scholar] [CrossRef]
- Myers, R.C.; Perry, M.J. Black holes in higher dimensional space-times. Ann. Phys. 1986, 172, 304. [Google Scholar] [CrossRef]
- Huang, J.H. No black hole bomb for D-dimensional extremal Reissner—Nordstrom black holes under charged massive scalar perturbation. Eur. Phys. J. C 2022, 82, 467. [Google Scholar] [CrossRef]
- Vieira, H.S. Scalar fields in a five-dimensional Lovelock black hole spacetime. Ann. Phys. 2020, 418, 168197. [Google Scholar] [CrossRef]
- Abu-Saleem, M.; Vieira, H.S. Some aspects of the five-dimensional Lovelock black hole spacetime: Strong homotopy retract, perihelion precession and quasistationary levels. Ann. Phys. 2021, 433, 168583. [Google Scholar] [CrossRef]
- Fox, R.H. Algebraic Geometry and Topology: A Symposium in Honor of Solomon Lefschetz: 1873; Princeton Legacy Library: Princeton, NJ, USA, 1957. [Google Scholar]
- Massey, W.S. Algebraic Topology: An Introduction; Springer: New York, NY, USA, 1977. [Google Scholar]
- Richter, B. From Categories Homotopy Theory; Cambridge University Press: Cambridge, UK, 2020. [Google Scholar]
- Robertson, S.A. Isometric folding of Riemannian manifolds. Proc. R. Soc. Edinb. A 1978, 79, 275. [Google Scholar] [CrossRef]
- Huang, J.H.; Zhao, R.D.; Zou, Y.F. Higher-dimensional non-extremal Reissner-Nordstrom black holes, scalar perturbation and superradiance: An analytical study. Phys. Lett. B 2021, 823, 136724. [Google Scholar] [CrossRef]
- Hyers, D.H. The Functions of Mathematical Physics (Harry Hochstadt). SIAM Rev. 1973, 15, 235. [Google Scholar] [CrossRef]
- Frye, C.R.; Efthimiou, C.J. Spherical harmonics in p dimensions. arXiv 2012, arXiv:1205.3548. [Google Scholar]
- del Castillo, G.F.T. A generating function for the spherical harmonics in p dimensions. Rev. Mex. Fis. 2013, 59, 248. [Google Scholar]
- Ronveaux, A. (Ed.) Heun’s Differential Equations; Oxford University Press: New York, NY, USA, 1995. [Google Scholar]
- Heun, K. Zur Theorie der Riemann’schen Functionen zweiter Ordnung mit vier Verzweigungspunkten. Math. Ann. 1888, 33, 161–179. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).