Abstract
Measurements of magnetic fields near seismic sources during solar flares are vital for understanding the dynamics of solar activity. We used spectropolarimetric observations of the X17.2/4B solar flare on 28 October 2003, over a wavelength interval of 43 Å, including the D3, D2, D1, and Ni I 5892.88 Å lines, to analyze the Stokes I ± V profiles. Effective magnetic fields within 0.5–1.5 kG were measured in the D1, D2, and D3 lines at different flare locations, with the photospheric Ni I 5892.88 Å line showing a weaker field of below 0.5 kG. The D3 line showed rapid plasma descents of up to 11 km/s, in contrast to the slower velocities within 2.3 km/s observed in other lines. The differing amplitudes in the I + V and I − V profiles indicated potential non-Zeeman polarization effects. Secondary Stokes V peaks were also detected up to 8 Å from the D3 emission core. Significant altitudinal inhomogeneity in the magnetic field strengths was detected, possibly indicating the local magnetic collapse, facilitating the Lorentz-force driven mechanism of the seismic source excitation.
1. Introduction
In this study, we analyze in detail the observational material for the large solar flare of 28 October 2003 at 11:15 UT. In previous research, relatively subtle spectral effects in the far wings of the D3 spectral line were reported [1], possibly indicative of extremely strong magnetic fields in the 105 G range. In the present study, we analyze new data for the D3, D2, D1 and Ni I 5892.88 Å spectral lines, primarily focusing on much stronger and more pronounced effects manifested in multiple lines.
The solar flare on 28 October 2003 of X17.2/4B class was one of the most powerful in recent decades—it holds the third position in the list of such flares according to the criterion of peak X-ray power recorded by the GOES detectors since 1976. This flare occurred in the active region NOAA 0486, in the same region that produced the strongest flare of X28+ class one week later, on 4 November 2003. Less than a day (approximately 18 h) after the flare of 28 October, a rank 9 magnetic storm arose on the Earth.
The peak of the Hα flare emission was observed in the time interval of 11:00 –11:10 UT [2]. According to GOES detectors, a sharp increase in the flux of high-energy protons took place during the flare; the next day, the proton flux exceeded the levels of 102, 103, and 104 particles per cm−2 s−1 sr−1 for the protons with energies of 100 MeV, 50 MeV, and 10 MeV, respectively. It should be noted that, for a quiet Sun, the typical proton flux is about 10−1 particles, suggesting that the proton flux increased by about 3 to 5 orders of magnitude after this flare.
Three seismic sources were detected in this flare according to [3,4]. One of these sources was close to the projection of the entrance slit of the Echelle spectrograph for our observations, especially for time 11:15 UT. Subsequently, it turned out that the position of the entrance slit of the instrument coincided quite well with the region of the local gamma source of the flare [5].
It should be noted that seismic sources are among the least studied phenomena accompanying the energy release of solar flares [6,7,8,9]. They are observed on the dopplerograms of the Sun’s photosphere as disturbances that spread concentrically from a certain point. Such waves were observed in ≈50% of solar flares, with some being accompanied by multiple seismic sources. Physically, these are acoustic waves propagating not on the surface but rather within the sun’s interior (hence the name—seismic). They are reflected due to the temperature gradient and reach the surface accelerated. A number of different mechanisms have been proposed to explain the driver of the flares’ acoustic emission, including chromospheric shocks, wave-mechanical transients, and Lorentz force transients [10,11]. In particular, high-energy beams of protons and electrons that are separated in the non-neutral reconnecting current sheets [12] can either directly impact the photosphere [4,13], or cause a chromospheric shock that descends and penetrates into the solar interior [14]. It should be noted that due to radiative losses, the energy that penetrates through the photosphere can be insufficient to cause the observed seismic radiation [15].
Another factor that can likely cause the seismic emission is related to the wave-mechanical transients that are driven by the back-heating of the photosphere. This scenario was highlighted in [13,16], where the details of the seismic emission of the 28 and 29 October 2003 solar flares were studied. It was concluded that in order for the flare to be acoustically active, there needs to be a rapid impulsive heating at the flare’s onset as opposed to the much more powerful but slow energy release during the flare. This explains why the absolute majority of the flares can be acoustically inactive, despite the fact that the required acoustic energy is several orders of magnitudes lower than that of the electromagnetic energy released during the flare. The seismic signatures are strongly associated with a hard X-ray emission near the footprints of the magnetic loops, as well as with the strong downward propagating shocks during the flare’s onset. This served as a basis for the hypothesis that solar interior emission can be a direct continuation of the chromospheric shocks. While the downward propagation of chromospheric transient does not always lead to significant seismic emission [17], it can still be an important indicator, especially when coupled with the presence of a white-light emission.
A different mechanism that couples the energy of the flare with the seismic waves was proposed in [18]. It highlights that the photospheric magnetic field changes that occur as the result of a coronal disturbance involve the work performed by Lorentz forces, which can generate sufficient energy to produce observable flare-driven seismic waves. Within this framework, sudden changes in the magnetic field configuration, known as the McClymont magnetic jerk [19], can excite the seismic waves.
The study on the role of the Lorentz force during large, eruptive solar flares and their effects on the solar atmosphere and interior was further expanded in [20]. It was shown that the Lorentz force perturbation in the outer solar atmosphere is balanced by an equal and opposite force perturbation on the solar photosphere and interior. The post-flare conditions suggest that the photospheric field becomes more horizontal after the magnetic eruptions, indicating a decrease in coronal magnetic energy and alignment with force-free assumptions, leading to a downward force change acting on the photosphere and solar interior. Given these circumstances, it is important to obtain new observational data on magnetic fields and plasma velocities in the region of seismic sources of flares.
For the mentioned solar flare on 28 October 2003, an analysis of spectra obtained with the gamma-ray spectrometer SPI onboard INTEGRAL of the GOES was performed in [21]. In the energy range of 0.6–8 MeV, three prominent narrow lines at 2.2, 4.4, and 6.1 MeV were detected, resulting from nuclear interactions of accelerated ions within the solar atmosphere. In [22], the analysis was focused on magnetic field data from SOHO/MDI, chromospheric and coronal observations from the NainiTal observatory and TRACE. By combining the data analysis with a model of the coronal magnetic field, it was concluded that a large-scale quadrupolar reconnection process exists in this flare.
The mentioned flare is reported to have exhibited rapidly moving transient features, reaching the speeds of 30 to 50 km s−1 during its impulsive phase [23,24]. In two locations within the flare, magnetic transients were associated with sign reversals in both magnetic field polarity and Doppler velocity, indicative of the rapid reconnection of successive magnetic field lines at higher levels of the corona.
Four FeI lines in this flare for the time of 11:13 UT were studied in [25], where spectral evidence for a three-component magnetic field structure. which included a background field with the strength of ≈300 G and two strong spatially unresolved components, was discovered. The existence of the latter two components follows from the unique shape of the Stokes V profiles of the FeI 5233.0 and FeI 5397.1 lines, with two positive and two negative peaks. Such peculiarities are possible for magnetic fields in two ranges, 1300–3100 G and 8–10 kG. From comparison of the Stokes I and V profiles, it follows that the mentioned extremely strong field had the opposite magnetic polarity compared to the other two magnetic components.
The results of magnetic field measurements and semi-empirical modeling for the time 11:06 which corresponds to a peak phase of this flare were presented in [26]. In order to study the physical conditions in the flare, twelve spectral lines were used, including several FeI and FeII lines, as well as , , , and . It was found that the flare had a unique Balmer decrement, with an outstanding ratio between the and intensities, which is unprecedented for all flares observed. Outside the sunspots, the effective magnetic field , measured by the ‘center of gravity’ (centroid) splitting of the I ± V profiles, was found to be within the range of 0–200 G in the middle photosphere, reaching 1200 G in the upper photosphere and the temperature minimum zone, and reducing back to 500 G in the chromosphere. Additionally, the broadening of the FeI 5250.2 Å line when compared to the FeI 5247.1 Å line was found, indicating the presence of a strong (800–1100 G) ‘turbulent’ field in the middle photosphere. A semi-empirical model of the flare constructed using the PANDORA code has an interesting peculiarity, namely, three discrete layers with an increased concentration and/or temperature, including a very dense and thin layer in the chromosphere with the following parameters: the concentration of hydrogen = 1018 cm3, the thickness = 3–5 km, and a height of km above the photosphere. It is interesting to note that three discrete layers in this flare, found in the indicated paper using lines of the Balmer series, are in good agreement with the data of the presented study, where this conclusion is made on the basis of data in the D3 line.
The flare on 28 October 2003 is also of interest from the point of view of the possible existence of particularly strong magnetic fields in it. Currently, there are very different estimates of local magnetic fields in solar flares, ranging from 102 up to 105 G [27,28,29,30,31,32,33]. That is, in some cases, the measured magnetic field in solar flares can exceed the magnetic field in sunspots, where it is typically found to be within 2–8 kG [34,35,36,37,38].
It is especially interesting that very strong magnetic fields are recorded in the flares at the levels of the chromosphere and even the lower corona, where, theoretically, one would expect magnetic fields of only a few tens of gauss within a model of simple untwisted flux tubes. However, observations in the microwave spectral region suggest that the coronal magnetic fields reach magnitudes of several hundred gauss [39,40,41]. Moreover, the measured coronal magnetic field could reach 2000–3000 G, assuming the thermal gyroresonance nature of the observed 17 GHz emission [40]. Apparently, there are specific mechanisms for maintaining significantly enhanced magnetic fields in a very sparse atmosphere with low static and dynamic pressures. It is possible that such mechanisms are related to certain topological features of the corresponding structures, which may be of the force-free type. This is confirmed by significant increases in the twist of photospheric magnetic fields observed during eruptive events [42]. Additionally, the coronal magnetic fields are transient in nature, and their decay is believed to drive the particle acceleration and energy release during flares [43,44], significantly complicating the analysis. Solving this problem requires not only further theoretical research but also careful examination of new observational data.
It can be expected that many spatially unresolved components with significantly different local parameters and filling factors may be present in the solar flare. At the same time, components with large filling factors should mainly contribute to the intense spectral manifestations, while other components with a small filling factors result in weaker features. In the previous paper [1], relatively weak spectral effects were highlighted in the D3 line. The main goal of the presented study is to compare magnetic fields and velocities in the strongest component across a wide range of heights, approximately 2 Mm, using data from the D3, D2, D1, and Ni I 5892.88 Å lines.
2. Observations and Methods
Observations of the flare were carried out with the Echelle spectrograph of the horizontal solar telescope of the Astronomical Observatory of Taras Shevchenko National University of Kyiv (HST AO KNU). Observers were Natalia Lozitska and Vsevolod Lozitsky.
The optical scheme of the telescope and some instrumental details were described in detail in [36]. The main value of observations with the Echelle spectrograph is that a wide spectrum interval, from 3800 to 6600 Å, can be recorded simultaneously, where many thousands of spectral lines can be registered. Another advantage of such observations is that I + V and I − V spectra are obtained simultaneously, on separate adjacent bands of the spectrograms. This was achieved with the circular polarization analyzer consisting of a plate in front of the entrance slit of the spectrograph, and a beam-splitting prism (analogous to the Wollaston prism) behind the entrance slit. Therefore, I + V and I − V spectra relate to the same moment of time and to the same locations on the sun.
The Echelle spectrograph is a cross-dispersion instrument. Its optical design simultaneously employs a diffraction grating with profiled grooves to intensify light concentration as well as a glass prism for dispersing diffraction orders. Therefore, the overlay of diffraction orders is entirely prevented, specifically due to the glass prism dispersing these orders to an appropriate degree. This is especially important for searching for subtle spectral effects far from the spectral line, in the spectral continuum region.
The D3 line was observed by this instrument in the 35th order of diffraction, and the total length of the spectrum, which is simultaneously registered near this line, is 160 Å in the range from −112 Å to +48 Å relative to the center of the D3 line. Dispersion in this diffraction order is 770 mÅ per mm, and the full width at half maximum (FWHM) of the instrumental profile is about 50 mÅ. All spectra were photographed on ORWO WP3 photographic plates, which have a signal-to-noise ratio of around 100 when optimally exposed. The length of the entrance slit of the spectrograph is 2.3 mm, and its width is 0.06 mm, which corresponds to about 37 and 0.9 arcsec, respectively. However, due to image vibration, the actual spatial resolution of our observations is ≈1.5 Mm.
When photographing the spectra of the flare in orthogonal circular polarizations, its brightest locations were selected. One of these locations, as a result of a lucky coincidence, turned out to be tangential to one of the seismic sources [3,4]. This can be seen from Figure 1, which shows the locations of the hard X-ray and gamma sources [3,5] overlaid on top of the white-light SOHO image of the NOOA 0486 active region. The position of the entrance slit of the spectrograph of AO KNU is marked with a red interval, which overlaps the area of rapid vertical plasma motions and the hard X-ray source of the seismic source #2. The results of the visual measurements of the magnetic field in spots are also given (in hundreds of gauss) and their magnetic polarities, measured in the Fe I 5250.2 line. The orientation of Figure 1 is such that east is on the left, west is on the right, and north is on top.

Figure 1.
A white-light image of the active region NOAA 0486 in from SOHO data. The locations of hard X-ray and gamma sources are marked with green and yellow circles, respectively [3,5]. The locations of vertical photospheric motions are outlined with blue ellipses [3]. The seismic sources are marked with purple numbers [3,4], and the position of the entrance slit of the spectrograph is shown with a red interval.
In this study, we investigate the mentioned flare at moment 11:15 UT, which has not been studied yet on a base of Zeeman spectrograms obtained with HST AO KNU. In order to obtain quantitative information on intensity distribution in spectra of the flare, the spectrogram for 11:15 UT was scanned using the Epson Perfection V 550 scanner. To transfer blackening into intensity, it is necessary to take into account the characteristic curve of the photographic material as well as the curve of the scanner itself. Both curves are non-linear and require preliminary determination by special methods. In order to do this, we used a step attenuator, for which transmittances are precisely known. When converting photometrical densities into intensities, the scattered light in the spectrograph was taken into account by subtracting the intensities corresponding to the intervals between images of different diffraction orders of the spectrum of the Echelle spectrograph.
During the pre-processing of observational data, spectrum recordings of I + V and I − V profiles were wavelength aligned using narrow telluric lines; the accuracy of this alignment is about 1–2 mÅ. The next step of data processing was to find the normalized intensities, i.e., local intensities, expressed in units of intensity of the local spectral continuum. After these two steps, I and V profiles were calculated using I + V and I − V profiles. The mentioned procedures were performed using a custom-made software, which facilitates the preparation and advanced processing of observational data in large volumes, while keeping track of the measurement error estimates.
The scanning approach to digitizing the spectrograms made it possible to obtain local values of intensities with a step of 3.846 mÅ. We used such very fine spectral discretization in order to reliably eliminate very narrow artifacts associated with small dust particles and other impurities on the spectrogram. The artifacts are typically much narrower than the FWHM of the instrumental profile, and can therefore be reliably detected and eliminated at fine discretization. If we had used spectral sampling with a step of 50 mÅ, some artifacts could have gone unnoticed, introducing significant distortions to the observational data.
In order to search for subtle effects in the spectrum, we found the averaged smoothed values of the intensities by averaging the data in 100 steps, i.e., 384.6 mÅ, which is approximately three times less than the observed emission width of the D3 line. Since the width of the instrument profile of the spectrograph is around 50 mÅ, corresponding to approximately 13 points on the registrogram, only those intensity values that are separated by more than the FWHM of the instrument profile can be considered to be independent measurements. Therefore, the signal-to-noise ratio of the 100-points-averaged data increases approximately by the square root of 7.7, that is, by a factor of 2.8. In order to reduce the influence of noise effects, we combined photometric data not only by wavelengths in the spectrum but also by different locations on the sun as presented below in Section 3.
3. Results
3.1. Selected Spectral Lines and Their I ± V Profiles
Table 1 lists the details of the selected spectral lines. In this table, is the line wavelength, EP is the excitation potential of the lower term according to [45], is the equivalent line width in the spectrum of the quiet sun [45], is the effective Lande factor calculated within the LS coupling scheme, and is the effective Lande factor corrected for the Paschen–Back effect.

Table 1.
Details of the selected spectral lines.
From the experimental [48,49] and theoretical [50] works, it follows that in lines D1 and D2, the Paschen–Back effect occurs at sub-kilogauss magnetic fields, which we confirmed by comparing the magnetic field strengths measured in lines No. 1, 2, and 4 in the sunspot on 24 July 2023. If we use the theoretical Lande factors for the LS coupling scheme to calibrate the splitting of the indicated lines, then an unrealistic picture occurs: the strongest magnetic field is indicated by the chromospheric D2 line (No. 2), the intermediate magnetic field is shown by the photospheric Ni I line (No. 4), and the weakest magnetic field is measured in the D1 line (No. 1). However, if we use the Lande factors corrected for the Paschen–Back, , for lines No. 1 and 2, then the situation becomes quite realistic: photospheric line No. 4 everywhere shows a stronger magnetic field in the sunspot than chromospheric lines No. 1 and 2. That is why the results presented below for lines D1 and D2 correspond to the Lande factors . The validity of using the Lande factors corrected for the Paschen–Back effect in the D3 line follows from the calculations by [33], performed using the HAZEL code [51]. It was found that for magnetic fields with a strength of 500–2000 G, the Paschen–Back effect cannot be neglected in the D3 HeI line.
In the studied flare, the D3, D1, and D2 lines had intense emission in their cores, which can be seen in Figure 2. Here, I ± V profiles are presented in the wavelength range from −14 to +29 Å relative to the D3 line, and to better identify the main effects, these profiles represent observed data averaged over intervals of approximately 300 mÅ. These data refer to the region of the seismic source of the flare, and more precisely, to a distance Mm from the position on the sun that corresponds to the extreme left border of the entrance slit of the spectrograph in Figure 1. According to such spatial binding, the region of the seismic source corresponds to the space interval 14–24 Mm. At the specified location, the emission intensity in the D3 line reaches a level of approximately 4.5 in the units of the local spectral continuum intensity, while the emission in the D1 and D2 lines reaches a level of about 1.45 units. This figure shows some displacement of the I − V profiles, shown by dashed lines, relative to the I + V profiles. This indicates the presence of magnetic fields in the region of formation of these emission peaks.
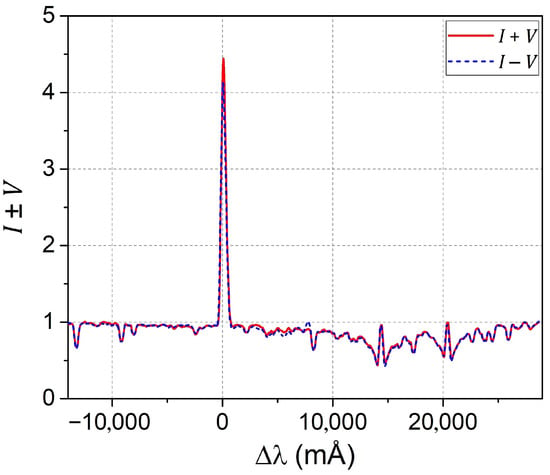
Figure 2.
Significantly smoothed I ± V profiles of the D3 line and its vicinity, which also includes D1 and D2 lines. These data correspond to position Mm along the entrance slit.
The emission profiles can be seen in more detail in Figure 3. Here, we present observational data averaged over an interval of 100 mÅ to reduce noise effects due to the graininess of the photo-emulsion in the spectrogram. It can be seen that the I ± V profiles of the D3 line are asymmetric and, in general, shifted to the red region of the spectrum relative to the zero point determined by the telluric lines. In addition, there is a relative displacement of I + V profiles relative to I − V, which indicates their Zeeman splitting by a magnetic field. It should also be noted that the I + V and I − V profiles for Mm have different central intensities, as well as a flat saturated top. These features will be discussed below.
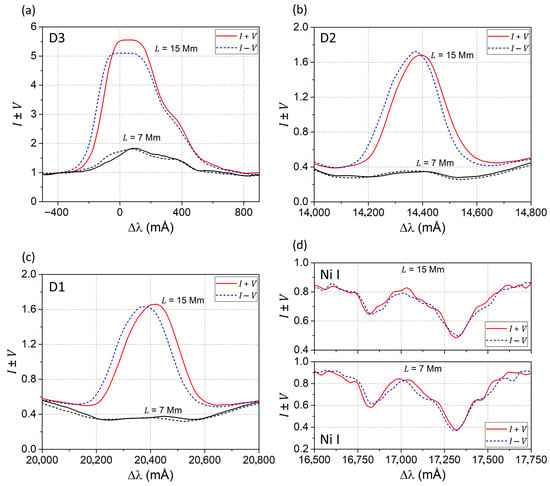
Figure 3.
I ± V profiles of D3 (a), D2 (b), D1 (c), and Ni I 5892.88 Å (d) lines at a location within ( Mm) and outside ( Mm) the seismic source.
Regarding the profiles of the chromospheric lines D2 and D1, they are more symmetrical and devoid of the mentioned saturation (Figure 3b,c). This was further confirmed with smaller data averaging intervals of 20–50 mÅ. The photospheric Ni I 5892.88 Å line (Figure 3d) had typical Fraunhofer absorption profiles along the entire entrance slit, with weak residual emission peaks at the locations where the strong emission peaks in the D3 line were observed.
3.2. Effective Magnetic Field
Since the observed splitting of the intense peaks in I ± V profiles was much smaller than their half-width (HWFM), only some effective magnetic field can be determined from the magnitude of such splitting. In the case of a uniform magnetic field, the value of should be close to the longitudinal component . If the magnetic field is heterogeneous and has, for example, two components—background and small-scale—the value of starts to depend on multiple parameters, such as local and background field intensities, angles of inclination of the field lines to the line of sight, as well as the corresponding magnetic polarities, the filling factor of the small-scale (spatially unresolved) component, etc. In this case, local values of magnetic fields can be obtained only as very rough estimates [52]. In the presence of unresolved magnetic structures, the local magnetic fields can be reliably measured only in the strong magnetic field regime, where the Zeeman splitting is larger than the HWFM of the spectral lines. Nevertheless, estimates of the value of can be useful in the case when it is not possible to determine the value of the field modulus in a more direct way because the value of can be treated as a lower estimate for local unresolved magnetic fields.
For a more reliable measurement of magnetic field in the flare, only the steepest sections of the profiles of these lines, outside the intense blend lines, were taken into account. Figure 4a illustrates the procedure used for measuring the magnetic splitting. For each wing of the emission (for the D1, D2, and D3 lines) or absorption (for the Ni I 5892.88 Å line) peaks, the displacement between the I + V and I − V profiles was measured at a half of the peak’s height. The Zeeman splittings and of the red and blue wings of the emission peaks were estimated in the approximation of a purely longitudinal magnetic field, i.e., assuming that the displacement between the I + V and I − V profiles is equal to the doubled Zeeman splitting. Finally, the splittings of the two wings of the emission peaks were averaged to calculate the resulting magnetic splitting . It should be noted that this method of measuring Zeeman splittings is similar in nature to classical magnetographic measurements [53], in which the polarization signal is recorded on the steepest sections of the profiles, where is the largest, which ensures the maximum sensitivity of the measurements.
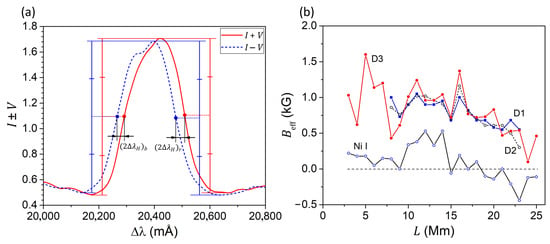
Figure 4.
(a) Stokes I ± V profiles of the D1 line, showing the details of how the magnetic splitting is measured. (b) Comparison of the effective (averaged) magnetic field along the entrance slit (see Figure 1), measured by different spectral lines. The measurements errors are approximately ±0.1 kG for all lines.
A simple calibration formula was used to relate the Zeeman splitting to the magnetic strength:
where the magnetic splitting is expressed in angstroms (Å), and the magnetic field strength B—in gauss (G). Constant C, taking into account the Lande factors in Table 1, has the values 2.20, 1.97, 1.51, and 1.62 for the D1, D2, D3, and Ni I 5892.88 Å lines, respectively.
The obtained measurements of are presented in Figure 4b, from which the following interesting features become apparent. The magnetic fields measured by D1, D2 and D3 agree well, despite the fact that the first two lines are formed in the chromosphere, while the third line forms significantly higher, in the transition zone between the chromosphere and the solar corona. As can be seen from Figure 4b, the value of , measured using the D3 line, varied quite significantly along the direction of the spectrograph entrance slit, reaching a maximum of 1.6 kG at Mm. This place was outside the seismic source, which, as mentioned, corresponds to 14–24 Mm in this figure.
Another interesting effect is that the value of , measured using the photospheric line Ni I 5892.883 Å, is almost in all locations smaller than the one indicate by the D3 line. Previously, a similar result was obtained in [54], comparing measurements of magnetic fields in five solar flares in the Fe I, Fe II, Hα, Hγ, D1, and D3 lines. However, in the mentioned paper, the magnetic fields were measured only at specific coordinates of flares, without investigating the distribution of the magnetic field along a certain direction on the sun. In addition, the mentioned work studied less powerful solar flares, which, however, had emission peaks in some metal lines as well as in the D3 line.
Figure 4b shows that magnetic polarity by the D3 and Ni I lines mostly matches, but in range L = 19–25, it is the opposite. This indicates a complex structure of the magnetic field in the flare, which includes the altitude change not only in the magnitude of the magnetic field but also in its polarity.
3.3. Doppler Velocities
The distribution of Doppler (longitudinal) velocities was determined by the displacement of lines under study relative to the H2O telluric lines. Figure 5a shows the Stokes I profiles of the D3, D2, D1 and Ni I 5892.88 Å lines, where the wavelength is measured as a deviation from the expected wavelength (Table 1) of each line. The figure also shows one of the H2O telluric lines used as the wavelength reference points. The displacements of the Stokes I emission (for D1, D2, and D3 lines) and absorption (for the Ni I 5892.88 Åline) peaks were calculated at the half-height of the peaks. It should be noted that while the line wavelengths have a slight variation across different sources [45,47,55,56], this variation is typically within 1 mÅ and therefore has a negligible impact on the velocity measurements.
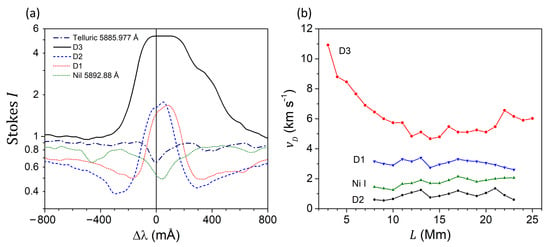
Figure 5.
(a) Stokes I profiles of the D3, D2, D1, Ni I 5892.88 Å, and one of the telluric lines used as a wavelength reference when measuring the Doppler (longitudinal) velocities . (b) Distributions of the Doppler velocities along the direction of the entrance slit, measured in different spectral lines. The measurement errors, estimated by the discrepancy between the positions of different telluric lines in the I + V and I − V spectra, are around 0.3 km s−1.
In general, the distribution of Doppler velocities is simpler than the magnetic field distribution, and has a maximum of +11 km s−1 at L = 3–4 Mm, that is, outside the seismic source (Figure 5b). In the region of the seismic source ( 14–24 Mm), the velocities were within 5–7 km s−1. In both cases, it was a descent of the plasma with the indicated speeds. As will be shown below, significantly higher rates follow from consideration of the weak spectral peculiarities—secondary peaks of the Stokes V profiles.
The most unexpected effect in Figure 5b is that the D2 line shows significantly slower velocities along the entire length of the entrance slit when compared to the D1 line. This is an unusual result, as these two sodium doublet lines relate to one multiplet (No. 1), have the same excitation potential of the lower term (0.00 eV), and fairly close equivalent widths (754 mÅ and 564 mÅ, respectively). Therefore, one would expect that since these two lines have virtually the same formation altitudes in the solar atmosphere, they should show similar observed velocities. Since this clearly is not the case, we make the conclusion that in the studied flare, there was a very fine height stratification of physical conditions, with closely located plasma volumes having significantly different velocities, possibly indicating the local magnetic collapse.
3.4. Possible Non-Zeeman Polarization
As it was noted above (Figure 3a), in some places of the flare, the I + V and I − V profiles of the D3 line have a significantly different amplitude of emission peaks. A similar effect was found in lines D1 and D2 too, but in the latter two lines, it is smaller in amplitude (Figure 3b,c). It is interesting to note that in the D3 line, this effect has a maximum at the location that roughly corresponds to the seismic source solar flare, while in lines D1 and D2, the location where this effect is present is narrower and corresponds to 18–22 Mm. At the same time, in the latter two lines, a fine detail at Mm is also repeated, namely, the change in the sign of this effect, if we bear in mind the difference in the parameters for the I + V and I − V profiles (Figure 6). Here, denotes the maximum peak intensity, and is the intensity of the local spectral continuum.
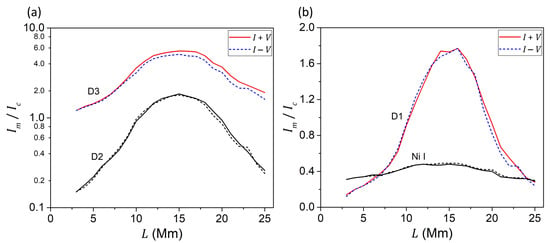
Figure 6.
Distribution of the relative peak amplitudes of the I + V and I − V profiles along the entrance slit for D2 and D3 lines (a), and D1 and Ni I 5892.883 Å lines (b). For the D1, D2, and D3 lines, denotes the amplitude of emission peaks in line profiles, and is the intensity of the nearest spectral continuum. For the Ni I line, the parameter is defined as the minimum intensity within the core of the Fraunhofer absorption profile.
Theoretically, such an effect should not occur with a uniform magnetic field of arbitrary orientation [57]. A similar effect can occur with a large inclination of the lines of force to the line of sight, accompanied by the effect of instrumental polarization [58,59,60]. In such a case, some portion of the linear polarization is transformed into circular polarization and creates a non-zero signal of circular polarization in the center of the line. In principle, this can cause a similar difference in the amplitudes of the emission peaks in the I + V and I − V spectra.
However, a similar appearance of circular polarization can also occur in the case of a transverse electric field. Such a field results in a linear polarization due to the Stark effect [61], which, being transformed partially into circular polarization by instrumental polarization, can also give, in principle, a similar picture in line profiles. If this is indeed the case, then the detected effects indicate strong electric fields in the flare.
An indirect argument in favor of such an interpretation is that similar effects of the predominance of polarization of one sign were also observed outside the intense emission peaks in this flare, which will be discussed further below. Since such unipolar peaks are observed far from the studied lines, then they could also manifest near the centers of the emission peaks.
In connection with the problem of the possible existence of extremely strong magnetic fields of the 104–105 G range [1,32,33], it is of particular interest to study the Stokes V profiles in a wide range of wavelengths around the D3 line (Figure 7). At the locations near the seismic source (Figure 7a), the largest amplitude changes in both Stokes V and profiles take place within approximately ±1 Å around the D3 line. A similar picture occurs at +14.37 Å and +20.33 Å, associated with the splitting of emission profiles of the D2 and D1 lines, respectively. However, at a wavelength of about +7.8 Å, a rather strong peak of one sign in the Stokes V profile is observed, not accompanied by the changes in the profile.
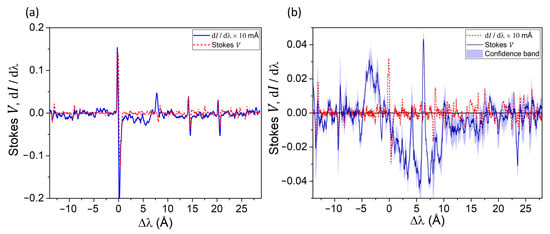
Figure 7.
Stokes V and profiles of the flare under study, within the seismic source at Mm (a), and outside it at L = 3–4 Mm (b). The spatial data averaging interval at L = 3–4 Mm is 2 Mm.
A much more complex picture is observed outside the seismic source, at L = 3–4 Mm (Figure 7b), where a rather complex pattern of secondary peaks is observed. The Stokes V profile has a sign-changing feature centered at the D3 line, similar to the one reported in [33] for a weaker solar flare. The amplitude of this feature reaches an outstanding 4% of the continuum intensity, with a width of 4–8 Å. Additionally, several narrow (≈0.6 Å) peaks are present at = +2 to +10 Å, with the most prominent ones at +4.1 and +6.3 Å. If we consider that this peak is superimposed on a larger-scale and sign-changing distribution of the Stokes V profile, spanning approximately from −5 to +10 Å, then the amplitude of this narrow peak should be considered equal to ≈8%. This feature may suggest some non-magnetic polarization of one sign with the Doppler velocity of about +320 km s−1. Moreover, the negative peak at +23.5 Å, if attributed to the D3 line, corresponds to even higher velocities of plasma descent, about +1200 km s−1. It seems most likely that all the specified features are related to the D3 line, as we could not reliably detect similar effects in the D1 and D2 lines.
3.5. Modeling Atmospheric Parameters
The broad peaks in the Stokes V profiles far from the D3 line core with the widths of 5–10 Å (Figure 7b) likely indicate some extreme conditions in the flare, such as a complex spatial structure or high-magnitude fields. In order to investigate the physical conditions that can lead to such polarization features, the performance of various atmospheric models was assessed, two of which we describe below. The first model—Model A—assumes a complex structure of the flare, while restricting the magnetic field intensities to several kG. The second model—Model B—lifts the restrictions on the magnetic field but in turn assumes a simpler atmosphere topology.
The calculations were performed using the HAZEL code [51], which solves the non-LTE radiative transfer problem for one or multiple constant-property slabs within the multi-term atom model [62]. The constant-property slabs can be arranged in series, or be merged by introducing a filling factor. Each slab is defined by the magnetic field vector, optical thickness , macroscopic and microscopic velocities, enhancement factor , and the Voigt profile damping a. The values of these parameters for Models A and B are summarized in Table 2. The parameters not mentioned in the table are set to zero.

Table 2.
Parameters of models A and B.
It was established that at least four components (slabs) are needed to produce the main peak and the broad polarization without the magnetic field growing beyond a few kG (Model A) (Figure 8). The optimal topology for Model A is A1→A2→A3→A4, meaning that the light travels consequently through each slab. The first component (A1) describes the intense emission in the core of the D3 line. The emissive components A2 and A3 form the broad polarization of the Stokes V profile. The last component A4 with a low emission enhancement factor serves as an absorbing layer which compensates for the contribution of A2 and A3 to the Stokes I profile, while the change in the sign of the magnetic field allows it to preserve the Stokes V polarization. Model A therefore captures a delicate balance between the emission and absorption of different components.
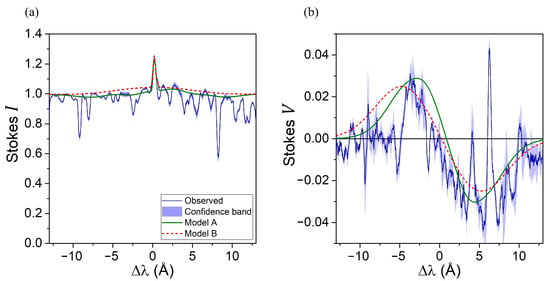
Figure 8.
Comparison between the obtained within models A and B Stokes I (a) and V (b) profiles and the corresponding observed profiles at L = 3–4 Mm.
If the restriction on the values of the magnetic field strength is lifted, the required complexity of the model significantly reduces. Model B is therefore much more straightforward, consisting of three components with an optimal (B1 + B2)→B3 topology. Here, the light passes through the components B1 and B2 that are merged with the filling factors of 0.8 and 0.2, respectively, before passing through B3. The component B1 produces the intense core of the D3 line, the component B2 forms the broad polarization, and the component B3 slightly reduces the contribution of B2 to the Stokes I profile. This model produces similar profiles (Figure 8) and is less sensitive to the exact parameter values compared to Model A.
The two models show how very different physical assumptions can be incorporated to explain the observed profiles. It should be noted that while increasing the number of components quickly leads to a much better model fit, this increase does not necessarily help in determining which model or combination of models should be preferred.
4. Discussion
The obtained data indicate a very complex altitudinal and lateral inhomogeneity of the magnetic field and radial velocities not only in the region of the seismic source of the flare but also beyond it. The altitudinal inhomogeneity of the magnetic field and velocities is well traced by the component with a large filling factor, which corresponds to the intense emission peaks in the D3, D1, and D2 lines, as well as the Fraunhofer absorption profiles of the Ni I 5892.88 Å line (Figure 2 and Figure 3). From these data, a non-trivial situation emerges—a positive height gradient of the magnetic field in the flare, given that the photospheric line Ni I 5892.88 Å shows a smaller measured field than the chromosphere lines D1 and D2, as well as D3 (Figure 4b). It is well known that in sunspots without flares, the altitudinal gradient of the magnetic field is negative [63]. The photospheric magnetic field plays a defining role in the formation and evolution of solar flares. Measurements of the field’s flux within the areas of high photospheric magnetic free energy density can be used as a reliable predictor for the intensity and overall nature of the flare [64]. Nevertheless, several studies have reported that the magnetic field at the upper levels of the atmosphere can be stronger than at the lower level during the solar flares [27,54]. Indeed, in these studies, the question remained open as to whether this is really an increase in the magnetic field intensity module with height, or a result of some complex interplay of multiple parameters. It should be emphasized that the corresponding measurements correspond to the weak-field regime, where the measured Zeeman splitting is much smaller than the spectral half-width (FWHM) of the line. In this case, the results of the measurements probably reflect not only the local and background magnetic field strengths, but also the corresponding filling factors, magnetic polarities, angles of inclination of field lines, etc. Reliable data on the absolute value of the magnetic field strength in the region of solar flares can be obtained only in the strong field regime, when the Zeeman splitting is larger than the half-width of the spectral line. This requires data on spectrally narrow lines that have large Lande factors.
To the best of our knowledge, the first results on this problem were obtained by [65], who used direct spectral-polarization measurements in the Ca I 6102.7 and Fe I 6302.5 lines with Lande factors of 2.0 and 2.5, respectively. While observing the complete Zeeman splitting of these lines in sunspots that were closest to solar flares, these authors found that before the flare emerges, the magnetic field strength at the upper level (indicated by the Ca I 6102.7 Å line) is 100–600 G higher than at the lower level (corresponding to the Fe I 6302.5 Å line). This difference persisted during the flare evolution, and underwent sign reversion in the post-flare phase so that the magnetic field at the upper level became weaker than at the lower one.
It is possible that solar flares are accompanied not only by strong magnetic fields but also by amplified electric fields. The spectral effects of electric fields in a flaring region were evaluated in [66] for the Hα line. As for the investigated flare of 28 October 2003, the electric fields in it can be indicated by the excess polarization at the tops of the emission peaks of the D3 line, and to a lesser extent, the D1 and D2 lines, which is not typical for the Zeeman and Paschen–Back effects (Figure 3 and Figure 6). A similar polarization of one sign was also found far from the intense emission in the D3 line, seemingly within the spectral continuum (Figure 7). This phenomenon likely indicates the Doppler effect with significant velocities along the line of sight, at least +320 km s−1, in the components with small filling factors.
Such high speeds clearly indicate some sort of the rapidly descending transients, which are expected in order for the energy transfer from the reconnection region into the solar interior [13,24]. The rapidly descending features are identified both within (Figure 7a, Å) and outside (Figure 7b, Å) the seismic source. While the speed and amplitude of the transients are marginally higher at the location within the seismic source, the question of whether they are directly associated with the seismic sources remains open. Nevertheless, the polarization imbalance in the spectra of these transients may indicate the manifestation of the Stark effect, which is consistent with the strong electric fields expected when the electron beams precipitate downward towards the photosphere [67].
Additionally, our study revealed a significant detail, namely, that in the background component with a large filling factor, the plasma movement from the level of the transition zone to the photosphere is significantly inhomogeneous. This is indicated by the fact that significantly different Doppler velocities were found using the chromospheric lines D1 and D2 (Figure 5b). It is interesting that this effect is observed with practically identical magnetic fields at the formation levels of not only the indicated lines but also the D3 line (Figure 4b). The detected difference in the Doppler velocities by D1 and D2 lines is also important from a methodological point of view, namely, for testing the possible use of these lines in the “line ratio” method [68] for diagnosing the spatially unresolved structure of the magnetic field in the chromosphere. For the photospheric level, the “line ratio” method was successfully applied by comparing the measurements in 2–3 specially selected Fe I photospheric lines—belonging to the same multiplet with almost identical excitation potentials of the lower term and oscillator strengths but significantly different Lande factors [52,68,69,70]. It was by this method that it was established for the first time that magnetic fields in quiet regions on the sun reach kilogauss values (1–2 kG), being localized within very thin spatially unresolvable magnetic tubes called fluxtubes. This conclusion is obtained on the basis of modeling in the framework of two-component models, assuming that the heights of the formations of the corresponding 2–3 suitable lines are the same. Another obstacle to the very attractive task of using these lines to diagnose the sub-telescopic structure of the magnetic field in the chromosphere is that their Lande factors actually differ little due to the Paschen–Back effect—only by ≈12% (see Table 1). If their Lande factors corresponded to the ones obtained within the LS coupling scheme, then they would differ by a factor of 1.78, which would be quite valuable in the “line ratio” method.
For the D1 and D2 lines, the assumption of matching formation heights, as indicated above, cannot be applied. In fact, the heights of the formation of these lines are so different in the investigated flare that the corresponding Doppler velocities differ by up to 2.5 km s−1 (Figure 5b). This difference in the plasma velocities inevitably leads to significant disturbances in the local plasma density. The latter, considered together with the increased values of the magnetic field (Figure 4b) and the saturated shape of the D3 line, characteristic of high optical density (Figure 3a), possibly indicates the collapse of the magnetic field and matter. The magnetic collapse, along with the increased magnitude of ≈1 kG in magnitude near the seismic source (Figure 4a), inevitably impacts various phenomena that are sensitive to the magnetic configuration of the solar atmosphere. Due to the proximity of the seismic source (Figure 1), the energy transfer and acoustic source excitation mechanism relying on the Lorentz forces [18,20] is likely to be amplified. Indeed, the increased chromospheric magnetic fields directly increase the Lorentz forces in the chromosphere, and, consequently, facilitate the transport of the magnetic energy toward the photosphere and the solar interior. Moreover, the magnetic collapse can serve as a perturbation that under certain conditions can contribute to triggering the rapid magnetic reconfiguration—the McClymont jerk [19].
Since the Doppler velocities of the component with a large filling factor (which gives strong emission manifestations) and of the components with small filling factors (which give weak secondary peaks far outside the main emission) differ by 1–2 orders of magnitude (2–11 km s−1 versus 320 km s−1), then it is a natural to assume that the local magnetic fields in these components can also differ significantly. Indeed, from a comparison of the distribution of magnetic fields and velocities in line D3 in Figure 4b and Figure 5b, the following general trend can be seen: the higher the speeds, the stronger the magnetic fields.
This assumption is confirmed by the highly averaged profile of the V parameter in the wavelength range of −5 Å to +10 Å (Figure 7b). The main effect is quite clearly visible: the change in the sign of the parameter V when passing through the center of the D3 line, which is characteristic of Zeeman and Paschen–Back effects. A similar effect was previously detected by [32,33] in the Hα and D3 lines in limb solar flares. Based on the significant splitting of the secondary peaks of the V parameter found in these works, corresponding to the Zeeman splitting of 2 to 3.6 Å, a conclusion was made about the possible existence of ultra-strong magnetic fields in the 105 G range.
Regarding the studied flare on 28 October 2003, the high splitting of almost 10 Å observed in the Stokes V profiles can potentially correspond to magnetic fields of similar magnitude (see Section 3.5, Model B). It should be noted that the complexity of the observed spectra necessitates the introduction of multi-component atmospheric models to reproduce only the most general trends. The increased number of fitted parameters significantly complicates the inversion problem, leading to substantial ambiguity (Figure 8). As a result, this complexity makes it impossible to definitively choose the preferred model without relying on some additional criteria in the future.
5. Conclusions
In the investigated solar flare on 28 October 2003, a significant height inhomogeneity of the magnetic field and Doppler velocities was found by the D3, D1, D2 and Ni I 5892.88 Å lines, which are formed in the height range of about 2 Mm—from the photosphere to the transition zone between the chromosphere and the corona. Over an interval of almost 27 Mm along the entrance slit of the spectrograph, the magnetic field in the photosphere (Ni I 5892.88 Å line) was weaker than in the chromosphere and the transition zone, which may indicate a local strengthening of the magnetic field in the flare region. This strengthening of the magnetic field (up to 1.6 kG) was possibly accompanied by a significant increase in the plasma concentration (its ‘collapse’) as can be seen by the characteristic signatures of a large optical depth in the D3 line (very intense emission with a flat saturated peak) and the significant difference in the Doppler velocities in the D1 and D2 lines. Such strengthening of the magnetic field likely amplifies the Lorentz force-based mechanism of the seismic source excitation. The Doppler shift of the emission in the D3 line indicates the descent of the plasma in the flare region with velocities in the range of 5–11 km s−1, which are significantly larger in absolute value than the ones in the chromosphere and photosphere. The specified features relate to the spatial component with a large filling factor; however, in the same flare, there was another component with a small filling factor as evidenced by the presence of weaker (up to 4%) emission peaks in the distance range from −5 to +10 Å relative to D3. The specific features of these peaks may indicate (a) significantly higher plasma descent velocities in the component with a small filling factor, at least up to +320 km s−1, (b) significantly stronger magnetic fields, and (c) non-Zeeman polarization, possibly due to strong electric fields. The latter feature is most significant in the area of the seismic source of the solar flare.
Author Contributions
Conceptualization, N.I.L. and V.G.L.; methodology, I.I.Y., N.I.L. and V.G.L.; software, I.I.Y.; formal analysis, I.I.Y., N.I.L. and V.G.L.; investigation, I.I.Y., N.I.L. and V.G.L.; data curation, I.I.Y., N.I.L. and V.G.L.; writing—original draft preparation, V.G.L.; writing—review and editing, I.I.Y., N.I.L. and V.G.L.; supervision, V.G.L.; project administration, V.G.L.; funding acquisition, V.G.L. All authors have read and agreed to the published version of the manuscript.
Funding
This study was funded by Ministry of Education and Science of Ukraine (Kyiv, UA), project No. 22 BF023-03.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Acknowledgments
SOHO is a project of international cooperation between ESA and NASA.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Lozitska, N.; Yakovkin, I.; Lozitsky, V. Unique spectral manifestations around the D3 line observed in the region close to the seismic source of a large solar flare. Mon. Not. R. Astron. Soc. Lett. 2024, 528, L1–L3. [Google Scholar] [CrossRef]
- Laba, I. Solar proton flare 4B/X17. 2 on 28 October 2003. Photometric results. Kinemat. Phys. Celest. Bodies 2007, 23, 36–40. [Google Scholar] [CrossRef]
- Kosovichev, A. Properties of flares-generated seismic waves on the Sun. Sol. Phys. 2006, 238, 1–11. [Google Scholar] [CrossRef]
- Zharkova, V.V.; Zharkov, S.I. On the origin of three seismic sources in the proton-rich flare of 28 October 2003. Astrophys. J. 2007, 664, 573. [Google Scholar] [CrossRef]
- Hurford, G.; Krucker, S.; Lin, R.; Schwartz, R.; Share, G.; Smith, D. Gamma-ray imaging of the 2003 October/November solar flares. Astrophys. J. 2006, 644, L93. [Google Scholar] [CrossRef]
- Kosovichev, A. The cause of photospheric and helioseismic responses to solar flares: High-energy electrons or protons? Astrophys. J. 2007, 670, L65. [Google Scholar] [CrossRef]
- Kosovichev, A.G. Sunquakes: Helioseismic response to solar flares. arXiv 2014, arXiv:1402.1249. [Google Scholar]
- Zharkova, V.; Zharkov, S.; Druett, M.; Matthews, S.; Inoue, S. Sunquake with a second bounce, other sunquakes, and emission associated with the X9. 3 flare of 6 September 2017-II. Proposed interpretation. Astron. Astrophys. 2020, 639, A79. [Google Scholar] [CrossRef]
- Zharkov, S.; Matthews, S.; Zharkova, V.; Druett, M.; Inoue, S.; Dammasch, I.E.; Macrae, C. Sunquake with a second bounce, other sunquakes, and emission associated with the X9. 3 flare of 6 September 2017-I. Observations. Astron. Astrophys. 2020, 639, A78. [Google Scholar] [CrossRef]
- Lindsey, C.; Donea, A.C. Mechanics of seismic emission from solar flares. In Helioseismology, Asteroseismology, and MHD Connections; Springer: New York, NY, USA, 2008; pp. 625–637. [Google Scholar]
- Martínez-Oliveros, J.C.; Donea, A.C. Magnetic field variations and seismicity of solar active regions. Mon. Not. R. Astron. Soc. Lett. 2009, 395, L39–L42. [Google Scholar] [CrossRef]
- Zharkova, V.V.; Gordovskyy, M. Energy spectra of particles accelerated in a reconnecting current sheet with the guiding magnetic field. Mon. Not. R. Astron. Soc. 2005, 356, 1107–1116. [Google Scholar] [CrossRef]
- Donea, A.C.; Lindsey, C. Seismic emission from the solar flares of 28 and 29 October 2003. Astrophys. J. 2005, 630, 1168. [Google Scholar] [CrossRef]
- Kosovichev, A.; Zharkova, V. X-ray flare sparks quake inside Sun. Nature 1998, 393, 317–318. [Google Scholar] [CrossRef]
- Ding, M.; Fang, C. On the propagation of chromospheric condensations in solar flares (I) Dynamic Simulations. Astrophys. Space Sci. 1994, 213, 233–246. [Google Scholar] [CrossRef]
- Donea, A.C.; Besliu-Ionescu, D.; Cally, P.S.; Lindsey, C.; Zharkova, V. Seismic emission from a M9. 5-class solar flare. Sol. Phys. 2006, 239, 113–135. [Google Scholar] [CrossRef]
- Moradi, H.; Donea, A.C.; Lindsey, C.; Besliu-Ionescu, D.; Cally, P.S. Helioseismic analysis of the solar flare-induced sunquake of 2005 January 15. Mon. Not. R. Astron. Soc. 2007, 374, 1155–1163. [Google Scholar] [CrossRef]
- Hudson, H.; Fisher, G.; Welsch, B. Flare energy and magnetic field variations. Subsurf. Atmos. Influ. Sol. Act. 2008, 383, 221. [Google Scholar]
- Anwar, B.; Acton, L.; Hudson, H.; Makita, M.; McClymont, A.; Tsuneta, S. Rapid sunspot motion during a major solar flare. Sol. Phys. 1993, 147, 287–303. [Google Scholar] [CrossRef]
- Fisher, G.H.; Bercik, D.J.; Welsch, B.T.; Hudson, H.S. Global forces in eruptive solar flares: The Lorentz force acting on the solar atmosphere and the solar interior. Sol. Phys. 2012, 277, 59–76. [Google Scholar] [CrossRef]
- Kiener, J.; Gros, M.; Tatischeff, V.; Weidenspointner, G. Properties of the energetic particle distributions during the 28 October 2003 solar flare from INTEGRAL/SPI observations. Astron. Astrophys. 2006, 445, 725–733. [Google Scholar] [CrossRef]
- Mandrini, C.H.; Démoulin, P.; Schmieder, B.; Deluca, E.; Pariat, E.; Uddin, W. Companion event and precursor of the X17 flare on 28 October 2003. Sol. Phys. 2006, 238, 293–312. [Google Scholar] [CrossRef]
- Maurya, R.A.; Ambastha, A. Magnetic and velocity field variations in the active regions NOAA 10486 and NOAA 10488. J. Astrophys. Astron. 2008, 29, 103–105. [Google Scholar] [CrossRef]
- Maurya, R.; Ambastha, A. Transient magnetic and doppler features related to the white-light flares in NOAA 10486. Sol. Phys. 2009, 258, 31–52. [Google Scholar] [CrossRef]
- Lozitsky, V. Magnetic fields and Fe I line profiles in the major solar flare on 28 October 2003. Astron. Lett. 2009, 35, 136–142. [Google Scholar] [CrossRef]
- Lozitsky, V.; Baranovsky, E.; Lozitska, N.; Tarashchuk, V. Profiles of spectral lines, magnetic fields, and thermodynamical conditions in the X17. 2/4B solar flare of 2003 October 28. Mon. Not. R. Astron. Soc. 2018, 477, 2796–2803. [Google Scholar] [CrossRef]
- Harvey, J. Chromospheric magnetic field measurements in a flare and an active region filament. Sol. Phys. 2012, 280, 69–81. [Google Scholar] [CrossRef]
- Wei, Y.; Chen, B.; Yu, S.; Wang, H.; Jing, J.; Gary, D.E. Coronal magnetic field measurements along a partially erupting filament in a solar flare. Astrophys. J. 2021, 923, 213. [Google Scholar] [CrossRef]
- Kleint, L. First detection of chromospheric magnetic field changes during an X1-flare. Astrophys. J. 2016, 834, 26. [Google Scholar] [CrossRef]
- Libbrecht, T.; de la Cruz Rodríguez, J.; Danilovic, S.; Leenaarts, J.; Pazira, H. Chromospheric condensations and magnetic field in a C3. 6-class flare studied via He I D3 spectro-polarimetry. Astron. Astrophys. 2019, 621, A35. [Google Scholar] [CrossRef]
- Yakovkin, I.; Veronig, A.; Lozitsky, V. Magnetic field measurements in a limb solar flare by hydrogen, helium and ionized calcium lines. Adv. Space Res. 2021, 68, 1507–1518. [Google Scholar] [CrossRef]
- Yakovkin, I.; Lozitsky, V. Signatures of superstrong magnetic fields in a limb solar flare from observations of the Hα line. Adv. Space Res. 2022, 69, 4408–4418. [Google Scholar] [CrossRef]
- Yakovkin, I.; Lozitsky, V. Search for superstrong magnetic fields in active processes on the Sun using spectro-polarimetry within 15 angstroms around the D3 line. Mon. Not. R. Astron. Soc. 2023, 523, 5812–5822. [Google Scholar] [CrossRef]
- Livingston, W.; Harvey, J.; Malanushenko, O.; Webster, L. Sunspots with the strongest magnetic fields. Sol. Phys. 2006, 239, 41–68. [Google Scholar] [CrossRef]
- van Noort, M.; Lagg, A.; Tiwari, S.; Solanki, S. Peripheral downflows in sunspot penumbrae. Astron. Astrophys. 2013, 557, A24. [Google Scholar] [CrossRef]
- Lozitsky, V. Indications of 8-kilogauss magnetic field existence in the sunspot umbra. Adv. Space Res. 2016, 57, 398–407. [Google Scholar] [CrossRef]
- Durán, J.C.; Lagg, A.; Solanki, S.K.; Van Noort, M. Detection of the strongest magnetic field in a sunspot light bridge. Astrophys. J. 2020, 895, 129. [Google Scholar] [CrossRef]
- Lozitsky, V.; Yurchyshyn, V.; Ahn, K.; Wang, H. Observations of Extremely Strong Magnetic Fields in Active Region NOAA 12673 Using GST Magnetic Field Measurement. Astrophys. J. 2022, 928, 41. [Google Scholar] [CrossRef]
- Brooks, D.H.; Warren, H.P.; Landi, E. Measurements of coronal magnetic field strengths in solar active region loops. Astrophys. J. Lett. 2021, 915, L24. [Google Scholar] [CrossRef]
- Zhu, R.; Tan, B.; Su, Y.; Tian, H.; Xu, Y.; Chen, X.; Song, Y.; Tan, G. Microwave diagnostics of magnetic field strengths in solar flaring loops. Sci. China Technol. Sci. 2021, 64, 169–178. [Google Scholar] [CrossRef]
- Landi, E.; Li, W.; Brage, T.; Hutton, R. Hinode/EIS coronal magnetic field measurements at the onset of a C2 flare. Astrophys. J. 2021, 913, 1. [Google Scholar] [CrossRef]
- Liu, Y.; Welsch, B.T.; Valori, G.; Georgoulis, M.K.; Guo, Y.; Pariat, E.; Park, S.H.; Thalmann, J.K. Changes of magnetic energy and helicity in solar active regions from major flares. Astrophys. J. 2023, 942, 27. [Google Scholar] [CrossRef]
- Fleishman, G.D.; Gary, D.E.; Chen, B.; Kuroda, N.; Yu, S.; Nita, G.M. Decay of the coronal magnetic field can release sufficient energy to power a solar flare. Science 2020, 367, 278–280. [Google Scholar] [CrossRef] [PubMed]
- Judge, P.; Rempel, M.; Ezzeddine, R.; Kleint, L.; Egeland, R.; Berdyugina, S.V.; Berger, T.; Bryans, P.; Burkepile, J.; Centeno, R.; et al. Measuring the Magnetic Origins of Solar Flares, Coronal Mass Ejections, and Space Weather. Astrophys. J. 2021, 917, 27. [Google Scholar] [CrossRef]
- Moore, C.E.; Minnaert, M.G.J.; Houtgast, J. The Solar Spectrum 2935 Å to 8770 Å: Second Revision of Rowland’s Preliminary Table of Solar Spectrum Wavelengths; National Bureau of Standards: Gaithersburg, MD, USA, 1966; Volume 61.
- Drake, G. High precision calculations for helium. In Springer Handbook of Atomic; Springer: New York, NY, USA, 2006; p. 199. [Google Scholar]
- Ryabchikova, T.; Piskunov, N.; Kurucz, R.; Stempels, H.; Heiter, U.; Pakhomov, Y.; Barklem, P.S. A major upgrade of the VALD database. Phys. Scr. 2015, 90, 054005. [Google Scholar] [CrossRef]
- Banasek, J.; Engelbrecht, J.; Pikuz, S.; Shelkovenko, T.; Hammer, D. Measuring 10-20 T magnetic fields in single wire explosions using Zeeman splitting. Rev. Sci. Instrum. 2016, 87, 103506. [Google Scholar] [CrossRef]
- Hori, H.; Miki, M.; Date, M. Paschen-back effect of D-lines in sodium under a high magnetic field. J. Phys. Soc. Jpn. 1982, 51, 1566–1570. [Google Scholar] [CrossRef]
- Momier, R.; Papoyan, A.V.; Leroy, C. Sub-Doppler spectra of sodium D lines in a wide range of magnetic field: Theoretical study. J. Quant. Spectrosc. Radiat. Transf. 2021, 272, 107780. [Google Scholar] [CrossRef]
- Ramos, A.A.; Bueno, J.T.; Degl’Innocenti, E.L. Advanced forward modeling and inversion of stokes profiles resulting from the joint action of the Hanle and Zeeman effects. Astrophys. J. 2008, 683, 542. [Google Scholar] [CrossRef]
- Rachkovsky, D.; Tsap, T.; Lozitsky, V. Small-scale magnetic field diagnostics outside sunspots: Comparison of different methods. J. Astrophys. Astron. 2005, 26, 435–445. [Google Scholar] [CrossRef]
- Babcock, H.W. The Solar Magnetograph. Astrophys. J. 1953, 118, 387. [Google Scholar] [CrossRef]
- Lozitskaia, N.; Lozitskii, V.; Solov’ev, A. Strong magnetic fields in solar flares: Observation data and theoretical model. Kinemat. I Fiz. Nebesnykh Tel 1991, 7, 40–47. [Google Scholar]
- Juncar, P.; Pinard, J.; Hamon, J.; Chartier, A. Absolute determination of the wavelengths of the sodium D1 and D2 lines by using a cw tunable dye laser stabilized on iodine. Metrologia 1981, 17, 77. [Google Scholar] [CrossRef]
- Striganov, A.R.; Sventitskii, N.S. Tables of Spectral Lines of Neutral and Ionized Atoms; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Unno, W. Line formation of a normal Zeeman triplet. Publ. Astron. Soc. Jpn. 1956, 8, 108. [Google Scholar]
- Jäger, F. Instrumental polarization concerning magnetographic measurements. Sol. Phys. 1972, 27, 481–488. [Google Scholar] [CrossRef]
- Jäger, F. Instrumental polarization concerning magnetographic measurements, II. Sol. Phys. 1974, 39, 499–504. [Google Scholar] [CrossRef]
- Grigor’ev, V.; Golovko, A. A study of the instrumental phase polarization of the horizontal solar telescope. Byulletin Solnechnye Dannye Akad. Nauk. SSSR 1975, 1975, 78–85. [Google Scholar]
- Frish, S. Optical Atom Spectra; Lan’: St. Peterburg, Russia, 2010; p. 656. [Google Scholar]
- Degl’Innocenti, M.L.; Landolfi, M. Polarization in Spectral Lines; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2006; Volume 307. [Google Scholar]
- Solanki, S.K. Sunspots: An overview. Astron. Astrophys. Rev. 2003, 11, 153–286. [Google Scholar] [CrossRef]
- Li, T.; Zheng, Y.; Li, X.; Hou, Y.; Li, X.; Zhang, Y.; Chen, A. Survey of Magnetic Field Parameters Associated with Large Solar Flares. arXiv 2024, arXiv:2402.18890. [Google Scholar] [CrossRef]
- Koval, A.; Stepanyan, N.; Stepanjan, N. Variations of magnetic fields of sunspots at two levels in connection with the development of active regions. Byulletin Solnechnye Dannye Akad. Nauk SSSR 1972, 1972, 83–91. [Google Scholar]
- Chen, B.; Shen, C.; Gary, D.E.; Reeves, K.K.; Fleishman, G.D.; Yu, S.; Guo, F.; Krucker, S.; Lin, J.; Nita, G.M.; et al. Measurement of magnetic field and relativistic electrons along a solar flare current sheet. Nat. Astron. 2020, 4, 1140–1147. [Google Scholar] [CrossRef]
- Zharkova, V.V.; Gordovskyy, M. The effect of the electric field induced by precipitating electron beams on hard X-ray photon and mean electron spectra. Astrophys. J. 2006, 651, 553. [Google Scholar] [CrossRef]
- Stenflo, J. Magnetic-field structure of the photospheric network. Sol. Phys. 1973, 32, 41–63. [Google Scholar] [CrossRef]
- Stenflo, J. Small-scale magnetic structures on the Sun. Astron. Astrophys. Rev. 1989, 1, 3–48. [Google Scholar] [CrossRef]
- Cerdeña, I.D.; Almeida, J.S.; Kneer, F. Inter-network magnetic fields observed with sub-arcsec resolution. Astron. Astrophys. 2003, 407, 741–757. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).