Abstract
Every numerical general relativistic investigation starts from the solution of the initial value equations at a given time. Astrophysically relevant initial values for different systems lead to distinct sets of equations that obey specific assumptions tied to the particular problem. Therefore, a robust and efficient solver for a variety of strongly gravitating sources is needed. In this work, we present the OpenMP version of the Compact Object CALculator (COCAL) on shared memory processors. We performed extensive profiling of the core COCAL modules in order to identify bottlenecks in efficiency, which we addressed. Using modest resources, the new parallel code achieves speedups of approximately one order of magnitude relative to the original serial COCAL code, which is crucial for parameter studies of computationally expensive systems such as magnetized neutron stars, as well as its further development towards more realistic scenarios. As a novel example of our new code, we compute a binary quark system where each companion has a dimensionless spin of aligned with the orbital angular momentum.
1. Introduction
Gravitational wave astronomy was launched in 2015 with the first-ever gravitational wave detection of the inspiral and merger from a binary black hole system, as reported by the LIGO scientific collaboration—event GW150914 [1]. Two years later, the simultaneous detection of gravitational waves from an inspiraling binary neutron star system, event GW170817, and its postmerger emission of electromagnetic radiation spurred the era of multimessenger astronomy [2,3,4,5,6]. Merging binary neutron stars and black hole–neutron stars are not only important sources of gravitational radiation, but also promising candidates for coincident electromagnetic counterparts, which could give new insight into their sources. To understand these observations and, in particular, to understand the physics of matter under extreme conditions, it is crucial to compare them with predictions from theoretical modeling which, due to the complexity of the underlying physical phenomena, are largely numerical in nature.
Numerical modeling of strongly gravitating systems typically involves two steps: first, the ab initio calculation of the initial values that describe the astrophysical system at a given time; and second, the evolution of these initial data in order to describe it at later times. These two general relativistic calculations involve two distinct codes: one that solves the elliptic problem to find out the initial data and another that solves the hyperbolic one that simulates their evolution. For these reasons, we have developed the Compact Object CALculator (COCAL) code, which is a serial code that solves for any compact object in equilibrium or quasiequilibrim in a variety of settings and/or mathematical formulations. In particular, COCAL has been used to calculate: (i) rotating neutron stars and quark stars (axisymmetric or triaxial, uniformly or differentially rotating) [7,8,9,10,11,12]; (ii) binary black holes in quasicircular orbits [13,14,15]; (iii) binary neutron stars and quark stars (irrotational or spinning) in quasicircular orbits [16,17]; (iv) magnetized rotating neutron stars with generic mixed poloidal and toroidal magnetic fields and a magnetosphere [18,19,20]; and (v) self-gravitating, tilted black hole-disks (where the angular momentum of the disk is tilted with respect to the angular momentum of the black hole) [21]. The main characteristics of the COCAL code is the use of finite differences and a Green’s function approach, as first developed in [22] for neutron stars and in [23] for black holes, to achieve a convergent solution through a Picard type of iteration, known as the Komatsu–Eriguchi–Hachisu (KEH) method [24,25]. The field equations are solved in spherical coordinates in multiple patches, and a smooth solution is obtained everywhere through boundary surface integrals. For the fluid equations, surface-fitted coordinates are being implemented that allow for an accurate representation of the neutron star surface, which is important in order to impose boundary conditions.
Similar to COCAL, there are a number of other codes whose purposes are to solve for initial data in general relativity. For binary as well as single compact object codes, these include the TwoPunctures [26], LORENE [27], KADATH/FUKA [28,29,30], SGRID [31], Spells [32], Elliptica [33], and NRPyElliptic [34] codes. Each code uses its own numerical methods, and depending on the problem, it may use different mathematical formulations too.
Compact systems (i)–(v) employ different mathematical formulations that nevertheless share common characteristics. For example, one well-known method for the calculation of initial data [35] is the Isenberg–Wilson–Mathews (IWM) [36,37,38,39] formulation, where the spatial three-dimensional metric is assumed to be conformally flat and the trace of the extrinsic curvature is zero. This method is applied from rotating neutron/quark stars [7,11] to binary black holes [13,14,15] and binary neutron stars [16,17] and results in five elliptic equations, i.e., a truncated system of the Einstein field equations. Notwithstanding the approximate nature of the method, its robustness and accuracy (especially for neutron stars) make the IWM method a workhorse in initial data construction. On the other hand, more intricate methods have been developed that can treat the full Einstein system, both for neutron stars and black holes. In [8], rotating axisymmetric or triaxial neutron stars were computed using the waveless method [40,41], while in [18,19,20], this method was employed to calculate generic magnetized equilibria with mixed poloidal and toroidal magnetic fields as well as a force-free magnetosphere. In [42,43], the same method was used to compute binary neutron stars in quasicircular orbits. This method is referred to as the “waveless” formulation. For spacetimes that contain a black hole, a new method has been developed in [21] that solves the complete initial data equations. Contrary to the IWM method, the formulations that try to address the whole Einstein system [21,40] result to a significantly larger number of elliptic equations. For neutron star spacetimes [40], we have fourteen nonlinear Poisson-like equations, with four of them resulting from imposing gauge conditions. For black hole spacetimes, we have a total of seventeen equations, with four of them resulting from imposing gauge conditions and another three being used for an additional decomposition of the extrinsic curvature [21]. The inclusion of magnetohydrodynamics will increase the total number of elliptic equations to be solved even more. Therefore, it is evident that in order to be able to study these astrophysically realistic systems in a systematic manner, an efficient parallelization scheme for the COCAL code needs to be developed.
In this paper, we present the OpenMP version of the COCAL code, which we call the Parallel Compact Object CALculator or PCOCAL for short. For the first time, we have systematically analyzed the whole serial COCAL code and identified the bottlenecks both for single objects (e.g., rotating neutron stars) as well as for binaries (e.g., binary neutron stars) using either the IWM or the waveless formulation. In order to implement the OpenMP directives for parallelization, we had to revise and sometimes completely rewrite many of the original subroutines. Using modest resources of 30–40 cores, both the single rotating neutron star module as well as the binary neutron star one achieve a speedup of an order of magnitude. In the binary case, we observed a smaller speedup than in the single star case, mainly due to the communication between different coordinate systems, which is absent in the latter calculation. As an application of our new code, we computed for the first time a spinning binary quark star system where each companion has a dimensionless spin of aligned with the orbital angular momentum.
In the equations presented, Greek indices are taken to run from 0 to 3 while Latin indices run from 1 to 3. We use a signature for the spacetime line element and a system of units in which (unless explicitly shown).
2. The Initial Value Equations
In this section, we summarize the 3 + 1 decomposition of Einstein’s equations for two representative problems that will be discussed below: (i) single rotating neutron stars in the waveless formalism [8,40] and (ii) spinning binary neutron stars in the IWM formalism [16,17]. While details on these methods can be found in the aforementioned papers, here we provide a broad overview of the equations that need to be solved in order to discuss the time footprint of each one in the iteration procedure, the possible bottlenecks with the parallelization, and the optimizations we perform.
We assume that a spacetime is foliated by a family of space-like hypersurfaces , parametrized by a time coordinate as . The future-pointing unit normal one form to , , is related to the generator of time translations as
where . Here, and are, respectively, the lapse function and the shift vector, which is spatial, . The projection tensor to is introduced as . The induced spatial metric on is the projection tensor restricted to it. By introducing a conformal spatial geometry with spatial metric , where is the conformal factor, we can write the line element on a chart of as
The conformal rescaling is determined from a condition , where and f are determinants of the rescaled spatial metric and the flat metric , respectively. We denote by and the differences between the conformal and flat metric
The extrinsic curvature of each slice is defined by
where is the Lie derivative along the normal vector on . Hereafter, we denote the trace of by K and the trace-free part of by . We define the conformal extrinsic curvature , similar to the conformal spatial metric.
In this paper, we consider perfect fluid spacetimes, whose stress–energy tensor is written as
where is the energy density and p is the pressure as measured by the co-moving observer, i.e., an observer with 4-velocity . As discussed in [18,19], in the case where we have magnetized neutron stars and total stress–energy tensor in addition to the perfect fluid contribution, Equation (5) will include the contribution of the magnetic field. We decompose the Einstein’s equations along the hypersurface as well as along its normal as follows,
which correspond, respectively, to the Hamiltonian constraint, momentum constraint, spatial trace part (combined with the Hamiltonian constraint), and spatial trace-free part.
As shown in [40], the above set of field Equations (6)–(9) are reduced to elliptic (Poisson) equations for , respectively, as follows,
where is the flat metric (in arbitrary coordinates) Laplacian, defined by . The sources , , , and [21] depend nonlinearly on the unknown potentials and are written in Appendix A. In the COCAL code, we use the Cartesian components of the elliptic Equations (10)–(13), on spherical grids (see Section 3). Equations (10)–(13) must be supplied with conditions on the boundary of our computational region. Because we will only consider isolated single or binary stars, the boundary conditions for the gravitational equations will only be at spatial infinity, where we impose asymptotic flatness, i.e.,
In case a black hole is present, COCAL uses excision, and boundary conditions are applied on the excised surface (typically a sphere). Depending on the method, we have employed Robin–Dirichlet, apparent horizon [13,14,23], or simply Kerr–Schild [21] boundary conditions.
2.1. Rotating Neutron Star in the Waveless Formalism
Coordinate gauge conditions such as the maximal slicing and generalized Dirac gauge
are assumed for rotating neutron stars. As described in Appendix A, . These conditions simplify Equations (A1)–(A4) significantly. In particular, . The asymptotic behavior of the metric potentials becomes a Coulomb-type fall-off,
Our choice of is the shift in an (asymptotically) inertial frame.
The Bianchi identity implies . Under the assumption of rest mass conservation and an isentropic law , it leads to the relativistic Euler equation
is the relativistic vorticity and the relativistic specific enthalpy. We consider two cases of single rotating stars, both of which are described by a 4-velocity
Here, is the helical symmetry vector, is the constant angular velocity of the star, and is the generator of rotational symmetry. For uniformly rotating stars, it is .
2.1.1. Axisymmetric Rotating Neutron Stars
For stationary and axisymmetric systems, we impose time symmetry on both the three dimensional metric as well as the extrinsic curvature
Note that we do not explicitly impose the axisymmetry on our formulation. Under these asumptions, in Equation (A2) and for Equation (A4). Note that the last terms involve second order derivatives of the shift vector .
The stationarity condition for the fluid variables
reduce the Euler Equation (19) to the simple algebraic equation
where C is a constant to be determined. Note that is computed by the normalization condition . In this work, we also assume that neutron stars are “cold”, i.e., they can be described by a zero-temperature equation of state (EOS),
or, equivalently, . This kind of one-parameter EOS is called barotropic. Equations (10)–(13) under gauge conditions (15) and (16) and Equation (23) determine all gravitational and fluid variables.
2.1.2. Triaxial Rotating Neutron Stars
For nonaxisymmetric rotating neutron stars, we impose time symmetry on the three metric but helical symmetry (stationarity in the rotating frame) on the extrinsic curvature
2.2. Binary Neutron Stars in the IWM Formalism
Binary neutron stars are computed within the IWM formalism, where
which means that Equation (13) is absent, while in Equations (10)–(12), the magenta terms in the sources (A1)–(A3) are zero. The spacetime helical symmetry
implies that Equation (A10) can be written as
where the corotating shift.
The 4-velocity of the fluid here can be written as
where is the fluid velocity in the corotating frame and the helical Killing vector refers to a binary system having orbital angular velocity . For irrotational binaries [44,45,46,47], we have , so the specific enthalpy current can be derived from a potential . In order to allow for arbitrary spinning binary configurations, a 3-vector is introduced according to [48]
where the part corresponds to the “irrotational part” of the flow and the “spinning part” of the flow. Equations (30) and (31) yield
For arbitrary spinning binaries under the assumptions of helical symmetry
and the additional assumption for the spin of the neutron star
yields
where C is a constant to be determined.
The conservation of rest mass and Equation (32) for the fluid velocity will produce an extra elliptic equation for the fluid potential
Note that because , the conformal geometry is flat and therefore . The boundary for the fluid is represented by the surface of the star; hence, the boundary condition for Equation (36) will be of the von Neumann type, that is, in terms of derivatives of the rest mass density and of
3. Numerical Methods
All elliptic equations are solved using the representation theorem of partial differential equations through a Picard type of iteration. Starting from
where S is a nonlinear function of f (here, f can be any of and S any combination of them), and by using an appropriate Green’s function
that satisfies certain boundary conditions, a solution for f can be written as
where V is the domain of integration, , the initial space-like hypersurface. The volume V and its boundary depend on the coordinate system used and are different for isolated rotating neutron stars and binary neutron stars. We will explain this difference in the next sections. This method is widely known as the KEH method [24,25].
For the evaluation of the integrals in Equation (40), a multipole expansion of in associated Legendre functions, , on spherical coordinates is used;
where the radial Green’s function depends on boundary conditions and the coefficients are and for . In practice, the sum over ℓ is truncated at . The standard value used for single rotating stars as well as binaries is . On the other hand, highly rotating black holes and magnetized neutron stars require a larger .
3.1. Single Rotating Neutron Star
For a single rotating neutron star, the only elliptic equations to be solved are the gravitational Equations (10)–(13). We employ a single spherical coordinate system that covers the region , where and , with M being the total mass of the system. The boundary conditions (14) are applied at . Coordinate grids with , , and , are freely specifiable except for the points at the boundary of the computational domain. The grid setup is the same as in [8]: the radial grid intervals are constant when , which typically extends up to ∼, where is the equatorial radius of the star, and increase thereafter in a geometric progression with . Here, k is a constant, and . For the angular coordinate grids , we choose equally spaced grids. Definitions of the parameters for the grid setups are listed in Table 1.

Table 1.
Summary of parameters used for single rotating star configurations. denotes the neutron star surface.
When applying Equation (40), we use the Green’s function . For the quadratures, a 2nd order midpoint rule is used in r and integrations, and a 4th order midpoint rule is used for integration. We also use a 2nd order finite difference formula for the r, , and derivatives evaluated at the midpoints , except for a 3rd order finite difference formula used in the first radial derivative evaluated at the midpoints. For derivatives at the grid points , a 4th order finite difference formula is used. We found [13,15] that these choices are necessary in order to maintain an overall second-order accuracy for the COCAL code and a small error near the possible black hole excised surface [15]. Note that we use the midpoint rule for numerical quadrature formula and hence compute the source terms, Equation (A1)–(A4), at the midpoints of the grids.
A relaxation parameter is used when updating a newly computed variable . If is the value at the n-th iteration, and the current result of the Poisson solver, Equation (40), then the -th iteration value will be
where . Usually, for all variables except for , where . The criterion used by the cocal to stop the iteration for a variable f is based on the relative error between two successive iterations and is given by
for all points of the grids and all variables. The coupled elliptic Equations (10)–(13) are solved sequentially (starting from , followed by , , and finally the ) at every iteration, and Equation (42) is applied separately to each potential before moving to the next elliptic equation.
3.2. Binary Systems
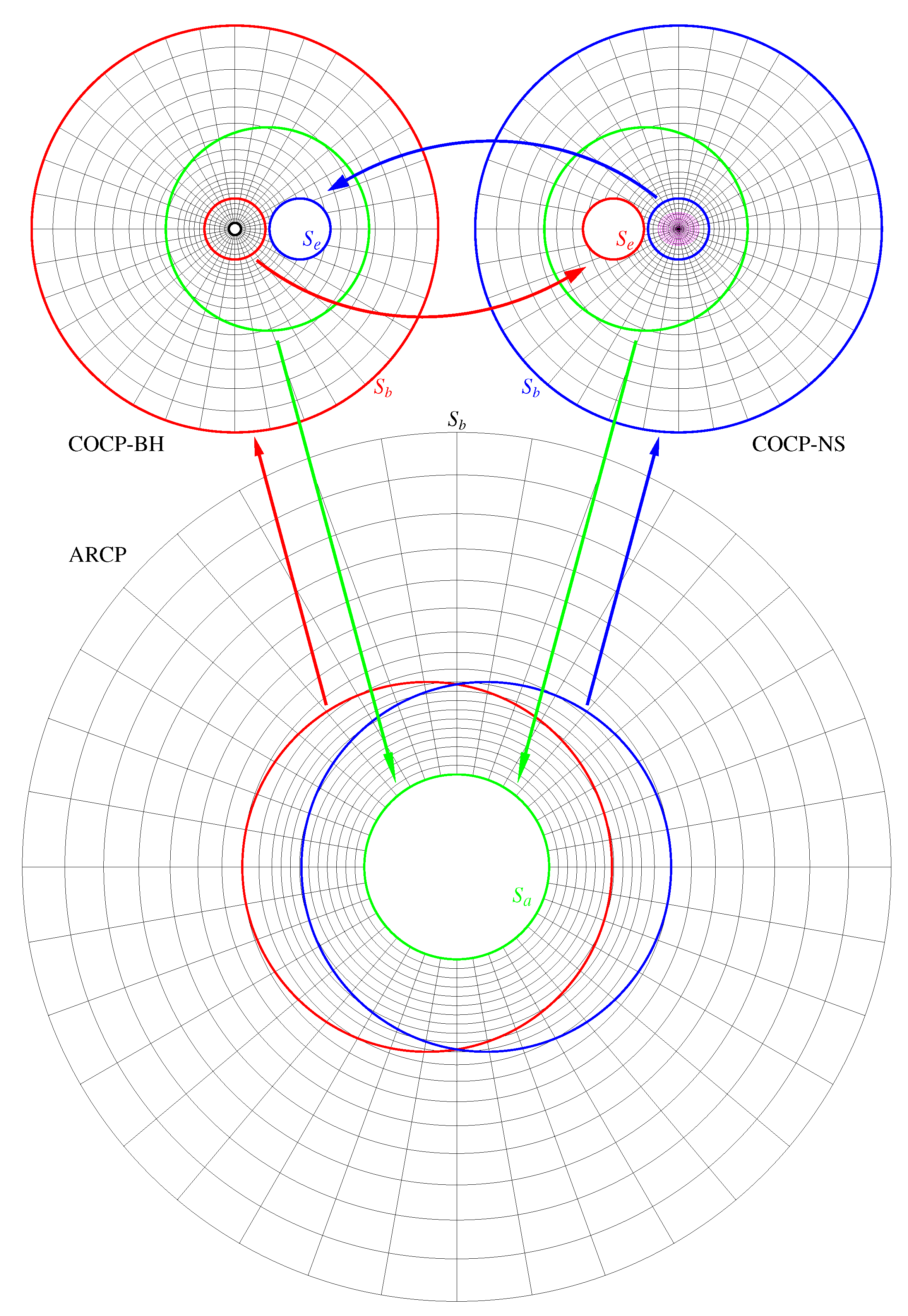
For binary configurations, the hypersurface is covered by at least three coordinate systems, as explained in detail in [13,14,15,16]. As an example of a general binary system, we show in Figure 1 a black hole–neutron star ( cross-section) that consists of the following: (i) Coordinate system COCP-BH (top-left coordinate system) centered around the black hole extending from an inner sphere (small black circle at its center) of radius to a sphere of radius (red outer circle). The surface denotes the black hole region and is excised from the grid. If M is the mass of the system, we have while ; (ii) Coordinate system COCP-NS (top-right coordinate system) centered around the neutron star, which extends from to a sphere of radius (blue outer circle). Both COCP-BH and COCP-NS contain an excised sphere (although we use the common symbol , these spheres are different in the two coordinate systems), which is introduced to improve the angular resolution and reduce the number of multipoles for resolving the companion object in a given coordinate system; and (iii) Coordinate system ARCP, which is positioned at the center of mass of the system and extends from an inner sphere of radius (green inner circle) to an outer sphere of radius (outer black circle). Definitions of the parameters for the grid setups are listed in Table 2.
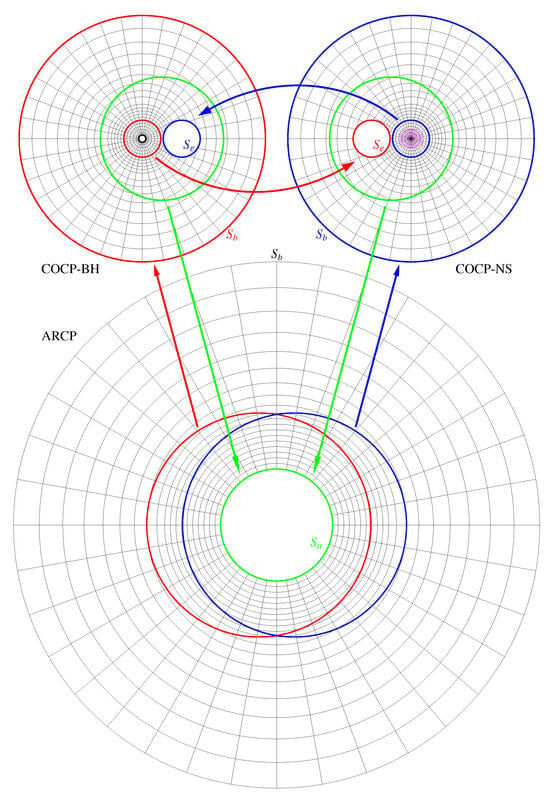
Figure 1.
A typical setup with multiple coordinate grid patches in the cocal code for a black hole–neutron star system. The left and right top patches are those for compact object coordinate patches (COCPs) centered at the black hole and the neutron star, respectively. The smallest circle with a thick curve in COCP-BH is the sphere , where the interior region is excised and certain boundary conditions are imposed. The ovals drawn in COCP-NS denote the neutron star. The bottom patch is that for asymptotic region coordinate patch (ARCP), centered at the mass center of the system. The arrows represent maps of potentials between the multiple patches. Note that the spheres , , and of these coordinate patches are distinct despite our use of a common symbol. The radius of each coordinate patch does not reflect the size used in actual computations.

Table 2.
Summary of the grid the parameters used for the binary systems and, in particular, the binary neutron stars computed here. denotes the neutron star surface. Every patch has its own set of parameters above.
In binary systems, elliptic Equations (10)–(12) are solved separately in all three coordinate systems (in Figure 1), and a smooth solution emerges in an iterative process. On the other hand, Equation (36) is only solved in coordinate systems where a neutron star exists. Therefore, the computational cost of a binary system is significantly larger than that of a single rotating star. Convergence to a smooth solution is achieved because in any given coordinate system, in the calculation of the surface integrals in Equation (40), we use the values of the potential functions f from another coordinate system as indicated by the red, green, and blue arrows in Figure 1. For example, when we calculate the contribution of the surface integral on the red sphere inside the COCP-NS coordinate system (top-right), we use the values of the potentials on the corresponding red sphere from the COCP-BH coordinate system (top-left) as indicated by the red curved arrow. In this way, a given potential () from one coordinate system is communicated to all others, and at the end of the iterative process, a smooth solution is obtained in the whole computational domain. For a detailed explanation of how the KEH method works in multiple coordinate systems, see [13,14,23].
4. Speedup and Efficiency Results
The original serial COCAL consists of more than 400,000 lines of Fortran 90 code, and in order to use OpenMP parallelization, many of its loops had to be rewritten in a way that would efficiently utilize OpenMP’s capabilities. In particular, in multiple loops, the code inside the innermost one had to be written in a way that is independent between threads. For example, in a typical triple loop over the r (loop 1), (loop 2), and (loop 3) coordinates, any code between loop 1 and loop 2 and/or between loop 2 and loop 3 is written only inside the innermost loop 3. The reason is to utilize the collapse clause, which collapses the multiple loops into a single one, which is then divided among the multiple threads. Most of our loops were three-dimensional, but there were many that were four or even five-dimensional, which result in large speedups through OpenMP parallelization. For example, in a binary system, Figure 1, the calculation of the surface integral on the excised sphere uses the Legendre functions with respect to the coordinate system at the center of . Assuming is the spherical angle with respect to the z-axis at the center of , the term will depend on all coordinates of that particular patch; therefore, these functions become five-dimensional, as they depend on the Legendre indices too.
Another commonly used command is the reduction clause, which is used to perform summations, for example in the calculation of the volume and surface integrals. In this case, the code is written in a way that the summation appears only inside the innermost loop so that a combination of the collapse and reduction clauses can execute this operation in multiple threads. The reduction clause is also used in finding the maximum error in Equation (43) for every variable in each coordinate system. The private clause is used extensively for local nested-loop variables so that multiple threads executing a parallel region are independently calculated. Listing a variable as private causes each thread that executes that construct to receive a new temporary variable of the same type, and the multiple loop can be performed independently in parallel.
Below, we will describe the two main modules of the PCOCAL code: (a) the parallelized single rotating star module (Section 2.1); and (b) the parallelized binary neutron star module (Section 2.2). For the single star solver (a), the computational infrastructure is straightforward (one spherical grid), but the mathematical formalism used requires the solution of 14 elliptic equations. On the other hand, for the binary solver (b), a simpler mathematical formalism requires the solution of six elliptic equations in a more intricate computational domain, which involves at least three coordinate systems (see Figure 1).
In order to quantify the speedup and efficiency of PCOCAL, we define the following measures:
- : CPU wall-clock time of parallelized part of the code using n threads.
- : CPU wall-clock time of serial (nonparallelized) part of the code. Input/Output (IO) and copying between arrays are excluded.
- : CPU wall-clock time of serial IO.
- : CPU wall-clock time of memory copy between arrays.
The reason for timing is because in COCAL/PCOCAL, every main variable (e.g., the 3D conformal factor ) exists in all coordinate systems (which are at least three) and is stored in a higher dimensional array (for the case of , in a 4D array) where the extra index determines the patch (COCP-1, COCP-2, or ARCP). When calculating quantities in one patch where we want to access a quantity in another patch, an array copy is necessary. The time for these copies is measured by .
The total time for a calculation is . We define the speedup of the code using n threads as
while the efficiency is defined as
The speedup and efficiency refer to the parallelized part of code (which constitutes the large majority of the solver), while and refer to the total speedup and efficiency, which include the serial parts of the code, the input/output, and memory handling. Note that for the tests performed in this paper, the input/output routines were neither optimized nor minimized (for diagnostic purposes), and thus, the total speedup shown underestimates the real one.
To make sure that the parallelized PCOCAL code produces the same results as COCAL itself, we perform a pointwise check for every parallelized subroutine against the serial code and confirm that the differences between the two codes are ≲ in all variables.
Most of the runs have been performed in server A, which has 36 cores with 2 threads per core (72 threads total) and an Intel(R) Xeon(R) Gold 6254 CPU 3.10 GHz (Intel, Santa Clara, CA, USA). We have also used server B, which has 40 cores with 2 threads per core (80 threads total) and an Intel(R) Xeon(R) Gold 6242R CPU 3.10 GHz. Both servers are dual-socket. An Intel compiler (2021.3.0 20210609) is being used.
4.1. Single Rotating Neutron Star
Following the methods of Section 2.1 and Section 3.1, we test our new code in three grid resolutions, as can be seen in Table 3. Resolution H2 has 442,368 intervals (number of points in the directions are , , and , respectively), while resolutions H3, H4 have twice and four times as many intervals in every dimension, i.e., 8 and 64 times more intervals in total, respectively. The default value of terms in the Legendre expansions is . Below, we also investigate the performance of the code with respect to L.

Table 3.
Three different resolutions used for the single rotating star tests. The parameters are shown in Table 1. The number of points that cover the largest star radius is . Resolutions H2, H3, and H4 correspondingly use 2, 10.3, and 80.1 GB of RAM.
In Algorithm 1, we sketch the most salient steps taken for a solution. In parentheses with green fonts, we show the percentage of time needed for a given calculation per iteration using a single core using the H3 resolution. Lines that do not have a number indicate that the time it took for completion was less than . The rest of the time is spent in the calculation of diagnostics as well as further output. Steps 2–12 are repeated iteratively until condition 13 is fulfilled, and hence, convergence to a solution is achieved. As we can see, the most time-consuming routines are the computation of the momentum constraint sources (15%), the calculation of the sources (13%), followed by the calculation of the conformal Ricci tensor (11%) and the Poisson solvers themselves (11%). The reason that the three source arrays of the momentum constraint took more time to be computed than the six source arrays was mainly due to the modular way that COCAL implements various mathematical formulations. In particular, for the waveless formulation, the sources (right-hand side of the Poisson equations) are split into two parts: (i) the part that comes from the conformal flat part of the metric and (ii) the ones that come from the nonconformal one. In this way, one has the flexibility of choosing a specific method (conformal flat vs. nonconformal flat) without repeating the writing of a code. The disadvantage is that triple loops all over the gridpoints may be repeated; therefore, speed is sacrificed in view of modularity. In the computation of the momentum constraint sources for the waveless formulation (which is not conformally flat), both the fluid part and the gravitational part of the source computation are performed twice, which leads to a larger time footprint than the six source arrays . Overall the bottleneck for the rotating neutron star module in the waveless formulation is the computation of the sources (lines 2–8) rather than the Poisson solvers (line 9). As we will see, this is in contrast with the binary neutron star module in the conformal flat approximation, where the latter dominates over the former.
| Algorithm 1 Rotating star in the waveless formalism | ||
| 1: | procedure RNS | |
| 2: | Interpolate variables to SFC | ▹ |
| 3: | Compute , , | ▹ |
| 4: | Compute volume sources , Equation (A1) | ▹ |
| 5: | Compute volume sources , Equation (A3) | ▹ |
| 6: | Compute volume sources , Equation (A2) | ▹ |
| 7: | Compute volume sources , Equation (A4) | ▹ |
| 8: | Compute right-hand side of Equation (A22) | ▹ |
| 9: | Compute , Equation (40) | ▹ |
| 10: | Variable update, Equation (42) | ▹ |
| 11: | Use Equation (23) to compute the rest mass density . | |
| 12: | Compute Equation (43) | ▹ |
| 13: | if then | |
| 14: | exit | |
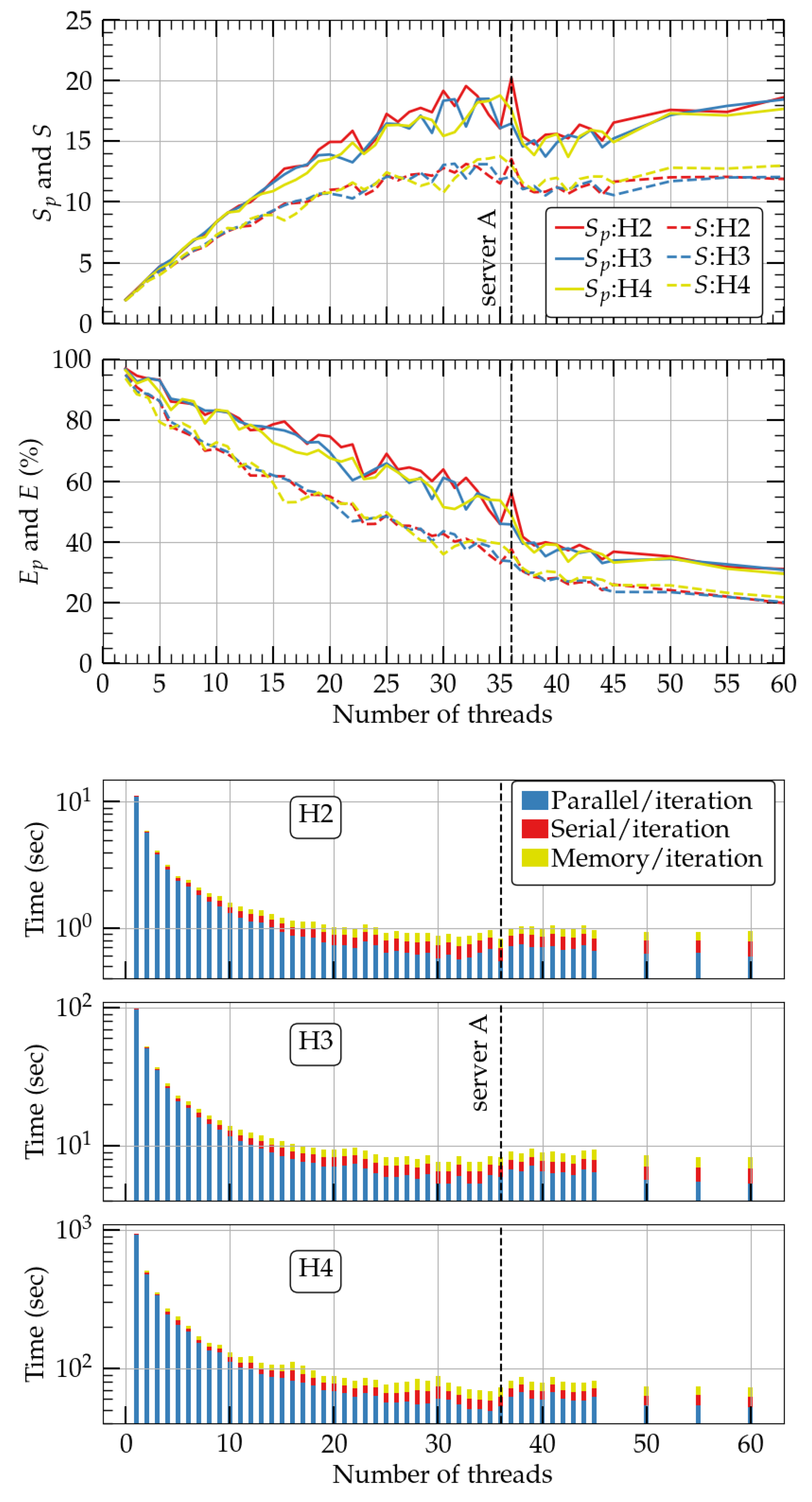
In Figure 2, we plot in the upper two panels the speedup (top) and efficiency (bottom) of the parallelized part of the code (solid lines), as well as the corresponding measures S and E for the total code (dashed lines). As we mentioned above, S underestimates the real speedup as the input/output routines were neither optimized nor minimized (for diagnostic purposes). Thus, in the discussion below, we focus on the speedup and efficiency . One characteristic of the speedup is that for all resolutions, it reaches a maximum at ∼36 threads and drops slightly afterwards, from which point it continues to increase. The maximum speedup of the parallelized part of the code is 18–20 times the serial one (when ≲60 threads are used) which can be achieved with a minimum of ∼36 threads. At that point, the efficiency is ∼50%. At maximum speedup, the whole rotating neutron star code (including the serial routines that are nonparallelized, such as the calculation of the parameters in Equation (20), C in Equation (23), and the coordinate scaling [8,16]) is ∼12, 13, and 14 times faster than the serial analog for resolutions H2, H3, and H4 and occurs at 36, 34, and 35 threads, respectively. This can be seen in Figure 2 on the lower three panels, where blue bars signify the parallelized routines of the code, red bars the serial part of the code, and yellow bars the memory copy between arrays. From this plot, we see that the parallelized code constitutes the vast majority of the total number of subroutines and is responsible for the achieved speedup. Also, we observe that the higher the resolution (H4), the larger the total speedup, which is a promising result for high-resolution campaigns.
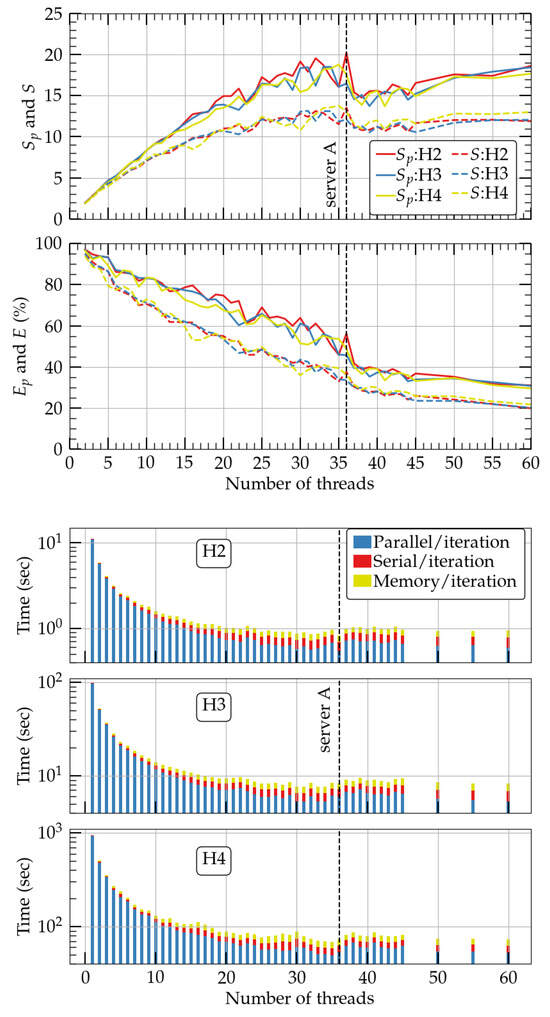
Figure 2.
Upper two panels: Speedup (top) and efficiency of the parallelized (solid lines) and total code (dashed lines) of a single rotating star module in the waveless formalism for three different resolutions, H2, H3, and H4. In all cases, the maximum number of terms in the Legendre expansion is . The vertical dashed line denotes the number of cores/CPU of server A. Bottom three panels: Performance time of the whole code in the three resolutions.
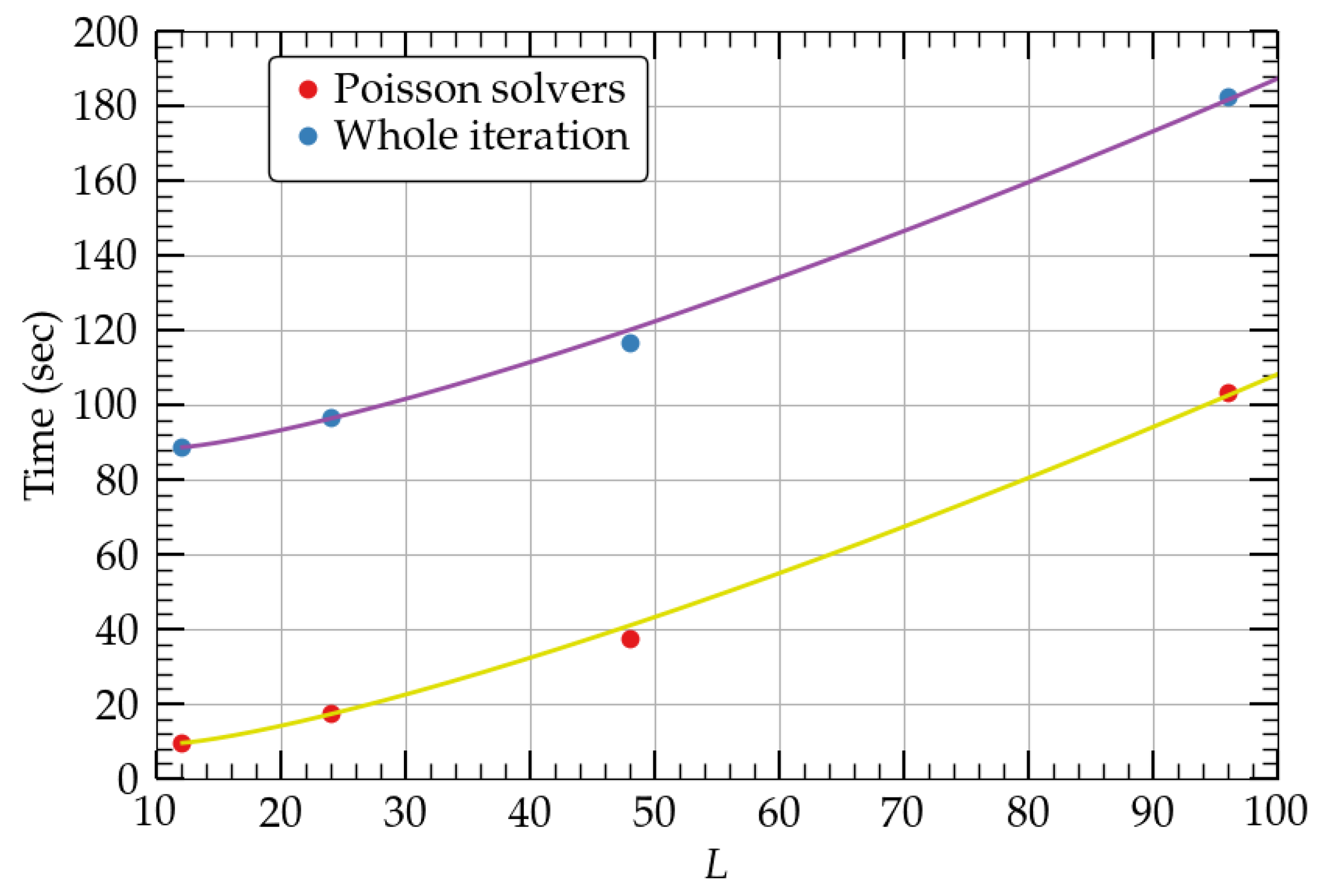
In all tests presented in Figure 2, we used terms in the Legendre expansion, Equation (41), and therefore all integrals, Equation (40). It is experimentally found that such a number of terms leads to accurate results without compromising the speed of the code. is commonly used in all nonmagnetized rotating star calculations [7,8,9,10,11,12] as well as in the binary neutron star calculations [16,17] that we will mention in the next section. On the other hand, accurate magnetized rotating neutron stars or black hole-disk solutions require a larger number (≲60) of terms to be included in the Legendre expansions. In Figure 3, we plot the time of a single iteration (blue dots), as well as the time for the Poisson solvers alone (red dots), using the H3 resolution and a single core. Increasing the number of Legendre terms L increases the time spent on the Poisson solvers as
where . This fitting function is plotted by a solid yellow line. At the same time, the time spent on the whole iteration is also fitted by the same relation Equation (46), but (as reported in Algorithm 1, line 9, the percentage of time spent for the Poisson solvers with respect to the whole iteration when is approximately ) and is plotted with a purple curve. In other words, for a given resolution, the increase in the number of Legendre terms essentially affects the Poisson solvers as well as the whole iteration in the same manner and scale as ∼.
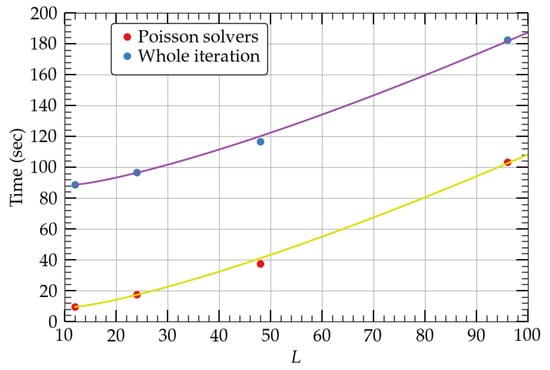
Figure 3.
Time for the Poisson solvers (red dots) as well as for a single iteration (blue dots) for the H3 resolution in a single core for various values of Legendre terms L. Solids lines represent fitting functions.
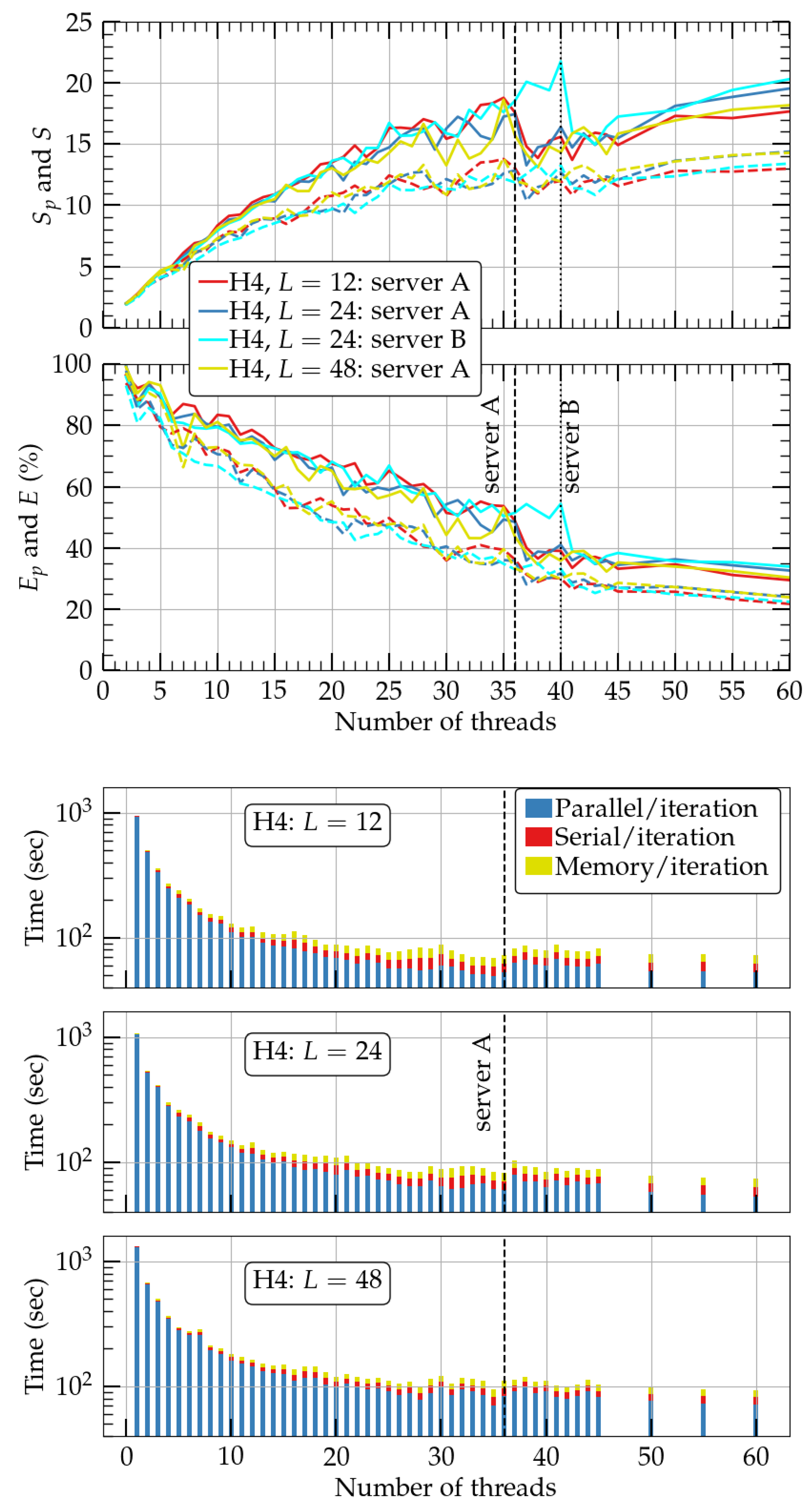
In order to evaluate our new code with respect to the number L, we performed the same tests using the H4 resolution for three different numbers of Legendre terms . The results are shown in the upper two panels of Figure 4 with red, blue, and yellow curves in server A. In addition, we show with a cyan curve the speedup and efficiency of the run in server B. The first conclusion is that the speedup is approximately preserved when the number of Legendre terms is increased. All runs in server A have a maximum at ∼35 threads. Beyond that point, and similarly to Figure 2, the speedup drops and then starts to increase again. This behavior is qualitatively the same as the run with at server B, with the maximum now happening at 40 threads and a speedup of larger than 20. Given than the server A CPUs have 36 cores while the server B CPUs have 40, we conclude that peak speedup with minimum amount of threads happens approximately at the number of cores a CPU has. The larger the number of cores, the larger the speedup will be. On the lower three panels, we plot the total performance time for in the H4 resolution and server A. We find that the maximum speedup of the total rotating neutron star code (including the routines that are nonparallelized) is ∼14, 13, and 14 times faster than the serial analog in the H4 resolutions for and occurs at 35, 36, and 35 threads, respectively. Therefore, the speedup is preserved when the number of Legendre terms is increased for the whole code as well, which is expected, given the fact that the parallelization scheme covers all of the main components of PCOCAL.
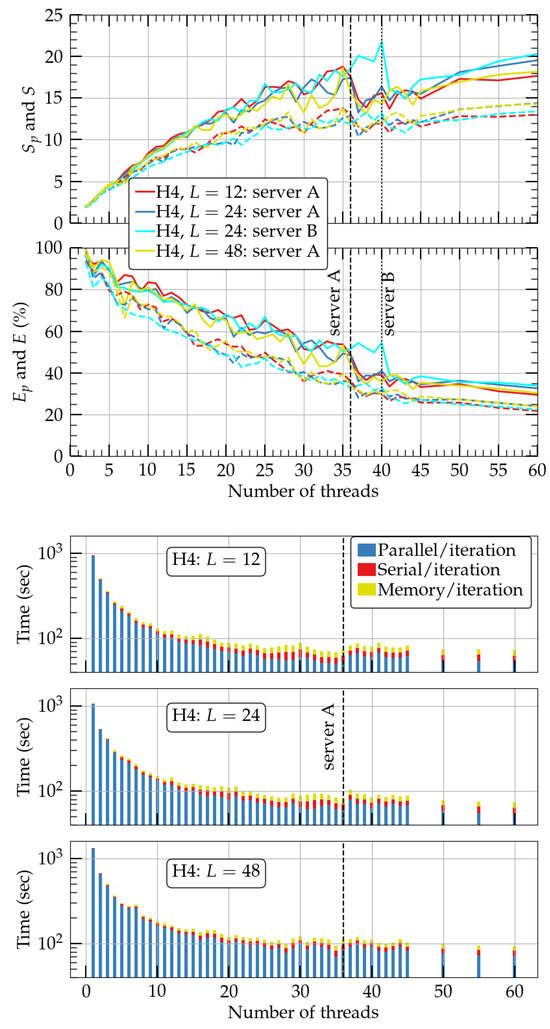
Figure 4.
Same as in Figure 2 but only for resolution H4 with . Speedup and efficiency in a second server (server B) is also shown for (cyan curve on the upper two panels). As in Figure 2, solid lines in the left panels correspond to and , while dashed lines correspond to S and E. Vertical dashed lines denote the number of cores/CPU of servers A and B.
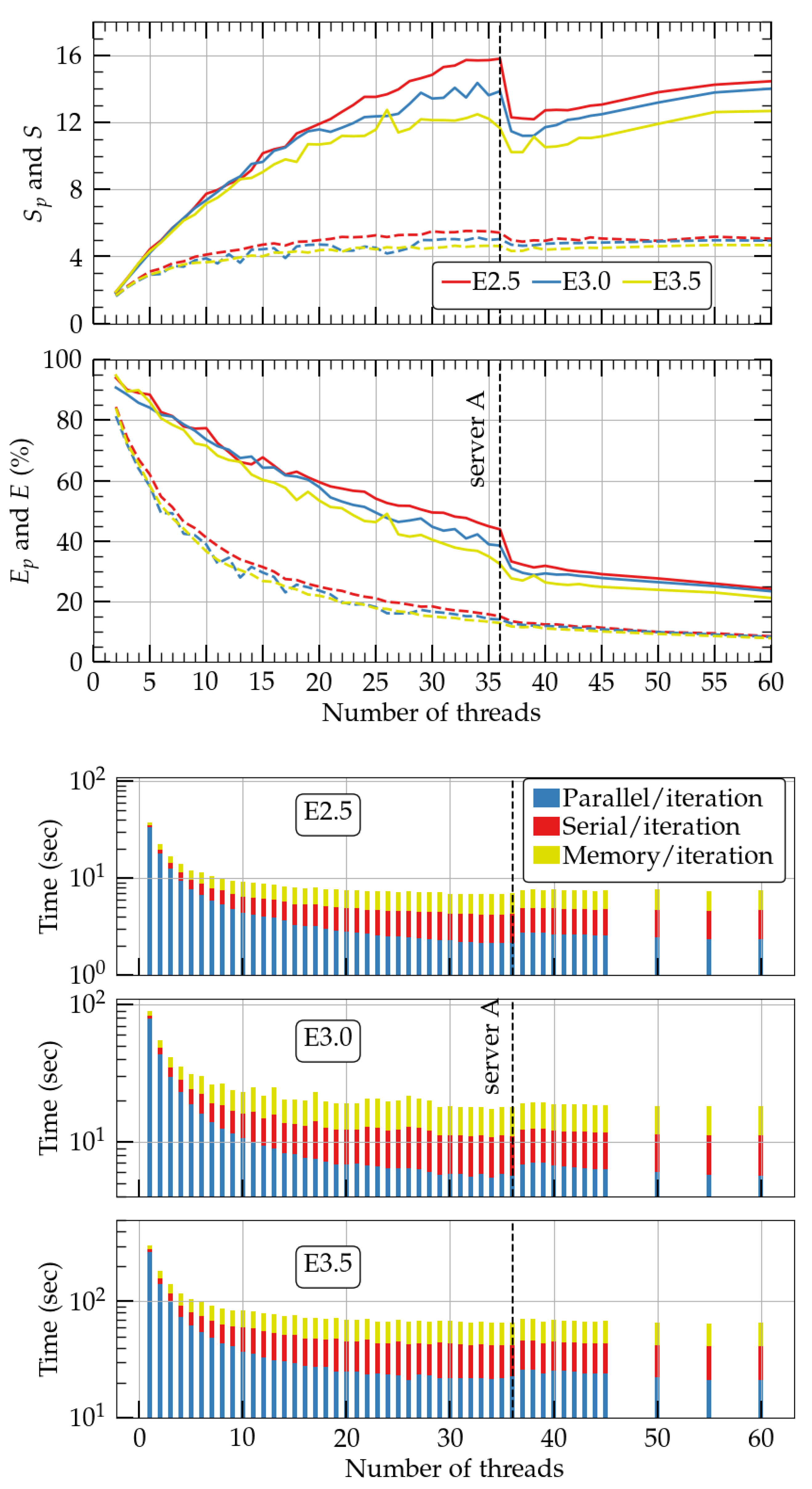
4.2. Binary Neutron Stars
Following the methods of Section 2.2 and Section 4, we test our new code in three resolutions as in Table 4. Resolution E2.5 has 1,492,992 intervals in each of the three coordinates systems (two COCPs and one ARCP in Figure 1), while resolutions E3.0 and E3.5 have ∼1.3, and 2 times as many intervals in every dimension, i.e., and 8 times more intervals in total, respectively. In all binary cases, we use as the number of terms in the Legendre expansions. Notice that the BH coordinate system (COCP-BH, top-left, red patch in Figure 1) is now replaced by an NS coordinate system, similar to the blue, top-right patch COCP-NS. Therefore, there is no inner surface (no boundary conditions), and for the red patch in Figure 1 for the binary neutron/quark case.

Table 4.
Three different grid structure parameters used for the circular binary computation in COCAL. The amount of RAM used in each resolution is written in the first column. All variables are explained in Table 2, and the distances are in normalized quantities [16]. There are two COCP grids centered around each neutron star and one ARCP centered at the center of mass of the system (see Figure 1). Resolutions E2.5, E3.0, and E3.5 correspondingly use 5.0, 9.9, and 30.6 GB of RAM.
In Algorithm 2, we sketch the most important steps taken for a binary neutron star solution using a single core in the E3.0 resolution. As in Algorithm 1, we report the percentage of time needed for the completion of each step with green fonts inside a parenthesis, while when such number is absent, it means that the time it took for completion was less than . The rest of the time is spent in the calculation of diagnostics as well as further output. Steps 2–14 are repeated iteratively until the condition in line 15 is fulfilled. The main differences between the RNS and NSNS modules are: (i) Steps 3–15 are performed in three coordinate systems (two for COCP-NS and the ARCP) as seen in Figure 1 instead of one in the RNS module; (ii) the calculation of every potential in the two COCP-NS coordinate systems is significantly more involved because of the excised sphere (the reason for the existence of in the COCP patches is explained in detail in [13,14,15]); (iii) the additional calculation of the velocity potential (∼4%) (absent in the RNS module) is another important difference between the NSNS module and the RNS one; (iv) because for binary neutron stars we solve for conformally flat initial data, potentials and, in addition, the source terms (Equation (A1)–(A3)) are significantly simpler as the magenta terms are zero.
As mentioned above, surface integrals (see Equation (40)) on do not exist in the single coordinate system of the RNS module. When computing those integrals as well as the surface integrals at and in a given coordinate system (e.g., on COCP-NS-1), the integrands are computed using the variables of another coordinate system (e.g., from COCP-NS-2). In this way, solutions between coordinate systems communicate between each other in order to achieve a smooth solution everywhere. Therefore, to compute the integrands on the surface integrals at , , and , three-dimensional interpolations from nearby points of another coordinate system is needed. In total, the Poisson solvers take ∼41% of the time of an iteration. The time of the Poisson solvers in each COCP-NS patch is ∼17%, while in the ARCP, it is ∼7%. The big difference between them is due to the fact that patch ARCP does not have an excised sphere . The surface integral in the off-center sphere is the most time-consuming operation (∼11%), and it involves the computation of the corresponding associated Legendre functions, which are five-dimensional arrays of (). In the current implementation, this time-consuming operation is performed on the fly every time such an integral is calculated in order to have a smaller memory footprint. Note that these functions do not change during the iteration procedure and in principle can only be calculated once. Such an array in the E3.5 resolution will be ∼9 GB.
| Algorithm 2 Binary neutron star | ||
| 1: | procedure NSNS | |
| 2: | for all Coordinate Systems A do | |
| 3: | Interpolate variables from SFC | ▹ |
| 4: | Compute | ▹ |
| 5: | Compute volume source Equation (A1), | |
| 6: | Compute volume source Equation (A3), | |
| 7: | Compute volume source Equation (A2), | ▹ |
| 8: | Compute sources on excised surface | ▹ |
| 9: | Compute Equation (40) | ▹ |
| 10: | Variable update Equation (42) | ▹ |
| 11: | Use Equation (35) to compute the rest mass density . | |
| 12: | Compute Equations (36) and (40) | ▹ |
| 13: | Compute | ▹ |
| 14: | Variable copy between CSs | ▹ |
| 15: | if | |
| for all A) then | ||
| 16: | exit | |
In Figure 5, we plot in the upper two panels the speedup (top) and efficiency (bottom) of the parallelized part of the binary NSNS code (solid lines), as well as the corresponding measures S and E for the total code (dashed lines). Similar to the RNS module, Figure 2, we find that for all resolutions the speedup increases until a certain number of threads; then, it exhibits a sudden small drop, from which point it continues to increase with the number of threads. One difference with respect to Figure 2 is that the speedup curves are distinct for resolutions E2.5, E3.0, and E3.0, while for the RNS module we observe a broad overlap of these curves between resolutions H2, H3, H4. The reason for this behavior is the communication between the different coordinate systems in the binary code, which is absent in the single neutron star module. Despite that, the speedup of the parallelized code reaches values of 12–16 using just ∼36 threads. The efficiency at that point is ∼40%. This speedup can further increase if more than 60 threads are used. Another finding in Figure 5 is the fact that for the highest resolution E3.5, the speedup is broadly constant from ∼26 to ∼35 threads, which is due to the domination of data communication between the different grids in the calculation process. In the lower three panels of Figure 5, we also see that the total binary code (including the routines that are nonparallelized) is six, five, and five times faster than the serial analogue for resolutions E2.5, E3.0, and E3.5 and occurs at 33, 34, and 26 threads, respectively. The distribution of times in the whole code can be seen on the lower three panels of Figure 5. In the future, we will address the data communication and memory handling in order to make the binary speedup scale similarly to the RNS code. In practice, a binary neutron star in quasicircular orbit that took approximately six days of continuous computation in the E3.0 resolution with the COCAL code; with PCOCAL, it needs approximately one day using a modest amount of ∼30 threads.
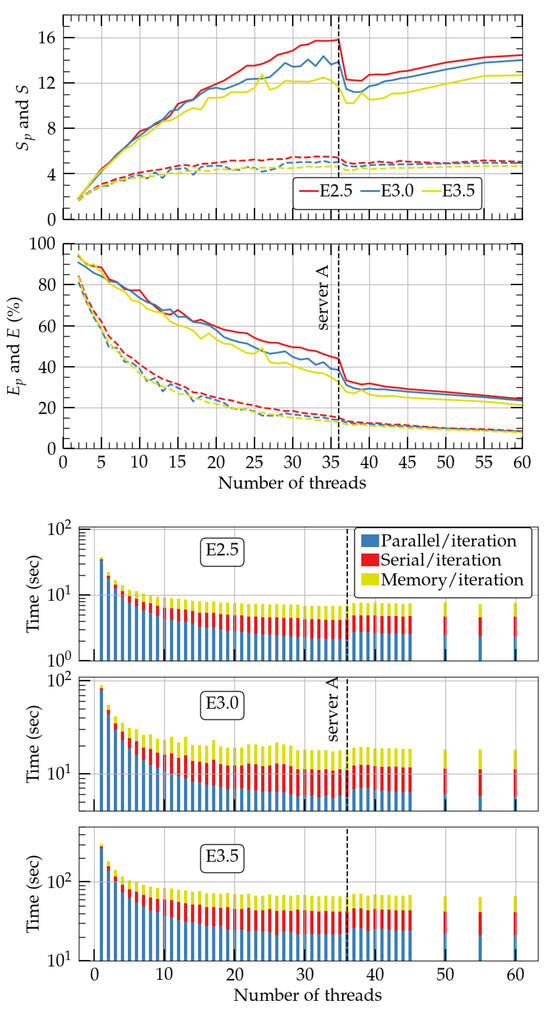
Figure 5.
Same as in Figure 2 but for binary neutron stars. The resolutions used are shown in Table 4 and are E2.5, E3.0, and E3.5. As in Figure 2, solid lines in the left panels correspond to and , while dashed lines correspond to S and E. Vertical dashed lines denote the number of cores/CPU of server A.
The differences between the PCOCAL and COCAL for a binary neutron or quark star are ≲ in all coordinate systems for the gravitational variables and fluid variables , as well as for the constants and that appear in the calculation.
5. Spinning Binary Quark Stars
Given the fact that the state of matter at supranuclear densities is an open question, there is the possibility that conventional neutron stars contain in their core a phase transition to strange quark matter, i.e., up, down, and strange free quarks. A quark-gluon plasma has been observed in heavy ion collision at CERN and RHIC [49]. Also, Bodmer and Witten [50,51] pointed out that it is possible that the ground state of matter at zero pressure and a large baryon number is not iron but strange quark matter. Thus, from a theoretical standpoint, one can have pure quark stars. In [11,12,52,53,54], we have computed rotating isolated axisymmetric, triaxial, and differentially rotating quark stars, while in [55], irrotational binary quark stars have been evolved in grid-based hydrodynamics. Here, we present an example using the PCOCAL code of a spinning binary quark star, where each companion has a spin along the axis of the orbital angular momentum.
As in our previous studies, the quark EOS is the MIT model with or in a parametric form
where is the bag constant, which is set to , and is the surface energy density. The parameter could be regarded as the rest mass density and K is constant. As explained in [54], changing K does not affect the EOS; thus, we choose this constant such that at the surface , i.e., . This is accomplished for
Assuming , this EOS predicts a maximum spherical mass of a quark star of with .
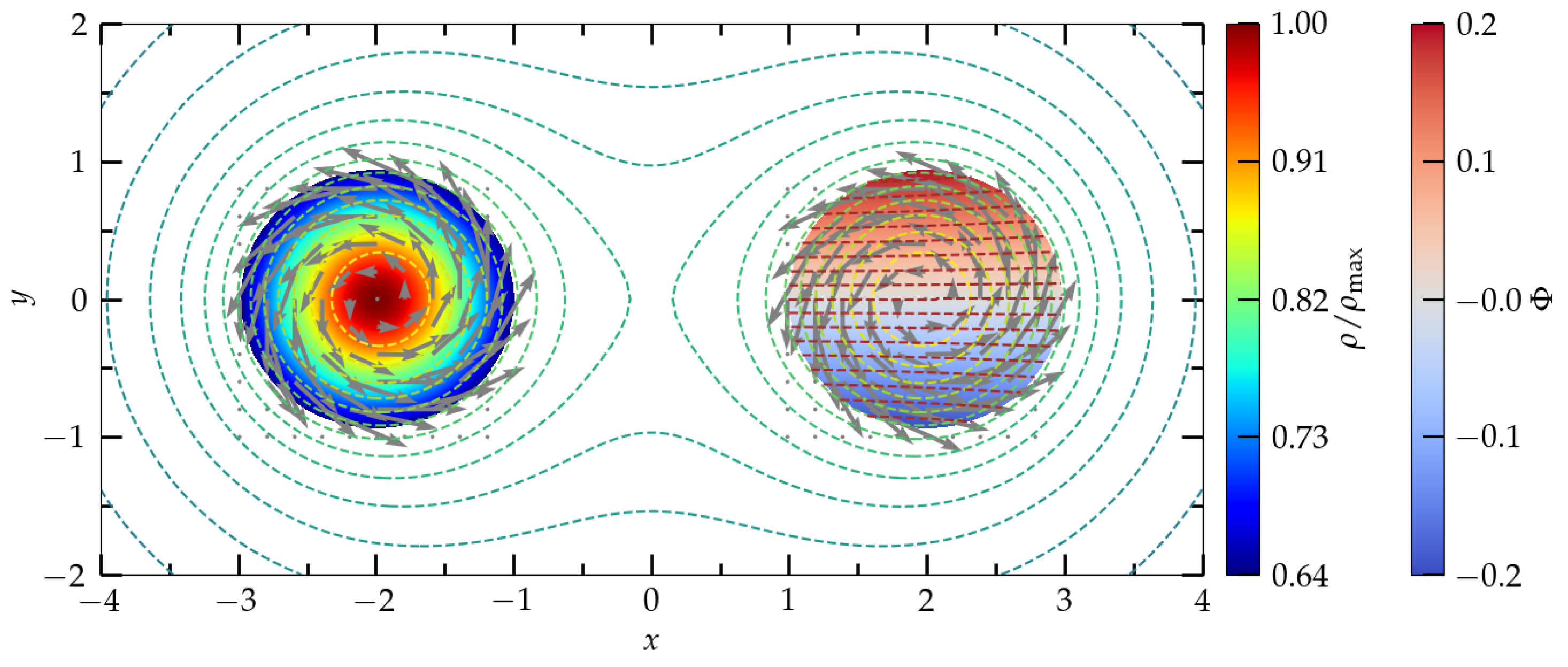
Using the formalism described in Section 2.2 with a spin vector
( are coordinates with respect to the quark star center) in Equation (31), and solving Equations (10)–(12), (31), (35) and (36), we compute here a spinning binary quark star at separation and Arnowitt–Deser–Misner mass of . The quasilocal spin [17] of each companion is along the axis of orbital motion. This spin angular momentum corresponds to an approximate dimensionless spin of . In Figure 6, we plot the rest mass density (left quark star), velocity potential (right quark star), contour plots of the conformal factor (green dashed lines), and velocity potential (brown dashed lines), as well as the fluid velocity with respect to the corotating frame. The direction of the velocity arrows show that the spin angular momentum is along the positive z-axis (contrary to the irrotational case) in accordance with Equation (50). From the density colorbar, we see that the central density is approximately times the surface density . The nonzero surface density is characteristic of the self-bound quark stars, contrary to their neutron star analogs. For nonspinning (irrotational) binaries of the same surface density (and rest mass), the central density is higher and . This behavior is similar to binary neutron stars as well as to isolated rotating neutron/quark stars. Note that in order to find the quasiequilibrium solution, a root finding method over the central quark star densities is needed, and therefore, a number of cycles (∼10) of Algorithm 2 is performed. Pointwise comparison between PCOCAL and COCAL solutions show differences ≲ for all variables.
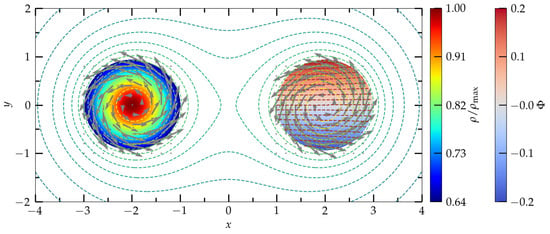
Figure 6.
A spinning binary quark star. The rest mass density is shown for the star on the left, while the velocity potential is plotted for the star on the right. Contour plots of the conformal factor (green dashed lines) and the velocity potential (brown dashed lines in the right quark star), as well as the fluid velocity with respect to the corotating observer, are shown.
6. Conclusions
In this work, we presented a new efficient parallelized code, PCOCAL, for general relativistic compact object initial data. PCOCAL is based on the serial COCAL code (which has been tested for a wide range of astrophysical scenarios) and employs extensive OpenMP practices. To optimize PCOCAL, a thorough profiling of the serial COCAL code is performed for the first time. Both the single and binary neutron star modules have been examined in detail, and timing of each subroutine was performed. The parallelized module that solves the full set of Einstein equations for a single rotating neutron star is found to be 12–14 times faster than the corresponding serial code, with the parallel part being 18–20 times faster than the serial one. The parallelized module that solves for a binary neutron star system in quasiequilibrim is 5–6 times faster than the corresponding serial code, with the parallel part being 12–16 times faster than the serial one. As a novel example, we computed initial data for a spinning binary quark star system that could be a binary neutron star mimicker. The achieved speedup will help us explore a larger set of problems that require intensive calculations, as for example in the calculation of magnetized neutron stars.
As a step forward, we plan to revisit the data communication and memory handling of the binary module in order to achieve better speedups for the highest resolutions, as in the single rotating star module. In addition, we will perform domain decomposition in order to implement a combined MPI-OpenMP scheme.
Author Contributions
Conceptualization, A.T.; methodology, L.B., A.T. and K.U.; software, L.B., A.T. and K.U.; validation, L.B.; formal analysis, L.B. and A.T.; investigation, L.B. and A.T.; resources, A.T. and K.U.; data curation, L.B.; writing - original draft, L.B. and A.T.; writing - review & editing, A.T. and K.U.; visualization, L.B. and A.T.; supervision, A.T.; project administration, A.T.; funding acquisition, A.T. and K.U. All authors have read and agreed to the published version of the manuscript.
Funding
A.T. is supported by National Science Foundation Grants No. PHY-2308242 and No. OAC-2310548 awarded to the University of Illinois at Urbana-Champaign. A.T. acknowledges support from the National Center for Supercomputing Applications (NCSA) at the University of Illinois at Urbana-Champaign through the NCSA Fellows program. K.U. is supported by the JSPS Grant-in-Aid for Scientific Research (C) 22K03636 awarded to the University of the Ryukyus.
Data Availability Statement
The authors declare that there are no data associated with this manuscript.
Acknowledgments
A.T. thanks E. Zhou for useful discussions.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A. Source Terms
The source terms , , , and in Equation (10)–(13) are
where with magenta color, we signify terms that are due to the nonconformal flat contribution . Such terms are zero in the IWM formulation used in the binary neutron star calculations of Section 2.2. We also define the conformally rescaled shift as ; therefore, . The covariant derivatives associated with , and are, respectively, , and . It is
where
and
as . In the case where Cartesian coordinates are used for the flat metric, i.e., , then is the usual partial derivative ∂ and is the Laplacian in Cartesian coordinates. The superscript TF means the trace-free part. The conformal trace-free extrinsic curvature is written as
where is the conformal Killing operator: .
Another important term in our system is the one that involves , the 3D Ricci tensor associated with the conformal geometry . One can show [56] that
where
and
Notice that the terms , enter into Equation (A4), which we discuss below. The nonlinear term is second order in and therefore smaller than the first-order terms and in Equation (A15). The term involves the gauge functions , which are the conformal connection functions in the BSSN formulation [57,58,59]. For initial data, in order for the whole system (A1)–(A4) to converge, these functions must be fixed [21,56]
where is known. Equation (A19) is related to our freedom in choosing spatial coordinates. In order to impose Equation (A19) to the solutions of the system Equation (A1)–(A4) and thereby having a self-consistent iteration scheme, an adjustment is necessary for the . Following [43], (or [8] Equations (29)–(32)) gauge vector potentials are introduced through the transformation
which are then used to adjust as
References
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. Observation of Gravitational Waves from a Binary Black Hole Merger. Phys. Rev. Lett. 2016, 116, 061102. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. GW170817: Observation of Gravitational Waves from a Binary Neutron Star Inspiral. Phys. Rev. Lett. 2017, 119, 161101. [Google Scholar] [CrossRef] [PubMed]
- Kozlova, A.; Golenetskii, S.; Aptekar, R.; Frederiks, D.; Svinkin, D.; Cline, T.; Hurley, K.; Connaughton, V.; Briggs, M.S.; Meegan, C.; et al. IPN Triangulation of GRB 170816A (short/hard). GRB Coordinates Network, Circular Service, No. 21517, #1 (2017). 2017, Volume 1517. Available online: https://ui.adsabs.harvard.edu/abs/2017GCN.21517....1K/abstract (accessed on 20 March 2024).
- Abbott, B.P. Multi-messenger Observations of a Binary Neutron Star Merger. Astrophys. J. Lett. 2017, 848, L12. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. Gravitational Waves and Gamma-Rays from a Binary Neutron Star Merger: GW170817 and GRB 170817A. Astrophys. J. Lett. 2017, 848, L13. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. Estimating the Contribution of Dynamical Ejecta in the Kilonova Associated with GW170817. Astrophys. J. Lett. 2017, 850, L39. [Google Scholar] [CrossRef]
- Huang, X.; Markakis, C.; Sugiyama, N.; Uryū, K. Quasi-equilibrium models for triaxially deformed rotating compact stars. Phys. Rev. D 2008, D78, 124023. [Google Scholar] [CrossRef]
- Uryū, K.; Tsokaros, A.; Galeazzi, F.; Hotta, H.; Sugimura, M.; Taniguchi, K.; Yoshida, S. New code for equilibriums and quasiequilibrium initial data of compact objects. III. Axisymmetric and triaxial rotating stars. Phys. Rev. D 2016, D93, 044056. [Google Scholar] [CrossRef]
- Uryū, K.; Tsokaros, A.; Baiotti, L.; Galeazzi, F.; Sugiyama, N.; Taniguchi, K.; Yoshida, S. Do triaxial supramassive compact stars exist? Phys. Rev. D 2016, 94, 101302. [Google Scholar] [CrossRef]
- Uryu, K.; Tsokaros, A.; Baiotti, L.; Galeazzi, F.; Taniguchi, K.; Yoshida, S. Modeling differential rotations of compact stars in equilibriums. Phys. Rev. D 2017, 96, 103011. [Google Scholar] [CrossRef]
- Zhou, E.; Tsokaros, A.; Rezzolla, L.; Xu, R.; Uryū, K. Uniformly rotating, axisymmetric and triaxial quark stars in general relativity. Phys. Rev. 2018, D97, 023013. [Google Scholar] [CrossRef]
- Zhou, E.; Tsokaros, A.; Uryu, K.; Xu, R.; Shibata, M. Differentially rotating strange star in general relativity. Phys. Rev. 2019, D100, 043015. [Google Scholar] [CrossRef]
- Uryū, K.; Tsokaros, A. New code for equilibriums and quasiequilibrium initial data of compact objects. Phys. Rev. D 2012, 85, 064014. [Google Scholar] [CrossRef]
- Tsokaros, A.; Uryū, K. Binary black hole circular orbits computed with cocal. J. Eng. Math. 2012, 82, 133–141. [Google Scholar] [CrossRef]
- Uryū, K.; Tsokaros, A.; Grandclement, P. New code for equilibriums and quasiequilibrium initial data of compact objects. II. Convergence tests and comparisons of binary black hole initial data. Phys. Rev. D 2012, D86, 104001. [Google Scholar] [CrossRef]
- Tsokaros, A.; Uryū, K.; Rezzolla, L. New code for quasiequilibrium initial data of binary neutron stars: Corotating, irrotational, and slowly spinning systems. Phys. Rev. D 2015, 91, 104030. [Google Scholar] [CrossRef]
- Tsokaros, A.; Uryu, K.; Ruiz, M.; Shapiro, S.L. Constant circulation sequences of binary neutron stars and their spin characterization. Phys. Rev. 2018, D98, 124019. [Google Scholar] [CrossRef]
- Uryu, K.; Gourgoulhon, E.; Markakis, C.; Fujisawa, K.; Tsokaros, A.; Eriguchi, Y. Equilibrium solutions of relativistic rotating stars with mixed poloidal and toroidal magnetic fields. Phys. Rev. 2014, D90, 101501. [Google Scholar] [CrossRef]
- Uryu, K.; Yoshida, S.; Gourgoulhon, E.; Markakis, C.; Fujisawa, K.; Tsokaros, A.; Taniguchi, K.; Eriguchi, Y. New code for equilibriums and quasiequilibrium initial data of compact objects. IV. Rotating relativistic stars with mixed poloidal and toroidal magnetic fields. Phys. Rev. 2019, D100, 123019. [Google Scholar] [CrossRef]
- Uryu, K.; Yoshida, S.; Gourgoulhon, E.; Markakis, C.; Fujisawa, K.; Tsokaros, A.; Taniguchi, K.; Zamani, M. Equilibriums of extremely magnetized compact stars with force-free magnetotunnels. Phys. Rev. D 2023, 107, 103016. [Google Scholar] [CrossRef]
- Tsokaros, A.; Uryu, K.; Shapiro, S.L. Complete initial value spacetimes containing black holes in general relativity: Application to black hole-disk systems. Phys. Rev. 2019, D99, 041501. [Google Scholar] [CrossRef]
- Uryū, K.; Eriguchi, Y. New numerical method for constructing quasiequilibrium sequences of irrotational binary neutron stars in general relativity. Phys. Rev. D 2000, 61, 124023. [Google Scholar] [CrossRef]
- Tsokaros, A.A.; Uryū, K. Numerical method for binary black hole/neutron star initial data: Code test. Phys. Rev. D 2007, 75, 044026. [Google Scholar] [CrossRef]
- Komatsu, H.; Eriguchi, Y.; Hachisu, I. Rapidly rotating general relativistic stars. I-Numerical method and its application to uniformly rotating polytropes. Mon. Not. R. Astron. Soc. 1989, 237, 355–379. [Google Scholar] [CrossRef]
- Komatsu, H.; Eriguchi, Y.; Hachisu, I. Rapidly rotating general relativistic stars. II–Differentially rotating polytropes. Mon. Not. R. Astron. Soc. 1989, 239, 153–171. [Google Scholar] [CrossRef]
- Ansorg, M.; Brügmann, B.; Tichy, W. A single-domain spectral method for black hole puncture data. Phys. Rev. D 2004, 70, 064011. [Google Scholar] [CrossRef]
- Langage Objet pour la RElativité Numérique. Available online: www.lorene.obspm.fr (accessed on 1 September 2008).
- Kadath Spectral Solver. Available online: https://kadath.obspm.fr (accessed on 1 May 2010).
- Grandclement, P. Kadath: A Spectral solver for theoretical physics. J. Comput. Phys. 2010, 229, 3334–3357. [Google Scholar] [CrossRef]
- Papenfort, L.J.; Tootle, S.D.; Grandclément, P.; Most, E.R.; Rezzolla, L. New public code for initial data of unequal-mass, spinning compact-object binaries. Phys. Rev. D 2021, 104, 024057. [Google Scholar] [CrossRef]
- Tichy, W. A New numerical method to construct binary neutron star initial data. Class. Quant. Grav. 2009, 26, 175018. [Google Scholar] [CrossRef]
- Pfeiffer, H.P.; Kidder, L.E.; Scheel, M.A.; Teukolsky, S.A. A multidomain spectral method for solving elliptic equations. Comput. Phys. Commun. 2003, 152, 253–273. [Google Scholar] [CrossRef]
- Rashti, A.; Fabbri, F.M.; Brügmann, B.; Chaurasia, S.V.; Dietrich, T.; Ujevic, M.; Tichy, W. New pseudospectral code for the construction of initial data. Phys. Rev. D 2022, 105, 104027. [Google Scholar] [CrossRef]
- Assumpcao, T.; Werneck, L.R.; Jacques, T.P.; Etienne, Z.B. Fast hyperbolic relaxation elliptic solver for numerical relativity: Conformally flat, binary puncture initial data. Phys. Rev. D 2022, 105, 104037. [Google Scholar] [CrossRef]
- Tsokaros, A.; Uryū, K. Methods for relativistic self-gravitating fluids: From binary neutron stars to black hole-disks and magnetized rotating neutron stars. Gen. Rel. Grav. 2022, 54, 52. [Google Scholar] [CrossRef]
- Isenberg, J.A. Waveless Approximation Theories of Gravity. Int. J. Mod. Phys. 2008, 17, 265–273. [Google Scholar] [CrossRef]
- Wilson, J.R.; Mathews, G.J. Relativistic hydrodynamics. In Frontiers in Numerical Relativity; Evans, C.R., Finn, L.S., Hobill, D.W., Eds.; Cambridge University Press: Cambridge, UK, 1989; pp. 306–314. [Google Scholar]
- Wilson, J.R.; Mathews, G.J. Instabilities in Close Neutron Star Binaries. Phys. Rev. Lett. 1995, 75, 4161. [Google Scholar] [CrossRef] [PubMed]
- Wilson, J.R.; Mathews, G.J.; Marronetti, P. Relativistic numerical model for close neutron-star binaries. Phys. Rev. D 1996, 54, 1317–1331. [Google Scholar] [CrossRef]
- Shibata, M.; Uryu, K.; Friedman, J.L. Deriving formulations for numerical computation of binary neutron stars in quasicircular orbits. Phys. Rev. 2004, D70, 044044. [Google Scholar] [CrossRef]
- Bonazzola, S.; Gourgoulhon, E.; Grandclement, P.; Novak, J. A constrained scheme for Einstein equations based on Dirac gauge and spherical coordinates. Phys. Rev. D 2004, 70, 104007. [Google Scholar] [CrossRef]
- Uryū, K.; Limousin, F.; Friedman, J.L.; Gourgoulhon, E.; Shibata, M. Binary Neutron Stars: Equilibrium Models beyond Spatial Conformal Flatness. Phys. Rev. Lett. 2006, 97, 171101. [Google Scholar] [CrossRef]
- Uryū, K.; Limousin, F.; Friedman, J.L.; Gourgoulhon, E.; Shibata, M. Non-conformally flat initial data for binary compact objects. Phys. Rev. D 2009, 80, 124004. [Google Scholar] [CrossRef]
- Bonazzola, S.; Gourgoulhon, E.; Marck, J.A. Relativistic formalism to compute quasiequilibrium configurations of nonsynchronized neutron star binaries. Phys. Rev. D 1997, 56, 7740–7749. [Google Scholar] [CrossRef]
- Asada, H. Formulation for the internal motion of quasiequilibrium configurations in general relativity. Phys. Rev. D 1998, 57, 7292–7298. [Google Scholar] [CrossRef]
- Shibata, M. Relativistic formalism for computation of irrotational binary stars in quasiequilibrium states. Phys. Rev. D 1998, 58, 024012. [Google Scholar] [CrossRef]
- Teukolsky, S.A. Irrotational Binary Neutron Stars in Quasi-Equilibrium in General Relativity. Astrophys. J. 1998, 504, 442–449. [Google Scholar] [CrossRef]
- Tichy, W. Initial data for binary neutron stars with arbitrary spins. Phys. Rev. D 2011, 84, 024041. [Google Scholar] [CrossRef]
- Rafelski, J. Melting Hadrons, Boiling Quarks. Eur. Phys. J. A 2015, 51, 114. [Google Scholar] [CrossRef]
- Bodmer, A.R. Collapsed Nuclei. Phys. Rev. D 1971, 4, 1601–1606. [Google Scholar] [CrossRef]
- Witten, E. Cosmic separation of phases. Phys. Rev. D 1984, 30, 272–285. [Google Scholar] [CrossRef]
- Zhou, E.; Tsokaros, A.; Rezzolla, L.; Xu, R. Maximum mass of axisymmetric rotating quark stars. Astron. Nachr. 2017, 338, 1044–1047. [Google Scholar] [CrossRef]
- Zhou, E.; Tsokaros, A.; Rezzolla, L.; Xu, R.; Uryū, K. Rotating Quark Stars in General Relativity. Universe 2018, 4, 48. [Google Scholar] [CrossRef]
- Zhou, E.; Kiuchi, K.; Shibata, M.; Tsokaros, A.; Uryu, K. Evolution of bare quark stars in full general relativity: Single star case. Phys. Rev. D 2021, 103, 123011. [Google Scholar] [CrossRef]
- Zhou, E.; Kiuchi, K.; Shibata, M.; Tsokaros, A.; Uryu, K. Evolution of equal mass binary bare quark stars in full general relativity: Could a supramassive merger remnant experience prompt collapse? Phys. Rev. D 2022, 106, 103030. [Google Scholar] [CrossRef]
- Shibata, M.; Sekiguchi, Y. Gravitational waves from axisymmetric rotating stellar core collapse to a neutron star in full general relativity. Phys. Rev. D 2004, 69, 084024. [Google Scholar] [CrossRef]
- Nakamura, T.; Oohara, K.; Kojima, Y. General Relativistic Collapse to Black Holes and Gravitational Waves from Black Holes. Prog. Theor. Phys. Suppl. 1987, 90, 1–218. [Google Scholar] [CrossRef]
- Shibata, M.; Nakamura, T. Evolution of three-dimensional gravitational waves: Harmonic slicing case. Phys. Rev. D 1995, 52, 5428–5444. [Google Scholar] [CrossRef]
- Baumgarte, T.W.; Shapiro, S.L. Numerical integration of Einstein’s field equations. Phys. Rev. D 1999, 59, 024007. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).