Abstract
In a recent study devoted to the influence of electromagnetic radiation reaction on the motion of radiating charged particles in magnetized black hole spacetimes the authors claim that the tail term cannot be neglected in the complete DeWitt–Brehme equation, putting into doubt the previous papers where such an approximation was used. Here, we demonstrate by using simple dimensional arguments that such a statement is misleading in many astrophysically relevant situations. In the case of relativistic electrons moving around a stellar-mass black hole, the tail term is ignorable if a magnetic field of at least a few Gauss is present.On the other hand, in different situations, the tail term can be relevant, as demonstrated in the case of orbital widening, where it can even amplify the effect.
1. Introduction
The motion of charged test particles in the background of magnetized black holes or neutron stars is of high astrophysical relevance, as it can explain the creation of ultrahigh-energy particles around supermassive black holes in galactic nuclei by the magnetic Penrose process or help in understanding high-frequency quasiperiodic oscillations observed in some microquasars [1,2,3]. Furthermore, it is a basis for understanding the complex Blandford–Znajek process of energy extraction from rotating black holes [4,5] or models of toroidal nonconducting or magnetohydrodynamical structures [6,7].
The influence of back-reaction forces on the radiating charged particles moving in the magnetized black-hole backgrounds seems to be of high relevance [3,8,9,10,11] and has a long history that comes back to pioneering works [12,13,14]. The full description of the influence of radiation reaction in curved backgrounds was given by the DeWitt–Brehme equation also containing a non-local tail term [15,16,17]. The influence of the tail term was later extensively studied in [18].
In some recent studies devoted to the charged particle motion in strong magnetic fields around black holes [10,19,20,21], the tail term was abandoned in the calculations. This approximation, used in [10,19,20,22] has been recently put into doubt in [23], where the authors derive, in the Newtonian approximation, a simple equation
relating the radiation reaction force to the dissipative tail force , and the Lorentz force to the gravitational force . This was an inspiration for the following claim: “neglecting the dissipative part of the tail term and keeping the radiation reaction due to the Lorentz force is equivalent to neglecting the gravitational force while keeping the Lorentz force”.
However, such a strict statement is clearly misleading, as we demonstrate by using simple dimensional arguments. We consider the DeWitt–Brehme equation in the complete form applied to the vacuum spacetimes where the Ricci terms vanish. We show that the back-reaction forces can have different characteristics under different conditions and can be very complex.
2. Dynamics of Radiating Particle
The motion of a relativistic particle with charge q and mass m is governed by the DeWitt–Brehme equation [10,15,17], which can be written in the form
where the last term of Equation (2) is the tail integral
The term containing the Ricci tensor vanishes in the vacuum metrics, so it is irrelevant in our case. The integral in the tail term is evaluated over the past history of the charged particle, with primes indicating its prior positions. The existence of the “tail” integral in (2) implies that the radiation reaction in curved spacetime has a non-local nature. A detailed derivation of the equations of motion for radiating charged particle can be found in [17].
One can reduce the order of the differential equation using the so-called Landau–Lifshits approach [24], which leads to the following result [10].
Different forces with different magnitudes are present in the system, and the question is whether some parts of this equation can be neglected under certain physical conditions.
3. Magnitude of the Forces
The motion of radiating charged particle, described by Equation (4), contains several terms of different magnitudes. Let us estimate the contribution of each of the terms in the equation separately and compare the individual terms with the gravitational force. We choose a system of units where the gravitational interaction given by the Christoffel symbols equals one.
Let us assume that the electromagnetic tensor is given by a uniform magnetic field with magnitude B; hence, we have in (4). The dimensionless parameter represents the relative ratio between the magnetic Lorentz and gravitational forces [10]
reflecting the relative influence of the magnetic and gravitational fields on the charged particle motion. Here, () corresponds to magnetic repulsion (attraction) where the Lorentz force is outward (inward) directed. Radiation reaction (RR) force and tail term self-interaction acting on a charged particle is represented by the dimensionless parameter k having the form
The value of parameter k is much lower than that of . For an electron orbiting stellar mass and supermassive black holes we have, respectively,
For protons, the values of k parameter are lower by the factor of , as in the case of . Despite the weakness of parameter k as compared to , it enters into the equations for ultrarelativistic particles as , which can make the effect of the radiation reaction force considerably large.
The left-hand side of (4) is a purely gravitational term given by the Christoffel symbols, which can be taken in the dimensionless units to be ∼1. On the right-hand side of (4), one can distinguish the Lorentz force (LF) , and three components of the back-reaction force: the two parts of the RR force that are proportional to and , and the tail term of the electromagnetic self-force, which is proportional to . In summary, Equation (4) can be presented in the following form
where one can identify the following forces: Gravitational ; Lorentz ; Radiation reaction and ; Self force (tail term) .
Representative values for all four forces in the case of an electron moving around a stellar-mass black hole are given in Table 1. All forces can have quite different magnitudes according to the two parameters k and . Here, we assume the particles to be relativistic , which allows us to use the magnitude estimates for distinguishing different forces of particle dynamics, but the exact values of individual forces at a given point of the spacetime do not differ much in their magnitudes.

Table 1.
Magnitudes of different forces acting on radiating charged particle in the dimensionless form of Equation (4) for different values of magnetic field strengths. The estimates correspond to a relativistic electron in the vicinity of a stellar-mass BH with . Electron electromagnetic self-force (tail term) and gravitational interaction is the same for all cases and .
Note that the estimates shown in Table 1 are valid for electrons at relativistic velocities, which is a reasonable assumption since the motion of particles in the vicinity of a black hole is always relativistic, i.e., velocity is a significant fraction of the speed of light.
4. Orbital Widening Effect
In [10,19], it has been shown that under certain values and signs of parameters k and the radiation reaction force leads to the widening of circular orbits of radiating charged particles, i.e., increasing their orbital radii due to radiation. The authors of [23] claim that such a counterintuitive result occurs due to a flawed ignoring of the tail term in the equations of motion. In particular, it has been pointed out in [23] that the tail term contains the conservative and dissipative parts and that the former is negligible, while the latter is not, despite being of a similar order of magnitude. Neglection of the dissipative part of the tail term, according to [23], leads to the orbital widening. Below, we demonstrate that the claim of [23] is wrong, as orbital widening can appear even when the tail term is fully considered.
The exact calculation of the tail force is rather complex. Here, we use the approximations obtained by [25] for the dissipative part of the tail term. For the conservative part we refer to [26]. Finally, the components of the tail term corresponding to the electromagnetic self-force in the case of the Schwarzschild black hole takes the following form
Here, we fix the motion at the equatorial plane , which reduces the number of components of the equation of motion to three. In this case, the corresponding energy loss is given by
Examples of charged particle trajectories with and without the inclusion of the tail term are plotted in Figure 1, where one can see that the effect of the orbital widening exists independently from the tail term. One can observe orbital widening in both cases (with and without the tail term). It must be noted that in astrophysically relevant scenarios, the orbital widening is likely undetectable due to the smallness of the radiation parameters k. Orbital widening occurs only for the repulsive Lorentz forces. In contrast, it is absent for the attractive Lorentz forces, and the back-reaction has a dumping effect causing infall in the black hole; see left subfigure in Figure 2. As a counter-example to the case presented in [23], here we show in Figure 1 an example of the orbital widening that occurs in both cases: with the inclusion of the tail term, and without the tail term.
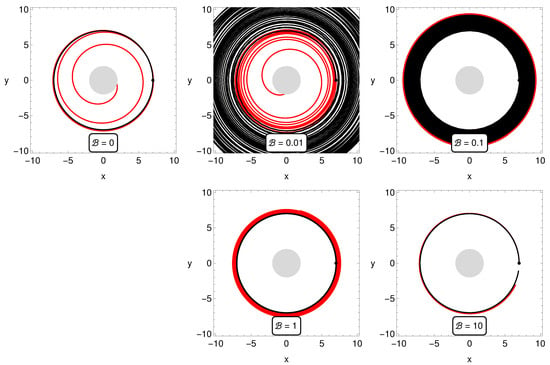
Figure 1.
Trajectories demonstrating orbital widening effect for the charged particle equation of motion with (red) and without (black) included. The radiation parameter is , and particle angular momentum depends on parameter , so the charged particle without radiation reaction will stay on a circular orbit with radius . A similar tendency will be obtained for the lower k parameter or larger initial radius , but the effect of orbital widening will not be so noticeable. Both situations with repulsive () and attractive () Lorentz force are plotted. For repulsive Lorentz force, the orbital widening effect is clearly visible without the tail term () and with the tail term () as well. For all orbits, the same integration time () has been used, demonstrating slow orbital speed for high values.
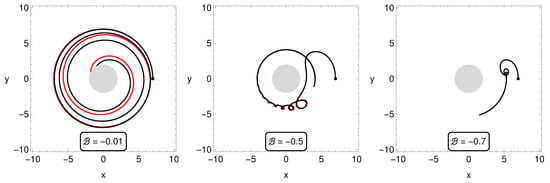
Figure 2.
Radiation reaction with (red curves) and without (black curves) tail term included for attractive () Lorentz force, similar to Figure 1. For attractive Lorentz force () the radiation reaction leads to infall into BH with or without the tail term. For larger magnetic field parameters (), the radiation reaction could even reverse the direction of the charged particle orbit, making the Lorentz force repulsive even in this case. All orbits are plotted for the same time interval () demonstrating the orbital motion slowing down with an increasing magnetic field parameter. The orbital widening effect will also appear in later phases of the test particle motion.
As we can see from formula (13), the energy increase in the case of pure self-interaction (tail term only, last negative term) is not possible. If the tail term is neglected, the presence of the second term (positive) can lead to an increase in energy. The second term is actually responsible for the orbital widening, which occurs only if . Radiating particle orbiting magnetized black hole with repulsive Lorentz force having energy oscillates around stable circular orbit and radiates away the oscillatory energy residing in the circular orbit, where it always has energy . Further, the positive term at circular orbit increases the energy of the particle towards unity, which causes the radiation reaction force to push the particle outwards the black hole. The energy, in this case, can only reach unity, i.e., rest mass energy at infinity. The orbital widening effect is relatively slow compared to the radiative cooling; however, for strong magnetic fields and a low density of plasma, the effect can potentially be faster than the particle collision timescale.
The interesting and complex problem of the “orbital widening” introduced in [19] was criticized in [23] based on an energetic argument. The detailed analysis using the relativistic equation of motion proves that orbital widening is a general theoretical phenomenon that can be present with and without the tail term. Still, for realistic astrophysical parameters, it is likely to be negligible. Here, one should take into account the charged particle’s mean free path, which could be comparable to one orbit around the black hole, but not to orbits needed for the orbital widening effect.
In Figure 3, we illustrate dependence of the influence of the tail term on the role of the back-reaction forces in dependence on the magnetic parameter and the reaction parameter k. When external magnetic field effect is not present () the particle without tail influence will stay on circular orbit. When the tail will be included, the particle will fall into the black hole with time of black hole capture depending on radiation parameter k. This scenario will remain valid for low values of external magnetic field (), but when external magnetic field is large () the orbital widening is reported for both trajectories with or without the tail term influence. Clearly, the combined effect of both and k is relevant and the appearance of the orbital widening effect occurs for a high enough .
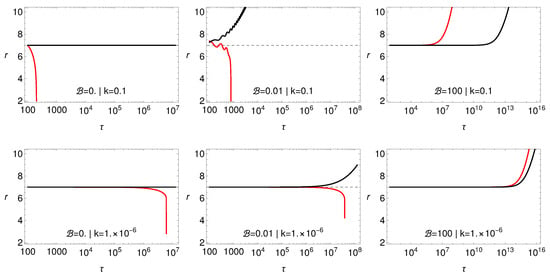
Figure 3.
Change of charged particle circular orbit radius with integration time due to the orbital widening effect. Trajectories for radiating charged particles with (red) and without the tail term (black) are compared. Different values for radiation k and magnetic filed parameters have been used.
Astrophysically, the most common and relevant situation is when the Lorentz force dominates the charged particle motion and synchrotron radiation causes radiation reaction. The gravitational force only slightly modifies the radiation process, and the electromagnetic tail term in this case can be ignored completely.
5. Astrophysical Implications
Due to the comparison of ratios of various components of the forces introduced above, we can immediately see those that are relevant in a given background and those that can be neglected. For example, it is useful to make a comparison of the following components
If only the first (classical) RR term is taken into account, while the relativistic term is neglected, we obtain the simple and elegant formula (1) from [23]. But even from this nonrelativistic formula, one cannot conclude that neglecting the tail term and keeping the radiation reaction is equivalent to neglecting the gravitational force while keeping the Lorentz force. For example, the formula (1) can be satisfied for theoretical situation ; obviously we can neglect the smallest tail term force. From the realistic ratios between forces presented in Table 1 one can conclude that the electron dynamics in a magnetic field of the order Gs (considered to be a typical magnetic field strength in many stellar black hole systems, such as microquasars) is driven by the Lorentz force, the second part of the radiation reaction force, and gravity, while the tail term is completely negligible in this case.
Large values of the magnetic field parameter in astrophysical settings suggest that the effects of EM interaction and RR can not be neglected since the LF and RR can be much stronger than gravity. Still, RR can overcome LF only for particles such as electrons (i.e., with large specific charge) in the presence of a very strong magnetic field with a magnitude of the order of Gs. In such a case, the gravitational interaction plays only a subtle role, while the tail term can be neglected completely. It appears that there is no astrophysical realistic combination of k and parameters, where all the forces would be of similar magnitudes.
6. Conclusions
When no external magnetic field is present or the magnetic field is very weak, gravity and the tail term remain, and the tail term cannot be neglected. In this case, the statement of [23] is applicable. However, even if a magnetic field of the order of a few Gauss arises, the LF and RR forces overcome the tail term by several orders of magnitude. Therefore, one can conclude that the tail term can be ignored for the dynamics of elementary particles in many astrophysical situations but can be relevant in other situations, depending on the ratio of relevant parameters, as demonstrated in Figure 4.
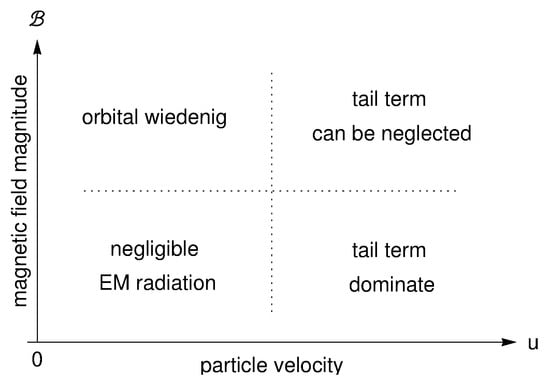
Figure 4.
The landscape of different radiating charged particle dynamical regimes demonstrating the parameter space, where the tail term can be relevant or negligible. For relativistic charged particles with high velocities, reflecting many astrophysical situations, the effect of the tail term can be neglected. Orbital widening has been reported for slowly moving particles under the combined gravitational and magnetic field influence.
The interesting problem of the “orbital widening” introduced in [10,19] is quite complex and depends on a wide variety of background conditions. Our results show a variety of possible behaviors of the circular orbit evolution under various relations of the relevant parameters reflecting different influences of the tail term—widening with and without the tail term, infall of the particle from the circular orbit due to radiative forces both with and without the tail term, and also the case of widening without the tail term, and fall with inclusion of the tail term. Similar to [23], we consider circular orbits at large distances from the black hole (Newtonian regime). Orbital widening can occur only under repulsive Lorentz force. In a future article, we plan to discuss the dynamics of charged particles under the influence of the tail term in considering various types of the background electromagnetic field.
Author Contributions
Conceptualization, Z.S. and M.K.; methodology, A.T.; validation, A.T. and D.G.; writing, Z.S., M.K. and A.T.; visualization, M.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research was partially funded (M.K. and A.T.) by the GAČR grant No. 23-07043S.
Data Availability Statement
Data are contained within the article.
Acknowledgments
The authors would like to acknowledge institutional support by the Research Centre for Theoretical Physics and Astrophysics, Institute of Physics, Silesian University in Opava.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Tursunov, A.; Dadhich, N. Fifty Years of Energy Extraction from Rotating Black Hole: Revisiting Magnetic Penrose Process. Universe 2019, 5, 125. [Google Scholar] [CrossRef]
- Stuchlík, Z.; Kološ, M.; Kovář, J.; Slaný, P.; Tursunov, A. Influence of Cosmic Repulsion and Magnetic Fields on Accretion Disks Rotating around Kerr Black Holes. Universe 2020, 6, 26. [Google Scholar] [CrossRef]
- Stuchlík, Z.; Kološ, M.; Tursunov, A. Penrose Process: Its Variants and Astrophysical Applications. Universe 2021, 7, 416. [Google Scholar] [CrossRef]
- Blandford, R.D.; Znajek, R.L. Electromagnetic extraction of energy from Kerr black holes. Mon. Not. R. Astron. Soc. 1977, 179, 433–456. [Google Scholar] [CrossRef]
- Dadhich, N.; Tursunov, A.; Ahmedov, B.; Stuchlík, Z. The distinguishing signature of magnetic Penrose process. Mon. Not. R. Astron. Soc. 2018, 478, L89–L94. [Google Scholar] [CrossRef]
- Nakamura, M.; Asada, K.; Hada, K.; Pu, H.; Noble, S.; Tseng, C.; Toma, K.; Kino, M.; Nagai, H.; Takahashi, K.; et al. Parabolic Jets from the Spinning Black Hole in M87. Astrophys. J. 2018, 868, 146. [Google Scholar] [CrossRef]
- Stuchlík, Z.; Blaschke, M.; Kovář, J.; Slaný, P. Charged fluid nonconducting toroidal structures orbiting a Schwarzschild black hole immersed in a split-monopole magnetic field. Phys. Rev. D 2022, 105, 103012. [Google Scholar] [CrossRef]
- Frolov, V.P.; Shoom, A.A. Motion of charged particles near a weakly magnetized Schwarzschild black hole. Phys. Rev. D 2010, 82, 084034. [Google Scholar] [CrossRef]
- Shoom, A.A. Synchrotron radiation from a weakly magnetized Schwarzschild black hole. Phys. Rev. D 2015, 92, 124066. [Google Scholar] [CrossRef]
- Tursunov, A.; Kološ, M.; Stuchlík, Z.; Galtsov, D.V. Radiation Reaction of Charged Particles Orbiting a Magnetized Schwarzschild Black Hole. Astrophys. J. 2018, 861, 2. [Google Scholar] [CrossRef]
- Kološ, M.; Shahzadi, M.; Tursunov, A. Charged particle dynamics in parabolic magnetosphere around Schwarzschild black hole. Eur. Phys. J. C 2023, 83, 323. [Google Scholar] [CrossRef]
- Johnston, M.; Ruffini, R.; Zerilli, F. Gravitationally Induced Electromagnetic Radiation. Phys. Rev. Lett. 1973, 31, 1317–1319. [Google Scholar] [CrossRef]
- Sokolov, A.A.; Gal’tsov, D.V.; Petukhov, V.I. Radiation emitted by relativistic particles moving in the vicinity of the Schwarzschild black hole, immersed in an external magnetic field. Phys. Lett. A 1978, 68, 1–2. [Google Scholar] [CrossRef]
- Zerilli, F.J. Gravitational and electromagnetic radiation around black holes. Nuovo Cimento B Ser. 2000, 115, 687. [Google Scholar]
- DeWitt, B.S.; Brehme, R.W. Radiation damping in a gravitational field. Ann. Phys. 1960, 9, 220–259. [Google Scholar] [CrossRef]
- Hobbs, J. A vierbein formalism of radiation damping. Ann. Phys. 1968, 47, 141–165. [Google Scholar] [CrossRef]
- Poisson, E. The Motion of Point Particles in Curved Spacetime. Living Rev. Relativ. 2004, 7, 6. [Google Scholar] [CrossRef] [PubMed]
- Gal’tsov, D.V. Radiation reaction in various dimensions. Phys. Rev. D 2002, 66, 025016. [Google Scholar] [CrossRef]
- Tursunov, A.A.; Kološ, M.; Stuchlík, Z. Orbital widening due to radiation reaction around a magnetized black hole. Astron. Nachrichten 2018, 339, 341–346. [Google Scholar] [CrossRef]
- Kološ, M.; Tursunov, A.; Stuchlík, Z. Radiative Penrose process: Energy gain by a single radiating charged particle in the ergosphere of rotating black hole. Phys. Rev. D 2021, 103, 024021. [Google Scholar] [CrossRef]
- Rueda, J.A.; Ruffini, R.; Kerr, R.P. Gravitomagnetic Interaction of a Kerr Black Hole with a Magnetic Field as the Source of the Jetted GeV Radiation of Gamma-Ray Bursts. Astrophys. J. 2022, 929, 56. [Google Scholar] [CrossRef]
- Tursunov, A.; Stuchlík, Z.; Kološ, M.; Dadhich, N.; Ahmedov, B. Supermassive Black Holes as Possible Sources of Ultrahigh-energy Cosmic Rays. Astrophys. J. 2020, 895, 14. [Google Scholar] [CrossRef]
- Santos, J.S.; Cardoso, V.; Natário, J. Electromagnetic radiation reaction and energy extraction from black holes: The tail term cannot be ignored. Phys. Rev. D 2023, 107, 064046. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. The Classical Theory of Fields; Butterworth-Heinemann: Oxford, UK, 1975. [Google Scholar]
- Gal’tsov, D.V. Radiation reaction in the Kerr gravitational field. J. Phys. A Math. Gen. 1982, 15, 3737–3749. [Google Scholar] [CrossRef]
- Poisson, E.; Pound, A.; Vega, I. The Motion of Point Particles in Curved Spacetime. Living Rev. Relativ. 2011, 14, 7. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).