Rotation Matrix of a Charged Symmetrical Body: One-Parameter Family of Solutions in Elementary Functions

Abstract

Euler–Poisson equations of a charged symmetrical body in external constant and homogeneous electric and magnetic fields are deduced starting from the variational problem, where the body is considered as a system of charged point particles subject to holonomic constraints. The final equations are written for the center-of-mass coordinate, rotation matrix and angular velocity. A general solution to the equations of motion is obtained for the case of a charged ball. For the case of a symmetrical charged body (solenoid), the task of obtaining the general solution is reduced to the problem of a one-dimensional cubic pseudo-oscillator. In addition, we present a one-parametric family of solutions to the problem in elementary functions.

1. Introduction

Spinning bodies represent an important object of study in modern research at different scales, from problems of attitude stability and control of a spacecraft to levitating nano-particles and elementary particles with spin. The behavior of a spinning object in special and general relativity as well as in quantum mechanics in many cases is considered in the first order by perturbation theory based on exact solutions to the classical problem [1]. Therefore, the search for new integrable cases and analytical solutions in the dynamics of a spinning body is important for further progress in such problems [2,3,4]. In the present work, we consider a charged spinning body in external constant and homogeneous electric and magnetic fields. While the case of a ferromagnet has been discussed quite widely in the literature [5,6,7,8,9,10], much less attention has been paid to a charged dielectric [11]. In this article we will try to fill this gap in the literature.

This work is organized as follows. In Section 2, we deduce equations of motion on the base of a Lagrangian action, formulated for the case under consideration. We will present a detailed derivation of the equations, since semi-empirical methods applied to a spinning body in some cases lead to either inaccuracies or erroneous interpretation of the final result [12,13,14,15]. In Section 3, we present a general solution to the obtained equations for the case of a charged ball. In Section 4, we reduce the problem of a symmetrical charged body to the problem of a one-dimensional non-linear pseudo-oscillator. In Section 5, we present a one-parametric family of solutions in elementary functions for the motions with specially chosen initial angular velocity of the symmetrical charged body. In the Appendix A, for the convenience of the reader, we summarized the motion of a point charged particle in an external electromagnetic field.

2. Charged Body in Constant and Homogeneous Electric and Magnetic Fields

Consider a rigid body that consists of n particles ${\mathbf{y}}_N\left(t\right)$ of charge $e_N$ and mass $m_N$, $N=1,2,\dots ,n$. Its Lagrangian action reads [12] as follows:

$$\begin{array}{c}\hfill S=\int dt\frac{1}{2}{\sum }_{N=1}^n{m}_N{\dot{\mathbf{y}}}_N^2+\frac{1}{2}{\sum }_{A,B=2}^4{\lambda }_{AB}\left[({\mathbf{y}}_A-{\mathbf{y}}_1,{\mathbf{y}}_B-{\mathbf{y}}_1)-a_{AB}\right]\\ \hfill +\frac{1}{2}{\sum }_{A=2}^4{\sum }_{\beta =5}^n{\lambda }_{A\beta }\left[({\mathbf{y}}_A-{\mathbf{y}}_1,{\mathbf{y}}_{\beta }-{\mathbf{y}}_1)-a_{A\beta }\right].\end{array}$$

(1)

The first term is the kinetic energy of all particles, while the remaining terms account for the presence of constraints that guarantee that distances and angles among the particles do not change with time1 The constraints were added with the help of the Lagrangian multiplier ${\lambda }_{AN}\left(t\right)$. In all calculations, these auxiliary variables should be treated on an equal footing with ${\mathbf{y}}_N\left(t\right)$. In particular, looking for the equations of motion, we take variations with respect to ${\mathbf{y}}_N$ and all ${\lambda }_{AN}$. The $3\times 3$ block ${\lambda }_{AB}$ of ${\lambda }_{AN}$ was chosen to be the symmetric matrix. The variations with respect to ${\lambda }_{AN}$ imply the constraints, which therefore arise as a part of conditions of the extreme of the action functional. So, the presence of ${\lambda }_{AN}$ allows $y_N^i$ to be treated as an unconstrained variable that should be varied independently in obtaining the equations of motion.

We consider the body immersed into constant and homogeneous electric and magnetic fields with scalar potential $A_0\left({\mathbf{y}}_N\right)$ and vector potential $\mathbf{A}\left({\mathbf{y}}_N\right)$, see Appendix A. Generally, its movement will produce a time-dependent distribution of charges and currents leading to the radiation of an electromagnetic field, see Chapter 17 in [16]. We neglect the resulting radiation and radiation damping effects. Then, summing up the potential energies (A15) of the body’s particles, we obtain the total potential energy

$$\begin{array}{c}\hfill -U=\sum _{N=1}^n{e}_N{A}_0\left({\mathbf{y}}_N\right)+\frac{e_N}{c}(\mathbf{A}\left({\mathbf{y}}_N\right),{\dot{\mathbf{y}}}_N).\end{array}$$

(2)

Adding it to Action (1), we obtain a variational problem for the body in external electric and magnetic fields. We assume that all particles of the body have the same charge to mass ratio, $\frac{e_N}{m_N}=\mu$ for any $N=1,2,\dots ,n$. Then, our action implies the following dynamical equations:

$$\begin{array}{c}\hfill m_1{\ddot{\mathbf{y}}}_1=-{\sum }_{AB}{\lambda }_{AB}[{\mathbf{y}}_B-{\mathbf{y}}_1]-\frac{1}{2}{\sum }_{A\alpha }{\lambda }_{A\alpha }[{\mathbf{y}}_A+{\mathbf{y}}_{\alpha }-2{\mathbf{y}}_1]+\mu m_1\mathbf{E}+\frac{\mu }{c}{m}_1[{\dot{\mathbf{y}}}_1,\mathbf{B}],\\ \hfill m_A{\ddot{\mathbf{y}}}_A={\sum }_B{\lambda }_{AB}[{\mathbf{y}}_B-{\mathbf{y}}_1]+\frac{1}{2}{\sum }_{\alpha }{\lambda }_{A\alpha }[{\mathbf{y}}_{\alpha }-{\mathbf{y}}_1]+\mu m_A\mathbf{E}+\frac{\mu }{c}{m}_A[{\dot{\mathbf{y}}}_A,\mathbf{B}],\\ \hfill m_{\alpha }{\ddot{\mathbf{y}}}_{\alpha }=\frac{1}{2}{\sum }_A{\lambda }_{A\alpha }[{\mathbf{y}}_A-{\mathbf{y}}_1]+\mu m_{\alpha }\mathbf{E}+\frac{\mu }{c}{m}_{\alpha }[{\dot{\mathbf{y}}}_{\alpha },\mathbf{B}].\end{array}$$

(3)

Introducing the center of mass, ${\mathbf{y}}_0=\frac{1}{{\mu }_0}\sum m_N{\mathbf{y}}_N$, where ${\mu }_0=\sum m_N$, Equations (3) imply

$$\begin{array}{c}\hfill {\ddot{\mathbf{y}}}_0=\mu \mathbf{E}+\frac{\mu }{c}[{\dot{\mathbf{y}}}_0,\mathbf{B}],\end{array}$$

(4)

that is, the center of mass behaves like the charged point particle discussed in the Appendix A. In particular, the rotational motion of the body does not affect its translational motion.

Substituting ${\mathbf{y}}_N={\mathbf{y}}_0+{\mathbf{x}}_N$ into Equation (3) and taking into account (4), we rewrite these equations in the center-of-mass coordinate system:

$$\begin{array}{c}\hfill m_1{\ddot{x}}_1^i=-{\sum }_{A,B=2}^4{\lambda }_{AB}[x_B^i-x_1^i]-\frac{1}{2}{\sum }_{A\alpha }{\lambda }_{A\alpha }[x_A^i+x_{\alpha }^i-2x_1^i]+m_1{\lambda }^i+\mu m_1\mathbf{E}+\frac{\mu }{c}{m}_1[{\dot{\mathbf{x}}}_1,\mathbf{B}],\\ \hfill m_A{\ddot{x}}_A^i={\sum }_{B=2}^4{\lambda }_{AB}[x_B^i-x_1^i]+\frac{1}{2}{\sum }_{\alpha =5}^n{\lambda }_{A\alpha }[x_{\alpha }^i-x_1^i]+m_A{\lambda }^i+\mu m_A\mathbf{E}+\frac{\mu }{c}{m}_A[{\dot{\mathbf{x}}}_A,\mathbf{B}],\\ \hfill m_{\alpha }{\ddot{x}}_{\alpha }^i=\frac{1}{2}{\sum }_{A=2}^4{\lambda }_{A\alpha }[x_A^i-x_1^i]+m_{\alpha }{\lambda }^i+\mu m_{\alpha }\mathbf{E}+\frac{\mu }{c}{m}_{\alpha }[{\dot{\mathbf{x}}}_{\alpha },\mathbf{B}].\end{array}$$

(5)

Each solution $x_N^i\left(t\right)$ to these equations is of the form $x_N^i\left(t\right)=R_{ik}\left(t\right)x_N^k\left(0\right)$, where $R_{ij}\left(t\right)$ is an orthogonal matrix that, by construction, obeys the universal initial data $R_{ij}\left(0\right)={\delta }_{ij}$. Substituting this expression into Equations (5), then multiplying the equation with number N by $x_N^j\left(0\right)$ and taking their sum, we obtain the following second-order equations for determining the rotation matrix $R_{ik}$:

$$\begin{array}{c}\hfill {\ddot{R}}_{ik}{g}_{kj}=-R_{ik}{\lambda }_{kj}+\mu E_i(\sum m_N{\mathbf{x}}_N)-A_{ia}{g}_{aj},R^{T}R=\mathbf{1},R\left(0\right)=\mathbf{1}.\end{array}$$

(6)

It is denoted

$$\begin{array}{c}\hfill A_{ia}=\frac{\mu }{c}{ϵ}_{inp}{B}_n{\dot{R}}_{pa}.\end{array}$$

(7)

In addition, $g_{ik}$ is the mass matrix

$$\begin{array}{c}\hfill g_{ij}\equiv \sum _{N=1}^n{m}_N{x}_N^i\left(0\right)x_N^j\left(0\right),\end{array}$$

(8)

while ${\lambda }_{jk}\left(t\right)$ is the symmetric matrix

$$\begin{array}{c}\hfill {\lambda }_{jk}=-\sum _{AB}{\lambda }_{AB}\left[x_1^j{x}_1^k+x_A^j{x}_B^k-x_B^{(j}{x}_1^{k)}\right]-\frac{1}{2}\sum _{A\alpha }{\lambda }_{A\alpha }\left[x_{\alpha }^{(j}{x}_A^{k)}-x_{\alpha }^{(j}{x}_1^{k)}-x_A^{(j}{x}_1^{k)}-2x_1^j{x}_1^k\right],\end{array}$$

(9)

where all $x_N^i$ are taken at the instant $t=0$.

Due to the identity $\sum m_N{\mathbf{x}}_N=0$, satisfied for the center-of-mass coordinates, the second term on the r. h. s. of Equation (6) vanishes. In the result, the electric field does not affect the motion of rotational degrees of freedom. In addition, the center-of-mass variable does not enter into this equation, so the translational motion does not affect the rotational motion of the body.

The variable ${\lambda }_{jk}\left(t\right)$ in Equation (6) depends on the unknown dynamical variable ${\lambda }_{AN}\left(t\right)$. Fortunately, we do not need to know ${\lambda }_{jk}\left({\lambda }_{AN}\left(t\right)\right)$, because these equations determine ${\lambda }_{jk}$ algebraically, as some functions of R and $\dot{R}$. This result, obtained with the use of the procedure described in [12], can be formulated as follows:

Affirmation. 

Consider the second-order system for determining the variables $R_{ij}\left(t\right)$ and ${\lambda }_{kj}\left(t\right)$

$$\begin{array}{c}\hfill {\ddot{R}}_{ik}{g}_{kj}=-R_{ik}{\lambda }_{kj}-A_{ik}{g}_{kj},R^{T}R=\mathbf{1},\end{array}$$

(10)

where $A_{ik}(R_{ab},{\dot{R}}_{ab})$ is some given matrix that does not depend on $g_{kj}$ and ${\lambda }_{kj}$ (as before, $g_{kj}$ is a numerical symmetric non-degenerate matrix, and ${\lambda }_{kj}\left(t\right)={\lambda }_{jk}\left(t\right)$).

Problem (10) is equivalent to the following Cauchy problem for the first-order system, written for the mutually independent variables $R_{ij}\left(t\right)$ and ${\Omega }_i\left(t\right)$:

$$\begin{array}{c}\hfill I_{ka}{\dot{\Omega }}_a={[I\mathbf{\Omega },\mathbf{\Omega }]}_k+\frac{1}{2}{ϵ}_{kij}\left[{\left(AI\right)}_{ai}{R}_{aj}+{\left(RI\right)}_{ai}{A}_{aj}\right]-\frac{1}{2}{I}_{ka}{ϵ}_{aij}{A}_{bi}{R}_{bj},\end{array}$$

(11)

$$\begin{array}{c}\hfill {\dot{R}}_{ij}=-{ϵ}_{jab}{\Omega }_a{R}_{ib},R_{ij}\left(0\right)={\delta }_{ij},\end{array}$$

(12)

where I is an inertia tensor of the body with the components $I_{ij}=(\sum g_{aa}){\delta }_{ij}-g_{ij}$.

Note that this system is composed of $SO\left(3\right)$ vectors and tensors, so it is covariant under the rotations. We will work with these equations assuming that the mass matrix and inertia tensor are of diagonal form. This implies [12] that at initial instant $t=0$ the Laboratory basis vector ${\mathbf{e}}_i$ was taken in the directions of the axes of inertia ${\mathbf{R}}_i\left(t\right)$ taken as the body-fixed frame: ${\mathbf{e}}_i={\mathbf{R}}_i\left(0\right)$. We also recall that the body-fixed basis vectors are columns of the rotation matrix: $R=({\mathbf{R}}_1,{\mathbf{R}}_2,{\mathbf{R}}_3)$. Eigenvalues of the mass matrix and inertia tensor are related as follows: $2g_1=I_2+I_3-I_1$, and so on.

Our Equation (6) are of the form (10), so they are equivalent to the first-order system (11) and (12) with A written in (7). To obtain an explicit form of Equation (11), we use (12) to rewrite the quantity $A_{ia}$ as follows:

$$\begin{array}{c}\hfill {ϵ}_{ijk}{B}_j{\dot{R}}_{ka}={ϵ}_{ijk}{ϵ}_{abc}{B}_j{\Omega }_b{R}_{kc}={ϵ}_{ijk}{ϵ}_{\alpha \beta \gamma }{R}_{\alpha a}{R}_{\beta b}{R}_{\gamma c}{B}_j{\Omega }_b{R}_{kc}=\\ \hfill {ϵ}_{ijk}{ϵ}_{\alpha \beta \gamma }{R}_{\alpha a}{B}_j{(R\mathbf{\Omega })}_{\beta }{\left(R{R}^T\right)}_{\gamma k}={ϵ}_{ijk}{ϵ}_{\alpha \beta k}{R}_{\alpha a}{B}_j{(R\mathbf{\Omega })}_{\beta }=R_{ia}(\mathbf{B}R\mathbf{\Omega })-{(R\mathbf{\Omega })}_i{\left(\mathbf{B}R\right)}_a.\end{array}$$

Thus,

$$\begin{array}{c}\hfill A_{ia}=-\frac{\mu }{c}{ϵ}_{ijk}{ϵ}_{abc}{B}_j{\Omega }_b{R}_{kc}=\frac{\mu }{c}\left[{(R\mathbf{\Omega })}_i{\left(\mathbf{B}R\right)}_a-R_{ia}(\mathbf{B}R\mathbf{\Omega })\right].\end{array}$$

(13)

Using the latter expression for $A_{ia}$ in Equation (11), after direct calculations, this acquires the form

$$\begin{array}{c}\hfill I\dot{\mathbf{\Omega }}=[I\mathbf{\Omega },\mathbf{\Omega }]-\frac{\mu }{2c}\left\{I[R^T\mathbf{B},\mathbf{\Omega }]-[I{R}^T\mathbf{B},\mathbf{\Omega }]+[R^T\mathbf{B},I\mathbf{\Omega }]\right\}.\end{array}$$

(14)

The vector composed of last three terms can be written in a more compact form in terms of the mass matrix. Indeed, writing the first component of this vector in explicit form we obtain

$$\begin{array}{c}{\left(I[R^T\mathbf{B},\mathbf{\Omega }]\right)}_1-{[I{R}^T\mathbf{B},\mathbf{\Omega }]}_1+{[R^T\mathbf{B},I\mathbf{\Omega }]}_1=\\ (I_1-I_2+I_3){\left(R^T\mathbf{B}\right)}_2{\Omega }_3-(I_1-I_3+I_2){\left(R^T\mathbf{B}\right)}_3{\Omega }_2=\\ 2g_2{\left(R^T\mathbf{B}\right)}_2{\Omega }_3-2g_3{\left(R^T\mathbf{B}\right)}_3{\Omega }_2=2{[g{R}^T\mathbf{B},\mathbf{\Omega }]}_1,\end{array}$$

(15)

and similar expressions for the second and third components. Then, Equation (11) acquires the final form

$$\begin{array}{c}\hfill I\dot{\mathbf{\Omega }}=[I\mathbf{\Omega },\mathbf{\Omega }]-\frac{\mu }{c}[g{R}^T\mathbf{B},\mathbf{\Omega }].\end{array}$$

(16)

For completeness, we also present equations for the vector of angular momentum $\mathbf{m}=RI\mathbf{\Omega }$ and for its components $\mathbf{M}=I\mathbf{\Omega }$ in the body-fixed frame

$$\begin{array}{c}\hfill \dot{\mathbf{m}}=-\frac{\mu }{c}[Rg{R}^T\mathbf{B},R{I}^{-1}{R}^T\mathbf{m}],\end{array}$$

(17)

$$\begin{array}{c}\hfill \dot{\mathbf{M}}=[\mathbf{M},I^{-1}\mathbf{M}]-\frac{\mu }{c}[g{R}^T\mathbf{B},I^{-1}\mathbf{M}].\end{array}$$

(18)

Let us consider Equation (16) in the Laboratory system with the third axis in the direction of magnetic vector $\mathbf{B}$. Denote by $I^{\prime }$ and $g^{\prime }$ the nondiagonal tensors of inertia and mass that will appear in these coordinates. Then, Equation (16) acquires the form $I^{\prime }\dot{\mathbf{\Omega }}=[I^{\prime }\mathbf{\Omega },\mathbf{\Omega }]-\frac{\mu \left|\mathbf{B}\right|}{c}[g^{\prime }{\mathbf{G}}_3,\mathbf{\Omega }]$, where ${\mathbf{G}}_3$ is the third row of the rotation matrix $R_{ij}$. They coincide with those deduced by G. Grioli, see [1,11].

In summary, we have succeeded in obtaining equations of motion (4), (12) and (16) for a spinning charged body in external electric and magnetic fields. The solution $R_{ij}\left(t\right)$, $y_0^i\left(t\right)$ to these equations contains complete information on the evolution of the body with respect to the Laboratory frame: dynamics of the body’s point $y_N^i\left(t\right)$ with initial position $y_N^i\left(0\right)=y_0^i\left(0\right)+x_N^i\left(0\right)$ is $y_N^i\left(t\right)=y_0^i\left(t\right)+R_{ij}\left(t\right)x_N^j\left(0\right)$.

3. General Solution to the Equations of a Charged Ball

Consider a totally symmetric charged body:

$$\begin{array}{c}\hfill I_1=I_2=I_3\equiv I_0.\end{array}$$

(19)

This could be a charged ball. Then, its center moves according to Equation (A13). From kinematic relations $\mathbf{m}={\sum }_{N=1}^n{m}_N[{\mathbf{x}}_N,{\dot{\mathbf{x}}}_N]={\sum }_i{g}_i[{\mathbf{R}}_i,{\dot{\mathbf{R}}}_i]=RI{R}^T\mathit{\omega }=RI\mathbf{\Omega }$ between angular momentum $\mathbf{m}$, angular velocity $\mathit{\omega }$ and its component ${\Omega }_i$ in the body-fixed frame, together with Equation (19), we obtain $\mathbf{m}=I_0\mathit{\omega }=I_{0}R\mathbf{\Omega }$. The first equality means that for all t the instantaneous rotation axis $\mathit{\omega }$ remains parallel with the vector of angular momentum. Substituting (19) into the equations of previous section, we obtain

$$\begin{array}{c}\hfill {\dot{R}}_{ij}=-{ϵ}_{jab}{\Omega }_a{R}_{ib},R_{ij}\left(0\right)={\delta }_{ij},\end{array}$$

(20)

$$\begin{array}{c}\hfill \dot{\mathbf{\Omega }}=-\frac{\mu }{2c}[R^T\mathbf{B},\mathbf{\Omega }];\end{array}$$

(21)

$$\begin{array}{c}\hfill \dot{\mathbf{m}}=-\frac{\mu }{2c}[\mathbf{B},\mathbf{m}].\end{array}$$

(22)

The last equation implies that angular momentum precesses around $\mathbf{B}$ with Larmor’s frequency $\alpha =\frac{\mu \left|\mathbf{B}\right|}{2c}$. In addition, the length of angular momentum and its projection on the $\mathbf{B}$-axis are the first integrals

$$\begin{array}{c}\hfill {\mathbf{m}}^2=\mathrm{const},(\mathbf{m},\mathbf{B})=\mathrm{const}.\end{array}$$

(23)

Components ${\Omega }_i$ of angular velocity $\mathit{\omega }$ with respect to the body-fixed frame precesses with the same frequency around components ${\left(R^T\mathbf{B}\right)}_i$ of magnetic field $\mathbf{B}$ in the body-fixed frame.

Substituting $\mathbf{\Omega }=\frac{1}{I_0}{R}^T\mathbf{m}$ into (21) and taking into account (20), we arrive at Equation (22). So, system (20), (21) is equivalent to ${\dot{R}}_{ij}=-\frac{1}{I_0}{ϵ}_{jab}{\left(R^T\mathbf{m}\right)}_a{R}_{ib}$, $\dot{\mathbf{m}}=-\frac{\mu }{2c}[\mathbf{B},\mathbf{m}]$. Further, the first (non-linear on R) equation of the latter system can be replaced on the linear equation ${\dot{R}}_{ij}=\frac{1}{I_0}{ϵ}_{iab}{m}_a{R}_{bj}$. The resulting system and the initial one have the same solutions in the set of orthogonal matrices. In the result, instead of Equations (20) and (21), a totally symmetric body can be described by the equations

$$\begin{array}{c}\hfill {\dot{R}}_{ij}=\frac{1}{I_0}{ϵ}_{iab}{m}_a{R}_{bj},\mathrm{or},\mathrm{equivalently}{\dot{\mathbf{R}}}_j=\frac{1}{I_0}[\mathbf{m},{\mathbf{R}}_j],\end{array}$$

(24)

$$\begin{array}{c}\hfill \dot{\mathbf{m}}=-\frac{\mu }{2c}[\mathbf{B},\mathbf{m}],\end{array}$$

(25)

where all quantities are defined with respect to the Laboratory system. The initial conditions are $R_{ij}\left(0\right)={\delta }_{ij}$. According to these equations, $\mathbf{m}\left(t\right)$ precesses around constant vector $\mathbf{B}$, while vectors ${\mathbf{R}}_j\left(t\right)$ instantaneously precess around $\mathbf{m}\left(t\right)$.

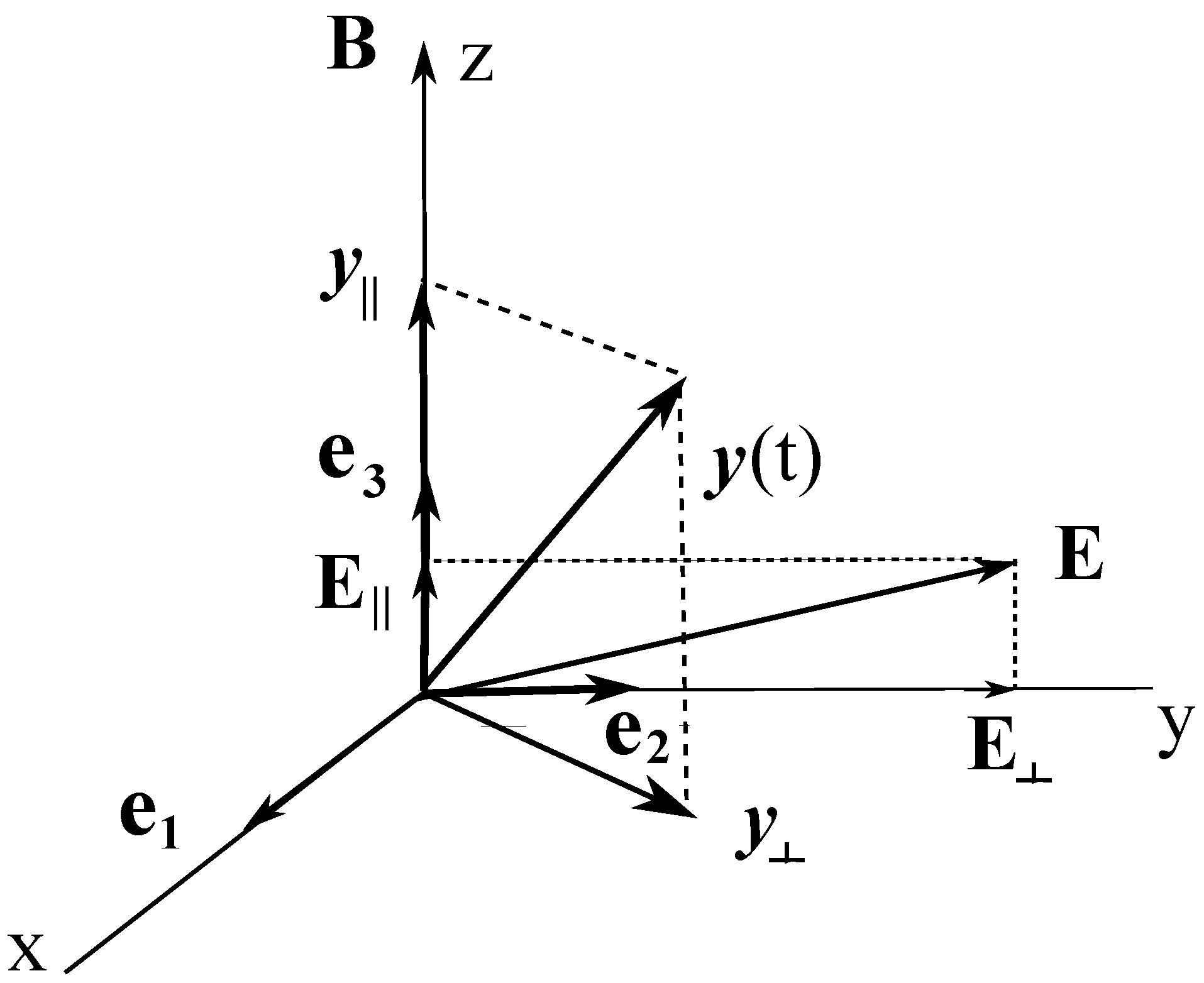
Let us obtain the general solution to system (24) and (25). For a totally symmetric body, we can choose the directions of Laboratory axes as convenient; this will not violate the diagonal form of the inertia tensor. Using this freedom, we choose the Laboratory system so that at $t=0$ the vectors $\mathbf{B}$ and $\mathbf{m}\left(0\right)$ lie in the plane of ${\mathbf{e}}_2$ and ${\mathbf{e}}_3$, and $\mathbf{B}$ is directed along ${\mathbf{e}}_3$, see Figure 1.

Then, $\mathbf{B}={(0,0,|\mathbf{B}\left|\right)}^T$, $\mathbf{m}\left(0\right)={(0,m_2,m_3)}^T$, and

$$\begin{array}{c}\hfill \mathbf{m}\left(t\right)=\left(\begin{array}{ccc}cos\alpha t& sin\alpha t& 0\\ -sin\alpha t& cos\alpha t& 0\\ 0& 0& 1\end{array}\right)\left(\begin{array}{c}0\\ m_2\\ m_3\end{array}\right)=\left(\begin{array}{c}{m}_{2}sin\alpha t\\ m_{2}cos\alpha t\\ m_3\end{array}\right),\end{array}$$

(26)

is a solution to Equation (25), where the precession frequency is the Larmor’s frequency

$$\begin{array}{c}\hfill \alpha =\frac{\mu \left|\mathbf{B}\right|}{2c}.\end{array}$$

(27)

To solve Equation (24) with this $\mathbf{m}\left(t\right)$, we look for its solution in the form

$$\begin{array}{c}\hfill {\displaystyle \left|\begin{array}{ccc}cos\gamma tcos\alpha t-{\widehat{k}}_{3}sin\gamma tsin\alpha t& {\widehat{k}}_{3}sin\gamma tcos\alpha t+B\left(t\right)sin\alpha t& -{\widehat{k}}_{2}sin\gamma tcos\alpha t+{\widehat{k}}_2{\widehat{k}}_{3}A\left(t\right)sin\alpha t\\ & & \\ -cos\gamma tsin\alpha t-{\widehat{k}}_{3}sin\gamma tcos\alpha t& -{\widehat{k}}_{3}sin\gamma tsin\alpha t+B\left(t\right)cos\alpha t& {\widehat{k}}_{2}sin\gamma tsin\alpha t+{\widehat{k}}_2{\widehat{k}}_{3}A\left(t\right)cos\alpha t\\ & & \\ {\widehat{k}}_{2}sin\gamma t& {\widehat{k}}_2{\widehat{k}}_{3}A\left(t\right)& {\widehat{k}}_3^2+{\widehat{k}}_2^{2}cos\gamma t\end{array}\right|}\end{array}$$

$$\begin{array}{c}\hfill =\left(\begin{array}{ccc}cos\alpha t& sin\alpha t& 0\\ -sin\alpha t& cos\alpha t& 0\\ 0& 0& 1\end{array}\right)\left(\begin{array}{ccc}cos\gamma t& {\widehat{k}}_{3}sin\gamma t& -{\widehat{k}}_{2}sin\gamma t\\ & & \\ -{\widehat{k}}_{3}sin\gamma t& B\left(t\right)& {\widehat{k}}_2{\widehat{k}}_{3}A\left(t\right)\\ & & \\ {\widehat{k}}_{2}sin\gamma t& {\widehat{k}}_2{\widehat{k}}_{3}A\left(t\right)& {\widehat{k}}_3^2+{\widehat{k}}_2^{2}cos\gamma t\end{array}\right),\end{array}$$

(28)

where it was denoted $A\left(t\right)=1-cos\gamma t$ and $C\left(t\right)={\widehat{k}}_2^2+{\widehat{k}}_3^{2}cos\gamma t$. To fix $\widehat{\mathbf{k}}$ and $\gamma$, we substitute the ansatz (28) into (24) and then take $t=0$ in the resulting expressions. They determine $\widehat{\mathbf{k}}$ as follows: ${\widehat{k}}_2=-\frac{m_2}{\gamma I_0}$, ${\widehat{k}}_3=-\frac{\alpha I_0+m_3}{\gamma I_0}$. Then, ${\widehat{k}}_2^2+{\widehat{k}}_3^2=1$ implies $I_0^2{\gamma }^2=m_2^2+{(\alpha I_0+m_3)}^2$. The obtained equalities allow us to represent $\mathbf{k}$ and $\gamma$ through $\mathbf{m}$ and $\alpha$ as follows:

$$\begin{array}{c}\hfill {\widehat{k}}_2=-\frac{m_2}{\sqrt{m_2^2+{(\alpha I_0+m_3)}^2}},\\ \hfill {\widehat{k}}_3=-\frac{m_3+\alpha I_0}{\sqrt{m_2^2+{(\alpha I_0+m_3)}^2}},\\ \hfill \gamma =\frac{1}{I_0}\sqrt{m_2^2+{(\alpha I_0+m_3)}^2}.\end{array}$$

(29)

By direct calculations, it can be verified that expression (28) with these $\widehat{\mathbf{k}}$ and $\gamma$ satisfies Equation (24).

In summary, we obtained an analytical solution for a charged ball launched with an initial angular velocity $\mathit{\omega }=\frac{1}{I_0}\mathbf{m}=\frac{1}{I_0}{(0,m_2,m_3)}^T$ in constant and homogeneous electric $\mathbf{E}$ and magnetic $\mathbf{B}$ fields. This is given by the double-frequency rotation matrix (28) and (29). The total motion can be thought of as a superposition of two rotations: the first around unit vector $\widehat{\mathbf{k}}={(0,{\widehat{k}}_2,{\widehat{k}}_3)}^T$ with frequency $\gamma$, and the second around the axis of magnetic field $\mathbf{B}={(0,0,|\mathbf{B}\left|\right)}^T$ with frequency $\alpha =\frac{\mu \left|\mathbf{B}\right|}{2c}$. The angular momentum vector $\mathbf{m}\left(t\right)$ precesses around the vector $\mathbf{B}$ with the Larmor’s frequency $\alpha =\frac{\mu \left|\mathbf{B}\right|}{2c}$.

Let us consider the ball launched with an initial vector of angular velocity parallel to the vector of magnetic field $\mathbf{B}$. That is, the initial conditions are $\mathbf{m}\left(0\right)={(0,0,m_3)}^T$. Then, $\mathbf{m}\left(t\right)={(0,0,m_3)}^T$, $\widehat{\mathbf{k}}={(0,0,-1)}^T$ and $\gamma =\alpha +\frac{m_3}{I_0}$. With these values, the rotation matrix (28) reduces to

$$\begin{array}{c}\hfill R=\left(\begin{array}{ccc}cos\frac{m_3}{I_0}t& -sin\frac{m_3}{I_0}t& 0\\ sin\frac{m_3}{I_0}t& cos\frac{m_3}{I_0}t& 0\\ 0& 0& 1\end{array}\right).\end{array}$$

(30)

As should be expected, the ball experiences a stationary rotation around the vector of magnetic field $\mathbf{B}$ with frequency $\frac{m_3}{I_0}$.

4. Symmetrical Charged Body and One-Dimensional Non-Linear Pseudo-Oscillator

In this section we start to study the symmetrical charged body. We show that, for any solution $R_{ij}\left(t\right)$, ${\Omega }_i\left(t\right)$ to the Euler–Poisson equations, the function ${\Omega }_3\left(t\right)$ obeys the equation of a one-dimensional cubic pseudo-oscillator, see Equation (47) below. In addition, when ${\Omega }_3\left(t\right)$ is known, the functions ${\Omega }_1\left(t\right)$ and ${\Omega }_2\left(t\right)$ can be found by quadratures, see Equations (44) and (45).

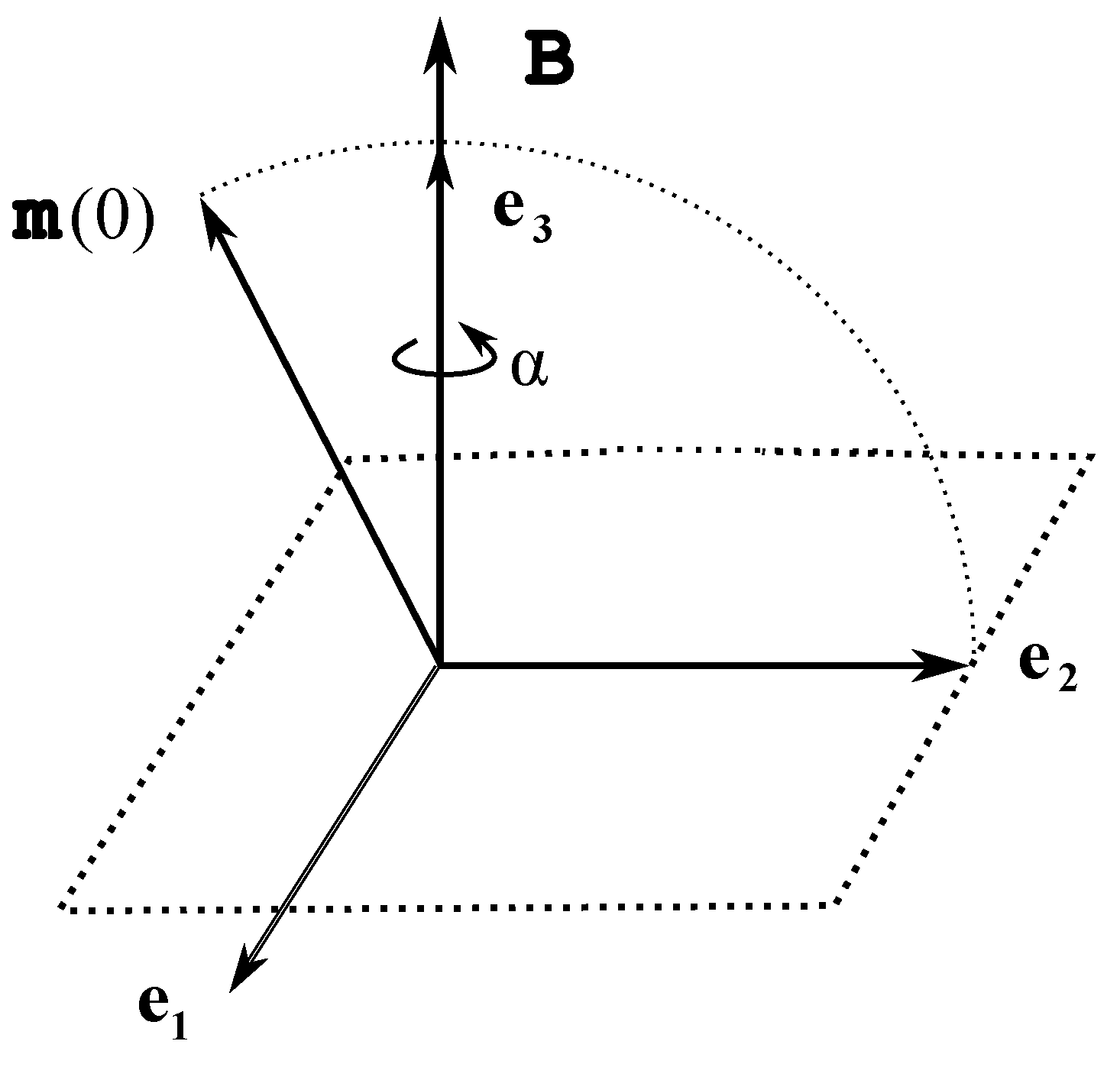
Consider Equations (12) and (16) for the symmetrical body2 $\mathbb{I}=diagonal(I_2,I_2,I_3)$. This implies the following mass matrix: $g=\frac{1}{2}diagonal(I_3,I_3,2I_2-I_3)$. We consider the positively charged body; then, the charge–mass ratio is a positive number, $\mu >0$. We assume that at $t=0$ the third inertia axis of the body is vertical. Then, without spoiling the diagonal form of the inertia tensor in our equations, the Laboratory system can be chosen as shown in Figure 2.

The basis vector ${\mathbf{e}}_3$ is directed along the third inertia axis ${\mathbf{R}}_3\left(0\right)$; the vectors ${\mathbf{e}}_2$ and ${\mathbf{e}}_3$ lie on the plane of a paper sheet together with the vector of constant magnetic field $\mathbf{B}={(0,B_2>0,B_3>0)}^T$. The initial instantaneous angular velocity of the body is

$$\begin{array}{c}\hfill \mathbf{\Omega }\left(0\right)=\mathit{\omega }\left(0\right)={({\omega }_1,{\omega }_2,{\omega }_3)}^T.\end{array}$$

(31)

It is convenient to introduce the following notation:

$$\begin{array}{c}\hfill {\mathbf{B}}^{\prime }\equiv \frac{\mu }{2c}\mathbf{B}=\left(\begin{array}{c}0\\ B_2^{\prime }>0\\ B_3^{\prime }>0\end{array}\right),\mathbf{K}\left(t\right)\equiv \frac{\mu }{2c}\mathbf{B}R\left(t\right)=\left(\begin{array}{c}{\left({\mathbf{B}}^{\prime }R\right)}_1\\ {\left({\mathbf{B}}^{\prime }R\right)}_2\\ {\left({\mathbf{B}}^{\prime }R\right)}_3\end{array}\right),\end{array}$$

(32)

then $\mathbf{K}\left(0\right)={\mathbf{B}}^{\prime }$. It was denoted

$$\begin{array}{c}\hfill I\equiv \frac{I_3}{I_2},E^{\prime }\equiv \frac{2E}{I_2}.\end{array}$$

(33)

Contracting the Poisson Equations (12) with $B_i^{\prime }$, we obtain $\dot{\mathbf{K}}=-[\mathbf{\Omega },\mathbf{K}]$. This equation together with (16) gives us the auxiliary system of $3+3$ closed equations for determining the variables $\mathbf{\Omega }\left(t\right)$ and $\mathbf{K}\left(t\right)$:

$$\begin{array}{c}\hfill \mathbb{I}\dot{\mathbf{\Omega }}=[\mathbb{I}\mathbf{\Omega },\mathbf{\Omega }]-2[\mathbf{K}g,\mathbf{\Omega }],\end{array}$$

(34)

$$\begin{array}{c}\hfill \dot{\mathbf{K}}=-[\mathbf{\Omega },\mathbf{K}].\end{array}$$

(35)

By construction, the initial conditions for $\mathbf{K}\left(t\right)$ are $\mathbf{K}\left(0\right)={\mathbf{B}}^{\prime }$. Any solution $R_{ij}\left(t\right)$, ${\Omega }_i\left(t\right)$ to the Euler–Poisson equations obeys this system. So, we can use the latter to look for the angular velocity ${\Omega }_i\left(t\right)$.

This system admits four integrals of motion. Two of them are

$$\begin{array}{c}\hfill {\Omega }_1^2+{\Omega }_2^2+I{\Omega }_3^2=E^{\prime }={\omega }_1^2+{\omega }_2^2+I{\omega }_3^2,\end{array}$$

(36)

$$\begin{array}{c}\hfill {\mathbf{K}}^2=B_2^{\prime 2}+B_3^{\prime 2}.\end{array}$$

(37)

To obtain two more integrals, we write our system in components:

$$\begin{array}{c}{\dot{\Omega }}_1=(1-I){\Omega }_3{\Omega }_2-I{\Omega }_3{K}_2+(2-I){\Omega }_2{K}_3,\hfill \\ {\dot{\Omega }}_2=-(1-I){\Omega }_3{\Omega }_1+I{\Omega }_3{K}_1-(2-I){\Omega }_1{K}_3,\hfill \\ {\dot{\Omega }}_3={\Omega }_1{K}_2-{\Omega }_2{K}_1;\hfill \end{array}$$

(38)

$$\begin{array}{c}{\dot{K}}_1={\Omega }_3{K}_2-{\Omega }_2{K}_3,\\ {\dot{K}}_2=-{\Omega }_3{K}_1+{\Omega }_1{K}_3,\\ {\dot{K}}_3=-({\Omega }_1{K}_2-{\Omega }_2{K}_1).\end{array}$$

(39)

The equations with ${\dot{\Omega }}_3$ and ${\dot{K}}_3$ imply the third integral:

$$\begin{array}{c}\hfill K_3+{\Omega }_3=c_3={\omega }_3+B_3^{\prime }.\end{array}$$

(40)

Combining the equations with ${\dot{\Omega }}_1$, ${\dot{\Omega }}_2$, ${\dot{K}}_1$ and ${\dot{K}}_2$, we obtain one more integral of motion:

$$\begin{array}{c}\hfill {\Omega }_1{K}_1+{\Omega }_2{K}_2-{\Omega }_3^2+(2-I)c_3{\Omega }_3=c_5={\omega }_2{B}_2^{\prime }-{\omega }_3^2+(2-I)({\omega }_3+B_3^{\prime }){\omega }_3.\end{array}$$

(41)

We have written them through the integration constants $c_3$ and $c_5$, as well as through the initial data ${\omega }_i$ and $B_i^{\prime }$ of the problem.

Using (40) and (41) and the equation with ${\dot{\Omega }}_3$ of system (38), we represent the variables $K_i$ through ${\Omega }_i$ as follows:

$$\begin{array}{c}\hfill K_1=\frac{{\Omega }_1({\Omega }_3^2-(2-I)c_3{\Omega }_3+c_5)-{\Omega }_2{\dot{\Omega }}_3}{E^{\prime }-I{\Omega }_3^2},\\ \hfill K_2=\frac{{\Omega }_2({\Omega }_3^2-(2-I)c_3{\Omega }_3+c_5)+{\Omega }_1{\dot{\Omega }}_3}{E^{\prime }-I{\Omega }_3^2},\\ \hfill K_3=-{\Omega }_3+c_3.\end{array}$$

(42)

Substituting them into the equations for ${\dot{\Omega }}_1$ and ${\dot{\Omega }}_2$ from (38), we obtain

$$\begin{array}{c}\hfill {\dot{\Omega }}_1=\varphi \left(t\right){\Omega }_2+\dot{f}\left(t\right){\Omega }_1,{\dot{\Omega }}_2=-\varphi \left(t\right){\Omega }_1+\dot{f}\left(t\right){\Omega }_2,\end{array}$$

(43)

where $\varphi \left(t\right)$ and $f\left(t\right)$ turn out to be the following functions of ${\Omega }_3\left(t\right)$:

$$\begin{array}{c}\hfill \varphi \left(t\right)\equiv \frac{(2-I)c_3{E}^{\prime }-(E^{\prime }+I{c}_5){\Omega }_3\left(t\right)}{E^{\prime }-I{\Omega }_3^2\left(t\right)},f\left(t\right)=ln\sqrt{E^{\prime }-I{\Omega }_3^2\left(t\right)}.\end{array}$$

(44)

If ${\Omega }_3\left(t\right)$ is known, Equations (43) can be immediately integrated as follows:

$$\begin{array}{c}\hfill {\Omega }_1\left(t\right)=f_0\sqrt{E^{\prime }-I{\Omega }_3^2\left(t\right)}sin(\Phi \left(t\right)+{\varphi }_0),{\Omega }_2\left(t\right)=f_0\sqrt{E^{\prime }-I{\Omega }_3^2\left(t\right)}cos(\Phi \left(t\right)+{\varphi }_0),\end{array}$$

(45)

where $\Phi \left(t\right)$ is the indefinite integral of $\varphi \left(t\right)$, while $f_0$ and ${\varphi }_0$ are the integration constants.

So, it remains to find the third component ${\Omega }_3\left(t\right)$. With this aim, we compute the time derivative of the last equation from (38), and use other equations of system (38) and (39) in the resulting expression, presenting it as follows:

$$\begin{array}{c}\hfill {\ddot{\Omega }}_3=[-2{\Omega }_3+(2-I)c_3]({\Omega }_1{K}_1+{\Omega }_2{k}_2)-I{\Omega }_3(K_1^2+K_2^2)+[c_3-{\Omega }_3]({\Omega }_1^2+{\Omega }_2^2).\end{array}$$

(46)

Using the integrals of motion (36), (37) and (41), we obtain a closed equation for determining ${\Omega }_3\left(t\right)$, that can be called the cubic pseudo-oscillator Equation:

$$\begin{array}{c}\hfill {\ddot{\Omega }}_3=a_0+a_1{\Omega }_3+a_2{\Omega }_3^2+a_3{\Omega }_3^3,\end{array}$$

(47)

where the numeric coefficient $a_i$ is a function of the initial data of the original problem

$$\begin{array}{c}{a}_0(\mathit{\omega },{\mathbf{B}}^{\prime })=[(2-I)c_5+E^{\prime }]c_3,\\ a_1(\mathit{\omega },{\mathbf{B}}^{\prime })=-2c_5+[I-{(2-1)}^2]c_3^2-E^{\prime }-I{\mathbf{B}}^{\prime 2},\\ a_2(\mathit{\omega },{\mathbf{B}}^{\prime })=6(1-I)c_3,a_3=-2(1-I).\end{array}$$

(48)

It is not difficult to obtain a two-parametric family of simple solutions to Equation (47). Note that ${\Omega }_3\left(t\right)={\omega }_3$ will be a (constant) solution to (47) if the third component ${\omega }_3$ of initial angular velocity is a root of the third-degree polynomial on the right side of (47). Substituting ${\Omega }_3\left(t\right)={\omega }_3$ into Equation (47), we obtain the condition on initial data ${\omega }_1,{\omega }_2,{\omega }_3$ under which ${\omega }_3$ satisfies this equation. To obtain this condition, it is convenient to represent Equation (47) in terms of the initial data, keeping combinations like ${\omega }_3-{\Omega }_3\left(t\right)$ as follows:

$$\begin{array}{c}\hfill {\ddot{\Omega }}_3=[(2-I)B_3^{\prime }-I{\omega }_3+2({\omega }_3-{\Omega }_3)][{\omega }_2{B}_2^{\prime }-({\omega }_3^2-{\Omega }_3^2)+\\ \hfill (2-I)(B_3^{\prime }+{\omega }_3)({\omega }_3-{\Omega }_3)]-I{\Omega }_3[{\mathbf{B}}^{\prime 2}-{(B_3^{\prime }+({\omega }_3-{\Omega }_3))}^2]+\\ \hfill { }_3^{\prime }+({\omega }_3-{\Omega }_3)][{\omega }_1^2+{\omega }_2^2+I({\omega }_3^2-{\Omega }_3^2)].\end{array}$$

(49)

Substituting ${\Omega }_3\left(t\right)={\omega }_3$, we get that (47) will be satisfied only for the initial data ${\omega }_i$ obeying the following equation:

$$\begin{array}{c}\hfill B_3^{\prime }({\omega }_1^2+{\omega }_2^2)-I{B}_2^{\prime }{\omega }_2{\omega }_3+(2-I)B_2^{\prime }{B}_3^{\prime }{\omega }_2-I{B}_2^{\prime 2}{\omega }_3=0,\end{array}$$

(50)

Substituting ${\Omega }_3\left(t\right)={\omega }_3$, we obtain that (47) will be satisfied only for the initial data ${\omega }_i$ obeying the following equation:

$$\begin{array}{c}\hfill B_3^{\prime }({\omega }_1^2+{\omega }_2^2)-I{B}_2^{\prime }{\omega }_2{\omega }_3+(2-I)B_2^{\prime }{B}_3^{\prime }{\omega }_2-I{B}_2^{\prime 2}{\omega }_3=0,\end{array}$$

(51)

or, equivalently,

$$\begin{array}{c}\hfill {\omega }_1^2+{({\omega }_2+B_2^{\prime })}^2-\frac{I{B}_2^{\prime }}{B_3^{\prime }}({\omega }_2+B_2^{\prime })({\omega }_3+B_3^{\prime })=(1-I)B_2^{\prime 2}.\end{array}$$

(52)

This is a surface of second order. Since the point with ${\omega }_i=0$ obeys this equation, the surface always passes through the origin of the coordinate system. Resolving (51) with respect to ${\omega }_3$, we obtain the following two-parametric family of constant solutions to cubic pseudo-oscillator Equation (47):

$$\begin{array}{c}\hfill {\Omega }_3\left(t\right)={\omega }_3({\omega }_1,{\omega }_2)=\frac{B_3^{\prime }[{\omega }_1^2+{\omega }_2^2+(2-I)B_2^{\prime }{\omega }_2]}{I{B}_2^{\prime }({\omega }_2+B_2^{\prime })},{\omega }_1\in \mathbb{R},{\omega }_2\in \mathbb{R}\setminus \{-B_2^{\prime }\}.\end{array}$$

(53)

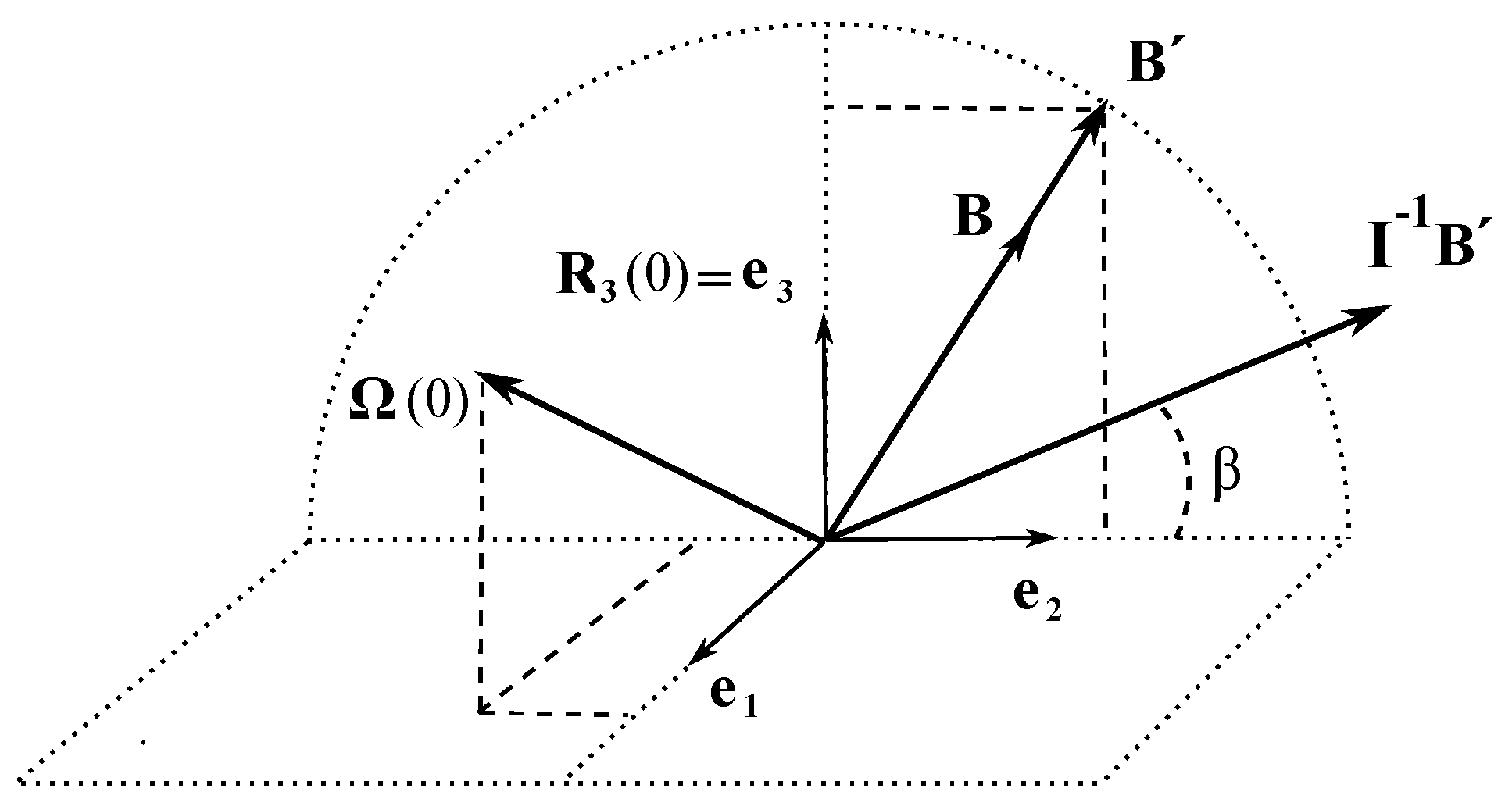
Let us find out which quadric is defined by Equation (52), by writing it in the canonical form. Following the standard procedure [17], we arrive at the new coordinates ${\omega }_i^{\prime }$:

$$\begin{array}{c}{\omega }_1^{\prime }={\omega }_1,\hfill \\ {\omega }_2^{\prime }=({\omega }_2+B_2^{\prime })cos\left(\frac{\beta }{2}+\frac{\pi }{4}\right)+({\omega }_3+B_3^{\prime })sin\left(\frac{\beta }{2}+\frac{\pi }{4}\right),\hfill \\ {\omega }_3^{\prime }=-({\omega }_2+B_2^{\prime })sin\left(\frac{\beta }{2}+\frac{\pi }{4}\right)+({\omega }_3+B_3^{\prime })cos\left(\frac{\beta }{2}+\frac{\pi }{4}\right),\hfill \end{array}$$

(54)

where $\beta$ is the angle between the vectors ${\mathbf{e}}_2$ and ${\mathbb{I}}^{-1}{\mathbf{B}}^{\prime }$, see Figure 3. The new coordinates are obtained from ${\omega }_i$ by shifting the origin of the coordinate system to the point $-{\mathbf{B}}^{\prime }$, and subsequent rotation counter-clockwise by the angle $\frac{\beta }{2}+\frac{\pi }{4}$ in the plane ${\mathbf{e}}_2,{\mathbf{e}}_3$. Note that $\frac{\pi }{4}<\frac{\beta }{2}+\frac{\pi }{4}<\frac{\pi }{2}$. In these coordinates, Equation (52) acquires the form

$$\begin{array}{c}\hfill {\omega }_1^{\prime 2}-\frac{{\omega }_2^{\prime 2}}{a_2}+\frac{{\omega }_3^{\prime 2}}{a_3}=(1-I)B_2^{\prime 2},\mathrm{where}{a}_2\equiv \frac{2sin\beta }{1-sin\beta },a_3\equiv \frac{2sin\beta }{1+sin\beta }.\end{array}$$

(55)

Depending on the relationship between the inertia moments $I_2$ and $I_3$, it describes different surfaces.

• 1. Let $1<I\equiv \frac{I_3}{I_2}<2$. This body could be a charged sufficiently short cylindrical surface. If it rotates around its coaxial axis, it will produce a magnetic field corresponding to a short solenoid. Equation (55) becomes

$$\begin{array}{c}\hfill \frac{{\omega }_1^{\prime 2}}{C_1^2}-\frac{{\omega }_2^{\prime 2}}{C_2^2}+\frac{{\omega }_3^{\prime 2}}{C_3^2}=-1,\end{array}$$

(56)

where

$$\begin{array}{c}\hfill C_1^2\equiv (I-1)B_2^{\prime 2},C_2^2\equiv \frac{2(I-1)B_2^{\prime 2}sin\beta }{1-sin\beta },C_3^2\equiv \frac{2(I-1)B_2^{\prime 2}sin\beta }{1+sin\beta }.\end{array}$$

Hence, the surface of the initial data is a hyperboloid of two sheets. Its upper sheet is shown in Figure 3a.

In the limiting case $I\equiv \frac{I_3}{I_2}=2$, we have a plane body that could be a charged circular loop. In this case, the sheets of the hyperboloid are tangent to the horizontal planes ${\omega }_3=0$ and ${\omega }_3=-2B_3^{\prime }$.

• 2. For the totally symmetric body $I\equiv \frac{I_3}{I_2}=1$, Equation (55) becomes the cone

  $$\begin{array}{c}\hfill {\omega }_1^{\prime 2}+\frac{{\omega }_3^{\prime 2}}{a_3}=\frac{{\omega }_2^{\prime 2}}{a_2},\end{array}$$

  (57)

  with semi-axes $a_2$ and $a_3$ written in Equation (55).
• 3. Let $0<I\equiv \frac{I_3}{I_2}<1$. This body could be a charged long cylindrical surface. If it rotates around its coaxial axis, it will produce a magnetic field corresponding to a long solenoid. Equation (55) becomes

$$\begin{array}{c}\hfill \frac{{\omega }_1^{\prime 2}}{C_1^2}-\frac{{\omega }_2^{\prime 2}}{C_2^2}+\frac{{\omega }_3^{\prime 2}}{C_3^2}=1,\end{array}$$

(58)

where

$$\begin{array}{c}\hfill C_1^2\equiv (1-I)B_2^{\prime 2},C_2^2\equiv \frac{2(1-I)B_2^{\prime 2}sin\beta }{1-sin\beta },C_3^2\equiv \frac{2(1-I)B_2^{\prime 2}sin\beta }{1+sin\beta }.\end{array}$$

Hence, the surface of the initial data is a hyperboloid of one sheet shown in Figure 3b.

In summary, we have shown that, for any solution to the Euler–Poisson Equations (12) and (16) of a symmetrical charged body, the function ${\Omega }_3\left(t\right)$ obeys the cubic pseudo-oscillator equation (47). We obtained a two-parameter family of constant solutions (53) to this equation. Not all of them generate solutions to the original problem. In the next section, they will help us to obtain a one-parameter family of solutions to the original Euler–Poisson equations in elementary functions.

5. Rotation Matrix: One-Parameter Family of Solutions in Elementary Functions

As we saw in the previous section, our problem (12) and (16) probably admits solutions with constant ${\Omega }_3\left(t\right)$. So, let us search for solutions of the auxiliary task (34) and (35) of the form

$$\begin{array}{c}\hfill \mathbf{\Omega }\left(t\right)={({\Omega }_1\left(t\right),{\Omega }_2\left(t\right),{\omega }_3=const)}^T,\mathbf{\Omega }\left(0\right)={({\omega }_1,{\omega }_2,{\omega }_3)}^T.\end{array}$$

(59)

Substituting this ansatz into the Equations (34) and (35), they become

$$\begin{array}{c}\hfill {\dot{\Omega }}_1=[(1-I){\omega }_3+(2-I)B_3^{\prime }]{\Omega }_2-I{\omega }_3{K}_2,\\ \hfill {\dot{\Omega }}_2=-[(1-I){\omega }_3+(2-I)B_3^{\prime }]{\Omega }_1+I{\omega }_3{K}_1,\\ \hfill {\Omega }_1{K}_2-{\Omega }_2{K}_1=0;\end{array}$$

(60)

$$\begin{array}{c}\hfill {\dot{K}}_1={\omega }_3{K}_2-B_3^{\prime }{\Omega }_2,{\dot{K}}_2=-{\omega }_3{K}_1+B_3^{\prime }{\Omega }_1,K_3=B_3^{\prime }.\end{array}$$

(61)

These equations admit three integrals of motion: $\frac{d}{dt}({\Omega }_1^2+{\Omega }_2^2)=0$, $\frac{d}{dt}(K_1^2+K_2^2)=0$ and $\frac{d}{dt}({\Omega }_1{K}_1+{\Omega }_2{K}_2)=0$. This implies the equalities

$$\begin{array}{c}\hfill {\Omega }_1^2\left(t\right)+{\Omega }_2^2\left(t\right)={\omega }_1^2+{\omega }_2^2,\\ \hfill K_1^2\left(t\right)+K_2^2\left(t\right)=B_2^{\prime 2},\\ \hfill {\Omega }_1\left(t\right)K_1\left(t\right)+{\Omega }_2\left(t\right)K_2\left(t\right)={\omega }_2{B}_2^{\prime }.\end{array}$$

(62)

Using the equations ${\Omega }_1{K}_1+{\Omega }_2{K}_2={\omega }_2{B}_2^{\prime }$ and $-{\Omega }_2{K}_1+{\Omega }_1{K}_2=0$, we obtain that $K_1$ and $K_2$ are just proportional to ${\Omega }_1$ and ${\Omega }_2$.

$$\begin{array}{c}\hfill K_1=\frac{{\omega }_2{B}_2^{\prime }}{{\omega }_1^2+{\omega }_2^2}{\Omega }_1,K_2=\frac{{\omega }_2{B}_2^{\prime }}{{\omega }_1^2+{\omega }_2^2}{\Omega }_2.\end{array}$$

(63)

Substituting these expressions into (60) and (61), we obtain the equations of precession

$$\begin{array}{c}\hfill {\dot{\Omega }}_1={\varphi }^{\prime }{\Omega }_2,{\dot{\Omega }}_2=-{\varphi }^{\prime }{\Omega }_1,\mathrm{where}{\varphi }^{\prime }\equiv (1-I){\omega }_3+(2-I)B_3^{\prime }-\frac{I{B}_2^{\prime }{\omega }_2{\omega }_3}{{\omega }_1^2+{\omega }_2^2};\end{array}$$

(64)

and

$$\begin{array}{c}\hfill {\dot{\Omega }}_1=\varphi {\Omega }_2,{\dot{\Omega }}_2=-\varphi {\Omega }_1,\mathrm{where}\varphi \equiv {\omega }_3-\frac{B_3^{\prime }({\omega }_1^2+{\omega }_2^2)}{B_2^{\prime }{\omega }_2}.\end{array}$$

(65)

They will be consistent only if ${\varphi }^{\prime }=\varphi$, that is, the initial data should lie on the surface

$$\begin{array}{c}\hfill B_3^{\prime }({\omega }_1^2+{\omega }_2^2)-I{B}_2^{\prime }{\omega }_2{\omega }_3+(2-I)B_2^{\prime }{B}_3^{\prime }{\omega }_2-\frac{I{B}_2^{\prime 2}{\omega }_2^2{\omega }_3}{{\omega }_1^2+{\omega }_2^2}=0.\end{array}$$

(66)

Combining this with the necessary condition (51)

$$\begin{array}{c}\hfill B_3^{\prime }({\omega }_1^2+{\omega }_2^2)-I{B}_2^{\prime }{\omega }_2{\omega }_3+(2-I)B_2^{\prime }{B}_3^{\prime }{\omega }_2-I{B}_2^{\prime 2}{\omega }_3=0,\end{array}$$

(67)

we conclude that the initial data should be taken on the second-order curve

$$\begin{array}{c}\hfill B_3^{\prime }{\omega }_2^2-I{B}_2^{\prime }{\omega }_2{\omega }_3+(2-I)B_2^{\prime }{B}_3^{\prime }{\omega }_2-I{B}_2^{\prime 2}{\omega }_3=0,\end{array}$$

(68)

that lies on the plane ${\omega }_1=0$. Geometrically, these are hyperbolas that appear as a result of the intersection of the hyperboloids in Figure 3 with this plane.

For the circular loop or short solenoid, they are

$$\begin{array}{c}\hfill \frac{{\omega }_2^{\prime 2}}{C_2^2}-\frac{{\omega }_3^{\prime 2}}{C_3^2}=1,\mathrm{where}{C}_2^2\equiv \frac{2(I-1)B_2^{\prime 2}sin\beta }{1-sin\beta },C_3^2\equiv \frac{2(I-1)B_2^{\prime 2}sin\beta }{1+sin\beta }.\end{array}$$

(69)

For the long solenoid, they are

$$\begin{array}{c}\hfill -\frac{{\omega }_2^{\prime 2}}{C_2^2}+\frac{{\omega }_3^{\prime 2}}{C_3^2}=1,\mathrm{where}{C}_2^2\equiv \frac{2(1-I)B_2^{\prime 2}sin\beta }{1-sin\beta },C_3^2\equiv \frac{2(1-I)B_2^{\prime 2}sin\beta }{1+sin\beta }.\end{array}$$

(70)

Lastly, for a totally symmetric body, they degenerate into the straight lines

$$\begin{array}{c}\hfill \frac{{\omega }_2^{\prime }}{a_2}=\pm \frac{{\omega }_3^{\prime }}{a_3},\mathrm{where}{a}_2\equiv \sqrt{\frac{2sin\beta }{1-sin\beta }},a_3\equiv \sqrt{\frac{2sin\beta }{1+sin\beta }}.\end{array}$$

(71)

Resolving Equation (68) with respect to ${\omega }_3$, we obtain

$$\begin{array}{c}\hfill {\omega }_3\left({\omega }_2\right)=\frac{B_3^{\prime }{\omega }_2[{\omega }_2+(2-I)B_2^{\prime }]}{I{B}_2^{\prime }({\omega }_2+B_2^{\prime })},{\omega }_2\in \mathbb{R}\setminus \{-B_2^{\prime }\}.\end{array}$$

(72)

With this ${\omega }_3$, the two systems (64) and (65) depend on the same frequency

$$\begin{array}{c}\hfill \varphi ={\omega }_3\left({\omega }_2\right)-\frac{B_3^{\prime }}{B_2^{\prime }}{\omega }_2=\frac{B_3^{\prime }{\omega }_2(1-I)({\omega }_2+2B_2^{\prime })}{I{B}_2^{\prime }({\omega }_2+B_2^{\prime })},\end{array}$$

(73)

and imply the following solution

$$\begin{array}{c}\hfill \mathbf{\Omega }\left(t\right)=\left(\begin{array}{c}{\omega }_{2}sin\varphi t\\ {\omega }_{2}cos\varphi t\\ {\omega }_3\left({\omega }_2\right)\end{array}\right),\mathrm{then}\mathbf{\Omega }\left(0\right)=\left(\begin{array}{c}0\\ {\omega }_2\\ {\omega }_3\left({\omega }_2\right)\end{array}\right).\end{array}$$

(74)

This means that the vector of angular velocity in the body-fixed frame ${\mathbf{R}}_i$ precesses around the third axis ${\mathbf{R}}_3$ with frequency $\varphi$.

The next step is to solve the Poisson Equation (12). We consider them in the form

$$\begin{array}{c}\hfill \dot{\gamma }=[\gamma ,\mathbf{\Omega }\left(t\right)],\end{array}$$

(75)

with $\mathbf{\Omega }\left(t\right)$ specified by Equations (72)–(74). Here, $\gamma$ is any row of the rotation matrix.

In components, this reads

$$\begin{array}{c}\hfill {\dot{\gamma }}_1={\gamma }_2{\omega }_3-{\gamma }_3{\Omega }_2\left(t\right),{\dot{\gamma }}_2={\gamma }_3{\Omega }_1\left(t\right)-{\gamma }_1{\omega }_3,{\dot{\gamma }}_3={\gamma }_1{\Omega }_2\left(t\right)-{\gamma }_2{\Omega }_1\left(t\right).\end{array}$$

(76)

This system admits the integral of motion

$$\begin{array}{c}\hfill {\Omega }_1{\gamma }_1+{\Omega }_2{\gamma }_2+\frac{{\widehat{B}}_3{\omega }_2}{{\widehat{B}}_2}{\gamma }_3=c,\end{array}$$

(77)

where ${\widehat{B}}_2\equiv B_2/\left|\mathbf{B}\right|$ and ${\widehat{B}}_3\equiv B_3/\left|\mathbf{B}\right|$ are components of the unit vector in the direction of magnetic vector $\mathbf{B}$. Preservation in time of quantity (77) can be verified by direct computation of its time derivative, with use of the identities

$$\begin{array}{c}\hfill \frac{B_3^{\prime }}{B_2^{\prime }}=\frac{B_3}{B_2}=\frac{{\widehat{B}}_3}{{\widehat{B}}_2}.\end{array}$$

(78)

We need to find the general solution to Equation (76). Then, according to [12], the rows of the rotation matrix $R_{ij}$ can be obtained taking the following three particular solutions. Row $R_{11},R_{12},R_{13}$ is $\gamma \left(t\right)$ with the initial data $\gamma \left(0\right)=(1,0,0)$ and with $c={\Omega }_1\left(0\right)=0$. Row $R_{21},R_{22},R_{23}$ is $\gamma \left(t\right)$ with the initial data $\gamma \left(0\right)=(0,1,0)$ and with $c={\Omega }_2\left(0\right)={\omega }_2$. Lastly, row $R_{31},R_{32},R_{33}$ is $\gamma \left(t\right)$ with the initial data $\gamma \left(0\right)=(0,0,1)$ and with $c={\widehat{B}}_3{\omega }_2/{\widehat{B}}_2$.

First, we solve algebraically the equations ${\Omega }_1{\gamma }_1+{\Omega }_2{\gamma }_2=c-\frac{{\widehat{B}}_3{\omega }_2}{{\widehat{B}}_2}{\gamma }_3$ and ${\Omega }_2{\gamma }_1-{\Omega }_1{\gamma }_2={\dot{\gamma }}_3$, representing ${\gamma }_1$ and ${\gamma }_2$ as follows:

$$\begin{array}{c}\hfill {\gamma }_1=\frac{1}{{\omega }_2^2}[{\Omega }_1(c-\frac{{\widehat{B}}_3{\omega }_2}{{\widehat{B}}_2}{\gamma }_3)+{\Omega }_2{\dot{\gamma }}_3],{\gamma }_2=\frac{1}{{\omega }_2^2}[{\Omega }_2(c-\frac{{\widehat{B}}_3{\omega }_2}{{\widehat{B}}_2}{\gamma }_3)-{\Omega }_1{\dot{\gamma }}_3],\end{array}$$

(79)

Substituting them into the equation for ${\dot{\gamma }}_1$, we obtain a closed equation of second order for ${\gamma }_3\left(t\right)$

$$\begin{array}{c}\hfill {\ddot{\gamma }}_3+k^2{\gamma }_3=c\frac{{\widehat{B}}_3{\omega }_2}{{\widehat{B}}_2},\mathrm{where}k=\frac{{\omega }_2}{{\widehat{B}}_2}.\end{array}$$

(80)

This is the equation of the harmonic oscillator with constant frequency k, under the action of an external constant force. Its general solution with the integration constants b and $k_0$ is

$$\begin{array}{c}\hfill {\gamma }_3\left(t\right)=bcos(kt+k_0)+c\frac{{\widehat{B}}_3{\omega }_2}{{\widehat{B}}_2{k}^2}.\end{array}$$

(81)

Substituting this result into expressions (79), we obtain the remaining variables

$$\begin{array}{c}{\gamma }_1\left(t\right)=\frac{1}{{\omega }_2}[c-b\frac{{\widehat{B}}_3{\omega }_2}{{\widehat{B}}_2}cos(kt+k_0)-c{\widehat{B}}_3^2]sin\varphi t-\frac{b}{{\widehat{B}}_2}sin(kt+k_0)cos\varphi t,\\ {\gamma }_2\left(t\right)=\frac{1}{{\omega }_2}[c-b\frac{{\widehat{B}}_3{\omega }_2}{{\widehat{B}}_2}cos(kt+k_0)-c{\widehat{B}}_3^2]cos\varphi t+\frac{b}{{\widehat{B}}_2}sin(kt+k_0)sin\varphi t.\end{array}$$

(82)

At $t=0$, we obtain

$$\begin{array}{c}\hfill {\gamma }_1\left(0\right)=-\frac{b}{{\widehat{B}}_2}sin{k}_0,\\ \hfill {\gamma }_2\left(0\right)=\frac{1}{{\omega }_2}[c-b\frac{{\widehat{B}}_3{\omega }_2}{{\widehat{B}}_2}cos{k}_0-c{\widehat{B}}_3^2],\\ \hfill {\gamma }_3\left(0\right)=bcos{k}_0+c\frac{{\widehat{B}}_2{\widehat{B}}_3}{{\omega }_2}.\end{array}$$

(83)

Solving Equations (83) with the data described below Equation (78), we obtain, in each case,

$$\begin{array}{c}\hfill c=0,b=-{\widehat{B}}_2,k_0=\frac{\pi }{2};\\ \hfill c={\omega }_2,b=-{\widehat{B}}_2{\widehat{B}}_3,k_0=0;\\ \hfill c=\frac{{\widehat{B}}_3{\omega }_2}{{\widehat{B}}_2},b=1-{\widehat{B}}_3^2={\widehat{B}}_2^2,k_0=0.\end{array}$$

(84)

Substituting these values into Equations (81) and (82) we obtain the rotation matrix of a symmetrical charged body, immersed into the magnetic field $\mathbf{B}={(0,B_2,B_3)}^T$, and launched with initial angular velocity (74)

$$\left(\begin{array}{ccc}cosktcos\varphi t-{\widehat{B}}_{3}sinktsin\varphi t& -cosktsin\varphi t-{\widehat{B}}_{3}sinktcos\varphi t& {\widehat{B}}_{2}sinkt\\ & & \\ {\widehat{B}}_{3}sinktcos\varphi t+C\left(t\right)sin\varphi t& -{\widehat{B}}_{3}sinktsin\varphi t+C\left(t\right)cos\varphi t& {\widehat{B}}_2{\widehat{B}}_{3}A\left(t\right)\\ & & \\ -{\widehat{B}}_{2}sinktcos\varphi t+{\widehat{B}}_2{\widehat{B}}_{3}A\left(t\right)sin\varphi t& {\widehat{B}}_{2}sinktsin\varphi t+{\widehat{B}}_2{\widehat{B}}_{3}A\left(t\right)cos\varphi t& {\widehat{B}}_3^2+{\widehat{B}}_2^{2}coskt\end{array}\right)$$

(85)

It was denoted $A\left(t\right)=1-coskt$ and $C\left(t\right)={\widehat{B}}_2^2+{\widehat{B}}_3^{2}coskt$. Two frequencies in the problem are $\varphi$ written in Equation (73), and $k={\omega }_2/{\widehat{B}}_2$. The dependence of the rotation matrix on the inertia moments $I_2$, $I_3$ as well as on the charge–mass ratio $\mu$ is hidden in the frequency $\varphi$.

By direct substitution of the obtained functions (74) and (85) into Equations (12) and (16), I verified that they are satisfied.

The rotation matrix can be decomposed as follows:

$$\begin{array}{c}\hfill R\left(t\right)=R_{\widehat{\mathbf{B}}}(t,k)\times R_{OZ}(t,\varphi )=\\ \hfill \left(\begin{array}{ccc}coskt& -{\widehat{B}}_{3}sinkt& {\widehat{B}}_{2}sinkt\\ & & \\ {\widehat{B}}_{3}sinkt& {\widehat{B}}_2^2+{\widehat{B}}_3^{2}coskt& {\widehat{B}}_2{\widehat{B}}_3(1-coskt)\\ & & \\ -{\widehat{B}}_{2}sinkt& {\widehat{B}}_2{\widehat{B}}_3(1-coskt)& {\widehat{B}}_3^2+{\widehat{B}}_2^{2}coskt\end{array}\right)\times \left(\begin{array}{ccc}cos\varphi t& -sin\varphi t& 0\\ sin\varphi t& cos\varphi t& 0\\ 0& 0& 1\end{array}\right)\end{array}$$

(86)

Then, the position $\mathbf{x}\left(t\right)$ of any point of the body at the instant t is $\mathbf{x}\left(t\right)=R_{\widehat{\mathbf{B}}}(t,k)\times R_{OZ}(t,\varphi )\mathbf{x}\left(0\right)$. This is obtained by rotating the initial position vector $\mathbf{x}\left(0\right)$ first around the Laboratory axis $OZ$ by the angle $\varphi t$ and then around the $\mathbf{B}$-axis by the angle $kt$.

It can be said that the motion is the composition of a proper rotation around the third inertia axis with precession of this axis around the vector of magnetic field $\mathbf{B}$. The final answer (85) admits the limit of the totally symmetric body $I_2=I_3$; this implies $\varphi =0$. The resulting motion is the precession around the magnetic vector $\mathbf{B}$ without a proper rotation.

Combining Equations (72), (73) and (80) we obtain the relation between two frequencies of the motion (85)

$$\begin{array}{c}\hfill {\varphi }_B=\frac{(I_2-I_3){\widehat{B}}_3\left(2\right|{\mathbf{B}}^{\prime }|+k_B)}{I_3\left(\right|{\mathbf{B}}^{\prime }|+k_B)}{k}_B.\end{array}$$

(87)

We recall that the most general motion of a free symmetrical body is the precession without nutation [12]. Observe that the rotation matrix (85) coincides with Equation (132) of the work [12] if we replace $\widehat{\mathbf{B}}$, $k_B$ and ${\varphi }_B$ on $\widehat{\mathbf{m}}$, k and $\varphi$. The physical meaning of this coincidence can be formulated as follows.

Affirmation. 

If a symmetrical charged body in the magnetic field $\mathbf{B}=(0,B_2,B_3)$ moves according (85) with the precession frequency $k_B$ around $\mathbf{B}$ and the proper rotation frequency ${\varphi }_B$, then in the absence of a magnetic field its precession with the same frequency $k_B$ around the unit vector $\widehat{\mathbf{B}}$ will happen with the proper rotation frequency

$$\begin{array}{c}\hfill \varphi =\frac{I_2-I_3}{I_3}{\widehat{B}}_3{k}_B.\end{array}$$

(88)

Indeed, consider the motion (85) with initial angular velocity $\mathit{\omega }\left(0\right)={(0,{\omega }_2,{\omega }_3\left({\omega }_2\right))}^T$. Let it then be launched in the absence of a magnetic field with initial angular velocity $\mathbf{\Omega }\left(0\right)={(0,{\omega }_2,\frac{I_2{\omega }_2{B}_3}{I_3{B}_2})}^T$. According to [12], it will precess around the vector of conserved angular momentum $\mathbf{m}=I\mathbf{\Omega }\left(0\right)=(0,I_2{\omega }_2,\frac{I_2{\omega }_2}{B_2}{B}_3)=\frac{I_2{\omega }_2}{B_2}\mathbf{B}\sim \mathbf{B}$ with the frequency $k=\frac{\left|\mathbf{m}\right|}{I_2}=\frac{{\omega }_2}{{\widehat{B}}_2}=k_B$ and with the proper rotation frequency $\varphi =\frac{I_2-I_3}{I_2{I}_3}{m}_3=\frac{I_2-I_3}{I_3}{\widehat{B}}_3\frac{{\omega }_2}{{\widehat{B}}_2}=\frac{I_2-I_3}{I_3}{\widehat{B}}_3{k}_B$.

Components of angular momentum $\mathbf{m}\left(t\right)$ for our solutions in elementary functions are not conserved quantities. But using the integrals of motion (36), (40) and (41) with ${\Omega }_3\left(t\right)={\omega }_2=\mathrm{const}$, we obtain

$$\begin{array}{c}\hfill \left(\mathbf{m}\right(t),\mathbf{B})=const.\end{array}$$

(89)

That is, the angular momentum always lies in the plane orthogonal to the constant vector of the magnetic field.

6. Conclusions

In this work we deduced the equations of motion of a charged symmetrical body in external constant and homogeneous electric and magnetic fields starting from the variational problems (1) and (2), where the body is considered as a system of charged point particles subject to holonomic constraints. The final equations are written in terms of center-of-mass coordinates, rotation matrix and angular velocity. They are (4), (12) and (16). According to these, the rotational motion of the body does not perturb its translational motion and vice versa. In particular, the center of mass obeys Equation (4) and behaves as a point charged particle in the electromagnetic field. In addition, the electric field does not affect the rotational motion of the body.

For the case of a totally symmetrical body (charged ball) we found a general solution (28) and (29) to the equations of motion. The resulting motion can be thought of as a superposition of two rotations: the first around unit vector $\widehat{\mathbf{k}}$ with the frequency $\gamma$, determined by initial values of angular velocity and Larmor’s frequency, and the second around the axis of magnetic field $\mathbf{B}={(0,0,|\mathbf{B}\left|\right)}^T$ with the frequency $\alpha =\frac{\mu \left|\mathbf{B}\right|}{2c}$. The angular momentum vector $\mathbf{m}\left(t\right)$ precesses around vector $\mathbf{B}$ with Larmor’s frequency $\alpha =\frac{\mu \left|\mathbf{B}\right|}{2c}$.

Analyzing Equations (12) and (16) for the case of a symmetrical charged top, we demonstrated that the task to find the component of angular velocity ${\Omega }_i\left(t\right)$ can be reduced to solving the equation of a one-dimensional cubic pseudo-oscillator (47). We found a two-parametric family of solutions (53) to this equation. This helped us later find a one-parametric family of solutions (85) for the rotation matrix of a symmetrical charged body, immersed into the magnetic field $\mathbf{B}={(0,B_2,B_3)}^T$, and launched with initial angular velocity (74). The resulting motions turn out to be the composition of a proper rotation around the third inertia axis with precession of this axis around the vector of magnetic field $\mathbf{B}$.