Abstract
We construct and examine a holonomy-corrected chiral fields model of cosmological relevance. Specifically, we holonomize the Hamiltonian corresponding to a quintom field scenario with additional kinetic interaction (governed by the constant chiral metric, ) on a flat FLRW background and contrast the resulting model with the corresponding purely classical system. In particular, it is shown that the single LQC bouncing stage is ensured to be realized, provided the full chiral kinetic energy function does not change sign during evolution. (As preparation, a particularly simple k-essence field is examined within the effective LQC scheme; some exact solutions are obtained in the process.) Additionally, under the said assumption, it is established that the landmark bouncing mechanism of standard (effective) LQC is still guaranteed to be featured even when taking any finite number of fields and to be dependent on such fields (the particular zero-potential case corresponding to a family of simple purely kinetic k-essence multi-field cosmology models).
1. Introduction
Multi-field cosmology has grown to be a sub-field of its own within theoretical (quantum) cosmology. The gained popularity of such a paradigm is due chiefly to the quite effective way in which it has managed to accommodate (within a single theoretical framework) such meaningful features as the inflationary scenario, dark matter and dark energy (see, e.g., [1]). However, it has been shown that, within the standard form of multi-field cosmology, there are obstructions to the crossing of the phantom divide line (unless the stability of the model is not considered as a requirement) [2,3]. Partly in order to circumvent this state of affairs, different types of couplings have been considered within the context of multi-field cosmology. A particular instance is the so-called standard quintom scenario, in which a quintessence and a phantom field interact in order to achieve the desired crossing. Furthermore, in particular instances, the quintom field scenario allows for the avoidance of the initial singularity by means of a bouncing mechanism (see the review in [2] and the references therein).
Within the standard multi-field cosmology paradigm, the interaction among the involved scalar fields is assumed to be of a canonical type, i.e., the corresponding Lagrangian density has the following general form:
A whole new set of possibilities in the multi-field cosmology paradigm is achieved by generalizing the above Lagrangian in order to include non-canonical interactions among the scalar fields (the usual quintom field scenario being a very simple particular case), where the couplings among the fields are controlled by a symmetric tensor field (whose components, in general, depend on the matter fields, , although this is usually assumed to be just a constant symmetric matrix). This new generalized multi-field cosmology framework is known as chiral cosmology [4,5].
Specifically, the Lagrangian (density) of chiral cosmology is of the following general form:1
As can be seen, the chiral cosmology paradigm simply amounts to replacing in (1) with (but care should be exercised: as already pointed out, in the most general case, is a tensor field which depends on the fields —just as depends on the gravitational potentials defined by the line element). The inclusion of the metric field, , of course, evokes the “internal space”-type frameworks which permeate the gauge theories of particle physics. This is no coincidence; the chiral cosmology paradigm is indeed inspired by such theories [4].
An even further generalization was put forward in [6] in order to account for general k-essence fields—in which the kinetic term can acquire more general non-canonical forms [7,8,9]. The corresponding Lagrangian density has the following general structure:
in which is any function of the following standard kinetic term:
(note that this idea is reminiscent of theories, in which the standard gravitational term R is replaced by an arbitrary function of it; for a review of theories, see, e.g., [10]). A multi-field k-essence scenario is achieved by taking (whereas the standard multi-field paradigm is obtained by additionally requiring to be the identity function). We will be referring to this more general framework as chiral k-essence cosmology.
On the other hand, it can be shown that certain scalar–tensor theories of gravity (when viewed in the Einstein frame) give rise to this kind of generalization of standard multi-field cosmology [11]. Additionally, the use of non-minimal couplings is necessary when scalar fields are quantized in the presence of non-flat space–time backgrounds [12].
The above remarks provide sufficient motivation for considering the quantum counterpart of classical theoretical frameworks of the Universe which involve non-canonical fields, with a focus on describing (at an effective level) its very early stages of evolution. In this respect, recently, the standard canonical (Wheeler–DeWitt) quantization of some particular chiral cosmology models has been undertaken (in particular, the flat FLRW (see, e.g., [6,13,14]) and Bianchi type I (see, e.g., [15,16]) backgrounds have been thoroughly studied).
The standard Wheeler–DeWitt quantization program (which dates back to the 1960’s) has now evolved into the framework known as loop quantum gravity (LQG) [17,18]. This upgraded Wheeler–DeWitt program has gained considerable attention as a viable candidate for a quantum theory of gravity. In very succinct terms, LQG is achieved by rewriting the traditional ADM formulation of general relativity [19] in terms of a certain type of connection variables and then quantizing the resulting Hamiltonian framework by way of techniques akin to gauge theory (rather complete accounts can be found in the monographs [18,20]).
The implementation of the ideas and methods of LQG in symmetry-reduced minisuperspace models is called loop quantum cosmology (LQC) [21,22]. In particular, as a result of the underlying quantum geometry predicted by LQG, it has been shown that the loop quantization of the FLRW models leads to an early bouncing stage, which enables the resolution of the cosmological singularity [21,23]. In order to extract the physics in a more simple way, an effective scheme (which can be interpreted as a kind of semi-classical limit of LQC) has been envisaged [21]. This effective setup has been successfully used to study the consequences of (a certain type of) loop quantum corrections in cosmological models. Moreover, it has been shown (via analytical and numerical investigations [24]) that the effective description of the FLRW models reproduces very well the behavior of the corresponding full-loop quantization of such models.
Given that LQC is in several respects an improvement to traditional Wheeler–DeWitt quantum cosmology and given the appealing characteristics of the chiral cosmology framework (some of which were highlighted above), it is only natural to attempt to construct a loop quantum-corrected chiral cosmology paradigm and, of course, to contrast it with its non-corrected counterparts. A rather direct route to achieve such a comparative investigation in a simple way is to consider only the so-called holonomy corrections, which are precisely the ones taken into account in the effective scheme of LQC.
The present investigation is therefore chiefly devoted to the implementation of the effective LQC scheme in the particular chiral cosmology family of models considered in Ref. [6] (and to performing a corresponding preliminary study of the resulting loop quantum-corrected framework), which considers quintom fields on a flat FLRW background (this is carried out in the main part of the manuscript, Section 4). The experience gained from undertaking such a task will enable us to arrive at a loop quantum correction for any chiral cosmology modeled on a flat FLRW background and to establish the viability of such an extended paradigm regarding the landmark feature of LQC—the quantum bounce.
Henceforth, we can assert that the main aim of our investigation is to present a rather broad and diverse chiral cosmology family consisting of an infinite number of particular (multi-field) cosmological models, all of which incorporate the celebrated LQC singularity resolution by means of a bounce. Away from the bounce, the models would rapidly transit, by construction, to their more standard, non-holonomized counterparts. These features impart to such a family great potential for addressing issues from (predominantly quantum) the very early stages to the (highly classical) late epochs.
The manuscript is organized as follows: In Section 2, we recall the loop quantization effective scheme for the flat FLRW model with a free standard scalar field. As a preparation for the non-canonical multi-field case, in Section 3, we implement the steps in Section 2 to arrive at an effective formulation for the flat FLRW model in the presence of a simple k-essence field, obtaining, in passing, some exact solutions. In Section 4, we construct and study an effective LQC scheme for a certain type of chiral field which the authors have found to be of sufficient cosmological relevance (and which has been thoroughly studied in the specialized literature). Aside from discussing the main results obtained, a general framework which incorporates holonomy corrections to any chiral cosmology based on a flat FLRW background is presented in Section 5. There, it is established that the LQC bouncing scenario is ensured to be realized in such an enlarged family, provided a somewhat mild condition involving the full kinetic energy is satisfied. We consider this finding to be the main result of our investigation.
2. Effective LQC Dynamics
This brief part is intended only as a quick guide to arriving at an effective formulation of LQC. Full comprehensive accounts can be found in Refs. [21,22,25].
Recall first that in the ADM formulation of general relativity, it is established that the full Hamiltonian, H, can be written as the combination (), where N and are Lagrange multipliers (called lapse and shift, respectively), which enforce the fulfillment of and (so that the full Hamiltonian, H, is constrained to vanish), and is the spacelike slice (see, e.g., §1 of Ref. [18]).
Now, when specializing to the flat FLRW spacetime,
the Einstein–Hilbert gravitational action,
leads to the full (particle-like) Lagrangian,
where the spatial integration has been carried over a region of a unit spatial coordinate volume.
The implementation of a standard canonical analysis to the above Lagrangian framework results in a Hamiltonian system specified by the full Hamiltonian function (see, e.g., §2 of Ref. [26]),
(where a matter contribution has been added) and the Hamiltonian constraint equation:
On the other hand, the Ashtekar–Barbero variables cast general relativity into the form of a gauge theory, in which phase space is described not by the four metric and its conjugate momentum but by an gauge connection (the so-called Ashtekar–Barbero connection), , and its canonical conjugate field, the densitized triad . The canonical pair has the following Poisson structure:
with , the Dirac delta distribution, on the spacelike hypersurface .
When imposing spatial homogeneity and isotropy, the connection and triad fields can be written as
with
where is a (auxiliary) flat metric and and are a constant triad and co-triad compatible with , with denoting the volume—with respect to —of the region of the spacelike slice in which the variational principle is well defined2.
These connection triad variables and the usual geometrodynamical ones are related via
In an effective description, it is customary to work with the following variables:
Taking a free standard homogeneous field as matter content, the Hamiltonian above can be written in terms of these variables as
We stress that this is the usual classical Hamiltonian of the flat FLRW in the presence of a free standard scalar field (as can be readily seen by using relations (13) and (14)), the only difference being that it is written in terms of the canonical pair (connection triad variables) .
Now, the holonomy correction due to the loop quantization is encoded by making the replacement [21]
in the Hamiltonian (15), where (with being the Planck length) is the smallest eigenvalue of the area operator (consistent with the imposed symmetries) in the full LQG [18]. The resulting effective Hamiltonian is thus given by
The corresponding equations of motion are ()
Taking into account the corresponding Hamiltonian constraint (i.e., the counterpart of Equation (9)) and the equation of motion for V, the Friedmann equation is updated to [21]
where
is the Hubble parameter, with
and is the maximum value that can take in view of the effective Hamiltonian constraint, i.e.,
In the loop quantum cosmology of the flat FLRW model with a free standard scalar field, it is established that
- ;
- ;
- The volume, V, reaches a minimum at ;
- is monotonic (in particular, decreasing).
As a consequence of the above statements, a single “Big Bounce” takes place during the evolution (for details, see, e.g., [21,27]).
Additionally, the usual Friedmann equation,
can intuitively be seen as the limiting case (which amounts to ) of the above modified Friedmann Equation (22).
Note also that in this simplistic view of effective LQC, such a framework is attained just by making the replacement (16) within the corresponding minisuperspace classical Hamiltonian (itself written in terms of symmetry-reduced connection variables). As already stated, the relevance of this simplified avenue to the effective scheme has been supported time and again in several (analytic and numerical) investigations.
To implement the effective LQC scheme in the chiral cosmology setup, it is therefore sufficient to first write the minisuperspace Hamiltonian (corresponding to a flat FLRW background) in terms of the symmetry-reduced holonomy variables with the help of (13) and then directly carry out the replacement (16) within this Hamiltonian. This will be the route that is exploited in the present investigation. We will exemplify such a route by first considering a single k-essence field. In passing, this intermediate step will additionally serve to (i) view this simple k-essence field as a kind of precursor to the chiral cosmology paradigm and (ii) aid in interpreting the crucial ingredient of the chiral cosmology paradigm (the symmetric field ) as conforming to a specific part of the metric arising in the full configuration manifold (i.e., full minisuperspace). This last point (ii) has a certain relevance on its own, since by interpreting as a part of the configuration manifold metric, we are implicitly further geometrizing the chiral cosmology scenario—thus prompting the use of additional geometric tools perhaps not readily available before. However, this last treatment will not be carried out in the holonomy-corrected case since the inverse problem (Hamiltonian framework → Lagrangian framework) is of a quite intricate nature (see, for instance, [28,29]).
3. Effective Dynamics with a Simple -Essence Field
Below, in one of the main parts of this section, we consider the particular case of the effective dynamics of a simple k-essence field with a non-canonical kinetic term of the form . Some aspects of this particular kind of family of fields have been studied in [30].
Consider, therefore, a single homogeneous scalar field, , with a Lagrangian density (recall (3))
where in a flat FLRW background.
Then, the corresponding Einstein–Hilbert action,
leads (after integration over a finite region of the spacelike slice of unit volume) to the Lagrangian
with and , where the minisuperspace metric is defined by
We note that (recall that contains terms which are set equal to unity upon spatial integration)
where is the standard kinetic term .
We will need below the corresponding Hamiltonian, which is
where is the inverse of and is given by
We now look at some more general situations.
3.1. A Further Geometrical Interpretation of the (k-Essence) Chiral Cosmology Scenario
Consider a single homogeneous free field, , with the Lagrangian density given by (generalized kinetic term)
In the presence of a homogeneous background arising from a diagonal spacetime metric (not necessarily in the FLRW family),
The corresponding Einstein–Hilbert action,
leads (after spatial integration) to the Lagrangian
with , , , and . We observe that in this more general situation, a quadratic form is well defined (in coordinates ) only for with . The “metric” in minisuperspace would be given by , where
which is degenerate.
In a more conventional situation, in order to keep a Riemannian structure for minisuperspace, we could just focus on the reduced system defined by the configuration variables , , and and set up the Lagrangian framework from there [31,32]. Then, one would go on to the Hamiltonian framework by implementing the Dirac–Bergmann algorithm (see, e.g., [33,34])—along with the gauge variable N. However, in the case at hand, it is not immediately clear how such an algorithm is to be carried out due to the velocity-dependent term . We can bypass this position (while at the same time retaining the Riemannian structure) by considering the following. In the context of ordinary classical mechanics, cannot be considered part of the kinetic energy; instead, it should be viewed as a velocity-dependent potential. Now, in order to have a well-defined (i.e., non-degenerate) metric structure in minisuperspace (coordinatized by all four configuration variables), we can simply assume to be analytic and interpret the first-order term, , in its Taylor expansion as completing the standard kinetic energy part while at the same time considering the remaining series term, , as an additional non-canonical kinetic component. One could then work with the approximated model resulting from keeping just some low-degree polynomial of the remaining series. In this case, we would have
We should state that even by keeping a small polynomial in the aforementioned remaining series, the inversion of momenta, , in terms of velocities, , could prove to be impossible.
In the case of several fields, , the situation is the same. In order to have a well-defined metric structure, we consider the linear term in of the Taylor expansion of as completing the quadratic form while taking the remaining part, , as a velocity-dependent potential function. The minisuperspace metric is then given by , where
Observe that enters the minisuperspace metric, , to satisfy
The situation is unaltered if we let the metric be homogeneous but not necessarily diagonal. We would simply have
where l could take values from one to three, according to the size of the gravitational part of the metric structure.
To summarize, the consideration of the generalized non-canonical kinetic term in the Lagrangian density (3) has the undesired consequence of heavily modifying the Riemannian structure of the corresponding minisuperspace (e.g., (36)). In general, such a modification renders the metric degenerate, and so the associated minisuperspace is no longer a (pseudo-)Riemannian manifold (if we are to consider the standard minisuperspace variables as defining a coordinate patch). In order to keep the Riemannian structure, a rewriting of the Lagrangian framework could be attempted, which in turn could lead to an ordinary Hamiltonian framework which incorporates a metric structure—which is very desirable if a standard quantization is to be attempted. A path towards fulfilling this goal in an approximated way, applicable for all analytic , has been delineated above.
For the rest of the paper, we will not have to worry about this issue since we assume to be the identity function. In this more restricted case, note that (39) still applies.
On the other hand, by identifying the chiral metric as conforming to the part of the minisuperspace metric consistent with (41), we are purporting a further geometrical interpretation of which always arises within the minisuperspace approximation. It is evident from (127) that plays an important role in the (infinite-dimensional) geometry of the full gravity–matter configuration space, but it is not straight forward to anticipate specifically in what way one should interpret in the finite-dimensional geometry defined by the minisuperspace approximation. Once realizing the very specific block in which enters the minisuperspace metric , it is, in principle, possible to extract valuable information regarding the behavior of the gravitational potentials and chiral fields simply by further studying the metric structure on its own. For instance, one could implement tools of global differential geometry specially tailored to (constrained) mechanical systems in order to arrive at meaningful conclusions about the general behavior of solution curves (see, e.g., [35]).
3.2. Classical Solutions in Connection Variables
Before addressing the effective scheme of LQC, we obtain purely classical exact solutions but using the connection triad variables defined by (13) and (14).
The Hamiltonian (31) can then be rewritten as ()
The corresponding Hamilton equations are
where we have made use of the Hamiltonian constraint in writing the equation for . Using Equations (44) and (45) and the Hamiltonian constraint, we can arrive at the Friedmann equation
where .
The Klein–Gordon equation for this non-canonical scalar field is given by
where a prime denotes differentiation with respect to .
The solutions for the gravitational variables are (with being an integration constant)
where we have fixed the initial condition so that the singularity is reached at .
From Equations (45) and (46), we have
so that
where is an integration constant. These relations will enable us to obtain solutions for and for particular forms of .
3.2.1. (Sáez–Ballester)
For this case (see [36] for the cosmological significance of this particular model), Equation (53) is
which gives (for )
with being an integration constant. Figure 1 shows the behavior of the scalar field for different values of the parameters, while Figure 2 shows the corresponding volume function.
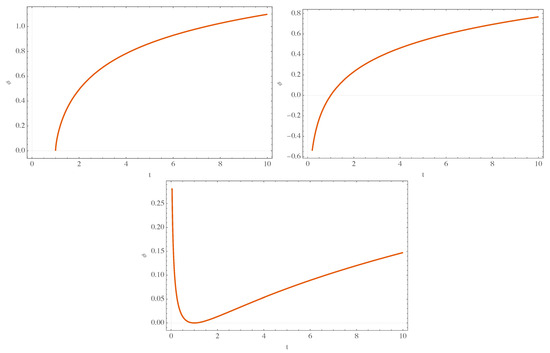
Figure 1.
Behavior of the scalar field (Equation (55)) for different values of m. For the left top panel, ; for the right top panel, ; and for the bottom panel, .
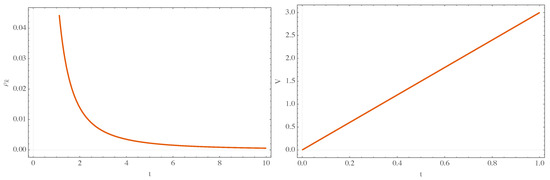
Figure 2.
Behavior of the energy density, , and the volume function, V, (Equation (55)). We can immediately spot the cosmological singularity.
For , we obtain
where is an integration constant. In Figure 3, we depict the scalar field given by Equation (56).
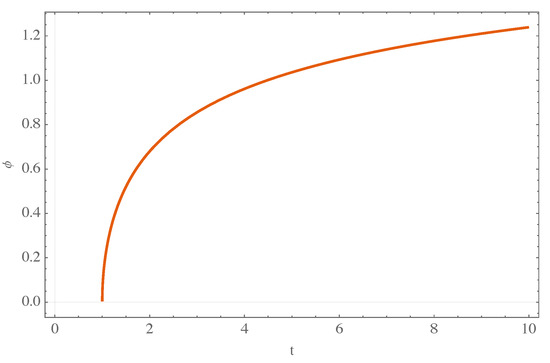
Figure 3.
Behavior of the scalar field given by Equation (56).
3.2.2.
In this case, the relation (53) is given by
which gives (for )
where is an integration constant. The behavior of this scalar field is shown in Figure 4.
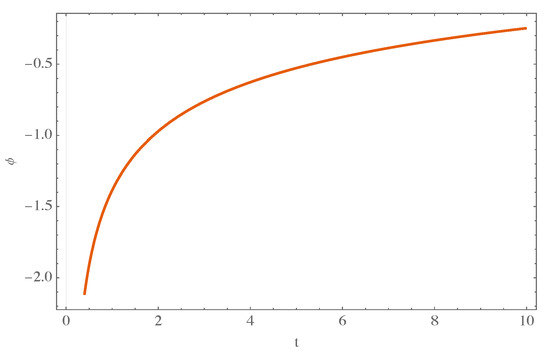
Figure 4.
Plot of the scalar field specified by Equation (58) for a given set of values.
For completeness, we consider the case (standard free homogenous field). We obtain
with being a constant arising from the integration. In Figure 5, we show how the scalar field evolves as a function of t, as given by Equation (59).
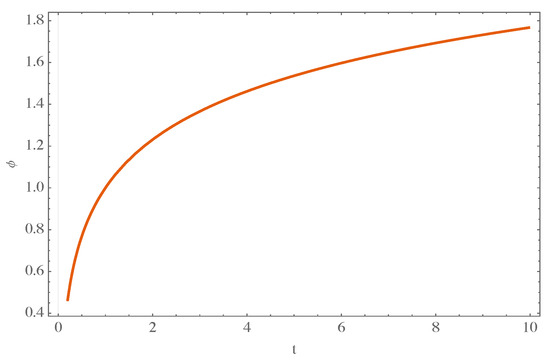
Figure 5.
We can see how the scalar field given by Equation (59) evolves as a function of t.
3.3. Holonomized Hamiltonian
The corresponding Hamilton equations are
where we have used the Hamiltonian constraint in writing Equation (61).
From Equation (63) and the Hamiltonian constraint, we can observe that the energy density function is bounded; its maximum value is (the same as for a standard field).
The corresponding Friedmann equation is
We observe from Equation (62) that a minimum in the volume function is reached at the time, , at which (the bounce takes place at ). We also note that for the k-essence field considered here, the critical value, , corresponds to a maximum in the effective density function, , as in the usual canonical case.
In a recent work [37], a more general k-essence model than the one presented in this part is studied from a qualitative point of view by directly replacing in (22) with the (highly exotic) energy density of the k-essence field, obtaining an equation analogous to (65). Recall, however, that (22) is obtained in effective LQC from the corresponding (holonomized) Hamiltonian framework. But, as already discussed, an “out-of-the-box” ordinary Hamiltonian framework is not available for more general forms of k-essence, so additional care should be taken in those cases. In any case, it would be safer to arrive at the modified Friedmann equation from the (previously constructed) holonomized Hamiltonian framework.
We now proceed to solve the equations of motion (61)–(64). The equation for is decoupled from the system and is the same as in the standard case. We have
where we have set so that (which corresponds to a minimum in the volume function); that is, the bounce takes place at .
The equation for the volume function is also the same as in the standard case. By substituting the solution for into Equation (62), we obtain
where is the volume at the bounce.
We observe that Equations (63) and (64) are the same as in the classical case, so we have
where B is an integration constant.
In the remaining part of this section, we exemplify our general findings regarding the initial bouncing scenario by considering the two specific forms for the function which were dealt with in the purely classical case and make a depiction of such a mechanism with the help of some simple plots in arbitrary units. No additional study will be carried out since, as already stated, the main aim of this brief part was just to warm up for the more demanding chiral case—which will be tackled in the next section.
3.3.1. (Sáez–Ballester)
For this case, Equation (70) takes the form
which can be integrated to give (for )
with C being an integration constant. The corresponding volume function is depicted In Figure 6. In Figure 7, we show the behavior of the energy density for the solution given in Equation (72).
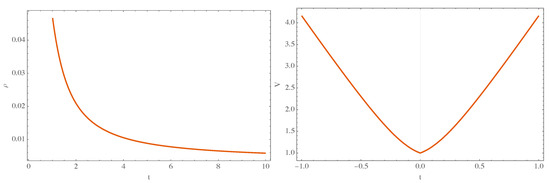
Figure 6.
Energy density for the scalar field given by Equation (72). Also, the volume function is depicted. Notice the bouncing scenario.
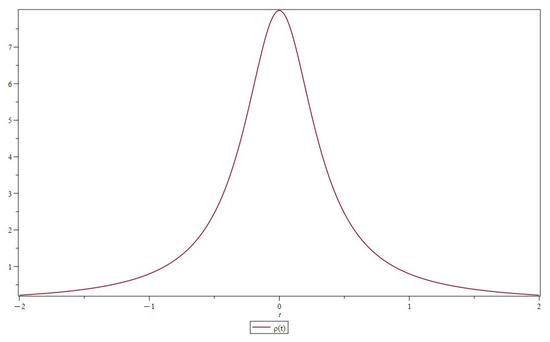
Figure 7.
Overall behavior of the energy density for the scalar field given by Equation (72) (arbitrary units).
For , we obtain
In Figure 8, we have plotted the energy density corresponding to the solution for the scalar field given by Equation (73).
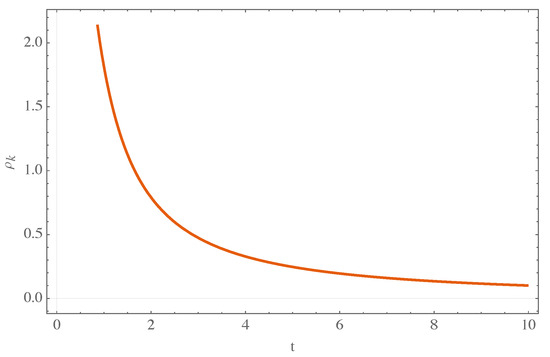
Figure 8.
Energy density for the scalar field given by Equation (73). We have choosen B and C to be imaginary.
3.3.2.
Here, relation (70) takes the form
which, upon integration, gives
where C is an integration constant. In Figure 9 below, the general behavior of the energy density function is portrayed (with the help of the exact solutions obtained above). As already emphasized in the general analysis of the equations of motion, the bouncing mechanism is featured.
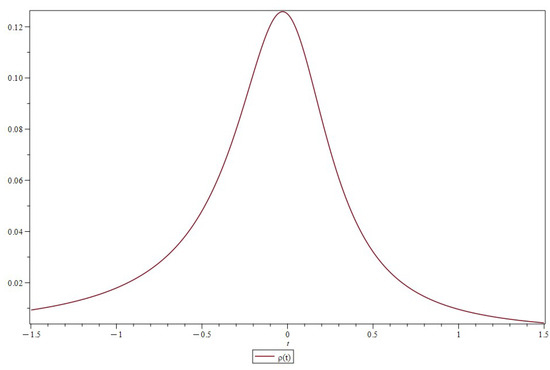
Figure 9.
Generic behavior of the energy density for the scalar field given by Equation (75) (arbitrary units).
We obviate the case since it corresponds to the free standard one, which has been extensively studied within the LQC community.
4. Chiral Fields in Effective LQC
4.1. Standard (Semi-)Classical and Quantum Treatments
We consider now a chiral cosmology model defined by two homogeneous scalar fields, and , interacting on a flat FLRW background according to the Lagrangian density
with , , being strictly positive numbers and ()
We also consider a barotropic equation of state for the chiral fields,
where (recall that some quantities in are to be set equal to unity upon integration of the spatial slice)
is the pressure and
is the energy density (with being the standard kinetic term (4)). Note that both quantities are the natural generalizations to chiral fields of the standard scalar field pressure and energy density.
The usual Einstein–Hilbert action,
leads (after spatial integration) to the particle-like Lagrangian
where , , , and
We observe that, in accordance with (41), the chiral ingredient enters the minisuperspace metric as (recall that contains terms which are set equal to unity upon spatial integration)
Three somewhat large classes of model families associated with both the classical and quantum scenarios given by this Hamiltonian system have been carefully examined in [6]. There, the relation
was imposed so that some families of classical solutions could be found in a closed, exact form. Although we will not be primarily concerned with purely classical analytical solutions in the rest of this paper, we will comply with such relations when generating numerical solutions, exemplifying the behavior regarding the bouncing mechanism of the corresponding holonomized framework.
The Hamilton equations for the phase-space dynamical variables are ()
For completeness, we present the starting point of the standard quantum and semi-classical dynamics associated with this Hamiltonian system.
The usual replacement () leads to the (naive-factor-ordered) Wheeler–DeWitt equation:
In ordinary quantum mechanics, it is well known that this usual prescription can lead to incorrect results if the coordinates used are not ones in which the configuration space metric takes the flat form . In a not necessarily flat configuration space, using a general coordinate system, it is safest to quantize using the Laplace–Beltrami operator directly (see, e.g., [38]) , which is defined by
where is the metric field on the considered (pseudo-)Riemannian manifold (in a chart with local coordinates ). The use of the Laplace–Beltrami operator in connection with the quantization of the gravitational field can be traced back to [39] (a recent discussion on the matter can be found in [40]). Note the prominent role played by the metric structure of the configuration manifold regarding quantization (this is quite often overlooked). If no metric structure is available in minisuperspace, one would run into serious difficulties when trying to setup the associated standard quantization scheme.
Specifically, the quantization is achieved by the following replacement (which reduces to the usual formula for ):
The corresponding Wheeler–DeWitt equation associated with the Hamiltonian (84) takes the slightly more general form
As we can notice, the only difference from the naive quantum prescription lies in the additional -term.
As is well known [41], the semi-classical scheme of standard quantum mechanics can be achieved by implementing the so-called eikonal approximation, i.e., by assuming , with , and keeping terms up to a desired order in ℏ. The zeroth-order approximation of (93) is given by
whereas the more general case (96) is approximated as
Needless to say, these Hamilton–Jacobi-like equations are extremely difficult to solve analytically.
A standard quantum and semi-classical analysis of the chiral model under consideration can be achieved by studying Equations (96) and (99), respectively. As already stated, some quantum versions of the present model have already been considered in some recent investigations, so we proceed directly with the inclusion of holonomy corrections due to LQC.
4.2. Holonomized Chiral Cosmology
For ease of comparison with the holonomy-corrected case, we embark on studying the classical dynamics associated with this Hamiltonian (with these connection triad variables).
The associated equations of motion are
Recall that these equations are to be solved by additionally taking into consideration the corresponding Hamiltonian constraint equation.
From the above equations and the Hamiltonian constraint equation, follow the following general remarks:
- The energy density function,is only bounded from below, and it is bounded from above provided is itself bounded (here, is not restricted to take values in the interval since no holonomization has been implemented);
- is not forbidden; in fact, it is observed that at , (this is, of course, a cosmological singularity);
- corresponds to either a maximum of V or a minimum of V, according to whether the full chiral kinetic term is positive or negative at , respectively;
- If the potential function, , is negative at , then the volume function reaches a maximum at .
The above statements can be summarized by asserting that the cosmological singularity is not generically resolved. However, given that is not definitely a monotonic function of time, several bouncing scenarios could occur for specific forms of the potential functions (since the equations of motion for the fields and their momenta crucially depend on the potential term). Indeed, in Ref. [6], particular bouncing models were spotted.
The Friedmann equation is the expected one,
The equation-of-state parameter is
In the following, we accentuate some characteristics of the dynamics of this Hamiltonian system via some numerical solutions (see Figure 10). Figure 11 shows the energy density, , which at takes the value .
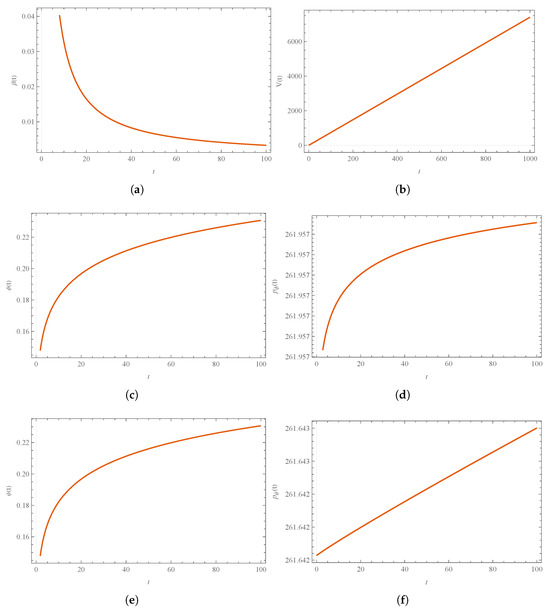
Figure 10.
Numerical solution of the Hamilton Equations (101)–(106): (a) , (b) , (c) , (d) , (e) , and (f) . We use arbitrary units, namely , , , , and , and the initial condition , .
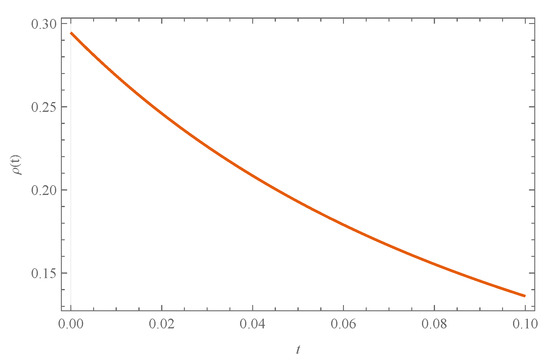
Figure 11.
Numerical solution for the energy density, (Equation (108)). We use arbitrary units, namely , , , , and , and the initial condition , .
Using the numerical solutions (101)–(106) and the equation of state (110), we find the behavior of ; see Figure 12. In Figure 12, we can see that there is an evolution dominated by the kinetic energy density, and then it moves to a domain of the potential energy density. This gives us indications of the existence of an inflationary stage, which will not be analyzed here. For completeness, Figure 13 shows the number of e-folds, which, for the given time, does not reach the minimum required limit .
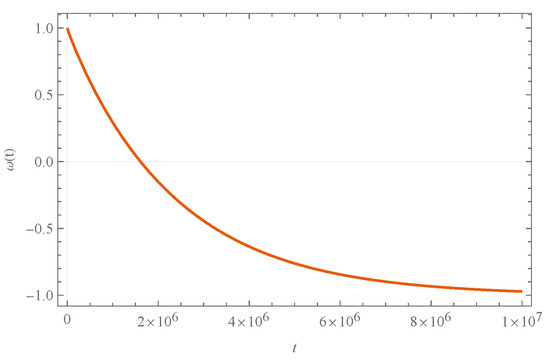
Figure 12.
Numerical solution for the equation-of-state variable, , (Equation (112)). We use arbitrary units, namely , , , , and , and the initial condition , .
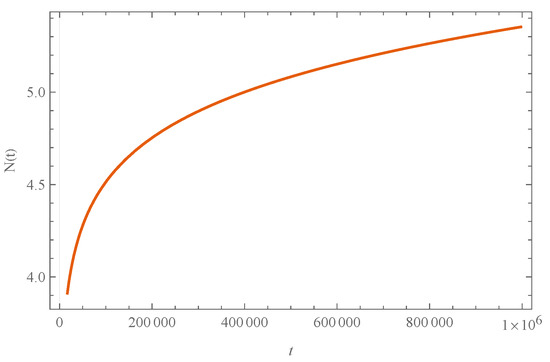
Figure 13.
Numerical solution for the e-folds, . We use arbitrary units, namely , , , , and , and the initial condition , .
The upgraded version of the Hamiltonian (84), which includes holonomy corrections due to loop quantum gravity, is achieved by implementing the replacement (16). The holonomy-corrected Hamiltonian is
We proceed now to study the corrected dynamics emanating from this holonomized Hamiltonian, taking into consideration the two cases which were studied above from standard perspectives.
The equations of motion associated with the Hamiltonian (113) (to be complemented with the corresponding Hamiltonian constraint equation) are given by
From the above equations and the Hamiltonian constraint equation, it follows that:
- The energy density function,takes values in the range , with (the same critical density featured in (22) in the standard case);
- The function is a monotonic function of time provided thatis fulfilled, in which case, the maximum is attained only once for solution curves lying at the surface of phase space defined by a specific condition;
- In the case at hand, a simple sufficient condition for the first relation in (122) to be satisfied is ;
- Provided (122) is fulfilled during evolution, the volume function reaches a minimum at —which corresponds to —and it is attained only once, given that the image of is in the interval .
These remarks can be summarized by stating that, if (122) is guaranteed, the initial singularity is removed by means of a bouncing scenario unfolding at , with and . This conclusion is still valid in the free case. We note that a negative definite potential ensures the first inequality in (122) (whereas the fulfillment of the second inequality in (122) implies that the potential energy is positive during evolution).
We highlight that if (122) is not fulfilled during evolution, it is still the case that the energy density function takes values in the interval (so V cannot take the value zero during evolution) and that the critical points of V are the ones for which . However, since in this situation is not ensured to be monotonic, several bouncing scenarios could arise.
The modified Friedmann equation is now given by
We observe that this equation incorporates, in a simple way, the observations stated above regarding the occurrence of bouncing stages (which are always associated with the attainment of the maximum energy density, ).
The equation-of-state parameter is given by
4.2.1. The First Case
In this case, we will take , in addition to taking the following initial conditions: , , . Figure 14 shows some numerical solutions for the dynamical variables (). These solutions exemplify the points mentioned above. It is shown that is a monotonic function (in this case, a decreasing function). The bounce is given for and corresponds to the maximum value, , of the energy density; see Figure 15a.
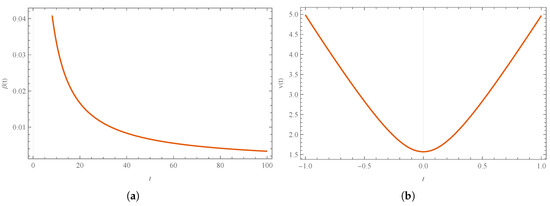
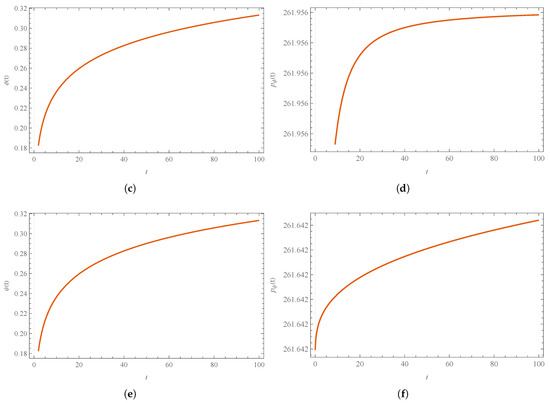
Figure 14.
Numerical solution of the Hamilton Equations (114)–(119): (a) , (b) , (c) , (d) , (e) , and (f) . The bounce is clearly noticeable in the behavior of the volume function. It was set to take place at . We use arbitrary units, namely , , , , and , and the initial condition , .
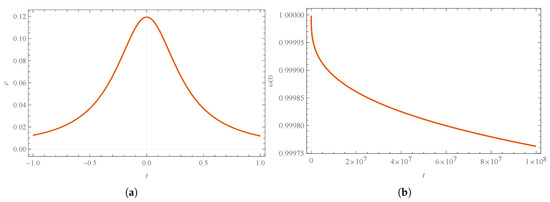
Figure 15.
Numerical solution for (a) energy density, (Equation (121)), and (b) the equation-of-state parameter, (Equation (126)). We use arbitrary units, namely , , , , and , and the initial condition , . Observe that the energy density function is bounded, with its maximum value being achieved precisely at the bounce.
For completeness, we also depict the behavior of the equation-of-state parameter. Unlike in the case without holonomy corrections, the equation-of-state parameter, , (see Figure 15b) indicates that the kinetic energy density dominates the evolution for the particular numerical solution considered.
4.2.2. The Second Case
In the second case, we will analyze while complying with the restriction . Figure 16 shows the numerical solutions (). We can notice that the behavior of the fields is similar to that in the first case. The bounce was set to take place at ; is a monotonic function; and the energy density takes its maximum value, , precisely at the bounce.
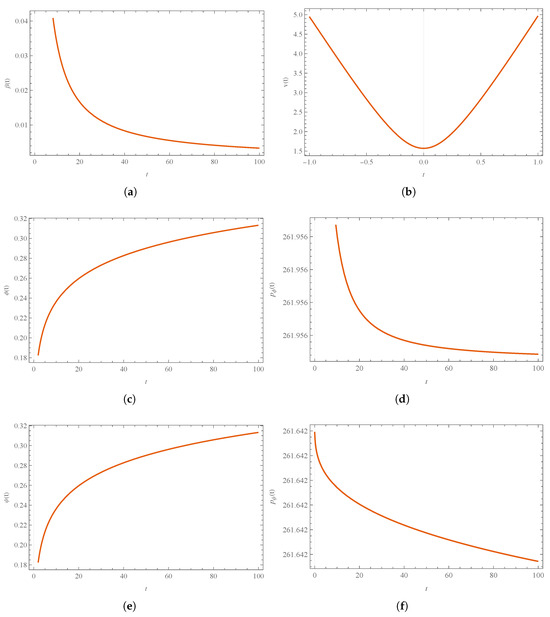
Figure 16.
Numerical solution of the Hamilton Equations (114)–(119): (a) , (b) , (c) , (d) , (e) , and (f) . The bounce is clearly noticeable in the behavior of the volume function. It was set to take place at . We use arbitrary units, namely , , , , and , and the initial condition , .
Regarding the equation-of-state parameter, , we note that the evolution is also dominated by the kinetic energy for the particular numerical solution considered (see Figure 17).
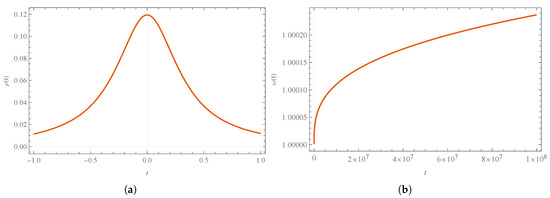
Figure 17.
Numerical solution for (a) energy density, (Equation (121)), and (b) the equation-of-state parameter, (Equation (126)). We use arbitrary units, namely , , , , and , and the initial condition , . Observe that the energy density function is bounded, with its maximum value being achieved precisely at the bounce.
5. Summary and Discussion
As a summary of the present work, we make the following remarks.
- In preparation for the main parts of the manuscript, in Section 3, a holonomization of a FLRW background with a particularly simple k-essence field was performed, and some exact solutions were found (which were shown to reduce to the standard classical ones in the limit of a vanishing area gap).
- In Section 4.2, we constructed a family of holonomy-corrected chiral quintom cosmology models. We established that the key single big bounce in the standard LQC paradigm is achieved provided the full chiral kinetic energy does note change sign during its evolution (which is ensured, in particular, by taking parameters ). We also analyzed the corresponding equation-of-state parameter.
- The main objective of Section 4.2.1 and Section 4.2.2 was to exemplify the general remarks given for the holonomy-corrected Hamiltonian system in Section 4.2 via particular numerical solutions.
A Larger Family of Loop Quantum-Corrected Chiral Models
The experience gained in Section 3 and Section 4 allows us to arrive at meaningful general conclusions regarding the bouncing scenario for an even broader chiral cosmology paradigm.
Consider a more general family of chiral fields defined by taking the Lagrangian (82) but with several scalar fields and assume additionally that the non-degenerate chiral metric, , is dependent on the scalar fields (i.e., take , where stands for the set ). This gives
In this case, the is given by particularizing (39)—which is still valid for a general —to the flat FLRW case, and so the corresponding Hamiltonian framework is well defined. The Hamiltonian takes the following specific form (for ):
where is such that . In terms of connection triad variables, this Hamiltonian is written as
The holonomy-corrected version of the above Hamiltonian is hence
where in the last line we have defined the phase space functions , , and U.
Since we are assuming a well-defined Hamiltonian system (in particular, is a non-degenerate metric field for the matter sector of the configuration manifold) the energy density will be given by , so the associated Hamiltonian constraint equation leads to
Now, the equation of motion for can be rewritten (with the help of the Hamiltonian constraint) as
Therefore, is monotonic provided that, during its evolution, either or . Under such an assumption and from the equation of motion for V (which is the same as in the more restricted case of (84)), it hence follows that the volume function reaches its minimum at only once. That is to say, the single initial bounce of standard LQC (the “big bounce”) takes place.
We have thus established the following result.
Regarding the family of holonomy-corrected chiral models defined by (130), if does not change sign during evolution, then the big bounce of standard LQC is ensured to occur.
Here are some additional remarks directly related to the above result.
- A negative definite K together with an identically zero U is not consistent with (131), and such a situation is therefore forbidden.
- If U is identically zero, must be satisfied during evolution, and hence the single big bounce takes place.
- The more restrictive situation in which K is positive and definite is, of course, a particular case of the result established above.
- If is satisfied during evolution, then the big bounce occurs. This includes the more restrictive situation in which U is negative and definite. Indeed, if , then from (131), it follows that during evolution.
- The more restrictive situation in which K is negative and definite (in which case it is necessary that during evolution) is, of course, a particular case of the result established above.
These remarks should help in the building of sensible cosmological models which ensure the occurrence of the LQC bounce within the considered larger family of holonomy-corrected chiral cosmology models.
The corresponding modified Friedmann equation for such a family of chiral models is
which, of course, reduces to the standard one in the limit of a vanishing area gap.
The equation-of-state parameter is given by
We stress that the construction of the modified Friedmann equation heavily relies on the underlying Hamiltonian framework (if the Hamiltonian framework is to be avoided, then one should start from a well-defined Lagrangian framework for effective LQC), and in general, it is not safe to pretend that such an equation is obtained just by inserting any desired ultra-exotic multi-field energy density into (22). (In the more conventional case of the family of chiral field cosmology models defined by (127), we have just shown that this replacement can be safely carried out). In particular, care should be taken when dealing with general k-essence chiral cosmology models since, in this case, an ordinary Hamiltonian framework might not be immediately available.
Nonetheless, it should be kept in mind that the family put forward here is to be viewed as only an effective framework—built directly upon the standard LQC effective scheme. In particular, we remark that this family was not obtained as a certain continuum limit of a full-loop quantized scenario. Serious issues and drawbacks are expected to be encountered along this more fundamental avenue. In fact, the usual (effective) LQC framework (which relies on just a single free standard homogeneous field) has been recently subject to scrutiny due to some serious caveats regarding, in particular, the evolution of the volume semiclassical states (see, e.g., [42]).
To sum up, it is concluded that, for the more general family of loop quantum-corrected chiral models defined by (130) (assuming does not change sign during evolution), the characteristic LQC single bouncing stage associated with the maximum, , of the energy density (and with the minimum of the volume function) is always realized. Note that the particular case corresponds to a family of purely kinetic k-essence multi-field theories whose kinetic term can be written in the form (which, in view of the Hamiltonian constraint, must evolve as ).
The importance of the above conclusion relies mostly on the large number of models contained in the family defined by (130) (since the finite number of homogeneous fields and the dependence of on such fields are left otherwise to be arbitrary). A bit away from the initial bounce, the family would rapidly transit to the set of standard chiral cosmological models defined by (128) (since most effects due to quantum gravity would dilute away during the inflationary epoch [21]). This implies that the inclusion of inflation, dark matter, and dark energy (and other features like the crossing of the phantom divide line) that has been achieved by particular multi-field cosmology scenarios (see, e.g., [43,44,45,46,47,48,49,50,51,52]) consistent with (128) can be “glued” to its singularity-free loop quantum-corrected counterpart given by (130). This gluing would, therefore, comprise a rather robust and considerably diverse paradigm to study the evolution of the universe from the very early quantum-dominated epochs up to the late stages.
Therefore, the main feature of the presented broad family of models is the possibility of addressing issues/tensions pertaining to any of the Universe’s stages of evolution within a single theoretical framework, with the benefit of automatically incorporating the avoidance of the initial singularity.
In relation to the remark above, it is instructive to emphasize the way in which this wide family of holonomy-corrected chiral cosmology models reduces to specific, more standard cosmological models:
- Standard models with holonomy corrections:
- −
- A standard quintom scenario in effective LQC is obtained by considering two scalar fields, and , with (see, e.g., [53]);
- −
- Inflationary scenarios within effective LQC are obtained by considering one scalar field, , with and suitable forms for (see, e.g., [54]);
- −
- The original effective scheme of LQC is achieved by considering one free scalar field, , with .
- Standard models without holonomy corrections: The replacement is to be performed in the Hamiltonian (130), and is no longer restricted to take values only in the range .
- −
- The standard quintom scenario is obtained by considering only two scalar fields, and , and taking with suitable potentials, and . Relevant potentials are reported in [1].
- −
- The standard quintessence scenario is obtained by considering only one scalar field, , and taking with a suitable potential, . Relevant potentials are reported in [1,55]. The standard ΛCDM model can, of course, be regarded as a limiting case of the quintessence scenario.
An interesting further widening of the family (130) would be achieved by considering anisotropic backgrounds, in particular the Bianchi type I and IX models (given their isotropic limit, their importance in the BKL conjecture [56], and the possible meaningful role of anisotropies in the very early universe). This could, in principle, be achieved with a similar method to the one followed here (the effective LQC scheme of some anisotropic models is already available and has been substantially studied; see, e.g., [57,58,59,60]).
Author Contributions
Conceptualization, A.E.-G.; methodology, A.E.-G.; writing—original draft, A.E.-G., L.R.D.-B., S.A.P.-P. and J.S.; writing—review and editing, A.E.-G., L.R.D.-B., S.A.P.-P. and J.S.; visualization, L.R.D.-B., S.A.P.-P. and J.S.; software, L.R.D.-B., S.A.P.-P. and J.S. All authors have read and agreed to the published version of the manuscript.
Funding
A.E.-G. was partially supported by SNI-CONAHCyT and Secretaria de Investigación y Posgrado del Instituto Politécnico Nacional, grant SIP20231739. L.R.D.-B. was partially supported by SNI-CONAHCyT and Secretaria de Investigación y Posgrado del Instituto Politécnico Nacional, grant SIP20241763. S.A.P.-P. was partially supported by SNI-CONAHCyT and Secretaria de Investigación y Posgrado del Instituto Politécnico Nacional, grant SIP20230366. J.S. was partially supported by SNI-CONAHCyT and PROMEP, grant UGTO-CA-3.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Acknowledgments
This work is part of a collaboration within the Instituto Avanzado de Cosmología and Red PROMEP: Gravitation and Mathematical Physics under project Quantum aspects of gravity in cosmological models, phenomenology and geometry of space-time. Many calculations where conducted with the Symbolic Program REDUCE 3.8.
Conflicts of Interest
The authors declare no conflicts of interest.
Notes
| 1 | In cosmology, one is usually restricted to homogenous (metric and scalar) fields. |
| 2 | The spatial integration featured in the action, when carried over the whole spacelike slice, diverges in the flat case. Due to homogeneity, we can restrict the action to a compact region of the spacelike slice. |
References
- Copeland, E.J.; Sami, M.; Tsujikawa, S. Dynamics of dark energy. Int. J. Mod. Phys. D 2006, 15, 1753–1936. [Google Scholar] [CrossRef]
- Cai, Y.F.; Saridakis, E.N.; Setare, M.R.; Xia, J.Q. Quintom Cosmology: Theoretical implications and observations. Phys. Rep. 2010, 493, 1–60. [Google Scholar] [CrossRef]
- Vikman, A. Can dark energy evolve to the phantom? Phys. Rev. D 2005, 71, 023515. [Google Scholar] [CrossRef]
- Chervon, S.V. On the chiral model of cosmological inflation. Russ. Phys. J. 1995, 38, 539–543. [Google Scholar] [CrossRef]
- Chervon, S.V. Chiral Cosmological Models: Dark Sector Fields Description. Quantum Matter 2013, 2, 71–82. [Google Scholar] [CrossRef]
- Socorro, J.; Pérez-Payán, S.; Hernández-Jiménez, R.; Espinoza-García, A.; Díaz-Barrón, L.R. Quintom Fields from Chiral K-essence Cosmology. Universe 2022, 8, 548. [Google Scholar] [CrossRef]
- Armendariz-Picon, C.; Damour, T.; Mukhanov, V.F. k—Inflation. Phys. Lett. B 1999, 458, 209–218. [Google Scholar] [CrossRef]
- Armendariz-Picon, C.; Mukhanov, V.; Steinbardt, P.J. Dynamical solution to the problem of a small cosmological constant and late-time cosmic acceleration. Phys. Rev. Lett. 2000, 85, 4438. [Google Scholar] [CrossRef]
- Armendariz-Picon, C.; Mukhanov, V.; Steinbardt, P.J. Essentials of k-essence. Phys. Rev. D 2001, 63, 103510. [Google Scholar] [CrossRef]
- De Felice, A.; Tsujikawa, S. f(R) theories. Living Rev. Relativ. 2010, 13, 3. [Google Scholar] [CrossRef]
- Kaiser, D.I. Conformal transformations with multiple scalar fields. Phys. Rev. D 2010, 81, 084044. [Google Scholar] [CrossRef]
- Birrell, N.D.; Davies, P.C.W. Quantum Fields in Curved Space; Cambridge University Press: New York, NY, USA, 1982. [Google Scholar]
- Paliathanasis, A.; Leon, G.; Pan, S. Exact Solutions in Chiral Cosmology. Gen. Relativ. Gravit. 2019, 51, 106. [Google Scholar] [CrossRef]
- Socorro, J.; Pérez-Payán, S.; Hernández-Jiménez, R.; Espinoza-García, A.; Díaz-Barrón, L.R. Classical and quantum exact solutions for a FRW in chiral like cosmology. Class. Quant. Grav. 2021, 38, 135027. [Google Scholar] [CrossRef]
- Paliathanasis, A. Bianchi I Spacetimes in Chiral–Quintom Theory. Universe 2022, 8, 503. [Google Scholar] [CrossRef]
- Socorro, J.; Pérez-Payán, S.; Hernández-Jiménez, R.; Espinoza-García, A.; Díaz-Barrón, L.R. Quintom fields from chiral anisotropic cosmology. Gen. Relativ. Gravit. 2023, 55, 75. [Google Scholar] [CrossRef]
- Ashtekar, A.; Lewandowski, J. Background independent quantum gravity: A status report. Class. Quant. Grav. 2004, 21, R53–R152. [Google Scholar] [CrossRef]
- Thiemann, T. Introduction to Modern Canonical Quantum General Relativity; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Arnowitt, R.; Deser, S.; Misner, C.W. Republication of: The dynamics of general relativity. Gen. Relativ. Gravit. 2008, 40, 1997–2027. [Google Scholar] [CrossRef]
- Rovelli, C. Quantum Gravity; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Ashtekar, A.; Singh, P. Loop quantum cosmology: A status report. Class. Quant. Grav. 2011, 28, 213001. [Google Scholar] [CrossRef]
- Bojowald, M. Loop quantum cosmology. Living Rev. Relativ. 2005, 8, 11. [Google Scholar] [CrossRef]
- Bojowald, M. Absence of singularity in loop quantum cosmology. Phys. Rev. Lett. 2001, 86, 5227–5230. [Google Scholar] [CrossRef]
- Diener, P.; Gupt, B.; Megevand, M.; Singh, P. Numerical evolution of squeezed and non-Gaussian states in loop quantum cosmology. Class. Quant. Grav. 2014, 31, 165006. [Google Scholar] [CrossRef]
- Ashtekar, A.; Bojowald, M.; Lewandowski, J. Mathematical structure of loop quantum cosmology. Adv. Theor. Math. Phys. 2003, 7, 233–268. [Google Scholar] [CrossRef]
- Bojowald, M. Canonical Gravity and Applications; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Ashtekar, A.; Corichi, A.; Singh, P. Robustness of key features of loop quantum cosmology. Phys. Rev. D 2008, 77, 024046. [Google Scholar] [CrossRef]
- Sotiriou, T.P. Covariant effective action for loop quantum cosmology from order reduction. Phys. Rev. D 2009, 79, 044035. [Google Scholar] [CrossRef]
- Ribeiro, A.R.; Vernieri, D.; Lobo, F.S.N. Effective f(R) Actions for Modified Loop Quantum Cosmologies via Order Reduction. Universe 2023, 9, 181. [Google Scholar] [CrossRef]
- Socorro, J.; Pimentel, L.O.; Espinoza-García, A. Classical Bianchi type I cosmology in K-essence theory. Adv. High Energy Phys. 2014, 2014, 805164. [Google Scholar] [CrossRef]
- Corben, H.C.; Stehle, P. Classical Mechanics; Dover Publications: Mineola, NY, USA, 1994. [Google Scholar]
- Goldstein, H.; Poole, C.; Safko, J. Classical Mechanics; Addison-Wesley: Reading, MA, USA, 2002. [Google Scholar]
- Dirac, P.A.M. Lectures on Quantum Mechanics; Dover Publications: Mineola, NY, USA, 2001. [Google Scholar]
- Wipf, A. Hamilton’s Formalism for Systems with Constraints. In Canonical Gravity: From Classical to Quantum; Ehlers, J., Friedright, H., Eds.; Springer: Berlin/Heidelberg, Germany, 1994. [Google Scholar]
- Christodoulakis, T.; Dimakis, N.; Terzis, P.A. Lie point and variational symmetries in minisuperspace Einstein gravity. J. Phys. A Math. Theor. 2014, 47, 095202. [Google Scholar] [CrossRef]
- Saez, D.; Ballester, V.J. A simple coupling with cosmological implications. Phys. Lett. A 1986, 113, 467–470. [Google Scholar] [CrossRef]
- Shi, J.; Wu, J. Dynamics of k-essence in loop quantum cosmology. Chin. Phys. C 2021, 45, 045104. [Google Scholar] [CrossRef]
- Abraham, R.; Marsden, J.E. Foundations of Mechanics; American Mathematical Society: Providence, RI, USA, 2008. [Google Scholar]
- De Witt, B.S. Quantum Theory of Gravity. I. The Canonical Theory. Phys. Rev. 1967, 160, 1113. [Google Scholar] [CrossRef]
- Ryan, M.P., Jr.; Turbiner, A.V. The conformally invariant Laplace–Beltrami operator and factor ordering. Phys. Lett. A 2004, 333, 30–34. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Course of Theoreitcal Physics. In Quantum Mechanics (Non-Relativistic Theory); Elsevier: Amsterdam, The Netherlands, 1977; Volume 3. [Google Scholar]
- Kaminski, W.; Kolanowski, M.; Lewandowski, J. Dressed metric predictions revisited. Class. Quant. Grav. 2020, 37, 095001. [Google Scholar] [CrossRef]
- Kim, S.A.; Liddle, A.R. Nflation: Multi-field inflationary dynamics and perturbations. Phys. Rev. D 2006, 74, 023513. [Google Scholar] [CrossRef]
- Lazkoz, R.; Leon, G.; Quiros, I. Quintom cosmologies with arbitrary potentials. Phys. Lett. B 2007, 649, 103–110. [Google Scholar] [CrossRef]
- Leon, G.; Paliathanasis, A.; Morales-Martínez, J.L. The past and future dynamics of quintom dark energy models. Eur. Phys. J. C 2018, 78, 753. [Google Scholar] [CrossRef]
- Dimakis, N.; Paliathanasis, A. Crossing the phantom divide line as an effect of quantum transitions. Class. Quant. Grav. 2021, 38, 075016. [Google Scholar] [CrossRef]
- Elizalde, E.; Nojiri, S.; Odintsov, S.D.; Saez-Gomez, D.; Faraoni, V. Reconstructing the universe history, from inflation to acceleration, with phantom and canonical scalar fields. Phys. Rev. D 2008, 77, 106005. [Google Scholar] [CrossRef]
- Christodoulidis, P.; Roest, D.; Sfakianakis, E.I. Scaling attractors in multi-field inflation. J. Cosmol. Astropart. Phys. 2019, 12, 59. [Google Scholar] [CrossRef]
- Beesham, A.; Chervon, S.V.; Maharaj, S.D.; Kubasov, A.S. An Emergent Universe with Dark Sector Fields in a Chiral Cosmological Model. Quantum Matter 2013, 2, 388–395. [Google Scholar] [CrossRef]
- Chervon, S.V.; Abbyazov, R.R.; Kryukov, S.V. Dynamics of Chiral Cosmological Fields in the Phantom-Canonical Model. Russ. Phys. J. 2015, 58, 597–605. [Google Scholar] [CrossRef]
- Socorro, J.; Núñez, O.E. Scalar potentials with Multi-scalar fields from quantum cosmology and supersymmetric quantum mechanics. Eur. Phys. J. Plus 2017, 132, 168. [Google Scholar] [CrossRef]
- Socorro, J.; Núñez, O.E.; Hernández-Jiménez, R. Classical and Quantum Exact Solutions for a FRW Multiscalar Field Cosmology with an Exponential Potential Driven Inflation. Adv. Math. Phys. 2018, 2018, 3468381. [Google Scholar] [CrossRef]
- Wei, H.; Zhang, S.N. Dynamics of quintom and hessence energies in loop quantum cosmology. Phys. Rev. D 2007, 76, 063005. [Google Scholar] [CrossRef]
- Barboza, L.N.; Graef, L.L.; Ramos, R.O. Warm bounce in loop quantum cosmology and the prediction for the duration of inflation. Phys. Rev. D 2020, 102, 103521. [Google Scholar] [CrossRef]
- Tsujikawa, S. Quintessence: A review. Class. Quant. Grav. 2013, 30, 214003. [Google Scholar] [CrossRef]
- Belinskii, V.A.; Khalatnikov, I.M.; Lifshitz, E.M. Oscillatory approach to a singular point in relativistic cosmology. Adv. Phys. 1970, 19, 525. [Google Scholar] [CrossRef]
- Chiou, D.W. Loop quantum cosmology in Bianchi Type I Models: Analytical Investigation. Phys. Rev. D 2007, 75, 024029. [Google Scholar] [CrossRef]
- Chiou, D.W. Effective dynamics, big bounces and scaling symmetry in Bianchi I loop quantum cosmology. Phys. Rev. D 2007, 76, 124037. [Google Scholar] [CrossRef]
- Ashtekar, A.; Wilson-Ewing, E. Loop quantum cosmology of Bianchi type I models. Phys. Rev. D 2009, 79, 083535. [Google Scholar] [CrossRef]
- Wilson-Ewing, E. Loop quantum cosmology of Bianchi type IX models. Phys. Rev. D 2010, 82, 043508. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).