The Non-Thermal Radio Emissions of the Solar Transition Region and the Proposal of an Observational Regime
Abstract
1. Introduction: Why Focus on the Solar Transition Region?
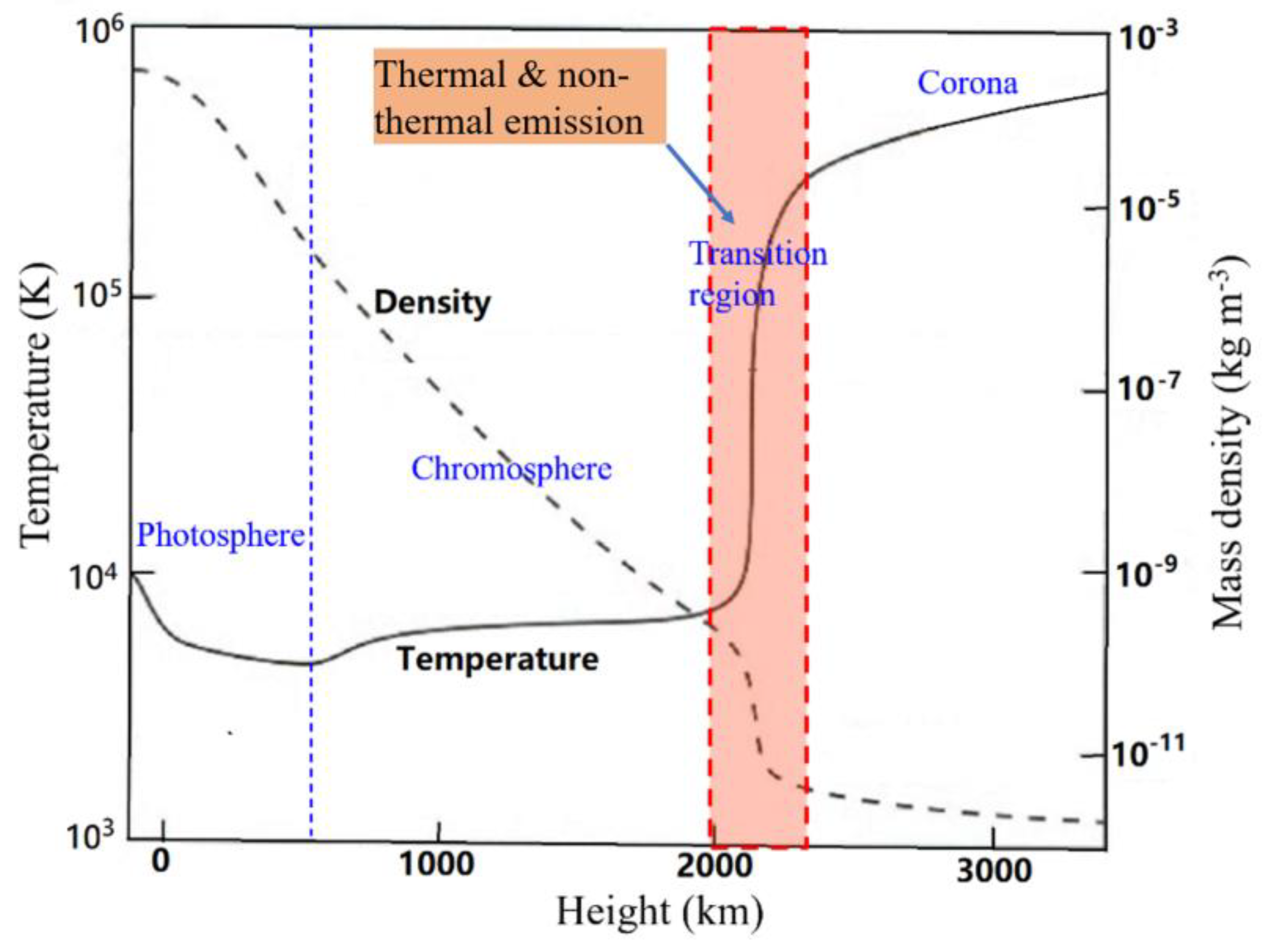
2. Non-Thermal Radio Emissions from the Solar Transition Region
2.1. Non-Thermal Electrons in the Transition Region
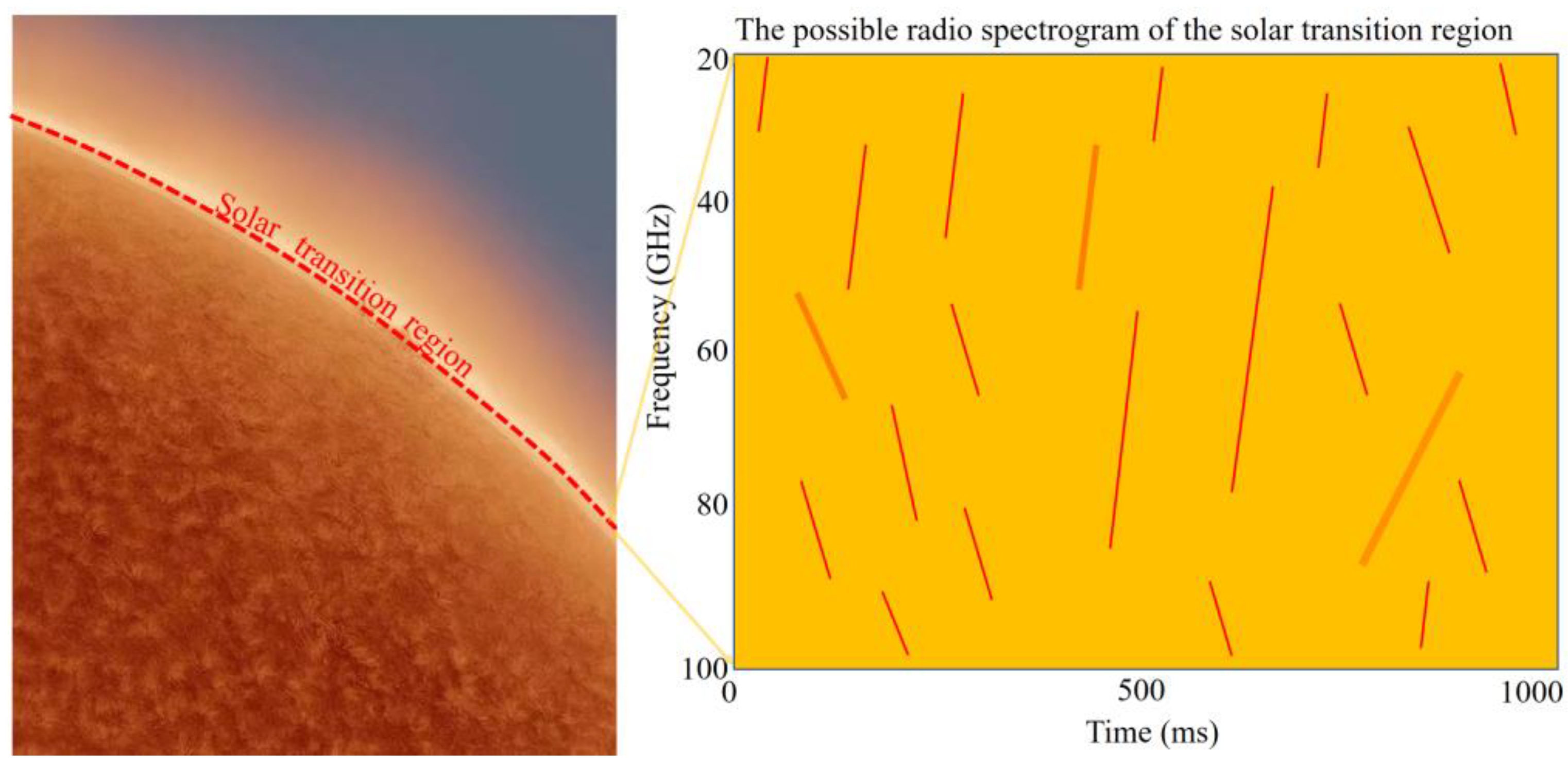
2.2. Radio Emissions by Non-Thermal Electrons in the Transition Region
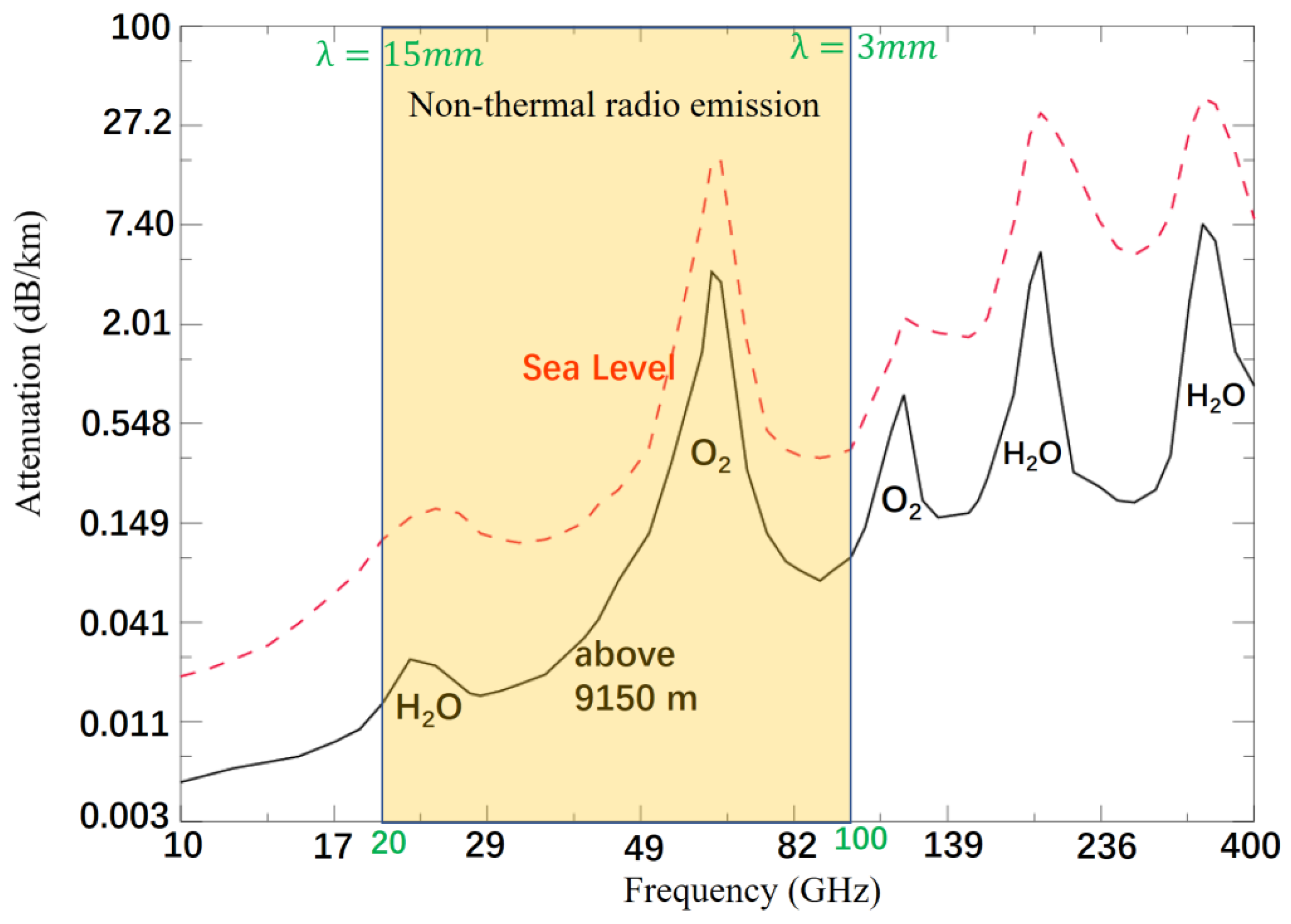
3. Limitations of Radio Observations of the Transition Region
4. The Proposed Solar Ultra-Wide Broadband Millimeter-Wave Spectrometer
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Alissandrakis, C.E. Where is the base of the Transition Region? Evidence from TRACE, SDO, IRIS and ALMA observations. Adv. Space Res. 2023, 71, 1907–1914. [Google Scholar] [CrossRef]
- Zhang, X.; Deng, L.; Fei, Y.; Li, C.; Tian, X. Temporal Variation of the Rotation in the Solar Transition Region. Astrophys. J. 2023, 951, L3. [Google Scholar] [CrossRef]
- Mariska, J.T. The Solar Transition Region; Cambridge University Press: Cambridge, UK, 1992. [Google Scholar]
- Kjeldseth-Moe, O. The Solar Transition Region Dynamic Sun; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Marsch, E.; Zhou, G.Q.; He, J.S.; Tu, C.Y. Magnetic structure of the solar transition region as observed in various ultraviolet lines emitted at different temperatures. Astron. Astrophys. 2006, 457, 699. [Google Scholar] [CrossRef]
- Kerr, R.A. Why Is the Sun’s Corona So Hot? Science 2012, 336, 1099. [Google Scholar] [CrossRef]
- Klimchuk, J.A. On Solving the Coronal Heating Problem. Sol. Phys. 2006, 234, 41–77. [Google Scholar] [CrossRef]
- Davila, J.M. Heating of the solar corona by the resonant absorption of Alfven waves. Astrophys. J. 1987, 317, 514–521. [Google Scholar] [CrossRef]
- De Pontieu, B.; McIntosh, S.W.; Carlsson, M.; Hansteen, V.H.; Tarbell, T.D.; Boerner, P.; Martinez-Sykora, J.; Schrijver, C.J.; Title, A.M. The Origins of Hot Plasma in the Solar Corona. Science 2011, 331, 55–58. [Google Scholar] [CrossRef] [PubMed]
- Parker, E.N. Nanoflares and the solar X-ray corona. Astrophys. J. 1988, 330, 474–479. [Google Scholar] [CrossRef]
- Cargill, P.J.; Klimchuk, J.A. Nanoflare Heating of the Corona Revisited. Astrophys. J. 2004, 605, 911–920. [Google Scholar] [CrossRef]
- Tan, B. Coronal heating driven by a magnetic gradient pumping mechanism in solar plasmas. Astrophys. J. 2014, 795, 140. [Google Scholar] [CrossRef]
- Tan, B. The Early Evolution of Solar Flaring Plasma Loops. Universe 2021, 7, 378. [Google Scholar] [CrossRef]
- Sigalotti, L.D.G.; Cruz, F. Unveiling the mystery of solar-coronal heating. Phys. Today 2023, 76, 34–40. [Google Scholar] [CrossRef]
- Tian, H.; DeLuca, E.E.; Cranmer, S.R.; De Pontieu, B.; Peter, H.; Martínez-Sykora, J.; Golub, L.; McKillop, S.; Reeves, K.K.; Miralles, M.P.; et al. Prevalence of small-scale jets from the networks of the solar transition region and chromosphere. Science 2014, 346, 1255711. [Google Scholar] [CrossRef]
- Wilhelm, K.; Curdt, W.; Marsch, E.; Lemaire, P.; Gabriel, A.; Vial, J.-C.; Grewing, M.; Huber, M.C.E.; Jordan, S.D.; Poland, A.I.; et al. SUMER—Solar Ultraviolet Measurements of Emitted Radiation. Sol. Phys. 1995, 162, 189–231. [Google Scholar] [CrossRef]
- Handy, B.; Acton, L.; Kankelborg, C.; Wolfson, C.; Akin, D.; Bruner, M.; Caravalho, R.; Catura, R.; Chevalier, R.; Duncan, D.; et al. The transition region and coronal explorer. Sol. Phys. 1999, 187, 229–260. [Google Scholar] [CrossRef]
- De Pontieu, B.; Title, A.M.; Lemen, J.R.; Kushner, G.D.; Akin, D.J.; Allard, B.; Berger, T.; Boerner, P.; Cheung, M.; Chou, C.; et al. The Interface Region Imaging Spectrograph (IRIS). Sol. Phys. 2014, 289, 2733–2779. [Google Scholar] [CrossRef]
- Warren, H.P.; Reep, J.W.; Crump, N.A.; Simões, P.J.A. Transition region and chromospheric signatures of impulsive heating events. i. observations. Astrophys. J. 2016, 829, 35. [Google Scholar] [CrossRef]
- Reep, J.W.; Warren, H.P.; Crump, N.A.; Simões, P.J.A. Transition region and chromospheric signatures of impulsive heating events. ii. modeling. Astrophys. J. 2016, 827, 145. [Google Scholar] [CrossRef]
- Chen, X.; Kontar, E.P.; Chrysaphi, N.; Zhang, P.; Krupar, V.; Musset, S.; Maksimovic, M.; Jeffrey, N.L.S.; Azzollini, F.; Vecchio, A. Source positions of an interplanetary type III radio burst and anisotropic radio-wave scattering. Astron. Astrophys. 2023, 680, A1. [Google Scholar] [CrossRef]
- Gary, D.E. New Insights from Imaging Spectroscopy of Solar Radio Emission. Annu. Rev. Astron. Astrophys. 2023, 61, 427–472. [Google Scholar] [CrossRef]
- Vernazza, J.E.; Avrett, E.H.; Loeser, R. Structure of the solar chromosphere. III—Models of the EUV brightness components of the quiet-sun. Astrophys. J. Suppl. Ser. 1981, 45, 635–725. [Google Scholar] [CrossRef]
- Avrett, E.H.; Loeser, R. Models of the Solar Chromosphere and Transition Region from SUMER and HRTS Observations: Formation of the Extreme-Ultraviolet Spectrum of Hydrogen, Carbon, and Oxygen. Astrophys. J. Suppl. Ser. 2008, 175, 229–276. [Google Scholar] [CrossRef]
- Dulk, G.A. Radio Emission from the Sun and Stars. Annu. Rev. Astron. Astrophys. 1985, 23, 169–224. [Google Scholar] [CrossRef]
- De Jager, C.; Kuijpers, J.; Correia, E.; Kaufmann, P. A high-energy solar flare burst complex and the physical properties of its source region. Sol. Phys. 1987, 110, 317–326. [Google Scholar] [CrossRef]
- Kaufmann, P.; Correia, E.; Costa, J.E.R.; Vaz, A.M.Z. A synchrotron-inverse Compton interpretation of a solar burst producing fast pulses at λ < 3 mm and hard X-rays. Astron. Astrophys. 1986, 157, 11. [Google Scholar]
- White, S.M.; Kundu, M.R. Solar observations with a millimeter-wavelength Array. Sol. Phys. 1992, 141, 347–369. [Google Scholar] [CrossRef]
- Kaufmann, P.; Correia, E.; Costa, J.E.R.; Zodi, A.M.; Dennis, B.R. Solar burst with millimeter-wave emission at high frequency only. Nature 1985, 313, 31. [Google Scholar] [CrossRef]
- Bastian, T.S.; Benz, A.O.; Gary, D.E. Radio emission from solar flares. Annu. Rev. Astron. Astrophys. 1998, 36, 131–188. [Google Scholar] [CrossRef]
- Petrosian, V.; Bykov, A.M. Particle Acceleration Mechanisms. Space Sci. Rev. 2008, 134, 207–227. [Google Scholar] [CrossRef]
- Li, Y.; Ni, L.; Ye, J.; Mei, Z.; Lin, J. Particle Accelerations in a 2.5-dimensional Reconnecting Current Sheet in Turbulence. Astrophys. J. 2022, 938, 24. [Google Scholar] [CrossRef]
- Li, X.C.; Guo, F.; Li, H.; Li, G. Particle Acceleration during Magnetic Reconnection in a Low-beta Plasma. Astrophys. J. 2017, 843, 21. [Google Scholar] [CrossRef]
- Gordovskyy, M.; Browning, P.K.; Vekstein, G.E. Particle acceleration in a transient magnetic reconnection event. Astron. Astrophys. 2010, 519, A21. [Google Scholar] [CrossRef]
- Porter, J.G.; Dere, K.P. The magnetic network location of explosive events observed in the solar transition region. Astrophys. J. 1991, 370, 775–778. [Google Scholar] [CrossRef]
- Singh, N. Reconnection-driven double layers in the stratified plasma of the solar transition region: Supply of hot plasma into the corona. Astrophys. J. 2015, 810, L1. [Google Scholar] [CrossRef]
- Moore, R.L.; Sterling, A.C.; Cirtain, J.W.; Falconer, D.A. Solar X-ray jets, type-ii spicules, granule-size emerging bipoles, and the genesis of the heliosphere. Astrophys. J. 2011, 731, L18. [Google Scholar] [CrossRef]
- Buchner, J.; Nikutowski, B.; Otto, A. Plasma acceleration due to transition region reconnection. Goephys. Monogr. Ser. 2005, 156, 161. [Google Scholar] [CrossRef]
- De la Luz, V.; Lara, A.; Raulin, J.-P. Synthetic spectra of radio, millimeter, sub-millimeter, and infrared regimes with non-local thermodynamic equilibrium approximation. Astrophys. J. 2011, 737, 1. [Google Scholar] [CrossRef]
- White, S.M.; Iwai, K.; Phillips, N.M.; Hills, R.E.; Hirota, A.; Yagoubov, P.; Siringo, G.; Shimojo, M.; Bastian, T.S.; Hales, A.S.; et al. Observing the Sun with the Atacama Large Millimeter/submillimeter Array (ALMA): Fast-Scan Single-Dish Mapping. Sol. Phys. 2017, 292, 88. [Google Scholar] [CrossRef]
- Nindos, A.; Patsourakos, S.; Alissandrakis, C.E.; Bastian, T.S. ALMA observations of the variability of the quiet Sun at millimeter wavelengths. Astron. Astrophys. 2021, 652, A92. [Google Scholar] [CrossRef]
- Bao-Lin, T.; Jun, C.; Cheng-Ming, T.; Hong-Xiang, K. Scaling-laws of Radio Spike Bursts and Their Constraints on New Solar Radio Telescopestwo. Chin. Astron. Astrophys. 2019, 43, 59–74. [Google Scholar] [CrossRef]
- Tan, B. Small-scale microwave bursts in long-duration solar flares. Astrophys. J. 2013, 773, 165. [Google Scholar] [CrossRef]
- Gelfreikh, G.B.; Pilyeva, N.A.; Ryabov, B.I. On the gradient of coronal magnetic fields from radio observations. Sol. Phys. 1997, 170, 253–264. [Google Scholar] [CrossRef]
- Nakajima, H.A.; Nishio, M.; Enome, S.; Shibasaki, K.; Takano, T.; Hanaoka, Y.; Torii, C.; Sekiguchi, H.; Bushimata, T.; Kawashima, S.; et al. New Nobeyama Radio Heliograph. J. Astrpphys. Astron. 1995, 16, 427. [Google Scholar]
- Nakajima, H.; Sekiguchi, H.; Sawa, M.; Kai, K.; Kawashima, S. The radiometer and polarimeters at 80, 35, and 17 GHz for solae observations at Nobeyama. Publ. Astron. Soc. Jpn. 1985, 37, 163. [Google Scholar]
- Kaufmann, P.; Strauss, F.M.; Schaal, R.E.; Laporte, C. The use of the large millimeter-wave antenna at Itaprtinga in high sensitivity solar research. Solar Phys. 1982, 78, 389. [Google Scholar] [CrossRef]
- Kaufmann, P.; Levato, H.; Cassiano, M.M.; Correia, E.; Costa, J.E.R.; de Castro, C.G.G.; Godoy, R.; Kingsley, R.K.; Kingsley, J.S.; Kudaka, A.S.; et al. New telescopes for ground-based solar observations at submillimeter and mid-infrared. Proc. SPIE 2008, 7012, 788889. [Google Scholar] [CrossRef]
- Kundu, M.R.; White, S.M.; Gopalswamy, N.; Bieging, J.H.; Hurford, G.J. First high spatial resolution interferometric observations of solar flares at millimeter wavelengths. Astrophys. J. 1990, 358, L69. [Google Scholar] [CrossRef]
- Wootten, A.; Thompson, A.R. The Atacama Large Millimeter/Submillimeter Array. Proc. IEEE 2009, 97, 1463–1471. [Google Scholar] [CrossRef]
- Bastian, T.S.; Shimojo, M.; Bárta, M.; White, S.M.; Iwai, K. Solar observing with the Atacama large millimeter-submillimeter array. Front. Astron. Space Sci. 2022, 9, 977368. [Google Scholar] [CrossRef]
- Fleishman, G.D.; Oliveros, J.C.M.; Landi, E.; Glesener, L. What aspects of solar flares can be clarified with mm/submm observations? Front. Astron. Space Sci. 2022, 9, 966444. [Google Scholar] [CrossRef]
- Nindos, A.; Patsourakos, S.; Jafarzadeh, S.; Shimojo, M. The dynamic chromosphere at millimeter wavelengths. Front. Astron. Space Sci. 2022, 9, 981205. [Google Scholar] [CrossRef]
- Skokić, I.; Benz, A.O.; Brajša, R.; Sudar, D.; Matković, F.; Bárta, M. Flares detected in ALMA single-dish images of the Sun. Astron. Astrophys. 2023, 669, A156. [Google Scholar] [CrossRef]
- Yan, F.; Wu, Z.; Shang, Z.; Wang, B.; Zhang, L.; Chen, Y. The First Flare Observation with a New Solar Microwave Spectrometer Working in 35–40 GHz. Astrophys. J. 2022, 942, L11. [Google Scholar] [CrossRef]
- Shang, Z.; Wu, Z.; Liu, Y.; Bai, Y.; Lu, G.; Zhang, Y.; Zhang, L.; Su, Y.; Chen, Y.; Yan, F. The Calibration of the 35–40 GHz Solar Radio Spectrometer with the New Moon and a Noise Source. Astrophys. J. Suppl. Ser. 2023, 268, 45. [Google Scholar] [CrossRef]
- Pol, S.L.C.; Ruf, C.S.; Keihm, S.J. Improved 20- to 32-GHz atmospheric absorption model. Radio Sci. 1998, 33, 1319–1333. [Google Scholar] [CrossRef]
- Belikovich, M.V.; Makarov, D.S.; Serov, E.A.; Kulikov, M.Y.; Feigin, A.M. Validation of Atmospheric Absorption Models within the 20–60 GHz Band by Simultaneous Radiosonde and Microwave Observations: The Advantage of Using ECS Formalism. Remote. Sens. 2022, 14, 6042. [Google Scholar] [CrossRef]
- Grec, G.; Fossat, E.; Brandt, P.; Deubner, F.L. Solar pulsations and anhular coherence of atmospheric transparency fluctuations. Astron. Astrophys. 1979, 77, 347. [Google Scholar]
| Telescope | Frequency (GHz) | Status |
|---|---|---|
| Nobeyama RadioHiograph (NoRH), Japan [45] | Imaging at 17, 34 | Closed in 2020 |
| Nobeyama Radio Polarimeters (NoRP), Japan [46] | 1.0, 2.0, 3.75, 9.4, 17, 35, 80 | Daily (80 GHz; has been closed since 2012). |
| Itapetiga radome-enclosed telescope, Brazil [47] | 7.0, 23.2, 30, 44.3, 90 | Occasional observation based on events |
| Solar Submillimeter Telescope (SST), Argentina [48] | 212, 405 | Occasional observation based on events |
| Berkeley-Illinois-Maryland Array (BIMA), USA [49] | Imaging at 86 | Occasional observation based on events |
| Atacama Large Millimeter/submillimeter Array, ALMA, Czeli [50,51,52,53,54] | Imaging at 100, 239 | Solar observation time: 2–3% |
| Chashan Broadband Solar millimeter spectrometer (CBS), China [55] | 35–40 with frequency resolution: 0.5 GHz | Daily observations since 2022 |
| Observing frequency | 20–100 GHz (4 elements: 20–40, 40–60, 60–80, 80–100 GHz) |
| radius of antenna | 98.3 cm, 65.5 cm, 49.2 cm, 39.3 cm, respectively |
| Antenna design | Front-fed parabolic reflector antenna, Cassegrain dual-reflector antenna |
| Feed design | Quadruple-ridged flared horn or Corrugated Horn |
| Dynamic range | >30 dB |
| Polarization | RCP and LCP |
| Sensitivity | <0.2 sfu |
| Frequency resolution | 100 MHz, 200 MHz, 250 MHz, 400 MHz, respectively |
| Frequency channel | 200, 100, 80, 50, respectively. A total of 430 channels |
| Time resolution | 0.2 ms |
| Calibration | Using the Y Factor method with Thot from noise input and Tcold from cold sky |
| Observing frequency | 20–35 GHz, or 75–100 GHz |
| radius of antenna | 112.4 cm, or 39.3 cm |
| Antenna design | Front-fed parabolic reflector antenna, Cassegrain dual-reflector antenna |
| Feed design | Quadruple-ridged flared horn or Corrugated Horn |
| Dynamic range | >30 dB |
| Polarization | RCP and LCP |
| Sensitivity | <0.2 sfu |
| Frequency resolution | 50 MHz or 250 MHz |
| Frequency channel | 300 or 100 |
| Time resolution | 0.2 ms or 0.4 ms |
| Construct site | Saisteng Mountain in Qinghai, China (altitude: 4030 m) |
| Calibration | Using the Y factor method with Thot from noise input and Tcold from cold sky |
| Atmospheric Absorption correction | Using an atmospheric absorption model [58,59] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tan, B.; Huang, J.; Zhang, Y.; Deng, Y.; Chen, L.; Liu, F.; Fan, J.; Shi, J. The Non-Thermal Radio Emissions of the Solar Transition Region and the Proposal of an Observational Regime. Universe 2024, 10, 82. https://doi.org/10.3390/universe10020082
Tan B, Huang J, Zhang Y, Deng Y, Chen L, Liu F, Fan J, Shi J. The Non-Thermal Radio Emissions of the Solar Transition Region and the Proposal of an Observational Regime. Universe. 2024; 10(2):82. https://doi.org/10.3390/universe10020082
Chicago/Turabian StyleTan, Baolin, Jing Huang, Yin Zhang, Yuanyong Deng, Linjie Chen, Fei Liu, Jin Fan, and Jun Shi. 2024. "The Non-Thermal Radio Emissions of the Solar Transition Region and the Proposal of an Observational Regime" Universe 10, no. 2: 82. https://doi.org/10.3390/universe10020082
APA StyleTan, B., Huang, J., Zhang, Y., Deng, Y., Chen, L., Liu, F., Fan, J., & Shi, J. (2024). The Non-Thermal Radio Emissions of the Solar Transition Region and the Proposal of an Observational Regime. Universe, 10(2), 82. https://doi.org/10.3390/universe10020082







