New Indication from Quantum Chromodynamics Calling for beyond the Standard Model

Abstract

We find that a big gap between indicators for the breaking strengths of the global chiral SU(2) and U(1) axial symmetries in the QCD of the standard model (SM) can be interpreted as a new fine-tuning problem. This may thus imply calling for a class beyond the SM, which turns out to favor having a new chiral symmetry, and the associated massless new quark is insensitive to the chiral SU(2) symmetry for the lightest up and down quarks so that the fine-tuning is relaxed. Our statistical estimate shows that QCD of the SM is by more than 300 standard deviations off the parameter space free from fine-tuning, and the significance will be greater as the lattice measurements on the QCD hadron observables become more accurate. We briefly address a dark QCD model with massless new quarks as one viable candidate.

1. Introduction

Several types of fine-tuning problems have so far been pointed out that cannot be resolved by the SM alone. All of these involve an unsatisfactory big cancellation, e.g., the gauge hierarchy problem [1,2,3,4] and the strong CP problem [5,6,7,8,9]. The associated fine-tuned small observables have been confirmed: the size of the Higgs mass is much smaller than the Planck scale and the yet-unobserved electromagnetic dipole moment of neutron, respectively.

Fine-tunings can generically be related to existence of a hidden new symmetry that relaxes the big cancellation so that the fine-tuning becomes absent in the symmetric limit, which includes the ‘t Hooft naturalness argument [10]1. Taking this seriously into account has so far motivated people to refine or go beyond standard theories with such a new hidden symmetry and opened numerous frontiers in research directions along the lines of theoretical particle and cosmological physics.

In this paper, we argue that a big gap between indicators for the breaking strengths of the global chiral $SU\left(2\right)$ and $U\left(1\right)$ axial symmetries in the QCD of the SM can be interpreted as a new fine-tuning problem.

QCD has been well explored and confirmed, but actually, we know less precisely how low-energy QCD and the vacuum depend on quark flavors (described like the Columbia plot); in particular, there is little understanding of how the relatively heavy strange quark contributes there. This important open issue is thought of as an analogy to the top quark contribution to the electroweak-symmetry broken vacuum in the Higgs potential of the SM, called the electroweak-vacuum stability problem. What the present work focuses on is such a still nontrivial quark–flavor structure of the QCD vacuum, in particular, the essential gap between the breaking strengths of the chiral $SU\left(2\right)$ symmetry for the light up and down quarks and $U\left(1\right)$ axial symmetry.

The proposed new fine-tuning issue arises in an anomalous chiral Ward–Takahashi identity, which dictates the chiral $SU\left(2\right)$ breaking strength as the subtraction of the $U\left(1\right)$ axial breaking and the rate of the fluctuation of the QCD topological charge (Equation (1)). There, a drastic cancellation between two independent infrared singularities is observed, at around the QCD scale, which is responsible for the existence of the soft pions and required to yield the finite quark condensate. This thus potentially causes fine-tuning and yields a gigantic gap between the chiral $SU\left(2\right)$ and $U\left(1\right)$ axial breaking strengths.

We find that the gap is big enough to require fine-tuning, which corresponds to more than 300 standard deviations for the QCD in the SM away from the parameter space free from fine-tuning. The prospected statistical significance is subject to the higher accuracy of the lattice QCD measurements on the hadronic observables. Thus, the fine-tuned big gap between the chiral $SU\left(2\right)$ and $U\left(1\right)$ axial breaking strengths can be interpreted as a new indication from QCD calling for beyond the SM.

As one viable candidate, a dark QCD model with massless new quarks is briefly addressed.

2. The Posed Fine-Tuning Problem and Hidden Symmetry

We begin by introducing a key equation, the anomalous-chiral Ward identity, showing a relation between the indicators for the breaking strengths of chiral $SU{\left(2\right)}_L\times SU{\left(2\right)}_R$ symmetry (${\chi }_{\mathrm{chiral}}$) and $U{\left(1\right)}_A$ axial symmetry (${\chi }_{\mathrm{axial}}$), together with the topological susceptibility (${\chi }_{\mathrm{top}}$). In light of the QCD of the SM, we consider massive three-flavor QCD only including the lightest up, down, and strange quarks relevant below the QCD scale of $\mathcal{O}\left(1\right)$ GeV. We perform the three-flavor chiral $SU\left(3\right)$ rotations to derive the anomalous Ward identities. Detailed definitions of susceptibilities, as well as the explicit derivation for the Ward identities, are supplied in Appendix A. Combining relevant identities, we thus find

$$\begin{array}{c}\hfill {\chi }_{\mathrm{chiral}}={\chi }_{\mathrm{axial}}+\frac{4}{m_l^2}{\chi }_{\mathrm{top}},\end{array}$$

(1)

where $m_l$ denotes the mass for the up and down quarks. ${\chi }_{\mathrm{chiral}}$ is given as the difference of the (volume-averaged) propagators of mesons forming the chiral partner, which becomes zero when the partner masses are identical. ${\chi }_{\mathrm{axial}}$ is the similar indicator for the breaking strength of the $U\left(1\right)$ axial symmetry. ${\chi }_{\mathrm{top}}$ measures the rate of fluctuation of the topological charge2.

In the case with small-enough $m_l$ and finite strange quark mass $m_s$ ($m_s\gg m_l\to 0$), as in the QCD of the SM at the physical point, the topological susceptibility ${\chi }_{\mathrm{top}}$ can approximately be evaluated as (see also Appendix A)3

$$\begin{array}{c}\hfill {\chi }_{\mathrm{top}}{|}_{m_l\ll m_s}\sim (\frac{\langle \overline{u}u\rangle }{m_l}+\frac{\langle \overline{d}d\rangle }{m_l}+\frac{\langle \overline{s}s\rangle }{m_s}){\overline{m}}^2,\end{array}$$

(2)

where $\overline{m}={(2/m_l+1/m_s)}^{-1}$. Noting that $\langle \overline{u}u\rangle$, $\langle \overline{d}d\rangle$, and $\langle \overline{s}s\rangle$ remain nonzero even when $m_l=0$, because of the dynamical generation of quark condensates in QCD at the scale of $\mathcal{O}\left(1\right)$ GeV, we find that for small $m_l\ll m_s$, the $\langle \overline{u}u\rangle$ and $\langle \overline{d}d\rangle$ terms are dominant in Equation (2) so that the ${\chi }_{\mathrm{top}}$ term in Equation (1) is well approximated as

$$\begin{array}{cc}\hfill \frac{{\chi }_{\mathrm{top}}}{m_l^2}{|}_{m_l\ll m_s}& \hfill \sim \left(\frac{\langle \overline{u}u\rangle }{m_l}+\frac{\langle \overline{d}d\rangle }{m_l}\right)\frac{{\overline{m}}^2}{m_l^2}\hfill \\ \hfill & \hfill \sim -\frac{{\left[\mathcal{O}\left(1\right)\mathrm{GeV}\right]}^3}{4m_l},\hfill \end{array}$$

(3)

with the minus sign of the quark-condensate value taken into account. Thus, the size of the ${\chi }_{\mathrm{top}}$ term becomes larger than ${\left[\mathcal{O}\left(1\right)\mathrm{GeV}\right]}^2$ (with minus sign). Note also that ${\chi }_{\mathrm{chiral}}>0$, ${\chi }_{\mathrm{axial}}>0$, and ${\chi }_{\mathrm{chiral}}<{\chi }_{\mathrm{axial}}$ due to the measured meson spectroscopy (for more details, see Appendix A). Therefore, in the case with small $m_l$ and finite $m_s$, we meet a big destructive cancellation in Equation (1) between ${\chi }_{\mathrm{axial}}$ and the ${\chi }_{\mathrm{top}}$ term, both of which are on the order bigger than ${\left[\mathcal{O}\left(1\right)\mathrm{GeV}\right]}^2$, to have a highly suppressed ${\chi }_{\mathrm{chiral}}$: Equation (1) looks like ${\left[\mathcal{O}\left(10\mathrm{GeV}\right)\right]}_{{\chi }_{\mathrm{axial}}}^2-{\left[\mathcal{O}\left(10\mathrm{GeV}\right)\right]}_{{\chi }_{\mathrm{top}}}^2={\chi }_{\mathrm{chiral}}\ll {\left[\mathcal{O}\left(1\mathrm{GeV}\right)\right]}^2$ for $m_l\lesssim$ MeV. This can be interpreted as a fine-tuning, unless some symmetry is present to explain the extraordinarily small ${\chi }_{\mathrm{chiral}}$, which can relax the big subtraction, as elaborated in the Introduction. Note, however, that even the conventional chiral $SU\left(2\right)$ symmetry ($m_l\to 0$) makes the accidental big cancellation more serious. As it will turn out later, the QCD of the SM with light up and down quarks and relatively heavier strange quarks actually suffers from this kind of big subtraction.

The original form of the anomalous Ward identity Equation (1), as given in Appendix A, is constructed from several susceptibilities. The anomalous Ward identity Equation (1) is derived by making a couple of the chiral $SU\left(3\right)$ transformations, corresponding to the $SU\left(3\right)$ adjoint indices $a=1,2,3,8$, on the vacuum expectation values of the pseudoscalar operators with $a=0,8$ (see also Appendix E), which gives some correspondence between the vacuum expectation values of scalar and pseudoscalar operators, leading to the relationship among susceptibilities. Once ${\chi }_{\mathrm{top}}$ is identified in terms of a set of the susceptibilities, other terms unambiguously correspond to ${\chi }_{\mathrm{chiral}}$ and ${\chi }_{\mathrm{axial}}$, which can be independently observed in the lattice simulation. Therefore, a big subtraction between ${\chi }_{\mathrm{axial}}$ and ${\chi }_{\mathrm{top}}$ to yield a small ${\chi }_{\mathrm{chiral}}$ is physical. In fact, such big destructive cancellation has been observed even at high temperatures [11].

The existence of the fine-tuning is due to the accidental cancellation between two individual infrared singularities responsible for the soft pions in QCD, as discussed in Ref. [12], ${\chi }_{\mathrm{axial}}\sim 1/m_{\pi }^2\sim 1/m_l$, ${\chi }_{\mathrm{chiral}}\sim$ constant, and ${\chi }_{\mathrm{top}}/m_l^2\sim 1/m_l$ (see also Equation (3)) for $m_l\ll m_s$ and $m_l\to 0$; hence, in this limit, Equation (1) looks like finite = $\infty -\infty$. This observation may imply that the chiral limit, on the basis of which the QCD can be expanded in the way of the chiral perturbation and hence widely accepted and well established, is faced with an accidental fine-tuning. Thus, the proposed fine-tuning is completely separated from the already existing fine-tuning, e.g., on the tiny mass difference between proton and neutron.

Going away from the QCD of the SM, we consider a counter limit where $m_s\to 0$, keeping $m_l$ finite. In Equation (1), the ${\chi }_{\mathrm{top}}$ term then vanishes as $m_s\to 0$ (see also Equation (2)), reflecting the flavor-singlet nature [12], so that the indicators for the breaking strengths of the chiral and axial symmetries become identically equal each other:

$$\begin{array}{c}\hfill ({\chi }_{\mathrm{chiral}}-{\chi }_{\mathrm{axial}})=\frac{4{\chi }_{\mathrm{top}}}{m_l^2}\to 0,\mathrm{as}{m}_s\to 0.\end{array}$$

(4)

In this case, the ${\chi }_{\mathrm{top}}$ term $({\chi }_{\mathrm{top}}/m_l^2)$ is adjusted to zero by a big destructive subtraction, i.e., a fine-tuning between ${\chi }_{\mathrm{chiral}}$ and ${\chi }_{\mathrm{axial}}$. However, this fine-tuning can be gone in the limit $m_s\to 0$, which makes $({\chi }_{\mathrm{top}}/m_l^2)$ become zero, in contrast to the QCD of the SM argued above, though the case with $m_l\gg m_s\to 0$, where ${\chi }_{\mathrm{chiral}}\sim {\chi }_{\mathrm{axial}}$, is unrealistic.

Note that the strange quark currently acts as a spectator for the chiral $SU\left(2\right)$ symmetry, being a singlet. Hence, the introduction of a new massless quark, protected by its own chiral symmetry, i.e., hidden new symmetry, should play the same role as the strange quark to solve the fine-tuning problem, keeping the massive-enough strange quark in accordance with the observation. We will later introduce an explicit and phenomenologically viable model having massless new quarks ($\chi$) with a new chiral symmetry, which makes the real-life QCD free from fine-tuning:

$$\begin{array}{c}\hfill ({\chi }_{\mathrm{chiral}}-{\chi }_{\mathrm{axial}})\to 0,\mathrm{as}{m}_{\chi }\to 0,\end{array}$$

(5)

with $m_l$ and $m_s$ at the physical point.

3. Quantifying the Fine-Tuning

We define the ratio [12]

$$\begin{array}{c}\hfill R\equiv \frac{{\chi }_{\mathrm{chiral}}}{{\chi }_{\mathrm{axial}}},\end{array}$$

(6)

which also reads $R=1-\frac{4{\chi }_{\mathrm{top}}/m_l^2}{{\chi }_{\mathrm{axial}}}=\frac{1}{1+\frac{4{\chi }_{\mathrm{top}}/m_l^2}{{\chi }_{\mathrm{chiral}}}}$ via the Ward identity in Equation (1). Thus, the deviation from $R=1$ dictates a fine-tuning, and hence R serves as the estimator of the fine-tuning.

To compute the estimator R, one needs to work on the QCD in the deep-infrared region, which is highly nonperturbative because of the strong coupling nature in the low-energy scale. The best method to compute such nonperturbative dynamics is the numerical simulations of QCD on the lattice. However, the lattice simulations have never measured the susceptibilities at vacuum with varying $m_s$4.

Instead of the lattice simulation, in the spirit of Weinberg [15], we can invoke effective models of low-energy QCD, which realize the same breaking structure of the chiral and axial symmetries, and so forth, as that in low-energy QCD. In this paper, as the low-energy QCD description, we thus adapt a class of the Nambu–Jona–Lasinio (NJL) model made of only quarks with several quarkonic interactions. The NJL model has extensively been utilized in the field of hadron physics and so far provided us with lots of qualitative interpretations for low-energy QCD features, associated with chiral and axial symmetry breaking, together with successful phenomenological predictions [16].

We evaluate R as a function of $m_s$ based on a best-fit NJL model, which exhibits good fitness with lattice data on 2 + 1 flavor-QCD at the physical point, such as the observed meson masses. Details are provided in Appendix B, Appendix C and Appendix D. Since the NJL model currently does not incorporate the isospin breaking as well as radiative electromagnetic and weak interactions, it would not be suitable to input experimental values of QCD observables that implicitly include all those corrections. We therefore have used as inputs observables in lattice QCD with 2 + 1 flavors in the isospin-symmetric limit at the physical point available from the literature [17,18], which are exclusive for the gauge interactions external to QCD, and applied the least-${\chi }^2$ test to fix the parameters by using five representative observables5.

We thus compute the estimator R at the best-fit point, including the errors associated with the lattice data, and find

$$\begin{array}{c}\hfill R=0.0469\pm 0.0028.\end{array}$$

(7)

This clarifies that the QCD at the physical point is by about 340 standard deviation off the theory free from fine-tuning with $R=1$! This is due to a too-large $m_s$, as noted above.

We may take into account a possible theoretical uncertainty of about 30%, which could arise from the leading order approximation in the $1/N_c$ expansion, on which the present NJL model prediction is based. Currently disregarded corrections, associated with the isospin breaking, electromagnetic, and electroweak interactions, would also be small enough to be covered by the 30% uncertainty. Therefore, the estimated value of R in Equation (7) with the theoretical uncertainty of 30% would be the one corresponding to the prediction of the SM. Combining this 30% (“theor.”) with the error in Equation (7) associated with the uncertainties of inputs from the lattice data (“lat.”), we would then have $R=0.0469\pm {\left(0.0028\right)}_{\mathrm{lat}.}\pm {\left(0.0141\right)}_{\mathrm{theor}.}$. It is still about 66 standard deviations.

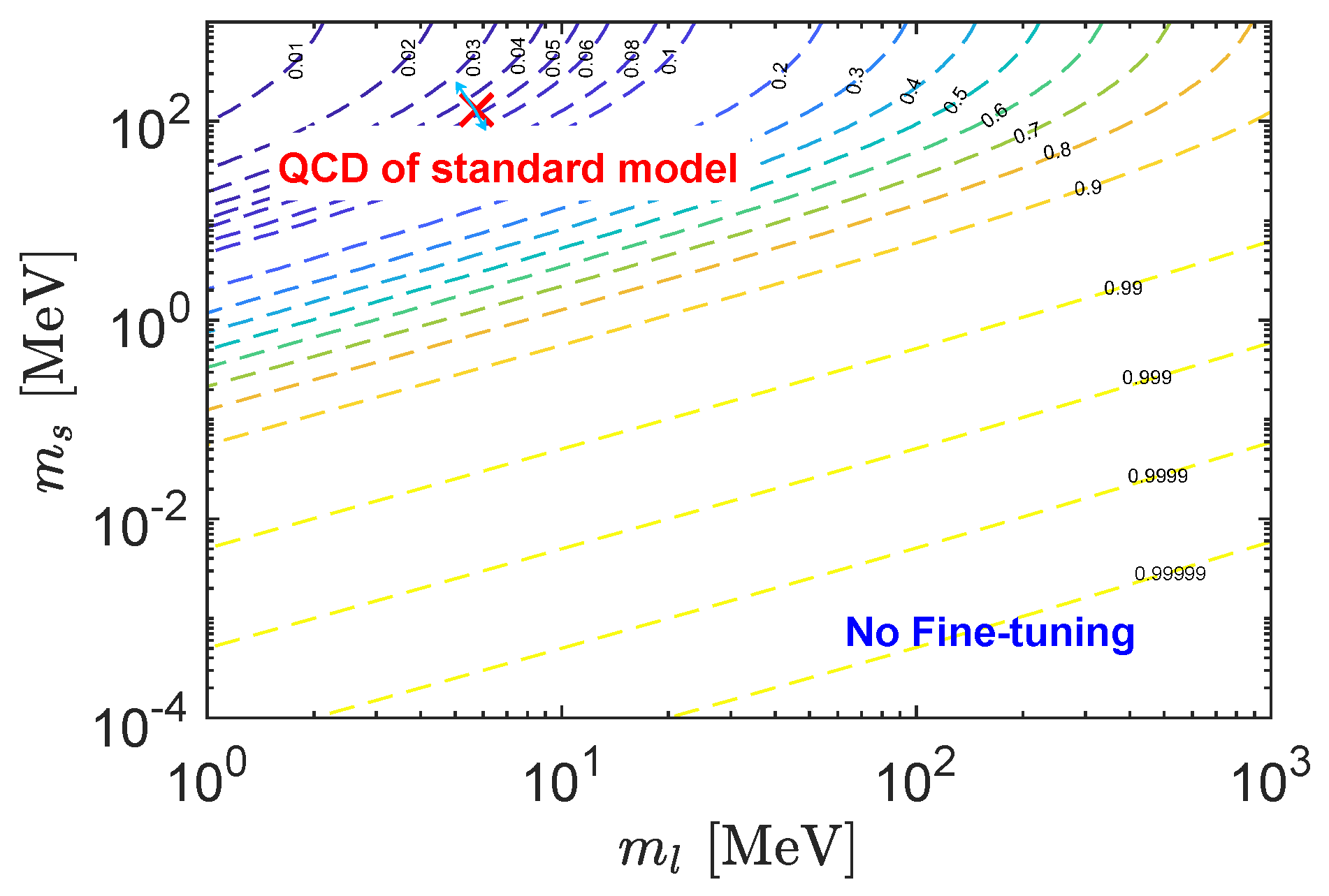
To make this disfavor visualized, varying the value of $m_s$ and $m_l$ with other model parameters fixed at the best-fit values, we plot contours of the estimator R on the $(m_l,m_s)$ plane, which is displayed in Figure 1.

The value of R tends to saturate to be ≃0.02, even in the massive two-flavor limit with $m_s\to \infty$ and $m_l=5.75$ MeV. This trend is exactly what we have suspected from the $m_s$ scaling of the ${\chi }_{\mathrm{top}}$ term in Equation (3). With $m_s$ fixed, say, to the physical point, R tends to get close to 1 as $m_l$ becomes larger and actually reaches 1 before the decoupling limit of the up and down quarks, as clarified in Ref. [12].

The deviation in Equation (7) can be interpreted as an indication of a violation of a new symmetry, as conjectured in Equation (5), which the SM does not possess. The significance of this new symmetry is subject to the accuracy in the current lattice simulation reflected in the size of the error of R, which is as low as 10%. This significance may therefore be compared to the significance for the discovery of the small isospin breaking in the W and Z boson masses observed at UA1 and UA2 experiments [21,22,23,24], which was the same 10% level in accuracy at the final stage of the discovery era (with data taking til 1985) [25,26]. The estimator R can be defined also for the W and Z masses as $R_{WZ}\equiv \frac{m_W}{m_Z}$ such that the mass difference is written as $\Delta m_{WZ}=m_Z-m_W=m_Z(1-R_{WZ})$, which actually forms a big cancellation structure and hence could be thought of as a fine-tuning in the same way as in ${\chi }_{\mathrm{axial}}$ and ${\chi }_{\mathrm{top}}/m_l^2$ with R in Equation (6). The final UA2 result reads [26] $R_{\mathrm{WZ}}^{1982–1985}=0.876\pm 0.026$, so it is about a 4.8$\sigma$ deviation from the isospin-symmetric limit $R_{\mathrm{WZ}}=1$. This is, however, of course, trivial and can be explained by the isospin breaking (related to the so-called custodial symmetry) in the SM due to the hypercharge gauge interaction and the presence of isospin breaking in the quark masses. Compared to this, the new indication from QCD in Equation (7) is by about one order of magnitude more significant.

Current precision measurements on $m_W$ and $m_Z$ give $R_{WZ}^{2022}=0.88147\pm 0.00013$ [27], which corresponds to 890$\sigma$ deviations from the isospin-symmetric limit. Similarly, the error of R in Equation (7) is also expected to become smaller as the precision in the lattice simulations becomes higher in the future; hence, the significance of the violation of a new symmetry will be enlarged to be as big as the current one for the isospin breaking.

This prospected significance might also become comparable with the current significance of the isospin breaking in the proton and neutron mass difference with $R_{pn}\equiv \frac{m_p}{m_n}=1-\frac{\Delta m_{pn}}{m_n}=\frac{1}{1\frac{\Delta m_{pn}}{m_p}}$, which is read as $R_{pn}^{2022}=0.998623477\left(316\right)$ [27], leading to $\sim 4\times {10}^4\sigma$.

The gauge hierarchy problem caused by the big destructive loop correction to the Higgs mass $m_h$ yields $R_H=\frac{m_h^2\left(m_h\right)}{m_h^2\left(M_p\right)}\approx 1-\frac{3}{8{\pi }^2}\frac{M_p^2-m_h^2}{m_h^2\left(M_p\right)}=\frac{1}{1+\frac{3}{8{\pi }^2}\frac{M_p^2-m_h^2}{m_h^2}}$, where $M_p$ denotes the Planck scale $\sim {10}^{18}$ GeV, $m_h\left(m_h\right)\sim 125$ GeV, and we have simply taken into account only the top loop with the top Yukawa coupling $\sim 1$. This $R_H$ is estimated to be ∼$6.3\times {10}^{-32}$. A similar estimate can be made also for the strong CP problem, which would yield $R_{\theta }=\frac{{\theta }_{\mathrm{QCD}}}{{\theta }_{\mathrm{EW}}}<{10}^{-10}$, where ${\theta }_{\mathrm{QCD}}$ and ${\theta }_{\mathrm{EW}}$, respectively, denote the QCD and electroweak origins for the CP phase of the quark mass term. Thus, the statistical significance of $R_H$ will remain the biggest unless the accuracy in measuring the Higgs mass and top Yukawa coupling becomes better than the level of $\sim {10}^{-32}$, the size of $R_H$.

The fine-tuning problem that we presently address is nothing sensory, but is essentially related to the existence of a hidden symmetry which makes $R=1$ or ${\chi }_{\mathrm{top}}/m_l^2=0$ or ${\chi }_{\mathrm{chiral}}={\chi }_{\mathrm{axial}}$ in terms of our estimator. This is in contrast to the conventional argument: Something delicately fine or not is controlled merely by whether the tuning, to some extent, is necessary to make a big cancellation. The quantification of the present fine-tuning is unambiguously made on the basis of the statistical significance, and the standard deviations are subject to the accuracy in the measurement of Rs, which should therefore be compared with those having the same level of accuracy, as seen above.

Note that the strong CP problem in the SM is trivially solved in the limit $m_l\to 0$, whereas the new fine-tuning problem becomes more serious ($R\to 0$). This discrepancy in the two problems can be understood via the Ward identity Equation (1), where ${\chi }_{\mathrm{top}}$ itself can be sent to zero when $m_l\to 0$, which is the massless up quark solution to the strong CP problem [5,28]; however, ${\chi }_{\mathrm{top}}/m_l^2$ then blows up, leaving the new fine-tuning problem. Thus, the two problems are generically separated within the framework of the SM. This fact also proves that the chiral $SU\left(2\right)$ symmetry (with $m_l\to 0$) does not make QCD free from fine-tuning, in sharp contrast to the naïve folklore. We will discuss a more definite discrimination from the strong CP problem in a later section (Section 5).

We could start with the definition of R, $R={\chi }_{\mathrm{chiral}}/{\chi }_{\mathrm{axial}}$, instead of the Ward identity Equation (1), and discuss the difference ${\Delta }_{\mathrm{axial}-\mathrm{chiral}}={\chi }_{\mathrm{axial}}-{\chi }_{\mathrm{chiral}}$, so that $R=1-{\Delta }_{\mathrm{axial}-\mathrm{chiral}}/{\chi }_{\mathrm{axial}}$. Then, the form of Equation (1) is unambiguously fixed as it stands, telling us that the symmetric limit $R=1$ is realized when ${\chi }_{\mathrm{top}}/m_l^2\to 0$, which cannot be made when $m_l\to 0$ (because ${\chi }_{\mathrm{top}}\sim m_l$ for small $m_l$), but can be achieved when $m_s\to 0$, which is based on the symmetry argument. This alternative view would also help readers to more definitely see that the $m_l=0$ limit separates the new fine-tuning problem from the strong CP problem, where $R\to 0$ and $R_{\theta }={\theta }_{\mathrm{QCD}}/{\theta }_{\mathrm{EW}}\to 1$, respectively.

4. A Solution: New Quarks with Dark QCD Colors

The proposed new fine-tuning problem is present at the scale only around the order of 1 GeV. When the electroweak symmetry becomes manifest at higher scales, the fine-tuning problem will be obscure. This is because the global chiral $SU\left(2\right)$ and $U\left(1\right)$ axial symmetries are explicitly broken by the electroweak interactions as well as quark masses (or Yukawa couplings between the Higgs and quarks). In that case, the key Equation (1) will be modified involving the electroweak “topological” susceptibilities. Also at scales $\lesssim m_{\pi }$, the fine-tuning will be nontransparent due to the decoupling of pions, which is the most dominant source to generate the big gap between ${\chi }_{\mathrm{chiral}}$ and ${\chi }_{\mathrm{axial}}$. Thus, the new fine-tuning problem needs to be solved by a new physics with the scale ${\Lambda }_{\mathrm{NEW}}$ in a range of $m_{\pi }\lesssim {\Lambda }_{\mathrm{NEW}}\lesssim$ 1 GeV.

The hint for this avenue is seen in Equation (4), which indicates introducing massless new quarks. In fact, the topological susceptibility ${\chi }_{\mathrm{top}}$ goes to zero when a massless new quark couples to the other three quarks due to the flavor-singlet nature so that Equation (5) is realized. The detailed proof is given in Appendix E. This motivates one to consider an explicit model beyond the SM.

We consider a new chiral quark ($\chi$) to be neutral under the electroweak charges, which, instead, carries a dark color of $SU\left(N_d\right)$ group under the fundamental representation. The group representation table for the $\chi$ quark thus goes like ${\chi }_{L,R}\sim {(N_d,3,1)}_0$ for $SU\left(N_d\right)\times SU{\left(3\right)}_c\times SU{\left(2\right)}_W\times U{\left(1\right)}_Y$, where the latter three symmetries correspond to the SM ones (QCD color, weak, and hypercharge). The dark color symmetry, as well as the electroweak neutrality, forbids creating extra light hadrons composed of the ordinary light quarks and the $\chi$ quark, such as $\overline{u}\chi$ and $uu\chi$. For simplicity, we also assume that the dark QCD coupling $g_d$ becomes strong almost at the same scale as the ordinary QCD coupling does, $({\Lambda }_d\sim {\Lambda }_{\mathrm{QCD}}=\mathcal{O}\left(1\right)\mathrm{GeV})$, namely, $g_d\sim g_s$.

Below the scale ∼ 1 GeV, the dark QCD dynamically breaks the dark chiral $U{\left(3\right)}_L\times U{\left(3\right)}_R$ symmetry for the $\chi$ quark, down to the vectorial part, where the extra factor of 3 in the number of flavors comes from the QCD color multiplicity. Only the hadrons singlet under both the dark and ordinary QCD colors survive in the vacuum. Then, there emerges only one composite Nambu–Goldstone boson, ${\eta }_d$, which becomes pseudo due to the axial anomaly in the dark QCD sector and acquires the mass of $\mathcal{O}\left(1\right)$ GeV. Moreover, at almost the same scale, the ordinary QCD breaks the approximate chiral $SU{(3+N_d)}_L\times SU{(3+N_d)}_R$ symmetry involving the $\chi$ quark down to the vectorial one, where, again, only the color singlets are relevant. The spontaneous breaking of this extended chiral symmetry does not yield excessive meson spectra made of ordinary quarks because of the double color symmetries, as aforementioned. Thus, the new low-lying spectra consist only of the dark sector: ${\eta }_d\sim \overline{\chi }i{\gamma }_5\chi$ and its dark chiral partner ${\sigma }_d\sim \overline{\chi }\chi$, as well as spin-1 dark mesons ($\overline{\chi }{\gamma }_{\mu }\chi$ and $\overline{\chi }{\gamma }_{\mu }{\gamma }_5\chi$) and dark baryons ($\sim \chi \chi \chi \cdots \chi$). All those low-lying dark hadrons have a mass on the order of 1 GeV by feeding the chiral breaking contributions from both the ordinary QCD and dark QCD sectors.

The most stringent phenomenological constraint on this type of model comes from the extra massless-quark contribution to the running evolution of the ordinary QCD coupling ${\alpha }_s$, where, in the present case, $N_d$ species of new quarks in the fundamental representation of $SU{\left(3\right)}_c$ group come into play. Collider experiments have confirmed the asymptotic freedom with high accuracy in a wide range of higher energy scales, in particular above 10 GeV, over 1 TeV [27]. When ${\alpha }_s$ is evolved up to higher scales using ${\alpha }_s\left(M_Z\right)$ measured at the Z boson pole as input, the tail of the asymptotic freedom around $\mathcal{O}\left(1\right)$ TeV can thus have sensitivity to exclude new quarks. Current data on ${\alpha }_s$ at the scale around $\mathcal{O}\left(1\right)$ TeV involve large theoretical uncertainties. This results in uncertainty of determination of ${\alpha }_s\left(M_Z\right)$ for various experiments (LHC-ATLAS, -CMS, Tevatron-CDF, D0, etc.), which yields ${\alpha }_s\left(M_Z\right)\simeq 0.110–0.130$, consistent with the world average ${\alpha }_s\left(M_Z\right)\simeq 0.118$ within the uncertainties [27]. We have worked on the two-loop perturbative computation of ${\alpha }_s$6, and find that as long as $N_d$ is moderately large $(N_d\le 5)$, the measured ultraviolet scaling (for the renormalization scale of $\mu$ = 10 GeV, a few TeV) can be consistent with the current data [27] within the range of ${\alpha }_s\left(M_z\right)$ above.

Precise measurements in lower scales $\lesssim 10$ GeV have not well been explored so far due to the deep-infrared complexity of QCD. The low-energy running of ${\alpha }_s$ is indeed still uncertain and can be variant as discussed in a recent review, e.g., [29]. The present dark QCD could dramatically alter the infrared running feature of ${\alpha }_s$, due to new quarks and the running of the dark QCD coupling ${\alpha }_d$. This will also supply a decisive answer to the possibility of the infrared-near conformality of the real-life QCD.

Thus, a few massless new quarks can still survive constraints on ${\alpha }_s$ at the current status7. More precise measurements of ${\alpha }_s$ in the future will clarify how many light or massless new quarks can be hidden in QCD, which will fix the value of $N_d$ in terms of the present dark QCD.

Regarding other phenomenological aspects, we have checked that the present dark QCD model can survive current constraints, such as the measurement of the ordinary QCD hadron physics, dark meson couplings to diphoton, and limits on the dark baryon as dark matter candidates, and so forth. Furthermore, the dark meson and dark baryon yield several smoking guns to be probed in the near future, respectively, through the triphoton ($3\gamma$) signal at the mass around 1 GeV, at the Belle II experiment with 20–50 ${\mathrm{fb}}^{-1}$ data [31], and a planned dark matter detection experiment aiming at the sub-GeV mass range [32] with the spin-independent dark matter–nucleon cross-section ∼${10}^{-43}{\mathrm{cm}}^2$8.

5. Conclusions

Toward a deeper understanding of the flavor dependence of the QCD vacuum, in the present work, we have focused on a gap between the breaking strengths of the chiral $SU\left(2\right)$ symmetry for light up and down quarks and $U\left(1\right)$ axial symmetry. It might be too premature to conclude that this gap is related merely to the mystery of the quark-generation structure in the SM. We have found an alternative interpretation based on the symmetry argument: the gap can be relaxed by a chiral symmetry for the strange quark, and the role of the massless/light strange quark can be replaced by a new massless/light quark (called $\chi$).

The existence of the symmetric limit $m_s\to 0$, where the “chiral $SU\left(2\right)$ = $U\left(1\right)$ axial” is realized as above, is manifest in the flavor dependence of the QCD vacuum, and we have shown how the gap, i.e., the fine-tuning, is seriously large on the basis of the statistical analysis along with comparison with the existing fine-tuned quantities.

Thus, the QCD of the SM may be yet incomplete if the fine-tuning is considered to be serious and hence may call for more quarks to keep the equivalence of the strengths of the chiral $SU\left(2\right)$ and $U\left(1\right)$ axial breaking. Given these new criteria, new quarks need protecting to be (nearly) massless by a new chiral symmetry and can be introduced in QCD consistently with existing experiments; that is what we have demonstrated in the present work. This symmetry is independent of the existing chiral or isospin symmetry, which ensures the smallness of masses of light quarks and has so far played the role to make QCD free from fine-tuning, e.g., for the small proton–neutron mass difference compared to individual proton and neutron masses.

The new fine-tuning problem is triggered due to the large strange quark mass, and brings a big gap between the chiral and axial order parameters, detected as a small size of the estimator R in Equation (6). This trend actually persists even in a whole temperature, as can be understood by tracing the analysis in the recent literature [12]. The present work is sort of an extension from the reference, and what is more, it essentially paves the way to a new criterion on the necessity of beyond the SM, which is completely out of the scope of the literature. Still, as noted also in [12], the characteristic small R can be checked on the lattice QCD simulations in the future, which will be an indirect observation of the proposed new indication.

In this paper, a benchmark of the fine-tuned QCD was placed based on the well-known low-energy effective model, NJL. This is a pioneering step and should be motivated and confirmed by various approaches in the future, such as the lattice calculation and functional-renormalization group analysis. One can also work on the chiral perturbation theory to evaluate R. No work has so far been conducted properly taking into account the flavor-singlet condition for ${\chi }_{\mathrm{top}}$; hence, it would also be an interesting issue to be left in the future.

Relaxing the new fine-tuning is tied with the vanishing curvature of the QCD vacuum at around the QCD scale: ${\chi }_{\mathrm{top}}\to 0$. The new fine-tuning problem is present irrespective of the place of the QCD vacuum, i.e., the value of the (net) QCD $\overline{\theta }$ parameter: even a shifted QCD vacuum with $\overline{\theta }$ gone, say by assumption of a QCD axion, keeps nonzero ${\chi }_{\mathrm{top}}$ as the developed axion potential energy, including the axion mass, which takes precisely the same flavor-singlet form as in Equation (2). Thus, the new fine-tuning problem is definitely separated from the strong CP problem.

In general, the dark QCD solution instead implies a nontrivial relation between $\overline{\theta }$ and ${\theta }_d$, the theta parameter in dark QCD, to realize ${\chi }_{\mathrm{top}}=0$ in the presence of the massless new $\chi$ quark: the anomalous axial rotation of the massless $\chi$ leaves the $\overline{\theta }$-dependence into the dark QCD topological sector, $({\theta }_d+(N_c/N_d)\overline{\theta })Q_{\mathrm{top}}^d$, where $Q_{\mathrm{top}}^d$ denotes the dark QCD topological charge. Thereby, one obtains ${\chi }_{\mathrm{top}}={(N_c/N_d)}^2{\chi }_{\mathrm{top}}^d\ne 0$, with ${\chi }_{\mathrm{top}}^d$ being the topological susceptibility in dark QCD, unless ${\theta }_d=-(N_c/N_d)\overline{\theta }$. This nontrivial relation is required no matter what size $\overline{\theta }$ is, i.e., which is independent of the strong CP problem.

The required relation might be trivial when QCD itself relaxes $\overline{\theta }$ to 0 at a deep-infrared fixed point to be consistent with realization of the confinement, as recently discussed in lattice QCD [34,35,36]. This self-relaxation is applicable also to dark QCD; hence, in that case, one has $\overline{\theta }={\theta }_d=0$, and ${\chi }_{\mathrm{top}}=0$ in the presence of the massless $\chi$ quark. In this sense, the proposed fine-tuning might be linked also with a deeper understanding of the color confinement.

In contrast, solving the new fine-tuning problem disfavors QCD axion models as the solution of the strong CP: first of all, the QCD axion needs not to be present until the QCD pions are decoupled from R, otherwise the axion potential energy necessarily yields nonzero ${\chi }_{\mathrm{top}}$ even along with massless new quarks. In this sense, a composite axion [37,38] with the dynamical/composite scale scaled down to the QCD scale (or lower) might be the candidate, where the composite scale is set to $\sim m_{\pi }\sim 4\pi f_a$ with the axion decay constant $f_a$. However, such a low-scale QCD axion model with both a QCD axion and its small decay constant on the QCD scale has already been ruled out by the LEP search for $Z\to \pi \gamma$ [39] due to too-large axion coupling to diphoton. Thus, the QCD axion is incompatible with the solution for the new fine-tuning problem.

Other solutions alternative to the presently addressed dark QCD are worth investigating. In closing, we provide one general “recipe”. First of all, try to introduce new Dirac massless quarks, which act as a spectator of the global chiral $SU\left(2\right)$ symmetry for the up and down quarks. They are generically allowed to feel the electroweak charge, whichever way it is ganged vectorlikely or chirally. The former case would be phenomenologically viable in light of the electroweak precision tests, and the limit on the number of quark generations placed from the Z boson decays. Those new quarks would be preferable not to form the Yukawa interaction with ordinary quarks and Higgs fields (doublets and triplets, and so on), which develop the vacuum expectation values at the weak scale, and yield the mass for the new quarks. If new quarks could be coupled to such Higgses, solving the strong CP problem (without introducing an axion), as well as keeping the light enough new quarks down until the QCD scale, would be hard and challenging.

Given this recipe, one might think that though it would sound somewhat ad hoc, the presumably most minimal setup would be to introduce an electroweak-singlet quark with a negative charge under a new parity while assigning a positive charge for ordinary quarks, so as to avoid spoiling the successful light hadron spectroscopy. In the dark QCD model introduced in the present paper, the role of such a new parity has been played by the dark QCD color charge. Such alternatives are to be addressed in detail elsewhere.