Abstract
Tensions in the measurements of neutron and kaon weak decays, such as of the neutron lifetime, may speak to the existence of new particles and dynamics not present in the Standard Model (SM). In scenarios with dark sectors, particles that couple feebly to those of the SM appear. We offer a focused overview of such possibilities and describe how the observations of neutron stars, which probe either their structure or dynamics, limit them. In realizing these constraints, we highlight how the assessment of particle processes within dense baryonic matter impacts the emerging picture—and we emphasize both the flavor structure of the constraints and their broader connections to cogenesis models of dark matter and baryogenesis.
1. Introduction
Various astronomical observations speak to the existence of dark matter and dark energy [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16], and the detections of neutrinos from extraterrestrial sources reveal nonzero neutrino masses [17,18,19]. Also, the cosmic excess of matter over antimatter [20,21], i.e., the baryon asymmetry of the universe (BAU), cannot be described within the SM, because the electroweak phase transition is not of the first order [22,23] for the empirically determined Higgs mass [24,25]. Thus, physics beyond the SM has been established, even if its origins continue to be mysterious. Although these may come from dynamics that is disjoint from the SM, the possibility of identifying its nature mandates the careful consideration of any experimental anomalies that appear, for they could point to new dynamics. In this article, we consider the neutron lifetime anomaly [26,27], which entails the possibility that it could, at least in part, derive from new physics [28,29,30,31], and how that possibility can be constrained by observations of neutron stars [32,33,34,35,36,37]. To set the stage, in this introduction we (i) place the neutron lifetime anomaly in the context of other low-energy decay experiments, (ii) motivate why new physics in neutron decay could be linked to models that explain both dark matter and the BAU, and (iii) discuss how neutron dark decays connect to neutron star structure and dynamics.
1.1. Low-Energy Experimental Anomalies in Beta Decay
The expected pattern of quark flavor mixing under charged current interactions in the SM make the Cabibbo angle, i.e., the mixing of the first- and second-generation of quarks, central to a unitarity test of the Cabibbo–Kobayashi–Maskawa (CKM) matrix with elements . This test probes the possibility of additional contributions to quark mixing and/or whether , the effective strength of the weak interactions as measured through the muon lifetime, is really universal. The so-called Cabibbo angle anomaly (CAA) has different components, and its resolution gains in importance, because possible non-SM effects need not be very small [38,39]. There are disagreements in the assessment of , which is most precisely probed through neutron decays or through superallowed () transitions in nuclei, as well as in , for which () and () decay studies are the most precise. Theoretical corrections and inputs are needed in the analysis of the experiments to determine . The determinations of from and decays do not agree [40,41,42], and the extracted values of are also in slight tension with each other [42]. The combined results are also at odds with CKM unitarity, with the differences predicated by the computed radiative corrections [43,44,45]. In the superallowed case, the effect of the axial vector current enters in the radiative corrections, which can be modified according to nuclear structure as well [46]. Recent developments in the theory of the radiative corrections in neutron decay have led to refined assessments of their value, thus impacting the value of [45]; we refer to [47] in this volume for a summary. It is worth noting that these determinations also differ from the value of determined from the ratio of rates in and () decays [41,42]. These anomalies could have various resolutions, thereby arising from either limitations in the experiments themselves (there is only one high quality measurement of ) or in the SM theoretical inputs; however, particular new physics models, such as those with right-handed currents, could be at work [39,42].
The mixed symmetry nature of neutron decay implies that at least two different experiments are needed to extract , and our interests make it important to flesh out the details. In the SM, the neutron lifetime is
where (the weak coupling constants of the nucleon), is the electron mass, f is a phase space factor, and is [44], [45], or [48], depending on the calculation of the radiative correction (and f) used. Following common practice, we use and interchangeably, which is also strongly supported by an analysis of the radiative corrections to [49]. The uncertainties in dominate those in and have been used to determine its reported error. Thus, we see that the right-hand side of Equation (1) is strongly constrained, and the parameter is determined separately through measurements of the neutron decay correlations, with the coefficients [50] termed as the “neutron alphabet [51]”. Thus, to determine , in order to combine with for a test of CKM unitarity, both the lifetime and a measured decay correlation are needed. The most precisely determined correlation coefficient is “A”, which is the correlation between the neutron spin and the momentum of the decay electron; thus, that determination has been commonly used. Recently, precise determinations of “a”, which is the correlation of the decay electron and antineutrino momenta, have been achieved. Thus, we shall compare the outcomes of combining the measurements of either the A or a correlation coefficients with the neutron lifetime for .
In Figure 1, we show the data set that constitutes the neutron lifetime anomaly—we see that the measured lifetime has been shown to be significantly different if the neutrons decay while stored in a bottle or trap, with the surviving neutrons counted after some storage time, or if the neutrons decay while in a beam within a device that counts the decay protons. The determined neutron lifetimes differ by some , which is a significant variation. One prominent impact this shift could have is on big bang nucleosynthesis (BBN), because the neutron lifetime determines, to a good approximation, the temperature at which the weak interactions freeze out in the early universe—and a shorter lifetime reduces the expected yield of 4He [52]. We refer to [53] for a review of the neutron lifetime’s impact on element yields from BBN. Since the bottle lifetime is shorter, the difference between the two determinations can be reasonably attributed to the possibility of neutron dark decays [28] coming from physics beyond the SM, and we refer to the review [54] in this volume for further discussion.
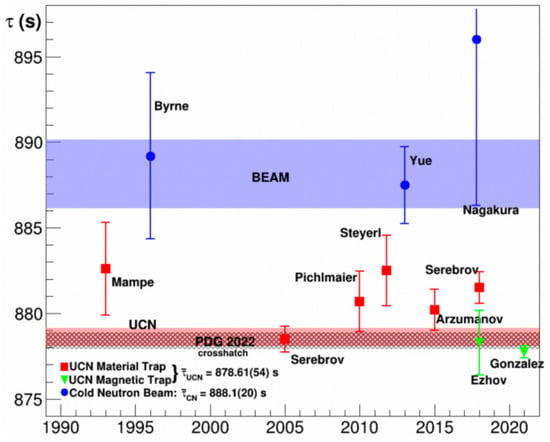
Figure 1.
Measured values of the neutron lifetime from beam (blue), material trap (red), and magnetic trap (green) experiments since 1990 from [55]. In all neutron trap experiments, which use ultracold neutrons (UCNs), the neutron lifetime was determined by counting the neutrons that persist, whereas in the beam experiments, it was determined by counting the decay protons. The central values of the two sets of experiments disagree by , with a significance in excess of —this is the neutron lifetime anomaly. The Particle Data Group (PDG) does not include the beam measurements in their fits [56].
Testing the structure of neutron (and nuclear) decay in the SM has been a focus of intense research for decades [51,57,58,59]. Here, the various decay observables, including the lifetimes and decay correlations, can constrain the possibility that the neutron lifetime anomaly comes from new physics [36,60,61]. That is, the agreement of the value of with CKM unitarity and the value of in a neutron lifetime and in a decay correlation limit the possibility of non- contributions, which could include neutron dark decays or the possibility of oscillations, to the lifetime. In that context, the PDG gives an average of with a scale factor of 2.7 from the A and a correlation coefficients [56], where the most precise determination, from an A measurement, is from PERKEO III [62]. The other two most precise determinations of , which are also determined from A [63,64], are consistent with that result. Recent and precise a determinations [65,66,67] have emerged, however, that differ significantly from the A results. We note, e.g., [65]—and the latest status of the various measurements is shown in Figure 2. This discrepancy cannot yet be challenged by direct calculation in lattice quantum chromodynamics (QCD). As for the lattice QCD results, we note the Flavour Lattice Averaging Group (FLAG) average from simulations with flavors, [68], as well as the CalLat-18 result of [69], which is compatible with the PERKEO III determination, though it has been updated to [70]. Placed in the context of a test of CKM unitarity, as shown in Figure 2 using the radiative corrections of [45], we see that the values of from the bottle lifetime and the PERKEO III A measurement are entirely consistent with the value determined in superallowed decays. Interestingly, the value of from the measured beam lifetime combined with from an a measurement is very comparable to its value determined using the bottle lifetime and the from A. In the presence of two possible solutions for and that are similarly compatible with CKM unitarity, it would seem we cannot (yet) limit a dark decay solution to the neutron lifetime anomaly on the basis of this comparison. This perspective differs from that of earlier work [60,61], and it is driven by the recent a measurements. Ultimately, any solution to the neutron lifetime anomaly using new physics is required to be compatible with the measured structure of the SM currents.
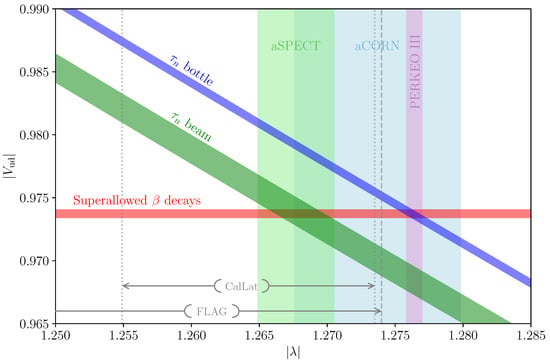
Figure 2.
The SM correlation between the CKM matrix element and the axial vector to vector coefficient ratio is presented utilizing the averaged neutron lifetime values from bottle (blue) and beam (green) methods given in Figure 1. This figure includes radiative corrections as per [45]. Vertical bands illustrate measurements from aSPECT [65] (light green), aCORN [67] (light blue), and PERKEO III [62] (light purple). The measured value of via superallowed nuclear transitions is shown by a red band [56]. Additionally, lattice values of are shown comprising the 2021 FLAG average for flavors [68] and the 2019 results from the CalLat collaboration [70].
1.2. From Anomalies to Dark Matter and the Cosmic Baryon Asymmetry
Although astronomical observations speak to the existence of dark matter that is (i) stable or nearly so on Gyr time scales [13,14], (ii) possessive of no substantial strong or electromagnetic charge [71], and (iii) engenders an “inside-out” formation of large-scale structure [7], many different sorts of dark matter candidates are possible [72,73], and they can impact astrophysical observations at small scales differently [74]. It is intriguing that the contributions of baryonic matter and of dark matter to the present cosmic density parameter are not too dissimilar, with the fraction in baryonic matter being some 20% of the dark matter one [13]. Perhaps, then, dark matter is asymmetric [75,76]—much as baryonic matter is—thereby suggesting that the two effects could share a common origin. That possibility could be realized through a dark cogenesis model [77,78,79], and interestingly there is also a connection between such models and a dark decay model of the neutron lifetime anomaly [28], thereby yielding the dark decay , where is a fermion with a baryon number of . This connection is concrete, even if the ultimate numerical impact of the decay rate on the neutron lifetime anomaly finally turns out to be small. Dark cogenesis models can act in counterpoint to other popular mechanisms, such as via weak-scale supersymmetry—in the latter, the severity of permanent EDM searches for the electron and neutron limit the possible phase space severely [80]. In contrast, the B mesogenesis [78] mechanism and its variants [32,79,81,82,83,84] do not require sources of CP violation beyond the SM to operate, and they are, moreover, testable mechanisms of baryogenesis [85]. The schematic illustration of B mesogenesis is presented in Figure 3. The branching ratio for decay cannot be too small [86], and experimental constraints exist from searches using BaBar data, with improvements expected from Belle-2 [87]. To generate the noted decays, new scalars ought to exist as well, and they can be probed through collider searches and through constraints from flavor physics [79,88]. Here, we discuss what further constraints come from precision studies of neutron stars and their dynamics [36,37].
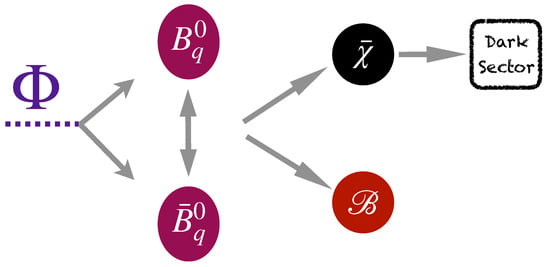
Figure 3.
A schematic illustration of B mesogenesis [78]: a late-scale dark cogenesis model. Here, a scalar , produced out of equilibrium, decays and hadronizes to a pair, with . The pair mixes in the presence of CP violation, and, finally, a B meson decays preferentially to , which is a baryon —a dark antibaryon pair. Since carries , the final states do not break the baryon number, yet this scenario produces a baryon asymmetry in the visible sector. The produced decays to other dark sector states, thus preventing washout of the baryon asymmetry, with the particles of the dark sector final states serving as dark matter candidates. Different dark sector choices, that we note in text, differ in their impacts on the dynamics of a neutron star [37].
1.3. Constraints from Neutron Star Structure and Dynamics
Taken at face value, the difference in the beam and bottle lifetimes reflects roughly a change in the neutron decay rate—and if the neutron does decay via or , where is a scalar that could also decay via [28], then the ability to form a protoneutron star is impacted [33,34,89]. In particular, its maximum mass is only some , which is in conflict with observations of neutron stars of much larger masses. This constraint can be sidestepped in different ways, such as if self-interactions are included in the model, as also studied in [90] as an example. We note [91] in this volume for a discussion of neutron star constraints on dark scalar boson production in this context. Here, rather, we focus on the new physics channels with dark fermions, particularly with a baryon-number-carrying particle and the connections of this possibility to models that describe dark matter and baryon asymmetry. In this context, must decay, though not to antibaryons, to avoid a washout of the baryon asymmetry, and the size of the realized baryon asymmetry relies on the rate of . Here then, the neutron dark decay rate can be smaller and thus be in accord with neutron star observations. It thus would not explain the full size of the neutron lifetime anomaly, but constraints on its size are useful in that they can be interpreted in terms of limits on the flavor structure of the quark–dark baryon couplings. Here we note that although must decay to other dark particles, different dark sector choices can be made. The precise energy loss constraints we are able to make from the study of existing neutron stars are sensitive to those choices, and we will explain how in Section 2. There are also dark decay models, such as the model of [92], that we cannot constrain with the methods we review in this paper, though that model is constrained by the would-be agreement between the decay correlations and the bottle lifetime, should the anomaly in the a and A determinations of (or ) be resolved.
In what follows, we discuss, in turn, the effects of the existence of dark sectors on stars and, particularly, how neutron stars can constrain models of neutron dark decays, how computations of particle processes in dense matter are important to determining those constraints, and, finally, what constraints emerge from neutron stars. We then conclude with a perspective on the neutron lifetime anomaly and a final summary.
2. Stellar Constraints on Dark Sectors
Neutron stars, which are remnants of stellar evolution, present a unique opportunity to study the intricate interactions of dark matter within extreme astrophysical environments. In this section, we place this in a broader context, thus delving into the multifaceted role of dark matter across different stages of stellar evolution, from the early universe’s first stars to the dynamic phenomena observed in supernovae. We explore how dark matter not only influences the life cycle of stars but also plays a crucial role in the formation, structure, and evolution of neutron stars.
2.1. Dark Matter’s Role in Stellar Evolution
The role of dark matter extends beyond the confines of neutron stars. Within the so-called CDM cosmological framework, cold dark matter (CDM) is a key driver of the universe’s “inside-out” structural growth, thereby crucially shaping the formation of galaxies and stars from the earliest density fluctuations [6]. Its influence is not limited to gravitational interactions: the dark sector potentially engages in a variety of interactions and phenomena that have a lasting impact on stellar evolution. This section explores these interactions, starting with the pivotal role of dark matter in the life cycle of the first stars.
2.1.1. Impact on First Stars and Population I Stars
In the earliest chapters of cosmic history, population III (Pop III) stars, the universe’s very first luminous bodies, emerged from the gravitational collapse of pockets of gas in small halos driven by dark matter [93]. These stars have been predicted to form at redshifts of 20–30 in halos with masses ranging from to . Recent reports suggest the possible identification of a Pop III star cluster in the remote fringes of a galaxy, thus highlighting ongoing efforts to deepen our understanding of these primordial objects [94]. Beyond its gravitational influence, dark matter, through its annihilation channels, might have significantly impacted the formation of Pop III stars. Such annihilation events could act as an additional heat sources, thereby potentially inhibiting protostar formation by offsetting essential cooling mechanisms [95,96]. In scenarios where a high dark matter density exists at the gas cloud’s location, if some annihilation products are trapped and thermalized within the cloud, and with this dark matter-induced heating surpassing expected cooling effects, a novel stellar phase, known as the “dark star” phase, could emerge. This phase could manifest itself as a giant hydrogen–helium star ( AU), which would be powered by dark matter annihilation instead of nuclear fusion [95]. Furthermore, with the ongoing capture of dark matter, these objects may evolve into supermassive dark stars, with masses larger than – and luminosities exceeding – [97]. Such objects could potentially be observable by the James Webb Space Telescope (JWST) [97,98]. Among the four metal-poor, high-redshift () sources discovered by the JWST Advanced Deep Extragalactic Survey (JADES) [99,100], three have been identified as potential supermassive dark star candidates [101].
Dark matter can significantly influence the evolution of Pop III stars postformation, especially for those near the Eddington limit. The additional heating from dark matter annihilation could destabilize the most massive Pop III stars, thereby effectively setting an upper mass limit. For instance, the impact of nonthermal, super heavy dark matter particles (mass range – GeV) is explored in [102]. It has been found that at a dark matter density of about , conforming to the XENON1T one-year detection bounds [103], the maximum mass of a Pop III star could be restricted to a few tens of solar masses. In environments with extreme dark matter densities, such as , the growth of Pop III stars might be limited to just a few solar masses due to the Eddington limit.
Pop III stars, which are luminous yet transient features of the early universe, concluded their short lifecycles in supernovae, thereby enriching the cosmos with heavy elements. However, the influence of dark matter could extend beyond the inception of these stars, thus significantly shaping the endpoint of their evolution. This influence is epitomized by the black hole mass gap (BHMG), which is a range delineated by where no black holes emerge from the direct collapse of massive stars due to pair instability.
The upper boundary of the BHMG results from supermassive stars bypassing pair-instability supernovae to form black holes directly, while the lower threshold arises from less massive stars that undergo pulsational pair-instability supernovae, thereby shedding significant mass through pulsations and leading to lower-mass black hole remnants than their progenitors. Modifications to Pop III stellar physics, potentially through new physics such as light particle emission, can shift the BHMG boundaries. Such particles can expedite helium burning and diminish stellar wind mass loss, thereby consequently reducing the available oxygen for burning and suppressing the pulsational pair-instability mechanisms in Pop III progenitors [104].
Transitioning from dark matter considerations in the stellar evolution in the early universe, we now turn our focus to the influence of dark sector physics on more contemporary stars. Luminosity measurements from the Sun and horizontal branch (HB) stars are instrumental in constraining dark sector particles, which are known for their potential to alter stellar cooling rates. The Sun’s emission of energy through a “dark channel”, such as dark photons, is particularly restricted by solar boron (8B) neutrino flux measurements [105]. These observations establish a conservative upper limit on the Sun’s dark luminosity, which is mandated to be less than 10% of the Sun’s total photon luminosity [106]. Furthermore, the emission of light particles such as neutrinos and axions from the cores of red giants can delay helium ignition. This results in the development of more massive cores, thus leading to a brighter phase prior to their evolution into HB stars [107]. The tip of the red giant branch (TRGB) is especially sensitive to new energy loss mechanisms, including those prompted by axions [108], dark photons [109], or millicharged particles [110], which can cause noticeable deviations in TRGB brightness from their standard values. Conversely, dark matter annihilation within a star’s core might trigger an earlier helium ignition, which could potentially lead to a dimming of the TRGB [111], thereby offering a contrasting perspective on the impact of dark matter within stellar environments.
Significant dark matter accumulation within stars can impact their structures by altering convective and radiative regions due to energy transfer by dark matter particles [112]. These structural changes influence stellar pulsations, with implications for asteroseismology [113,114]. In asymmetric dark matter (ADM) scenarios, where a primordial asymmetry determines the dark matter relic abundance instead of annihilation processes [115], ADM can accumulate without annihilation counterbalance. This accumulation leads to notable effects on stellar evolution, such as altered thermal transport in main sequence stars [116,117,118]. Specifically, ADM interactions, depending on their nature, can modify the temperature gradient in a star’s core by evacuating nuclear energy, with spin-dependent interactions playing a significant role during core hydrogen burning [119].
2.1.2. Influence on Supernovae Dynamics
The deaths of stars are also not free from potential dark sector influences. Specifically, the study of core-collapse supernovae, which mark the cataclysmic end of massive stars (with masses exceeding approximately ) offers a unique window for probing possible hidden sector interactions with ordinary matter. The emission of light particles from supernova remnants introduces an additional cooling mechanism, which operates by draining energy from the protoneutron star (PNS). This process is subject to constraints, as it could lead to a reduction in the duration of the neutrino burst observed from SN 1987A, which is a pivotal discriminant among astrophysical observations [120,121,122]. To maintain consistency with these observations, a conservative upper limit on the luminosity of dark particles () has been established, thus ensuring that it remains below the neutrino luminosity observed during the Kelvin–Helmholtz cooling phase, which takes place approximately one second after the core bounce. This constraint results in the formulation of a specific condition: , which is imposed one second after the bounce [107]. Supernova 1987A has also been instrumental in establishing limits on various extensions of the dark sector. These include constraints on axions [123], dark photons [124], and, notably, on muonic dark forces [125,126]. The latter, particularly the gauged model [127,128], has garnered interest for potentially resolving both the muon anomaly [129,130] and the Hubble constant tension [21,131,132]. Moreover, SN 1987A has been critical in constraining hyperon decay processes, thereby encompassing both decays into light bosons [133] and those leading to GeV-scale dark sector particles [79] —this is a constraint that we revisit in our study of neutron dark decay constraints in neutron stars.
The exploration of supernovae, which is crucial for understanding the dynamics of dark sectors, culminates in the birth of compact star remnants, which leads us to our next topic.
2.2. Neutron Stars as Dark Matter Laboratories
Among these remnants, neutron stars stand out due to their extreme densities and strong gravitational fields, thus making them ideal laboratories for probing dark matter effects in dense matter [134,135]. In this discussion, we categorize the effects of the dark sector on neutron stars into two distinct types: static and dynamic.
Static effects pertain to modifications in the equation of state (EoS) that governs the dense matter within neutron stars, with [136] as an explicit example. These alterations reshape the neutron stars’ configuration space in hydrostatic equilibrium, as dictated by the EoS. Such effects reach their complete manifestation well within the age (its observation time) of the star, thus acting in a time-independent manner during our observations.
Dynamic effects, in contrast, involve changes that occur over time, thereby impacting the neutron star’s structure, such as its temperature and spin. These changes evolve with the star, thus reflecting ongoing transformations.
It is important to recognize that a new physics model can induce both static and dynamic effects on neutron stars. There are models that exclusively yield dynamic effects while still preserving the original EoS. In such cases, these models facilitate a quasi-equilibrium transformation of the star, thereby unfolding within a configuration space that is derived from, and remains consistent with, the unaltered EoS [36].
2.2.1. Static Effects of Dark Matter on Neutron Stars
Building on the concept of static dark effects, a notable example is the introduction of a dark baryon. This particle, comparable to a baryon in mass but with markedly weaker interactions, results in a decrease in the pressure within neutron stars. Such a phenomenon effectively “softens” the EoS. This softening consequently reduces the maximum stable mass for neutron stars () as determined by the Tolman–Oppenheimer–Volkoff (TOV) equations for hydrostatic equilibrium [137,138]. Such modifications present significant challenges to the simplest models aimed at resolving the neutron lifetime anomaly [54], as we have noted in Section 1.3. They reduce to about [33,34,89], which is markedly below the mass of the most massive observed neutron stars, which exceed [139,140,141]. To reconcile these discrepancies, the introduction of repulsive interactions either within the dark sector or between dark particles and baryons becomes necessary [33,34,89,91,142,143]. Alternatively, a dark decay channel leading to a significantly lower equilibrium density of dark particles could circumvent this stringent bound [92]. In contrast, the condensation of light scalar fields, such as axions, within neutron stars—induced by the star’s baryonic content—results in a reduction of the baryon masses. This phenomenon can precipitate the emergence of a new ground state in nuclear matter, thereby potentially leading to an increased maximum mass for neutron stars [144,145].
2.2.2. Dark Dynamics of Neutron Stars
Dynamical effects on neutron stars can manifest themselves in various forms, ranging from abrupt, dramatic events to more gradual changes. A prime example of a sudden effect is the collapse of a neutron star into a black hole. Such extreme transformations can be triggered by specific interactions with dark matter, as seen in three distinct scenarios.
In one scenario, certain weakly interacting massive particle (WIMP) variants can accumulate within neutron stars. Over time, these WIMPs may gravitate towards the star’s center, thus eventually forming a self-gravitating core. This class of possibilities includes massive bosons lacking vectorial repulsive interactions and both bosons and fermions with strong attractive scalar interactions. Such a concentration of WIMPs could precipitate the rapid destruction of neutron stars in a period shorter than their observed lifespans [146].
In a parallel scenario, the accretion of nonannihilating dark matter within a neutron star can result in the formation of a degenerate dark core. If this core expands beyond its Chandrasekhar limit [147], the neutron star hosting it might undergo collapse [148,149]. This process potentially leads to the creation of anomalously low-mass black holes within a mass range of approximately –. Such black holes, if they merge, could produce gravitational waves detectable by the LIGO-Virgo-KAGRA network. The absence of detections thus far provides constraints on the interactions of nonannihilating dark matter, as suggested by recent studies [150]. However, the possibility of dark matter-induced core collapse can be highly sensitive to dark matter self-interactions [151]. Even extremely weak repulsive self-interactions can prevent black hole formation, which is a scenario that is particularly relevant in the context of realistic bosonic dark matter models [152]. Furthermore, the coannihilation of dark matter with nucleons, which is a common feature in many asymmetric dark matter models, can also act to inhibit black hole formation [152].
A third avenue explores the impact of dark matter realized as charged massive particles, with masses ranging from to . These particles can accumulate in collapsing protostellar clouds. After the formation of a neutron star, they fall to its center, thereby potentially forming a black hole on a time scale of the order of a year. This black hole could then grow rapidly through accretion, thus leading to the host neutron star’s destruction on a similar time scale. The existence of old neutron stars suggests that these charged massive particles, if present, make up no more than of the dark halo’s mass [153].
Gradual dynamical effects can also occur. The thermal history of neutron stars can deviate from the predictions of standard cooling theory [154]. This deviation, potentially speaking to new heating mechanisms, has been supported by observations of several old warm neutron stars [155,156]. These stars exhibit surface temperatures higher than those predicted by standard cooling models. They could arise from the inclusion of further SM effects [157,158], including nonequilibrium processes [159] such as rotochemical heating, which results from the spin-down behavior of pulsars [160]. However, heating could also be incurred through dark matter scattering and capture [158,161,162,163] or annihilation [164]. Alternatively, dark matter effects could alter the structure of dense matter altogether through the appearance of axion quark nuggets [165] or of finite density-seeded vacuum instabilities [166,167].
There are various heating effects. Kinetic heating, resulting from dark matter capture, involves dark matter particles being gravitationally accelerated to velocities exceeding half the speed of light. As these particles scatter within neutron stars, they deposit significant kinetic energy, thus possibly heating the stars to infrared black body temperatures [161]. Although the dynamics within neutron star cores, the primary region of such scattering, are not fully understood, the role of the crust has been emphasized in dark matter interactions. Scattering with just the neutron star’s low-density crust can still kinetically heat the star to infrared temperatures, which are detectable by forthcoming telescopes, thereby highlighting the crust’s importance in dark matter detection and annihilation processes [168]. Moreover, inelastic dark matter could significantly influence neutron star heating. Its interactions would be suppressed in standard nuclear recoil direct detection experiments, where small momentum transfers are insufficient relative to the mass splitting between dark matter states. However, neutron stars enable effective inelastic scattering, even with large mass splittings, due to the acceleration of dark matter particles to velocities approaching the speed of light during their infall [162,169]. Additionally, the annihilation of WIMPs inside neutron stars can impact their thermal properties. This is particularly evident in neutron stars older than 10 million years that are situated nearer to the Galactic center, where the density of dark matter is expected to be significantly higher than in the vicinity of the Earth. For instance, in regions where the dark matter density is at least , such interactions could lead to an asymptotic internal temperature of around [164]. Conversely, in regions with comparatively lower dark matter densities, other heating mechanisms may play a more dominant role in shaping the thermal evolution of neutron stars [157].
Studies of young neutron stars also give constraints. Temperature observations of NS1987A, the remnant of SN1987A [170,171], and of Cassiopeia A (Cas A), the second-youngest known neutron star with an approximate age of 340 years, were shown to impose constraints on anomalous cooling processes in neutron stars. These observations play a crucial role in constraining the emissions of novel bosonic particles that could serve as additional cooling mechanisms, thereby altering the thermal evolution of stars [172,173].
As a separate tack, binary pulsar systems offer unparalleled insights into both gravitational physics and particle physics, particularly in the context of dark sectors. These systems enable precision tests of fundamental theories, thereby providing constraints on new physics beyond the SM. In gravitational physics, binary pulsars have been instrumental in rigorously testing general relativity and alternative theories of gravity in strong-field regimes [174,175]. Notably, the Hulse–Taylor pulsar (PSR B1913+16) [176,177], in a binary system of a pulsar and a neutron star, and the double pulsar system (PSR J0737-3039A/B) [178,179] have played key roles in validating general relativity’s predictions [180,181]. Furthermore, the sensitivity of binary pulsar orbital periods to energy loss mechanisms [182,183,184] makes them ideal for investigating particle interactions that extend beyond the SM [185]. Observations of these periods have led to constraints on ultralight dark matter candidates [186,187,188,189] and limits on dark baryon processes involving neutron–mirror neutron mixing [190], as well as broader constraints on various forms of the quasi-equilibrium baryon number violation (BNV) [36,37]. The implications of these constraints, derived from binary pulsar period observations, on quasi-equilibrium BNV and specific dark decays of baryons are further explored in Section 4.
The precision of pulsar timing has become an essential tool in astrophysics, especially through pulsar timing arrays (PTAs), which have been used to find evidence for a stochastic gravitational wave background [191,192,193,194]. This technique also plays a pivotal role in exploring ultralight dark matter (ULDM), as ULDM candidates with masses around eV have been predicted to create oscillating gravitational potentials at nanohertz frequencies [195]. Such oscillations lead to periodic variations in the arrival times of radio pulses from pulsars, thereby overlapping with the frequency range for gravitational waves detectable by PTAs [196]. The European Pulsar Timing Array has effectively used this aspect to constrain scenarios in which dark matter interacts only gravitationally, thereby demonstrating that ultralight particles in the mass range cannot fully account for the observed local dark matter density [197]. Additionally, pulsar timing exhibits sensitivity to the effects of heavier dark matter candidates, including primordial black holes and compact subhalos, thereby extending its utility in constraining a wide mass range of dark matter candidates [198]. In addition, pulsar timing shows potential for probing BNV [199]. Anomalies in pulsar spin-down rates and braking indices could be indicative of BNV processes, thereby possibly leading to pulsar spin-up behavior and the reactivation of dormant pulsars. With current timing precision being sensitive to the BNV rates of , PTAs are increasingly becoming a crucial tool for future BNV detection or constraints, particularly as their precision improves in the context of gravitational wave detection.
2.3. Quasi-Equilibrium Dynamics of Baryon Loss in Neutron Stars
In Section 2.2, we explored the ways in which dark sector extensions to the SM can impact neutron stars. Building on this foundation, this section delves further into these phenomena, with a particular focus on the implications of specific dark decays of baryons within neutron stars.
One intriguing example involves neutron dark decays, such as . These should occur at a rate of around to resolve the neutron lifetime anomaly. If the dark decay products, such as , remain stable over short timescales, they could swiftly saturate the interior of a neutron star shortly after the collapse of its progenitor star’s core. This process is expected to drive dynamical effects whose outcomes would be chemical equilibrium between the decay products and the star’s baryons. Modeling the EoS under these circumstances necessitates incorporating the new degrees of freedom, such as and other dark sector particles, affecting the star’s pressure and energy density. The ground state of this system would be determined by the lowest energy state, subject to charge conservation and an extended baryon number concept, where . Should maintain stability over long timescales, the neutron star would eventually settle into a static state. This scenario illustrates a static dark sector influence, thereby altering the star’s configuration space via its EoS. In this case, static limits such as the maximum mass of neutron stars can be used to constrain the dark decays.
If neutron decay products such as further decay or engage in annihilation, leading to particles that escape the star, the situation becomes dynamically complex. It is important to note that these depletion processes need not be direct; they may involve a series of reactions. For instance, if decays into leptons, then baryon number conservation would be explicitly violated. This, in turn, would trigger a sequence of baryon-conserving reactions within the neutron star. The resulting depletion of baryons manifests itself not only through neutrino emission but also through contributions to the thermal energy and work done on the stellar fluid. In this case, continuous neutron decays could dynamically influence the neutron star properties over its lifetime. Ongoing processes like these could lead to observable changes in neutron stars, including modifications in thermal evolution, variations in pulsar spins, or alterations in the orbital periods of binary pulsars. In this context, neutron stars offer an observational platform for constraining and potentially revealing active dark decay processes.
Broadening our perspective, the overall influence of baryon dark decays, which should dominate dark baryon processes in neutron stars because of the sheer number of neutrons involved, depends on the production () and depletion () rates of dark particles, as well as the sensitivity () of neutron star observations. While the depletion mechanisms themselves vary—manifesting as either the direct escape of dark particles from the star or an explicit BNV—the crucial factor in modeling these effects is their rate, with one notable exception. The thermal evolution of a neutron star does require a more detailed examination of the depletion mechanism, since it is influenced by the specific sequence of reactions involved in the process. These diverse scenarios necessitate distinct computational approaches, as depicted in Figure 4.
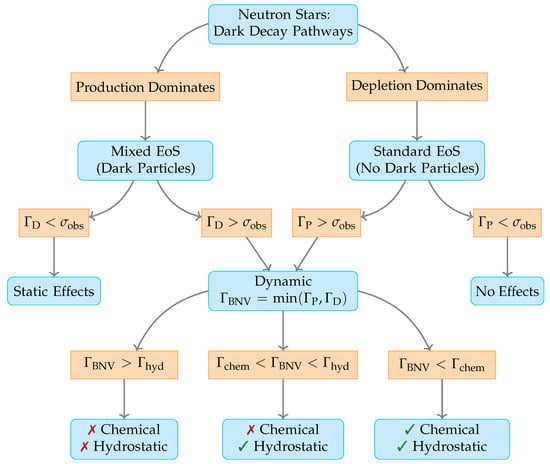
Figure 4.
The potential pathways and resultant states stemming from neutron decays to dark final states in neutron stars, which are dictated by production () and depletion () rates. Observational sensitivity () and the star’s response rates—chemical () and hydrodynamic () ones—further influence these pathways. A departure from chemical and/or hydrostatic quasi-equilibrium (denoted by ✗) necessitates numerical simulations for precise stellar modeling, with the expectation that stars transition from a nonequilibrium to a quasi-equilibrium state over time.
In cases where depletion () exceeds production (), the star primarily comprises SM particles. Here, becomes the effective BNV rate to compare against . Conversely, if production () surpasses depletion (), dark sector particles must be included in the EoS. The depletion rate () then serves as the effective BNV rate, because this determines the time scale over which the star changes.
In scenarios in which the neutron star observations are not sensitive to the BNV rate (), we have the following:
- Production dominance () leads to static effects via EoS modifications, thus incorporating dark particles.
- Depletion dominance () results in no observable effects.
Conversely, when observations are sufficiently sensitive to possible BNV effects () and under the assumption that in degenerate cold neutron stars the hydrodynamic response rate exceeds the chemical rate (), we have the following:
- I.
- The star is in both chemical and hydrostatic quasi-equilibrium if . This state warrants a quasi-equilibrium analysis, as developed in [36].
- II.
- The star remains only in hydrostatic quasi-equilibrium if . A hydrostatic equilibrium description is valid on short timescales (). However, a complete reaction chain must be considered, as chemical equilibrium is absent in the EoS.
- III.
- The absence of both equilibria when requires comprehensive simulations of the star’s hydrodynamic and chemical evolution.
Notably, in the quasi-equilibrium scenario (I.), baryon number conservation on short timescales forms a key constraint in the derivation of its EOS. The primary distinction between production- and depletion-dominated states lies in the inclusion or exclusion of dark sector elements and the extended definition of the baryon number.
The quasi-equilibrium framework posits that if dark sector perturbations, such as baryon decays, proceed at a slower rate than the star’s responses, the star will evolve within an equilibrium configuration space defined by the EoS. In scenarios where dark particle production dominates, this EoS incorporates the pertinent dark degrees of freedom. Conversely, in cases where depletion prevails, the EoS remains akin to the standard formulation, which is exclusive of dark sector influences. This approach effectively balances the dynamical aspects of dark sector interactions against the inherent stabilizing mechanisms of neutron stars. The computational simplicity in depletion-dominated scenarios is significant, as the EoS needs not reflect intricate dark sector details, thus facilitating a model-independent analysis.
Building upon this framework, the configuration space of neutron stars can be effectively parameterized by a set of n independent parameters, which is denoted as . Variations in the neutron star observables, symbolized as , can then be quantified through the following expression:
where each term represents the sensitivity of the observable to changes in the ith parameter, as governed by the EoS. The rates of change for these parameters, , are determined by imposing constraints on the system’s quasi-equilibrium dynamics. These constraints may include theoretical principles, such as the conservation or specific rate of violation of the baryon number, alongside observational data like the spin-down rates of pulsars. Together, these factors provide a comprehensive framework to model and understand the evolution of neutron star observables within the prescribed parameter space.
Before exploring specific examples, we think it crucial to recognize that certain neutron star characteristics, such as its surface temperature, rotational period, or its magnetic field, may not always be central to our framework, particularly when these factors do not significantly influence the observable under study. Neutron stars, which are composed of cold, degenerate matter, experience minimal thermal contributions to their structure. Similarly, rotational effects are often minor for pulsars with longer periods, generally those exceeding a few milliseconds [200]. Therefore, dynamical evolution within the configuration space can often be treated as independent from changes in the magnetic field, temperature, or rotation period. However, it is important to note that these elements should be explicitly included in the analysis when they directly impact the observable being studied. For example, when investigating pulsar spin-down behavior, rotation remains a crucial component within the formalism. Similarly, temperature may be a vital factor in processes that are subject to Pauli blocking mechanisms.
We now illustrate the application of the quasi-equilibrium framework with three distinct examples, each of which is succinctly summarized in Table 1. In each case, we note what configuration space is modified through the dynamical change indicated, as well as the constraints that act on those dynamics.

Table 1.
Quasi-equilibrium frameworks for neutron star evolution under various scenarios. Parameters include the central energy densities for the entire star (), visible sector (), and dark sector (), as well as the central angular velocity (). The observed spin-down rate is indicated by , while the rate of baryon number violation or conversion in dark sector processes is denoted by .
- Standard Baryon-Conserving Spin-Down Rate of a Pulsar:
- Configuration Space: This is defined by , where represents the central energy density, and denotes the central angular velocity of the local inertial frames [200,201].
- Constraints: These are governed by the observed spin-down rate () while maintaining baryon number conservation ().
- Formation of a Dark Core without Depletion:
- Configuration Space: This is defined by , which represents the central energy densities of the visible (V) and dark (D) sectors at the star’s core. The formation rate is generally assumed to be comparable to or slower than the star’s age. This rate does not result in thermalization between the two sectors. Consequently, the sectors are characterized by distinct energy densities and pressures, thereby interacting primarily through gravitational influence.
- Constraints: The total baryon number conservation () acts as a constraint, thereby ensuring a balanced rate of baryon conversion between the dark and visible sectors. The conversion rate from visible to dark baryons () is derived from the specifics of the particle physics governing the decay or conversion processes.
- Baryon Dark Decays Followed by Efficient Depletion:
- Configuration Space: This space, also known as the single-parameter sequence (illustrated in Figure 5), is singularly defined by (if the star is not rapidly rotating). Here, denotes the central energy density of the neutron star. This simplified configuration space reflects the scenario where baryon dark decays and subsequent depletion processes dominantly influence the neutron star’s structure.
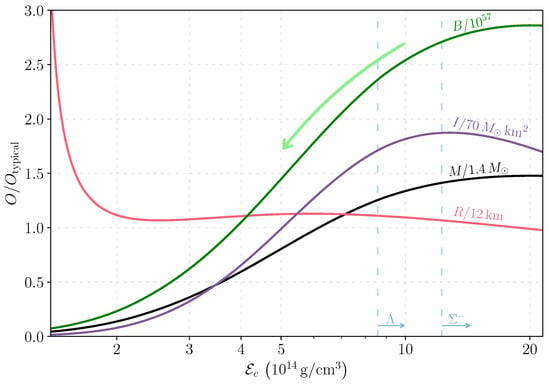 Figure 5. Variations in neutron star properties as functions of central energy density (): mass (M), radius (R), baryon number (B), and moment of inertia (I), all normalized to typical values. Namely, , , , and . The calculations employ the DS(CMF)-1 EoS [202]. Notable features include the quasi-equilibrium baryon loss (indicated by the green arrow) and the onset of hyperon appearance (denoted by cyan vertical dashed lines) at sufficiently large central energy density.
Figure 5. Variations in neutron star properties as functions of central energy density (): mass (M), radius (R), baryon number (B), and moment of inertia (I), all normalized to typical values. Namely, , , , and . The calculations employ the DS(CMF)-1 EoS [202]. Notable features include the quasi-equilibrium baryon loss (indicated by the green arrow) and the onset of hyperon appearance (denoted by cyan vertical dashed lines) at sufficiently large central energy density. - Constraints: The evolution is primarily governed by the total baryon loss rate . This rate is instrumental in dictating the evolution of the star’s core composition and overall structure, as indicated by the green arrow in Figure 5, which represents the quasi-equilibrium evolution along the single-parameter sequence.
Transitioning from the comprehensive analysis of neutron stars’ quasi-equilibrium dynamics, we now shift our focus to specialized dark sector models, particularly those that expand neutron dark decay scenarios to encompass dark cogenesis. Such models propose a unified origin for the observed baryon asymmetry and a corresponding asymmetry within the dark sector. This approach intriguingly links the physics of neutron stars to wider cosmological narratives.
2.4. Illustrative Dark Sector Models
We have considered neutron decays in which a dark baryon appears, and the manner in which we can probe this possibility in a neutron star depends on if and how decays to other dark sector particles. In this section, we consider just one particular dark sector interaction, but its impact on a neutron star can vary significantly depending on the assumed spectrum of particles in the dark sector. Indeed, with suitable choices, we will see that it can sample all the scenarios outlined in the previous section.
Although we certainly expect to decay were it to play a role in mesogenesis, it need not—perhaps is stable and a possible dark matter candidate in and of itself. This would require, of course, that the is light enough that it cannot decay to light antibaryons, and we presume it does not decay just to mesons and/or leptons alone, so that true baryon number-violating () processes do not appear in this context. Thus, as in [78,79], we introduce two new particles: a scalar baryon with and a Majorana fermion . It is important that neither nor decay, nor that they transform into each other. However, may decay via [78]
where either or or both could be dark matter candidates. This interaction can destabilize the proton, produce decay, or produce annihilation, with examples as shown in Figure 6a,b. For different choices of the particles’ masses, different processes appear. For example, we have the following:
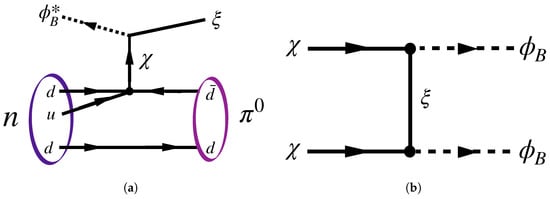
Figure 6.
(a) Induced nucleon decay. (b) annihilation from [37].
If does not decay, the neutron dark decay rate is constrained, or alternatively, self-interactions must be present, as previously noted in Section 1, to align with observed neutron star masses. This scenario corresponds to the production dominance route depicted in Figure 4, thereby leading to static effects such as the modification of the maximum theoretical neutron star mass.
However, with a suitable choice of dark sector masses, subsequent to neutron decay to a final state with a particle, either and/or can appear. These outcomes can act with different effects within a neutron star. Either sort of particle could fall to the core of the star and modify its evolution—and possibly act with a destabilizing effect [149]. Alternatively, if and are light enough, they can escape the star. Thus, the scenarios described in the previous section can all be sampled through the dark sector interaction of Equation (3). In our own investigations [36,37], we have used a quasi-static approach to determine the evolution of the star in the presence of a slow apparent BNV to dark final states. The consistency of this analysis, that new physics dynamics does not impact the evolution of the star, requires that we have an effective mechanism to remove energy from the star upon decay to a dark final state. Accordingly, our analysis is predicated on the assumptions inherent in the depletion dominance pathway of Figure 4, which culminates in a quasi-equilibrium evolution of the star. As a concrete example of such, we have supposed that , thus realizing removal through decay, with being light enough to escape the star.
Additional physical constraints appear if we work within the context of a dark cogenesis model. For example, if could occur, and it would under the conditions we have just outlined for quasi-static evolution of the star, then if is heavy enough, and can also appear. In a broader context, such processes would act to dilute a cosmic baryon asymmetry. Thus, either the flavor structure of the pertinent quark– couplings must be sufficiently small, or the mass of is further constrained. Following the latter path, we note that successful baryogenesis within the dark sector scenario of Equation (3) (and masses such that occurs) can be realized if . This and nuclear stability considerations gives us the following window on [37]:
though in what follows, we consider neutron star constraints on –baryon mixing over a larger mass window in anticipation of other model building solutions. We now turn to the evaluation of these decays within the dense medium of a neutron star.
3. Neutron Stars and Particle Decays in Dense Matter
The consideration of dense matter phenomena is crucial for investigating baryon interactions in neutron stars, where intense gravitational forces compress baryonic matter to densities exceeding nuclear saturation. Such extreme conditions push the system into the strongly repulsive domain of nuclear interactions, thus resulting in an elevation of the ground state energies of the baryons. This increase in energy levels potentially allows for decay processes that are otherwise kinematically forbidden in both a vacuum and within nuclei [37]. Consequently, neutron stars present themselves as unique astrophysical laboratories, thereby offering the possibility to observe baryon dark decays that bypass the constraints usually encountered in earthbound experiments such as Super-Kamiokande or KamLAND [203,204]. To gain a more comprehensive and quantitative insight into this phenomenon, we delve into a particular formalism of dense matter. This exploration aims to uncover the unique role of heavy neutron stars as cosmic laboratories, thus offering new probes of dark sectors.
In this vein, a hadronic relativistic mean field (RMF) theory offers a robust framework for addressing dense matter interactions in such extreme environments [205,206,207,208]. Within RMF theory, baryon interactions are mediated through various Lorentz scalar and vector mesons. The Euler–Lagrange equations that govern the dynamics of these meson fields include baryon currents as source terms, thus taking the form of for scalar mesons and for vector mesons. As the baryon density increases, these currents intensify, thereby leading to a significant vacuum expectation value (VEV) for the meson fields. Within this framework, the mesonic degrees of freedom are thus effectively represented by their classical VEVs, which is a simplification that sees scalar meson VEVs contributing to the baryon masses and vector mesons to their four-momentums. This theoretical construct provides the foundation for understanding baryon behavior in the dense, locally uniform medium of neutron stars.
In such a medium, the wave function for a baryon with a canonical four-momentum is expressed as
where represents the kinetic four-momentum. The vector self-energy (), generated by the vector meson VEVs, is characterized by in the nuclear matter frame. The time component of is given by , with signifying the baryon’s effective mass. The baryon spinor satisfying the Dirac equation
is solved in the Dirac–Pauli representation as
where are the Pauli matrices, and is the Pauli spinor with and . The baryons’ energy spectrum () is delineated by
where we note that in the RMF approximation, and are density-dependent but independent of . The CM energy of the baryons, denoted as , is a function of their effective mass and momentum in the nuclear matter frame. It is expressed by the following equation:
This energy reaches its minimum when the momentum is zero and reaches its maximum at the Fermi momentum. The numerical values of , , and for the baryons within neutron stars under the DS(CMF)-1 EoS [202], which comes from a more sophisticated descendent [208] of the RMF model we have noted, are depicted as functions of density in Figure 7. (We anticipate further evolutionary development of the RMF approach through a determination of its parameters from a description of pure neutron matter within chiral effective theory [209].) As evidenced in Figure 7, a notable reduction in the effective baryon masses () at higher densities is observed, which is indicative of chiral symmetry restoration in these high-density regimes in this model. Furthermore, the dynamics between and (in the nuclear matter frame) are such that while decreases, increases, thereby cumulatively leading to an increase in the total energy of the baryons as delineated by Equation (8) at higher densities. The core (maximum) density of four pulsars (in binary systems) are denoted by vertical dot–dashed lines for comparison. This sets the stage for understanding how each neutron star, with its unique density profile, represents a distinct astrophysical laboratory.
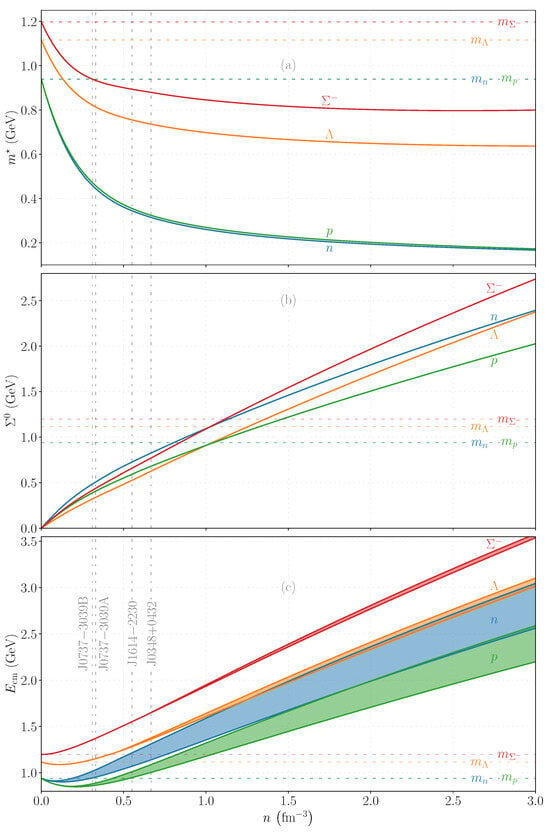
Figure 7.
Variations in baryonic properties under the DS(CMF)-1 EoS depicted as functions of density. (a) Effective masses of various baryons. (b) Vector self-energies of the baryons in the nuclear matter frame. (c) Range of center of mass (CM) frame energies for the baryons. Vertical lines in all panels represent the central number densities () of the pulsar systems examined in Section 4, while horizontal lines correspond to the vacuum masses of the respective baryons.
Figure 8 further demonstrates how each neutron star offers a unique probe that is intrinsically linked to its specific density profile. The CM energy spectrum of the baryons (, neutron (n), and proton (p)) in neutron stars in PSR J1614-2230, PSR J0348+0432, and PSR J0737-3039A has been observed to surpass their vacuum rest mass within the stars’ cores, as shown in the figure. Notably, heavier neutron stars such as in PSR J1614-2230 and PSR J0348+0432 have been shown to exhibit a higher energy density reach, thereby underscoring the relationship between a star’s mass and its potential for exploring baryon dark decays. This characteristic of neutron stars, particularly the more massive ones, highlights their capability to facilitate baryonic decays into states that are kinematically forbidden in vacuum conditions. The unique energy reaches offered by these pulsar systems offer invaluable insights into dark matter models beyond the scope of terrestrial experiments. In the ensuing section, we demonstrate how observations of binary pulsars, in conjunction with the considerations of dense matter outlined herein, pave the way for novel constraints on the dark decays of baryons.
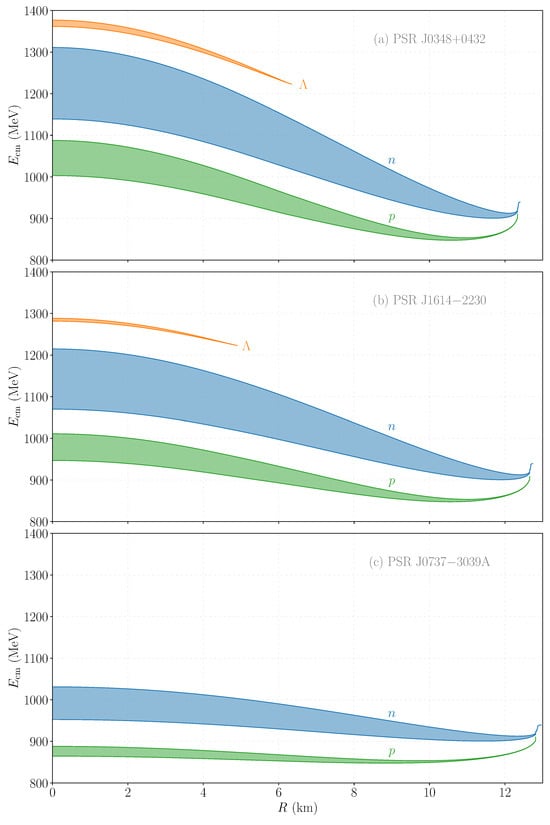
Figure 8.
Energy spectra of baryons (, neutron (n), and proton (p)) in their center of mass (CM) frames within specific neutron stars of (a) PSR J0348+0432, (b) PSR J1614-2230, and (c) PSR J0737-3039A plotted as functions of stellar radius. We have chosen to represent only PSR J0737-3039A here and henceforth, as it is nearly identical in mass to PSR J0737-3039B. The plot highlights how the CM energy in high-density regions exceeds the baryons’ vacuum rest mass, thus hinting at the possibility of decay into states that are kinematically forbidden in vacuum. Detailed analysis of these phenomena is provided in the main text.
4. Baryon Loss Constraints from Energy Loss Limits in Pulsar Binaries
Binary pulsar orbital periods, which are sensitive to energy loss mechanisms, present an effective observational tool for probing quasi-equilibrium BNV processes. In scenarios with efficient depletion, such as Example 3 in Section 2.3, the quasi-equilibrium BNV at a rate contributes to an energy loss from neutron stars as follows [36]:
where represents the partial derivative with respect to the central energy density of stars, M is the mass, I denotes the moment of inertia, and is the angular spin frequency. This energy loss affects the binary pulsar orbital period [182,183,184]:
in which 1 and 2 represent binary components. The observed orbital period decay rate, , combines gravitational radiation (), intrinsic energy loss (), and extrinsic factors ():
The precision in these terms determines the sensitivity of the BNV limits, thus making binary pulsars with accurate timing ideal for realizing stringent constraints. Moreover, as noted in Section 3, each pulsar, especially the more massive ones, offers a unique opportunity for the study of the BNV. Their larger mass extends the density reach, thereby enabling constraints on higher mass ranges of dark particles such as in processes such as . Furthermore, selecting binary systems with heavier pulsars is essential for constraining the dark decays of hyperons. In EoSs that incorporate hyperon degrees of freedom, hyperons start populating the medium only in extremely dense environments [210], specifically in the cores of heavier neutron stars (as illustrated in Figure 8).
In our pursuit of comprehensive coverage of the model parameter space, a strategic combination of binary pulsars—both heavy and precisely measured—is essential. Ideal candidates are systems with accurately determined masses, orbital periods, and well-quantified contributions to each term in Equation (12). It is critical to select binary systems that are free from mass transfer between their components to avoid complex alterations in the observed orbital period decay rate, as mass transfer can significantly influence [211]. Excluding the heavy candidate PSR J0952-0607, a “black widow” pulsar with substantial mass uncertainty and significant rotational effects on its structure [139], our attention turns to the following candidate binary pulsar systems:
- PSR J0740+6620: [140],
- PSR J0348+0432: [141],
- PSR J1614-2230: [212].
- We ultimately selected PSR J0348+0432 and PSR J1614-2230, which offer the advantages of smaller errors in and , thus ensuring more precise constraints. Complementing this selection, we also considered pulsar systems that are renowned for their high-precision measurements. Among these, the double pulsar J0737-3039A/B [179] and the Hulse–Taylor pulsar system [176] stand out. Since both are characterized by similar mass profiles, we focused on the double pulsar J0737-3039A/B, which was chosen for its superior precision.
The constraints derived from our selected pulsar systems were applied to a specific model involving baryon decays , which was dictated by an effective mixing parameter . The in-medium Lagrangian governing these decays is represented as:
In this equation, we have employed , where are the Dirac gamma matrices, and represents the spacetime derivatives. Furthermore, and correspond to the field operators for visible and dark baryons, respectively. To construct a combined limit () from the individual pulsar constraints (), we utilize the following relation:
The resulting limits, as derived in [37], are depicted for individual systems and their combined limits under the assumption of the DS(CMF)-1 EoS [202] from the hadronic EoS of [208] with a crust [213] from the CompOSE database [214] in Figure 9.
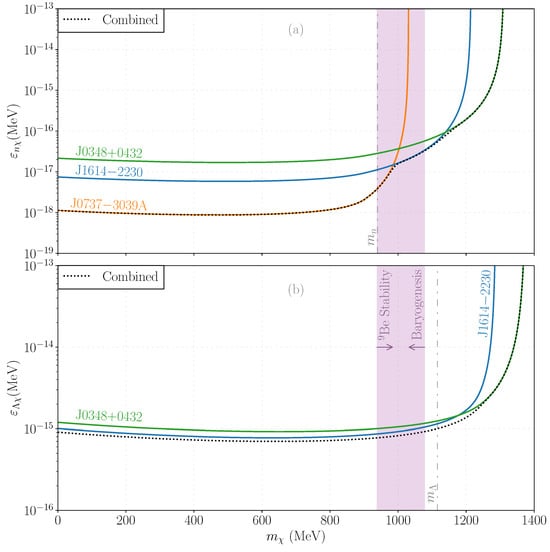
Figure 9.
Two- exclusion constraints on the mixing parameters for baryon–dark baryon interactions derived under the depletion dominance scenario [37] as illustrated in Figure 4 and based on the DS(CMF)-1 EoS [37]. The vertical purple band indicates the range for the dark baryon mass (), which is essential for nuclear stability and successful baryogenesis as defined in Equation (4). (a) Neutron (n)–dark baryon () interaction constraints as functions of . The colored lines represent the exclusion limits from the pulsars in PSR J0348+0432 (green), PSR J1614-2230 (blue), and pulsar A in the double pulsar system PSR J0737-3039A/B (orange), with the combined limits depicted by a dotted black curve. The vertical dashed lines mark the vacuum rest mass of the neutron. (b) Similar constraints for the – interaction using the same color scheme and presentation. Here, the vertical dashed lines represent the vacuum rest mass of the hyperon.
As depicted in Figure 9, the pulsars provided constraints on models with dark baryon masses extending several hundred MeV above the mass of the decaying baryon. Specifically, the heaviest pulsar, in PSR J0348+0432, demonstrated the broadest energy reach, while the most precisely measured system, the double pulsar J0737-3039A/B, yielded the most stringent limits for lower mass ranges. By varying the choice of EoS, we can explore the robustness of our assessments. We have explored this for the entire family of DS(CMF) EoSs: DS(CMF)-1-8 [202,215] in [37]. Interestingly, the combined constraint changed negligibly below , thus effectively covering our window of interest, Equation (4), whereas variations in of a factor of a few appeared over the entire mass range studied—and only DS(CMF)-1,3,7 supported the appearance of strange baryons for the parameters of our candidate pulsars. We note that the parameter at was bounded to be no larger than for the entire window in the mass we have supposed in a dark cogenesis scenario.
We consider the implications of these results in the next section.
5. Perspectives on the Neutron Lifetime Anomaly and Dark Cogenesis
We now determine the outcomes from our neutron star analysis in regard to the in-vacuum limits on neutron dark decay. We can translate the constraints on that we report in Figure 9 to ones on the in-vacuum decay rate of using the following equation:
We note that signifies the baryon magnetic moment (Landé) g factor, where for neutrons, and for baryons [56]. The resulting constraints on the vacuum branching ratios are illustrated in Figure 10.
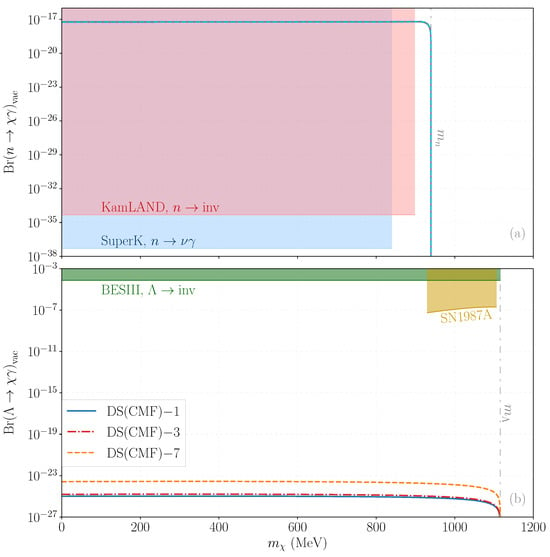
Figure 10.
Two- exclusion limits on the vacuum branching fraction for processes are depicted in panels (a) for neutrons and (b) for baryons. The green region represents limits from Super-Kamiokande [203]. We highlight that the KamLAND constraint (red) [204] is pertinent to our study of decay, as the prompt photon would not pass the correlation cuts and would remain undetected. Panel (b) also presents limits from neutron star studies for the DS(CMF)-7, DS(CMF)-3, and DS(CMF)-1 EoSs in order of increasing severity, along with constraints from the BES-III experiment (blue) [216], noting that the in this case would also be undetected, and the SN1987A limits (gold) [79].
In Figure 11, we focus on the particular range of masses pertinent to the neutron lifetime anomaly, thus reporting both and . It is apparent that terrestrial searches for baryon number-violating processes in underground detectors give the most stringent limits on the possibility of , yet the windows on the mass open in such searches did not overlap with the possible mass window for the neutron lifetime anomaly—the nuclear stability constraint we have noted yielded the lowest possible mass, reported in Equation (4), and this precludes that possibility. Nevertheless, we include the KamLAND [204] and Super-Kamiokande [203] limits, as well as the limit on from BESIII [216] and that from the SN1987A study of [79] for context. Specifically, the KamLAND constraints are relevant to our study of the decay ; in these scenarios, the prompt photon would not meet the correlation cuts, thus rendering it invisible. We observe that our neutron star limit is about times more severe than the accelerator limit and is similarly less sensitive to the BNV than the underground experiments. Additionally, we incorporated constraints arising from the influence of decay on the neutrino signal duration observed from SN1987A [79]. These constraints have been derived from a supernova simulation involving an progenitor leading to a remnant [217]. Theoretically, these constraints could extend to lower masses as well. Notably, our derived limits significantly surpass the bounds established by the supernova data [79].
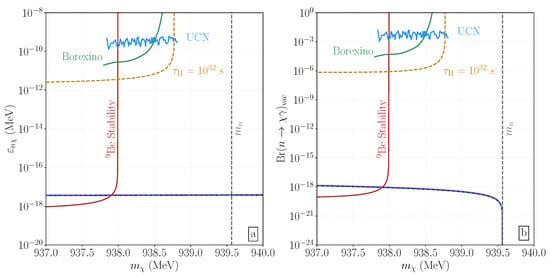
Figure 11.
Exclusion limits at 2 on (a) and (b) the vacuum branching fraction for from our quasi-static neutron star analysis in the particular mass region pertinent to an explanation of the neutron lifetime anomaly. Additional constraints and expected limits (dashed) as per [218] have been included. This figure has been taken from [37].
The outcome of our analysis appears to exclude a new physics interpretation of the neutron lifetime anomaly, but the context in which we performed this analysis is crucial: different choices within the dark sector could lead to alternate outcomes, as explored in Section 2.3. In our case, we have chosen a dark sector content and interaction as per Equation (3) and the accompanying discussion so that the SM dynamics of the neutron star determine the evolution of the star under a change in its baryon number—with the injected energy from the exotic neutron decay, particularly from production, removed through decay, with subsequently removed from the star. Our approach aligns with the depletion dominance route depicted in Figure 4, thus resulting in a quasi-static evolution of the neutron star. However, in alternative scenarios, the establishing limits would depend on varying pathways of dark decay, as outlined in the same figure.
As for dark cogenesis models, to which our neutron dark decay studies connect, such as B mesogenesis [78], we constrain the flavor structure of the quark– couplings through the limits we report [37]—and we show our limits in our favored mass region according to the shaded band in Figure 9.
6. Summary
There is an increasing recognition that the solution to the dark matter problem may involve an entire sector of dark particles with dark dynamics. The presence of such dynamics can be probed in terrestrial experiments that are sensitive to the determination of missing momentum [219] in hadron decays, and in this article, we have considered this broader possibility in the context of neutron stars. Particularly, we have noted the consequences from limits on the observation of energy loss in neutron stars, especially those that emerge from the timing of the period of binary pulsars on baryon dark decays, specifically of neutrons and baryons.
Neutron star observables have multiple points of contact with the problem of the neutron lifetime anomaly and with the broader possibility of the simultaneous generation of dark matter and the BAU. We have noted models that would give rise to or to all dark decays, as described in [54,91] in this volume, which are limited by the need to form neutron stars of sufficient mass. An unwanted softening of the neutron EoS through such neutron decay effects can be mitigated through the possibility of self-interactions or by reducing the neutron dark decay rate. We have studied the possibility of using dark sector interactions to eradicate the particles produced via dark decays through annihilation to light, which are dark sector particles that can escape from the star. Here, we have studied the limit in which the dark decays proceed slowly with respect to the usual Urca processes that operate in the neutron star, thereby enforcing chemical and thermal equilibrium. Thus, in this quasi-static framework we are able to study the consequences of the observed energy loss constraints from pulsar timing studies on dark decays in the neutron stars. The constraints we have found thus far are severe, but broader possibilities remain—and they beckon. Certainly, there are models of the neutron lifetime anomaly that are not constrained by our concerns. Here, we note the model that yields [92]. That model does not soften the EoS unduely, nor does it give rise to substantial energy loss effects that could be constrained through our pulsar timing studies. Thus, the possibility of a new physics solution to the neutron lifetime anomaly remains, with the future neutron decay correlation and lifetime studies offering the possibility of setting the controversy to rest, though effects in neutron stars, as well as in isolated ones, through observed heating or spin effects may finally serve to identify the effects of dark sectors in a positive way.
Author Contributions
All authors contributed equally to this work. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the U.S. Department of Energy Office of Nuclear Physics under contract DE-FG02-96ER40989.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Acknowledgments
We thank Jeffrey M. Berryman for his past collaboration on many of the topics in this overview.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Zwicky, F. Die Rotverschiebung von extragalaktischen Nebeln. Helv. Phys. Acta 1933, 6, 110–127. [Google Scholar]
- Zwicky, F. On the Masses of Nebulae and of Clusters of Nebulae. Astrophys. J. 1937, 86, 217. [Google Scholar] [CrossRef]
- Peebles, P.J.E.; Yu, J.T. Primeval Adiabatic Perturbation in an Expanding Universe. Astrophys. J. 1970, 162, 815. [Google Scholar] [CrossRef]
- Press, W.H.; Schechter, P. Formation of Galaxies and Clusters of Galaxies by Self-Similar Gravitational Condensation. Astrophys. J. 1974, 187, 425–438. [Google Scholar] [CrossRef]
- White, S.D.M.; Rees, M.J. Core condensation in heavy halos: A two-stage theory for galaxy formation and clustering. Mon. Not. R. Astron. Soc. 1978, 183, 341–358. [Google Scholar] [CrossRef]
- Peebles, P.J.E. Large-scale background temperature and mass fluctuations due to scale-invariant primeval perturbations. Astrophys. J. 1982, 263, L1–L5. [Google Scholar] [CrossRef]
- Blumenthal, G.R.; Faber, S.M.; Primack, J.R.; Rees, M.J. Formation of galaxies and large-scale structure with cold dark matter. Nature 1984, 311, 517–525. [Google Scholar] [CrossRef]
- Davis, M.; Efstathiou, G.; Frenk, C.S.; White, S.D.M. The evolution of large-scale structure in a universe dominated by cold dark matter. Astrophys. J. 1985, 292, 371–394. [Google Scholar] [CrossRef]
- Rubin, V.C.; Ford, W.K.J.; Thonnard, N. Extended rotation curves of high-luminosity spiral galaxies. IV. Systematic dynamical properties, Sa -> Sc. Astrophys. J. Lett. 1978, 225, L107–L111. [Google Scholar] [CrossRef]
- Faber, S.M.; Gallagher, J.S. Masses and mass-to-light ratios of galaxies. Annu. Rev. Astron. Astrophys. 1979, 17, 135–187. [Google Scholar] [CrossRef]
- Rubin, V.C.; Ford, W.K.J.; Thonnard, N. Rotational properties of 21 SC galaxies with a large range of luminosities and radii, from NGC 4605 (R = 4kpc) to UGC 2885 (R = 122kpc). Astrophys. J. 1980, 238, 471–487. [Google Scholar] [CrossRef]
- Hu, W.; Dodelson, S. Cosmic Microwave Background Anisotropies. Annu. Rev. Astron. Astrophys. 2002, 40, 171–216. [Google Scholar] [CrossRef]
- Aghanim, N. et al. [Planck Collaboration] Planck 2018 results. I. Overview and the cosmological legacy of Planck. Astron. Astrophys. 2020, 641, A1. [Google Scholar] [CrossRef]
- Eisenstein, D.J.; Zehavi, I.; Hogg, D.W.; Scoccimarro, R.; Blanton, M.R.; Nichol, R.C.; Scranton, R.; Seo, H.J.; Tegmark, M.; Zheng, Z.; et al. Detection of the Baryon Acoustic Peak in the Large-Scale Correlation Function of SDSS Luminous Red Galaxies. Astrophys. J. 2005, 633, 560–574. [Google Scholar] [CrossRef]
- Riess, A.G.; Filippenko, A.V.; Challis, P.; Clocchiatti, A.; Diercks, A.; Garnavich, P.M.; Gilliland, R.L.; Hogan, C.J.; Jha, S.; Kirshner, R.P.; et al. Observational Evidence from Supernovae for an Accelerating Universe and a Cosmological Constant. Astron. J. 1998, 116, 1009–1038. [Google Scholar] [CrossRef]
- Perlmutter, S.; Aldering, G.; Goldhaber, G.; Knop, R.A.; Nugent, P.; Castro, P.G.; Deustua, S.; Fabbro, S.; Goobar, A.; Groom, D.E.; et al. Measurements of Ω and Λ from 42 High-Redshift Supernovae. Astrophys. J. 1999, 517, 565–586. [Google Scholar] [CrossRef]
- Davis, R., Jr.; Harmer, D.S.; Hoffman, K.C. Search for neutrinos from the sun. Phys. Rev. Lett. 1968, 20, 1205–1209. [Google Scholar] [CrossRef]
- Fukuda, Y. et al. [Super-Kamiokande Collaboration] Evidence for oscillation of atmospheric neutrinos. Phys. Rev. Lett. 1998, 81, 1562–1567. [Google Scholar] [CrossRef]
- Ahmad, Q.R. et al. [SNO Collaboration] Direct evidence for neutrino flavor transformation from neutral current interactions in the Sudbury Neutrino Observatory. Phys. Rev. Lett. 2002, 89, 011301. [Google Scholar] [CrossRef] [PubMed]
- Sakharov, A.D. Violation of CP Invariance, C asymmetry, and baryon asymmetry of the universe. Pisma Zh. Eksp. Teor. Fiz. 1967, 5, 32–35. [Google Scholar] [CrossRef]
- Aghanim, N. et al. [Planck Collaboration] Planck 2018 results. VI. Cosmological parameters. Astron. Astrophys. 2020, 641, A6, Erratum in Astron. Astrophys. 2021, 652, C4. [Google Scholar] [CrossRef]
- Kajantie, K.; Laine, M.; Rummukainen, K.; Shaposhnikov, M.E. Is there a hot electroweak phase transition at mH≳mW? Phys. Rev. Lett. 1996, 77, 2887–2890. [Google Scholar] [CrossRef] [PubMed]
- Csikor, F.; Fodor, Z.; Heitger, J. Endpoint of the hot electroweak phase transition. Phys. Rev. Lett. 1999, 82, 21–24. [Google Scholar] [CrossRef]
- Aad, G. et al. [ATLAS Collaboration] Observation of a new particle in the search for the Standard Model Higgs boson with the ATLAS detector at the LHC. Phys. Lett. B 2012, 716, 1–29. [Google Scholar] [CrossRef]
- Chatrchyan, S. et al. [CMS Collaboration] Observation of a New Boson at a Mass of 125 GeV with the CMS Experiment at the LHC. Phys. Lett. B 2012, 716, 30–61. [Google Scholar] [CrossRef]
- Serebrov, A.P.; Aleksandrov, E.B.; Dovator, N.A.; Dmitriev, S.P.; Fomin, A.K.; Geltenbort, P.; Kharitonov, A.G.; Krasnoschekova, I.A.; Lasakov, M.S.; Murashkin, A.N.; et al. Search for neutron-mirror neutron oscillations in a laboratory experiment with ultracold neutrons. Nucl. Instrum. Meth. A 2009, 611, 137–140. [Google Scholar] [CrossRef]
- Wietfeldt, F.E.; Greene, G.L. Colloquium: The neutron lifetime. Rev. Mod. Phys. 2011, 83, 1173–1192. [Google Scholar] [CrossRef]
- Fornal, B.; Grinstein, B. Dark Matter Interpretation of the Neutron Decay Anomaly. Phys. Rev. Lett. 2018, 120, 191801. [Google Scholar] [CrossRef]
- Berezhiani, Z. Neutron lifetime puzzle and neutron–mirror neutron oscillation. Eur. Phys. J. C 2019, 79, 484. [Google Scholar] [CrossRef]
- Barducci, D.; Fabbrichesi, M.; Gabrielli, E. Neutral Hadrons Disappearing into the Darkness. Phys. Rev. D 2018, 98, 035049. [Google Scholar] [CrossRef]
- Rajendran, S.; Ramani, H. Composite solution to the neutron lifetime anomaly. Phys. Rev. D 2021, 103, 035014. [Google Scholar] [CrossRef]
- Nelson, A.; Reddy, S.; Zhou, D. Dark halos around neutron stars and gravitational waves. J. Cosmol. Astropart. Phys. 2019, 7, 012. [Google Scholar] [CrossRef]
- Baym, G.; Beck, D.H.; Geltenbort, P.; Shelton, J. Testing Dark Decays of Baryons in Neutron Stars. Phys. Rev. Lett. 2018, 121, 061801. [Google Scholar] [CrossRef] [PubMed]
- Motta, T.F.; Guichon, P.A.M.; Thomas, A.W. Implications of Neutron Star Properties for the Existence of Light Dark Matter. J. Phys. G 2018, 45, 05LT01. [Google Scholar] [CrossRef]
- Berezhiani, Z.; Biondi, R.; Mannarelli, M.; Tonelli, F. Neutron-mirror neutron mixing and neutron stars. Eur. Phys. J. C 2021, 81, 1036. [Google Scholar] [CrossRef]
- Berryman, J.M.; Gardner, S.; Zakeri, M. Neutron Stars with Baryon Number Violation, Probing Dark Sectors. Symmetry 2022, 14, 518. [Google Scholar] [CrossRef]
- Berryman, J.M.; Gardner, S.; Zakeri, M. How Macroscopic Limits on Neutron Star Baryon Loss Yield Microscopic Limits on Non-Standard-Model Baryon Decay. arXiv 2023, arXiv:2305.13377. [Google Scholar] [CrossRef]
- Coutinho, A.M.; Crivellin, A.; Manzari, C.A. Global Fit to Modified Neutrino Couplings and the Cabibbo-Angle Anomaly. Phys. Rev. Lett. 2020, 125, 071802. [Google Scholar] [CrossRef]
- Crivellin, A.; Mellado, B. Anomalies in Particle Physics. arXiv 2023, arXiv:2309.03870. [Google Scholar]
- Moulson, M. Experimental determination of Vus from kaon decays. PoS 2017, CKM2016, 033. [Google Scholar] [CrossRef][Green Version]
- Seng, C.Y.; Galviz, D.; Marciano, W.J.; Meißner, U.G. Update on |Vus| and |Vus/Vud| from semileptonic kaon and pion decays. Phys. Rev. D 2022, 105, 013005. [Google Scholar] [CrossRef]
- Cirigliano, V.; Crivellin, A.; Hoferichter, M.; Moulson, M. Scrutinizing CKM unitarity with a new measurement of the Kμ3/Kμ2 branching fraction. Phys. Lett. B 2023, 838, 137748. [Google Scholar] [CrossRef]
- Czarnecki, A.; Marciano, W.J.; Sirlin, A. Precision measurements and CKM unitarity. Phys. Rev. D 2004, 70, 093006. [Google Scholar] [CrossRef]
- Marciano, W.J.; Sirlin, A. Improved calculation of electroweak radiative corrections and the value of Vud. Phys. Rev. Lett. 2006, 96, 032002. [Google Scholar] [CrossRef] [PubMed]
- Seng, C.Y.; Gorchtein, M.; Ramsey-Musolf, M.J. Dispersive evaluation of the inner radiative correction in neutron and nuclear β decay. Phys. Rev. D 2019, 100, 013001. [Google Scholar] [CrossRef]
- Towner, I.S.; Hardy, J.C. Calculated corrections to superallowed Fermi beta decay: New evaluation of the nuclear structure dependent terms. Phys. Rev. C 2002, 66, 035501. [Google Scholar] [CrossRef]
- Gorchtein, M.; Seng, C.Y. The Standard Model Theory of Neutron Beta Decay. Universe 2023, 9, 422. [Google Scholar] [CrossRef]
- Czarnecki, A.; Marciano, W.J.; Sirlin, A. Radiative Corrections to Neutron and Nuclear Beta Decays Revisited. Phys. Rev. D 2019, 100, 073008. [Google Scholar] [CrossRef]
- Gorchtein, M.; Seng, C.Y. Dispersion relation analysis of the radiative corrections to gA in the neutron β-decay. J. High Energy Phys. 2021, 10, 053. [Google Scholar] [CrossRef]
- Jackson, J.D.; Treiman, S.B.; Wyld, H.W. Possible tests of time reversal invariance in Beta decay. Phys. Rev. 1957, 106, 517–521. [Google Scholar] [CrossRef]
- Abele, H. The neutron. Its properties and basic interactions. Prog. Part. Nucl. Phys. 2008, 60, 1–81. [Google Scholar] [CrossRef]
- Mathews, G.J.; Kajino, T.; Shima, T. Big Bang nucleosynthesis with a new neutron lifetime. Phys. Rev. D 2005, 71, 021302. [Google Scholar] [CrossRef]
- Yeh, T.H.; Olive, K.A.; Fields, B.D. The Neutron Mean Life and Big Bang Nucleosynthesis. Universe 2023, 9, 183. [Google Scholar] [CrossRef]
- Fornal, B. Neutron Dark Decay. Universe 2023, 9, 449. [Google Scholar] [CrossRef]
- A New Era of Discovery: The 2023 Long Range Plan for Nuclear Science. Available online: https://nuclearsciencefuture.org/#:~:text=The%20plan%2C%20released%20in%20October,leadership%20and%20training%20the%20workforce (accessed on 15 November 2023).
- Workman, R.L. et al. [Particle Data Group] Review of Particle Physics. PTEP 2022, 2022, 083C01. [Google Scholar] [CrossRef]
- Dubbers, D.; Schmidt, M.G. The Neutron and Its Role in Cosmology and Particle Physics. Rev. Mod. Phys. 2011, 83, 1111–1171. [Google Scholar] [CrossRef]
- Cirigliano, V.; Gardner, S.; Holstein, B. Beta Decays and Non-Standard Interactions in the LHC Era. Prog. Part. Nucl. Phys. 2013, 71, 93–118. [Google Scholar] [CrossRef]
- Dubbers, D.; Märkisch, B. Precise Measurements of the Decay of Free Neutrons. Ann. Rev. Nucl. Part. Sci. 2021, 71, 139–163. [Google Scholar] [CrossRef]
- Czarnecki, A.; Marciano, W.J.; Sirlin, A. Neutron Lifetime and Axial Coupling Connection. Phys. Rev. Lett. 2018, 120, 202002. [Google Scholar] [CrossRef] [PubMed]
- Dubbers, D.; Saul, H.; Märkisch, B.; Soldner, T.; Abele, H. Exotic decay channels are not the cause of the neutron lifetime anomaly. Phys. Lett. B 2019, 791, 6–10. [Google Scholar] [CrossRef]
- Märkisch, B.; Mest, H.; Saul, H.; Wang, X.; Abele, H.; Dubbers, D.; Klopf, M.; Petoukhov, A.; Roick, C.; Soldner, T.; et al. Measurement of the Weak Axial-Vector Coupling Constant in the Decay of Free Neutrons Using a Pulsed Cold Neutron Beam. Phys. Rev. Lett. 2019, 122, 242501. [Google Scholar] [CrossRef] [PubMed]
- Mund, D.; Maerkisch, B.; Deissenroth, M.; Krempel, J.; Schumann, M.; Abele, H.; Petoukhov, A.; Soldner, T. Determination of the Weak Axial Vector Coupling from a Measurement of the Beta-Asymmetry Parameter A in Neutron Beta Decay. Phys. Rev. Lett. 2013, 110, 172502. [Google Scholar] [CrossRef] [PubMed]
- Brown, M.A.P. et al. [UCNA Collaboration] New result for the neutron β-asymmetry parameter A0 from UCNA. Phys. Rev. C 2018, 97, 035505. [Google Scholar] [CrossRef]
- Beck, M.; Ayala Guardia, F.; Baeßler, S.; Borg, M.; Glück, F.; Heil, W.; Kahlenberg, J.; Klopf, M.; Konrad, G.; Maisonobe, R.; et al. Improved determination of the β-ν¯e angular correlation coefficient a in free neutron decay with the aSPECT spectrometer. Phys. Rev. C 2020, 101, 055506. [Google Scholar] [CrossRef]
- Beck, M.; Heil, W.; Schmidt, C.; Baeßler, S.; Glück, F.; Konrad, G.; Schmidt, U. Reanalysis of the angular correlation measurement aSPECT with new constrains on Fierz interference. arXiv 2023, arXiv:2308.16170. [Google Scholar]
- Wietfeldt, F.E.; Byron, W.A.; Collett, B.; Dewey, M.S.; Gentile, T.R.; Hassan, M.T.; Jones, G.L.; Komives, A.; Nico, J.S.; Stephenson, E.J. Recoil-Order and Radiative Corrections to the aCORN Experiment. arXiv 2023, arXiv:2306.15042. [Google Scholar]
- Aoki, Y. et al. [Flavour Lattice Averaging Group (FLAG)] FLAG Review 2021. Eur. Phys. J. C 2022, 82, 869. [Google Scholar] [CrossRef]
- Chang, C.C.; Nicholson, A.N.; Rinaldi, E.; Berkowitz, E.; Garron, N.; Brantley, A.D.; Monge-Camacho, H.; Monahan, C.J.; Bouchard, C.; Clark, M.A.; et al. A per-cent-level determination of the nucleon axial coupling from quantum chromodynamics. Nature 2018, 558, 91–94. [Google Scholar] [CrossRef]
- Walker-Loud, A.; Walker-Loud, A.; Berkowitz, E.; Gambhir, A.S.; Brantley, D.; Vranas, P.; Bouchard, C.; Clark, M.A.; Garron, N.; Chang, C.C.; et al. Lattice QCD Determination of gA. PoS 2020, CD2018, 020. [Google Scholar] [CrossRef]
- Clowe, D.; Bradac, M.; Gonzalez, A.H.; Markevitch, M.; Randall, S.W.; Jones, C.; Zaritsky, D. A direct empirical proof of the existence of dark matter. Astrophys. J. Lett. 2006, 648, L109–L113. [Google Scholar] [CrossRef]
- Battaglieri, M.; Belloni, A.; Chou, A.; Cushman, P.; Echenard, B.; Essig, R.; Estrada, J.; Feng, J.L.; Flaugher, B.; Fox, P.J.; et al. US Cosmic Visions: New Ideas in Dark Matter 2017: Community Report. In Proceedings of the U.S. Cosmic Visions: New Ideas in Dark Matter, College Park, MD, USA, 23–25 March 2017. [Google Scholar]
- Chou, A.S.; Soares-Santos, M.; Tait, T.M.P.; Adhikari, R.X.; Anchordoqui, L.A.; Annis, J.; Chang, C.L.; Cooley, J.; Drlica-Wagner, A.; Fang, K.; et al. Snowmass Cosmic Frontier Report. arXiv 2022, arXiv:2211.09978. [Google Scholar]
- Gardner, S.; McDermott, S.D.; Yanny, B. The Milky Way, coming into focus: Precision astrometry probes its evolution and its dark matter. Prog. Part. Nucl. Phys. 2021, 121, 103904. [Google Scholar] [CrossRef]
- Nussinov, S. Technocosmology—Could a technibaryon excess provide a “natural” missing mass candidate? Phys. Lett. B 1985, 165, 55–58. [Google Scholar] [CrossRef]
- Barr, S.M.; Chivukula, R.S.; Farhi, E. Electroweak Fermion Number Violation and the Production of Stable Particles in the Early Universe. Phys. Lett. B 1990, 241, 387–391. [Google Scholar] [CrossRef]
- Davoudiasl, H.; Mohapatra, R.N. On Relating the Genesis of Cosmic Baryons and Dark Matter. New J. Phys. 2012, 14, 095011. [Google Scholar] [CrossRef]
- Elor, G.; Escudero, M.; Nelson, A. Baryogenesis and Dark Matter from B Mesons. Phys. Rev. D 2019, 99, 035031. [Google Scholar] [CrossRef]
- Alonso-Álvarez, G.; Elor, G.; Escudero, M.; Fornal, B.; Grinstein, B.; Martin Camalich, J. Strange physics of dark baryons. Phys. Rev. D 2022, 105, 115005. [Google Scholar] [CrossRef]
- Morrissey, D.E.; Ramsey-Musolf, M.J. Electroweak baryogenesis. New J. Phys. 2012, 14, 125003. [Google Scholar] [CrossRef]
- Elahi, F.; Mohammadi Najafabadi, M. Neutron Decay to a Non-Abelian Dark Sector. Phys. Rev. D 2020, 102, 035011. [Google Scholar] [CrossRef]
- Elor, G.; McGehee, R. Making the Universe at 20 MeV. Phys. Rev. D 2021, 103, 035005. [Google Scholar] [CrossRef]
- Alonso-Álvarez, G.; Elor, G.; Escudero, M. Collider signals of baryogenesis and dark matter from B mesons: A roadmap to discovery. Phys. Rev. D 2021, 104, 035028. [Google Scholar] [CrossRef]
- Elahi, F.; Elor, G.; McGehee, R. Charged B mesogenesis. Phys. Rev. D 2022, 105, 055024. [Google Scholar] [CrossRef]
- Barrow, J.L.; Golubeva, E.S.; Paryev, E.; Richard, J.M. Progress and simulations for intranuclear neutron-antineutron transformations in 1840Ar. Phys. Rev. D 2020, 101, 036008. [Google Scholar] [CrossRef]
- Elor, G.; Guerrera, A.W.M. Branching fractions of B meson decays in Mesogenesis. J. High Energy Phys. 2023, 2, 100. [Google Scholar] [CrossRef]
- Lees, J.P. et al. [The BaBaR Collaboration] Search for B mesogenesis at BaBar. Phys. Rev. D 2023, 107, 092001. [Google Scholar] [CrossRef]
- Fajfer, S.; Susič, D. Colored scalar mediated nucleon decays to an invisible fermion. Phys. Rev. D 2021, 103, 055012. [Google Scholar] [CrossRef]
- McKeen, D.; Nelson, A.E.; Reddy, S.; Zhou, D. Neutron Stars Exclude Light Dark Baryons. Phys. Rev. Lett. 2018, 121, 061802. [Google Scholar] [CrossRef]
- Cline, J.M.; Cornell, J.M. Dark decay of the neutron. J. High Energy Phys. 2018, 7, 81. [Google Scholar] [CrossRef]
- Husain, W.; Sengupta, D.; Thomas, A.W. Constraining Dark Boson Decay Using Neutron Stars. Universe 2023, 9, 307. [Google Scholar] [CrossRef]
- Strumia, A. Dark Matter interpretation of the neutron decay anomaly. J. High Energy Phys. 2022, 2, 67. [Google Scholar] [CrossRef]
- Ciardi, B.; Ferrara, A. The First cosmic structures and their effects. Space Sci. Rev. 2005, 116, 625–705. [Google Scholar] [CrossRef]
- Maiolino, R.; Uebler, H.; Perna, M.; Scholtz, J.; D’Eugenio, F.; Witten, C.; Laporte, N.; Witstok, J.; Carniani, S.; Tacchella, S.; et al. JWST-JADES. Possible Population III signatures at z=10.6 in the halo of GN-z11. arXiv 2023, arXiv:2306.00953. [Google Scholar]
- Spolyar, D.; Freese, K.; Gondolo, P. Dark matter and the first stars: A new phase of stellar evolution. Phys. Rev. Lett. 2008, 100, 051101. [Google Scholar] [CrossRef]
- Iocco, F.; Bressan, A.; Ripamonti, E.; Schneider, R.; Ferrara, A.; Marigo, P. Dark matter annihilation effects on the first stars. Mon. Not. Roy. Astron. Soc. 2008, 390, 1655–1669. [Google Scholar] [CrossRef]
- Freese, K.; Ilie, C.; Spolyar, D.; Valluri, M.; Bodenheimer, P. Supermassive Dark Stars: Detectable in JWST. Astrophys. J. 2010, 716, 1397–1407. [Google Scholar] [CrossRef]
- Zackrisson, E.; Scott, P.; Rydberg, C.E.; Iocco, F.; Edvardsson, B.; Östlin, G.; Sivertsson, S.; Zitrin, A.; Broadhurst, T.; Gondolo, P. Finding High-redshift Dark Stars with the James Webb Space Telescope. Astrophys. J. 2010, 717, 257–267. [Google Scholar] [CrossRef]
- Robertson, B.E.; Tacchella, S.; Johnson, B.D.; Hainline, K.; Whitler, L.; Eisenstein, D.J.; Endsley, R.; Rieke, M.; Stark, D.P.; Alberts, S.; et al. Identification and properties of intense star-forming galaxies at redshifts z > 10. Nat. Astron. 2023, 7, 611–621. [Google Scholar] [CrossRef]
- Curtis-Lake, E.; Carniani, S.; Cameron, A.; Charlot, S.; Jakobsen, P.; Maiolino, R.; Bunker, A.; Witstok, J.; Smit, R.; Chevallard, J.; et al. Spectroscopic confirmation of four metal-poor galaxies at z = 10.3-13.2. arXiv 2023, arXiv:2212.04568. [Google Scholar] [CrossRef]
- Ilie, C.; Paulin, J.; Freese, K. Supermassive Dark Star candidates seen by JWST. Proc. Nat. Acad. Sci. USA 2023, 120, e2305762120. [Google Scholar] [CrossRef] [PubMed]
- Ilie, C.; Zhang, S. Multiscatter capture of superheavy dark matter by Pop. III stars. J. Cosmol. Astropart. Phys. 2019, 12, 51, Erratum in J. Cosmol. Astropart. Phys. 2020, 10, E01. [Google Scholar] [CrossRef]
- Aprile, E.; Aalbers, J.; Agostini, F.; Alfonsi, M.; Althueser, L.; Amaro, F.D.; Anthony, M.; Arneodo, F.; Baudis, L.; Bauermeister, B.; et al. Dark Matter Search Results from a One Ton-Year Exposure of XENON1T. Phys. Rev. Lett. 2018, 121, 111302. [Google Scholar] [CrossRef]
- Croon, D.; McDermott, S.D.; Sakstein, J. Missing in axion: Where are XENON1T’s big black holes? Phys. Dark Univ. 2021, 32, 100801. [Google Scholar] [CrossRef]
- Haxton, W.C.; Hamish Robertson, R.G.; Serenelli, A.M. Solar Neutrinos: Status and Prospects. Ann. Rev. Astron. Astrophys. 2013, 51, 21–61. [Google Scholar] [CrossRef]
- Redondo, J.; Raffelt, G. Solar constraints on hidden photons re-visited. J. Cosmol. Astropart. Phys. 2013, 08, 34. [Google Scholar] [CrossRef]
- Raffelt, G. Stars as Laboratories for Fundamental Physics: The Astrophysics of Neutrinos, Axions, and Other Weakly Interacting Particles; Theoretical Astrophysics, University of Chicago Press: Chicago, IL, USA, 1996. [Google Scholar]
- Capozzi, F.; Raffelt, G. Axion and neutrino bounds improved with new calibrations of the tip of the red-giant branch using geometric distance determinations. Phys. Rev. D 2020, 102, 083007. [Google Scholar] [CrossRef]
- An, H.; Pospelov, M.; Pradler, J. New stellar constraints on dark photons. Phys. Lett. B 2013, 725, 190–195. [Google Scholar] [CrossRef]
- Davidson, S.; Campbell, B.; Bailey, D. Limits on particles of small electric charge. Phys. Rev. D 1991, 43, 2314–2321. [Google Scholar] [CrossRef] [PubMed]
- Lopes, J.; Lopes, I. Dark matter capture and annihilation in stars: Impact on the red giant branch tip. Astron. Astrophys. 2021, 651, A101. [Google Scholar] [CrossRef]
- Martins, A.; Lopes, I.; Casanellas, J. Asteroseismic constraints on asymmetric dark matter: Light particles with an effective spin-dependent coupling. Phys. Rev. D 2017, 95, 023507. [Google Scholar] [CrossRef]
- Rato, J.a.; Lopes, J.; Lopes, I. On asymmetric dark matter constraints from the asteroseismology of a subgiant star. Mon. Not. Roy. Astron. Soc. 2021, 507, 3434–3443. [Google Scholar] [CrossRef]
- Ayala, A. Looking into dark matter with asteroseismology. Front. Astron. Space Sci. 2022, 9, 958502. [Google Scholar] [CrossRef]
- Zurek, K.M. Asymmetric Dark Matter: Theories, signatures, and constraints. Phys. Rep. 2014, 537, 91–121. [Google Scholar] [CrossRef]
- Spergel, D.N.; Press, W.H. Effect of hypothetical, weakly interacting, massive particles on energy transport in the solar interior. Astrophys. J. 1985, 294, 663–673. [Google Scholar] [CrossRef]
- Iocco, F.; Taoso, M.; Leclercq, F.; Meynet, G. Main sequence stars with asymmetric dark matter. Phys. Rev. Lett. 2012, 108, 061301. [Google Scholar] [CrossRef] [PubMed]
- Banks, H.; Ansari, S.; Vincent, A.C.; Scott, P. Simulation of energy transport by dark matter scattering in stars. J. Cosmol. Astropart. Phys. 2022, 4, 2. [Google Scholar] [CrossRef]
- Raen, T.J.; Martínez-Rodríguez, H.; Hurst, T.J.; Zentner, A.R.; Badenes, C.; Tao, R. The Effects of Asymmetric Dark Matter on Stellar Evolution I: Spin-Dependent Scattering. Mon. Not. R. Astron. Soc. 2021, 503, 5611–5623. [Google Scholar] [CrossRef]
- Hirata, K.; Kajita, T.; Koshiba, M.; Nakahata, M.; Oyama, Y.; Sato, N.; Suzuki, A.; Takita, M.; Totsuka, Y.; Kifune, T.; et al. Observation of a neutrino burst from the supernova SN1987A. Phys. Rev. Lett. 1987, 58, 1490–1493. [Google Scholar] [CrossRef] [PubMed]
- Bionta, R.M.; Blewitt, G.; Bratton, C.B.; Casper, D.; Ciocio, A.; Claus, R.; Cortez, B.; Crouch, M.; Dye, S.T.; Errede, S.; et al. Observation of a neutrino burst in coincidence with supernova 1987A in the Large Magellanic Cloud. Phys. Rev. Lett. 1987, 58, 1494–1496. [Google Scholar] [CrossRef] [PubMed]
- Raffelt, G.G. Astrophysical methods to constrain axions and other novel particle phenomena. Phys. Rep. 1990, 198, 1–113. [Google Scholar] [CrossRef]
- Raffelt, G.; Seckel, D. Bounds on exotic-particle interactions from SN1987A. Phys. Rev. Lett. 1988, 60, 1793–1796. [Google Scholar] [CrossRef] [PubMed]
- Dent, J.B.; Ferrer, F.; Krauss, L.M. Constraints on Light Hidden Sector Gauge Bosons from Supernova Cooling. arXiv 2012, arXiv:1201.2683. [Google Scholar]
- Croon, D.; Elor, G.; Leane, R.K.; McDermott, S.D. Supernova Muons: New Constraints on Z’ Bosons, Axions and ALPs. J. High Energy Phys. 2021, 1, 107. [Google Scholar] [CrossRef]
- Manzari, C.A.; Martin Camalich, J.; Spinner, J.; Ziegler, R. Supernova Limits on Muonic Dark Forces. arXiv 2023, arXiv:2307.03143. [Google Scholar] [CrossRef]
- He, X.G.; Joshi, G.C.; Lew, H.; Volkas, R.R. New-Z′ phenomenology. Phys. Rev. D 1991, 43, R22–R24. [Google Scholar] [CrossRef]
- Ma, E.; Roy, D.P.; Roy, S. Gauged L(mu)–L(tau) with large muon anomalous magnetic moment and the bimaximal mixing of neutrinos. Phys. Lett. B 2002, 525, 101–106. [Google Scholar] [CrossRef]
- Aoyama, T.; Asmussen, N.; Benayoun, M.; Bijnens, J.; Blum, T.; Bruno, M.; Caprini, I.; Carloni Calame, C.M.; Cè, M.; Colangelo, G.; et al. The anomalous magnetic moment of the muon in the Standard Model. Phys. Rept. 2020, 887, 1–166. [Google Scholar] [CrossRef]
- Abi, B. et al. [Muon g − 2 Collaboration] Measurement of the Positive Muon Anomalous Magnetic Moment to 0.46 ppm. Phys. Rev. Lett. 2021, 126, 141801. [Google Scholar] [CrossRef] [PubMed]
- Escudero, M.; Hooper, D.; Krnjaic, G.; Pierre, M. Cosmology with A Very Light Lμ − Lτ Gauge Boson. J. High Energy Phys. 2019, 03, 071. [Google Scholar] [CrossRef]
- Di Valentino, E.; Mena, O.; Pan, S.; Visinelli, L.; Yang, W.; Melchiorri, A.; Mota, D.F.; Riess, A.G.; Silk, J. In the realm of the Hubble tension—a review of solutions. Class. Quant. Grav. 2021, 38, 153001. [Google Scholar] [CrossRef]
- Camalich, J.M.; Terol-Calvo, J.; Tolos, L.; Ziegler, R. Supernova Constraints on Dark Flavored Sectors. Phys. Rev. D 2021, 103, L121301. [Google Scholar] [CrossRef]
- Baryakhtar, M.; Caputo, R.; Croon, D.; Perez, K.; Berti, E.; Bramante, J.; Buschmann, M.; Brito, R.; Chen, T.Y.; Cole, P.S.; et al. Dark Matter In Extreme Astrophysical Environments. arXiv 2022, arXiv:2203.07984. [Google Scholar]
- Bramante, J.; Raj, N. Dark matter in compact stars. arXiv 2023, arXiv:2307.14435. [Google Scholar] [CrossRef]
- Berryman, J.M.; Gardner, S. Neutron star structure with a new force between quarks. Phys. Rev. C 2021, 104, 045802. [Google Scholar] [CrossRef]
- Oppenheimer, J.R.; Volkoff, G.M. On massive neutron cores. Phys. Rev. 1939, 55, 374–381. [Google Scholar] [CrossRef]
- Tolman, R.C. Static solutions of Einstein’s field equations for spheres of fluid. Phys. Rev. 1939, 55, 364–373. [Google Scholar] [CrossRef]
- Romani, R.W.; Kandel, D.; Filippenko, A.V.; Brink, T.G.; Zheng, W. PSR J0952-0607: The Fastest and Heaviest Known Galactic Neutron Star. Astrophys. J. Lett. 2022, 934, L17. [Google Scholar] [CrossRef]
- Fonseca, E.; Cromartie, H.T.; Pennucci, T.T.; Ray, P.S.; Kirichenko, A.Y.; Ransom, S.M.; Demorest, P.B.; Stairs, I.H.; Arzoumanian, Z.; Guillemot, L.; et al. Refined Mass and Geometric Measurements of the High-mass PSR J0740+6620. Astrophys. J. Lett. 2021, 915, L12. [Google Scholar] [CrossRef]
- Antoniadis, J.; Freire, P.C.C.; Wex, N.; Tauris, T.M.; Lynch, R.S.; Van Kerkwijk, M.H.; Kramer, M.; Bassa, C.; Dhillon, V.S.; Driebe, T.; et al. A Massive Pulsar in a Compact Relativistic Binary. Science 2013, 340, 6131. [Google Scholar] [CrossRef]
- Grinstein, B.; Kouvaris, C.; Nielsen, N.G. Neutron Star Stability in Light of the Neutron Decay Anomaly. Phys. Rev. Lett. 2019, 123, 091601. [Google Scholar] [CrossRef]
- Zhou, D. Neutron Star Constraints on Neutron Dark Decays. Universe 2023, 9, 484. [Google Scholar] [CrossRef]
- Balkin, R.; Serra, J.; Springmann, K.; Weiler, A. The QCD axion at finite density. J. High Energy Phys. 2020, 07, 221. [Google Scholar] [CrossRef]
- Balkin, R.; Serra, J.; Springmann, K.; Stelzl, S.; Weiler, A. Heavy neutron stars from light scalars. arXiv 2023, arXiv:2307.14418. [Google Scholar]
- Goldman, I.; Nussinov, S. Weakly interacting massive particles and neutron stars. Phys. Rev. D 1989, 40, 3221–3230. [Google Scholar] [CrossRef] [PubMed]
- Chandrasekhar, S. The Maximum Mass of Ideal White Dwarfs. Astrophys. J. 1931, 74, 81. [Google Scholar] [CrossRef]
- De Lavallaz, A.; Fairbairn, M. Neutron Stars as Dark Matter Probes. Phys. Rev. D 2010, 81, 123521. [Google Scholar] [CrossRef]
- McDermott, S.D.; Yu, H.B.; Zurek, K.M. Constraints on Scalar Asymmetric Dark Matter from Black Hole Formation in Neutron Stars. Phys. Rev. D 2012, 85, 023519. [Google Scholar] [CrossRef]
- Bhattacharya, S.; Dasgupta, B.; Laha, R.; Ray, A. Can LIGO Detect Nonannihilating Dark Matter? Phys. Rev. Lett. 2023, 131, 091401. [Google Scholar] [CrossRef]
- Bramante, J.; Fukushima, K.; Kumar, J. Constraints on bosonic dark matter from observation of old neutron stars. Phys. Rev. D 2013, 87, 055012. [Google Scholar] [CrossRef]
- Bell, N.F.; Melatos, A.; Petraki, K. Realistic neutron star constraints on bosonic asymmetric dark matter. Phys. Rev. D 2013, 87, 123507. [Google Scholar] [CrossRef]
- Gould, A.; Draine, B.T.; Romani, R.W.; Nussinov, S. Neuton stars: Graveyard of charged dark matter. Phys. Lett. B 1990, 238, 337–343. [Google Scholar] [CrossRef]
- Yakovlev, D.G.; Gnedin, O.Y.; Gusakov, M.E.; Kaminker, A.D.; Levenfish, K.P.; Potekhin, A.Y. Neutron star cooling. Nucl. Phys. A 2005, 752, 590–599. [Google Scholar] [CrossRef]
- Rangelov, B.; Pavlov, G.G.; Kargaltsev, O.; Reisenegger, A.; Guillot, S.; Reyes, C.; van Kerkwijk, M.H. Hubble Space Telescope Detection of the Millisecond Pulsar J2124-3358 and its Far-ultraviolet Bow Shock Nebula. Astrophys. J. 2017, 835, 264. [Google Scholar] [CrossRef]
- Durant, M.; Kargaltsev, O.; Pavlov, G.G.; Kowalski, P.M.; Posselt, B.; van Kerkwijk, M.H.; Kaplan, D.L. The Spectrum of the Recycled PSR J0437-4715 and Its White Dwarf Companion. Astrophys. J. 2012, 746, 6. [Google Scholar] [CrossRef]
- Gonzalez, D.; Reisenegger, A. Internal heating of old neutron stars: Contrasting different mechanisms. Astron. Astrophys. 2010, 522, A16. [Google Scholar] [CrossRef]
- Köpp, F.; Horvath, J.E.; Hadjimichef, D.; Vasconcellos, C.A.Z.; Hess, P.O. Internal heating mechanisms in neutron stars. Int. J. Mod. Phys. D 2023, 32, 2350046. [Google Scholar] [CrossRef]
- Yanagi, K.; Nagata, N.; Hamaguchi, K. Cooling Theory Faced with Old Warm Neutron Stars: Role of Non-Equilibrium Processes with Proton and Neutron Gaps. Mon. Not. R. Astron. Soc. 2020, 492, 5508–5523. [Google Scholar] [CrossRef]
- Reisenegger, A. Deviations from chemical equilibrium due to spindown as an internal heat source in neutron stars. Astrophys. J. 1995, 442, 749. [Google Scholar] [CrossRef][Green Version]
- Baryakhtar, M.; Bramante, J.; Li, S.W.; Linden, T.; Raj, N. Dark Kinetic Heating of Neutron Stars and An Infrared Window On WIMPs, SIMPs, and Pure Higgsinos. Phys. Rev. Lett. 2017, 119, 131801. [Google Scholar] [CrossRef]
- Bell, N.F.; Busoni, G.; Robles, S. Heating up Neutron Stars with Inelastic Dark Matter. J. Cosmol. Astropart. Phys. 2018, 9, 18. [Google Scholar] [CrossRef]
- Bell, N.F.; Busoni, G.; Robles, S.; Virgato, M. Improved Treatment of Dark Matter Capture in Neutron Stars. J. Cosmol. Astropart. Phys. 2020, 9, 28. [Google Scholar] [CrossRef]
- Kouvaris, C. WIMP Annihilation and Cooling of Neutron Stars. Phys. Rev. D 2008, 77, 023006. [Google Scholar] [CrossRef]
- Zhitnitsky, A. Neutron Stars as the Dark Matter detectors. arXiv 2023, arXiv:2312.12500. [Google Scholar]
- Balkin, R.; Serra, J.; Springmann, K.; Stelzl, S.; Weiler, A. Runaway relaxion from finite density. J. High Energy Phys. 2022, 6, 23. [Google Scholar] [CrossRef]
- Balkin, R.; Serra, J.; Springmann, K.; Stelzl, S.; Weiler, A. Density induced vacuum instability. SciPost Phys. 2023, 14, 071. [Google Scholar] [CrossRef]
- Acevedo, J.F.; Bramante, J.; Leane, R.K.; Raj, N. Warming Nuclear Pasta with Dark Matter: Kinetic and Annihilation Heating of Neutron Star Crusts. J. Cosmol. Astropart. Phys. 2020, 3, 38. [Google Scholar] [CrossRef]
- Alvarez, G.; Joglekar, A.; Phoroutan-Mehr, M.; Yu, H.B. Heating neutron stars with inelastic dark matter and relativistic targets. Phys. Rev. D 2023, 107, 103024. [Google Scholar] [CrossRef]
- Cigan, P.; Matsuura, M.; Gomez, H.L.; Indebetouw, R.; Abellán, F.; Gabler, M.; Richards, A.; Alp, D.; Davis, T.A.; Janka, H.-T.; et al. High angular resolution ALMA images of dust and molecules in the SN 1987A ejecta. Astrophys. J. 2019, 886, 51. [Google Scholar] [CrossRef]
- Page, D.; Beznogov, M.V.; Garibay, I.; Lattimer, J.M.; Prakash, M.; Janka, H.T. NS 1987A in SN 1987A. Astrophys. J. 2020, 898, 125. [Google Scholar] [CrossRef]
- Hong, D.K.; Shin, C.S.; Yun, S. Cooling of young neutron stars and dark gauge bosons. Phys. Rev. D 2021, 103, 123031. [Google Scholar] [CrossRef]
- Shin, C.S.; Yun, S. Dark gauge boson production from neutron stars via nucleon-nucleon bremsstrahlung. J. High Energy Phys. 2022, 02, 133. [Google Scholar] [CrossRef]
- Freire, P.C.C.; Wex, N.; Esposito-Farèse, G.; Verbiest, J.P.W.; Bailes, M.; Jacoby, B.A.; Kramer, M.; Stairs, I.H.; Antoniadis, J.; Janssen, G.H.; et al. The relativistic pulsar-white dwarf binary PSR J1738+0333—II. The most stringent test of scalar-tensor gravity. Mon. Not. R. Astron. Soc. 2012, 423, 3328–3343. [Google Scholar] [CrossRef]
- Stairs, I.H. Testing general relativity with pulsar timing. Living Rev. Relativ. 2003, 6, 5. [Google Scholar] [CrossRef]
- Hulse, R.A.; Taylor, J.H. Discovery of a pulsar in a binary system. Astrophys. J. Lett. 1975, 195, L51–L53. [Google Scholar] [CrossRef]
- Weisberg, J.M.; Huang, Y. Relativistic Measurements from Timing the Binary Pulsar PSR B1913+16. Astrophys. J. 2016, 829, 55. [Google Scholar] [CrossRef]
- Lyne, A.G.; Burgay, M.; Kramer, M.; Possenti, A.; Manchester, R.N.; Camilo, F.; Mclaughlin, M.A.; Lorimer, D.R.; D’Amico, N.; Joshi, B.C.; et al. A double-pulsar system: A rare laboratory for relativistic gravity and plasma physics. Science 2004, 303, 1153–1157. [Google Scholar] [CrossRef]
- Kramer, M.; Stairs, I.H.; Manchester, R.N.; Wex, N.; Deller, A.T.; Coles, W.A.; Ali, M.; Burgay, M.; Camilo, F.; Cognard, I.; et al. Strong-Field Gravity Tests with the Double Pulsar. Phys. Rev. X 2021, 11, 041050. [Google Scholar] [CrossRef]
- Peters, P.C. Gravitational Radiation and the Motion of Two Point Masses. Phys. Rev. 1964, 136, B1224–B1232. [Google Scholar] [CrossRef]
- Peters, P.C.; Mathews, J. Gravitational Radiation from Point Masses in a Keplerian Orbit. Phys. Rev. 1963, 131, 435–440. [Google Scholar] [CrossRef]
- Huang, S.S. Modes of Mass Ejection by Binary Stars and the Effect on Their Orbital Periods. Astrophys. J. 1963, 138, 471. [Google Scholar] [CrossRef]
- Jeans, J.H. Cosmogonic Problems associated with a Secular Decrease of Mass. Mon. Not. R. Astron. Soc. 1924, 85, 2–11. [Google Scholar] [CrossRef]
- Jeans, J.H. The Effect of Varying Mass on a Binary System. Mon. Not. R. Astron. Soc. 1925, 85, 912–914. [Google Scholar] [CrossRef]
- Goldman, I.; Nussinov, S. Limit on Continuous Neutrino Emission from Neutron Stars. J. High Energy Phys. 2010, 8, 91. [Google Scholar] [CrossRef]
- Blas, D.; Nacir, D.L.; Sibiryakov, S. Ultralight Dark Matter Resonates with Binary Pulsars. Phys. Rev. Lett. 2017, 118, 261102. [Google Scholar] [CrossRef]
- Armaleo, J.M.; López Nacir, D.; Urban, F.R. Binary pulsars as probes for spin-2 ultralight dark matter. J. Cosmol. Astropart. Phys. 2020, 1, 53. [Google Scholar] [CrossRef]
- Kumar Poddar, T.; Mohanty, S.; Jana, S. Vector gauge boson radiation from compact binary systems in a gauged Lμ − Lτ scenario. Phys. Rev. D 2019, 100, 123023. [Google Scholar] [CrossRef]
- Dror, J.A.; Laha, R.; Opferkuch, T. Probing muonic forces with neutron star binaries. Phys. Rev. D 2020, 102, 023005. [Google Scholar] [CrossRef]
- Goldman, I.; Mohapatra, R.N.; Nussinov, S. Bounds on neutron-mirror neutron mixing from pulsar timing. Phys. Rev. D 2019, 100, 123021. [Google Scholar] [CrossRef]
- Agazie, G.; Anumarlapudi, A.; Archibald, A.M.; Arzoumanian, Z.; Baker, P.T.; Bécsy, B.; Blecha, L.; Brazier, A.; Brook, P.R.; Burke-Spolaor, S.; et al. The NANOGrav 15 yr Data Set: Evidence for a Gravitational-wave Background. Astrophys. J. Lett. 2023, 951, L8. [Google Scholar] [CrossRef]
- Antoniadis, J.; Arumugam, P.; Arumugam, S.; Babak, S.; Bagchi, M.; Bak Nielsen, A.-S.; Bassa, C.G.; Bathula, A.; Berthereau, A.; Bonetti, M.; et al. The second data release from the European Pulsar Timing Array III. Search for gravitational wave signals. Astron. Astrophys. 2023, 678, A50. [Google Scholar] [CrossRef]
- Reardon, D.J.; Zic, A.; Shannon, R.M.; Hobbs, G.B.; Bailes, M.; Marco, V.D.; Kapur, A.; Rogers, A.F.; Thrane, E.; Askew, J.; et al. Search for an Isotropic Gravitational-wave Background with the Parkes Pulsar Timing Array. Astrophys. J. Lett. 2023, 951, L6. [Google Scholar] [CrossRef]
- Xu, H.; Chen, S.; Guo, Y.; Jiang, J.; Wang, B.; Xu, J.; Xue, Z.; Caballero, R.N.; Yuan, J.; Xu, Y.; et al. Searching for the Nano-Hertz Stochastic Gravitational Wave Background with the Chinese Pulsar Timing Array Data Release I. Res. Astron. Astrophys. 2023, 23, 075024. [Google Scholar] [CrossRef]
- Khmelnitsky, A.; Rubakov, V. Pulsar timing signal from ultralight scalar dark matter. J. Cosmol. Astropart. Phys. 2014, 2, 19. [Google Scholar] [CrossRef]
- Porayko, N.K.; Zhu, X.; Levin, Y.; Hui, L.; Hobbs, G.; Grudskaya, A.; Postnov, K.; Bailes, M.; Bhat, N.D.R.; Coles, W.; et al. Parkes Pulsar Timing Array constraints on ultralight scalar-field dark matter. Phys. Rev. D 2018, 98, 102002. [Google Scholar] [CrossRef]
- Smarra, C.; Goncharov, B.; Barausse, E.; Antoniadis, J.; Babak, S.; Nielsen, A.S.B.; Bassa, C.G.; Berthereau, A.; Bonetti, M.; Bortolas, E.; et al. Second Data Release from the European Pulsar Timing Array: Challenging the Ultralight Dark Matter Paradigm. Phys. Rev. Lett. 2023, 131, 171001. [Google Scholar] [CrossRef]
- Dror, J.A.; Ramani, H.; Trickle, T.; Zurek, K.M. Pulsar Timing Probes of Primordial Black Holes and Subhalos. Phys. Rev. D 2019, 100, 023003. [Google Scholar] [CrossRef]
- Zakeri, M. Pulsar Timing Anomalies: A Window into Baryon Number Violation. arXiv 2023, arXiv:2311.05586. [Google Scholar]
- Glendenning, N.K. Compact Stars: Nuclear Physics, Particle Physics, and General Relativity; Springer: New York, NY, USA, 1997. [Google Scholar]
- Hartle, J.B. Slowly rotating relativistic stars. 1. Equations of structure. Astrophys. J. 1967, 150, 1005–1029. [Google Scholar] [CrossRef]
- Dexheimer, V. The Relativistic SU(3) Chiral Mean Field (CMF) Equation of State. (DS(CMF)-1). 2021. Available online: https://compose.obspm.fr/eos/180 (accessed on 22 April 2023).
- Takhistov, V. et al. [The Super-Kamiokande Collaboration] Search for Nucleon and Dinucleon Decays with an Invisible Particle and a Charged Lepton in the Final State at the Super-Kamiokande Experiment. Phys. Rev. Lett. 2015, 115, 121803. [Google Scholar] [CrossRef] [PubMed]
- Araki, T. et al. [KamLAND Collaboration] Search for the invisible decay of neutrons with KamLAND. Phys. Rev. Lett. 2006, 96, 101802. [Google Scholar] [CrossRef] [PubMed]
- Walecka, J.D. A Theory of highly condensed matter. Ann. Phys. 1974, 83, 491–529. [Google Scholar] [CrossRef]
- Serot, B.D.; Walecka, J.D. The Relativistic Nuclear Many Body Problem. Adv. Nucl. Phys. 1986, 16, 1–327. [Google Scholar]
- Serot, B.D.; Walecka, J.D. Recent progress in quantum hadrodynamics. Int. J. Mod. Phys. E 1997, 6, 515–631. [Google Scholar] [CrossRef]
- Dexheimer, V.; Schramm, S. Proto-Neutron and Neutron Stars in a Chiral SU(3) Model. Astrophys. J. 2008, 683, 943–948. [Google Scholar] [CrossRef]
- Alford, M.G.; Brodie, L.; Haber, A.; Tews, I. Relativistic mean-field theories for neutron-star physics based on chiral effective field theory. Phys. Rev. C 2022, 106, 055804. [Google Scholar] [CrossRef]
- Ambartsumyan, V.A.; Saakyan, G.S. The Degenerate Superdense Gas of Elementary Particles. Sov. Astron. 1960, 4, 187. [Google Scholar]
- Rawley, L.A.; Taylor, J.H.; Davis, M.M. Period derivative and orbital eccentricity of binary pulsar 1953+29. Nature 1986, 319, 383–384. [Google Scholar] [CrossRef]
- Arzoumanian, Z.; Brazier, A.; Burke-Spolaor, S.; Chamberlin, S.; Chatterjee, S.; Christy, B.; Cordes, J.M.; Cornish, N.J.; Crawford, F.; Cromartie, H.T.; et al. The NANOGrav 11-year Data Set: High-precision timing of 45 Millisecond Pulsars. Astrophys. J. Suppl. 2018, 235, 37. [Google Scholar] [CrossRef]
- Gulminelli, F.; Raduta, A.R. Unified treatment of subsaturation stellar matter at zero and finite temperature. Phys. Rev. C 2015, 92, 055803. [Google Scholar] [CrossRef]
- Typel, S. et al. [CompOSE Core Team] CompOSE Reference Manual. Eur. Phys. J. A 2022, 58, 221. [Google Scholar] [CrossRef]
- Dexheimer, V. The Relativistic SU(3) Chiral Mean Field (CMF) Equation of State. (DS(CMF)-8). 2021. Available online: https://compose.obspm.fr/eos/187 (accessed on 20 April 2023).
- Ablikim, M. et al. [BESIII Collaboration] Search for invisible decays of the Λ baryon. Phys. Rev. D 2022, 105, L071101. [Google Scholar] [CrossRef]
- Garching Core-Collapse Supernova Archive. Available online: https://wwwmpa.mpa-garching.mpg.de/ccsnarchive (accessed on 6 November 2023).
- McKeen, D.; Pospelov, M. How long does the hydrogen atom live? arXiv 2020, arXiv:2003.02270. [Google Scholar] [CrossRef]
- Berlin, A.; Blinov, N.; Krnjaic, G.; Schuster, P.; Toro, N. Dark Matter, Millicharges, Axion and Scalar Particles, Gauge Bosons, and Other New Physics with LDMX. Phys. Rev. D 2019, 99, 075001. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).