Constraining the Initial Mass Function via Stellar Transients
Abstract
1. Introduction
2. Methods
2.1. UV Luminosity Density
2.2. Local Stellar Mass Density
2.3. Core-Collapse Supernova Rate
2.4. Type Ia Supernova Rate
2.5. Long Gamma-Ray Burst Rate
2.6. MCMC
3. Results
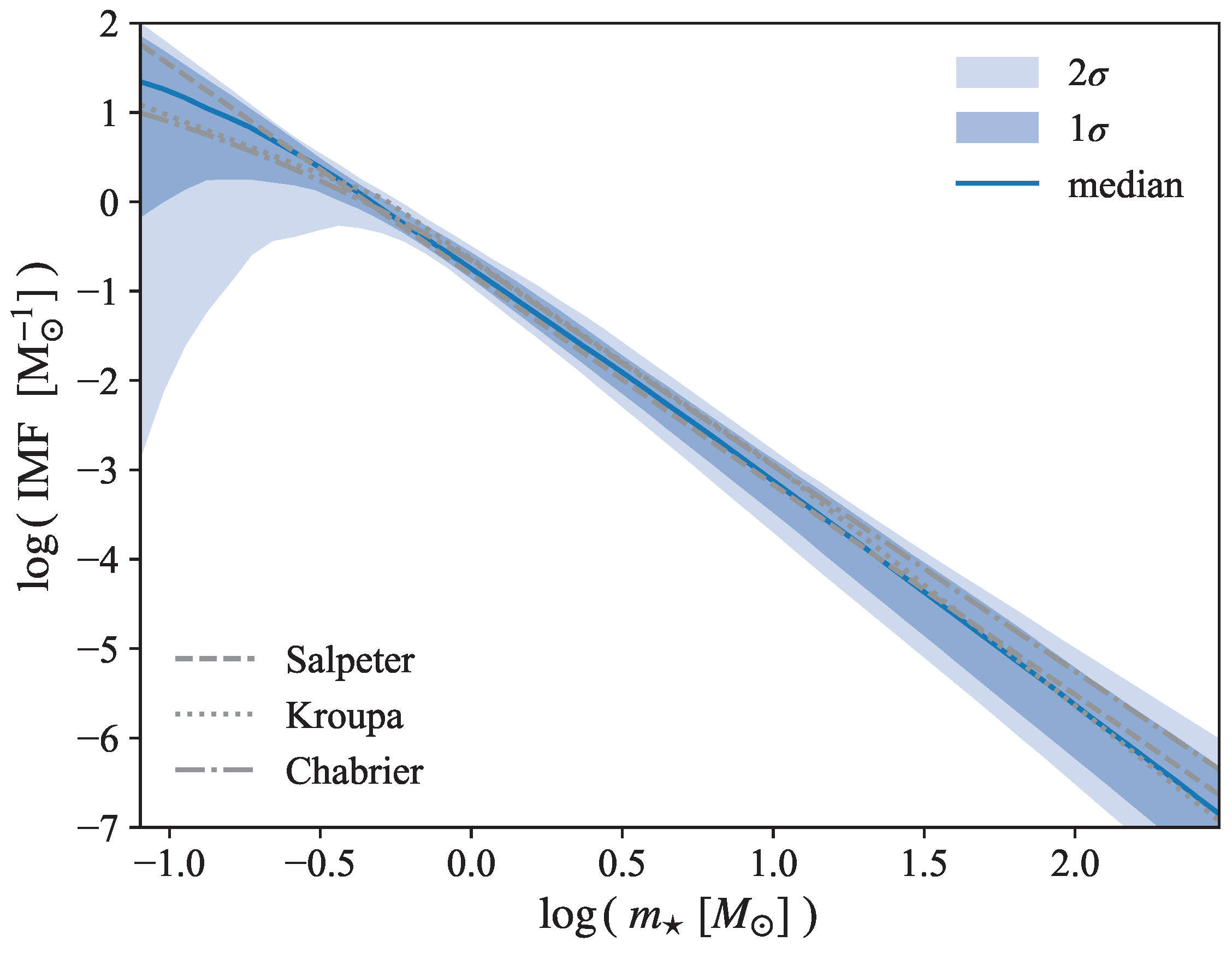
3.1. Stellar Initial Mass Function, Type Ia Supernovae, and Core-Collapse Supernovae
3.2. Long Gamma-Ray Bursts and Cosmic Metallicity Evolution
3.3. IMF Evolution with Redshift
4. Discussion
4.1. Initial Mass Function
4.2. Type Ia and Core-Collapse Supernova Progenitors
4.3. Long Gamma-Ray Bursts and Cosmic Metallicity Evolution
4.4. Variation on the Cosmic Z Evolution Prescription
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Update on LGRB Rate Determination by Ghirlanda and Salvaterra 2022
Appendix B. Additional MCMC Results
| - | ||
| - | ||
| - | ||
| - | ||
| - | ||
| - |
Appendix C. Additional Results for IMF Variation
| - | ||
| - | ||
| - | ||
| - | ||
| - | ||
| - | ||
| - | ||
| — | - | |
| - | ||
| - | ||
| - | ||
| - |
Appendix D. Parameter Estimates for the FMR Variation




References
- Hennebelle, P.; Grudíc, M. The Physical Origin of the Stellar Initial Mass Function. arXiv 2024, arXiv:2404.07301. [Google Scholar] [CrossRef]
- Salpeter, E.E. The Luminosity Function and Stellar Evolution. Astrophys. J. 1955, 121, 161. [Google Scholar] [CrossRef]
- Scalo, J.M. The Stellar Initial Mass Function. FCPh 1986, 11, 1–278. [Google Scholar]
- Kroupa, P.; Tout, C.A.; Gilmore, G. The Distribution of Low-Mass Stars in the Galactic Disc. Mon. Not. R. Astron. Soc. 1993, 262, 545–587. [Google Scholar] [CrossRef]
- Scalo, J.; Vázquez-Semadeni, E.; Chappell, D.; Passot, T. On the Probability Density Function of Galactic Gas. I. Numerical Simulations and the Significance of the Polytropic Index. Astrophys. J. 1998, 504, 835–853. [Google Scholar] [CrossRef]
- Kroupa, P. On the variation of the initial mass function. Mon. Not. R. Astron. Soc. 2001, 322, 231–246. [Google Scholar] [CrossRef]
- Chabrier, G. Galactic Stellar and Substellar Initial Mass Function. PASP 2003, 115, 763–795. [Google Scholar] [CrossRef]
- Kroupa, P.; Weidner, C.; Pflamm-Altenburg, J.; Thies, I.; Dabringhausen, J.; Marks, M.; Maschberger, T. The Stellar and Sub-Stellar Initial Mass Function of Simple and Composite Populations. In Planets, Stars and Stellar Systems. Volume 5: Galactic Structure and Stellar Populations; Oswalt, T.D., Gilmore, G., Eds.; Springer: Dordrecht, The Netherlands, 2013; Volume 5, p. 115. [Google Scholar] [CrossRef]
- Kroupa, P.; Jerabkova, T. Star-Formation Rates of Galaxies; Cambridge University Press: Cambridge, UK, 2021. [Google Scholar] [CrossRef]
- Weisz, D.R.; Fouesneau, M.; Hogg, D.W.; Rix, H.W.; Dolphin, A.E.; Dalcanton, J.J.; Foreman-Mackey, D.T.; Lang, D.; Clifton Johnson, L.; Beerman, L.C.; et al. The Panchromatic Hubble Andromeda Treasury. IV. A Probabilistic Approach to Inferring the High-Mass Stellar Initial Mass Function and other Power-Law Functions. Astrophys. J. 2012, 762, 123. [Google Scholar] [CrossRef]
- Wainer, T.M.; Williams, B.F.; Johnson, L.C.; Weisz, D.R.; Dalcanton, J.J.; Seth, A.C.; Dolphin, A.; Durbin, M.J.; Bell, E.F.; Chen, Z.; et al. The Panchromatic Hubble Andromeda Treasury: Triangulum Extended Region (PHATTER). VI. The High-Mass Stellar Initial Mass Function of M33. arXiv 2024, arXiv:2406.12129. [Google Scholar] [CrossRef]
- Strolger, L.G.; Dahlen, T.; Rodney, S.A.; Graur, O.; Riess, A.G.; McCully, C.; Ravindranath, S.; Mobasher, B.; Shahady, A.K. The Rate of Core Collapse Supernovae to Redshift 2.5 from the Candels and Clash Supernova Surveys. Astrophys. J. 2015, 813, 93. [Google Scholar] [CrossRef]
- Stanway, E.R.; Eldridge, J.J. Initial mass function variations cannot explain the ionizing spectrum of low metallicity starbursts. Astron. Astrophys. 2019, 621, A105. [Google Scholar] [CrossRef]
- Ziegler, J.J.; Edwards, T.D.P.; Suliga, A.M.; Tamborra, I.; Horiuchi, S.; Ando, S.; Freese, K. Non-universal stellar initial mass functions: Large uncertainties in star formation rates at z = 2–4 and other astrophysical probes. Mon. Not. R. Astron. Soc. 2022, 517, 2471–2484. [Google Scholar] [CrossRef]
- Li, J.; Liu, C.; Zhang, Z.Y.; Tian, H.; Fu, X.; Li, J.; Yan, Z.Q. Stellar initial mass function varies with metallicity and time. Nature 2023, 613, 460–462. [Google Scholar] [CrossRef]
- Martín-Navarro, I.; de Lorenzo-Cáceres, A.; Gadotti, D.A.; Méndez-Abreu, J.; Falcón-Barroso, J.; Sánchez-Blázquez, P.; Coelho, P.; Neumann, J.; van de Ven, G.; Pérez, I. The universal variability of the stellar initial mass function probed by the TIMER survey. arXiv 2023, arXiv:2312.13355. [Google Scholar] [CrossRef]
- Maksymowicz-Maciata, M.; Spiniello, C.; Martín-Navarro, I.; Ferré-Mateu, A.; Bevacqua, D.; Cappellari, M.; D’Ago, G.; Tortora, C.; Arnaboldi, M.; Hartke, J.; et al. INSPIRE: INvestigating Stellar Population In RElics VI—The low-mass end slope of the stellar Initial Mass Function and chemical composition. arXiv 2024, arXiv:2401.15769. [Google Scholar] [CrossRef]
- Bouwens, R.J.; Oesch, P.A.; Stefanon, M.; Illingworth, G.; Labbe, I.; Reddy, N.; Atek, H.; Montes, M.; Naidu, R.; Nanayakkara, T.; et al. New Determinations of the UV Luminosity Functions from z=9 to 2 Show a Remarkable Consistency with Halo Growth and a Constant Star Formation Efficiency. Astron. J. 2021, 162, 47. [Google Scholar] [CrossRef]
- Bouwens, R.; Illingworth, G.; Oesch, P.; Stefanon, M.; Naidu, R.; van Leeuwen, I.; Magee, D. UV luminosity density results at z>8 from the first JWST/NIRCam fields: Limitations of early data sets and the need for spectroscopy. Mon. Not. R. Astron. Soc. 2023, 523, 1009–1035. [Google Scholar] [CrossRef]
- Donnan, C.T.; McLeod, D.J.; Dunlop, J.S.; McLure, R.J.; Carnall, A.C.; Begley, R.; Cullen, F.; Hamadouche, M.L.; Bowler, R.A.A.; Magee, D.; et al. The evolution of the galaxy UV luminosity function at redshifts z = 8 – 15 from deep JWST and ground-based near-infrared imaging. Mon. Not. R. Astron. Soc. 2022, 518, 6011–6040. [Google Scholar] [CrossRef]
- Harikane, Y.; Ouchi, M.; Oguri, M.; Ono, Y.; Nakajima, K.; Isobe, Y.; Umeda, H.; Mawatari, K.; Zhang, Y. A Comprehensive Study of Galaxies at z = 9–16 Found in the Early JWST Data: Ultraviolet Luminosity Functions and Cosmic Star Formation History at the Pre-reionization Epoch. Astrophys. J. Suppl. Ser. 2023, 265, 5. [Google Scholar] [CrossRef]
- Kennicutt, R.C.; Evans, N.J. Star Formation in the Milky Way and Nearby Galaxies. Annu. Rev. Astron. Astrophys. 2012, 50, 531–608. [Google Scholar] [CrossRef]
- Foreman-Mackey, D.; Hogg, D.W.; Lang, D.; Goodman, J. emcee: The MCMC Hammer. Publ. Astron. Soc. Pac. 2013, 125, 306–312. [Google Scholar] [CrossRef]
- Madau, P.; Dickinson, M. Cosmic Star-Formation History. Annu. Rev. Astron. Astrophys. 2014, 52, 415–486. [Google Scholar] [CrossRef]
- Cai, Z.Y.; Lapi, A.; Bressan, A.; De Zotti, G.; Negrello, M.; Danese, L. A Physical Model for the Evolving Ultraviolet Luminosity Function of High Redshift Galaxies and their Contribution to the Cosmic Reionization. Astrophys. J. 2014, 785, 65. [Google Scholar] [CrossRef]
- Robertson, B.E.; Ellis, R.S.; Furlanetto, S.R.; Dunlop, J.S. Cosmic Reionization and Early Star-Forming Galaxies: A Joint Analysis of New Constraints from Planck and the Hubble Space Telescope. Astrophys. J. 2015, 802, L19. [Google Scholar] [CrossRef]
- Finkelstein, S.L.; D’Aloisio, A.; Paardekooper, J.P.; Ryan, R., Jr.; Behroozi, P.; Finlator, K.; Livermore, R.; Sanderbeck, P.R.U.; Vecchia, C.D.; Khochfar, S. Conditions for Reionizing the Universe with a Low Galaxy Ionizing Photon Escape Fraction. Astrophys. J. 2019, 879, 36. [Google Scholar] [CrossRef]
- Madau, P.; Della Valle, M.; Panagia, N. On the evolution of the cosmic supernova rates. Mon. Not. R. Astron. Soc. 1998, 297, L17–L22. [Google Scholar] [CrossRef]
- Maoz, D.; Mannucci, F.; Nelemans, G. Observational Clues to the Progenitors of Type Ia Supernovae. Annu. Rev. Astron. Astrophys. 2014, 52, 107–170. [Google Scholar] [CrossRef]
- Bethe, H.A.; Wilson, J.R. Revival of a stalled supernova shock by neutrino heating. Astrophys. J. 1985, 295, 14–23. [Google Scholar] [CrossRef]
- Burrows, A.; Hayes, J.; Fryxell, B.A. On the Nature of Core-Collapse Supernova Explosions. Astrophys. J. 1995, 450, 830. [Google Scholar] [CrossRef]
- Janka, H.T.; Müller, E. Neutrino heating, convection, and the mechanism of Type-II supernova explosions. Astron. Astrophys. 1996, 306, 167. [Google Scholar]
- Burrows, A.; Radice, D.; Vartanyan, D. Three-dimensional supernova explosion simulations of 9-, 10-, 11-, 12-, and 13-Msun stars. Mon. Not. R. Astron. Soc. 2019, 485, 3153–3168. [Google Scholar] [CrossRef]
- Aguilera-Dena, D.R.; Müller, B.; Antoniadis, J.; Langer, N.; Dessart, L.; Vigna-Gómez, A.; Yoon, S.C. Stripped-envelope stars in different metallicity environments: II. Type I supernovae and compact remnants. Astron. Astrophys. 2023, 671, A134. [Google Scholar] [CrossRef]
- Heger, A.; Woosley, S.E. The Nucleosynthetic Signature of Population III. Astrophys. J. 2002, 567, 532. [Google Scholar] [CrossRef]
- Heger, A.; Fryer, C.L.; Woosley, S.E.; Langer, N.; Hartmann, D.H. How Massive Single Stars End Their Life. Astrophys. J. 2003, 591, 288. [Google Scholar] [CrossRef]
- Smartt, S.J. Observational Constraints on the Progenitors of Core-Collapse Supernovae: The Case for Missing High-Mass Stars. Publ. Astron. Soc. Aust. 2015, 32, e016. [Google Scholar] [CrossRef]
- Timmes, F.X.; Woosley, S.E.; Weaver, T.A. The Neutron Star and Black Hole Initial Mass Function. Astrophys. J. 1996, 457, 834. [Google Scholar] [CrossRef]
- Zhang, W.; Woosley, S.E.; Heger, A. Fallback and Black Hole Production in Massive Stars. Astrophys. J. 2008, 679, 639. [Google Scholar] [CrossRef]
- Coughlin, E.R.; Quataert, E.; Fernández, R.; Kasen, D. A physical model of mass ejection in failed supernovae. Mon. Not. R. Astron. Soc. 2018, 477, 1225–1238. [Google Scholar] [CrossRef]
- Antoni, A.; Quataert, E. Numerical simulations of the random angular momentum in convection—II. Delayed explosions of red supergiants following ’failed’ supernovae. Mon. Not. R. Astron. Soc. 2023, 525, 1229–1245. [Google Scholar] [CrossRef]
- Mészáros, P. Gamma-ray bursts. Rep. Prog. Phys. 2006, 69, 2259–2321. [Google Scholar] [CrossRef]
- Iwamoto, K.; Mazzali, P.; Nomoto, K.; Umeda, H.; Nakamura, T.; Patat, F.; Danziger, I.; Young, T.; Suzuki, T.; Shigeyama, T.; et al. A hypernova model for the supernova associated with the γ-ray burst of 25 April 1998. Nature 1998, 395, 672–674. [Google Scholar] [CrossRef]
- Nomoto, K.; Maeda, K.; Tominaga, N.; Ohkubo, T.; Umeda, H.; Deng, J.; Mazzali, P. Hypernovae: Their Properties and Gamma-Ray Burst Connection. Prog. Theor. Phys. Suppl. 2004, 155, 299–302. [Google Scholar] [CrossRef]
- Woosley, S.; Bloom, J. The Supernova Gamma-Ray Burst Connection. Annu. Rev. Astron. Astrophys. 2006, 44, 507–556. [Google Scholar] [CrossRef]
- Mazzali, P.A.; Deng, J.; Nomoto, K.; Sauer, D.N.; Pian, E.; Tominaga, N.; Tanaka, M.; Maeda, K.; Filippenko, A.V. A neutron-star-driven X-ray flash associated with supernova SN 2006aj. Nature 2006, 442, 1018–1020. [Google Scholar] [CrossRef] [PubMed]
- Mazzali, P.A.; Valenti, S.; Della Valle, M.; Chincarini, G.; Sauer, D.N.; Benetti, S.; Pian, E.; Piran, T.; D’Elia, V.; Elias-Rosa, N.; et al. The Metamorphosis of Supernova SN 2008D/XRF 080109: A Link Between Supernovae and GRBs/Hypernovae. Science 2008, 321, 1185. [Google Scholar] [CrossRef]
- Valenti, S.; Benetti, S.; Cappellaro, E.; Patat, F.; Mazzali, P.; Turatto, M.; Hurley, K.; Maeda, K.; Gal-Yam, A.; Foley, R.; et al. The broad-lined Type Ic supernova 2003jd. Mon. Not. R. Astron. Soc. 2008, 383, 1485–1500. [Google Scholar] [CrossRef]
- Hjorth, J.; Bloom, J.S. The Gamma-Ray Burst—Supernova Connection. arXiv 2011, arXiv:1104.2274. [Google Scholar] [CrossRef]
- Caffau, E.; Ludwig, H.G.; Steffen, M.; Freytag, B.; Bonifacio, P. Solar Chemical Abundances Determined with a CO 5BOLD 3D Model Atmosphere. Sol. Phys. 2010, 268, 255–269. [Google Scholar] [CrossRef]
- Larson, R.B. Early star formation and the evolution of the stellar initial mass function in galaxies. Mon. Not. R. Astron. Soc. 1998, 301, 569–581. [Google Scholar] [CrossRef]
- Bressan, A.; Marigo, P.; Girardi, L.; Salasnich, B.; Cero, C.D.; Rubele, S.; Nanni, A. Stellar tracks and isochrones with the PAdova and TRieste Stellar Evolution Code. Mon. Not. R. Astron. Soc. 2012, 427, 127–145. [Google Scholar] [CrossRef]
- Chen, Y.; Girardi, L.; Bressan, A.; Marigo, P.; Barbieri, M.; Kong, X. Improving PARSEC models for very low mass stars. Mon. Not. R. Astron. Soc. 2014, 444, 2525–2543. [Google Scholar] [CrossRef]
- Chen, Y.; Bressan, A.; Girardi, L.; Marigo, P.; Kong, X.; Lanza, A. parsec evolutionary tracks of massive stars up to 350 at metallicities 0.0001 Z 0.04. Mon. Not. R. Astron. Soc. 2015, 452, 1068–1080. [Google Scholar] [CrossRef]
- Tang, J.; Bressan, A.; Rosenfield, P.; Slemer, A.; Marigo, P.; Girardi, L.; Bianchi, L. New PARSEC evolutionary tracks of massive stars at low metallicity: Testing canonical stellar evolution in nearby star-forming dwarf galaxies. Mon. Not. R. Astron. Soc. 2014, 445, 4287–4305. [Google Scholar] [CrossRef]
- Costa, G.; Girardi, L.; Bressan, A.; Marigo, P.; Rodrigues, T.S.; Chen, Y.; Lanza, A.; Goudfrooij, P. Mixing by overshooting and rotation in intermediate-mass stars. Mon. Not. R. Astron. Soc. 2019, 485, 4641–4657. [Google Scholar] [CrossRef]
- Costa, G.; Bressan, A.; Mapelli, M.; Marigo, P.; Iorio, G.; Spera, M. Formation of GW190521 from stellar evolution: The impact of the hydrogen-rich envelope, dredge-up, and 12C(a,g)16O rate on the pair-instability black hole mass gap. Mon. Not. R. Astron. Soc. 2020, 501, 4514–4533. [Google Scholar] [CrossRef]
- Nguyen, C.T.; Costa, G.; Girardi, L.; Volpato, G.; Bressan, A.; Chen, Y.; Marigo, P.; Fu, X.; Goudfrooij, P. PARSEC V2.0: Stellar tracks and isochrones of low- and intermediate-mass stars with rotation. Astron. Astrophys. 2022, 665, A126. [Google Scholar] [CrossRef]
- Goswami, S.; Slemer, A.; Marigo, P.; Bressan, A.; Silva, L.; Spera, M.; Boco, L.; Grisoni, V.; Pantoni, L.; Lapi, A. The effects of the initial mass function on Galactic chemical enrichment. Astron. Astrophys. 2021, 650, A203. [Google Scholar] [CrossRef]
- Goswami, S.; Silva, L.; Bressan, A.; Grisoni, V.; Costa, G.; Marigo, P.; Granato, G.L.; Lapi, A.; Spera, M. Impact of very massive stars on the chemical evolution of extremely metal-poor galaxies. Astron. Astrophys. 2022, 663, A1. [Google Scholar] [CrossRef]
- Gruppioni, C.; Pozzi, F.; Rodighiero, G.; Delvecchio, I.; Berta, S.; Pozzetti, L.; Zamorani, G.; Andreani, P.; Cimatti, A.; Ilbert, O.; et al. The Herschel PEP/HerMES luminosity function—I. Probing the evolution of PACS selected Galaxies to z=4. Mon. Not. R. Astron. Soc. 2013, 432, 23–52. [Google Scholar] [CrossRef]
- Rowan-Robinson, M.; Oliver, S.; Wang, L.; Farrah, D.; Clements, D.L.; Gruppioni, C.; Marchetti, L.; Rigopoulou, D.; Vaccari, M. The star formation rate density from z = 1 to 6. Mon. Not. R. Astron. Soc. 2016, 461, 1100–1111. [Google Scholar] [CrossRef]
- Dunlop, J.S.; McLure, R.J.; Biggs, A.D.; Geach, J.E.; Michałowski, M.J.; Ivison, R.J.; Rujopakarn, W.; van Kampen, E.; Kirkpatrick, A.; Pope, A.; et al. A deep ALMA image of the Hubble Ultra Deep Field. Mon. Not. R. Astron. Soc. 2016, 466, 861–883. [Google Scholar] [CrossRef]
- Novak, M.; Smolčić, V.; Delhaize, J.; Delvecchio, I.; Zamorani, G.; Baran, N.; Bondi, M.; Capak, P.; Carilli, C.L.; Ciliegi, P.; et al. The VLA-COSMOS 3 GHz Large Project: Cosmic star formation history since z=5. Astron. Astrophys. 2017, 602, A5. [Google Scholar] [CrossRef]
- Liu, D.; Daddi, E.; Dickinson, M.; Owen, F.; Pannella, M.; Sargent, M.; Béthermin, M.; Magdis, G.; Gao, Y.; Shu, X.; et al. “Super-deblended” Dust Emission in Galaxies. I. The GOODS-North Catalog and the Cosmic Star Formation Rate Density out to Redshift 6. Astrophys. J. 2018, 853, 172. [Google Scholar] [CrossRef]
- Oesch, P.A.; Bouwens, R.J.; Illingworth, G.D.; LabbE, I.; Stefanon, M. The Dearth of z=10 Galaxies in All HST Legacy Fields—The Rapid Evolution of the Galaxy Population in the First 500 Myr. Astrophys. J. 2018, 855, 105. [Google Scholar] [CrossRef]
- Bhatawdekar, R.; Conselice, C.J.; Margalef-Bentabol, B.; Duncan, K. Evolution of the galaxy stellar mass functions and UV luminosity functions at z= 6-9 in the Hubble Frontier Fields. Mon. Not. R. Astron. Soc. 2019, 486, 3805–3830. [Google Scholar] [CrossRef]
- Gruppioni, C.; BEthermin, M.; Loiacono, F.; Le Fèvre, O.; Capak, P.; Cassata, P.; Faisst, A.L.; Schaerer, D.; Silverman, J.; Yan, L.; et al. The ALPINE-ALMA [CII] survey: The nature, luminosity function, and star formation history of dusty galaxies up to z=6. Astron. Astrophys. 2020, 643, A8. [Google Scholar] [CrossRef]
- Spera, M.; Mapelli, M. Very massive stars, pair-instability supernovae and intermediate-mass black holes with the sevn code. Mon. Not. R. Astron. Soc. 2017, 470, 4739–4749. [Google Scholar] [CrossRef]
- Cummings, J.D.; Kalirai, J.S.; Tremblay, P.E.; Ramirez-Ruiz, E.; Choi, J. The White Dwarf Initial–Final Mass Relation for Progenitor Stars from 0.85 to 7.5 Msun. Astrophys. J. 2018, 866, 21. [Google Scholar] [CrossRef]
- Marigo, P.; Cummings, J.D.; Curtis, J.L.; Kalirai, J.; Chen, Y.; Tremblay, P.E.; Ramirez-Ruiz, E.; Bergeron, P.; Bladh, S.; Bressan, A.; et al. Carbon star formation as seen through the non-monotonic initial–final mass relation. Nat. Astron. 2020, 4, 1102–1110. [Google Scholar] [CrossRef]
- Marigo, P. The Initial-Final Mass Relation of White Dwarfs: A Tool to Calibrate the Third Dredge-up. arXiv 2022, arXiv:2204.06470. [Google Scholar]
- Weaver, J.R.; Davidzon, I.; Toft, S.; Ilbert, O.; McCracken, H.J.; Gould, K.M.L.; Jespersen, C.K.; Steinhardt, C.; Lagos, C.D.P.; Capak, P.L.; et al. COSMOS2020: The galaxy stellar mass function: The assembly and star formation cessation of galaxies at 0.2< z ≤ 7.5. Astron. Astrophys. 2023, 677, A184. [Google Scholar] [CrossRef]
- Cappellaro, E.; Evans, R.; Turatto, M. A new determination of supernova rates and a comparison with indicators for galactic star formation. Astron. Astrophys. 1999, 351, 459. [Google Scholar]
- Cappellaro, E.; Riello, M.; Altavilla, G.; Botticella, M.T.; Benetti, S.; Clocchiatti, A.; Danziger, J.I.; Mazzali, P.; Pastorello, A.; Patat, F.; et al. Death rate of massive stars at redshift∼0.3. Astron. Astrophys. 2005, 430, 83–93. [Google Scholar] [CrossRef]
- Botticella, M.T.; Riello, M.; Cappellaro, E.; Benetti, S.; Altavilla, G.; Pastorello, A.; Turatto, M.; Greggio, L.; Patat, F.; Valenti, S.; et al. Supernova rates from the Southern inTermediate Redshift ESO Supernova Search (STRESS). Astron. Astrophys. 2007, 479, 49–66. [Google Scholar] [CrossRef]
- Bazin, G.; Palanque-Delabrouille, N.; Rich, J.; Ruhlmann-Kleider, V.; Aubourg, E.; Le Guillou, L.; Astier, P.; Balland, C.; Basa, S.; Carlberg, R.G.; et al. The core-collapse rate from the Supernova Legacy Survey. Astron. Astrophys. 2009, 499, 653–660. [Google Scholar] [CrossRef]
- Graur, O.; Poznanski, D.; Maoz, D.; Yasuda, N.; Totani, T.; Fukugita, M.; Filippenko, A.V.; Foley, R.J.; Silverman, J.M.; Gal-Yam, A.; et al. Supernovae in the Subaru Deep Field: The rate and delay-time distribution of Type Ia supernovae out to redshift 2: Supernovae in the Subaru Deep Field. Mon. Not. R. Astron. Soc. 2011, 417, 916–940. [Google Scholar] [CrossRef]
- Li, W.; Chornock, R.; Leaman, J.; Filippenko, A.V.; Poznanski, D.; Wang, X.; Ganeshalingam, M.; Mannucci, F. Nearby supernova rates from the Lick Observatory Supernova Search—III. The rate-size relation, and the rates as a function of galaxy Hubble type and colour. Mon. Not. R. Astron. Soc. 2011, 412, 1473–1507. [Google Scholar] [CrossRef]
- Dahlen, T.; Strolger, L.G.; Riess, A.G.; Mattila, S.; Kankare, E.; Mobasher, B. The Extended Hubble Space Telescope Supernova Survey: The Rate of Core Collapse Supernovae to z = 1. Astrophys. J. 2012, 757, 70. [Google Scholar] [CrossRef]
- Mattila, S.; Dahlen, T.; Efstathiou, A.; Kankare, E.; Melinder, J.; Alonso-Herrero, A.; PErez-Torres, M.A.; Ryder, S.; Väisänen, P.; Östlin, G. Core-Collapse Supernovae Missed by Optical Surveys. Astrophys. J. 2012, 756, 111. [Google Scholar] [CrossRef]
- Melinder, J.; Dahlen, T.; Mencía Trinchant, L.; Östlin, G.; Mattila, S.; Sollerman, J.; Fransson, C.; Hayes, M.; Kankare, E.; Nasoudi-Shoar, S. The rate of supernovae at redshift 0.1–1.0: The Stockholm VIMOS Supernova Survey III. Astron. Astrophys. 2012, 545, A96. [Google Scholar] [CrossRef]
- Taylor, M.; Cinabro, D.; Dilday, B.; Galbany, L.; Gupta, R.R.; Kessler, R.; Marriner, J.; Nichol, R.C.; Richmond, M.; Schneider, D.P.; et al. The Core Collapse Supernova Rate from the SDSS-II Supernova Survey. Astrophys. J. 2014, 792, 135. [Google Scholar] [CrossRef]
- Cappellaro, E.; Botticella, M.T.; Pignata, G.; Grado, A.; Greggio, L.; Limatola, L.; Vaccari, M.; Baruffolo, A.; Benetti, S.; Bufano, F.; et al. Supernova rates from the SUDARE VST-OmegaCAM search: I. Rates per unit volume. Astron. Astrophys. 2015, 584, A62. [Google Scholar] [CrossRef]
- Graur, O.; Bianco, F.B.; Modjaz, M. A unified explanation for the supernova rate-galaxy mass dependence based on supernovae detected in Sloan galaxy spectra. Mon. Not. R. Astron. Soc. 2015, 450, 905–925. [Google Scholar] [CrossRef]
- Petrushevska, T.; Amanullah, R.; Goobar, A.; Fabbro, S.; Johansson, J.; Kjellsson, T.; Lidman, C.; Paech, K.; Richard, J.; Dahle, H.; et al. High-redshift supernova rates measured with the gravitational telescope A1689. Astron. Astrophys. 2016, 594, A54. [Google Scholar] [CrossRef]
- Frohmaier, C.; Angus, C.R.; Vincenzi, M.; Sullivan, M.; Smith, M.; Nugent, P.E.; Cenko, S.B.; Gal-Yam, A.; Kulkarni, S.R.; Law, N.M.; et al. From core collapse to superluminous: The rates of massive stellar explosions from the Palomar Transient Factory. Mon. Not. R. Astron. Soc. 2020, 500, 5142–5158. [Google Scholar] [CrossRef]
- Kobayashi, C.; Tsujimoto, T.; Nomoto, K. The History of the Cosmic Supernova Rate Derived from the Evolution of the Host Galaxies. Astrophys. J. 2000, 539, 26–38. [Google Scholar] [CrossRef]
- Strolger, L.; Riess, A.G.; Dahlen, T.; Livio, M.; Panagia, N.; Challis, P.; Tonry, J.L.; Filippenko, A.V.; Chornock, R.; Ferguson, H.; et al. The Hubble Higher z Supernova Search: Supernovae to z=1.6 and Constraints on Type Ia Progenitor Models. Astrophys. J. 2004, 613, 200–223. [Google Scholar] [CrossRef]
- Dahlen, T.; Strolger, L.; Riess, A.G.; Mobasher, B.; Chary, R.; Conselice, C.J.; Ferguson, H.C.; Fruchter, A.S.; Giavalisco, M.; Livio, M.; et al. High-Redshift Supernova Rates. Astrophys. J. 2004, 613, 189–199. [Google Scholar] [CrossRef]
- Valiante, R.; Matteucci, F.; Recchi, S.; Calura, F. Theoretical cosmic Type Ia supernova rates. New Astron. 2009, 14, 638–648. [Google Scholar] [CrossRef]
- Petrecca, V.; Botticella, M.T.; Cappellaro, E.; Greggio, L.; Sánchez, B.; Möller, A.; Sako, M.; Graham, M.; Paolillo, M.; Bianco, F.; et al. Recovered SN Ia rate from simulated LSST images. arXiv 2024, arXiv:2402.17612. [Google Scholar]
- Palicio, P.A.; Matteucci, F.; Valle, M.D.; Spitoni, E. Cosmic Type Ia SN rate and constraints on SN Ia progenitors. arXiv 2024, arXiv:2402.16635. [Google Scholar]
- Kobayashi, C.; Tsujimoto, T.; Nomoto, K.; Hachisu, I.; Kato, M. Metallicity effects on type Ia supernovae and cosmic supernova rates in cluster vs. field galaxies. Mem. Soc. Astron. Ital. 2000, 71, 461–470. [Google Scholar]
- Toonen, S.; Nelemans, G.; Portegies Zwart, S. Supernova Type Ia progenitors from merging double white dwarfs: Using a new population synthesis model. Astron. Astrophys. 2012, 546, A70. [Google Scholar] [CrossRef]
- Kistler, M.D.; Stanek, K.Z.; Kochanek, C.S.; Prieto, J.L.; Thompson, T.A. The Impact of Metallicity on the Rate of Type Ia Supernovae. Astrophys. J. 2013, 770, 88. [Google Scholar] [CrossRef]
- Claeys, J.S.W.; Pols, O.R.; Izzard, R.G.; Vink, J.; Verbunt, F.W.M. Theoretical uncertainties of the Type Ia supernova rate. Astron. Astrophys. 2014, 563, A83. [Google Scholar] [CrossRef]
- Maoz, D.; Mannucci, F. Type-Ia Supernova Rates and the Progenitor Problem: A Review. Publ. Astron. Soc. Aust. 2012, 29, 447–465. [Google Scholar] [CrossRef]
- Pain, R.; Hook, I.; Perlmutter, S.; Deustua, S.; Gabi, S.; Goldhaber, G.; Groom, D.; Kim, A.; Kim, M.; Lee, J.; et al. The Type Ia Supernova Rate at z sim 0.4. arXiv 1996, arXiv:astro-ph/9602125. [Google Scholar]
- Hardin, D.; Afonso, C.; Alard, C.; Albert, J.N.; Amadon, A.; Andersen, J.; Ansari, R.; Aubourg, E.; Bareyre, P.; Bauer, F.; et al. Type Ia supernova rate at z∼0.1. arXiv 2000, arXiv:astro-ph/0006424. [Google Scholar]
- Pain, R.; Fabbro, S.; Sullivan, M.; Ellis, R.S.; Aldering, G.; Astier, P.; Deustua, S.E.; Fruchter, A.S.; Goldhaber, G.; Goobar, A.; et al. The Distant Type Ia Supernova Rate. Astrophys. J. 2002, 577, 120–132. [Google Scholar] [CrossRef]
- Madgwick, D.S.; Hewett, P.C.; Mortlock, D.J.; Wang, L. Spectroscopic Detection of Type Ia Supernovae in the Sloan Digital Sky Survey. Astrophys. J. 2003, 599, L33–L36. [Google Scholar] [CrossRef]
- Tonry, J.L.; Schmidt, B.P.; Barris, B.; Candia, P.; Challis, P.; Clocchiatti, A.; Coil, A.L.; Filippenko, A.V.; Garnavich, P.; Hogan, C.; et al. Cosmological Results from High-zSupernovae. Astrophys. J. 2003, 594, 1–24. [Google Scholar] [CrossRef]
- Blanc, G.; Afonso, C.; Alard, C.; Albert, J.N.; Aldering, G.; Amadon, A.; Andersen, J.; Ansari, R.; Aubourg, E.; Balland, C.; et al. Type Ia supernova rate at a redshift of sim0.1. Astron. Astrophys. 2004, 423, 881–894. [Google Scholar] [CrossRef]
- Scannapieco, E.; Bildsten, L. The Type Ia Supernova Rate. Astrophys. J. 2005, 629, L85–L88. [Google Scholar] [CrossRef]
- Barris, B.J.; Tonry, J.L. The Rate of Type Ia Supernovae at High Redshift. Astrophys. J. 2006, 637, 427–438. [Google Scholar] [CrossRef]
- Neill, J.D.; Sullivan, M.; Balam, D.; Pritchet, C.J.; Howell, D.A.; Perrett, K.; Astier, P.; Aubourg, E.; Basa, S.; Carlberg, R.G.; et al. The Type Ia Supernova rate at z=0.5 from the Supernova Legacy Survey. Astron. J. 2006, 132, 1126–1145. [Google Scholar] [CrossRef]
- Neill, J.D.; Sullivan, M.; Balam, D.; Pritchet, C.J.; Howell, D.A.; Perrett, K.; Astier, P.; Aubourg, E.; Basa, S.; Carlberg, R.G.; et al. The Supernova Type Ia Rate Evolution with SNLS. AIP Conf. Proc. 2007, 924, 421–424. [Google Scholar] [CrossRef]
- Poznanski, D.; Maoz, D.; Yasuda, N.; Foley, R.J.; Doi, M.; Filippenko, A.V.; Fukugita, M.; Gal-Yam, A.; Jannuzi, B.T.; Morokuma, T.; et al. Supernovae in the Subaru Deep Field: An initial sample and Type Ia rate out to redshift 1.6. Mon. Not. R. Astron. Soc. 2007, 382, 1169–1186. [Google Scholar] [CrossRef]
- Dahlen, T.; Strolger, L.; Riess, A.G. The Extended HST Supernova Survey: The Rate of SNe Ia at z > 1.4 Remains Low. Astrophys. J. 2008, 681, 462–469. [Google Scholar] [CrossRef]
- Kuznetsova, N.; Barbary, K.; Connolly, B.; Kim, A.G.; Pain, R.; Roe, N.A.; Aldering, G.; Amanullah, R.; Dawson, K.; Doi, M.; et al. A New Determination of the High-Redshift Type Ia Supernova Rates with the Hubble Space Telescope Advanced Camera for Surveys. Astrophys. J. 2008, 673, 981–998. [Google Scholar] [CrossRef]
- Dilday, B.; Kessler, R.; Frieman, J.A.; Holtzman, J.; Marriner, J.; Miknaitis, G.; Nichol, R.C.; Romani, R.; Sako, M.; Bassett, B.; et al. A Measurement of the Rate of Type Ia Supernovae at Redshift z=0.1 from the First Season of the SDSS-II Supernova Survey. Astrophys. J. 2008, 682, 262–282. [Google Scholar] [CrossRef]
- Horesh, A.; Poznanski, D.; Ofek, E.O.; Maoz, D. The rate of Type Ia supernovae at z = 0.2 from SDSS-I overlapping fields: Supernova rate from SDSS-I. Mon. Not. R. Astron. Soc. 2008, 389, 1871–1880. [Google Scholar] [CrossRef]
- Graham, M.L.; Pritchet, C.J.; Sullivan, M.; Howell, D.A.; Gwyn, S.D.J.; Astier, P.; Balland, C.; Basa, S.; Carlberg, R.G.; Conley, A.; et al. The Type Ia Supernova Rate in Radio and Infrared Galaxies from the Canada-France-Hawaii Telescope Supernova Legacy Survey. Astron. J. 2010, 139, 594–605. [Google Scholar] [CrossRef]
- Dilday, B.; Smith, M.; Bassett, B.; Becker, A.; Bender, R.; Castander, F.; Cinabro, D.; Filippenko, A.V.; Frieman, J.A.; Galbany, L.; et al. Measurements of the Rate of Type Ia Supernovae at Redshift <0.3 From the Sloan Digital Sky Survey II Supernova Survey. Astrophys. J. 2010, 713, 1026–1036. [Google Scholar] [CrossRef]
- Dilday, B.; Bassett, B.; Becker, A.; Bender, R.; Castander, F.; Cinabro, D.; Frieman, J.A.; Galbany, L.; Garnavich, P.; Goobar, A.; et al. A Measurement of the Rate of Type Ia Supernovae in Galaxy Clusters from the SDSS-II Supernova Survey. Astrophys. J. 2010, 715, 1021–1035. [Google Scholar] [CrossRef]
- Rodney, S.A.; Tonry, J.L. Revised Supernova Rates from the IfA Deep Survey. Astrophys. J. 2010, 723, 47–53. [Google Scholar] [CrossRef]
- Barbary, K.; Aldering, G.; Amanullah, R.; Brodwin, M.; Connolly, N.; Dawson, K.S.; Doi, M.; Eisenhardt, P.; Faccioli, L.; Fadeyev, V.; et al. The Hubble Space Telescope Cluster Supernova Survey. II. The Type Ia Supernova Rate in High-Redshift Galaxy Clusters. Astrophys. J. 2011, 745, 32. [Google Scholar] [CrossRef]
- Barbary, K.; Aldering, G.; Amanullah, R.; Brodwin, M.; Connolly, N.; Dawson, K.S.; Doi, M.; Eisenhardt, P.; Faccioli, L.; Fadeyev, V.; et al. The Hubble Space Telescope Cluster Supernova Survey. VI. The Volumetric Type Ia Supernova Rate. Astrophys. J. 2011, 745, 31. [Google Scholar] [CrossRef]
- Krughoff, K.S.; Connolly, A.J.; Frieman, J.; SubbaRao, M.; Kilper, G.; Schneider, D.P. Spectroscopic Determination of the Low-Redshift Type Ia Supernova Rate from the SLOAN Digital Sky Survey. Astrophys. J. 2011, 731, 42. [Google Scholar] [CrossRef]
- Sand, D.J.; Graham, M.L.; Bildfell, C.; Zaritsky, D.; Pritchet, C.; Hoekstra, H.; Just, D.W.; Herbert-Fort, S.; Sivanandam, S.; Foley, R.J.; et al. The Multi-Epoch Nearby Cluster Survey: Type Ia Supernova Rate Measurement in z=0.1 Clusters and the Late-Time Delay Time Distribution. Astrophys. J. 2012, 746, 163. [Google Scholar] [CrossRef]
- Perrett, K.; Sullivan, M.; Conley, A.; González-Gaitán, S.; Carlberg, R.; Fouchez, D.; Ripoche, P.; Neill, J.D.; Astier, P.; Balam, D.; et al. Evolution in the Volumetric Type Ia Supernova Rate from the Supernova Legacy Survey. Astron. J. 2012, 144, 59. [Google Scholar] [CrossRef]
- Graur, O.; Maoz, D. Discovery of 90 Type Ia supernovae among 700 000 Sloan spectra: The Type Ia supernova rate versus galaxy mass and star formation rate at redshift = 0.1. Mon. Not. R. Astron. Soc. 2013, 430, 1746–1763. [Google Scholar] [CrossRef]
- Graur, O.; Rodney, S.A.; Maoz, D.; Riess, A.G.; Jha, S.W.; Postman, M.; Dahlen, T.; Holoien, T.W.S.; McCully, C.; Patel, B.; et al. Type-Ia Supernova Rates to Redshift 2.4 from CLASH: The Cluster Lensing and Supernova Survey with Hubble. Astrophys. J. 2014, 783, 28. [Google Scholar] [CrossRef]
- Okumura, J.E.; Ihara, Y.; Doi, M.; Morokuma, T.; Pain, R.; Totani, T.; Barbary, K.; Takanashi, N.; Yasuda, N.; Aldering, G.; et al. The Type Ia supernovae rate with Subaru/XMM-Newton Deep Survey. Publ. Astron. Soc. Jpn. 2014, 66. [Google Scholar] [CrossRef]
- Rodney, S.A.; Riess, A.G.; Strolger, L.G.; Dahlen, T.; Graur, O.; Casertano, S.; Dickinson, M.E.; Ferguson, H.C.; Garnavich, P.; Hayden, B.; et al. Type Ia Supernova Rate Measurements to Redshift 2.5 From CANDELS: Searching for Prompt Explosions in the Early Universe. Astron. J. 2014, 148, 13. [Google Scholar] [CrossRef]
- Frohmaier, C.; Sullivan, M.; Nugent, P.E.; Smith, M.; Dimitriadis, G.; Bloom, J.S.; Cenko, S.B.; Kasliwal, M.M.; Kulkarni, S.R.; Maguire, K.; et al. The volumetric rate of normal type Ia supernovae in the local Universe discovered by the Palomar Transient Factory. Mon. Not. R. Astron. Soc. 2019, 486, 2308–2320. [Google Scholar] [CrossRef]
- Perley, D.A.; Fremling, C.; Sollerman, J.; Miller, A.A.; Dahiwale, A.S.; Sharma, Y.; Bellm, E.C.; Biswas, R.; Brink, T.G.; Bruch, R.J.; et al. The Zwicky Transient Facility Bright Transient Survey. II. A Public Statistical Sample for Exploring Supernova Demographics. Astrophys. J. 2020, 904, 35. [Google Scholar] [CrossRef]
- Sharon, A.; Kushnir, D. The ZTF-BTS Type Ia supernovae luminosity function is consistent with a single progenitor channel for the explosions. Mon. Not. R. Astron. Soc. 2021, 509, 5275–5297. [Google Scholar] [CrossRef]
- Desai, D.D.; Kochanek, C.S.; Shappee, B.J.; Jayasinghe, T.; Stanek, K.Z.; Holoien, T.W.S.; Thompson, T.A.; Ashall, C.; Beacom, J.F.; Do, A.; et al. Supernova Rates and Luminosity Functions from ASAS-SN I: 2014–2017 Type Ia SNe and Their Sub-Types. arXiv 2023, arXiv:2306.11100. [Google Scholar] [CrossRef]
- MacFadyen, A.I.; Woosley, S.E. Collapsars: Gamma-Ray Bursts and Explosions in “Failed Supernovae”. Astrophys. J. 1999, 524, 262. [Google Scholar] [CrossRef]
- Hirschi, R.; Meynet, G.; Maeder, A. Stellar evolution with rotation: XIII. Predicted GRB rates at various Z. Astron. Astrophys. 2005, 443, 581–591. [Google Scholar] [CrossRef]
- Yoon, S.-C.; Langer, N. Evolution of rapidly rotating metal-poor massive stars towards gamma-ray bursts. Astron. Astrophys. 2005, 443, 643–648. [Google Scholar] [CrossRef]
- Woosley, S.E.; Heger, A. The Progenitor Stars of Gamma-Ray Bursts. Astrophys. J. 2006, 637, 914–921. [Google Scholar] [CrossRef]
- Yoon, S.C.; Langer, N.; Norman, C. Single star progenitors of long gamma-ray bursts: I. Model grids and redshift dependent GRB rate. Astron. Astrophys. 2006, 460, 199–208. [Google Scholar] [CrossRef]
- Curti, M.; Mannucci, F.; Cresci, G.; Maiolino, R. The mass–metallicity and the fundamental metallicity relation revisited on a fully -based abundance scale for galaxies. Mon. Not. R. Astron. Soc. 2019, 491, 944–964. [Google Scholar] [CrossRef]
- Curti, M.; Maiolino, R.; Curtis-Lake, E.; Chevallard, J.; Carniani, S.; D’Eugenio, F.; Looser, T.J.; Scholtz, J.; Charlot, S.; Cameron, A.; et al. JADES: Insights on the low-mass end of the mass–metallicity–star-formation rate relation at 3 < z < 10 from deep JWST/NIRSpec spectroscopy. arXiv 2023, arXiv:2304.08516. [Google Scholar]
- Boco, L.; Lapi, A.; Chruslinska, M.; Donevski, D.; Sicilia, A.; Danese, L. Evolution of Galaxy Star Formation and Metallicity: Impact on Double Compact Object Mergers. Astrophys. J. 2021, 907, 110. [Google Scholar] [CrossRef]
- Popesso, P.; Concas, A.; Cresci, G.; Belli, S.; Rodighiero, G.; Inami, H.; Dickinson, M.; Ilbert, O.; Pannella, M.; Elbaz, D. The main sequence of star-forming galaxies across cosmic times. Mon. Not. R. Astron. Soc. 2022, 519, 1526–1544. [Google Scholar] [CrossRef]
- Chruślińska, M.; Nelemans, G.; Boco, L.; Lapi, A. The impact of the FMR and starburst galaxies on the (low metallicity) cosmic star formation history. Mon. Not. R. Astron. Soc. 2021, 508, 4994–5027. [Google Scholar] [CrossRef]
- Chrimes, A.A.; Stanway, E.R.; Eldridge, J.J. Binary population synthesis models for core-collapse gamma-ray burst progenitors. Mon. Not. R. Astron. Soc. 2019, 491, 3479–3495. [Google Scholar] [CrossRef]
- Ghirlanda, G.; Salvaterra, R. The Cosmic History of Long Gamma Ray Bursts. arXiv 2022, arXiv:2206.06390. [Google Scholar] [CrossRef]
- Gabrielli, F.; Lapi, A.; Boco, L.; Ugolini, C.; Costa, G.; Sgalletta, C.; Shepherd, K.; Di Carlo, U.N.; Bressan, A.; Limongi, M.; et al. The Cosmic Rate of Pair-Instability Supernovae. arXiv 2024, arXiv:2408.13076. [Google Scholar] [CrossRef]
- Davé, R. The galaxy stellar mass–star formation rate relation: Evidence for an evolving stellar initial mass function? Mon. Not. R. Astron. Soc. 2008, 385, 147–160. [Google Scholar] [CrossRef]
- Fryer, C.L.; Lien, A.Y.; Fruchter, A.; Ghirlanda, G.; Hartmann, D.; Salvaterra, R.; Upton Sanderbeck, P.R.; Johnson, J.L. Properties of High-redshift Gamma-Ray Bursts. Astrophys. J. 2022, 929, 111. [Google Scholar] [CrossRef]
- Lapi, A.; Gandolfi, G.; Boco, L.; Gabrielli, F.; Massardi, M.; Haridasu, B.S.; Baccigalupi, C.; Bressan, A.; Danese, L. Constraining the Initial Mass Function in the Epoch of Reionization from Astrophysical and Cosmological Data. Universe 2024, 10, 141. [Google Scholar] [CrossRef]
- Mitra, S.; Chatterjee, A. Non-parametric reconstruction of photon escape fraction from reionization. Mon. Not. R. Astron. Soc. Lett. 2023, 523, L35–L39. [Google Scholar] [CrossRef]
- Horiuchi, S.; Beacom, J.F. Revealing Type Ia Supernova Physics with Cosmic Rates and Nuclear Gamma Rays. Astrophys. J. 2010, 723, 329–341. [Google Scholar] [CrossRef]
- Sana, H.; de Mink, S.E.; de Koter, A.; Langer, N.; Evans, C.J.; Gieles, M.; Gosset, E.; Izzard, R.G.; Bouquin, J.B.L.; Schneider, F.R.N. Binary Interaction Dominates the Evolution of Massive Stars. Science 2012, 337, 444–446. [Google Scholar] [CrossRef]
- Moe, M.; Di Stefano, R. Mind Your Ps and Qs: The Interrelation between Period (P) and Mass-ratio (Q) Distributions of Binary Stars. Astrophys. J. Suppl. Ser. 2017, 230, 15. [Google Scholar] [CrossRef]
- Winters, J.G.; Henry, T.J.; Jao, W.C.; Subasavage, J.P.; Chatelain, J.P.; Slatten, K.; Riedel, A.R.; Silverstein, M.L.; Payne, M.J. The Solar Neighborhood. XLV. The Stellar Multiplicity Rate of M Dwarfs Within 25 pc. Astron. J. 2019, 157, 216. [Google Scholar] [CrossRef]
- Refregier, A.; Amara, A.; Kitching, T.D.; Rassat, A.; Scaramella, R.; Weller, J. Euclid Imaging Consortium Science Book. arXiv 2010, arXiv:1001.0061. [Google Scholar]
- Laureijs, R.; Amiaux, J.; Arduini, S.; Auguères, J.L.; Brinchmann, J.; Cole, R.; Cropper, M.; Dabin, C.; Duvet, L.; Ealet, A.; et al. Euclid Definition Study Report. arXiv 2011, arXiv:1110.3193. [Google Scholar]
- Feindt, U.; Nordin, J.; Rigault, M.; Brinnel, V.; Dhawan, S.; Goobar, A.; Kowalski, M. simsurvey: Estimating transient discovery rates for the Zwicky transient facility. J. Cosmol. Astropart. Phys. 2019, 2019, 005. [Google Scholar] [CrossRef]
- Regos, E.; Vinkó, J. Detection and Classification of Supernovae Beyond z ∼ 2 Redshift with the James Webb Space Telescope. Astrophys. J. 2019, 874, 158. [Google Scholar] [CrossRef]
- Rose, B.M.; Baltay, C.; Hounsell, R.; Macias, P.; Rubin, D.; Scolnic, D.; Aldering, G.; Bohlin, R.; Dai, M.; Deustua, S.E.; et al. A Reference Survey for Supernova Cosmology with the Nancy Grace Roman Space Telescope. arXiv 2021, arXiv:2111.03081. [Google Scholar]
- Kocevski, D.; West, A.A.; Modjaz, M. Modeling the GRB Host Galaxy Mass Distribution: Are GRBs Unbiased Tracers of Star Formation? Astrophys. J. 2009, 702, 377. [Google Scholar] [CrossRef]
- Vergani, S.D.; Salvaterra, R.; Japelj, J.; Le Floc’h, E.; D’Avanzo, P.; Fernandez-Soto, A.; Krühler, T.; Melandri, A.; Boissier, S.; Covino, S.; et al. Are long gamma-ray bursts biased tracers of star formation? Clues from the host galaxies of the Swift/BAT6 complete sample of LGRBs—I. Stellar mass at z<1. Astron. Astrophys. 2015, 581, A102. [Google Scholar] [CrossRef]
- Perley, D.A.; Tanvir, N.R.; Hjorth, J.; Laskar, T.; Berger, E.; Chary, R.; de Ugarte Postigo, A.; Fynbo, J.P.U.; Krühler, T.; Levan, A.J.; et al. The Swift GRB Host Galaxy Legacy Survey. II. Rest-Frame Near-IR Luminosity Distribution and Evidence for a Near-Solar Metallicity Threshold. Astrophys. J. 2016, 817, 8. [Google Scholar] [CrossRef]
- Vergani, S.D.; Palmerio, J.; Salvaterra, R.; Japelj, J.; Mannucci, F.; Perley, D.A.; D’Avanzo, P.; Krühler, T.; Puech, M.; Boissier, S.; et al. The chemical enrichment of long gamma-ray bursts nurseries up to z = 2. Astron. Astrophys. 2017, 599, A120. [Google Scholar] [CrossRef]
- Palmerio, J.T.; Vergani, S.D.; Salvaterra, R.; Sanders, R.L.; Japelj, J.; Vidal-García, A.; D’Avanzo, P.; Corre, D.; Perley, D.A.; Shapley, A.E.; et al. Are long gamma-ray bursts biased tracers of star formation? Clues from the host galaxies of the Swift/BAT6 complete sample of bright LGRBs—III. Stellar masses, star formation rates, and metallicities at z > 1. Astron. Astrophys. 2019, 623, A26. [Google Scholar] [CrossRef]
- Langer, N.; Norman, C.A. On the Collapsar Model of Long Gamma-Ray Bursts:Constraints from Cosmic Metallicity Evolution. ApJL 2006, 638, L63–L66. [Google Scholar] [CrossRef]
- White, N.E.; Bauer, F.E.; Baumgartner, W.; Bautz, M.; Berger, E.; Cenko, B.; Chang, T.C.; Falcone, A.; Fausey, H.; Feldman, C.; et al. The Gamow Explorer: A Gamma-Ray Burst Observatory to study the high redshift universe and enable multi-messenger astrophysics. In Proceedings of the UV, X-ray, and Gamma-Ray Space Instrumentation for Astronomy XXII; Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series; Siegmund, O.H., Ed.; SPIE: St Bellingham, WA, USA, 2021; Volume 11821, p. 1182109. [Google Scholar] [CrossRef]
- Bozzo, E.; Amati, L.; Baumgartner, W.; Chang, T.C.; Cordier, B.; Angelis, N.D.; Doi, A.; Feroci, M.; Froning, C.; Gaskin, J.; et al. Future Perspectives for Gamma-ray Burst Detection from Space. arXiv 2024, arXiv:2404.11808. [Google Scholar]
- Foley, R.J.; Koekemoer, A.M.; Spergel, D.N.; Bianco, F.B.; Capak, P.; Dai, L.; Dore, O.; Fazio, G.G.; Ferguson, H.; Filippenko, A.V.; et al. LSST Observing Strategy White Paper: LSST Observations of WFIRST Deep Fields. arXiv 2018, arXiv:1812.00514. [Google Scholar] [CrossRef]
- Foley, R.; Bloom, J.S.; Cenko, S.B.; Chornock, R.; Dimitriadis, G.; Doré, O.; Filippenko, A.V.; Fox, O.D.; Hirata, C.M.; Jha, S.W.; et al. WFIRST: Enhancing Transient Science and Multi-Messenger Astronomy. Bull. Am. Astron. Soc. 2019, 51, 305. [Google Scholar] [CrossRef]
- Moriya, T.J.; Wong, K.C.; Koyama, Y.; Tanaka, M.; Oguri, M.; Hilbert, S.; Nomoto, K. Searches for Population III pair-instability supernovae: Predictions for ULTIMATE-Subaru and WFIRST. Publ. Astron. Soc. Jpn. 2019, 71, 59. [Google Scholar] [CrossRef]
- Wang, L.; Mould, J.; Baade, D.; Baron, E.; Bromm, V.; Cooke, J.; Fan, X.; Foley, R.; Fruchter, A.; Gal-Yam, A.; et al. JWST: Probing the Epoch of Reionization with a Wide Field Time-Domain Survey. Bull. Am. Astron. Soc. 2019, 51, 399. [Google Scholar] [CrossRef]
- Dessart, L.; Prieto, J.L.; Hillier, D.J.; Kuncarayakti, H.; Hueichapan, E.D. Using LSST late-time photometry to constrain Type Ibc supernovae and their progenitors. Astron. Astrophys. 2022, 666, L14. [Google Scholar] [CrossRef]
- Bailey, A.C.; Vincenzi, M.; Scolnic, D.; Cuillandre, J.C.; Rhodes, J.; Hook, I.; Peterson, E.R.; Popovic, B. Type Ia supernova observations combining data from the Euclid mission and the Vera C. Rubin Observatory. Mon. Not. R. Astron. Soc. 2023, 524, 5432–5441. [Google Scholar] [CrossRef]
- Subrayan, B.M.; Milisavljevic, D.; Moriya, T.J.; Weil, K.E.; Lentner, G.; Linvill, M.; Banovetz, J.; Garretson, B.; Reynolds, J.; Sravan, N.; et al. Inferencing Progenitor and Explosion Properties of Evolving Core-collapse Supernovae from Zwicky Transient Facility Light Curves. Astrophys. J. 2023, 945, 46. [Google Scholar] [CrossRef]
- Arendse, N.; Dhawan, S.; Carracedo, A.S.; Peiris, H.V.; Goobar, A.; Wojtak, R.; Alves, C.; Biswas, R.; Huber, S.; Birrer, S.; et al. Detecting strongly-lensed type Ia supernovae with LSST. arXiv 2024, arXiv:2312.04621. [Google Scholar] [CrossRef]
- Strotjohann, N.L.; Ofek, E.O.; Gal-Yam, A.; Sollerman, J.; Chen, P.; Yaron, O.; Zackay, B.; Rehemtulla, N.; Gris, P.; Masci, F.J.; et al. Search for Supernova Progenitor Stars with ZTF and LSST. Astrophys. J. 2023, 960, 72. [Google Scholar] [CrossRef]
- Salvaterra, R.; Campana, S.; Vergani, S.D.; Covino, S.; D’Avanzo, P.; Fugazza, D.; Ghirlanda, G.; Ghisellini, G.; Melandri, A.; Nava, L.; et al. A Complete Sample of Bright Swift Long Gamma-Ray Bursts. I. Sample Presentation, Luminosity Function and Evolution. Astrophys. J. 2012, 749, 68. [Google Scholar] [CrossRef]







| - | ||
| - | ||
| - | ||
| - | ||
| - | ||
| - | ||
| - | ||
| - | ||
| - |
| - | ||
| - | ||
| - | ||
| - | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gabrielli, F.; Boco, L.; Ghirlanda, G.; Salafia, O.S.; Salvaterra, R.; Spera, M.; Lapi, A. Constraining the Initial Mass Function via Stellar Transients. Universe 2024, 10, 383. https://doi.org/10.3390/universe10100383
Gabrielli F, Boco L, Ghirlanda G, Salafia OS, Salvaterra R, Spera M, Lapi A. Constraining the Initial Mass Function via Stellar Transients. Universe. 2024; 10(10):383. https://doi.org/10.3390/universe10100383
Chicago/Turabian StyleGabrielli, Francesco, Lumen Boco, Giancarlo Ghirlanda, Om Sharan Salafia, Ruben Salvaterra, Mario Spera, and Andrea Lapi. 2024. "Constraining the Initial Mass Function via Stellar Transients" Universe 10, no. 10: 383. https://doi.org/10.3390/universe10100383
APA StyleGabrielli, F., Boco, L., Ghirlanda, G., Salafia, O. S., Salvaterra, R., Spera, M., & Lapi, A. (2024). Constraining the Initial Mass Function via Stellar Transients. Universe, 10(10), 383. https://doi.org/10.3390/universe10100383







