Abstract
We imagine spherically symmetric configurations made of both dark matter and dark energy in the halo of spiral galaxies. Adopting a polytropic equation of state for dark matter and the Extended Chaplygin gas equation of state for dark energy, we model the same object with three different dark matter–dark energy compositions. We compute the frequencies and the corresponding eigenfunctions of the ten lowest modes, integrating the equations for the radial perturbations by imposing the appropriate boundary conditions at the center and the surface of the object. Also, a comparison between the different models is made.
1. Introduction
The concordance cosmological model, the CDM model, describes the formation and structure of the Universe at large scales, and is based on cold dark matter and , the cosmological constant. The existence of dark matter, still of unknown nature and origin, originates from old studies that showed that the Universe is mostly composed of an invisible material that affects galaxies and galaxy clusters only gravitationally. The pioneer works belong to F. Zwicky [1] in the 30s, and several decades later to V. Rubin, who studied the Andromeda’s rotation curve and discovered that at any distance from the bulge of the galaxy, the rotation speed was constant [2]. These studies showed that approximately 85% of the mass of the Universe corresponds to dark matter [3].
In addition to dark matter, there is another dark component in the Universe, called dark energy. This is also of unknown nature as of today, but has a repulsive rather than attractive character, since the current accelerating expansion of the Universe is produced by it [4,5,6]. Current modern data seem to show that approximately 70% of the Universe is made of dark energy, 25% of dark matter, and 5% of ordinary matter [7].
Compact stars [8], the final products of very massive stars, are extremely dense objects with a mass of the order of one solar mass, and a radius of a few kilometers, such as neutron stars [9] and strange quark stars [10,11,12,13,14,15], although the latter class of compact objects remain hypothetical for the time being. In the same way, there are studies that contemplate the possibility that relativistic exotic stars may exist, composed of dark matter [16,17,18], or dark energy even [19,20,21,22]. In a recent study, we considered configurations composed of both dark matter and dark energy adopting the two-fluid formalism [23]. In that study we gave a relativistic description based on the field equations of General Relativity.
To determine the radius and mass of those stars, we require the EoS of each fluid component, i.e., one for dark matter and another for dark energy, under the condition that there is no direct interaction between the fluids other than the gravitational force. Dark matter may be viewed as a Bose–Einstein condensate [24], and so we adopt the polytropic equation of state for dark matter [25,26]. Regarding dark energy, we consider the Extended Chaplygin gas equation of state [27,28], which was introduced with the aim of unifying dark energy and non-relativistic matter working with a single fluid instead of two.
Regarding plausible scenarios and astrophysical mechanisms that may produce dark stars in the Universe, it has been proposed that the first stars to exist in the Cosmos, contrary to ordinary main sequence stars, were powered by dark matter heating rather than fusion [29,30]. Dark matter particles might have accumulated in the interior of the first stars and been annihilated, producing a heat source that can power such stars. Moreover, if Bose–Einstein condensation took place in the very early Universe, at very high redshifts, as suggested by the analysis performed in [16], at the moment of star formation most of the DM was already in a condensate form. Hence, one may naturally expect the formation of stellar type objects made of pure condensate dark matter stars [16].
Asteroseismology is a widely used technique, since the frequencies of the oscillation modes of pulsating stars are very sensitive to the inner structure and composition of the object. It has been proven to be a powerful tool at our disposal, since it allows us to probe the interior of the Sun, solar-like stars, and other classes of stars [31,32], such as nuclear reactions, their compositions, equations of state, differential rotation rates, and meridional circulation. Currently, asteroseismology has been extended to the study of compact stars [33,34,35,36], like white dwarfs [37] and neutron stars [38]. In addition, there are studies of exotic stars such as strange quark stars [39], dark matter stars [39,40,41], and dark energy stars [21]. For more details, the interested reader may consult for instance [42,43,44,45,46,47,48,49,50].
Regarding excitation and detectability, there are numerous astrophysical mechanisms that may excite oscillation modes of stars, such as tidal effects in binaries, starquakes caused by cracks during supernova explosions, magnetic reconfiguration, or any other form of instability [38,51,52,53,54,55]. The Kepler and CoRoT missions have already measured the oscillation spectra of solar-like, white dwarf, and red giant stars [56,57,58,59,60,61]. Actual wave detectors, like LIGO [38], do not detect the radial oscillations studied here, due to their low sensitivity at the kHz frequency range. However, the third-generation of ground-based gravitational wave detectors are expected to have a much higher sensitivity (by an order of magnitude), such as the Cosmic Explorer [62] and the Einstein Telescope [63]. These detections could give us information related to neutron star masses, frequencies, tidal Love numbers, amplitudes of the modes, damping times, and moments of inertia.
In the present work, we compute the frequencies and corresponding eigenfunctions of the 10 lowest radial oscillation modes of spherical configurations from the dark sector, namely both dark matter and dark energy. To that end, we model an object of a given mass and radius with three different models, which differ in their internal structure and composition.
The present article is structured as follows: after this introductory section, we present the structure equations governing the hydrostatic equilibrium and the equations of state employed here. Radial oscillations are discussed in Section 3, and we present and discuss our main results in Section 4. Finally, we conclude our work in Section 5.
Throughout the manuscript, we adopt the mostly positive metric signature (−, +, +, +) and we work in natural geometrical units, setting G = c = 1 for the Newton’s constant and speed of light in vacuum, respectively. All units used here are measured in GeV: 1 m , 1 kg , 1 s , and the Planck mass .
2. Relativistic Spheres in General Relativity
We assume that the objects are non-rotating and are electrically neutral. Also, we work with relativistic configurations in four dimensions, with a vanishing cosmological constant.
2.1. Structure Equations
The metric tensor in Schwarzschild coordinates (t, r, , ) for static and spherically symmetric space-times is given by
To obtain interior solutions describing hydrostatic equilibrium of stars composed of dark matter and dark energy, we need to integrate the Tolman–Oppenheimer–Volkoff (TOV) equations [64,65] for two-fluid formalism [66,67], which are given by
which we consider a spherical configuration composed of dark matter and dark energy, whose pressure and energy density are and , for dark matter, and and for dark energy, respectively. is the mass function, and a prime denotes differentiation with respect to the radial coordinate r.
The total pressure p and total density are the sum of the pressures and densities of both fluids, i.e.,
The TOV equations are to be integrated imposing the following initial conditions at the centre of the star
where and are the central pressure for dark matter and dark energy, respectively. Moreover, the the surface conditions of the star that must be satisfied are
with R being the radius of the star and M its mass.
2.2. Equations of State
To solve the TOV equations, we will require the equations of state. Since each fluid is independent, dark matter and dark energy have their own equation of state.
Dark matter may be interpreted as a Bose–Einstein condensate [24], since it solves the core–cusp problem [68]. Hence, a polytropic EoS of the following form is obtained [16,25,26]
where k is the constant of proportionality, determined by [16,26,39]
with m being the mass of the dark matter particle, and l being the scattering length that determines the elastic cross-section at low energies, [16,26,39]. Each model is characterized by its own numerical value of k, which can be seen in Table 1. Nowadays, the DM self-interacting cross section must satisfy the constraint [69,70,71]

Table 1.
Numerical values of the parameters A, B, k and f for each model. For all three models considered in this work we assume a sphere of mass M = 1.216 and radius R = 8.145 km.
The numerical values of k displayed in Table 1 may be achieved if, e.g., and 1 GeV, and the bounds on are satisfied. We comment in passing that regarding the fuzzy DM model based on a free ultra-light scalar field, recent works have put an upper bound on its mass, [72,73], violating the from the linear matter power spectrum.
As far as dark energy is concerned, following [20], we consider the Extended Chaplygin equation of state [27,28].
where A is dimensionless and B has dimensions of energy density and pressure, both positive constants. Note that the equation of state of Chaplygin gas is given by [74], while the additional barotropic term, , provides us with another viable dark energy model [75]; as it predicts a transition from deceleration to acceleration, it fits supernovae data, while at the same time the equation-of-state parameter w interpolates between 0 and −1, unifying thus non-relativistic matter and DE. What is more, at low red shift, the energy density becomes a constant, mimicking thus a positive cosmological constant, see Equation (11) of [75]. Table 1 shows the numerical values for A and B that we have considered.
It must be taken into account that given the form of the EoS, the pressure and density cannot become zero at the same time. Therefore, a vanishing pressure at the surface of the star implies a non-vanishing value for the energy density, which is computed to be .
Additionally, it is convenient to introduce a new dimensionless factor related to the central conditions of the stars defined as
The numerical values for A, B, k, and f that we have chosen for three different models are displayed in Table 1 in order to compare stars of the same mass and radius but with different inner composition and obtain realistic solutions. The values are M = 1.216 for the mass, and R = 8.145 km for the radius. The chosen values are motivated by the fact that there are a few observed objects with known masses and radii around those values, see for instance Table 1 of [76].
In a recent work, we studied some properties of dark stars made of dark matter and dark energy [23], and here we propose to study radial oscillations and frequencies for this class of objects.
3. Radial Oscillations
The equations for radial perturbations of the stars, given below, are satisfied by the radial displacement, , and the pressure perturbation, , defined by
which satisfy the following first order differential equations [77,78]:
where is defined to be
and are the metric potentials, which are computed as follows
with M the mass of the star and R its radius, while is the frequency oscillation mode, where s is a dimensionless number, while the constant is computed by
Finally
with being the relativistic adiabatic index, and is the the speed of sound.
The unknown frequencies are determined solving the Sturm–Liouville boundary value problem imposing the following boundary conditions [38], both at the center and at the surface of the star
since must be finite as , and must be finite at the surface as , so . Furthermore, since the system of equations is linear, the scaling factor is free and therefore the oscillating functions may be normalized, setting [78].
Before we proceed, a comment is in order here. When dealing with radial oscillations of objects made of two fluid components, in general there are two approaches [79]. In the first, a consistent general relativistic formalism to deal with the couplings between oscillation amplitudes and Lagrangian perturbations for each fluid was developed in [36,80]. Unfortunately, dealing with a system of highly coupled and non-linear differential equations requires very time-consuming numerical calculations. In the second approach, which is in fact simpler, only the radial oscillation of the whole admixed star, namely treated as a single fluid sphere, is studied without explicitly considering the gravitational coupling between the two fluid components, see, e.g., [39,81]. This is the approach we are taking in the discussion to follow.
4. Results and Discussion
We have studied radial oscillations and frequencies of dark stars made of dark matter and dark energy for their first 10 lowest modes shown in Table 2. For this, we have selected three different models, which all have the same radius R = 8.145 km and mass M = 1.216 but different dark energy mass fractions. The precise numerical values of the parameters A, B, k, and f, are shown in Table 1. The three models considered in this work are as follows

Table 2.
Frequencies (in kHz) of radial oscillation modes for the three models discussed here, see text for more details.
In Figure 1, we show the eigenfunctions and versus normalized (dimensionless) radial coordinate for low, intermediate, and highly excited modes for all three models considered here. We recall that in a Sturm–Liouville boundary value problem, the number of zeros of the eigenfunctions corresponds to the overtone number n. In the graphs, it can be observed that this is indeed the case. For instance, the fundamental mode has no zeros, while the first excited mode and the second excited mode have one and two zeros, respectively. And so on and so forth for higher modes.
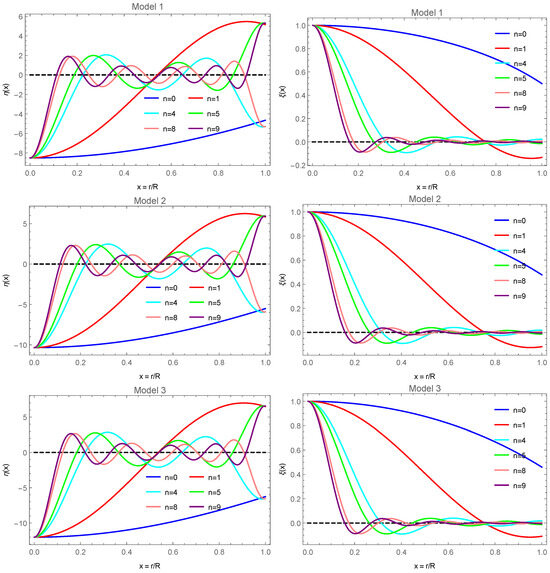
Figure 1.
Perturbations (left panels) and (right panels) vs. for low order modes (blue) and (red), intermediate modes (cyan) and (green), and highly excited modes (pink) and (purple). Shown are Model 1 (top panels), Model 2 (center panels), and Model 3 (bottom panels).
In Table 2, where the numerical values of the frequencies are shown, we see that the frequencies are higher for Model 3 and lower for Model 1. In Figure 2, the large frequency separations defined as [38]
are displayed for all three models, where is the overtone number. As usual, for highly excited modes, the large frequency separations tend to a constant which is different from one model to another. They are also larger for Model 3 and smaller for Model 1. It is worth mentioning that Model 3 is characterized by the largest sound speed, see Figure 5 below, while regarding the fundamental mode, the function of Model 3 decreases faster than the corresponding function of the other two models. Those features are in agreement with the results of [38], where radial oscillations of neutron stars were studied, and a similar behavior was observed.
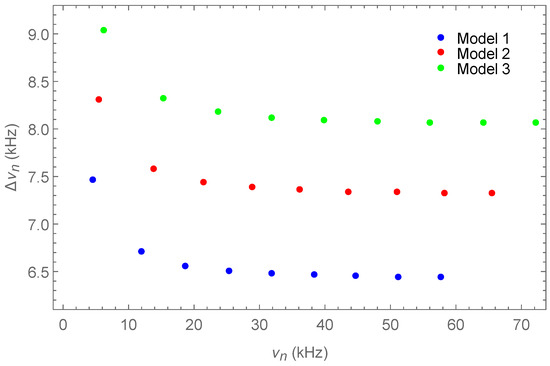
Figure 2.
Large frequency separation vs. frequencies , both in kHz, for the lowest 10 modes. Blue is for Model 1, red for Model 2 and green for Model 3.
Figure 3 and Figure 4 show the perturbations and , respectively, for the three models and for the fundamental mode and the first excited mode. Depending on the model, the values of start with different values, whereas for they all start with . In the three models, the values of are very similar for each mode. However, in they differ, except for the zeros, which for each mode the three models are the same, as is .
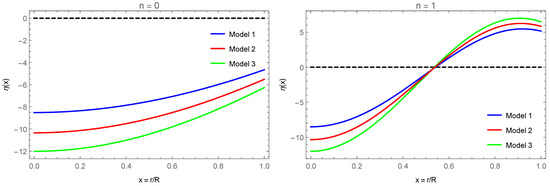
Figure 3.
perturbations for the fundamental mode n = 0 (left) and the first excited mode n = 1 (right). Blue represents Model 1, red represents Model 2, and green represents Model 3.
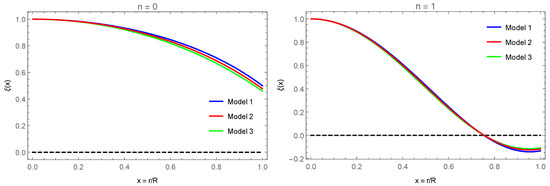
Figure 4.
perturbations for the fundamental mode n = 0 (left) and the first excited mode n = 1 (right). Blue denotes Model 1, red Model 2, and green Model 3.
We obtained that the dark energy mass fraction differs in all models, obtaining 49%, 44%, and 41% in Models 1, 2, and 3, respectively. If radial oscillations are discovered in dark stars, it will be possible to use their frequencies to infer the properties of their internal structure, and check if there is evidence for dark matter and dark energy inside the star, and their percentages or mass fraction.
Furthermore, we have checked that the results comply with the criteria for realistic solutions. The Buchdahl limit [82] is satisfied since . Stability, [83], energy conditions and [21,84,85,86,87], and causality, [21], are fulfilled as well, as can be seen in Figure 5. The values for the speed of sound of Model 3 are the highest and those of Model 1 are the lowest.
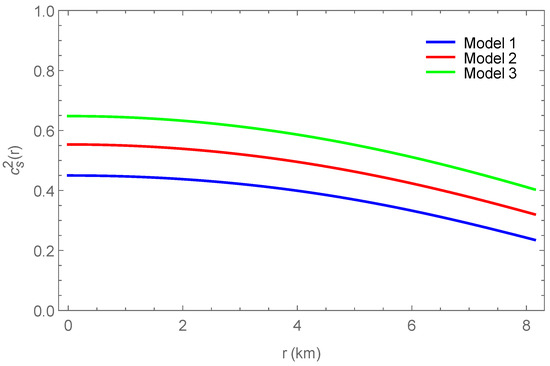
Figure 5.
Speed of sound vs. radial coordinate r in . Blue represents Model 1, red Model 2, and green Model 3.
5. Conclusions
To summarize our work, in the present article, we studied radial oscillations of spherical, non-rotating configurations made of both dark matter and dark energy. For the latter, we adopted the Extended Chaplygin gas EoS, while for the former, viewed as Bose–Einstein condensate, we assumed a polytropic EoS with index . We modeled the same object with mass and radius km in three different dark matter–dark energy compositions. We integrated the equations for the perturbations, imposing the appropriate boundary conditions, both at the center and the surface of the objects, and we computed the frequencies as well as the corresponding eigenfunctions for the 10 lowest modes, namely fundamental (f mode) and nine excited modes. The large frequency separations are displayed as well for all three models considered here. A direct comparison between the three models is made showing (i) the two eigenfunctions of the fundamental and first excited mode as well as (ii) the speed of sound of the interior solution. We find that as the objects contain less and less dark energy, the sound speed and the frequencies increase.
Author Contributions
Conceptualization: G.P., Methodology: G.P., Formal analysis: G.P., Investigation: C.S. and G.P., Writing original draft preparation: C.S., Software: C.S., Writing-review and editing: C.S. and G.P., Visualization: C.S. and G.P. All authors have read and agreed to the published version of the manuscript.
Funding
The author C.S. acknowledges financial support from Universidad de la Frontera.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zwicky, F. The redshift of extragalactic nebulae. Helv. Phys. Acta 1933, 6, 110. [Google Scholar]
- Rubin, V.C.; Ford, W.K., Jr. Rotation of the Andromeda Nebula from a Spectroscopic Survey of Emission Regions. Astrophys. J. 1970, 159, 379–403. [Google Scholar] [CrossRef]
- Munoz, C. Dark matter detection in the light of recent experimental results. Int. J. Mod. Phys. A 2004, 19, 3093–3170. [Google Scholar] [CrossRef]
- Riess, A.G. et al. [Supernova Search Team] Observational evidence from supernovae for an accelerating universe and a cosmological constant. Astron. J. 1998, 116, 1009–1038. [Google Scholar] [CrossRef]
- Perlmutter, S. et al. [Supernova Cosmology Project] Measurements of Ω and Λ from 42 high redshift supernovae. Astrophys. J. 1999, 517, 565–586. [Google Scholar] [CrossRef]
- Freedman, W.L.; Turner, M.S. Measuring and understanding the universe. Rev. Mod. Phys. 2003, 75, 1433–1447. [Google Scholar] [CrossRef]
- Aghanim, N. et al. [Planck] Planck 2018 results. VI. Cosmological parameters. Astron. Astrophys. 2020, 641, A6, Erratum in Astron. Astrophys. 2021, 652, C4. [Google Scholar] [CrossRef]
- Shapiro, S.L.; Teukolsky, S.A. Black Holes, White Dwarfs, and Neutron Stars: The Physics of Compact Objects; Wiley: New York, NY, USA, 1983; p. 645. [Google Scholar]
- Lattimer, J.M.; Prakash, M. Neutron Star Observations: Prognosis for Equation of State Constraints. Phys. Rep. 2007, 442, 109–165. [Google Scholar] [CrossRef]
- Alcock, C.; Farhi, E.; Olinto, A. Strange stars. Astrophys. J. 1986, 310, 261–272. [Google Scholar] [CrossRef]
- Alcock, C.; Olinto, A. Exotic Phases of Hadronic Matter and their Astrophysical Application. Ann. Rev. Nucl. Part. Sci. 1988, 38, 161–184. [Google Scholar] [CrossRef]
- Madsen, J. Physics and astrophysics of strange quark matter. Lect. Notes Phys. 1999, 516, 162–203. [Google Scholar] [CrossRef]
- Weber, F. Strange quark matter and compact stars. Prog. Part. Nucl. Phys. 2005, 54, 193–288. [Google Scholar] [CrossRef]
- Yue, Y.L.; Cui, X.H.; Xu, R.X. Is psr b0943+10 a low-mass quark star? Astrophys. J. Lett. 2006, 649, L95–L98. [Google Scholar] [CrossRef]
- Leahy, D.; Ouyed, R. Supernova SN2006gy as a first ever Quark Nova? Mon. Not. R. Astron. Soc. 2008, 387, 1193. [Google Scholar] [CrossRef]
- Li, X.Y.; Harko, T.; Cheng, K.S. Condensate dark matter stars. J. Cosmol. Astropart. Phys. 2012, 6, 1. [Google Scholar] [CrossRef]
- Maselli, A.; Pnigouras, P.; Nielsen, N.G.; Kouvaris, C.; Kokkotas, K.D. Dark stars: Gravitational and electromagnetic observables. Phys. Rev. D 2017, 96, 023005. [Google Scholar] [CrossRef]
- Panotopoulos, G.; Lopes, I. Dark stars in Starobinsky’s model. Phys. Rev. D 2018, 97, 024025. [Google Scholar] [CrossRef]
- Singh, K.N.; Ali, A.; Rahaman, F.; Nasri, S. Compact stars with exotic matter. Phys. Dark Univ. 2020, 29, 100575. [Google Scholar] [CrossRef]
- Tello-Ortiz, F.; Malaver, M.; Rincón, Á.; Gomez-Leyton, Y. Relativistic anisotropic fluid spheres satisfying a non-linear equation of state. Eur. Phys. J. C 2020, 80, 371. [Google Scholar] [CrossRef]
- Panotopoulos, G.; Rincón, Á.; Lopes, I. Radial oscillations and tidal Love numbers of dark energy stars. Eur. Phys. J. Plus 2020, 135, 856. [Google Scholar] [CrossRef]
- Panotopoulos, G.; Rincón, Á.; Lopes, I. Slowly rotating dark energy stars. Phys. Dark Univ. 2021, 34, 100885. [Google Scholar] [CrossRef]
- Sepúlveda, C.; Panotopoulos, G. On exotic objects made of dark energy and dark matter: Mass-to-radius profiles and tidal Love numbers. Galaxies 2023, 11, 101. [Google Scholar] [CrossRef]
- Boehmer, C.G.; Harko, T. Can dark matter be a Bose-Einstein condensate? J. Cosmol. Astropart. Phys. 2007, 6, 025. [Google Scholar] [CrossRef]
- Fan, J. Ultralight Repulsive Dark Matter and BEC. Phys. Dark Univ. 2016, 14, 84–94. [Google Scholar] [CrossRef]
- Chavanis, P.H. Phase transitions between dilute and dense axion stars. Phys. Rev. D 2018, 98, 023009. [Google Scholar] [CrossRef]
- Pourhassan, B.; Kahya, E.O. Extended Chaplygin gas model. Results Phys. 2014, 4, 101–102. [Google Scholar] [CrossRef]
- Pourhassan, B.; Kahya, E.O. FRW cosmology with the extended Chaplygin gas. Adv. High Energy Phys. 2014, 2014, 231452. [Google Scholar] [CrossRef]
- Freese, K.; Spolyar, D.; Bodenheimer, P.; Gondolo, P. Dark Stars: A New Study of the FIrst Stars in the Universe. New J. Phys. 2009, 11, 105014. [Google Scholar] [CrossRef]
- Spolyar, D.; Bodenheimer, P.; Freese, K.; Gondolo, P. Dark Stars: A new look at the First Stars in the Universe. Astrophys. J. 2009, 705, 1031–1042. [Google Scholar] [CrossRef]
- Turck-Chieze, S.; Couvidat, S. Solar neutrinos, helioseismology and the solar internal dynamics. Rep. Prog. Phys. 2011, 74, 086901. [Google Scholar] [CrossRef]
- Chaplin, W.J.; Miglio, A. Asteroseismology of Solar-Type and Red-Giant Stars. Ann. Rev. Astron. Astrophys. 2013, 51, 353. [Google Scholar] [CrossRef]
- Kokkotas, K.D.; Schmidt, B.G. Quasinormal modes of stars and black holes. Living Rev. Rel. 1999, 2, 2. [Google Scholar] [CrossRef] [PubMed]
- Paschalidis, V.; Stergioulas, N. Rotating Stars in Relativity. Living Rev. Rel. 2017, 20, 7. [Google Scholar] [CrossRef] [PubMed]
- Clemente, F.D.; Mannarelli, M.; Tonelli, F. Reliable description of the radial oscillations of compact stars. Phys. Rev. D 2020, 101, 103003. [Google Scholar] [CrossRef]
- Kain, B. Radial oscillations and stability of multiple-fluid compact stars. Phys. Rev. D 2020, 102, 023001. [Google Scholar] [CrossRef]
- Córsico, A.H.; Althaus, L.G.; Bertolami, M.M.M.; Kepler, S.O. Pulsating white dwarfs: New insights. Astron. Astrophys. Rev. 2019, 27, 7. [Google Scholar] [CrossRef]
- Sagun, V.; Panotopoulos, G.; Lopes, I. Asteroseismology: Radial oscillations of neutron stars with realistic equation of state. Phys. Rev. D 2020, 101, 063025. [Google Scholar] [CrossRef]
- Panotopoulos, G.; Lopes, I. Radial oscillations of strange quark stars admixed with condensed dark matter. Phys. Rev. D 2017, 96, 083013. [Google Scholar] [CrossRef]
- Leung, S.C.; Chu, M.C.; Lin, L.M. Dark-matter admixed neutron stars. Phys. Rev. D 2011, 84, 107301. [Google Scholar] [CrossRef]
- Leung, S.C.; Chu, M.C.; Lin, L.M. Equilibrium Structure and Radial Oscillations of Dark Matter Admixed Neutron Stars. Phys. Rev. D 2012, 85, 103528. [Google Scholar] [CrossRef]
- Lopes, I.P. A New Look at the Eckart-Scuflaire-Osaki Classification Scheme of Stellar Oscillations. Astrophys. J. 2000, 542, 1071–1074. [Google Scholar] [CrossRef][Green Version]
- Lopes, I.P. Nonradial adiabatic oscillations of stars. Astron. Astrophys. 2001, 373, 916–931. [Google Scholar] [CrossRef]
- Kokkotas, K.D.; Ruoff, J. Radial oscillations of relativistic stars. Astron. Astrophys. 2001, 366, 565. [Google Scholar] [CrossRef]
- Miniutti, G.; Pons, J.A.; Berti, E.; Gualtieri, L.; Ferrari, V. Non-radial oscillation modes as a probe of density discontinuities in neutron stars. Mon. Not. R. Astron. Soc. 2003, 338, 389. [Google Scholar] [CrossRef]
- Passamonti, A.; Bruni, M.; Gualtieri, L.; Sopuerta, C.F. Coupling of radial and non-radial oscillations of relativistic stars: Gauge-invariant formalism. Phys. Rev. D 2005, 71, 024022. [Google Scholar] [CrossRef]
- Passamonti, A.; Bruni, M.; Gualtieri, L.; Nagar, A.; Sopuerta, C.F. Coupling of radial and axial non-radial oscillations of compact stars: Gravitational waves from first-order differential rotation. Phys. Rev. D 2006, 73, 084010. [Google Scholar] [CrossRef]
- Savonije, G.J. Non-radial oscillations of the rapidly rotating Be star HD 163868. Astron. Astrophys. 2007, 469, 1057. [Google Scholar] [CrossRef]
- Flores, C.V.; Lugones, G. Radial oscillations of color superconducting self-bound quark stars. Phys. Rev. D 2010, 82, 063006. [Google Scholar] [CrossRef]
- Brillante, A.; Mishustin, I.N. Radial oscillations of neutral and charged hybrid stars. Europhys. Lett. 2014, 105, 39001. [Google Scholar] [CrossRef]
- Franco, L.M.; Link, B.; Epstein, R.I. Quaking neutron stars. Astrophys. J. 2000, 543, 987. [Google Scholar] [CrossRef]
- Andersson, N.; Jones, D.I.; Kokkotas, K.D.; Stergioulas, N. R mode runaway and rapidly rotating neutron stars. Astrophys. J. Lett. 2000, 534, L75. [Google Scholar] [CrossRef]
- Tsang, D.; Read, J.S.; Hinderer, T.; Piro, A.L.; Bondarescu, R. Resonant Shattering of Neutron Star Crusts. Phys. Rev. Lett. 2012, 108, 011102. [Google Scholar] [CrossRef]
- Hinderer, T.; Taracchini, A.; Foucart, F.; Buonanno, A.; Steinhoff, J.; Duez, M.; Kidder, L.E.; Pfeiffer, H.P.; Scheel, M.A.; Szilagyi, B.; et al. Effects of neutron-star dynamic tides on gravitational waveforms within the effective-one-body approach. Phys. Rev. Lett. 2016, 116, 181101. [Google Scholar] [CrossRef] [PubMed]
- Chirenti, C.; Gold, R.; Miller, M.C. Gravitational waves from f-modes excited by the inspiral of highly eccentric neutron star binaries. Astrophys. J. 2017, 837, 67. [Google Scholar] [CrossRef]
- Michel, E.; Baglin, A.; Auvergne, M.; Catala, C.; Samadi, R. CoRoT measures solar-like oscillations and granulation in stars hotter than the Sun. Science 2008, 322, 558–560. [Google Scholar] [CrossRef] [PubMed]
- Mosser, B.; Belkacem, K.; Goupil, M.J.; Miglio, A.; Morel, T.; Barban, C.; Baudin, F.; Hekker, S.; Samadi, R.; Ridder, J.D.; et al. Red-giant seismic properties analyzed with CoRoT. Astron. Astrophys. 2010, 517, A22. [Google Scholar] [CrossRef]
- Mosser, B.; Belkacem, K.; Goupil, M.J.; Michel, E.; Elsworth, Y.; Barban, C.; Kallinger, T.; Hekker, S.; DeRidder, J.; Samadi, R.; et al. The universal red-giant oscillation pattern: An automated determination with CoRoT data. Astron. Astrophys. 2011, 525, L9. [Google Scholar] [CrossRef]
- Bischoff-Kim, A.; Østensen, R.H. Asteroseismology of the Kepler field DBV White Dwarf—It’s a hot one! Astrophys. J. Lett. 2011, 742, L16. [Google Scholar] [CrossRef]
- Corsico, A.H.; Althaus, L.G.; Bertolami, M.M.M.; Bischoff-Kim, A. Asteroseismology of the Kepler V777 Her variable white dwarf with fully evolutionary models. Astron. Astrophys. 2012, 541, A42. [Google Scholar] [CrossRef]
- Hekker, S. CoRoT and Kepler results: Solar-like oscillators. Adv. Space Res. 2013, 52, 1581–1592. [Google Scholar] [CrossRef]
- Evans, M.; Adhikari, R.X.; Afle, C.; Ballmer, S.W.; Biscoveanu, S.; Borhanian, S.; Brown, D.A.; Chen, Y.; Eisenstein, R.; Gruson, A.; et al. A Horizon Study for Cosmic Explorer: Science, Observatories, and Community. arXiv 2021, arXiv:2109.09882. [Google Scholar]
- Punturo, M.; Abernathy, M.; Acernese, F.; Allen, B.; Andersson, N.; Arun, K.; Barone, F.; Barr, B.; Barsuglia, M.; Beker, M.; et al. The Einstein Telescope: A third-generation gravitational wave observatory. Class. Quant. Grav. 2010, 27, 194002. [Google Scholar] [CrossRef]
- Oppenheimer, J.R.; Volkoff, G.M. On massive neutron cores. Phys. Rev. 1939, 55, 374–381. [Google Scholar] [CrossRef]
- Tolman, R.C. Static solutions of Einstein’s field equations for spheres of fluid. Phys. Rev. 1939, 55, 364–373. [Google Scholar] [CrossRef]
- Sandin, F.; Ciarcelluti, P. Effects of mirror dark matter on neutron stars. Astropart. Phys. 2009, 32, 278–284. [Google Scholar] [CrossRef]
- Ciarcelluti, P.; Sandin, F. Have neutron stars a dark matter core? Phys. Lett. B 2011, 695, 19–21. [Google Scholar] [CrossRef]
- Harko, T. Bose-Einstein condensation of dark matter solves the core/cusp problem. J. Cosmol. Astropart. Phys. 2011, 5, 022. [Google Scholar] [CrossRef]
- Markevitch, M.; Gonzalez, A.H.; Clowe, D.; Vikhlinin, A.; David, L.; Forman, W.; Jones, C.; Murray, S.; Tucker, W. Direct constraints on the dark matter self-interaction cross-section from the merging galaxy cluster 1E0657-56. Astrophys. J. 2004, 606, 819–824. [Google Scholar] [CrossRef]
- Robertson, A.; Massey, R.; Eke, V. What does the Bullet Cluster tell us about self-interacting dark matter? Mon. Not. Roy. Astron. Soc. 2017, 465, 569–587. [Google Scholar] [CrossRef]
- Young, B.L. A survey of dark matter and related topics in cosmology. Front. Phys. 2017, 12, 121201, Erratum in Front. Phys. 2017, 12, 121202. [Google Scholar] [CrossRef]
- Meinert, J.; Hofmann, R. Axial Anomaly in Galaxies and the Dark Universe. Universe 2021, 7, 198. [Google Scholar] [CrossRef]
- Bañares-Hernández, A.; Castillo, A.; Camalich, J.M.; Iorio, G. Confronting fuzzy dark matter with the rotation curves of nearby dwarf irregular galaxies. Astron. Astrophys. 2023, 676, A63. [Google Scholar] [CrossRef]
- Kamenshchik, A.Y.; Moschella, U.; Pasquier, V. An Alternative to quintessence. Phys. Lett. B 2001, 511, 265–268. [Google Scholar] [CrossRef]
- Panotopoulos, G.; Lopes, I.; Rincón, Á. Lagrangian formulation for an extended cosmological equation-of-state. Phys. Dark Univ. 2021, 31, 100751. [Google Scholar] [CrossRef]
- Aziz, A.; Ray, S.; Rahaman, F.; Khlopov, M.; Guha, B.K. Constraining values of bag constant for strange star candidates. Int. J. Mod. Phys. D 2019, 28, 1941006. [Google Scholar] [CrossRef]
- Chanmugan, G. Radial oscillations of zero-temperature white dwarfs and neutron stars below nuclear densities. Astrophys. J. 1977, 217, 799. [Google Scholar] [CrossRef]
- Vath, H.M.; Chanmugan, G. Radial oscillations of neutron stars and strange stars. Astron. Astrophys. 1992, 260, 250–254. [Google Scholar]
- Jiménez, J.C.; Fraga, E.S. Radial Oscillations of Quark Stars Admixed with Dark Matter. Universe 2022, 8, 34. [Google Scholar] [CrossRef]
- Kain, B. Dark matter admixed neutron stars. Phys. Rev. D 2021, 103, 043009. [Google Scholar] [CrossRef]
- Panotopoulos, G.; Lopes, I. Radial oscillations of strange quark stars admixed with fermionic dark matter. Phys. Rev. D 2018, 98, 083001. [Google Scholar] [CrossRef]
- Buchdahl, H.A. General Relativistic Fluid Spheres. Phys. Rev. 1959, 116, 1027. [Google Scholar] [CrossRef]
- Moustakidis, C.C. The stability of relativistic stars and the role of the adiabatic index. Gen. Rel. Grav. 2017, 49, 68. [Google Scholar] [CrossRef]
- Mak, M.K.; Harko, T. An Exact Anisotropic Quark Star Model. Chin. J. J. Astron. Astrophys. 2002, 2002, 248. [Google Scholar] [CrossRef]
- Deb, D.; Chowdhury, S.R.; Ray, S.; Rahaman, F.; Guha, B.K. Relativistic model for anisotropic strange stars. Ann. Phys. 2017, 387, 239. [Google Scholar] [CrossRef]
- Deb, D.; Chowdhury, S.R.; Ray, S.; Rahaman, F. A New Model for Strange Stars. Gen. Rel. Grav. 2018, 50, 112. [Google Scholar] [CrossRef]
- Balart, L.; Panotopoulos, G.; Rincón, Á. Regular charged black holes, energy conditions and quasinormal modes. arXiv 2023, arXiv:2309.01910. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).