Abstract
The ALICE collaboration recently reported the mean transverse momentum as a function of charged-particle multiplicity for different pp-collision classes defined based on the “jettiness” of the event. The event “jettiness” is quantified using transverse spherocity that is measured at midpseudorapidity () considering charged particles with transverse momentum within GeV/c. Comparisons to PYTHIA 8 (tune Monash) predictions show a notable disagreement between the event generator and data for jetty events that increases as a function of charged-particle multiplicity. This paper reports on the origin of such a disagreement. Since at intermediate and high ( GeV/c), the spectral shape is expected to be modified by color reconnection or jets, their effects on the average are studied. The results indicate that the origin of the discrepancy is the overpredicted multijet yield by PYTHIA 8, which increases with the charged-particle multiplicity. This finding is important to understand the way transverse spherocity and multiplicity bias the pp collisions and how well models like PYTHIA 8 reproduce those biases. The studies are pertinent since transverse spherocity is currently used as an event classifier by experiments at the LHC.
1. Introduction
One of the most unexpected results at the LHC has been the discovery of collective-like effects in high-multiplicity pp interactions (small-collision systems) [1]. Thus, the study of high-multiplicity pp collisions has become more than pertinent. Several theoretical approaches have been suggested to explain these effects. For example, in the range of applicability of the color-glass condensate effective field theory, the flow-like behavior can be produced in the early stages of the collision [2,3]. Alternatively, the effects could develop during the collective evolution, where hydrodynamics is applicable [4,5,6]. Other approaches implemented in Monte Carlo event generators like PYTHIA 8 [7] employ effects such as color reconnection or rope hadronization to perform a microscopic description of the system [3,8]. Indeed, it has been shown that PYTHIA 8 tune Monash [9] can produce flow-like effects in pp collisions [10]. Therefore, any important discrepancy between PYTHIA 8 and data must be understood and aimed at checking whether a trivial effect can explain such a discrepancy or a more fundamental mechanism is missing to fully describe the data.
Charged-particle multiplicities () and distributions have been extensively studied by experiments at the LHC and at RHIC in small systems [11,12,13,14,15,16,17]. The data indicate a clear increase of the with increasing multiplicity. On one hand, this phenomenon is described in PYTHIA 8 by multiparton interactions (MPI) and allowing the interaction among partons before the hadronization via color strings (color reconnection), thus hardening the spectra at intermediate but decreasing the average multiplicity [18]. On the other hand, in EPOS LHC, an event generator featuring the core–corona effect, the increase of the is determined by the collective expansion of the system [19].
One issue when pp collisions are analyzed as a function of the charged-particle multiplicity (measured in a narrow pseudorapidity interval) is that high-multiplicity events are biased towards multijet final states. The effect is illustrated when the spectra of high-multiplicity pp collisions are normalized to the analogous quantity measured in minimum-bias pp collisions. The ratio shows a continuous rise with increasing , and it becomes steeper for larger multiplicity values [20]. One way to mitigate the bias was proposed some years ago. The idea consists of measuring the “jettiness” of the event using event-shape observables like transverse spherocity [21,22,23]. Since then, different measurements have been reported using event-shape selections [24,25]. The ALICE collaboration reported the first measurement of the as a function of multiplicity for different spherocity classes [20]. Although results for minimum-bias and high-spherocity pp collisions (isotropic events) were well described by PYTHIA 8 tune Monash, the agreement was broken for low-spherocity pp collisions (jetty events). This was a surprise since Monash was obtained from a tune to LHC data and, therefore, is known to describe several observables of unidentified charged particles [9]. In this paper, the origin of this discrepancy is studied, focusing on color reconnection as it is known to modify the -spectral shape at intermediate ( GeV/c). Since in this range, the transition between soft and hard processes occurs, the impact of color reconnection and jets is also explored. Another motivation is the bias of the high-multiplicity pp sample towards multijet final states.
This paper is organized as follows: Section 2 provides a brief description of event shapes and the Monte Carlo event generator. Section 3 explores the origin of the difference between data and PYTHIA 8, as well as the impact of jets on reconciling the event generator and data. Finally, Section 4 summarizes the conclusions.
2. Spherocity and PYTHIA 8 Event Generators
Event shapes are sensitive to the spatial distribution of particles produced in a collision. They have been extensively used to characterize QCD in electron-positron collisions, for example, in the extraction of the strong-coupling constant, understanding the hadronization process, or even in the parton shower tuning in event generators [26]. In hadronic interactions, event shapes are restricted to the transverse plane relative to the beam direction, making the observables insensitive to the boost along the beam direction [27].
Among the event shapes currently in use, transverse spherocity () has shown to be a good tool to classify the high-multiplicity pp collisions as either multijet final states (jetty) or uniform particle emission (isotropic) [24]. Jetty events are associated with jet topologies surrounded by the underlying event, while isotropic events are related to collisions dominated by the underlying event, i.e., several semi-hard parton-parton scatterings taking place within the same pp collision. Transverse spherocity, from now on called spherocity, is defined relative to a unit vector () that minimizes the ratio:
the sum runs over all primary charged particles with GeV/c and within . The primary charged particles [28] are those with a mean proper lifetime larger than 1 cm/c, which are either produced directly in the interaction or from decays of particles with mean proper lifetime smaller than 1 cm/c. Spherocity is a normalized quantity and consequently has extreme values of 0 and 1, corresponding to jetty and isotropic events, respectively. Since spherocity is implicitly multiplicity dependent, in order to disentangle the multiplicity from the event-shape effects, the analysis must be double differential. For a fixed multiplicity value, the multiplicity effect becomes factorized, and therefore, any modification in particle production can be attributed to the event-shape selection. Nonetheless, selecting pp collisions with high charged-particle multiplicity biases the sample, affecting different observables. For instance, the neutral-to-charged kaon ratio is known to decrease when the midrapidity charged-particle multiplicity increases [29]. In PYTHIA 8, events with an isotropic distribution of particles are associated with high underlying-event (UE) activity and, therefore, with many MPI. Contrarily, the UE activity decreases when spherocity is reduced.
As different physics aspects cannot be extracted from theoretical grounds, event generators rely on some sets of tuned parameters to enhance the predictive power. In this paper, the tune Monash, a set of parameters extracted from and data, is used in the PYTHIA 8 simulations [7,9]. During the developing parton shower of a hadronic collision, quarks and gluons are connected by colored strings. Originally, string models were based on the leading color approximation where generated partons were colored and connected only to their parent emitters. In this sense, the products from different MPIs were kept independent. Color reconnection (CR) allows the interaction among partons from originally non-correlated MPIs, implying a far richer colored topology than the original leading color method [30]. The MPI-based color reconnection model implemented in PYTHIA 8 Monash sets the probability of a low- parton to be merged with a higher- one in such a way that the total string length becomes minimized. The CR mechanism is governed by a parameter called reconnection range (), with a value of 1.8 for the Monash tune.
3. Average Transverse Momentum as a Function of Multiplicity and Spherocity
To compare with available ALICE data, only pp collisions producing at least one charged particle with in the pseudorapidity interval are used. This particular selection is called INEL > 0. Following the experimental definition of spherocity, the minimum number of particles in the selected event must be at least three, and a restricted range of 0.15 to 10 GeV/c is demanded [20]. With this information, it is possible to compute a distribution for each event multiplicity and derive the percentiles corresponding to each interval. For multiplicity, all primary charged particles with and within are considered. Events falling within the 0–10% spherocity class are labeled as a jetty, while those in the opposite extreme range of 90–100% are the isotropic events. Finally, the is computed per event multiplicity in each class.
3.1. Color Reconnection Effects
Figure 1 presents the as a function of d/d for isotropic and jetty events. Data are compared with PYTHIA 8 Monash and EPOS LHC predictions [19], and the results are fully consistent with those reported in Ref. [20]. For isotropic events, both event generators can correctly reproduce the data when d/d> 12. For jetty events, only EPOS LHC can describe the data within the full multiplicity range. Indeed, PYTHIA 8 Monash completely falls away from the systematic uncertainties. Furthermore, the data-to-model ratio shows a minimum at d/d ≈ 6 followed by a maximum and then a fast-increasing divergence. The main difference between the two models is the way the soft component of the collision is treated. In PYTHIA 8, during the hard scattering process, partons may emit initial- and final-state radiation (ISR and FSR), which are simulated using parton shower algorithms [7]. In PYTHIA 8-tune Monash, the hard scattering and parton showers are accompanied by MPI and beam remnants. Colored strings are formed, connecting all the final-state partons and beam remnants. The hadronization mechanism in PYTHIA 8 is based on the Lund string fragmentation model [7], followed by particle decays. The hadronization process leads to the production of jets and the UE. On the other hand, the event generation process in EPOS LHC [19] arises from the parton-based Gribov–Regge theory [31], pQCD, and the Lund string model. As discussed in Ref. [19], an elementary scattering corresponds to a scattering of primary partons, which contains a hard scattering (pQCD) accompanied by ISR and FSR. String hadronization relies on the local density of string segments per volume unit with respect to a critical density parameter. Each string is classified according to a core–corona approach where a low-density corona region accompanies a high-density core region [31]. In the core, the string energy density is sufficient to invoke a quark–gluon plasma description that is subject to hydrodynamic evolution [32].
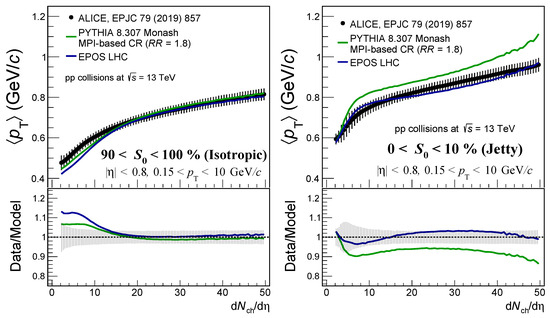
Figure 1.
Average transverse momentum as a function of d/d for pp collisions at = 13 TeV for two different spherocity classes: isotropic (left) and jetty (right). Black points correspond to data, and error bars are the associated systematic uncertainties. Data are compared to two different Monte Carlo predictions (solid lines). The green line is the result of PYTHIA 8 Monash, while the blue line is the result of the EPOS LHC. The bottom panel presents the data-to-model ratio, where the shaded area around unity is the systematic uncertainty.
To understand the disagreement between PYTHIA 8 Monash and data for jetty events, the contribution of particles within different intervals to is studied. Figure 2 presents the as a function of d/d for isotropic and jetty events. The contribution of particles with transverse momentum within GeV/c (low- particles), GeV/c (intermediate- particles) and GeV/c (high- particles) is shown. Isotropic events are fully dominated by low- particles up to d/d ≈ 30. As a result, below this threshold, the shape of closely resembles the shape dictated by the most inclusive . For high-multiplicity events, the increase of the is influenced by intermediate- particles. Jetty events show a completely different behavior. Up to d/d ≈ 30, the shape of the most inclusive is mostly due to low- and intermediate- particles, but there is also a non-negligible contribution from high- particles. Finally, the fast increase of the in the high-multiplicity regime (the third rise of the average as a function of multiplicity) is mainly driven by high- particles.
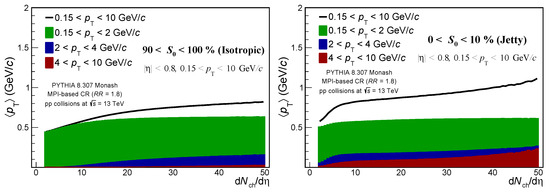
Figure 2.
Average as a function of d/d for pp collisions at = 13 TeV for two different spherocity classes: isotropic (left) and jetty (right). Black line is the -integrated distribution, green area is for low- particles with GeV/c, blue for intermediate- particles with GeV/c, and red area for high- particles with GeV/c.
Since CR is known to modify the spectral shape, different CR models were tested. The first one employs a new CR method available in PYTHIA 8 that is based on QCD rules to determine the string length minimization. This model allows the formation of topological structures (junctions) when three colored strings meet at a single point. This implies that baryon production is enhanced with respect to the default CR approach [18]. The simulation with this method is labeled as PYTHIA 8 Monash (QCD-based CR) in Figure 3. The agreement with data in isotropic events becomes worse, in particular for d/d< 25. For jetty events, there is basically no difference relative to PYTHIA 8 Monash. The second simulation is also based on PYTHIA 8 Monash but with a reconnection range value of 1.4, slightly smaller than the default one. This is labeled as PYTHIA 8 Monash () in Figure 3. Lowering the reduces the reconnection probability, increasing the particle multiplicity and decreasing the of the emitted particles. As a consequence, the average transverse momentum of the event is also reduced. Results confirm this statement both for isotropic and jetty events, from PYTHIA 8 Monash () is systematically below the prediction from PYTHIA 8 Monash (). This slight modification in the greatly improves the agreement with data in jetty events; however, the third rise of is still observed. For isotropic events, the predicted by PYTHIA 8 Monash () is worst in the full multiplicity interval relative to the default case.
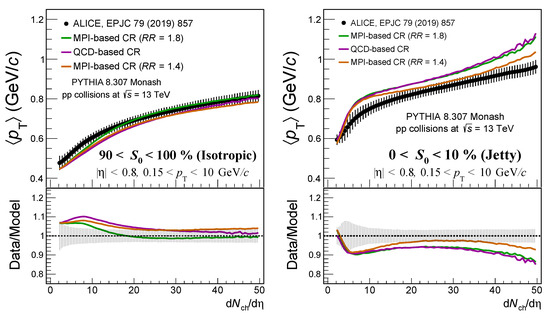
Figure 3.
Average as a function of d/d for pp collisions at = 13 TeV for two different spherocity classes: isotropic (left) and jetty (right). Black markers correspond to data, and error bars are the associated systematic uncertainties. Data are compared to three different Monte Carlo predictions (solid lines). The green line is the result from PYTHIA 8 Monash (default ), purple represents the PYTHIA 8 color reconnection based on a QCD model, and the orange line is PYTHIA 8 Monash (). The bottom panel presents the data-to-model ratio, where the shaded area around unity is the systematic uncertainty.
Figure 4 shows the probability density of charged-particle multiplicity for PYTHIA 8 Monash with the reconnection rage values and (default). As mentioned above, a variation of induces a modification of the particle production. As a matter of fact, both sets of simulations have the same results for d/d ≲ 25. Above this value, setting over predicts the number of high-multiplicity pp collisions by a maximum of ∼20% relative to at .
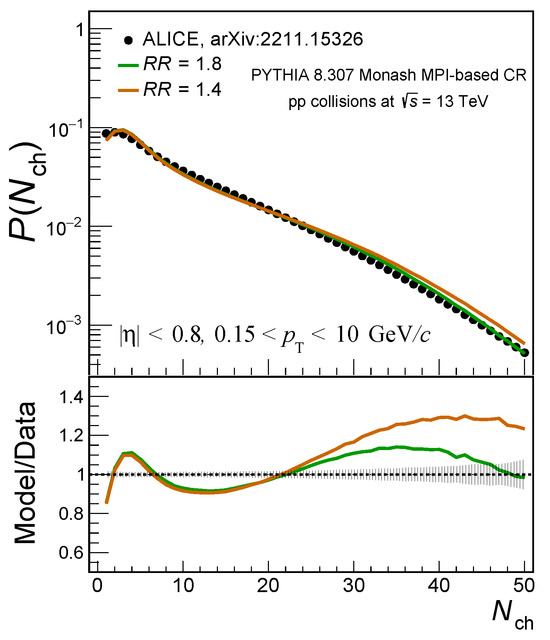
Figure 4.
Probability density of charged-particle multiplicity for PYTHIA 8 Monash with (default) and , denoted by the green and orange solid lines, respectively. Markers correspond to data, and error bars are the associated systematic uncertainties. The bottom panel shows the model-to-data ratio.
3.2. Impact of Jets on Mean
Modification of improves the agreement between PYTHIA 8 and data for jetty events, and it affects the isotropic ones. Besides that, as already stated, the third increase in at high multiplicity () is still observed even varying the parameters. We, therefore, also studied the impact of jets in the discrepancy between PYTHIA 8 Monash and data because jets are expected to modify the spectral shape at high ( GeV/c). Bear in mind that CR effects on jet observables are expected to be negligible because, for example, in the MPI-based CR model, it is easy to merge a low- system with any other but difficult to merge two high- ones [33].
A recent publication has reported the inclusive charged-particle jet differential cross-section as a function of the jet- for different jet radius (R) in pp collisions at TeV for two configurations: with and without background subtraction [34]. For both sets of results and small values of R, PYTHIA 8 Monash overestimates the minimum-bias data up to 40% at ≈ 10 GeV/c and by 10% at very high-. The discrepancy is even larger if R is increased. This is a clear indication that PYTHIA 8 Monash overestimates the jet yield. Moreover, the discrepancy becomes worse with increasing charged-particle multiplicity. This could in turn explain the overpredicted for large d/d in jetty events. A procedure aimed at quantifying the effect of such jet excess on is followed.
PYTHIA 8 Monash simulations are employed using similar event and track selection described above with some modifications: no upper limit for the particle’s transverse momentum and . FastJet is used as a jet finder with anti- recombination algorithm [35]. Transverse momentum for jets is calculated with a boosted invariant recombination scheme and (in this case is used). The inclusive charged-particle jet cross-section measured by ALICE is normalized to the corresponding MC prediction. For 5 GeV/c, a survival probability given by this ratio is assigned to each jet- interval. A random number generator is implemented to decide whether the event is kept or not. For a given jet , if the number is smaller than the corresponding survival probability, the event is kept. Otherwise, the event is discarded. At this point, two different selections are applied. The first one keeps events with at least one surviving jet (loose condition), and the second one requires events with all their jets surviving the selection (tight condition). Figure 5 shows the fraction of accepted events applying the survival probability to the leading jet (loose selection) and all jets in the event (tight selection). Since low-multiplicity events are associated with soft physics like diffractive events, the hard selection removes most of the events for . This is not an issue for our discussion because we are interested in the impact of jets at high multiplicities. The rejection factor is higher for the tight selection than for the loose selection at high multiplicity.
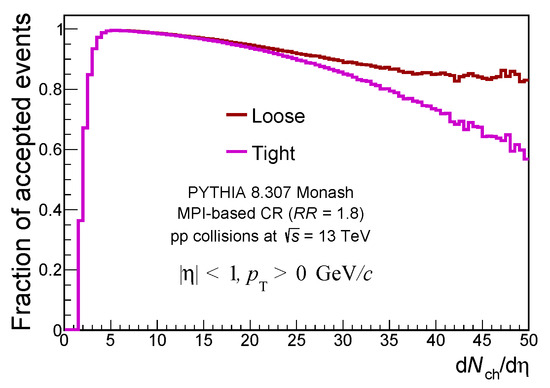
Figure 5.
Fraction of accepted events as a function of the charged-particle multiplicity. Accepted events are obtained by applying the survival probability considering the loose (red) and tight (magenta) requirements.
The selected events are, in turn, used to compute the as a function of d/d in the two spherocity classes. As the “excess” of jets has been removed, it is expected that jetty events will become depleted in the distributions, shifting the average spherocity towards values closer to one. Figure 6 presents the spherocity distributions for low (left), intermediate (center) and high (right) multiplicities considering INEL > 0 and those surviving the loose and tight selections. Only results considering PYTHIA 8 Monash are shown. For quantitative comparison, the mean values for each distribution are also displayed. These plots confirm the expected behavior already stated: jetty events are now depleted towards larger values. Furthermore, the effect is more pronounced as the multiplicity increases.
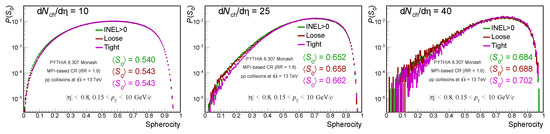
Figure 6.
PYTHIA 8 Monash spherocity distributions for low (left), intermediate (center) and high (right) multiplicity. The green line displays the spherocity-integrated result, and the other two lines are obtained for events surviving the jet excess removal: red for the loose selection and magenta for the tight one. The corresponding mean values of the distributions are also shown.
Figure 7 presents as a function of d/d in pp collisions at TeV for isotropic and jetty events. PYTHIA 8 Monash results, including INEL > 0 collisions, are compared with results obtained after applying the loose and tight selections. The prediction for isotropic events remains completely unaffected for both loose and tight selections, while for jetty events, there is a noticeable difference. Regarding the loose selection, the result is closer to data as compared to INEL > 0 for , above this threshold both results are basically the same. Regarding the tight selection, the average as a function of multiplicity is modified in the full multiplicity interval. Indeed, with this selection, the model is able to describe data nicely within systematic uncertainties. These results suggest that for PYTHIA 8 Monash to describe the data, the high-multiplicity regime should be dominated by minijet topologies rather than multijet final states. A similar conclusion was reached by applying a Machine Learning technique to data, which suggested that in data, multiparton interactions are more relevant than in MC to produce high multiplicities [36]. In other words, the bias towards hard physics is not the same in data and MC.
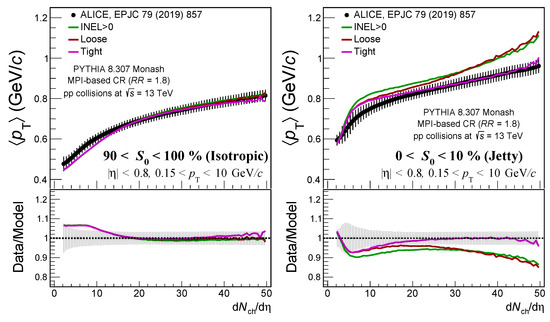
Figure 7.
Average as a function of d/d for pp collisions at = 13 TeV for two different spherocity classes: isotropic (left) and jetty (right). Black markers correspond to data, and error bars are the associated systematic uncertainties. Data are compared to three different Monte Carlo predictions (solid lines). The green line displays the result considering INEL > 0 collisions, and the other two lines are obtained for events surviving the jet excess removal: red for the loose selection and magenta for the tight one. The bottom panel presents the data-to-model ratio, where the shaded area around unity is the systematic uncertainty.
4. Conclusions
A study of the as a function of charged-particle multiplicity and spherocity has been presented. The main goal is to understand the origin of the discrepancy between data and PYTHIA 8 Monash for pp collisions with spherocity close to zero (jetty events). There, the average in PYTHIA 8 Monash exhibits a steep increase with increasing multiplicity () that is not seen in data. This effect is called the third increase of the average with multiplicity. This paper reports that the overestimate from PYTHIA 8 Monash at high-charged-particle multiplicity is mainly due to high- particles (4 10 GeV/c). Different color reconnection models were tested, as well as the impact of jets.
- Regarding color reconnection, we show that slightly decreasing the reconnection range parameter notably reduces the discrepancy, improving the agreement for jetty events but keeping the third increase of the average with multiplicity. The reduction affects the results for isotropic pp collisions in the full measured multiplicity range. Other predictions like multiplicity distributions are still in agreement with data within 20%. Results from a new color reconnection model based on QCD rules yield the same predictions as PYTHIA 8 Monash for both jetty and isotropic events.
- Regarding the impact of jets at high multiplicity, PYTHIA 8 Monash is known to overestimate jet production, in particular at high multiplicities. Based on comparisons between jet yields measured in INEL > 0 collisions, the jet excess in PYTHIA 8 Monash relative to data was estimated and used to obtain a rough estimate of the potential impact of this discrepancy on . We define the survival probability of the event based on a data-motivated selection criterion applied to the leading jet. With this implementation, PYTHIA 8 Monash keeps a very good description of the data in isotropic events, but it reconciles the simulation with experimental measurements for d/d ≲ 30 in jetty events. If the selectivity in PYTHIA 8 Monash is applied to both leading and subleading jets, the agreement between data and PYTHIA 8 Monash for jetty events becomes significantly improved in the full multiplicity interval. The results suggest that the third rise of the average for in PYTHIA 8 Monash can be attributed to the presence of multijet topologies. The implication is that, in data, high multiplicities may be dominated by minijet topologies (MPI) rather than by multijet final states.
Author Contributions
Conceptualization, A.O.; methodology, A.O. and L.V.P.; validation, A.O., L.V.P. and V.M.M.N.; formal analysis, A.O., L.V.P. and V.M.M.N.; investigation, A.O., L.V.P. and V.M.M.N.; writing—original draft preparation, A.O. and L.V.P.; writing—review and editing, A.O. and L.V.P. All authors have read and agreed to the published version of the manuscript.
Funding
A.O. and L.V.P. have received support for this work from CONAHCyT under the Grants CB No. A1-S-22917, A1-S-21560 and CF No. 2042. A.O. acknowledges the support from PAPIIT-UNAM under the Grant No. IG100524.
Data Availability Statement
Publicly available datasets were analyzed in this study. This data can be found here: https://www.hepdata.net/record/ins1735345, accessed on 5 December 2023.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Nagle, J.L.; Zajc, W.A. Small System Collectivity in Relativistic Hadronic and Nuclear Collisions. Ann. Rev. Nucl. Part. Sci. 2018, 68, 211–235. [Google Scholar] [CrossRef]
- Bzdak, A.; Schenke, B.; Tribedy, P.; Venugopalan, R. Initial state geometry and the role of hydrodynamics in proton-proton, proton-nucleus and deuteron-nucleus collisions. Phys. Rev. C 2013, 87, 064906. [Google Scholar] [CrossRef]
- Dusling, K.; Venugopalan, R. Evidence for BFKL and saturation dynamics from dihadron spectra at the LHC. Phys. Rev. D 2013, 87, 051502. [Google Scholar] [CrossRef]
- Mäntysaari, H.; Schenke, B.; Shen, C.; Tribedy, P. Imprints of fluctuating proton shapes on flow in proton-lead collisions at the LHC. Phys. Lett. B 2017, 772, 681–686. [Google Scholar] [CrossRef]
- Greif, M.; Greiner, C.; Schenke, B.; Schlichting, S.; Xu, Z. Importance of initial and final state effects for azimuthal correlations in p+Pb collisions. Phys. Rev. D 2017, 96, 091504. [Google Scholar] [CrossRef]
- Schenke, B.; Venugopalan, R. Eccentric protons? sensitivity of flow to system size and shape in p + p, p + Pb, and Pb + Pb collisions. Phys. Rev. Lett. 2014, 113, 102301. [Google Scholar] [CrossRef] [PubMed]
- Sjöstrand, T.; Ask, S.; Christiansen, J.R.; Corke, R.; Desai, N.; Ilten, P.; Mrenna, S.; Prestel, S.; Rasmussen, C.O.; Skands, P.Z. An introduction to PYTHIA 8.2. Comput. Phys. Commun. 2015, 191, 159–177. [Google Scholar] [CrossRef]
- Bierlich, C.; Gustafson, G.; Lönnblad, L.; Tarasov, A. Effects of overlapping strings in pp collisions. J. High Energy Phys. 2015, 2015, 148. [Google Scholar] [CrossRef]
- Skands, P.; Carrazza, S.; Rojo, J. Tuning PYTHIA 8.1: The monash 2013 tune. Eur. Phys. J. C 2014, 74, 3024. [Google Scholar] [CrossRef]
- Ortiz, A.; Christiansen, P.; Flores, E.C.; Cervantes, I.M.; Paić, G. Color reconnection and flowlike patterns in p p collisions. Phys. Rev. Lett. 2013, 111, 042001. [Google Scholar] [CrossRef]
- Adams, J.; Aggarwal, M.M.; Ahammed, Z.; Amonett, J.; Anderson, B.D.; Anderson, M.; Arkhipkin, D.; Averichev, G.S.; Bai, Y.; Balewski, J.; et al. The Multiplicity dependence of inclusive pt spectra from pp collisions at = 200-GeV. Phys. Rev. D 2006, 74, 032006. [Google Scholar] [CrossRef]
- Adare, A.; Afanasiev, S.; Aidala, C.; Ajitanand, N.N.; Akiba, Y.; Al-Bataineh, H.; Alexander, J.; Aoki, K.; Aphecetche, L.; Armendariz, R.; et al. Identified charged hadron production in p + p collisions at = 200 and 62.4 GeV. Phys. Rev. C 2011, 83, 064903. [Google Scholar] [CrossRef]
- Aamodt, K.; Abel, N.; Abeysekara, U.; Quintana, A.A.; Abramyan, A.; Adamová, D.; Aggarwal, M.M.; Rinella, G.A.; Agocs, A.G.; Salazar, S.A.; et al. Transverse momentum spectra of charged particles in proton–proton collisions at = 900 gev with ALICE at the LHC. Phys. Lett. B 2010, 693, 53–68. [Google Scholar] [CrossRef]
- Khachatryan, V.; Sirunyan, A.M.; Tumasyan, A.; Adam, W.; Bergauer, T.; Dragicevic, M.; Erö, J.; Fabjan, C.; Friedl, M.; Frühwirth, R.; et al. Charged Particle Multiplicities in pp Interactions at = 0.9, 2.36, and 7 TeV. J. High Energy Phys. 2011, 1, 79. [Google Scholar] [CrossRef]
- Aad, G.; Borjanović, I.; Božović-Jelisavčić, I.; Krstić, J.; Mamužić, J.; Mudrinić, M.; Popović, D.S.; Reljić, D.; Sijacki, D.; Simić, L.; et al. Charged-particle multiplicities in pp interactions measured with the ATLAS detector at the LHC. New J. Phys. 2011, 13, 053033. [Google Scholar] [CrossRef]
- Adam, J.; Adamová, D.; Aggarwal, M.M.; Rinella, G.A.; Agnello, M.; Agrawal, N.; Ahammed, Z.; Ahn, S.U.; Aiola, S.; Akindinov, A.; et al. Pseudorapidity and transverse-momentum distributions of charged particles in proton–proton collisions at = 13 TeV. Phys. Lett. B 2016, 753, 319–329. [Google Scholar] [CrossRef]
- ALICE Collaboration. Charged-particle production as a function of the relative transverse activity classifier in pp, p-Pb, and Pb-Pb collisions at the LHC. arXiv 2023, arXiv:2310.07490. [CrossRef]
- Christiansen, J.R.; Skands, P.Z. String formation beyond leading colour. J. High Energy Phys. 2015, 2015, 3. [Google Scholar] [CrossRef]
- Pierog, T.; Karpenko, I.; Katzy, J.M.; Yatsenko, E.; Werner, K. Epos lhc: Test of collective hadronization with data measured at the cern large hadron collider. Phys. Rev. C 2015, 92, 034906. [Google Scholar] [CrossRef]
- Acharya, S.; Adamová, D.; Adhya, S.P.; Adler, A.; Adolfsson, J.; Aggarwal, M.M.; Rinella, G.A.; Agnello, M.; Agrawal, N.; Ahammed, Z.; et al. Charged-particle production as a function of multiplicity and transverse spherocity in pp collisions at = 5.02 and 13 TeV. Eur. Phys. J. C 2019, 79, 857. [Google Scholar] [CrossRef]
- Ortiz, A.; Paić, G.; Cuautle, E. Mid-rapidity charged hadron transverse spherocity in pp collisions simulated with Pythia. Nucl. Phys. A 2015, 941, 78–86. [Google Scholar] [CrossRef]
- Ortiz, A. Experimental results on event shapes at hadron colliders. Adv. Ser. Direct. High Energy Phys. 2018, 29, 343–357. [Google Scholar] [CrossRef]
- Ortiz, A.; Khuntia, A.; Vázquez-Rueda, O.; Tripathy, S.; Bencedi, G.; Prasad, S.; Fan, F. Unveiling the effects of multiple soft partonic interactions in pp collisions at s = 13.6 TeV using a new event classifier. Phys. Rev. D 2023, 107, 076012. [Google Scholar] [CrossRef]
- ALICE Collaboration. Light-flavor particle production in high-multiplicity pp collisions at = 13 TeV as a function of transverse spherocity. arXiv 2023, arXiv:2310.10236. [CrossRef]
- ALICE Collaboration. Femtoscopic correlations of identical charged pions and kaons in pp collisions at = 13 TeV with event-shape selection. arXiv 2023, arXiv:2310.07509. [CrossRef]
- Banfi, A.; Salam, G.P.; Zanderighi, G. Phenomenology of event shapes at hadron colliders. J. High Energy Phys. 2010, 2010, 38. [Google Scholar] [CrossRef]
- Velasquez, A.O.; Paic, G. Event Shape Analysis in ALICE. arXiv 2009, arXiv:0912.0909. [Google Scholar] [CrossRef]
- ALICE Collaboration. The ALICE Definition of Primary Particles; ALICE-PUBLIC-2017-005 (2017). Available online: https://cds.cern.ch/record/2270008 (accessed on 1 January 2024).
- Acharya, S.; Adamová, D.; Adler, A.; Adolfsson, J.; Aggarwal, M.M.; Rinella, G.A.; Agnello, M.; Agrawal, N.; Ahammed, Z.; Ahn, S.U.; et al. Multiplicity dependence of light-flavor hadron production in pp collisions at = 7 TeV. Phys. Rev. C 2019, 99, 024906. [Google Scholar] [CrossRef]
- Buckley, A.; Butterworth, J.; Gieseke, S.; Grellscheid, D.; Höche, S.; Hoeth, H.; Krauss, F.; Lönnblad, L.; Nurse, E.; Richardson, P.; et al. General-purpose event generators for LHC physics. Phys. Rep. 2011, 504, 145–233. [Google Scholar] [CrossRef]
- Ene, A.C.; Jipa, A.; Giubega, L.-E. Study of Monte Carlo event generators for proton-proton collisions at LHC energies in the forward region. Chin. Phys. C 2019, 43, 083001. [Google Scholar] [CrossRef]
- The ALICE experiment—A journey through QCD. arXiv 2022, arXiv:2211.04384. [CrossRef]
- Bierlich, C.; Chakraborty, S.; Desai, N.; Gellersen, L.; Helenius, I.; Ilten, P.; Lönnblad, L.; Mrenna, S.; Prestel, S.; Preuss, C.T.; et al. A comprehensive guide to the physics and usage of PYTHIA 8.3. Scipost Phys. Codebases 2022, 008. [Google Scholar] [CrossRef]
- Acharya, S.; Adamova, D.; Adler, A.; Adolfsson, J.; Aglieri Rinella, G.; Agnello, M.; Agrawal, N.; Ahammed, Z.; Ahmad, S.; Ahn, S.U.; et al. Multiplicity dependence of charged-particle jet production in pp collisions at = 13 TeV. Eur. Phys. J. C 2022, 82, 514. [Google Scholar] [CrossRef]
- Cacciari, M.; Salam, G.P.; Soyez, G. FastJet user manual. Eur. Phys. J. C 2012, 72, 1896. [Google Scholar] [CrossRef]
- Ortiz, A.; Zepeda, E.A. Extraction of the multiplicity dependence of multiparton interactions from LHC pp data using machine learning techniques. J. Phys. G 2021, 48, 085014. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).