Generalized ƒ(R,Φ, X) Gravity and the Late-Time Cosmic Acceleration
Abstract
:1. Introduction
2. Generalised Gravity Models: Formalism
3. Cosmological Applications: Late-Time Cosmic Acceleration
3.1. Brans–Dicke Type Models
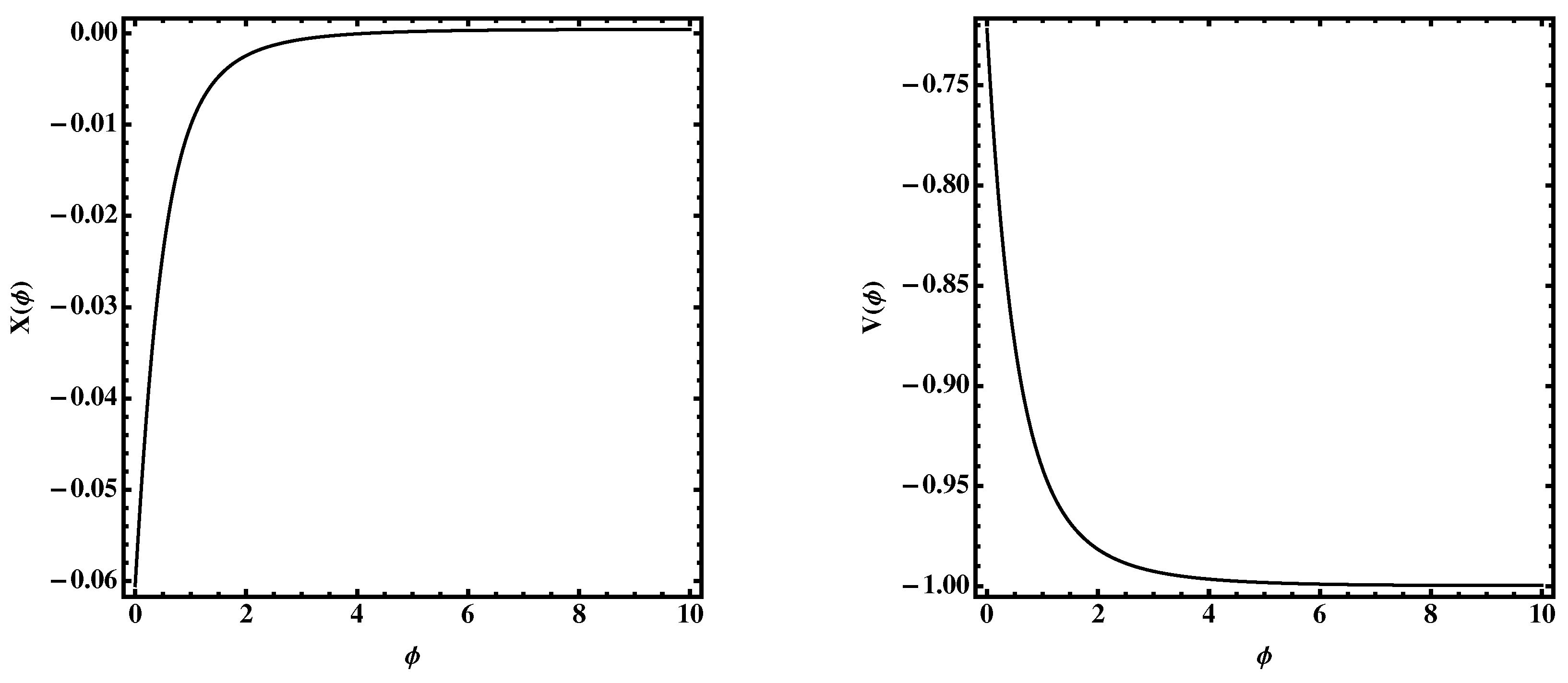
3.2. Minimally-Coupled Field Model
4. Conclusions
Acknowledgements
Author Contributions
Conflicts of Interest
References
- Perlmutter, S.; Aldering, G.; Goldhaber, G.; Knop, R.A.; Nugent, P.; Castro, P.G.; Deustua, S.; Fabbro, S.; Goobar, A.; Groom, D.E.; et al. Measurements of Omega and Lambda from 42 high red shift supernovae. Astrophys. J. 1999, 517, 565–586. [Google Scholar]
- Riess, A.G.; Filippenko, A.V.; Challis, P.; Clocchiattia, A.; Diercks, A.; Garnavich, P.M.; Gilliland, R.L.; Hogan, C.J.; Jha, S.; Kirshner, R.P.; et al. Observational evidence from supernovae for an accelerating universe and a cosmological constant. Astron. J. 1998, 116, 1009–1038. [Google Scholar] [CrossRef]
- Maartens, R. Brane world gravity. Living Rev. Relativ. 2004, 7. [Google Scholar] [CrossRef]
- Dvali, G.R.; Gabadadze, G.; Porrati, M. 4-D gravity on a brane in 5-D Minkowski space. Phys. Lett. B 2000, 485, 208–214. [Google Scholar] [CrossRef]
- De Rham, C.; Hofmann, S.; Khoury, J.; Tolley, A.J. Cascading Gravity and Degravitation. J. Cosmol. Astropart. Phys. 2008, 2008, 011. [Google Scholar] [CrossRef]
- Sotiriou, T.P.; Faraoni, V. f(R) Theories Of Gravity. Rev. Mod. Phys. 2010, 82, 451–497. [Google Scholar] [CrossRef]
- De Felice, A.; Tsujikawa, S. f(R) theories. Living Rev. Relativ. 2010, 13, 3. [Google Scholar] [CrossRef]
- Capozziello, S.; De Laurentis, M. Extended Theories of Gravity. Phys. Rep. 2011, 509, 167–321. [Google Scholar] [CrossRef]
- Lobo, F.S.N. The Dark side of gravity: Modified theories of gravity. 2008; arXiv:0807.1640[gr-qc]. [Google Scholar]
- Nojiri, S.; Odintsov, S.D. Unified cosmic history in modified gravity: From F(R) theory to Lorentz non-invariant models. Phys. Rep. 2011, 505, 59–144. [Google Scholar] [CrossRef]
- De la Cruz-Dombriz, A.; Saez-Gomez, D. Black holes, cosmological solutions, future singularities, and their thermodynamical properties in modified gravity theories. Entropy 2012, 14, 1717–1770. [Google Scholar] [CrossRef]
- Boehmer, C.G.; Tamanini, N. A New Approach to Modifying Theories of Gravity. Found. Phys. 2013, 43, 1478–1488. [Google Scholar] [CrossRef]
- Boehmer, C.G.; Tamanini, N.; Wright, M. On galaxy rotation curves from a new approach to modified gravity. 2014; arXiv:gr-qc/1403.4110. [Google Scholar]
- Allemandi, G.; Borowiec, A.; Francaviglia, M.; Odintsov, S.D. Dark energy dominance and cosmic acceleration in first order formalism. Phys. Rev. D 2005, 72, 063505. [Google Scholar] [CrossRef]
- Bertolami, O.; Boehmer, C.G.; Harko, T.; Lobo, F.S.N. Extra force in f(R) modified theories of gravity. Phys. Rev. D 2007, 75, 104016. [Google Scholar] [CrossRef]
- Harko, T.; Koivisto, T.S.; Lobo, F.S.N. Palatini formulation of modified gravity with a nonminimal curvature-matter coupling. Mod. Phys. Lett. A 2011, 26, 1467–1480. [Google Scholar] [CrossRef]
- Harko, T.; Lobo, F.S.N. Generalized curvature-matter couplings in modified gravity. Galaxies 2014, 2, 410–465. [Google Scholar] [CrossRef]
- Harko, T.; Lobo, F.S.N.; Nojiri, S.; Odintsov, S.D. f(R,T) gravity. Phys. Rev. D 2011, 84, 024020. [Google Scholar] [CrossRef]
- Haghani, Z.; Harko, T.; Lobo, F.S.N.; Sepangi, H.R.; Shahidi, S. Further matters in space-time geometry: f(R,T,RμνTμν) gravity. Phys. Rev. D 2013, 88, 044023. [Google Scholar] [CrossRef]
- Odintsov, S.D.; Sáez-Gómez, D. f(R,T,RμνTμν) gravity phenomenology and ΛCDM universe. Phys. Lett. B 2013, 725, 437–444. [Google Scholar] [CrossRef]
- Carroll, S.M.; Duvvuri, V.; Trodden, M.; Turner, M.S. Is cosmic speed-up due to new gravitational physics? Phys. Rev. D 2004, 70, 043528. [Google Scholar] [CrossRef]
- Copeland, E.J.; Sami, M.; Tsujikawa, S. Dynamics of dark energy. Int. J. Mod. Phys. D 2006, 15, 1753–1936. [Google Scholar] [CrossRef]
- Olmo, G.J. Palatini Approach to Modified Gravity: f(R) Theories and Beyond. Int. J. Mod. Phys. D 2011, 20, 413–462. [Google Scholar] [CrossRef]
- Sotiriou, T.P.; Liberati, S. Metric-affine f(R) theories of gravity. Ann. Phys. 2007, 322, 935–966. [Google Scholar] [CrossRef]
- Harko, T.; Koivisto, T.S.; Lobo, F.S.N.; Olmo, G.J. Metric-Palatini gravity unifying local constraints and late-time cosmic acceleration. Phys. Rev. D 2012, 85, 084016. [Google Scholar] [CrossRef]
- Goheer, N.; Larena, J.; Dunsby, P.K.S. Power-law cosmic expansion in f(R) gravity models. Phys. Rev. D 2009, 80, 061301. [Google Scholar] [CrossRef]
- Myrzakulov, R.; Sáez-Gómez, D.; Tureanu, A. On the ΛCDM Universe in f(G) gravity. Gen. Relativ. Gravit. 2011, 43, 1671–1684. [Google Scholar] [CrossRef]
- De la Cruz-Dombriz, A.; Dobado, A. A f(R) gravity without cosmological constant. Phys. Rev. D 2006, 74, 087501. [Google Scholar] [CrossRef]
- Elizalde, E.; Myrzakulov, R.; Obukhov, V.V.; Sáez-Gómez, D. LambdaCDM epoch reconstruction from F(R,G) and modified Gauss-Bonnet gravities. Class. Quant. Grav. 2010, 27, 095007. [Google Scholar] [CrossRef]
- Dunsby, P.K.S.; Elizalde, E.; Goswami, R.; Odintsov, S.; Sáez-Gómez, D. On the LCDM Universe in f(R) gravity. Phys. Rev. D 2010, 82, 023519. [Google Scholar] [CrossRef]
- Ade, P.A.R.; Aghanim, N.; Arnaud, M.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Banday, A.J.; Barreiro, R.B.; Bartlett, J.G.; Bartolo, N.; et al. Planck 2015 results. XIII. Cosmological parameters. 2015; arXiv:astro-ph.CO/1502.01589. [Google Scholar]
- Starobinsky, A.A. A New Type of Isotropic Cosmological Models Without Singularity. Phys. Lett. B 1980, 91, 99–102. [Google Scholar] [CrossRef]
- Tsujikawa, S.; Sami, M. A Unified approach to scaling solutions in a general cosmological background. Phys. Lett. B 2004, 603, 113–123. [Google Scholar] [CrossRef]
- Copeland, E.J.; Lee, S.J.; Lidsey, J.E.; Mizuno, S. Generalised cosmological scaling solutions. Phys. Rev. D 2005, 71, 023526. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bahamonde, S.; Böhmer, C.G.; Lobo, F.S.N.; Sáez-Gómez, D. Generalized ƒ(R,Φ, X) Gravity and the Late-Time Cosmic Acceleration. Universe 2015, 1, 186-198. https://doi.org/10.3390/universe1020186
Bahamonde S, Böhmer CG, Lobo FSN, Sáez-Gómez D. Generalized ƒ(R,Φ, X) Gravity and the Late-Time Cosmic Acceleration. Universe. 2015; 1(2):186-198. https://doi.org/10.3390/universe1020186
Chicago/Turabian StyleBahamonde, Sebastian, Christian G. Böhmer, Francisco S.N. Lobo, and Diego Sáez-Gómez. 2015. "Generalized ƒ(R,Φ, X) Gravity and the Late-Time Cosmic Acceleration" Universe 1, no. 2: 186-198. https://doi.org/10.3390/universe1020186
APA StyleBahamonde, S., Böhmer, C. G., Lobo, F. S. N., & Sáez-Gómez, D. (2015). Generalized ƒ(R,Φ, X) Gravity and the Late-Time Cosmic Acceleration. Universe, 1(2), 186-198. https://doi.org/10.3390/universe1020186








