Anti-Evaporation of Black Holes in Bigravity
Abstract
:1. Introduction
2. Bigravity Theory
2.1. The Action and Equation of Motion
2.2. Proportional Solutions
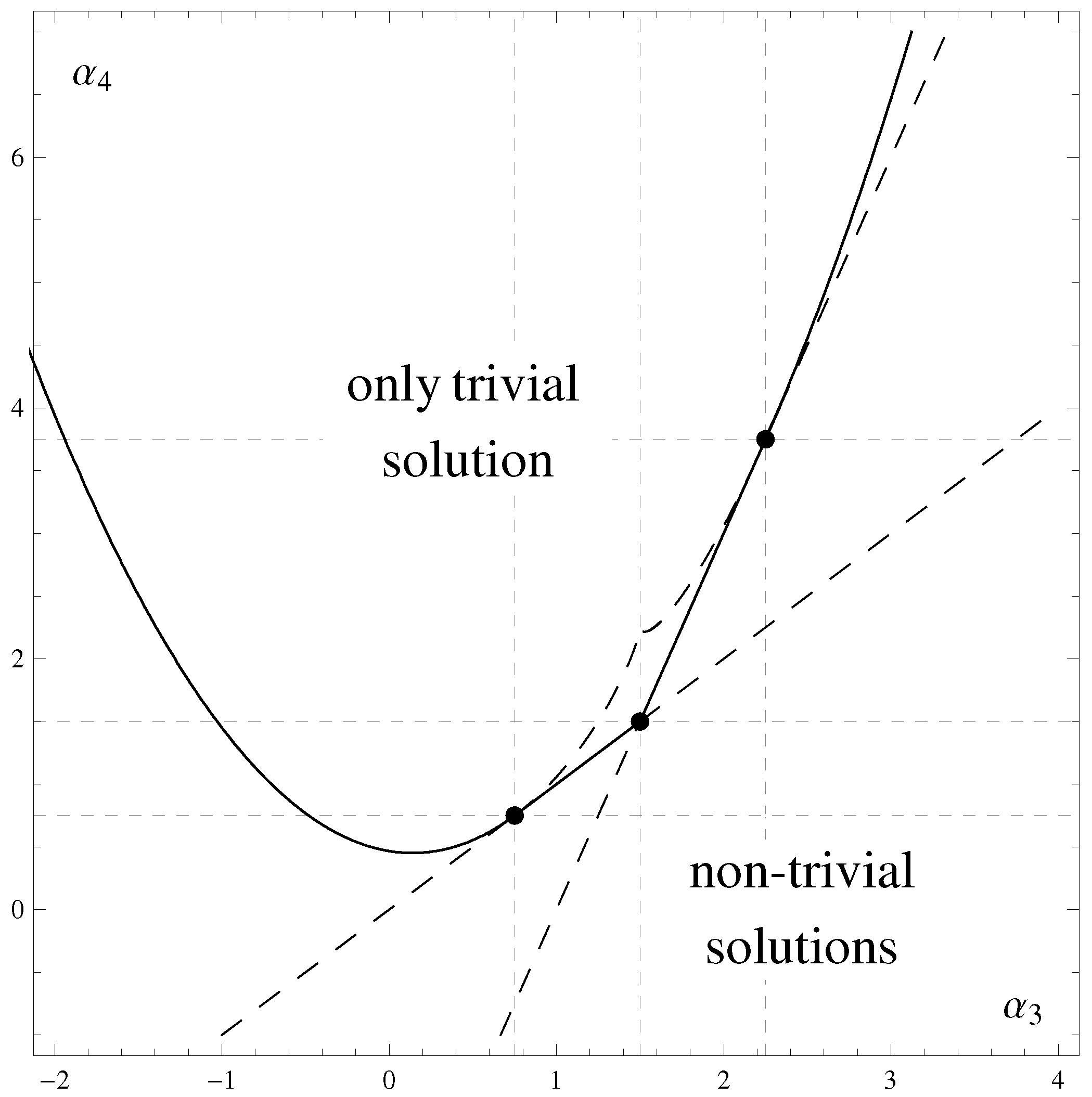
3. Stability and Anti-Evaporation of the Schwarzschild–de Sitter Space-Time
3.1. Nariai Space-Time and Anti-Evaporation
3.2. Perturbations and Stability of Bi-Diagonal Narial Solution
4. Results and Discussion
Acknowledgments
Conflicts of Interest
References
- Hassan, S.F.; Rosen, R.A. Bimetric Gravity from Ghost-free Massive Gravity. J. High Energ. Phys. 2012, 1202, 126. [Google Scholar] [CrossRef]
- Hassan, S.F.; Rosen, R.A.; Schmidt-May, A. Ghost-free Massive Gravity with a General Reference Metric. J. High Energ. Phys. 2012, 2012, 26. [Google Scholar] [CrossRef]
- de Rham, C.; Gabadadze, G. Generalization of the Fierz-Pauli Action. Phys. Rev. D 2010, 82, 044020. [Google Scholar] [CrossRef]
- de Rham, C.; Gabadadze, G.; Tolley, A.J. Resummation of Massive Gravity. Phys. Rev. Lett. 2011, 106, 231101. [Google Scholar] [CrossRef]
- Hassan, S.F.; Rosen, R.A. Resolving the Ghost Problem in non-Linear Massive Gravity. Phys. Rev. Lett. 2012, 108, 041101. [Google Scholar] [CrossRef]
- Hinterbichler, K. Theoretical Aspects of Massive Gravity. Rev. Mod. Phys. 2012, 84, 671–710. [Google Scholar] [CrossRef]
- de Rham, C. Massive Gravity. Living Rev. Rel. 2014, 17, 7. [Google Scholar] [CrossRef]
- Fierz, M.; Pauli, W. On relativistic wave equations for particles of arbitrary spin in an electromagnetic field. Proc. Roy. Soc. Lond. A 1939, 173, 211–232. [Google Scholar] [CrossRef]
- van Dam, H.; Veltman, M.J.G. Massive and massless Yang-Mills and gravitational fields. Nucl. Phys. B 1970, 22, 397–411. [Google Scholar] [CrossRef]
- Zakharov, V.I. Linearized gravitation theory and the graviton mass. JETP Lett. 1970, 12, 312–314. [Google Scholar]
- Vainshtein, A.I. To the problem of nonvanishing gravitation mass. Phys. Lett. B 1972, 39, 393–394. [Google Scholar] [CrossRef]
- Boulware, D.G.; Deser, S. Can gravitation have a finite range? Phys. Rev. D 1972, 6, 3368–3382. [Google Scholar] [CrossRef]
- Arkani-Hamed, N.; Georgi, H.; Schwartz, M.D. Effective field theory for massive gravitons and gravity in theory space. Ann. Phys. 2003, 305, 96–118. [Google Scholar] [CrossRef]
- Boulanger, N.; Damour, T.; Gualtieri, L.; Henneaux, M. Inconsistency of interacting, multigraviton theories. Nucl. Phys. B 2001, 597, 127–171. [Google Scholar] [CrossRef]
- Rosen, N. General Relativity and Flat Space. I. Phys. Rev. 1940, 57, 147–150. [Google Scholar] [CrossRef]
- Rosen, N. General Relativity and Flat Space. II. Phys. Rev. 1940, 57, 150–153. [Google Scholar] [CrossRef]
- Rosen, N. Bimetric Theory of Gravitation. In Proceedings of the topics in theoretical and experimental gravitation physics, Erice 1975, New York, NY, USA, 13-25 March 1975; 1977; pp. 273–294. [Google Scholar]
- Isham, C.J.; Salam, A.; Strathdee, J.A. F-dominance of gravity. Phys. Rev. D 1971, 3, 867–873. [Google Scholar] [CrossRef]
- Isham, C.J.; Storey, D. Exact Spherically Symmetric Classical Solutions for the F-G Theory of Gravity. Phys. Rev. D 1978, 18, 1047–1052. [Google Scholar] [CrossRef]
- Salam, A.; Sivaram, C. Strong gravity approach to QCD and confinement. Mod. Phys. Lett. A 1993, 8, 321–326. [Google Scholar] [CrossRef]
- Hinterbichler, K. Ghost-Free Derivative Interactions for a Massive Graviton. J. High Energ. Phys. 2013, 2013, 102. [Google Scholar] [CrossRef]
- Kimura, R.; Yamauchi, D. Derivative interactions in de Rham-Gabadadze-Tolley massive gravity. Phys. Rev. D 2013, 88, 084025. [Google Scholar] [CrossRef]
- Ohara, Y.; Akagi, S.; Nojiri, S. Renormalizable toy model of massive spin two field and new bigravity. Phys. Rev. D 2014, 90, 043006:1–043006:4. [Google Scholar] [CrossRef]
- Ohara, Y.; Akagi, S.; Nojiri, S. Stability analysis for new theories of massive spin-two particle and black hole entropy of new bigravity. 2014. arXiv:1407.5765 [hep-th]. [Google Scholar]
- Akagi, S.; Ohara, Y.; Nojiri, S. New massive spin two model on a curved spacetime. Phys. Rev. D 2014, 90, 123013:1–123013:12. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Modified gravity with negative and positive powers of the curvature: Unification of the inflation and of the cosmic acceleration. Phys. Rev. D 2003, 68, 123512. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Unified cosmic history in modified gravity: From F(R) theory to Lorentz non-invariant models. Phys. Rept. 2011, 505, 59–144. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D.; Shirai, N. Variety of cosmic acceleration models from massive F(R) bigravity. J. Cosmol. Astropart. Phys. 2013, 2013, 020. [Google Scholar]
- Nojiri, S.; Odintsov, S.D. Ghost-free F(R) bigravity and accelerating cosmology. Phys. Lett. B 2012, 716, 377–383. [Google Scholar] [CrossRef]
- Klusoň, J.; Nojiri, S.; Odintsov, S.D. New proposal for non-linear ghost-free massive F(R) gravity: Cosmic acceleration and Hamiltonian analysis. Phys. Lett. B 2013, 726, 918–925. [Google Scholar] [CrossRef]
- Bamba, K.; Makarenko, A.N.; Myagky, A.N.; Nojiri, S.; Odintsov, S.D. Bounce cosmology from F(R) gravity and F(R) bigravity. J. Cosmol. Astropart. Phys. 2014, 2014, 008. [Google Scholar]
- Berg, M.; Buchberger, I.; Enander, J.; Mortsell, E.; Sjors, S. Growth Histories in Bimetric Massive Gravity. J. Cosmol. Astropart. Phys. 2012, 2012, 021. [Google Scholar] [CrossRef]
- von Strauss, M.; Schmidt-May, A.; Enander, J.; Mortsell, E.; Hassan, S.F. Cosmological Solutions in Bimetric Gravity and their Observational Tests. J. Cosmol. Astropart. Phys. 2012, 2012, 042. [Google Scholar] [CrossRef]
- Akrami, Y.; Koivisto, T.S.; Sandstad, M. Accelerated expansion from ghost-free bigravity: A statistical analysis with improved generality. J. High Energ. Phys. 2013, 2013, 99. [Google Scholar] [CrossRef]
- Akrami, Y.; Koivisto, T.S.; Mota, D.F.; Sandstad, M. Bimetric gravity doubly coupled to matter: Theory and cosmological implications. J. Cosmol. Astropart. Phys. 2013, 2013, 046. [Google Scholar] [CrossRef]
- Tamanini, N.; Saridakis, E.N.; Koivisto, T.S. The Cosmology of Interacting Spin-2 Fields. J. Cosmol. Astropart. Phys. 2014, 2014, 15. [Google Scholar] [CrossRef]
- Rossi, N. Dark Halo or Bigravity? Eur. Phys. J. ST 2008, 163, 291–296. [Google Scholar] [CrossRef]
- Banados, M.; Gomberoff, A.; Rodrigues, D.C.; Skordis, C. A Note on bigravity and dark matter. Phys. Rev. D 2009, 79, 063515. [Google Scholar] [CrossRef]
- Aoki, K.; Maeda, K. Cosmology in ghost-free bigravity theory with twin matter fluids: The origin of “dark matter”. Phys. Rev. D 2014, 89, 064051. [Google Scholar] [CrossRef]
- Aoki, K.; Maeda, K. Dark matter in ghost-free bigravity theory: From a galaxy scale to the universe. Phys. Rev. D 2014, 90, 124089. [Google Scholar] [CrossRef]
- De Felice, A.; Nakamura, T.; Tanaka, T. Possible existence of viable models of bi-gravity with detectable graviton oscillations by gravitational wave detectors. Prog. Theor. Exp. Phys. 2014, 2014, 043E01:1–043E01:4. [Google Scholar] [CrossRef]
- Katsuragawa, T. Properties of Bigravity Solutions in a Solvable Class. Phys. Rev. D 2014, 89, 124007. [Google Scholar] [CrossRef]
- Katsuragawa, T.; Nojiri, S. Stability and Anti-evaporation of the Schwarzschild-de Sitter Black Holes in Bigravity. Phys. Rev. D 2015, 91, 084001:1–084001:8. [Google Scholar] [CrossRef]
- de Rham, C.; Heisenberg, L.; Ribeiro, R.H. Ghosts and matter couplings in massive gravity, bigravity and multigravity. Phys. Rev. D 2014, 90, 124042. [Google Scholar] [CrossRef]
- de Rham, C.; Heisenberg, L.; Ribeiro, R.H. On couplings to matter in massive (bi-)gravity. Class. Quant. Grav. 2015, 32, 035022. [Google Scholar] [CrossRef]
- Bousso, R.; Hawking, S.W. (Anti)evaporation of Schwarzschild-de Sitter black holes. Phys. Rev. D 1998, 57, 2436–2442. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Anti-Evaporation of Schwarzschild-de Sitter Black Holes in F(R) gravity. Class. Quant. Grav. 2013, 30, 125003. [Google Scholar] [CrossRef]
- Sebastiani, L.; Momeni, D.; Myrzakulov, R.; Odintsov, S.D. Instabilities and (anti)-evaporation of Schwarzschild-de Sitter black holes in modified gravity. Phys. Rev. D 2013, 88, 104022:1–104022:10. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Instabilities and anti-evaporation of Reissner-Nordstrom black holes in modified F(R) gravity. Phys. Lett. B 2014, 735, 376–382. [Google Scholar] [CrossRef]
- Bousso, R.; Hawking, S.W. Trace anomaly of dilaton coupled scalars in two-dimensions. Phys. Rev. D 1997, 56, 7788–7791. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Trace anomaly and nonlocal effective action for 2-D conformally invariant scalar interacting with dilaton. Mod. Phys. Lett. A 1997, 12, 2083–2087. [Google Scholar] [CrossRef]
- Hayward, J.D. Entropy in the Russo-Susskind-Thorlacius model. Phys. Rev. D 1995, 52, 2239–2244. [Google Scholar] [CrossRef]
- Brito, R.; Cardoso, V.; Pani, P. Massive spin-2 fields on black hole spacetimes: Instability of the Schwarzschild and Kerr solutions and bounds on the graviton mass. Phys. Rev. D 2013, 88, 023514:1–023514:2. [Google Scholar] [CrossRef]
- Brito, R.; Cardoso, V.; Pani, P. Partially massless gravitons do not destroy general relativity black holes. Phys. Rev. D 2013, 87, 124024:1–124024:12. [Google Scholar] [CrossRef]
- Babichev, E.; Fabbri, A. Instability of black holes in massive gravity. Class. Quant. Grav. 2013, 30, 152001. [Google Scholar] [CrossRef]
- Babichev, E.; Fabbri, A. Stability analysis of black holes in massive gravity: A unified treatment. Phys. Rev. D 2014, 89, 081502. [Google Scholar] [CrossRef]
© 2015 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Katsuragawa, T. Anti-Evaporation of Black Holes in Bigravity. Universe 2015, 1, 158-172. https://doi.org/10.3390/universe1020158
Katsuragawa T. Anti-Evaporation of Black Holes in Bigravity. Universe. 2015; 1(2):158-172. https://doi.org/10.3390/universe1020158
Chicago/Turabian StyleKatsuragawa, Taishi. 2015. "Anti-Evaporation of Black Holes in Bigravity" Universe 1, no. 2: 158-172. https://doi.org/10.3390/universe1020158
APA StyleKatsuragawa, T. (2015). Anti-Evaporation of Black Holes in Bigravity. Universe, 1(2), 158-172. https://doi.org/10.3390/universe1020158




