Using Expert Driven Machine Learning to Enhance Dynamic Metabolomics Data Analysis
Abstract
1. Introduction
2. Materials and Methods
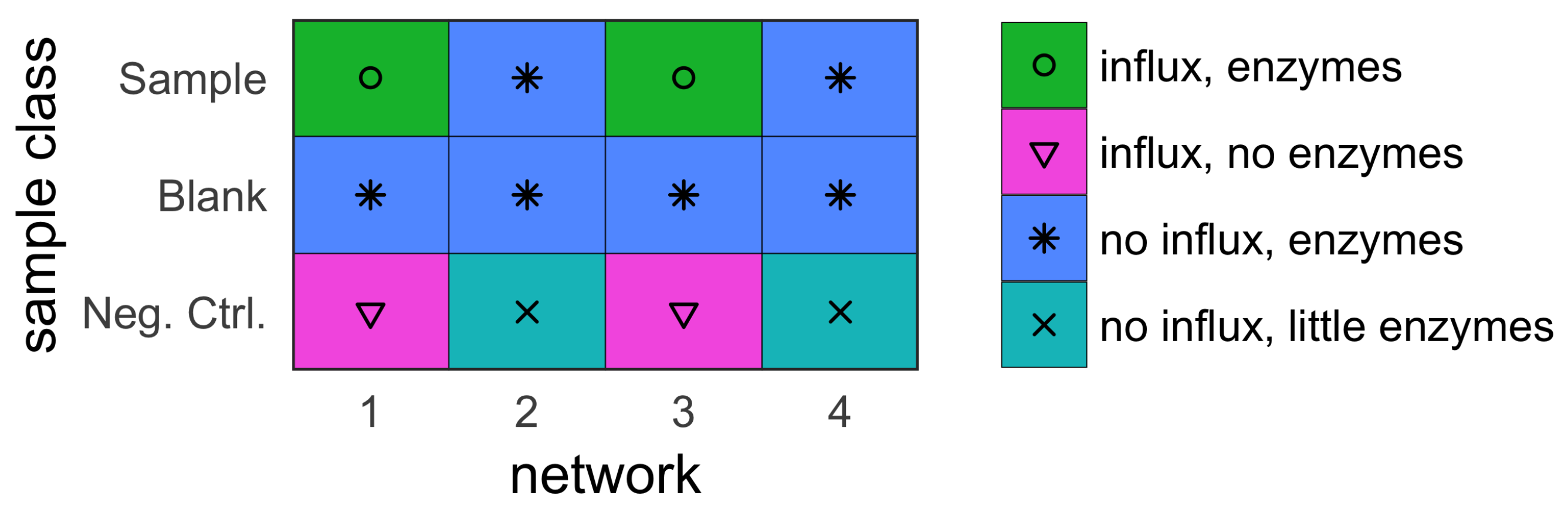
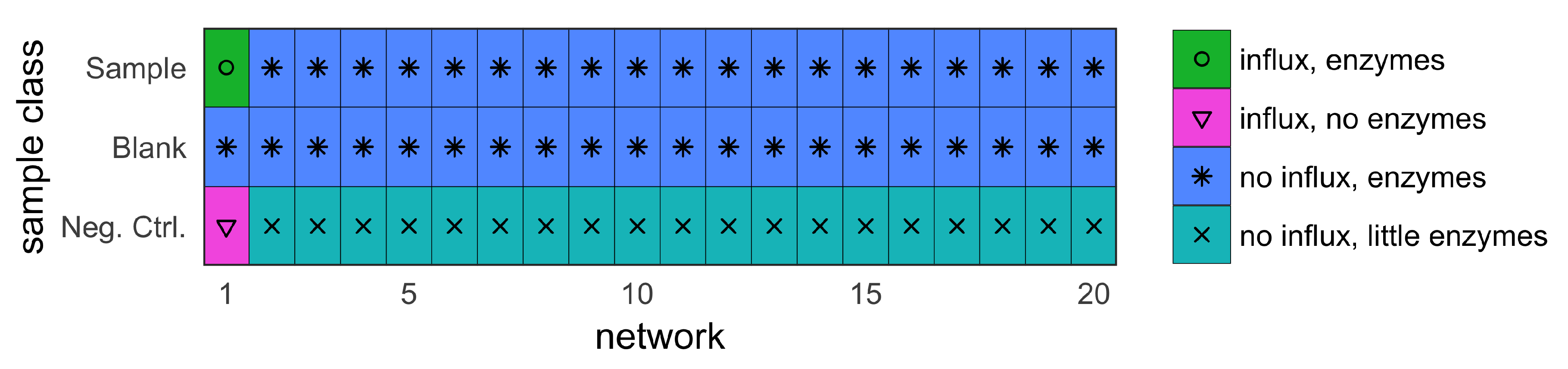
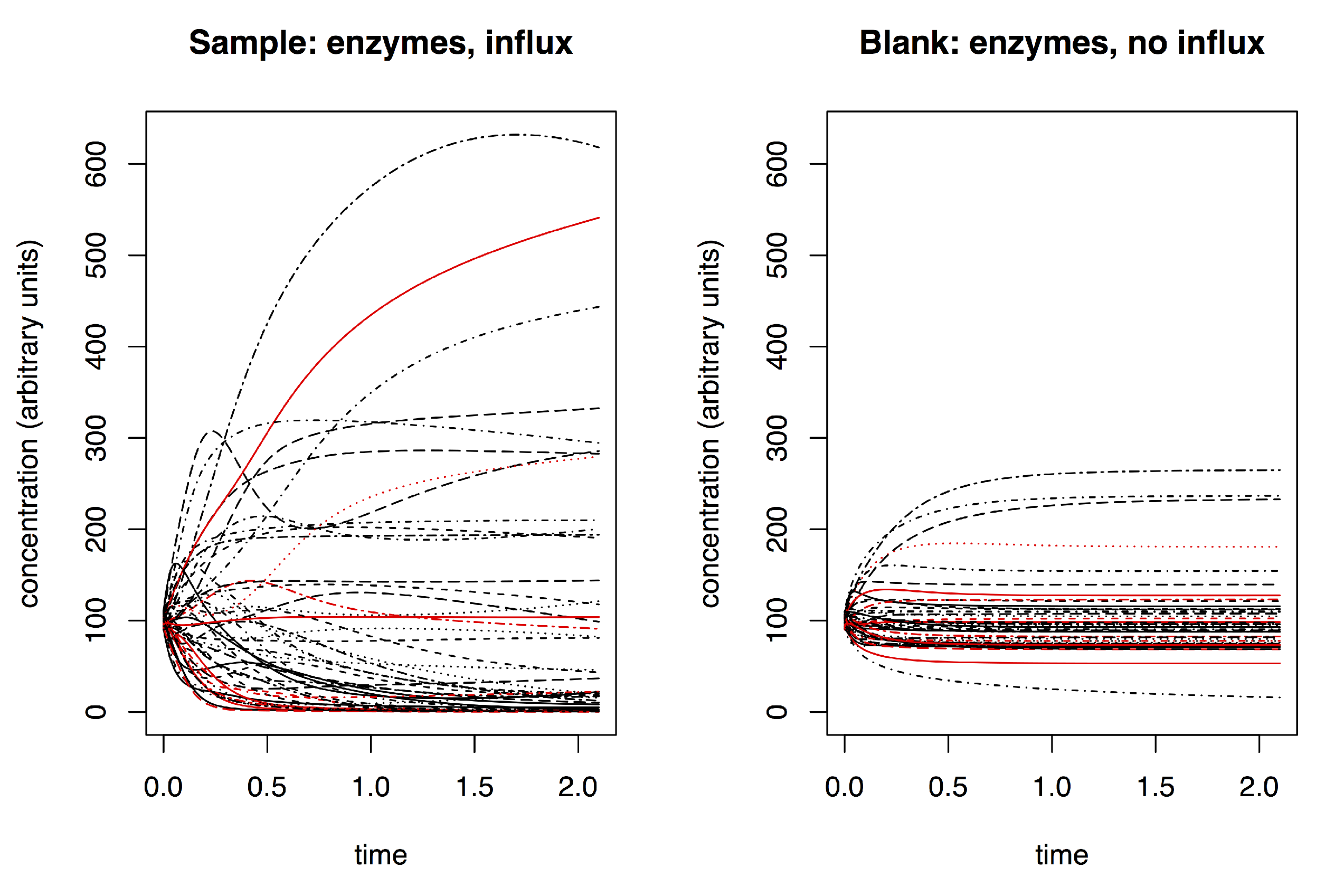
2.1. Simulating Dynamic Metabolomics Data
- (1)
- The dynamics in the data are governed by an underlying network with an appropriate connectivity distribution (the Barabási-Albert model was chosen [11,12], see Section S1 in Supplementary Materials for further discussion).
- (2)
- Nodes in the network are metabolites, which have certain starting concentrations that evolve over time.
- (3)
- Transitions in concentrations are caused by enzymes. Effectively, these are the rates/fluxes that govern flow in the network.
- (4)
- Some of these enzymes are assigned to multiple edges and are also influenced by the adjacent nodes/metabolites. That way, an external influx in metabolite X can cause a depletion of metabolite Y somewhere else in the network (X increases, thus rate/flux of X to X’ increases, which is the same rate/flux as the one from Y to Y’, thus Y depletes).
- (5)
- The intake of certain compounds (e.g., nutrients) causes an external influx in specific metabolites, (temporary rise in concentration).
- (6)
- The rate/flux increases or decreases depending on the concentration of the metabolite causing the reaction. This increasing rate is limited and follows a sigmoidal curve.
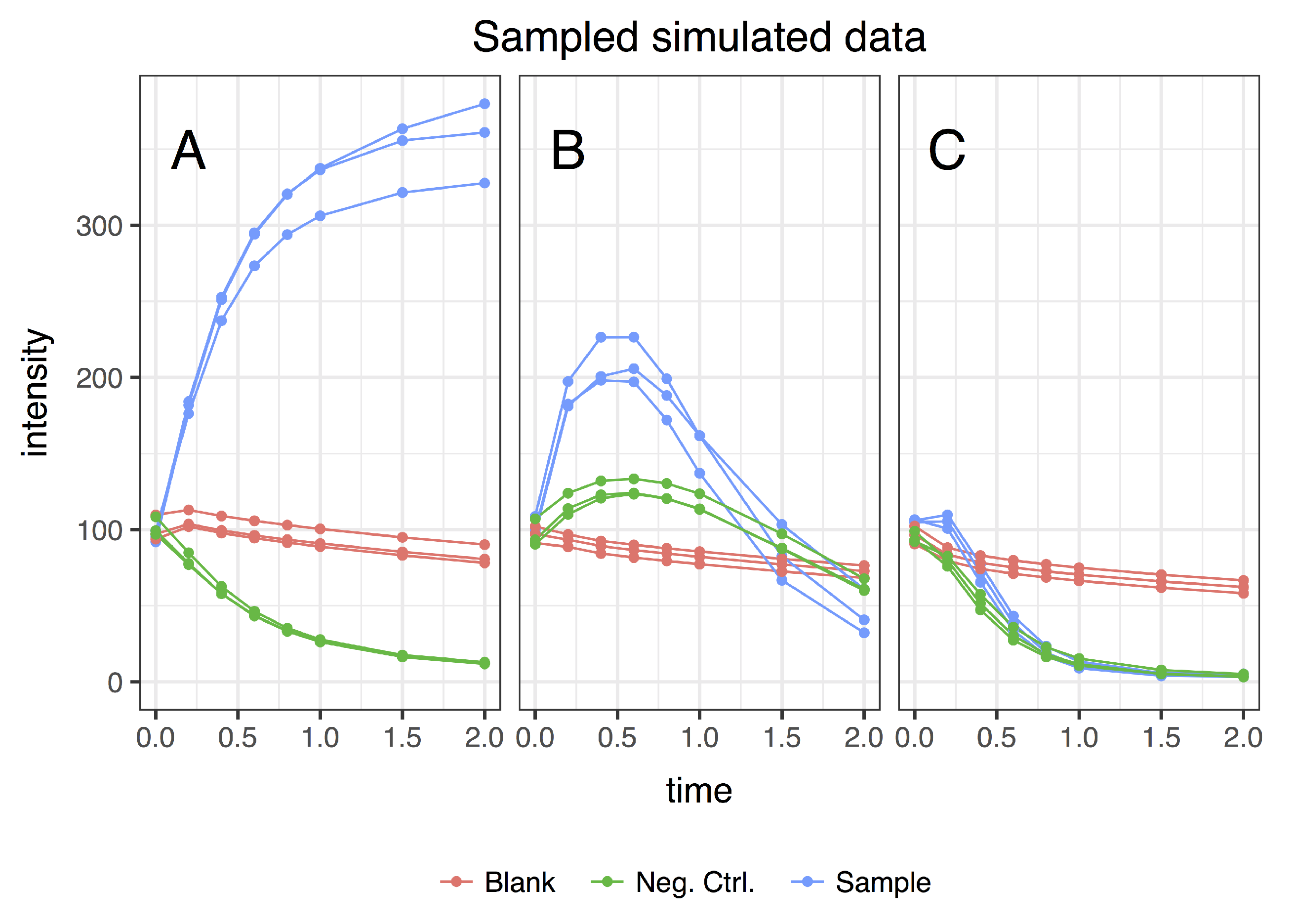
- sample (with influx and includes enzymes);
- blank (no influx, includes enzymes); and
- negative control (with influx, no enzymes).
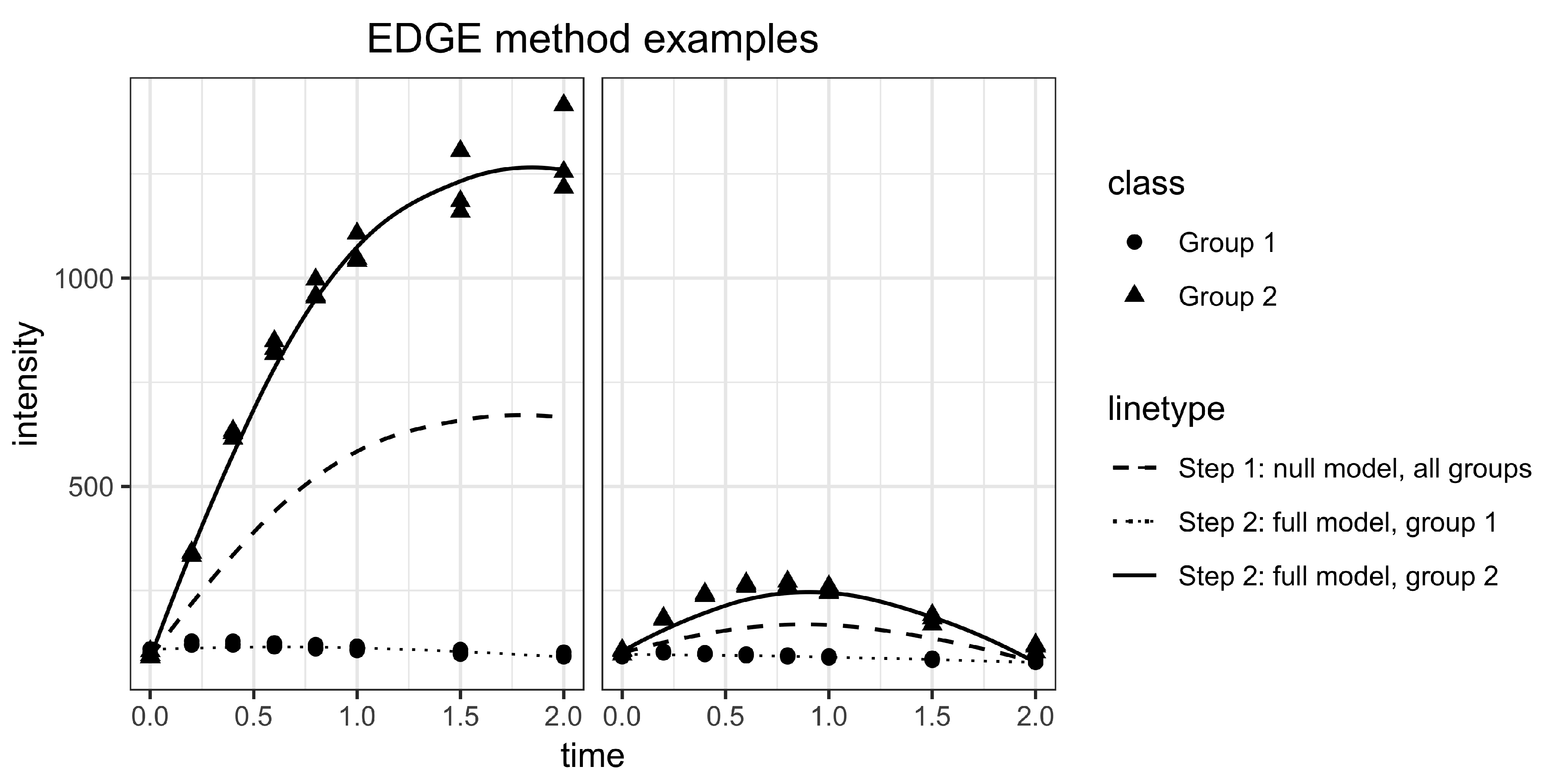
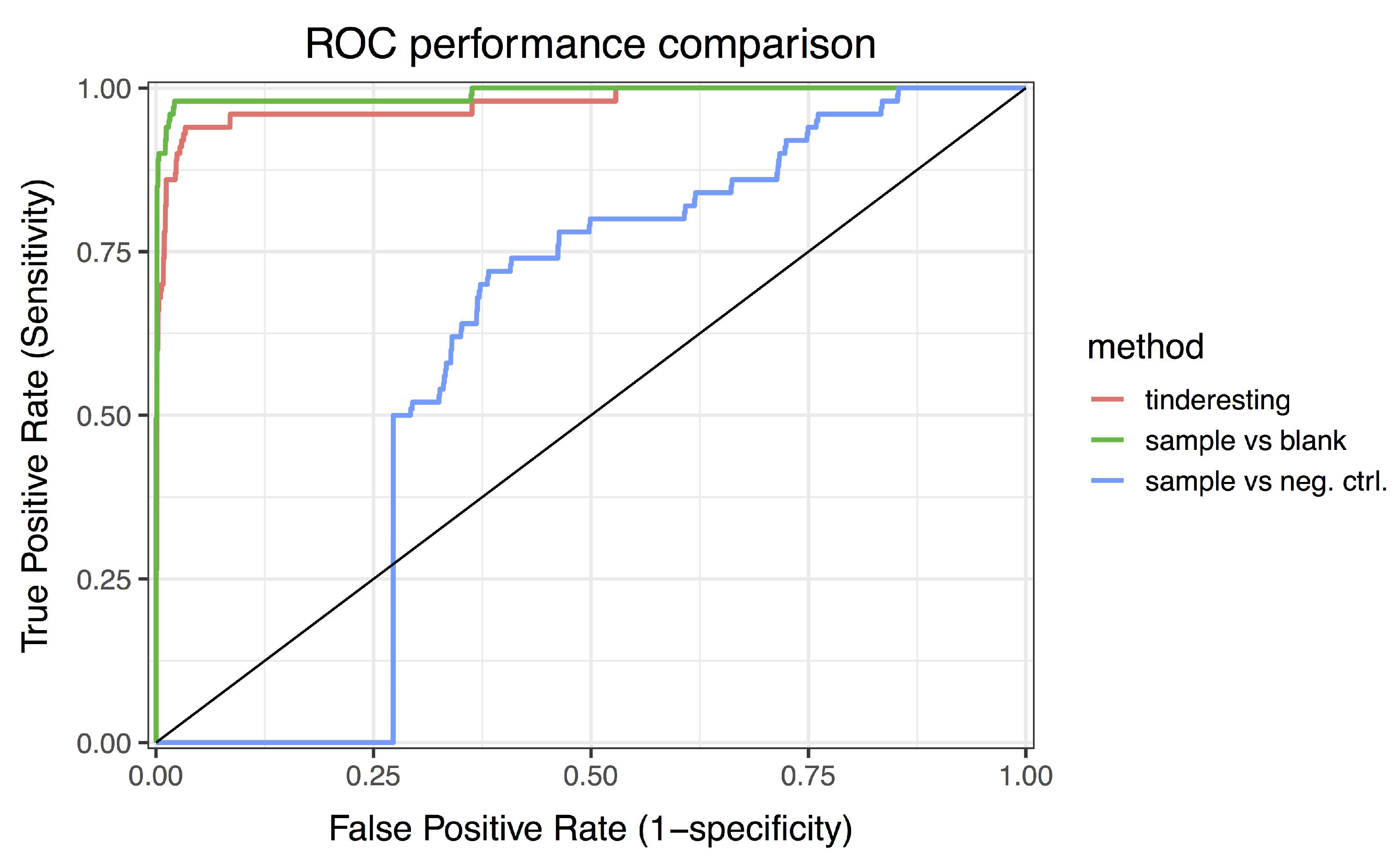
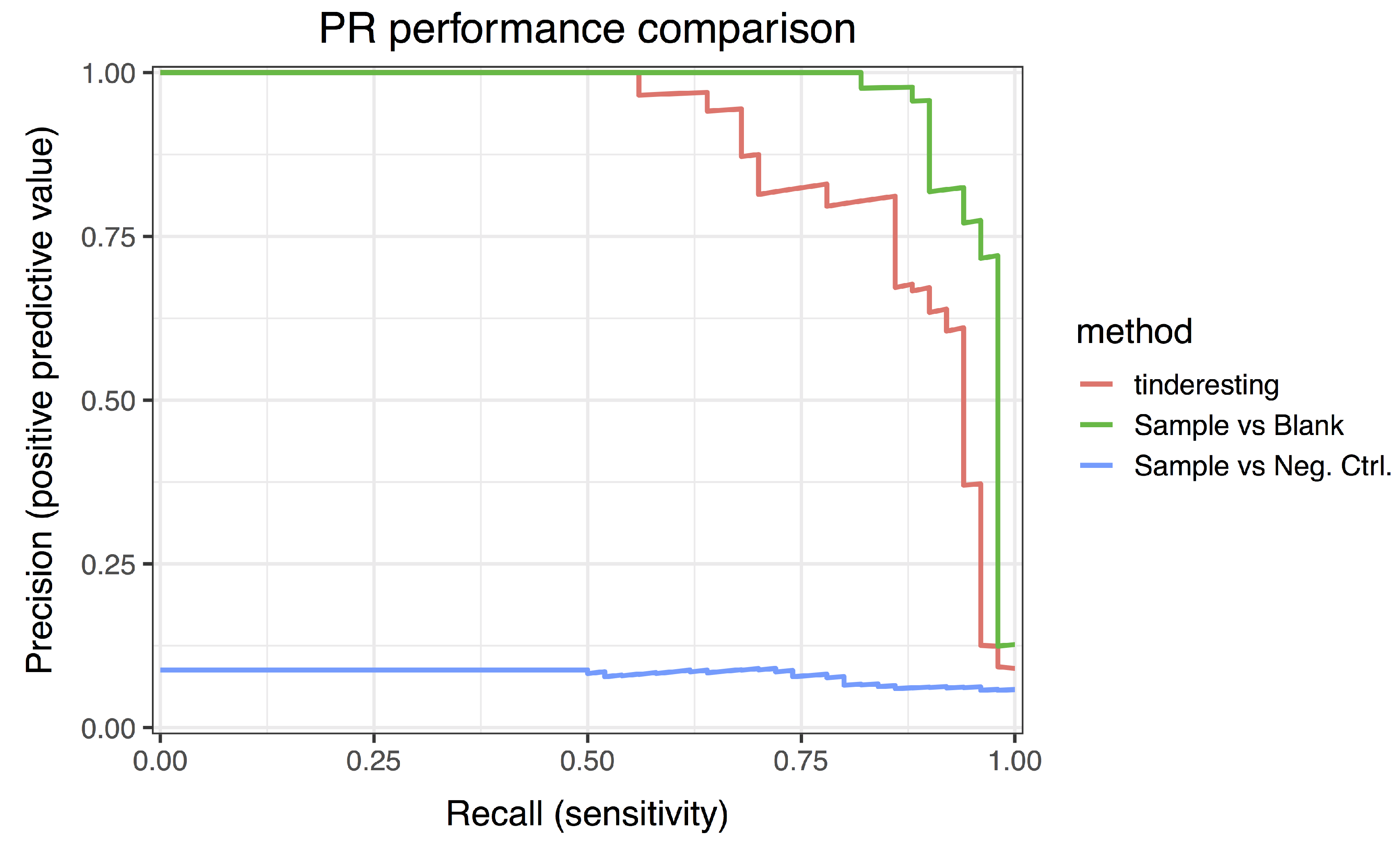
2.2. Statistical Methods for Differential Metabolism
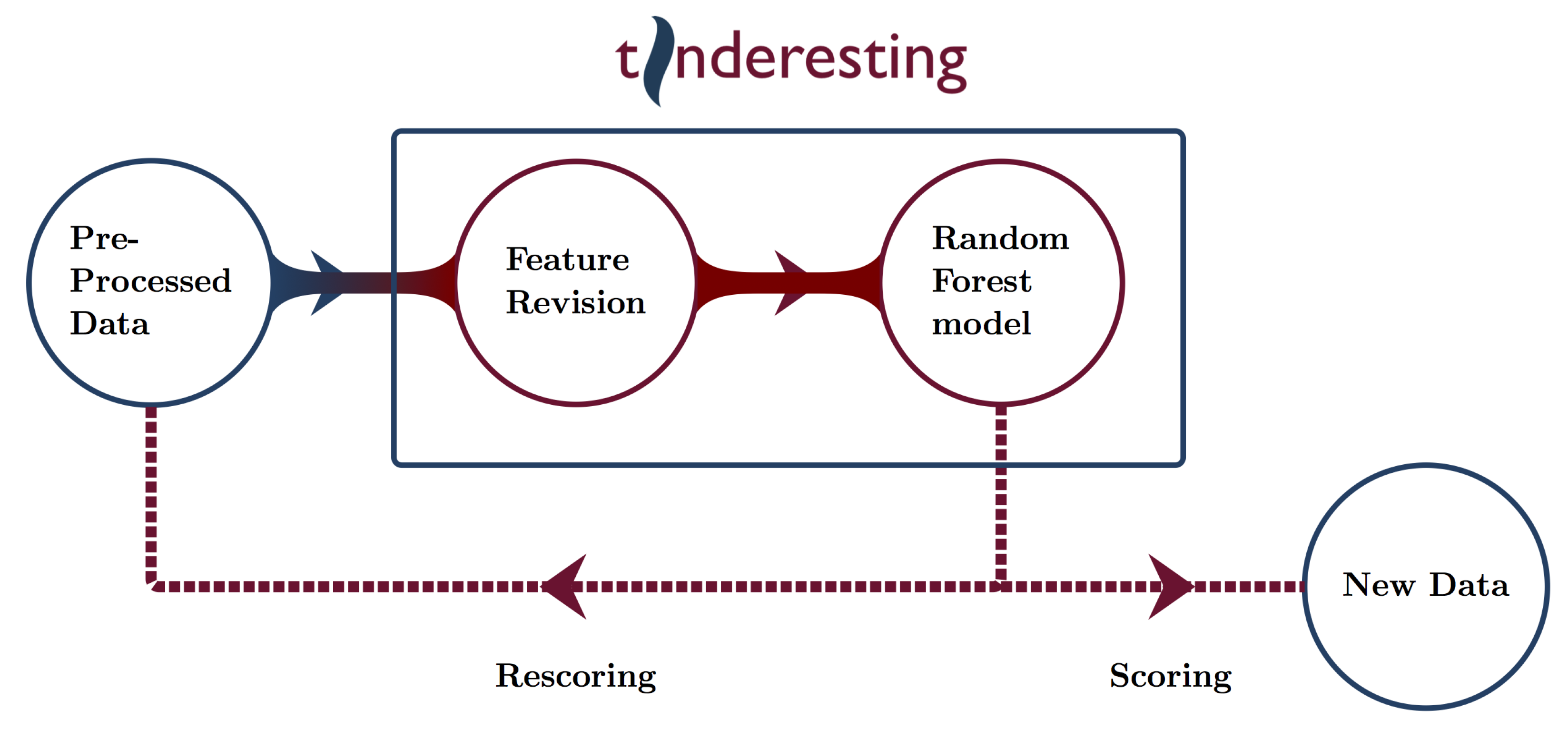
2.3. Machine Learning and Tinderesting
3. Results
3.1. Simulating Dynamic Metabolomics Data
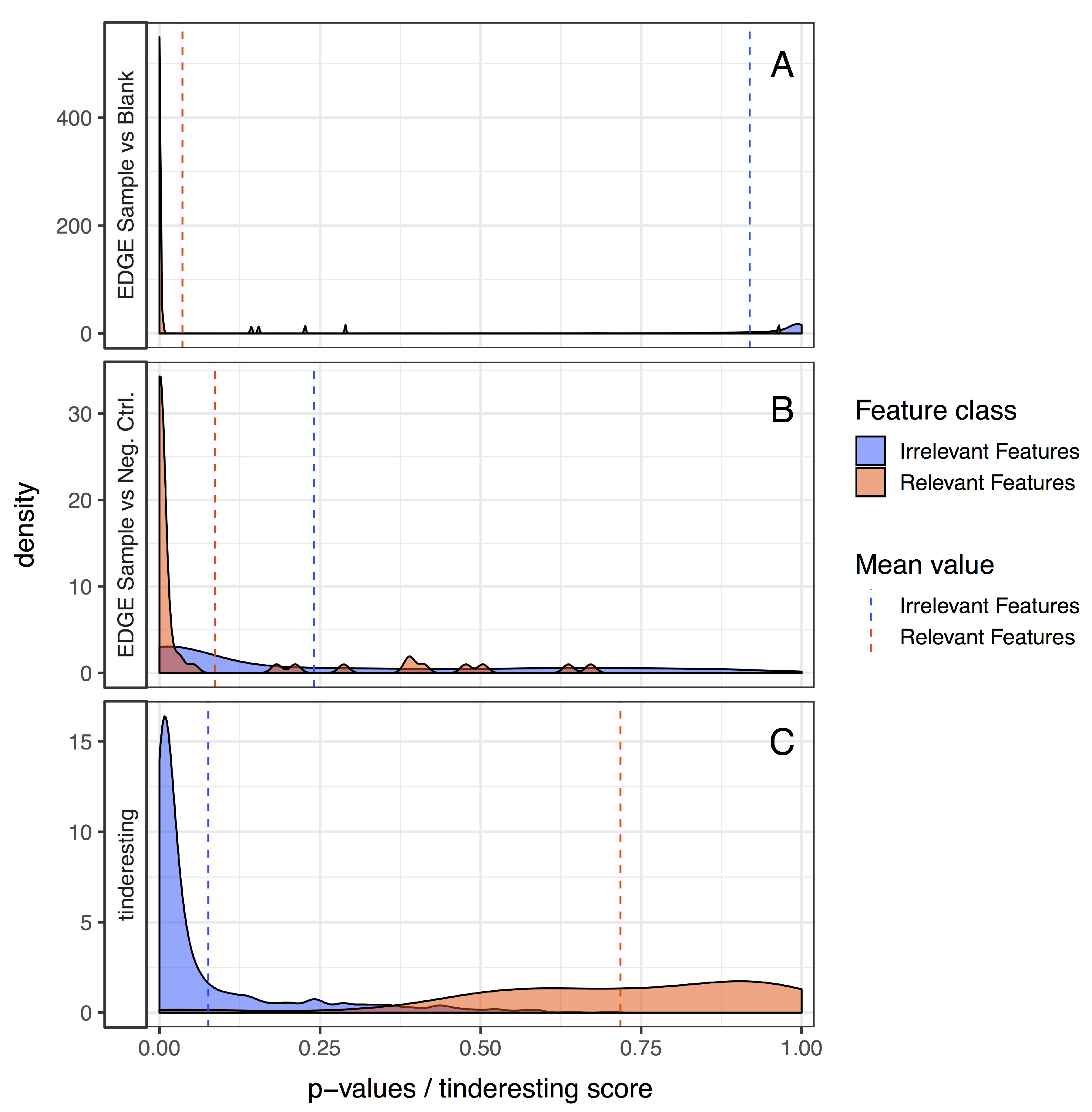
3.2. Statistical Analysis and tinderesting
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Giacomoni, F.; Le Corguillé, G.; Monsoor, M.; Landi, M.; Pericard, P.; Pétéra, M.; Duperier, C.; Tremblay-Franco, M.; Martin, J.F.; Jacob, D.; et al. Workflow4Metabolomics: A collaborative research infrastructure for computational metabolomics. Bioinformatics 2015, 31, 1493–1495. [Google Scholar] [CrossRef]
- Weber, R.J.M.; Lawson, T.N.; Salek, R.M.; Ebbels, T.M.D.; Glen, R.C.; Goodacre, R.; Griffin, J.L.; Haug, K.; Koulman, A.; Moreno, P.; et al. Computational tools and workflows in metabolomics: An international survey highlights the opportunity for harmonisation through Galaxy. Metabolomics 2017, 13, 12. [Google Scholar] [CrossRef]
- Chong, J.; Soufan, O.; Li, C.; Caraus, I.; Li, S.; Bourque, G.; Wishart, D.S.; Xia, J. MetaboAnalyst 4.0: Towards more transparent and integrative metabolomics analysis. Nucleic Acids Res. 2018, 46, W486–W494. [Google Scholar] [CrossRef] [PubMed]
- Chong, J.; Xia, J. MetaboAnalystR: An R package for flexible and reproducible analysis of metabolomics data. Bioinformatics 2018, 34, 4313–4314. [Google Scholar] [CrossRef] [PubMed]
- Smilde, A.K.; Westerhuis, J.A.; Hoefsloot, H.C.J.; Bijlsma, S.; Rubingh, C.M.; Vis, D.J.; Jellema, R.H.; Pijl, H.; Roelfsema, F.; van der Greef, J. Dynamic metabolomic data analysis: A tutorial review. Metabolomics 2010, 6, 3–17. [Google Scholar] [CrossRef] [PubMed]
- Higgs, G.A.; Salmon, J.A.; Henderson, B.; Vane, J.R. Pharmacokinetics of aspirin and salicylate in relation to inhibition of arachidonate cyclooxygenase and antiinflammatory activity. PNAS 1987, 84, 1417–1420. [Google Scholar] [CrossRef] [PubMed]
- Storey, J.D.; Xiao, W.; Leek, J.T.; Tompkins, R.G.; Davis, R.W. Significance analysis of time course microarray experiments. PNAS 2005, 102, 12837–12842. [Google Scholar] [CrossRef] [PubMed]
- Leek, J.T.; Monsen, E.; Dabney, A.R.; Storey, J.D. EDGE: Extraction and analysis of differential gene expression. Bioinformatics 2005, 22, 507–508. [Google Scholar] [CrossRef]
- Von Ahn, L.; Maurer, B.; McMillen, C.; Abraham, D.; Blum, M. reCAPTCHA: Human-Based Character Recognition via Web Security Measures. Science 2008, 321, 1465–1468. [Google Scholar] [CrossRef]
- Peeters, L.; Beirnaert, C.; Van der Auwera, A.; Bijttebier, S.; Laukens, K.; Pieters, L.; Hermans, N.; Foubert, K. Revelation of the metabolic pathway of Hederacoside C using an innovative data analysis strategy for dynamic multiclass biotransformation experiments. J. Chromatogr. A 2019, in press. [Google Scholar] [CrossRef] [PubMed]
- Barabási, A.L.; Albert, A. Emergence of scaling in random networks. Science 1999, 286, 509–512. [Google Scholar] [PubMed]
- Csardi, G.; Nepusz, T. The igraph software package for complex network research. InterJ. Complex Syst. 2006, 1695, 1–9. [Google Scholar]
- Pfeiffer, T.; Soyer, O.S.; Bonhoeffer, S. The evolution of connectivity in metabolic networks. PLoS Biol. 2005, 3, e228. [Google Scholar] [CrossRef]
- Jeong, H.; Tombor, B.; Albert, R.; Oltvai, Z.N.; Barabási, A.L. The large-scale organization of metabolic networks. Nature 2000, 407, 651–654. [Google Scholar] [CrossRef] [PubMed]
- Storey, J.D.; Tibshirani, R. Statistical significance for genomewide studies. PNAS 2003, 100, 9440–9445. [Google Scholar] [CrossRef] [PubMed]
- Liaw, A.; Wiener, M. Classification and Regression by randomForest. R News 2002, 2, 18–22. [Google Scholar]
- Beirnaert, C.; Cuyckx, M.; Bijttebier, S. MetaboMeeseeks: Helper functions for metabolomics analysis. R package version 0.1.2. Available online: https://github.com/Beirnaert/MetaboMeeseeks (accessed on 19 March 2019).
- Chawla, N.V.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: Synthetic minority over-sampling technique. J. Artif. Intell. Res. 2002, 16, 321–357. [Google Scholar] [CrossRef]
- Venkatraman, E.S.; Begg, C.B. A distribution-free procedure for comparing receiver operating characteristic curves from a paired experiment. Biometrika 1996, 83, 835–848. [Google Scholar] [CrossRef]
- DeLong, E.R.; DeLong, D.M.; Clarke-Pearson, D.L. Comparing the areas under two or more correlated receiver operating characteristic curves: A nonparametric approach. Biometrics 1988, 44, 837–845. [Google Scholar] [CrossRef]
- Breynaert, A.; Bosscher, D.; Kahnt, A.; Claeys, M.; Cos, P.; Pieters, L.; Hermans, N. Development and validation of an in vitro experimental gastrointestinal dialysis model with colon phase to study the availability and colonic metabolisation of polyphenolic compounds. Planta Medica 2015, 81, 1075–1083. [Google Scholar] [CrossRef]
- Stevens, J.F.; Maier, C.S. The chemistry of gut microbial metabolism of polyphenols. Phytochem. Rev. 2016, 15, 425–444. [Google Scholar] [CrossRef] [PubMed]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Beirnaert, C.; Peeters, L.; Meysman, P.; Bittremieux, W.; Foubert, K.; Custers, D.; Van der Auwera, A.; Cuykx, M.; Pieters, L.; Covaci, A.; et al. Using Expert Driven Machine Learning to Enhance Dynamic Metabolomics Data Analysis. Metabolites 2019, 9, 54. https://doi.org/10.3390/metabo9030054
Beirnaert C, Peeters L, Meysman P, Bittremieux W, Foubert K, Custers D, Van der Auwera A, Cuykx M, Pieters L, Covaci A, et al. Using Expert Driven Machine Learning to Enhance Dynamic Metabolomics Data Analysis. Metabolites. 2019; 9(3):54. https://doi.org/10.3390/metabo9030054
Chicago/Turabian StyleBeirnaert, Charlie, Laura Peeters, Pieter Meysman, Wout Bittremieux, Kenn Foubert, Deborah Custers, Anastasia Van der Auwera, Matthias Cuykx, Luc Pieters, Adrian Covaci, and et al. 2019. "Using Expert Driven Machine Learning to Enhance Dynamic Metabolomics Data Analysis" Metabolites 9, no. 3: 54. https://doi.org/10.3390/metabo9030054
APA StyleBeirnaert, C., Peeters, L., Meysman, P., Bittremieux, W., Foubert, K., Custers, D., Van der Auwera, A., Cuykx, M., Pieters, L., Covaci, A., & Laukens, K. (2019). Using Expert Driven Machine Learning to Enhance Dynamic Metabolomics Data Analysis. Metabolites, 9(3), 54. https://doi.org/10.3390/metabo9030054






