Current limitations in quantitatively predicting biological behavior hinder our efforts to engineer biological systems to produce biofuels and other desired chemicals [
1]. Determination of internal metabolic fluxes (i.e., the amount of metabolites traversing each biochemical reaction per unit time [
2,
3]) is a useful tool in this effort because they map how carbon and electrons flow through metabolism to enable cell function [
3,
4] and can produce actionable insights to increase biofuel production [
5]. Several methods are available for calculating internal metabolic fluxes. Arguably, the most popular are Flux Balance Analysis (FBA) and
C Metabolic Flux Analysis (
C MFA). FBA determines fluxes by using comprehensive genome-scale models and by assuming that cells closely follow an evolutionary principle of maximizing biomass.
C MFA calculates fluxes by constraining small models of central carbon metabolism with the strong flux constraints obtained from
C labeling experiments [
6,
7,
8]. Proponents of each of these two techniques rarely combine them, except for a few exceptions (e.g., [
9,
10,
11,
12,
13,
14,
15]). FBA and COnstraint Based Reconstruction and Analysis (COBRA) can predict all fluxes in a large genome scale model using an optimization principle, but do not directly constrain internal fluxes with high resolution experimental data. Conversely,
C MFA models are well constrained by experimental data, but only measure a small number of central carbon metabolism fluxes, and do not model the full complexity and plasticity of a large metabolic network. However, metabolic engineering can benefit from uniting the advantages of both approaches: a method that provides fluxes for comprehensive genome-scale models as constrained by the very informative
C labeling experimental data.
While
C MFA has been performed at the genome scale for
E. coli [
16], it is a computationally expensive method and requires knowledge of all of the carbon transitions in the network. This knowledge is nontrivial to obtain systematically for any desired organism [
17,
18,
19,
20,
21,
22]. Two-scale
C Metabolic Flux Analysis [
23] (2S-
C MFA) is an alternative technique that constrains genome-scale models with
C labeling experimental data. 2S-
C MFA constrains all fluxes in the genome-scale model simultaneously using stochiometric and
C labeling constraints, but does so at two resolution scales: for core reactions, both stochiometric and
C labeling constraints are used, whereas, for non-core reactions, only stochiometric constraints are used. 2S-
C MFA is meant to obtain the same results as genome-scale
C MFA if we assume that flux flows from core to peripheral metabolism and there is limited flow back. This assumption is named the two-scale or bow tie approximation (
Figure 1 and
Figure 2) and stems from the bow tie structure of cellular metabolism, a universally conserved product of evolution [
24,
25]. Hence, in this paper, we will refer to it indistinctly as the bow tie approximation or the two-scale approximation. The bow tie structure entails, as shown in
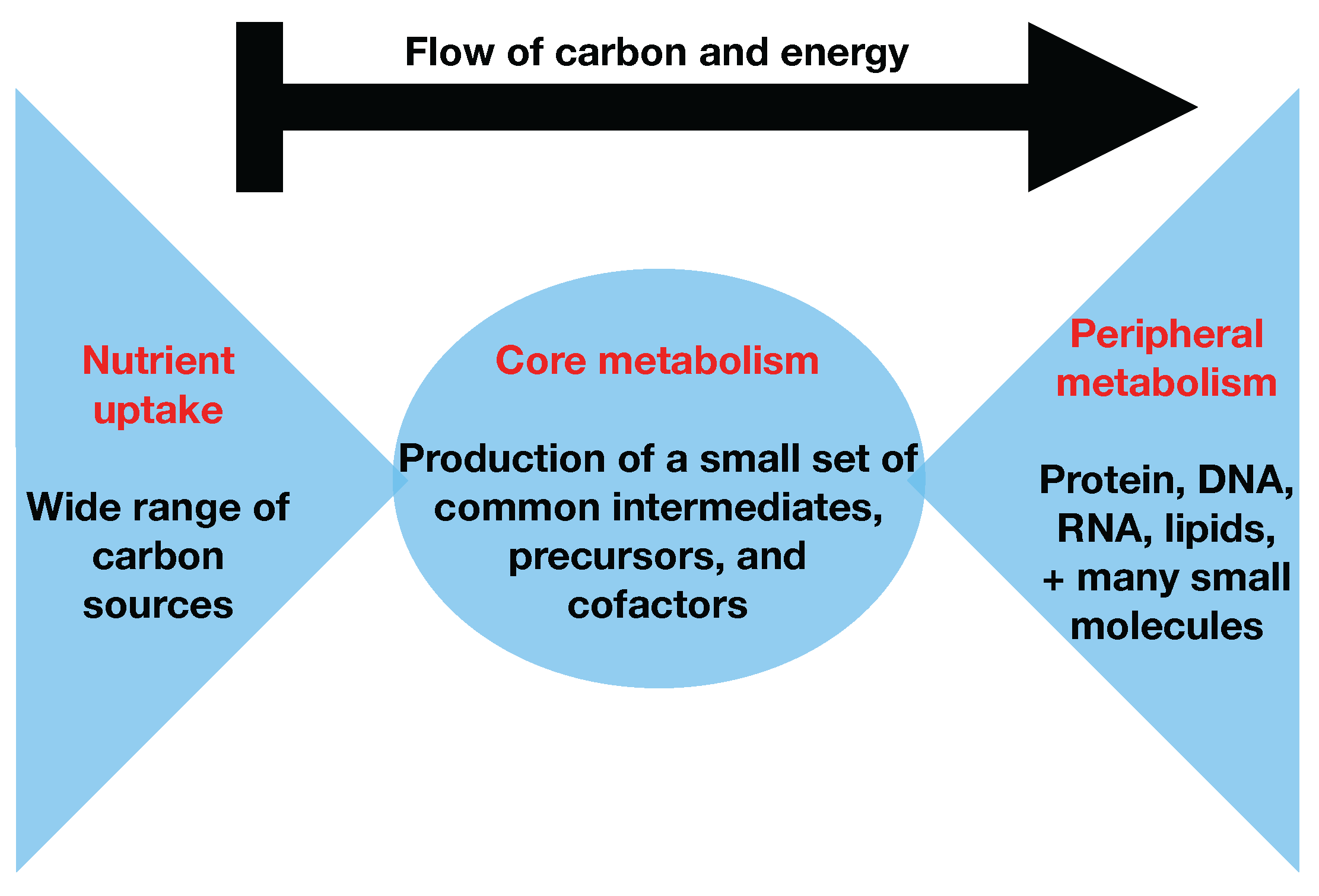
Figure 1, that almost all carbon and energy sources are converted through central carbon metabolism pathways into a set of twelve precursor metabolites (glucose-6-phosphate, fructose-6-phosphate, ribose-5-phosphate, erythrose-4-phosphate, glyceraldehyde-3-phosphate, 3-phosphoglycerate, phosphoenol-pyruvate, pyruvate, acetyl-CoA, 2-oxoglutarate, succinyl-CoA, and oxaloacetate), which are the building blocks of most cellular components and natural products synthesized by cells [
26]. Hence, if carbon sources are included in the core metabolism, the bow tie structure implies that flux flows from core to peripheral metabolism and there is limited flow back. This bow tie approximation is experimentally justified by the fact that traditional
C MFA, using only core metabolism models, can convincingly explain labeling patterns for amino acids and intracellular metabolites for model organisms [
27,
28,
29,
30], and by experimentally verified metabolic engineering predictions using 2S-
C MFA [
5].
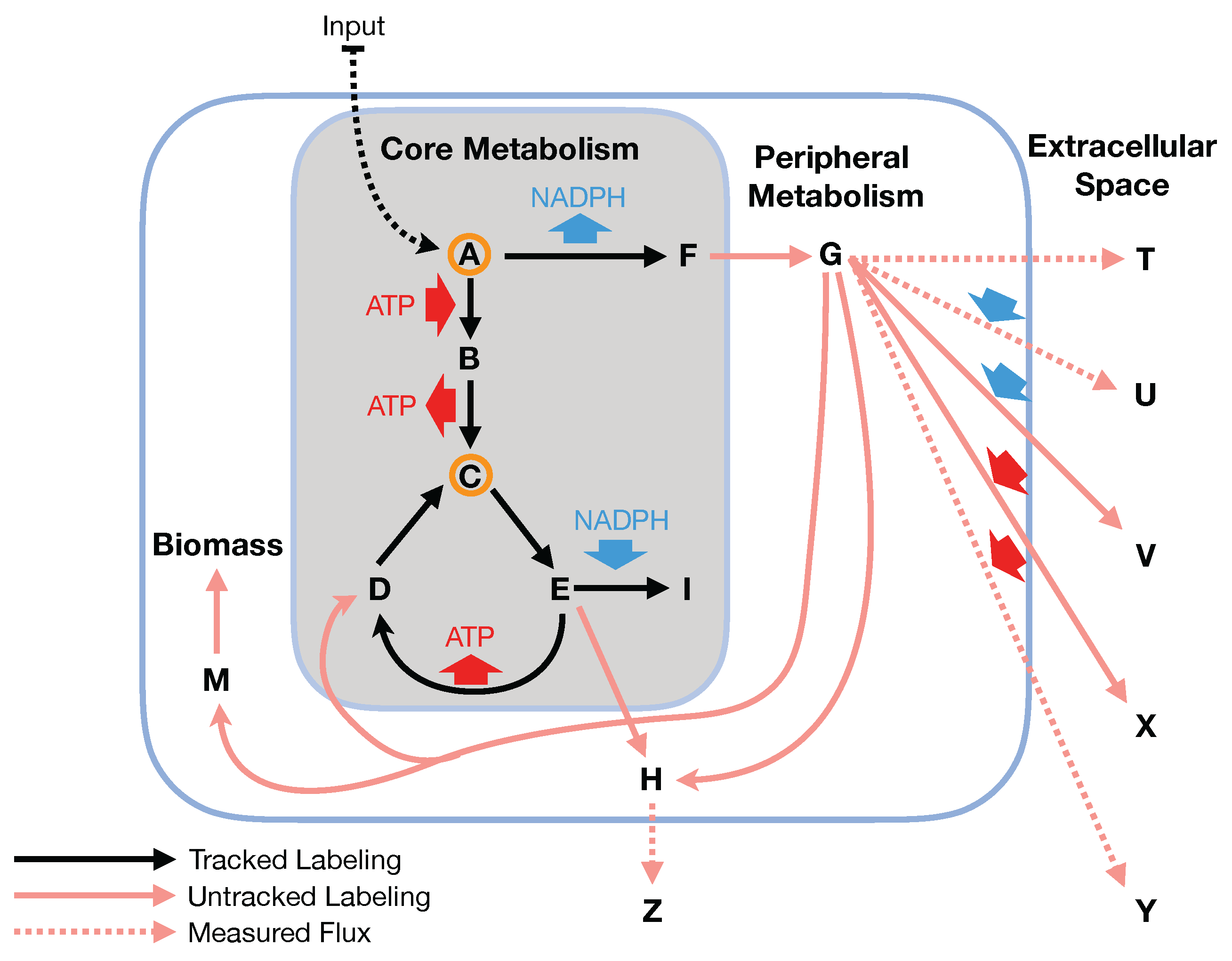
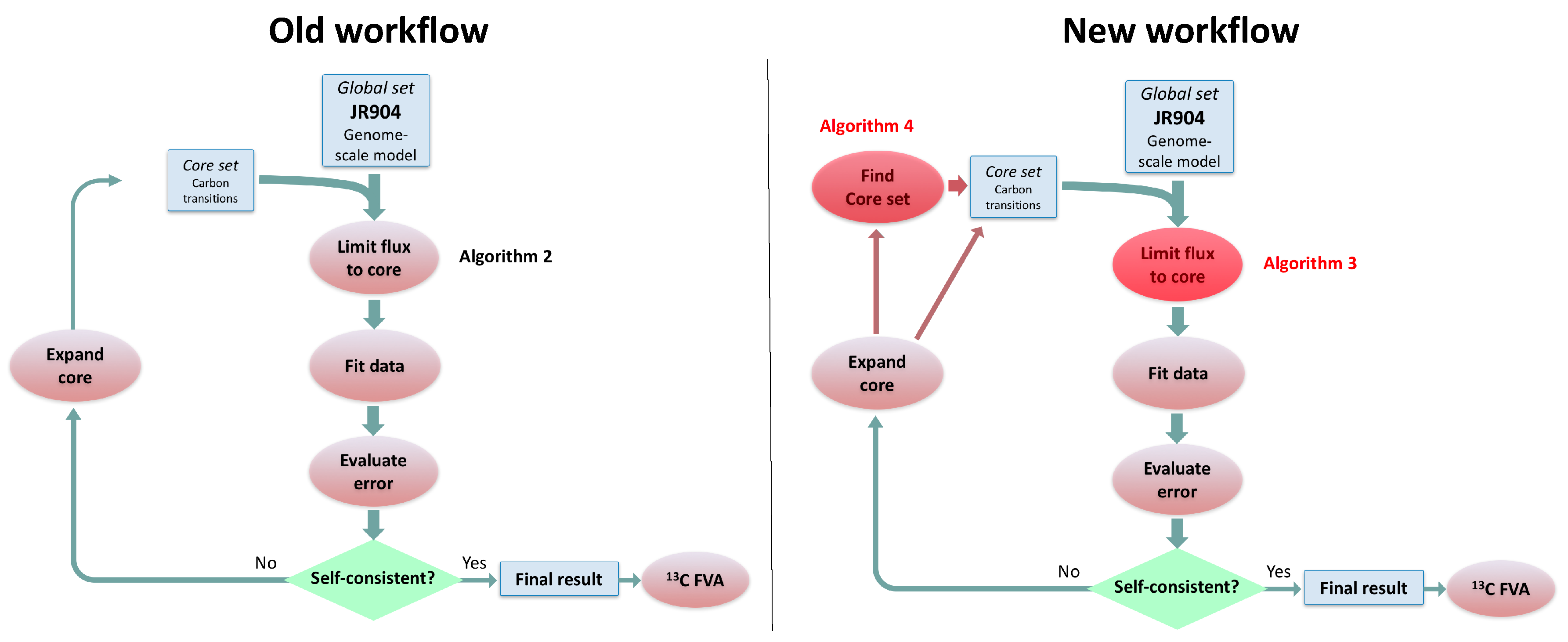
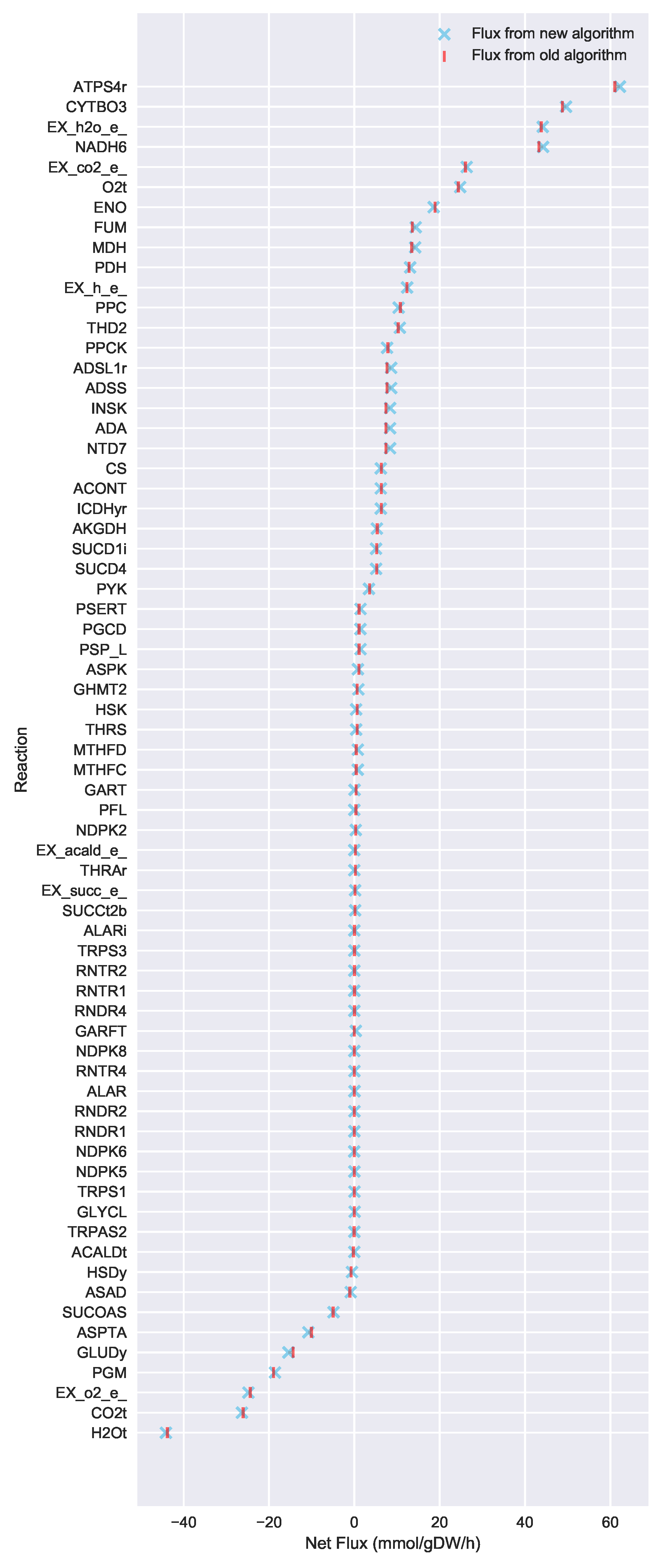
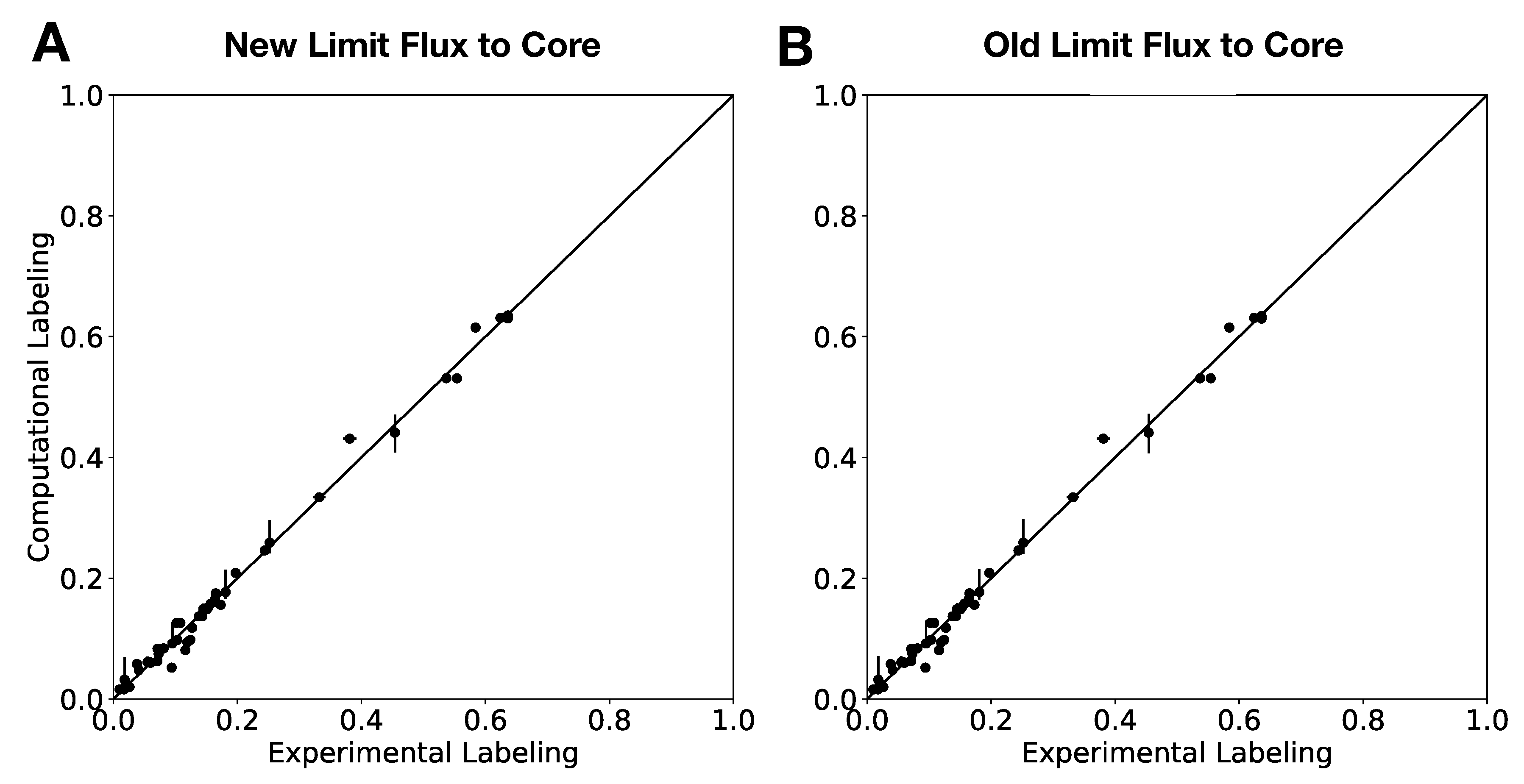
In this paper, we formalize the bow tie approximation (a.k.a. two-scale approximation) in terms of genome-scale models by providing improved and systematic methods to (1) constrain fluxes in accordance with this approximation and (2) determine the boundaries of core metabolism. In the context of genome-scale models, the bow tie approximation is implemented by setting the upper bound of all reactions with products in core metabolism to zero, or the lowest value consistent with the observed growth rate (see “Limit Flux to Core” step in Figure 2 of [
23] and
Figure 2). The previously published 2S-
C MFA [
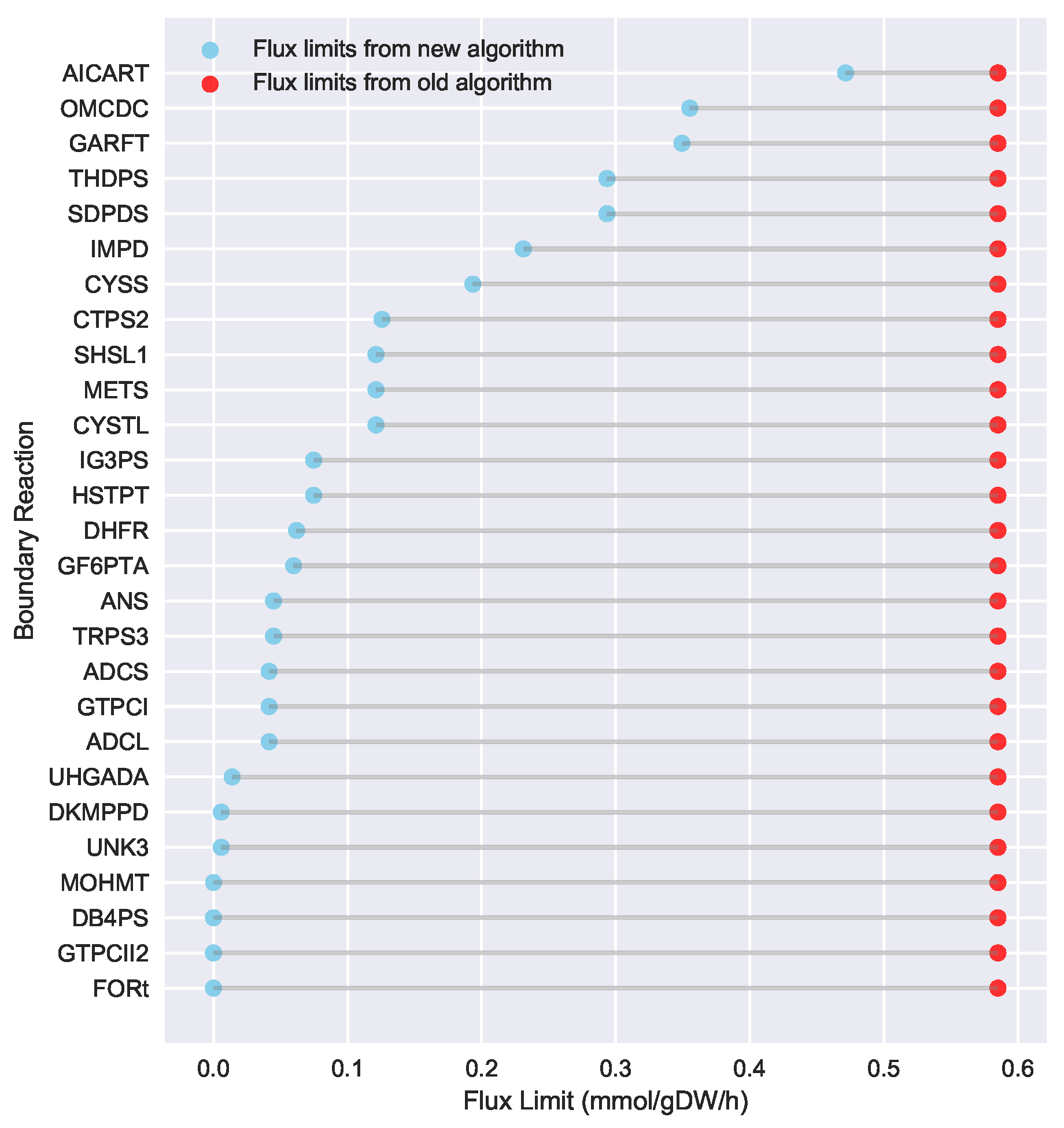
23] implementation of the “Limit Flux to Core” step used an algorithm that limited the upper bounds of fluxes into the core using an inefficient and ad hoc process which relied on trial and error, arbitrary cutoff values, and sequential execution. Here, we present an improved method which uses linear optimization to find the minimum flux bounds into the core, which is computationally more efficient, and also more biologically relevant, as we identify the lowest flux into core metabolism consistent with observed experimental data. Minimizing the flux of reactions into the core through linear programming is complicated by the reversible nature of some reactions which cross the core boundary. We solve this problem by constructing a minimization procedure which considers only the unidirectional component of each boundary flux that has products in core metabolism.
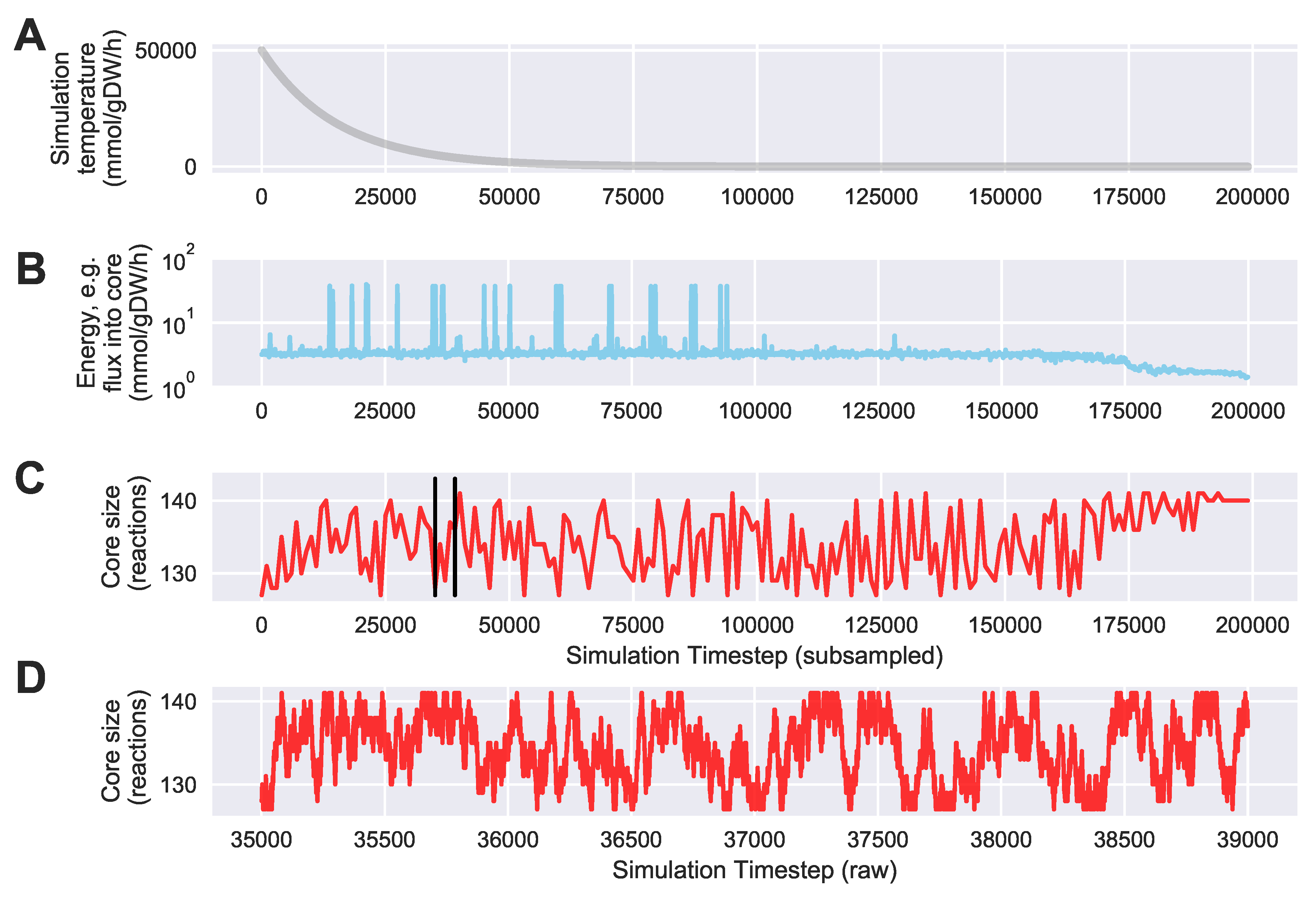
For a given core, a metric to quantitatively determine to what degree the bow tie approximation holds, is the sum of fluxes into the core (zero for a perfect case of the bow tie structure). Therefore, we also introduce a Simulated Annealing algorithm to computationally explore the space of alternate core metabolism reaction sets, minimizing the sum of fluxes flowing into core metabolism. This process can automatically identify an improved core (displaying less total flux into core) which has more or less reactions as needed to better satisfy the bow tie approximation and be more suitable for subsequent C MFA or 2S-C MFA modeling.