Design Principles as a Guide for Constraint Based and Dynamic Modeling: Towards an Integrative Workflow
Abstract
:1. Introduction
The Chess Metaphor
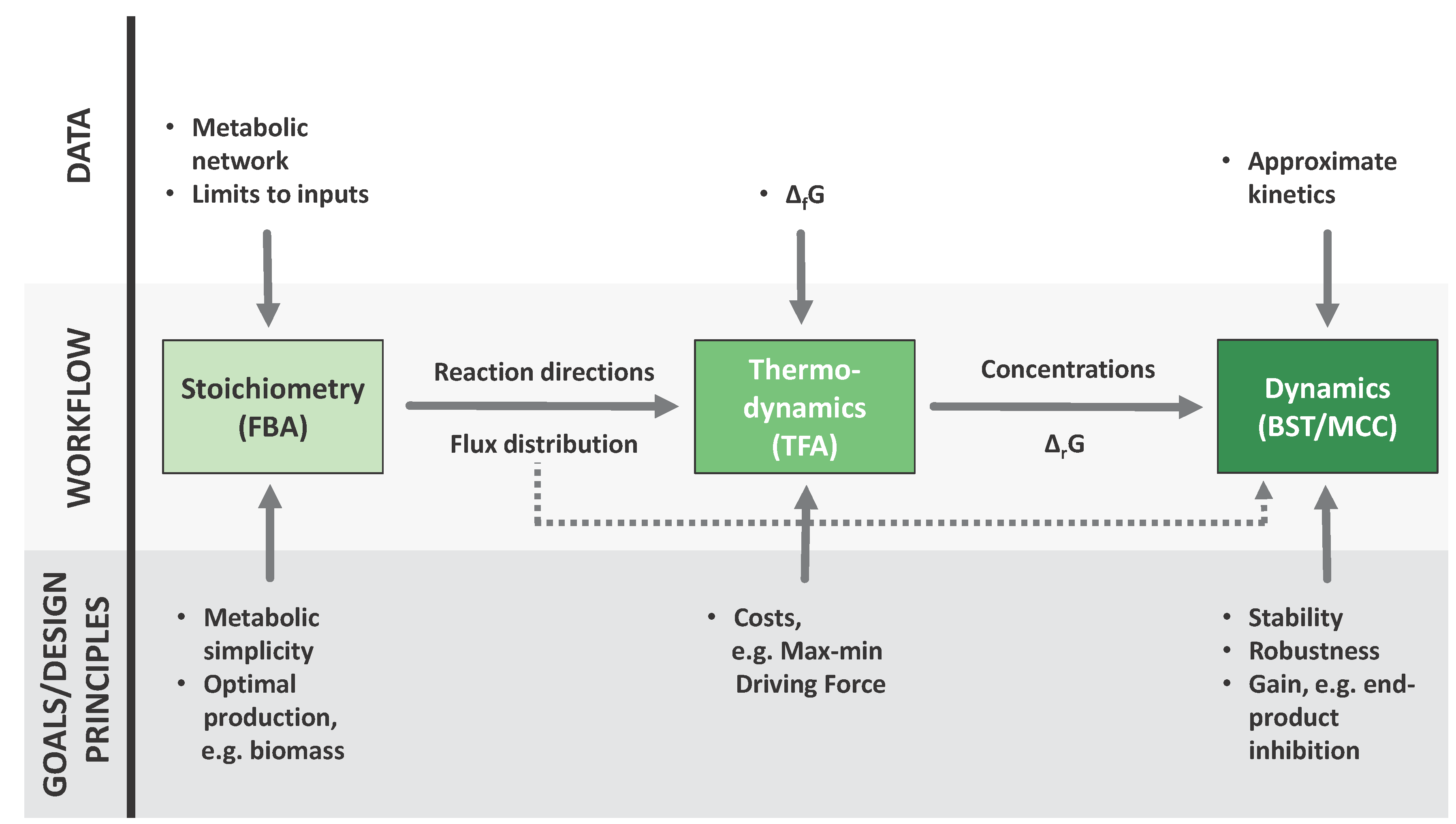
2. Established Methods
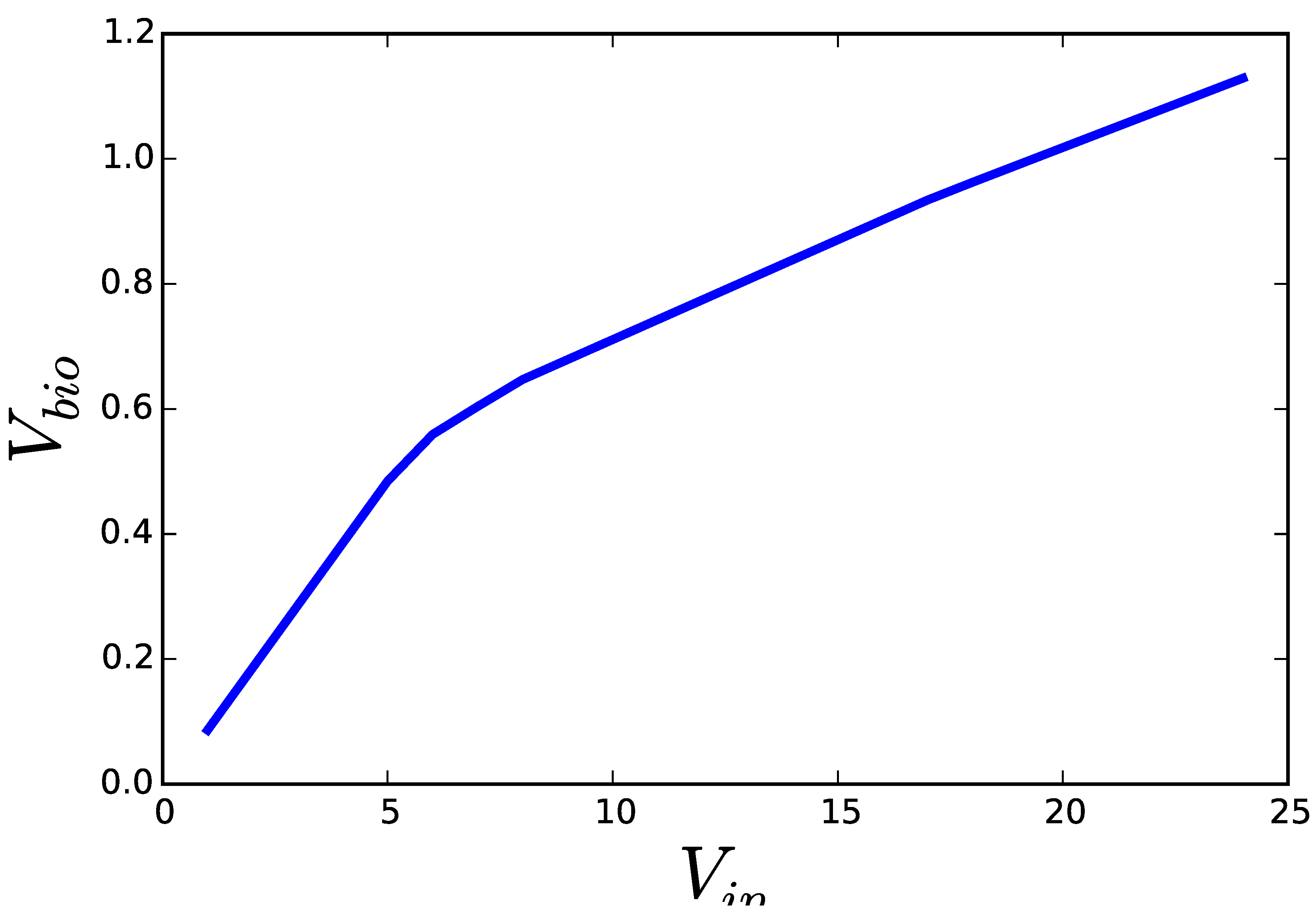
2.1. Flux Centric Approaches: Constraining the Flux Space
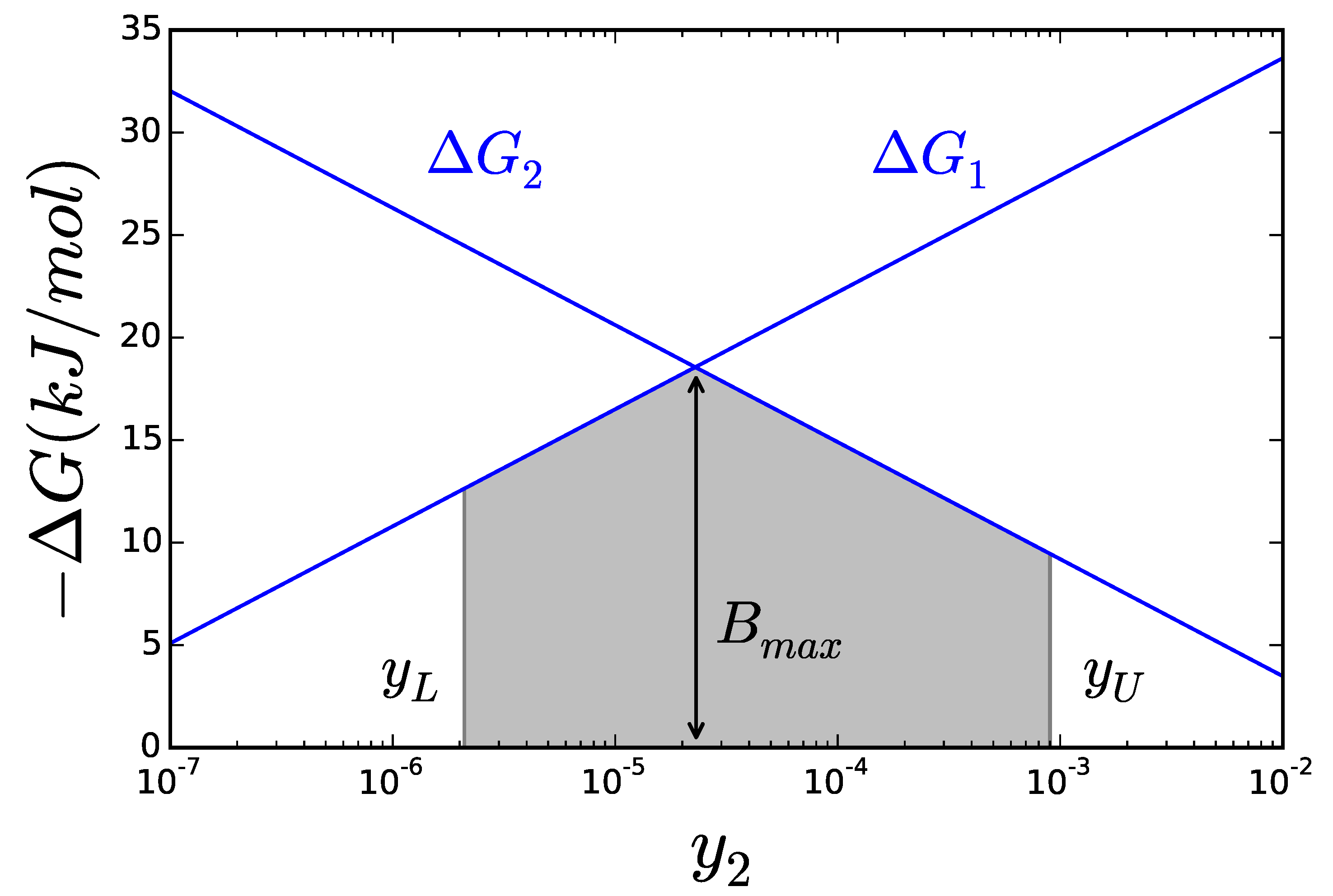
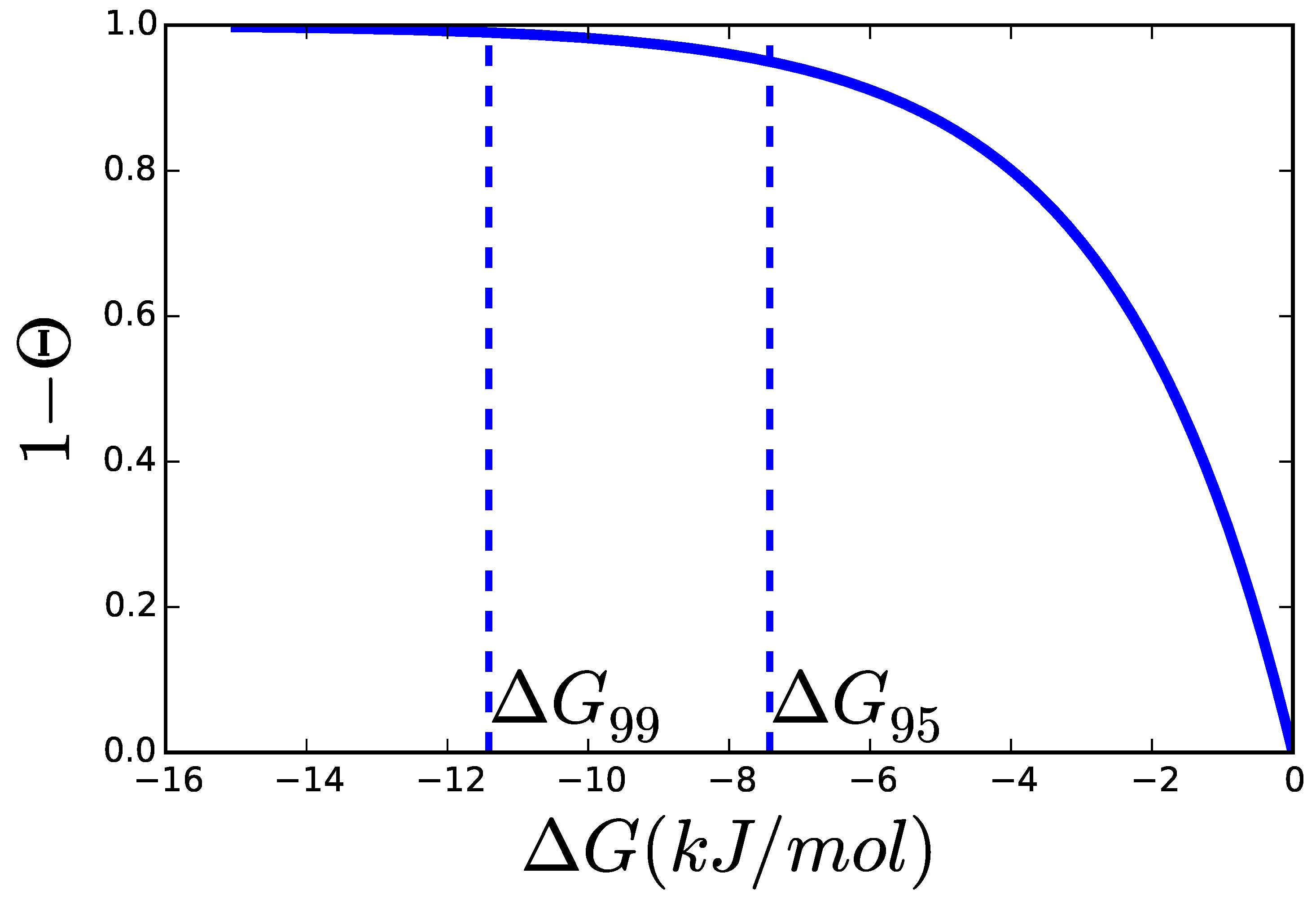
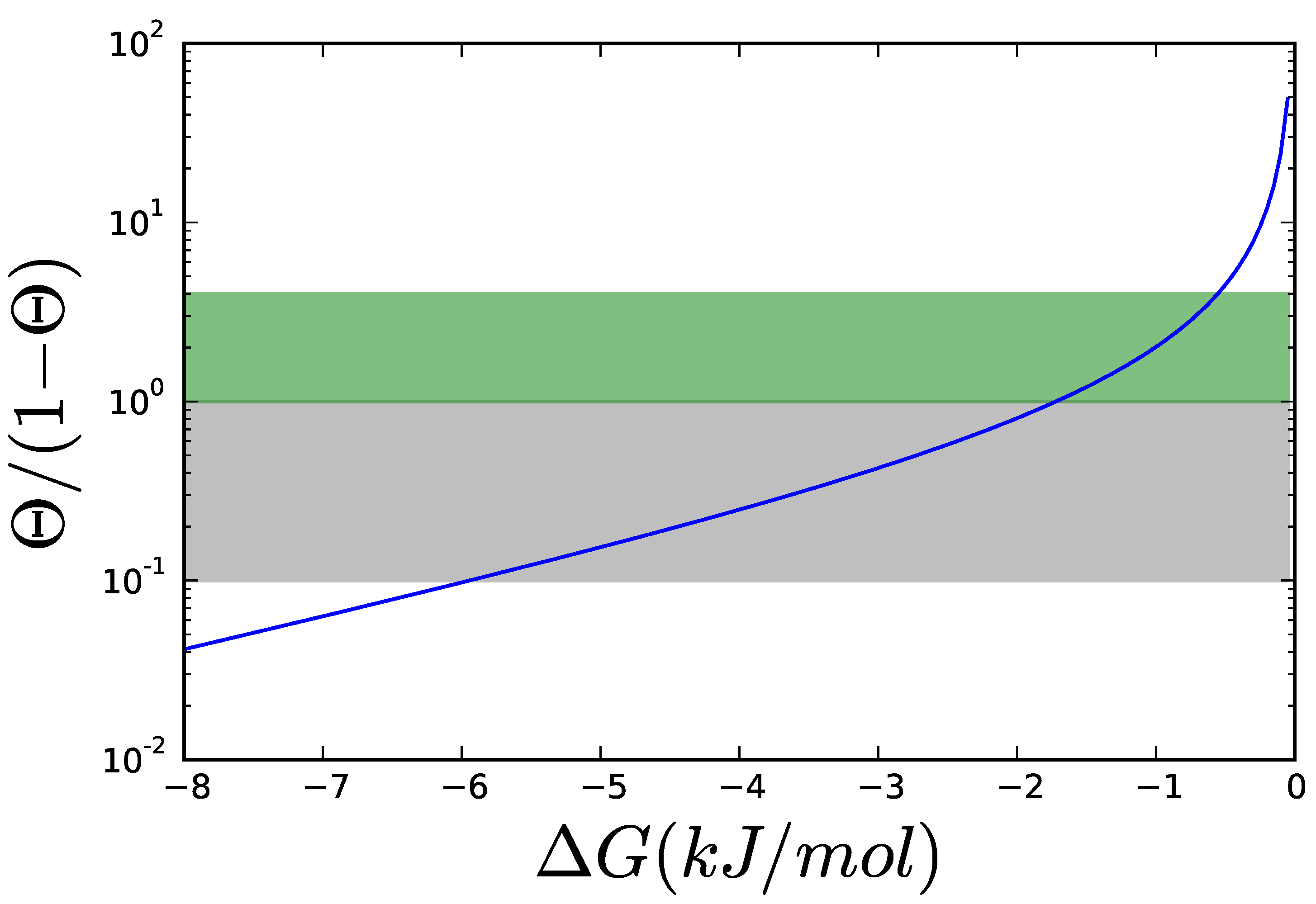
2.2. Thermodynamics: The Bridge to Metabolites
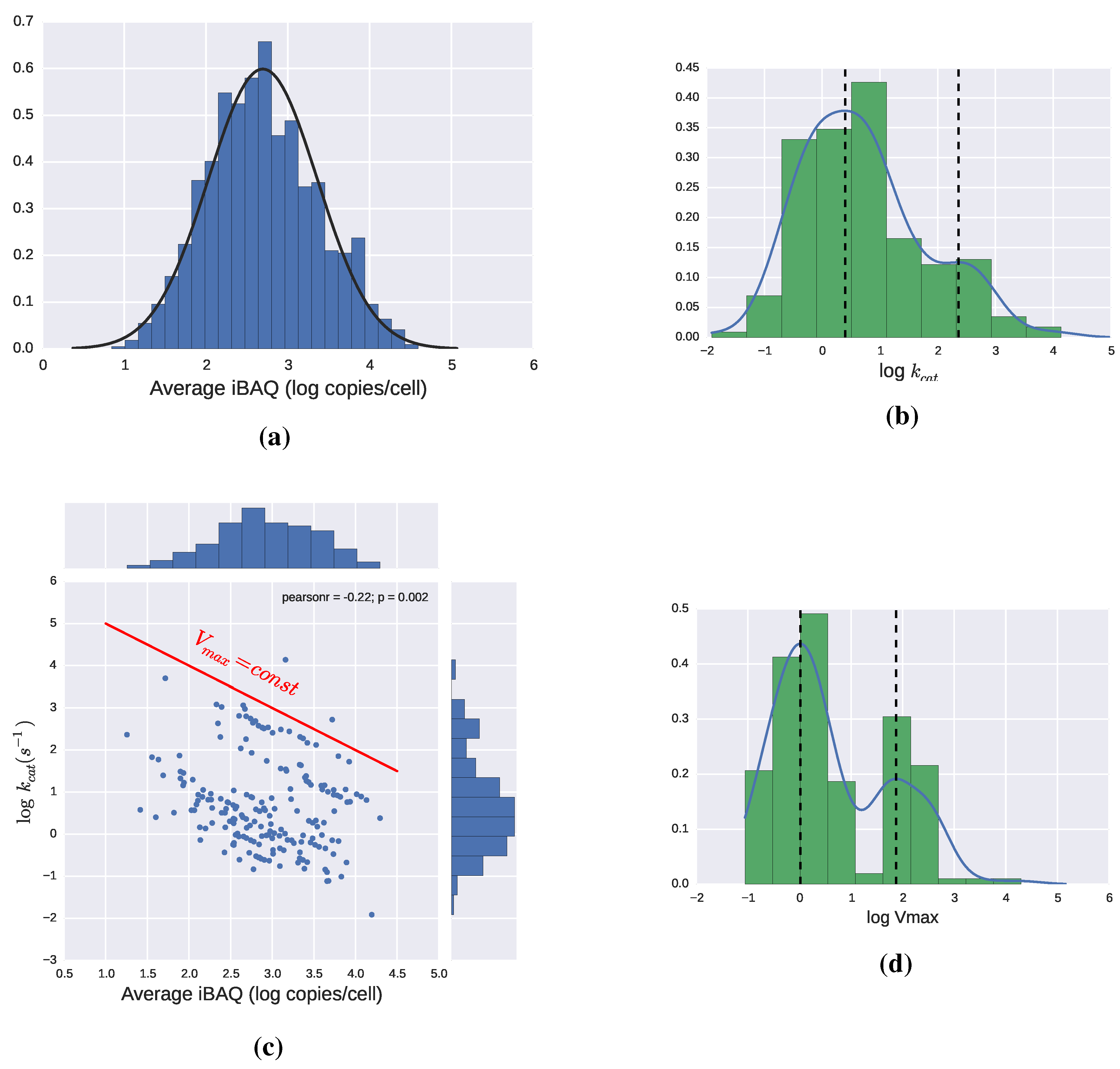
2.3. Catalytic Efficiency of Enzymes
2.3.1. Theoretical Limits and Some Reference Values
2.4. Adding Regulation to Obtain a Dynamic Model
2.5. Mathematically Controlled Comparison (MCC)
3. Results
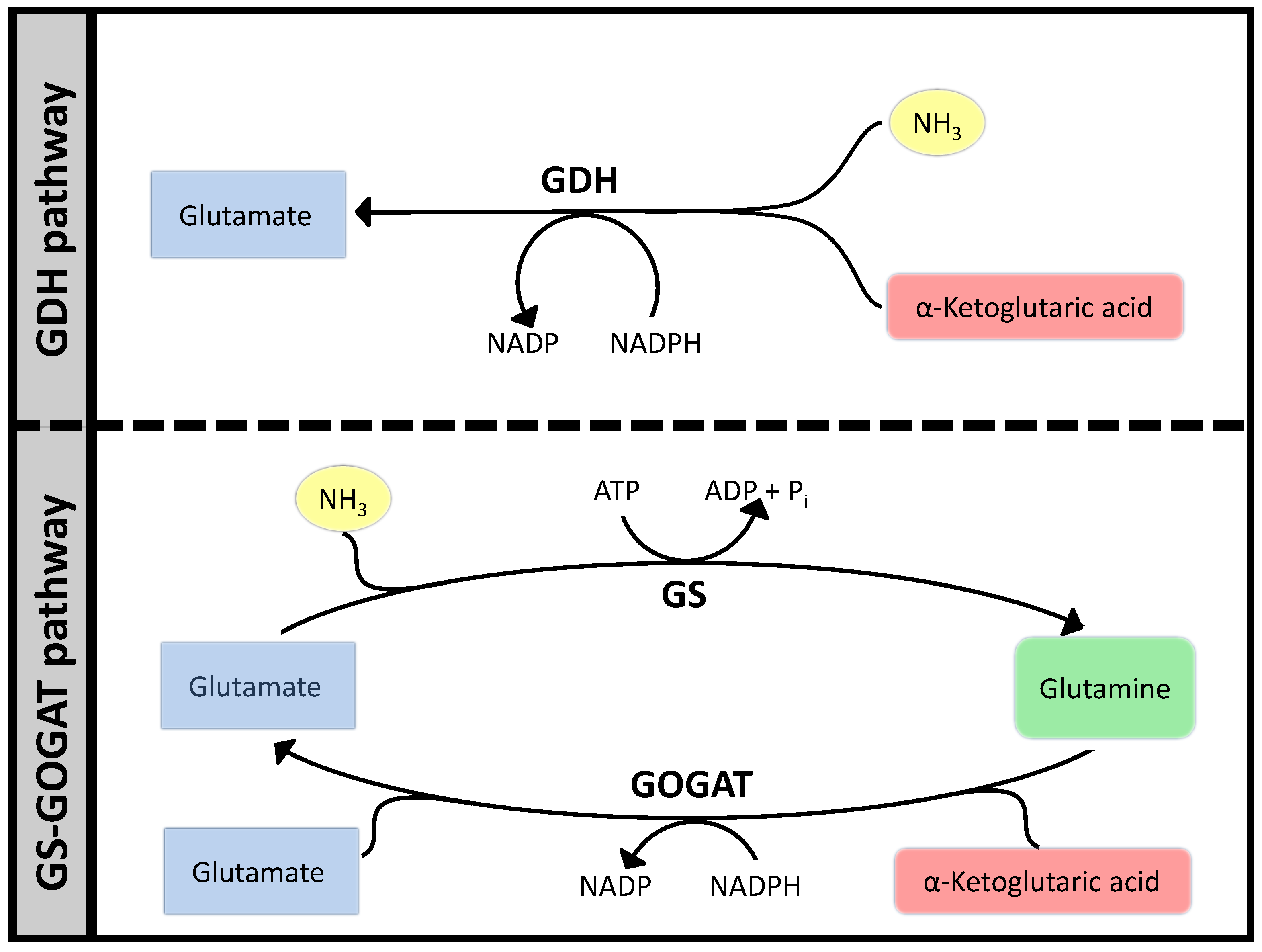
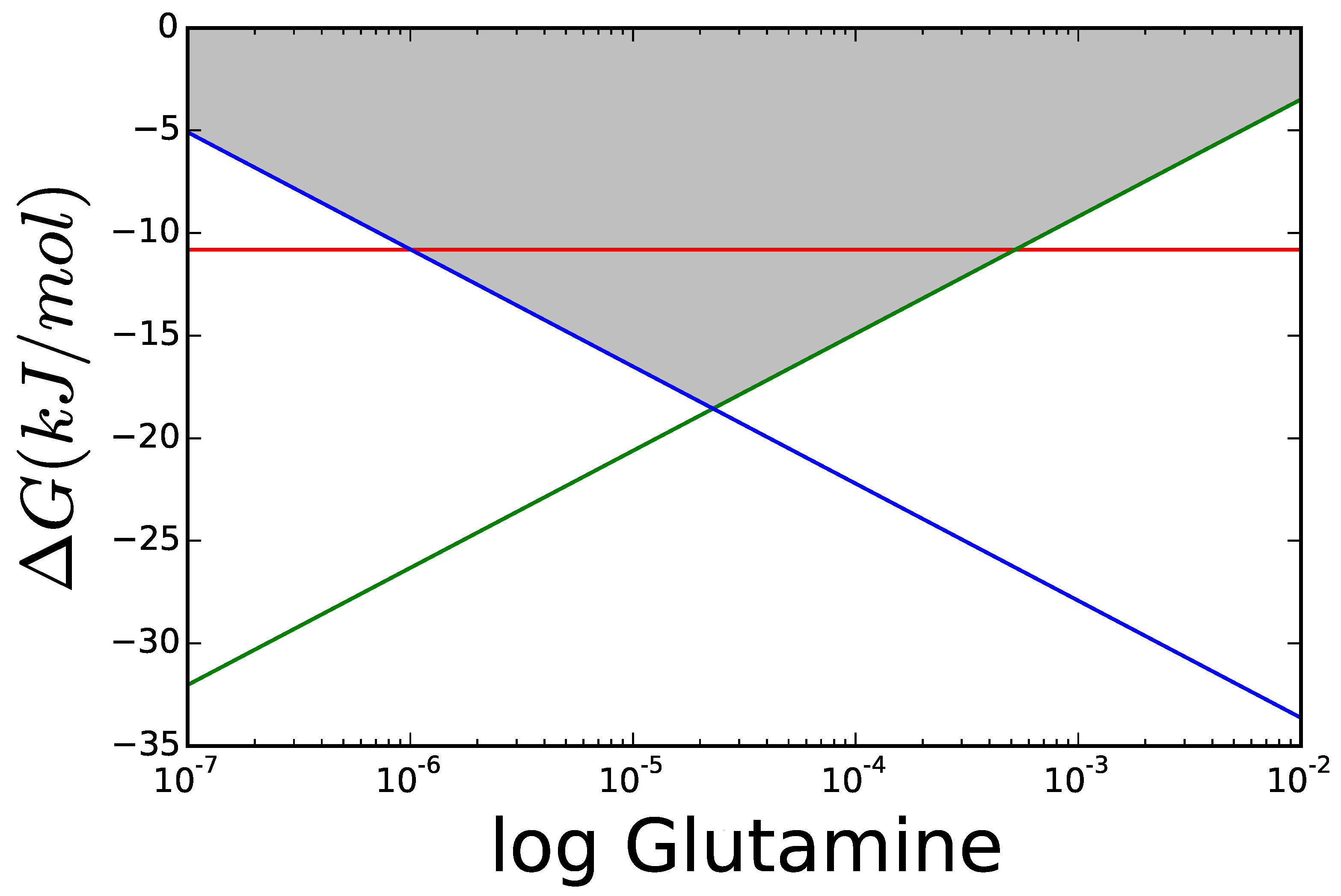
3.1. Case Study 1: Ammonia Assimilation
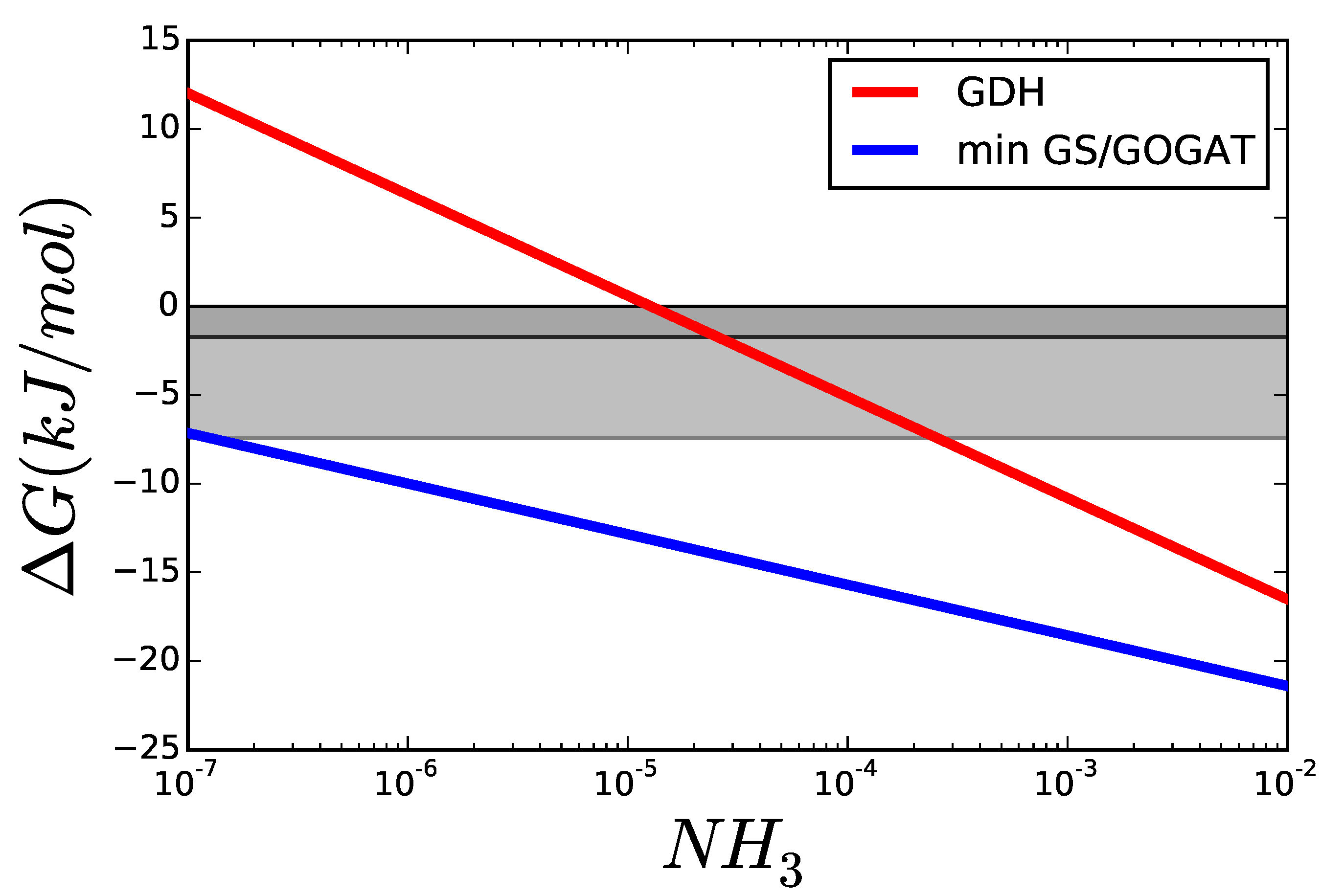
3.2. Case Study 2: Thermodynamic Shortening of an Unbranched Pathway
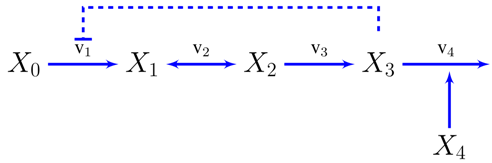
3.3. Case Study 3: Two Alternative Designs for an Unbranched Pathway
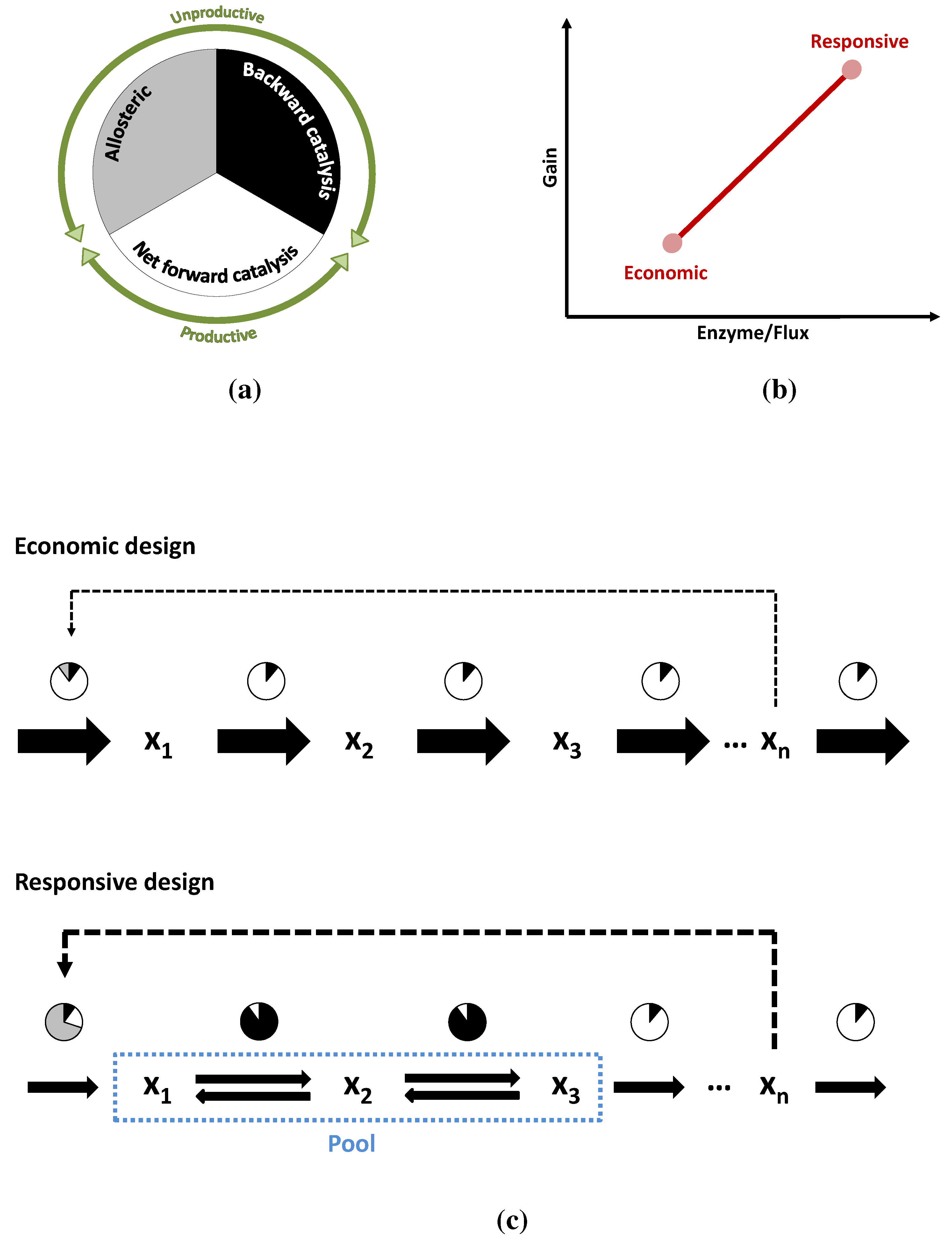
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix
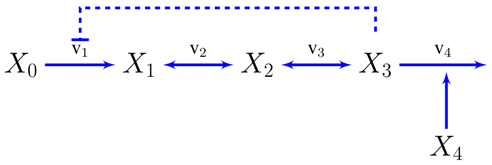
A. Supplementary Information: The Unbranched Pathway
B. Supplementary Information: Ammonia Assimilation
References
- Palsson, B.Ø. Systems Biology; Cambridge University Press: Cambridge, UK, 2015. [Google Scholar]
- Shoval, O.; Sheftel, H.; Shinar, G.; Hart, Y.; Ramote, O.; Mayo, A.; Dekel, E.; Kavanagh, K.; Alon, U. Evolutionary trade-offs, pareto optimality, and the geometry of phenotype space. Science 2012, 336, 1157–1160. [Google Scholar] [CrossRef] [PubMed]
- Savageau, M.A. Biochemical Systems Analysis: A Study of Function and Design in Molecular Biology; Addison-Wesley: Boston, NJ, USA, 1976. [Google Scholar]
- Varma, A.; Palsson, B.Ø. Metabolic capabilities of Escherichia coli: I. Synthesis of biosynthetic precursors and cofactors. J. Theor. Biol. 1993, 165, 477–502. [Google Scholar] [CrossRef] [PubMed]
- Varma, A.; Palsson, B.Ø. Metabolic capabilities of Escherichia coli ii. Optimal growth patterns. J. Theor. Biol. 1993, 165, 503–522. [Google Scholar] [CrossRef]
- Maskow, T.; von Stockar, U. How reliable are thermodynamic feasibility statements of biochemical pathways? Biotechnol. Bioeng. 2005, 92, 223–230. [Google Scholar] [CrossRef] [PubMed]
- Savageau, M.A. Biochemical systems analysis: I. Some mathematical properties of the rate law for the component enzymatic reactions. J. Theor. Biol. 1969, 25, 365–369. [Google Scholar] [CrossRef]
- Savageau, M.A. Biochemical systems analysis: II. The steady-state solutions for an n-pool system using a power-law approximation. J. Theor. Biol. 1969, 25, 370–379. [Google Scholar] [CrossRef]
- Savageau, M.A. Biochemical systems analysis: III. Dynamic solutions using a power-law approximation. J. Theor. Biol. 1970, 26, 215–226. [Google Scholar] [CrossRef]
- Schuster, S.; Pfeiffer, T.; Fell, D.A. Is maximization of molar yield in metabolic networks favoured by evolution? J. Theor. Biol. 2008, 252, 497–504. [Google Scholar] [CrossRef] [PubMed]
- Crabtree, H.G. Observations on the carbohydrate metabolism of tumours. Biochem. J. 1929, 23, 536–545. [Google Scholar] [CrossRef] [PubMed]
- Dantzig, G.B. Linear Programming and Extensions; Princeton Landmarks in Mathematics and Physics; Princeton University Press: Princeton, NJ, USA, 1963. [Google Scholar]
- Steuer, R.E. Multiple Criteria Optimization: Theory, Computation, and Applications; Wiley: New York City, NY, USA, 1986. [Google Scholar]
- Jamshidi, N.; Palsson, B.Ø. Flux-concentration duality in dynamic nonequilibrium biological networks. Biophys. J. 2009, 97, L11–L13. [Google Scholar] [CrossRef] [PubMed]
- Marin-Sanguino, A.; Mendoza, E.R.; Voit, E.O. Flux duality in nonlinear gma systems: Implications for metabolic engineering. J. Biotechnol. 2010, 149, 166–172. [Google Scholar] [CrossRef] [PubMed]
- Smallbone, K.; Simeonidis, E. Flux balance analysis: A geometric perspective. J. Theor. Biol. 2009, 258, 311–315. [Google Scholar] [CrossRef] [PubMed]
- Schellenberger, J.; Lewis, N.E.; Palsson, B.Ø. Elimination of thermodynamically infeasible loops in steady-state metabolic models. Biophys. J. 2011, 100, 544–553. [Google Scholar] [CrossRef] [PubMed]
- Kelk, S.M.; Olivier, B.G.; Stougie, L.; Bruggeman, F.J. Optimal flux spaces of genome-scale stoichiometric models are determined by a few subnetworks. Sci. Rep. 2012, 2. [Google Scholar] [CrossRef] [PubMed]
- Alberty, R.A. Thermodynamics of Biochemical Reactions; John Wiley & Sons: New York City, NY, USA, 2005. [Google Scholar]
- Henry, C.S.; Broadbelt, L.J.; Hatzimanikatis, V. Thermodynamics-based metabolic flux analysis. Biophys. J. 2007, 92, 1792–1805. [Google Scholar] [CrossRef] [PubMed]
- Bar-Even, A.; Noor, E.; Savir, Y.; Liebermeister, W.; Davidi, D.; Tawfik, D.S.; Milo, R. The moderately efficient enzyme: Evolutionary and physicochemical trends shaping enzyme parameters. Biochemistry 2011, 50, 4402–4410. [Google Scholar] [CrossRef] [PubMed]
- Noor, E.; Bar-Even, A.; Flamholz, A.; Reznik, E.; Liebermeister, W.; Milo, R. Pathway thermodynamics highlights kinetic obstacles in central metabolism. PLoS Comput. Biol. 2014, 10, e1003483. [Google Scholar] [CrossRef] [PubMed]
- Beard, D.A.; Qian, H. Relationship between thermodynamic driving force and one-way fluxes in reversible processes. PLoS ONE 2007, 2, e144. [Google Scholar] [CrossRef] [PubMed]
- Flamholz, A.; Noor, E.; Bar-Even, A.; Liebermeister, W.; Milo, R. Glycolytic strategy as a tradeoff between energy yield and protein cost. Proc. Natl. Acad. Sci. USA 2013, 110, 10039–10044. [Google Scholar] [CrossRef] [PubMed]
- Meléndez-Hevia, E.; Isidoro, A. The game of the pentose phosphate cycle. J. Theor. Biol. 1985, 117, 251–263. [Google Scholar] [CrossRef]
- Noor, E.; Eden, E.; Milo, R.; Alon, U. Central carbon metabolism as a minimal biochemical walk between precursors for biomass and energy. Mol. Cell 2010, 39, 809–820. [Google Scholar] [CrossRef] [PubMed]
- Meléndez-Hevia, E.; Waddell, T.G.; Montero, F. Optimization of metabolism: The evolution of metabolic pathways toward simplicity through the game of the pentose phosphate cycle. J. Theor. Biol. 1994, 166, 201–220. [Google Scholar] [CrossRef]
- Sorribas, A.; Hernández-Bermejo, B.; Vilaprinyo, E.; Alves, R. Cooperativity and saturation in biochemical networks: A saturable formalism using taylor series approximations. Biotechnol. Bioeng. 2007, 97, 1259–1277. [Google Scholar] [CrossRef] [PubMed]
- Garcia-Viloca, M.; Gao, J.; Karplus, M.; Truhlar, D.G. How enzymes work: analysis by modern rate theory and computer simulations. Science 2004, 303, 186–195. [Google Scholar] [CrossRef] [PubMed]
- Klipp, E.; Heinrich, R. Evolutionary optimization of enzyme kinetic parameters: Effect of constraints. J. Theor. Biol. 1994, 171, 309–323. [Google Scholar] [CrossRef] [PubMed]
- Warshel, A. Electrostatic origin of the catalytic power of enzymes and the role of preorganized active sites. J. Biol. Chem. 1998, 273, 27035–27038. [Google Scholar] [CrossRef] [PubMed]
- Fersht, A.R. Catalysis, binding and enzyme-substrate complementarity. Proc. R. Soc. Lond. B Biol. Sci. 1974, 187, 397–407. [Google Scholar] [CrossRef] [PubMed]
- Bennett, B.D.; Kimball, E.H.; Gao, M.; Osterhout, R.; van Dien, S.J.; Rabinowitz, J.D. Absolute metabolite concentrations and implied enzyme active site occupancy in Escherichia coli. Nat. Chem. Biol. 2009, 5, 593–599. [Google Scholar] [CrossRef] [PubMed]
- Burbaum, J.J.; Raines, R.T.; Albery, W.J.; Knowles, J.R. Evolutionary optimization of the catalytic effectiveness of an enzyme. Biochemistry 1989, 28, 9293–9305. [Google Scholar] [CrossRef] [PubMed]
- Pettersson, G. Evolutionary optimization of the catalytic efficiency of enzymes. Eur. J. Biochem. 1992, 206, 289–295. [Google Scholar] [CrossRef] [PubMed]
- Shoup, D.; Lipari, G.; Szabo, A. Diffusion-controlled bimolecular reaction rates: The effect of rotational diffusion and orientation constraints. Biophys. J. 1981, 36, 697. [Google Scholar] [CrossRef]
- Chou, K.C.; Li, T.-T.; Zhou, G.-Q. A semi-analytical expression for the concentration distribution of substrate molecules in fast, enzyme-catalysed reaction systems. Biochim. Biophys. Acta (BBA) Enzymol. 1981, 657, 304–308. [Google Scholar] [CrossRef]
- Mavrovouniotis, M.L.; Stephanopoulos, G.; Stephanopoulos, G. Estimation of upper bounds for the rates of enzymatic reactions. Chem. Eng. Commun. 1990, 93, 211–236. [Google Scholar] [CrossRef]
- Hammes, G.G. Multiple conformational changes in enzyme catalysis. Biochemistry 2002, 41, 8221–8228. [Google Scholar] [CrossRef] [PubMed]
- Arike, L.; Valgepea, K.; Peil, L.; Nahku, R.; Adamberg, K.; Vilu, R. Comparison and applications of label-free absolute proteome quantification methods on Escherichia coli. J. Proteom. 2012, 75, 5437–5448. [Google Scholar] [CrossRef] [PubMed]
- Link, H.; Christodoulou, D.; Sauer, U. Advancing metabolic models with kinetic information. Curr. Opin. Biotechnol. 2014, 29, 8–4. [Google Scholar] [CrossRef] [PubMed]
- Voit, E.O. Biochemical systems theory: A review. ISRN Biomath. 2013, 2013. [Google Scholar] [CrossRef]
- Kacser, H.; Burns, J.A. The control of flux. Symp. Soc. Exp. Biol. 1973, 27, 65–104. [Google Scholar] [CrossRef] [PubMed]
- Heinrich, R.; Rapoport, T.A. A linear steady-state treatment of enzymatic chains. Eur. J. Biochem. 1974, 42, 89–95. [Google Scholar] [CrossRef] [PubMed]
- Dorf, R.C.; Bishop, R.H. Modern Control Systems; Pearson: London, UK, 2011. [Google Scholar]
- Di Lampedusa, G.T. IL Gattopardo; Feltrinelli Editore: Milan, Italy, 2002; Volume 4. [Google Scholar]
- Alves, R.; Savageau, M.A. Systemic properties of ensembles of metabolic networks: Application of graphical and statistical methods to simple unbranched pathways. Bioinformatics 2000, 16, 534–547. [Google Scholar] [CrossRef] [PubMed]
- Goel, G.; Chou, I.-C.; Voit, E.O. System estimation from metabolic time-series data. Bioinformatics 2008, 24, 2505–2511. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Gunawan, R. Parameter estimation of dynamic biological network models using integrated fluxes. BMC Syst. Biol. 2014, 8, 127. [Google Scholar] [CrossRef] [PubMed]
- Pozo, C.; Miró, A.; Guillén-Gosálbez, G.; Sorribas, A.; Alves, R.; Jiménez, L. Gobal optimization of hybrid kinetic/fba models via outer-approximation. Comput. Chem. Eng. 2015, 72, 325–333. [Google Scholar] [CrossRef]
- Gerdtzen, Z.P.; Daoutidis, P.; Hu, W.-S. Non-linear reduction for kinetic models of metabolic reaction networks. Metab. Eng. 2004, 6, 140–154. [Google Scholar] [CrossRef] [PubMed]
- Van Heeswijk, W.C.; Westerhoff, H.V.; Boogerd, F.C. Nitrogen assimilation in Escherichia coli: Putting molecular data into a systems perspective. Microbiol. Mol. Biol. Rev. 2013, 77, 628–695. [Google Scholar] [CrossRef] [PubMed]
- Flamholz, A.; Noor, E.; Bar-Even, A.; Milo, R. eQuilibrator—The biochemical thermodynamics calculator. Nucleic Acids Res. 2012. [Google Scholar] [CrossRef] [PubMed]
- Windass, J.D.; Worsey, M.J.; Pioli, E.M.; Pioli, D.; Barth, P.T.; Atherton, K.T.; Dart, E.C.; Byrom, D.; Powell, K.; Senior, P.J. Improved conversion of methanol to single-cell protein by methylophilus methylotrophus. Nature 1980, 287, 396–401. [Google Scholar] [CrossRef] [PubMed]
- Alves, R.; Savageau, M.A. Irreversibility in unbranched pathways: Preferred positions based on regulatory considerations. Biophys. J. 2001, 80, 1174–1185. [Google Scholar] [CrossRef]
- Ederer, M.; Gilles, E.D. Thermodynamically feasible kinetic models of reaction networks. Biophys. J. 2007, 92, 1846–1857. [Google Scholar] [CrossRef] [PubMed]
- Noor, E.; Bar-Even, A.; Flamholz, A.; Lubling, Y.; Davidi, D.; Milo, R. An integrated open framework for thermodynamics of reactions that combines accuracy and coverage. Bioinformatics 2012, 28, 2037–2044. [Google Scholar] [CrossRef] [PubMed]
- Alves, R.; Savageau, M.A. Extending the method of mathematically controlled comparison to include numerical comparisons. Bioinformatics 2000, 16, 786–798. [Google Scholar] [CrossRef] [PubMed]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sehr, C.; Kremling, A.; Marin-Sanguino, A. Design Principles as a Guide for Constraint Based and Dynamic Modeling: Towards an Integrative Workflow. Metabolites 2015, 5, 601-635. https://doi.org/10.3390/metabo5040601
Sehr C, Kremling A, Marin-Sanguino A. Design Principles as a Guide for Constraint Based and Dynamic Modeling: Towards an Integrative Workflow. Metabolites. 2015; 5(4):601-635. https://doi.org/10.3390/metabo5040601
Chicago/Turabian StyleSehr, Christiana, Andreas Kremling, and Alberto Marin-Sanguino. 2015. "Design Principles as a Guide for Constraint Based and Dynamic Modeling: Towards an Integrative Workflow" Metabolites 5, no. 4: 601-635. https://doi.org/10.3390/metabo5040601
APA StyleSehr, C., Kremling, A., & Marin-Sanguino, A. (2015). Design Principles as a Guide for Constraint Based and Dynamic Modeling: Towards an Integrative Workflow. Metabolites, 5(4), 601-635. https://doi.org/10.3390/metabo5040601




