Computational Strategies for a System-Level Understanding of Metabolism
Abstract
:1. Introduction
- Establish from the beginning the scientific question that motivates the development of the model. Consequently, the analysis of the model is expected to increase the current knowledge on the system, thanks to novel predictions on its functioning and to their experimental validation. In this phase, initial experimental data are necessary to define a plausible mathematical model, since they can aid to discriminate among different hypotheses on the structure of the system.
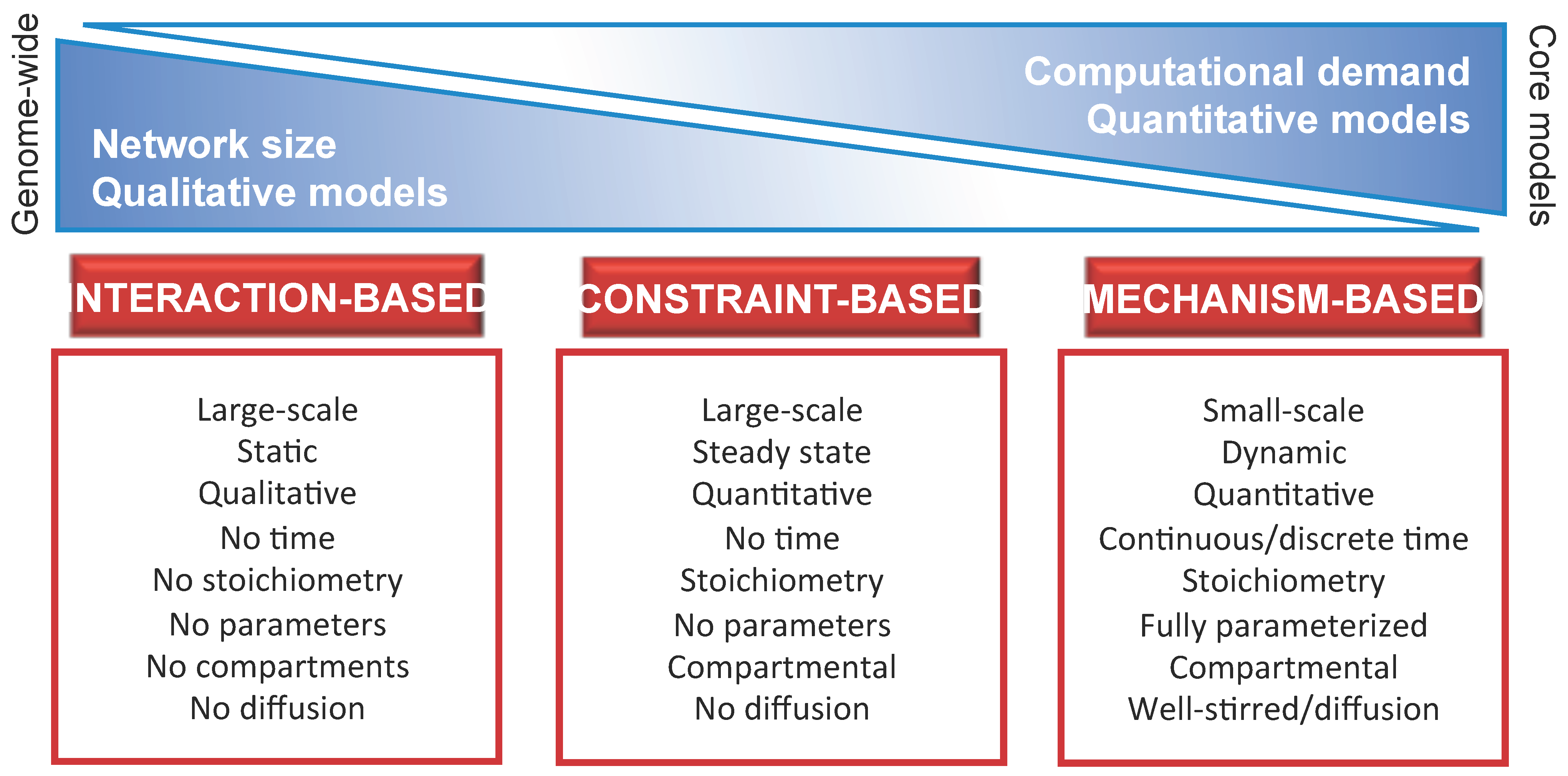
- Identify the proper level of abstraction necessary to formally describe the components of thesystem and their mutual interactions. In particular, the model should take into account all available knowledge on the biochemical, physical or regulatory properties of all system components and interactions. In so doing, any detectable emergent property of the system—either in the physiological state or in response to genetic, chemical or environmental perturbations—can be discovered with the appropriate computational methods. The choice of the level of abstraction will bring to the definition of either fine-grained (e.g., mechanism-based) or coarse-grained (e.g., interaction-based or constraint-based) models. Typically, the mechanism-based approach deals with toy or core models, while the interaction-based and constraint-based approaches are more suited for the analysis of genome-wide or core models. A schematic overview of the three main modeling approaches is given in Figure 1, including a list of their principal dichotomic features [23], such as quantitative vs. qualitative, static vs. dynamic, parameterized vs. non parameterized, single volume vs. compartmental, well-stirred vs. heterogeneous (diffusion), etc.Figure 1. Schematic overview of the main modeling approaches for biological systems, together with their principal characteristics and differences. Moving from the coarse-grained (interaction-based, constraint-based) to the fine-grained (mechanism-based) approach, models vary with respect to: (i) the size of the system, defined in terms of the number of components and respective interactions included in the model, which decrease from genome-wide to core models (Section 2.1); (ii) the computational costs required for the analysis of the model, which increase from the analysis of the topological properties of the network typical of interaction-based models (Section 3.1), to the study of flux distributions typical of constraint-based models (Section 3.2), to the investigation of the system dynamics typical of mechanism-based models (Section 3.3); (iii) the nature of the computational results together with the predictive capability, which changes from qualitative to quantitative while moving from interaction-based models (characterized by a high level of abstraction) to mechanism-based models (fully parameterized and describing the system at the level of the functional chemical interactions).Figure 1. Schematic overview of the main modeling approaches for biological systems, together with their principal characteristics and differences. Moving from the coarse-grained (interaction-based, constraint-based) to the fine-grained (mechanism-based) approach, models vary with respect to: (i) the size of the system, defined in terms of the number of components and respective interactions included in the model, which decrease from genome-wide to core models (Section 2.1); (ii) the computational costs required for the analysis of the model, which increase from the analysis of the topological properties of the network typical of interaction-based models (Section 3.1), to the study of flux distributions typical of constraint-based models (Section 3.2), to the investigation of the system dynamics typical of mechanism-based models (Section 3.3); (iii) the nature of the computational results together with the predictive capability, which changes from qualitative to quantitative while moving from interaction-based models (characterized by a high level of abstraction) to mechanism-based models (fully parameterized and describing the system at the level of the functional chemical interactions).
- Choose the most appropriate mathematical formalism. A one-to-one correspondence between each modeling approach and a specific modeling purpose would facilitate the choice of the most suitable strategy to be employed. Unfortunately, a sharp-cutting separation is not always possible. In general, mechanism-based (dynamical) models—which are usually defined as systems of differential equations—are considered the most likely candidates to achieve a detailed comprehension of cellular processes. Nonetheless, the usual lack of quantitative parameters represents a limit to a wide applicability of this approach for large metabolic networks. Various attempts have been proposed for the automatic estimation of missing parameters or the characterization of the parameters space [24,25,26].On the other side of the spectrum of modeling approaches, interaction-based models are characterized by a simplified representation of the biological process and allow to achieve qualitative knowledge only. These models can be analyzed by using, for instance, graph theory or topological analysis to investigate the “design principles” of metabolic networks, that can be considered transversal to different organisms [27]. Moreover, they allow to easily identify the so-called hubs (highly interconnected components, essential for the existence of several metabolic processes), as well as the metabolites and reactions connecting them, which can be of particular interest within the scope of, e.g., drug target discovery [28].Considering the limitations of these modeling approaches, the common practice for the computational investigation of metabolism usually relies on constraint-based models. These models are based on the definition and manipulation of stoichiometric matrices, whose native application pertains to the field of metabolic engineering. In this case, the methodologies that were initially developed for the optimization of microbial strains or for the maximization of some product yields in biotechnological applications, are now widely used with different goals in the study of metabolic networks.
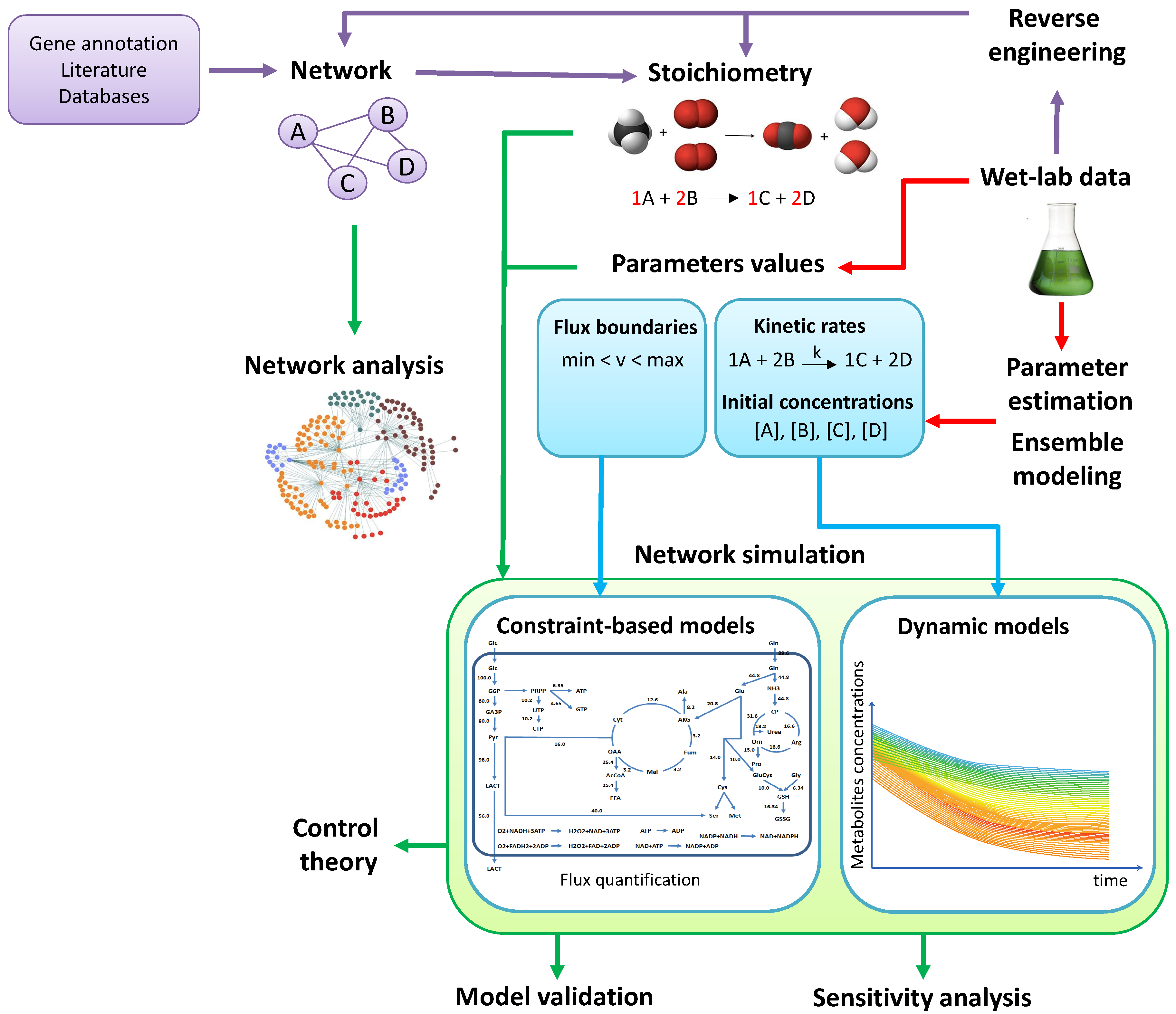
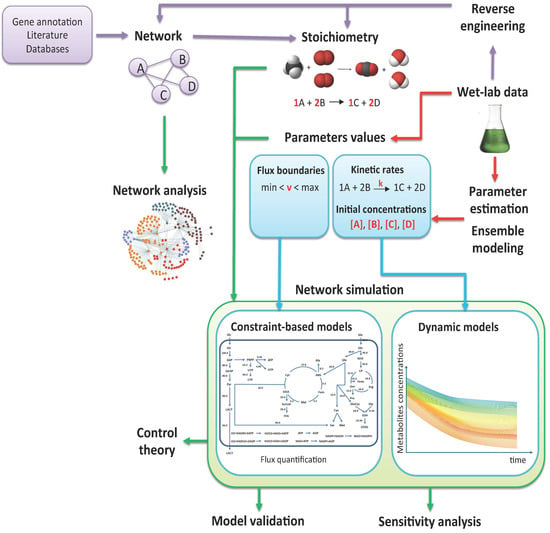
2. From Experimental Data to Models
2.1. Metabolic Network Reconstruction
2.2. Parameter Estimation
2.3. Reverse Engineering
2.4. Ensemble Modeling
3. From Models to in Silico Data
3.1. Topological Analysis
3.2. Flux Balance Analysis
3.3. Simulation of the Dynamics
4. From In Silico Data to Experimental Hypothesis
4.1. Model Validation
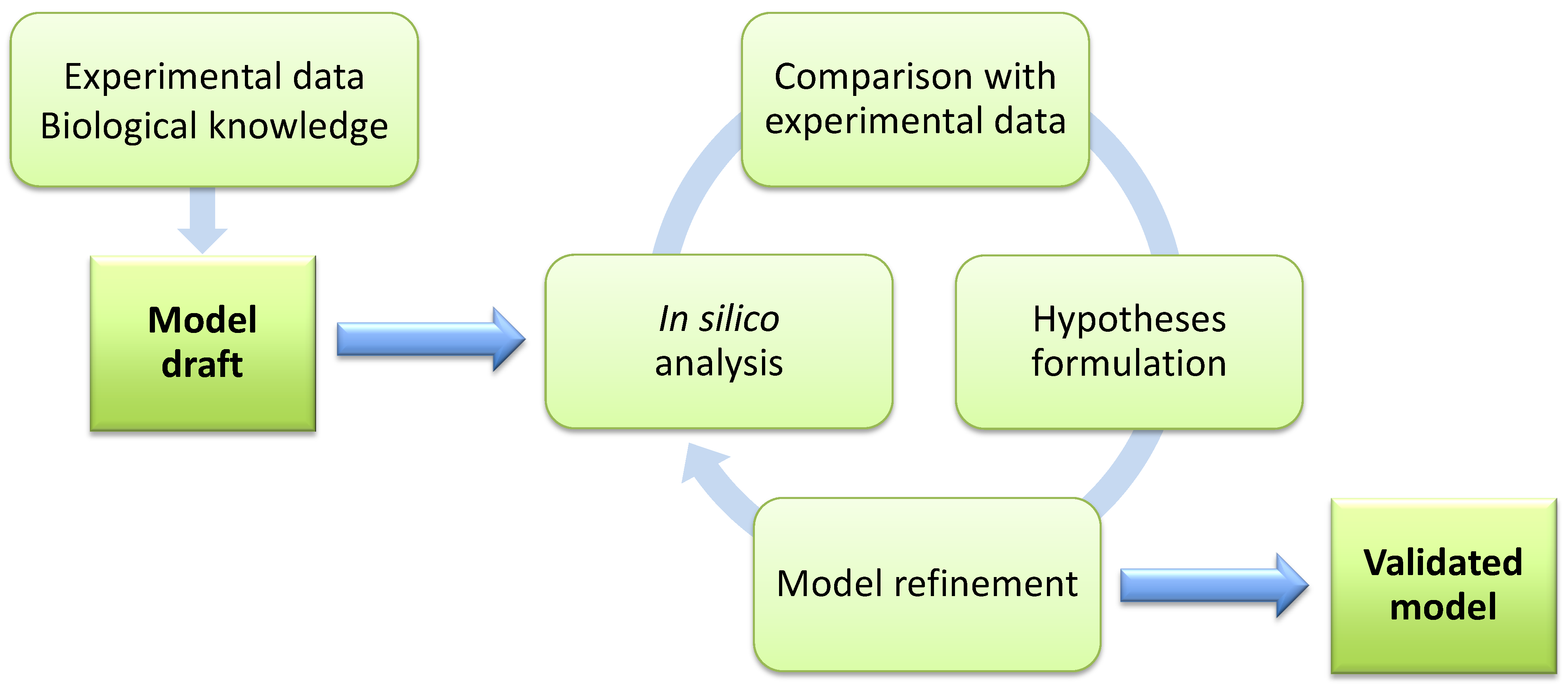
4.2. Sensitivity Analysis
4.3. Control Theory
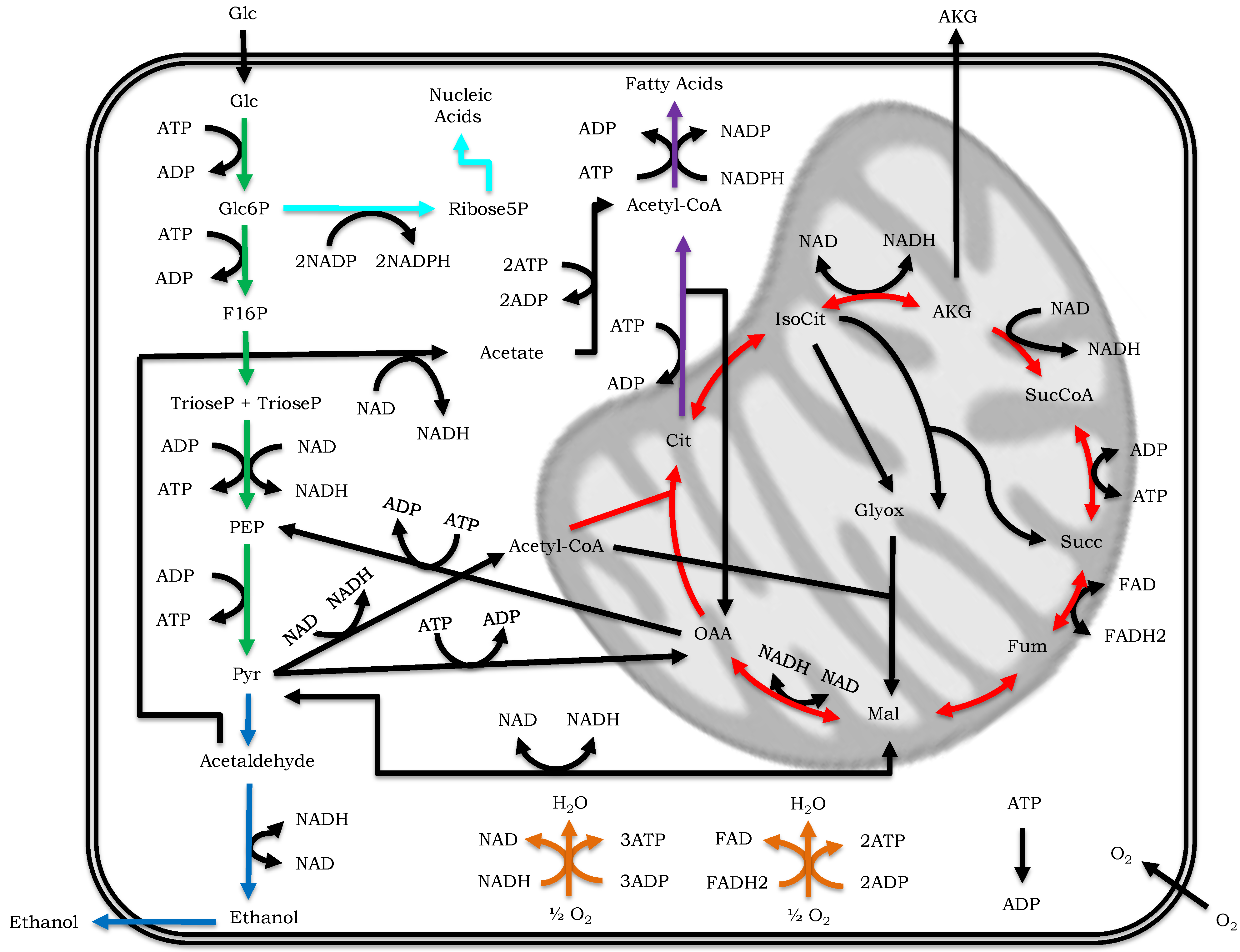
5. Computational Strategies at Work: Gaining Novel Insights on Metabolism
5.1. Increase, Integrate and Validate Biological Knowledge
5.2. Generate Experimentally Testable Hypotheses: Identify Regulatory Nodes and Drug Targets
5.3. Design Microbial Strains for Metabolic Engineering and Industrial Applications
6. Conclusions and Perspectives
| Pathway/Aim ofthe Model | Cell Type/Organ | Organism | Modeling Approach &Methodology | ExperimentalData | Reference |
|---|---|---|---|---|---|
| Glycolysis | - | T. brucei | CM, ODE | L | Achcar et al. [159] |
| GW metabolic network and succinic acid production | - | S. cerevisiae | GW, FBA | M | Agren et al. [58] |
| GW metabolic network | - | A. niger | GW, FBA | L | Andersen et al. [173] |
| Mitochondrial energy metabolism, Na+/Ca2+ cycle, K+ cycle | Heart, liver | B. taurus, S. scrofa, R. norvegicus | CM, DAE, PE, SA | L, M | Bazil et al. [80] |
| OXPHOS | Cardiomyocytes | R. norvegicus | CM, ODE | L | Beard [156] |
| Electron transport chain | Heart homogenates | R. norvegicus | CM, ODE, CRL | L, M | Chang et al. [154] |
| Glycolysis, OXPHOS | Not specified | Eukaryotic, H. sapiens | CM, Control theory | L | Cloutier et al. [200] |
| Bow-tie architecture of metabolism | Not specified | H. sapiens | GW, Topological analysis | L | Csete et al. [118] |
| Central metabolism | - | Yeast | CM, FBA | L | Damiani et al. [65] |
| Energy metabolism | Skeletal muscle cell | Mammal | CM, PDE | L | Dasika et al. [165] |
| Glycolysis and pentose phosphate pathway | - | E. coli | CM, ODE, SA | L | Degenring et al. [179] |
| Glycolysis and pentose phosphate pathway | - | E. coli | CM, ODE, SA | L | Degenring et al. [179] |
| Biosynthesis of valine and leucine | - | C. glutaminicum | CM, ODE, SDE | M | Dräger et al. [76] |
| Anabolic, catabolic, chemiosmosis pathways | - | E. coli | GW, Control theory | M | Federowicw et al. [202] |
| Small world behavior of metabolism | Not specified | H. sapiens | GW, Topological analysis | L | Fell et al. [116] |
| GW metabolic network | Not specified | H. sapiens | GW, FBA | L | Duarte et al. [39] |
| GW metabolic network | - | E. coli MG1655 | GW, FBA | M | Edwards and Palsson [175] |
| GW metabolic network | - | H. influenzae | GW, FBA | L | Edwards et al. [36] |
| Cancer metabolic networks | Various (NCI-60 collection) | H. sapiens | Network reconstruction, FBA, gene (pair) analysis | L | Folger et al. [208] |
| GW metabolic network HepatoNet1 | Hepatocytes | H. sapiens | GW. Network reconstruction | L | Gille et al. [220] |
| Cytochrome bc1 complex, ROS production | Muscle, heart, liver, kidney, brain | R. norvegicus | CM, ODE | L | Guillaud et al. [153] |
| GW metabolic network EHMN | Not specified | H. sapiens | GW, Network reconstruction | L | Hao et al. [221] |
| GW metabolic network | - | S. cerevisiae S288c | GW, Network reconstruction, FBA | L | Heavner et al. [3] |
| GW metabolic network | - | S. cerevisiae | Network reconstruction | L | Herrgård et al. [43] |
| Topological properties of metabolism | - | 43 different organisms | GW, Topological analysis | L | Jeong et al. [27] |
| Glycolysis, OXPHOS | - | Not specified | CM, ODE, Game theory | - | Kareva [189] |
| Whole-cell life cycle model | - | M. genitalium | GW, FBA, ODE | L, M | Karr et al. [204] |
| Glycolysis, pentose phosphate pathway | - | T. brucei | CM, ODE | L | Kerkhoven et al. [64] |
| Energy metabolism | Colorectal cells | H. sapiens | CM, FBA, EM | M | Khazaei et al. [214] |
| GW metabolic network | - | Synechocystis sp. PCC 6803 | GW, FBA | L | Knoop et al. [37] |
| Glycolysis, gluconeogenesys, glycogen metabolism | Hepatocytes | H. sapiens | CM, ODE | L | König et al. [157] |
| Adenine nucleotide translocase | Heart mitochondria | B. taurus | CM, ODE, PE, SA | L | Metelkin et al. [152] |
| GW metabolic network | - | Z. mays L. subsp. mays | GW, Network reconstruction | L | Monaco et al. [40] |
| Xylose metabolism | - | L. lactis IO-1 | CM, ODE, SA | M | Oshiro et al. [183] |
| GW metabolic network | - | S. cerevisiae | GW, Network reconstruction, FBA | L | Österlund et al. [222] |
| GW metabolic network and succinic acid production | - | S. cerevisiae | GW, FBA | M | Otero et al. [57] |
| Topological properties of metabolism | - | 43 different organisms, E. coli | GW, Topological analysis | L | Ravasz et al. [122] |
| One-carbon metabolism, trans-sulfuration pathway, synthesis of glutathione | Hepatocyte | H. sapiens | CM, ODE | L | Reed et al. [158] |
| Glycolysis, TCA cycle, pentose phosphate pathway, glutaminolysis, OXPHOS | HeLa cell | H. sapiens | CM, FBA | M | Resendis-Antonio et al. [67] |
| Modularity of metabolism | Not specified | H. sapiens | GW, Topological analysis | L | Resendis-Antonio et al. [120] |
| GW metabolic network | Not specified | H. sapiens | GW, Network reconstruction | L | Sahoo et al. [223] |
| Acetone, butanol and ethanol production | - | C. acetobutylicum | CM, ODE, SA | M | Shinto et al. [184] |
| Cancer metabolic networks | Various (NCI-60 collection) | H. sapiens | FBA | L | Shlomi et al. [206] |
| GW metabolic network | - | S. cerevisiae | GW, FBA | L | Simeonidis et al. [130] |
| Glycolysis | - | S. cerevisiae | CM, ODE | M | Teusink et al. [62] |
| GW metabolic network | Not specified | H. sapiens | GW, FBA | L | Thiele et al. [4] |
| Primary metabolism | - | E. coli | CM, ODE, EM | - | Tran et al. [101] |
| Fueling reaction network | - | E. coli W3110 | CM, FBA | M | Varma et al. [174] |
| Reduced model of cell metabolism | - | - | CM, FBA | L | Vazquez et al. [61] |
| Small-world property of metabolism | - | E. coli | GW. Topological analysis | L | Wagner et al. [117] |
| GW metabolic network | - | C. glabrata | GW, FBA | L | Xu et al. [38] |
| Erythrocyte metabolism | Red blood cell | H. sapiens | Hybrid: ODE + MFA | - | Yugi et al. [166] |
| Mitochondrial energy metabolism | Various tissues | Mammal | CM, ODE | - | Yugi [224] |
| Modularity of metabolism | Not specified | H. sapiens | GW, Topological analysis | L | Zhao et al. [119] |
| ROS-induced ROS release in mitochondria network | Cardiomyocytes | C. porcellus | CM, ODE, PDE, RD, Finite Difference Method | M | Zhou et al. [164] |
| Tool name | Purpose | Interaction-based | Constraint-Based | Mechanism-Based | Reference |
|---|---|---|---|---|---|
| BioMet Toolbox | Genome-wide metabolic model validation, FBA, probabilistic FBA, gene set analysis | √ | [225] | ||
| Cobra Toolbox | FBA, FVA, dFBA, gap filling, network visualization | √ | [226] | ||
| COPASI | Determinstic, stochastic and hybrid simulation, PE, SA, MCA | √ | [227,228] | ||
| cupSODA | Deterministic simulations on GPUs | √ | [171] | ||
| Cytoscape | Complex networks visualization and topological analysis | √ | [229,230] | ||
| FAME | Web based FBA and FVA | √ | [231] | ||
| FASIMU | FBA, FVA, gene deletion analysis, gap filling | √ | [232] | ||
| OptFlux | FBA, FVA, EFM, gene deletion analysis | √ | [233] | ||
| Pathway Tools | GW reconstruction, FBA, gap filling | √ | [234] | ||
| Raven Toolbox | GW reconstructions, FBA, network analysis and visualization | √ | √ | [235] | |
| SurreyFBA | FBA, FVA, EFM | √ | [236] |
| Database | Contents | Reference |
|---|---|---|
| BiGG | Genome-scale metabolic networks | [237] |
| BioCyc | Collection of more than 3000 pathways / genome databases | [238] |
| BioModels | SBML models of biological processes | [239] |
| Brenda | Molecular and biochemical information on enzymes | [240] |
| CellML | XML-based models of biological processes | [241] |
| Ensembl | Genome browser for genomic information | [242] |
| ExPASy | Portal to existing databases and tools categorized by life science areas | [243] |
| GeneCards | Omics data on human genes | [244] |
| HumanCyc | Human metabolism pathways | [245] |
| Human Metabolic Atlas | Human metabolism models | [52] |
| Human Protein Atlas | Human protein expression profiles with spatial localization in tissues and cells | [53] |
| JWS | Curated models of biochemical pathways and simulation tools | [246] |
| KEGG | Manually curated pathway maps integrating molecular-level information | [32] |
Acknowledgments
Author Contributions
Conflicts of Interest
List of Acronyms
| BDO | 1,4-butanediol |
| CM | Core Model |
| DE | Differential Evolution |
| dFBA | Dynamic Flux Balance Analysis |
| dNTP | Deoxyribonucleotide Triphosphate |
| EFM | Elementary Flux Modes |
| EM | Ensemble Modeling |
| FBA | Flux Balance Analysis |
| FDG-PET | 18F-fluorodeoxyglucose–positron emission tomography |
| FVA | Flux Variability Analysis |
| GA | Genetic Algorithm |
| GC | Gas Chromatography |
| GC-MS | Gas Chromatography Mass Spectrometry |
| GP | Genetic Programming |
| GPU | Graphical Processing Unit |
| GW | Genome-Wide |
| MCA | Metabolic Control Analysis |
| MFA | Metabolic Flux Analysis |
| MID | Mass Isoptomers Distribution |
| MS | Mass Spectrometry |
| OAT | One-factor-at-A-Time |
| ODE | Ordinary Differential Equation |
| OF | Objective Function |
| PE | Parameter Estimation |
| PSO | Particle Swarm Optimization |
| RD | Reaction-Diffusion |
| RE | Reverse Engineering |
| ROS | Reactive Oxygen Species |
| SA | Sensitivity Analysis |
| SiAn | Simulated Annealing |
| SDE | Stochastic Differential Equation |
| TCA | Tricarboxylic Acid |
Appendix I: Experimental Methodologies for Metabolic Data Generation
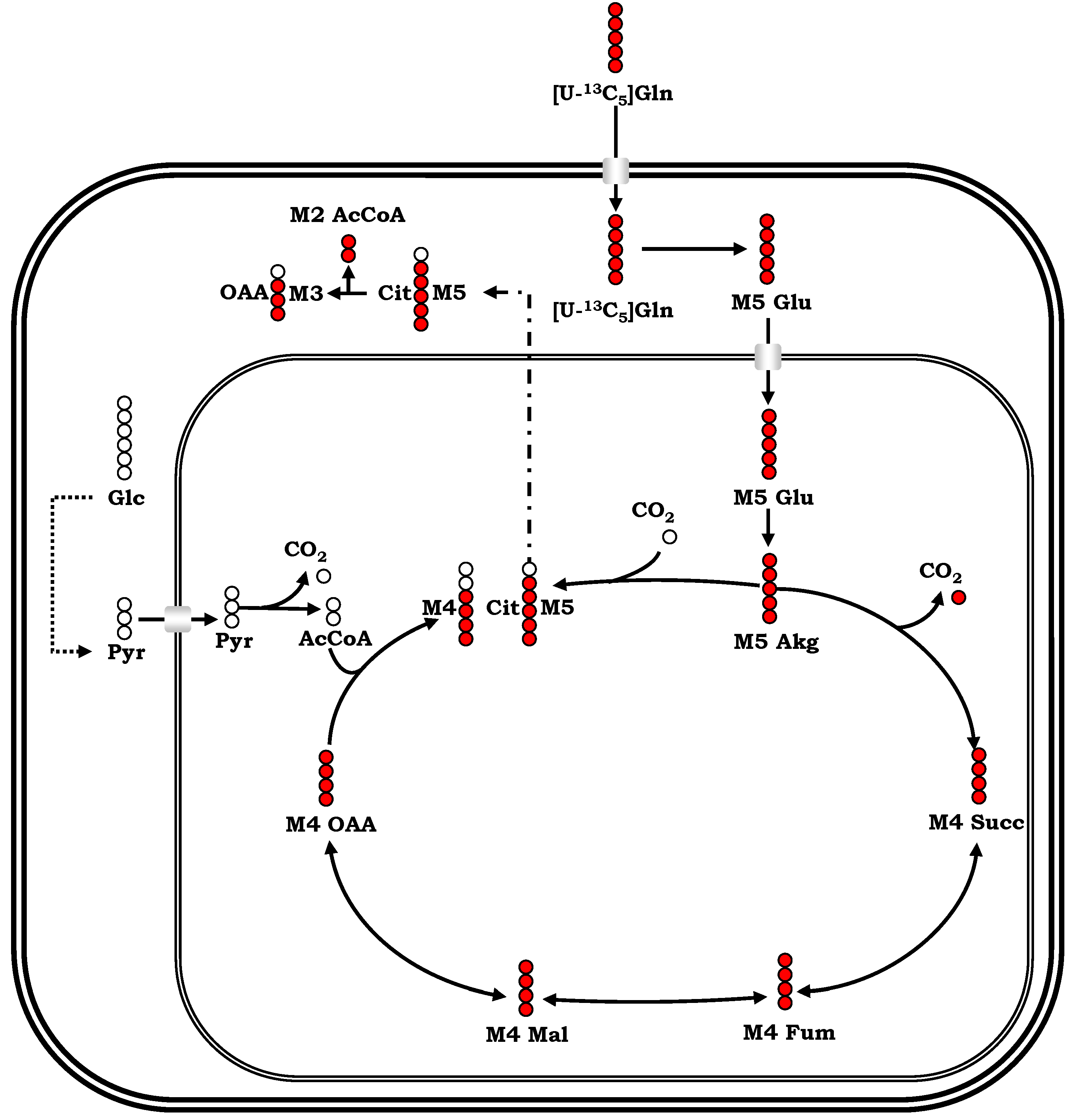
References
- Suthers, P.F.; Dasika, M.S.; Kumar, V.S.; Denisov, G.; Glass, J.I.; Maranas, C.D. A genome-scale metabolic reconstruction of Mycoplasma genitalium, iPS189. PLoS Comput. Biol. 2009, 5, e1000285. [Google Scholar] [CrossRef] [PubMed]
- Monk, J.M.; Charusanti, P.; Aziz, R.K.; Lerman, J.A.; Premyodhin, N.; Orth, J.D.; Feist, A.M.; Palsson, B.Ø. Genome-scale metabolic reconstructions of multiple Escherichia coli strains highlight strain-specific adaptations to nutritional environments. Proc. Natl. Acad. Sci. USA 2013, 110, 20338–20343. [Google Scholar] [CrossRef] [PubMed]
- Heavner, B.D.; Smallbone, K.; Price, N.D.; Walker, L.P. Version 6 of the consensus yeast metabolic network refines biochemical coverage and improves model performance. Database-Oxford 2013, 2013, 1. [Google Scholar]
- Thiele, I.; Swainston, N.; Fleming, R.M.T.; Hoppe, A.; Sahoo, S.; Aurich, M.K.; Haraldsdottir, H.; Mo, M.L.; Rolfsson, O.; Stobbe, M.D.; et al. A community-driven global reconstruction of human metabolism. Nat. Biotechnol. 2013, 31, 419–425. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kubota, K.; Fukushima, T.; Yuji, R.; Miyano, H.; Hirayama, K.; Santa, T.; Imai, K. Development of an HPLC-fluorescence determination method for carboxylic acids related to the tricarboxylic acid cycle as a metabolome tool. Biomed. Chromatogr. 2005, 19, 788–795. [Google Scholar] [CrossRef] [PubMed]
- Nielsen, J.; Oliver, S. The next wave in metabolome analysis. Trends Biotechnol. 2005, 23, 544–546. [Google Scholar] [CrossRef] [PubMed]
- Griffin, J.L. Metabolic profiles to define the genome: can we hear the phenotypes? Philos. Trans. R. Soc. B 2004, 359, 857–871. [Google Scholar] [CrossRef]
- Griffin, J.L.; Shockcor, J.P. Metabolic profiles of cancer cells. Nat. Rev. Cancer 2004, 4, 551–561. [Google Scholar] [CrossRef] [PubMed]
- Patton, A.L.; Seely, K.A.; Chimalakonda, K.C.; Tran, J.P.; Trass, M.; Miranda, A.; Fantegrossi, W.E.; Kennedy, P.D.; Dobrowolski, P.; Radominska-Pandya, A.; et al. Targeted metabolomic approach for assessing human synthetic cannabinoid exposure and pharmacology. Anal. Chem. 2013, 85, 9390–9399. [Google Scholar]
- Robertson, D.G.; Watkins, P.B.; Reily, M.D. Metabolomics in toxicology: preclinical and clinical applications. Toxicol. Sci. 2011, 120, S146–S170. [Google Scholar] [CrossRef] [PubMed]
- Roessner, U.; Luedemann, A.; Brust, D.; Fiehn, O.; Linke, T.; Willmitzer, L.; Fernie, A.R. Metabolic profiling allows comprehensive phenotyping of genetically or environmentally modified plant systems. Plant Cell 2001, 13, 11–29. [Google Scholar] [CrossRef] [PubMed]
- Nordström, A.; Lewensohn, R. Metabolomics: Moving to the clinic. J. Neuroimmune Pharm. 2010, 5, 4–17. [Google Scholar] [CrossRef]
- Alberghina, L.; Gaglio, D.; Moresco, R.M.; Gilardi, M.C.; Messa, C.; Vanoni, M. A systems biology road map for the discovery of drugs targeting cancer cell metabolism. Curr. Pharm. Design 2014, 20, 2648–2666. [Google Scholar]
- Ward, P.S.; Thompson, C.B. Metabolic reprogramming: A cancer hallmark even Warburg did not anticipate. Cancer Cell 2012, 21, 297–308. [Google Scholar] [CrossRef] [PubMed]
- Hanahan, D.; Weinberg, R.A. Hallmarks of cancer: The next generation. Cell 2011, 144, 646–674. [Google Scholar] [CrossRef] [PubMed]
- Senn, T.; Hazen, S.L.; Tang, W. Translating metabolomics to cardiovascular biomarkers. Prog. Cardiovasc. Dis. 2012, 55, 70–76. [Google Scholar] [CrossRef]
- Trushina, E.; Mielke, M.M. Recent advances in the application of metabolomics to Alzheimer’s disease. BBA-Mol. Basis Dis. 2014, 1842, 1232–1239. [Google Scholar] [CrossRef]
- Vermeersch, K.A.; Styczynski, M.P. Applications of metabolomics in cancer research. J. Carcinog. 2013, 12, 9. [Google Scholar] [CrossRef] [PubMed]
- Toya, Y.; Shimizu, H. Flux analysis and metabolomics for systematic metabolic engineering of microorganisms. Biotechnol. Adv. 2013, 31, 818–826. [Google Scholar] [CrossRef] [PubMed]
- Feng, X.; Page, L.; Rubens, J.; Chircus, L.; Colletti, P.; Pakrasi, H.B.; Tang, Y.J. Bridging the gap between fluxomics and industrial biotechnology. Biomed. Res. Int. 2011, 2010. Article ID460717. [Google Scholar]
- Gianchandani, E.P.; Chavali, A.K.; Papin, J.A. The application of flux balance analysis in systems biology. WIREs Syst. Biol. Med. 2010, 2, 372–382. [Google Scholar] [CrossRef]
- Alberghina, L.; Westerhoff, H.V. Systems Biology: Definitions and Perspectives; Topics in Current Genetics; Springer-Verlag Berlin: Heidelberg, Germany, 2005. [Google Scholar]
- Stelling, J. Mathematical models in microbial systems biology. Curr. Opin. Microbiol. 2004, 7, 513–518. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Hatzimanikatis, V. Metabolic engineering under uncertainty. I: Framework development. Metab. Eng. 2006, 8, 133–141. [Google Scholar] [CrossRef] [PubMed]
- Steuer, R.; Gross, T.; Selbig, J.; Blasius, B. Structural kinetic modeling of metabolic networks. Proc. Natl. Acad. Sci. USA 2006, 103, 11868–11873. [Google Scholar] [CrossRef] [PubMed]
- Murabito, E.; Smallbone, K.; Swinton, J.; Westerhoff, H.V.; Steuer, R. A probabilistic approach to identify putative drug targets in biochemical networks. J. R. Soc. Interface 2011, 8, 880–895. [Google Scholar] [PubMed]
- Jeong, H.; Tombor, B.; Albert, R.; Oltvai, Z.N.; Barabási, A.L. The large-scale organization of metabolic networks. Nature 2000, 407, 651–654. [Google Scholar] [CrossRef] [PubMed]
- Hopkins, A.L. Network pharmacology: the next paradigm in drug discovery. Nat. Chem. Biol. 2008, 4, 682–690. [Google Scholar] [CrossRef] [PubMed]
- Feist, A.M.; Herrgård, M.J.; Thiele, I.; Reed, J.L.; Palsson, B.Ø. Reconstruction of biochemical networks in microorganisms. Nat. Rev. Microbiol. 2008, 7, 129–143. [Google Scholar] [CrossRef] [PubMed]
- Karp, P.D.; Riley, M.; Paley, S.M.; Pelligrini-Toole, A. EcoCyc: An encyclopedia of Escherichia coli genes and metabolism. Nucleic Acids Res. 1996, 24, 32–39. [Google Scholar] [CrossRef] [PubMed]
- Karp, P.D.; Ouzounis, C.A.; Paley, S.M. HinCyc: A knowledge base of the complete genome and metabolic pathways of H. influenzae. In Proceedings of the International Conference on Intelligent Systems for Molecular Biology (ISMB), St. Louis, MO, USA, 12–25 June 1996; Volume 4, pp. 116–124.
- Kanehisa, M.; Goto, S. KEGG: Kyoto Encyclopedia of Genes and Genomes. Nucleic Acids Res. 2000, 28, 27–30. [Google Scholar] [CrossRef] [PubMed]
- Levchenko, A. Dynamical and integrative cell signaling: Challenges for the new biology. Biotechnol. Bioeng. 2003, 84, 773–782. [Google Scholar] [CrossRef] [PubMed]
- Soon, W.W.; Hariharan, M.; Snyder, M.P. High-throughput sequencing for biology and medicine. Mol. Syst. Biol. 2013. [Google Scholar] [CrossRef]
- Hyduke, D.R.; Lewis, N.E.; Palsson, B.Ø. Analysis of omics data with genome-scale models of metabolism. Mol. Biosyst. 2013, 9, 167–174. [Google Scholar] [CrossRef] [PubMed]
- Edwards, J.S.; Palsson, B.Ø. Systems properties of the Haemophilus influenzae Rd metabolic genotype. J. Biol. Chem. 1999, 274, 17410–17416. [Google Scholar] [CrossRef] [PubMed]
- Knoop, H.; Gründel, M.; Zilliges, Y.; Lehmann, R.; Hoffmann, S.; Lockau, W.; Steuer, R. Flux balance analysis of cyanobacterial metabolism: The metabolic network of Synechocystis sp. PCC 6803. PLoS Comput. Biol. 2013, 9, e1003081. [Google Scholar] [CrossRef] [PubMed]
- Xu, N.; Liu, L.; Zou, W.; Liu, J.; Hua, Q.; Chen, J. Reconstruction and analysis of the genome-scale metabolic network of Candida glabrata. Mol. Biosyst. 2013, 9, 205–216. [Google Scholar] [CrossRef] [PubMed]
- Duarte, N.C.; Becker, S.A.; Jamshidi, N.; Thiele, I.; Mo, M.L.; Vo, T.D.; Srivas, R.; Palsson, B.Ø. Global reconstruction of the human metabolic network based on genomic and bibliomic data. Proc. Natl. Acad. Sci. USA 2007, 104, 1777–1782. [Google Scholar] [CrossRef] [PubMed]
- Monaco, M.K.; Sen, T.Z.; Dharmawardhana, P.D.; Ren, L.; Schaeffer, M.; Naithani, S.; Ama-rasinghe, V.; Thomason, J.; Harper, L.; Gardiner, J.; et al. Maize metabolic network construc- tion and transcriptome analysis. Plant Genome 2013. [Google Scholar] [CrossRef]
- McCloskey, D.; Palsson, B.Ø.; Feist, A.M. Basic and applied uses of genome-scale metabolic network reconstructions of Escherichia coli. Mol. Syst. Biol. 2013, 9. Article number 661. [Google Scholar]
- Thiele, I.; Palsson, B.Ø. A protocol for generating a high-quality genome-scale metabolic reconstruction. Nat. Protoc. 2010, 5, 93–121. [Google Scholar] [CrossRef] [PubMed]
- Herrgård, M.J.; Swainston, N.; Dobson, P.; Dunn, W.B.; Arga, K.Y.; Arvas, M.; Blüthgen, N.; Borger, S.; Costenoble, R.; Heinemann, M.; et al. A consensus yeast metabolic network reconstruction obtained from a community approach to systems biology. Nat. Biotechnol. 2008, 26, 1155–1160. [Google Scholar] [CrossRef] [PubMed]
- Devoid, S.; Overbeek, R.; deJongh, M.; Vonstein, V.; Best, A.A.; Henry, C. Automated genome annotation and metabolic model reconstruction in the SEED. In Systems Metabolic Engineering; Springer: New York, NY, USA, 2013; pp. 17–45. [Google Scholar]
- Kumar, V.S.; Dasika, M.S.; Maranas, C.D. Optimization based automated curation of metabolic reconstructions. BMC Bioinform. 2007, 8, 212. [Google Scholar] [CrossRef]
- Henry, C.S.; DeJongh, M.; Best, A.A.; Frybarger, P.M.; Linsay, B.; Stevens, R.L. High-throughput generation, optimization and analysis of genome-scale metabolic models. Nat. Biotechnol. 2010, 28, 977–982. [Google Scholar] [CrossRef] [PubMed]
- Latendresse, M.; Krummenacker, M.; Trupp, M.; Karp, P.D. Construction and completion of flux balance models from pathway databases. Bioinformatics 2012, 28, 388–396. [Google Scholar] [CrossRef] [PubMed]
- Latendresse, M. Efficiently gap-filling reaction networks. BMC Bioinform. 2014, 15, 225. [Google Scholar] [CrossRef]
- Thorleifsson, S.G.; Thiele, I. rBioNet: A COBRA toolbox extension for reconstructing high-quality biochemical networks. Bioinformatics 2011, 27, 2009–2010. [Google Scholar] [CrossRef] [PubMed]
- Stobbe, M.D.; Houten, S.M.; Jansen, G.A.; van Kampen, A.H.C.; Moerland, P.D. Critical assessment of human metabolic pathway databases: a stepping stone for future integration. BMC Syst. Biol. 2011, 5, 165. [Google Scholar] [CrossRef] [PubMed]
- Stobbe, M.D.; Swertz, M.A.; Thiele, I.; Rengaw, T.; van Kampen, A.H.C.; Moerland, P.D. Consensus and conflict cards for metabolic pathway databases. BMC Syst. Biol. 2013, 7, 50. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Agren, R.; Bordel, S.; Mardinoglu, A.; Pornputtapong, N.; Nookaew, I.; Nielsen, J. Reconstruction of genome-scale active metabolic networks for 69 human cell types and 16 cancer types using INIT. PLoS Comput. Biol. 2012, 8, e1002518. [Google Scholar] [CrossRef] [PubMed]
- Uhlen, M.; Oksvold, P.; Fagerberg, L.; Lundberg, E.; Jonasson, K.; Forsberg, M.; Zwahlen, M.; Kampf, C.; Wester, K.; Hober, S.; et al. Towards a knowledge-based Human Protein Atlas. Nat. Biotechnol. 2010, 28, 1248–1250. [Google Scholar] [CrossRef] [PubMed]
- Monk, J.; Nogales, J.; Palsson, B.Ø. Optimizing genome-scale network reconstructions. Nat. Biotechnol. 2014, 32, 447–452. [Google Scholar] [CrossRef] [PubMed]
- Schellenberger, J.; Lewis, N.E.; Palsson, B.Ø. Elimination of thermodynamically infeasible loops in steady-state metabolic models. Biophys. J. 2011, 100, 544–553. [Google Scholar] [CrossRef] [PubMed]
- De Martino, D.; Capuani, F.; Mori, M.; De Martino, A.; Marinari, E. Counting and correcting thermodynamically infeasible flux cycles in genome-scale metabolic networks. Metabolites 2013, 3, 946–966. [Google Scholar] [CrossRef] [PubMed]
- Otero, J.M.; Cimini, D.; Patil, K.R.; Poulsen, S.G.; Olsson, L.; Nielsen, J. Industrial systems biology of Saccharomyces cerevisiae enables novel succinic acid cell factory. PLoS One 2013, 8, e54144. [Google Scholar] [CrossRef] [PubMed]
- Agren, R.; Otero, J.M.; Nielsen, J. Genome-scale modeling enables metabolic engineering of Saccharomyces cerevisiae for succinic acid production. J. Ind. Microbiol. Biotechnol. 2013, 40, 735–747. [Google Scholar] [CrossRef] [PubMed]
- Oberhardt, M.A.; Palsson, B.Ø.; Papin, J.A. Applications of genome-scale metabolic reconstructions. Mol. Syst. Biol. 2009. [Google Scholar] [CrossRef]
- Molenaar, D.; van Berlo, R.; de Ridder, D.; Teusink, B. Shifts in growth strategies reflect tradeoffs in cellular economics. Mol. Syst. Biol. 2009, 5, 323. [Google Scholar] [CrossRef] [PubMed]
- Vazquez, A.; Liu, J.; Zhou, Y.; Oltvai, Z.N. Catabolic efficiency of aerobic glycolysis: The Warburg effect revisited. BMC Syst. Biol. 2010, 4, 58. [Google Scholar] [CrossRef] [PubMed]
- Teusink, B.; Passarge, J.; Reijenga, C.A.; Esgalhado, E.; van der Weijden, C.C.; Schepper, M.; Walsh, M.C.; Bakker, B.M.; van Dam, K.; Westerhoff, H.V.; et al. Can yeast glycolysis be understood in terms of in vitro kinetics of the constituent enzymes? Testing biochemistry. Eur. J. Biochem. 2000, 267, 5313–5329. [Google Scholar] [CrossRef]
- Smallbone, K.; Messiha, H.L.; Carroll, K.M.; Winder, C.L.; Malys, N.; Dunn, W.B.; Murabito, E.; Swainston, N.; Dada, J.O.; Khan, F.; et al. A model of yeast glycolysis based on a consistent kinetic characterisation of all its enzymes. FEBS Lett. 2013, 587, 2832–2841. [Google Scholar]
- Kerkhoven, E.J.; Achcar, F.; Alibu, V.P.; Burchmore, R.J.; Gilbert, I.H.; Trybiło, M.; Driessen, N.N.; Gilbert, D.; Breitling, R.; Bakker, B.M.; et al. Handling uncertainty in dynamic models: The pentose phosphate pathway in Trypanosoma brucei. PLoS Comput. Biol. 2013, 9, e1003371. [Google Scholar] [CrossRef] [PubMed]
- Damiani, C.; Pescini, D.; Colombo, R.; Molinari, S.; Alberghina, L.; Vanoni, M.; Mauri, G. An ensemble evolutionary constraint-based approach to understand the emergence of metabolic phenotypes. Nat. Comput. 2014, 13, 321–331. [Google Scholar] [CrossRef]
- Diaz-Ruiz, R.; Rigoulet, M.; Devin, A. The Warburg and Crabtree effects: On the origin of cancer cell energy metabolism and of yeast glucose repression. BBA-Bioenergetics 2011, 1807, 568–576. [Google Scholar] [CrossRef] [PubMed]
- Resendis-Antonio, O.; Checa, A.; Encarnación, S. Modeling core metabolism in cancer cells: Surveying the topology underlying the Warburg effect. PLoS One 2010, 5, e12383. [Google Scholar] [CrossRef] [PubMed]
- Mogilner, A.; Wollman, R.; Marshall, W.F. Quantitative modeling in cell biology: What is it good for? Dev. Cell 2006, 11, 279–287. [Google Scholar] [CrossRef] [PubMed]
- Ingolia, N.T.; Murray, A.W. The ups and downs of modeling the cell cycle. Curr. Biol. 2004, 14, R771–R777. [Google Scholar] [CrossRef] [PubMed]
- Moles, C.G.; Mendes, P.; Banga, J.R. Parameter estimation in biochemical pathways: A comparison of global optimization methods. Genome Res. 2003, 13, 2467–2474. [Google Scholar] [CrossRef] [PubMed]
- Nobile, M.S.; Besozzi, D.; Cazzaniga, P.; Mauri, G.; Pescini, D. A GPU-based multi-swarm PSO method for parameter estimation in stochastic biological systems exploiting discrete-time target series. In Evolutionary Computation Machine Learning and Data Mining in Bioinformatics; Giacobini, M., Vanneschi, L., Bush, W., Eds.; Springer-Verlag Berlin: Heidelberg, Germany, 2012; Volume 7246, LNCS; pp. 74–85. [Google Scholar]
- Guillén-Gosálbez, G.; Miró, A.; Alves, R.; Sorribas, A.; Jiménez, L. Identification of regulatory structure and kinetic parameters of biochemical networks via mixed-integer dynamic optimization. BMC Syst. Biol. 2013, 7, 113. [Google Scholar] [CrossRef] [PubMed]
- Hendrickx, D.M.; Hendriks, M.M.W.B.; Eilers, P.H.C.; Smilde, A.K.; Hoefsloot, H.C.J. Reverse engineering of metabolic networks, a critical assessment. Mol. Biosyst. 2011, 7, 511–520. [Google Scholar] [CrossRef] [PubMed]
- Quach, M.; Brunel, N.; d’Alché Buc, F. Estimating parameters and hidden variables in non-linear state-space models based on ODEs for biological networks inference. Bioinformatics 2007, 23, 3209–3216. [Google Scholar] [CrossRef] [PubMed]
- Raue, A.; Becker, V.; Klingmüller, U.; Timmer, J. Identifiability and observability analysis for experimental design in nonlinear dynamical models. Chaos 2010, 20, 045105. [Google Scholar] [CrossRef] [PubMed]
- Dräger, A.; Kronfeld, M.; Ziller, M.J.; Supper, J.; Planatscher, H.; Magnus, J.B.; Oldiges, M.; Kohlbacher, O.; Zell, A. Modeling metabolic networks in C. glutamicum: A comparison of rate laws in combination with various parameter optimization strategies. BMC Syst. Biol. 2009, 3, 5. [Google Scholar] [CrossRef] [PubMed]
- Caspi, R.; Altman, T.; Dreher, K.; Fulcher, C.A.; Subhraveti, P.; Keseler, I.M.; Kothari, A.; Krummenacker, M.; Latendresse, M.; Mueller, L.A.; et al. The MetaCyc database of metabolic pathways and enzymes and the BioCyc collection of pathway/genome databases. Nucleic Acids Res. 2012, 40, D742–D753. [Google Scholar] [CrossRef] [PubMed]
- Dash, R.K.; Li, Y.; Kim, J.; Saidel, G.M.; Cabrera, M.E. Modeling cellular metabolism and energetics in skeletal muscle: large-scale parameter estimation and sensitivity analysis. IEEE Trans. Bio-Med. Eng. 2008, 55, 1298–1318. [Google Scholar] [CrossRef]
- Lasdon, L.; Waren, A.; Jain, A.; Ratner, M. Design and testing of a generalized reduced gradient code for nonlinear programming. ACM Trans. Math. Software 1978, 4, 34–50. [Google Scholar] [CrossRef]
- Bazil, J.N.; Buzzard, G.T.; Rundell, A.E. Modeling mitochondrial bioenergetics with integrated volume dynamics. PLoS Comput. Biol. 2010, 6, e1000632. [Google Scholar] [CrossRef] [PubMed]
- Kirkpatrick, S.; Gelatt, C.D.; Vecchi, M.P. Optimization by simulated annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef] [PubMed]
- Eberhart, R.C.; Kennedy, J. A new optimiser using particle swarm theory. In Proceedings of the IEEE Sixth International Symposium on Micro Machine and Human Science, Nagoya, Japan, 4–6 October 1995; pp. 39–43.
- Storn, R. On the usage of differential evolution for function optimization. In Proceedings of the Biennial Conference of the North American Fuzzy Information Processing Society, Berkeley, CA, USA, 19–22 June 1996; pp. 519–523.
- Besozzi, D.; Cazzaniga, P.; Mauri, G.; Pescini, D.; Vanneschi, L. A compar-ison of genetic algorithms and particle swarm optimization for parameter estimation in stochastic biochemical systems. In Evolutionary Computation, Machine Learn-ing and Data Mining in Bioinformatics; Pizzuti, C., Ritchie, M.D., Giacobini, M., Eds.; Springer-Verlag Berlin: Heidelberg, Germany, 2009; Volume 5483, LCNS; pp. 116–127. [Google Scholar]
- Clerc, M. Particle Swarm Optimization; ISTE: London, UK, 2010. [Google Scholar]
- Mendes, P.; Kell, D.B. Non-linear optimization of biochemical pathways: Applications to metabolic engineering and parameter estimation. Bioinformatics 1998, 14, 869–883. [Google Scholar] [CrossRef] [PubMed]
- Marquardt, D.W. An algorithm for least-squares estimation of nonlinear parameters. J. Soc. Ind. Appl. Math. 1963, 11, 431–441. [Google Scholar] [CrossRef]
- Villaverde, A.F.; Egea, J.A.; Banga, J.R. A cooperative strategy for parameter estimation in large scale systems biology models. BMC Syst. Biol. 2012, 6, 75. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Koza, J.R.; Mydlowec, W.; Lanza, G.; Yu, J.; Keane, M.A. Reverse engineering of metabolic pathways from observed data using genetic programming. In Proceedings of the IEEE Pacific Symposium on Biocomputing, Big Island of Hawaii, HI, USA, 3–7 January 2001; Volume 6, pp. 434–445.
- Koza, J.R. Genetic Programming: On the Programming of Computers by Means of Natural Selection; The MIT Press: Cambridge, MA, USA, 1992. [Google Scholar]
- Sugimoto, M.; Kikuchi, S.; Tomita, M. Reverse engineering of biochemical equations from time-course data by means of genetic programming. Biosystems 2005, 80, 155–164. [Google Scholar] [CrossRef] [PubMed]
- Cho, D.; Cho, K.; Zhang, B. Identification of biochemical networks by S-tree based genetic programming. Bioinformatics 2006, 22, 1631–1640. [Google Scholar] [CrossRef] [PubMed]
- Nobile, M.S.; Besozzi, D.; Cazzaniga, P.; Pescini, D.; Mauri, G. Reverse engineering of kinetic reaction networks by means of cartesian genetic programming and particle swarm optimization. In Proceedings of the IEEE Congress on Evolutionary Computation (CEC), Cancún, Mexico, 20–23 June 2013; pp. 1594–1601.
- Miller, J.; Thomson, P. Cartesian Genetic Programming. In Proceedings of the Third European Conference on Genetic Programming (EuroGP2000), Edinburgh, Scotland, UK, 15–16 April 2000; Volume 182, pp. 121–132.
- Szederkenyi, G.; Banga, J.R.; Alonso, A.A. Inference of complex biological networks: distinguishability issues and optimization-based solutions. BMC Syst. Biol. 2011, 5, 177. [Google Scholar] [Green Version]
- Çakır, T.; Hendriks, M.M.W.B.; Westerhuis, J.A.; Smilde, A.K. Metabolic network discovery through reverse engineering of metabolome data. Metabolomics 2009, 5, 318–329. [Google Scholar] [CrossRef] [PubMed]
- Arkin, A.; Ross, J. Statistical construction of chemical reaction mechanisms from measured time-series. J. Phys. Chem. 1995, 99, 970–979. [Google Scholar] [CrossRef]
- Damiani, C.; Lecca, P. Model identification using correlation-based inference and transfer entropy estimation. In Proceedings of the IEEE Fifth UKSim European Symposium on Computer Modeling and Simulation (EMS), Madrid, Spain, 16–18 November 2011; pp. 129–134.
- Schreiber, T. Measuring information transfer. Phys. Rev. Lett. 2000, 85, 461. [Google Scholar] [CrossRef] [PubMed]
- Vance, W.; Arkin, A.; Ross, J. Determination of causal connectivities of species in reaction networks. Proc. Natl. Acad. Sci. USA 2002, 99, 5816–5821. [Google Scholar] [CrossRef] [PubMed]
- Tran, L.M.; Rizk, M.L.; Liao, J.C. Ensemble modeling of metabolic networks. Biophys. J. 2008, 95, 5606–5617. [Google Scholar]
- Jia, G.; Stephanopoulos, G.; Gunawan, R. Ensemble kinetic modeling of metabolic networks from dynamic metabolic profiles. Metabolites 2012, 2, 891–912. [Google Scholar] [CrossRef] [PubMed]
- Henry, C.S.; Broadbelt, L.J.; Hatzimanikatis, V. Thermodynamics-based metabolic flux analysis. Biophys. J. 2007, 92, 1792–1805. [Google Scholar] [CrossRef] [PubMed]
- Miškovic´, L.; Hatzimanikatis, V. Modeling of uncertainties in biochemical reactions. Biotechnol. Bioeng. 2011, 108, 413–423. [Google Scholar] [CrossRef] [PubMed]
- Link, H.; Kochanowski, K.; Sauer, U. Systematic identification of allosteric protein-metabolite interactions that control enzyme activity in vivo. Nat. Biotechnol. 2013, 31, 357–361. [Google Scholar] [CrossRef] [PubMed]
- Zomorrodi, A.R.; Lafontaine Rivera, J.G.; Liao, J.C.; Maranas, C.D. Optimization-driven identification of genetic perturbations accelerates the convergence of model parameters in ensemble modeling of metabolic networks. Biotechnol. J. 2013, 8, 1090–1104. [Google Scholar] [CrossRef]
- Link, H.; Christodoulou, D.; Sauer, U. Advancing metabolic models with kinetic information. Curr. Opin. Biotech. 2014, 29, 8–14. [Google Scholar] [CrossRef] [PubMed]
- Bollobás, B. Modern Graph Theory; Springer: New York, NY, USA, 1998; Volume 184. [Google Scholar]
- Aittokallio, T.; Schwikowski, B. Graph-based methods for analysing networks in cell biology. Brief Bioinform. 2006, 7, 243–255. [Google Scholar] [CrossRef] [PubMed]
- Albert, R. Scale-free networks in cell biology. J. Cell Sci. 2005, 118, 4947–4957. [Google Scholar] [CrossRef] [PubMed]
- Caldarelli, G. Scale-Free Networks. Complex Webs in Nature and Technology; Oxford University Press: Oxford, UK, 2007. [Google Scholar]
- Romero, P.; Karp, P.D. Nutrition-related analysis of pathway/genome databases. In Proceedings of the Pacific Symposium on Biocomputing, Big Island of Hawaii, HI, USA, 3–7 January 2001; pp. 471–482.
- Light, S.; Kraulis, P.; Elofsson, A. Preferential attachment in the evolution of metabolic networks. BMC Genomics 2005, 6, 159. [Google Scholar] [CrossRef] [PubMed]
- Hordijk, W.; Steel, M. Detecting autocatalytic, self-sustaining sets in chemical reaction systems. J. Theor. Biol. 2004, 227, 451–461. [Google Scholar] [CrossRef] [PubMed]
- Albert, R.; Jeong, H.; Barabási, A.L. Error and attack tolerance of complex networks. Nature 2000, 406, 378–382. [Google Scholar] [CrossRef] [PubMed]
- Fell, D.A.; Wagner, A. The small world of metabolism. Nat. Biotechnol. 2000, 18, 1121–1122. [Google Scholar] [CrossRef] [PubMed]
- Wagner, A.; Fell, D.A. The small world inside large metabolic networks. Proc. R. Soc. B-Biol. Sci. 2001, 268, 1803–1810. [Google Scholar] [CrossRef]
- 118. Csete, M.E.; Doyle, J.C. Bow ties, metabolism and disease. Trends Biotechnol. 2004, 22, 446–450. [Google Scholar] [CrossRef] [PubMed]
- Zhao, J.; Yu, H.; Luo, J.H.; Cao, Z.W.; Li, Y.X. Hierarchical modularity of nested bow-ties in metabolic networks. BMC Bioinform. 2006, 7, 386. [Google Scholar] [CrossRef]
- Resendis-Antonio, O.; Hernández, M.; Mora, Y.; Encarnación, S. Functional modules, structural topology, and optimal activity in metabolic networks. PLoS Comput. Biol. 2012, 8, e1002720. [Google Scholar] [CrossRef] [PubMed]
- Montañez, R.; Medina, M.A.; Solé, R.V.; Rodríguez-Caso, C. When metabolism meets topology: Reconciling metabolite and reaction networks. Bioessays 2010, 32, 246–256. [Google Scholar] [CrossRef] [PubMed]
- Ravasz, E.; Somera, A.L.; Mongru, D.A.; Oltvai, Z.N.; Barabási, A.L. Hierarchical organization of modularity in metabolic networks. Science 2002, 297, 1551–1555. [Google Scholar] [CrossRef] [PubMed]
- Chen, M.; Hofestädt, R. Quantitative Petri net model of gene regulated metabolic networks in the cell. In Silico Biol. 2003, 3, 347–365. [Google Scholar] [PubMed]
- Reddy, V.N.; Mavrovouniotis, M.L.; Liebman, M.N. Petri net representations in metabolic pathways. In Proceedings of the ISMB, Bethesda, MD, USA, 21–23 July 1993; Volume 93, pp. 328–336.
- Zevedei-Oancea, I.; Schuster, S. Topological analysis of metabolic networks based on Petri net theory. In Silico Biol. 2003, 3, 323–345. [Google Scholar] [PubMed]
- Lewis, N.E.; Nagarajan, H.; Palsson, B.Ø. Constraining the metabolic genotype–phenotype relationship using a phylogeny of in silico methods. Nat. Rev. Microbiol. 2012, 10, 291–305. [Google Scholar] [PubMed]
- COBRA Methods. Available online: http://cobramethods.wikidot.com/methods (accessed on 1November 2014).
- Orth, J.D.; Thiele, I.; Palsson, B.Ø. What is flux balance analysis? Nat. Biotechnol. 2010, 28, 245–248. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.M.; Gianchandani, E.P.; Papin, J.A. Flux balance analysis in the era of metabolomics. Brief Bioinform. 2006, 7, 140–150. [Google Scholar] [CrossRef] [PubMed]
- Simeonidis, E.; Murabito, E.; Smallbone, K.; Westerhoff, H.V. Why does yeast ferment? A flux balance analysis study. Biochem. Soc. T 2010, 38, 1225–1229. [Google Scholar] [CrossRef]
- Bro, C.; Regenberg, B.; Förster, J.; Nielsen, J. In silico aided metabolic engineering of Saccharomyces cerevisiae for improved bioethanol production. Metab. Eng. 2006, 8, 102–111. [Google Scholar] [CrossRef] [PubMed]
- Burgard, A.P.; Maranas, C.D. Optimization-based framework for inferring and testing hypothesized metabolic objective functions. Biotechnol. Bioeng. 2003, 82, 670–677. [Google Scholar] [CrossRef] [PubMed]
- Ramakrishna, R.; Edwards, J.S.; McCulloch, A.; Palsson, B.Ø. Flux-balance analysis of mitochondrial energy metabolism: consequences of systemic stoichiometric constraints. Am. J. Physiol.-Reg. I 2001, 280, R695–R704. [Google Scholar]
- Schuster, S.; Hilgetag, C. On elementary flux modes in biochemical reaction systems at steady state. J. Biol. Syst. 1994, 2, 165–182. [Google Scholar] [CrossRef]
- Schilling, C.H.; Letscher, D.; Palsson, B.Ø. Theory for the systemic definition of metabolic pathways and their use in interpreting metabolic function from a pathway-oriented perspective. J. Theor. Biol. 2000, 203, 229–248. [Google Scholar] [CrossRef] [PubMed]
- Hunt, K.A.; Folsom, J.P.; Taffs, R.L.; Carlson, R.P. Complete enumeration of elementary flux modes through scalable, demand-based subnetwork definition. Bioinformatics 2014, 30, 1569–1578. [Google Scholar] [CrossRef] [PubMed]
- De Figueiredo, L.F.; Podhorski, A.; Rubio, A.; Kaleta, C.; Beasley, J.E.; Schuster, S.; Planes, F.J. Computing the shortest elementary flux modes in genome-scale metabolic networks. Bioinformatics 2009, 25, 3158–3165. [Google Scholar] [CrossRef] [PubMed]
- Mahadevan, R.; Schilling, C.H. The effects of alternate optimal solutions in constraint-based genome-scale metabolic models. Metab. Eng. 2003, 5, 264–276. [Google Scholar] [CrossRef] [PubMed]
- Gudmundsson, S.; Thiele, I. Computationally efficient flux variability analysis. BMC Bioinform. 2010, 11, 489. [Google Scholar] [CrossRef]
- Feist, A.; Palsson, B.Ø. The biomass objective function. Curr. Opin. Microbiol. 2010, 13, 344–349. [Google Scholar] [CrossRef] [PubMed]
- Schellenberger, J.; Palsson, B.Ø. Use of randomized sampling for analysis of metabolic networks. J. Biol. Chem. 2009, 284, 5457–5461. [Google Scholar]
- Mahadevan, R.; Edwards, J.S.; Doyle III, F.J. Dynamic flux balance analysis of diauxic growth in Escherichia coli. Biophys. J. 2002, 83, 1331–1340. [Google Scholar] [CrossRef] [PubMed]
- Covert, M.W.; Schilling, C.H.; Palsson, B.Ø. Regulation of gene expression in flux balance models of metabolism. J. Theor. Biol. 2001, 213, 73–88. [Google Scholar] [CrossRef] [PubMed]
- Herrgård, M.J.; Lee, B.S.; Portnoy, V.; Palsson, B.Ø. Integrated analysis of regulatory and metabolic networks reveals novel regulatory mechanisms in Saccharomyces cerevisiae. Genome Res. 2006, 16, 627–635. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.M.; Gianchandani, E.P.; Eddy, J.A.; Papin, J.A. Dynamic analysis of integrated signaling, metabolic, and regulatory networks. PLoS Comput. Biol. 2008, 4, e1000086. [Google Scholar] [CrossRef] [PubMed]
- Machado, D.; Herrgård, M. Systematic evaluation of methods for integration of transcriptomic data into constraint-based models of metabolism. PLoS Comput. Biol. 2014, 10, e1003580. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Burgard, A.P.; Nikolaev, E.V.; Schilling, C.H.; Maranas, C.D. Flux coupling analysis of genome-scale metabolic network reconstructions. Genome Res. 2004, 14, 301–312. [Google Scholar] [CrossRef] [PubMed]
- Papin, J.A.; Reed, J.L.; Palsson, B.Ø. Hierarchical thinking in network biology: the unbiased modularization of biochemical networks. Trends Biochem. Sci. 2004, 29, 641–647. [Google Scholar] [CrossRef] [PubMed]
- Reed, J.L.; Palsson, B.Ø. Genome-scale in silico models of E. coli have multiple equivalent phenotypic states: Assessment of correlated reaction subsets that comprise network states. Genome Res. 2004, 14, 1797–1805. [Google Scholar] [CrossRef] [PubMed]
- Petzold, L.R. Automatic selection of methods for solving stiff and nonstiff systems of ordinary differential equations. SIAM J. Sci. Stat. Comput. 1983, 4, 136–148. [Google Scholar] [CrossRef]
- Brown, P.N.; Byrne, G.D.; Hindmarsh, A.C. VODE: A variable-coefficient ODE solver. SIAM J. Sci. Stat. Comput. 1989, 10, 1038–1051. [Google Scholar] [CrossRef]
- Metelkin, E.; Goryanin, I.; Demin, O. Mathematical modeling of mitochondrial adenine nucleotide translocase. Biophys. J. 2006, 90, 423–432. [Google Scholar] [CrossRef] [PubMed]
- Guillaud, F.; Dröse, S.; Kowald, A.; Brandt, U.; Klipp, E. Superoxide production by cytochrome bc1 complex: A mathematical model. BBA-Bioenergetics 2014, 1837, 1643–1652. [Google Scholar] [CrossRef] [PubMed]
- Chang, I.; Heiske, M.; Letellier, T.; Wallace, D.; Baldi, P. Modeling of mitochondria bioenergetics using a composable chemiosmotic energy transduction rate law: Theory and experimental validation. PLoS One 2011, 6, e14820. [Google Scholar]
- Korzeniewski, B.; Zoladz, J.A. A model of oxidative phosphorylation in mammalian skeletal muscle. Biophys. Chem. 2001, 92, 17–34. [Google Scholar] [CrossRef] [PubMed]
- Beard, D.A. A biophysical model of the mitochondrial respiratory system and oxidative phosphorylation. PLoS Comput. Biol. 2005, 1, e36. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- König, M.; Bulik, S.; Holzhütter, H.G. Quantifying the contribution of the liver to glucose homeostasis: A detailed kinetic model of human hepatic glucose metabolism. PLoS Comput. Biol. 2012, 8, e1002577. [Google Scholar] [CrossRef] [PubMed]
- Reed, M.C.; Thomas, R.L.; Pavisic, J.; James, S.J.; Ulrich, C.M.; Nijhout, H.F. A mathematical model of glutathione metabolism. Theor. Biol. Med. Model. 2008, 5, 8. [Google Scholar] [CrossRef] [PubMed]
- Achcar, F.; Kerkhoven, E.J.; The SilicoTryp Consortium; Bakker, B.M.; Barrett, M.P.; Breitling, R. Dynamic modelling under uncertainty: The case of Trypanosoma brucei energy metabolism. PLoS Comput. Biol. 2012, 8, e1002352. [Google Scholar] [CrossRef] [PubMed]
- Kinsey, S.T.; Locke, B.R.; Dillaman, R.M. Molecules in motion: influences of diffusion on metabolic structure and function in skeletal muscle. J. Exp. Biol. 2011, 214, 263–274. [Google Scholar] [CrossRef] [PubMed]
- Baras, F.; Mansour, M.M. Reaction-diffusion master equation: A comparison with microscopic simulations. Phys. Rev. E 1996, 54, 6139–6148. [Google Scholar] [CrossRef]
- Bernstein, D. Simulating mesoscopic reaction-diffusion systems using the Gillespie algorithm. Phys. Rev. E 2005, 71, 041103. [Google Scholar] [CrossRef]
- Gruenert, G.; Ibrahim, B.; Lenser, T.; Lohel, M.; Hinze, T.; Dittrich, P. Rule-based spatial modeling with diffusing, geometrically constrained molecules. BMC Bioinform. 2010, 11, 307. [Google Scholar] [CrossRef]
- Zhou, L.; Aon, M.; Almas, T.; Cortassa, S.; Winslow, R.; O’Rourke, B. A reaction-diffusion model of ROS-induced ROS release in a mitochondrial network. PLoS Comput. Biol. 2010, 6, e1000657. [Google Scholar] [CrossRef] [PubMed]
- Dasika, S.K.; Kinsey, S.T.; Locke, B.R. Facilitated diffusion of myoglobin and creatine kinase and reaction–diffusion constraints of aerobic metabolism under steady-state conditions in skeletal muscle. Biotechnol. Bioeng. 2012, 109, 545–558. [Google Scholar] [CrossRef] [PubMed]
- Yugi, K.; Nakayama, Y.; Kinoshita, A.; Tomita, M. Hybrid dynamic/static method for large-scale simulation of metabolism. Theor. Biol. Med. Model. 2005, 2, 42. [Google Scholar] [CrossRef] [PubMed]
- Ishii, N.; Nakayama, Y.; Tomita, M. Distinguishing enzymes using metabolome data for the hybrid dynamic/static method. Theor. Biol. Med. Model. 2007, 4, 19. [Google Scholar] [CrossRef] [PubMed]
- Osana, Y.; Fukushima, T.; Yoshimi, M. An FPGA-based multi-model simulation method for biochemical systems. In Proceedings of the 19th IEEE International Parallel and Distributed Processing Symposium, 4–8 April 2005; IEEE Computer Society: Denver, CO, USA.
- Li, H.; Cao, H.; Petzold, L.R.; Gillespie, D.T. Algorithms and software for stochastic simulation of biochemical reacting systems. Biotechnol. Prog. 2008, 24, 56–61. [Google Scholar] [CrossRef] [PubMed]
- Nobile, M.S.; Cazzaniga, P.; Besozzi, D.; Pescini, D.; Mauri, G. cuTauLeaping: A GPU-powered tau-leaping stochastic simulator for massive parallel analyses of biological systems. PLoS One 2014, 9, e91963. [Google Scholar] [CrossRef] [PubMed]
- Nobile, M.S.; Besozzi, D.; Cazzaniga, P.; Mauri, G. GPU-accelerated simulations of mass-action kinetics models with cupSODA. J. Supercomput. 2014, 69, 17–24. [Google Scholar] [CrossRef]
- Kiviet, D.J.; Nghe, P.; Walker, N.; Boulineau, S.; Sunderlikova, V.; Tans, S.J. Stochasticity of metabolism and growth at the single-cell level. Nature 2014, in press. [Google Scholar]
- Andersen, M.R.; Nielsen, M.L.; Nielsen, J. Metabolic model integration of the bibliome, genome, metabolome and reactome of Aspergillus niger. Mol. Syst. Biol. 2008, 4. [Google Scholar] [CrossRef]
- Varma, A.; Palsson, B.Ø. Stoichiometric flux balance models quantitatively predict growth and metabolic by-product secretion in wild-type Escherichia coli W3110. Appl. Environ. Microbiol. 1994, 60, 3724–3731. [Google Scholar]
- Edwards, J.; Palsson, B.Ø. The Escherichia coli MG1655 in silico metabolic genotype: its definition, characteristics, and capabilities. Proc. Natl. Acad. Sci. USA 2000, 97, 5528–5533. [Google Scholar] [CrossRef] [PubMed]
- Förster, J.; Famili, I.; Palsson, B.Ø.; Nielsen, J. Large-scale evaluation of in silico gene deletions in Saccharomyces cerevisiae. OMICS 2003, 7, 193–202. [Google Scholar] [CrossRef] [PubMed]
- Saltelli, A.; Ratto, M.; Andres, T.; Campolongo, F.; Cariboni, J.; Gatelli, D.; Saisana, M.; Tarantola, S. Global Sensitivity Analysis: The Primer; Wiley: Hoboken, NJ, USA, 2008. [Google Scholar]
- Saltelli, A.; Tarantola, S.; Campolongo, F. Sensitivity anaysis as an ingredient of modeling. Stat. Sci. 2000, 15, 377–395. [Google Scholar] [CrossRef]
- Degenring, D.; Froemel, C.; Dikta, G.; Takors, R. Sensitivity analysis for the reduction of complex metabolism models. J. Process Contr. 2004, 14, 729–745. [Google Scholar] [CrossRef]
- Fell, D.A. Metabolic control analysis: A survey of its theoretical and experimental development. Biochem. J. 1992, 286, 313–330. [Google Scholar] [PubMed]
- Kohn, M.C. Computer simulation of metabolism in palmitate-perfused rat heart. III. Sensitivity analysis. Ann. Biomed. Eng. 1983, 11, 533–549. [Google Scholar] [CrossRef] [PubMed]
- Zi, Z. Sensitivity analysis approaches applied to systems biology models. IET Syst. Biol. 2011, 5, 336–346. [Google Scholar] [CrossRef] [PubMed]
- Oshiro, M.; Shinto, H.; Tashiro, Y.; Miwa, N.; Sekiguchi, T.; Okamoto, M.; Ishizaki, A.; Sonomoto, K. Kinetic modeling and sensitivity analysis of xylose metabolism in Lactococcus lactis IO-1. J. Biosci. Bioeng. 2009, 108, 376–384. [Google Scholar] [CrossRef] [PubMed]
- Shinto, H.; Tashiro, Y.; Yamashita, M.; Kobayashi, G.; Sekiguchi, T.; Hanai, T.; Kuriya, Y.; Okamoto, M.; Sonomoto, K. Kinetic modeling and sensitivity analysis of acetone-butanol-ethanol production. J. Biotechnol. 2007, 131, 45–56. [Google Scholar] [CrossRef] [PubMed]
- Chan, K.; Saltelli, A.; Tarantola, S. Sensitivity analysis of model output: Variance-based methods make the difference. In Proceedings of the 29th conference on Winter simulation, 7–10 December 1997; IEEE Computer Society: Washington, DC, USA; pp. 261–268.
- Di Maggio, J.; Diaz Ricci, J.C.; Diaz, M.S. Global sensitivity analysis in dynamic metabolic networks. Comput. Chem. Eng. 2010, 34, 770–781. [Google Scholar] [CrossRef]
- Helton, J.C.; Davis, F.J. Illustration of sampling-based methods for uncertainty and sensitivity analysis. Risk Anal. 2002, 22, 591–622. [Google Scholar] [CrossRef] [PubMed]
- Damiani, C.; Filisetti, A.; Graudenzi, A.; Lecca, P. Parameter sensitivity analysis of stochastic models: Application to catalytic reaction networks. Comput. Biol. Chem. 2013, 42, 5–17. [Google Scholar] [CrossRef] [PubMed]
- Kareva, I. Prisoner’s dilemma in cancer metabolism. PLoS One 2011, 6, e28576. [Google Scholar] [CrossRef] [PubMed]
- Sajitz-Hermstein, M.; Nikoloski, Z. Restricted cooperative games on metabolic networks reveal functionally important reactions. J. Theor. Biol. 2012, 314, 192–203. [Google Scholar] [CrossRef] [PubMed]
- Yang, R.; Lenaghan, S.C.; Wikswo, J.P.; Zhang, M. External control of the GAL network in S. cerevisiae: A view from control theory. PLoS One 2011, 6, e19353. [Google Scholar] [CrossRef] [PubMed]
- Palumbo, P.; Mavelli, G.; Farina, L.; Alberghina, L. Networks and circuits in cell regulation. Biochem. Biophys. Res. Commun. 2010, 396, 881–886. [Google Scholar] [CrossRef] [PubMed]
- Hinze, T.; Schumann, M.; Bodenstein, C.; Heiland, I.; Schuster, S. Biochemical frequency control by synchronisation of coupled Repressilators: An in silico study of modules for circadian clock systems. Comput. Intell. Neurosci. 2011, 2011. Article ID 262189. [Google Scholar]
- Broom, M.; Rychtáˇr, J. Game-Theoretical Models in Biology; CRC Press Chapman and Hall: London, UK, 2013. [Google Scholar]
- Cosentino, C.; Bates, D. Feedback Control in Systems Biology; CRC Press Chapman and Hall: London, UK, 2012. [Google Scholar]
- Sontag, E.D. Some new directions in control theory inspired by systems biology. Syst. Biol. 2004, 1, 9–18. [Google Scholar] [CrossRef]
- Csete, M.E.; Doyle, J.C. Reverse engineering of biological complexity. Science 2002, 295, 1664–1669. [Google Scholar] [CrossRef] [PubMed]
- Wellstead, P.; Bullinger, E.; Kalamatianos, D.; Mason, O.; Verwoerd, M. The rôle of control and system theory in systems biology. Annu. Rev. Control 2008, 32, 33–47. [Google Scholar] [CrossRef]
- Szallasi, Z.; Stelling, J.; Periwal, V. Systems Modeling in Cellular Biology; The MIT Press: Cambridge, MA, USA, 2006. [Google Scholar]
- Cloutier, M.; Wellstead, P. The control systems structures of energy metabolism. J. R. Soc. Interface 2010, 7, 651–665. [Google Scholar] [CrossRef] [PubMed]
- Wellstead, P.; Cloutier, M. An energy systems approach to Parkinson’s disease. WIREs Syst. Biol. Med. 2011, 3, 1. [Google Scholar] [CrossRef]
- Federowicz, S.; Kim, D.; Ebrahim, A.; Lerman, J.; Nagarajan, H.; Cho, B.K.; Zengler, K.; Palsson, B.Ø. Determining the control circuitry of redox metabolism at the genome-scale. PLoS Genet. 2014, 10, e1004264. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Reeves, G.T.; Fraser, S.E. Biological systems from an engineer’s point of view. PLoS Biol. 2009, 7, e1000021. [Google Scholar]
- Karr, J.R.; Sanghvi, J.C.; Macklin, D.N.; Gutschow, M.V.; Jacobs, J.M.; Bolival, B.; Assad-Garcia, N.; Glass, J.I.; Covert, M.W. A whole-cell computational model predicts phenotype from genotype. Cell 2012, 150, 389–401. [Google Scholar] [CrossRef] [PubMed]
- Vander Heiden, M.G.; Cantley, L.C.; Thompson, C.B. Understanding the Warburg effect: The metabolic requirements of cell proliferation. Science 2009, 324, 1029–1033. [Google Scholar] [CrossRef] [PubMed]
- Shlomi, T.; Benyamini, T.; Gottlieb, E.; Sharan, R.; Ruppin, E. Genome-scale metabolic modeling elucidates the role of proliferative adaptation in causing the Warburg effect. PLoS Comput. Biol. 2011, 7, e1002018. [Google Scholar] [CrossRef] [PubMed]
- Yizhak, K.; Le Dévédec, S.E.; Rogkoti, V.M.; Baenke, F.; Boer, V.C.; Frezza, C.; Schulze, A.; Water, B.; Ruppin, E. A computational study of the Warburg effect identifies metabolic targets inhibiting cancer migration. Mol. Syst. Biol. 2014. [Google Scholar] [CrossRef]
- Folger, O.; Jerby, L.; Frezza, C.; Gottlieb, E.; Ruppin, E.; Shlomi, T. Predicting selective drug targets in cancer through metabolic networks. Mol. Syst. Biol. 2011, 7, 501. [Google Scholar] [CrossRef] [PubMed]
- Frezza, C.; Zheng, L.; Folger, O.; Rajagopalan, K.; MacKenzie, E.; Jerby, L.; Micaroni, M.; Chaneton, B.; Adam, J.; Hedley, A.; et al. Haem oxygenase is synthetically lethal with the tumour suppressor fumarate hydratase. Nature 2011, 477, 225–228. [Google Scholar] [CrossRef] [PubMed]
- Nam, H.; Campodonico, M.; Bordbar, A.; Hyduke, D.R.; Kim, S.; Zielinski, D.C.; Bernhard, O.P. A systems approach to predict oncometabolites via context-specific genome-scale metabolic networks. PLoS Comput. Biol. 2014, 10, e1003837. [Google Scholar] [CrossRef] [PubMed]
- Brynildsen, M.P.; Winkler, J.A.; Spina, C.S.; MacDonald, I.C.; Collins, J.J. Potentiating antibacterial activity by predictably enhancing endogenous microbial ROS production. Nat. Biotechnol. 2013, 31, 160–165. [Google Scholar] [CrossRef] [PubMed]
- Kim, H.U.; Kim, S.Y.; Jeong, H.; Kim, T.Y.; Kim, J.J.; Choy, H.E.; Yi, K.Y.; Rhee, J.H.; Lee, S.Y. Integrative genome-scale metabolic analysis of Vibrio vulnificus for drug targeting and discovery. Mol. Syst. Biol. 2011. [Google Scholar] [CrossRef]
- Van Heerden, J.H.; Wortel, M.T.; Bruggeman, F.J.; Heijnen, J.J.; Bollen, Y.J.M.; Planqué, R.; Hulshof, J.; O’Toole, T.G.; Wahl, S.A.; Teusink, B. Lost in transition: Start-up of glycolysis yields subpopulations of nongrowing cells. Science 2014, 343, 1245114. [Google Scholar] [CrossRef] [PubMed]
- Khazaei, T.; McGuigan, A.; Mahadevan, R. Ensemble modeling of cancer metabolism. Front Physiol. 2012, 3, 135. [Google Scholar] [CrossRef] [PubMed]
- Nielsen, J. Metabolic engineering. Appl. Microbiol. Biotech. 2001, 55, 263–283. [Google Scholar] [CrossRef]
- Bordbar, A.; Monk, J.M.; King, Z.A.; Palsson, B.Ø. Constraint-based models predict metabolic and associated cellular functions. Nat. Rev. Genet. 2014, 15, 107–120. [Google Scholar] [CrossRef] [PubMed]
- Edwards, J.S.; Ibarra, R.U.; Palsson, B.Ø. In silico predictions of Escherichia coli metabolic capabilities are consistent with experimental data. Nat. Biotechnol. 2001, 19, 125–130. [Google Scholar]
- Lee, S.Y.; Lee, D.Y.; Kim, T.Y. Systems biotechnology for strain improvement. Trends Biotechnol. 2005, 23, 349–358. [Google Scholar] [CrossRef] [PubMed]
- Yim, H.; Haselbeck, R.; Niu, W.; Pujol-Baxley, C.; Burgard, A.; Boldt, J.; Khandurina, J.; Trawick, J.D.; Osterhout, R.E.; Stephen, R.; et al. Metabolic engineering of Escherichia coli for direct production of 1, 4-butanediol. Nat. Chem. Biol. 2011, 7, 445–452. [Google Scholar] [CrossRef] [PubMed]
- Gille, C.; Bölling, C.; Hoppe, A.; Bulik, S.; Hoffmann, S.; Hübner, K.; Karlstädt, A.; Ganeshan, R.; König, M.; Rother, K.; et al. HepatoNet1: A comprehensive metabolic reconstruction of the human hepatocyte for the analysis of liver physiology. Mol. Syst. Biol. 2010. [Google Scholar] [CrossRef]
- Hao, T.; Ma, H.; Zhao, X.; Goryanin, I. Compartmentalization of the Edinburgh human metabolic network. BMC Bioinform. 2010, 11, 393. [Google Scholar] [CrossRef]
- Österlund, T.; Nookaew, I.; Bordel, S.; Nielsen, J. Mapping condition-dependent regulation of metabolism in yeast through genome-scale modeling. BMC Syst. Biol. 2013, 7, 36. [Google Scholar] [CrossRef] [PubMed]
- Sahoo, S.; Franzson, L.; Jonsson, J.J.; Thiele, I. A compendium of inborn errors of metabolism mapped onto the human metabolic network. Mol. Biosyst. 2012, 8, 2545–2558. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yugi, K. Dynamic kinetic modeling of mitochondrial energy metabolism. In E-Cell System; Springer: New York, NY, USA, 2013; pp. 105–142. [Google Scholar]
- BioMet Toolbox. Available online: http://biomet-toolbox.org/ (accessed on 1 November 2014).
- Schellenberger, J.; Que, R.; Fleming, R.M.; Thiele, I.; Orth, J.D.; Feist, A.M.; Zielinski, D.C.; Bordbar, A.; Lewis, N.E.; Rahmanian, S.; et al. Quantitative prediction of cellular metabolism with constraint-based models: The COBRA Toolbox v2. 0. Nat. Protoc. 2011, 6, 1290–1307. [Google Scholar] [CrossRef] [PubMed]
- Hoops, S.; Sahle, S.; Gauges, R.; Lee, C.; Pahle, J.; Simus, N.; Singhal, M.; Xu, L.; Mendes, P.; Kummer, U. COPASI–a COmplex PAthway SImulator. Bioinformatics 2006, 22, 3067–3074. [Google Scholar] [CrossRef] [PubMed]
- COPASI. Available online: http://www.copasi.org/ (accessed on 1 November 2014).
- Shannon, P.; Markiel, A.; Ozier, O.; Baliga, N.S.; Wang, J.T.; Ramage, D.; Amin, N.; Schwikowski, B.; Ideker, T. Cytoscape: A software environment for integrated models of biomolecular interaction networks. Genome Res. 2003, 13, 2498–2504. [Google Scholar] [CrossRef] [PubMed]
- Saito, R.; Smoot, M.E.; Ono, K.; Ruscheinski, J.; Wang, P.L.; Lotia, S.; Pico, A.R.; Bader, G.D.; Ideker, T. A travel guide to Cytoscape plugins. Nat. Methods 2012, 9, 1069–1076. [Google Scholar] [CrossRef] [PubMed]
- Boele, J.; Olivier, B.G.; Teusink, B. FAME, the flux analysis and modeling environment. BMC Syst. Biol. 2012, 6, 8. [Google Scholar] [CrossRef] [PubMed]
- Hoppe, A.; Hoffmann, S.; Gerasch, A.; Gille, C.; Holzhütter, H.G. FASIMU: Flexible software for flux-balance computation series in large metabolic networks. BMC Bioinform. 2011, 12, 28. [Google Scholar] [CrossRef]
- Rocha, I.; Maia, P.; Evangelista, P.; Vilaça, P.; Soares, S.; Pinto, J.P.; Nielsen, J.; Patil, K.R.; Ferreira, E.C.; Rocha, M. OptFlux: An open-source software platform for in silico metabolic engineering. BMC Syst. Biol. 2010, 4, 45. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Karp, P.D.; Paley, S.M.; Krummenacker, M.; Latendresse, M.; Dale, J.M.; Lee, T.J.; Kaipa, P.; Gilham, F.; Spaulding, A.; Popescu, L.; et al. Pathway Tools version 13.0: Integrated software for pathway/genome informatics and systems biology. Brief Bioinform. 2009, 11, 40–79. [Google Scholar] [CrossRef] [PubMed]
- Agren, R.; Liu, L.; Shoaie, S.; Vongsangnak, W.; Nookaew, I.; Nielsen, J. The RAVEN toolbox and its use for generating a genome-scale metabolic model for Penicillium chrysogenum. PLoS Comput. Biol. 2013, 9, e1002980. [Google Scholar] [CrossRef] [PubMed]
- Gevorgyan, A.; Bushell, M.E.; Avignone-Rossa, C.; Kierzek, A.M. SurreyFBA: A command line tool and graphics user interface for constraint-based modeling of genome-scale metabolic reaction networks. Bioinformatics 2011, 27, 433–434. [Google Scholar] [CrossRef] [PubMed]
- Schellenberger, J.; Park, J.O.; Conrad, T.M.; Palsson, B.Ø. BiGG: A Biochemical Genetic and Genomic knowledgebase of large scale metabolic reconstructions. BMC Bioinform. 2010, 11, 213. [Google Scholar] [CrossRef]
- Caspi, R.; Altman, T.; Dale, J.M.; Dreher, K.; Fulcher, C.A.; Gilham, F.; Kaipa, P.; Karthikeyan, A.S.; Kothari, A.; Krummenacker, M.; et al. The MetaCyc database of metabolic pathways and enzymes and the BioCyc collection of pathway/genome databases. Nucleic Acids Res. 2010, 38, D473–D479. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Donizelli, M.; Rodriguez, N.; Dharuri, H.; Endler, L.; Chelliah, V.; Li, L.; He, E.; Henry, A.; Stefan, M.I.; et al. BioModels Database: An enhanced, curated and annotated resource for published quantitative kinetic models. BMC Syst. Biol. 2010, 4, 92. [Google Scholar] [CrossRef] [PubMed]
- Schomburg, I.; Chang, A.; Placzek, S.; Sohngen, C.; Rother, M.; Lang, M.; Munaretto, C.; Ulas, S.; Stelzer, M.; Grote, A.; et al. BRENDA in 2013: Integrated reactions, kinetic data, enzyme function data, improved disease classification: New options and contents in BRENDA. Nucleic Acids Res. 2012, 41, D764–D772. [Google Scholar] [CrossRef] [PubMed]
- Lloyd, C.M.; Lawson, J.R.; Hunter, P.J.; Nielsen, P.F. The CellML model repository. Bioinformatics 2008, 24, 2122–2123. [Google Scholar] [CrossRef] [PubMed]
- Flicek, P.; Amode, M.R.; Barrell, D.; Beal, K.; Billis, K.; Brent, S.; Carvalho-Silva, D.; Clapham, P.; Coates, G.; Fitzgerald, S.; et al. Ensembl 2014. Nucleic Acids Res. 2013, 42, D749–D755. [Google Scholar] [CrossRef] [PubMed]
- Artimo, P.; Jonnalagedda, M.; Arnold, K.; Baratin, D.; Csardi, G.; de Castro, E.; Duvaud, S.; Flegel, V.; Fortier, A.; Gasteiger, E.; et al. ExPASy: SIB bioinformatics resource portal. Nucleic Acids Res. 2012, 40, W597–W603. [Google Scholar]
- Safran, M.; Dalah, I.; Alexander, J.; Rosen, N.; Stein, T.I.; Shmoish, M.; Nativ, N.; Bahir, I.; Doniger, T.; Krug, H.; et al. GeneCards Version 3: The human gene integrator. Database 2010, 2010. Article ID baq020. [Google Scholar] [CrossRef]
- Romero, P.; Wagg, J.; Green, M.L.; Kaiser, D.; Krummenacker, M.; Karp, P.D. Computational prediction of human metabolic pathways from the complete human genome. Genome Biol. 2004, 6, R2. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Olivier, B.G.; Snoep, J.L. Web-based kinetic modelling using JWS Online. Bioinformatics 2004, 20, 2143–2144. [Google Scholar] [CrossRef] [PubMed]
- Christensen, B.; Nielsen, J. Isotopomer analysis using GC-MS. Metab. Eng. 1999, 1, 282–290. [Google Scholar] [CrossRef] [PubMed]
- Kelleher, J.K. Flux estimation using isotopic tracers: Common ground for metabolic physiology and metabolic engineering. Metab. Eng. 2001, 3, 100–110. [Google Scholar] [CrossRef] [PubMed]
- Kohlstedt, M.; Becker, J.; Wittmann, C. Metabolic fluxes and beyond-systems biology understanding and engineering of microbial metabolism. Appl. Microbiol. Biotech. 2010, 88, 1065–1075. [Google Scholar] [CrossRef]
- Claudino, W.M.; Quattrone, A.; Biganzoli, L.; Pestrin, M.; Bertini, I.; di Leo, A. Metabolomics: Available results, current research projects in breast cancer, and future applications. J. Clin. Oncol. 2007, 25, 2840–2846. [Google Scholar] [CrossRef] [PubMed]
- Malet-Martino, M.; Holzgrabe, U. NMR techniques in biomedical and pharmaceutical analysis. J. Pharmaceut. Biomed. 2011, 55, 1–15. [Google Scholar] [CrossRef]
- Van, Q.N.; Veenstra, T.D. How close is the bench to the bedside? Metabolic profiling in cancer research. Genome Med. 2009, 1, 5. [Google Scholar] [CrossRef] [PubMed]
- Chan, S.C.; Ng, S.H.; Chang, J.T.C.; Lin, C.Y.; Chen, Y.C.; Chang, Y.C.; Hsu, C.L.; Wang, H.M.; Liao, C.T.; Yen, T.C. Advantages and pitfalls of 18F-fluoro-2-deoxy-D-glucose positron emission tomography in detecting locally residual or recurrent nasopharyngeal carcinoma: Comparison with magnetic resonance imaging. Eur. J. Nucl. Med. Mol. I 2006, 33, 1032–1040. [Google Scholar] [CrossRef]
- Chang, J.M.; Lee, H.J.; Goo, J.M.; Lee, H.Y.; Lee, J.J.; Chung, J.K.; Im, J.G. False positive and false negative FDG-PET scans in various thoracic diseases. Korean J. Radiol. 2006, 7, 57–69. [Google Scholar] [CrossRef] [PubMed]
- Antoniewicz, M.R. Using multiple tracers for 13C metabolic flux analysis. In Systems Metabolic Engineering; Springer-Verlag Berlin: Heidelberg, Germany, 2013; pp. 353–365. [Google Scholar]
- Metallo, C.M.; Walther, J.L.; Stephanopoulos, G.; et al. Evaluation of 13C isotopic tracers for metabolic flux analysis in mammalian cells. J. Biotechnol. 2009, 144, 167–174. [Google Scholar] [CrossRef] [PubMed]
- Gaglio, D.; Metallo, C.M.; Gameiro, P.A.; Hiller, K.; Sala Danna, L.; Balestrieri, C.; Alberghina, L.; Stephanopoulos, G.; Chiaradonna, F.; et al. Oncogenic K-Ras decouples glucose and glutamine metabolism to support cancer cell growth. Mol. Syst. Biol. 2011, 7, 523. [Google Scholar] [CrossRef] [PubMed]
- Ahn, W.S.; Antoniewicz, M.R. Towards dynamic metabolic flux analysis in CHO cell cultures. Biotechnol. J. 2012, 7, 61–74. [Google Scholar] [CrossRef] [PubMed]
- Antoniewicz, M.R. Tandem mass spectrometry for measuring stable-isotope labeling. Curr. Opin. Biotech. 2013, 24, 48–53. [Google Scholar] [CrossRef] [PubMed]
- Crown, S.B.; Antoniewicz, M.R. Publishing 13C metabolic flux analysis studies: A review and future perspectives. Metab. Eng. 2013, 20, 42–48. [Google Scholar] [CrossRef] [PubMed]
- Hiller, K.; Metallo, C.M.; et al. Profiling metabolic networks to study cancer metabolism. Curr. Opin. Biotech. 2013, 24, 60–68. [Google Scholar] [CrossRef] [PubMed]
- Metallo, C.M.; Gameiro, P.A.; Bell, E.L.; Mattaini, K.R.; Yang, J.; Hiller, K.; Jewell, C.M.; Johnson, Z.R.; Irvine, D.J.; Guarente, L.; et al. Reductive glutamine metabolism by IDH1 mediates lipogenesis under hypoxia. Nature 2012, 481, 380–384. [Google Scholar]
- Stephanopoulos, G. Metabolic fluxes and metabolic engineering. Metab. Eng. 1999, 1, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Sugiura, Y.; Honda, K.; Kajimura, M.; Suematsu, M. Visualization and quantification of cerebral metabolic fluxes of glucose in awake mice. Proteomics 2014, 14, 829–838. [Google Scholar] [CrossRef] [PubMed]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cazzaniga, P.; Damiani, C.; Besozzi, D.; Colombo, R.; Nobile, M.S.; Gaglio, D.; Pescini, D.; Molinari, S.; Mauri, G.; Alberghina, L.; et al. Computational Strategies for a System-Level Understanding of Metabolism. Metabolites 2014, 4, 1034-1087. https://doi.org/10.3390/metabo4041034
Cazzaniga P, Damiani C, Besozzi D, Colombo R, Nobile MS, Gaglio D, Pescini D, Molinari S, Mauri G, Alberghina L, et al. Computational Strategies for a System-Level Understanding of Metabolism. Metabolites. 2014; 4(4):1034-1087. https://doi.org/10.3390/metabo4041034
Chicago/Turabian StyleCazzaniga, Paolo, Chiara Damiani, Daniela Besozzi, Riccardo Colombo, Marco S. Nobile, Daniela Gaglio, Dario Pescini, Sara Molinari, Giancarlo Mauri, Lilia Alberghina, and et al. 2014. "Computational Strategies for a System-Level Understanding of Metabolism" Metabolites 4, no. 4: 1034-1087. https://doi.org/10.3390/metabo4041034
APA StyleCazzaniga, P., Damiani, C., Besozzi, D., Colombo, R., Nobile, M. S., Gaglio, D., Pescini, D., Molinari, S., Mauri, G., Alberghina, L., & Vanoni, M. (2014). Computational Strategies for a System-Level Understanding of Metabolism. Metabolites, 4(4), 1034-1087. https://doi.org/10.3390/metabo4041034