Bucket Fuser: Statistical Signal Extraction for 1D 1H NMR Metabolomic Data
Abstract
:1. Introduction
2. Methods
2.1. Algorithm
2.2. Metabolomic Data Acquisition and Processing
2.2.1. Datasets
2.2.2. Feature Extraction
3. Results
3.1. Bucket Fuser Dynamically Constructs NMR Metabolite Features
- (1)
- BF fits plateaus, as shown by the thick blue and red lines;
- (2)
- The plateaus start and end at the same position for all spectra;
- (3)
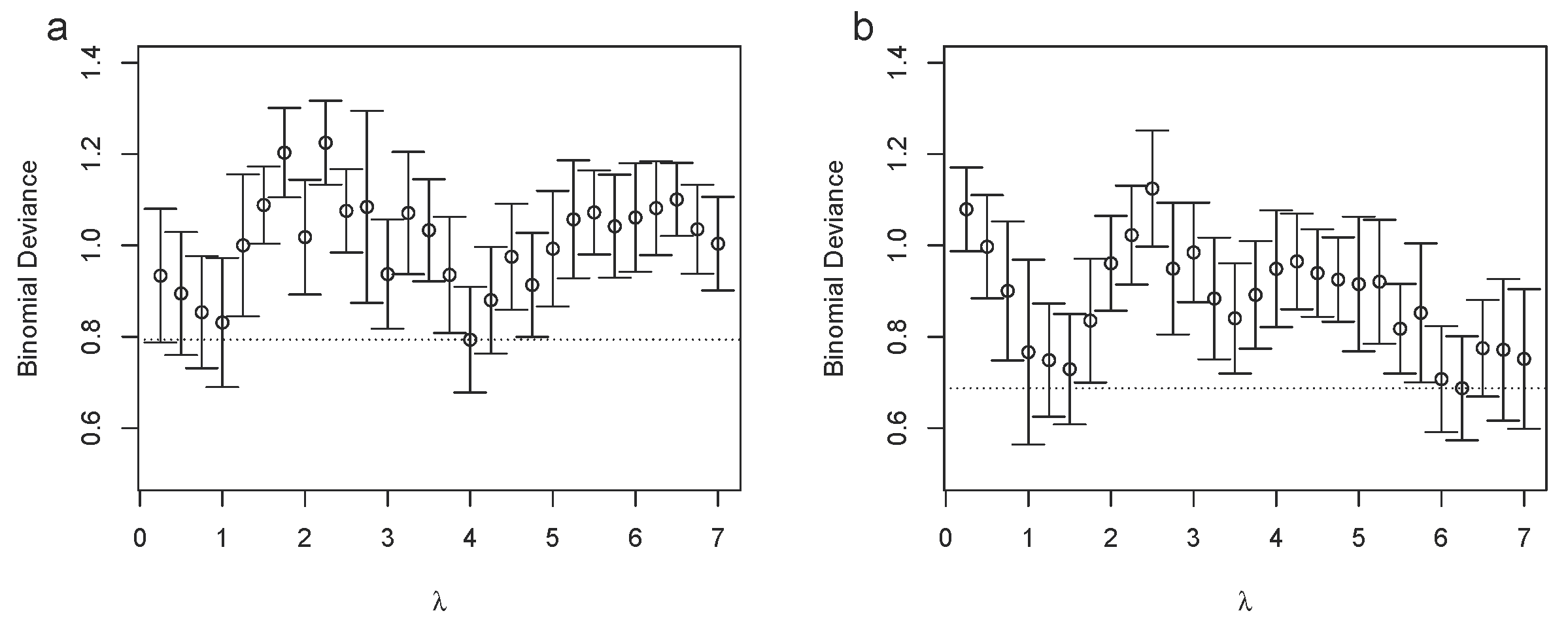
- The regularization parameter calibrates the plateau width: yields larger plateaus than and yields larger plateaus than .
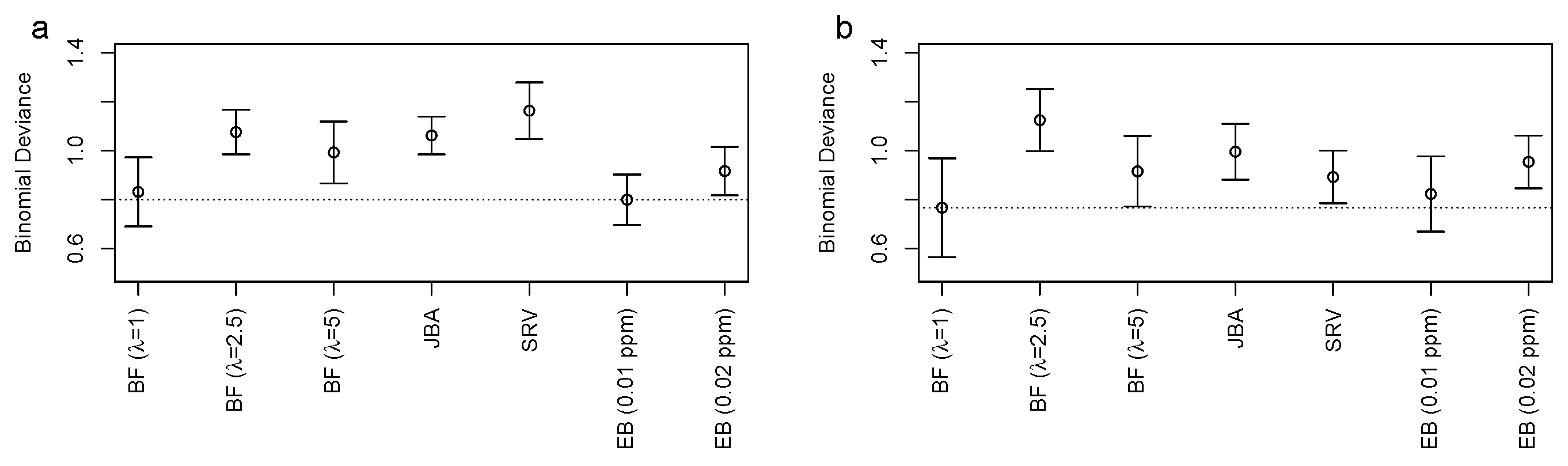
3.2. Bucket Fuser Improved Signal Extraction
3.3. Metabolite Identification
3.4. The Bucket Fuser Can Deal with Small Sample Sizes
3.5. The Bucket Fuser Improved the Detection of Metabolic Biomarkers for Acute Kidney Injury after Cardiac Surgery
4. Discussion and Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zacharias, H.U.; Schley, G.; Hochrein, J.; Klein, M.S.; Köberle, C.; Eckardt, K.U.; Willam, C.; Oefner, P.J.; Gronwald, W. Analysis of human urine reveals metabolic changes related to the development of acute kidney injury following cardiac surgery. Metabolomics 2013, 9, 697–707. [Google Scholar] [CrossRef]
- Zacharias, H.U.; Hochrein, J.; Vogl, F.C.; Schley, G.; Mayer, F.; Jeleazcov, C.; Eckardt, K.U.; Willam, C.; Oefner, P.J.; Gronwald, W. Identification of plasma metabolites prognostic of acute kidney injury after cardiac surgery with cardiopulmonary bypass. J. Proteome Res. 2015, 14, 2897–2905. [Google Scholar] [CrossRef]
- Zacharias, H.U.; Altenbuchinger, M.; Schultheiss, U.T.; Samol, C.; Kotsis, F.; Poguntke, I.; Sekula, P.; Krumsiek, J.; Köttgen, A.; Spang, R.; et al. A novel metabolic signature to predict the requirement of dialysis or renal transplantation in patients with chronic kidney disease. J. Proteome Res. 2019, 18, 1796–1805. [Google Scholar] [CrossRef]
- Gronwald, W.; Klein, M.S.; Zeltner, R.; Schulze, B.D.; Reinhold, S.W.; Deutschmann, M.; Immervoll, A.K.; Böger, C.A.; Banas, B.; Eckardt, K.U.; et al. Detection of autosomal dominant polycystic kidney disease by NMR spectroscopic fingerprinting of urine. Kidney Int. 2011, 79, 1244–1253. [Google Scholar] [CrossRef]
- Brindle, J.T.; Antti, H.; Holmes, E.; Tranter, G.; Nicholson, J.K.; Bethell, H.W.; Clarke, S.; Schofield, P.M.; McKilligin, E.; Mosedale, D.E.; et al. Rapid and noninvasive diagnosis of the presence and severity of coronary heart disease using 1 H-NMR-based metabonomics. Nat. Med. 2002, 8, 1439–1445. [Google Scholar] [CrossRef]
- Delles, C.; Rankin, N.J.; Boachie, C.; McConnachie, A.; Ford, I.; Kangas, A.; Soininen, P.; Trompet, S.; Mooijaart, S.P.; Jukema, J.W.; et al. Nuclear magnetic resonance-based metabolomics identifies phenylalanine as a novel predictor of incident heart failure hospitalisation: Results from PROSPER and FINRISK 1997. Eur. J. Heart Fail. 2018, 20, 663–673. [Google Scholar] [CrossRef]
- Fischer, K.; Kettunen, J.; Würtz, P.; Haller, T.; Havulinna, A.S.; Kangas, A.J.; Soininen, P.; Esko, T.; Tammesoo, M.L.; Mägi, R.; et al. Biomarker profiling by nuclear magnetic resonance spectroscopy for the prediction of all-cause mortality: An observational study of 17,345 persons. PLoS Med. 2014, 11, e1001606. [Google Scholar] [CrossRef]
- Deelen, J.; Kettunen, J.; Fischer, K.; van der Spek, A.; Trompet, S.; Kastenmüller, G.; Boyd, A.; Zierer, J.; van den Akker, E.B.; Ala-Korpela, M.; et al. A metabolic profile of all-cause mortality risk identified in an observational study of 44,168 individuals. Nat. Commun. 2019, 10, 3346. [Google Scholar] [CrossRef] [PubMed]
- Anderson, P.E.; Reo, N.V.; DelRaso, N.J.; Doom, T.E.; Raymer, M.L. Gaussian binning: A new kernel-based method for processing NMR spectroscopic data for metabolomics. Metabolomics 2008, 4, 261–272. [Google Scholar] [CrossRef]
- Davis, R.A.; Charlton, A.J.; Godward, J.; Jones, S.A.; Harrison, M.; Wilson, J.C. Adaptive binning: An improved binning method for metabolomics data using the undecimated wavelet transform. Chemom. Intell. Lab. Syst. 2007, 85, 144–154. [Google Scholar] [CrossRef]
- De Meyer, T.; Sinnaeve, D.; Van Gasse, B.; Tsiporkova, E.; Rietzschel, E.R.; De Buyzere, M.L.; Gillebert, T.C.; Bekaert, S.; Martins, J.C.; Van Criekinge, W. NMR-based characterization of metabolic alterations in hypertension using an adaptive, intelligent binning algorithm. Anal. Chem. 2008, 80, 3783–3790. [Google Scholar] [CrossRef] [PubMed]
- Anderson, P.E.; Mahle, D.A.; Doom, T.E.; Reo, N.V.; DelRaso, N.J.; Raymer, M.L. Dynamic adaptive binning: An improved quantification technique for NMR spectroscopic data. Metabolomics 2011, 7, 179–190. [Google Scholar] [CrossRef]
- Blaise, B.J.; Shintu, L.; Elena, B.; Emsley, L.; Dumas, M.E.; Toulhoat, P. Statistical recoupling prior to significance testing in nuclear magnetic resonance based metabonomics. Anal. Chem. 2009, 81, 6242–6251. [Google Scholar] [CrossRef] [PubMed]
- Rodriguez-Martinez, A.; Ayala, R.; Posma, J.M.; Harvey, N.; Jiménez, B.; Sonomura, K.; Sato, T.A.; Matsuda, F.; Zalloua, P.; Gauguier, D.; et al. pJRES Binning Algorithm (JBA): A new method to facilitate the recovery of metabolic information from pJRES 1H NMR spectra. Bioinformatics 2019, 35, 1916–1922. [Google Scholar] [CrossRef]
- Bleakley, K.; Vert, J.P. The group fused lasso for multiple change-point detection. arXiv 2011, arXiv:1106.4199. [Google Scholar]
- Tibshirani, R.; Saunders, M.; Rosset, S.; Zhu, J.; Knight, K. Sparsity and smoothness via the fused lasso. J. R. Stat. Soc. Ser. B Stat. Methodol. 2005, 67, 91–108. [Google Scholar] [CrossRef]
- Tibshirani, R.; Wang, P. Spatial smoothing and hot spot detection for CGH data using the fused lasso. Biostatistics 2008, 9, 18–29. [Google Scholar] [CrossRef]
- Meier, L.; Van De Geer, S.; Bühlmann, P. The group lasso for logistic regression. J. R. Stat. Soc. Ser. B Stat. Methodol. 2008, 70, 53–71. [Google Scholar] [CrossRef]
- Boyd, S.; Parikh, N.; Chu, E. Distributed Optimization and Statistical Learning via the Alternating Direction Method of Multipliers; Now Publishers: Boston, MA, USA, 2011. [Google Scholar]
- Zacharias, H.U.; Hochrein, J.; Klein, M.S.; Samol, C.; Oefner, P.J.; Gronwald, W. Current experimental, bioinformatic and statistical methods used in nmr based metabolomics. Curr. Metabolomics 2013, 1, 253–268. [Google Scholar] [CrossRef]
- Altenbuchinger, M.; Zacharias, H.U.; Solbrig, S.; Schäfer, A.; Büyüközkan, M.; Schultheiß, U.T.; Kotsis, F.; Köttgen, A.; Spang, R.; Oefner, P.J.; et al. A multi-source data integration approach reveals novel associations between metabolites and renal outcomes in the German Chronic Kidney Disease study. Sci. Rep. 2019, 9, 13954. [Google Scholar] [CrossRef]
- Wallmeier, J.; Samol, C.; Ellmann, L.; Zacharias, H.U.; Vogl, F.C.; Garcia, M.; Dettmer, K.; Oefner, P.J.; Gronwald, W.; GCKD study Investigators. Quantification of Metabolites by NMR Spectroscopy in the Presence of Protein. J. Proteome Res. 2017, 16, 1784–1796. [Google Scholar] [CrossRef] [PubMed]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2019. [Google Scholar]
- Dieterle, F.; Ross, A.; Schlotterbeck, G.; Senn, H. Probabilistic quotient normalization as robust method to account for dilution of complex biological mixtures. Application in 1H NMR metabonomics. Anal. Chem. 2006, 78, 4281–4290. [Google Scholar] [CrossRef] [PubMed]
- Zacharias, H.U.; Rehberg, T.; Mehrl, S.; Richtmann, D.; Wettig, T.; Oefner, P.J.; Spang, R.; Gronwald, W.; Altenbuchinger, M. Scale-invariant biomarker discovery in urine and plasma metabolite fingerprints. J. Proteome Res. 2017, 16, 3596–3605. [Google Scholar] [CrossRef] [PubMed]
- Hedjazi, L.; Gauguier, D.; Zalloua, P.A.; Nicholson, J.K.; Dumas, M.E.; Cazier, J.B. mQTL. NMR: An integrated suite for genetic mapping of quantitative variations of 1H NMR-based metabolic profiles. Anal. Chem. 2015, 87, 4377–4384. [Google Scholar] [CrossRef]
- Rodriguez-Martinez, A.; Posma, J.M.; Ayala, R.; Neves, A.L.; Anwar, M.; Petretto, E.; Emanueli, C.; Gauguier, D.; Nicholson, J.K.; Dumas, M.E. MWASTools: An R/bioconductor package for metabolome-wide association studies. Bioinformatics 2018, 34, 890–892. [Google Scholar] [CrossRef]
- Lin, W.; Shi, P.; Feng, R.; Li, H. Variable selection in regression with compositional covariates. Biometrika 2014, 101, 785–797. [Google Scholar] [CrossRef]
- Altenbuchinger, M.; Rehberg, T.; Zacharias, H.; Stämmler, F.; Dettmer, K.; Weber, D.; Hiergeist, A.; Gessner, A.; Holler, E.; Oefner, P.J.; et al. Reference point insensitive molecular data analysis. Bioinformatics 2017, 33, 219–226. [Google Scholar] [CrossRef]
- Kadkhodaie, M.; Christakopoulou, K.; Sanjabi, M.; Banerjee, A. Accelerated alternating direction method of multipliers. In Proceedings of the 21th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Sydney, Australia, 10–13 August 2015; pp. 497–506. [Google Scholar]
- Krishnamurthy, K. CRAFT (complete reduction to amplitude frequency table)—Robust and time-efficient Bayesian approach for quantitative mixture analysis by NMR. Magn. Reson. Chem. 2013, 51, 821–829. [Google Scholar] [CrossRef]



| BF ( = 1) | BF ( = 2.5) | BF ( = 5) | SRV | JBA | EB (0.01 ppm) | EB (0.02 ppm) |
|---|---|---|---|---|---|---|
| 360 + 261 = 621 | 398 + 234 = 632 | 507 + 301 = 808 | 531 | 538 | 749 | 375 |
| BF ( = 1) | BF ( = 2.5) | BF ( = 5) | JBA | SRV | EB (0.01 ppm) | EB (0.02 ppm) | |
|---|---|---|---|---|---|---|---|
| 3-Hydroxybutyrate | 0.768 | 0.720 | 0.689 | 0.768 | 0.600 | 0.547 | 0.498 |
| Acetate | 0.757 | 0.983 | 0.968 | 0.966 | 0.908 | 0.946 | 0.892 |
| Acetoacetate | 0.670 | 0.664 | 0.610 | 0.670 | 0.611 | 0.614 | 0.603 |
| Acetone | 0.528 | 0.748 | 0.568 | 0.530 | 0.472 | 0.455 | 0.350 |
| Alanine | 0.680 | 0.927 | 0.947 | 0.722 | 0.915 | 0.926 | 0.905 |
| Asparagine | 0.685 | 0.662 | 0.635 | 0.563 | 0.698 | 0.683 | 0.659 |
| Betaine | 0.509 | 0.637 | 0.480 | 0.689 | 0.481 | 0.630 | 0.221 |
| Carnitine | 0.678 | 0.419 | 0.427 | 0.692 | 0.412 | 0.444 | 0.445 |
| Creatine | 0.929 | 0.907 | 0.584 | 0.909 | 0.842 | 0.763 | 0.626 |
| Creatinine | 0.772 | 0.893 | 0.881 | 0.443 | 0.749 | 0.703 | 0.619 |
| Dimethylamine | 0.895 | 0.649 | 0.649 | 0.598 | 0.684 | 0.587 | 0.592 |
| Glucose | 0.990 | 0.990 | 0.989 | 0.987 | 0.989 | 0.990 | 0.988 |
| Glutamine | 0.873 | 0.870 | 0.905 | 0.612 | 0.779 | 0.897 | 0.878 |
| Glycine | 0.838 | 0.808 | 0.741 | 0.332 | 0.778 | 0.655 | 0.543 |
| Histidine | 0.548 | 0.764 | 0.523 | 0.453 | 0.571 | 0.558 | 0.631 |
| Isobutyrate | 0.845 | 0.793 | 0.568 | 0.445 | 0.687 | 0.618 | 0.522 |
| Isoleucine | 0.866 | 0.911 | 0.808 | 0.735 | 0.762 | 0.792 | 0.790 |
| Lactate | 0.988 | 0.989 | 0.989 | 0.979 | 0.983 | 0.990 | 0.985 |
| Phenylalanine | 0.850 | 0.874 | 0.888 | 0.819 | 0.818 | 0.810 | 0.800 |
| Proline | 0.754 | 0.937 | 0.699 | 0.676 | 0.871 | 0.680 | 0.609 |
| Pyruvate | 0.884 | 0.968 | 0.941 | 0.884 | 0.931 | 0.857 | 0.692 |
| Threonine | 0.494 | 0.502 | 0.490 | 0.426 | 0.472 | 0.490 | 0.474 |
| TMAO | 0.282 | 0.401 | 0.403 | 0.449 | 0.279 | 0.400 | 0.231 |
| Tyrosine | 0.931 | 0.941 | 0.947 | 0.816 | 0.935 | 0.939 | 0.924 |
| Valine | 0.811 | 0.947 | 0.961 | 0.725 | 0.924 | 0.952 | 0.952 |
| BF ( = 1) | BF ( = 2.5) | BF ( = 5) | JBA | SRV | EB (0.01 ppm) | EB (0.02 ppm) | |
|---|---|---|---|---|---|---|---|
| BF () | 11 | - | - | 7 | 3 | 5 | 1 |
| BF () | - | 14 | - | 6 | 2 | 3 | 0 |
| BF () | - | - | 11 | 6 | 5 | 2 | 1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Altenbuchinger, M.; Berndt, H.; Kosch, R.; Lang, I.; Dönitz, J.; Oefner, P.J.; Gronwald, W.; Zacharias, H.U.; Investigators GCKD Study. Bucket Fuser: Statistical Signal Extraction for 1D 1H NMR Metabolomic Data. Metabolites 2022, 12, 812. https://doi.org/10.3390/metabo12090812
Altenbuchinger M, Berndt H, Kosch R, Lang I, Dönitz J, Oefner PJ, Gronwald W, Zacharias HU, Investigators GCKD Study. Bucket Fuser: Statistical Signal Extraction for 1D 1H NMR Metabolomic Data. Metabolites. 2022; 12(9):812. https://doi.org/10.3390/metabo12090812
Chicago/Turabian StyleAltenbuchinger, Michael, Henry Berndt, Robin Kosch, Iris Lang, Jürgen Dönitz, Peter J. Oefner, Wolfram Gronwald, Helena U. Zacharias, and Investigators GCKD Study. 2022. "Bucket Fuser: Statistical Signal Extraction for 1D 1H NMR Metabolomic Data" Metabolites 12, no. 9: 812. https://doi.org/10.3390/metabo12090812
APA StyleAltenbuchinger, M., Berndt, H., Kosch, R., Lang, I., Dönitz, J., Oefner, P. J., Gronwald, W., Zacharias, H. U., & Investigators GCKD Study. (2022). Bucket Fuser: Statistical Signal Extraction for 1D 1H NMR Metabolomic Data. Metabolites, 12(9), 812. https://doi.org/10.3390/metabo12090812








