Next-Generation Genome-Scale Metabolic Modeling through Integration of Regulatory Mechanisms
Abstract
1. Introduction
2. Modeling of Metabolic Regulation
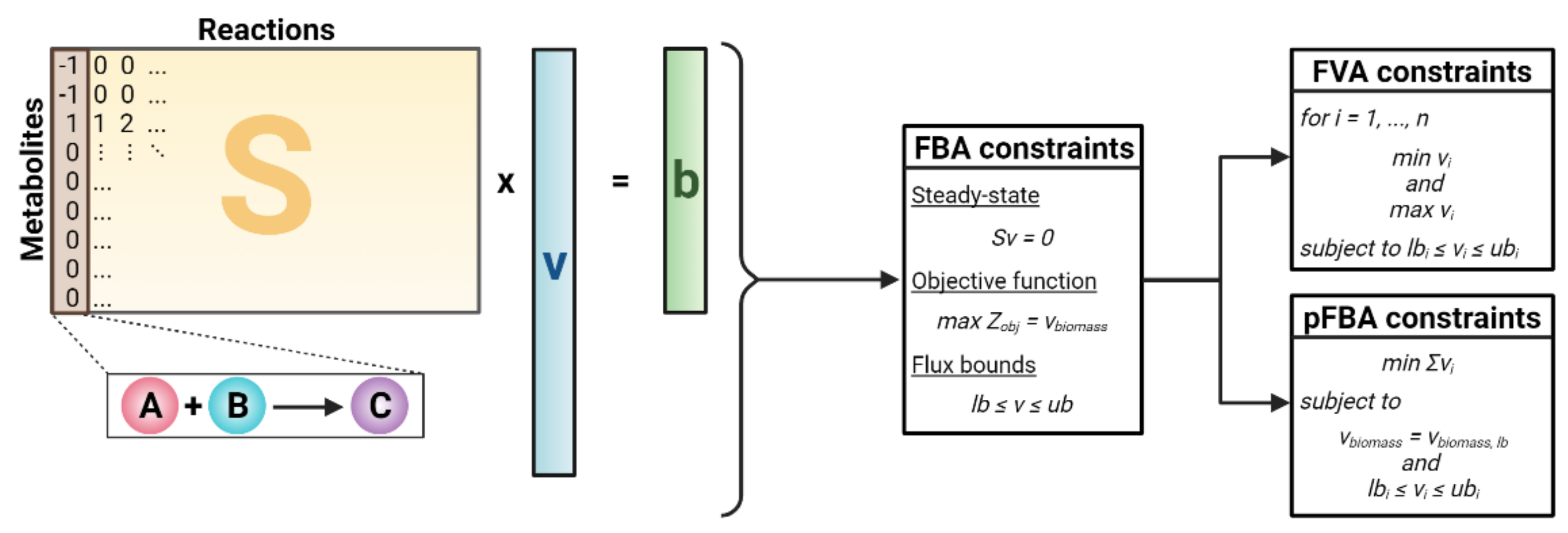
2.1. Simulating Metabolic Networks Using Constraint-Based Modeling (CBM)
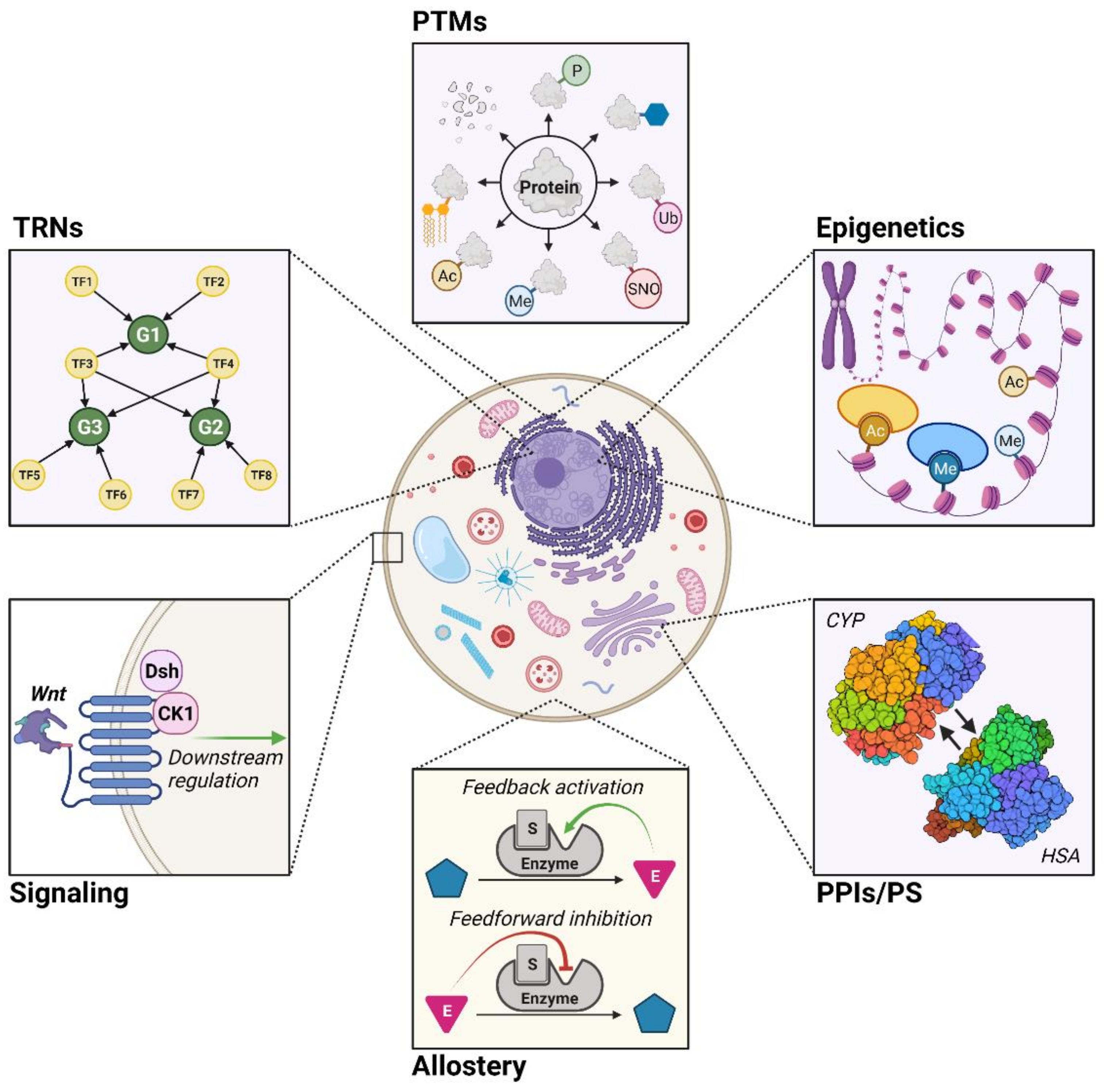
2.2. Transcriptional Regulatory Networks (TRNs)
2.2.1. Boolean TRNs
2.2.2. Continuous TRNs
2.3. Post-Translational Modifications (PTMs)
2.4. Epigenetics
2.5. Protein–Protein Interactions and Protein Stability (PPIs/PS)
2.6. Allostery
2.7. Signaling
3. Areas for Improvement
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zhu, J.; Thompson, C.B. Metabolic Regulation of Cell Growth and Proliferation. Nat. Rev. Mol. Cell Biol. 2019, 20, 436–450. [Google Scholar] [CrossRef] [PubMed]
- Metallo, C.M.; Vander Heiden, M.G. Understanding Metabolic Regulation and Its Influence on Cell Physiology. Mol. Cell 2013, 49, 388–398. [Google Scholar] [CrossRef] [PubMed]
- Chubukov, V.; Gerosa, L.; Kochanowski, K.; Sauer, U. Coordination of Microbial Metabolism. Nat. Rev. Microbiol. 2014, 12, 327–340. [Google Scholar] [CrossRef] [PubMed]
- Gerosa, L.; Sauer, U. Regulation and Control of Metabolic Fluxes in Microbes. Curr. Opin. Biotechnol. 2011, 22, 566–575. [Google Scholar] [CrossRef] [PubMed]
- Kochanowski, K.; Sauer, U.; Noor, E. Posttranslational Regulation of Microbial Metabolism. Curr. Opin. Microbiol. 2015, 27, 10–17. [Google Scholar] [CrossRef]
- Nielsen, J. Systems Biology of Metabolism. Annu. Rev. Biochem. 2017, 86, 245–275. [Google Scholar] [CrossRef] [PubMed]
- Heinemann, M.; Sauer, U. Systems Biology of Microbial Metabolism. Curr. Opin. Microbiol. 2010, 13, 337–343. [Google Scholar] [CrossRef]
- Mardinoglu, A.; Gatto, F.; Nielsen, J. Genome-Scale Modeling of Human Metabolism—A Systems Biology Approach. Biotechnol. J. 2013, 8, 985–996. [Google Scholar] [CrossRef]
- Price, N.D.; Reed, J.L.; Palsson, B. Genome-Scale Models of Microbial Cells: Evaluating the Consequences of Constraints. Nat. Rev. Microbiol. 2004, 2, 886–897. [Google Scholar] [CrossRef] [PubMed]
- Thiele, I.; Palsson, B. A Protocol for Generating a High-Quality Genome-Scale Metabolic Reconstruction. Nat. Protoc. 2010, 5, 93–121. [Google Scholar] [CrossRef] [PubMed]
- Lewis, N.E.; Nagarajan, H.; Palsson, B.O. Constraining the Metabolic Genotype-Phenotype Relationship Using a Phylogeny of In Silico Methods. Nat. Rev. Microbiol. 2012, 10, 291–305. [Google Scholar] [CrossRef] [PubMed]
- Fang, X.; Lloyd, C.J.; Palsson, B.O. Reconstructing Organisms in Silico: Genome-Scale Models and Their Emerging Applications. Nat. Rev. Microbiol. 2020, 18, 931–943. [Google Scholar] [CrossRef] [PubMed]
- Edwards, J.S.; Ibarra, R.U.; Palsson, B.O. In Silico Predictions of Escherichia coli Metabolic Capabilities Are Consistent with Experimental Data. Nat. Biotechnol. 2001, 19, 125–130. [Google Scholar] [CrossRef]
- Fong, N.L.; Lerman, J.A.; Lam, I.; Palsson, B.O.; Charusanti, P. Reconciling a Salmonella enterica Metabolic Model with Experimental Data Confirms That Overexpression of the Glyoxylate Shunt Can Rescue a Lethal PPC Deletion Mutant. FEMS Microbiol. Lett. 2013, 342, 62–69. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Gu, C.; Kim, G.B.; Kim, W.J.; Kim, H.U.; Lee, S.Y. Current Status and Applications of Genome-Scale Metabolic Models. Genome Biol. 2019, 20, 121. [Google Scholar] [CrossRef] [PubMed]
- Covert, M.W.; Schilling, C.H.; Palsson, B. Regulation of Gene Expression in Flux Balance Models of Metabolism. J. Theor. Biol. 2001, 213, 73–88. [Google Scholar] [CrossRef]
- Liu, G.; Marras, A.; Nielsen, J. The Future of Genome-Scale Modeling of Yeast through Integration of a Transcriptional Regulatory Network. Quant. Biol. 2014, 2, 30–46. [Google Scholar] [CrossRef]
- Monk, J.; Nogales, J.; Palsson, B.O. Optimizing Genome-Scale Network Reconstructions. Nat. Biotechnol. 2014, 32, 447–452. [Google Scholar] [CrossRef]
- Chandrasekaran, S. A Protocol for the Construction and Curation of Genome-Scale Integrated Metabolic and Regulatory Network Models. Methods Mol. Biol. 2019, 1927, 203–214. [Google Scholar] [CrossRef]
- Kim, M.; Tagkopoulos, I. Data Integration and Predictive Modeling Methods for Multi-Omics Datasets. Mol. Omi. 2018, 14, 8–25. [Google Scholar] [CrossRef]
- Noor, E.; Cherkaoui, S.; Sauer, U. Biological Insights through Omics Data Integration. Curr. Opin. Syst. Biol. 2019, 15, 39–47. [Google Scholar] [CrossRef]
- Cho, J.S.; Gu, C.; Han, T.H.; Ryu, J.Y.; Lee, S.Y. Reconstruction of Context-Specific Genome-Scale Metabolic Models Using Multiomics Data to Study Metabolic Rewiring. Curr. Opin. Syst. Biol. 2019, 15, 1–11. [Google Scholar] [CrossRef]
- Dahal, S.; Yurkovich, J.T.; Xu, H.; Palsson, B.O.; Yang, L. Synthesizing Systems Biology Knowledge from Omics Using Genome-Scale Models. Proteomics 2020, 20, 1900282. [Google Scholar] [CrossRef]
- Covert, M.W.; Palsson, B. Transcriptional Regulation in Constraints-Based Metabolic Models of Escherichia coli. J. Biol. Chem. 2002, 277, 28058–28064. [Google Scholar] [CrossRef]
- Shlomi, T.; Eisenberg, Y.; Sharan, R.; Ruppin, E. A Genome-Scale Computational Study of the Interplay between Transcriptional Regulation and Metabolism. Mol. Syst. Biol. 2007, 3, 101. [Google Scholar] [CrossRef]
- Lee, S.G.; Park, J.H.; Hou, B.K.; Kim, Y.H.; Kim, C.M.; Hwang, K.S. Effect of Weight-Added Regulatory Networks on Constraint-Based Metabolic Models of Escherichia coli. BioSystems 2007, 90, 843–855. [Google Scholar] [CrossRef]
- Covert, M.W.; Xiao, N.; Chen, T.J.; Karr, J.R. Integrating Metabolic, Transcriptional Regulatory and Signal Transduction Models in Escherichia coli. Bioinformatics 2008, 24, 2044–2050. [Google Scholar] [CrossRef] [PubMed]
- Chandrasekaran, S.; Price, N.D. Probabilistic Integrative Modeling of Genome-Scale Metabolic and Regulatory Networks in Escherichia coli and Mycobacterium tuberculosis. Proc. Natl. Acad. Sci. USA 2010, 107, 17845–17850. [Google Scholar] [CrossRef] [PubMed]
- Jensen, P.A.; Lutz, K.A.; Papin, J.A. TIGER: Toolbox for Integrating Genome-Scale Metabolic Models, Expression Data, and Transcriptional Regulatory Networks. BMC Syst. Biol. 2011, 5, 147. [Google Scholar] [CrossRef] [PubMed]
- Marmiesse, L.; Peyraud, R.; Cottret, L. FlexFlux: Combining Metabolic Flux and Regulatory Network Analyses. BMC Syst. Biol. 2015, 9, 93. [Google Scholar] [CrossRef] [PubMed]
- Ma, S.; Minch, K.J.; Rustad, T.R.; Hobbs, S.; Zhou, S.-L.; Sherman, D.R.; Price, N.D. Integrated Modeling of Gene Regulatory and Metabolic Networks in Mycobacterium tuberculosis. PLoS Comput. Biol. 2015, 11, e1004543. [Google Scholar] [CrossRef]
- Banos, D.T.; Trébulle, P.; Elati, M. Integrating Transcriptional Activity in Genome-Scale Models of Metabolism. BMC Syst. Biol. 2017, 11, 134. [Google Scholar] [CrossRef]
- Wang, Z.; Danziger, S.A.; Heavner, B.D.; Ma, S.; Smith, J.J.; Li, S.; Herricks, T.; Simeonidis, E.; Baliga, N.S.; Aitchison, J.D.; et al. Combining Inferred Regulatory and Reconstructed Metabolic Networks Enhances Phenotype Prediction in Yeast. PLoS Comput. Biol. 2017, 13, e1005489. [Google Scholar] [CrossRef]
- Motamedian, E.; Mohammadi, M.; Shojaosadati, S.A.; Heydari, M. TRFBA: An Algorithm to Integrate Genome-Scale Metabolic and Transcriptional Regulatory Networks with Incorporation of Expression Data. Bioinformatics 2017, 33, 1057–1063. [Google Scholar] [CrossRef]
- Shen, F.; Sun, R.; Yao, J.; Li, J.; Liu, Q.; Price, N.D.; Liu, C.; Wang, Z. OptRAM: In-Silico Strain Design via Integrative Regulatory-Metabolic Network Modeling. PLoS Comput. Biol. 2019, 15, e1006835. [Google Scholar] [CrossRef] [PubMed]
- Brunk, E.; Chang, R.L.; Xia, J.; Hefzi, H.; Yurkovich, J.T.; Kim, D.; Buckmiller, E.; Wang, H.H.; Cho, B.K.; Yang, C.; et al. Characterizing Posttranslational Modifications in Prokaryotic Metabolism Using a Multiscale Workflow. Proc. Natl. Acad. Sci. USA 2018, 115, 11096–11101. [Google Scholar] [CrossRef] [PubMed]
- Smith, K.; Shen, F.; Lee, H.J.; Chandrasekaran, S. Metabolic Signatures of Regulation by Phosphorylation and Acetylation. bioRxiv 2021, 838243. [Google Scholar] [CrossRef]
- Chandrasekaran, S.; Zhang, J.; Sun, Z.; Zhang, L.; Ross, C.A.; Huang, Y.C.; Asara, J.M.; Li, H.; Daley, G.Q.; Collins, J.J. Comprehensive Mapping of Pluripotent Stem Cell Metabolism Using Dynamic Genome-Scale Network Modeling. Cell Rep. 2017, 21, 2965–2977. [Google Scholar] [CrossRef] [PubMed]
- Shen, F.; Boccuto, L.; Pauly, R.; Srikanth, S.; Chandrasekaran, S. Genome-Scale Network Model of Metabolism and Histone Acetylation Reveals Metabolic Dependencies of Histone Deacetylase Inhibitors. Genome Biol. 2019, 20, 49. [Google Scholar] [CrossRef] [PubMed]
- Chang, R.L.; Andrews, K.; Kim, D.; Li, Z.; Godzik, A.; Palsson, B.O. Structural Systems Biology Evaluation of Metabolic Thermotolerance in Escherichia coli. Science 2013, 340, 1220–1223. [Google Scholar] [CrossRef]
- Brunk, E.; Mih, N.; Monk, J.; Zhang, Z.; O’Brien, E.J.; Bliven, S.E.; Chen, K.; Chang, R.L.; Bourne, P.E.; Palsson, B.O. Systems Biology of the Structural Proteome. BMC Syst. Biol. 2016, 10, 1–16. [Google Scholar] [CrossRef]
- Lee, S.; Zhang, C.; Kilicarslan, M.; Piening, B.D.; Bjornson, E.; Hallström, B.M.; Groen, A.K.; Ferrannini, E.; Laakso, M.; Snyder, M.; et al. Integrated Network Analysis Reveals an Association between Plasma Mannose Levels and Insulin Resistance. Cell Metab. 2016, 24, 172–184. [Google Scholar] [CrossRef]
- Machado, D.; Herrgård, M.J.; Rocha, I. Modeling the Contribution of Allosteric Regulation for Flux Control in the Central Carbon Metabolism of E. coli. Front. Bioeng. Biotechnol. 2015, 3, 154. [Google Scholar] [CrossRef][Green Version]
- Hackett, S.R.; Zanotelli, V.R.T.; Xu, W.; Goya, J.; Park, J.O.; Perlman, D.H.; Gibney, P.A.; Botstein, D.; Storey, J.D.; Rabinowitz, J.D. Systems-Level Analysis of Mechanisms Regulating Yeast Metabolic Flux. Science 2016, 354. [Google Scholar] [CrossRef] [PubMed]
- Min Lee, J.; Gianchandani, E.P.; Eddy, J.A.; Papin, J.A. Dynamic Analysis of Integrated Signaling, Metabolic, and Regulatory Networks. PLoS Comput. Biol. 2008, 4, e1000086. [Google Scholar] [CrossRef] [PubMed]
- Orth, J.D.; Thiele, I.; Palsson, B.Ø. What Is Flux Balance Analysis? Nat. Biotechnol. 2010, 28, 245–248. [Google Scholar] [CrossRef] [PubMed]
- Reimers, A.M.; Reimers, A.C. The Steady-State Assumption in Oscillating and Growing Systems. J. Theor. Biol. 2016, 406, 176–186. [Google Scholar] [CrossRef] [PubMed]
- Feist, A.M.; Palsson, B.O. The Biomass Objective Function. Curr. Opin. Microbiol. 2010, 13, 344–349. [Google Scholar] [CrossRef]
- Schuetz, R.; Kuepfer, L.; Sauer, U. Systematic Evaluation of Objective Functions for Predicting Intracellular Fluxes in Escherichia coli. Mol. Syst. Biol. 2007, 3, 119. [Google Scholar] [CrossRef]
- Mahadevan, R.; Schilling, C.H. The Effects of Alternate Optimal Solutions in Constraint-Based Genome-Scale Metabolic Models. Metab. Eng. 2003, 5, 264–276. [Google Scholar] [CrossRef]
- Lewis, N.E.; Hixson, K.K.; Conrad, T.M.; Lerman, J.A.; Charusanti, P.; Polpitiya, A.D.; Adkins, J.N.; Schramm, G.; Purvine, S.O.; Lopez-Ferrer, D.; et al. Omic Data from Evolved E. coli Are Consistent with Computed Optimal Growth from Genome-Scale Models. Mol. Syst. Biol. 2010, 6, 390. [Google Scholar] [CrossRef]
- Vivek-Ananth, R.P.; Samal, A. Advances in the Integration of Transcriptional Regulatory Information into Genome-Scale Metabolic Models. BioSystems 2016, 147, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.-F.; Zhang, Y.; Xu, H.; Bu, G. Transcriptional Regulation and Its Misregulation in Alzheimer’s Disease. Mol. Brain 2013, 6, 44. [Google Scholar] [CrossRef]
- Lee, T.I.; Young, R.A. Transcriptional Regulation and Its Misregulation in Disease. Cell 2013, 152, 1237–1251. [Google Scholar] [CrossRef] [PubMed]
- Bonneau, R.; Facciotti, M.T.; Reiss, D.J.; Schmid, A.K.; Pan, M.; Kaur, A.; Thorsson, V.; Shannon, P.; Johnson, M.H.; Bare, J.C.; et al. A Predictive Model for Transcriptional Control of Physiology in a Free Living Cell. Cell 2007, 131, 1354–1365. [Google Scholar] [CrossRef] [PubMed]
- Chubukov, V.; Uhr, M.; Le Chat, L.; Kleijn, R.J.; Jules, M.; Link, H.; Aymerich, S.; Stelling, J.; Sauer, U. Transcriptional Regulation Is Insufficient to Explain Substrate-Induced Flux Changes in Bacillus subtilis. Mol. Syst. Biol. 2013, 9, 709. [Google Scholar] [CrossRef]
- Rocks, O.; Peyker, A.; Kahms, M.; Verveer, P.J.; Koerner, C.; Lumbierres, M.; Kuhlmann, J.; Waldmann, H.; Wittinghofer, A.; Bastiaens, P.I.H. An Acylation Cycle Regulates Localization and Activity of Palmitoylated Ras Isoforms. Science 2005, 307, 1746–1752. [Google Scholar] [CrossRef] [PubMed]
- Maeda, A.; Okano, K.; Park, P.S.-H.; Lem, J.; Crouch, R.K.; Maeda, T.; Palczewski, K. Palmitoylation Stabilizes Unliganded Rod Opsin. Proc. Natl. Acad. Sci. USA 2010, 107, 8428–8433. [Google Scholar] [CrossRef]
- Mann, M.; Jensen, O.N. Proteomic Analysis of Post-Translational Modifications. Nat. Biotechnol. 2003, 21, 255–261. [Google Scholar] [CrossRef]
- Deribe, Y.L.; Pawson, T.; Dikic, I. Post-Translational Modifications in Signal Integration. Nat. Struct. Mol. Biol. 2010, 17, 666–672. [Google Scholar] [CrossRef]
- Zhao, S.; Xu, W.; Jiang, W.; Yu, W.; Lin, Y.; Zhang, T.; Yao, J.; Zhou, L.; Zeng, Y.; Li, H.; et al. Regulation of Cellular Metabolism by Protein Lysine Acetylation. Science 2010, 327, 1000–1004. [Google Scholar] [CrossRef]
- Oliveira, A.P.; Sauer, U. The Importance of Post-Translational Modifications in Regulating Saccharomyces cerevisiae Metabolism. FEMS Yeast Res. 2012, 12, 104–117. [Google Scholar] [CrossRef]
- Pisithkul, T.; Patel, N.M.; Amador-Noguez, D. Post-Translational Modifications as Key Regulators of Bacterial Metabolic Fluxes. Curr. Opin. Microbiol. 2015, 24, 29–37. [Google Scholar] [CrossRef]
- Nam, H.; Lewis, N.E.; Lerman, J.A.; Lee, D.-H.; Chang, R.L.; Kim, D.; Palsson, B.O. Network Context and Selection in the Evolution to Enzyme Specificity. Science 2012, 337, 1101–1104. [Google Scholar] [CrossRef] [PubMed]
- Feizi, A.; Österlund, T.; Petranovic, D.; Bordel, S.; Nielsen, J. Genome-Scale Modeling of the Protein Secretory Machinery in Yeast. PLoS ONE 2013, 8, e63284. [Google Scholar] [CrossRef] [PubMed]
- Carnino, J.M.; Ni, K.; Jin, Y. Post-Translational Modification Regulates Formation and Cargo-Loading of Extracellular Vesicles. Front. Immunol. 2020, 11, 948. [Google Scholar] [CrossRef] [PubMed]
- Gutierrez, J.M.; Feizi, A.; Li, S.; Kallehauge, T.B.; Hefzi, H.; Grav, L.M.; Ley, D.; Hizal, D.B.; Betenbaugh, M.J.; Voldborg, B.; et al. Genome-Scale Reconstructions of the Mammalian Secretory Pathway Predict Metabolic Costs and Limitations of Protein Secretion. Nat. Commun. 2020, 11, 68. [Google Scholar] [CrossRef]
- Moore, L.D.; Le, T.; Fan, G. DNA Methylation and Its Basic Function. Neuropsychopharmacology 2012, 38, 23–38. [Google Scholar] [CrossRef] [PubMed]
- Chuang, J.C.; Jones, P.A. Epigenetics and MicroRNAs. Pediatr. Res. 2007, 61, 24–29. [Google Scholar] [CrossRef] [PubMed]
- Bannister, A.J.; Kouzarides, T. Regulation of Chromatin by Histone Modifications. Cell Res. 2011, 21, 381–395. [Google Scholar] [CrossRef]
- Reid, M.A.; Dai, Z.; Locasale, J.W. The Impact of Cellular Metabolism on Chromatin Dynamics and Epigenetics. Nat. Cell Biol. 2017, 19, 1298–1306. [Google Scholar] [CrossRef] [PubMed]
- Su, X.; Wellen, K.E.; Rabinowitz, J.D. Metabolic Control of Methylation and Acetylation. Curr. Opin. Chem. Biol. 2016, 30, 52–60. [Google Scholar] [CrossRef]
- Kaelin, W.G.; McKnight, S.L. Influence of Metabolism on Epigenetics and Disease. Cell 2013, 153, 56–69. [Google Scholar] [CrossRef] [PubMed]
- Etchegaray, J.P.; Mostoslavsky, R. Interplay between Metabolism and Epigenetics: A Nuclear Adaptation to Environmental Changes. Mol. Cell 2016, 62, 695–711. [Google Scholar] [CrossRef] [PubMed]
- Lu, C.; Thompson, C.B. Metabolic Regulation of Epigenetics. Cell Metab. 2012, 16, 9–17. [Google Scholar] [CrossRef]
- Chandrasekaran, S. Tying Metabolic Branches with Histone Tails Using Systems Biology. Epigenet. Insights 2019, 12. [Google Scholar] [CrossRef] [PubMed]
- Campit, S.; Chandrasekaran, S. Inferring Metabolic Flux from Time-Course Metabolomics. In Methods in Molecular Biology; Humana Press Inc.: Totowa, NJ, USA, 2020; Volume 2088, pp. 299–313. [Google Scholar]
- Campit, S.E.; Meliki, A.; Youngson, N.A.; Chandrasekaran, S. Nutrient Sensing by Histone Marks: Reading the Metabolic Histone Code Using Tracing, Omics, and Modeling. BioEssays 2020, 42, 2000083. [Google Scholar] [CrossRef]
- Barretina, J.; Caponigro, G.; Stransky, N.; Venkatesan, K.; Margolin, A.A.; Kim, S.; Wilson, C.J.; Lehár, J.; Kryukov, G.V.; Sonkin, D.; et al. The Cancer Cell Line Encyclopedia Enables Predictive Modelling of Anticancer Drug Sensitivity. Nature 2012, 483, 603–607. [Google Scholar] [CrossRef]
- Pacheco, M.P.; John, E.; Kaoma, T.; Heinäniemi, M.; Nicot, N.; Vallar, L.; Bueb, J.L.; Sinkkonen, L.; Sauter, T. Integrated Metabolic Modelling Reveals Cell-Type Specific Epigenetic Control Points of the Macrophage Metabolic Network. BMC Genom. 2015, 16, 809. [Google Scholar] [CrossRef]
- Salehzadeh-Yazdi, A.; Asgari, Y.; Saboury, A.A.; Masoudi-Nejad, A. Computational Analysis of Reciprocal Association of Metabolism and Epigenetics in the Budding Yeast: A Genome-Scale Metabolic Model (GSMM) Approach. PLoS ONE 2014, 9, e111686. [Google Scholar] [CrossRef]
- Shen, F.; Cheek, C.; Chandrasekaran, S. Dynamic Network Modeling of Stem Cell Metabolism. Methods Mol. Biol. 2019, 1975, 305–320. [Google Scholar] [CrossRef] [PubMed]
- Friedman, A.; Perrimon, N. Genetic Screening for Signal Transduction in the Era of Network Biology. Cell 2007, 128, 225–231. [Google Scholar] [CrossRef] [PubMed]
- Nyfeler, B.; Michnick, S.W.; Hauri, H.-P. Capturing Protein Interactions in the Secretory Pathway of Living Cells. Proc. Natl. Acad. Sci. USA 2005, 102, 6350–6355. [Google Scholar] [CrossRef]
- Pandey, A.V.; Henderson, C.J.; Ishii, Y.; Kranendonk, M.; Backes, W.L.; Zanger, U.M. Editorial: Role of Protein-Protein Interactions in Metabolism: Genetics, Structure, Function. Front. Pharmacol. 2017, 8, 881. [Google Scholar] [CrossRef] [PubMed]
- De Las Rivas, J.; Fontanillo, C. Protein-Protein Interactions Essentials: Key Concepts to Building and Analyzing Interactome Networks. PLoS Comput. Biol. 2010, 6, 1–8. [Google Scholar] [CrossRef]
- Kangueane, P.; Nilofer, C. Databases for Protein-Protein Interaction. In Protein-Protein and Domain-Domain Interactions; Springer: Singapore, 2018; pp. 113–124. [Google Scholar]
- Ivanov, A.A.; Khuri, F.R.; Fu, H. Targeting Protein-Protein Interactions as an Anticancer Strategy. Trends Pharmacol. Sci. 2013, 34, 393–400. [Google Scholar] [CrossRef] [PubMed]
- Zinzalla, G.; Thurston, D.E. Targeting Protein-Protein Interactions for Therapeutic Intervention: A Challenge for the Future. Future Med. Chem. 2009, 1, 65–93. [Google Scholar] [CrossRef]
- Gómez-Moreno, C.; Martínez-Júlvez, M.; Medina, M.; Hurley, J.K.; Tollin, G. Protein-Protein Interaction in Electron Transfer Reactions: The Ferrodoxin/Flavodoxin/ferredoxin:NADP+ Reductase System from Anabaena. Biochimie 1998, 80, 837–846. [Google Scholar] [CrossRef]
- Frieden, C. Protein-Protein Interaction and Enzymatic Activity. Annu. Rev. Biochem. 1971, 40, 653–696. [Google Scholar] [CrossRef]
- Vinayagam, A.; Zirin, J.; Roesel, C.; Hu, Y.; Yilmazel, B.; Samsonova, A.A.; Neumüller, R.A.; Mohr, S.E.; Perrimon, N. Integrating Protein-Protein Interaction Networks with Phenotypes Reveals Signs of Interactions. Nat. Methods 2014, 11, 94–99. [Google Scholar] [CrossRef]
- Lee, S.; Zhang, C.; Liu, Z.; Klevstig, M.; Mukhopadhyay, B.; Bergentall, M.; Cinar, R.; Ståhlman, M.; Sikanic, N.; Park, J.K.; et al. Network Analyses Identify Liver-Specific Targets for Treating Liver Diseases. Mol. Syst. Biol. 2017, 13, 938. [Google Scholar] [CrossRef]
- Goodey, N.M.; Benkovic, S.J. Allosteric Regulation and Catalysis Emerge via a Common Route. Nat. Chem. Biol. 2008, 4, 474–482. [Google Scholar] [CrossRef]
- Macpherson, J.A.; Anastasiou, D. Allosteric Regulation of Metabolism in Cancer: Endogenous Mechanisms and Considerations for Drug Design. Curr. Opin. Biotechnol. 2017, 48, 102–110. [Google Scholar] [CrossRef]
- Komiya, Y.; Habas, R. Wnt Signal Transduction Pathways. Organogenesis 2008, 4, 68–75. [Google Scholar] [CrossRef]
- MacDonald, B.T.; Tamai, K.; He, X. Wnt/β-Catenin Signaling: Components, Mechanisms, and Diseases. Dev. Cell 2009, 17, 9–26. [Google Scholar] [CrossRef] [PubMed]
- Logan, C.Y.; Nusse, R. The Wnt Signaling Pathway in Development and Disease. Annu. Rev. Cell Dev. Biol. 2004, 20, 781–810. [Google Scholar] [CrossRef] [PubMed]
- Habas, R.; Dawid, I.B. Dishevelled and Wnt Signaling: Is the Nucleus the Final Frontier? J. Biol. 2005, 4, 2. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Swameye, I.; Müller, T.G.; Timmer, J.; Sandra, O.; Klingmüller, U. Identification of Nucleocytoplasmic Cycling as a Remote Sensor in Cellular Signaling by Databased Modeling. Proc. Natl. Acad. Sci. USA 2003, 100, 1028–1033. [Google Scholar] [CrossRef] [PubMed]
- Samaga, R.; Klamt, S. Modeling Approaches for Qualitative and Semi-Quantitative Analysis of Cellular Signaling Networks. Cell Commun. Signal. 2013, 11, 43. [Google Scholar] [CrossRef]
- Rajagopal, S.; Shenoy, S.K. GPCR Desensitization: Acute and Prolonged Phases. Cell. Signal. 2018, 41, 9–16. [Google Scholar] [CrossRef] [PubMed]
- Kumar, A.; Christofides, P.D.; Daoutidis, P. Singular Perturbation Modeling of Nonlinear Processes with Nonexplicit Time-Scale Multiplicity. Chem. Eng. Sci. 1998, 53, 1491–1504. [Google Scholar] [CrossRef]
- Gerdtzen, Z.P.; Daoutidis, P.; Hu, W.S. Non-Linear Reduction for Kinetic Models of Metabolic Reaction Networks. Metab. Eng. 2004, 6, 140–154. [Google Scholar] [CrossRef]
- Wilkins, O.; Hafemeister, C.; Plessis, A.; Holloway-Phillips, M.-M.; Pham, G.M.; Nicotra, A.B.; Gregorio, G.B.; Jagadish, S.V.K.; Septiningsih, E.M.; Bonneau, R.; et al. EGRINs (Environmental Gene Regulatory Influence Networks) in Rice That Function in the Response to Water Deficit, High Temperature, and Agricultural Environments. Plant Cell 2016, 28, 2365–2384. [Google Scholar] [CrossRef] [PubMed]
- Huang, Z.; Zhu, L.; Cao, Y.; Wu, G.; Liu, X.; Chen, Y.; Wang, Q.; Shi, T.; Zhao, Y.; Wang, Y.; et al. ASD: A Comprehensive Database of Allosteric Proteins and Modulators. Nucleic Acids Res. 2011, 39, 663–669. [Google Scholar] [CrossRef] [PubMed]
- Senior, A.W.; Evans, R.; Jumper, J.; Kirkpatrick, J.; Sifre, L.; Green, T.; Qin, C.; Žídek, A.; Nelson, A.W.R.; Bridgland, A.; et al. Improved Protein Structure Prediction Using Potentials from Deep Learning. Nature 2020, 577, 706–710. [Google Scholar] [CrossRef]
- Chandrasekaran, S.; Price, N.D. Metabolic Constraint-Based Refinement of Transcriptional Regulatory Networks. PLoS Comput. Biol. 2013, 9, e1003370. [Google Scholar] [CrossRef] [PubMed]
- Sánchez, B.J.; Zhang, C.; Nilsson, A.; Lahtvee, P.; Kerkhoven, E.J.; Nielsen, J. Improving the Phenotype Predictions of a Yeast Genome-Scale Metabolic Model by Incorporating Enzymatic Constraints. Mol. Syst. Biol. 2017, 13, 935. [Google Scholar] [CrossRef]
- Ryu, J.Y.; Kim, H.U.; Lee, S.Y. Deep Learning Enables High-Quality and High-Throughput Prediction of Enzyme Commission Numbers. Proc. Natl. Acad. Sci. USA 2019, 116, 13996–14001. [Google Scholar] [CrossRef] [PubMed]
- Chandrasekaran, S.; Danos, N.; George, U.Z.; Han, J.-P.; Quon, G.; Müller, R.; Tsang, Y.; Wolgemuth, C. The Axes of Life: A Roadmap for Understanding Dynamic Multiscale Systems. Integr. Comp. Biol. 2021. [Google Scholar] [CrossRef]
- Harcombe, W.R.; Riehl, W.J.; Dukovski, I.; Granger, B.R.; Betts, A.; Lang, A.H.; Bonilla, G.; Kar, A.; Leiby, N.; Mehta, P.; et al. Metabolic Resource Allocation in Individual Microbes Determines Ecosystem Interactions and Spatial Dynamics. Cell Rep. 2014, 7, 1104–1115. [Google Scholar] [CrossRef]
- Dukovski, I.; Bajić, D.; Chacón, J.M.; Quintin, M.; Vila, J.C.; Sulheim, S.; Pacheco, A.R.; Bernstein, D.B.; Rieh, W.J.; Korolev, K.S.; et al. Computation of Microbial Ecosystems in Time and Space (COMETS): An Open Source Collaborative Platform for Modeling Ecosystems Metabolism. arXiv 2020, arXiv:2009.01734. Available online: https://arxiv.org/abs/2009.01734 (accessed on 26 August 2021).
- Cole, J.A.; Kohler, L.; Hedhli, J.; Luthey-Schulten, Z. Spatially-Resolved Metabolic Cooperativity within Dense Bacterial Colonies. BMC Syst. Biol. 2015, 9, 15. [Google Scholar] [CrossRef] [PubMed]
- Mahadevan, R.; Edwards, J.S.; Doyle, F.J. Dynamic Flux Balance Analysis of Diauxic Growth in Escherichia coli. Biophys. J. 2002, 83, 1331–1340. [Google Scholar] [CrossRef]
- Garcia-Albornoz, M.A.; Nielsen, J. Application of Genome-Scale Metabolic Models in Metabolic Engineering. Ind. Biotechnol. 2013, 9, 203–214. [Google Scholar] [CrossRef]
- Suthers, P.F.; Maranas, C.D. Challenges of Cultivated Meat Production and Applications of Genome-Scale Metabolic Modeling. AIChE J. 2020, 66, e16235. [Google Scholar] [CrossRef]
- Karr, J.R.; Sanghvi, J.C.; MacKlin, D.N.; Gutschow, M.V.; Jacobs, J.M.; Bolival, B.; Assad-Garcia, N.; Glass, J.I.; Covert, M.W. A Whole-Cell Computational Model Predicts Phenotype from Genotype. Cell 2012, 150, 389–401. [Google Scholar] [CrossRef]
- DuShane, J.K.; Mayberry, C.L.; Wilczek, M.P.; Nichols, S.L.; Maginnis, M.S. JCPyV-Induced MAPK Signaling Activates Transcription Factors during Infection. Int. J. Mol. Sci. 2019, 20, 4779. [Google Scholar] [CrossRef]
- Beckett, D. Regulating Transcription Regulators via Allostery and Flexibility. Proc. Natl. Acad. Sci. USA 2009, 106, 22035–22036. [Google Scholar] [CrossRef]
- Liao, S.-Y.; Kuo, I.-Y.; Chen, Y.-T.; Liao, P.-C.; Liu, Y.-F.; Wu, H.-Y.; Lai, W.-W.; Wang, Y.-C. AKT-Mediated Phosphorylation Enhances Protein Stability and Transcription Activity of ZNF322A to Promote Lung Cancer Progression. Oncogene 2019, 38, 6723–6736. [Google Scholar] [CrossRef]
- Dunphy, L.J.; Papin, J.A. Biomedical Applications of Genome-Scale Metabolic Network Reconstructions of Human Pathogens. Curr. Opin. Biotechnol. 2018, 51, 70–79. [Google Scholar] [CrossRef] [PubMed]
- Sen, P.; Orešič, M. Metabolic Modeling of Human Gut Microbiota on a Genome Scale: An Overview. Metabolites 2019, 9, 22. [Google Scholar] [CrossRef] [PubMed]
- Chowdhury, S.; Fong, S.S. Leveraging Genome-Scale Metabolic Models for Human Health Applications. Curr. Opin. Biotechnol. 2020, 66, 267–276. [Google Scholar] [CrossRef] [PubMed]
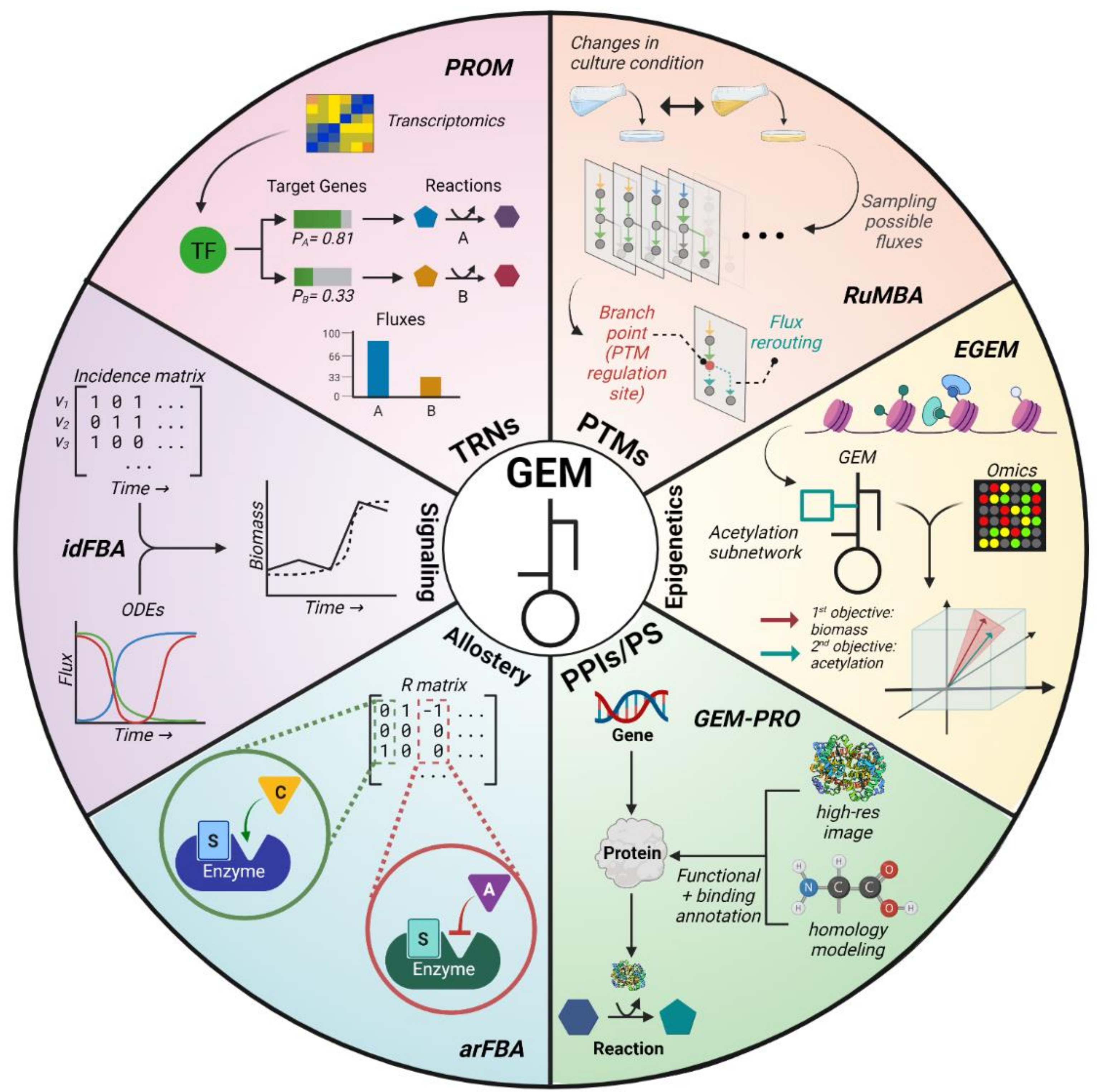
| Method | Regulation | TRN Type | Year | Organism | Language | Summary | Ref. |
|---|---|---|---|---|---|---|---|
| rFBA | TRN | Boolean | 2002 | E. coli | MATLAB | Uses Boolean TRN to predict fluxes | [24] |
| SR-FBA | TRN | Boolean | 2007 | E. coli | MATLAB | Uses Boolean TRN to better characterize steady-state fluxes | [25] |
| Lee et al. | TRN | Discrete | 2007 | E. coli | LINGO + LabView | Integrates TRN with eight weight parameters to predict fluxes | [26] |
| iFBA | TRN/Signaling | Boolean | 2008 | E. coli | MATLAB | Uses Boolean TRN with kinetic parameters and ODEs to better predict fluxes | [27] |
| PROM | TRN | Continuous | 2010 | E. coli, M. tuberculosis | MATLAB | Uses transcriptomics and TF–target relationships to integrate a continuous TRN | [28] |
| TIGER | TRN | Boolean | 2011 | S. cerevisiae | MATLAB | Integrates TRN + GEM + transcriptomics | [29] |
| FlexFlux | TRN | Boolean/ Continuous | 2015 | E. coli | Java | Integrates TRN + GEMs in SBML format | [30] |
| PROM 2.0 | TRN | Continuous | 2015 | M. tuberculosis | MATLAB | Uses transcriptomics and TF–target relationships to integrate an expanded continuous TRN | [31] |
| CoRegFlux | TRN | Continuous | 2017 | S. cerevisiae | R | Predicts fluxes with reverse-engineered TRN | [32] |
| IDREAM | TRN | Continuous | 2017 | S. cerevisiae | MATLAB | Predicts fluxes with continuous reverse-engineered TRN | [33] |
| TRFBA | TRN | Continuous | 2017 | E. coli, S. cerevisiae | MATLAB | Uses transcriptomics and TF–target relationships to more intuitively integrate a continuous TRN | [34] |
| OptRAM | TRN | Continuous | 2019 | S. cerevisiae | MATLAB | Strain design algorithm that uses IDREAM | [35] |
| RuMBA | PTMs | N/A | 2018 | E. coli | MATLAB | Identifies branch-point reactions regulated by PTMs via flux sampling | [36] |
| CAROM | PTMs | N/A | 2019 | E. coli, S. cerevisiae | MATLAB | Integrative analysis of multi-omics data to predict PTM regulation | [37] |
| Chandrasekaran et al. | Epigenetics | N/A | 2017 | Stem cell | MATLAB | Uses time-course metabolomics data to infer fluxes, such as those involved in methylation | [38] |
| EGEM | Epigenetics | N/A | 2019 | Cancer cell | MATLAB | Simulation of multi-objective model with an acetylation subnetwork | [39] |
| Chang et al. | PPIs/PS | N/A | 2013 | E. coli | MATLAB | Integrated protein binding and structure information into the E. coli GEM | [40] |
| GEM-PRO | PPIs/PS | N/A | 2016 | E. coli, T. maritima | Python | Describes general process of integrating protein information into GEMs | [41] |
| Lee et al. | PPIs/PS | N/A | 2016 | Liver cells | MATLAB | Integrated TRNs and PPIs to construct cell-specific networks to study liver metabolism | [42] |
| arFBA | Allostery | N/A | 2015 | E. coli | Python | Integrates allosteric interactions into GEMs | [43] |
| SIMMER | Allostery | N/A | 2016 | S. cerevisiae | R | Accounted for allosteric regulation but mostly relied on ODE modeling | [44] |
| idFBA | Signaling | N/A | 2008 | S. cerevisiae | MATLAB | Incorporates ODEs and an incidence matrix to model dynamics | [45] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chung, C.H.; Lin, D.-W.; Eames, A.; Chandrasekaran, S. Next-Generation Genome-Scale Metabolic Modeling through Integration of Regulatory Mechanisms. Metabolites 2021, 11, 606. https://doi.org/10.3390/metabo11090606
Chung CH, Lin D-W, Eames A, Chandrasekaran S. Next-Generation Genome-Scale Metabolic Modeling through Integration of Regulatory Mechanisms. Metabolites. 2021; 11(9):606. https://doi.org/10.3390/metabo11090606
Chicago/Turabian StyleChung, Carolina H., Da-Wei Lin, Alec Eames, and Sriram Chandrasekaran. 2021. "Next-Generation Genome-Scale Metabolic Modeling through Integration of Regulatory Mechanisms" Metabolites 11, no. 9: 606. https://doi.org/10.3390/metabo11090606
APA StyleChung, C. H., Lin, D.-W., Eames, A., & Chandrasekaran, S. (2021). Next-Generation Genome-Scale Metabolic Modeling through Integration of Regulatory Mechanisms. Metabolites, 11(9), 606. https://doi.org/10.3390/metabo11090606






