Mathematical Models for FDG Kinetics in Cancer: A Review
Abstract
1. Introduction
- Image reconstruction inverse problem [6]: to reconstruct the spatio-temporal distribution of FDG inside the tissue by solving the integral equation that connects the FDG densito to the measured radiation by means of the Radon transform.
- Compartmental inverse problem [7]: to model the tracer kinetics by solving the non-linear time-dependent equation that connects the tracer coefficients to the reconstructed FDG concentration.
- Only one compartment is allowed to exchange tracer with the environment.
- The input function, i.e., the tracer concentration introduced into the tissue by the blood, is known by means of either experimental measurements or mathematical modeling.
- The overall tracer concentration associated to the organ of interest (typically, the tumor) is known as a function of time.
- Both the linearity of fluxes between compartments and vanishing initial conditions hold.
- The kinetic coefficients are constant and homogeneous in the tissue.
2. The Experimental Data in the Compartmental Game
2.1. Standardized Uptake Value
2.2. Input Function
2.3. Activity Concentration of Target Tissue
3. The Construction of Compartmental Models
3.1. Generalities
3.2. Basic Applicability Conditions
- Tracer is administered in trace amounts. The number of injected molecules is supposed to be sufficiently high so that diffusion may described by application of a continuous model. However, such a number is not so high as to influence physiological processes and molecular interactions. In particular, tracer does not affect glucose metabolism.
- During an experiment, physiologic conditions are in a steady state which is not affected by measurement devices of tracer concentration. This holds true, in particular, for glucose metabolism.
- The well-mixing condition holds for each compartment. In practice, this means that equilibrium is reached in a time interval, which is rather short with respect to the time of data acquisition. As a consequence, the spatial homogeneity condition follows, which implies that the tracer concentration in each compartment depends only on time.
- Transport of tracer molecules and related composites between compartments follows a first order kinetics, which ultimately leads to linear ODEs.
- Bound tracer in blood is disregarded, and the arterial concentration of tracer available for tissue uptake is regarded as a valuable approximation of capillary concentration.
3.3. Examples of Standard CMs
3.3.1. 1-Compartment Model
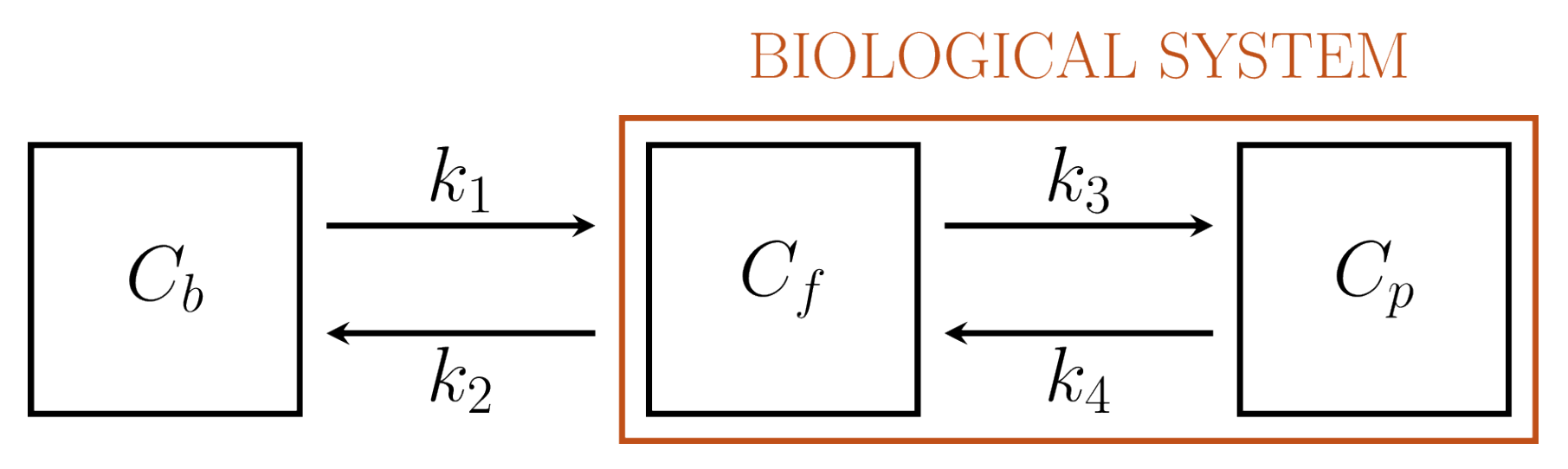
3.3.2. 2-Compartment Model
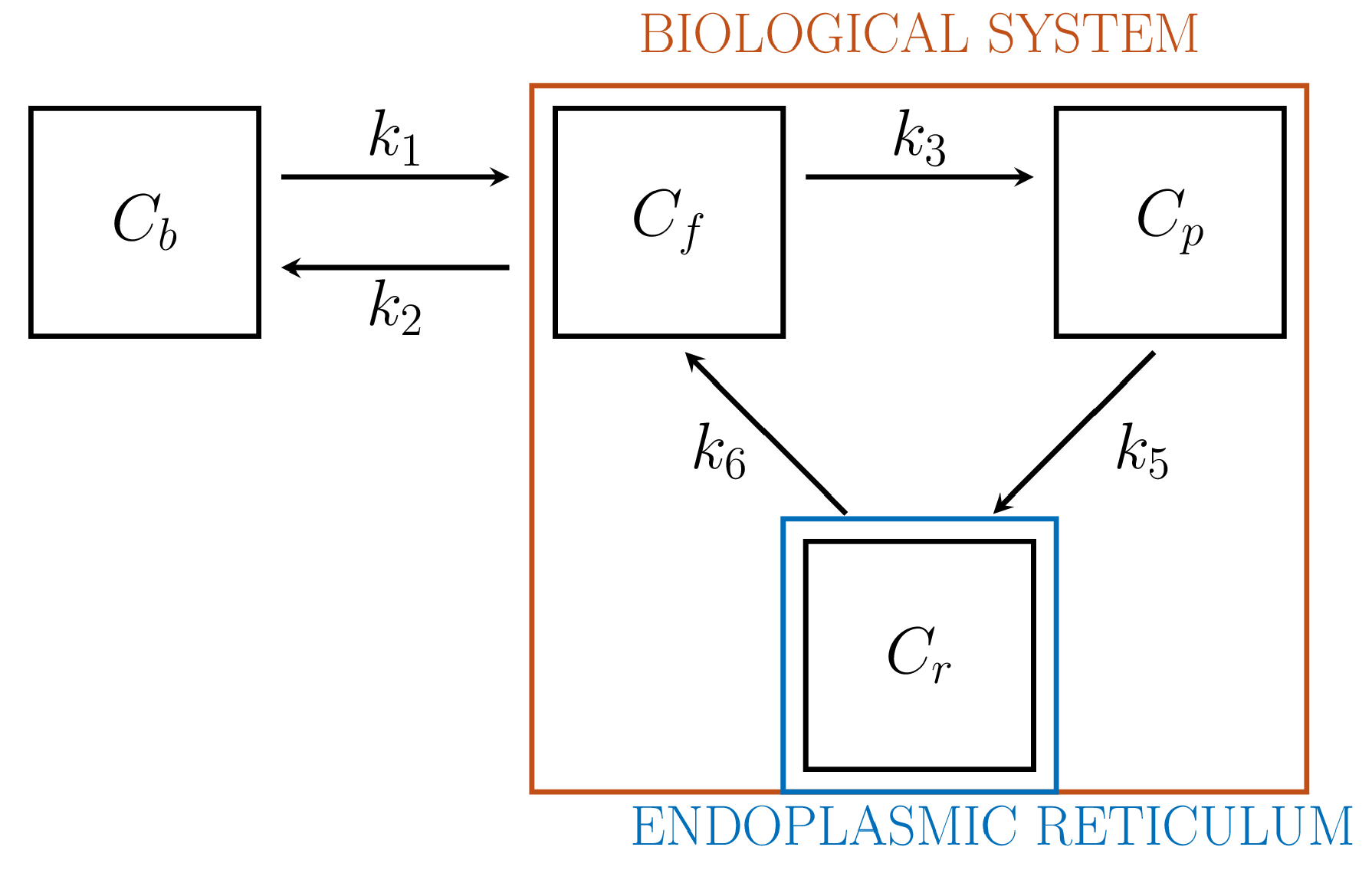
3.3.3. 3-Compartment Model
3.4. Compact Formulation and General Formal Solution of the Direct Problem
4. Patlak and Logan Graphical Approaches
4.1. PGA
- First step. The vector solution of the irreversible system of ODE (29) is substituted into the IPE (33), which is then divided by . The resulting equation takes the form(see the Appendix A) where [min] is a constant macroparameter [25], and depends on and the components of .
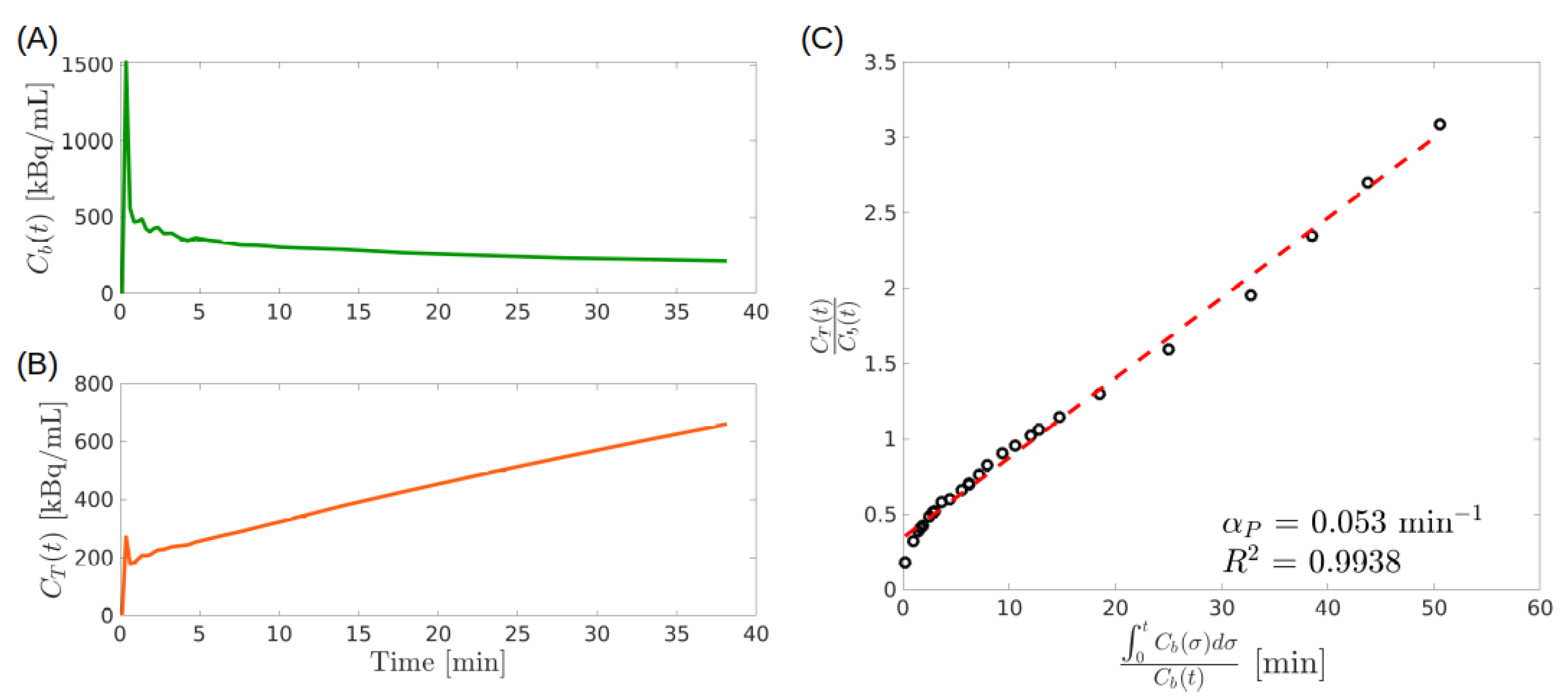
- Second step. In a number of relevant cases it may be shown that is asymptotically constant. Then, in the plane referred to Cartesian coordinates , define the functions and by. The points give the parametric representation of a curve which is known as the standard Patlak plot [38]. Comparison with Equation (34) and the condition on show that the curve is asymptotically linear. Thus the slope and the adimensional constant intercept are estimated in terms of the data by linear regression [38]. The procedure may be applied pixel-wise.
- Third step. The interpretation of is achieved by comparison with the stationary solution of the system of ODEs (29), corresponding to a constant IF. It is shown that measures the rate of tracer uptake by the tissue at stationary conditions.
4.1.1. PGA for 2-CM
4.1.2. PGA for 3-CM
4.2. LGA
- First step. Consider the integral in time of the IPE equation in the compact form (33):where is related to data through the ODE (29). Indeed, multiplication of (29) by yieldsFurther multiplication by , and integration with respect to time from 0 to t givesSubstitution into (46), followed by division by gives the necessary conditionwhere the dimensionless constant and the function [min are defined as
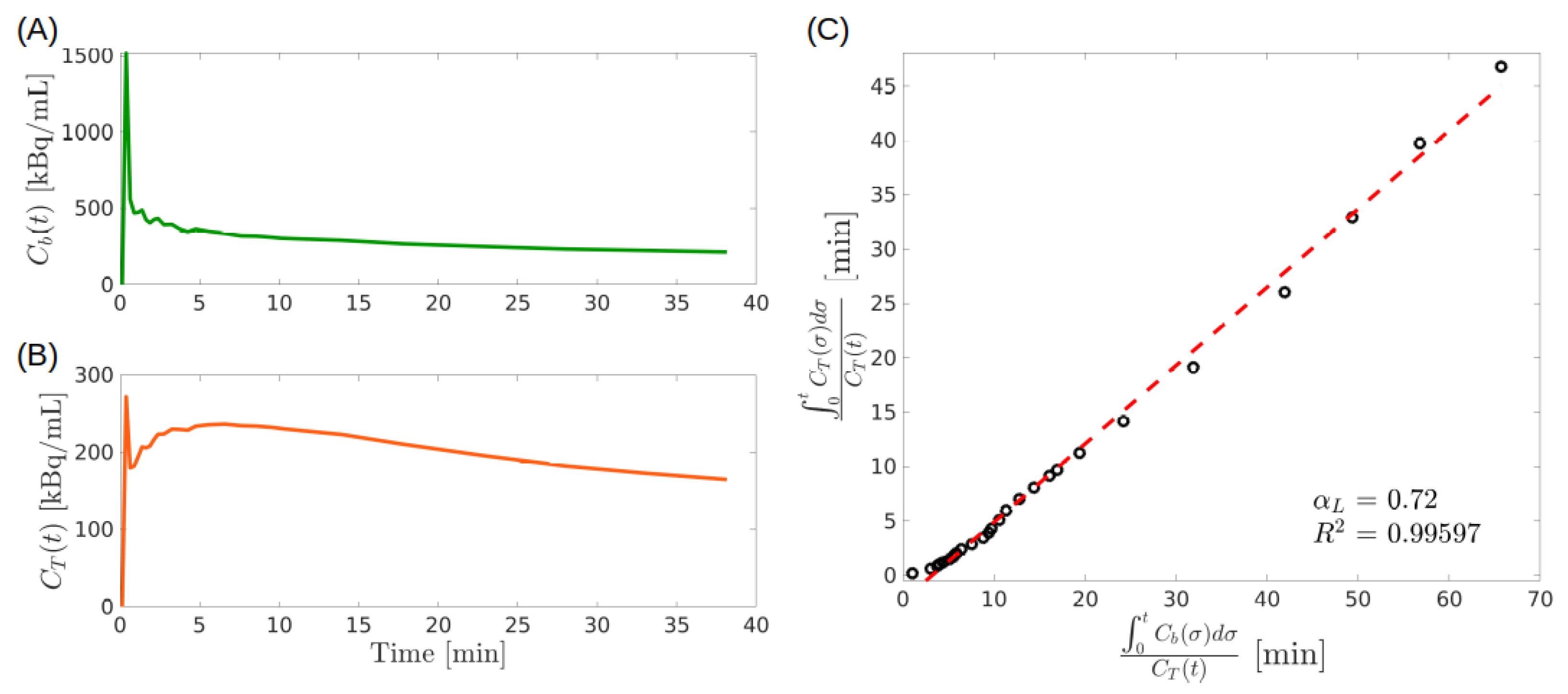
- Second step. Following the analogy with the GPA approach of Section 4.1, in a number of relevant cases it may be shown that is asymptotically constant. In such a case, consider the functions and defined by. In analogy with (34) the points of the Cartesian plane define a parametric representation of the standard Logan plot, which is an asymptotically linear curve. The adimensional slope and the intercept are macroparameters determined by the data, which are estimated by linear regression.
- Third step. The interpretation of follows from the equilibrium solution of the system (29) at constant IF . The equilibrium state is given byAccording to the IPE (33), the previous equation, and the definition of , it follows thatThus, the slope is the ratio between the constant equilibrium value of the total tissue concentration and the blood concentration.
4.2.1. LGA for 2-CM
4.2.2. LGA for 3-CM
5. Issues on the Solvability of the Inverse Problem
5.1. Identifiability of Linear CMs
5.2. Sensitivity Analysis
6. Physiology-Driven Compartmental Models
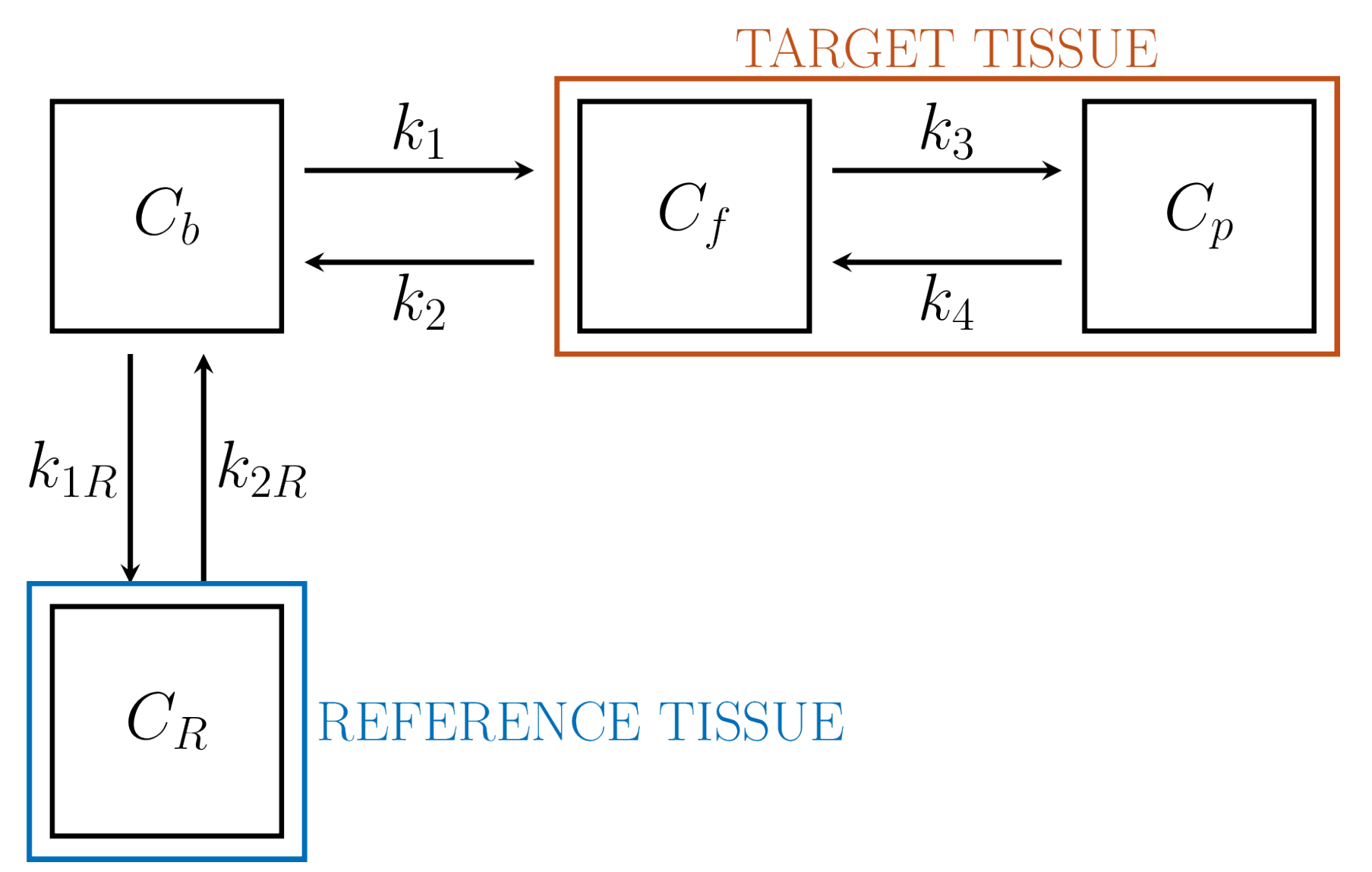
6.1. Reference Tissue Models
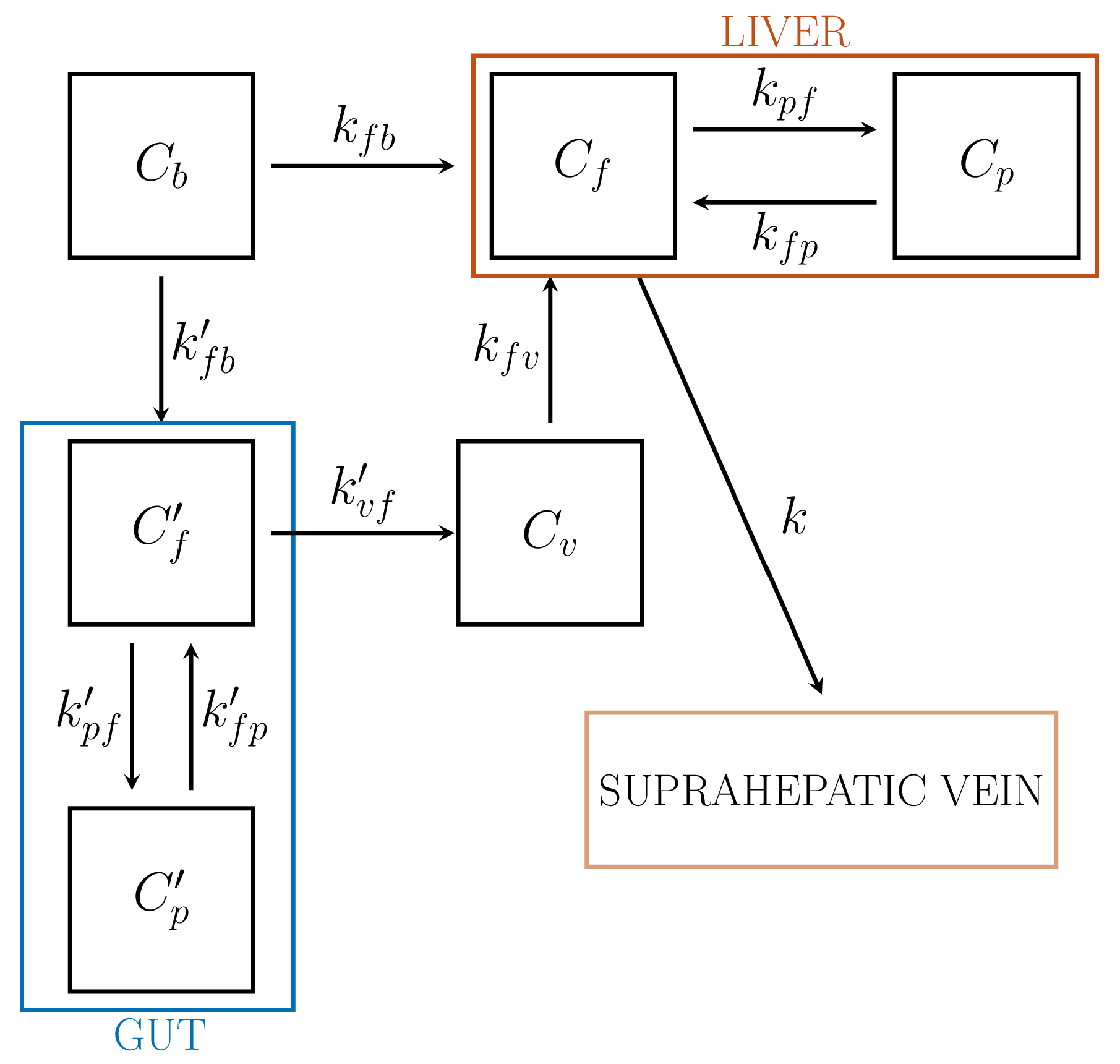
6.2. CMs for Liver
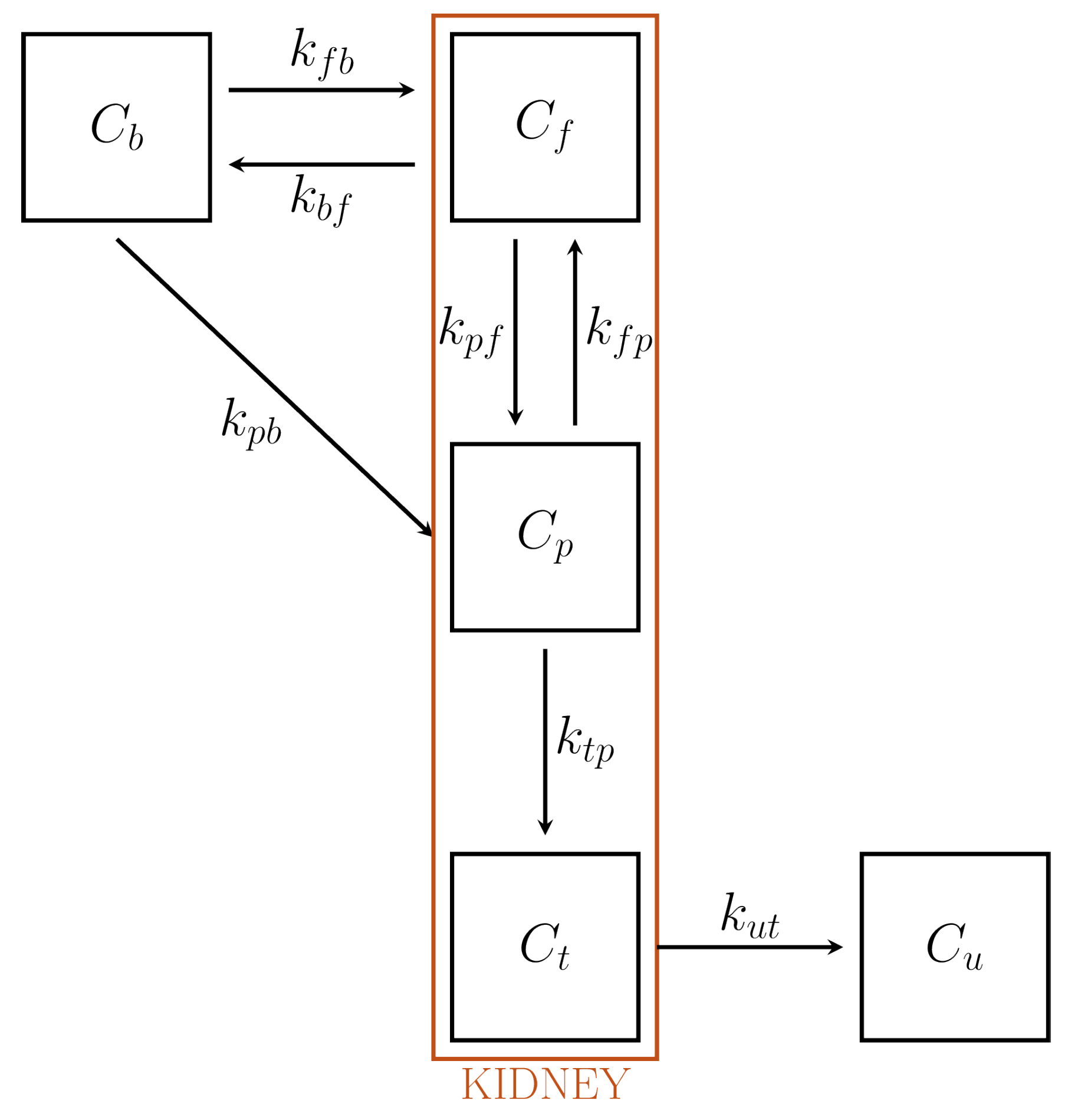
6.3. CMs for the Renal System
- An extravascular compartment accounting for tracer outside cells, whose exchange with blood is free.
- A compartment containing the phosphorylated FDG, the FDG in the cells, and the preurine pool. In particular, following the flow of liquid, tracer is filtered in the preurines and carried towards the proximal tubule. This compartment has been denoted as because tracer can also be in phosphorylated form.
- A tubular compartment , where tracer flows towards bladder. Here, the concentration varies (increases) because of the re-absorption of liquids through the tubular walls.
- The urinary pool , anatomically identified with the bladder, where the tracer carried by the urine is accumulated. Notice the bladder volume varies with time.
6.4. The Role of the Endoplasmic Reticulum
6.5. Comparison among Different Models
7. Some Numerics: Optimization Schemes
- They typically suffer numerical instabilities related to the non-uniqueness and sensitivity limitations discussed in Section 5.
- Since the operator is clearly non linear and, further, the space where possible minimizers can be searched for is typically big, they may suffer local minima.
- Particularly, in the case of three-compartment models, the number of kinetic parameters to determine is high, which implies that they are computationally demanding.
7.1. Deterministic Approaches
7.2. Statistical Approaches
7.3. Biology-Inspired Approaches
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Shaw, R.J. Glucose metabolism and cancer. Curr. Opin. Cell Biol. 2006, 18, 598–608. [Google Scholar] [CrossRef]
- Liberti, M.V.; Locasale, J.W. The Warburg effect: How does it benefit cancer cells? Trends Biochem. Sci. 2016, 41, 211–218. [Google Scholar] [CrossRef]
- Warburg, O. The metabolism of carcinoma cells. J. Cancer Res. 1925, 9, 148–163. [Google Scholar] [CrossRef]
- Pacák, J.; Točík, Z.; Černỳ, M. Synthesis of 2-deoxy-2-fluoro-D-glucose. J. Chem. Soc. D 1969, 2, 77. [Google Scholar] [CrossRef]
- Reske, S.N.; Kotzerke, J. FDG-PET for clinical use. Eur. J. Nucl. Med. 2001, 28, 1707–1723. [Google Scholar] [CrossRef] [PubMed]
- Ollinger, J.M.; Fessler, J.A. Positron-emission tomography. IEEE Sign. Proc. Mag. 1997, 14, 43–55. [Google Scholar] [CrossRef]
- Watabe, H.; Ikoma, Y.; Kimura, Y.; Naganawa, M.; Shidahara, M. PET kinetic analysis–compartmental model. Ann. Nucl. Med. 2006, 20, 583–588. [Google Scholar] [CrossRef] [PubMed]
- Vander Heiden, M.G.; Cantley, L.C.; Thompson, C.B. Understanding the Warburg effect: The metabolic requirements of cell proliferation. Science 2009, 324, 1029–1033. [Google Scholar] [CrossRef] [PubMed]
- Cherry, S.R.; Sorenson, J.A.; Phelps, M.E. Physics in Nuclear Medicine; Elsevier Health Sciences: Amsterdam, The Netherlands, 2012. [Google Scholar]
- Muzi, M.; Freeman, S.D.; Burrows, R.C.; Wiseman, R.W.; Link, J.M.; Krohn, K.A.; Graham, M.M.; Spence, A.M. Kinetic characterization of hexokinase isoenzymes from glioma cells: Implications for FDG imaging of human brain tumors. Nucl. Med. Biol. 2001, 28, 107–116. [Google Scholar] [CrossRef]
- Maddalena, F.; Lettini, G.; Gallicchio, R.; Sisinni, L.; Simeon, V.; Nardelli, A.; Venetucci, A.A.; Storto, G.; Landriscina, M. Evaluation of glucose uptake in normal and cancer cell lines by positron emission tomography. Mol. Imag. 2015, 14, 490–498. [Google Scholar] [CrossRef]
- Williams, S.P.; Flores-Mercado, J.E.; Port, R.E.; Bengtsson, T. Quantitation of glucose uptake in tumors by dynamic FDG-PET has less glucose bias and lower variability when adjusted for partial saturation of glucose transport. Eur. J. Nucl. Med. Mol. Imag. Res. 2012, 2, 1–13. [Google Scholar] [CrossRef]
- Scussolini, M.; Bauckneht, M.; Cossu, V.; Bruno, S.; Orengo, A.M.; Piccioli, P.; Capitanio, S.; Yosifov, N.; Ravera, S.; Morbelli, S.; et al. G6Pase location in the endoplasmic reticulum: Implications on compartmental analysis of FDG uptake in cancer cells. Sci. Rep. 2019, 9, 1–14. [Google Scholar] [CrossRef]
- Garbarino, S.; Caviglia, G.; Sambuceti, G.; Benvenuto, F.; Piana, M. A novel description of FDG excretion in the renal system: Application to metformin-treated models. Phys. Med. Biol. 2014, 59, 2469. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Signorini, M.; Paulesu, E.; Friston, K.; Perani, D.; Colleluori, A.; Lucignani, G.; Grassi, F.; Bettinardi, V.; Frackowiak, R.; Fazio, F. Rapid assessment of regional cerebral metabolic abnormalities in single subjects with quantitative and nonquantitative [18F]FDG PET: A clinical validation of statistical parametric mapping. Neuroimage 1999, 9, 63–80. [Google Scholar] [CrossRef]
- Garbarino, S.; Vivaldi, V.; Delbary, F.; Caviglia, G.; Piana, M.; Marini, C.; Capitanio, S.; Calamia, I.; Buschiazzo, A.; Sambuceti, G. A new compartmental method for the analysis of liver FDG kinetics in small animal models. EJNMMI Res. 2015, 5, 35. [Google Scholar] [CrossRef]
- Büsing, K.A.; Schönberg, S.O.; Brade, J.; Wasser, K. Impact of blood glucose, diabetes, insulin, and obesity on standardized uptake values in tumors and healthy organs on 18F-FDG PET/CT. Nucl. Med. Biol. 2013, 40, 206–213. [Google Scholar] [CrossRef] [PubMed]
- Adams, M.C.; Turkington, T.G.; Wilson, J.M.; Wong, T.Z. A systematic review of the factors affecting accuracy of SUV measurements. AJR Am. J. Roentgenol. 2010, 195, 310–320. [Google Scholar] [CrossRef]
- Schmidt, K.C.; Turkheimer, F.E. Kinetic modeling in positron emission tomography. Quart J. Nucl. Med. 2002, 46, 70–85. [Google Scholar]
- Schain, M.; Fazio, P.; Mrzljak, L.; Amini, N.; Al-Tawil, N.; Fitzer-Attas, C.; Bronzova, J.; Landwehrmeyer, B.; Sampaio, C.; Halldin, C.; et al. Revisiting the Logan plot to account for non-negligible blood volume in brain tissue. Eur. J. Nucl. Med. Mol. Imag. Res. 2017, 7, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Zanotti-Fregonara, P.; Chen, K.; Liow, J.S.; Fujita, M.; Innis, R.B. Image-derived input function for brain PET studies: Many challenges and few opportunities. J. Cer. Blood Flow Metab. 2011, 31, 1986–1998. [Google Scholar] [CrossRef] [PubMed]
- Vriens, D.; de Geus-Oei, L.F.; Oyen, W.J.; Visser, E.P. A curve-fitting approach to estimate the arterial plasma input function for the assessment of glucose metabolic rate and response to treatment. J. Nucl. Med. 2009, 50, 1933–1939. [Google Scholar] [CrossRef]
- Wernick, M.N.; Aarsvold, J.N. Emission Tomography: The Fundamentals of PET and SPECT; Elsevier: Amsterdam, The Netherlands, 2004. [Google Scholar]
- Lawson, R.S. Application of mathematical methods in dynamic nuclear medicine studies. Phys. Med. Biol. 1999, 44, R57–R98. [Google Scholar] [CrossRef] [PubMed]
- Gunn, R.N.; Gunn, S.R.; Cunningham, V.J. Positron emission tomography compartmental models. J. Cer. Blood Flow Metab. 2001, 21, 635–652. [Google Scholar] [CrossRef] [PubMed]
- Piana, M.; Caviglia, G.; Sommariva, S. Mathematical modelling of nuclear medicine data. In Proceedings of the 2020 IEEE 20th Mediterranean Electrotechnical Conference (MELECON), Palermo, Italy, 16–18 June 2020; pp. 415–418. [Google Scholar] [CrossRef]
- Bertoldo, A.; Rizzo, G.; Veronese, M. Deriving physiological information from PET images: From SUV to compartmental modelling. Clin. Transl. Imaging 2014, 2, 239–251. [Google Scholar] [CrossRef]
- Munk, O.L.; Keiding, S.; Baker, C.; Bass, L. A microvascular compartment model validated using 11C-methylglucose liver PET in pigs. Phys. Med. Biol. 2017, 63, 015032. [Google Scholar] [CrossRef]
- Sokoloff, L.; Reivich, M.; Kennedy, C.; Rosiers, M.D.; Patlak, C.; Pettigrew, K.E.A.; Sakurada, O.; Shinohara, M. The [14C]deoxyglucose method for the measurement of local cerebral glucose utilization: Theory, procedure, and normal values in the conscious and anesthetized albino rat. J. Neurochem. 1977, 28, 897–916. [Google Scholar] [CrossRef]
- Ghosh, A.; Shieh, J.J.; Pan, C.J.; Sun, M.S.; Chou, J.Y. The catalytic center of glucose-6-phosphatase. HIS176 is the nucleophile forming the phosphohistidine-enzyme intermediate during catalysis. J. Biol. Chem. 2002, 277, 32837–32842. [Google Scholar] [CrossRef]
- Marini, C.; Ravera, S.; Buschiazzo, A.; Bianchi, G.; Orengo, A.M.; Bruno, S.; Bottoni, G.; Emionite, L.; Pastorino, F.; Monteverde, E.; et al. Discovery of a novel glucose metabolism in cancer: The role of endoplasmic reticulum beyond glycolysis and pentose phosphate shunt. Sci. Rep. 2016, 6, 1–13. [Google Scholar]
- Csala, M.; Marcolongo, P.; Lizák, B.; Senesi, S.; Margittai, É.; Fulceri, R.; Magyar, J.É.; Benedetti, A.; Bánhegyi, G. Transport and transporters in the endoplasmic reticulum. Biochim. Biophys. Acta Biomembr. 2007, 1768, 1325–1341. [Google Scholar] [CrossRef] [PubMed]
- Sommariva, S.; Scussolini, M.; Cossu, V.; Marini, C.; Sambuceti, G.; Caviglia, G.; Piana, M. The role of endoplasmic reticulum in in vivo cancer FDG kinetics. PLoS ONE 2021, 16, e0252422. [Google Scholar] [CrossRef]
- Hearon, J.Z. Theorems on linear systems. Ann. N. Y. Acad. Sci. 1963, 108, 36–68. [Google Scholar] [CrossRef] [PubMed]
- Schmidt, K. Which linear compartmental systems can be analyzed by spectral analysis of PET output data summed over all compartments? J. Cereb. Blood Flow Metab. 1999, 19, 560–569. [Google Scholar] [CrossRef] [PubMed]
- Patlak, C.S.; Blasberg, R.G.; Fenstermacher, J.D. Graphical evaluation of blood-to-brain transfer constants from multiple-time uptake data. J. Cereb. Blood Flow Metab. 1983, 3, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Logan, J.; Fowler, J.S.; Volkow, N.D.; Wolf, A.P.; Dewey, S.L.; Schlyer, D.J.; MacGregor, R.R.; Hitzemann, R.; Bendriem, B.; Gatley, S.J.; et al. Graphical analysis of reversible radioligand binding from time–activity measurements applied to [N-11C-methyl]-(–)-cocaine PET studies in human subjects. J. Cereb. Blood Flow Metab. 1990, 10, 740–747. [Google Scholar] [CrossRef]
- Zuo, Y.; Qi, J.; Wang, G. Relative Patlak plot for dynamic PET parametric imaging without the need for early-time input function. Phys. Med. Biol. 2018, 63, 165004. [Google Scholar] [CrossRef]
- Kimura, Y.; Naganawa, M.; Shidahara, M.; Ikoma, Y.; Watabe, H. PET kinetic analysis—Pitfalls and a solution for the Logan plot. Ann. Nucl. Med. 2007, 21, 1–8. [Google Scholar] [CrossRef]
- Chis, O.T.; Banga, J.R.; Balsa-Canto, E. Structural identifiability of systems biology models: A critical comparison of methods. PLoS ONE 2011, 6, e27755. [Google Scholar] [CrossRef]
- Cobelli, C.; Foster, D.; Toffolo, G. Tracer Kinetics in Biomedical Research; Kluwer Academic Publishers: New York, NY, USA, 2002. [Google Scholar]
- Gonnet, P.; Dimopoulos, S.; Widmer, L.; Stelling, J. A specialized ODE integrator for the efficient computation of parameter sensitivities. BMC Syst. Biol. 2012, 6, 1–13. [Google Scholar] [CrossRef]
- Saltelli, A.; Ratto, M.; Tarantola, S.; Campolongo, F. Sensitivity analysis for chemical models. Chem. Rev. 2005, 105, 2811–2828. [Google Scholar] [CrossRef]
- Goulet, D. Modeling, simulating, and parameter fitting of biochemical kinetic experiments. SIAM Rev. 2016, 58, 331–353. [Google Scholar] [CrossRef][Green Version]
- Pianosi, F.; Sarrazin, F.; Wagener, T. A Matlab toolbox for global sensitivity analysis. Environ. Model. Softw. 2015, 70, 80–85. [Google Scholar] [CrossRef]
- Herman, J.; Usher, W. SALib: An open-source Python library for sensitivity analysis. J. Open Source Softw. 2017, 2, 97. [Google Scholar] [CrossRef]
- Juillet, B.; Bos, C.; Gaudichon, C.; Tomé, D.; Fouillet, H. Parameter Estimation for Linear Compartmental Models—A Sensitivity Analysis Approach. Ann. Biomed. Eng. 2009, 37, 1028–1042. [Google Scholar] [CrossRef] [PubMed]
- Scussolini, M.; Garbarino, S.; Piana, M.; Sambuceti, G.; Caviglia, G. Reference tissue models for FDG-PET data: Identifiability and solvability. IEEE Trans. Rad. Plasma Med. Sci. 2018, 2, 177–186. [Google Scholar] [CrossRef]
- Garbarino, S.; Caviglia, G.; Brignone, M.; Massollo, M.; Sambuceti, G.; Piana, M. Estimate of FDG excretion by means of compartmental analysis and ant colony optimization of nuclear medicine data. Comput. Math. Methods Med. 2013, 2013, 793142. [Google Scholar] [CrossRef] [PubMed]
- Gunn, R.N.; Gunn, S.R.; Turkheimer, F.E.; Aston, J.A.; Cunningham, V.J. Positron emission tomography compartmental models: A basis pursuit strategy for kinetic modeling. J. Cer. Blood Flow. Metab. 2002, 22, 1425–1439. [Google Scholar] [CrossRef] [PubMed]
- Hong, Y.T.; Fryer, T.D. Kinetic modelling using basis functions derived from two-tissue compartmental models with a plasma input function: General principle and application to [18F] fluorodeoxyglucose positron emission tomography. Neuroimage 2010, 51, 164–172. [Google Scholar] [CrossRef] [PubMed]
- Kadrmas, D.J.; Oktay, M.B. Generalized separable parameter space techniques for fitting 1K-5K serial compartment models. Nucl. Med. Phys. 2013, 40, 072502. [Google Scholar] [CrossRef]
- Zhang, J.L.; Morey, A.M.; Kadrmas, D.J. Application of separable parameter space techniques to multi-tracer PET compartment modeling. Phys. Med. Biol. 2016, 61, 1238. [Google Scholar] [CrossRef]
- Scussolini, M.; Garbarino, S.; Sambuceti, G.; Caviglia, G.; Piana, M. A physiology-based parametric imaging method for FDG–PET data. Inverse Probl. 2017, 33, 125010. [Google Scholar] [CrossRef]
- Crisci, S.; Piana, M.; Ruggiero, V.; Scussolini, M. A Regularized Affine-Scaling Trust-Region Method for Parametric Imaging of Dynamic PET Data. SIAM J. Imaging Sci. 2021, 14, 418–439. [Google Scholar] [CrossRef]
- Cheng, X.; Li, Z.; Liu, Z.; Navab, N.; Huang, S.C.; Keller, U.; Ziegler, S.I.; Shi, K. Direct parametric image reconstruction in reduced parameter space for rapid multi-tracer PET imaging. IEEE Trans. Med. Imaging. 2015, 34, 1498–1512. [Google Scholar] [CrossRef] [PubMed]
- Szirmay-Kalos, L.; Kacsó, Á.; Magdics, M.; Tóth, B. Robust compartmental model fitting in direct emission tomography reconstruction. Visu. Comput. 2021, 1–14. [Google Scholar] [CrossRef]
- Kamasak, M.E.; Bouman, C.A.; Morris, E.D.; Sauer, K. Direct reconstruction of kinetic parameter images from dynamic PET data. IEEE Trans. Med. Imag. 2005, 24, 636–650. [Google Scholar] [CrossRef]
- Peng, J.Y.; Aston, J.A.; Gunn, R.N.; Liou, C.Y.; Ashburner, J. Dynamic positron emission tomography data-driven analysis using sparse Bayesian learning. IEEE Trans. Med. Imag. 2008, 27, 1356–1369. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Zhou, Y.; Aston, J.A.; Johansen, A.M. Bayesian model comparison for compartmental models with applications in positron emission tomography. J. Appl. Stat. 2013, 40, 993–1016. [Google Scholar] [CrossRef]
- Malave, P.; Sitek, A. Bayesian analysis of a one-compartment kinetic model used in medical imaging. J. Appl. Stat. 2015, 42, 98–113. [Google Scholar] [CrossRef]
- Zhu, W.; Ouyang, J.; Rakvongthai, Y.; Guehl, N.; Wooten, D.; El Fakhri, G.; Normandin, M.; Fan, Y. A Bayesian spatial temporal mixtures approach to kinetic parametric images in dynamic positron emission tomography. Med. Phys. 2016, 43, 1222–1234. [Google Scholar] [CrossRef]
- Castellaro, M.; Rizzo, G.; Tonietto, M.; Veronese, M.; Turkheimer, F.E.; Chappell, M.A.; Bertoldo, A. A Variational Bayesian inference method for parametric imaging of PET data. NeuroImage 2017, 150, 136–149. [Google Scholar] [CrossRef]
- Pan, L.; Cheng, C.; Haberkorn, U.; Dimitrakopoulou-Strauss, A. Machine learning-based kinetic modeling: A robust and reproducible solution for quantitative analysis of dynamic PET data. Phys. Med. Biol. 2017, 62, 3566. [Google Scholar] [CrossRef]
- Xu, J.; Liu, H. Deep-learning-based separation of a mixture of dual-tracer single-acquisition PET signals with equal half-Lives: A simulation study. IEEE Trans. Rad. Plasma Med. Sci. 2019, 3, 649–659. [Google Scholar] [CrossRef]
- Kuttner, S.; Wickstrøm, K.K.; Lubberink, M.; Tolf, A.; Burman, J.; Sundset, R.; Jenssen, R.; Appel, L.; Axelsson, J. Cerebral blood flow measurements with 15O-water PET using a non-invasive machine-learning-derived arterial input function. J. Cereb. Blood Flow Metab. 2021, 0271678X21991393. [Google Scholar] [CrossRef]
- Wang, G.; Qi, J. Direct estimation of kinetic parametric images for dynamic PET. Theranostics 2013, 3, 802. [Google Scholar] [CrossRef] [PubMed]
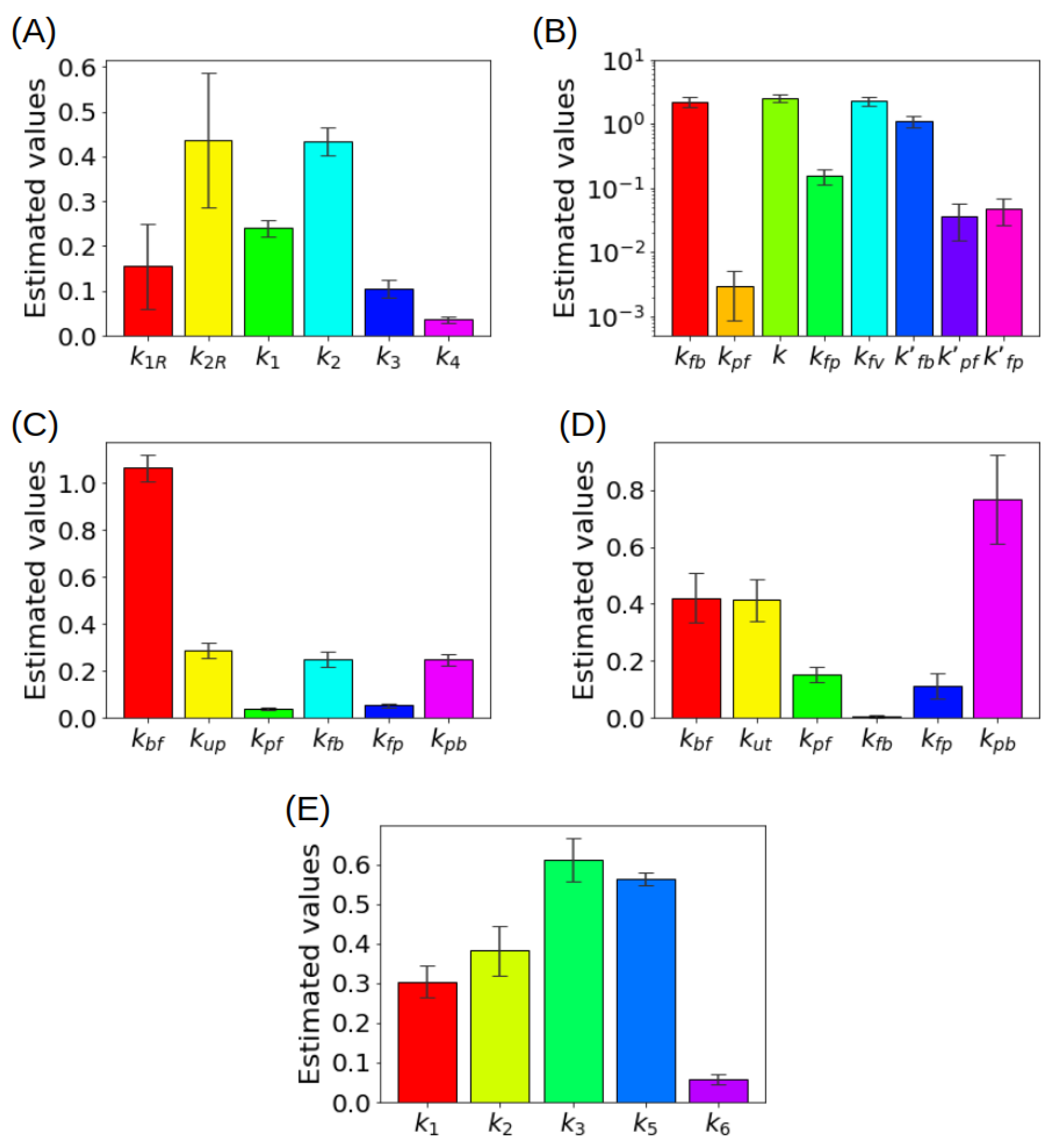
| Model | Scope | Compartments | Size of k | PGA | Identifiability |
|---|---|---|---|---|---|
| 2-CM | Basic standard model | , | 4 | ✓ | ✓ |
| 3-CM | Focus on endoplasmic reticulum | , , | 5 | ✓ | ✓ |
| RTM | Avoids use of IF | , , | 6 | ✕ | ✓ |
| Liver | Role of gut for the dual input (HA and PV) | , , , , | 8 | ✕ | ✕ |
| Kidney | Focus on tubules and bladder | , , , | 7 | ✕ | ✓ |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sommariva, S.; Caviglia, G.; Sambuceti, G.; Piana, M. Mathematical Models for FDG Kinetics in Cancer: A Review. Metabolites 2021, 11, 519. https://doi.org/10.3390/metabo11080519
Sommariva S, Caviglia G, Sambuceti G, Piana M. Mathematical Models for FDG Kinetics in Cancer: A Review. Metabolites. 2021; 11(8):519. https://doi.org/10.3390/metabo11080519
Chicago/Turabian StyleSommariva, Sara, Giacomo Caviglia, Gianmario Sambuceti, and Michele Piana. 2021. "Mathematical Models for FDG Kinetics in Cancer: A Review" Metabolites 11, no. 8: 519. https://doi.org/10.3390/metabo11080519
APA StyleSommariva, S., Caviglia, G., Sambuceti, G., & Piana, M. (2021). Mathematical Models for FDG Kinetics in Cancer: A Review. Metabolites, 11(8), 519. https://doi.org/10.3390/metabo11080519







