Diffuse Optical Spectroscopy Assessment of Resting Oxygen Metabolism in the Leg Musculature
Abstract
1. Introduction
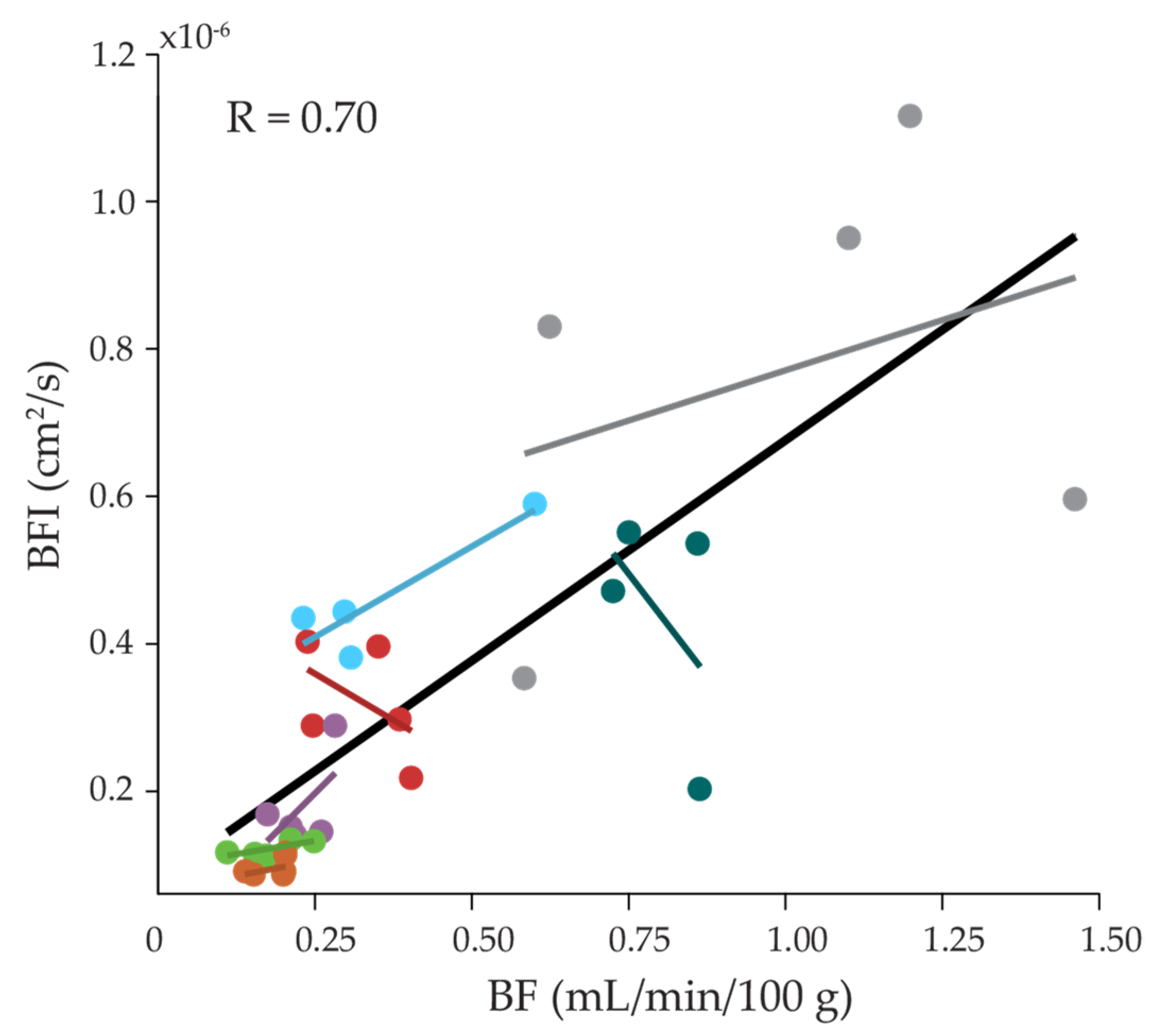
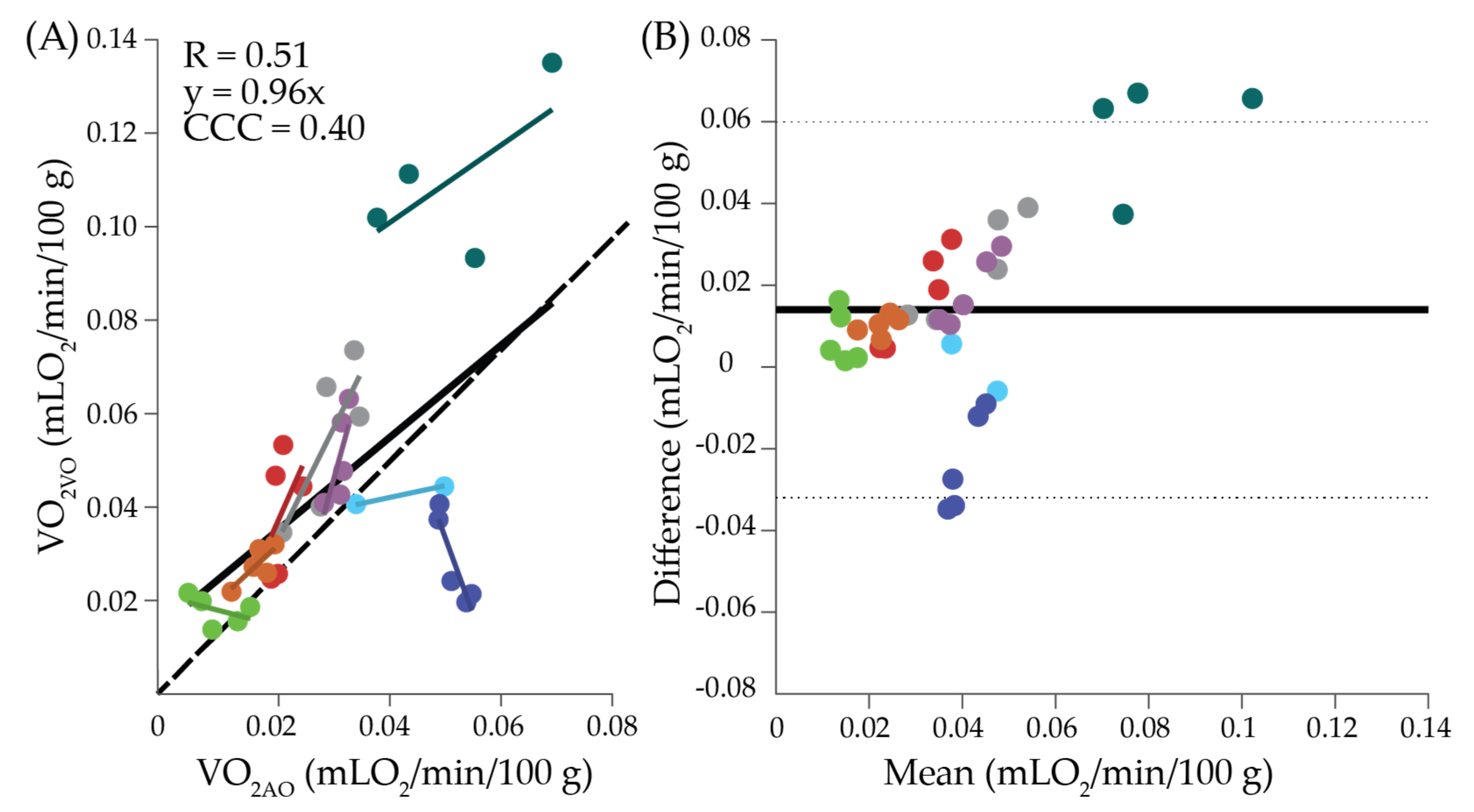
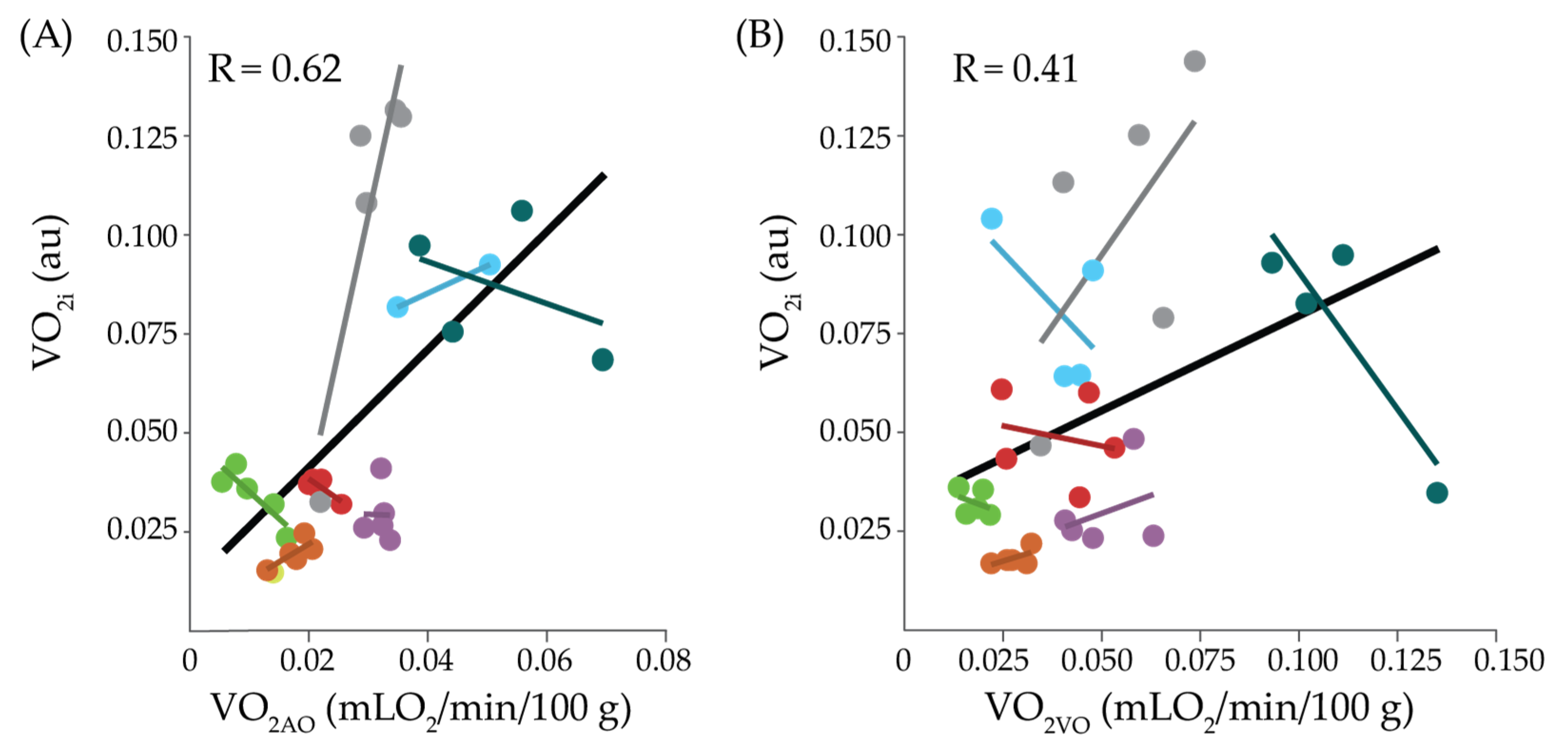
2. Results
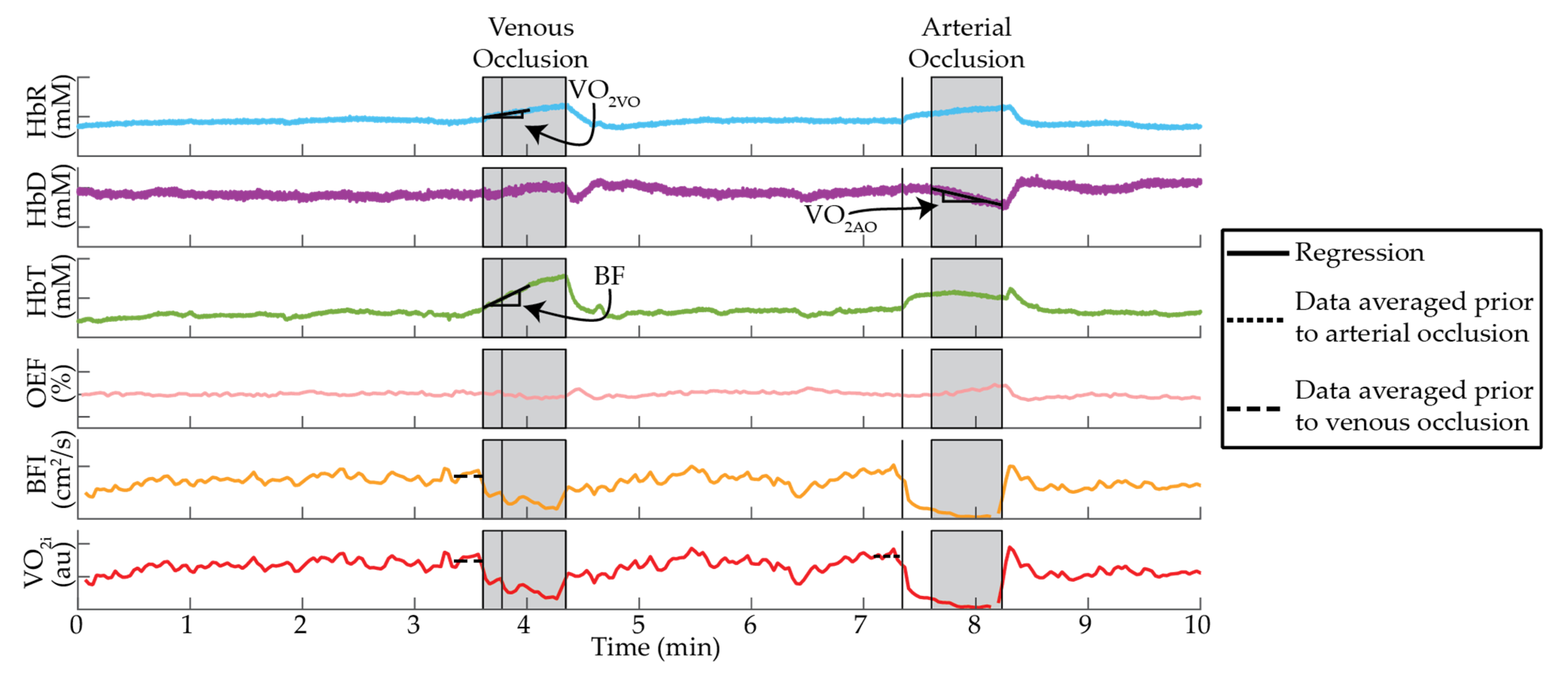
3. Discussion
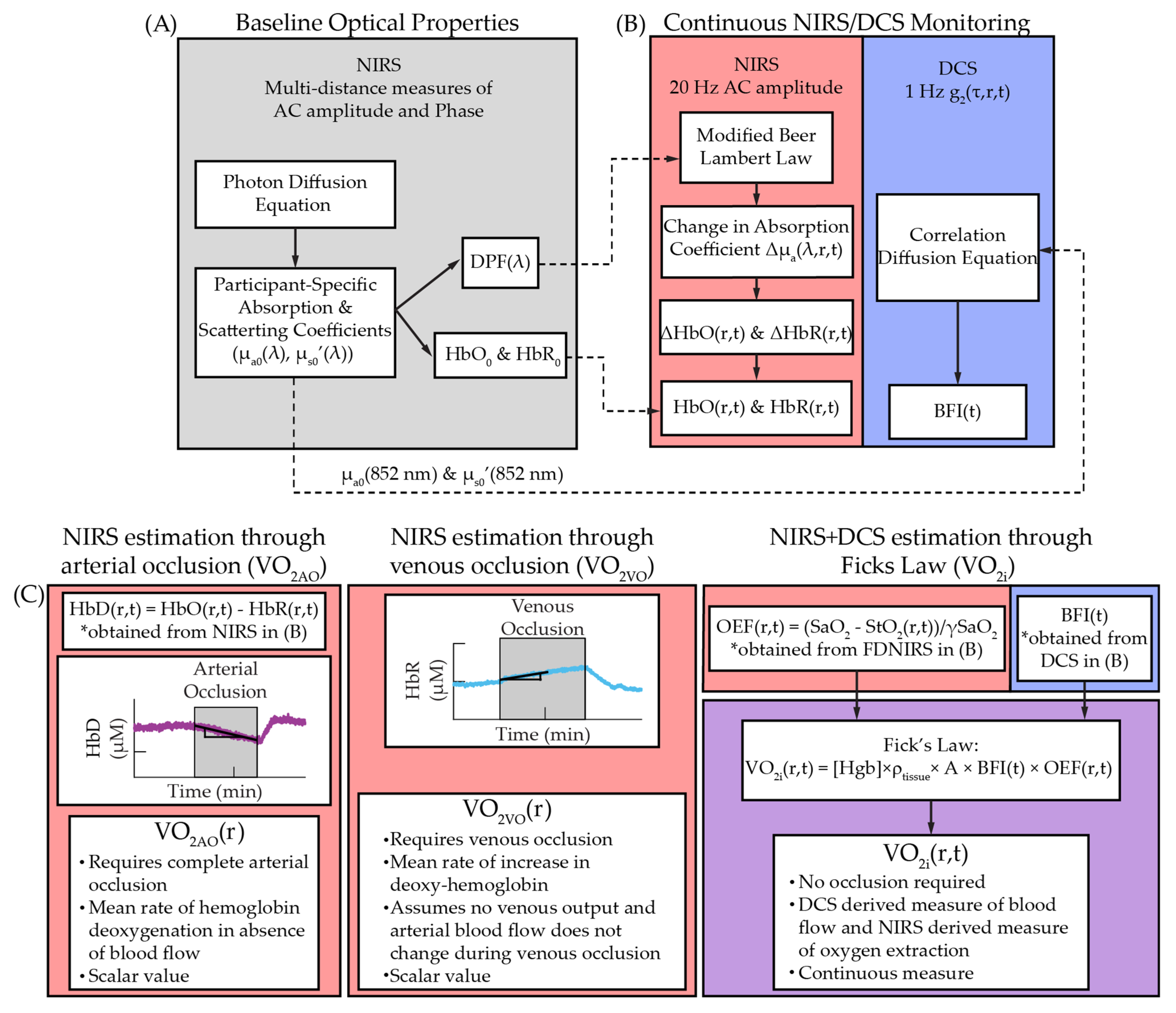
4. Materials and Methods
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dietz, V.; Quintern, J.; Berger, W. Electrophysiological studies of gait in spasticity and rigidityevidence that altered mechanical properties of muscle contribute to hypertonia. Brain 1981, 104, 431–449. [Google Scholar] [CrossRef] [PubMed]
- Dietz, V.; Sinkjaer, T. Spastic movement disorder: Impaired reflex function and altered muscle mechanics. Lancet Neurol. 2007, 6, 725–733. [Google Scholar] [CrossRef]
- Patrick, S.K.; Denington, A.A.; Gauthier, M.J.A.; Gillard, D.M.; Prochazka, A. Quantification of the UPDRS rigidity scale. IEEE Trans. Neural. Syst. Rehabil. Eng. 2001, 9, 31–41. [Google Scholar] [CrossRef]
- Prochazka, A.; Bennett, D.J.; Stephens, M.J.; Patrick, S.K.; Sears-Duru, R.; Roberts, T.; Jhamandas, J.H. Measurement of rigidity in Parkinson’s disease. Mov. Disord. 1997, 12, 24–32. [Google Scholar] [CrossRef] [PubMed]
- Powell, D.; Hanson, N.; Threlkeld, A.J.; Fang, X.; Xia, R. Enhancement of parkinsonian rigidity with contralateral hand activation. Clin. Neurophysiol. 2011, 122, 1595–1601. [Google Scholar] [CrossRef]
- Xia, R.; Powell, D.; Rymer, W.Z.; Hanson, N.; Fang, X.; Threlkeld, A.J. Differentiation between the contributions of shortening reaction and stretch-induced inhibition to rigidity in Parkinson’s disease. Exp. Brain Res. 2011, 209, 609–618. [Google Scholar] [CrossRef]
- Xu, F.; Ge, Y.; Lu, H. Noninvasive quantification of whole-brain cerebral metabolic rate of oxygen (CMRO2) by MRI. Magn. Reson. Med. 2009, 62, 141–148. [Google Scholar] [CrossRef]
- Ferrannini, E. The theoretical bases of indirect calorimetry: A review. Metabolism 1988, 37, 287–301. [Google Scholar] [CrossRef]
- Mtaweh, H.; Tuira, L.; Floh, A.A.; Parshuram, C.S. Indirect calorimetry: History, technology, and application. Front. Pediatr. 2018, 6, 257. [Google Scholar] [CrossRef]
- Stringer, K.A.; Younger, J.G.; McHugh, C.; Yeomans, L.; Finkel, M.A.; Puskarich, M.A.; Jones, A.E.; Trexel, J.; Karnovsky, A. Whole blood reveals more metabolic detail of the human metabolome than serum as measured by 1H-NMR spectroscopy: Implications for sepsis metabolomics. Shock 2015, 44, 200–208. [Google Scholar] [CrossRef]
- Basmajian, J.V. Muscles Alive, Their Functions Revealed by Electromyography; Williams & Wilkins: Baltimore, MD, USA, 1978; ISBN 0-683-00413-1. [Google Scholar]
- Nordander, C.; Willner, J.; Hansson, G.-Å.; Larsson, B.; Unge, J.; Granquist, L.; Skerfving, S. Influence of the subcutaneous fat layer, as measured by ultrasound, skinfold calipers and BMI, on the EMG amplitude. Eur. J. Appl. Physiol. 2003, 89, 514–519. [Google Scholar] [CrossRef]
- Kuiken, T.A.; Lowery, M.M.; Stoykov, N.S. The effect of subcutaneous fat on myoelectric signal amplitude and cross-talk. Prosthet. Orthot. Int. 2003, 27, 48–54. [Google Scholar] [CrossRef] [PubMed]
- Day, S. Important Factors in Surface EMG Measurement; Bortec Biomedical Ltd.: Calgary, AB, Canada, 2002. [Google Scholar]
- Henry, B.; Zhao, M.; Shang, Y.; Uhl, T.; Thomas, D.T.; Xenos, E.S.; Saha, S.P.; Yu, G. Hybrid diffuse optical techniques for continuous hemodynamic measurement in gastrocnemius during plantar flexion exercise. J. Biomed. Opt. 2015, 20. [Google Scholar] [CrossRef]
- Gurley, K.; Shang, Y.; Yu, G. Noninvasive optical quantification of absolute blood flow, blood oxygenation, and oxygen consumption rate in exercising skeletal muscle. J. Biomed. Opt. 2012, 17, 075010. [Google Scholar] [CrossRef]
- De Blasi, R.A.; Cope, M.; Elwell, C.; Safoue, F.; Ferrari, M. Noninvasive measurement of human forearm oxygen consumption by near infrared spectroscopy. Eur. J. Appl. Physiol. 1993, 67, 20–25. [Google Scholar] [CrossRef]
- De Blasi, R.A.; Ferrari, M.; Natali, A.; Conti, G.; Mega, A.; Gasparetto, A. Noninvasive measurement of forearm blood flow and oxygen consumption by near-infrared spectroscopy. J. Appl. Physiol. 1994, 76, 1388–1393. [Google Scholar] [CrossRef] [PubMed]
- Blasi, R.A.D.; Almenrader, N.; Aurisicchio, P.; Ferrari, M. Comparison of two methods of measuring forearm oxygen consumption (VO2) by near infrared spectroscopy. J. Biomed. Opt. 1997, 2, 171–175. [Google Scholar] [CrossRef]
- Hamaoka, T.; Iwane, H.; Shimomitsu, T.; Katsumura, T.; Murase, N.; Nishio, S.; Osada, T.; Kurosawa, Y.; Chance, B. Noninvasive measures of oxidative metabolism on working human muscles by near-infrared spectroscopy. J. Appl. Physiol. 1996, 81, 1410–1417. [Google Scholar] [CrossRef]
- Beekvelt, M.C.P.V.; Borghuis, M.S.; Engelen, B.G.M.V.; Wevers, R.A.; Colier, W.N.J.M. Adipose tissue thickness affects in vivo quantitative near-IR spectroscopy in human skeletal muscle. Clin. Sci. 2001, 101, 21–28. [Google Scholar] [CrossRef] [PubMed]
- Van Beekvelt, M.C.P.; Colier, W.N.J.M.; Wevers, R.A.; Van Engelen, B.G.M. Performance of near-infrared spectroscopy in measuring local O2 consumption and blood flow in skeletal muscle. J. Appl. Physiol. 2001, 90, 511–519. [Google Scholar] [CrossRef] [PubMed]
- Cheatle, T.R.; Potter, L.A.; Cope, M.; Delpy, D.T.; Smith, P.D.C.; Scurr, J.H. Near-infrared spectroscopy in peripheral vascular disease. Br. J. Surg. 1991, 78, 405–408. [Google Scholar] [CrossRef]
- Casavola, C.; Paunescu, L.A.; Fantini, S.; Gratton, E. Blood flow and oxygen consumption with near-infrared spectroscopy and venous occlusion: Spatial maps and the effect of time and pressure of inflation. J. Biomed. Opt. 2000, 5, 269–276. [Google Scholar] [CrossRef][Green Version]
- Homma, S.; Eda, H.; Ogasawara, S.; Kagaya, A. Near-infrared estimation of O2 supply and consumption in forearm muscles working at varying intensity. J. Appl. Physiol. 1996, 80, 1279–1284. [Google Scholar] [CrossRef]
- Yu, G.; Durduran, T.; Lech, G.; Zhou, C.; Chance, B.; Mohler, E.R.; Yodh, A.G. Time-dependent blood flow and oxygenation in human skeletal muscles measured with noninvasive near-infrared diffuse optical spectroscopies. J. Biomed. Opt. 2005, 10, 024027. [Google Scholar] [CrossRef] [PubMed]
- Tucker, W.J.; Rosenberry, R.; Trojacek, D.; Chamseddine, H.H.; Arena-Marshall, C.A.; Zhu, Y.; Wang, J.; Kellawan, J.M.; Haykowsky, M.J.; Tian, F.; et al. Studies into the determinants of skeletal muscle oxygen consumption: Novel insight from near-infrared diffuse correlation spectroscopy. J. Physiol. 2019, 597, 2887–2901. [Google Scholar] [CrossRef] [PubMed]
- Cheung, C.; Culver, J.P.; Takahashi, K.; Greenberg, J.H.; Yodh, A.G. In vivo cerebrovascular measurement combining diffuse near-infrared absorption and correlation spectroscopies. Phys. Med. Biol. 2001, 46, 2053–2065. [Google Scholar] [CrossRef] [PubMed]
- Durduran, T.; Yu, G.; Burnett, M.G.; Detre, J.A.; Greenberg, J.H.; Wang, J.; Zhou, C.; Yodh, A.G. Diffuse optical measurement of blood flow, blood oxygenation, and metabolism in a human brain during sensorimotor cortex activation. Opt. Lett. 2004, 29, 1766–1768. [Google Scholar] [CrossRef]
- Shang, Y.; Gurley, K.; Symons, B.; Long, D.; Srikuea, R.; Crofford, L.J.; Peterson, C.A.; Yu, G. Noninvasive optical characterization of muscle blood flow, oxygenation, and metabolism in women with fibromyalgia. Arthritis Res. Ther. 2012, 14, R236. [Google Scholar] [CrossRef]
- Mesquita, R.C.; Durduran, T.; Yu, G.; Buckley, E.M.; Kim, M.N.; Zhou, C.; Choe, R.; Sunar, U.; Yodh, A.G. Direct measurement of tissue blood flow and metabolism with diffuse optics. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2011, 369, 4390–4406. [Google Scholar] [CrossRef]
- Baker, W.B.; Li, Z.; Schenkel, S.S.; Chandra, M.; Busch, D.R.; Englund, E.K.; Schmitz, K.H.; Yodh, A.G.; Floyd, T.F.; Mohler, E.R. Effects of exercise training on calf muscle oxygen extraction and blood flow in patients with peripheral artery disease. J. Appl. Physiol. 2017, 123, 1599–1609. [Google Scholar] [CrossRef]
- Li, Z.; Baker, W.B.; Parthasarathy, A.B.; Ko, T.S.; Wang, D.; Schenkel, S.; Durduran, T.; Li, G.; Yodh, A.G. Calibration of diffuse correlation spectroscopy blood flow index with venous-occlusion diffuse optical spectroscopy in skeletal muscle. J. Biomed. Opt. 2015, 20. [Google Scholar] [CrossRef] [PubMed]
- Leahy, S.; Toomey, C.; McCreesh, K.; O’Neill, C.; Jakeman, P. Ultrasound measurement of subcutaneous adipose tissue thickness accurately predicts total and segmental body fat of young adults. Ultrasound Med. Biol. 2012, 38, 28–34. [Google Scholar] [CrossRef] [PubMed]
- Amery, A.; Bossaert, H.; Deruyttere, M.; Vanderlinden, L.; Verstraete, M. Influence of body posture on leg blood flow. J. Vasc. Res. 1973, 10, 152–163. [Google Scholar] [CrossRef]
- Mosti, G.; Partsch, H. Inelastic bandages maintain their hemodynamic effectiveness over time despite significant pressure loss. J. Vasc. Surg. 2010, 52, 925–931. [Google Scholar] [CrossRef][Green Version]
- Mayrovitz, H.N. Compression-induced pulsatile blood flow changes in human legs. Clin. Physiol. 1998, 18, 117–124. [Google Scholar] [CrossRef] [PubMed]
- Durduran, T.; Choe, R.; Baker, W.B.; Yodh, A.G. Diffuse optics for tissue monitoring and tomography. Rep. Prog. Phys. 2010, 73. [Google Scholar] [CrossRef]
- Fantini, S.; Hueber, D.; Franceschini, M.A.; Gratton, E.; Rosenfeld, W.; Stubblefield, P.G.; Maulik, D.; Stankovic, M.R. Non-invasive optical monitoring of the newborn piglet brain using continuous-wave and frequency-domain spectroscopy. Phys. Med. Biol. 1999, 44, 1543–1563. [Google Scholar] [CrossRef]
- Barstow, T.J. Understanding near infrared spectroscopy and its application to skeletal muscle research. J. Appl. Physiol. 2019, 126, 1360–1376. [Google Scholar] [CrossRef]
- Billett, H.H. Hemoglobin and hematocrit. In Clinical Methods: The History, Physical, and Laboratory Examinations; Walker, H.K., Hall, W.D., Hurst, J.W., Eds.; Butterworths: Boston, MA, USA, 1990; ISBN 978-0-409-90077-4. [Google Scholar]
- Hamlett, A.C.; Ryan, L.; Wolfinger, R. On the use of PROC MIXED to estimate correlation in the presence of repeated measures. Proc. Stat. Data Anal. 2004, 198, 29. [Google Scholar]
- Bland, J.M.; Altman, D. Statistical methods for assessing agreement between two methods of clinical measurement. Lancet 1986, 327, 307–310. [Google Scholar] [CrossRef]
- Koo, T.K.; Li, M.Y. A Guideline of selecting and reporting intraclass correlation coefficients for reliability research. J. Chiropr. Med. 2016, 15, 155–163. [Google Scholar] [CrossRef] [PubMed]
- Cicchetti, D.V. Guidelines, criteria, and rules of thumb for evaluating normed and standardized assessment instruments in psychology. Psychol. Assess. 1994, 6, 284–290. [Google Scholar] [CrossRef]

| Participant | μa0 (cm−1) | μs0′ (cm−1) | A | b | HbO0 (μM) | HbR0 (μM) | HbT0 (μM) | StO20 (%) |
|---|---|---|---|---|---|---|---|---|
| 1 | 0.163 ± 0.008 | 6.61 ± 0.66 | 485 ± 1322 | 0.22 ± 0.34 | 33.5 ± 2.9 | 25.7 ± 2.6 | 59.1 ± 3.4 | 56.6 ± 3.6 |
| 2 | 0.159 ± 0.001 | 5.34 ± 0.14 | 178 ± 130 | 0.41 ± 0.27 | 34.2 ± 0.6 | 22.1 ± 0.7 | 56.3 ± 0.4 | 60.8 ± 1.1 |
| 3 | 0.157 ± 0.004 | 5.71 ± 0.12 | 345 ± 154 | 0.59 ±0.08 | 31.57 ± 1.6 | 24.7 ± 1.8 | 56.3 ± 2.0 | 56.1 ± 2.4 |
| 4 | 0.122 ± 0.004 | 6.00 ± 0.40 | 445 ± 238 | 0.58 ± 0.20 | 26.1 ± 1.4 | 13.3 ± 0.5 | 39.4 ± 1.8 | 66.2 ± 0.6 |
| 5 | 0.146 ± 0.003 | 8.03 ± 0.39 | 134 ± 78 | 0.39 ± 0.10 | 29.9 ± 1.0 | 20.9 ± 0.7 | 50.8 ± 1.3 | 58.9 ± 1.1 |
| 6 | 0.127 ± 0.025 | 6.74 ± 1.18 | 14 ± 13 | 0.11 ± 0.10 | 25.9 ± 7.6 | 16.2 ± 2.8 | 42.1 ± 10.5 | 61.2 ± 2.9 |
| 7 | 0.205 ± 0.007 | 5.86 ± 0.15 | 216 ± 76 | 0.53 ± 0.05 | 46.5 ± 2.1 | 30.5 ± 1.2 | 77.0 ± 3.1 | 60.4 ± 0.8 |
| 8 | 0.061 ± 0.001 | 4.71 ± 0.06 | 11 ± 5 | 0.12 ± 0.07 | 4.5 ± 0.3 | 9.7 ± 0.3 | 14.2 ± 0.3 | 31.4 ± 1.8 |
| 9 | 0.109 ± 0.003 | 5.68 ± 0.18 | 21 ± 6 | 0.19 ± 0.04 | 17.9 ± 0.6 | 17.3 ± 1.1 | 35.2 ± 1.6 | 50.9 ± 1.2 |
| Group | 0.139 ± 0.041 | 6.02 ± 1.00 | 218 ± 469 | 0.37 ± 0.24 | 27.9 ± 1 | 20.3 ± 6.5 | 48.1 ± 18.2 | 55.5 ± 9.9 |
| Participant | VO2AO (mLO2/min/100 g) | VO2VO (mLO2/min/100 g) | VO2i (au) | BF (mL/min/100 mL) | BFI (×10−7 cm2/s) |
|---|---|---|---|---|---|
| 1 | 0.043 ± 0.011 | 0.039 ± 0.012 | 8.34 ± 2.15 | 0.36 ± 0.16 | 4.28 ± 1.10 |
| 2 | 0.022 ± 0.002 | 0.039 ± 0.013 | 3.62 ± 0.26 | 0.33 ± 0.08 | 3.22 ± 0.78 |
| 3 | 0.052 ± 0.014 | 0.113 ± 0.016 | 8.59 ± 1.54 | 0.78 ± 0.07 | 4.45 ± 1.41 |
| 4 | 0.030 ± 0.006 | 0.057 ± 0.014 | 10.52 ± 4.18 | 1.05 ± 0.32 | 7.69 ± 3.00 |
| 5 | 0.032 ± 0.002 | 0.051 ± 0.010 | 2.91 ± 0.71 | 0.23 ± 0.04 | 1.80 ± 0.62 |
| 6 | 0.014 | NA | 1.44 | NA | NA |
| 7 | 0.052 ± 0.003 | 0.029 ± 0.010 | NA | 0.18 ± 0.07 | NA |
| 8 | 0.011 ± 0.005 | 0.018 ± 0.004 | 3.40 ± 0.70 | 0.18 ± 0.05 | 1.29 ± 0.01 |
| 9 | 0.018 ± 0.003 | 0.028 ± 0.004 | 1.95 ± 0.34 | 0.18 ± 0.03 | 0.94 ± 0.12 |
| Group | 0.031 ± 0.016 | 0.045 ± 0.028 | 5.50 ± 3.66 | 0.40 ± 0.34 | 3.37 ± 2.55 |
| Repeatability Measure | VO2AO | VO2VO | VO2i | BF | BFI | HbT0 | StO20 |
|---|---|---|---|---|---|---|---|
| ICC | 0.88 | 0.85 | 0.77 | 0.83 | 0.62 | 0.99 | 0.99 |
| CV | 0.19 ± 0.13 | 0.24 ± 0.13 | 0.24 ±0.09 | 0.27 ± 0.12 | 0.25 ± 0.11 | 0.06 ± 0.07 | 0.03 ± 0.02 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Boebinger, S.E.; Brothers, R.O.; Bong, S.; Sanders, B.; McCracken, C.; Ting, L.H.; Buckley, E.M. Diffuse Optical Spectroscopy Assessment of Resting Oxygen Metabolism in the Leg Musculature. Metabolites 2021, 11, 496. https://doi.org/10.3390/metabo11080496
Boebinger SE, Brothers RO, Bong S, Sanders B, McCracken C, Ting LH, Buckley EM. Diffuse Optical Spectroscopy Assessment of Resting Oxygen Metabolism in the Leg Musculature. Metabolites. 2021; 11(8):496. https://doi.org/10.3390/metabo11080496
Chicago/Turabian StyleBoebinger, Scott E., Rowan O. Brothers, Sistania Bong, Bharat Sanders, Courtney McCracken, Lena H. Ting, and Erin M. Buckley. 2021. "Diffuse Optical Spectroscopy Assessment of Resting Oxygen Metabolism in the Leg Musculature" Metabolites 11, no. 8: 496. https://doi.org/10.3390/metabo11080496
APA StyleBoebinger, S. E., Brothers, R. O., Bong, S., Sanders, B., McCracken, C., Ting, L. H., & Buckley, E. M. (2021). Diffuse Optical Spectroscopy Assessment of Resting Oxygen Metabolism in the Leg Musculature. Metabolites, 11(8), 496. https://doi.org/10.3390/metabo11080496





